Закон Ома для полной цепи

Если закон Ома для участка цепи знают почти все, то  закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!

Идеальный источник ЭДС

Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС – это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?

Внутреннее сопротивление источника ЭДС

Дело все в том, что в аккумуляторе “спрятано” сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой “r “.

Выглядит все это в аккумуляторе примерно вот так:

Цепляем лампочку

Итак, что у нас получается в чистом виде?

Лампочка – это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:

Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью  делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.

На резисторе R падает напряжение U_R , а на внутреннем резисторе r падает напряжение U_r .

Теперь вспоминаем статью делитель тока. Сила тока, протекающая  через последовательно соединенные сопротивления везде одинакова.

Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Далее

Закон Ома для полной цепи

Итак, последнее выражение носит название “закон Ома для полной цепи”

где

Е – ЭДС источника питания, В

R – сопротивление всех внешних элементов в цепи, Ом

I – сила ток в цепи, А

r – внутреннее сопротивление источника питания, Ом

Просадка напряжения

Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Наш подопечный готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.

Первым делом давайте замеряем напряжение на клеммах аккумулятора

12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.

Подключаем  галогенную лампу к аккумулятору и снова замеряем напряжение:

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!

А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:

Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

Смотрим на показания приборов:

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Смотрим показания:

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.

Как найти внутреннее сопротивление источника ЭДС

Давайте снова вернемся к этой фотографии

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило

U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r

Вывод

Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.

Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R

), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.

Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.

ЭДС. Закон Ома для полной цепи

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи

, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная

против движения заряда (т.е. против направления тока).

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

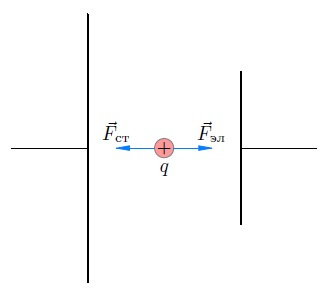
Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят,

неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

(1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

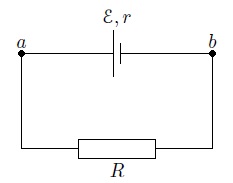
Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:

(2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

(4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

(5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .

Если сила тока в цепи равна , то

Некоторое количество теплоты выделяется также на источнике тока:

Полное количество теплоты, которое выделяется в цепи, равно:

КПД электрической цепи — это отношение полезного тепла к полному:

КПД цепи равен единице лишь в том случае, если источник тока идеальный .

Закон Ома для неоднородного участка

Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (усли внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).

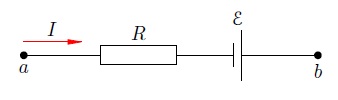
Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным элетрическим полем и сторонними силами источника, целиком превращается в тепло: .

Подставляем сюда выражения для , и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

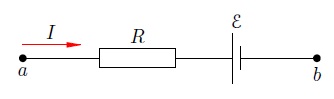
Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Закон Ома

В 1826 величайший немецкий физик Георг Симон Ом публикует свою работу «Определение закона, по которому металлы проводят контактное электричество», где дает формулировку знаменитому закону. Ученые того времени встретили враждебно публикации великого физика. И лишь после того, как другой ученый – Клод Пулье, пришел к тем же выводам опытным путем, закон Ома признали во всем мире.

Закон Ома – физическая закономерность, которая определяет взаимосвязь между током, напряжением и сопротивлением проводника. Он имеет две основные формы.

Закон Ома для участка цепи

Формулировка закона Ома для участка цепи – сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению.

Это простое выражение помогает на практике решать широчайший круг вопросов. Для лучшего запоминания решим задачу.

  Задача 1.1

Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм², если к концам провода приложено напряжение 12 B.

Задача простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.

Закон Ома для полной цепи

Формулировка закона Ома для полной цепи — сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.

Здесь могут возникнуть вопросы. Например, что такое ЭДС? Электродвижущая сила — это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электродвижущая говорит о том, что эта сила двигает электричество, то есть заряд.

В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.

Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.

Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.

  Задача 2.1

Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

 

Теперь решим задачу посложнее.

  Задача 2.2

Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм². Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.

Приступим.

Мнемоническая диаграмма

Для лучшего запоминания закона Ома существует мнемоническая диаграмма, благодаря которой можно всегда напомнить себе формулу. Пользоваться этой диаграммой очень просто. Достаточно закрыть искомую величину и две другие укажут, как её найти. Потренируйтесь, это может вам пригодится.

Успехов в изучении электричества! Рекомендуем прочесть статью — законы Кирхгофа.

Просмотров: 14452

Закон Ома для полной цепи — Студопедия

Формулировка закона Ома для полной цепи — сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.

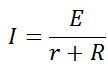
Электродвижущая сила — это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электродвижущаяговорит о том, что эта сила двигает электричество, то есть заряд.

В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.

Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.

Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.

Задача

Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

 

ЛЕКЦИЯ 4. РЕЗИСТОРЫ: ПОНЯТИЕ, СПОСОБЫ СОЕДИНЕНИЯ. СЛОЖНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ: ПОНЯТИЕ, ЗАКОНЫ КИРХГОФА, МЕТОД КОНТУРНЫХ ТОКОВ.

Рези́стор — пассивный элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления, предназначенный для линейного преобразования тока в напряжение и напряжения в ток, ограничения тока, поглощения электрической энергии и др.

Весьма широко используемый компонент практически всех электрических и электронных устройств.

Закон

Ома

Закон Ома гласит, что

«ток через проводник между двумя точками прямо пропорционален разности потенциалов или напряжению между двумя точками, и обратно пропорционален сопротивлению между ними».

Закон Ома может быть выражен как

I = U / R (1)

где

I = ток (ампер, А)

U = электрический потенциал (вольт, В)

R = сопротивление (Ом, Ом )

Пример — закон Ома

Батарея 12 вольт обеспечивает питание до сопротивления 18 Ом .Ток в электрической цепи можно рассчитать как

I = (12 вольт) / (18 Ом)

= 0,67 ампер

Эквивалентные выражения закона Ома

Закон Ома (1) также может быть выражено как

U = RI (2)

или

R = U / I (3)

Загрузите и распечатайте диаграмму закона Ома !

Пример — сопротивление электрической цепи

Ток 1 ампер протекает через электрическую цепь 230 В, .На приведенной выше диаграмме это означает сопротивление

R ≈ 220 Ом

Его можно также рассчитать по закону Ома

R = (230 В) / (1 А)

= 230 Ом

Пример — Закон Ома и кратные и подмножители

Токи, напряжения и сопротивления в электрических цепях часто могут быть очень маленькими или очень большими, поэтому часто используются кратные и подкратные.

Требуемое напряжение, подаваемое на 3.Резистор 3 кОм для создания тока 20 мА можно рассчитать как

U = (3,3 кОм) (1000 Ом / кОм) (20 мА) (10 ^-3 А / мА)

= 66 В

Номограмма электрического сопротивления

Загрузите и распечатайте номограмму зависимости электрического сопротивления от вольт и ампер!

Значения по умолчанию на номограмме выше указывают 230 вольт , сопротивление 24 Ом и ток 10 ампер .

Мощность

Электрическая мощность может быть выражена как

P = UI

= RI ²

= U ² / R (4)

где

P = электрическая мощность (Вт, Вт)

Пример — потребляемая мощность

Мощность, потребляемая в указанной выше электрической цепи 12 В , может быть рассчитана как

P = (12 вольт) ² / ( 18 Ом)

= 8 Вт

Пример — мощность и электрическое сопротивление

Электрическая лампочка 100 Вт подключена к источнику питания 230 В и .Текущий ток можно рассчитать путем преобразования (4) в

I = P / U

= (100 Вт) / (230 В)

= 0,43 ампера

Сопротивление может быть вычислено путем реорганизации (4) в

R = U ² / P

= (230 В) ² / (100 Вт)

= 529 Ом

Номограмма электрической мощности

Эта номограмма может использоваться для оценки зависимости мощности отнапряжение и ампер.

Загрузите и распечатайте номограмму зависимости электрической мощности от вольт и ампер!

Значения по умолчанию на номограмме выше: 240 В, , сопротивление 10 ампер и мощность 2,4 кВт, для постоянного или однофазного переменного тока и 4 кВт, для трехфазного переменного тока.

.

Обобщение импеданса для распространения закона Ома на конденсаторы и индукторы

2. Образование
3. Наука
4. Электроника
5. Обобщение импеданса для распространения закона Ома на конденсаторы и индукторы

Автор: Джон Сантьяго

Используйте концепцию импеданса, чтобы гернализировать закон Ома в векторной форме, чтобы вы могли применить и расширить закон на конденсаторы и катушки индуктивности. После описания импеданса вы используете векторные диаграммы, чтобы показать разность фаз между напряжением и током.Эти диаграммы показывают, как соотношение фаз между напряжением и током различается для резисторов, конденсаторов и катушек индуктивности.

Закон Ома и импеданс

Для схемы, состоящей только из резисторов, закон Ома гласит, что напряжение равно току, умноженному на сопротивление, или В = IR . Но когда вы добавляете в схему устройства хранения данных, связь i-v становится немного сложнее. Резисторы избавляются от энергии в виде тепла, а конденсаторы и катушки индуктивности накапливают энергию.

Конденсаторы сопротивляются изменениям напряжения, а катушки индуктивности — изменениям тока. Импеданс обеспечивает прямую зависимость между напряжением и током для резисторов, конденсаторов и катушек индуктивности, когда вы анализируете цепи с векторными напряжениями или токами.

Как и сопротивление, вы можете думать об импедансе как о константе пропорциональности, которая связывает векторное напряжение В и векторный ток I в электрическом устройстве. В терминах закона Ома можно соотнести В , I и импеданс Z следующим образом:

В = I Z

Импеданс Z — это комплексное число:

Z = R + jX

Вот что означают действительная и мнимая части Z :

• Реальная часть R — это сопротивление от резисторов .Вы никогда не вернете энергию, потерянную при протекании тока через резистор. Когда у вас есть резистор, подключенный последовательно с конденсатором, начальное напряжение конденсатора постепенно снижается до 0, если к цепи не подключена батарея.

  Почему? Потому что резистор использует начальную накопленную энергию конденсатора в виде тепла, когда через цепь протекает ток. Точно так же резисторы заставляют начальный ток катушки индуктивности постепенно снижаться до 0.

• Мнимая часть X — это реактивное сопротивление , которое возникает из-за воздействия конденсаторов или катушек индуктивности .Всякий раз, когда вы видите воображаемое число для импеданса, речь идет о запоминающих устройствах. Если мнимая часть импеданса отрицательна, тогда в мнимой части импеданса преобладают конденсаторы. Если он положительный, то в импедансе преобладают индукторы.

Когда у вас есть конденсаторы и катушки индуктивности, импеданс изменяется с частотой. Это большое дело! Зачем? Вы можете разрабатывать схемы, чтобы принимать или отклонять определенные диапазоны частот для различных приложений. Когда в этом контексте используются конденсаторы или катушки индуктивности, цепи называются фильтрами.Вы можете использовать эти фильтры для таких вещей, как создание необычных рождественских дисплеев с мигающими разноцветными огнями и танцами под музыку.

Величина, обратная импедансу Z , называется проводимостью Y :

Действительная часть G называется проводимостью , а мнимая часть B называется проводимостью .

Диаграммы и резисторы, конденсаторы и катушки индуктивности

Фазорные диаграммы объясняют различия между резисторами, конденсаторами и катушками индуктивности, где напряжение и ток либо совпадают по фазе, либо не совпадают по фазе на 90 ^o .Напряжение и ток резистора совпадают по фазе, потому что мгновенное изменение тока соответствует мгновенному изменению напряжения.

Но для конденсаторов напряжение не изменяется мгновенно, поэтому даже если ток изменяется мгновенно, напряжение будет отставать от тока. Для катушек индуктивности ток не изменяется мгновенно, поэтому при мгновенном изменении напряжения ток отстает от напряжения.

Вот векторные диаграммы этих трех устройств.Для резистора ток и напряжение совпадают по фазе, потому что векторное описание резистора составляет В _R = I _R R . Напряжение конденсатора отстает от тока на 90 ^o из-за — j / (ω C) , а напряжение индуктора опережает ток на 90 ^o из-за j ω L ,

Положите закон Ома для конденсаторов в векторной форме

Для конденсатора емкостью C у вас будет следующий ток:

Поскольку производная фазора просто умножает вектор на j ω , описание вектора для конденсатора составляет

Описание вектора для конденсатора имеет форму, аналогичную закону Ома, показывая, что импеданс конденсатора равен

Ранее вы видели векторную диаграмму конденсатора.Напряжение конденсатора отстает от тока на 90 90 10 3 o 90 10 4, как вы можете видеть из формулы Эйлера:

Представьте себе мнимое число j как оператор, который поворачивает вектор на 90, ^o против часовой стрелки. –j вращает вектор по часовой стрелке. Следует также отметить, что j ² поворачивает вектор на 180 ^o и равен –1.

Мнимая составляющая конденсатора отрицательна.По мере увеличения радианной частоты ω сопротивление конденсатора уменьшается. Поскольку частота батареи равна 0, а напряжение батареи постоянное, сопротивление конденсатора бесконечно. Конденсатор действует как разомкнутая цепь для источника постоянного напряжения.

Положите закон Ома для индукторов в векторной форме

Для индуктора с индуктивностью L , напряжение

Соответствующее описание вектора для индуктора:

Импеданс катушки индуктивности

Z _L = jωL

Ранее вы видели векторную диаграмму индуктора.Напряжение индуктора опережает ток на 90 ^o по формуле Эйлера:

Мнимая составляющая для индукторов положительна. По мере увеличения радианной частоты ω сопротивление катушки индуктивности увеличивается. Поскольку радианная частота для батареи равна 0, а батарея имеет постоянное напряжение, импеданс равен 0. Катушка индуктивности действует как короткое замыкание для источника постоянного напряжения.

Об авторе книги

Джон М.Сантьяго-младший, доктор философии, , прослужил в ВВС США (USAF) 26 лет. В течение этого времени он занимал различные руководящие должности в области технического управления программами, развития приобретения и поддержки операционных исследований. Находясь в Европе, он возглавлял более 40 международных научных и технических конференций / семинаров.

,Принципиальная схема закона Ома

[Как читать символы] • Закон Ома

Простая электрическая схема по закону Ома состоит из сопротивления, подключенного последовательно к источнику постоянного напряжения.

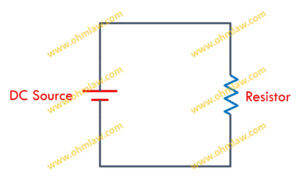
Две параллельные линии, одна из которых имеет сравнительно большую длину, представляют источник постоянного тока, а символ зигзага представляет резистор. В то время как простые линии используются для обозначения проводов.

Приведенная выше диаграмма верна для общего случая, на практике нам нужно добавить амперметр и вольтметр для измерения.Теперь наша диаграмма с инструментами будет выглядеть так:

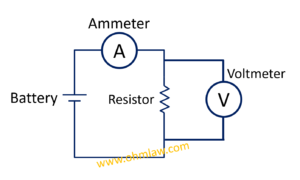
Давайте разберемся с компонентами нашей принципиальной схемы.

Батарея: это источник постоянного напряжения, обеспечивающий питание внутренней цепи. Как мы изучили утверждение Ома: V = IR. Фактически, V — это батарея или источник напряжения, который питает всю схему.

Амперметр: он считывает ток, протекающий по всей цепи. Помните, что амперметр всегда подключается последовательно к цепи.

Вольтметр: Считывает напряжение на резисторе. Помните, что вольтметр всегда подключается параллельно компоненту.

А теперь давайте начнем изучать основы математики права на 5 различных примерах.

Пример 1: Аккумулятор 10 В подключается последовательно с сопротивлением 20 кОм. Найдите ток, протекающий по цепи.

Решение: Использование V ₁ = I ₁ R ₁ .

I ₁ = V ₁ / R ₁ = 0.5 мА

Пример 2: Источник 15 В подключается к неизвестному резистору. Значение тока измеряется как 5 мА. Найдите значение

р.

Решение: R ₂ = В ₂ / I ₂ = 15 В / 5 мА = 3 кОм

Пример 3: Резистор 50 кОм подключается к переменному источнику питания 25 В постоянного тока. Найдите значение неизвестного тока, протекающего по этой цепи.

Решение: I ₃ = В ₃ / R ₃ = 25 В / 50 кОм = 0,5 мА

Пример 4: Рассеиваемая мощность через сопротивление 29 кОм составляет 15 Вт.Найдите значение тока и входного напряжения, подаваемого источником.

Решение: Здесь будут использоваться формулы: I = SQRT (P / R) и V = SQRT (P * R). Вы можете узнать обо всех этих формулах из Ohmic Wheel.

Пример 5: R5 = 10 Ом и P5 = 20 Вт

Решение: V5 = 14,14 и I5 = 1,414

,Закон

Ома — Простая английская Википедия, бесплатная энциклопедия

Закон Ома гласит, что в электрической цепи ток, проходящий через резистор между двумя точками, связан с разностью напряжений между двумя точками и связан с электрическое сопротивление между двумя точками.

Пример) р знак равно В я {\ displaystyle R = {\ frac {V} {I}}}

Где I — ток в амперах, В, — разность потенциалов в вольтах, а R — постоянная, измеряемая в омах, называемая сопротивлением.

Ток прямо пропорционален потере напряжения через резистор. То есть, если ток удваивается, то увеличивается и напряжение. Чтобы ток проходил через сопротивление, на этом сопротивлении должно быть напряжение. Закон Ома показывает взаимосвязь между напряжением (V), током (I) и сопротивлением (R). Это можно записать тремя способами:

я знак равно В р или В знак равно я р или р знак равно В я {\ displaystyle I = {\ frac {V} {R}} \ quad {\ text {or}} \ quad V = IR \ quad {\ text {or}} \ quad R = {\ frac {V} {I }}} ,

Изложение закона Ома — закона Ома гласит, что «ток, протекающий в проводнике, прямо пропорционален разности потенциалов, приложенной к его концам, при условии, что физические условия и температура проводника остаются постоянными».

Напряжение [изменить | изменить источник]

Напряжение — это количество энергии между двумя точками цепи. Эти две точки имеют разные заряды, одна выше, а другая ниже. Разница между этими двумя точками заряда заключается в том, как мы измеряем напряжение.Единица измерения «вольт» — это имя итальянского физика Алессандро Вольта, создавшего первую химическую батарею. Буква «V» обозначает напряжение.

Текущее [изменение | изменить источник]

Ток — это скорость прохождения заряда. Чем выше заряд, тем быстрее ток. Ток связан с движением электронов по цепи. Ток измеряет скорость движения электронов. Единица измерения тока — «ампер», и обычно человек записывает ее как «амперы». Букву «I» можно представить как ток.

Сопротивление [изменение | изменить источник]

Сопротивление — это то, насколько цепь сопротивляется потоку заряда. Это гарантирует, что заряд не будет течь слишком быстро и не повредит компоненты. В цепи лампочка может быть резистором. Если электроны проходят через лампочку, то лампочка загорается. Если сопротивление велико, то лампа будет тусклее. Единицей измерения сопротивления является «Ом», которая называется омега, и произносится как «ом», это имя изобретателя закона Ома.18 электронов. ^[2]

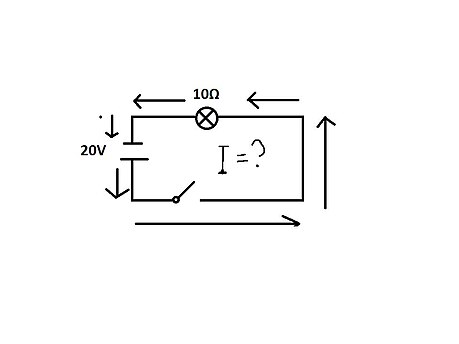
Например, ученый знает, что значение напряжения составляет 20 В. Как известно, сопротивление, которое есть в лампочке, составляет 10 Ом. Теперь нам нужно найти другую неизвестную переменную, которая является текущей. Для ее решения можно использовать формулу закона Ома. С двумя известными переменными, V (напряжение) и R (сопротивление), единственная переменная, которую нужно найти, — это I (ток).

20 В = 10 Ом * I

I = 2A

В задаче ученый всегда получает достаточно информации, чтобы решить другие значения, единственное, что ученый должен запомнить, — это формула закона Ома.Затем он используется с тем, что дано, для решения неизвестной части. В приведенном выше примере сила тока составляет 2 ампера.

^[1]

1. ↑ Ссылка , Get; facebook; Twitter; Pinterest; Эл. адрес; Приложения, Другое. «Калькулятор закона Ома | Расчет сопротивления и силы напряжения и тока». Проверено 21 августа 2019.

,

No related posts.