Закон Джоуля — Ленца описывает выделение тепла в проводнике при прохождении тока. Закон можно

ПОЖАЛУЙСТА СРОЧНО!! ДАЮ 60 БАЛЛОВЗадание 1 (15 баллов).Перевести величины в СИ:1. 114 см2.2. 0,0015 км3.3. 11 ч.4. 750 мг.5. 1,5 л.6. 8 дней.7. 5 мс8. … 50 км2.Задание 2 (10 баллов).Определите цену деления и показания у приведенных ниже мензурок с учетом погрешности. СКРИН ПРИКРЕПИЛА!!!!!!! Задание 3 (15 баллов).Предлагаемую ниже таблицу расчертите на бланке и аргументированно укажите, в какой столбец (один или несколько) Вы впишете следующие явления: тиканье часов, летит пуля, горит свеча, раскаты грома, ползет черепаха, пчелы жужжат, эхо, планшет заряжается, фейерверк, фары освещают дорогу, батарея обогревает комнату, течет река, солнце нагревает поверхность пустыни, лунное затмение, кипит чайник.МеханическиеТепловыеЗвуковыеЭлектрическиеСветовыеЗадание 4 (20 баллов).Чтобы определить диаметр проволоки, ученик вплотную намотал 40 витков проволоки на карандаш, которые заняли 1/3 длины карандаша.

Какой диаметр проволоки (в мм), если длина карандаша 12 см?Задание 5 (15 баллов).Дети во время похода попали в грозу. Они обратили внимание на то, что гром слышен всегда после удара молнии. Какую гипотезу можно выдвинуть на основании этих наблюдений?Задание 6 (15 баллов).Вам поставили задачу: найти средний диаметр частичек риса. Как с помощью линейки и стакана данной крупы можно достаточно точно определить средний диаметр частичек риса?Задание 7 (10 баллов).Изобразите циферблат с ценой деления1) 2 часа.2) 20 минут.

ДАЮ 30 БАЛЛОВ НУЖНА ПОМОЩЬ В ТЕСТЕ

ДАЮ 25 БАЛЛОВ, СРОЧНО!

Тело было выпущено вертикально вверх со скоростью 30 м / с. К моменту съемки, что Будет ли его скорость на высоте 15 м / с? Равно 0

Какую максимальную скорость может дать сжатая пружина с потенциальной энергией 40 Дж? 500 грамм на массу тела?

Каково центростремительное ускорение тела, движущегося по окружности, радиусом 50 дм со скоростью 10 м/сек?​

со скольки километров надо сбросить 1000 кг чтобы разогнать его до скорости звука?​

Камень какого веса и массы способен поднять мальчик на Луне , если на Земле он может поднять камень весом 160 Н ? gз=10 м/с^2 , gл=1,6 м/с^2?​

распишите пожалуйста решение, очень нужно

Сколько электронов действует на заряд , помещённых в однородное поле напряжённостью 20000 Н/Кл по действием силы 0. 32 нН (Ответ выразите в степени 5)* … ​ А)1 В)8 С)32 В)16

Работа и мощность тока. Закон Джоуля — Ленца

6 Дуговая печь потребляет ток I=200 А от сети с напряжением V=120B через ограничивающее сопротивление R = 0,2 Ом. Найти мощность, потребляемую печью.

Решение:
N=I(V-IR)=16 кВт.

7 Нагревательная спираль электроаппарата для испарения воды имеет при температуре t=100°С сопротивление R= 10 Ом. Какой ток I надо пропускать через эту спираль, чтобы аппарат испарял массу воды m=100г за время τ=1 мин? Удельная теплота парообразования воды λ = 2,3 МДж/кг.

Решение:
Считая, что вся электрическая энергия затрачивается на испарение воды, получим

8 Электропечь должна давать количество теплоты Q = 0,1 МДж за время τ = 10 мин. Какова должна быть длина нихромовой проволоки сечения S=0,5 мм², если печь предназначается для сети с напряжением V=36 В? Удельное сопротивление нихрома ρ=1,2мкОм⋅м.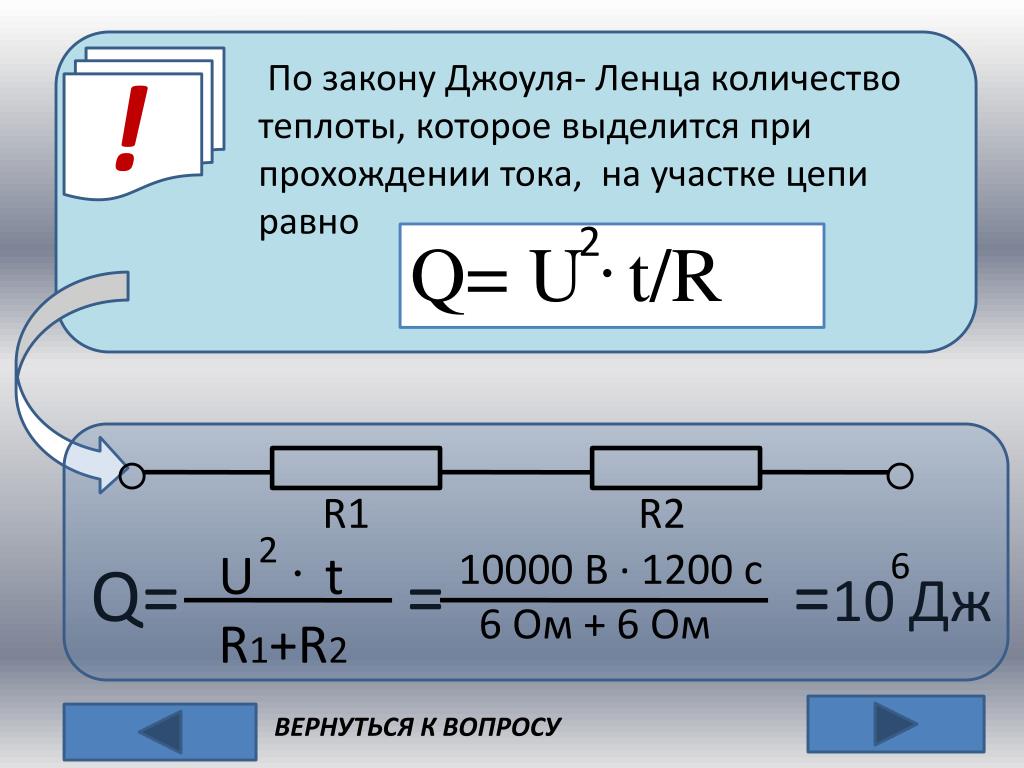
Решение:
По закону Джоуля — Ленца
-сопротивление проволоки, l-ее длина; отсюда

9 Комната теряет в сутки количество теплоты Q = 87 МДж. Какой длины l надо взять нихромовую проволоку диаметра D = 1 мм для намотки электропечи, поддерживающей температуру комнаты неизменной? Печь включается в сеть с напряжением V=120В, удельное сопротивление нихрома ρ=1,2мкОм⋅м.

Решение:

10 В сосуд, содержащий массу воды m = 480 г, помещен электронагреватель мощности N=40 Вт. Насколько изменилась температура воды в сосуде, если ток через нагреватель проходил в течение времени τ = 21 мин? Удельная теплоемкость воды с=4,2 кДж/(кг·К), теплоемкость сосуда вместе с нагревателем С_с=100Дж/К.

Решение:
Полученное количество теплоты идет на нагревание воды и сосуда с нагревателем, поэтому

где t1 и t2-начальная и конечная температуры воды. Изменение температуры воды

11 Найти мощность N электронагревателя кастрюли, если в ней за время τ = 20 мин можно вскипятить объем воды V=2 л. К.п.д. электронагревателя η = 70%. Удельная теплоемкость воды с = 4,2 кДж/(кг·К), начальная температура воды t₁ = 20° С.

Решение:
Электрическая энергия, идущая на нагревание воды,

где

— масса воды, t2 = 100° С- конечная температура воды; отсюда

12 Сколько времени надо нагревать на электроплитке мощности N=600 Вт при к.п.д. η = 75% массу льда m_л = 2кг, взятого при температуре t₁ = —16° С, чтобы обратить его в воду, а воду нагреть до температуры t₂ = 100°C? Удельная теплоемкость льда с_л = 2,1 кДж/(кг·К), удельная теплота плавления льда r=0,33 МДж/кг, удельная теплоемкость воды с = 4,2 кДж/(кг·К).

Решение:
Время нагревания определяется из уравнения теплового баланса (tо=0°С):

13 Какова должна быть длина нихромовой проволоки диаметра D = 0,3 мм, чтобы при включении последовательно с 40-ваттной лампочкой, рассчитанной на 127 В, проволока давала нормальный накал при напряжении в сети V=220 В? Удельное сопротивление нихрома ρ = 1,2 мкОм⋅м.

Решение:


14 Реостат с полным сопротивлением R подключен к сети с напряжением V (рис. 134). Во сколько раз изменится потребляемая от сети мощность, если движок реостата переместить на 1/4 длины от его конца?

Решение:
Отношение выделяемых на реостате мощностей N₀/N=4/3.

15 Найти к.п.д. насосной установки, которая подает в единицу времени объем воды V_τ = 75 л/с на высоту h = 4,7 м через трубу, имеющую сечение S=0,01 м², если мотор потребляет мощность N=10 кВт.

Решение:
Для подачи воды на высоту А необходима мощность

К. п. д. установки


16 Моторы электропоезда при движении со скоростью υ = 54 км/ч потребляют мощность N=900 кВт. К.п.д. моторов и передающих механизмов h = 80%. Найти силу тяги F, развиваемую моторами.
Решение:
Мощность, необходимая для движения поезда, равна

отсюда

17 Железная и медная проволоки одинаковых длин и сечений соединены последовательно и включены в сеть. Найти отношение количеств теплоты, выделившихся в каждой проволоке. Удельные сопротивления железа и меди равны ρ₁ =0,12 мкОм⋅м и ρ₂ = 0,017 мкОм⋅м. Решить эту же задачу для случая параллельного соединения проволок.

Решение:
Токи, идущие через обе проволоки, соединенные последовательно, одинаковы и равны I. При этом в проволоках за время t выделяются количества теплоты

-сопротивления железной и медной проволок, l и S-их длина и площадь сечения. Отношение количеств теплоты при последовательном соединении

При параллельном соединении токи в железной и медной проволоках

где V-напряжение в сети. В этом случае за время τ в проволоках выделяются количества теплоты
Их отношение


18 Железная и медная проволоки одинаковых длин и сечений включены в сеть на равные промежутки времени сначала последовательно, затем параллельно. Найти отношение количеств теплоты, выделившихся в проволоках в обоих случаях, если по железной проволоке тек один и тот же ток. Удельные сопротивления железа и меди ρ₁ =0,12 мкОм·м и ρ₂ = 0,017 мкОм·м.

Решение:


19 За время τ₁=40c в цепи из трех одинаковых проводников, соединенных параллельно и включенных в сеть, выделилось некоторое количество теплоты. За какое время τ₂ выделится такое же количество теплоты, если проводники соединить последовательно?

Решение:


20 Два одинаковых электронагревателя, потребляющих каждый мощность N = 200 Вт при напряжении V= 120 В, длинными и тонкими проводами подключены к источнику тока. Найти сопротивление проводов R, если при последовательном и при параллельном соединениях нагревателей они выделяют в единицу времени одно и то же количество теплоты.

Решение:


21 В электрочайнике с двумя нагревателями необходимо нагреть объем воды V=2 л от комнатной температуры (t₀ = 20° С) до температуры кипения. Каждый нагреватель, включенный в сеть отдельно, выделяет мощность N₁ = 250 Вт. Через какое время закипит вода, если ее подогревать одним нагревателем или двумя, включенными в ту же сеть последовательно или параллельно друг другу? К.п.д. нагревателя η = 80%. Удельная теплоемкость воды с = 4,2 кДж/(кг·К).

Решение:
Для нагревания воды до температуры кипения t=100° С необходимо количество теплоты
—
масса воды в чайнике. При включении одного нагревателя его мощность N₁=IV, где I-ток, текущий через него, и V-напряжение сети. В этом случае на нагревание воды идет часть теплоты, выделяемой нагревателем,

отсюда время нагревания воды одним нагревателем

При параллельном включении двух нагревателей, как и при включении одного из них, на каждом нагревателе будет напряжение сети V. Следовательно, в каждом из них будет выделяться та же мощность N₁ и общая мощность будет N₂ = 2N₁; отсюда время нагревания воды двумя нагревателями

При последовательном включении нагревателей общий ток через них будет равен 1/2.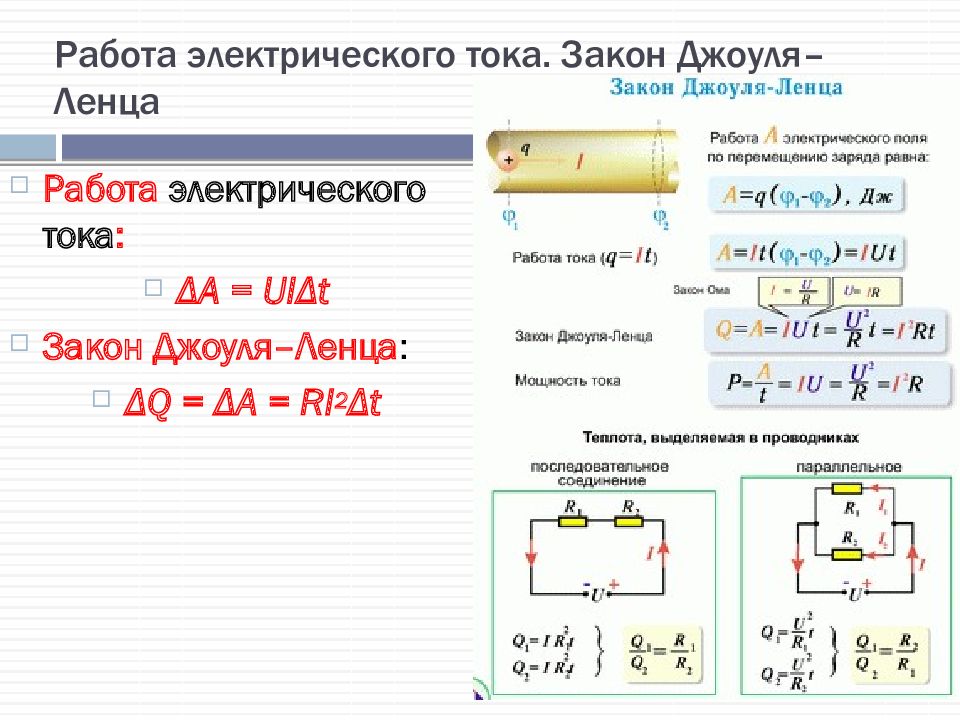 Поэтому общая мощность, выделяемая в них,

Следовательно, время нагревания воды в этом случае

22 Электрочайник имеет в нагревателе две секции. При включении первой секции вода в чайнике закипает за время τ₁ = 10 мин, а при включении второй секции — за время τ₂ = 40мин. Через какое время закипит вода, если включить обе секции параллельно или последовательно?

Решение:
При последовательном соединении секций

при параллельном соединении секций

23 Две лампы имеют одинаковые мощности. Одна из них рассчитана на напряжение V₁ = 120 В, другая—на напряжение V₂ = 220 В. Во сколько раз отличаются сопротивления ламп?

Решение:
Используя закон Джоуля-Ленца

находим

24 Какое сопротивление имеют 40- и 75-ваттные лампы, рассчитанные на включение в сеть с напряжением V=120 В? Какой ток течет через каждую лампу?

Решение:
Мощность лампы

где I-ток, текущий через лампу, R-ее сопротивление; отсюда для первой и второй ламп имеем

25 Какую мощность будет потреблять 25-ваттная лампочка, рассчитанная на напряжение V₁ = 120 В, если ее включить в сеть с напряжением V₂ = 220 В?

Решение:


26 100-ваттная лампа включена в сеть с напряжением V=120В. Сопротивление лампы в накаленном состоянии больше, чем в холодном (при температуре t₀ = 0° С), в 10 раз. Найти температурный коэффициент сопротивления материала нити и сопротивление лампы в холодном состоянии, если во время горения лампы температура нити t = 2000° С.

Решение:
Когда лампа включена,

-сопротивление нити горящей лампы и Ro=R/10-сопротивление нити лампы при температуре t0; отсюда

27 Найти сопротивление 100-ваттной лампы при комнатной температуре t₀ = 20° С, если при напряжении сети V=220 В температура нити t = 2800° С. Температурный коэффициент сопротивления материала нити .

Решение:


28 К источнику тока с э.д.с. ε = 140 В на расстоянии l=400 м от него подключена лампа, рассчитанная на напряжение V=120B и мощность N=100 Вт. Как изменится падение напряжения на лампе, если параллельно ей подключить вторую такую же лампу? Удельное сопротивление провода ρ = 0,028 мкОм⋅м, его сечение S=1 мм².

Решение:
Сопротивления лампы и проводов

Ток, текущий по линии, и падение напряжения на лампе равны

При подключении второй лампы сопротивление двух ламп равно R₁/2. Поэтому ток, текущий по линии, и падение напряжения на лампах равны

Изменение напряжения на лампе

Знак минус показывает, что при включении второй лампы падение напряжения на первой уменьшается.

29 На какое расстояние l можно передавать электроэнергию от источника тока с э.д.с. ε = 5 кВ так, чтобы на нагрузке с сопротивлением R=1,6 кОм выделялась мощность N=10 кВт? Удельное сопротивление провода ρ = 0,017 мкОм⋅м, его сечение S=1 мм².

Решение:


30 Под каким напряжением V нужно передавать электроэнергию на расстояние l=10 км, чтобы при плотности тока j = 0,5 А/мм² в стальных проводах двухпроводной линии электропередачи потери в линии составляли 1% передаваемой мощности? Удельное сопротивление стали ρ = 0,12 мкОм⋅м.

Решение:

31 Цепь состоит из двух параллельно включенных ламп мощности N=30 Вт каждая. Потери мощности в подводящих проводах составляют 10% полезной мощности. Найти напряжение на зажимах источника тока, если он обеспечивает в цепи ток I=2 A.

Решение:
Напряжение на зажимах источника тока

где V₁ и V₂ — падения напряжения на нагрузке и на проводах линии.
Мощность, выделяемая на нагрузке,

Потери мощности в линии

отсюда


32 От источника тока с напряжением V=750 В необходимо передать мощность N=5 кВт на некоторое расстояние. Какое наибольшее сопротивление R может иметь линия передачи, чтобы потери энергии в ней не превышали 10% передаваемой мощности?

Решение:

33 Какой наибольшей мощности электропечь можно установить в конце двухпроводной линии, имеющей сопротивление R=10 Ом, если источник тока развивает мощность N=6 кВт при напряжении V= 1 кВ?

Решение:
Ток в линии I=N/V. Потери мощности в линии

Мощность электропечи

34 Два параллельно соединенных резистора с сопротивлениями R₁=6 Ом и R₂ = 12 Ом подключены последовательно с резистором, имеющим сопротивление R= 15 Ом, к зажимам генератора с э.д.с. ε = 200 В и внутренним сопротивлением r=1 Ом. Найти мощность, выделяющуюся на резисторе R.

Решение:

35 Элемент с э.д.с. ε = 12 В и внутренним сопротивлением r = 4 Ом замкнут на сопротивление R = 8 Ом. Какое количество теплоты будет выделяться во внешней цепи в единицу времени?

Решение:
Ток в цепи I=ε/(R+r). Количество теплоты, выделяемое во внешней цепи в единицу времени,

36 Найти полную мощность элемента при сопротивлении внешней цепи R = 4 Ом, если внутреннее сопротивление элемента r = 2 Ом, а напряжение на его зажимах V=6 В.

Решение:
Полная мощность элемента

где I-ток в цепи. Так как

37 Батарея элементов, замкнутая на сопротивление R₁ = 2 Ом, дает ток I₁ = 1,6 А. Та же батарея, замкнутая на сопротивление R₂ = 1 Ом, дает ток I₂ = 2 А. Найти мощность, теряемую внутри батареи во втором случае.

Решение:
Внутри батареи теряется мощность

где r-внутреннее сопротивление батареи. Если ε — э. д. с. батареи, то по закону Ома для полной цепи в первом и втором случаях

отсюда


38 Найти э.д.с. ε и внутреннее сопротивление r аккумулятора, если при токе I₁ = 15 А он отдает во внешнюю цепь мощность N₁=135 Вт, а при токе I₂ = 6 А — мощность N₂ = 64,8 Вт.

Решение:


39 К источнику тока с э.д.с. ε = 8 В подключена нагрузка. Напряжение на зажимах источника V=6,4 В. Найти к.п.д. схемы.

Решение:
К. п. д.- это отношение полезной работы (мощности) ко всей затраченной работе (полной мощности). Полезной мощностью в данном случае является мощность, выделяемая на нагрузке, N₁=IV, где I-ток в цепи. Так как э. д. с. ε по определению представляет собой полную работу, совершаемую источником тока при перемещении по цепи единичного заряда, а в единицу времени через сечение проводника проходит заряд, численно равный I, то полная мощность источника тока равна

Таким образом, к.п.д. схемы

40 Найти к.п.д. схемы, изображенной на рис. 135. Сопротивления резисторов R₁ = 2 Ом и R₂ = 5 Ом, внутреннее сопротивление источника тока r = 0,5 Ом.

Калькулятор законов Ома и Джоуля — Ленца • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения

Определения и формулы

Электрическая схема простейшей цепи, иллюстрирующая параметры U, I и R закона Ома

Мы окружены электронными устройствами и электрическими цепями. От компьютеров, планшетов, смартфонов и автомобилей до кредитных карточек, ключей к автомобилям и домам — во всех этих устройствах используются электрические цепи. И работа всех этих цепей основана на законе Ома:

Все мы помним (ладно, не все, только некоторые) эту простую формулу из уроков физики, а некоторые знают ее даже с раннего детства. Европейцы знают первую формулу, а те, кто живет в Северной Америке, привыкли ко второй. Европейцы предпочитают обозначать напряжение буквой U, а американцы предпочитают V. Поэтому мы можем смело заявить, что закон Ома — везде. Попробуем понять его чуть лучше.

Закон Ома

Георг Симон Ом (1789–1854)

Закон Ома назван в честь немецкого физика и математика Георга Симона Ома (1789–1854), который, будучи школьным учителем в школе с хорошо оборудованной физической лабораторией, исследовал недавно изобретенный Вольтов столб (в 1799 г.) и термопару, изобретенную в 1821 г. Он обнаружил, что ток в проводнике был прямо пропорционален разности потенциалов на концах проводника. Ом опубликовал результаты своих исследований в 1827 г. в знаменитой книге Die galvanische Kette, mathematisch bearbeitet (Математическое исследование гальванической цепи). Это соотношение между током, напряжением и сопротивлением, известное теперь под названием закона Ома, является фундаментом всей электроники. Единица сопротивления ом также названа в честь ученого. Работы ученого были признаны не сразу и ему пришлось много лет бороться за признание на своей родине.

Элемент электрических цепей, основной целью которого является ввод в цепь электрического сопротивления, называется резистором. На принципиальных схемах он обозначается двумя символами, один из которых используется в Европе и стандартизован Международной электротехнической комиссией (МЭК), а другой — в Северной Америке и стандартизован Институтом инженеров электротехники и электроники (IEEE).

Резисторы и их символы — европейский, стандартизованный МЭК (слева), и американский, стандартизованный IEEE (справа)

В законе Ома сопротивление, измеренное в омах — просто коэффициент пропорциональности между током и напряжением:

где I — ток, V и U — напряжение и R — сопротивление.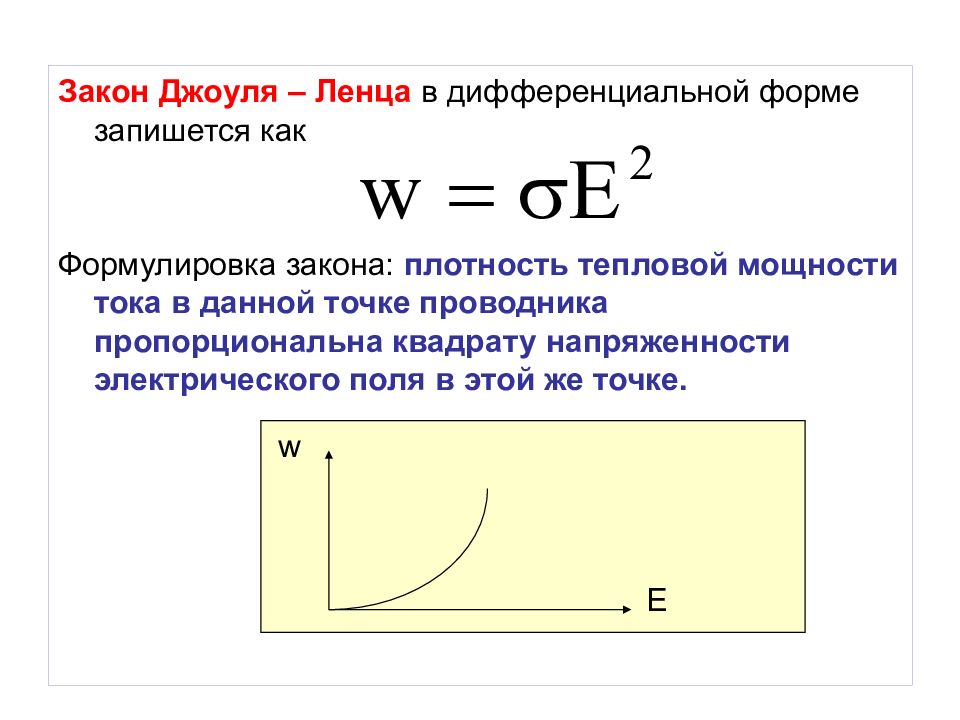 Отметим, что в этом выражении R ≥ 0. Отметим также, что в этой формуле предполагается, что резистор имеет постоянное сопротивление, не зависящее от приложенного напряжения или протекающего тока. Если величина R или отношение U/I постоянны, то можно построить график зависимости тока от напряжения, который будет иметь вид прямой линии.

В резистивных цепях, например, в проводах и резисторах, ток и напряжение линейно пропорциональны. В математике линейной функцией называется такая функция, график которой представляет собой прямую линию (см. рисунок ниже). Например, функция y = 2x — линейная. Если две величины связаны линейным соотношением, то при увеличении или уменьшении одной величины, скажем, в три раза, вторая величина также увеличивается или уменьшается в то же самое число раз. В приложении к закону Ома это означает, что, если напряжение на резисторе увеличится втрое, ток через него также увеличится втрое. Однако, это справедливо только в предположении, что сопротивление резистора постоянно.

График, показывающий соотношение между током и напряжением для определенного электронного элемента, называется его вольт-амперной характеристикой. Резисторы имеют линейную вольт-амперную характеристику.

Более подробную информацию о резисторах и других электронных компонентах вы найдете в наших Электротехнических и радиотехнических калькуляторах, а также в Электротехнических конвертерах.

Нелинейные элементы

Графики вольт-амперных характеристик некоторых электронных элементов: 1 — резистор, 2 — диод, 3 — лампа накаливания, 4 — полупроводниковый стабилитрон; как мы видим, только резистор имеет линейную характеристику

Несмотря на то, что при изучении закона Ома мы всегда предполагаем, что вольт-амперные характеристики резисторов линейные, важно отметить, что многие очень нужные электрические и электронные элементы, такие как лампы накаливания, диоды и транзисторы, широко применяемые в электрических схемах, имеют нелинейные характеристики сопротивления. То есть, их вольт-амперные характеристики не являются прямыми линиями, проходящими через начало координат.

В этой цепи повышение напряжения не приведет к пропорциональному увеличению тока, так как сопротивление горячей лампы накаливания при подаче на нее номинального напряжения 12 В выше, чем оно было при 4 или 6 В. Вольт-амперная характеристика становится более пологой при повышении напряжения, что означает увеличение сопротивления лампы (см. рисунок выше)

Во многих случаях предположение о линейности резисторов неверное. Возьмем, например, схему с лампой накаливания и источником переменного напряжения. Эту схему можно найти во многих школьных учебниках, где обсуждается зависимость тока от напряжения в предположении, что сопротивление лампы накаливания постоянное. Там объясняют, что, если напряжение, приложенное к 12-вольтовой лампе, увеличивать, ток также пропорционально увеличивается. Однако это совсем не так! Если включить амперметр и измерить ток, мы увидим, что он не прямо пропорционален напряжению. Это связано с тем, что сопротивление ламы изменяется — оно растет, когда нить накаливания начинает светиться, так как лампа имеет нелинейную вольт-амперную характеристику.

Когда молодые люди начинают изучать электротехнику, законы Ома и Джоуля — Ленца будут, скорее всего первыми законами, которые нужно будет понять. Однако, когда они увидят эти законы в форме «колеса закона Ома», они могут испугаться, особенно если они поймут, что им придется зазубрить все эти формулы — потому что их учителям намного проще проверить память своих учеников, чем разобраться в том, понимают они предмет или нет. Поэтому многие преподаватели заставляют студентов зазубривать 12 формул вместо того, чтобы получше объяснить и показать на опыте суть закона и попросить их запомнить, а еще лучше, понять всего две из них:

и

Несмотря на то, что этот круг чаще всего называют «колесом закона Ома», здесь объединены два закона: Ома и Джоуля — Ленца.

Недорогой набор для изучения школьниками законов электротехники

Остальные 10 «страшных» формул можно просто вывести их этих двух. И даже эти две формулы не нужно запоминать. Запомнить и понять нужно то, что ток через элемент прямо пропорционален разности потенциалов, приложенной к этому элементу, и обратно пропорционален его сопротивлению. Это и есть закон Ома. А также то, что мощность прямо пропорциональна току и напряжению — это закон Джоуля — Ленца.

Эти два закона очень интуитивны, если студенты понимают что такое ток, напряжение, сопротивление и мощность. А понять это можно, если поиграть с батарейкой, несколькими резисторами и мультиметром. Можно также поиграть и с этим калькулятором.

Для понимания закона Ома удобно использовать гидравлический аналог с водяным насосом (представляющим источник питания), обеспечивающим давление жидкости (представляющее напряжение), которое толкает воду (ток) по трубе (цепи) с узким местом (сопротивление). Все остальные формулы, показанные в «колесе», выводятся из этих двух формул и, если они используются ежедневно, их в конце концов не трудно будет запомнить без лишних усилий.

Закон Джоуля — Ленца

Джеймс Прескотт Джоуль (1818–1889)

Для молодого Джеймса Джоуля, который работал менеджером в пивоварне, занятия наукой были просто хобби. Его отец был богатым пивоваром и Джеймс начал работать в пивоварне в 15 лет. Именно там, в 23 года, Джеймс Джоуль открыл закон, который теперь носит его имя. Его интересовало какой привод более эффективен в его работе: привычный паровой двигатель или недавно изобретенный электродвигатель. Этим экспериментам он посвящал много времени. В результате Джоуль установил соотношение между током, текущим через электрическое сопротивление (провод), и теплом, которое выделялось при этом.

Закон Джоуля утверждает, что мощность выделяемого в проводнике тепла P при прохождении через него электрического тока I пропорциональна произведению квадрата тока на сопротивление проводника R:

Если объединить этот закон с законом Ома, получается несколько полезных формул, которые можно использовать для расчета мощности, рассеиваемой резистором, определять сопротивление по известным току и напряжению, определять ток, текущий через резистор, а также приложенное к резистору напряжение. Эти формулы часто изображают в виде «колеса закона Ома» (вид довольно устрашающий) или не такого страшного «треугольника закона Ома». Ниже приведены примеры использования этих формул. Примеры кликабельные и результат расчетов можно посмотреть в калькуляторе. Нагрев провода при протекании через него тока иногда называют также омическим или резистивным нагревом.

Эмилий Ленц (1804–1865)

Выделение тепла в проводнике при прохождении через него электрического тока было независимо исследовано также русским физиком Эмилием Ленцем, который изучал электромагнетизм с 1831 г. Ленц известен прежде всего правилом о направлении индукционного тока в проводнике в изменяющемся магнитном поле, носящим его имя. Он также независимо от Джоуля открыл закон о выделении тепла в проводнике, поэтому он носит и его имя — закон Джоуля-Ленца.

Следует отметить, что в некоторых учебниках на английском языке закон Джоуля-Ленца неправильно называют законом Уатта, особенно если используется формула P = UI.

Закон Ома для цепей переменного тока

Закон Ома используется не только для анализа описанных выше цепей постоянного тока. Если напряжение имеет форму изменяющейся во времени функции, например, к цепи приложено синусоидальное напряжение, то закон Ома не прекращает свое действие. Если к резистору приложено синусоидальное напряжение, то через него течет синусоидальный ток. Этот ток находится в фазе с приложенным напряжением, так как при изменении полярности напряжения, в тот же момент изменяет полярность и ток. Когда напряжение проходит через максимум, ток делает то же самое.

При использовании закона Ома для анализа цепей переменного тока всегда необходимо выражать ток и напряжение единообразно. Это означает, что ток и напряжение нужно выражать в виде или среднеквадратичных значений, или пиковых значений, или двойной амплитуды. Если закон Джоуля — Ленца используется для определения рассеиваемой резистором мощности, действует аналогичное правило: ток и напряжение должны быть выражены одинаковым образом, например:

Здесь индекс RMS означает среднеквадратичное значение (англ. root mean square). Или

Здесь индекс p означает пиковое (англ. peak) значение. Если цепь переменного тока содержит реактивные элементы, такие как конденсаторы или катушки индуктивности, или обмотки двигателей, то закон Ома применим и к ним. В этом случае вместо активного сопротивления используется реактивное сопротивление:

Здесь X может быть реактивным сопротивлением конденсатора X_C или катушки индуктивности X_L, которые рассчитываются по известным формулам:

и

Подробную информацию о реактивном сопротивлении различных элементов электронных схем, а также об их параллельном и последовательном соединении вы найдете в наших электротехнических и радиотехнических калькуляторах и конвертерах.

Что касается мощности, потребляемой реактивными элементами, они не преобразуют энергию в тепло и, следовательно, энергия на их нагрев не теряется и рассеиваемая на них в виде тепла активная мощность P равна нулю. Мгновенная мощность (точнее, энергия) перемещается туда-сюда между конденсатором или катушкой и источником питания (помним, что соединительные провода при этом нагреваются и энергия теряется!). Скорость, с которой реактивный элемент сохраняет или возвращает энергию, называется реактивной мощностью Q и определяется по следующим формулам:

Реактивная мощность измеряется в вольт-амперах реактивных (вар) и эту единицу можно использовать со всеми десятичными приставками, например: квар, Мвар, и т. д.

Параллельная RLC-цепь

Чтобы применить законы Ома и Джоуля-Ленца для цепей с реактивными и активными компонентами нужно использовать комплексные величины импеданса Z, напряжения U и тока I. В связи с тем, что при расчетах по этим законам нужно выполнять умножение и деление комплексных чисел, удобно представлять их в полярной форме. Для конвертирования величин тока, напряжения, комплексной мощности и импеданса из алгебраической формы в тригонометрическую и наоборот можно воспользоваться нашим калькулятором. Для определения импеданса различных параллельных и последовательных цепей с активными и реактивными компонентами пользуйтесь нашими Электротехническими и радиотехническими калькуляторами.

Формулы закона Ома для переменного тока

Вначале отметим, что оригинал этой статьи написан на английском языке для англоязычной аудитории. В учебниках по теоретическим основам электротехники и основам теории цепей на английском языке, в отличие от учебников на русском языке, широко используется анализ с помощью векторных диаграмм на комплексной плоскости в полярной системе координат, который здесь и рассматривается. Причем, в отличие от учебников на русском языке, где в таких случаях обычно используется формула Эйлера, в англоязычной (особенно американской) литературе принято обозначение комплексных числе в полярной системе координат с углом (∠), который обычно обозначается в градусах:

Здесь U∠φ — сокращение для Ue^jφ.

Ниже приведены формулы, используемые в этом калькуляторе. Расчёты выполняются с комплексными величинами, представленными в тригонометрической форме и в соответствии с правилами умножения и деления комплексных чисел в тригонометрической (векторной) форме.

где φ_U, φ_I и φ_Z — соответственно фазовые углы напряжения, тока и импеданса.

Все комплексные величины вводятся в калькулятор в алгебраической или в тригонометрической форме. Несмотря на то, что импеданс и комплексная мощность не являются векторами, как напряжение и ток, их можно представлять в комплексной форме, потому что они являются комплексными числами, как ток и напряжение. Если они вводятся в алгебраической форме, то для удобства вычислений они преобразуются в тригонометрическую форму по формулам, описанным в нашем Калькуляторе преобразования алгебраической формы комплексного числа в тригонометрическую.

В качестве примера рассчитаем общий ток I_T, в параллельной RLC-цепи с R = 10 Ом, L = 100 мкГн и C = 1 мкФ. Источник переменного тока подает в цепь синусоидальное напряжение 0,5 В с частотой 10 кГц (щелкните для просмотра результата вычислений).

Величина модуля импеданса этой RLC-цепи равна

Фазовый угол (аргумент):

Положительный фазовый угол означает, что нагрузка имеет индуктивный характер и ток отстает от напряжения. Полный импеданс в тригонометрической форме:

Для расчета полного тока воспользуемся законом Ома и правилом деления чисел в тригонометрической форме (модули делятся, углы вычитаются):

Мощность в цепях переменного тока

В нашем калькуляторе мощности переменного тока показано, что активную P, реактивную Q, полную |S| и комплексную S мощность можно рассчитать по следующим формулам:

и

Еще раз напомним, что, поскольку при расчете мощности нужно выполнять умножение и деление комплексных чисел, это удобно делать в тригонометрической форме. Можно показать, что комплексная мощность равна произведению комплексного значения напряжения и сопряженного комплексного значения тока, то есть

Здесь U и I — напряжение в комплексной форме, а I*, U* и Z* — сопряженные комплексные значения тока, напряжения и импеданса соответственно. Полужирным шрифтом выделены комплексные значения. Отметим, что здесь комплексная мощность S измеряется в вольт-амперах (ВА). В тригонометрической форме имеем:

Здесь φ_U — фазовый угол напряжения и φ_I — фазовый угол тока. Эти формулы использованы для «колеса закона Ома для переменного тока». Его удобно использовать в качестве шпаргалки для вычислений.

«Колесо закона Ома»; полужирный шрифт показывает комплексные значения тока, напряжения, мощности и индуктивности. Звездочкой в I* показано, что это сопряженное комплексное значение тока I.

Подробную информацию о расчете мощности переменного тока вы найдете в нашем Калькуляторе мощности переменного тока. Ниже приведено несколько примеров расчетов с использованием данного калькулятора.

Примеры расчетов

Пример 3. Нагреватель с сопротивлением 10 Ом подключен к розетке с напряжением 120 В. Рассчитайте потребляемую мощность и протекающий через нагреватель ток.

Пример 4. Установленная в холодильнике маломощная лампа накаливания с сопротивлением 2300 Ом подключена к напряжению питания 120 В. Рассчитайте потребляемую лампой мощность и протекающий через нее ток.

Пример 5. Ток 0,15 А от солнечной батареи протекает через резистор сопротивлением 220 Ом. Рассчитайте напряжение на резисторе и мощность, которую он рассеивает.

Пример 6. Рассчитайте сопротивление галогенной лампы и потребляемую ею мощность, если она потребляет ток 1,5 А от автомобильной аккумуляторной батареи напряжением 12 В.

Пример 7. Рассчитайте ток, протекающий через 12-килоомный резистор и падение напряжения на нем, если на резисторе рассеивается мощность 1 Вт.

Последовательная RC-цепь (см. Пример 6). Дано: R = 10 Ом, C = 0,1 мкФ, I = 0,2∠0°. Определить: U

Пример 8. 10-омный резистор и конденсатор ёмкостью 0,01 мкФ, соединенные последовательно, подключены к источнику переменного напряжения частотой 1 МГц. Определите напряжение источника в тригонометрической форме, если потребляемый от источника ток равен I = 0,2∠0° А. Подсказка: используйте Калькулятор импеданса последовательной RC-цепи для определения импеданса в тригонометрической форме (Z = 18.8 ∠–57.86°), затем используйте этот калькулятор для определения напряжения источника питания (V = 3.76∠–57.8° V).

Автор статьи: Анатолий Золотков

Задачи на применение закона Джоуля-Ленца с решением

Закон Джоуля-Ленца описывает тепловое действие электрического тока и находит широкое применение в электротехнике. В сегодняшней статье разберем несколько задач на закон Джоуля-Ленца.

Лень решать задачи? Зайдите на наш телеграм-канал: там найдется много интересного для всех учащихся. А если вы решили обратиться к нам за помощью, не упустите выгоду и обязательно прочекайте приятные скидки и акции на нашем втором канале.

Закон Джоуля-Ленца: задачи с решением

Для решения любой физической задачи существует алгоритм: сначала записываются все известные данные, затем определяются величины, которые нужно найти. Подробнее о решении физических задач читайте в нашей памятке для студентов. Также советуем держать под рукой формулы, это существенно облегчит процесс решения.

Кстати, если вы интересуетесь задачами на закон Джоуля-Ленца, вам также может быть полезно ознакомиться с задачами на мощность тока.

Задача на закон Джоуля-Ленца №1

Условие

Какое количество теплоты выделяет за 5 минут нагреватель электрочайника, если его сопротивление равно 30 Ом, а сила тока в цепи 1,5 А?

Решение

Это простейшая задача на закон Джоуля-Ленца для участка цепи. Запишем сам закон:

Q=I2Rt

Подставив значения из условия в формулу, найдем:

Q=1,52·30·300=20250 Дж

Ответ: 20,25 кДж.

Задача на закон Джоуля-Ленца №2

Условие

Какое количество теплоты выделит за 40 минут спираль электроплитки, если сила тока в цепи 3 А, а напряжение 220 В?

Решение

Эта также простейшая задача на закон Джоуля-Ленца, но, в отличие от первой задачи, при ее решении используется другая формулировка закона. Сначала запишем закон Джоуля-Ленца:

Q=I2Rt

Теперь перепишем его с учетом закона Ома:

I=URR=UIQ=I2UIt=IUt

Осталось подставить значения и вычислить:

Q=3·220·2400=1,584 МДж

Ответ: 1,584 МДж.

Задача на закон Джоуля-Ленца №3

Условие

Сколько минут ток шел по проводнику сопротивлением 25 Ом, если при силе тока 1 А проводник вылелил 6 кДж теплоты.

Решение

Запишем закон Джоуля-Ленца и выразим время:

Q=I2Rtt=QI2R

Найдем:

t=600012·25=240 c=4 мин

Ответ: 4 минуты.

При расчетах не забывайте переводить все величины из условия в систему СИ.

Задача на закон Джоуля-Ленца №4

Условие

Электрическая плитка при силе тока 4 А за 20 минут потребляет 1000 кДж энергии. Рассчитайте сопротивление плитки.

Решение

Выразим сопротивление из закона Джоуля-Ленца:

Q=I2RtR=QI2t

Подставим значения и вычислим:

R=1000·10316·1200=52 Ом

Ответ: 52 Ом.

Задача на закон Джоуля-Ленца №5

Условие

По проводнику с сопротивлением 6 Ом пропускали постоянный ток в течение 9 c. Какое количество теплоты выделилось в проводнике за это время, если через его сечение прошел заряд 3 Кл?

Решение

Заряд можно определить, зная время и силу тока. А зная заряд и врямя, за которое он прошел по проводнику, найдем силу тока:

I=qt

Запишем закон Джоуля-Ленца для количества теплоты:

Q=I2RtQ=q2t2Rt=q2Rt

Подставим значения и вычислим:

Q=32·69=6 Дж

Ответ: 6 Дж.

Вопросы на закон Джоуля-Ленца

Вопрос 1. Как звучит закон Джоуля-Ленца?

Ответ. Закон Джоуля-Ленца гласит:

Количество теплоты, выделившейся в проводнике при прохождении по нему электрического тока, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока.

Q=I2Rt

Вопрос 2. Почему проводник с током нагревается?

Ответ. При прохождении тока по проводнику положительные ионы в узлах кристаллических решеток проводника за счет энергии тока начинают сильнее колебаться. Это сопровождается увеличением внутренней энергии проводника, т.е. его нагреванием. При этом энергия тока выделяется в виде теплоты, которую называют джоулевым теплом.

Вопрос 3. Как был открыт закон Джоуля-Ленца?

Ответ.  По спирали, помещенной в калориметр с водой, пропускали электрический ток. Через некоторое время вода нагревалась. По температуре воды можно было вычислить количество выделившейся теплоты. Эмпирическим путем было доказано, что при прохождении тока по проводнику, обладающему определенным сопротивлением, в течение времени током совершается работа, проявляющаяся в виде выделившейся теплоты.

Английский физик Джеймс Джоуль и русский физик Эмилий Ленц изучали зависимость количества выделяемой теплоты от силы тока одновременно. Они пришли к одному и тому же выводу независимо друг от друга.

Вопрос 4. Как еще можно записать закон Джоуля-Ленца?

Ответ. Воспользовавшись законом Ома для участа цепи, закон Джоуля-Ленца можно переписать следующим образом:

Q=UIt=U2Rt

Вопрос 5. Каково практическое применение закона Джоуля-Ленца?

Ответ. Закон Джоуля-Ленца находит широкое применение на практике:

1. На нем основан принцип действия многих нагревательных приборов (чайник, электроплитка, фен, утюг, паяльник и т.д).
2. На принципе закона Джоуля-Ленца основана контактная сварка, где создание неразъемного сварного соединения достигается путем нагрева металла за счет проходящего через него электрического тока и пластической деформации свариваемых деталей путем сжатия. Электродуговая сварка также использует закон Джоуля-Ленца.
3. Расчеты на основе закона Джоуля-Ленца позволяют стабилизировать и минимизировать тепловые потери в линиях электропередач.

Нужна помощь в решении задач и выполнении других заданий по учебе? Обращайтесь в профессиональный сервис для учащихся в любое время.

Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца | ЕГЭ по физике

Закон Кулона

Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.

Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.

Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.2}$

где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.

Сила взаимодействия между зарядами зависит также от среды между заряженными телами.

В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.

Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.

За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.

То есть $1$ Кл$= 1А·с$.

Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т.2$ — электрическая постоянная.

Электрическая емкость конденсатора

Электроемкость

Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:

$C={q}/{φ}$

Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.

Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.

Электрический конденсатор

Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.

Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика.2}/{2}$

где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.

Сила тока

Электрическим током называется упорядоченное (направленное) движение заряженных частиц.

Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:

$I={∆q}/{∆t}$

Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.

Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.

Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц.2$, дает весьма незначительную величину — $∼0.1$ мм/с.

Закон Ома для участка цепи

Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.

Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.

Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:

$I={U}/{R}$

Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.

Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I={U}/{R}$, и растворов электролитов. Знание ВАХ играет большую роль при изучении тока.

Закон Ома — это основа всей электротехники. Из закона Ома $I={U}/{R}$ следует:

1. сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
2. сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.

Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).

Электрическое сопротивление

Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.

Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.

Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.

Удельное сопротивление

Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:

$R=ρ{l}/{S}$

где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.

Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.

Из формулы $R=ρ{l}/{S}$ следует, что

$ρ={RS}/{l}$

Величина, обратная $ρ$, называется удельной проводимостью $σ$:

$σ={1}/{ρ}$

Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м.{-1}$. Для растворов электролитов $α

Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.

Параллельное и последовательное соединение проводников

Для параллельного соединения проводников справедливы следующие соотношения:

1) электрический ток, поступающий в точку $А$ разветвления проводников (она называется также узлом), равен сумме токов в каждом из элементов цепи:

$I=I_1+I_2;$

2) напряжение $U$ на концах проводников, соединенных параллельно, одно и то же:

$U=U_1=U_2;$

3) при параллельном соединении проводников складываются их обратные сопротивления:

${1}/{R}={1}/{R_1}+{1}/{R_2}, R={R_1·R_2}/{R_1+R_2};$

4) сила тока и сопротивление в проводниках связаны соотношением:

${I_1}/{I_2}={R_2}/{R_1}$

Для последовательного соединения проводников в цепи справедливы следующие соотношения:

1) для общего тока $I$:

$I=I_1=I_2,$

где $I_1$ и $I_2$ — ток в проводниках $1$ и $2$ соответственно; т. е. при последовательном соединении проводников сила тока на отдельных участках цепи одинакова;

2) общее напряжение $U$ на концах всего рассматриваемого участка равно сумме напряжений на отдельных его участках:

$U=U_1+U_2;$

3) полное сопротивление $R$ всего участка цепи равно сумме последовательно соединенных сопротивлений:

$R=R_1+R_2;$

4) также справедливо соотношение:

${U_1}/{U_2}={R_1}/{R_2}$

Работа электрического тока. Закон Джоуля-Ленца

Работа, совершаемая током, проходящим по некоторому участку цепи, согласно ($U=φ_1-φ_2={A}/{q}$) равна:

$A=qU$

где $А$ — работа тока; $q$ — электрический заряд, прошедший за данное время через рассматриваемый участок цепи. Подставляя в последнее равенство формулу $q=It$, получаем:

$A=IUt$

Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.

Закон Джоуля-Ленца

Закон Джоуля — Ленца гласит: количество теплоты, выделяемое в проводнике на участке электрической цепи с сопротивлением $R$ при протекании по нему постоянного тока $I$ в течение времени $t$ равно произведению квадрата тока на сопротивление и время:

$Q=I^2Rt$

Закон был установлен в 1841 г.2}/{R}$

Из соотношения для ЭДС легко получить мощность источника тока:

$P_ε=εI$

В СИ работу выражают в джоулях (Дж), мощность — в ваттах (Вт), а время -в секундах (с). При этом

$1$Вт$=1$Дж/с, $1$Дж$=1$Вт$·$с.

Рассчитаем наибольшую допустимую мощность потребителей электроэнергии, которые могут одновременно работать в квартире. Так как в жилых зданиях сила тока в проводке не должна превышать $I=10$А, то при напряжении $U=220$В соответствующая электрическая мощность оказывается равной:

$Р=10А·220В=2200Вт=2.2кВт.$

Одновременное включение в сеть приборов с большей суммарной мощностью приведет к увеличению силы тока, и потому недопустимо.

В быту работу тока (или израсходованную на совершение этой работы электроэнергию) измеряют с помощью специального прибора, называемого электрическим счетчиком (счетчиком электроэнергии). При прохождении тока через этот счетчик внутри его начинает вращаться легкий алюминиевый диск. Скорость его вращения прямо пропорциональна силе тока и напряжению. Поэтому по числу оборотов, сделанных им за данное время, можно судить о работе, совершенной током за это время. Работа тока при этом выражается обычно в киловатт-часах ($кВт·ч$).

$1кВт·ч$ — это работа, совершаемая электрическим током мощностью $1кВт$ в течение $1ч$. Так как $1кВт=1000Вт$, а $1ч=3600с$, то $1кВт·ч=1000Вт·3600с=3600000 Дж$.

Закон джоуля ленца. Закон джоуля-ленца Количество теплоты через сопротивление и напряжение

Содержание:

Знаменитый русский физик Ленц и английский физик Джоуль, проводя опыты по изучению тепловых действий электрического тока, независимо друг от друга вывели закон Джоуля-Ленца. Данный закон отражает взаимосвязь количества теплоты, выделяемого в проводнике, и электрического тока, проходящего по этому проводнику в течение определенного периода времени.

Свойства электрического тока

Когда электрический ток проходит через металлический проводник, его электроны постоянно сталкиваются с различными посторонними частицами. Это могут быть обычные нейтральные молекулы или молекулы, потерявшие электроны. Электрон в процессе движения может отщепить от нейтральной молекулы еще один электрон. В результате, его кинетическая энергия теряется, а вместо молекулы происходит образование положительного иона. В других случаях электрон, наоборот, соединиться с положительным ионом и образовать нейтральную молекулу.

В процессе столкновений электронов и молекул происходит расход энергии, в дальнейшем превращающейся в тепло. Затраты определенного количества энергии связаны со всеми движениями, во время которых приходится преодолевать сопротивление. В это время происходит превращение работы, затраченной на преодоление сопротивления трения, в тепловую энергию.

Закон джоуля Ленца формула и определение

Согласно закону джоуля Ленца, электрический ток, проходящий по проводнику, сопровождается количеством теплоты, прямо пропорциональным квадрату тока и сопротивлению, а также времени течения этого тока по проводнику.

В виде формулы закон Джоуля-Ленца выражается следующим образом: Q = I 2 Rt, в которой Q отображает количество выделенной теплоты, I — , R — сопротивление проводника, t — период времени. Величина «к» представляет собой тепловой эквивалент работы и применяется в тех случаях, когда количество теплоты измеряется в калориях, сила тока — , сопротивление — в Омах, а время — в секундах. Численное значение величины к составляет 0,24, что соответствует току в 1 ампер, который при сопротивлении проводника в 1 Ом, выделяет в течение 1 секунды количество теплоты, равное 0,24 ккал. Поэтому для расчетов количества выделенной теплоты в калориях применяется формула Q = 0,24I 2 Rt.

При использовании системы единиц СИ измерение количества теплоты производится в джоулях, поэтому величина «к», применительно к закону Джоуля-Ленца, будет равна 1, а формула будет выглядеть: Q = I 2 Rt. В соответствии с I = U/R. Если это значение силы тока подставить в основную формулу, она приобретет следующий вид: Q = (U 2 /R)t.

Основная формула Q = I 2 Rt очень удобна для использования при расчетах количества теплоты, которое выделяется в случае последовательного соединения. Сила тока во всех проводниках будет одинаковая. При последовательном соединении сразу нескольких проводников, каждый из них выделит столько теплоты, которое будет пропорционально сопротивлению проводника. Если последовательно соединить три одинаковые проволочки из меди, железа и никелина, то максимальное количество теплоты будет выделено последней. Это связано с наибольшим удельным сопротивлением никелина и более сильным нагревом этой проволочки.

При параллельном соединении этих же проводников, значение электрического тока в каждом из них будет различным, а напряжение на концах — одинаковым. В этом случае для расчетов больше подойдет формула Q = (U 2 /R)t. Количество теплоты, выделяемое проводником, будет обратно пропорционально его проводимости. Таким образом, закон Джоуля — Ленца широко используется для расчетов установок электрического освещения, различных отопительных и нагревательных приборов, а также других устройств, связанных с преобразованием электрической энергии в тепловую.

Закон Джоуля-Ленца. Работа и мощность электрического тока

Задача по теме «Законы постоянного тока». Задача может быть интересна учащимся 10-х классов и выпускникам для подготовки к ЕГЭ. Кстати, подобного рода задача была на ЕГЭ в части 1 с несколько иным вопросом (необходимо было найти отношение количеств теплоты, выделяющихся на резисторах).

На каком из резисторов выделится наибольшее (наименьшее) количество теплоты? R1 = R4 = 4 Ом, R2 = 3 Ом, R3 = 2Ом. Дать решение. Чтобы ответить на вопрос задачи, необходимо сравнить количество теплоты, выделяющееся на каждом их резисторов. Для этого воспользуемся формулой закона Джоуля — Ленца. То есть основной задачей будет являться определение силы тока (или сравнение), протекающей через каждый резистор.

Согласно законам последовательного соединения, сила тока, протекающая через резисторы R1 и R2, и R3 и R4, одинаковая.Чтобы определить силу тока в верхней и в нижней ветвях, воспользуемся законом параллельного соединения, согласно которому, напряжение на этих ветвях одинаковое.Расписывая напряжение на нижней и верхней ветвях по закону Ома для участка цепи, имеем: Подставляя численные значения сопротивлений резисторов, получаем:То есть получаем соотношение между токами, протекающими в верхней и в нижней ветви:Определив силу тока через каждый из этих резисторов, определяем количество теплоты, выделяющееся на каждом из резисторов.Сравнивая числовые коэффициенты, приходим к выводу, что максимальное количество теплоты выделится на четвёртом резисторе, а минимальное количество теплоты — на втором.

Вы можете оставить комментарий, или поставить трэкбек со своего сайта.

Написать комментарий

fizika-doma.ru

Тепловая мощность — формула расчета

С теплотехническими расчётами приходится сталкиваться владельцам частных домов, квартир или любых других объектов. Это основа основ проектирования зданий.

Понять суть этих расчётов в официальных бумагах, не так сложно, как кажется.

Для себя также можно научиться выполнять вычисления, чтобы решить, какой утеплитель применять, какой толщины он должен быть, какой мощности приобретать котёл и достаточно ли имеющихся радиаторов на данную площадь.

Ответы на эти и многие другие вопросы можно найти, если понять, что такое тепловая мощность. Формула, определение и сферы применения – читайте в статье.

Что такое тепловой расчет?

Если говорить просто, тепловой расчёт помогает точно узнать, сколько тепла хранит и теряет здание, и сколько энергии должно вырабатывать отопление, чтобы поддерживать в жилье комфортные условия.

Оценивая теплопотери и степень теплоснабжения, учитываются следующие факторы:

1. Какой это объект: сколько в нём этажей, наличие угловых комнат, жилой он или производственный и т. д.
2. Сколько человек будет «обитать» в здании.
3. Важная деталь — это площадь остекления. И размеры кровли, стен, пола, дверей, высота потолков и т. д.
4. Какова продолжительность отопительного сезона, климатические характеристики региона.
5. По СНиПам определяют нормы температур, которые должны быть в помещениях.
6. Толщина стен, перекрытий, выбранные теплоизоляторы и их свойства.

Могут учитываться и другие условия и особенности, например, для производственных объектов считаются рабочие и выходные дни, мощность и тип вентиляции, ориентация жилья по сторонам света и др.

Для чего нужен тепловой расчет?

Как умудрялись обходиться без тепловых расчётов строители прошлого?

Сохранившиеся купеческие дома показывают, что всё делалось просто с запасом: окна поменьше, стены — потолще. Получалось тепло, но экономически не выгодно.

Теплотехнический расчёт позволяет строить наиболее оптимально. Материалов берётся ни больше — ни меньше, а ровно столько, сколько нужно. Сокращаются габариты строения и расходы на его возведение.

Вычисление точки росы позволяет строить так, чтобы материалы не портились как можно дольше.

Для определения необходимой мощности котла также не обойтись без расчётов. Суммарная мощность его складывается из затрат энергии на обогрев комнат, нагрев горячей воды для хозяйственных нужд, и способности перекрывать теплопотери от вентиляции и кондиционирования. Прибавляется запас мощности, на время пиковых холодов.

При газификации объекта требуется согласование со службами. Рассчитывается годовой расход газа на отопление и общая мощность тепловых источников в гигакалориях.

Нужны расчёты при подборе элементов отопительной системы. Обсчитывается система труб и радиаторов – можно узнать, какова должна быть их протяжённость, площадь поверхности. Учитывается потеря мощности при поворотах трубопровода, на стыках и прохождении арматуры.

При расчетах затрат тепловой энергии могут пригодиться знания, как перевести Гкал в Квт и обратно. В следующей статье подробно рассмотрена эта тема с примерами расчета.

Полный расчет теплого водяного пола приведен в этом примере.

Знаете ли вы, что количество секций радиаторов отопления не берется «с потолка»? Слишком малое их количество приведет к тому, что в доме будет холодно, а чрезмерно больше создаст жару и приведет к чрезмерной сухости воздуха. По ссылке http://microklimat.pro/sistemy-otopleniya/raschet-sistem-otopleniya/kolichestva-sekcij-radiatorov.html приведены примеры правильного расчета радиаторов.

Расчет тепловой мощности: формула

Рассмотрим формулу и приведем примеры, как произвести расчет для зданий с разным коэффициентом рассеивания.

Vx(дельта)TxK= ккал/ч (тепловая мощность), где:

• Первый показатель «V» – объем рассчитываемого помещения;
• Дельта «Т» — разница температур – это та величина, которая показывает насколько градусов внутри помещения теплее, чем снаружи;
• «К» — коэффициент рассеивания (его еще называют «коэффициент пропускания тепла»). Величина берется из таблицы. Обычно цифра колеблется от 4 до 0,6.

Примерные величины коэффициента рассеивания для упрощенного расчёта

• Если это неутепленный металлопрофиль или доска то «К» будет = 3 – 4 единицы.
• Одинарная кирпичная кладка и минимальное утепление – «К» = от 2 до 3-ёх.
• Стена в два кирпича, стандартное перекрытие, окна и
• двери – «К» = от 1 до 2.
• Самый теплый вариант. Стеклопакеты, кирпичные стены с двойным утеплителем и т. п. – «К» = 0,6 – 0,9.

Более точный расчет можно произвести, высчитывая точные размеры отличающихся по свойствам поверхностей дома в м2 (окна, двери и т. д.), производя расчёт для них отдельно и складывая получившиеся показатели.

Пример расчета тепловой мощности

Возьмем некое помещение 80 м2 с высотой потолков 2,5 м и посчитаем, какой мощности котел нам потребуется для его отопления.

Вначале высчитываем кубатуру: 80 х 2,5 = 200 м3. Дом у нас утеплен, но недостаточно – коэффициент рассеивания 1,2.

Морозы бывают до -40 °C, а в помещении хочется иметь комфортные +22 градуса, разница температур (дельта «Т») получается 62 °C.

Подставляем в формулу мощности тепловых потерь цифры и перемножаем:

200 х 62 х 1,2 = 14880 ккал/ч.

Полученные килокалории переводим в киловатты, пользуясь конвертером:

• 1 кВт = 860 ккал;
• 14880 ккал = 17302,3 Вт.

Округляем в большую сторону с запасом, и понимаем, что в самый сильный мороз -40 градусов нам потребуется 18 кВт энергии в час.

Умножаем периметр дома на высоту стен:

(8 + 10) х 2 х 2,5 = 90 м2 поверхности стены + 80 м2 потолок = 170 м2 поверхности, контактирующей с холодом. Теплопотери, высчитанные нами выше, составили 18 кВт/ч, делим поверхность дома на расчетную израсходованную энергию получаем, что 1 м2 теряет примерно 0,1 кВт или 100 Вт ежечасно при температуре на улице -40 °C, а в помещении +22 °С.

Эти данные могут стать основой для расчёта требуемой толщины утеплителя на стены.

Приведем другой пример расчета, он в некоторых моментах сложнее, но более точный.

Формула:

Q = S x (дельта)T / R:

• Q– искомая величина теплопотерь дома в Вт;
• S– площадь охлаждающих поверхностей в м2;
• T– разница температур в градусах Цельсия;
• R– тепловое сопротивление материала (м2 х К/Вт) (Метры квадратные умноженные на Кельвин и делёный на Ватт).

Итак, чтобы найти «Q» того же дома, что и в примере выше, подсчитаем площадь его поверхностей «S» (пол и окна считать не будем).

• «S» в нашем случае = 170 м2, из них 80 м2 потолок и 90 м2 — стены;
• T = 62 °С;
• R– тепловое сопротивление.

Ищем «R» по таблице тепловых сопротивлений или по формуле. Формула для расчета по коэффициенту теплопроводности такая:

R= H/ К.Т. (Н – толщина материала в метрах, К.Т. – коэффициент теплопроводности).

В этом случае, дом у нас имеет стены в два кирпича обшитые пенопластом толщиной 10 см. Потолок засыпан опилками толщиной 30 см.

Отопительную систему частного дома нужно устраивать с учетом экономии средств на энергоносители. Расчет системы отопления частного дома, а также рекомендации по выбору котлов и радиаторов — читайте внимательно.

Чем и как утеплить деревянный дом изнутри, вы узнаете, прочитав эту информацию. Выбор утеплителя и технология утепления.

Из таблицы коэффициентов теплопроводности (измеряется Вт / (м2 х К) Ватт делёный на произведение метра квадратного на Кельвин). Находим значения для каждого материала, они будут:

• кирпич — 0,67;
• пенопласт – 0,037;
• опилки – 0,065.

Подставляем данные в формулу (R= H/ К.Т.):

• R (потолка 30 см толщиной) = 0,3 / 0,065 = 4,6 (м2 х К) / Вт;
• R (кирпичной стены 50 см) = 0,5 / 0,67 = 0,7 (м2 х К) / Вт;
• R (пенопласт 10 см) = 0,1 / 0,037 = 2,7 (м2 х К) / Вт;
• R (стен) = R(кирпич) + R(пенопласт) = 0,7 + 2,7 = 3,4 (м2 х К) / Вт.

Теперь можем приступить к расчету теплопотерь «Q»:

• Q для потолка = 80 х 62 / 4,6 = 1078,2 Вт.
• Q стен = 90 х 62 / 3,4 = 1641,1 Вт.
• Остается сложить 1078,2 + 1641,1 и перевести в кВт, получается (если сразу округлить) 2,7 кВт энергии за 1 час.

Можно обратить внимание, насколько большая разница получилась в первом и втором случае, хотя объём домов и температура за окном в первом и втором случае были совершенно одинаковыми.

Всё дело в степени утомлённости домов (хотя, конечно, данные могли быть и иными, если бы мы рассчитывали пол и окна).

Заключение

Приведённые формулы и примеры показываю, что при теплотехнических расчётах очень важно учитывать как можно больше факторов, влияющих на теплопотери. Сюда входит и вентиляция, и площадь окон, степень их утомлённости и т. д.

А подход, когда на 10 м2 дома берётся 1 кВт мощности котла – слишком приблизительный, чтобы всерьёз опираться на него.

Видео на тему

microklimat.pro

13 Тепловой расчет

10. Тепловой расчет.

Конструкция ИМС должна быть такой, чтобы теплота, выделяющаяся при ее функционировании, не приводила в наиболее неблагоприятных условиях эксплуатации к отказам элементов в результате перегрева. К основным тепловыделяющим элементам следует отнести, прежде всего, резисторы, активные элементы и компоненты. Мощности, рассеиваемые конденсаторами и индуктивностями, невелики. Пленочная коммутация ИМС, благодаря малому электрическому сопротивлению и высокой теплопроводности металлических пленок, способствует отводу теплоты от наиболее нагретых элементов и выравниванию температуры платы ГИС и кристалла полупроводниковой ИМС.

Рис. 10.1. Вариант крепления платы на корпус.

Тепловой расчёт резисторов.

Тепловое сопротивление резистора вычислим по формуле (10.1)

п = 0.03 [Вт/см °С] — коэффициент теплопроводности материала подложки;

δп = 0.06 см – толщина платы.

RT=0.06/0.03=2 см2∙°С/Вт

Рассчитаем температуру пленочных резисторов по формуле

PR – мощность, выделяемая на резисторе;

SR – площадь, занимаемая резистором на плате;

P0 – суммарная мощность, выделяемая всеми компонентами микросхемы;

Sп – площадь платы.

PR = 0.43 мВт – мощность выделяемая на резисторе;

SR = 0.426мм2 – площадь занимаемая резистором;

Sn = 80 мм2 – площадь платы;

RT = 2 см2∙°С/Вт – тепловое сопротивление резистора;

Токр.ср = 40С – максимальная температура окружающей среды;

T = 125С = максимально допустимая температура пленочных резисторов.

TR=(0.43∙10-3∙200)/0.426+(24.82∙10-3∙200)/80+40=40.26 С

Температура остальных резисторов рассчитывается аналогично с помощью программы MathCad. Результаты расчётов представлены в Таблице10.1

Таблица. 10.1

Из таблицы видно, что для всех пленочных резисторов заданный тепловой режим соблюдается.

Тепловой расчет для навесного элемента.

Тепловое сопротивление будет вычисляться по формуле:

k = 0.003 [Вт/см °С] — коэффициент теплопроводности клея;

δк1 = 0.01 см – толщина клея.

Rт=(0.06/0.03)+(0.01/0.003)=5.33 см2∙°С/Вт

Рассчитаем температуру навесного элемента по формуле:

Расчет транзистор КТ202А, VT14

Pнэ = 2,6 мВт – мощность выделяемая на транзисторе;

Sнэ = 0,49 мм2 – площадь занимаемая транзистором;

P0 = 24.82 мВт – мощность выделяемая всеми компонентами платы;

Sn = 80 мм2 – площадь платы;

Т0С = 40С – максимальная температура окружающей среды;

T = 85С = максимально допустимая температура транзистора.

Tнэ=(2.6∙10-3∙533)/0.49+(24.82∙10-3∙533)/80+40=42.99С

Следовательно заданный тепловой режим соблюдается.

Температура остальных транзисторов рассчитывается аналогично с помощью программы MathCad. Результаты расчётов представлены в Таблице10.2

Таблица 10.2

Из таблицы видно, что для всех транзисторов заданный тепловой режим соблюдается. Следовательно и тепловые условия для всей схемы выполняются.

studfiles.net

Тепловая мощность электрического тока и ее практическое применение

Причина нагревания проводника кроется в том, что энергия движущихся в нем электронов (иными словами, энергия тока) при последовательном столкновении частиц с ионами молекулярной решётки металлического элемента преобразуется в тёплый тип энергии, или Q, так образуется понятие «тепловая мощность».

Работу тока измеряют с помощью международной системы единиц СИ, применяя к ней джоули (Дж), мощность тока определяют как «ватт» (Вт). Отступая от системы на практике, могут применять в том числе и внесистемные единицы, измеряющие работу тока. Среди них ватт-час (Вт × ч), киловатт-час (сокращённо кВт × ч). Например, 1 Вт × ч обозначает работу тока с удельной мощностью 1 ватт и длительностью времени на один час.

Если электроны движутся по неподвижному проводнику из металла, в этом случае вся полезная работа вырабатываемого тока распределяется на нагревание металлической конструкции, и, исходя из положений закона сохранения энергии, это можно описать формулой Q=A=IUt=I2Rt=(U2/R)*t. Такие соотношения с точностью выражают известный закон Джоуля-Ленца. Исторически он впервые был определён опытным путём учёным Д. Джоулем в середине 19-го века, и в то же время независимо от него ещё одним учёным — Э.Ленцем. Практическое применение тепловая мощность нашла в техническом исполнении с изобретения в 1873 году русским инженером А. Ладыгиным обыкновенной лампы накаливании.

Тепловая мощность тока задействуется в целом ряде электрических приборов и промышленных установок, а именно, в тепловых измерительных приборах, нагревательного типа электрических печках, электросварочной и инвенторной аппаратуре, очень распространены бытовые приборы на электрическом нагревательном эффекте – кипятильники, паяльники, чайники, утюги.

Находит себя тепловой эффект и в пищевой промышленности. С высокой долей использования применяется возможность электроконтактного нагрева, что гарантирует тепловая мощность. Он обуславливается тем, что ток и его тепловая мощность, оказывая влияние на пищевой продукт, который обладает определённой степенью сопротивления, вызывает в нем равномерное разогревание. Можно привести в пример то, как производятся колбасные изделия: через специальный дозатор мясной фарш поступает в металлические формы, стенки которых одновременно служат электродами. Здесь обеспечивается постоянная равномерность нагрева по всей площади и объёму продукта, поддерживается заданная температура, сохраняется оптимальная биологическая ценность пищевого продукта, вместе с этими факторами длительность технологических работ и расход энергии остаются наименьшими.

Удельная тепловая мощность электрического тока (ω), иными словами — количество теплоты, что выделяется в единице объёма за определённую единицу времени, рассчитывается следующим образом. Элементарный цилиндрический объём проводника (dV), с поперечным проводниковым сечением dS, длиной dl, параллельной направлению тока, и сопротивлением составляют уравнения R=p(dl/dS), dV=dSdl.

Согласно определениям закона Джоуля-Ленца, за отведённое время (dt) во взятом нами объёме выделится уровень теплоты, равный dQ=I2Rdt=p(dl/dS)(jdS)2dt=pj2dVdt. В таком случае ω=(dQ)/(dVdt)=pj2 и, применяя здесь закон Ома для установления плотности тока j=γE и соотношение p=1/γ, мы сразу получаем выражение ω=jE= γE2. Оно в дифференциальной форме даёт понятие о законе Джоуля-Ленца.

fb.ru

Страничка эмбеддера » Тепловые расчеты

Все электронные компоненты выделяют тепло, поэтому умение рассчитывать радиаторы так, чтобы не пролетать в прикидках на пару порядков очень полезно любому электронщику.

Тепловые расчеты очень просты и имеют очень много общего с расчетами электронных схем. Вот, посмотрите на обычную задачу теплового расчета, с которой я только что столкнулся

Задача

Нужно выбрать радиатор для 5-вольтового линейного стабилизатора, который питается от 12вольт максимум и выдает 0.5А. Максимальная выделяемая мощность получается (12-5)*0.5 = 3.5Вт

Погружение в теорию

Для того, чтобы не плодить сущностей, люди почесали тыковку и поняли, что тепло очень похоже на электрической ток, и для тепловых расчетов можно использовать обычный закон Ома, только

Напряжение (U) заменяется температурой (T)

Ток (I) заменяется мощностью (P)

Сопротивление заменяется тепловым сопротивлением. Обычное сопротивление имеет размерность Вольт/Ампер, а тепловое – °C/Ватт

В итоге, закон Ома заменяется на свой тепловой аналог:

Небольшой замечание – для того, чтобы обозначить, что имеется ввиду тепловое (а не электрическое) сопротивление, к букве R, дописывают букву тэта:на клавиатуре у меня такой буквы нет, а копировать из таблицы символов лень, поэтому я буду пользоваться просто буквой R.

Продолжаем

Тепло выделяется в кристалле стабилизатора, а наша цель – не допустить его перегрева (не допустить перегрева именно кристалла, а не корпуса, это важно!).

До какой температуры можно нагревать кристалл, написано в даташите:

Обычно, предельную температуру кристалла называют Tj (j = junction = переход – термочувствительные внутренности микросхем в основном состоят из pn переходов. Можно считать, что температура переходов равна температуре кристалла)

Без радиатора

Тепловая схема выглядит очень просто:

Специально для случаев использования корпуса без радиатора, в даташитах пишут тепловое сопротивление кристалл-атмосфера (Rj-a) (что такое j вы уже в курсе, a = ambient = окружающая среда)

Заметьте, что температура “земли” не нулевая, а равняется температуре окружающего воздуха (Ta). Температура воздуха зависит от того, в каких условиях находится радиатор Если стоит на открытом воздухе, то можно положить Ta = 40 °C, а вот, если в закрытой коробке, то температура может быть значительно выше!

Записываем тепловой закон Ома: Tj = P*Rj-a + Ta. Подставляем P = 3.5, Rj-a = 65, получаем Tj = 227.5 + 40 = 267.5 °C. Многовато, однако!

Цепляем радиатор

Тепловая схема нашего примера со стабилизатором на радиаторе становится вот такой:

• Rj-c – сопротивление от кристалла до теплоотвода корпуса (c = case = корпус). Дается в даташите. В нашем случае – 5 °C/Вт – из даташита
• Rc-r – сопротивление корпус-радиатор. Тут не все так просто. Это сопротивление зависит от того, что находится между корпусом и радиатором. К примеру, силиконовая прокладка имеет коэффициент теплопроводности 1-2 Вт/(м*°C), а паста КПТ-8 – 0.75Вт/(м*°C). Тепловое сопротивление можно получить из коэффициента теплопроводности по формуле:

  R = толщина прокладки/(коэффициент теплопроводности * площадь одной стороны прокладки)

  Часто Rc-r вообще можно игнорировать. К примеру, в нашем случае (используем корпус TO220, с пастой КПТ-8, средняя глубина пасты, взятая с потолка – 0.05мм). Итого, Rc-r = 0.5 °C/Вт. При мощности 3.5вт, разница температур корпуса стабилизатора и радиатора — 1.75градуса. Это – не много. Для нашего примера, возьмем Rc-r = 2 °C/Вт

Rr-a – тепловое сопротивление между радиатором и атмосферой. Определяется геометрией радиатора, наличием обдува, и кучей других факторов. Этот параметр намного проще измерить, чем посчитать (см в конце статьи). Для примера — Rr-c = 12.5 °C/Вт

Ta = 40°C – тут мы прикинули, что атмосферная температура редко выше, можно взять и 50 градусов, чтобы уж точно было.

Подставляем все эти данные в закон Ома, и получаем Tj = 3.5*(5+2+12.5) + 40 = 108.25 °C

Это значительно меньше, чем предельные 150 °C. Такой радиатор можно использовать. При этом, корпус радиатора будет греться до Tc = 3.5*12.5 + 40 = 83.75 °C. Такая температура уже способна размягчить некоторые пластики, поэтому нужно быть осторожным.

Измерение сопротивления радиатор-атмосфера.

Скорее-всего, у вас уже валяется куча радиаторов, которые можно задействовать. Тепловое сопротивление измеряется очень легко. Это этого нужно сопротивление и источник питания.

Лепим сопротивление на радиатор, используя термопасту:

Подключаем источник питания, и выставляем напряжение так, чтобы на сопротивлении выделялась некая мощность. Лучше, конечно, нагревать радиатор той мощностью, которую он будет рассеивать в конечном устройстве (и в том положении, в котором он будет находиться, это важно!). Я обычно оставляю такую конструкцию на пол часа, чтобы она хорошо прогрелась.

После того, как измерили температуру, можно рассчитать тепловое сопротивление

Rr-a = (T-Ta)/P. К примеру, у меня радиатор нагрелся до 81 градуса, а температура воздуха – 31 градус. таким образом, Rr-a = 50/4 = 12.5 °C/Вт.

Прикидка площади радиатора

В древнем справочнике радиолюбителя приводился график, по которому можно прикинуть площадь радиатора. Вот он:

Работать с ним очень просто. Выбираем перегрев, который хочется получить и смотрим, какая площадь соответствует необходимой мощности при таком перегреве.

К примеру, при мощности 4вт и перегреве 20 градусов, понадобится 250см^2 радиатора. Этот график дает завышенную оценку площади, и не учитывает кучу факторов как то принудительный обдув, геометрия ребер, итп.

bsvi.ru

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка

Закон Джоуля Ленца в интегральной форме в тонких проводах:

Если сила тока изменяется со временем, проводник неподвижен и химических превращений в нем нет, то в проводнике выделяется тепло.

— Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля

Преобразование электрической энергии в тепловую широко используется в электрических печах и различных электронагревательных приборах. Тот же эффект в электрических машинах и аппаратах приводит к непроизвольным затратам энергии (потере энергии и снижении КПД). Тепло, вызывая нагрев этих устройств, ограничивает их нагрузку; при перегрузке повышение температуры может вызвать повреждение изоляции или сокращение срока службы установки.

В формуле мы использовали:

Количество теплоты

Работа тока

Напряжение в проводнике

Сила тока в проводнике

Промежуток времени

Джеймс Прескотт Джоуль (слева) и Эмилий Христианович Ленц (справа)

Электрические нагреватели всевозможных типов используются человечеством уже столетия, благодаря свойству электрического тока выделять тепло при прохождении через проводник. У этого явления есть и негативный фактор – перегретая электропроводка из-за слишком большого тока часто становилась причиной короткого замыкания и возникновения пожаров. Выделение тепла от работы электрического тока изучалось в школьном курсе физики, но многие позабыли эти знания.

Впервые зависимость выделения теплоты от силы электрического тока была сформулирована и математически определена Джеймсом Джоулем в 1841 году, и чуть позже, в 1842 г., независимо от него, Эмилем Ленцем. В честь этих физиков и был назван закон Джоуля-Ленца, по которому рассчитывают мощность электронагревателей и потери на тепловыделение в линиях электропередач.

Определение закона Джоуля – Ленца

В словесном определении, согласно исследований Джоуля и Ленца закон звучит так:

Количество теплоты, выделяемой в определенном объеме проводника при протекании электрического тока прямо пропорционально умножению плотности электрического тока и величины напряженности электрического поля

В виде формулы данный закон выглядит следующим образом:

Выражение закона Джоуля — Ленца

Поскольку описанные выше параметры редко применяются в обыденной жизни, и, учитывая, что почти все бытовые расчеты выделения теплоты от работы электрического тока касаются тонких проводников (кабели, провода, нити накаливания, шнуры питания, токопроводящие дорожки на плате и т. п.), используют закон Джоуля Ленца с формулой, представленной в интегральном виде:

Интегральная форма закона

В словесном определении закон Джоуля Ленца звучит так:

Словесное определение закона Джоуля — Ленца

Если принять, что сила тока и сопротивление проводника не меняется в течение времени, то закон Джоуля — Ленца можно записать в упрощенном виде:

Применив закон Ома и алгебраические преобразования, получаем приведенные ниже эквивалентные формулы:

Эквивалентные выражения теплоты согласно закона Ома

Применение и практическое значение закона Джоуля – Ленца

Исследования Джоуля и Ленца в области тепловыделения от работы электрического тока существенно продвинули научное понимание физических процессов, а выведенные основные формулы не претерпели изменений и используются по сей день в различных отраслях науки и техники. В сфере электротехники можно выделить несколько технических задач, где количество выделяемой при протекании тока теплоты имеет критически важное значение при расчете таких параметров:

• теплопотери в линиях электропередач;
• характеристики проводов сетей электропроводки;
• тепловая мощность (количество теплоты) электронагревателей;
• температура срабатывания автоматических выключателей;
• температура плавления плавких предохранителей;
• тепловыделение различных электротехнических аппаратов и элементов радиотехники.

Электроприборы, в которых используется тепловая работа тока

Тепловое действие электрического тока в проводах линий электропередач (ЛЭП) является нежелательным из-за существенных потерь электроэнергии на тепловыделение.

По различным данным в линиях электропередач теряется до 40% всей производимой электрической энергии в мире. Для уменьшения потерь при передаче электроэнергии на большие расстояния, поднимают напряжение в ЛЭП, производя расчеты по производным формулам закона Джоуля – Ленца.

Диаграмма всевозможных потерь электроэнергии, среди которых теплопотери на воздушных линиях составляют львиную долю (64%)

Очень упрощенно тепловую работу тока можно описать следующим образом: двигаются электроны между молекулами, и время от времени сталкиваются с ними, отчего их тепловые колебания становятся более интенсивными. Наглядная демонстрация тепловой работы тока и ассоциативные пояснения процессов показаны на видео ниже:

Расчеты потерь электроэнергии в линиях электропередач

В качестве примера можно взять гипотетический участок линии электропередач от электростанции до трансформаторной подстанции. Поскольку провода ЛЭП и потребитель электроэнергии (трансформаторная подстанция) соединены последовательно , то через них течет один и тот же ток I. Согласно рассматриваемому тут закону Джоуля – Ленца количество выделяемой на проводах теплоты Q w (теплопотерь) рассчитывается по формуле:

Производимая электрическим током мощность (Q c) в нагрузке рассчитывается согласно закону Ома:

Таким образом, при равенстве токов, в первую формулу можно вставить вместо I выражение Q c /U c , поскольку I = Q c /U c:

Если проигнорировать зависимость сопротивления проводников от изменения температуры, то можно считать R w неизменным (константой). Таким образом, при стабильном энергопотреблении потребителя (трансформаторной подстанции), тепловыделение в проводах ЛЭП будет обратно пропорционально квадрату напряжения в конечной точке линии. Другими словами, чем больше напряжение электропередачи, тем меньше потери электроэнергии.

Для передачи электроэнергии высокого напряжения требуются большие опоры ЛЭП

Работа закона Джоуля – Ленца в быту

Данные расчеты справедливы также и в быту при передаче электроэнергии на малые расстояния – например, от ветрогенератора до инвертора. При автономном энергоснабжении ценится каждый Ватт выработанной низковольтным ветряком энергии, и возможно, будет выгодней поднять напряжение трансформатором прямо у ветрогенератора, чем тратиться на большое сечение кабеля, чтобы уменьшить потери электроэнергии при передаче.

При значительном удалении низковольтного ветрогенератора переменного тока для уменьшения потерь электроэнергии будет выгодней подключение через повышающий трансформатор

В бытовых сетях электропроводки расстояния крайне малы, чтобы уменьшения тепловых потерь поднимать напряжение, поэтому при расчете проводки учитывается тепловая работа тока, согласно закону Джоуля – Ленца при выборе поперечного сечения проводов, чтобы их тепловой нагрев не привел к оплавлению и возгоранию изоляции и окружающих материалов. Выбор кабеля по мощности и электропроводки проводятся согласно таблиц и нормативных документов ПУЭ, и подробно описаны на других страницах данного ресурса.

Соотношения силы тока и поперечного сечения проводников

При расчете температуры нагрева радиотехнических элементов, биметаллической пластины автоматического выключателя или плавкого предохранителя используется закон Джоуля – Ленца в интегральной форме, так как при росте температуры изменяется сопротивление данных материалов. При данных сложных расчетах также учитываются теплоотдача, нагрев от других источников тепла, собственная теплоемкость и множество других факторов.

Программное моделирование тепловыделения полупроводникового прибора

Полезная тепловая работа электрического тока

Тепловыделяющая работа электрического тока широко применяется в электронагревателях, в которых используется последовательное соединение проводников с различным сопротивлением. Данный принцип работает следующим образом: в соединенных последовательно проводниках течет одинаковый ток, значит, согласно закону Джоуля – Ленца, тепла выделится больше у материала проводника с большим сопротивлением.

Спираль с повышенным сопротивлением накаляется, но питающие провода остаются холодными

Таким образом, шнур питания и подводящие провода электроплитки остаются относительно холодными, в то время как нагревательный элемент нагревается до температуры красного свечения. В качестве материала для проводников нагревательных элементов используются сплавы с повышенным (относительно меди и алюминия электропроводки) удельным сопротивлением — нихром, константан, вольфрам и другие.

Нить лампы накаливания изготовляют из тугоплавких вольфрамовых сплавов

При параллельном соединении проводников тепловыделение будет больше на нагревательном элементе с меньшим сопротивлением, так как при его уменьшении возрастает ток относительного соседнего компонента цепи. В качестве примера можно привести очевидный пример свечения двух лампочек накаливания различной мощности – у более мощной лампы тепловыделение и световой поток больше.

Если прозвонить омметром лампочки, то окажется, что у более мощной лампы сопротивление меньше. На видео ниже автор демонстрирует последовательное и параллельное подключение, но к сожалению, он ошибся в комментарии — будет ярче светить лампа с большим сопротивлением, а не наоборот.

Закон Джоуля – Ленца – закон физики, определяющий количественную меру теплового действия электрического тока. Сформулирован этот закон был в 1841 году английским учёным Д. Джоулем и совершенно отдельно от него в 1842 году известным русским физиком Э. Ленцем. Поэтому он получил своё двойное название — закон Джоуля – Ленца.

Определение закона и формула

Словесная формулировка имеет следующий вид: мощность тепла, выделяемого в проводнике при протекании сквозь него , пропорционально произведению значения плотности электрического поля на значение напряженности.

Математически закон Джоуля — Ленца выражается следующим образом:

ω = j E = ϭ E²,

где ω — количество тепла, выделяемого в ед. объема;

E и j – напряжённость и плотность, соответственно, электрического полей;

σ — проводимость среды.

Физический смысл закона Джоуля – Ленца

Закон можно объяснить следующим образом: ток, протекая по проводнику, представляет собой перемещение электрического заряда под воздействием . Таким образом, электрическое поле совершает некоторую работу. Эта работа расходуется на нагрев проводника.

Другими словами, энергия переходит в другое свое качество – тепло.

Но чрезмерный нагрев проводников с током и электрооборудования допускать нельзя, поскольку это может привести к их повреждению. Опасен сильный перегрев при проводов, когда по проводниках могут протекать достаточно большие токи.

В интегральной форме для тонких проводников закон Джоуля – Ленца звучит следующим образом: количество теплоты, которое выделяется в единицу времени в рассматриваемом участке цепи, определяется как произведение квадрата силы тока на сопротивление участка.

Математически эта формулировка выражается следующим образом:

Q = ∫ k I² R t,

при этом Q – количество выделившейся теплоты;

I – величина тока;

R — активное сопротивление проводников;

t – время воздействия.

Значение параметра k принято называть тепловым эквивалентом работы. Величина этого параметра определяется в зависимости от разрядности единиц, в которых выполняются измерения значений, используемых в формуле.

Закон Джоуля-Ленца имеет достаточно общий характер, поскольку не имеет зависимости от природы сил, генерирующих ток.

Из практики можно утверждать, что он справедлив, как для электролитов, так проводников и полупроводников.

Область применения

Областей применения в быту закона Джоуля Ленца – огромное количество. К примеру, вольфрамовая нить в лампе накаливания, дуга в электросварке, нагревательная нить в электрообогревателе и мн. др. Это наиболее широко распространенный физический закон в повседневной жизни.

Работа, энергия, теплота тока. Полезная, полная мощность. Закон Джоуля-Ленца

Мы уже выяснили, что источником движения электронов в проводнике служит электрическое поле, которое совершает работу по переносу заряда:

(1)

Проходя через проводник, ток оказывает тепловое воздействие на сам проводник. Данное тепловое воздействие можно описать энергетически:

(2)

Формула (2) описывает все энергетические характеристики, связанные с током, для упрощения, мы будем называть данный параметр через 

.

Используя определения силы тока: 

, можем получить:

(3)

• где
  • — время течения тока.

Соотношение (3) называется законом Джоуля-Ленца.

Учитывая закон Ома для участка цепи (

), можно получить следующий ряд уравнений:

(4)

• где
  • — полное сопротивление цепи.

Использование каждого из этих уравнений диктуется условиями задачи.

Мы уже ввели понятие механической мощности 

. Тогда соотношения (4) можно адаптировать под мощность:

(5)

Соотношение (5) определяет полную мощность, потребляемую участком цепи.

Для полной цепи постоянного тока, мощность источника тока/напряжения (т.е. мощность, выдаваемую самим источником), то необходимо использовать закон Ома для полной цепи: 

, тогда:

(6)

• где
  • — ЭДС источника,
  • — внутреннее сопротивление источника.

Соотношение (6) определяет полную мощность, генерируемую источником тока/напряжения.

Тогда для полной цепи можем определить, так называемую, полезную мощность, т.е. мощность, расходуемую, непосредственно, на потребителя. Пусть в цепи потребляется напряжение 

, тогда:

(7)

Исходя из закона Ома для участка цепи:

(8)

Зная связь между ЭДС и напряжением:

Можем получить:

(9)

 Выражение (7) и (9) — полезная мощность, выдаваемая источником.

Вывод: любая энергетическая характеристика, связанная с током, может быть найдена, исходя из закона Джоуля-Ленца и его форм (4). По поводу мощности дела сложнее: по задаче нужно определить мощность чего нужно определить. Для этого выясняем, с какой цепью работаем:

• для участка цепи: формулы (5)
• для полной цепи:
  • в случае вопроса о мощности источника, то формулы (6)
  • в случае вопроса о полезной мощности, то формулы (7) и (9)

Поделиться ссылкой:

Термодинамика — Вывод закона Джоуля-Ленца

Давайте поговорим о законе джоулева нагрева. Проводник — это материал (например, проводник из металла), который имеет свою собственную структуру, а это означает, что в нем есть атомы. Эти атомы связаны между собой связями. Под током понимается жидкость (жидкость или газ), движущаяся внутри проводника вдоль оси. В моем случае жидкость — это поток электронов (электронный газ). Вот что я должен был понять.Тогда идея становится ясной; и станет понятнее после прочтения закона в Википедии. Я считаю, что мне следует собрать больше благодарностей по этой теме с точки зрения квантовой физики.

Вопросы:

1. Есть ли термодинамическая система?
2. $ dU = 0 $?
3. Как вывести формулу?

Чтобы ответить на все эти вопросы, нужно понимать, что происходит внутри проводника. Естественно сказать, что электроны движутся под действием силы $ \ vec {E} $, порождаемой разностью потенциалов.Применение второго закона Ньютона дает нам некоторую информацию: $$ q \ cdot \ vec {E} = m \ cdot \ vec {a} \ Rightarrow a = \ frac {q \ cdot E} {m} \ ne 0 $$ Следовательно, все электроны ускоряются силой. Это означает, что скорость жидкости должна увеличиваться и, следовательно, вызывать изменение кинетической энергии — это было бы полезно. Теперь мы должны понять, от чего и где генерируется тепло. Ключ кроется в законах сохранения (энергии и импульса). Почему? Потому что электроны могут сталкиваться с атомами проводника; после этого возникают изменения кинетических энергий.2 \ cdot \ tau} {2m} $$ Последнее, что нужно сделать, это положить $ q = e $, потому что жидкость представляет собой поток электронов. Теперь осталось учесть передачу энергии. Когда электрон сталкивается с атомом, он передает ему некоторую энергию; эта энергия равна $ T $. Итак, тепло передается путем диффузии: электроны получают кинетическую энергию и отдают ее проводнику — именно это и произошло с проводником.

Ответим на первый вопрос. Как мы наблюдали, электроны движутся внутри проводника с ускорением, полученным от электрического поля $ E $, от которого они также получают кинетическую энергию.Энергия передается проводнику в виде джоулева нагрева. Что такое термодинамическая система? Это система (закрытая, изолированная, открытая), в которой происходит процесс (например, изотермический процесс). Система может состоять из нескольких объектов, которые взаимодействуют между собой. В результате он излучает некоторую энергию (рассмотрим двигатель автомобиля, где посредством сжигания нефти тепловая энергия газа преобразуется в движущую силу, чтобы автомобиль мог двигаться). Работа этого процесса определяется $ A = \ nu \ cdot R \ cdot T \ cdot \ ln \ left (\ frac {V_2} {V_1} \ right) $.Теперь вернемся к процессу передачи кинетической энергии атомам от электронов. Исходя из сказанного, процесс, происходящий внутри проволоки, должен быть термодинамическим. Рассмотрим еще одну идею, как вывести формулу. Перед выводом запишем уравнения сохранения импульса и энергии, учитывая три типа столкновений. Первый — элластический: электрон движется с $ u_0 $, а атом перед столкновением находится в состоянии покоя; после этого электрон приобретает скорость $ u $, а атом $ v $.2} {2} $$ Теперь мы подходим к другому подходу. Мы предполагаем, что внутри проводника находятся движущиеся атомы и электроны, и рассматриваем сталкивающиеся жидкости. Идея здесь в том, что электрическое поле снабжает электронный газ энергией. Атомы получают меньшую энергию, чем электроны из электрического поля. Следовательно, если мы обозначим температуру электронного газа через $ T_e $, а атомов через $ T_a $, мы получим неравенство $ T_e> T_a $, означающее, что энергия, получаемая электронами от атомов, меньше энергии, полученной от электронных поле.2} {2} = \ frac {3} {2} \ cdot k \ cdot T_e $$ Результирующий поток — это сумма всех потоков; она должна быть пропорциональна разнице между этими потоками, числом столкновений и средней кинетической энергией, получаемой атомами от электронов: $$ w = \ frac {N} {\ tau} \ cdot \ frac {2 \ cdot m_e} {m_a} \ cdot \ frac {3} {2} \ cdot k \ cdot \ left (T_e — T_a \ right) $$ Используя первую формулу для $ w $, имеем $$ \ frac {N} {\ tau} \ cdot \ frac {2 \ cdot m_e} {m_a} \ cdot \ frac {3} {2} \ cdot k \ cdot \ left (T_e — T_a \ right) = \ гидроразрыв {N \ cdot q ^ 2 \ cdot \ tau} {2m} \ cdot E ^ 2 $$ откуда $$ T_e — T_a = \ frac {1} {6} \ cdot \ frac {m_a} {m_e} \ cdot \ frac {q ^ 2 \ cdot \ tau ^ 2} {k \ cdot} \ cdot E ^ 2 $ $

В первом подходе мы получили, что $ w = \ sigma \ cdot E ^ 2 $, которое можно переписать в векторной форме как $$ w = \ left (\ sigma \ cdot \ vec {E} \ right) \ cdot \ vec {E} = \ vec {j} \ cdot \ vec {E} $$, что верно в соответствии с законом Ома (дифференциальную форму можно получить из исходной формы с помощью $ R = \ rho \ cdot \ frac { l} {A} $ и взятие дифференциалов).Отсюда нетрудно получить $ P = V \ cdot I $, потому что мы знаем, что $$ V = — \ Delta \ varphi = \ vec {E} \ cdot \ vec {dl}, \\ j = \ frac {dI} {dS} $$ Итак, величина $ w $ — это мощность на объем! Далее, $ Q = I \ cdot V \ cdot \ Delta t $, потому что $ w $ — это мощность выделения тепла. Тогда согласно первому закону термодинамики получаем $$ dU = \ delta Q — \ delta W = 0 $$ потому что $ \ delta A = dK = -q d \ varphi $, где K обозначает кинетическую энергию. Так, $$ Q = A = I \ cdot V \ cdot \ Delta t $$

Калькулятор закона Ома

• Электрические, радиочастотные и электронные калькуляторы • Онлайн-преобразователи единиц

Определения и формулы

Схема простой схемы, иллюстрирующей параметры закона Ома U , I и R

Мы окружены электрическим схемы в нашей повседневной жизни.От компьютеров, планшетов, смартфонов и автомобилей до кредитных карт и ключей от наших автомобилей и домов — все они сделаны с использованием электрических цепей. И все они работают по закону Ома:

Мы все (хорошо, не все, только некоторые) знаем эту простую формулу со школы, а некоторые из нас знают ее даже с раннего возраста. Европейцы знают первую формулу, а жители Северной Америки знают вторую. Европейцы предпочитают U для напряжения, в то время как американцы предпочитают V для того же физического количества.Итак, мы можем сказать, что закон Ома действует везде. Попробуем лучше понять этот закон.

Закон Ома

Георг Симон Ом (1789–1854)

Закон Ома назван в честь немецкого физика и математика Георга Симона Ома (1789–1854), который был школьным учителем в школе с хорошо оборудованной физической лабораторией. , исследовал недавно изобретенную (в 1799 году) гальваническую батарею и термопару, изобретенную в 1821 году. Он обнаружил, что ток в проводнике прямо пропорционален разности потенциалов на проводнике.Он опубликовал результаты своих исследований в 1827 году в знаменитой книге Die galvanische Kette, Mathematisch Bearbeitet (Математическое исследование гальванической цепи) . В результате его работы отряд сопротивления назван его именем. Эта взаимосвязь между током, напряжением и сопротивлением, известная теперь как закон Ома, является основной основой всей электроники. Ом годами боролся за признание своей работы.

Элемент схемы, основным назначением которого является создание электрического сопротивления, называется резистором.На схемах он представлен двумя видами символов: один используется в основном в Европе и стандартизирован Международной электротехнической комиссией (МЭК), а другой — в Северной Америке и стандартизирован Институтом инженеров по электротехнике и электронике (IEEE).

Резисторы и их электронные символы — европейские, стандартизированные IEC (слева) и американские, стандартизованные IEEE (справа)

По закону Ома сопротивление, измеренное в омах, представляет собой просто константу пропорциональности между током и напряжением:

, где I — ток, В и U — напряжение, а R — сопротивление.Обратите внимание, что в этом выражении R ≥ 0. Также обратите внимание, что в этом выражении мы предположили, что резистор имеет постоянное сопротивление, которое не зависит от напряжения или тока. Если значение R или отношение U / I является постоянным, то ток можно изобразить как функцию напряжения в виде прямой линии.

В резистивных цепях, например, в проводах и резисторах, ток и напряжение линейно пропорциональны. В математике линейная функция — это функция, график которой представляет собой прямую линию (см. Иллюстрацию ниже).Например, y = 2 x является линейной функцией. В линейных отношениях, если одна из величин увеличивается или уменьшается, например, в три раза, другая также будет увеличиваться или уменьшаться на ту же величину. По закону Ома это означает, что если напряжение на резисторе утроится, ток также утроится. Это предполагает постоянное сопротивление.

График, показывающий соотношение между током и напряжением для конкретного электронного компонента, называется вольт-амперной характеристикой.Резисторы имеют линейную вольт-амперную характеристику.

Дополнительную информацию о резисторах и других электронных компонентах можно найти в наших электрических, радиочастотных и электронных калькуляторах и электротехнических преобразователях.

Неомические компоненты

Графическое изображение вольт-амперных кривых нескольких устройств: 1 — резистор, 2 — диод, 3 — лампа накаливания, 4 — стабилитрон; как мы видим, только резистор имеет линейную вольт-амперную характеристику

Хотя при изучении закона Ома мы всегда предполагаем, что вольт-амперные характеристики резисторов линейны, важно отметить, что многие очень полезные электрические и электронные компоненты как лампы накаливания, диоды и транзисторы, которые широко используются в электрических цепях, демонстрируют нелинейную характеристику сопротивления.То есть для них соотношение напряжения и тока не является прямой линией, проходящей через начало координат.

В этой схеме увеличение напряжения не будет производить пропорционально увеличивающийся ток, потому что сопротивление горячей лампы при номинальном напряжении 12 В выше, чем ее сопротивление при 4 или 6 В. Кривая вольт-амперной характеристики сглаживается по мере того, как увеличивается напряжение и увеличивается сопротивление лампы (см. рисунок выше)

Во многих случаях это предположение о линейности резисторов неверно.Рассмотрим, например, схему с лампой накаливания и блоком питания с переменным напряжением. Эту схему можно найти во многих школьных учебниках, где обсуждается, как ток зависит от напряжения, при условии, что сопротивление лампы постоянно. Они объясняют, что если напряжение на 12-вольтовых выводах лампы увеличивается, пропорционально увеличивается и ток. Тем не менее, это не так! Если мы поместим амперметр и измерим ток, мы заметим, что он не прямо пропорционален напряжению.Это связано с тем, что сопротивление лампы изменяется, когда ее нить накаливания начинает светиться — лампа имеет нелинейную вольт-амперную характеристику.

Когда молодые люди начинают изучать электричество, законы Ома и Джоуля — первые два закона, которые они узнают, и довольно часто они видят их в форме колеса закона Ома, что действительно пугает, особенно когда они понимают, что им нужно запомнит это колесо — потому что для их учителей намного проще проверить память учеников, чем проверить их понимание.Учителя часто заставляют своих учеников запоминать все 12 формул вместо запоминания или, что еще лучше, понимают только их двоих, а именно:

и

Хотя это колесо обычно называют колесом закона Ома, это колесо на самом деле объединяет два закона — закон Ома и закон нагрева Джоуля, также называемый первым законом Джоуля, и закон Джоуля-Ленца

Недорогой комплект электричества для детей

Остальные 10 страшных формул могут быть легко выведены из этих двух.И даже эти две формулы запоминать не нужно. Что действительно необходимо помнить и понимать, так это то, что ток через компонент прямо пропорционален разности потенциалов, приложенной к этому компоненту, и обратно пропорционален его сопротивлению. Это закон Ома. И что мощность прямо пропорциональна току и напряжению — это закон Джоуля.

Эти два закона очень интуитивно понятны, если учащиеся понимают, что такое ток, напряжение, сопротивление и мощность.Они поймут, если поиграют с батареей, несколькими резисторами и мультиметром. Они также могут поиграть с этим калькулятором.

Это легко, если они используют аналогию водяного насоса с ограничением и трубой, в которой насос оказывает давление (представляющее напряжение), чтобы протолкнуть воду (ток) по контуру (трубе) с ограничением (сопротивлением). Все остальные формулы, представленные в колесе закона Ома, могут быть выведены из этих двух формул, и если человек использует другие формулы ежедневно, он в конечном итоге запомнит их без каких-либо усилий.

Закон Джоуля

Джеймс Прескотт Джоуль (1818–1889)

Для молодого английского пивовара Джеймса Прескотта Джоуля, который зарабатывал себе на жизнь, работая менеджером пивоварни, наука была просто хобби. Его отец был богатым пивоваром, и молодой Джеймс начал работать на пивоварне в возрасте пятнадцати лет. Когда Джоуля было всего 23 года, он открыл закон, который теперь носит его имя, проводя эксперименты, пытаясь выяснить, что более эффективно в их пивоварне: паровой двигатель или недавно изобретенные электродвигатели.В результате он установил взаимосвязь между током, протекающим через сопротивление (провод), и выделяемым теплом.

Закон Джоуля гласит, что мощность нагрева P , генерируемая электрическим током I в проводнике, пропорциональна произведению квадрата тока и сопротивления провода R :

Если мы сложим Используя закон Джоуля и закон Ома, мы можем вывести несколько полезных формул, которые можно использовать для расчета мощности, рассеиваемой в резисторе, сопротивления на основе известных значений напряжения и тока, тока, протекающего в резисторе, и напряжения на резисторе.Эти формулы часто отображаются в виде страшного колеса закона Ома или (менее страшного) треугольника закона Ома. Щелкните примеры ниже, чтобы узнать, как использовать эти формулы. Этот нагрев провода электрическим током также называется омическим нагревом, джоулевым нагревом или резистивным нагревом.

Эмиль Ленц (1804–1865)

Омический нагрев был независимо изучен русским физиком Эмилем Ленцем, который изучал электромагнетизм с 1831 года и наиболее известен благодаря открытию минимума, связывающего направление индуцированного электрического тока с движущимся магнитным полем. который назван в его честь.Он также независимо открыл закон Джоуля, и этот закон часто носит также имя Ленца — «закон Джоуля-Ленца».

Следует также отметить, что в некоторых учебниках этот закон неверно именуется законом Ватта, особенно если они ссылаются на формулу P = UI .

Закон Ома в цепях переменного тока

Закон Ома используется не только для анализа цепей постоянного тока, описанных выше. Когда переменное во времени напряжение, например синусоидальное напряжение, прикладывается к цепи, закон Ома все еще применяется.Если на резистор подается синусоидальное напряжение, в нем будет течь синусоидальный ток. Этот ток находится в фазе с приложенным напряжением, потому что, когда напряжение меняет полярность, ток также меняет ее. Когда напряжение на максимуме, ток также на максимуме.

При применении закона Ома для анализа цепи переменного тока всегда необходимо последовательно выражать напряжение и ток. Это означает, что напряжение и ток должны быть выражены как среднеквадратичные значения, так и пиковое или размах.При применении закона Джоуля для определения мощности, рассеиваемой в резисторе, применяется то же правило: и ток, и напряжение должны выражаться с использованием одних и тех же значений. Например:

, где субиндекс RMS обозначает среднеквадратичное значение, или

Здесь p означает пиковое значение. Если цепь переменного тока содержит реактивные компоненты, такие как конденсаторы и катушки индуктивности, к ним также применяется закон Ома. В этом случае их реактивные сопротивления используются вместо сопротивления:

, где X может быть реактивным сопротивлением конденсатора X _C или катушки индуктивности X _L , которые рассчитываются по следующим формулам :

и

Дополнительную информацию о реактивном сопротивлении различных компонентов и их последовательном и параллельном сочетании можно найти в наших электрических, радиочастотных и электронных калькуляторах и электротехнических преобразователях.

Что касается мощности в реактивных компонентах, они не преобразуют энергию в тепло и, следовательно, энергия не теряется, и истинная (активная, активная) мощность P равна нулю. Мгновенная мощность передается между конденсатором или катушкой индуктивности и источником питания. Скорость, с которой реактивный компонент накапливает или возвращает энергию, называется его реактивной мощностью Q и определяется по следующим формулам:

Реактивная мощность измеряется в вольт-амперах реактивной (вар) и может использоваться с обычными десятичные префиксы, например квар, мвар и т. д.

Параллельная цепь RLC

В схемах, содержащих активные и реактивные компоненты, применение закона Ома включает использование комплексных величин импеданса Z , напряжения U и тока I . Поскольку для вычислений по законам Ома и Джоуля используются операции умножения и деления, удобно выражать комплексные значения в полярной форме. Вы можете использовать наш калькулятор преобразования прямоугольного фазора для преобразования значений комплексной мощности, тока, напряжения и импеданса между комплексными и полярными формами.Чтобы определить полное сопротивление различных параллельных и последовательных цепей с активными и реактивными компонентами, используйте наши электрические, высокочастотные и электронные калькуляторы.

Формулы закона Ома переменного тока

Примечание для читателей, которые не знакомы с обозначениями углов, используемыми в американских учебниках по электронике и электротехнике. Специальное обозначение, называемое обозначением вектора или угла, используется с символом угла (∠). Используется для описания векторов. Вектор — это комплексное число U , используемое для обозначения синусоиды.Он представлен в полярных координатах вектором с величиной U и углом φ , который обычно выражается в градусах. Фазоры предоставляют простые средства анализа электрических цепей. Формула Эйлера лежит в основе векторного анализа:

Это U∠φ — всего лишь сокращенное обозначение для Ue ^jφ .

Следующие формулы используются в этом калькуляторе. Расчеты производятся со значениями в форме векторов в соответствии с правилами умножения и деления векторов:

, где φ _U , φ _I и φ _Z — напряжение, ток и фазовые углы импеданса.

Все комплексные значения вводятся в форму калькулятора либо в прямоугольной, либо в векторной форме. Хотя импеданс и комплексная мощность не являются векторными величинами, они могут быть представлены в сложной форме, потому что, как и напряжение и ток, они являются комплексными числами и имеют как величину, так и угол. Если они введены в прямоугольной форме, они преобразуются в форму вектора перед вычислением с использованием формул, описанных в нашем Калькуляторе комплекса в фазор.

В качестве примера мы рассчитаем полный ток I _T в параллельной RLC-цепи с R = 10 Ом, L = 100 мкГн и C = 1 мкФ.Источник переменного тока подает синусоидальное напряжение 0,5 В с частотой 10 кГц (нажмите, чтобы просмотреть результат расчетов).

Величина импеданса этой цепи RLC в прямоугольной форме составляет

Фазовый угол

Положительный фазовый угол означает, что нагрузка является индуктивной, а ток отстает от напряжения. Общий импеданс в полярной форме равен

Используя закон Ома и правило деления чисел в полярной форме, мы определим полный ток:

Мощность в цепях переменного тока

В нашем калькуляторе мощности переменного тока мы показали, что активный P , реактивный Q , кажущийся | S | и комплексную мощность S можно рассчитать по следующим формулам:

и

Опять же, поскольку умножения и деления участвуют в расчетах мощности, удобно выражать комплексные значения в полярной форме .Математически можно показать, что комплексная мощность равна произведению векторного напряжения и комплексно-сопряженного векторного тока, то есть

Здесь U и I — напряжение и ток в комплексная форма и I * , U * и Z * представляют собой сопряженные значения тока, напряжения и импеданса в сложной форме. Жирный шрифт означает, что эти значения являются векторными величинами.Обратите внимание, что здесь комплексная мощность S измеряется в вольт-амперах (ВА). В векторной форме мы имеем

, где φ _U — фазовый угол напряжения, а φ _I — текущий фазовый угол. Эти формулы были использованы для создания колеса закона Ома переменного тока.

Колесо закона Ома переменного тока; Полужирный шрифт используется для отображения комплексных значений тока, напряжения, мощности и импеданса. Звездочка, например, в I * , показывает комплексное сопряжение комплексного тока I

Более подробную информацию о расчетах мощности переменного тока вы найдете в нашем калькуляторе мощности переменного тока.Ниже приведены несколько примеров расчетов с помощью этого калькулятора.

Примеры расчетов

Пример 3 . К розетке на 120 В. подключается электронагреватель сопротивлением 10 Ом. Рассчитайте потребляемую мощность и ток, потребляемый нагревателем.

Пример 4 . Маленькая лампочка с сопротивлением 2300 Ом в холодильнике подключается к линии питания 120 В. Рассчитайте потребляемую мощность и ток, потребляемый лампой.

Пример 5 . Ток 0,15 А от солнечной панели протекает через резистор 220 Ом. Рассчитайте напряжение на этом резисторе и мощность, которую он рассеивает в виде тепла.

Пример 6 . Вычислите сопротивление галогенной лампы накаливания и мощность, которую она рассеивает, если потребляет 1,5 А от 12-вольтового автомобильного аккумулятора.

Пример 7 . Вычислите ток через резистор 12 кОм и напряжение на нем, если резистор рассеивает мощность 1 Вт.RC-цепочка серии

(см. Пример 6). Дано: R = 10 Ом, C = 0,1 мкФ, I = 0,2∠0 °. Требуется: U

Пример 8 . К источнику питания синусоидальной формы с частотой 1 МГц последовательно подключены резистор на 10 Ом и конденсатор 0,01 мкФ. Определите напряжение источника в полярной форме, если ток, потребляемый от источника, составляет I = 0,2∠0 ° A. Подсказка: используйте наш калькулятор импеданса последовательной RC-цепи, чтобы определить полное сопротивление RC-цепи в полярной форме (Z = 18.8 – 57,86 °), затем с помощью этого калькулятора определите напряжение источника (V = 3,76–57,8 ° В).

Эту статью написал Анатолий Золотков

Электроэнергия — Резюме — Гипертекст по физике

• … электрическое сопротивление
• электрическая мощность
• контуров-р…

Гипертекст по физике
© 1998–2021 Glenn Elert
Автор, иллюстратор, веб-мастер

Нет постоянных условий.

1. Механика
   1. Кинематика
      1. Движение
      2. Расстояние и перемещение
      3. Скорость и скорость
      4. Разгон
      5. Уравнения движения
      6. Свободное падение
      7. Графики движения
      8. Кинематика и расчет
      9. Кинематика в двух измерениях
      10. Снарядов
      11. Параметрические уравнения
   2. Динамика I: Сила
      1. Силы
      2. Сила и масса
      3. Действие-реакция
      4. Масса
      5. Динамика
      6. Статика
      7. Трение
      8. Силы в двух измерениях
      9. Центростремительная сила
      10. Кадры справки
   3. Энергия
      1. Работа
      2. Энергия
      3. Кинетическая энергия
      4. Потенциальная энергия
      5. Сохранение энергии
      6. Мощность
      7. Простые машины
   4. Dynamics II: Импульс
      1. Импульс и импульс
      2. Сохранение импульса
      3. Импульс и энергия
      4. Импульс в двух измерениях
   5. Вращательное движение
      1. Кинематика вращения
      2. Инерция вращения
      3. Вращательная динамика
      4. Статика вращения
      5. Угловой момент
      6. Энергия вращения
      7. Прокатный
      8. Вращение в двух измерениях
      9. Сила Кориолиса
   6. Планетарное движение
      1. Геоцентризм
      2. Гелиоцентризм
      3. Вселенская гравитация
      4. Орбитальная механика I
      5. Гравитационная потенциальная энергия
      6. Орбитальная механика II
      7. Плотность вытянутых тел
   7. Периодическое движение
      1. Пружины
      2. Генератор простых гармоник
      3. Маятники
      4. Резонанс
      5. Эластичность
   8. Жидкости
      1. Плотность
      2. Давление
      3. Плавучесть
      4. Расход жидкости
      5. Вязкость
      6. Аэродинамическое сопротивление
      7. Режимы потока
2. Теплофизика
   1. Тепло и температура
      1. Температура
      2. Тепловое расширение
      3. Атомная природа вещества
      4. Закон о газе
      5. Кинетико-молекулярная теория
      6. Фазы
   2. Калориметрия
      1. Явное тепло
      2. Скрытое тепло
      3. Химическая потенциальная энергия
   3. Теплопередача
      1. Проводимость
      2. Конвекция
      3. Радиация
   4. Термодинамика
      1. Тепло и работа
      2. Диаграммы давление-объем
      3. Двигатели
      4. Холодильники
      5. Энергия и энтропия
      6. Абсолютный ноль
3. Волны и оптика
   1. Волновые явления
      1. Природа волн
      2. Периодические волны
      3. Интерференция и суперпозиция
      4. Интерфейсы и барьеры
   2. Звук
      1. Природа звука
      2. Интенсивность
      3. Эффект Доплера (звук)
      4. Ударные волны
      5. Дифракция и интерференция (звук)
      6. Стоячие волны
      7. ударов
      8. Музыка и шум
   3. Физическая оптика
      1. Природа света
      2. Поляризация
      3. Эффект Доплера (световой)
      4. Черенковское излучение
      5. Дифракция и интерференция (свет)
      6. Тонкопленочная интерференция
      7. Цвет
   4. Геометрическая оптика
      1. Отражение
      2. Преломление
      3. Зеркала сферические
      4. Сферические линзы
      5. Аберрация
4. Электричество и магнетизм
   1. Электростатика
      1. Электрический заряд
      2. Закон Кулона
      3. Электрическое поле
      4. Электрический потенциал
      5. Закон Гаусса
      6. Проводников
   2. Электростатические приложения
      1. Конденсаторы
      2. Диэлектрики
      3. Батареи
   3. Электрический ток
      1. Электрический ток
      2. Электрическое сопротивление
      3. Электроэнергия
   4. цепей постоянного тока
      1. Резисторы в цепях
      2. Батареи в цепях
      3. Конденсаторы в цепях
      4. Правила Кирхгофа
   5. Магнитостатика
      1. Магнетизм
      2. Электромагнетизм
      3. Закон Ампера
      4. Электромагнитная сила
   6. Магнитодинамика
      1. Электромагнитная индукция
      2. Закон Фарадея
      3. Закон Ленца
      4. Индуктивность
   7. цепей переменного тока
      1. Переменный ток
      2. RC цепи
      3. Цепи РЛ
      4. Цепи LC
   8. Электромагнитные волны
      1. Уравнения Максвелла
      2. Электромагнитные волны
      3. Электромагнитный спектр
5. Современная физика
   1. Относительность
      1. Пространство-время
      2. Масса-энергия
      3. Общая теория относительности
   2. Quanta
      1. Излучение черного тела
      2. Фотоэффект
      3. Рентгеновские снимки
      4. Антиматерия
   3. Волновая механика
      1. Волны материи
      2. Атомарные модели
      3. Полупроводники
      4. Конденсированные вещества
   4. Ядерная физика
      1. Изотопы
      2. Радиоактивный распад
      3. Период полураспада
      4. Энергия связи
      5. Деление
      6. Fusion
      7. Нуклеосинтез
      8. Ядерное оружие
      9. Радиобиология
   5. Физика элементарных частиц
      1. Квантовая электродинамика
      2. Квантовая хромодинамика
      3. Квантовая динамика вкусов
      4. Стандартная модель
      5. Помимо стандартной модели
6. Фонды
   1. квартир
      1. Международная система единиц
      2. Гауссова система единиц
      3. Британо-американская система единиц
      4. Разные единицы
      5. Время
      6. Преобразование единиц
   2. Измерение
      1. Значащие цифры
      2. По порядку величины
   3. Графики
      1. Графическое представление данных
      2. Линейная регрессия
      3. Подгонка кривой
      4. Исчисление
   4. Векторы
      1. Тригонометрия
      2. Сложение и вычитание векторов
      3. Векторное разрешение и компоненты
      4. Умножение векторов
   5. ссылку
      1. Специальные символы
      2. Часто используемые уравнения
      3. Физические константы
      4. Астрономические данные
      5. Периодическая таблица элементов
      6. Люди в физике
7. Назад дело
   1. Предисловие
      1. Об этой книге
   2. Связаться с автором
      1. гленнелерт.нас
      2. Behance
      3. Instagram
      4. Твиттер
      5. YouTube
   3. Аффилированные сайты
      1. hypertextbook.com
      2. midwoodscience.org

Закон индукции Фарадея: Закон Ленца

Цели обучения

К концу этого раздела вы сможете:

• Рассчитайте ЭДС, ток и магнитные поля, используя закон Фарадея.
• Объясните физические результаты Закона Ленца

Закон Фарадея и Ленца

Эксперименты Фарадея показали, что ЭДС, вызванная изменением магнитного потока, зависит только от нескольких факторов. Во-первых, ЭДС прямо пропорциональна изменению магнитного потока Δ Φ . Во-вторых, ЭДС является наибольшей, когда изменение во времени Δ t является наименьшим, то есть ЭДС обратно пропорциональна Δ t . Наконец, если катушка имеет Н витков, будет создана ЭДС, которая в Н в раз больше, чем для одиночной катушки, так что ЭДС прямо пропорциональна Н .Уравнение для ЭДС, вызванной изменением магнитного потока, равно

[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex].

Это соотношение известно как закон индукции Фарадея . Обычно единицами измерения ЭДС являются вольты. Знак минус в законе индукции Фарадея очень важен. Минус означает, что ЭДС создает ток I и магнитное поле B, которые противодействуют изменению магнитного потока Δ Φ — это известно как закон Ленца . Направление (обозначенное знаком минус) ЭДС настолько важно, что оно было названо законом Ленца в честь русского Генриха Ленца (1804–1865), который, подобно Фарадею и Генри, независимо исследовал аспекты индукции.Фарадей знал о направлении, но Ленц так ясно изложил его, что ему приписывают его открытие. (См. Рисунок 1.)

Рис. 1. (a) Когда стержневой магнит вставляется в катушку, сила магнитного поля в катушке увеличивается. Ток, наведенный в катушке, создает другое поле в направлении, противоположном направлению стержневого магнита, чтобы противодействовать увеличению. Это один из аспектов закона Ленца: индукция препятствует любому изменению потока. (b) и (c) — две другие ситуации. Убедитесь сами, что показанное направление индуцированной катушки B действительно противодействует изменению магнитного потока и что показанное направление тока согласуется с RHR-2.

Стратегия решения проблем закона Ленца

Чтобы использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС:

1. Сделайте набросок ситуации для использования при визуализации и записи направлений.
2. Определите направление магнитного поля B.
3. Определите, увеличивается или уменьшается поток.
4. Теперь определите направление индуцированного магнитного поля B. Оно противодействует изменению потока на , добавляя или вычитая из исходного поля.
5. Используйте RHR-2 для определения направления индуцированного тока I, ответственного за индуцированное магнитное поле B.
6. Направление (или полярность) наведенной ЭДС теперь будет управлять током в этом направлении и может быть представлено как ток, выходящий из положительного вывода ЭДС и возвращающийся к его отрицательному выводу.

Для практики примените эти шаги к ситуациям, показанным на Рисунке 1, и другим, которые являются частью следующего текстового материала.

Применение электромагнитной индукции

Существует множество применений закона индукции Фарадея, которые мы исследуем в этой и других главах. На этом этапе позвольте нам упомянуть несколько, которые имеют отношение к хранению данных и магнитным полям. Очень важное приложение связано с аудио и видео , записывающими лентами . Пластиковая лента, покрытая оксидом железа, проходит мимо записывающей головки. Эта записывающая головка представляет собой круглое железное кольцо, вокруг которого намотана катушка с проволокой — электромагнит (рис. 2).Сигнал в виде переменного входного тока от микрофона или камеры поступает на записывающую головку. Эти сигналы (которые являются функцией амплитуды и частоты сигнала) создают переменные магнитные поля на записывающей головке. Когда лента движется мимо записывающей головки, ориентация магнитного поля молекул оксида железа на ленте изменяется, таким образом записывая сигнал. В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по конструкции записывающей головке. Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в проволочной катушке в воспроизводящей головке.Затем этот сигнал отправляется на громкоговоритель или видеоплеер.

Рис. 2. Головки для записи и воспроизведения, используемые с аудио- и видеомагнитными лентами. (кредит: Стив Джурветсон)

Аналогичные принципы применимы и к жестким дискам компьютеров, но с гораздо большей скоростью. Здесь записи находятся на вращающемся диске с покрытием. Исторически считывающие головки создавались по принципу индукции. Однако входная информация передается в цифровой, а не аналоговой форме — на вращающемся жестком диске записывается серия нулей или единиц.Сегодня большинство считывающих устройств с жестких дисков не работают по принципу индукции, а используют технологию, известную как гигантское магнитосопротивление . (Открытие того факта, что слабые изменения магнитного поля в тонкой пленке из железа и хрома могут вызывать гораздо большие изменения электрического сопротивления, было одним из первых крупных успехов нанотехнологии.) Еще одно применение индукции можно найти на магнитной полосе на оборотной стороне вашей личной кредитной карты, которая использовалась в продуктовом магазине или в банкомате.Это работает по тому же принципу, что и аудио- или видеопленка, упомянутая в последнем абзаце, в которой голова считывает личную информацию с вашей карты.

Другое применение электромагнитной индукции — это когда электрические сигналы должны передаваться через барьер. Рассмотрим кохлеарный имплант , показанный ниже. Звук улавливается микрофоном на внешней стороне черепа и используется для создания переменного магнитного поля. Ток индуцируется в приемнике, закрепленном в кости под кожей, и передается на электроды во внутреннем ухе.Электромагнитная индукция может использоваться и в других случаях, когда электрические сигналы должны передаваться через различные среды.

Рис. 3. Электромагнитная индукция, используемая при передаче электрического тока через среды. Устройство на голове ребенка индуцирует электрический ток в приемнике, закрепленном в кости под кожей. (кредит: Бьорн Кнетч)

Еще одна современная область исследований, в которой электромагнитная индукция успешно реализуется (и имеет значительный потенциал), — это транскраниальное магнитное моделирование.Множество расстройств, включая депрессию и галлюцинации, можно объяснить нерегулярной локальной электрической активностью в головном мозге. В транскраниальной магнитной стимуляции быстро меняющееся и очень локализованное магнитное поле помещается рядом с определенными участками мозга, идентифицированными. В идентифицированных участках индуцируются слабые электрические токи, которые могут привести к восстановлению электрических функций в тканях мозга.

Апноэ сна («остановка дыхания») поражает как взрослых, так и младенцев (особенно недоношенных детей, и это может быть причиной внезапной детской смерти [SID]).У таких людей дыхание может многократно останавливаться во время сна. Прекращение действия более чем на 20 секунд может быть очень опасным. Инсульт, сердечная недостаточность и усталость — вот лишь некоторые из возможных последствий для человека, страдающего апноэ во сне. У младенцев проблема заключается в задержке дыхания на это более длительное время. В одном из типов мониторов, предупреждающих родителей о том, что ребенок не дышит, используется электромагнитная индукция. В проводе, обмотанном вокруг груди младенца, проходит переменный ток. Расширение и сжатие грудной клетки младенца во время дыхания изменяет площадь спирали.В расположенной рядом катушке датчика индуцируется переменный ток из-за изменения магнитного поля исходного провода. Если ребенок перестанет дышать, наведенный ток изменится, и родители могут быть предупреждены.

Подключение: сохранение энергии

Закон Ленца — это проявление сохранения энергии. Индуцированная ЭДС создает ток, который противодействует изменению потока, потому что изменение потока означает изменение энергии.Энергия может входить или уходить, но не мгновенно. Закон Ленца — следствие. Когда изменение начинается, закон гласит, что индукция противодействует и, таким образом, замедляет изменение. Фактически, если бы индуцированная ЭДС была в том же направлении, что и изменение потока, была бы положительная обратная связь, которая не давала бы нам бесплатную энергию из любого видимого источника — закон сохранения энергии был бы нарушен.

Пример 1. Расчет ЭДС: насколько велика наведенная ЭДС?

Рассчитайте величину наведенной ЭДС, когда магнит, показанный на Рисунке 1 (а), вдавливается в катушку, учитывая следующую информацию: одноконтурная катушка имеет радиус 6.00 см, а среднее значение B cos θ (это дано, поскольку поле стержневого магнита сложное) увеличивается с 0,0500 Тл до 0,250 Тл за 0,100 с.

Стратегия

Чтобы найти величину ЭДС , мы используем закон индукции Фарадея, как указано в [latex] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex], но без знака минус, указывающего направление:

[латекс] \ text {emf} = N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex].

Решение

Нам дано, что N = 1 и Δ t = 0.100 с, но мы должны определить изменение потока Δ Φ , прежде чем мы сможем найти ЭДС. Поскольку площадь петли фиксирована, мы видим, что

ΔΦ = Δ ( BA cos θ ) = AΔ ( B cos θ ).

Теперь Δ ( B cos θ ) = 0.200 Тл, поскольку было задано, что B cos θ изменяется от 0,0500 до 0,250 Тл. Площадь контура A = πr2 = (3,14…) ( 0,060 м) ² = 1,13 × 10 ⁻² м ² .{2} \ right) \ left (0.200 \ text {T} \ right)} {0.100 \ text {s}} = 22.6 \ text {mV} \\ [/ latex].

Обсуждение

Хотя это напряжение легко измерить, его явно недостаточно для большинства практических приложений. Больше петель в катушке, более сильный магнит и более быстрое движение делают индукцию практическим источником напряжения, которым она и является.

Исследования PhET: Электромагнитная лаборатория Фарадея

Поиграйте с стержневым магнитом и катушками, чтобы узнать о законе Фарадея.Поднесите стержневой магнит к одной или двум катушкам, чтобы лампочка загорелась. Просмотрите силовые линии магнитного поля. Измеритель показывает направление и величину тока. Просмотрите силовые линии магнитного поля или используйте измеритель, чтобы показать направление и величину тока. Вы также можете играть с электромагнитами, генераторами и трансформаторами!

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

Концептуальные вопросы

1. Человек, работающий с большими магнитами, иногда помещает голову в сильное поле.Она сообщает, что у нее кружится голова, когда она быстро поворачивает голову. Как это может быть связано с индукцией?
2. Ускоритель частиц отправляет заряженные частицы с высокой скоростью по откачанной трубе. Объясните, как катушка с проволокой, намотанная вокруг трубы, может обнаруживать прохождение отдельных частиц. Нарисуйте график выходного напряжения катушки при прохождении через нее одиночной частицы.

Задачи и упражнения

1. Как показано на Рисунке 5 (а), каково направление тока, индуцируемого в катушке 2: (а) Если ток в катушке 1 увеличивается? (b) Если ток в катушке 1 уменьшается? (c) Если ток в катушке 1 постоянный? Ясно покажите, как вы следуете шагам из приведенной выше стратегии решения проблем для закона Ленца .

Рис. 5. (a) Катушки лежат в одной плоскости. (б) Проволока находится в плоскости катушки.

2. Как показано на Рисунке 5 (b), в каком направлении индуцируется ток в катушке: (a) Если ток в проводе увеличивается? (б) Если ток в проводе уменьшится? (c) Если ток в проводе внезапно меняет направление? Ясно покажите, как вы следуете шагам из приведенной выше стратегии решения проблем для закона Ленца .

3. Как показано на рисунке 6, каковы направления токов в катушках 1, 2 и 3 (предположим, что катушки лежат в плоскости цепи): (a) Когда переключатель в первый раз замыкается? (б) Когда выключатель был замкнут в течение длительного времени? (c) Сразу после размыкания переключателя?

Рисунок 6.

4. Повторите предыдущую проблему с перевернутой батареей.

5. Убедитесь, что единицами измерения Δ Φ / Δ t являются вольты. То есть показать, что 1 Тл м ² / с = 1 В.

6. Предположим, катушка с 50 витками находится в плоскости страницы в однородном магнитном поле, направленном внутрь страницы. Змеевик изначально имел площадь 0,250 м ² . Он растягивается, чтобы не было площади за 0,100 с. Каковы направление и величина наведенной ЭДС, если однородное магнитное поле имеет напряженность 1.50 т?

7. (a) Техник МРТ перемещает свою руку из области очень низкой напряженности магнитного поля в поле 2,00 Тл сканера МРТ, указывая пальцами в направлении поля. Найдите среднюю ЭДС, индуцированную в его обручальном кольце, учитывая его диаметр 2,20 см и предполагая, что для его перемещения в поле требуется 0,250 с. (б) Обсудите, может ли этот ток существенно изменить температуру кольца.

8. Integrated Concepts Обратимся к ситуации в предыдущей задаче: (a) Какой ток индуцируется в кольце, если его сопротивление равно 0.0100 Ом? (б) Какая средняя мощность рассеивается? (c) Какое магнитное поле индуцируется в центре кольца? (d) Каково направление индуцированного магнитного поля относительно поля МРТ?

9. ЭДС индуцируется вращением катушки с 1000 витками диаметром 20,0 см в магнитном поле Земли 5,00 × 10 ⁻⁵ Тл. Какая средняя ЭДС индуцируется, если плоскость катушки изначально перпендикулярна полю Земли и повернута параллельно полю за 10,0 мс?

10.Катушка с 500 витками радиусом 0,250 м поворачивается на одну четверть оборота за 4,17 мс, первоначально ее плоскость перпендикулярна однородному магнитному полю. (Это 60 об / с.) Найдите напряженность магнитного поля, необходимую для индукции средней ЭДС 10 000 В.

11. Integrated Concepts Примерно как ЭДС, наведенная в петле на рисунке 5 (b), зависит от расстояния центра петли от провода?

12. Integrated Concepts (a) Молния создает быстро меняющееся магнитное поле.Если болт ударяется о землю вертикально и действует как ток в длинном прямом проводе, он вызывает напряжение в петле, выровненной, как показано на рисунке 5 (b). Какое напряжение индуцируется в петле диаметром 1,00 м и 50,0 м от удара молнии 2,00 × 10 6 , если ток падает до нуля за 25,0 мкс? (b) Обсудите обстоятельства, при которых такое напряжение может привести к заметным последствиям.

Глоссарий

Закон индукции Фарадея:

средство вычисления ЭДС в катушке из-за изменения магнитного потока, заданное как [latex] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex]

Закон Ленца:

знак минус в законе Фарадея, означающий, что ЭДС, индуцированная в катушке, противодействует изменению магнитного потока

Избранные решения проблем и упражнения

1.(a) CCW (b) CW (c) Нет наведенного тока

3. (a) 1 против часовой стрелки, 2 против часовой стрелки, 3 по часовой стрелке (b) 1, 2 и 3 без наведенного тока (c) 1 CW, 2 CW, 3 CCW

7. (a) 3,04 мВ (b) В качестве нижнего предела для кольца, оценка R = 1,00 мОм. Передаваемое тепло составит 2,31 мДж. Это небольшое количество тепла.

9. 0,157 В

11. пропорционально [латексу] \ frac {1} {r} \\ [/ latex]

Закон Ленца — обзор

3.3 Диамагнитные, парамагнитные и ферромагнитные материалы

В этом разделе мы внимательно следим за книгой Бланделла [26], и читатели могут отсылать к этой книге для получения дополнительных сведений.

В диамагнитном материале магнитное поле индуцирует магнитный момент, который противодействует тому самому магнитному полю, которое его действительно вызывает. Диамагнетизм — это квантово-механическое явление, и его классическое объяснение в терминах закона Ленца не совсем корректно. Для материала с объемом ионов V и N (каждый с Z числом электронов с массой m _e и ионным радиусом r ) со всеми заполненными оболочками диамагнитная восприимчивость выражается как Уравнение(21.23) [26]:

(21.23) χ = Ne2μ0V6me∑i = 1Z 〈ri2〉

Диамагнитная восприимчивость в значительной степени не зависит от температуры. Он присутствует во всех материалах и связан с закрытыми атомными оболочками материалов, но обычно намного слабее, чем другие магнитные эффекты. Материалы с делокализованными π электронами, такие как нафталин и графит, демонстрируют большую диамагнитную восприимчивость. Эффективный диаметр кольца в молекулярном нафталине и слабо связанных листах гексагональных слоев в графите в несколько раз больше, чем диаметр атома, что приводит к большой диамагнитной восприимчивости в таких материалах.

В парамагнитных материалах приложенное магнитное поле индуцирует намагниченность, которая стремится выровняться с магнитным полем. В отличие от диамагнитных материалов с замкнутыми атомными оболочками и, следовательно, без магнитного момента, атомы в парамагнитных материалах обладают ненулевым моментом, возникающим из неспаренных электронов. Этот ненулевой магнитный момент атома связан с его полным угловым моментом, который является суммой орбитального углового момента L и спинового углового момента S .Эти магнитные моменты, связанные с атомами, однако, указывают в случайных направлениях из-за очень слабого взаимодействия между собой, и для любых практических целей они считаются независимыми. Магнитные моменты в парамагнитных материалах имеют тенденцию выравниваться при приложении внешнего магнитного поля, а степень выравнивания зависит от силы магнитного поля. С другой стороны, повышение температуры материалов будет случайным образом изменять моменты; следовательно, намагниченность парамагнитных материалов будет зависеть от отношения внешнего магнитного поля B и температуры T , т.е.е., В / Т .

В общем случае парамагнитного материала, где полный угловой момент Дж может принимать любое целое или полуцелое значение, индуцированная намагниченность в приложенном магнитном поле может быть выражена как уравнение. (21.24) [26]:

(21.24) M = MSBJ (y)

, где уравнение. (21.25):

(21.25) y = gJμBJBkBT

и уравнение. (21.26):

(21.26) MS = ngJμBJ

и B _J ( y ) — функция Бриллюэна, заданная уравнением.(21.27):

(21.27) BJ (y) = (2J + 1) 2Jcoth (2J + 12Jy) −12Jcoth (y2J)

За исключением очень низкой температуры и / или очень сильных магнитных полей, экспериментальная ситуация соответствует к y << 1, что приводит к формуле. (21.28):

(21.28) BJ (y) = (J + 1) y3J + O (y3)

Таким образом, для слабых магнитных полей восприимчивость парамагнитных материалов определяется формулой. (21.29):

(21.29) ξ≈μ0MB = ημ0μeff23kBT

, что является законом Кюри – Вейсса. Таким образом, измерение восприимчивости парамагнитных материалов позволяет вывести значение эффективного магнитного момента μ _eff (уравнение.21.30):

(21.30) μeff = gJμBJ (J + 1)

, где уравнение. (21.31):

(21.31) gJ = 32 + S (S + 1) −L (L + 1) 2J (J + 1)

и g _J известен как Lande- g-фактор .

В ферромагнитных (ФМ) материалах спонтанная намагниченность существует даже в отсутствие приложенного магнитного поля. Этот эффект возникает из-за обменного взаимодействия (которое имеет квантово-механическое происхождение и намного сильнее, чем дипольное взаимодействие между магнитными моментами) между моментами в узлах атомов.Одной из первых моделей, объясняющих ферромагнетизм, является модель Вейсса, в которой суммарный эффект обменного взаимодействия представлен эффективным молекулярным полем, как показано в формуле. (21.32):

(21.32) Bmf = −2gμB∑jJijSj

Здесь предполагается, что мы имеем дело с системой с нулевым угловым моментом, т. Е. L = 0 и J = S , и все магнитные атомы испытывают одно и то же молекулярное поле. Это молекулярное поле B _mf является мерой эффекта упорядочения системы, поэтому можно записать уравнение.(21.33):

(21.33) Bmf = λM

Теперь можно приступить к исследованию отклика FM-материала таким же образом, как и в случае парамагнитного материала, помещенного в магнитное поле B + B _mf , где B — внешнее магнитное поле. При достаточно низких температурах внутреннее молекулярное поле B _mf может выравнивать магнитные моменты даже в отсутствие приложенного магнитного поля.Для нахождения решения модели Вейсса графически решаются следующие уравнения [26]:

(21,34) MMS = BJ (y)

и

(21,35) y = gJμBJ (B + λM) kBT

Эта обработка в отсутствие термина λM будет идентично обработке парамагнитного материала (описанной ранее в этом разделе). Ограничение случаем B = 0, следовательно, M = k _B Ty / g _J μ _B прямое Линия, полученная при построении графика M против y , имеет градиент, который пропорционален температуре T .Не существует одновременного решения предыдущих уравнений, кроме как в начале координат, где y = 0 и M _S = 0 (рис. 21.8). Ситуация, однако, меняется ниже критической температуры T _C , когда градиент линии M по сравнению с y меньше, чем функция Бриллюэна B _J ( y ) в начале координат. При температурах T < T _C , есть три решения: 1 при M _S = 0 и еще два для M _S при ± некотором ненулевом значении ( Инжир.21,8). Обнаружено, что ненулевые решения устойчивы, а нулевое решение неустойчиво. Таким образом, ненулевая спонтанная намагниченность возникает в FM-материалах ниже критической температуры T _C , даже в отсутствие внешнего магнитного поля, и эта спонтанная намагниченность растет дальше с понижением температуры. Выше этой критической температуры T _C FM-материалы ведут себя как парамагнетики.

Рисунок 21.8. Графические решения уравнений. (21.34) и (21.35).

S.J. Бланделл, Магнетизм в конденсированных средах, Cambridge University Press, 2001. Авторское право 2001 г., воспроизведено с разрешения Oxford University Press.

Эта критическая температура в материалах FM известна как температура Кюри , и ее можно оценить, найдя, когда градиенты линии M = k _B Ty / g _J μ _B JλM _S и кривая M = M _S B _{Y 909 происхождение [26].Для малых значений y , B J ( y ) = ( J + 1) y /3 J + O ( y ³ ) и температура Кюри T C затем определяется как уравнение. (21.36):}

(21.36) TC = gJμB (J + 1) MS3kB = nλμeff23kB

Молекулярное поле определяется уравнением. (21.37):

(21.37) Bmf = λMS = 3kBTCgJμB (J + 1)

Для ферромагнетика с J = 1/2 и T _C ≈ 1000 K, B _{B 9098 mf} оценивается примерно в 1500 Тл [26].Это эффективное поле представляет собой огромное магнитное поле, которое отражает силу обменного взаимодействия.

Влияние приложенного магнитного поля в материалах FM заключается в смещении прямой линии в графическом решении уравнений вправо, что приводит к ненулевому решению для M для всех температур. С энергетической точки зрения всегда есть преимущество FM-материалов в приложенном магнитном поле — иметь ненулевую намагниченность с моментами, выстраивающимися вдоль магнитного поля.

RL Circuits — University Physics Volume 2

Цели обучения

К концу этого раздела вы сможете:

• Анализировать цепи, в которых последовательно соединены индуктор и резистор
• Опишите, как ток и напряжение экспоненциально растут или затухают в зависимости от начальных условий.

Цепь с сопротивлением и самоиндукцией называется цепью RL . (Рисунок) (a) показывает схему RL , состоящую из резистора, катушки индуктивности, постоянного источника ЭДС и переключателей, а в замкнутом состоянии схема эквивалентна одноконтурной цепи, состоящей из резистора и катушки индуктивности. подключен через источник ЭДС ((Рисунок) (б)).Когда открыт и закрыт, схема становится одноконтурной схемой только с резистором и катушкой индуктивности ((Рисунок) (c)).

Сначала рассмотрим схему RL (рисунок) (b). Когда он замкнут и разомкнут, источник ЭДС создает ток в цепи. Если бы в цепи не было самоиндукции, ток немедленно повысился бы до постоянного значения. Однако, согласно закону Фарадея, возрастающий ток вызывает на катушке индуктивности ЭДС. В соответствии с законом Ленца наведенная ЭДС противодействует увеличению тока и направлена, как показано на рисунке.В результате I (t) начинается с нуля и асимптотически увеличивается до своего конечного значения.

Применяя к этой схеме правило петли Кирхгофа, получаем

, которое является дифференциальным уравнением первого порядка для I (t) . Обратите внимание на его сходство с уравнением для последовательно соединенных конденсатора и резистора (см. RC Circuits). Точно так же решение (рисунок) можно найти, сделав замены в уравнениях, связывающих конденсатор с катушкой индуктивности. Это дает

где

— индуктивная постоянная времени цепи.

Текущее значение I (t) показано на (Рисунок) (а). Он начинается с нуля, и по мере того, как I (t) приближается асимптотически. Индуцированная ЭДС прямо пропорциональна dI / dt или наклону кривой. Следовательно, в то время как наивысшая сразу после включения переключателей, наведенная ЭДС уменьшается до нуля со временем, когда ток приближается к своему конечному значению. Схема становится эквивалентной резистору, подключенному к источнику ЭДС.

Изменение во времени (а) электрического тока и (б) величины индуцированного напряжения на катушке в цепи (рисунок) (б).

Энергия, запасенная в магнитном поле индуктора, составляет

.

Таким образом, по мере того, как ток приближается к максимальному значению, запасенная в катушке индуктивности энергия увеличивается от нуля и асимптотически приближается к максимуму

.

Постоянная времени показывает, насколько быстро ток увеличивается до своего конечного значения. При токе в цепи, начиная с (рисунок),

, который имеет окончательное значение. Чем меньше индуктивная постоянная времени, тем быстрее приближается ток.

Мы можем найти временную зависимость индуцированного напряжения на катушке индуктивности в этой цепи, используя и (рисунок):

Величина этой функции показана на (Рисунок) (b). Наибольшее значение имеет место, когда dI / dt является наибольшим, то есть сразу после закрытия и открытия. При приближении к установившемуся режиму dI / dt уменьшается до нуля. В результате напряжение на катушке индуктивности также обращается в нуль как

Постоянная времени также говорит нам, как быстро спадает наведенное напряжение.По величине наведенного напряжения

Таким образом, напряжение на катушке индуктивности падает примерно до своего начального значения после одной постоянной времени. Чем короче постоянная времени, тем быстрее падает напряжение.

По прошествии достаточного количества времени, чтобы ток практически достиг своего конечного значения, положения переключателей на (Рисунок) (a) меняются местами, давая нам схему в части (c). При токе в цепи согласно правилу петли Кирхгофа получаем

Решение этого уравнения аналогично решению уравнения для разряжающегося конденсатора с аналогичными заменами.Текущее значение на момент времени т. равно

.

Ток начинается и уменьшается со временем по мере того, как энергия, запасенная в катушке индуктивности, истощается ((рисунок)).

Зависимость напряжения на катушке индуктивности от времени можно определить из

Это напряжение изначально, и оно спадает до нуля, как и ток. Энергия, запасенная в магнитном поле индуктора, также экспоненциально уменьшается со временем, поскольку она рассеивается за счет джоулева нагрева в сопротивлении цепи.

Изменение во времени электрического тока в цепи RL (рисунок) (c). Индуцированное напряжение на катушке также экспоненциально спадает.

Проверьте свое понимание Убедитесь, что RC и L / R имеют измерения времени.

а. 2,2 с; б. 43 H; c. 1.0 с

Проверьте свое понимание Для схемы на (Рисунок) (b) покажите, что когда достигается устойчивое состояние, разница в полных энергиях, производимых батареей и рассеиваемых в резисторе, равна энергии, хранящейся в магнитном поле. поле катушки.

Концептуальные вопросы

Используйте закон Ленца, чтобы объяснить, почему начальный ток в цепи RL (рисунок) (b) равен нулю.

По мере прохождения тока через катушку индуктивности по закону Ленца возникает обратный ток, который создается, чтобы поддерживать чистый ток на уровне нуля ампер — начальном токе.

Когда ток в цепи RL (рисунок) (b) достигает своего конечного значения, какое напряжение на катушке индуктивности? Через резистор?

Зависит ли время, необходимое для того, чтобы ток в цепи RL достиг какой-либо части своего установившегося значения, от ЭДС батареи?

Катушка индуктивности подключена к клеммам батареи.Зависит ли ток, который в конечном итоге протекает через катушку индуктивности, от внутреннего сопротивления батареи? Зависит ли время, необходимое для того, чтобы ток достиг своего конечного значения, от этого сопротивления?

В какое время напряжение на катушке индуктивности цепи RL (рисунок) (b) является максимальным?

В, или когда переключатель впервые включен.

В простой схеме RL (Рисунок) (b), может ли ЭДС, индуцированная на катушке индуктивности, когда-либо быть больше, чем ЭДС батареи, используемой для создания тока?

Если ЭДС батареи (рисунок) (b) уменьшается в 2 раза, насколько изменится установившаяся энергия, накопленная в магнитном поле индуктора?

Постоянный ток течет по цепи с большой индуктивной постоянной времени.Когда переключатель в цепи размыкается, на выводах переключателя возникает большая искра. Объяснять.

Обсудите возможные практические применения схем RL .

Глоссарий

индуктивная постоянная времени

, обозначенное как, характерное время, заданное количеством L / R конкретной серии RL цепи

Логический класс

| Дом

ТОК ЭЛЕКТРИЧЕСТВА

Введение:

Когда через проводник проходит электрический ток, через некоторое время проводник нагревается и выделяет тепло.Это происходит из-за преобразования некоторой электрической энергии, проходящей через проводник, в тепловую. Этот эффект электрического тока называется тепловым эффектом тока.

Когда ток течет по проводнику, в проводнике генерируется тепловая энергия. Нагревательный эффект электрического тока зависит от трех факторов:

• Сопротивление R проводника. Чем выше сопротивление, тем больше тепла.
• Время t, в течение которого течет ток.Чем больше время, тем больше выделяется тепла
• Величина тока I. Чем выше сила тока, тем больше выделяется тепла.

Следовательно, эффект нагрева, создаваемый электрическим током I через проводник сопротивления R в течение некоторого времени, t определяется как H = I ² Rt. Это уравнение называется уравнением Джоуля электрического нагрева.

Электроэнергия и мощность

Работа, совершаемая при проталкивании заряда по электрической цепи, определяется выражением w.d = VIt

Таким образом, мощность, P = w.d / t = VI

Электрическая мощность, потребляемая электроприбором, определяется как P = VI = I ² R = V ² / R

Области применения нагрева электрическим током

Большинство бытовых электроприборов таким образом преобразуют электрическую энергию в тепло. К ним относятся лампы накаливания, электрический нагреватель, электрический утюг, электрический чайник и т. Д.

В осветительных приборах

1. Лампы накаливания — изготовлены из вольфрамовой проволоки, заключенной в стеклянную колбу, из которой удален воздух.Это потому, что воздух окисляет нить. Нить нагревается до высокой температуры и становится раскаленной добела. Вольфрам используется из-за его высокой температуры плавления; 3400 ⁰ Колба заполнена неактивным газом, например. аргон или азот при низком давлении, что снижает испарение вольфрамовой проволоки. Однако одним из недостатков инертного газа является то, что он вызывает конвекционные токи, которые охлаждают нить накала. Эта проблема сводится к минимуму за счет наматывания проволоки так, чтобы она занимала меньшую площадь, что снижает потери тепла за счет конвекции.
2. Люминесцентные лампы — эти лампы более эффективны по сравнению с лампами накаливания и служат намного дольше. У них есть пары ртути в стеклянной трубке, которая при включении испускает ультрафиолетовое излучение. Это излучение заставляет порошок в трубке светиться (флуоресцировать), то есть испускать видимый свет. Из разных порошков получаются разные цвета. Обратите внимание, что люминесцентные лампы дороги в установке, но их эксплуатационные расходы намного меньше.

В электронагревателе

1. Электрические плиты — электрические плиты раскалены докрасна, и произведенная тепловая энергия поглощается кастрюлей посредством теплопроводности.
2. Электрические обогреватели — лучистые обогреватели становятся красными при температуре около 900 ⁰ C, а испускаемое излучение направляется в комнату с помощью полированных отражателей.
3. Электрочайники — нагревательный элемент размещается на дне чайника так, чтобы нагреваемая жидкость покрывала его. Затем тепло поглощается водой и распределяется по всей жидкости за счет конвекции.

Электрические утюги — когда через нагревательный элемент протекает ток, выделяемая тепловая энергия передается на основание из тяжелого металла, повышая его температуру.Затем эта энергия используется для прессования одежды. Температуру утюга можно контролировать с помощью термостата (биметаллической планки).

Когда между концами резистора приложена разность потенциалов V, электрический

Поле

будет действовать на свободные электроны. Работа электрического поля на бесплатном

электронов за время t равно W = Vq

Вт = V это W = i2 Rt

ii) Эта работа, совершаемая полем, преобразуется в тепловую энергию резистора через столкновения с решеткой.{2}} \)

б) Тепло, выделяемое в данном резисторе заданным током, пропорционально времени, в течение которого в нем существует ток, т. Е. \ (H \ propto t \)

c) Тепло, выделяемое в резисторе заданным током в заданное время, пропорционально его сопротивлению.

v) Электрический нагреватель, электрический утюг, электрическая лампочка, электрическая плита — вот некоторые из инструментов, которые воздействуют на тепловой эффект Джоуля и преобразуют электрическую энергию в тепловую.Эффект Джоуля необратим .

Джоулев нагрев , также известный как омический нагрев и резистивный нагрев , представляет собой процесс, при котором прохождение электрического тока через проводник производит тепло. Первый закон Джоуля , также известный как закон Джоуля-Ленца , ^[1] , утверждает, что мощность нагрева, генерируемая электрическим проводником, пропорциональна произведению его сопротивления и квадрата тока: Джоулевое нагревание влияет на весь электрический проводник, в отличие от эффекта Пельтье, который передает тепло от одного электрического спая к другому.

Постоянный ток :

Самая общая и основная формула для джоулева нагрева:

{\ displaystyle P = (V_ {A} -V_ {B}) I}, где

• P — мощность (энергия в единицу времени), преобразованная из электрической энергии в тепловую,
• I — ток, протекающий через резистор или другой элемент,
• {\ displaystyle V_ {A} -V_ {B}} — падение напряжения на элементе. { 2} / R}, где «avg» обозначает среднее значение за один или несколько циклов, а «rms» обозначает среднеквадратичное значение.{*}} \ right) \)

  , где \ (\ varnothing \) — разность фаз между током и напряжением, {\ displaystyle \ operatorname {Re}} Re — действительная часть, Z — комплексное сопротивление, а Y * — комплексное сопряжение проводимости. (равно 1/ Z * ).

  Химическое воздействие электрического тока :

  Прохождение электрического тока через проводящую жидкость вызывает химические реакции.Возникающие в результате эффекты называют химическими

  .

  воздействия токов. Процесс нанесения слоя любого желаемого металла на другой материал с помощью электричества называется гальваникой.

  1. Найдите энергию, рассеиваемую за 5 минут электрической лампочкой с нитью накала 500 Ом, подключенной к источнику питания 240 В.

  Решение:

  E = Pt = V2 / R * t = (240 ² * 5 * 60) / 500 = 34,560 Дж.

  2. Электрическая лампочка имеет маркировку 100 Вт, 240 В. Вычислить:
  i) Ток через нить накала
  ii) Сопротивление нити накала лампы .

  Решение:

  P = VI I = P / V = ​​100/240 = 0,4167A
  По закону Ома V = IR R = V / I = 240 / 0,4167 = 575,95 Ом.

  1. Для нагрева воды используется погружной нагреватель мощностью 2,5 кВт. Вычислить:

  i) Рабочее напряжение нагревателя, если его сопротивление составляет 24 Ом 90 102

  ii) Преобразование электрической энергии в тепловую за 2 часа.

  Решение

  P = VI = I ² R

  I = (2500/24) ^1/2 = 10,2062A

  В = ИК = 10,2062 * 24 = 244,9488 В

  E = VIt = Pt = 2500 * 2 * 60 * 60 = 1,8 * 10 ⁷ Дж

  ИЛИ E = VIt = 244,9488 * 10,2062 * 2 * 60 * 60 = 1,8 * 10 ⁷ Дж.

  1. Найдите напряжение на клеммах E ₁ и E ₂ , как показано на рисунке.

  Решение:

  Ток на рисунке

  \ (I = \ frac {9-3} {10} = 0,6A \)

  \ ({{V} _ {1}} = {{E} _ {1}} + I {{r} _ {1}} = 3 + 0,6 \ times 1 = 3,6 В; {{V} _ {2}} = {{E} _ {2}} — Я {{r} _ {2}} = 9-0,6 \ умножить на 2 = 7,8 В \)

  2. Рассчитайте установившийся ток в показанном резисторе 2 Вт .Внутренний Сопротивление батареи незначительно, а емкость конденсатора 0,2 м F.

  Решение:

  Сопротивление параллельной комбинации резисторов 2 Вт и 3 Вт равно

  .

  \ (\ frac {1} {R} = \ frac {1} {2} + \ frac {1} {3} = \ frac {5} {6} \ Rightarrow \, \, \, \, \, R = 1.2 \, \, \ Omega \)

  Это сопротивление последовательно с 2.

  No related posts.