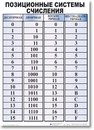
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
0 1 2 3 4 5 6 7 8 9 A B C D E F |
000 001 002 003 004 005 006 007 010 011 012 013 014 015 016 017 |
00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001110 00001111 |
| 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F |
020 021 022 023 024 025 026 027 030 031 032 034 035 036 037 |
00010000 00010001 00010010 00010011 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111 |
| Десятичное Dec |
Шестнадцатеричное Hex |
Восьмеричное Oct |
Двоичное Bin |
| 32 33 34 35 36 37 39 40 41 42 43 44 45 46 47 |
20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F |
040 041 042 043 044 045 046 047 050 051 052 053 054 055 056 057 |
00100000 00100001 00100011 00100100 00100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111 |
| 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
30 31 32 33 34 35 36 37 38 39 3B 3C 3D 3E 3F |
060 061 062 063 064 065 066 067 070 071 072 073 074 075 076 077 |
00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 |
| Десятичное Dec | Шестнадцатеричное Hex |
Восьмеричное Oct |
Двоичное Bin |
| 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F |
100 101 102 103 104 105 106 110 111 112 113 114 115 116 117 |
01000000 01000001 01000010 01000011 01000100 01000101 01000110 01000111 01001000 01001001 01001010 01001011 01001100 01001101 01001110 01001111 |
| 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 |
50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F |
120 121 122 123 124 125 126 127 130 131 132 133 134 135 136 137 |
01010000 01010001 01010010 01010011 01010100 01010101 01010110 01010111 01011001 01011010 01011011 01011100 01011101 01011110 01011111 |
| 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 |
60 61 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F |
140 142 143 144 145 146 147 150 151 152 153 154 155 156 157 |
01100000 01100001 01100010 01100011 01100100 01100101 01100110 01100111 01101000 01101001 01101010 01101011 01101100 01101101 01101110 01101111 |
| Десятичное Dec |
Шестнадцатеричное Hex |
Восьмеричное Oct |
Двоичное |
| 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 |
70 71 72 73 74 75 76 77 78 79 7A 7B 7C 7D 7E 7F |
160 161 162 163 164 165 166 167 170 171 172 173 174 176 177 |
01110000 01110001 01110010 01110011 01110100 01110101 01110110 01110111 01111000 01111001 01111010 01111011 01111100 01111101 01111110 01111111 |
| 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 |
80 81 82 83 85 86 87 88 89 8A 8B 8C 8D 8E 8F |
200 201 202 203 204 205 206 207 210 211 212 213 214 215 216 217 |
10000000 10000001 10000010 10000011 10000100 10000101 10000110 10000111 10001000 10001001 10001010 10001011 10001100 10001101 10001110 10001111 |
| 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 |
90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F |
220 221 222 223 224 225 226 227 230 231 232 233 234 235 236 237 |
10010000 10010001 10010010 10010011 10010100 10010101 10010110 10010111 10011000 10011001 10011010 10011011 10011100 10011101 10011110 10011111 |
| Десятичное Dec |
Шестнадцатеричное Hex |
Восьмеричное Oct |
Двоичное Bin |
| 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 |
A0 A1 A2 A3 A4 A5 A6 A7 A8 A9 AA AB AC AD AE AF |
240 241 242 243 244 245 246 247 250 251 252 253 254 255 256 257 |
10100000 10100001 10100010 10100011 10100100 10100101 10100110 10100111 10101000 10101001 10101010 10101011 10101100 10101101 10101110 10101111 |
| 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 |
B0 B1 B2 B3 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF |
260 261 262 263 264 265 266 267 270 271 272 273 274 275 276 277 |
10110000 10110001 10110010 10110011 10110100 10110101 10110110 10110111 10111000 10111001 10111010 10111011 10111100 10111101 10111110 10111111 |
| Десятичное Dec |
Шестнадцатеричное Hex |
Восьмеричное Oct |
Двоичное Bin |
| 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 |
C0 C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF |
300 301 302 303 304 305 306 307 310 311 312 313 314 315 316 317 |
11000000 11000001 11000010 11000011 11000100 11000101 11000110 11000111 11001000 11001001 11001010 11001011 11001100 11001101 11001110 11001111 |
| 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 |
D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF |
320 321 322 323 324 325 326 327 330 331 332 333 334 335 336 337 |
11010000 11010001 11010010 11010011 11010100 11010101 11010110 11010111 11011000 11011001 11011010 11011011 11011100 11011101 11011110 11011111 |
| 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 |
E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF |
340 341 342 343 344 345 346 347 350 351 352 353 354 355 356 357 |
11100000 11100001 11100010 11100011 11100100 11100101 11100110 11100111 11101000 11101001 11101010 11101011 11101100 11101101 11101110 11101111 |
| Десятичное Dec |
Шестнадцатеричное Hex |
Восьмеричное Oct |
Двоичное Bin |
| 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 |
F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF |
360 361 362 363 364 365 366 367 370 371 372 373 374 375 376 377 |
11110000 11110001 11110010 11110011 11110100 11110101 11110110 11110111 11111000 11111001 11111010 11111011 11111100 11111101 11111110 11111111 |
десятичная, двоичная, таблица перевода чисел
Система счисления – это способ записи чисел с помощью определенных знаков.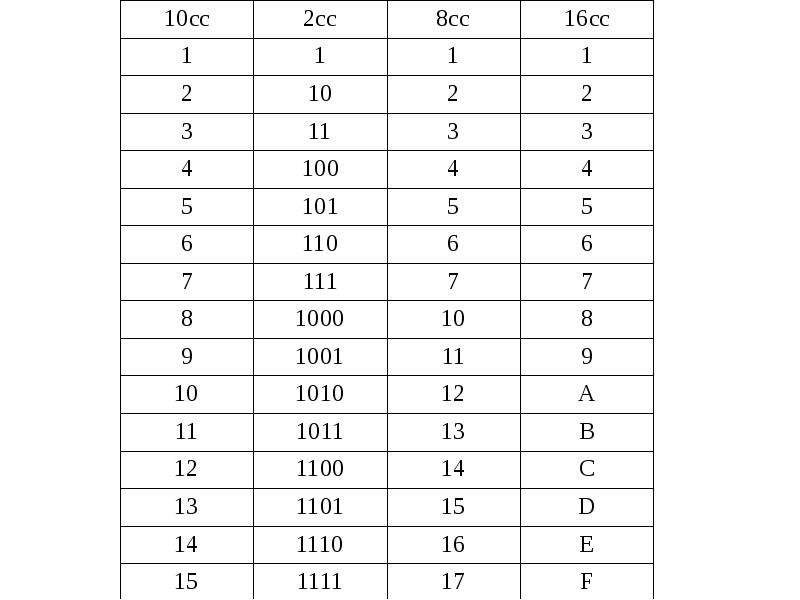
Давайте рассмотрим самые распространенные позиционные системы – в зависимости от местоположения (разряда) в записи числа один и тот же знак имеет различные значения.
Целое число “x” в позиционной системе счисления можно выразить следующим образом:
- b – основание системы
- ak – цифры числа (0 ≤ ak ≤ b-1)
- k – количество разрядов
Развернутая форма записи целого числа:
Двоичная система счисления: основание – 2
Используется в дискретной математике, информатике и программировании. Содержит только две цифры – 0 и 1. Число, записанное в данной системе, обозначается буквой B на конце (префикс).
Примеры:
- 101012 = 10101B = 1×24+0×23+1×22+0×21+1×20 = 16+4+1= 21
- 101112 = 10111B = 1×24+0×23+1×22+1×21+1×20 = 16+4+2+1= 23
- 1000112 = 100011B = 1×25+0×24+0×23+0×22+1×21+1×20 =32+2+1= 35
Восьмеричная система счисления: основание – 8
Для записи числа используются восемь цифр – от 0 до 7.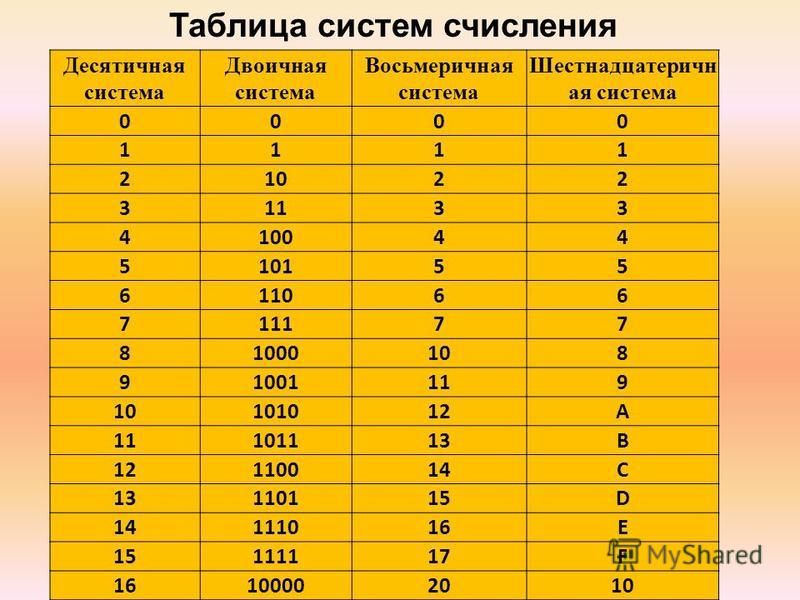
Примеры:
- 278 = 2×81+7×80 = 16+7 = 23
- 308 = 3×81+0×80 = 24
- 43078 = 4×83+3×82+0×81+7×80= 2247
Десятичная система счисления: основание -10
Самая распространенная система, которая используется повсеместно. Содержит цифры от 0 до 9.
Пример:
253810 = 2×103+5×102+3×101+8×100
Шестнадцатеричная система счисления: основание – 16
Используются цифры от 0 до 9, а также буквы от A до F. Для обозначения чисел служит префикс H. Система применяется в информатике и программировании.
Примеры:
- 2816 = 28H = 2×161+8×160 = 40
- 2F16 = 2FH = 2×161+15×160 = 47
- BC1216 = BC12H = 11×163+12×162+1×161+2×160= 48146
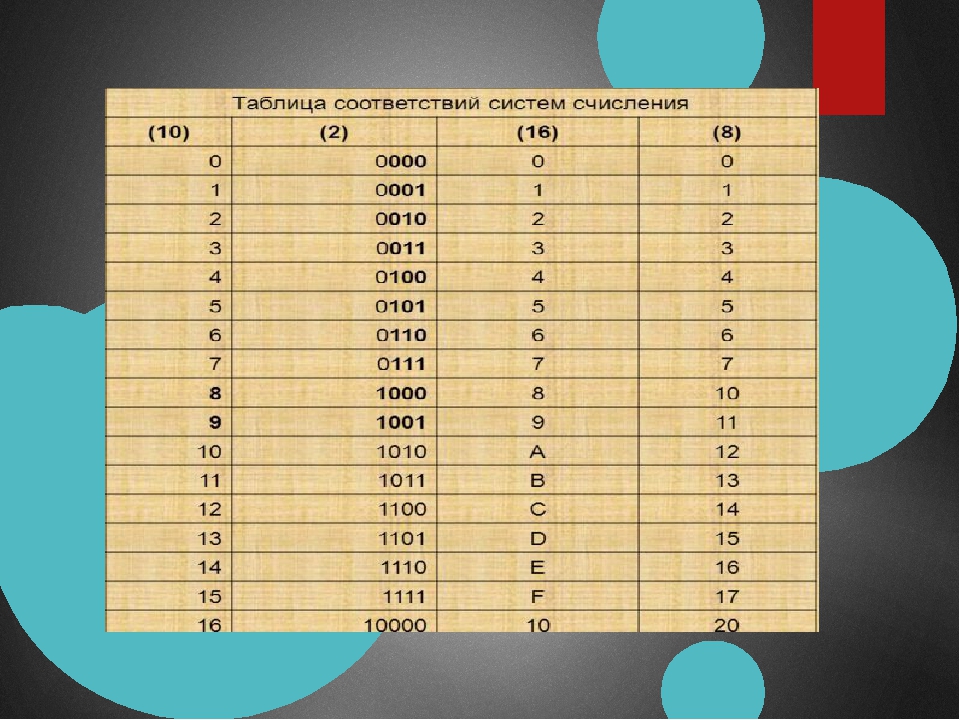
Таблица соответствия чисел систем счисления
система
система
система
система
Система счисления — презентация онлайн
ВСЕ2.
 План урока 3.
План урока 3.4.
5.
5.
6.
7.
8.
Систематизация теоретических знаний.
Графический диктант.
Кроссворд «Системы счисления. Основные
понятия».
Заполнение таблицы.
Решение задач.
Решение неравенств.
Загадка поэта.
Творческие задания.
Русская поговорка.
Рождение цветка.
Числовой лабиринт.
Рисуем по точкам.
Задание на дом.
1.
2.
Итоговая таблица
Конец
3. Систематизация теоретических знаний.
Учащиеся выполняют задания напроверку теоретического материала по
теме урока. Для выполнения данных
заданий используется дидактический
раздаточный материал (приложение 1).
Все задания (1 -3) данного этапа урока
выполняются каждым учащимся
индивидуально.
4. Задание 1. Графический диктант.
Если утверждение верно, ученик ставит знак _ , если неверно –знак /\ .
1.Система счисления – это способ записи чисел с помощью
заданного набора специальных знаков (цифр).
2.Информация, хранящаяся в компьютере, представлена в
троичной системе счисления.
3.В двоичной системе счисления 11 + 1 = 12.
4.Существует множество позиционных систем счисления, и они
отличаются друг от друга алфавитами.
5.В 16-ричной системе счисления символ F используется для
обозначения числа 15.
6.Римская система счисления – это позиционная система
счисления.
7.В двоичной системе счисления: один + один = один ноль.
Ответ
5. Задание 2. Кроссворд «Системы счисления. Основные понятия»
21
1
3
2
По горизонтали:
Система счисления, в которой вклад каждой цифры в величину числа
зависит от ее положения в последовательности цифр, изображающей число.
2.
Система счисления, которая используется для организации машинных
операций по преобразованию информации.
3.
Символы, при помощи которых записывается число.
По вертикали:
1.
Количество различных знаков или символов, используемых для изображения
цифр в данной системе.
2.
Совокупность различных цифр, используемых в позиционной системе
счисления для записи чисел.
1.
Ответы на кроссворд.
6. Задание 3. Заполнение таблицы.
Системасчисления
Десятичная
Основание
Алфавит
10
0;1;2;3;4;
5;6;7;8;9
Восьмиричная 8
0; 1
16
Подведение итогов
Ответ
7. Подведение итогов 1,2,3 заданий
После выполнения заданий 1-3 ученики проверяютработы друг друга и выставляют оценку по
следующим критериям:
1. Каждый правильный ответ во всех заданиях
оценивается одним баллом. Поэтому, максимальное
число баллов за правильно выполненное задание
«Графический диктант» — 7, за задание «Кроссворд» 5, за задание «Заполнение таблицы» — 3.
2. Набранные баллы суммируются. Оценка «отлично»
выставляется, если ученик набрал 14-15
баллов, «хорошо» — 13-11 баллов,
«удовлетворительно» — 8-10 баллов.
3. Работы передаются учителю, который заносит
результаты индивидуальной работы учащихся в
итоговую таблицу.
8. Решение задач.
На данном этапе урока учащиесявыполняют задания 4 и 5 в группах, не
используя при этом компьютер. Работа
каждой команды проверяется и
оценивается учителем. Учитель заносит
результаты в итоговую таблицу и
объявляет суммы баллов каждой
команды за выполненные задания.
9. Задание 4. Решение неравенств. Работа в группах. Каждая группа выполняет вариант задания, указанный учителем. (Задание
оценивается 2-мя баллами.)Поставьте вместо знака ? знак или =.
1.
2.
3.
4.
28510 ?
1111112
6С16 ?
5516 ?
11D16
? 11118
1010012
1258
Таблица перевода
Ответ
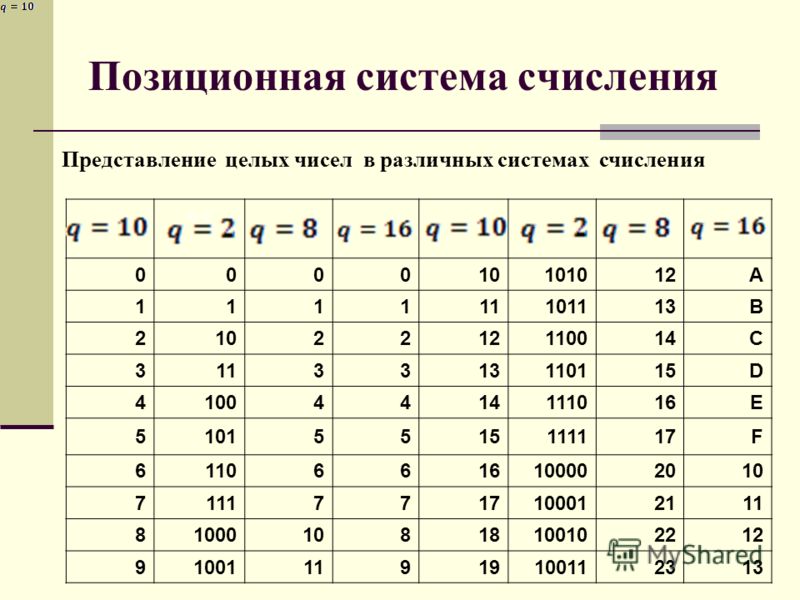
10. Таблица перевода чисел из одной системы счисления в другую
10-я 2-я8-я
16-я
10-я 2-я
8-я
16-я
0
0
0
0
10
1010
12
A
1
1
1
1
11
1011
13
B
2
10
2
2
12
1100
14
C
3
11
3
3
13
1101
15
D
4
100
4
4
14
1110
16
E
5
101
5
5
15
1111
17
F
6
110
6
6
16
10000
20
10
7
111
7
7
17
10001
21
11
8
1000
10
8
18
10010
22
12
9
1001
11
9
19
10011
23
13
11.
 Задание 5. Загадка поэта. (Работа в группах. Задание оценивается 2-мя баллами.) Прочитайте шуточное стихотворение А. Н. Старикова
Задание 5. Загадка поэта. (Работа в группах. Задание оценивается 2-мя баллами.) Прочитайте шуточное стихотворение А. Н. Старикова«Необыкновенная девочка» и попробуйте разгадать загадку поэта.
Для этого выпишите упомянутые в стихотворении числа и
переведите их в десятичную систему счисления.
Ей было тысяча сто лет,
Она в сто первый класс ходила,
В портфеле по сто книг носила.
Все это правда, а не бред. Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали. Когда, пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий. И десять темно-синих глаз
Рассматривали мир привычно …
Но станет все совсем обычным,
Когда поймете наш рассказ.
Ребята переводят числа в десятичную систему счисления и
читают стихотворение.
Ответ
12. Творческие задания.
Учащиеся выполняют задания (6 — 9) вгруппах, используя таблицу перевода чисел
из различных систем счисления в
десятичную и программу «Инженерный
калькулятор» на компьютере.
 Работа
Работакаждой команды проверяется и оценивается
учителем. Учитель заносит результаты в
итоговую таблицу и объявляет суммы
баллов каждой команды за выполненные
задания.
13. Задание 6. Русская поговорка. (Задание оценивается 5-ю баллами.)
Здесь зашифрована известная русская поговорка. Прочитайтеее, двигаясь с помощью двоичных цифр в определенной
последовательности.
Ответ
14. Задание 7. Рождение цветка. (Задание оценивается 5-ю баллами.)
Понаблюдаем за рождением цветка: сначала появился одинлисточек, затем второй … и вот распустился бутон. Постепенно
подрастая, цветок показывает нам некоторое двоичное число.
Если вы до конца проследите за ростом цветка, то узнаете,
сколько дней ему понадобилось, чтобы вырасти. Полученное
двоичное число перевести в десятичное.
Ответ
15. Задание 8. Числовой лабиринт. (Задание оценивается 10-ю баллами.)
Переведите числа, записанные в различных системахсчисления, в десятичную систему счисления; затем
полученные после вычисления числа замените буквами
русского алфавита, которые имеют соответствующие
порядковые номера; запишите полученное слово.
1316
1012
128
11002
100002
516
112
208
Алфавит
Ответ
16. АЛФАВИТ (к заданию 8).
АБВГДЕËЖЗИЙКЛМНОПРСТУФХ
Ц Ч Ш Щ Ъ ЫË Ь Э Ю Я
17. Задание 9. Рисуем по точкам.
Каждая группа учащихся получает карточку с двумя таблицами.Правильно выполненная работа по таблице 1 оценивается 10-ю
баллами, а по таблице 2 – 20-ю баллами. Ученики сами выбирают,
по какой таблице им работать.
В таблице 1 приведены номер точки и ее координаты, записанные
в двоичной системе счисления.
В таблице 2 приведены номер точки и ее координаты, записанные
в различных системах счисления.
Координаты некоторых точек нужно найти, выполнив
арифметические действия в указанных системах счисления.
Для каждой точки выполните перевод ее координат в десятичную
систему счисления и отметьте точку на координатной плоскости.
Правильно сделав перевод и соединив последовательно все
точки, вы получите некоторый рисунок.
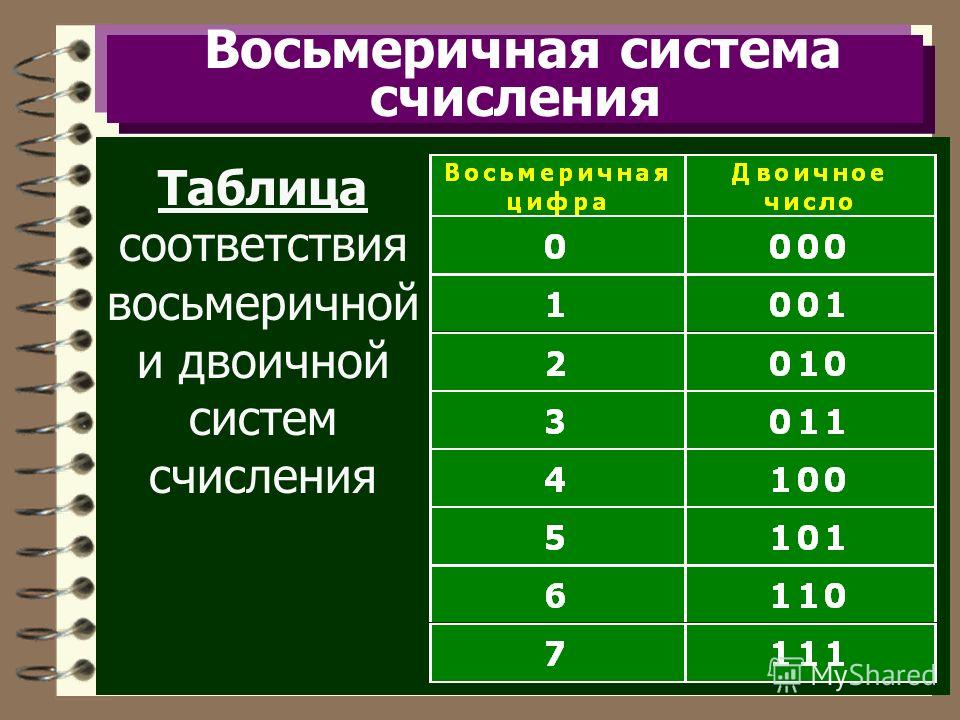 Рисунок можно
Рисунок можновыполнить в PAINT.
Координатная
плоскость
Таблица 1
Таблица 2
Ответ
18. Таблица 1.
№ точкиКоординаты точки
X
Y
1
1002
102
2
1012
1012
3
12
1012
4
112
10102
5
1002
10102
6
112
1102
7
1012
1102
8
1102
1012+1002
9
1112
10012
10
1102
1102
11
1002*102
1102
12
10002
1012
13
1102
1012
14
1012
102
19. Таблица 2.
№ точкиКоординаты точки
№
точки
Координаты точки
X
Y
12
48
100012-1012
102
13
102
78
112
12
14
2
1102
4
10002
12
15
112
1102
5
1012+1002
102
16
1112
1112
6
10012
1012
17
11002 -1002
68
7
10002
1002*102
18
10002
1002
8
112
716
19
1112
102
9
1012
816
20
416
28
10
112*112
138
21
112
34
11
10012
C16
22
38
1002
X
Y
1
102
1002
2
102
3
20.
 Результат выполнения задания 1 Графический диктант_ /\ /\ _ _ /\_
Результат выполнения задания 1 Графический диктант_ /\ /\ _ _ /\_21. Ответы на задание 2: кроссворд.
По горизонтали:1. Позиционная.
2. Двоичная. 3. Цифры.
По вертикали:
1. Основание.
2. Алфавит.
22. Ответ на задание 3. Правильно заполненная таблица имеет вид.
Системысчисления
Десятичная
Восьмеричная
Двоичная
Шестнадцатиричная
Алфавит
Основание
10
0;1;2;3;4;5;6;
7;8;9
8
0; 1; 2; 3; 4; 5; 6; 7
2
0; 1
16
0;1;2;3;4;5;6;7;8;9;
A;B;C;D;E;F
23. Ответы к заданию 4.
1. 28510 = 285102. 6310
3. 10810 > 4110
4. 8510 = 8510
24. Ответ к заданию 5.
Ей было 12 лет,Она в 5 класс ходила,
В портфеле по четыре книги носила.
Все это правда, а не бред. Она ловила каждый звук
Своими двумя ушами,
И две загорелые руки
Портфель и поводок держали.
Когда, пыля двумя ногами,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато четырехногий.
И двое темно-синих глаз
Рассматривали мир привычно …
Но станет все совсем обычным,
Когда поймете наш рассказ.
25. Ответ к заданию 6.
ЧТО ПОСЕЕШЬ,ТО И ПОЖНЕШЬ
26. Ответ к заданию 7.
100100012=145 дней27. Ответ к заданию 8.
ДИСКОВОД28. Ответ к заданию 9.
Выполнив правильно задания,ученики должны получить рисунок
цифры 4 для таблицы 1 и цифры
5 для таблицы 2.
29. Задание на дом.
Придумайте свой вариант рисунка накоординатной плоскости и составьте
для него таблицу координат,
представленных в различных системах
счисления.
30. Итоговая таблица
Перевод чисел в различные системы счисления в Excel
Изучим стандартные способы перевода чисел в различные системы счисления в Excel: двоичную, восьмеричную, десятичную и шестнадцатеричную.
Помимо повсеместно распространенной и всем нам хорошо известной десятичной системы счисления также используются и системы с другими основаниями (отличными от 10), например, двоичная, троичная, восьмеричная и т. д.
д.
Большинство из них имеют достаточно широкое применение практически во всех современных электронных устройствах, в программировании или компьютерной документации.
Системы счисления в Excel
В Excel есть возможность стандартными средствами переводить данные в четырех системах счисления:
Давайте подробно остановимся на основных вариантах преобразования данных.
Перевод числа из десятичной в двоичную систему в Excel
Для преобразования данных в двоичную запись в Excel существует стандартная функция ДЕС.В.ДВ (имя функции получается как первые буквы от слов ДЕСятичное В ДВоичное, дополнительно разделенное точками):
ДЕС.В.ДВ(число; [разрядность])
Преобразует десятичное число в двоичное.
- Число (обязательный аргумент) — десятичное целое число, которое требуется преобразовать;
- Разрядность (необязательный аргумент) — количество знаков для использования в записи.
 Данный аргумент необходим если нужно приписать к двоичной записи данных ведущие нули. К примеру, число 1101 с разрядностью 7 будет иметь вид 0001101.
Данный аргумент необходим если нужно приписать к двоичной записи данных ведущие нули. К примеру, число 1101 с разрядностью 7 будет иметь вид 0001101.
Обратите внимание, что Excel накладывает определенные ограничения на размер преобразуемых данных.
Двоичная запись не должна занимать более 10 знаков, поэтому десятичное число, соответственно, не должно быть больше 511 или меньше -512, иначе в качестве значения функция ДЕС.В.ДВ вернет ошибку.
Перевод числа из двоичной в десятичную систему в Excel
Для осуществления обратного перевода можно воспользоваться функцией ДВ.В.ДЕС:
ДВ.В.ДЕС(число)
Преобразует двоичное число в десятичное.
- Число (обязательный аргумент) — двоичное число, которое требуется преобразовать.
При этом разрядность в качестве аргумента функции для десятичной записи не используется.
Как и в случае с функцией ДЕС.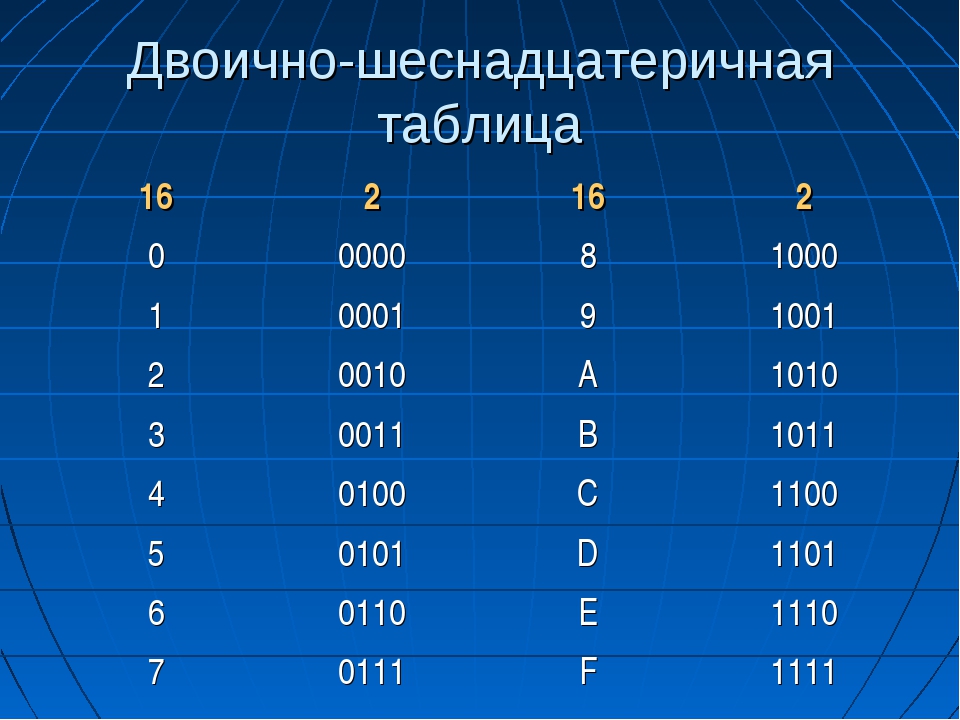 В.ДВ при использовании ДВ.В.ДЕС существует ограничение на размер преобразуемых данных — не более 10 знаков в записи, в ином случае функция вернет значение ошибки.
В.ДВ при использовании ДВ.В.ДЕС существует ограничение на размер преобразуемых данных — не более 10 знаков в записи, в ином случае функция вернет значение ошибки.
Перевод в других системах счисления
Для других систем счисления (восьмеричной, шестнадцатеричной) также определен набор стандартных формул.
Для удобства мы составили таблицу со схемой выбора формулы для преобразования данных (в левом столбце указано откуда переводим данные, в верхней строчке — куда переводим):
Как и в примерах выше имена функций образуются по достаточно простому правилу — берутся первые буквы от названий систем в которых преобразуются данные и разделяются точками (ВОСЬМеричное В ШЕСТНадцатеричное и пр.)
Арифметические операции с данными
Операции в Excel осуществляются в десятичной системе счисления, поэтому при применении арифметических действий (сложение, вычитание и т.д.) для преобразованных данных учитывайте, что конечный результат также будет записан в десятичной записи:
Чтобы избежать подобной проблемы, необходимо сначала перевести все данные в десятичный вид, произвести требуемые вычисления, а уже затем вновь преобразовать полученный результат в исходную систему счисления:
Удачи вам и до скорых встреч на страницах блога Tutorexcel. ru!
ru!
Поделиться с друзьями:
Поиск по сайту:
Системы счисления
Основные понятия систем счисления
Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: ; ; и т. д.
Различают два типа систем счисления:
позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.
Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно.
Любое целое число в позиционной системе можно записать в форме многочлена:
где S — основание системы счисления;
— цифры числа, записанного в данной системе счисления;
n — количество разрядов числа.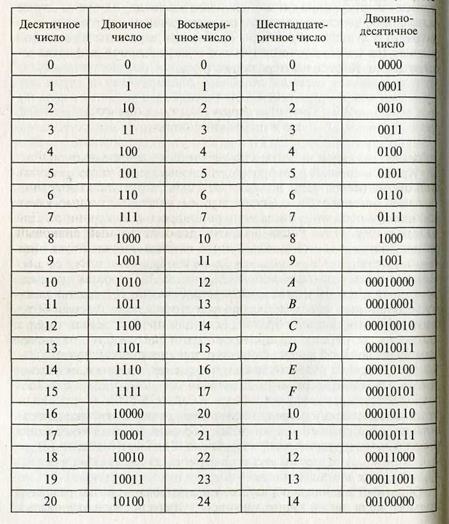
Пример. Число запишется в форме многочлена следующим образом:
Виды систем счисления
Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При этом буква I всегда означает единицу, буква — V пять, X — десять, L — пятьдесят, C — сто, D — пятьсот, M — тысячу и т.д. Например, число 264 записывается в виде CCLXIV. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.
Таблица 2. Запись чисел в римской системе счисления
|
1 |
2 |
3 |
4 |
5 |
|
I |
II |
III |
IV |
V |
|
6 |
7 |
8 |
9 |
10 |
|
VI |
VII |
VIII |
IX |
X |
|
11 |
13 |
18 |
19 |
22 |
|
XI |
XIII |
XVIII |
XIX |
XXII |
|
34 |
39 |
40 |
60 |
99 |
|
XXXIV |
XXXIX |
XL |
LX |
XCIX |
|
200 |
438 |
649 |
999 |
1207 |
|
CC |
CDXXXVIII |
DCXLIX |
CMXCIX |
MCCVII |
|
2045 |
3555 |
3678 |
3900 |
3999 |
|
MMXLV |
MMMDLV |
MMMDCLXXVIII |
MMMCM |
MMMCMXCIX |
Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами.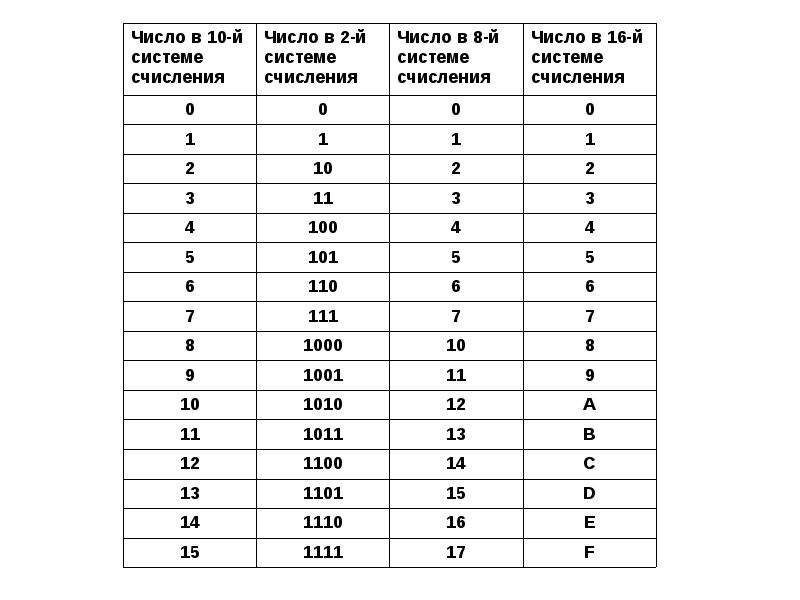 По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
Десятичня система счисления – в настоящее время наиболее известная и используемая. Изобретение десятичной системы счисления относится к главным достижениям человеческой мысли. Без нее вряд ли могла существовать, а тем более возникнуть современная техника. Причина, по которой десятичная система счисления стала общепринятой, вовсе не математическая. Люди привыкли считать в десятичной системе счисления, потому что у них по 10 пальцев на руках.
Древнее изображение десятичных цифр (рис. 1) не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.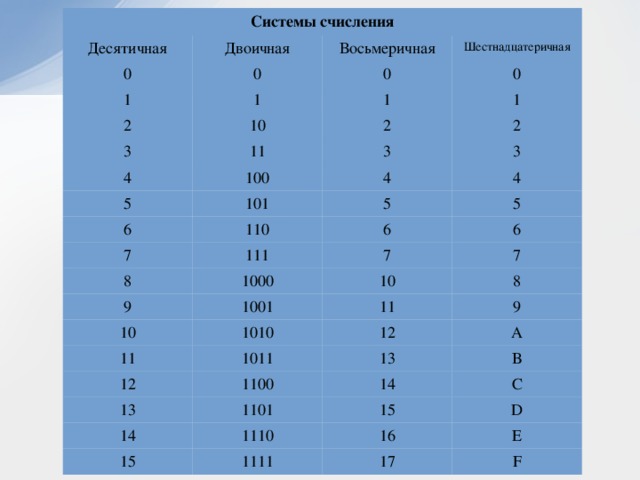
Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции. В ранних индийских рукописях, дошедших до нас, числа записывались в обратном порядке — наиболее значимая цифра ставилась справа. Но вскоре стало правилом располагать такую цифру с левой стороны. Особое значение придавалось нулевому символу, который вводился для позиционной системы обозначений. Индийская нумерация, включая нуль, дошла и до нашего времени. В Европе индусские приёмы десятичной арифметики получили распространение в начале ХIII в. благодаря работам итальянского математика Леонардо Пизанского (Фибоначчи). Европейцы заимствовали индийскую систему счисления у арабов, назвав ее арабской. Это исторически неправильное название удерживается и поныне.
Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.
В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1. Вопреки распространенному заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, еще в ХVII — ХIХ веках. Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу (1670 г.). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г. В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие.
Выбор двоичной системы для применения в вычислительной технике объясняется тем, что электронные элементы — триггеры, из которых состоят микросхемы ЭВМ, могут находиться только в двух рабочих состояниях.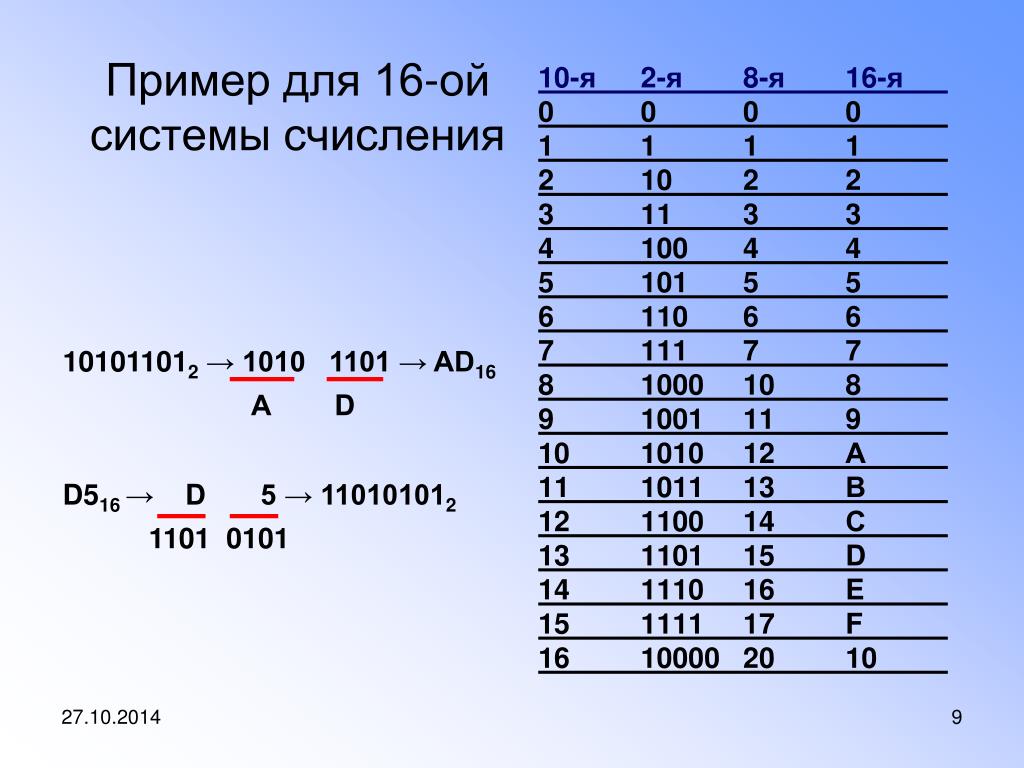
С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе. Телеграфист, используя только два символа этой азбуки — точки и тире, может передать практически любой текст.
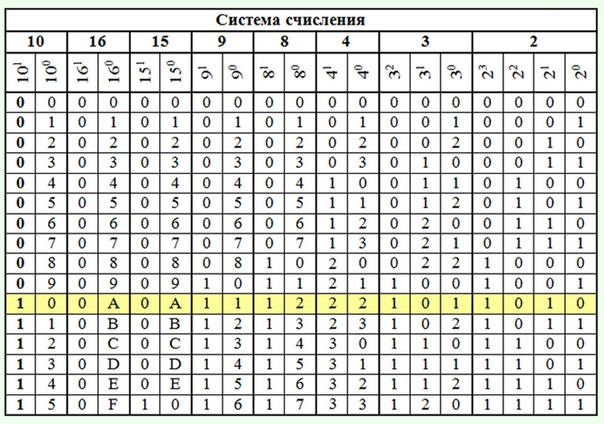
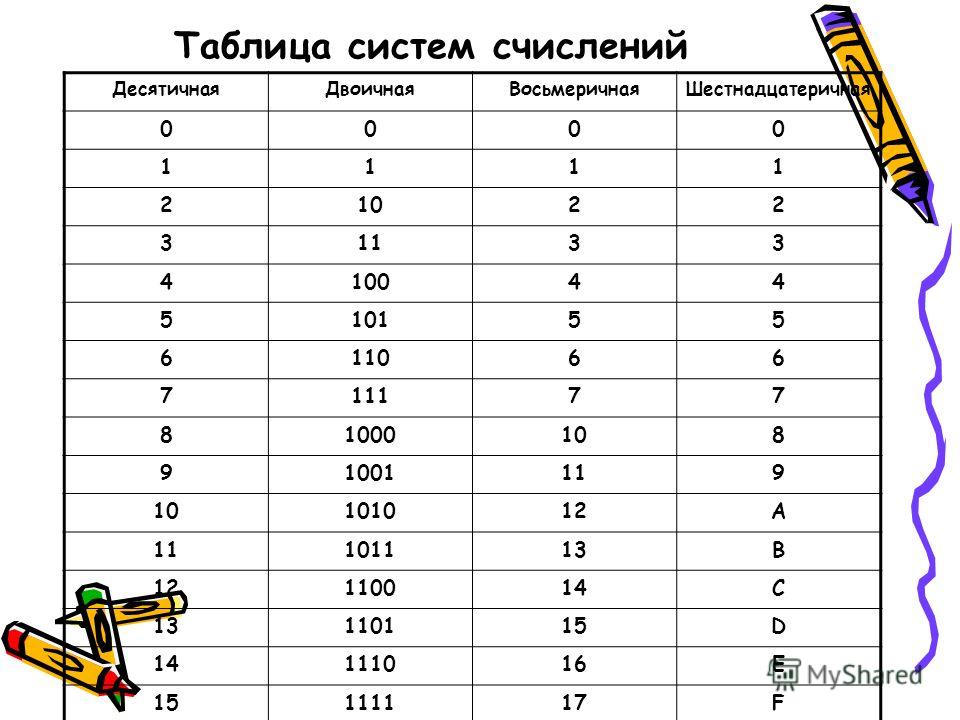
Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.
Ниже приведена таблица соответствия чисел, записанных в разных системах.
Таблица 3. Соответствие чисел, записанных в различных системах счисления
|
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
|
1 |
001 |
1 |
1 |
|
2 |
010 |
2 |
2 |
|
3 |
011 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
A |
|
11 |
1011 |
13 |
B |
|
12 |
1100 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
E |
|
15 |
1111 |
17 |
F |
|
16 |
10000 |
20 |
10 |
Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
Пример .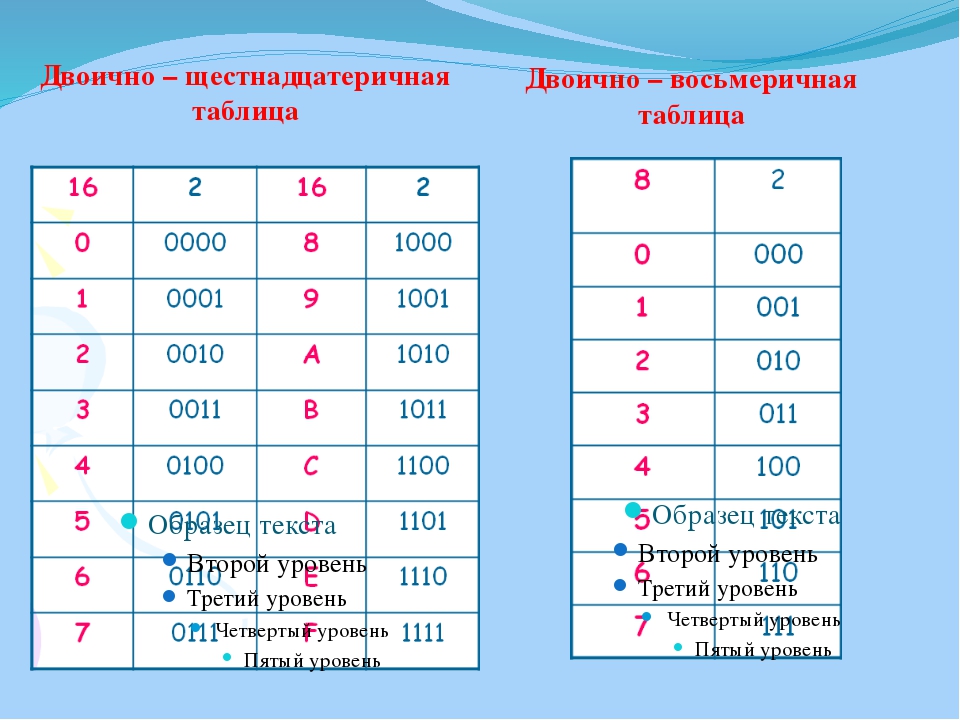 Число перевести в десятичную систему счисления.
Число перевести в десятичную систему счисления.
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
8 |
64 |
512 |
4096 |
32768 |
262144 |
Пример . Число перевести в десятичную систему счисления.
Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
16 |
256 |
4096 |
65536 |
1048576 |
16777216 |
Пример . Число перевести в десятичную систему счисления.
Число перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в двоичную систему счисления.
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в восьмеричную систему счисления.
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15.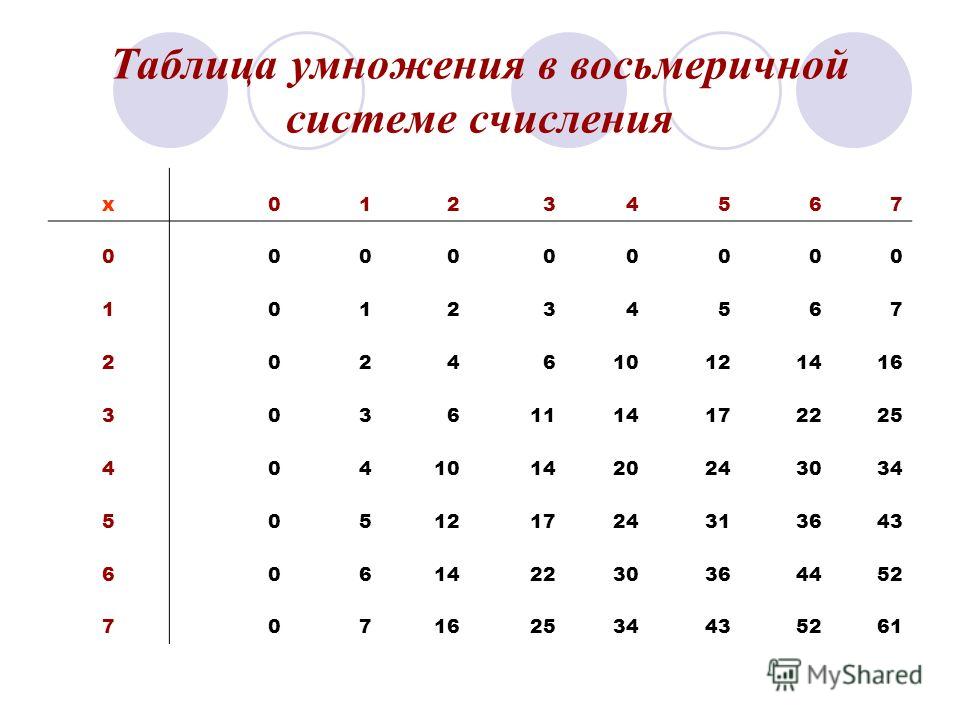 Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.
7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число перевести в восьмеричную систему счисления.
8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число перевести в шестнадцатеричную систему счисления.
9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.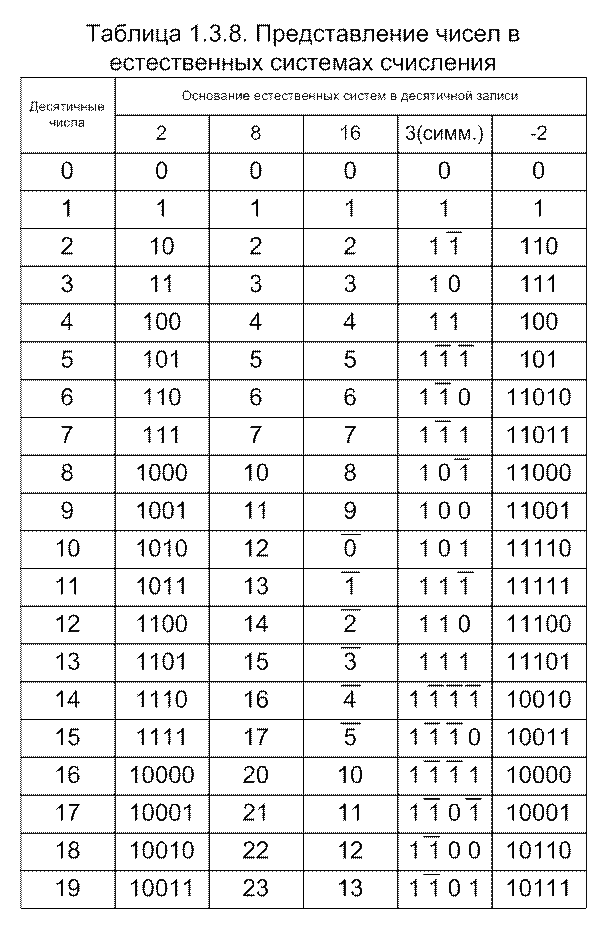
Пример. Число перевести в двоичную систему счисления.
10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Число перевести в двоичную систему счисления.
11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1. Число перевести в восьмеричную систему счисления.
Пример 2. Число перевести в шестнадцатеричную систему счисления.
Системы счисления. Таблица триад и тетрад. Быстрые способы перевода. | Самостоятельная учеба. САМ
Привет! Это второй урок базового курса по подготовке к ЕГЭ по информатике. На этом уроке мы с вами изучим метод триад и тетрад. А еще разберем полезности для двоичной СС.
С помощью метода триад и тетрад вы научитесь легко переводить числа между СС основанием которых является степень двойки. Это двоичная, четверичная, восьмеричная и шестнадцатиричная СС.
Для этого нам с вами нужно научится строить таблицу триад и тетрад. Сделать это очень просто.Таблица заполняется столбиками, поочередно.
Первый столбик — Выписываем 8 нулей, затем 8 единиц.
Второй столбик — уменьшаем количество 0 и 1 в два раза, т.е. записываем 4 нуля и 4 единицы, повторяем это дважды.
Третий столбик — еще в два раза уменьшаем нули и единицы. Чередуем 2 нуля и 2 единицы до конца столбика.
Четвертый столбик — чередуем нули и единицы.
Таким образом мы с вами построили таблицу тетрад(нужна для шестнадцатиричной СС), но внутри нее есть есть таблица триад(для восьмеричной СС). А внутри таблицы триад, есть таблица диад(для четверичной СС).
Для вашего удобства давайте запишем таблицу и выпишем значения для десятичной СС и шестнадцатиричной СС.
Как пользоваться этой таблицей?
Давайте представим что у нас с вами есть некоторое шестнадцатиричное число СE5. Нам нужно перевести это число в двоичную СС.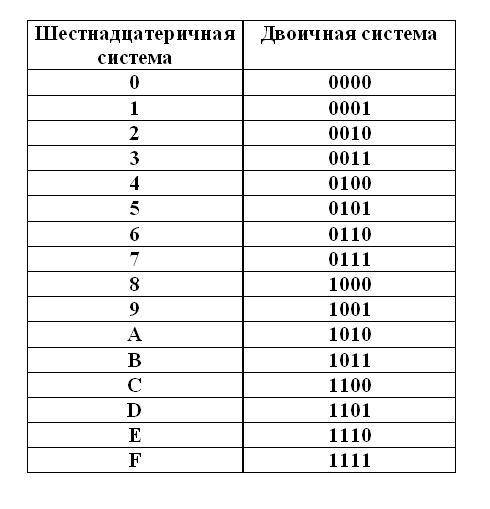 Мы могли бы воспользоваться тем что уже умеем, т.е. перевести это число в десятичную СС, а потом в двоичную. Но это долго, можно запутаться и т.д. Поэтому мы сделаем с вами все намного проще. Смотрим по таблице:
Мы могли бы воспользоваться тем что уже умеем, т.е. перевести это число в десятичную СС, а потом в двоичную. Но это долго, можно запутаться и т.д. Поэтому мы сделаем с вами все намного проще. Смотрим по таблице:
С = 1100, Е = 1110, 5 = 0101, отсюда следует что СЕ5 = 110011100101.
Каждая шестнадцатиричная цифра является тетрадой в двоичной системе счисления
Каждая восьмеричная цифра является триадой в двоичной системе счисления
Каждая четвертичная цифра является диадой в двоичной системе счисления
Рассмотрим пример когда у нас есть двоичное число
Число 1101001011 в двоичной СС, нам нужно перевести в восьмеричную СС. Нам нужно разделить это число на триады, начиная справа. Получится 1 101 002 011 и добавим к единице два незначащих нуля.
Я советую вам потренироваться самостоятельно переводить числа с помощью этой таблицы.
Задание 1
Число 10101000100111 в двоичной СС переведите в 4 СС, 8 СС, 16 СС
Задание 2
Переведите в двоичную систему счисления числа: 3256(8 СС), 1311(4 СС), FD91 (16 СС)
Если возникнут трудности и нужны будут ответы, то пишите коментарии, обязательно отвечу. 5 = 100000
5 = 100000
На этом наш второй урок базового курса по подготовке к ЕГЭ по информатике заканчивается. А тем кто еще не успел, я советую познакомится с демоверсией ЕГЭ по информатике 2021
Таблицы сложения и умножения
Таблицы сложения и умноженияТаблицы сложения и умножения в различных системах счисления
Двоичная система счисления
Троичная система счисления
| Таблица сложения | Таблица умножения | ||
| 1+1=2 | 1*1=1 | ||
| 1+2=10 | 2+2=11 | 1*2=2 | 2*2=11 |
Восьмеричная система счисления
| Таблица сложения | ||||||
| 1+1=2 | ||||||
| 1+2=3 | 2+2=4 | |||||
| 1+3=4 | 2+3=5 | 3+3=6 | ||||
| 1+4=5 | 2+4=6 | 3+4=7 | 4+4=10 | |||
| 1+5=6 | 2+5=7 | 3+5=10 | 4+5=11 | 5+5=12 | ||
| 1+6=7 | 2+6=10 | 3+6=11 | 4+6=12 | 5+6=13 | 6+6=14 | |
| 1+7=10 | 2+7=11 | 3+7=12 | 4+7=13 | 5+7=14 | 6+7=15 | 7+7=16 |
| Таблица умножения | ||||||
| 1*1=2 | ||||||
| 1*2=2 | 2*2=4 | |||||
| 1*3=3 | 2*3=6 | 3*3=11 | ||||
| 1*4=4 | 2*4=10 | 3*4=14 | 4*4=20 | |||
| 1*5=5 | 2*5=12 | 3*5=17 | 4*5=24 | 5*5=31 | ||
| 1*6=6 | 2*6=14 | 3*6=22 | 4*6=30 | 5*6=36 | 6*6=44 | |
| 1*7=7 | 2*7=16 | 3*7=25 | 4*7=34 | 5*7=43 | 6*7=52 | 7*7=61 |
Шестнадцатеричная система счисления
| Таблица сложения | ||||||||||||||
| 1+1=2 | ||||||||||||||
| 1+2=3 | 2+2=4 | |||||||||||||
| 1+3=4 | 2+3=5 | 3+3=6 | ||||||||||||
| 1+4=5 | 2+4=6 | 3+4=7 | 4+4=8 | |||||||||||
| 1+5=6 | 2+5=7 | 3+5=8 | 4+5=9 | 5+5=A | ||||||||||
| 1+6=7 | 2+6=8 | 3+6=9 | 4+6=A | 5+6=B | 6+6=C | |||||||||
| 1+7=8 | 2+7=9 | 3+7=A | 4+7=B | 5+7=C | 6+7=D | 7+7=E | ||||||||
| 1+8=9 | 2+8=A | 3+8=B | 4+8=C | 5+8=D | 6+8=E | 7+8=F | 8+8=10 | |||||||
| 1+9=A | 2+9=B | 3+9=C | 4+9=D | 5+9=E | 6+9=F | 7+9=10 | 8+9=11 | 9+9=12 | ||||||
| 1+A=B | 2+A=C | 3+A=D | 4+A=E | 5+A=F | 6+A=10 | 7+A=11 | 8+A=12 | 9+A=13 | A+A=14 | |||||
| 1+B=C | 2+B=D | 3+B=E | 4+B=F | 5+B=10 | 6+B=11 | 7+B=12 | 8+B=13 | 9+B=14 | A+B=15 | B+B=16 | ||||
| 1+C=D | 2+C=E | 3+C=F | 4+C=10 | 5+C=11 | 6+C=12 | 7+C=13 | 8+C=14 | 9+C=15 | A+C=16 | B+C=17 | C+C=18 | |||
| 1+D=E | 2+D=F | 3+D=10 | 4+D=11 | 5+D=12 | 6+D=13 | 7+D=14 | 8+D=15 | 9+D=16 | A+D=17 | B+D=18 | C+D=19 | D+D=1A | ||
| 1+E=F | 2+E=10 | 3+E=11 | 4+E=12 | 5+E=13 | 6+E=14 | 7+E=15 | 8+E=16 | 9+E=17 | A+E=18 | B+E=19 | C+E=1A | D+E=1B | E+E=1C | |
| 1+F=10 | 2+F=11 | 3+F=12 | 4+F=13 | 5+F=14 | 6+F=15 | 7+F=16 | 8+F=17 | 9+F=18 | A+F=19 | B+F=1A | C+F=1B | D+F=1C | E+F=1D | F+F=1E |
| Таблица умножения | ||||||||||||||
| 1*1=1 | ||||||||||||||
| 1*2=2 | 2*2=4 | |||||||||||||
| 1*3=3 | 2*3=6 | 3*3=9 | ||||||||||||
| 1*4=4 | 2*4=8 | 3*4=C | 4*4=10 | |||||||||||
| 1*5=5 | 2*5=A | 3*5=F | 4*5=14 | 5*5=19 | ||||||||||
| 1*6=6 | 2*6=C | 3*6=12 | 4*6=18 | 5*6=1E | 6*6=24 | |||||||||
| 1*7=7 | 2*7=E | 3*7=15 | 4*7=1C | 5*7=23 | 6*7=2A | 7*7=31 | ||||||||
| 1*8=8 | 2*8=10 | 3*8=18 | 4*8=20 | 5*8=28 | 6*8=30 | 7*8=38 | 8*8=40 | |||||||
| 1*9=9 | 2*9=12 | 3*9=1B | 4*9=24 | 5*9=2D | 6*9=36 | 7*9=3F | 8*9=48 | 9*9=51 | ||||||
| 1*A=A | 2*A=14 | 3*A=1E | 4*A=28 | 5*A=32 | 6*A=3C | 7*A=46 | 8*A=50 | 9*A=5A | A*A=64 | |||||
| 1*B=B | 2*B=16 | 3*B=21 | 4*B=2C | 5*B=37 | 6*B=42 | 7*B=4D | 8*B=58 | 9*B=63 | A*B=6E | B*B=79 | ||||
| 1*C=C | 2*C=18 | 3*C=24 | 4*C=30 | 5*C=3C | 6*C=48 | 7*C=54 | 8*C=60 | 9*C=6C | A*C=78 | B*C=84 | C*C=90 | |||
| 1*D=D | 2*D=1A | 3*D=27 | 4*D=34 | 5*D=41 | 6*D=4E | 7*D=5B | 8*D=68 | 9*D=75 | A*D=82 | B*D=8F | C*D=9C | D*D=A9 | ||
| 1*E=E | 2*E=1C | 3*E=2A | 4*E=38 | 5*E=46 | 6*E=54 | 7*E=62 | 8*E=70 | 9*E=7E | A*E=8C | B*E=9A | C*E=A8 | D*E=B6 | E*E=C4 | |
| 1*F=F | 2*F=1E | 3*F=2D | 4*F=3C | 5*F=4B | 6*F=5A | 7*F=69 | 8*F=78 | 9*F=87 | A*F=96 | B*F=A5 | C*F=B4 | D*F=C3 | E*F=D2 | F*F=E1 |
Задачи
Контрольная работа
К оглавлению
Системы счисления (двоичная, восьмеричная, десятичная, шестнадцатеричная)
Прежде чем мы сможем объяснить некоторые конкретные системы счисления, нам нужно знать, что такое система счисления.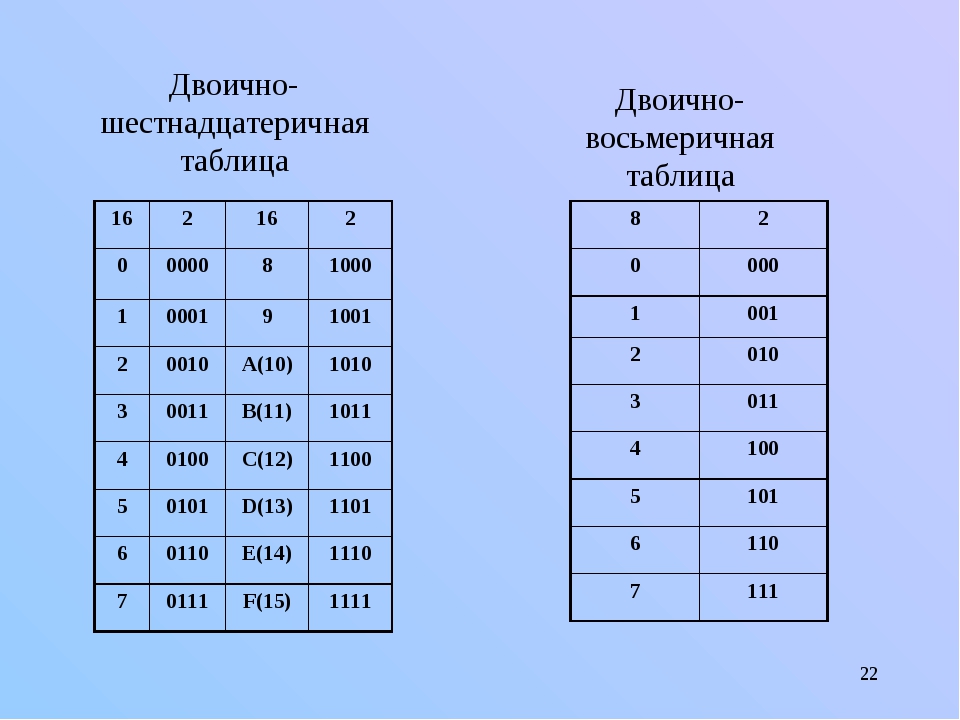 Проще говоря, система счисления — это способ представления чисел.
Проще говоря, система счисления — это способ представления чисел.
Мы можем классифицировать системы счисления по типу нотации в зависимости от того, используют ли они позиционную нотацию (также известную как нотация с числовыми значениями), и произвести дальнейшую категоризацию по основанию или основанию.
1. Непозиционная система счисления
Для объяснения непозиционной системы счисления мы возьмем в качестве примера римские цифры.В таблице ниже вы можете найти десятичные значения для основных символов римской системы счисления.
Вы можете спросить, есть ли какой-то узор для формирования всех остальных символов? Ответ положительный.
- Когда символ с меньшим значением помещается после символа, имеющего такое же или большее значение, значения складываются. Примеры приведены в таблице ниже.
- Когда символ с меньшим значением помещается перед символом, имеющим большее значение, меньшее значение вычитается из большего.
 Примеры приведены в таблице ниже.
Примеры приведены в таблице ниже.
2. Позиционная система счисления
Позиционная система счисления позволяет расширить исходный набор символов, чтобы их можно было использовать для представления любого произвольно большого (или маленького) значения. В разных системах число может быть представлено по-разному.
Например, два числа $ (2A) _ {16} $ и $ (52) _ {8} $ оба относятся к одному и тому же количеству $ (42) _ {10} $.
Система счисления, которую мы используем каждый день, называется десятичной системой счисления или системой счисления с основанием десять.Как видно из названия системы счисления, основание определяет всю систему.
Десятичная система счисления имеет основание 10, потому что мы работаем с 10 цифрами (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), и любое другое большее число может быть составлено из этих 10 цифр. Другими словами, мы используем тот же набор символов, но присваиваем символу другое значение в зависимости от его положения в числе.
Положение символа по отношению к другим символам в номере позволяет отдельному символу представлять большие (или меньшие) значения.{0}
долл. США$ = 3 \ cdot 100 + 4 \ cdot 10 + 2 \ cdot 1 $
$ = 300 + 40 + 2 $
В этом уроке мы не будем подробно объяснять десятичную систему, так как на странице, посвященной ей, есть много уроков.
Помимо десятичной системы счисления, существует множество других систем счисления. Мы упомянем только три из них, так как это наиболее часто используемые системы счисления после десятичной. Это: двоичная система счисления, восьмеричная система счисления и шестнадцатеричная система счисления. Мы дадим краткое объяснение каждой из них и узнаем, как преобразовывать числа из одной системы в другую.
2.1. Двоичная система счисления
Двоичная система счисления содержит две уникальные цифры (0 и 1). Таким образом, эта система является системой счисления с основанием 2. Относительные величины символов равны 0 <1. Символы в этой системе часто называются двоичными цифрами или просто битами. Двоичная система счисления — это позиционная система счисления. Позже мы увидим, что, например, $ 1010_ {2} \ neq 1100_ {2} $.
Символы в этой системе часто называются двоичными цифрами или просто битами. Двоичная система счисления — это позиционная система счисления. Позже мы увидим, что, например, $ 1010_ {2} \ neq 1100_ {2} $.
2.2. Восьмеричная система счисления
Восьмеричная система счисления содержит 8 уникальных цифр (0, 1, 2, 3, 4, 5, 6, 7).Таким образом, эта система является системой счисления с основанием 8. Относительные величины символов: 0 <1 <2 <3 <4 <5 <6 <7. Восьмеричная система счисления - еще один пример позиционной системы счисления.
2.3. Шестнадцатеричная система счисления
Шестнадцатеричная система счисления содержит 16 уникальных цифр. Поскольку в десятичной системе всего 10 арабских цифр, нам нужно использовать другие символы для представления оставшихся 6 цифр. Мы используем
буквенных знаков A – F, чтобы расширить систему до 16 цифр.16 цифр в шестнадцатеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Относительные величины символов равны
0. <1 <2 <3 <4 <5 <6 <7 <8 <9 Шестнадцатеричная система счисления также является позиционной системой счисления.
<1 <2 <3 <4 <5 <6 <7 <8 <9 Шестнадцатеричная система счисления также является позиционной системой счисления.
3. Базовая конверсия
Каждая цифра в числе «с основанием b» представляет степень $ b $. Итак, когда мы пишем число с основанием b, каждая цифра с основанием b умножается на соответствующую степень $ b $ в зависимости от позиции в числе.
3.1. Преобразование в десятичную систему
Преобразовать число из любой системы счисления в десятичную довольно просто. Мы знаем, что значение каждой цифры в числе основано на индивидуальном значении цифры и позиции цифры. Мы узнали это, когда узнали о десятичных числах. Используя это правило, мы можем преобразовать число из любой системы счисления в десятичное число.
Давайте посмотрим на общий пример:
Представьте, что у нас есть число $ d_ {2} d_ {1} d_ {0}.{-2} = 3 \ cdot 8 + 4 \ cdot 1 + 1 \ cdot \ displaystyle {\ frac {1} {8}} + 5 \ cdot \ displaystyle {\ frac {1} {64}} = 28. 203125 $
203125 $
3,2. Преобразование из десятичного числа в любое другое основание
Мы можем преобразовать десятичное число в любое другое, используя всего несколько простых шагов:
- Разделите десятичное число, которое нужно преобразовать, на значение нового основания.
- Запишите остаток в сторону
- Разделите частное предыдущего деления на новое основание.
- Запишите остаток в сторону
- Повторяйте шаги 3 и 4, пока частное на шаге 3 не станет равным нулю.
Требуемое число состоит из остатков, записываемых снизу вверх, слева направо.
Пример 2. Преобразует 25 в двоичное число.
Согласно правилу преобразования десятичных чисел в любое другое основание, необходимое число — $ 11001_ {2} $.
Пример 3. Преобразует 2489 в шестнадцатеричное число.
Помните, что эквивалент числа 11 в шестнадцатеричной системе счисления — буква B.
Согласно правилу преобразования десятичных чисел в любое другое основание, необходимое число — $ 9B9_ {16} $.
3.3. Эквивалентность различных систем счисления
4. Быстрые клавиши для переключения между основанием 2 и основанием 8 и между основанием 2 и основанием 16
Мы узнали, что можно преобразовать число из любого основания в число из любого основания, предварительно преобразовав его в десятичное. Например, если мы хотим преобразовать число с основанием 3 в число с основанием 7, сначала нужно преобразовать число с основанием 3 в десятичное, а затем преобразовать это десятичное число в число с основанием 7.
Мы можем использовать ту же процедуру для преобразования двоичного числа в восьмеричное или шестнадцатеричное, но есть несколько полезных сокращений, которые упростят этот процесс. Давайте посмотрим на следующий пример:
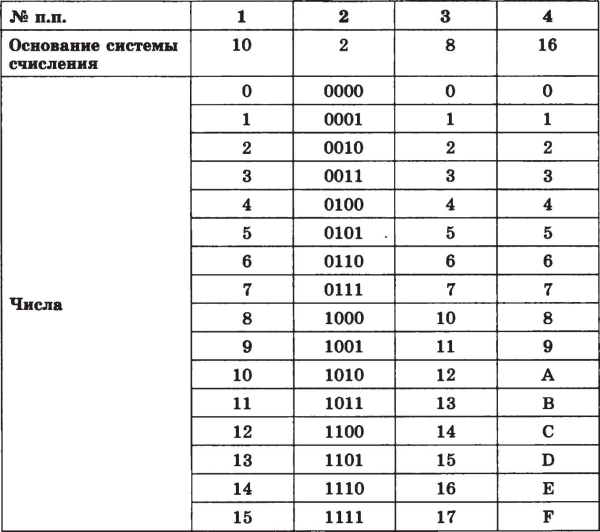
Пример 4. Преобразует $ 100100010101111_ {2} $ в шестнадцатеричное число.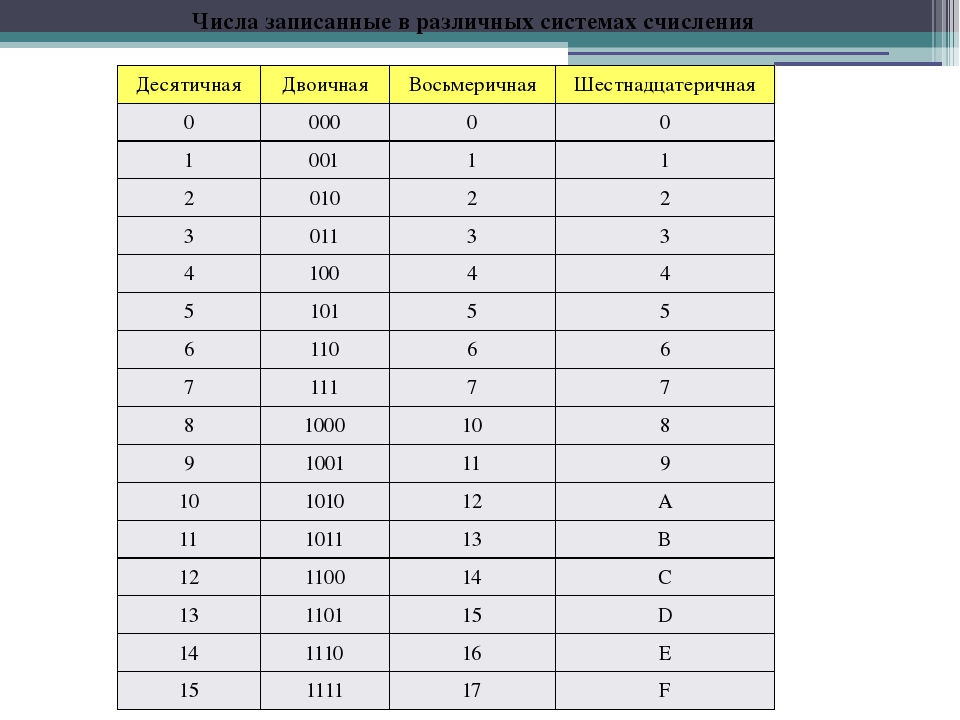
Чтобы преобразовать двоичное число в шестнадцатеричное, мы могли бы просто разбить двоичное число на группы из 4 цифр (начиная справа и добавляя ведущие нули, если цифры заканчиваются), а затем переинтерпретировать эти группы из 4 как перечисленные шестнадцатеричные значения. в таблице выше.При этом у нас есть:
$ 100100010101111_ {2} = 0100 1000 1010 1111 $
$ 0100 = 4 $, 1000 $ = 8 $, 1010 $ = A $, 1111 $ =
F $$ 100100010101111_ {2} = 48AF_ {16}
$Аналогично этому, чтобы преобразовать двоичное число в восьмеричное, мы могли бы просто разбить двоичное число на группы по 3 цифры, а остальная часть процедуры такая же, как преобразование двоичного числа в шестнадцатеричное число. Давайте превратим то же двоичное число в восьмеричное:
$ 100100010101111_ {2} = 100 100 010 101 111 $
100 долларов = 4
долларов010 долларов = 2
доллара101 доллар = 5
доллара111 долларов = 7
долларов$ 100100010101111_ {2} = 44257_ {8}
$ Обратить процесс еще проще. Предположим, мы хотим преобразовать $ FC7_ {16} $ в двоичную форму. Из таблицы мы можем прочитать двоичные значения для каждой цифры шестнадцатеричного числа:
Предположим, мы хотим преобразовать $ FC7_ {16} $ в двоичную форму. Из таблицы мы можем прочитать двоичные значения для каждой цифры шестнадцатеричного числа:
$ F_ {16} = 1111_ {2} $ C_ {16} = 1100_ {2} $ 7_ {16} = 0111_ {2}
$$ FC7_ {16} = 111111000111_ {2}
$Процесс преобразования восьмеричного числа в двоичную форму такой же.
Системы счисления — десятичная, двоичная, восьмеричная и шестнадцатеричная | Рукшани Атхапату | Coder’s Corner
Изображение предоставлено: PexelsДавайте рассмотрим несколько различных систем счисления, которые используются сегодня, и посмотрим, как с помощью трех простых правил мы можем построить любую систему счисления, какую захотим.
В математике «основание» или «основание» — это количество различных цифр или комбинаций цифр и букв, которые система счета использует для представления чисел. ~ Wiki ~
Например,
- Base 10 ( Decimal) — Представляет любое число, используя 10 цифр [0–9]
- Base 2 ( Binary ) — Представляет любое число, используя 2 цифры [0 –1]
- Base 8 ( Octal ) — представляет любое число, используя 8 цифр [0–7]
- Base 16 (Hexadecimal) — Представляет любое число, используя 10 цифр и 6 символов [0–9, A, B, C, D, E, F]
В любой из упомянутых выше систем счисления ноль очень важен как значение места.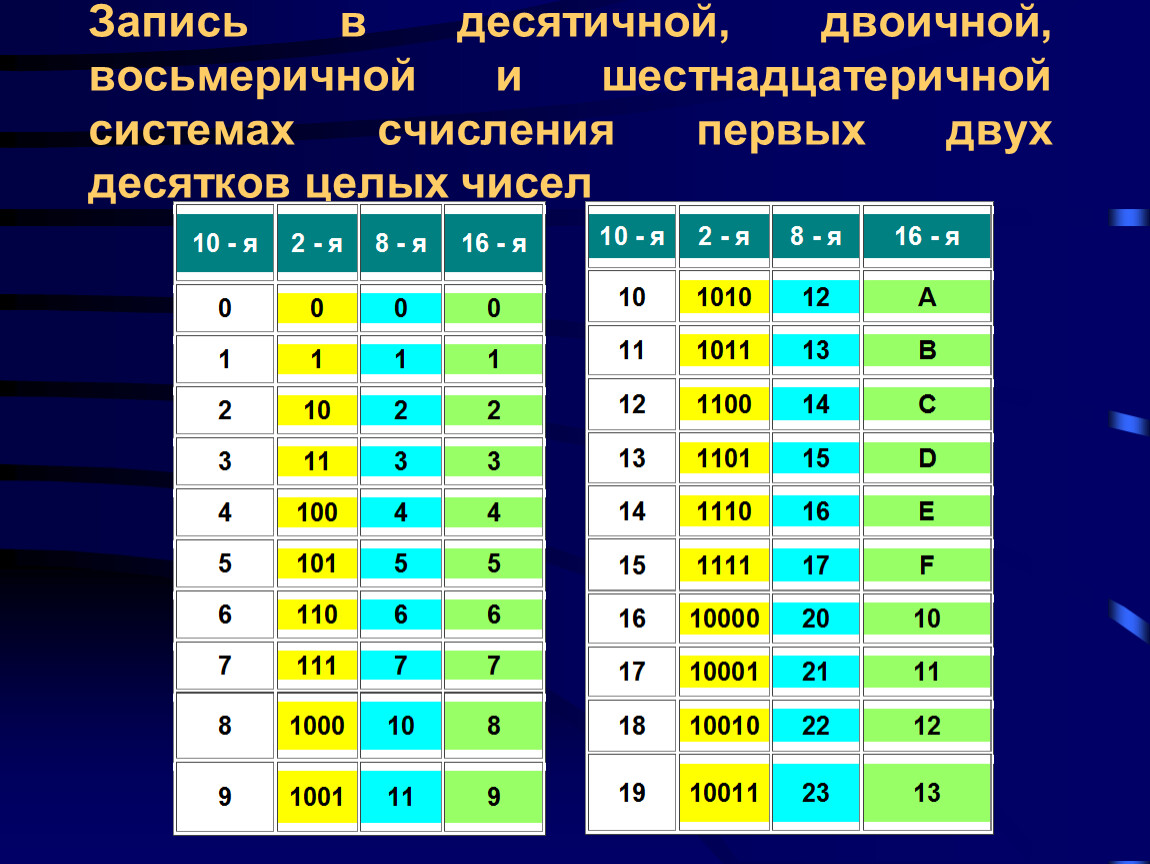 Возьмем число 1005. Как нам записать это число, чтобы знать, что в нем нет десятков и сотен? Мы не можем записать его как 15, потому что это другое число, а как записать миллион (1000000) или миллиард (1000000000) без нулей? Вы понимаете это значение?
Возьмем число 1005. Как нам записать это число, чтобы знать, что в нем нет десятков и сотен? Мы не можем записать его как 15, потому что это другое число, а как записать миллион (1000000) или миллиард (1000000000) без нулей? Вы понимаете это значение?
Сначала мы увидим, как построена десятичная система счисления, а затем мы будем использовать те же правила и для других систем счисления.
Мы все умеем писать числа до 9, не так ли? Что тогда? Что ж, это действительно просто.Когда вы израсходуете все свои символы, вы сделаете
- , вы добавите еще одну цифру слева и сделаете правую цифру 0.
- Затем снова поднимитесь до, пока не закончите все символы с правой стороны. и когда вы нажмете последний символ, увеличьте цифру слева на 1.
- Когда вы израсходовали все символы как на правой, так и на левой цифре, сделайте оба из них 0 и добавьте еще 1 слева, и это продолжится. и тому подобное.
Если вы используете 3 приведенных выше правила в десятичной системе,
- Запишите числа 0–9.
- Как только вы дойдете до 9, сделайте крайнюю правую цифру 0 и прибавьте 1 к левой, что означает 10.
- Затем на правой цифре мы продвинемся до 9, а когда мы достигнем 19, мы используем 0 на правой цифре и добавим 1 к слева, поэтому мы получаем 20.
- Точно так же, когда мы достигаем 99, мы используем 0 в местах обеих этих цифр и добавляем 1 слева, что дает нам 100.
Итак, вы видите, когда у нас есть десять разных символов, когда мы добавляем цифры в левую часть числа, каждая позиция будет стоить в 10 раз больше, чем предыдущая.
Возьмем ту же десятичную систему счисления. На самом деле есть только два правила.
- У вас есть символ для представления количества [0–9]
- Затем значение цифры в зависимости от ее положения — давайте это немного проясним.
Возьмем однозначное число «8». Это просто означает 8, другими словами, это именно то, что, как написано, представляет. А как насчет 24? В случае двух цифр правая цифра говорит то, что она означает, а левая цифра означает в десять раз больше, чем она говорит.То есть 4 равно 4, 2 равно 20. Всего получается 24.
Если мы возьмем трехзначное число, крайняя правая цифра означает то, что оно говорит, средняя цифра в десять раз больше того, что она говорит, а крайняя левая цифра в 100 раз больше того, что она говорит. Просто, если мы возьмем число 546, это означает 6 + (10 * 4) + (5 * 100) = 546.
В двоичном формате у нас есть только две цифры для представления числа, 0 и 1, и у нас уже закончились символы. . Так что же нам делать? Давайте применим те же правила, которые мы использовали для десятичной системы счисления.
Делаем правую цифру 0 и прибавляем 1 к левой, то есть наше следующее число — «10».Затем мы продвигаемся вверх, пока не израсходовали все символы с правой стороны. Итак, следующее число в строке — 11.
После «11» мы ставим 0 в обоих этих местах и прибавляем 1 слева, и получаем 100.
Затем 101, 110, 111, затем 1000…
Эта двоичная система счисления основана на двух цифрах, и каждая позиция стоит в два раза больше, чем предыдущая.
Чтение двоичного числа почти аналогично чтению десятичного числа. Правая цифра означает, что это означает, следующая означает два раза предыдущую, после этого 4 раза и т.д.
Итак, 101 означает 5 в десятичной системе счисления.
Эти же правила применяются также к восьмеричной и шестнадцатеричной системам счисления. В восьмеричном формате у нас есть только 8 цифр для представления чисел, поэтому, как только мы дойдем до 7, следующим числом будет 10, а в шестнадцатеричном формате у нас будет 10 цифр и 6 букв для представления чисел. В этом случае, когда мы дойдем до 9, следующая цифра будет представлена буквой «А». Следующая буква «Б». Точно так же мы поднимаемся до буквы «F», а после «F» идет «10».
Я просто перечислю несколько чисел в этих 4 различных системах счисления и посмотрю, сможете ли вы применить правила, которые мы обсуждали выше, чтобы получить следующее число.
Чтобы понять, как компьютеры представляют положительные и отрицательные числа, прочтите это, а другие сведения о шестнадцатеричном формате можно найти здесь.
Список литературы
№ 2535: Временные таблицы
Компьютеры считают, что проще всего работать с двумя цифрами — ноль и единица. Эти двоичные цифры называются битами. Чтобы записать возраст Вселенной, требуется тридцать четыре бита. Это больше, чем одиннадцать в нашей десятичной системе, но в компьютере есть гораздо более простые таблицы умножения: ноль умножить на ноль, ноль умножить на единицу и один умножить на единицу.Это оно!
Широко распространено мнение, что мы используем десять цифр, потому что именно столько у нас пальцев. Это более чем необходимо для хорошей работоспособной системы счисления. Я бы предпочел восемь. Но я просто рад, что мы не родились с двадцатью пальцами. Я бы никогда не просмотрел свои таблицы умножения.
Я Энди Бойд из Хьюстонского университета, где интересовался тем, как работают изобретательные умы.
[аудио: тройка — магическое число]
(Музыкальная тема)Для связанных эпизодов см. БОЛЬШИЕ ЧИСЛА и НОЛЬ, среди многих других.
Системы счисления, обсуждаемые в этом эпизоде, известны как позиционные системы . Позиционные системы счисления работают, выбирая по основанию , которое равно количеству цифр в системе. Положение цифры в цепочке цифр соответствует степени основания.
Например, в нашей стандартной десятичной системе счисления мы имеем
52,907 (базовая десятка) =
5 x 10 4 + 2 x 10 3 + 9 x 10 2 + 0 x 10 1 + 7 x 10 0 .
В восьмерке у нас
147,253 (базовая восьмерка) =
1 x 8 5 + 4 x 8 4 + 7 x 8 3 + 2 x 8 2 + 5 x 8 1 + 3 x 8 0 .
Обратите внимание, что оба этих числа, 52 907 (десять по основанию) и 147 253 (восемь по основанию), представляют одно и то же количество; они просто выражаются в двух разных системах счисления.
Таблицы умножениядля двоичной (основание два), четвертичной (основание четыре), восьмеричной (основание восемь) и десятичной (основание десять) систем счисления показаны ниже. Обратите внимание, что необходимо запомнить лишь немногим более половины значений в этих таблицах, поскольку изменение порядка умножения на обратное не меняет результата (например, 6 x 8 = 8 x 6).
Следует отметить, что однозначные таблицы сложения , подобные таблицам умножения, также необходимы для освоения базовой арифметики, но не обсуждаются в этом эпизоде.Большинство людей осваивают эти таблицы без особых проблем.
Дополнительную информацию о позиционных системах счисления см., Например, на http://en.wikipedia.org/wiki/Positional_notation.
Изображения таблиц умножения были вырезаны с веб-сайта http://www.cut-the-knot.org/blue/SysTable.shtml.
Двигатели нашей изобретательности Авторские права © 1988-2009, Джон Х.Линхард.
систем представления чисел — десятичных, двоичных, восьмеричных и шестнадцатеричных — x-engineer.org
В этой статье мы обсудим различные системы представления чисел, где они используются и почему они полезны. Вкратце мы рассмотрим представление чисел в десятичном формате , в двоичном формате , в восьмеричном и шестнадцатеричном формате .
Десятичное (основание 10)
Наиболее распространенной системой представления чисел является десятичная система .Все используют это. Это настолько распространено, что большинство людей не может поверить в то, что это единственное. Его используют в финансах, инженерии и биологии почти везде, где мы видим и используем числа.
Если кто-то просит вас думать над числом, вы наверняка будете думать над десятичным числом. Если вы думаете в двоичном или шестнадцатеричном формате, у вас должна быть крайняя страсть к арифметике или программному обеспечению / программированию.
Как следует из названия, десятичная система счисления использует 10 символов / знаков.В латинском языке 10 — это «decem», поэтому десятичное число может быть связано с латинским словом.
| Десятичные символы | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 можно увидеть 9 10 символов от 0 до 9 . С помощью этих символов мы можем построить все числа в десятичной системе. Все числа в десятичной системе могут быть составлены с помощью вышеупомянутых символов ( |
| N | … | 100000 | 10000 | 1000 | 100 | 10 | 1 | ||
В приведенном ниже примере десятичное число 670 делится на десятичное число. с номерами от 0 до 9 . Это просто, чтобы показать, что любое число в десятичной системе может быть разложено на сумму членов, составленных из произведения степени 10 и символов 0… 9 .0 \\
& = 60000 & + 7000 & + 0 & + 40 & + 9
\ end {split} \ end {формула *} \]
Тот же метод будет применен к двоичному файлу, восьмеричная и шестнадцатеричная системы, являющиеся по сути способом преобразования числа из десятичной системы в другой формат (основание).
Мы можем иметь в виду следующие характеристики десятичной системы счисления:
- использует 10 символов
- можно разложить на множители, содержащие степени 10
- это наиболее распространенная система представления чисел
Двоичная (основание 2)
Давайте теперь перейдем на сторону компьютерных фанатов.
Другая система представления чисел — это двоичная . Как следует из названия и по аналогии с десятичной системой, мы можем сказать, что двоичная система использует только 2 символа / символа:
В двоичном представлении мы используем только 0 (нули) и 1 (единицы) для представления числа.
Двоичная система используется везде, где требуется хранить информацию в электронном формате. Все компьютеры, которые вы знаете, интеллектуальные устройства, все, что связано с электроникой и микроконтроллерами, используют двоичную систему.
В электронике (цифровой) все операции выполняются с использованием двух уровней напряжения: высокого и низкого. Каждому уровню напряжения присваивается значение / символ: ВЫСОКИЙ для 1 и НИЗКИЙ для 0. Для микроконтроллера, на который подается напряжение + 5 В, значение 1 (высокое) будет представлено как +5 В, а значение 0 (низкое). ) на 0 В.
Примерно можно сказать, что используется двоичная система, потому что она может быть переведена в электронный сигнал.
Все десятичные числа, которые мы можем придумать, можно представить в виде двоичных символов.0 \\
& = 128 & + 0 & + 0 & + 16 & + 0 & + 4 & + 0 & + 1
\ end {split} \ end {формула *} \]
Как вы можете см. десятичное число 149 представлено в двоичной системе серией нулей и единиц ( 10010101 ). Обычно, чтобы различать десятичное и двоичное число, мы должны указать основание, на которое мы ссылаемся. Основание описывается как нижний индекс после последнего символа числа
Пример:
| Десятичное (основание 10) | Двоичное (основание 2) |
| \ [149_ {10} \] | \ [10010101_ {2} \] |
Указав основание числа, мы исключаем вероятность путаницы, потому что одно и то же представление (например.грамм. 11) может означать разные вещи для разных баз.
Другой способ избежать путаницы — использовать специальную нотацию (префикс) для двоичных чисел. Это потому, что 1100 может представлять одиннадцать сотен в десятичной системе или десятичные двенадцать в двоичной системе. Поэтому, если нужно указать двоичное число, мы используем префикс 0b . Пример: 0b1100 .
Вкратце характеристики двоичной системы:
- в ней используются 2 символа
- можно разложить на множители, содержащие степени 2
- используется в компьютерах, микроконтроллерах
Восьмеричное (основание 8)
Все числа в восьмеричной системе представлены с использованием 8 символов / знаков, от 0 до 7 .Причины использования восьмеричной системы вместо десятичной могут быть разными. Один из них заключается в том, что вместо того, чтобы использовать пальцы для счета, мы используем промежутки между пальцами.
У людей есть 4 промежутка между пальцами одной руки; Всего у нас будет 8 мест для обеих рук. В этом случае имеет смысл использовать восьмеричную систему представления чисел вместо десятичной. Недостатком является то, что для более высоких чисел потребуется больше символов по сравнению с десятичным.
Чтобы преобразовать десятичное представленное число в восьмеричную систему, мы разбиваем его на члены, содержащие степень 8:
| \ [8 ^ k \] | … | \ [8 ^ 5 \] | \ [8 ^ 4 \] | \ [8 ^ 3 \] | \ [8 ^ 2 \] | \ [8 ^ 1 \] | \ [8 ^ 0 \] |
| N | … | 32768 | 4096 | 512 | 64 | 8 | 1 |
В качестве примера мы собираемся представить десятичное число 67049 в восьмеричной системе счисления:
| \ [8 ^ 5 \] | \ [8 ^ 4 \] | \ [8 ^ 3 \] | \ [8 ^ 2 \] | \ [8 ^ 1 \] | \ [8 ^ 0 \] |
| 2 | 0 | 2 | 7 | 5 | 1 |
| \ [\ begin {уравнение *} \ begin {split} 67049 & = 2 \ cdot 8 ^ 5 & + 0 \ cdot 8 ^ 4 & + 2 \ cdot 8 ^ 3 & + 7 \ cdot 8 ^ 2 & + 5 \ cdot 8 ^ 1 & + 1 \ cdot 8 ^ 0 \\ & = 65535 & + 0 & + 1024 & + 448 & + 40 & + 1 \ end {split} \ end {формула *} \] | |||||
Шестнадцатеричное (основание 16)
Шестнадцатеричная система представления чисел использует 16 символов / знаков для определения чисел.Он используется в информатике в основном потому, что может представлять большие десятичные числа с меньшим количеством символов.
| Шестнадцатеричные символы | |||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9039 C D | E | F | ||||
По сравнению с десятичной системой, здесь также используются цифровые символы от 0 до 9.0 \\
& = 65536 & + 0 & + 1280 & + 224 & + 9
\ end {split} \ end {формула *} \]
Представление десятичного числа 67049 в шестнадцатеричном формате это 105E9 . Как и в случае с двоичной системой, обычной практикой является использование префикса « 0x » для отличия от десятичной системы счисления. Пример: 0x105E9 .
Кратко характеристики системы представления шестнадцатеричных чисел:
- в ней используются 16 символов
- можно разложить на множители, содержащие степени 16
- Используется в компьютерах, микроконтроллерах
В таблице ниже приведены характеристики вышеупомянутые системы представления чисел.
| Система | Количество символов | Символы | Префикс | Пример |
| Десятичный | 10 | , 2394 5, 6, 7, 8, 9 | Нет | 147 |
| Двоичный | 2 | 0, 1 | 0b | 0b10010011 |
| Шестнадцатеричный | Шестнадцатеричный | 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F | 0x | 0x93 |
Системы представления восьмеричных и шестнадцатеричных чисел связаны с компьютерной системой , в основном с процессорами и микроконтроллерами.Например, если микропроцессор использует 8-битные данные, восьмеричная система подходит для интерфейса данных. Если микропроцессор использует 16 бит, то для представления данных подходит шестнадцатеричная система.
Двоичные, восьмеричные и шестнадцатеричные числа
| Динарный (основание 10) | Шестнадцатеричное (основание 16) | Восьмеричное (основание 8) | Двоичное (основание 2) | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 0 1 2 3 4 5 6 7 8 9 A B C D E F | 000 001 002 003 004 005 006 007 010 011 012 013 014 015 016 017 | 00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 00001111 |
|---|---|---|---|---|
| 16 1 17 18 9 20 21 22 23 24 25 26 27 28 29 30 31 | 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F | 020 021 022 023 024 025 026 027 030 031 032 033 034 035 036 037 | 0001010000 900 00035 00035 000 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111 | |
| 32 33 34 35 36 39 900 35 39 35 43 44 45 46 47 | 20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F 9039 1 | 040 041 042 043 044 045 046 047 050 051 052 053 054 055 056 057 | 00100000 00100001 00100010 0035 0010 011 035 00100100100100 | |
| 48 49 50 51 52 53 54 55 56 57 60 59 61 57 60 59 63 | 30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F | 060 061 062 063 064 065 066 067 070 071 072 073 074 075 076 077 | 00110000 00110001 00110010 00110011 00110100 00110101 9003 5 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 | |
| 64 65 66 67 68 69 70 71 71 77 78 79 | 40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F | 100 101 102 103 104 105 106 107 110 111 112 113 114 115 116 117 | 01000000 01000001 01000010 01000011 01000100 01000101 01000110 01000111 01001000 0100101 1000111 01001000 01001001 1000111 01001000 01001001 100035 01001035 01001100 01001110 01001111 | |
| 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 | 50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F | 120 121 122 123 124 125 126 127 130 131 132 133 134 135 136 137 | 01010000 01010001 01010010 01010011 01010100 01010101 01010110 01010110035 01010110035 900 01011011 01011100 01011101 01011110 01011111 | |
| 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 | 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F | 140 141 142 143 14 4 145 146 147 150 151 152 153 154 155 156 157 | 01100000 01100001 01100010 01100011 01100100 01100101 01100110 011010111 900 011010111 900 01101101 01101110 01101111 | |
| 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 | 70 71 72 73 74 75 76 77 78 79 7A 7B 7C 7D 7E 7F | 160 161 162 163 164 165 166 167 170 171 172 173 174 175 176 177 | 01110000 01110001 01110010 01110011 01110100 01110101 01110110 01110111 0111 1000 01111001 01111010 01111011 01111100 01111101 01111110 01111111 | |
| 128 129 130 131 132 143 143 134 135 136 137 140 138 13935 900 900 | 80 81 82 83 84 85 86 87 88 89 8A 8B 8C 8D 8E 8F | 200 201 202 203 204 205 206 207 210 211 212 213 214 215 216 217 | 10000000 10000001 10000010 10000011 10000100 10000101 10000110 10000111 10001000 10001001 10001010 10001011 100011 10001001 10001010 10001011 100011 | |
| 144 145 146 147 148 149 150 151 152 153 154 15 5 156 157 158 159 | 90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F | 220 221 222 223 224 225 226 227 230 231 232 233 234 235 236 237 | 10010000 10010001 10010010 10010011 10010100 10010101 10010110 100101000 100101101 900 900 | |
| 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 A1 | 240 241 242 243 24 4 245 246 247 250 251 252 253 254 255 256 257 | 10100000 10100001 10100010 10100011 10100100 101001035 10101135 1010101135 10100110 10100111 1035 1010101135 101011100 900 900 | ||
| 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 | B0 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF | 260 261 262 263 264 265 266 267 270 271 272 273 274 275 276 277 | 10110000 10110001 10110010 10110011 10110100 10110101 10110110 10110111 1011 1000 10111001 10111010 10111011 10111100 10111101 10111110 10111111 | |
| 192 193 194 195 196 197 198 199 200 201 202 202 203 900 900 900 | C0 C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF | 300 301 302 303 304 305 306 307 310 311 312 313 314 315 316 317 | 11000000 11000001 11000010 11000011 11000100 11000101 11000110 110001135 11001000 11001001 110001135 11001000 11001001 1100101110 900001100 900001100 900 1100101100 900 | |
| 208 209 210 211 212 213 214 215 216 217 218 21 9 220 221 222 223 | D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF | 320 321 322 323 324 325 326 327 330 331 332 333 334 335 336 337 | 11010000 11010001 11010010 11010011 11010100 11010101 11010110 11010100 11010101 11010110 11010111 11035 11035 11035 110101 11010110 11010111 11035 11035 11035 11011100 11011101 11011110 11011111 | |
| 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 9039 E 900 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF | 340 341 342 343 34 4 345 346 347 350 351 352 353 354 355 356 357 | 11100000 11100001 11100010 11100011 11100100 11100101 11100110 11100111 11100101 11100110 11100111 111035 1110111 11100110 11100111 111035 11101101 11101110 11101111 | ||
| 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 | 35 F 253 254 255 | 900 F1 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF | 360 361 362 363 364 365 366 367 370 371 372 373 374 375 376 377 | 11110000 11110001 11110010 11110011 11110100 11110101 11110110 11110111 1111 1000 11111001 11111010 11111011 11111100 11111101 11111110 11111111 |
- Denary — Денарная система счисления (десятичная) — это система счисления с основанием 10, используемая людьми с 10 уникальными цифрами от 0 до 9
- Octal — восьмеричная система счисления (Oct) — это система счисления с основанием 8, в которой используются цифры от 0 до 7
- Шестнадцатеричный — Шестнадцатеричная система счисления (Hex) представляет собой систему счисления с основанием 16, использующую цифры 0-9 и буквы A — F
- Двоичная — Двоичная система счисления (Bin) — это система счисления с основанием 2, использующая число 1 и 0
Преобразование двоичного числа в десятичное
В десятичной системе счисления используется основание системы счисления 10.
Динарное (десятичное) число может быть выражено как
10,5
= 1 x 10 1 + 0 x 10 0 + 5 x 10 -1
Двоичная система счисления имеет основание системы счисления 2.
Двоичное число может быть выражено как
1011,1
= 1 x 2 3 + 0 x 2 2 + 1 x 2 1 + 1 x 2 0 + 1 x 2 -1
= 8 + 0 + 1 + 1 + 1/2
= 10.5
Различие двоичных и денарных чисел может быть указано как
1011,1 2 = 10,5 10
Преобразование шестнадцатеричных чисел в десятичные
Шестнадцатеричная система счисления имеет основание 16 и использует следующие 16 различные цифры
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F
‘A’ соответствует 10 в денарной системе, От B до 11, C до 12 …
Шестнадцатеричное число может быть выражено как
1BC
= 1 x 16 2 + C x 16 1 + F x 16 0
= 1 x 16 2 + 12 x 16 1 + 15 x 16 0
= 256 + 192 + 15
= 463
Системы счисления
Системы счисления
Структуры данных и системы счисления
© Авторские права Брайан Браун, 1984–1999.Все права
зарезервированный.
В данном учебном курсе используются расширения HTML 3.0
Введение
Система счисления определяет набор значений, используемых для представления количество. Мы говорим о количестве людей, посещающих занятия, количество модулей, взятых на одного студента, а также используйте числа для представляют собой оценки, полученные учащимися на тестах.
Количественная оценка значений и предметов по отношению друг к другу является помогает нам разобраться в окружающей среде.Мы делаем это в ранний возраст; выясняя, есть ли у нас еще игрушки, с которыми можно поиграть, еще подарки, еще леденцы и так далее.
Изучение систем счисления не ограничивается компьютерами. Мы применяем числа каждый день, и, зная, как работают числа, мы дать нам представление о том, как компьютер манипулирует и хранит числа.
Человечество на протяжении веков использовало знаки и символы для представляют собой числа. Ранние формы были прямыми линиями или группами линий, как в фильме Робинзон Крузо , где группа из шести вертикальных линий с диагональной линией поперек представлена одна неделя.
Сложно представить большие или очень маленькие числа с помощью такой графический подход. Еще в 3400 г. до н.э. в Египте и в 3000 г. до н.э. в Месопотамии они разработали символ, представляющий единицу 10. Это было большим достижением, поскольку уменьшило количество обязательные символы. Например, 12 можно представить как 10 и две единицы (три символа вместо 12, что требовалось ранее).
Римляне изобрели систему счисления, которая могла представлять все числа от 1 до 1000000 с использованием всего семи символов
- I = 1
- В = 5
- Х = 10
- L = 50
- С = 100
- D = 500
- M = 1000
Маленькая полоса над символом указывает на то, что номер умножить на 1000.
Наиболее распространенной сегодня системой счисления является арабский . система. Впервые он был разработан индусами и использовался как еще в 3 веке до нашей эры. Введение символа 0, используется для обозначения позиционного значения цифр, было очень важный. Таким образом, мы познакомились с концепцией групп единиц, десятков единиц, сотен единиц, тысяч единиц и скоро.
В системах счисления часто полезно думать о повторяющихся устанавливает , где набор значений повторяется снова и снова.
В десятичной системе счисления имеет набор значений. диапазон от 0 до 9. Этот базовый набор повторяется снова и снова. над, создавая большие числа.
Обратите внимание, как повторяется набор значений от 0 до 9, и для каждого повторить, столбец слева увеличивается (с 0 до 1, затем 2).
Каждое увеличение значения происходит до значения наибольшего число в наборе (9), на этом этапе следующее значение является наименьшим в наборе (0), и новое значение создается в левый столбец (т. е. следующее значение после 9 — 10).
09, 10–19, 20–29, 30–39 и т. Д.
Мы всегда записываем цифру с наибольшим значением на слева от номера
База
Значения
Базовое значение системы счисления — это количество различных
значения, которые имеет набор до повторения. Например, десятичный
имеет базу из десяти значений от 0 до 9.
- Двоичный = 2 (0, 1)
- Восьмеричное число = 8 (0-7)
- Десятичное число = 10 (0-9)
- Двенадцатеричный = 12 (использовался для некоторых целей римлянами)
- Шестнадцатеричный = 16 (0-9, A-F)
- Vigesimal = 20 (используется майя)
- Шестидесятеричный = 60 (используется вавилонянами)
Взвешивание
Фактор
Весовой коэффициент — это значение множителя, применяемое к каждому
положение столбца номера.Например, десятичное число имеет
весовой коэффициент TEN в каждом столбце слева
указывает на увеличение значения умножения на 10 по сравнению с предыдущим
столбец справа, т.е. каждый столбец перемещается влево увеличивается
с коэффициентом умножения 10.
200 = ----- 0 * 10 0 = 0 * 1 = 0 ------ 0 * 10 1 = 0 * 10 = 0 ------- 2 * 10 2 = 2 * 100 = 200 ----- 200 (суммируя) -----
Рассмотрим еще один пример десятичного числа 312.
312 = ----- 2 * 10 0 = 2 * 1 = 2 ------ 1 * 10 1 = 1 * 10 = 10 ------- 3 * 10 2 = 3 * 100 = 300 ----- 312 (суммируя) -----
десятичный
Система счисления [База-10]
В этой системе счисления используется ДЕСЯТЬ.
разные символы для представления значений.Установленные значения, используемые в
десятичный:
0 1 2 3 4 5 6 7 8 9
, где 0 имеет наименьшее значение, а девять — наибольшее. значение. Цифра или столбец слева имеет наибольшее значение, в то время как цифра справа имеет наименьшее значение.
Если при вычислении высшая цифра (9)
превышено, происходит перенос, который переносится в следующий столбец
(Слева).
Пример добавления и превышения диапазона базовой настройки 8 + 4 8 9 +1 10 +2 Примечание 1: 11 +3 12 +4 Примечание 1: при превышении 9 мы возвращаемся к началу набора (0), и перенесите значение 1 в следующий столбец слева. Другой пример добавления и превышения диапазона базовой установки 198 + 4 198 199 +1 200 +2 Примечание 2: 201 +3 202 +4 Примечание 2: при превышении 9 мы возвращаемся к началу набора (0), и перенесите значение 1 в следующий столбец слева. Таким образом в средний столбец (9) добавлен 1, следующее значение в наборе - 0, и мы переносим 1 (потому что набор был превышен) в следующий левый столбец.Добавление значение переноса от 1 до 1 в крайнем левом столбце дает.
Позиционные значения [единицы, десятки, сотни, тысячи и т. Д.
Колонны]
Наверное, в школе нас учили позиционным ценностям, в том, что
столбцы представляют степени 10. Это выражается нам как
столбцы единиц (0-9), десятки (группы по 10), сотни (группы
100) и так далее.
237 = (2 группы по 100) + (3 группы по 10) + (7 групп по 1) = (100 + 100) + (10 + 10 + 10) + (1 + 1 + 1 + 1 + 1 + 1 + 1) = (200) + (30) + (7) = 237
Каждый столбец, перемещаемый влево, в 10 раз превышает предыдущее значение.
двоичный
Система счисления [База-2]
В двоичной системе счисления используются ДВА
значения для представления чисел. Значения:
, где 0 имеет наименьшее значение, а 1 — наибольшее значение. Столбцы используются так же, как и в десятичная система, в которой крайний левый столбец используется для представления наибольшего значения.
Как мы видели в десятичной системе,
значения в наборе (0 и 1) повторяются как по вертикали, так и по
горизонтальные направления.
0 1 10 Примечание: перейти к наименьшему значению в наборе, перенести влево 11 100 Примечание: перейти к наименьшему значению в наборе, перенести влево 101 110 Примечание: перейти к наименьшему значению в наборе, перенести влево 111
. В компьютере двоичная переменная, способная хранить двоичные данные. значение (0 или 1) называется BIT.
В десятичной системе столбцы представляют умножение.
значения 10.Это произошло потому, что было 10 значений (0–9) в
набор. В этой двоичной системе всего два значения (0 — 1)
в наборе, поэтому столбцы представляют собой значения умножения 2.
1011 = ---- 1 * 2 0 = 1 ----- 1 * 2 1 = 2 ------ 0 * 2 2 = 0 ------- 1 * 2 3 = 8 ---- 11 (в десятичной системе)
Числовые диапазоны в двоичном формате с использованием указанного числа битов
Сколько разных значений может быть представлено определенным числом
бит?
количество различных значений = 2 n где n - количество бит например.2 8 = 256 разных значений
Правила сложения двоичных файлов
| Эксплуатация | Результат |
| 0 + 0 | 0 |
| 0 + 1 | 1 |
| 1 + 0 | 1 |
| 1 + 1 | 0 и Carry 1 |
1011 + 101 = 1011 101 1.Начните с самого правого столбца и примените правила. 2. 1 + 1 равно 0 и переносит 1 в следующий столбец слева. 1011 101 ------ 0 и нести 1 что действительно похоже 1011 111 ------ 0 3. Теперь займитесь вторым столбцом. 4. 1 + 1 равно 0, перенесите 1 в следующий столбец слева. 1011 111 ------ 00 и нести 1 что действительно похоже 1011 111 1 ------ 00 5.Теперь сделайте третий столбец 6. 1 + 1 равно 0, перенесите 1 в следующий столбец слева. 1011 111 1 ------ 000 и нести 1 что действительно похоже 1011 111 1 ------ 000 7. Теперь займитесь последней колонкой слева. 8. 1 + 1 равно 0 и переносится 1 слева. 1011 101 ------ 10000
Правила двоичного вычитания
| Эксплуатация | Результат |
| 0-0 | 0 |
| 0–1 | 1 и займ 1 |
| 1-0 | 1 |
| 1–1 | 0 |
Правила двоичного умножения
| Эксплуатация | Результат |
| 0 * 0 | 0 |
| 0 * 1 | 0 |
| 1 * 0 | 0 |
| 1 * 1 | 1 |
Примеры задач для двоичного сложения
и вычитание
Преобразование
Десятичное в двоичное
Существует несколько способов преобразования между десятичным и двоичным числами.Начнем с преобразования десятичного значения 254 в
двоичный.
Метод 1: Разделите число на 2, затем разделите полученное осталось на 2 и так далее, пока ничего не останется (0). Записывать остаток (который равен 0 или 1) на каждом этапе деления. Как только делений больше нет, перечислите оставшиеся значения в обратный порядок. Это двоичный эквивалент.
254/2, что дает 127 с остатком 0 127/2, что дает 63 с остатком 1 63/2 получается 31 с остатком 1 31/2 получается 15 с остатком 1 15/2 получается 7 с остатком 1 7/2 дает 3 с остатком 1 3/2 дает 1 с остатком 1 1/2 дает 0 с остатком 1 таким образом, двоичный эквивалент 11111110 Другой пример, 132 в десятичной системе счисления 132/2, что дает 66 с остатком 0 66/2, что дает 33 с остатком 0 33/2, что дает 16 с остатком 1 16/2 - 8 с остатком 0 8/2 - 4 с остатком 0 4/2 дает 2 с остатком 0 2/2 дает 1 с остатком 0 1/2 дает 0 с остатком 1 таким образом, двоичный эквивалент 10000100
Метод 2: Каждый столбец представляет степень двойки, поэтому используйте
это как основа для расчета числа.Иногда бывает
называется подходом 8: 4: 2: 1.
Запишите двоичное число. Где 1 появляется в
столбец, добавьте значение столбца как степень двойки к итоговому значению.
| Взвешивание | 8 | 4 | 2 | 1 | Ответ |
| Двоичное значение | 1 | 0 | 1 | 1 | 11 |
| Взвешивание | 8 | 4 | 2 | 1 | Ответ |
| Двоичное значение | 0 | 1 | 1 | 1 | 7 |
| Взвешивание | 32 | 16 | 8 | 4 | 2 | 1 | Ответ |
| Двоичное значение | 1 | 1 | 1 | 0 | 1 | 1 | 59 |
| Взвешивание | 32 | 16 | 8 | 4 | 2 | 1 | Ответ |
| Двоичное значение | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
Примеры задач для преобразования десятичных чисел в двоичные
Преобразование
Двоичные числа
- громоздко записывать
- длинный
- не имеет большого значения для обычного пользователя
- понимаются компьютерами
O кталл
Система счисления [База-8]
В восьмеричной системе счисления используется ВОСЕМЬ
значения для представления чисел.Значения:
0 1 2 3 4 5 6 7
, где 0 имеет наименьшее значение, а семь — наибольшее. значение. Столбцы используются так же, как и в десятичной системе, в этом крайнем левом столбце используется для представления наибольшего значения.
Как мы видели в десятичной системе,
значения в наборе (0 и 1) повторяются как по вертикали, так и по
горизонтальные направления.
0-7, 10-17, 20-27, 30-37......
Задача: Преобразовать восьмеричное число 176 в десятичное.
Каждый столбец представляет степень 8, 176 = ---- 6 * 8 0 = 6 ----- 7 * 8 1 = 56 ------ 1 * 8 2 = 64 ---- 126
Octal широко использовался в ранних мэйнфреймах. системы.
шестнадцатеричный
Система счисления [База-16]
В шестнадцатеричной системе счисления используется ШЕСТНАДЦАТЬ.
значения для представления чисел.Значения:
0 1 2 3 4 5 6 7 8 9 А Б В Г Д Е Ф
, где 0 имеет наименьшее значение, а F — наибольшее значение. Столбцы используются так же, как и в десятичной системе счисления. система, в которой крайний левый столбец используется для представления наибольшая ценность.
Как мы видели в десятичной системе,
значения в наборе (0 и 1) повторяются как по вертикали, так и по
горизонтальные направления.
0 - F, 10 - 1 этаж, 20 - 2 этаж, 30 - 3 этаж......
Шестнадцатеричный формат часто используется для представления значений [чисел и адреса памяти] в компьютерных системах.
| Десятичное | двоичный | Шестнадцатеричный |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | B |
| 12 | 1100 | С |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Преобразование шестнадцатеричного числа в десятичное
Задача: Преобразование 176 из шестнадцатеричного числа в десятичное.
Каждый столбец представляет степень 16, 176 = ---- 6 * 16 0 = 6 ----- 7 * 16 1 = 112 ------ 1 * 16 2 = 256 ---- 374
Преобразование двоичного числа в шестнадцатеричное
Проблема: Преобразование 10110 в шестнадцатеричное.
Каждая шестнадцатеричная цифра представляет 4 двоичных бита. Разделить двоичное число на группы по 4 бита, начиная справа.1 0110 = 1 = 6 = 16 в шестнадцатеричной системе счисления
Преобразование десятичного числа в шестнадцатеричное
Задача: Преобразование десятичного числа 232 в шестнадцатеричное.
Используйте тот же метод, который использовался ранее, чтобы разделить десятичную дробь на двоичный, но разделить на 16. 232/16 = 14 с остатком 8 14/16 = 0 с остатком от E (14 в десятичной системе = E) = E8 16
Во избежание путаницы мы часто добавляем суффикс для обозначения основания номера
162 h h означает шестнадцатеричный 162 16 16 означает основание 16 162 d d означает десятичное число 162 10 10 означает основание 10 162 o o означает восьмеричное 162 8 8 означает основание 8 101 b b означает двоичный 101 2 2 означает основание 2
Примеры задач для шестнадцатеричной системы
Преобразование
Представляя положительные и
отрицательные числа в двоичном формате
Когда для хранения значений используется несколько битов, наиболее
значащий бит [бит, имеющий наибольшее значение, в
крайний левый столбец] используется для хранения знака [положительный или
отрицательный] числа.Остальные биты содержат фактическое
значение.
Если число отрицательное, знак будет 1 , а для положительные числа, знак 0 .
Вопрос: Что такое диапазон чисел, доступных при использовании 8 бит.
Для 8 бит один бит предназначен для знака, 7 - для числа, поэтому диапазон значений равен 2 7 = 127 комбинаций
Из-за проблем с сложением и вычитанием отрицательный числа обычно хранятся в формате, отличном от положительного числа.
Дополнительная информация о представлении чисел
Дополнение
Дополнение до 1 — это метод хранения отрицательных значений. Это просто
инвертирует все 0 в 1 и все 1 в 0.
| Оригинальный номер | Двоичное значение | Дополняющее значение до 1 |
| 7 | 00000111 | 11111000 |
| 32 | 00100000 | 11011111 |
| 114 | 01110010 | 10001101 |
Дополнение до двух
Дополнение до 2 — это еще один метод хранения отрицательных значений.Это
получается добавлением 1 к значению дополнения до 1.
| Оригинальный номер | Двоичное значение | Дополняющее значение до 1 | Дополняющее значение 2 |
| 7 | 00000111 | 11111000 | 11111001 |
| 32 | 00100000 | 11011111 | 11100000 |
| 114 | 01110010 | 10001101 | 10001110 |
Другой способ создания дополнительного числа до 2 — начать наименьший значащий бит и скопируйте все 0 до достигается первая 1.Скопируйте первую 1, затем инвертируйте все оставшиеся биты.
В следующей таблице показаны как единицы, так и двойки.
дополнить, используя диапазон 4 бита.
| Двоичный | Дополнение до 1 | Дополнение до 2 | Без знака |
| 0111 | 7 | 7 | 7 |
| 0110 | 6 | 6 | 6 |
| 0101 | 5 | 5 | 5 |
| 0100 | 4 | 4 | 4 |
| 0011 | 3 | 3 | 3 |
| 0010 | 2 | 2 | 2 |
| 0001 | 1 | 1 | 1 |
| 0000 | 0 | 0 | 0 |
| 1111 | -0 | –1 | 15 |
| 1110 | –1 | -2 | 14 |
| 1101 | -2 | -3 | 13 |
| 1100 | -3 | -4 | 12 |
| 1011 | -4 | -5 | 11 |
| 1010 | -5 | -6 | 10 |
| 1001 | -6 | -7 | 9 |
| 1000 | -7 | -8 | 8 |
Примечание: Посмотрите, как в случае дополнения до 1 есть два представления для 0
Серый Код
Это циклический взвешенный код .Это значит, что он устроен так
что каждый переход от одного значения к следующему включает
только изменение одного бита .
Код Грея иногда называют отраженным двоичным кодом , потому что первые восемь значений сравниваются с последними 8 значения, но в обратном порядке.
| Десятичное | Двоичный | Серый |
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
Код Грея часто используется в механических приложениях, таких как энкодеры вала.
Арифметика по модулю 2
Это двоичное сложение, но перенос игнорируется.
Преобразование серого в двоичное
- запишите число серым кодом
- старший бит двоичного числа является самым старшим значащий бит кода Грея
- добавить (используя по модулю 2) следующий значащий бит двоичное число до следующего значащего бита серого закодированное число для получения следующего двоичного бита
- повторяйте шаг 3, пока все биты серого закодированного числа не добавлено по модулю 2
- результирующее число является двоичным эквивалентом серого номер
Пример, преобразование 1101101 кода Грея в двоичный Серый двоичный 1.1101101 2. 1 101101 1 копия в старшем младшем разряде 3. 1 1 1101 1 0 1 по модулю 2 1 = 0 4. 11 0 1101 1 0 0 0 по модулю 2 0 = 0 3/4 110 1 101 10 0 1 0 по модулю 2 1 = 1 3/4 1101 1 01100 1 0 1 по модулю 2 1 = 0 3/4 11011 0 1 1001 0 0 0 по модулю 2 0 = 0 3/4 110110 1 10010 0 1 0 по модулю 2 1 = 1 Ответ: 1001001
Преобразование двоичного изображения в серый
- запишите число в двоичном коде
- старший бит серого числа является самым старшим значащий бит двоичного кода
- добавить (используя по модулю 2) следующий значащий бит двоичное число до следующего значащего бита двоичного число для получения следующего бита с кодом серого
- повторяйте шаг 3 до тех пор, пока все биты двоичного числа не закодированы. были добавлены по модулю 2
- результирующее число является серым эквивалентом двоичное число
Пример, преобразование двоичного кода 1001001 в код Грея Бинарный серый 1.1001001 2. 1 001001 1 копировать вниз старший бит 3. 10 01001 11 1 по модулю 2 0 = 1 4. 1 00 1001110 0 по модулю 2 0 = 0 3/4 10 01 001 1101 0 по модулю 2 1 = 1 3/4 100 10 01 11011 1 по модулю 2 0 = 1 3/4 1001 00 1 110110 0 по модулю 2 0 = 0 3/4 10010 01 1101101 0 по модулю 2 1 = 1 Ответ 1101101
Превышение 3 Серый код
Во многих приложениях желательно иметь код, который является двоично-десятичным кодом, а также единицей расстояния.Блок А код расстояния получил свое название от того факта, что существует
изменение только одного бита между двумя последовательными числами. Превышение 3
Код Грея является таким кодом, значения для нуля и девяти различаются
только 1 бит, как и все значения для последовательных чисел.
Выходы линейных устройств или угловых энкодеров могут кодироваться более 3 кодов Грея для получения многозначных чисел BCD.
| Десятичное | Излишек 3 Серый |
| 0 | 0010 |
| 1 | 0110 |
| 2 | 0111 |
| 3 | 0101 |
| 4 | 0100 |
| 5 | 1100 |
| 6 | 1101 |
| 7 | 1111 |
| 8 | 1110 |
| 9 | 1010 |
Главная | Другие курсы | Обратная связь | Примечания | Тесты
© Copyright B Brown / Peter Henry.1984–1999 годы.
Все права защищены.
Что такое система счисления? — Определение, факты и примеры
Система счисления
Десятичная система счисления:Десятичная система счисления состоит из 10 цифр 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 и является наиболее часто используемой системой счисления. Мы используем комбинацию этих 10 цифр для образования всех остальных чисел. Значение цифры в числе зависит от ее положения в номере. Таблица значений десятичной системы счисления выглядит так:
Каждое место слева в десять раз больше, чем место справа от него, то есть, когда мы перемещаемся справа налево, разрядное значение увеличивается в десять раз с каждым местом.
Десятичная система счисления также называется системой счисления с основанием 10.
Число 49 365 читается как сорок девять тысяч триста шестьдесят пять, где значение 4 — сорок тысяч, 9 — девять тысяч, 3 — триста, 6 — шестьдесят и 5 — пять.
В двоичной системе счисления мы используем только две цифры 0 и 1. Это означает двойную систему счисления.
Пример двоичного числа: 1011; 101010; 1101101
Каждая цифра двоичного числа называется битом.Итак, двоичное число 101 имеет 3 бита. 499787080
В компьютерах и других цифровых устройствах используется двоичная система. В двоичной системе счисления используется основание 2.
Шестнадцатеричная система счисленияСлово шестнадцатеричное происходит от шестнадцатеричного, означающего 6, и десятичного значения 10. Итак, в шестнадцатеричной системе счисления 16 цифр. Он состоит из цифр от 0 до 9 и первых 5 букв алфавита:
В таблице ниже числа от 1 до 20 показаны в десятичном, двоичном и шестнадцатеричном формате.
Десятичное | двоичный | Шестнадцатеричный |
0 | 0 | 0 |
1 | 1 | 1 |
2 | 10 | 2 |
3 | 11 | 3 |
4 | 100 | 4 |
5 | 101 | 5 |
6 | 110 | 6 |
7 | 111 | 7 |
8 | 1000 | 8 |
9 | 1001 | 9 |
10 | 1010 | 10 |
11 | 1011 | А |
12 | 1100 | В |
13 | 1101 | С |
14 | 1110 | D |
15 | 1111 | E |
16 | 10000 | Ф |
17 | 10001 | 11 |
18 | 10010 | 12 |
19 | 10011 | 13 |
20 | 10100 | 14 |
Интересные факты
|

 Данный аргумент необходим если нужно приписать к двоичной записи данных ведущие нули. К примеру, число 1101 с разрядностью 7 будет иметь вид 0001101.
Данный аргумент необходим если нужно приписать к двоичной записи данных ведущие нули. К примеру, число 1101 с разрядностью 7 будет иметь вид 0001101.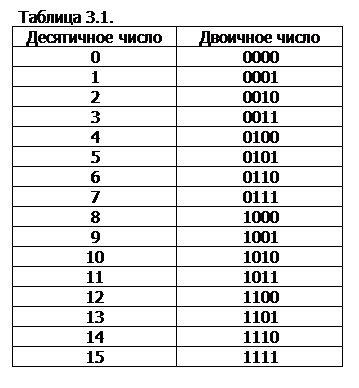 Примеры приведены в таблице ниже.
Примеры приведены в таблице ниже.