Закон Ома.

Закон Ома.

Программа КИП и А

В программу «КИП и А», в разделе «Электрика» включен блок расчета закона Ома для постоянного и переменного тока. Сначала немного теории..

Для постоянного тока

Закон Ома определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи. Наиболее популярна формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, т.е.

I = U / R	где	I — сила тока, измеряемая в Амперах, (A)
		U — напряжение, измеряемое в Вольтах, (V)
		R — сопротивление, измеряется в Омах, (Ω)

Закон Ома, является основополагающим в электротехнике и электронике. Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, — «Не знаешь закон Ома, — сиди дома..».

Помимо закона Ома, важнейшим является понятие электрической мощности, P:

Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U), т.е.

P = I × U	где	P — эл. мощность, измеряемая в Ваттах, (W)
		I — сила тока, измеряемая в Амперах, (A)
		U — напряжение, измеряемое в Вольтах, (V)

Комбинируя эти две формулы, выведем зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:

Сила тока,	I=	U/R	P/U	√(P/R)
Напряжение,	U=	I×R	P/I	√(P×R)
Сопротивление,	R=	U/I	P/I²	U²/P
Мощность,	P=	I×U	I²×R	U²/R

Практический пример использования таблицы: Покупая в магазине утюг, мощностью 1 кВт (1 кВт = 1000 Вт), высчитываем на какой минимальный ток должна быть рассчитана розетка в которую предполагается включать данную покупку:
Несмотря на то, что утюг включается в сеть переменного тока, пренебрегаем его реактивным сопротивлением (см. ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.

Наиболее распространенные множительные приставки:

• Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А. 1 миллиампер (1 mA) = 0,001 A. 1 микроампер (1 µA) = 0,000001 A.
• Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V. 1 милливольт (1 mV) = 0,001 V. 1 микровольт (1 µV) = 0,000001 V.
• Сопротивление, Омы (Om): 1 мегаом (1 MOm) = 1000000 Om. 1 килоом (1 kOm) = 1000 Om.
• Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W. 1 киловатт (1 kW) = 1000 W. 1 милливатт (1 mW) = 0,001 W.

Для переменного тока

В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.

Импеданс, Z

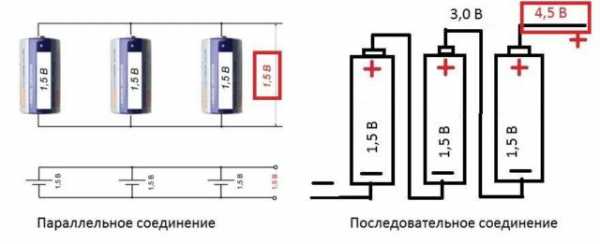
В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.

Последовательное включение R, L, C
Параллельное включение R, L, C

Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.

Импеданс, Полное сопротивление, Z
При последовательном включении R, L, C	При параллельном включении R, L, C
Z=√(R2+(ωL-1/ωC)2)	Z=1/ √(1/R2+(1/ωL-ωC)2)
где,
ω = 2πγ — циклическая, угловая частота; γ — частота переменного тока.

Коэффициент мощности, Cos(φ)

Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.

Cos(φ) = P / S

Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.
Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.

Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:

I = U / Z	где	I — сила переменного тока, измеряемая в Амперах, (A)
		U — напряжение переменного тока, измеряемое в Вольтах, (V)
		Z — полное сопротивление (импеданс), измеряется в Омах, (Ω)

Производные формулы:

Сила тока,	I=	U/Z	P/(U×Cos(φ))	√(P/Z)
Напряжение,	U=	I×Z	P/(I×Cos(φ))	√(P×Z)
Полное сопротивление, импеданс	Z=	U/I	P/I²	U²/P
Мощность,	P=	I²×Z	I×U×Cos(φ)	U²/Z

Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу:

Закон Ома для постоянного тока
Закон Ома для переменного тока
Расчет полного сопротивления
Расчет коэффициента мощности Cos(φ)

 

www.axwap.com

1. Электрическое сопротивление. Закон Ома для участка электрической цепи

Соберём электрическую цепь, состоящую из источника тока (который позволяет плавно менять напряжение), амперметра, спирали из никелиновой проволоки (проводника), ключа и параллельно присоединённого к спирали вольтметра (схема этой цепи показана рядом, прямоугольником условно обозначен проводник).

 

 

Замкнём цепь и отметим показания приборов. Затем при помощи источника тока плавно изменим напряжение (лучше всего увеличить его вдвое). Напряжение на спирали при этом тоже увеличится вдвое, и амперметр покажет вдвое большую силу тока. Увеличивая напряжение в \(3\) раза, напряжение на спирали увеличивается втрое, во столько же раз увеличивается сила тока.
Таким образом, опыт показывает, что во сколько раз увеличивается напряжение, приложенное к одному и тому же проводнику, во столько же раз увеличивается сила тока в нём. Другими словами:

 

Обрати внимание!

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника.

Эту зависимость можно изобразить графически. Её называют зависимостью силы тока в проводнике от напряжения между концами этого проводника.

 

 

Включая в электрическую цепь источника тока различные проводники и амперметр, можно заметить, что при разных проводниках показания амперметра различны, т.е. сила тока в данной цепи различна.

 

 

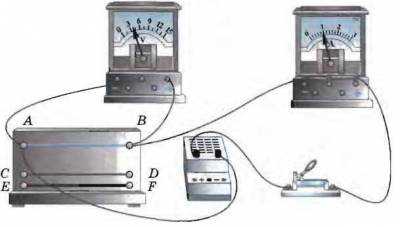
Графики тоже будут отличаться.

 

 

Вольтметр, поочерёдно подключаемый к концам этих проводников, показывает одинаковое напряжение. Значит, сила тока в цепи зависит не только от напряжения, но и от свойств проводников, включённых в цепь. Зависимость силы тока от свойств проводника объясняется тем, что разные проводники обладают различным электрическим сопротивлением.

 

Обрати внимание!

Электрическое сопротивление — физическая величина. Обозначается оно буквой R.

За единицу сопротивления принимают \(1\) ом — сопротивление такого проводника, в котором при напряжении на концах \(1\)вольт сила тока равна \(1\) амперу.

Кратко это записывают так: 1 Ом =1 В1 А.Применяют и другие единицы сопротивления: миллиом (мОм), килоом (кОм), мегаом (МОм).

 

\(1\) мОм = \(0,001\) Ом;

\(1\) кОм = \(1000\) Ом;

\(1\) МОм = \(1 000 000\) Ом.

 

Причина сопротивления заключается в следующем: электроны взаимодействуют с ионами кристаллической решётки металла. При этом замедляется упорядоченное движение электронов, и сквозь поперечное сечение проводника проходит за \(1\) с меньшее их число. Соответственно, уменьшается и переносимый электронами за \(1\) с заряд, т.е. уменьшается сила тока. Таким образом, каждый проводник как бы противодействует электрическому току, оказывает ему сопротивление. Итак:

 

Обрати внимание!

Причиной сопротивления является взаимодействие движущихся электронов с ионами кристаллической решётки.

Чтобы ответить на вопрос, как зависит сила тока в цепи от сопротивления, обратимся к опыту.

 

 

На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор. В эту цепь по очереди включают проводники, обладающие различным сопротивлением. Напряжение на концах проводника во время опыта поддерживается постоянным. За этим следят по показаниям вольтметра. Силу тока в цепи измеряют амперметром. Ниже приведены результаты опытов с тремя различными проводниками.

 

Напряжение на концах проводника, В	Сопротивление проводника, Ом	Сила тока в цепи, А
\(2\)	\(1\)	\(2\)
\(2\)	\(2\)	\(1\)
\(2\)	\(4\)	\(0,5\)

Обобщая результаты опытов, приходим к выводу, что:

 

Обрати внимание!

Сила тока в проводнике обратно пропорциональна сопротивлению проводника.

Зависимость силы тока от напряжения на концах участка цепи и сопротивления этого участка называется законом Ома — по имени немецкого учёного Георга Ома, открывшего этот закон в \(1827\) году.
Закон Ома читается так:

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

И записывается так:

 

I=UR,

 

где \(I\) — сила тока в участке цепи, \(U\) — напряжение на этом участке, \(R\) — сопротивление участка.

Зависимость силы тока от сопротивления проводника при одном и том же напряжении на его концах может быть показана графически:

 

 

 

Найти сопротивление экспериментально можно несколькими способами:

 

 

Где  — обозначение омметра в цепи (или мультиметра в режиме измерения сопротивления).

Источники:

Пёрышкин А.В. Физика, 8 класс// ДРОФА, 2013.

http://xn--h2adlho.xn--g1ababalj7azb.xn--p1ai/375/
http://radiolove.ucoz.com/index/ne_znaesh_zakona_oma_sidi_doma/0-8

www.yaklass.ru

Закон Ома | Закон Ома для участка цепи, формула

Как говорится в среде радиолюбителей: “Если не знаешь закон Ома, то сиди-ка лучше дома”.

Закон Ома с точки зрения гидравлики

Как вы уже знаете, электрический ток имеет аналогию с гидравликой. Напряжение – это уровень воды в башне. Сопротивление – это  труба или шланг. Сила тока – это объем воды за какой-то период времени.

Теперь давайте рассмотрим такой случай. Пусть вместо башни у нас будет сосуд с водой, в котором пробиты три одинаковых отверстия на разной высоте сосуда. Так как сосуд у нас наполнен водой, следовательно, на дне сосуда давление будет больше, чем на  его поверхности.

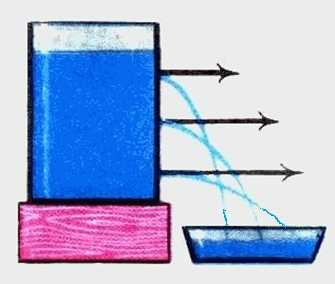
Как вы видите, нижняя струя, которая находится ближе ко дну, стреляет дальше, чем средняя струя. А средняя струя стреляет дальше, чем верхняя.  Заметьте, что отверстия у нас везде  одинакового диаметра. То есть можно сказать, что сопротивление каждого отверстия воде одинаково. За одинаковое время, объем воды, вытекаемый с самого нижнего отверстия намного больше, чем объем воды, вытекаемый со среднего и самого верхнего отверстия. А что у нас такое объем воды  за какое-то время? Да это же сила тока!

Итак, какую закономерность мы тут видим? Учитывая, что сопротивление везде одинаковое, получается что с увеличением напряжения увеличивается и сила тока!

Опыт №1

Думаю, у каждого из вас есть садовый участок. Где-то недалеко от вас всегда есть водонапорная башня

Для чего нужна водонапорная башня? Для контроля уровня расхода воды, а также для создания давления в трубах, иначе как вы  будете поливать свои огурцы? Вы никогда  не замечали, что башню возводят  где-нибудь на возвышенности? Для чего это делается? Как раз для того, чтобы создать давление.

Предположим, что ваш садовый участок находится выше, чем верхушка водобашни. Что произойдет в этом случае? Вода просто-напросто не дойдет до вас! Физика… закон сообщающихся сосудов.

У всех на кухне и в ванной есть краник. После очередного трудового дня вы решили помыть руки. Для этого вы на полную катушку включаете воду, и она начинает течь бурным потоком из краника:

Но вас не устраивает такой поток воды, поэтому, покрутив ручку крана, вы уменьшаете поток воды на минимум:

Что только что сейчас произошло?

Поменяв сопротивление потоку с помощью ручки краника, вы добились того, что этот поток воды стал течь очень слабо.

Давайте же проведем аналогию этой ситуации с электрическим током. Итак, что имеем? Напряжение потока мы не меняли. Где-то там вдалеке стоит водобашня и создает давление в трубах. Мы ведь не имеем права трогать водобашню, а тем более ее сносить). Поэтому уровень воды в башне все время полный, так как насос все время подкачивает воду до максимального уровня. Следовательно, напряжение у нас постоянное и не меняется.

Закрутив обратно ручку краника, мы  только что поменяли сопротивление трубы, из которой сделан краник. В данном случае мы увеличили сопротивление потоку воды. А что у нас получилось с потоком водички? Она стала бежать медленнее! То есть, можно сказать, что количество молекул воды за какое-то время при полностью открытом и полузакрытом кранике получилось разное. Ну-ка, вспоминаем, что такое сила тока 😉 Кто забыл, напомню – это количество электронов протекающих через поперечное сечение проводника за какой-то период времени. И что у нас стало с этой силой тока? Она уменьшилась!

Делаем вывод:

При увеличении сопротивления, сила тока, проходящая через это сопротивление, уменьшается.

Опыт N2

Итак. Имеем вот такую схему водоснабжения:

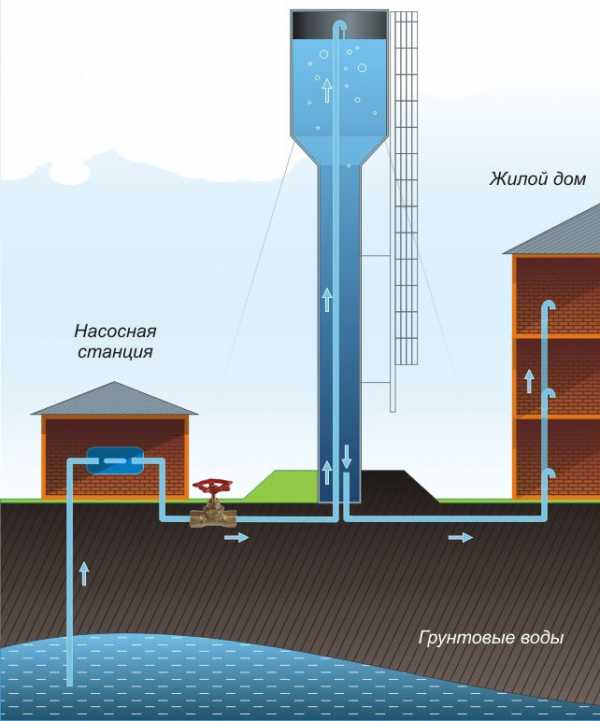
Теперь представьте, что вы поливаете огород и вам  надо наполнить  бочку с водой из шланга за 10 минут. Ни секундой раньше и не позже! У вас в огороде поток воды бежит примерно вот так:

Допустим, с водобашни у нас идет простой резиновый шланг. Сосед случайно припарковал свой автомобиль прямо на шланге и чуть-чуть придавил его

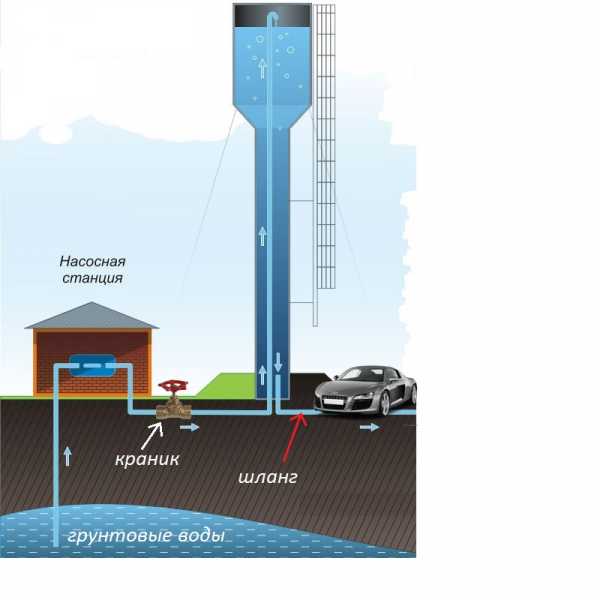
У вас поток воды стал убывать. Идти ругаться с соседом? Он уже ушел по делам, а бочку за 10 минут  наполнить не успеете. Потребуется больше времени. Как же быть? А почему бы нам не открыть краник перед водобашней чуток побольше? А это хорошая идея! Открываем краник на полную катушку и добиваемся, чтобы уровень воды в башне стал еще больше, чем был до этого (хотя  в башнях стоят защиты от переполнения какого-либо максимального уровня, но для примера упустим этот момент).

Итак, что у нас получается? Сосед придавил шланг, значит увеличил сопротивление. Поэтому сила тока у нас стала меньше. Чтобы восстановить силу тока, мы для этого увеличивали напряжение, то есть уровень воды в башне.

Вывод: при увеличении напряжения увеличивается и сила тока.

Опыт №3

Но беда не приходит одна. На башне сломалось реле контроля водонасоса! Насос качает воду и не отключается! Башня переполняется и поток воды из шланга с каждой секундой становиться все больше и больше! Что же делать? Мы же переполним нашу бочку за отведенное нам время! Спокойствие, только спокойствие… Выход есть! Для этого бежим и чуток перекрываем краник , добиваясь того, чтобы поток воды из шланга тек также, как и раньше 😉

В этом случае уровень воды (напряжение) на водобашне стал увеличиваться из-за того, что насос не отключался и все время качал воду. Поэтому, поток воды (сила тока) у нас тоже стала  расти. Чтобы выровнять силу тока, мы увеличили сопротивление краника ;-), тем самым привели в норму уровень воды в водобашне (напряжение) до приемлемого уровня.

Формула Закона Ома

Ну как, увидели закономерность из всего вышеописанного? А вот немецкий физик Георг Ом с помощью простых опытов нашел все-таки связь между этими тремя величинами и с тех пор этот закон носит его имя:

где

I – это сила тока, выражается в Амперах (А)

U – напряжение, выражается в Вольтах (В)

R – сопротивление, выражается в Омах (Ом)

Заключение

Закон Ома является самым главным законом в электронике. Абсолютно вся теория цепей построена именно на законе Ома. Поэтому, чтобы научиться читать электрические схемы, вам очень важно знать, как связаны напряжение, сила тока и сопротивление на участке цепи. В этой статье мы с вами разобрали закон Ома для участка цепи, но есть еще закон Ома для полной цепи, о котором можно прочитать в этой статье.

Более подробно про закон Ома для участка цепи вы можете также прочитать в этой статье.

www.ruselectronic.com

Закон Ома для участка цепи. Сопротивление

Закон Ома для участка цепи. Сопротивление

«Физика — 10 класс»

Что заставляет заряды двигаться вдоль проводника?
Как электрическое поле действует на заряды?

Вольт-амперная характеристика.

В предыдущем параграфе говорилось, что для существования тока в проводнике необходимо создать разность потенциалов на его концах. Сила тока в проводнике определяется этой разностью потенциалов. Чем больше разность потенциалов, тем больше напряжённость электрического поля в проводнике и, следовательно, тем большую скорость направленного движения приобретают заряженные частицы. Это означает увеличение силы тока.

Для каждого проводника — твёрдого, жидкого и газообразного — существует определённая зависимость силы тока от приложенной разности потенциалов на концах проводника.

Зависимость силы тока в проводнике от напряжения, подаваемого на него, называют вольт-амперной характеристикой проводника.

Её находят, измеряя силу тока в проводнике при различных значениях напряжения. Знание вольт-амперной характеристики играет большую роль при изучении электрического тока.

Закон Ома.

Наиболее простой вид имеет вольт- амперная характеристика металлических проводников и растворов электролитов. Впервые (для металлов) её установил немецкий учёный Георг Ом, поэтому зависимость силы тока от напряжения носит название закона Ома.

На участке цепи, изображённой на рисунке 15.3, ток направлен от точки 1 к точке 2. Разность потенциалов (напряжение) на концах проводника равна U = φ₁ — φ₂. Так как ток направлен слева направо, то напряжённость электрического поля направлена в ту же сторону и φ₁ > φ₂.

Измеряя силу тока амперметром, а напряжение вольтметром, можно убедиться в том, что сила тока прямо пропорциональна напряжению.

Закон Ома для участка цепи:

Сила тока на участке цепи прямо пропорциональна приложенному к нему напряжению U и обратно пропорциональна сопротивлению этого участка R.

Применение обычных приборов для измерения напряжения — вольтметров — основано на законе Ома. Принцип устройства вольтметра такой же, как и у амперметра. Угол поворота стрелки прибора пропорционален силе тока.

Сила тока, проходящего по вольтметру, определяется напряжением между точками цепи, к которой он подключён. Поэтому, зная сопротивление вольтметра, можно по силе тока определить напряжение. На практике прибор градуируют так, чтобы он сразу показывал напряжение в вольтах.

Сопротивление.

Основная электрическая характеристика проводника — сопротивление. От этой величины зависит сила тока в проводнике при заданном напряжении.

Свойство проводника ограничивать силу тока в цепи, т. е. противодействовать электрическому току, называют электрическим сопротивлением проводника.

С помощью закона Ома (15.3) можно определить сопротивление проводника:

Для этого нужно измерить напряжение на концах проводника и силу тока в нём.

На рисунке 15.4 приведены графики вольт-амперных характеристик двух проводников. Очевидно, что сопротивление проводника, которому соответствует график 2, больше, чем сопротивление проводника, которому соответствует график 1.

Сопротивление проводника не зависит от напряжения и силы тока.

Сопротивление зависит от материала проводника и его геометрических размеров.

Сопротивление проводника длиной l с постоянной площадью поперечного сечения S равно:

где ρ — величина, зависящая от рода вещества и его состояния (от температуры в первую очередь).

Величину ρ называют удельным сопротивлением проводника.

Удельное сопротивление материала численно равно сопротивлению проводника из этого материала длиной 1 м и площадью поперечного сечения 1 м².

Единицу сопротивления проводника устанавливают на основе закона Ома и называют её омом.

Проводник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нём 1 А.

Единицей удельного сопротивления является 1 Ом • м. Удельное сопротивление металлов мало. А вот диэлектрики обладают очень большим удельным сопротивлением. Например, удельное сопротивление серебра 1,59 • 10^-8 Ом • м, а стекла порядка 10¹⁰ Ом • м. В справочных таблицах приводятся значения удельного сопротивления некоторых веществ.

Значение закона Ома.

Из закона Ома следует, что при заданном напряжении сила тока на участке цепи тем больше, чем меньше сопротивление этого участка. Если по какой-то причине (нарушение изоляции близко расположенных проводов, неосторожные действия при работе с электропроводкой и пр.) сопротивление между двумя точками, находящимися под напряжением, оказывается очень малым, то сила тока резко возрастает (возникает короткое замыкание), что может привести к выходу из строя электроприборов и даже возникновению пожара.

Именно из-за закона Ома нельзя говорить, что чем выше напряжение, тем оно опаснее для человека. Сопротивление человеческого тела может сильно изменяться в зависимости от условий (влажности, температуры окружающей среды, внутреннего состояния человека), поэтому даже напряжение 10—20 В может оказаться опасным для здоровья и жизни человека. Следовательно, всегда необходимо учитывать не только напряжение, но и силу электрического тока. При работе в физической лаборатории нужно строго соблюдать правила техники безопасности!

Закон Ома — основа расчётов электрических цепей в электротехнике.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика

Электрический ток. Сила тока — Закон Ома для участка цепи. Сопротивление — Электрические цепи. Последовательное и параллельное соединения проводников — Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» — Работа и мощность постоянного тока — Электродвижущая сила — Закон Ома для полной цепи — Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

class-fizika.ru

для участка цепи, для полной цепи +ВИДЕО

Чтобы хоть немного разбираться в электрике, необходимо знать основополагающие законы. Один из них — закон Ома. С него начинают изучение электрики и не зря. Он иллюстрирует зависимость параметров электрической цепи друг от друга. 

Содержание статьи

Как звучит закон Ома для участка цепи

Есть говорить об официальной формулировке, то закон Ома можно озвучить так:

Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.

Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.

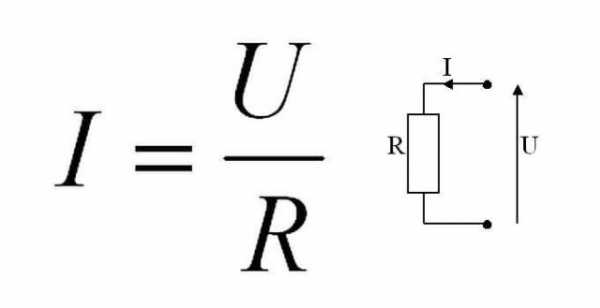
Формула закона Ома

• Чем больше напряжение, тем больше ток.
• Чем больше сопротивление, тем ток меньше.

Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.

Разбираемся что такое ток и сопротивление

Начнем с понятия электрического тока. Если говорить коротко, электрический ток применительно к металлам — это направленное движение электронов — отрицательно заряженных частиц. Их обычно представляют в виде небольших кружочков. В спокойном состоянии они передвигаются хаотически, постоянно меняя свое направление. При определенных условиях — возникновении разницы потенциалов — эти частицы начинают определенное движение в какую-то сторону. Вот это движение и есть электрический ток.

Чтобы было понятнее,  можно сравнить электроны с водой, разлитой на какой-то плоскости. Пока плоскость неподвижна, вода не движется. Но, как только появился наклон (возникла разница потенциалов), вода пришла в движение. С электронами примерно так же.

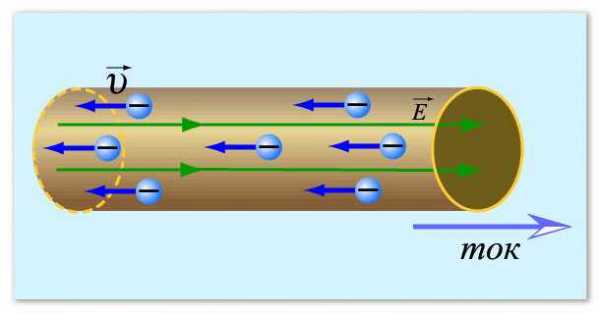
Примерно так можно себе представить электрический ток

Теперь надо понять, что такое сопротивление и почему с силой тока у них обратная связь: чем выше сопротивление, тем меньше ток. Как известно, электроны движутся по проводнику. Обычно это металлические провода, так как металлы обладают хорошей способностью проводить электрический ток. Мы знаем, что металл имеет плотную кристаллическую решетку: много частиц, которые расположены близко и связаны между собой. Электроны, пробираясь между атомами металла, на них наталкиваются, что затрудняет их движение. Это помогает проиллюстрировать сопротивление, которое оказывает проводник. Вот теперь становится понятным, почему, чем выше сопротивление, тем меньше сила тока — чем больше частиц, тем электронам сложнее преодолевать путь, делают они это медленнее. С этим, вроде, разобрались.

Если у вас есть желание проверить эту зависимость опытным путем, найдите переменный резистор, соедините последовательно резистор — амперметр — источник тока (батарейка). Еще желательно в цепь вставить выключатель — обычный тумблер.

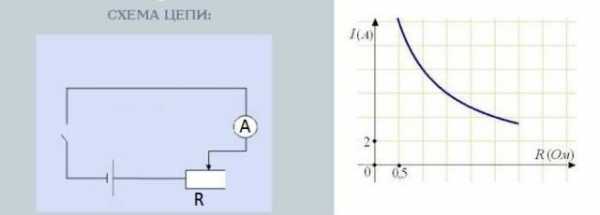
Цепь для проверки зависимости силы тока от сопротивления

Крутя ручку резистора вы изменяете сопротивление. При этом показания на амперметре, который измеряет силу тока, тоже меняются. Причем чем больше сопротивление, тем меньше отклоняется стрелка — меньше ток. Чем сопротивление меньше — тем сильнее отклоняется стрелка — ток больше.

Вместо стрелочного прибора можно использовать цифровой мультиметр в режиме измерения постоянного тока. В этом случае отслеживаются показания на жидкокристаллическом цифровом табло.

Зависимость тока от сопротивления почти линейная, то есть на графике отражается почти прямой линией. Почему почти — об этом надо говорить отдельно, но это другая история.

Говорим о напряжении

Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду. Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).

Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.

На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.

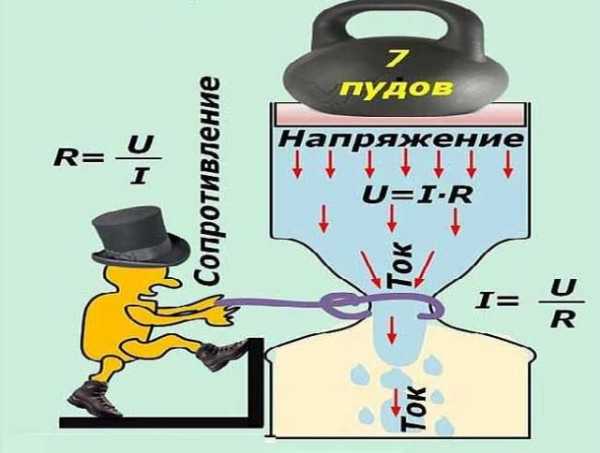
Благодаря картинке просто понять зависимость тока от напряжения и сопротивления

Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).

В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.

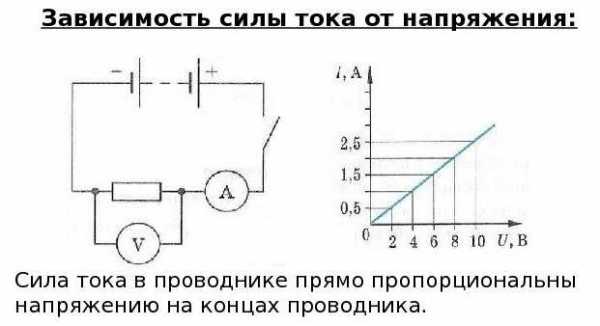
Схема для иллюстрации закона Ома

Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.

Что изменится для полной цепи

В ситуации выше рассмотрен только некоторый участок цепи, обладающий каким-то фиксированным сопротивлением. Мы предполагаем, что при определенных условиях электроны начнут движение. Причина этого движения — тот самый груз на картинке. В реальных условиях это — источник тока. Это может быть батарейка, генератор постоянного тока, подключенный шнур блока питания и т.д. При подключении источника питания к проводнику в нем начинает протекать ток. Это мы тоже знаем и наблюдаем, когда включаем лампу в сеть, ставим заряжаться мобильный телефон и т.д.

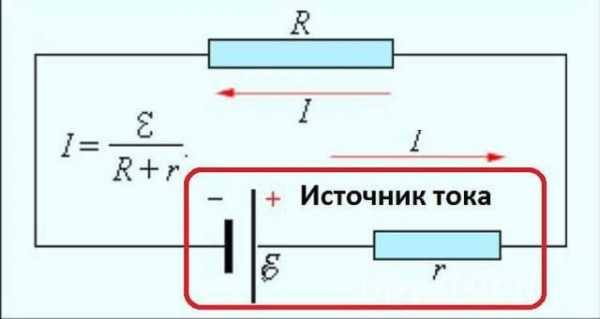
Полная цепь включает в себя источник питания

Участок цепи имеет какое-то сопротивление. Это понятно. Но источник  питания тоже имеет сопротивление. Его обычно обозначают маленько буквой r. Так как ток бежит по кругу, ему приходится преодолевать сопротивление провода и сопротивление источника тока. Вот это суммарное сопротивление цепи и источника питания — называют импеданс. Говорят еще что это комплексное сопротивление. В формуле Ома для полной цепи его отображают при помощи суммы. В знаменателе стоит сумма сопротивлений цепи и внутреннего сопротивления источника тока (R + r).

Всем, наверное, понятно, что именно источник тока создает нужные условия для движения электронов. Все благодаря тому, что он обладает ЭДС — электродвижущей силой. Эта величина обозначается обычно E. Чем больше эта сила, тем больше ток. Это тоже, вроде, понятно. Поэтому обозначение ЭДС — латинскую букву E — ставят в числитель. Таким образом, формулировка закона Ома для полной цепи звучит так:

Сила тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника тока.

Вроде не слишком сложно, но можно попробовать еще проще:

• Чем выше ЭДС источника тока, тем больше ток.
• Чем больше суммарное сопротивление, тем ток меньше.

Как найти сопротивление, напряжение

Зная формулу закона Ома для участка цепи, мы можем рассчитать напряжение и сопротивление. Напряжение находится как произведение силы тока и сопротивления.

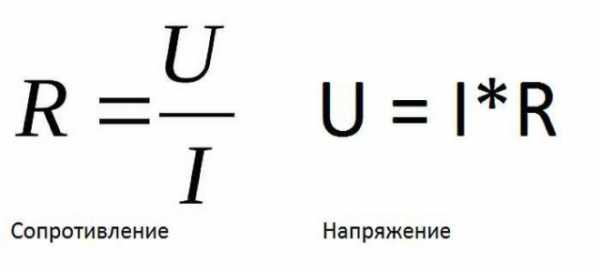
Формула напряжения и сопротивления по закону Ома

Сопротивление можно найти, разделив напряжение на ток. Все действительно несложно. Если мы знаем, что к участку цепи было проложено определенное напряжение и знаем какой при этом был ток, мы можем рассчитать сопротивление. Для этого напряжение делим на ток. Получаем как раз величину сопротивления этого куска цепи.

С другой стороны, если мы знаем сопротивление и силу тока, которая должна быть, мы сможем рассчитать напряжение. Надо всего лишь перемножить силу тока и сопротивление. Это даст напряжение, которое необходимо подать на этот участок цепи чтобы получить требуемый ток.

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

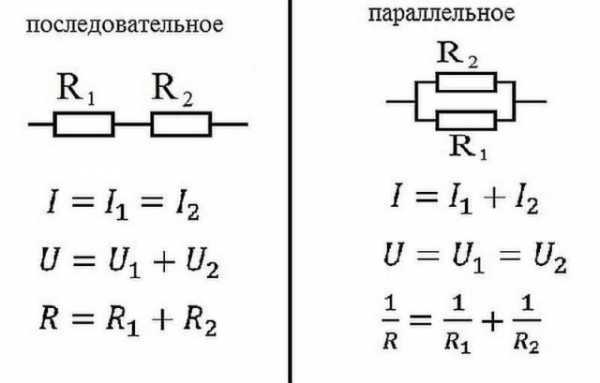
Закон Ома для параллельного и последовательного соединения

Последовательное соединение

Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи

При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.

Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

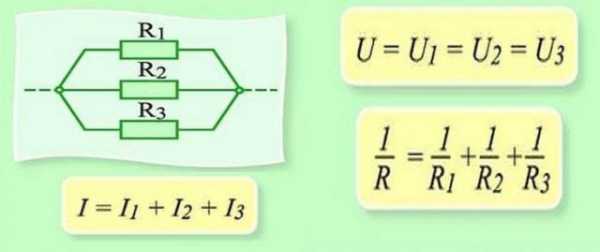
Законы для параллельного соединения

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.

Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

• Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
• Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

  Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока

В общем, это наиболее распространенные варианты использования этих соединений.

elektroznatok.ru

Закон Ома — это… Что такое Закон Ома?

V — напряжение,
I — сила тока,
R — сопротивление.

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде : ,

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r^[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

Из закона Ома для полной цепи вытекают следствия:

• При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
• При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто^[2] выражение:

(3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

(4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

(5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

(6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо^[3], впоследствии переименованный в Си́менс (обозначение: См, S).

Мнемоническая диаграмма для Закона

Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

В соответствии с этой диаграммой формально может быть записано выражение:

(7)

Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

(8)

где:

•  — удельное сопротивление материала, из которого сделан проводник,
•  — его длина
•  — площадь его поперечного сечения

Закон Ома и ЛЭП

Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением:

= (9)

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома в дифференциальной форме

Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.

Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re^−iδ — комплексное сопротивление (импеданс),
• R = (R_a² + R_r²)^1/2 — полное сопротивление,
• R_r = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = − arctg (R_r/R_a) — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Трактовка закона Ома

Закон Ома можно просто объяснить при помощи теории Друде:

Здесь:

См. также

Примечания

Ссылки

dic.academic.ru

Обсуждение:Закон Ома — Википедия

Материал из Википедии — свободной энциклопедии

Э… Это не совсем закон Ома.

На самом деле Ом экспериментальным путем установил что:
Сила электрического тока в проводнике пропорциональна приложенному напряжению:

I ~ U

где:
I — сила тока,
U — приложенное напряжение.

Ом сформулировал свой закон безотносительно к системе единиц.

Закон Ома можно сформулировать в нескольких формах (в том числе и в дифференциальной), но на самом деле закон имеет именно такую форму.

В системе Си закон Ома имеет вид:

I = U/R

где:
I — сила тока в Амперах,
U — приложенное напряжение в Вольтах,
R — сопротивление в Омах.

В других системах единиц закон Ома имеет, конечно же, другой вид.

Проводники — это такие вещества. Резистор — это устройство. К закону Ома отношения не имеет. snv

Согласен с тем, что единицы измерения тут указывать не следует. Убрал. Изменил резистор на проводник. Остальное считаю правильным. Закон Ома — в его современной формулировке (а не так, как его сам Ом формулировал) — есть именно равенство (I = U/R), которое можно записать в любой системе единиц, а не пропорциональность. Igorivanov 16:22, 12 Окт 2004 (UTC)

В системе Си коэффициен пропорциональности 1/R. В других системах едениц коэффициент пропорциональности другой. Хотя за последние 10 лет система Си стала настолько популярной, что я даже сходу не могу привести пример систем едениц в которых коэффициент пропорциональности отличен от 1/R.snv 16:42, 12 Окт 2004 (UTC)

Вовсе нет. Этот коэффициент пропорциональности есть просто определение сопротивления. Т.е. активное сопротивление (ну или эе проводимость) проводника есть, по определению, этот самый коэффициент. От системы единиц зависит, в чем его выражать. Igorivanov 16:54, 12 Окт 2004 (UTC)

Г-н Panaioty, подписи в статье не стоит ставить. Описывайте вашу правку и её причины в обсуждении. Булат Ш. 05:02, 24 июня 2008 (UTC)

Не статья, а какое-то дурное нагромождение разрозненных фактов из учебника ТОЭ. Собственно закон Ома приведён только в пятой (!) формуле, зато в первом же предложении мы зачем-то узнаём про 1826 год и как звали Ома. Надо полагать, до 1826 года этот закон не действовал, а Омов в науке как Поповых в Архангельской губернии. Сравните этот вики-срам хотя бы с английской версией. Там сначала — сам закон, внятно сформулированный и наглядно проиллюстрированный, а затем уже история открытия, имя Ома, размер его ноги и прочая лирика. 89.105.158.250 01:48, 14 октября 2014 (UTC)

Эмпирическая сущность закона Ома[править код]

Закон Ома является эмпирическим, а не фундаментальным, что я отразил во вводной части и в разделе «Трактовка и пределы применимости». Заодно дополнил этот раздел примерами нарушения закона Ома. Raoul NK 16:46, 22 июня 2013 (UTC)

Стрелки, указывающие направления тока и напряжения, должны быть направлены в одну сторону. См. Рис. 3-11 Л.Р. Нейман, К.С. Демирчян Теоретические основы электротехники, т.1, Л., Энергоиздат, 1981 Vnbiryukov (обс.) 13:59, 13 апреля 2017 (UTC)vnbiryukov

Этот рисунок, вообще, не несёт никакого смысла. Стрелки есть у векторов. У напряжения нет стрелок. Alexander Mayorov (обс.) 15:11, 13 апреля 2017 (UTC)

фраза про «математически корректное утверждение…», которое «физически ложно» очень понравилась. Показал его многим коллегам, все (позитивно) оценили. Автору огромное спасибо, как ныне говорят «респект»! 92.243.107.243 07:58, 7 марта 2019 (UTC)АИ.

ru.wikipedia.org