Закон Ома. Для цепей и тока. Формулы и применение
Георг Симон Ом начал свои исследования вдохновляясь знаменитым трудом Жана Батиста Фурье «Аналитическая теория тепла». В этой работе Фурье представлял тепловой поток между двумя точками как разницу температур, а изменение теплового потока связывал с его прохождением через препятствие неправильной формы из теплоизолирующего материала. Аналогично этому Ом обуславливал возникновение электрического тока разностью потенциалов.
История
Исходя из этого Ом стал экспериментировать с разными материалами проводника. Для того, чтобы определить их проводимость он подключал их последовательно и подгонял их длину таким образом, чтобы сила тока была одинаковой во всех случаях.
Важно при таких измерениях было подбирать проводники одного и того же диаметра. Ом, замеряя проводимость серебра и золота, получил результаты, которые по современным данным не отличаются точностью. Так, серебряный проводник у Ома проводил меньше электрического тока, чем золотой. Сам Ом объяснял это тем, что его проводник из серебра был покрыт маслом и из-за этого, по всей видимости, опыт не дал точных результатов.
Однако не только с этим были проблемы у физиков, которые в то время занимались подобными экспериментами с электричеством. Большие трудности с добычей чистых материалов без примесей для опытов, затруднения с калибровкой диаметра проводника искажали результаты тестов. Еще большая загвоздка состояла в том, что сила тока постоянно менялась во время испытаний, поскольку источником тока служили переменные химические элементы. В таких условиях Ом вывел логарифмическую зависимость силы тока от сопротивления провода.
Немногим позже немецкий физик Поггендорф, специализировавшийся на электрохимии, предложил Ому заменить химические элементы на термопару из висмута и меди. Ом начал свои эксперименты заново. В этот раз он пользовался термоэлектрическим устройством, работающем на эффекте Зеебека в качестве батареи. К нему он последовательно подключал 8 проводников из меди одного и того же диаметра, но различной длины. Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.
Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.
В результате нового эксперимента Ом пришел к формуле:
Х = a / b + l
Здесь X – интенсивность магнитного поля провода, l – длина провода, a – постоянная величина напряжения источника, b – постоянная сопротивления остальных элементов цепи.
Если обратиться к современным терминам для описания данной формулы, то мы получим, что Х – сила тока, а – ЭДС источника, b + l – общее сопротивление цепи.
Закон Ома для участка цепиЗакон Ома для отдельного участка цепи гласит: сила тока на участке цепи увеличивается при возрастании напряжения и уменьшается при возрастании сопротивления этого участка.
I = U / R
Исходя из этой формулы, мы можем решить, что сопротивление проводника зависит от разности потенциалов. С точки зрения математики, это правильно, но ложно с точки зрения физики. Эта формула применима только для расчета сопротивления на отдельном участке цепи.
Чтобы рассчитать сопротивление проводника, нужно перемножить его длину на удельное сопротивление его материала и разделить на площадь поперечного сечения.
Таким образом формула для расчета сопротивления проводника примет вид:
R = p ⋅ l / s
Закон Ома для полной цепиОтличие закона Ома для полной цепи от закона Ома для участка цепи заключается в том, что теперь мы должны учитывать два вида сопротивления. Это «R» сопротивление всех компонентов системы и «r» внутреннее сопротивление источника электродвижущей силы. Формула таким образом приобретает вид:
Формула таким образом приобретает вид:
I = U / R + r
Закон Ома для переменного токаПеременный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Попробуем разобраться, в чем реальная разница между реактивным и активным сопротивлением в цепи с переменным током. Вы уже должны были понять, что значение напряжение и силы тока в такой цепи меняется со временем и имеют, грубо говоря, волновую форму.
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера примененияЗакон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Похожие темы:
Закон Ома для участка цепи. Расчет электрического сопротивления проводника
|
Цель |
Обобщить знания учащихся об электрическом токе и напряжении и установить на опыте зависимость силы тока от напряжения на однородном участке электрической цепи и от сопротивления этого участка, вывести закон Ома для участка цепи. |
|
Задачи урока |
|
|
|
Урок формирования новых знаний с использованием электронных образовательных ресурсов. |
|
Формы работы учащихся |
Фронтальная, групповая, индивидуальная. |
|
Используемые приемы обучения |
проблемный; исследовательский. |
|
Методы |
Словесный, частично-поисковый, Практический, методы контроля и самоконтроля. |
|
Средства обучения |
Мел, доска, компьютер, мультимедийный проектор, наличие доступа в Интернет. |
|
Демонстрации |
1.Зависимость силы тока от сопротивления проводника при постоянном напряжении; ЦОР Физика. |
|
Формируемые УУД |
|
|
Ожидаемые результаты |
|
Ход урока
1.
 Организационный момент (приветствие, присутствие).
Организационный момент (приветствие, присутствие).2. Этап актуализации знаний
Учитель: Ребята, обратите внимание на слайд. Как Вы видите тема нашего сегодняшнего урока звучит как «Закон Ома для участка цепи. Расчет электрического сопротивления».
Но прежде, чем начать изучать новый материал, следует выяснить, к каким из физических явлений относится данная тема? (выслушиваются варианты ответа, возможно, понадобится вспомнить все остальные пять физических явлений). Итак, подведем итог, явления, к которым имеет отношение тема сегодняшнего урока называются электрические . Давайте вспомним, что же такое электрические явления? (выслушиваются предположения детей, далее работа по слайду).
Учитель: замечательно, ребята! Теперь когда мы знаем что такое электрические явления, необходимо поставить цель нашего урока, к которой мы будем стараться прийти в конце.
3. Мотивационный этап
Ребята, прежде чем устанавливать зависимости между физическими величинами, нам необходимо четко усвоить каждую из этих величин. Для этого давайте повторим по слайдам все физические величины, ос которыми нам сегодня придется работать при решении задач, а также повторим составные части электрической цепи, какие приборы помогают нам снимать показания.
Чтобы было легче понять, что такое сила тока, представьте, что перед Вами вместо провода труба, в которой находится вода, а воде плавают маленькие рыбки. Так вот рыбки, благодаря действию течения потока воды, начинают одновременно плыть в одном направлении. Если мы представим, что вместо рыбок у нас электроны, а вместо течения воды — электрическое поле, то в таком случае в проводнике возникает электрический ток, то есть упорядоченное движение заряженных частиц. За направление тока мы принимаем направление движения положительно заряженных частиц, то есть от + к -.
А теперь вспомним, что такое напряжение.
Если мы представим, что под действием течения воды в трубе одна из рыбок переместилась влево на расстояние 1 м, то мы можем сказать, что течение совершило работу по перемещению рыбки. Так и в случае электричества. Электрическое поле, перемещая заряженную частицу совершает работу, и если мы разделим значение этой работы на величину заряда частицы, то получим величину, которая называется электрическое напряжение.
Обратимся к еще одной физической величине
Электроны, передвигаясь вдоль проводника испытывают различные препятствия. Так, например, хорошими проводниками электрического тока являются металлы, а у них имеется кристаллическая решетка, чем более плотно устроена эта решетка, тем и электронам сложнее перемещаться из одного места проводника в другое, а следовательно электроны встречают некоторое сопротивление. Я неспроста сказала сопротивление, именно из этого физического смысла и вытекает понятие электрического сопротивления. Чем сложнее электронам передвигаться по проводнику, тем меньшее их количество в единицу времени будет перемещаться сквозь поперечное сечение и следовательно сила тока также будет меньше.
Давайте выясним, от каких параметров зависит электрическое сопротивление
И последнее, что мы сделаем перед изучением нового материала, это повторим, как правильно собираться электрические цепи по схемам, основные составные части электрической цепи.
4. Этап изучения нового материала
Ребята, зависимость этих трех физических величин друг от друга в 1827 году впервые вывел немецкий ученый Георг Ом. Поэтому и формула носит название его фамилии. Закон Ома.
Рассматривая зависимость друг от друга двух величин, третья должна оставаться постоянной. Мы с Вами сейчас опытным путем подтвердим что сила тока на участке цепи действительно будет увеличиваться при увеличении напряжения, но с учетом того, что сопротивление у нас будет величиной постоянной. (обращаемся к ЦОР).
Мы с Вами сейчас опытным путем подтвердим что сила тока на участке цепи действительно будет увеличиваться при увеличении напряжения, но с учетом того, что сопротивление у нас будет величиной постоянной. (обращаемся к ЦОР).
По графику мы видим, что сила тока увеличивалась ровно настолько же, насколько мы увеличивали напряжение, а значит первое утверждение из закона Ома о том, «что сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка,» ВЕРНО!
Теперь выясним, как же сила тока зависит от сопротивления при постоянном напряжении и прав ли бы Георг Ом в своих суждениях.
По графику мы убедились с Вами «Что сила тока обратно пропорциональна сопротивлению».
А теперь предлагаю Вам правило треугольника, для более удобного запоминая данной формулы
5. Этап применения нового знания
Приступим к решению задач. От простого к сложному.
Задача №1
Напряжение на зажимах электрического утюга 220(В), сопротивление нагревательного элемента утюга 50 (Ом). Чему равна сила тока в нагревательном элементе? Рассчитайте величину электрического заряда, проходящего через проводник за время 0,5 сек?
Задача №2
Используя данные предыдущей задачи, рассчитайте длину проводника (спирали в нагревательном элементе утюга), если известно, что площадь поперечного сечения проводника S равна 0,8 кв.мм., и проводник выполнен из меди.
Задача №3
Сборник ОГЭ физика 2017. автор ЗОРИН Н. И.
Вариант 6 № 16
Через поперечное сечение проводника прошел заряд, равный 6 Кл, за время, равное 5 минутам. Сопротивление проводника 5 (Ом). Рассчитайте напряжение проводника.
Задача №4
Вариант 8 № 18
Задача №5
Вариант 9 № 16
Как изменится сила тока в электрической цепи, если площадь поперечного сечения проводника уменьшить вдвое?
Задача №6
Вариант 9 №15
6.
 Рефлексивный этап
Рефлексивный этапУчитель: А сейчас подведем итог нашего урока. Вспомним цели, которые мы ставили перед собой! Как Вы считаете, удалось ли нам их добиться? Тогда давайте ответим на следующие вопросы: Какую взаимозависимость между силой тока, напряжением и сопротивлением на участке цепи мы раскрыли?
Ученики: Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.(слайд)
Учитель: В какой формуле выражена эта взаимозависимость?
Ученики: Взаимозависимость силы тока, напряжения и сопротивления выражена законом Ома для участка цепи.
Учитель: Кто впервые установил эту зависимость?
Ученики: Георг Ом (немецкий физик) в 1927 году.
Учитель: А как зависит электрическое сопротивление от длины проводника и площади поперечного сечения?
Ученики:Чем больше длина, тем больше сопротивление, чем больше площадь поперечного сечения, тем меньше сопротивление.
Учитель: Замечательно, надеюсь, данное занятие было полезным для Вас и теперь Вы сможете применять полученные знания на практике при решении задач.
Ток, напряжение, сопротивление. Закон Ома.
Мы начинаем публикацию материалов новой рубрики «Основы электроники«, и в сегодняшней статье речь пойдет о фундаментальных понятиях, без которых не проходит обсуждение ни одного электронного устройства или схемы. Как вы уже догадались, я имею ввиду ток, напряжение и сопротивление 🙂 Кроме того, мы не обойдем стороной закон Ома, который определяет взаимосвязь этих величин, но не буду забегать вперед, давайте двигаться постепенно.
Итак, давайте начнем с понятия напряжения.
Напряжение.

По определению напряжение — это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом в точку с высоким потенциалом (т. е. первая точка имеет более отрицательный потенциал по сравнению со второй). Из курса физики мы помним, что потенциал электростатического поля — это скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду. Давайте рассмотрим небольшой пример:
В пространстве действует постоянное электрическое поле, напряженность которого равна E. Рассмотрим две точки, расположенные на расстоянии d друг от друга. Так вот напряжение между двумя точками представляет из себя ни что иное, как разность потенциалов в этих точках:
U = \phi_1\medspace-\medspace \phi_2
В то же время не забываем про связь напряженности электростатического поля и разности потенциалов между двумя точками:
\phi_1\medspace-\medspace \phi_2 = Ed
И в итоге получаем формулу, связывающую напряжение и напряженность:
U = Ed
В электронике, при рассмотрении различных схем, напряжение все-таки принято считать как разность потенциалов между точками. Соответственно, становится понятно, что напряжение в цепи — это понятие, связанное с двумя точками цепи. То есть говорить, к примеру, «напряжение в резисторе» — не совсем корректно. А если говорят о напряжении в какой-то точке, то подразумевают разность потенциалов между этой точкой и «землей». Вот так плавно мы вышли к еще одному важнейшему понятию при изучении электроники, а именно к понятию «земля» 🙂 Так вот «землей» в электрических цепях чаще всего принято считать точку нулевого потенциала (то есть потенциал этой точки равен 0).
Давайте еще пару слов скажем о единицах, которые помогают охарактеризовать величину напряжения. Единицей измерения является Вольт (В). Глядя на определение понятия напряжения мы можем легко понять, что для перемещения заряда величиной 1 Кулон между точками, имеющими разность потенциалов 1 Вольт, необходимо совершить работу, равную 1 Джоулю.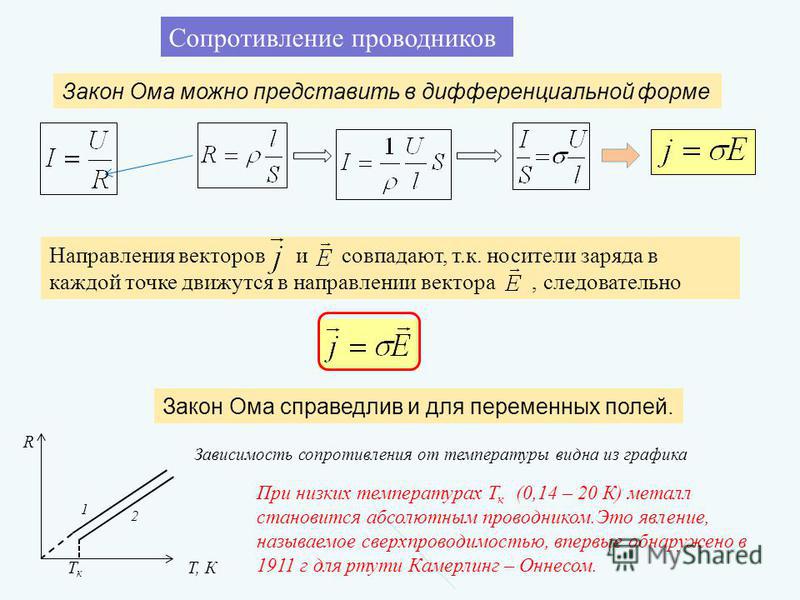 С этим вроде бы все понятно и можно двигаться дальше 🙂
С этим вроде бы все понятно и можно двигаться дальше 🙂
А на очереди у нас еще одно понятие, а именно ток.
Ток, сила тока в цепи.
Что же такое электрический ток?
Давайте подумаем, что будет происходить если под действие электрического поля попадут заряженные частицы, например, электроны… Рассмотрим проводник, к которому приложено определенное напряжение:
Из направления напряженности электрического поля (E) мы можем сделать вывод о том, что \phi_1 > \phi_2 (вектор напряженности всегда направлен в сторону уменьшения потенциала). На каждый электрон начинает действовать сила:
F = Ee
где e − это заряд электрона.
И поскольку электрон является отрицательно заряженной частицей, то вектор силы будет направлен в сторону противоположную направлению вектора напряженности поля. Таким образом, под действием силы частицы наряду с хаотическим движением приобретают и направленное (вектор скорости V на рисунке). В результате и возникает электрический ток 🙂
Ток — это упорядоченное движение заряженных частиц под воздействием электрического поля.
Важным нюансом является то, что принято считать, что ток протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, несмотря на то, что электрон перемещается в противоположном направлении.
Носителями заряда могут выступать не только электроны. Например, в электролитах и ионизированных газах протекание тока в первую очередь связано с перемещением ионов, которые являются положительно заряженными частицами. Соответственно, направление вектора силы, действующей на них (а заодно и вектора скорости) будет совпадать с направлением вектора E. И в этом случае противоречия не возникнет, ведь ток будет протекать именно в том направлении, в котором движутся частицы 🙂
Для того, чтобы оценить ток в цепи придумали такую величину как сила тока. Итак, сила тока (I) — это величина, которая характеризует скорость перемещения электрического заряда в точке. Единицей измерения силы тока является Ампер. Сила тока в проводнике равна 1 Амперу, если за 1 секунду через поперечное сечение проводника проходит заряд 1 Кулон.
Единицей измерения силы тока является Ампер. Сила тока в проводнике равна 1 Амперу, если за 1 секунду через поперечное сечение проводника проходит заряд 1 Кулон.
Мы уже рассмотрели понятия силы тока и напряжения, теперь давайте разберемся каким образом эти величины связаны. И для этого нам предстоит изучить, что же из себя представляет сопротивление проводника.
Сопротивление проводника/цепи.
Термин «сопротивление» уже говорит сам за себя 🙂
Итак, сопротивление — физическая величина, характеризующая свойства проводника препятствовать (сопротивляться) прохождению электрического тока.
Рассмотрим медный проводник длиной l с площадью поперечного сечения, равной S:
Сопротивление проводника зависит от нескольких факторов:
- удельного сопротивления проводника \rho
- длины проводника l
- площади поперечного сечения проводника S
Удельное сопротивление — это табличная величина. Формула, с помощью которой можно вычислить сопротивление проводника выглядит следующим образом:
R = \rho\medspace \frac{l}{S}
Для нашего случая \rho будет равно 0,0175 (Ом * кв. мм / м) — удельное сопротивление меди. Пусть длина проводника составляет 0.5 м, а площадь поперечного сечения равна 0.2 кв. мм. Тогда:
R =0,0175 \cdot \frac{0.5}{0.2} = 0.04375\medspace Ом
Как вы уже поняли из примера, единицей измерения сопротивления является Ом 🙂
С сопротивлением проводника все ясно, настало время изучить взаимосвязь напряжения, силы тока и сопротивления цепи.
Закон Ома.
И тут на помощь нам приходит основополагающий закон всей электроники — закон Ома:
Сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению рассматриваемого участка цепи.
Рассмотрим простейшую электрическую цепь:Как следует из закона Ома напряжение и сила тока в цепи связаны следующим образом:
I = \frac{U}{R}
Пусть напряжение составляет 10 В, а сопротивление цепи равно 200 Ом. Тогда сила тока в цепи вычисляется следующим образом:
Тогда сила тока в цепи вычисляется следующим образом:
I = \frac{10}{200} = 0.05 = 50\medspaceмА
Как видите, все несложно 🙂 Пожалуй на этом мы и закончим сегодняшнюю статью, спасибо за внимание и до скорых встреч!
Глава 21. Электрический ток. Законы Ома и Джоуля-Ленца
Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.
Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени
(21.1) |
Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю. Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.
Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то
(21. |
Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21.2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид
(21.3) |
Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова resistance — сопротивление).
Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения
(21.4) |
где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.
Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников
(21.4) |
Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно (см. рисунок), то электрическое напряжение на каждом проводнике будет одинаковым , ток через участок будет равен сумме токов, текущих через каждый проводник , а величина, обратная эквивалентному сопротивлению всего участка, равно сумме обратных сопротивлений отдельных проводников
(21.5) |
Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду
Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду
(21.6) |
В этом случае сила тока в цепи равна
(21.7) |
Формула (21.7) называется законом Ома для замкнутой электрической цепи.
При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно
(21.8) |
(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения. Поэтому отношение
(21.9) |
которое называется мощностью тока, не зависит от времени наблюдения. Формулу (21.9) также называют законом Джоуля-Ленца.
Рассмотрим теперь задачи.
Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21. 1.1 — ответ 2).
1.1 — ответ 2).
Согласно определению (21.1) находим среднюю силу тока в канале молнии (задача 21.1.2)
(ответ 2).
Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).
По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21.1.4)
Таким образом, сила тока уменьшилась в 4 раза (ответ 3).
Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем. Поэтому в задаче 21.1.5 имеем, например, используя крайнюю точку графика
(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.
Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6
где — удельное сопротивление меди, — длина проводника, — его радиус. Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
(ответ 3).
Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21. 1.7) сила тока в проводнике не изменится (ответ 4).
1.7) сила тока в проводнике не изменится (ответ 4).
В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21.7). Имеем
где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).
В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
где — внутреннее сопротивление источника (ответ 3).
Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (задача 21.1.10) приведет к увеличению мощности тока в 4 раза (ответ 2).
В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).
Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21.2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно
(ответ 2).
Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что
(ответ 2).
При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что
(ответ 1).
Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка
а затем и эквивалентное сопротивление всей цепи
(ответ 3).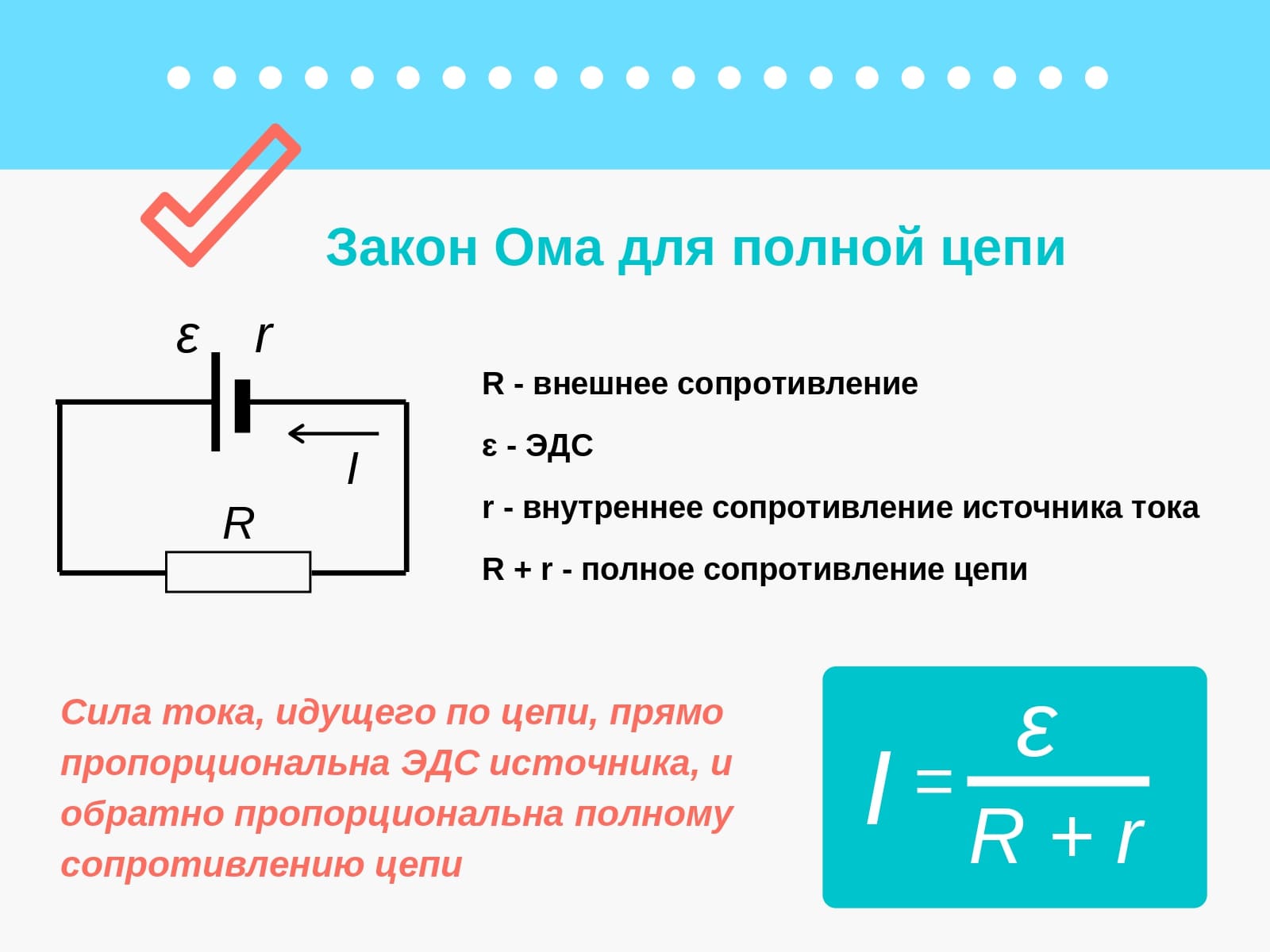
При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т.к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).
Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна
где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:
(ответ 2).
Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
(ответ 1).
Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22.8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).
Введение в электронику. Закон Ома
Серия статей известного автора множества радиолюбительских публикаций Дригалкина В.В. для начинающих радиолюбителей
Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“
В школе Вы, несомненно, проходили, а, если еще нет – обязательно будете изучать Закон Ома. Он определяет соотношение между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома.
Суть закона следующая: порождаемый напряжением ток обратно пропорционален сопротивлению, которое ему приходится преодолевать, и прямо пропорционален порождающему напряжению.
Именно такое определение содержит учебник по физике. Я же попробую объяснить этот процесс на примере с водопроводной трубой. Припоминаете, что такая же аналогия использовалась, когда мы говорили о токе? Представьте себе, что вода – некое подобие электрического тока, образуемого направленным движением электронов в проводнике, а напряжение – аналог давления (напора) воды. Сопротивление – это та сила противодействия среды их движению, которую приходится преодолевать электронам (воде), в результате выделяется теплота. Именно такая модель представлялась Георгу Ому в 1820-е годы, когда он занялся исследованием природы происходящего в электрических цепях. Чем выше давление воды в трубе, тем относительно большая доля энергии расходуется на преодоление сопротивления, поскольку в трубах усиливается турбулентность потока. Из этого исходил Ом, приступая к опытам по измерению зависимости силы тока от напряжения. Очень скоро выяснилось, что ничего подобного в электрических проводниках не происходит: сопротивление вещества электрическому току вовсе не зависит от приложенного напряжения. В этом, по сути, и заключается закон Ома, который (для отдельного участка цепи) записывается так:
Чем выше давление воды в трубе, тем относительно большая доля энергии расходуется на преодоление сопротивления, поскольку в трубах усиливается турбулентность потока. Из этого исходил Ом, приступая к опытам по измерению зависимости силы тока от напряжения. Очень скоро выяснилось, что ничего подобного в электрических проводниках не происходит: сопротивление вещества электрическому току вовсе не зависит от приложенного напряжения. В этом, по сути, и заключается закон Ома, который (для отдельного участка цепи) записывается так:
I = V/R,
В этой формуле I – сила тока, V – напряжение, приложенное к участку цепи, а R – электрическое сопротивление участка цепи (см. Рис. 1).
На этой схеме V иногда называют электродвижущей силой (ЭДС) , которая создает ток I. Этот ток, протекая по сопротивлениям, создает на них падения напряжения. Так если сопротивлений два, то XJ1 + U2 = ЭДС. Причем XJ1 = IRx, U2 = IR2. В реальных условиях эта схема содержит целых три сопротивления: R (сопротивление участка цепи), внутреннее сопротивление амперметра и внутреннее сопротивление источника тока.
Сегодня мы понимаем, что электрическая проводимость обусловлена движением свободных электронов, а сопротивление – столкновением этих электронов с атомами кристаллической решетки. При каждом таком столкновении часть энергии свободного электрона передается атому, который, начинает колебаться более интенсивно, и в результате мы наблюдаем нагревание проводника под действием электрического тока. Повышение напряжения в цепи никак не сказывается на доле тепловых потерь такого рода, и соотношение напряжения и электрического тока остается постоянным. Однако, когда Георг Ом сформировал свой закон, атомная теория строения вещества находилась в зачаточном состоянии, а до открытия электрона было еще несколько десятилетий. Таким образом, для него формула I = V/R была чисто экспериментальным результатом. Сегодня мы имеем достаточно стройную и одновременно сложную теорию электропроводности и понимаем, что закон Ома в его первозданном виде – всего лишь грубое приближение. Однако это не мешает нам с успехом использовать его для расчета самых сложных электрических цепей, применяющихся в промышленности и быту. Так как же применить Закон Ома на практике? Возьмем, к примеру, светодиод, который необходимо “запитать” от 9 В. Источником питания будет батарейка типа РРЗ, известная в народе как “Крона” (см. Рис. 2).
Таким образом, для него формула I = V/R была чисто экспериментальным результатом. Сегодня мы имеем достаточно стройную и одновременно сложную теорию электропроводности и понимаем, что закон Ома в его первозданном виде – всего лишь грубое приближение. Однако это не мешает нам с успехом использовать его для расчета самых сложных электрических цепей, применяющихся в промышленности и быту. Так как же применить Закон Ома на практике? Возьмем, к примеру, светодиод, который необходимо “запитать” от 9 В. Источником питания будет батарейка типа РРЗ, известная в народе как “Крона” (см. Рис. 2).
Если светодиод подключить в “Кроне” напрямую, он попросту сгорит. Светодиод имеет определенное напряжение и силу тока, которая через него может проходить . В большинстве случаев ток ограничивается несколькими десятками мА (миллиампер) и напряжение 2..4,5 В. Яркие светодиоды обычно рассчитаны на напряжение 3 В и ток 30 мА, т.е. при данном токе потребления светодиод находится под напряжением 3 В. Следовательно, напряжение на светодиоде зависит от тока и по Закону Ома, для нормальной работы светодиода нужно подобрать всего лишь сопротивление (R) в цепи светодиода (см. Рис. 2).
Для начала необходимо получить разность напряжения питания цепи от напряжения светодиода: 9 – 3 = 6 В. Переводим ток светодиода в амперы: 30 мА = 0,03 А. И находим сопротивление, поделив полученное напряжение на ток светодиода: 6/0,03 = 200 Ом. Отсюда следует, что резистор R в данной цепи должен иметь сопротивление 200 Ом. Вот так мы применили на практике Закон Ома. Понятное дело, что более сложные цепи требует сложнейших расчетов. Здесь мы сделает отступление, чтобы получше узнать батарейку. Батарейка – источник электричества для автономного питания разнообразных устройств, который делится на солевые, щелочные и литиевые (Рис. 3). Солевые батарейки предназначены для использования в приборах с низким потреблением энергии, например, в пультах дистанционного управления. Щелочные элементы (Alkalin) идеально подходят для питания настольных часов. Литиевые батарейки обычно имеют напряжение, кратное 3 В, и нашли применение в компьютерных системных платах (материнских) для сохранения настроек BlOSa. Цилиндрические батарейки имеют несколько типов: “AAA” (мизинчиковые), “АА” (пальчиковые) , “С” и “D” . Чем больше размером батарейка, тем большей мощностью она обладает. 3R12 пришла к нам из XX века и сегодня практически не применяется в устройствах, ведь ее можно составить из трех последовательно соединенных полторовольтовых батареек: 1,5В + 1,5В + 1,5В = 4,5В. Старение батареек приводит к химической реакции, которая разрушает корпус источника питания. Поэтому батарейки текут. Хотя производители и заявляют, что герметизация корпуса стала идеальной, даже дорогие батарейки протекают. Предупредить этот процесс можно периодической проверкой срока годности.
Литиевые батарейки обычно имеют напряжение, кратное 3 В, и нашли применение в компьютерных системных платах (материнских) для сохранения настроек BlOSa. Цилиндрические батарейки имеют несколько типов: “AAA” (мизинчиковые), “АА” (пальчиковые) , “С” и “D” . Чем больше размером батарейка, тем большей мощностью она обладает. 3R12 пришла к нам из XX века и сегодня практически не применяется в устройствах, ведь ее можно составить из трех последовательно соединенных полторовольтовых батареек: 1,5В + 1,5В + 1,5В = 4,5В. Старение батареек приводит к химической реакции, которая разрушает корпус источника питания. Поэтому батарейки текут. Хотя производители и заявляют, что герметизация корпуса стала идеальной, даже дорогие батарейки протекают. Предупредить этот процесс можно периодической проверкой срока годности.
Какие только детали не потребуются для изготовления электронных схем. Здесь и резисторы, и транзисторы, и конденсаторы, и диоды… Из всего разнообразия деталей необходимо выбрать по внешнему виду нужную, расшифровать надпись на ее корпусе, определить выводы и распознать ее на принципиальной схеме. О том, как это сделать, и будет рассказано далее. Принципиальная схема – изображение устройства в виде значков, которые в реальности представляют радиодетали, и связующих между ними линий (соединений). Рядом с каждым из таких элементов указывают их буквенно-цифровой индекс и номинал . Например, прямоугольником обозначают резистор, а надпись рядом с ним Rl lO kOm расшифровывается так: R – резистор; 1 – его индекс; lO kOm – сопротивление.
Перейти к следующей статье: “Резисторы”
§ 7. Закон Ома | Электротехника
Закон Ома для электрической цепи.
Согласно этому закону сила тока I в электрической цепи равна э. д. с. Е источника, поделенной на сопротивление цепи Rц, т. е.
I = E / Rц (7)
Полное сопротивление замкнутой электрической цепи (рис. 13) можно представить в виде суммы сопротивления внешней цепи R (например, какого-либо приемника электрической энергии) и внутреннего сопротивления Ro источника. Поэтому сила тока
13) можно представить в виде суммы сопротивления внешней цепи R (например, какого-либо приемника электрической энергии) и внутреннего сопротивления Ro источника. Поэтому сила тока
I = E / (R+Ro) (8)
Чем больше э. д. с. Е источника и чем меньше сопротивление электрической цепи, тем больший ток проходит по этой цепи.
Из формулы (7) следует, что э. д. с. источника электрической энергии равна произведению силы тока на полное сопротивление электрической цепи:
E = IRц (7)
Закон Ома для участка электрической цепи.
Закон Ома может быть применен не только ко всей цепи, но и к любому ее участку, например между точками а и б (см. рис. 13).
Рис. 13. Схема простейшей электрической цепи и Рис 14. Прохождение электрического тока по проводникам аналогично прохождению воды по трубам
В этом случае э. д. с. Е источника в формуле (7) должна быть заменена разностью потенциалов между началом и концом рассматриваемого участка, т. е. напряжением U, а вместо сопротивления всей цепи в формулу должно быть подставлено сопротивление R данного участка. В этом случае закон Ома формулируется следующим образом. Сила тока I на данном участке электрической цепи равна напряжению U, приложенному к участку, поделенному на сопротивление R этого участка:
I = U / R (9)
Прохождение электрического тока по проводникам полностью аналогично прохождению воды по трубам (рис. 14).
Чем больше разность уровней воды при входе и выходе из трубы (напор) и чем больше поперечное сечение трубы, тем больше воды протекает сквозь трубу в единицу времени. Точно так же, чем больше разность электрических потенциалов (напряжение) на зажимах источника или приемника электрической энергии и чем меньше его сопротивление (т. е. чем больше площадь поперечного сечения проводника), тем больший ток проходит по нему.
Из формулы (9) следует, что напряжение U, действующее на некотором участке цепи, равно произведению силы тока I на сопротивление R этого участка:
U = IR (10)
Так как потенциал электрического поля в начале участка электрической цепи больше, чем в конце, разность потенциалов, или напряжение U, приложенное к участку электрической цепи, часто называют падением напряжения на данном участке.
Сопротивление R участка цепи равно напряжению, приложенному к данному участку, поделенному на силу тока на этом участке, т. е.
R = U / I (11)
Если сопротивление R не зависит от проходящего по нему тока и приложенного к нему напряжения, то его вольт-амперная характеристика, т. е. зависимость силы тока I от напряжения U, представляет собой прямую линию 1 (рис. 15).
Рис. 15. Вольт-амперные характеристики линейных и нелинейных сопротивлений
Такие сопротивления называют линейными, а электрические цепи, в которых включены подобные сопротивления,— линейными цепями.
Однако в электротехнике широко применяют и такие устройства, сопротивление которых резко изменяется в зависимости от силы или направления проходящего через них тока либо приложенного напряжения. Подобные сопротивления имеют вольт-амперную характеристику, отличающуюся от прямой (кривая 2 на рис. 15), и называются поэтому нелинейными сопротивлениями.
Простейшим нелинейным сопротивлением является электрическая лампа накаливания. При протекании тока по металлической нити лампа нагревается и сопротивление ее возрастает. Следовательно, при увеличении приложенного к лампе напряжения сила тока будет возрастать не прямо пропорционально напряжению, а в несколько меньшей степени.
В принципе большинство электрических устройств может быть представлено в виде нелинейного сопротивления, так как при изменении силы тока меняется температура данного устройства, а следовательно, и его сопротивление. Однако у многих из них вольт-амперные характеристики в рабочем диапазоне изменений напряжения и тока мало отличаются от прямой, поэтому приближенно можно их считать линейными сопротивлениями.
К сопротивлениям с нелинейной вольт-амперной характеристикой относятся электрические лампы накаливания, термисторы (полупроводниковые резисторы, сопротивление которых сильно изменяется при изменении температуры), полупроводниковые диоды, тиристоры и транзисторы, электронные лампы и пр.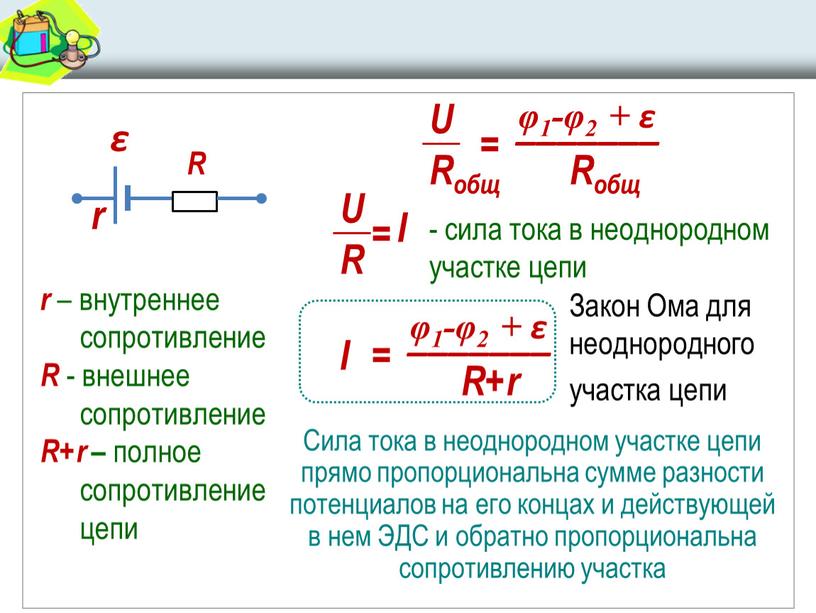 Нелинейные сопротивления широко используют в электротехнике для автоматического регулирования силы тока и напряжения в электрических цепях, электрических измерений, выпрямления тока и пр.
Нелинейные сопротивления широко используют в электротехнике для автоматического регулирования силы тока и напряжения в электрических цепях, электрических измерений, выпрямления тока и пр.
Закон Ома. Методические материалы
Цифровой ресурс может использоваться для обучения в рамках программы основной и средней школы (базового уровня).
Компьютерная программа позволяет провести серию экспериментов по теме «Закон Ома».
Краткая теория
Немецкий физик Георг Симон Ом (16.III.1787–7.VII.1854) в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику, пропорциональна напряжению U на концах проводника:
|
|
где R = const.
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
|
|
Эта формула выражает закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений внутреннего и внешнего участков цепи. Сопротивление r неоднородного участка можно рассматривать как внутреннее сопротивление источника тока.
Сопротивление r неоднородного участка можно рассматривать как внутреннее сопротивление источника тока.
Работа с моделью
Можно выбрать три варианта проведения опытов:
- . В качестве сопротивления выступает лампочка накаливания. Можно изменять напряжение источника питания, замыкать и размыкать цепь с помощью ключа, снимать показания с амперметра и вольтметра.
- . Вместо лампочки в данной работе присутствует реостат и сопротивление, с которого можно снимать показания амперметра и вольтметра при фиксированном источнике питания. Можно замыкать и размыкать цепь с помощью ключа, изменять сопротивление реостата.
- . Предназначена для изучения темы «Закон Ома для полной цепи». На схеме присутствует источник питания (батарейка), имеется возможность изменять его внутреннее сопротивление. Можно замыкать и размыкать цепь с помощью ключа, изменять сопротивление реостата, снимать показания с вольтметра и амперметра.
Рекомендации по применению модели
Данная модель может быть применена в качестве иллюстрации на уроках изучения нового материала и решения задач по теме «Закон Ома для участка цепи», «Закон Ома для полной цепи»». На примере этой модели можно рассмотреть с учащимися зависимость силы тока в цепи от напряжения, от внешнего и внутреннего сопротивления.
Пример планирования урока с использованием модели
Тема «Закон Ома»
Цель урока: с помощью компьютерной модели получить зависимость силы тока на участке цепи от напряжения на этом участке и его сопротивления.
|
|||||||||||||||||||||||||
|
Таблица 1. |
Примеры заданий для лабораторной работы
-
Выберите цепь 1 в модели «Закон Ома».
Проведя измерения, заполните таблицу.
U, В 2,4 3,6 4,2 6 I, А Постройте график зависимости силы тока от напряжения (можно сразу дать систему координат). Сделайте вывод о зависимости силы тока от напряжения.
-
Выберите модель «Экспериментальная проверка закона Ома». Изменяя сопротивление реостата заполните таблицу:
R, Ом 2 4 6 8 10 I, А Постройте график зависимости силы тока от сопротивления (можно сразу дать систему координат). Сделайте вывод о зависимости силы тока от сопротивления.
-
Сформулируйте зависимость силы тока от напряжения и сопротивления. Сравните свои результаты с формулировкой закона Ома для участка цепи в учебнике.
Сопротивление и закон Ома | Книга Ultimate Electronics
Ultimate Electronics: практическое проектирование и анализ схем
Как решить задачи закона Ома для резисторов. Микроскопические причины макроскопической линейности закона Ома. Читать 11 мин
Читать 11 мин
В разделе «Электроны в движении» мы обсуждали, как электрические поля вызывают силу → F = qe → E на электрон. Так же, как любой объект, испытывающий чистую силу, электрон будет ускоряться → Fnet = me → a в ответ на эту силу.Со временем это ускорение вызывает увеличение скорости: → a = d → vdt . Скорость носителей заряда можно описать как электрический ток.
Для свободных электронов, летающих в вакууме, это конец истории.
Однако для электронов, движущихся в материале — обычно, но не всегда в твердом теле — столкновения между электроном и самим материалом являются невероятно доминирующим фактором в общем движении электрона.
Хотя электрон все еще ускоряется электрическим полем, он часто теряет энергию из-за столкновений с материалом.Каждое столкновение рассеивает кинетическую энергию , которую электрон накопил в материале, который становится теплом.
В результате, чтобы электроны двигались через материал с постоянной средней скоростью (нулевое среднее ускорение), нам все еще нужно продолжать добавлять энергию, чтобы преодолеть кинетическую энергию, потерянную при столкновениях с неподвижным материалом. Это свойство называется сопротивлением .
(Из изучения механики и кинематики, существует спектр между упругими столкновениями, которые сохраняют полную кинетическую энергию, и неупругими столкновениями, которые не сохраняют полную кинетическую энергию, потому что часть этой энергии преобразуется в тепло, звук, деформацию материал и т. д.В случае трения или омического сопротивления мы имеем в виду неупругие столкновения.)
Электрическое сопротивление при столкновении аналогично сопротивлению воздуха.
Представьте себе мяч для настольного тенниса, упавший с башни. Под действием силы тяжести мяч ускоряется по направлению к земле. Если бы не было сопротивления воздуха, скорость мяча продолжала бы расти и расти без ограничений. Но в воздухе происходят столкновения между мячом и молекулами воздуха, поэтому мяч достигает некоторой установившейся скорости, которую в этой ситуации часто называют «конечной скоростью».При этой установившейся скорости энергия, полученная при движении вниз в поле гравитационной потенциальной энергии, равна энергии, потерянной в результате столкновений при выталкивании воздуха с пути. Когда мы усредняем многие из этих микроскопических столкновений, оказывается, что мяч не ускоряется и не замедляется, а вместо этого продолжает падать с постоянной скоростью.
Это действительно рассеивающая кинетическая энергия. В противном случае добавление энергии привело бы к постоянному ускорению, а не просто к поддержанию постоянной скорости.
Разумна и жидкая аналогия. Для проталкивания жидкости по трубе требуется энергия (обычно определяемая как разность давлений) для поддержания постоянной скорости (обычно указываемой как расход), потому что поток постоянно теряет энергию из-за сопротивления внутренних стенок трубы, а также вязким взаимодействиям между молекулами жидкости. Эти силы сопротивления действительно рассеиваются в виде тепла. (Однако, поскольку вода имеет такую высокую удельную теплоемкость, мы обычно не замечаем этого повышения температуры в повседневной жизни!)
Автомобиль, движущийся с постоянной скоростью по ровной автомагистрали, демонстрирует и то, и другое: для поддержания постоянной скорости необходимо добавлять энергию из-за сопротивления воздуха, а также сопротивления жидкостей внутри двигателя и трансмиссии, трения в колесе. подшипники, неупругая деформация резиновых покрышек и т. д.Если бы это было не так, мы могли бы просто поставить машину на нейтраль и выключить двигатель, как только наберем крейсерскую скорость.
Когда мы движемся через что-либо, кроме вакуума без трения (или сверхпроводника!), Материалы будут взаимодействовать, сталкиваться, деформироваться и вызывать потери кинетической энергии. Независимо от того, едет ли это автомобиль по шоссе или электрон, путешествующий по металлу, результат один: нужно постоянно добавлять больше энергии просто для поддержания постоянной средней кинетической энергии.
Закон Ома обычно называют:
В = ИК
где R — сопротивление резистора, В — падение напряжения на резисторе, а I ток через резистор. (См. Оставшуюся часть этой главы, в том числе Закон Кирхгофа о напряжении (KVL) и Закон Кирхгофа по току (KCL), Обозначение напряжений, токов и узлов, а также Решение схемных систем для получения дополнительной информации о правильном указании напряжения и тока!)
Поскольку напряжение является мерой работы на единицу заряда, закон Ома означает, что для материалов с более высоким сопротивлением требуется больше работы, чтобы протолкнуть такой же поток тока.
Закон Ома гласит, что сопротивление является линейной функцией, но это правило не универсально ; на самом деле это эмпирический (основанный на наблюдениях, а не на теории). На самом деле это линеаризованная модель триллионов или более взаимодействий атомного масштаба внутри материала, и оказывается, что в среднем , агрегированное поведение выглядит примерно линейным.
Если мы знаем любые два из V, I или R , мы можем найти третью переменную:
В = I⋅RI = VRR = VI
Это одно из самых основных практических уравнений в электронике, поэтому мы уделяем ему особое внимание во всех его формах.
Эти отношения можно рассматривать с теоретической точки зрения при установлении связи токов и напряжений в цепи, но они также имеют практическое значение:
- Если у нас есть известный ток , протекающий через известное сопротивление , мы можем умножить два, чтобы получить напряжение: V = I⋅R .
- Если у нас есть известное напряжение на известном сопротивлении , мы можем разделить два, чтобы получить ток: I = VR .
- Наконец, если у нас есть известное напряжение и известный ток , мы можем разделить два, чтобы получить сопротивление: R = VI .
В математическом смысле, когда мы используем слово известное , мы противопоставляем его переменной неизвестно , для которой мы вычисляем. (См. Системы уравнений.)
Но в практическом смысле известный может означать две несколько разные вещи:
- «Известный» может означать , управляемый извне, или , фиксированный . Например, если у нас есть источник тока, который всегда выдает 2 А, то этот ток известен, потому что он контролируется и устанавливается на определенное значение.
- «Известный» может означать , измеренный . Например, мы можем измерить напряжение 6 В на выходе источника тока. Это напряжение известно, потому что оно измеряется, а не фиксируется каким-либо процессом.
В большинстве вопросов, связанных с законом Ома, мы комбинируем два типа «известных». Чтобы объединить два приведенных выше примера, если наши 2 A источник тока подключен к неизвестному сопротивлению, и мы измеряем 6 В. на выходе мы можем определить, что неизвестное сопротивление составляет:
R = VI = 62 = 3 Ом
Линейность закона Ома чрезвычайно полезна при проведении измерений.Резисторы — это компоненты, которые линейно преобразуют разность напряжений в ток и наоборот, и это полезный эффект во многих аналоговых схемах. Подробнее о вольтметрах, амперметрах и омметрах мы поговорим в разделе «Мультиметры и измерения».
Наш первый пример — одиночный 100 Ом резистор R1, подключенный к источнику напряжения:
Exercise Щелкните схему, затем щелкните «Simulate» и щелкните «Run DC Solver». Это покажет расчетный ток:
I = VR = 5 В 100 Ом = 0.05 А = 50 мА
Затем нажмите «Run DC Sweep». Это настроено для регулировки значения источника напряжения от -5 до +5. Симулятор мгновенно построит график с настройкой напряжения по оси x и результирующим током по оси y.
Вместо того, чтобы управлять сопротивлением с источником напряжения, мы можем вместо этого подключить его к фиксированному источнику тока:
Exercise Щелкните схему, щелкните «Simulate» и «Run DC Solver». Это покажет расчетное напряжение:
ВА = I⋅R = (1 A) ⋅ (100 Ом) = 100 В
Затем нажмите «Run DC Sweep».Это настроено для регулировки значения текущего источника. Симулятор мгновенно построит график с текущими настройками по оси x и результирующим напряжением по оси y.
Использование симулятора CircuitLab для изменения токов и напряжений и построения графика DC Sweep — это очень простая функциональность. Немного более сложный случай — варьировать сопротивление:
Exercise Щелкните схему, щелкните «Simulate» и «Run DC Sweep». Теперь имитатор подключает различные резисторы от 1 до 1000 Ом и строит результирующую кривую тока с сопротивлением в Ом по оси x и током по оси y.
Это работает, устанавливая для параметра DC Sweep значение «R1.R», что означает «сопротивление резистора с именем R1». Просмотр параметров компонента — мощный инструмент моделирования схем.
Сопротивление — это свойство выбора материала (например, алюминия по сравнению с медью) и его физических размеров. Для твердого тела постоянной площади поперечного сечения A и длиной L , сопротивление:
R = ρLA
Размеры имеют смысл: если мы сделаем резистор вдвое длиннее, то расстояние между столкновениями и отводом энергии будет вдвое больше, как у резисторов, соединенных последовательно.Вместо этого, если мы увеличим площадь поперечного сечения, средняя скорость дрейфа будет ниже для того же количества тока, поэтому при каждом столкновении теряется меньше энергии.
Удельное сопротивление ρ является свойством материала, а также функцией температуры: подробнее см. раздел «Практические резисторы: температурный коэффициент».
Почему ток в резистивном материале линейно пропорционален напряжению?
Это часто считается само собой разумеющимся, но на самом деле это не очевидно. В свободном пространстве заряд в постоянном электрическом поле будет иметь линейно возрастающую скорость , а не (в среднем) постоянную скорость в резистивном материале.
Вот одна из возможных моделей:
Даже при нулевом приложенном электрическом поле (т. Е. Нулевом напряжении) заряды не остаются. Из-за теплового движения они постоянно натыкаются.
Теперь давайте приложим электрическое поле (т.е. ненулевое напряжение). Это поле → E поле вызывает силу на заряд:
→ F = q → E = m → а
Эта сила действует для небольшого ускорения заряда в направлении поля. Однако, прежде чем он начнет работать особенно быстро, заряд сталкивается с другими зарядами в материале.Это столкновение вызывает потерю кинетической энергии (преобразованной в тепло в материале), и заряд должен снова начать с нулевой скорости. Оттуда он начинает ускоряться из-за поля, и цикл ускорения и столкновения повторяется.
Предположим, что среднее время между столкновениями равно tcollision . В этом случае между столкновениями → E поле может ускорить заряд от v = 0 до некоторой скорости vmax до столкновения. В этом случае (при фиксированной коллизии ), средняя скорость частицы будет пропорциональна ускорению, обусловленному полем.(Если это неясно, постройте график зависимости скорости заряда от времени. Это будет похоже на пилообразную форму: увеличение от 0 до vmax во время столкновения , затем внезапно падает до 0 и повторяется снова. Средняя скорость ¯¯¯¯¯vd = vmax2 .)
Для получения более подробной информации о том, как все это проявляется со случайными тепловыми колебаниями в трех измерениях, посмотрите модель Drude .
Вы можете спросить, почему у нас среднее время между столкновениями, а не среднее расстояние между столкновениями.Это связано с тем, что тепловая скорость намного больше, чем скорость дрейфа, поэтому эти случайные тепловые скорости в основном определяют, когда происходит столкновение, а не скорость дрейфа, которая важна для определения скорости столкновения.
Для большинства материалов более высокая температура означает более высокие тепловые скорости и более короткое столкновение. , поэтому более высокое сопротивление. Подробнее о взаимосвязи между сопротивлением и температурой см. В разделе «Практические резисторы: температурный коэффициент».
Резисторы
обычно имеют линейную характеристику на много порядков величины тока — в отличие от полупроводникового перехода, как мы увидим позже.
Резисторыобычно имеют линейную характеристику независимо от того, в каком направлении течет ток — также в отличие от полупроводникового перехода.
Подумайте о механической винтовой пружине: сила линейна для крошечных толчков и для больших толчков, но в какой-то момент вы начинаете необратимо деформировать металл (пластическая деформация) и получаете нелинейное поведение.
Таким же образом, если вы превысите пределы резистора, вы можете навсегда изменить его, обычно путем перегрева. Дополнительные сведения см. В следующих нескольких разделах «Мощность и практические резисторы: номинальная мощность (мощность)».
Сверхпроводники когда-то были экзотическими материалами, но становятся все более и более распространенными по мере того, как дешевеют и растут в диапазоне рабочих температур. В настоящее время нет известных материалов, которые были бы сверхпроводниками при комнатной температуре и давлении, но исследования в этой области обнаружили материалы, которые работают при все более высоких температурах.
Сверхпроводники не только имеют низкое сопротивление , но предлагают действительно нулевое сопротивление при протекании тока.
В сверхпроводнике нет внутренних неупругих столкновений между носителями заряда и материалом.
Существуют практические ограничения на сверхпроводники в нескольких измерениях:
- Ток. Сверхпроводник может поддерживать только определенную максимальную плотность тока, известную как критический ток .
- Магнитное поле. Сверхпроводящие материалы имеют ограничения на напряженность магнитного поля, в которой они могут работать.
- Рабочая температура. Сверхпроводящие материалы перестают быть сверхпроводящими при превышении некоторого максимального предела температуры.
В дополнение к этому, сверхпроводники и сверхпроводящие провода все еще относительно сложны с точки зрения производства. Материалы часто бывают хрупкими, их необходимо охлаждать до чрезвычайно низких температур, их трудно соединять и соединять с другими компонентами.
В следующем разделе, Power, мы поговорим о том, куда уходит тепло от этих резистивных столкновений, и больше подумаем о потоках энергии и мощности в целом.
Роббинс, Майкл Ф. Ultimate Electronics: Практическое проектирование и анализ схем. CircuitLab, Inc., 2020, ultimateelectronicsbook.com. Доступно. (Авторские права © CircuitLab, Inc., 2020)
Электрическое сопротивление и закон Ома | Основная теория постоянного тока (DC)
Для обзора, напряжение — это мера потенциальной энергии, доступной для электрических зарядов. Ток — это равномерный дрейф электрических зарядов в ответ на напряжение.У нас может быть напряжение без тока, но у нас не может быть тока без напряжения, которое его мотивирует. Ток без напряжения был бы эквивалентен движению без движущей силы.
Когда электрические заряды проходят через такой материал, как металл, они, естественно, сталкиваются с некоторым трением, точно так же, как жидкость, движущаяся по трубе, неизбежно сталкивается с трением. У нас есть название для этого трения движения электрического заряда: сопротивление . Подобно напряжению и току, сопротивление имеет свою особую единицу измерения: Ом, , названную в честь немецкого физика Георга Симона Ома.
На этом этапе было бы хорошо обобщить и сравнить символы и единицы, которые мы используем для напряжения, тока и сопротивления:
| Кол-во | Алгебраический символ | Единица измерения и Аббревиатура единиц | |
|---|---|---|---|
| Напряжение | $ V $ (или E $) | Вольт | В |
| Текущий | $ I $ | ампер (или ампер) | A |
| Сопротивление | $ | реаловОм | $ \ Omega $ |
Сопротивление определяется как математическое соотношение между приложенным напряжением и результирующим током.Эта формула стала известна как закон Ома , возможно, самая основная формула во всей электротехнике (показана здесь в трех разных формах, каждая из которых решает разные переменные):
\ [R = {V \ over I} \ hskip 30pt V = IR \ hskip 30pt I = {V \ over R} \]
Устно сопротивление — это то, сколько напряжения требуется, чтобы протолкнуть ток определенной скорости через проводящий материал. Многие материалы обладают относительно стабильным сопротивлением, а другие — нет. Продаются устройства, называемые резисторами , которые производятся с очень точным сопротивлением с целью ограничения тока в цепях (среди прочего).
Вот пример действия закона Ома: вычислите величину тока в цепи с источником напряжения 25 В и общим сопротивлением 3500 \ (\ Omega \). Взяв 25 вольт и разделив на 3500 Ом, вы должны получить результат 0,007143 ампера, или 7,143 миллиампер (7,143 мА).
Один из самых сложных аспектов закона Ома — это не забывать, что необходимо сохранять все переменные в контексте . Это обычная проблема для многих студентов, изучающих физику: ни одно из уравнений, изученных на уроке физики, не даст правильных результатов, если все переменные не относятся к одному и тому же объекту или ситуации.2 \)). Аналогичным образом, согласно закону Ома, мы должны убедиться, что значения напряжения, тока и сопротивления, которые мы используем, относятся к одной и той же части одной и той же цепи.
Если рассматриваемая схема имеет только один источник напряжения, одно сопротивление и один путь для тока, мы не можем неправильно применить закон Ома. Представляя предыдущий пример схематической диаграммой:
Однако, если мы посмотрим на более сложную схему, мы столкнемся с возможностью неправильного применения закона Ома, потому что у нас есть несколько сопротивлений в цепи, а не только одно сопротивление:
Какое сопротивление мы используем для расчета тока в этой цепи? Делим ли мы наши 25 вольт на 3500 Ом, как в прошлый раз, или мы делим их на 1500 Ом, или что-то совсем другое? Ответ на этот вопрос заключается в идентификации напряжений и токов.Мы знаем, что потенциал 25 В будет приложен к общим из двух сопротивлений \ (R_1 \) и \ (R_2 \), и, поскольку существует только один путь для тока, они должны разделять один и тот же ток. Таким образом, у нас фактически есть три напряжения (\ (V_1 \), \ (V_2 \) и \ (V_ {total} \)), три сопротивления (\ (R_1 \), \ (R_2 \), и \ (R_ {total} \)), и только один ток (\ (I \)):
Используя форму \ (V = IR \) закона Ома, чтобы связать эти три напряжения (\ (V_1 \), \ (V_2 \) и \ (V_ {total} \)) с одним током (\ (I \)), получаем три уравнения для этой схемы:
\ [V_ {1} = I R_ {1} \]
\ [V_ {2} = I R_ {2} \]
\ [V_ {total} = I R_ {total} = I (R_1 + R_2) \]
Мы можем решать только одну неизвестную переменную за раз в любом уравнении.Это означает, что мы пока не можем решить для \ (V_1 \), потому что, хотя нам известно значение резистора \ (R_1 \) (3500 Ом), мы еще не знаем ток цепи (\ (I \)). То же самое для \ (V_2 \), потому что мы еще не знаем значение \ (I \). Однако третье уравнение разрешимо, поскольку мы знаем полное напряжение, а также значения обоих резисторов, оставив ток цепи \ (I \) в качестве единственной неизвестной переменной. Обработка этого уравнения и решение для \ (I \):
\ [I = {V_ {total} \ over R_ {total}} = {V_ {total} \ over R_1 + R_2} = {25 \ hbox {V} \ over 3500 \> \ Omega + 1500 \> \ Omega } = 0.005 \ hbox {A} = 5 \ hbox {mA} \]
Теперь, когда мы знаем величину тока в этой цепи, мы можем решить для \ (V_1 \) и \ (V_2 \) в других уравнениях, чтобы найти, что напряжение на резисторе \ (R_1 \) составляет 17,5 вольт, и что напряжение на резисторе \ (R_2 \) составляет 7,5 вольт.
Что такое сопротивление? | Fluke
Сопротивление — это мера сопротивления току в электрической цепи.
Сопротивление измеряется в омах и обозначается греческой буквой омега (Ом).Ом назван в честь Георга Симона Ома (1784-1854), немецкого физика, изучавшего взаимосвязь между напряжением, током и сопротивлением. Ему приписывают формулировку закона Ома.
Все материалы в некоторой степени сопротивляются току. Они делятся на две большие категории:
- Проводники: Материалы с очень низким сопротивлением, в которых электроны могут легко перемещаться. Примеры: серебро, медь, золото и алюминий.
- Изоляторы: Материалы, обладающие высоким сопротивлением и ограничивающие поток электронов.Примеры: резина, бумага, стекло, дерево и пластик.
Измерения сопротивления обычно проводятся для определения состояния компонента или цепи.
- Чем выше сопротивление, тем меньше ток. Если он слишком высокий, одной из возможных причин (среди многих) может быть повреждение проводов из-за горения или коррозии. Все проводники выделяют определенное количество тепла, поэтому перегрев часто связан с сопротивлением.
- Чем меньше сопротивление, тем больше ток. Возможные причины: повреждение изоляторов из-за влаги или перегрева.
Многие компоненты, такие как нагревательные элементы и резисторы, имеют фиксированное значение сопротивления. Эти значения часто печатаются на паспортных табличках компонентов или в руководствах для справки.
Когда указывается допуск, измеренное значение сопротивления должно находиться в пределах указанного диапазона сопротивления. Любое значительное изменение значения фиксированного сопротивления обычно указывает на проблему.
«Сопротивление» может звучать отрицательно, но в электричестве его можно использовать с пользой.
Примеры: Ток должен с трудом проходить через маленькие катушки тостера, достаточный для выделения тепла, которое подрумянивает хлеб. Лампы накаливания старого образца заставляют ток течь через такие тонкие нити, что возникает свет.
Невозможно измерить сопротивление в рабочей цепи. Соответственно, специалисты по поиску и устранению неисправностей часто определяют сопротивление, измеряя напряжение и ток и применяя закон Ома:
E = I x R
То есть, вольт = амперы x Ом.R в этой формуле означает сопротивление. Если сопротивление неизвестно, формулу можно преобразовать в R = E / I (Ом = вольт, деленный на амперы).
Примеры: В цепи электрического нагревателя, как показано на двух рисунках ниже, сопротивление определяется путем измерения напряжения и тока цепи с последующим применением закона Ома.
Пример нормального сопротивления цепи Пример увеличенного сопротивления цепиВ первом примере, общее обычное сопротивление цепи, известное опорное значение, составляет 60 Ω (240 ÷ 4 = 60 Ω).Сопротивление 60 Ом может помочь определить состояние цепи.
Во втором примере, если ток в цепи составляет 3 А вместо 4, сопротивление цепи увеличилось с 60 Ом до 80 Ом (240 ÷ 3 = 80 Ом). Увеличение общего сопротивления на 20 Ом может быть вызвано неплотным или грязным соединением или обрывом катушки. Секции с разомкнутой катушкой увеличивают общее сопротивление цепи, что снижает ток.
Ссылка: Принципы цифрового мультиметра Глена А. Мазура, American Technical Publishers.
2.2.4 Закон Ома и почему мы заботимся о сопротивлении
2.2.4 Закон Ома и почему мы заботимся о сопротивлении
Устройство, известное нам как тостер, на удивление простое. Он состоит в основном из провода, по которому пропускается ток. Проволока нагревается, поджаривая хлеб. Вот и все!
а почему нагревается провод? Ответ в том, что провод имеет некоторое сопротивление. Когда ток проходит через материал с некоторым сопротивлением, материал нагревается. Это тепло в первую очередь является рассеянием некоторой части электроэнергии, проходящей через материал.Это рассеяние мощности в виде тепла называется «потерями» в электросети.
Сопротивление материала, через который проходит ток, помогает определить потери, но это не единственный фактор. Напряжение, при котором энергия проходит через материал, также имеет значение, как и величина тока.
Эта взаимосвязь четко резюмируется в законе Ома, который гласит, что напряжение равно произведению тока и сопротивления, или V = I × R.Закон Ома используется для определения величины напряжения, необходимого для перемещения заданного количества тока (I) через некоторый материал с заданным сопротивлением (R).
Между тем, вспомните наше определение мощности: P = I × V. По сути, это количество мощности, передаваемой в цепи, подобной той, что была в нашем последнем упражнении.
Мы можем включить закон Ома в наше определение мощности, чтобы получить:
P = I × V = I × (I × R) = I2 × R
Это уравнение описывает количество мощности, рассеиваемой в цепи.Он также описывает количество потерь. Таким образом, закон Ома говорит нам, что потери будут увеличиваться пропорционально квадрату тока. Таким образом, если мы сохраним постоянное напряжение и удвоим ток, потери увеличатся в четыре раза.
Чтобы понять важность этого, предположим, что мы пропускаем 1000 ампер тока через цепь с падением напряжения 100 В. Итак, у нас есть мощность 100 кВт. Потери в цепи будут пропорциональны I2 × R, или 10002 × R в этом случае.
Но, если бы нам нужно было 100 кВт мощности, мы могли бы сделать это по-другому, пропустив через цепь 100 А при напряжении 1000 В.Сопротивление в цепи не изменится, но потери в цепи теперь будут пропорциональны 100 2 × R.
Таким образом, увеличивая напряжение (и уменьшая ток) в 10 раз, мы уменьшили наши потери в 100 раз. Это объясняет причину того, что у нас есть сеть переменного тока вместо сети постоянного тока. Помните, что в технологии питания постоянного тока Эдисона напряжение в источнике должно быть близко к напряжению в точке потребления.Но с помощью технологии переменного тока, разработанной Tesla и Westinghouse, мощность могла генерироваться и передаваться при очень высоких напряжениях, а затем снижаться до более низких напряжений в точке потребления. Это имело два больших преимущества: во-первых, можно было существенно снизить потери при передаче, а во-вторых, для домов и предприятий было намного безопаснее использовать электроэнергию низкого напряжения, а не высокого напряжения.
20.2: Закон Ома — сопротивление и простые схемы
Что управляет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока.Все такие устройства создают разность потенциалов и условно называются источниками напряжения. Когда источник напряжения подключен к проводнику, он создает разность потенциалов \ (V \), которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Закон Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению \ (В \). Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке равен , прямо пропорционально приложенному напряжению :
\ [I \ propto V.\ label {20.3.1} \]
Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда.
Сопротивление и простые схемы
Если напряжение управляет током, что ему мешает? Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением \ (R \).Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току, или
.\ [I \ propto \ frac {1} {R}. \ label {20.3.2} \]
Таким образом, например, ток уменьшается вдвое, если сопротивление увеличивается вдвое. Комбинируя отношения тока к напряжению и тока к сопротивлению, получаем
\ [I = \ frac {V} {R}. \ label {20.3.3} \]
Это соотношение также называется законом Ома.Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых справедлив закон Ома, называются омическими . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление \ (R \), которое не зависит от напряжения \ (V \) и тока \ (I \). Объект, который имеет простое сопротивление, называется резистором , даже если его сопротивление невелико.Единица измерения сопротивления — Ом, и обозначается символом \ (\ Omega \) (греческая омега в верхнем регистре). Перестановка \ (I = V / R \) дает \ (R = V / I \), и поэтому единицы сопротивления равны 1 Ом = 1 вольт на ампер:
\ [1 \ Omega = 1 \ frac {V} {A}. \ label {20.3.4} \]
На рисунке \ (\ PageIndex {1} \) показана схема простой схемы. Простая схема имеет один источник напряжения и один резистор. Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в \ (R \).
Рисунок \ (\ PageIndex {1} \): Простая электрическая цепь, в которой замкнутый путь для прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленной красными параллельными линиями. Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.Пример \ (\ PageIndex {1} \): Расчет сопротивления: Автомобильная фара:
Какое сопротивление проходит у автомобильной фары? 2.50 А течет при подаче на него 12,0 В?
Стратегия
Мы можем изменить закон Ома, как указано в \ (I = V / R \), и использовать его для определения сопротивления.
Решение:
Преобразование уравнения \ ref {20.3.3} и замена известных значений дает
\ [\ begin {align *} R & = \ frac {V} {I} \\ [5pt] & = \ frac {12,0 V} {2,50 A} \\ [5pt] & = 4,80 \ Omega. \ end {align *} \]
Обсуждение:
Это относительно небольшое сопротивление, но оно больше, чем хладостойкость фары.{-5} \ Omega \), а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделах «Сопротивление и удельное сопротивление».
Дополнительное понимание достигается путем решения \ (I = V / R \) для \ (V \), что дает
\ [V = ИК. \ label {20.3.5} \]
Выражение для \ (V \) можно интерпретировать как падение напряжения на резисторе, вызванное минимальным током \ (I \). Для обозначения этого напряжения часто используется фраза \ (IR \) drop .Например, у фары в примере падение \ (IR \) составляет 12,0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления. Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию).В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку \ (PE = q \ Delta V \), и то же самое \ (q \) проходит через каждую . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразованная резистором, равны (Рисунок \ (\ PageIndex {2} \)).
Рисунок \ (\ PageIndex {2} \): Падение напряжения на резисторе в простой схеме равно выходному напряжению батареи.ПОДКЛЮЧЕНИЕ: СОХРАНЕНИЕ ЭНЕРГИИ
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму.Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму только с помощью резистора. Мы обнаружим, что сохранение энергии имеет и другие важные применения в схемах и является мощным инструментом анализа схем.
ЗаконОма и сопротивление — Закон Ома — Национальная редакция 5 по физике
Изменение сопротивления
Если вы увеличите количество ламп в последовательной цепи, ток будет меньше. Лампы противостоят току, поэтому, если вы включите больше ламп, сопротивление будет больше.
Две последовательные цепи, одна с одной лампой, другая с двумяВы можете увеличить или уменьшить сопротивление в цепи, используя переменный резистор.
Три последовательные цепи, каждая из которых содержит ячейку, амперметр, лампу и переменный резисторВеличины напряжение, ток и сопротивление связаны соотношением:
\ [напряжение = ток \ умноженное на сопротивление \]
Это соотношение называется законом Ома. Обычно мы пишем закон Ома как;
\ [V = IR \]
Обозначение сопротивления — R, оно измеряется в омах \ ((\ Omega) \).
Обозначение напряжения — В, оно измеряется в вольтах \ ((В) \).
Обозначение тока — I, он измеряется в амперах \ ((A) \).
Убедитесь, что если проблема связана с более чем одним напряжением или током, вы используете напряжение на резисторе и ток через него, а не только любые значения, которые вы видите в вопросе.
Когда резистор поддерживается при постоянной температуре, его сопротивление остается неизменным. Мы можем подтвердить это экспериментально, подключив резистор к источнику питания и измерив ток в резисторе при увеличении напряжения питания.
График зависимости напряжения (разности потенциалов) от тока для резистора дает прямолинейный график, проходящий через начало координат.
График зависимости разности потенциалов (В) от тока (А)- Вопрос
Лампа фонаря потребляет ток 0,3 ампера от 3-вольтовой батареи. Рассчитайте его сопротивление.
- Показать ответ
\ [V = IR \]
\ [3 = 0,3 \ times R \]
\ [R = \ frac {3} {{0.{-3} A \]
Изменение температуры может вызвать изменение сопротивления некоторых материалов. Эти материалы известны как неомические проводники.
Например, сопротивление термистора зависит от его температуры.
График «напряжение-ток» для термистора не является прямой линией. График
напряжение — ток для термистораЭто означает, что сопротивление термистора не является постоянным для разных значений тока. Когда ток уменьшается на , сопротивление термистора увеличивается на .
Закон Ома
Электрические цепи используются в авиакосмической технике, от систем управления полетом до приборов в кабине и двигателей системы управления, чтобы аэродинамическая труба приборостроение и эксплуатация. Самая простая схема включает в себя один резистор и источник электрического потенциала или напряжения . Электроны проходят через схема, производящая ток электроэнергии.Сопротивление, напряжение и ток связаны друг с другом соотношением Закон Ома , как показано на рисунке. Если обозначить сопротивление R , ток и , а напряжение В , то закон Ома гласит, что:
V = i RСопротивление — это свойство цепи, которое противодействует потоку электронов. через провод. Это аналог трения в механической системе или аэродинамической системе. тащить.Сопротивление измеряется в Ом и зависит от геометрия резистора и материал, из которого он изготовлен. На атомном уровне свободные электроны в материале находятся в постоянном случайном движении, постоянно сталкиваясь друг с другом и с окружающими атомами материала. При приложении электрического поля электроны преимущественно движутся в направлении, противоположном полю. Атомы образуют матрицу, через которую электроны двигаться. В зависимости от шага, размера и ориентации матрицы скорость потока электронов будет меняться.Разные материалы имеют разные значения электропроводности . Удельное сопротивление материала является обратным проводимости и обозначается rho . Если материал имеет длину l и площадь поперечного сечения A , сопротивление равно предоставлено:
R = (rho * l) / АПоскольку электроны движутся через материал, сталкиваясь друг с другом и с атомной матрицей, электроны генерируют случайную тепловую энергию или тепло.

 Установить, что электрическое сопротивление зависит от длины проводника, удельного сопротивления и площади поперечного сечения.
Установить, что электрическое сопротивление зависит от длины проводника, удельного сопротивления и площади поперечного сечения.

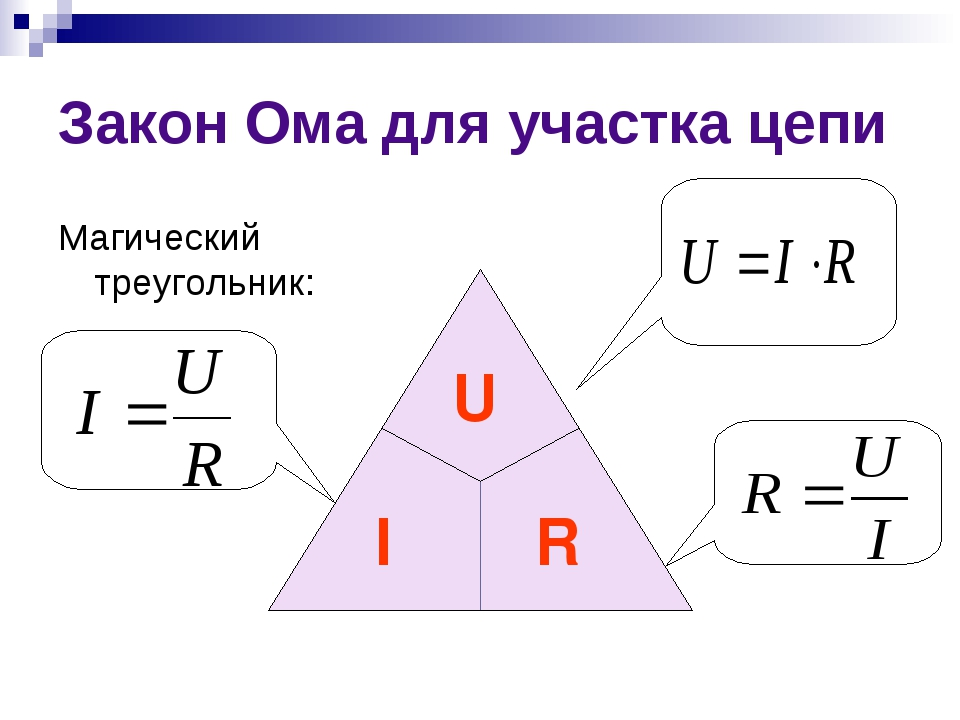 2)
2)