Продолжаем обсуждение катушек индуктивности! В первой статье (ссылка) мы обсудили все основные аспекты, а именно устройство катушек, принцип работы и их поведение при использовании в цепях постоянного и переменного тока. Но некоторые моменты остались незатронутыми, собственно, их мы и обсудим в этой статье 🙂 И начнем с очень важной характеристики, а именно добротности катушки индуктивности.
Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
Рассматривая примеры включения катушек в различные цепи мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
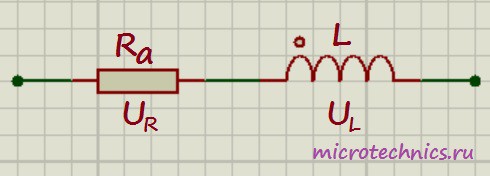
Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
U_L = IR_а
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление будет равно:
X_L = 2\pi f L = 0
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давай разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
u = iR + u_L
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -\varepsilon_L = L\frac{di}{dt}
И мы получаем для напряжения на реальной катушке индуктивности:
u = iR + L\frac{di}{dt}
Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:
Q = \frac{X_L}{R}
Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. Соответственно, чем выше добротность катушки индуктивности, тем она ближе к идеальной. Итак, активное сопротивление катушки мы рассмотрели, давайте перейдем к следующему вопросу.
Энергия катушки индуктивности.
Электрический ток, протекающий через катушку способствует накоплению энергии в магнитном поле катушки. При пропадании/отключении тока эта энергия будет возвращена в электрическую цепь. С этим мы и столкнулись при рассмотрении катушек индуктивности в цепях постоянного тока. Больше тут добавить особо нечего, просто приведу формулу, по которой можно определить величину накопленной энергии катушки индуктивности:
W = \frac{LI^2}{2}
Давайте переходить к вариантам соединения катушек между собой… Все расчеты мы будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0 и его необходимо учитывать при проведении любых расчетов.
Последовательное соединение катушек индуктивности.
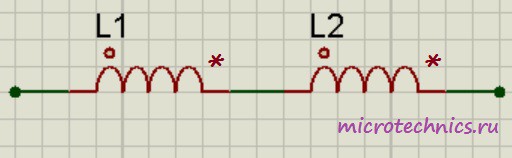
При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
L_0 = L_1 + L_2
Вроде бы все просто, проще некуда, но тут есть один важный момент. Данная формула справедлива только в том случае, если катушки расположены на на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:
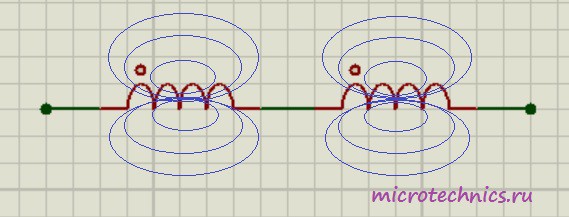
Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация совсем другая. Возможно два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек – начало второй катушки подключается к концу первой. А второй вариант называют встречным включением – конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом “*“. Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
L = L_1 + L_2 + 2M
Где M – взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:
L = L_1 + L_2\medspace-\medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу – уменьшается на ту же самую величину.
Параллельное соединение катушек индуктивности.
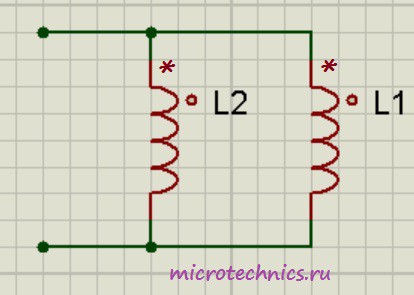
При параллельном соединении катушек индуктивности также возможны три варианта:
- Магнитное поле одной катушки не пересекает витков второй катушки, тогда: \frac{1}{L_0} = \frac{1}{L_1} +\frac{1}{L_2} или L_0 = \frac{L_1L_2}{L_1 + L_2}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены согласно (как изображено на рисунке – то есть начала обеих катушек подключены к одному узлу). В этом случае: L_0 = \frac{L_1L_2\medspace-\medspace M^2}{L_1 + L_2\medspace-\medspace 2M}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены встречно. В этом случае: L_0 = \frac{L_1L_2\medspace-\medspace M^2}{L_1 + L_2 + 2M}
Также как и в случае с последовательным соединением, при согласном включении общая индуктивность будет больше, чем при встречном включении, поскольку знаменатель дроби будет меньше.
Собственно, на этом мы и заканчиваем рассмотрение катушек индуктивности. Ранее мы изучили конденсаторы и резисторы, а в будущих статьях нам предстоит работать с цепями, включающие все эти элементы в разных комбинациях 🙂 Так что подписывайтесь на обновления и не пропускайте новые статьи на нашем сайте!
Соединение катушек — Основы электроники
Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.
Последовательное соединение катушек индуктивности.
Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.
Рисунок 1. Последовательное соединение катушект индуктивности.
Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:
где L1, L2 и L3 — индуктивности отдельных катушек.
Параллельное соединение катушек индуктивности.
Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:
Рисунок 2. Параллельное соединение катушек индуктивности.
Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:
Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или параллельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопротивления цепи при последовательном и параллельном соединении резисторов.
Соединение катушек при наличии взаимного влияния их магнитных полей.
Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:
- Магнитные потоки обеих катушек имеют одинаковые направления
- Магнитные потоки обеих катушек направлены навстречу друг другу
Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.
Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.
Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.
Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:
В первом случае ставится знак + (плюс), а во втором случае знак — (минус).
Величина М, называемая коэффициентом взаимной индукции, представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основано устройство вариометров. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Что такое катушка индуктивности
Что вы себе представляете под словом “катушка” ? Ну… это, наверное, какая-нибудь “фиговинка”, на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.
Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!
Индуктивность
Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC – метра.
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:
где
В – магнитное поле, Вб
I – сила тока, А
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
С научной же точки зрения, индуктивность – это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
где
I – сила тока в катушке , А
U – напряжение в катушке, В
R – сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух – это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Дроссель
Также есть особый вид катушек индуктивностей. Это так называемые
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей – это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Что влияет на индуктивность?
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
где
1 – это каркас катушки
2 – это витки катушки
3 – сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо “виток к витку”.
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков – тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.
Замеряем индуктивность
15 микрогенри
Отдалим витки катушки друг от друга
Замеряем снова
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Замеряем
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от “витков в квадрате”. Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Обозначение на схемах
Последовательное и параллельное соединение катушек индуктивности
При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Резюме
Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.
Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:
Пусть две катушки, обладающие сопротивлениями R1 и R2 , индуктивностями L1 и L2 и взаимной индуктивностью M, соединены последовательно (рис. 30.1).
Возможны два вида их соединения – согласное и встречное. Если считать, что звездочками отмечены начала обмоток, то при согласном включении начало второй подключается к концу первой (рис. 30.1, а). Токи в обеих катушках направлены одинаково относительно одноименных зажимов: от начала к концу. При встречном включении катушек конец второй присоединяется к концу первой (рис. 30.1, б).
Напряжение на каждой из катушек содержит три составляющих: падение напряжения на активном сопротивлении, напряжение самоиндукции и напряжение взаимной индукции:
Последние имеют одинаковые знаки при согласном включении и разные при встречном. Напряжение на входе цепи равно сумме этих двух напряжений:
Входное комплексное сопротивление цепи получим из совместного рассмотрения трех последних уравнений:
где Z1 и Z2 – комплексные сопротивления катушек, а ZM – комплексное сопротивление взаимной индукции:
Из формулы выше вытекают формулы, определяющие общую индуктивность цепи и суммарное индуктивное сопротивление:
причем
т.е.
Можно определить результирующее индуктивное сопротивление каждой катушки. У первой оно равно X1+-XM. И здесь при согласном включении оно больше чем при встречном. Физически это объясняется тем, что в первом случае магнитный поток, охватывающий каждую катушку, больше чем во втором; например, для первой катушки ФIсогл=Ф1+Ф21, а ФIвстр=Ф1-Ф21. Вследствие этого ЭДС электромагнитной индукции, оказывающая току индуктивное сопротивление, при согласном включении больше, чем при встречном.
На рис. 30.1 изображены векторные диаграммы, построенные по уравнениям (30.1) и (30.2).
При встречном включении возможен так называемый «емкостный» эффект, когда у одной из катушек напряжение на зажимах отстает по фазе от тока (напряжение на рис. 30.1, б). Это имеет место, когда индуктивность катушки меньше величины взаимной индуктивности. В этом случае результирующая индуктивность рассматриваемой катушки (с учетом взаимной индукции) отрицательна: L2-M < 0. Для всей цепи такой эффект невозможен. Ее индуктивность всегда положительна, и цепь носит активно-индуктивный характер.
Приветствую всех на нашем сайте!
Мы продолжаем изучать электронику с самых основ, и темой сегодняшней статьи будет катушка индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.
Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку 🙂 То есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:
Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название 🙂 Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:
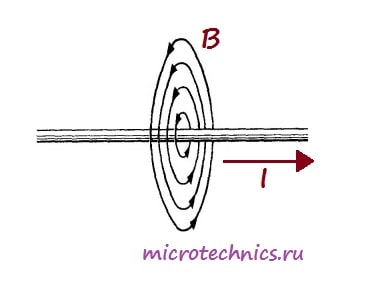
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:
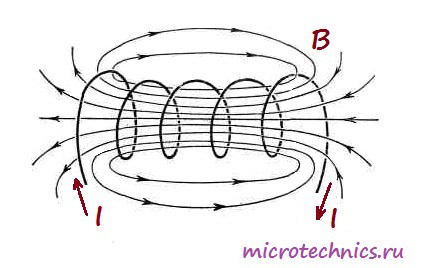
В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри – это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:
L = \frac{\mu_0\thinspace \mu S N^2}{l}
Давайте разберемся, что за величину входят в это выражение:
- \mu_0 – магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению: \mu_0 = 4 \pi \cdot 10^{-7}\medspace\frac{Гн}{м}
- \mu – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз
- S – площадь поперечного сечения катушки
- N – количество витков
- l – длина катушки
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.
С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет 🙂 Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:
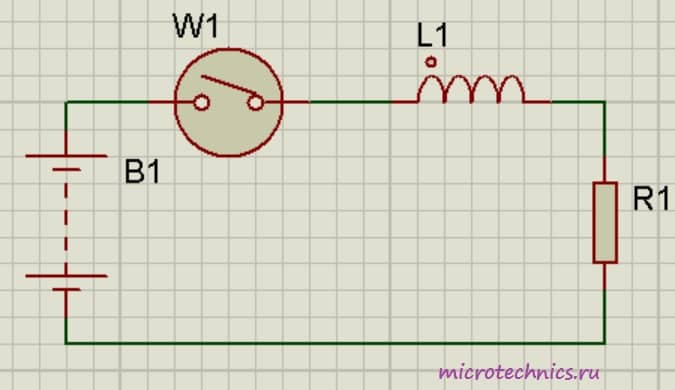
Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
\varepsilon_s = -\frac{d\Phi}{dt}
Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
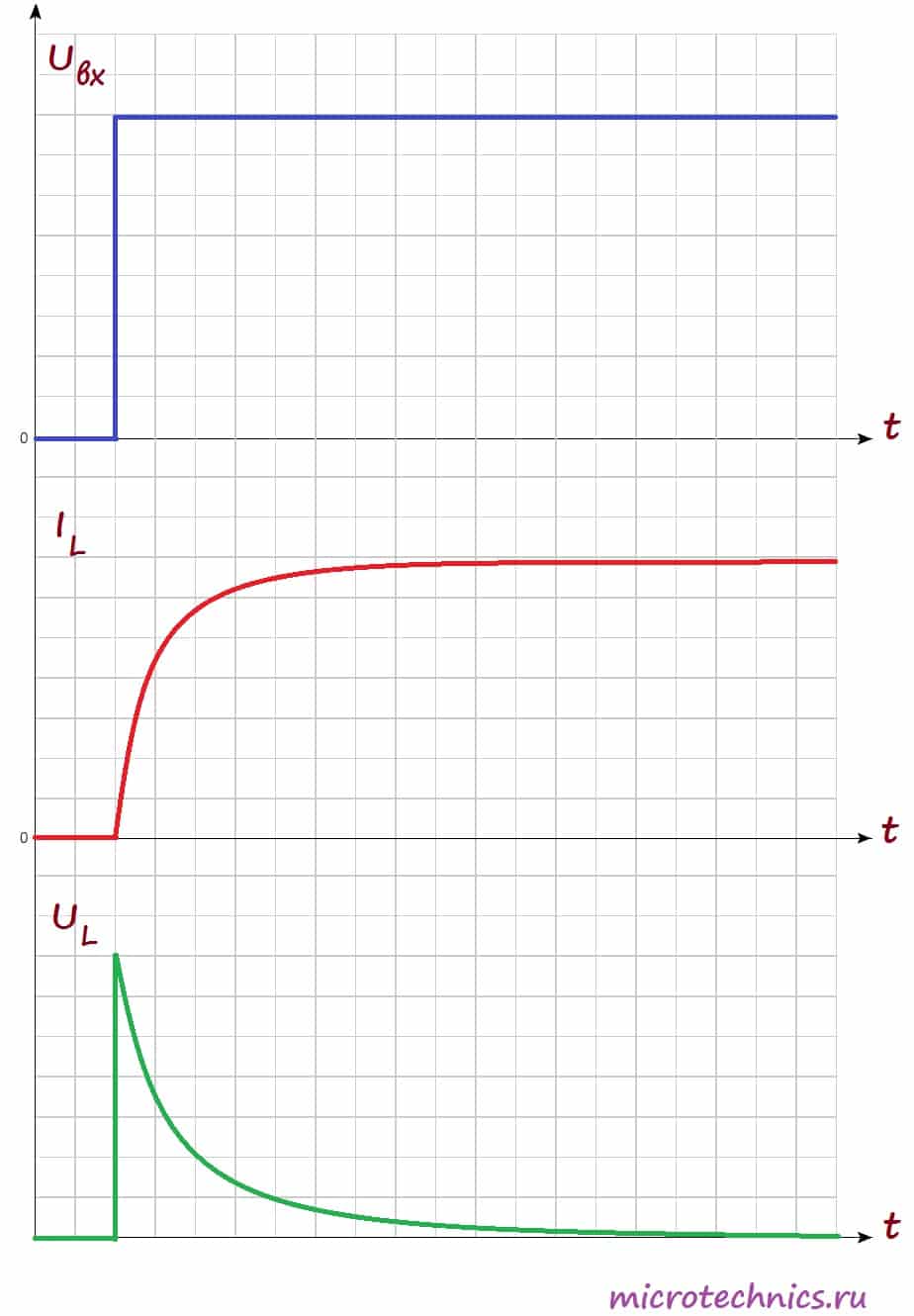
На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.
Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
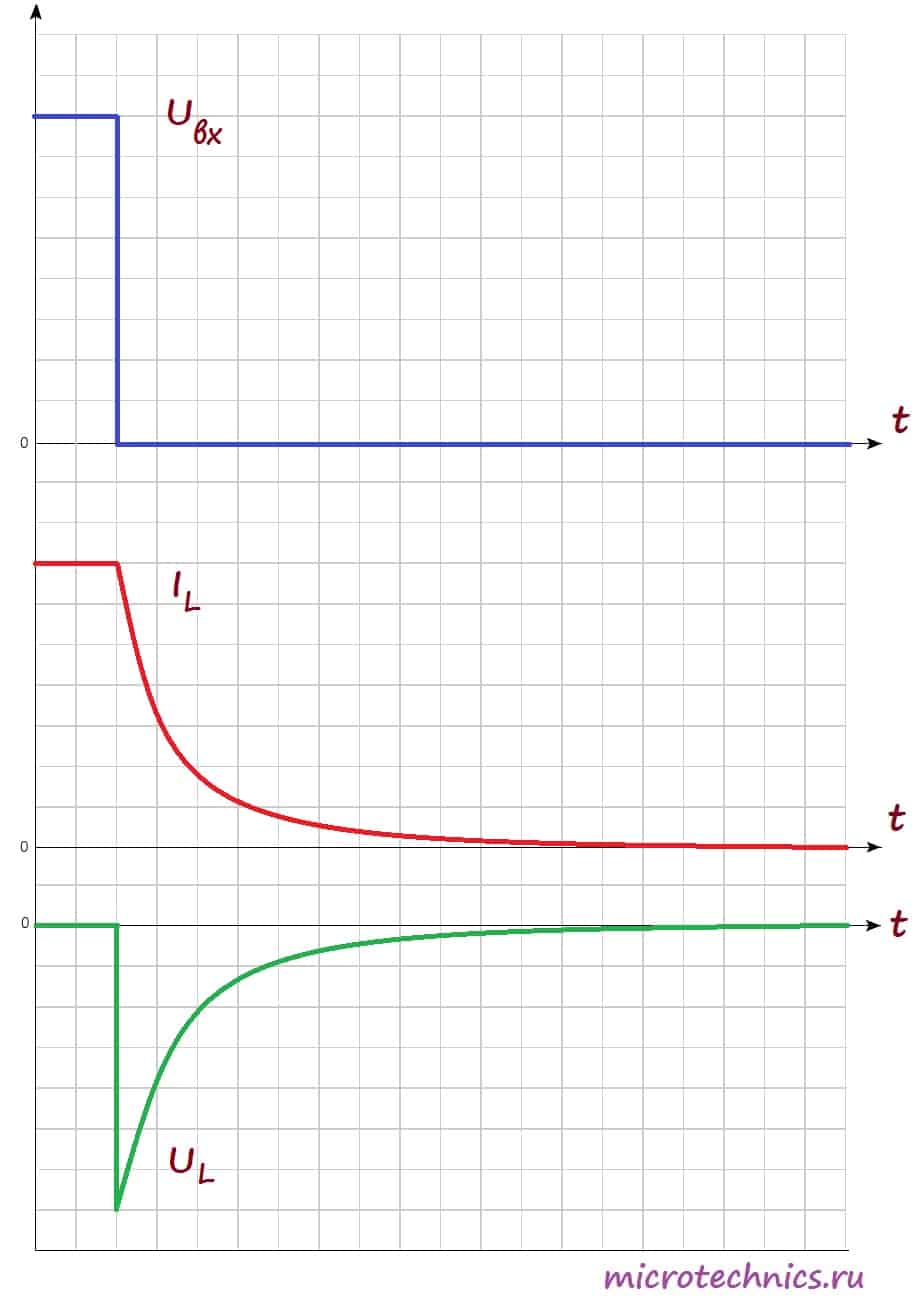
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:
\varepsilon_s = -L\medspace\frac{dI}{dt}
На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Катушка индуктивности в цепи переменного тока.
Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:
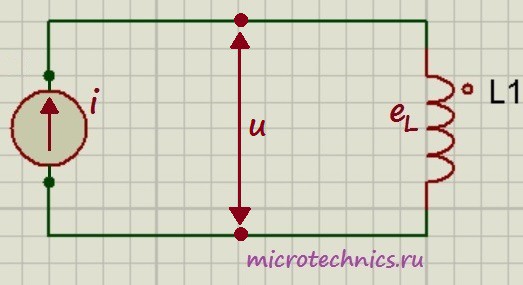
Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:
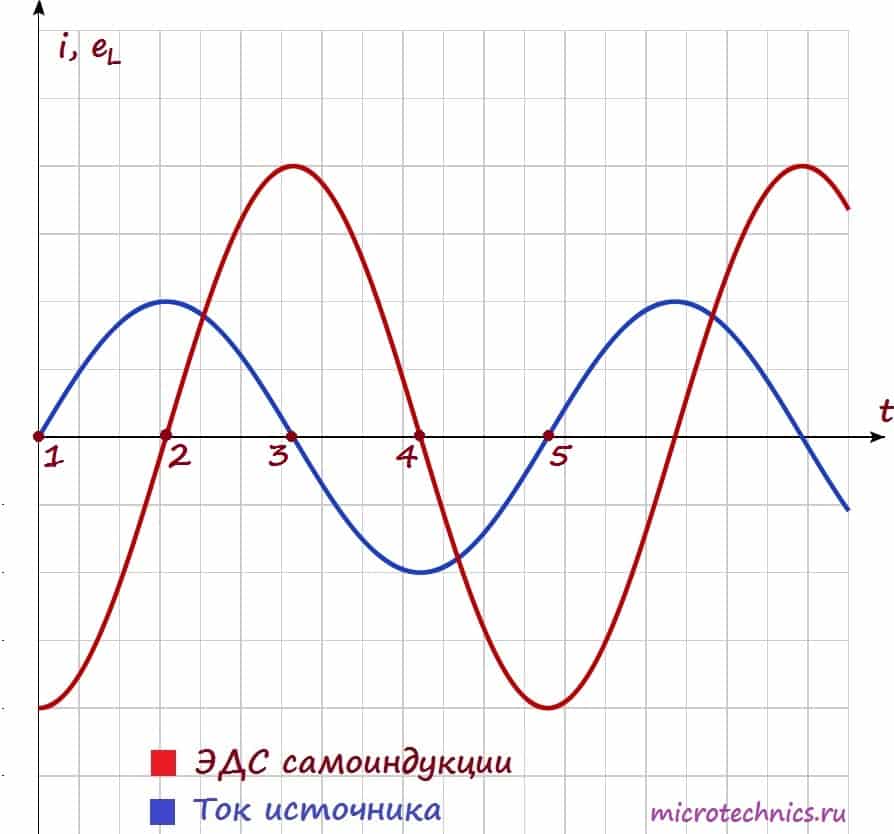
Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:
\varepsilon_L = -L\medspace\frac{dI}{dt}
Собственно, график нам и демонстрирует эту зависимость! Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.
Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу 🙂
Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: \varepsilon < 0, i > 0, участок 3-4: \varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника).
А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).
И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:
X_L = w\medspace L
Где w – круговая частота: w = 2 \pi f. [/latex]f[/latex] – это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все на самом деле просто! По 2-му закону Кирхгофа:
u + \varepsilon_L = 0
А следовательно:
u = – \varepsilon_L
Построим на одном графике зависимости тока и напряжения в цепи от времени:
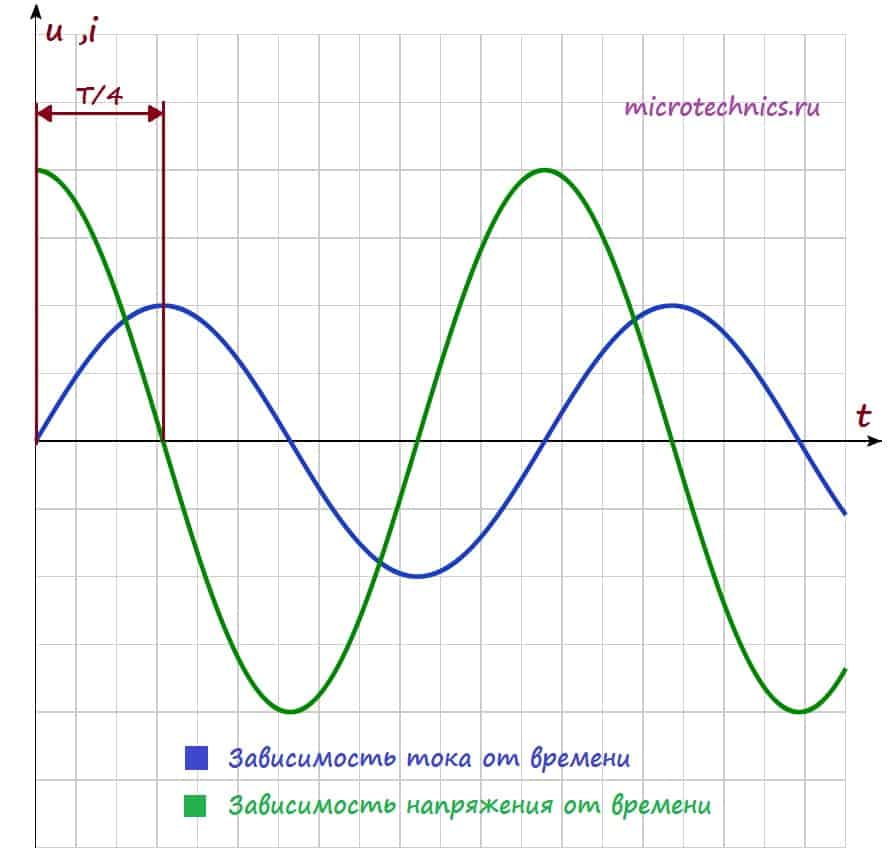
Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:
При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.
Вот и с включением катушки в цепь переменного тока мы разобрались!
На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!
Выбор статьи по меткам 03 (1) 5 марта 2020 (1) 5 мая Статград (2) 9 класс (3) 10 класс (1) 11 класс (2) 12 (1) 13 (С1) (3) 14 ноября (2) 14 февраля (1) 15 задание ЕГЭ (2) 16 задача профиль (1) 16 профильного ЕГЭ (1) 16 января Статград (2) 18 (С5) (2) 18 задача ЕГЭ (2) 18 мая 2020 физика (1) 23 марта (1) 31 января (1) 2016 (2) 140319 (1) 14032019 (1) C5 (1) RC-цепь (1) А9 (1) Александрова (2) Ампера (2) Архимед (2) Бернулли (1) Бойля-Мариотта (1) В8 (1) В12 (1) В13 (1) В15 (1) ВК (1) ВШЭ (2) ГИА физика задания 5 (1) Герона (1) Герцшпрунга-Рассела (1) Гринвич (1) ДВИ (1) ДПТ (1) Деление отрезка (1) Десятичные приставки (1) Дж (1) Диэлектрические проницаемости веществ (1) ЕГЭ 11 (2) ЕГЭ 14 (1) ЕГЭ 15 (2) ЕГЭ 18 (1) ЕГЭ С1 (1) ЕГЭ по математике (25) ЕГЭ по физике (49) ЕГЭ профиль (6) Европа (1) Задача 17 ЕГЭ (6) Задачи на движение (1) Закон Архимеда (2) Законы Ньютона (1) Земля (1) Ио (1) КПД (9) Каллисто (1) Кельвин (1) Кирхгоф (1) Кирхгофа (1) Койпера (1) Колебания (1) Коши (1) Коэффициенты поверхностного натяжения жидкостей (1) Кулона-Амонтона (1) Ломоносов (2) Лоренца (1) Луна (1) МГУ (1) МКТ (7) МФТИ олимпиада (1) Максвелл (2) Максвелла (1) Максимальное удаление тела от точки бросания (1) Менделеева-Клапейрона (3) Менелая (3) Метод наложения (2) Метод узловых потенциалов (1) Метод эквивалентных преобразований (1) НОД (1) Нансен (1) НеИСО (1) ОГЭ (11) ОГЭ (ГИА) по математике (27) ОГЭ 3 (ГИА В1) (1) ОГЭ 21 (3) ОГЭ 21 (ГИА С1) (4) ОГЭ 22 (2) ОГЭ 25 (3) ОГЭ 26 (1) ОГЭ 26 (ГИА С6) (1) ОГЭ по физике 5 (1) ОДЗ (13) Обыкновенная дробь (1) Оорта (1) Основные физические константы (1) Отношение объемов (1) Плюк (1) Показатели преломления (1) Показательные неравенства (1) Противо-эдс (1) Работа выхода электронов (1) Радиус кривизны траектории (1) Расстояние между скрещивающимися (1) Релятивистское замедление времени (1) Релятивистское изменение массы (1) С1 (1) С1 ЕГЭ (1) С2 (2) С3 (1) С4 (3) С6 (5) СУНЦ МГУ (2) Савченко (1) Сиена (1) Синхронная машина (1) Снеллиуса (2) Солнечной системы (1) Солнце (2) СпБ ГУ вступительный (1) Средняя кинетическая энергия молекул (1) Статград физика (6) Таблица Менделеева (1) Текстовые задачи (8) Тьерри Даксу (1) ФИПИ (1) Фазовые переходы (1) Фаренгейт (1) Фобос (1) Френеля (1) Цельсий (1) ЭДС (6) ЭДС индукции (2) Эйлера (1) Электрохимические эквиваленты (1) Эрастофен (1) абсолютная (1) абсолютная влажность (2) абсолютная звездная величина (3) абсолютная температура (1) абсолютный ноль (1) адиабаты (1) аксиомы (1) алгоритм Евклида (2) алгоритм Робертса (1) аморфное (1) амплитуда (3) аналитическое решение (1) анекдоты (1) апериодический переходной процесс (2) аргумент (1) арифметическая прогрессия (5) арифметической прогрессии (1) арки (1) арккосинус (1) арккотангенс (1) арксинус (1) арктангенс (1) архимеда (3) асинхронный (1) атмосферное (2) атмосферном (1) атомная масса (2) афелий (2) база (1) балка (1) банк (1) без калькулятора (1) без отрыва (1) белого карлика (1) бензин (1) бесконечная периодическая дробь (1) бесконечный предел (1) биквадратные уравнения (1) бипризма (1) биссектриса (4) биссектрисы (2) благоприятный исход (1) блеск (4) блок (2) блоки (2) боковой поверхности (1) большая полуось (1) большем давлении (1) бревно (2) бригада (2) бросили вертикально (1) бросили под углом (3) бросили со скоростью (2) броуновское движение (1) брошенного горизонтально (2) бруски (1) брусок (4) брусок распилили (1) бусинка (1) быстрый способ извлечения (1) вариант (3) вариант ЕГЭ (12) вариант ЕГЭ по физике (18) вариант по физике (1) варианты ЕГЭ (6) вариент по физике (1) введение дополнительного угла (1) вектор (5) векторное произведение (2) велосипедисты (1) вероятность (1) вертикальная составляющая (1) вертикально вверх (1) вертикальные углы (1) вес (3) весов (1) вес тела (1) ветви (1) ветвь (2) ветер (1) взаимодействие зарядов (1) видеоразбор (2) видеоразбор варианта (1) видимая звездная величина (2) виртуальная работа (1) виртуальный банк (1) виртуальных перемещений (1) витка (1) витков (1) виток (1) вклад (1) влажность (3) влажность воздуха (1) влетает (2) вневписанная окружность (2) внутреннее сопротивление (1) внутреннее сопротивление источника (1) внутреннюю энергию (1) внутренняя энергия (8) вода (1) вода течет (1) воды (1) возведение в квадрат (1) возвратное уравнение (1) возвратность (1) возвратные уравнения (2) воздушный шар (1) возрастающая (1) возрастет (1) волны (1) вписанная (1) вписанная окружность (3) вписанной окружности (1) вписанный угол (4) в правильной пирамиде (1) вращается (1) вращение (1) времени (2) время (24) время в минутах (1) время выполнения (1) время движения (2) время минимально (1) время падения (1) все значения а (1) всесибирская олимпиада (1) в стоячей воде (1) встретились (1) встретятся (1) вступительный (1) вступительный экзамен (1) вторая половина пути (1) вторичная (1) вторичная обмотка (1) вторичные изображения (1) второй закон (1) второй закон Ньютона (4) выбор двигателя (1) выборка корней (4) выколотая точка (1) выплаты (2) выразить вектор (1) высота (5) высота Солнца (1) высота столба (1) высота столба жидкости (1) высота столбика (1) высоте (3) высоту (1) высоты (3) выталкивающая сила (2) вычисления (2) газ (3) газа (1) газов (1) газовая атмосфера (1) галочка (1) гамма-лучей (1) гармоника (2) гвоздя (1) геометрическая вероятность (1) геометрическая прогрессия (4) геометрические высказывания (1) геометрический смысл (2) геометрическую прогрессию (1) геометрия (7) гигрометр (1) гидродинамика (1) гидростатика (3) гимназия при ВШЭ (1) гипербола (2) гипотенуза (3) гистерезисный двигатель (1) главный период (1) глубина (1) глухозаземленная нейтраль (1) гомотетия (2) гонщик (1) горизонтальная сила (1) горизонтальной спицы (1) горизонтальную силу (1) горка (1) гравитационная постоянная (1) градус (1) грани (2) график (2) графики функций (5) графически (1) графический способ (1) графическое решение (3) груз (2) грузик (2) грузовик (1) грузы (1) группа (1) давление (28) давление жидкости (3) давление пара (1) дальность полета (1) двигатель с активным ротором (1) движение под углом (1) движение под углом к горизонту (4) движение по кругу (1) движение по течению (1) движение с постоянной скоростью (2) движется груз (1) двойное неравенство (1) двойной фокус (1) двугранный угол при вершине (1) девальвация (1) действительная часть (1) действующее значение (2) деление (1) деление многочленов (2) деление уголком (1) делимость (23) делимость чисел (1) делители (1) делитель (2) делится (3) демонстрационный варант (1) деталей в час (1) диаграмма (1) диаметр (2) диаметру (1) динамика (4) диод (1) диск (2) дискриминант (5) дифракционная решетка (2) дифференцированный платеж (2) диффузия (1) диэлектрик (1) диэлектрическая проницаемость (1) длина (4) длина вектора (1) длина волны (7) длина медианы (1) длина отрезка (2) длина пружины (1) длина тени (1) длиной волны (2) длину нити (1) длины поездов (1) длительность разгона (1) длительный режим (1) добротность (1) догнал (1) догоняет (1) докажите (1) долг (1) доля (1) дополнительный угол (2) досок (1) досрочный (2) досрочный вариант (1) дптр (1) дуга (1) единицы продукции (1) единичный источник (1) единичных кубов (1) единмтвенное решение (1) единственный корень (1) ежесекундно (1) емкость (7) емкость заряженного шара (1) естественная область определения (1) желоб (2) жесткость (6) жеткость (1) живая математика (2) жидкости (1) жидкость (1) завод (1) загадка (2) задание 13 (2) задание 15 (3) задание 23 (1) задания 1-14 ЕГЭ (1) задача 9 (1) задача 13 профиль (1) задача 14 профиль (3) задача 15 профиль (1) задача 16 (1) задача 16 ЕГЭ (1) задача 16 профиль (4) задача 17 (1) задача 18 (1) задача 19 (2) задача 26 ОГЭ (2) задача с параметром (7) задачи (1) задачи на доказательство (4) задачи на разрезание (4) задачи на совместную работу (3) задачи про часы (1) задачи с фантазией (1) задерживающее напряжение (1) заземление (1) заказ (1) закон Бернулли (1) закон Гука (1) закон Ома (3) закон Снеллиуса (1) закона сохранения (1) закон движения (1) закон кулона (7) закон палочки (3) закон сложения классических скоростей (1) закон сохранения импульса (7) закон сохранения энергии (4) законы Кирхгофа (6) законы коммутации (1) законы сохранения (1) закрытым концом (1) замена переменной (2) замкнутая система (2) зануление (1) запаянная (2) заряд (9) заряда (1) заряд конденсатора (1) заряженная сфера (1) заряженный шар (1) защитная характеристика (1) звездочка (1) звезды (1) зенит (1) зенитное расстояние (1) зеркало (2) знак неравенства (1) знаменатель (1) знаменатель прогрессии (4) значение выражения (1) идеальный блок (1) идеальный газ (5) извлечение в столбик (1) излом (1) излучение (2) изменение длины (2) изменение импульса (2) изобара (1) изобаричесикй (1) изобарический (2) изобарный (1) изобарный процесс (1) изображение (3) изолированная нейтраль (1) изопроцессы (1) изотерма (2) изотермически (1) изотермический (2) изотермический процесс (1) изотоп (1) изохора (1) изохорический (1) изохорный процесс (1) импульс (11) импульса (1) импульс силы (2) импульс системы (1) импульс системы тел (4) импульс тела (4) импульс частицы (1) инвариантность (1) индуктивно-связанные цепи (1) индуктивное сопротивление (1) индуктивность (1) индукцией (1) индукция (8) интеграл Дюамеля (1) интервал (1) интересное (3) интерференционных полос (1) иррациональность (2) испарение (2) исследование функции (4) источник (1) источник света (1) исход (1) камень (1) камешек (1) капилляр (1) карлик (2) касательная (4) касательного (1) касательные (1) касаются (1) катер (2) катет (3) катится (2) катушка (6) качаний (2) квадлратичная зависимость (1) квадрант (1) квадрат (3) квадратичная функция (3) квадратное (1) квадратное уравнение (4) квадратную рамку (1) квазар (1) квант (1) квантов (1) кинематика (2) кинематическая связь (1) кинематические связи (5) кинетическая (12) кинетическая энергия (5) кинетической (1) кинетической энергии (1) кинетическую энегрию (1) кинетическую энергию (1) классический метод (3) классический метод расчета (1) клин (3) ключ (1) кодификатор (1) колебаний (1) колене (1) колесо (1) количество вещества (1) количество теплоты (9) коллектор (1) кольцо (2) комбинаторика (1) комбинированное (1) коммутация (1) комплексное сопротивление (1) комплексное число (1) комплексные числа (1) компонент (1) конвекция (3) конденсатор (10) конденсаторы (1) конденсации (1) конечная скорость (1) конечная температура (1) конечная температура смеси (1) конечный предел (1) консервативные (1) консоль (1) контрольная (1) контрольные (1) контур (5) конус (4) концентрация (7) концентрически (1) концентрическим (1) координата (5) координатный метод (2) координаты (3) координаты вектора (2) координаты середины отрезка (1) координаты точки (1) корабля (1) корень (4) корень квадратный (1) корень кубический (2) корни (3) корни иррациональные (1) корни квадратного уравнения (3) корни уравнения (1) корпоративных (1) косинус (2) косинус разности (1) косинусы (1) котангенс (1) коэффициент (1) коэффициент жесткости (1) коэффициент наклона (3) коэффициент поверхностного натяжения (3) коэффициент подобия (5) коэффициент трансформации (1) коэффициент трения (5) коэффициенты (1) красное смещение (1) красной границы (1) красный (1) кратковременный режим (1) кратные звезды (1) кредит (11) кредитная ставка (4) кредиты (1) криволинейная трапеция (2) кристаллизация (1) критерии оценки (1) круговая частота (1) круговой контур (1) кружок (1) кубическая парабола (1) кулонова сила (1) кульминация (1) кусочная функция (1) левом колене (1) лед (2) лет (1) линейная скорость (2) линейное напряжение (1) линейное уравнение (2) линейный размер (1) линза (2) линзы (2) линии излома (1) линиями поля (1) линия отвеса (1) литров (1) лифт (1) лифта (1) лифте (1) логарифм (10) логарифмические неравенства (3) логарифмические уравнения (1) логарифмическое неравенство (3) логарифмическое с переменным основанием (1) логарифмы (1) лунка (1) лучевая (1) льда (1) магнитное поле (2) магнитном поле (2) магнитные цепи (1) максимальная высота (1) максимальная скорость (1) максимум (1) малых колебаний (1) масса (24) масса воздуха (1) массе (1) массивная звезда (1) массовое содержание (1) массой (1) массу (1) математика (4) математический маятник (1) математического маятника (2) маятник (4) мгновенный центр вращения (1) медиана (2) меридиан (1) мертвая вода (1) мертвая петля (1) металлическая оболочка (1) метод виртуальных (1) метод внутреннего проецирования (1) метод замены переменной (4) метод интервалов (3) метод комплексных амплитуд (3) метод контурных токов (1) метод координат (1) метод линий (1) методом внутреннего проецирования (1) метод переброски (1) метод переменных состояния (1) метод подстановки (4) метод рационализации (4) метод решетки (1) метод следов (5) метод сложения (4) метод телескопирования (1) метод узловых напряжений (1) методы расчета цепей (2) методы расчета цепей постоянного тока (1) метод эквивалентного генератора (2) механика (1) механическая характеристика (1) механическое напряжение (1) миля (1) минимальная скорость (1) минимальное (1) минимальной высоты (1) минимальной скоростью (1) минимум (2) мишени (1) мнимая единица (1) мнимая часть (1) многоугольник (1) многочлены (1) мода (2) модули (1) модуль (13) модуль Юнга (1) модуль средней скорости (1) молекулярно-кинетическая теория (2) моль (2) молярная масса (5) момент (7) момент инерции (2) момент инерции двигателя (1) момент нагрузки (1) момент сил (1) монета (1) монотонная (1) монотонность функции (1) монохроматического (1) московская олимпиада (1) мощности силы тяжести (1) мощность (9) мощностью (1) мяч (1) наблюдатель (1) нагревание (1) нагреватель (1) нагревателя (1) нагрели (1) наибольшее (1) наивысшая точка (1) наименьшая работа (1) наименьшее (1) наименьшее общее кратное (1) наклон (1) наклонная плоскость (2) налог (1) на направление (2) на отрезке (2) на подумать (2) направление (1) направление обхода (3) направлении (1) направляющий вектор (1) напряжение (9) напряжение на зажимах (1) напряжение смещения нейтрали (2) напряженность (4) напряженность поля (6) нарушенная схема (3) насос (2) насоса (1) насыщенный пар (4) натуральное (9) натуральные (10) натуральных (1) натяжение нити (5) натяжения (1) находился в полете (2) начальная температура (1) начальной скоростью (1) недовозбуждение (1) незамкнутая система (2) нелинейное сопротивление (1) неопределенность типа бесконечность на бесконечность (1) неопределенность типа ноль на ноль (1) непериодическая дробь (1) неравенства (8) неравенство (22) неравенство профиль (1) неразрывности струи (1) нерастяжима (3) нерастяжимой (1) нерастяжимой нити (1) нерастянутой резинки (1) несимметричная нагрузка (1) несинусоидальный ток (3) нестандартные задачи (1) нестрогое (1) неупругим (1) нецентральный (1) нечетная функция (2) нечетное (1) нечетность (1) неявнополюсный (1) нити (3) нити паутины (1) нитку (1) нить (2) нить нерастяжима (1) новости (1) нормаль (1) нормальное ускорение (11) нормальной реакции опоры (1) нулевой ток (2) обкладками (1) обкладках (1) обкладки (1) область допустимых значений (9) область значений (1) область определения (8) область определения функции (4) оборот (1) обратные тригонометрические функции (1) обратные функции (1) общая хорда (1) общее сопротивление (1) общее сопротивление цепи (1) объем (37) объемный расход (1) объемом (1) объем пара (1) объем параллелепипеда (1) объем пирамиды (1) одинаковые части (1) одновременно (1) одновременно из одной точки (1) однозначное (1) окружность (13) окружность описанная (1) олимпиада (2) олимпиады по физике (2) они встретятся (1) операторный метод (4) описанная (1) оптика (1) оптимальный выбор (1) оптимизация (1) оптическая разность хода (1) оптический центр (1) орбитам (1) орбитой (1) оригинал (1) осевое сечение (1) оси (1) основание (2) основание логарифма (2) основания трапеции (1) основное тригонометрическое тождество (1) основное уравнение МКТ (2) основной газовый закон (1) основной период (1) основной уровень (1) основные углы (1) остаток (1) ось (1) отбор корней (5) ответ (1) отданное (1) отличная (1) относительная (2) относительная влажность (3) относительная скорость (1) относительно (4) относительность движениия (1) относительность движения (2) относительность скоростей (1) отношение (6) отношение времен (1) отношение длин (1) отношение площадей (3) отношение скоростей (2) отрезке (1) отрезок (1) отсечение невидимых граней (1) очки (1) падает (1) падает луч (1) падает под углом (1) падение (3) падение напряжения (2) падения (1) пар (3) парабола (5) параболы (1) параллакс (5) параллелепепед (2) параллелепипед (3) параллелограмм (4) параллелограмм Виньера (1) параллельно (2) параллельно двум векторам (1) параллельное соединение (3) параллельные прямые (1) параллельными граням (1) параметр (32) параметры (1) парообразование (1) парсек (1) парциальное (1) парциальное давление (1) пары (1) паскаль (1) первая треть (1) первичная (1) переброски (1) перевозбуждение (1) перегородка (1) перегрузок (1) перелетит (1) переливания (1) переменное магнитное поле (1) переменное основание (2) перемещение (6) перемычка (5) перемычке (1) перемычку (1) переносная (1) переносная скорость (1) пересекает (1) пересечение (1) пересечения (1) переходная проводимость (1) переходное сопротивление (1) переходной процесс (1) переходные процессы (9) перигелий (2) периметр (3) период (15) периодическая дробь (1) период колебаний (3) период малых колебаний (1) период обращения (2) период функции (1) периоды (1) перпендикулярно (1) песок (1) пион (1) пипетка (1) пирамида (7) пирамида шестиугольная (1) пирамиды (2) пирсона (1) плавание (1) плавкие предохранители (1) плавление (1) план (1) планете (1) планеты (3) планиметрия (14) планиметрия профиль (1) пластинами (1) пластинка (1) платеж (8) плечо (2) плоского зеркала (1) плоскопараллельная (1) плоскость (4) плоскость сечения (1) плотности веществ (1) плотность (23) плотность пара (3) плотность сосуда (1) плотность энергии (1) площади (2) площади фигур на клетчатой бумаге (1) площадь (30) площадь круга (1) площадь пластин (1) площадь поверхности (1) площадь под кривой (2) площадь проекции (1) площадь проекции сечения (1) площадь сектора (1) площадь сечения (5) площадь треугольника (3) поверхностная плотность заряда (1) поворот (1) повторно-кратковременный режим (1) по гладкому стержню (1) погрешность (1) погружено (1) подвесили (1) подготовка к контрольным (3) под каким углом (1) подмодульное (1) подмодульных выражений (1) подобен (1) подобие (8) подобия треугольников (1) подобны (1) подпереть (1) под углом (2) под углом к горизонту (3) показателем преломления (1) показательное (1) показатель преломления (4) поле (1) полезной работы (1) полезную мощность (1) полигон частот (1) по линиям сетки (1) полное ускорение (1) половина времени (1) половинный угол (1) положение равновесия (1) положительный знаменатель (1) полония (1) полость (1) полуокружность (1) полупроводник (1) полученное (1) понижение горизонта (1) по окружности (1) по переменному основанию (1) поправка часов (1) по прямой (1) поршень (4) поршня (1) порядок решетки (2) последовательно (1) последовательное соединение (3) последовательность (4) по сторонам клеток (1) посторонние корни (4) постоянная Авогадро (1) постоянная Хаббла (1) постоянная времени (1) постоянная скорость (1) постоянная составляющая (2) постоянный ток (5) построение (2) построение графика функции (1) потенциал (6) потенциал сферы (1) потенциал шара (2) потенциальная (13) потенциальная энергия (3) потенциальной (1) потери в стали (2) потеря корней (4) поток (5) по физике (1) правило левой (1) правило моментов (5) правильная пирамида (1) правильной пирамиде (1) правильную пирамиду (1) правильный многоугольник (1) правом колене (1) предел функции (1) преломляющий угол (1) преобразование графиков функций (1) преобразования (3) преподаватели (2) пресс (2) призма (7) призмы (3) признаки подобия (4) признаки равенства треугольников (3) пробн (1) пробник (206) пробник по физике (12) пробниук (1) пробный (1) пробный ЕГЭ (2) пробный ЕГЭ по физике (4) пробный вариант (25) пробный вариант ЕГЭ (17) пробный вариант ЕГЭ по физике (148) пробный вариант по физике (2) провода (1) проводник (1) проводник с током (1) проводящая оболочка (1) проводящего шара (1) проволока (1) проволоки (1) прогрессия (5) проекции (1) проекции скоростей (1) проекции ускорения (2) проекция (7) проекция перемещения (1) проекция скорости (6) проекция ускорения (2) производительность (2) производная (3) промежутка времени (1) промежуток (1) промежуток знакопостоянства (1) пропорциональны (1) проскальзывает (1) проскальзывания (1) противоположное событие (1) противостояние (1) протона (1) прототипы (1) профиль (2) профильный ЕГЭ (1) процент (5) процентная ставка (6) процентное отношение (1) процентное содержание (2) проценты (3) пружин (1) пружина (6) пружинный маятник (1) пружины (1) прямая (7) прямое восхождение (2) прямой (1) прямой АВ (1) прямолинейные разрезы (1) прямоугольник (1) пузырек (1) пульсар (1) пуля (1) пути (1) путь (27) пушка (1) пять корней (1) работа (16) работа газа (5) работа тока (1) работу выхода (2) рабочее тело (1) рабочие (1) равнобедренный (1) равновеликий (1) равновесие (4) равновесия (2) равновесное (1) равнодействующая (1) равномерно (1) равноускоренно (2) равноускоренное (3) равные (1) равные фигуры (1) радиальную ось (1) радикал (1) радикалы (1) радиус (11) радиус колеса (1) радиус кривизны (2) радиус описанной сферы (1) радиус темного кольца в отраженном свете (1) разбор (1) разбор Статграда по физике (4) разложение на множители (2) размах (1) разности температур (1) разность (2) разность потенциалов (2) разность прогрессии (3) разность хода (1) разрежьте (2) разрезание (6) разрешающая сила (1) разрыв функции (1) рамка (8) рамка с током (1) раскрытие модуля (1) расписание (1) расположение корней квадратного трехчлена (1) распределение частот (1) рассеивающая (1) расстояние (21) расстояние между зарядами (1) расстояние между прямыми (1) расстояние между скрещивающимися прямыми (1) расстояние на карте (1) расстояние от точки (1) расстояния (2) раствор (2) растяжение (2) расходуется (1) расцепители (1) расчеты по формулам (1) рационализация (4) рациональное (1) рациональные неравенства (1) реактивные элементы (1) реактивный двигатель (1) реакция опоры (4) реакция якоря (1) реальные 17 задачи (3) ребра (1) ребус (2) резервуар (1) резистор (1) рейки (2) рельс (1) рельса (1) рентгеновскую трубку (1) репетитор (1) решебник (1) решение тригонометрических уравнений (1) решение уравнений (2) решение уравнений больших степеней (1) решить в натуральных (1) решить в целых (1) ровно один (1) розетка (1) ромб (1) ряд Фурье (1) сарай с покатой крышей (1) сближаются (1) сближения (1) сбрасывают с высоты (1) сверхгигант (2) сверхновая (1) светимость (3) свободно (1) свободного падения (1) свободно падает (2) свойства (2) свойства отрезков (1) свойства степени (1) свойства функции (1) свойства функций (2) свойства чисел (1) свойство биссектрисы (2) свойству биссектрисы (1) сдвинуть (1) сегмент (1) сектор (1) секущая (2) серия решений (1) сертификация (6) сессия (1) сечение (14) сечение наклонной плоскостью (1) сидерический (1) сила (7) сила Архимеда (5) сила Лоренца (4) сила ампера (9) сила взаимодействия (4) сила давления (1) сила на дно (1) сила натяжения (8) сила натяжения нити (4) сила поверхностного натяжения (3) сила реакции опоры (1) сила трения (3) сила тяготения (1) сила тяжести (7) сила упругости (2) силой (2) силу (1) силу натяжения (1) силы от перемещения (1) силы трения (2) символический метод (3) симметричная нагрузка (1) симметрия (3) синодический (1) синус (4) синусоида (1) синусоидальный закон (1) синусоидальный ток (5) синус половинного аргумента (1) синусы (1) синхронный компенсатор (1) система (5) система неравенств (7) система отсчета (3) система счисления (1) система уравнений (3) системы уравнений (3) скалярное произведение (3) склонение (1) скольжение (2) скользит (1) скользит равномерно (1) скоросмть (1) скоростей (1) скорости (3) скорости течения (1) скорость (45) скорость реки (1) скорость сближения (3) скорость света (1) скорость теплохода (1) скорость удаления (1) скорость частицы (1) скоростью (1) скрещивающиеся прямые (1) с лестницы (1) сложение векторов (1) сложная задача на разрезание (1) сложная функция (1) сложные экономические задачи (3) смежные углы (1) смекалка (2) смеси (1) смешанное число (1) смещение (2) с нарушенной схемой (1) снаряд (2) собирающая (2) событие (1) соединение звездой (1) соединение треугольником (1) сокращение (1) сокращение дробей (1) соленоид (1) солнечная постоянная (3) солнечная система (1) сообразительность (1) сообщающиеся сосуды (2) соприкосновения (1) сопротивление (13) сопротивления (1) сопряженное (3) составить квадрат (1) составляет с направлением (1)
Рассмотрим параллельное соединение индуктивно связанных катушек (рис 5.9)
Рис 5.9
Запишем уравнения для каждой из ветвей цепи в комплексной форме:
Знак
(+) перед 
соответствует согласному включению,
знак (–) – встречному.
Введем обозначения
, 
, 
и перепишем последнюю систему уравнений
в виде :
Определим из этих уравнений токи в ветвях
Из последнего соотношения определим входное сопротивление параллельно соединенных индуктивно связанных катушек:
При
отсутствии индуктивной связи, т.е при
ZM =0 входное
сопротивление преобразуется к известному
выражению 
Полагая в предыдущем выражении r1=0, r2=0, получим выражение для полной индуктивности при согласном включении:
или в встречном включении
5.6 Расчет цепей со взаимной индуктивностью.
Расчет разветвленных ветвей при наличии взаимной индуктивности можно вести по уравнениям составленным по первому и второму законам Кирхгофа или методом контурных токов. Метод узловых потенциалов непосредственно не применим. Объясняется это тем, что ток в ветви зависит не только от разности потенциалов на зажимах ветви и от ЭДС, находящихся в ветви, но и от токов других ветвей с которым рассматриваемая ветвь индуктивно связана.
Ограниченное применение находит метод эквивалентного генератора. Его можно применить в том случае, если ветвь, в которой требуется определить ток, индуктивно не связанна с другими ветвями.
В противном случае исключение этой ветви привело бы к потере индуктивной связи.
В качестве примера запишем уравнения по законах Кирхгофа для цепи, изображенной на рис 5.10
Рис 5.10
Направления обхода контуров обозначим стрелками.
В
полученной системе трех уравнений
неизвестными являются токи 
.
Решая систему, получаем их численные значения.
Развязка индуктивных связей
Выше было сказано, что не все методы пригодны для расчета индуктивно связанных цепей. Анализ и расчет цепи упрощается, если часть цепи содержащую индуктивные связи заменить эквивалентной схемой без индуктивных связей. Эта замена является называется развязкой индуктивных связей.
Рассмотрим часть цепи с индуктивной связью (рис 5.11)
Рис 5.11
Запишем для нее уравнения в комплексной форме
где
знак (+) перед 
соответствует согласному включению
индуктивностей, а знак (–) встречному.
Выразив из первого уравнения ток
и подставив в выражение для
,
получим
,
а выразив
и
подставив в 
,
получим:
.
Полученным
уравнениям для 
и
соответствует
электрическая цепь, изображенная на
рис 5.12
Рис 5.12
В цепи на рис 5.12 отсутствует индуктивные связи, однако изменились величины индуктивностей и появился дополнительный элемент. Верхний знак перед М соответствует согласному включению, а нижний знак –встречное включение индуктивностей.
Для расчета цепи преобразованной таким образом можно использовать любые методы расчета цепей без ограничения.
Воздушный трансформатор
Трансформатор слово латинского происхождения и переводится как преобразователь. Этим определяется его назначение. Трансформатор служит для преобразования переменного напряжения, когда требуется изменить величину напряжения или осуществить передачу электрической энергии между контурами лишенными гальванической связи.
Конструктивно трансформатор представляет собой две или несколько индуктивно связных катушек, называемых обмотками трансформатора. Обмотки трансформатора могут быть помещены на общий ферромагнитный сердечник. Однако сердечник может отсутствовать. Тогда трансформатор называется воздушным трансформатором или трансформатором без сердечника.
Рассмотрим простейший воздушный трансформатор, состоящий из 2-х обмоток.
Такие трансформаторы находят широкое применение в устройствах работающих на высоких частотах, например, в радиоприемных устройствах. Схема трансформатора представлена на рис 5.13
Рис 5.13
Обмотка трансформатора, подключаемая к источнику переменного напряжения, называется первичной. На рис 5.13 она представлена индуктивностью L1 и активным сопротивлением проводника r1, из которого она изготовлена. Вторичная обмотка, к которой подключается нагрузка ZН, представлена индуктивностью L2 и активным сопротивлением r2. Между обмотками трансформатора имеется индуктивная связь, характеризуемая взаимной индуктивностью M.
Уравнения по второму закону Кирхгофа для первичной и вторичной цепи трансформатора запишутся в виде:
Векторные
диаграммы трансформатора для случаев
активно-индуктивной 
и активно-емкостной
нагрузки, построенные по уравнениям
приведены на рис. 5.14 а, б соответственно
:
Рис. 5.14
Порядок
построения векторной диаграммы
трансформатора проследим на рисунке
5.14а. Зададимся положительным направлением
тока 
во вторичной обмотке трансформатора.
Напряжение на активном сопротивлении
вторичной обмотки трансформатора
совпадает по фазе стоком.
Напряжение на индуктивности вторичной
катушки
опережает ток
на 900.
Совмещаем начало вектора 
концом вектора
.
Напряжение на активной составляющей
сопротивления нагрузке
совпадает по фазе с током
.
Откладываем вектор
параллельно вектору тока
с конца вектора
.
Вектор напряжения на индуктивной
составляющей сопротивления нагрузки
опережает ток
на 900,
откладываем с конца вектора 
под углом 900 к вектору 
.
Векторная сумма
равна
вектору напряжения
,
возникающего за счёт индуктивной связи
между первичной и вторичной катушками.
Вектор тока
относительно
сдвинут на –900.
Определив таким образом направление
тока 
строим векторы напряжений на элементах
первичной цепи трансформатора согласно
первому уравнению трансформатора.
Вектор
напряжения на активном сопротивлении
первичной катушки 
совпадает с током
.
Вектор напряжения на индуктивности
первой катушки
опережает
ток
на 900.
Совмещаем начало вектора 
с концом вектора
.
Падение напряжения
,
вызванное в первичной цепи током
вторичной цепи имеет сдвиг фазы – 900 по отношению к току 
.
Откладываем вектор
с
конца вектора
под углом –900 к току 
.
Сумма векторов
даёт вектор входного напряжения
трансформатора
.
Определим входное сопротивление трансформатора. Уравнения описывающие воздушный трансформатор запишем в виде
где 
— реактивное сопротивление первичной
цепи
—
активное сопротивление вторичной цепи
—
реактивное сопротивление вторичной
цепи трансформатора. Из системы уравнений
определим ток.
Разделим
числитель и знаменатель последнего
выражения на 
Полученное соотношение
выражает закон Ома для первичной цепи. Следовательно, знаменатель представляет собой выражение для входного сопротивления трансформатора.
Выделим в выражении для входного сопротивления трансформатора действительную и мнимую часть, умножив числитель и знаменатель третьего слагаемого на число комплексно — сопряженное знаменателю
Таким образом, входное сопротивление трансформатора представлено в виде последовательного соединения двух активных и двух реактивных сопротивлений. Входное сопротивление трансформатора может быть изображено в виде двухполюсника на рис 5.15
Рис 5.15
где 
активное сопротивление, вносимое из
вторичной цепи в первичной.
x1вн=
реактивное сопротивление, вносимое в
первичную цепь из вторичной .
Следует заметить, что вносимое реактивное сопротивление имеет знак противоположный знаку собственного реактивного сопротивления вторичного контура x22.
Из представления воздушного трансформатора в виде двухполюсника следует условие передачи максимальной мощности в нагрузку Zист=ZH*.
Другой подход к анализу трансформатора предполагает исключение индуктивной связи между обмотками и получения эквивалентной схемы замещения трансформатора.
Запишем уравнения трансформатора в виде
Добавим
и вычтем к левой части первого уравнения
слагаемое 
,
а к левой части второго уравнения
Преобразуем полученные уравнения
Из
последних уравнений следует, что цепь
описываемая ими состоит из 2-х контуров,
имеющих общее сопротивление 
.
В первом контуре протекает ток
во втором – ток
. Схема цепи , описываемая этими уравнениями
приведена на рис 5.16
Рис 5.16
Полученная
схема цепи может рассматриваться как
эквивалентная исходной в отношении
напряжений
и
и
токов
и
.
Как отмечалось выше, основное назначение трансформатора – повышение или понижение в некоторое число раз напряжения и тока. В идеальном случае такое преобразование не должно завесить ни от частоты приложенного напряжения ни от величины нагрузки. Рассмотрим ,при каких условиях это возможно.
Введём
понятия функции передачи тока и функции
передачи напряжения, 
и
,
соответственно.
Из
второго уравнения системы 5.1 выразим 
.
Разделив
левую и правую части полученного
соотношения на 
получим
Из
последнего выражения с учётом 
, получим функцию передачи тока.
Функцию передачи напряжения получим как отношение второго уравнения к первому из системы 5.1
Разделив
числитель и знаменатель последнего
выражения на 
, получим соотношение
включающее
в себя функцию передачи тока 
.Подставив
значение
,
окончательно получим функцию передачи
напряжения в виде
Как следует из выражений для функции передачи тока и напряжения, они зависят от многих величин.
Если можно пренебречь потерями в обмотках трансформатора, т. е. если r1=r2=0, то функция передачи напряжения запишется в виде
Полагая,
что потоки рассеяния отсутствуют, т.е.
коэффициент связи 
,
получим
Индуктивность
обмотки трансформатора пропорциональна
квадрату витков обмотки 
,
где
-магнитная
проводимость пути, по которому протекает
поток.
Выразив
величины индуктивностей 
и
через число витков
и
,
получим функцию передачи напряжения в
виде
Отношение 
назовем коэффициентом трансформации
и обозначим буквойn.
Таким
образом независимость от частоты и
нагрузки функции передачи напряжения
обеспечивается при нулевом активном
сопротивлении и коэффициенте связи 
.
Рассмотрим условие независимости от частоты функции передачи тока
Если
индуктивное сопротивление вторичной
цепи значительно больше сопротивления
нагрузки и активного сопротивления 
и
,
,
то
Идеальным трансформатором называется идеализированный элемент электрической цепи с двумя парами зажимов –первичных и вторичных , обладающий следующими свойствами : при любых условиях отношение первичного и вторичного комплексных токов равны постоянному числу
n-коэффициенту трансформации.
Если n>1, то трансформатор называется понижающим, если n<1, то трансформатор – повышающий.
Рассмотрим свойства идеального трансформатора.
Пусть
ко вторичным зажимам подключена нагрузка
с комплексным сопротивлением 
. Тогда входное сопротивление будет
равным :
Т.е входное сопротивление изменилось в n2 раз. Это позволяет применять трансформатор для согласования источника и нагрузки , например, по условию передачи в нагрузку максимальной мощности .
Например,
если сопротивление источника равно ri,
а сопротивление нагрузки – rH,
то входное сопротивление относительно
первичной обмотки равно 
и условие согласования запишется в
виде
откуда 
Установим связь между мощностью на входе и выходе идеального трансформатора.
–мощность
на входе трансформатора
–мощность
на выходе трансформатора
Таким образом, идеальный трансформатор передает энергию с входа на выход цепи без потерь.
Сформулируем условия, которые должны выполнятся для того, что бы трансформатор был идеальным:
1.Должны
отсутствовать потоки рассеяния, т. е . 
2.
Должны отсутствовать потери, т.е 
3.
Должны быть великими индуктивности
обмоток, т.е 
Реальные трансформаторы могут обеспечить выполнение условий лишь приближенно за счет технических решений:
Для отсутствия потока рассеяния обмотки трансформатора помещают на замкнутом сердечнике , выполненном из материала с высокой магнитной проводимостью.
Второе условие обеспечивает выбором обмоточного проводника , обладающего низким удельным сопротивлением .
Для выполнения условия
,обмотки должны иметь большое число
витковии высокую магнитную проводимость
материала сердечника.
,
обмотки должны иметь большое число
витков
и
и высокую магнитную проводимость
материала сердечника.По своим свойствам к идеальному трансформатору приближается трансформатор с ферромагнитным сердечником . Трансформатор с ферромагнитным сердечником может рассматриваться как линейный элемент , если магнитный поток не насыщает сердечника . Это условие обычно выполняется за исключением приборов , где насыщение принципиально необходимо.
90000 What is Inductor Coupling — Inductors in Series & Parallel Combinations 90001 90002 In previous tutorial, we started with Understanding an Inductor and It’s Working, now it is time to explore the different combinations of Inductors. In electronics, Inductors are the most commonly used components after the capacitors and resistors, which are used in different combinations for different applications. We have also used inductor to build metal detectors and measured the value of inductor using different techniques, all the links are given below: 90003 90002 90003 90006 90007 What is coupled circuits? 90008 90009 90002 The combinations of components are together to create coupled circuits.The meaning of coupled circuit is that the energy transfer takes place from one to other when either of the circuits is energized. Major components in the electronics circuit are coupled by either conductively or electromagnetically. 90003 90002 90003 90002 However, in this tutorial, the electromagnetic coupling and the combination of inductors, like 90007 inductors in series or parallel 90008 combinations will be discussed. 90003 90002 90003 90006 90007 Mutual Inductance 90008 90009 90002 In the previous article, we discussed the self-inductance of an inductor and its parameter.During the self-inductance related operation, there was no mutual inductance took place. 90003 90002 When the rate of current change occurs, a voltage is induced inside a coil. Which can be further demonstrated using the below formula where, 90003 90002 V (t) is the induced voltage inside the coil, 90029 i 90030 Is the current flowing through the coil, and the inductance of the coil is L. 90003 90032 90007 V (t) = L {di (t) / dt} 90008 90035 90002 The above condition is true only for the self-inductance related circuit element where two terminals are present.In such a case, no mutual inductance is taken into the order. 90003 90002 90003 90002 Now, at the same scenario, if two coils are situated in a close distance, the inductive coupling will happen. 90003 90002 90043 90003 90002 90003 90002 In the above image, two coils are shown. These two coils are very close to each other. Due to the current i1 flowing through the coil L1, 90007 magnetic flux is induced which will then get transferred to the other coil L2. 90008 90003 90002 90052 90003 90002 90003 90002 In the above image, the same circuit is now tightly wrapped in a core material so that the coils can not move.As the material is a magnetic core, it has 90007 permeability 90008. The two separate coils are now magnetically coupled. Now, interestingly, if one of the coils faces the rate of current change, the other coil will induce a voltage which is directly proportional to the rate of current change in the other coil. 90003 90002 90003 90002 Therefore, when a voltage source V1 is applied in the coil L1, the current i1 will start to flow through the L1. The rate of current change produces a flux which flows through the magnetic core and produces a voltage in the coil L2.The rate of current change in L1 also changes the flux which can further manipulate the induced voltage in L2. 90003 90002 90003 90002 The 90007 induced voltage in the L2 90008 can be calculated in the below formula- 90003 90032 90007 V 90072 2 90073 = M {di 90072 1 90073 (t) / dt} 90008 90035 90002 In the above equation, there is an unknown entity. That is 90007 M 90008. This is because, mutual inductances are responsible for the mutually induced voltage in two independent circuits.This 90007 M, mutual inductance is the coefficient proportionality 90008. 90003 90002 90003 90002 Same for the first coil L1, the mutually induced voltage due to mutual inductance for the first coil can be — 90003 90032 90007 V 90072 2 90073 = M {di 90072 2 90073 (t) / dt} 90008 90035 90002 90003 90002 Same as like the inductance, mutual inductance is also measured in Henry. The maximum value of mutual inductance can be √L 90072 1 90073 L 90072 2 90073. As the inductance induces voltage with the rate of current change, mutual inductance also induces a voltage, which is termed as mutual voltage M (di / dt).This mutual voltage can be positive or negative which is highly dependable on the physical construction of the coil and the direction of the current. 90003 90002 90003 90006 90007 DOT Convention 90008 90009 90002 The 90007 Dot Convention 90008 is an essential tool to determine the polarity of the mutually induced voltage. As the name suggests, the dot mark which is in a circular shape is a special symbol which is used at the end of two coils in mutually coupled circuits. This dot also provides the information of the winding construction around its magnetic core.90003 90002 90115 90003 90002 90003 90002 In the above circuit, two mutually coupled inductors are shown. These two inductors have self-inductances of L1 and L2. 90003 90002 90003 90002 The voltages V1 and V2 are developed across the inductors are the result of current entering into the inductors on the dotted terminals. By assuming that the mutual inductance of those two inductors is M, The induced voltage can be calculated using the below formula, 90003 90002 90003 90002 For the first inductor L1, the induced voltage will be — 90003 90032 90007 V 90072 1 90073 = L 90072 1 90073 (di 90072 1 90073 / dt) ± M (di 90072 2 90073 / dt) 90008 90035 90002 90003 90002 The same formula can be used for calculating the induced voltage of the second Inductor, 90003 90032 90007 V 90072 2 90073 = L 90072 2 90073 (di 90072 2 90073 / dt) ± M (di 90072 1 90073 / dt) 90008 90035 90002 90003 90002 Therefore, the circuit contains two types of induced voltage, the induced voltage due to self-inductance and the mutually induced voltage due to the mutual inductance.The induced voltage depending on the self-inductance is calculated using the formula V = L (di / dt) which is positive, but the mutually induced voltage can be negative or positive depending on the winding construction as well as the flow of current. The use of dot is an important parameter to determine the polarity of this mutually induced voltage. 90003 90002 90003 90002 In a coupled circuit where two terminals belong two different coils and identically marked with dots, then for the same direction of the current which is relative to like terminals, the magnetic flux of self and mutual induction in each coil will add up together.90003 90002 90003 90006 90007 Coefficient of Coupling 90008 90009 90002 The coefficient of inductor coupling is an important parameter for coupled circuits to determine the amount of coupling between the inductively coupled coils. The 90007 coefficient of coupling is expressed by the letter K. 90008 90003 90002 90003 90002 The formula of the coefficient of coupling is K = M / √L 90072 1 90073 + L 90072 2 90073 where L1 is the self inductance of the first coil and the L2 is the self inductance of the second coil.90003 90002 90003 90002 Two inductively coupled circuits are linked using the magnetic flux. If the entire flux of one inductor is coupled or linked the other inductor is called perfect coupling. During this situation, the K can be expressed as 1 which is the short form of 100% coupling. The coefficient of coupling will always less than the unity and the maximum value of the coefficient of coupling can be 1 or 100%. 90003 90002 90003 90002 The mutual inductance is highly dependable on the coefficient of coupling between the two inductively coupled coil circuits.If the coefficient of coupling is higher so the mutual inductance will be higher, on the other side, if the coefficient of coupling is at a lower amount that will highly decrease the mutual inductance in the coupling circuit. The coupling coefficient can not be a negative number and it has no dependencies on the direction of current inside the coils. The coupling coefficient depends on the core materials. In iron or ferrite core materials the coupling coefficient can be very high like 0.99 and for the air core, it can be as low as 0.4 to 0.8 depending on the space between the two coils. 90003 90002 90003 90006 90007 Inductor in Series Combination 90008 90009 90002 Inductors can be added together in series. There are 90007 two ways to connect inductors 90008 in series, by using 90007 Aiding Method 90008 or by using 90007 Opposition Method. 90008 90003 90002 90206 90003 90002 90003 90002 In the above image, two types of series connections are shown. 90007 For the first one on the left side 90008, the inductors are connected in series by 90007 Aiding Method 90008.In this method, the current flowing through the two inductors is in the same direction. As the current flowing in the same direction, the magnetic fluxes of self and mutual induction will end up linking with each other and add together. 90003 90002 90003 90002 Therefore, the total inductance can be calculated using the below formula- 90003 90032 90007 L 90072 eq 90073 = L 90072 1 90073 + L 90072 2 90073 + 2M 90008 90035 90002 Where, L 90072 eq 90073 is the total equivalent inductance and M is the mutual inductance.90003 90002 90003 90002 90007 For the right image, the Opposition Connection is shown 90008. In such a case, the current flow through the inductors is in the opposite direction. Therefore, the total inductance can be calculated using the below formula, 90003 90032 90007 L 90072 eq 90073 = L 90072 1 90073 + L 90072 2 90073 — 2M 90008 90035 90002 Where, L 90072 eq 90073 is the total equivalent inductance and M is the mutual inductance. 90003 90002 90003 90006 90007 Inductors in Parallel Combination 90008 90009 90002 Same as the series inductor combination, the parallel combination of two inductors can be two types, by using 90007 aiding method and by using opposition method 90008.90003 90002 90265 90003 90002 90003 90002 For the 90007 Aiding Method 90008, as seen on the left image, the dot convention clearly shows that the current flow through the inductors is in the same direction. To calculate the total inductance, below formula can be very helpful. In such a case, the self-induced electromagnetic field in two coils allows the mutually induced emf. 90003 90032 90007 L 90072 eq 90073 = (L 90072 1 90073 L 90072 2 90073 — M 90281 2 90282) / (L 90072 1 90073 + L 90072 2 90073 + 2M) 90008 90035 90002 90003 90002 For the 90007 Opposition Method 90008, the inductors are connected in parallel with the opposite direction of each other.In such a case, the mutual inductance creates a voltage which opposes the self-induced EMF. The equivalent inductance of the parallel circuit can be calculated using the below formula- 90003 90032 90007 L 90072 eq 90073 = (L 90072 1 90073 L 90072 2 90073 — M 90281 2 90282) / (L 90072 1 90073 + L 90072 2 90073 + 2M) 90008 90035 90002 90003 90006 90007 Applications of Inductor 90008 90009 90002 One of the best usage of coupled inductors is in the creation of 90007 transformers. 90008 A transformer uses coupled inductors wrapped around iron or ferrite core.An ideal transformer has zero loss and hundred percent 90007 coupling coefficients 90008. Other than the transformer, 90007 coupled inductors 90008 are also used in sepic or 90007 flyback converter 90008. This is an excellent choice to isolate the primary input with the secondary output of power supply by using the 90007 coupled inductor or transformers 90008. 90003 90002 90003 90002 Apart from that coupled inductors are also used to make a single or double tuned circuit in 90007 radio transmitting or receiving circuit 90008 90003 .90000 Introduction to Inductors — What is Inductor, Basics, Types and Working of Inductors 90001 90002 One Passive component that always remains obscure is the 90003 inductors 90004. These are the coil like structures that you find in most power electronic circuits and it is because of its properties your transformers work. The reason why many people do not understand Inductors is that they not only alter electric field but also the magnetic field around it. In this tutorial let us understand the 90003 basics of an Inductor 90004 and demystify it so that we will know how and when to use one in our applications.90007 90002 90007 90010 90003 What is an Inductor? 90004 90013 90002 The 90003 inductor 90004 is perhaps the simplest of all electronic components, constructed much like a resistor — a simple length of wire that is coiled up. However, here, resistance is not the property we’re looking for. It is something that happens because of the shape of the wire — a coil — it creates a magnetic field when a current is passed through it. This induced magnetic field gives this bit of wire some interesting electrical properties, especially inductance — which gives these parts their name.90007 90002 90007 90010 90003 Difference Between an Inductor and Capacitor 90004 90013 90002 We have already learnt about the capacitor in the previous article. And now that you have known the basics of inductor you might get a question, «90003 What is the difference between an Inductor and Capacitor? 90004 «90007 90002 First things first both store energy when a voltage potential is applied across it, but a Capacitor stores energy in form of an Electric Field and an Inductor stores energy in form of a Magnetic felid.Okay, but how does it affect its performance. 90007 90002 We need a dig a lot deep in to understand that, but for now you can just remember that a Capacitor tries to level the voltage in a circuit, that is it does not like the change in potential across each component and hence it will charge or discharge to level up the voltage. An Inductor on the other hand does not like the change in current within a circuit so it the current changes it will charge or discharge to equalize the current through the circuit.90007 90002 Also remember that an Inductor changes it polarity while discharging so the potential during charging will be opposite to the potential during dis-charge. 90007 90002 90007 90010 90003 Symbols for Inductors 90004 90013 90002 Like many other electronic components, the symbol for an inductor is a simplified pictogram of what it actually looks like: 90007 90002 90043 90007 90002 The lines near the symbol represent the core material — something we will discuss later.90007 90002 90007 90010 90003 Working of an Inductor 90004 90013 90002 An inductor, as already mentioned, is just a coil of wire. 90007 90002 Before we go into anything else, let’s ask the question, why a coil? 90007 90002 As we already know, any current carrying conductor generates a magnetic field in the following fashion: 90007 90002 90007 90002 However, if you plug in the value of the current into the formulas, then you’ll realize that the magnetic field produced is tiny — almost negligible, unless the currents are impossibly high, in the order of mega-amps.90007 90002 So in order to increase the magnetic field created by a specific length of wire, we wrap it into the form of a coil. This increases the magnetic field, like so: 90007 90002 90066 90007 90002 This shape is also called a 90003 solenoid 90004. 90007 90002 When a voltage is applied across the terminals of an inductor, the current flowing creates a magnetic field. This magnetic field again creates an induced current in the inductor of opposite polarity, according to Lenz’s law.The currents do not cancel each other out — rather, the induced current actively tries to oppose the incoming current due to the voltage across the inductor. The overall result of this battle is that the current through an inductor can not change rapidly — it is always a linear slope. 90007 90002 90007 90010 90003 Measuring an Inductor 90004 90013 90002 The 90003 working behavior of an inductor 90004 poses an interesting question — how do we quantitatively measure the behavior of an inductor in terms that is easily measurable? 90007 90002 We could try measuring inductors by the magnetic field that they create.As soon as we do that, we run into problems. The magnetic field created by an inductor depends on the current that passes through it, so even a small inductor can create a large magnetic field. 90007 90002 Instead, we could use the same approach we used for capacitors, and we can define inductance of a circuit as the voltage change induced when the current changes at a certain rate. 90007 90002 Mathematically, 90007 90002 90003 V = L (dI / dt) 90004 90007 90002 Where V is the voltage, L is the inductance, I is the current and t is the time period.90007 90002 Inductance, ‘L’, is measured in Henrys, named after Joseph Henry, the American scientist who discovered electromagnetic induction. 90007 90002 The formula for calculating the inductance of a coil of wire is given by this formula: 90007 90002 90003 L = (μn2a) / l 90004 90007 90002 Where L is the inductance in Henrys, μ is the permeability constant, i.e. a coefficient of how easily the magnetic field can be created in a given medium, n is the number of turns, a is the area of the coil and l is the length of the coil.90007 90002 Again, the Henry is a very large unit, so practically inductors are measured in microHenrys, uH, which is a millionth of a Henry, or milliHenrys, mH, which is a thousandth of a Henry. Occasionally you might even find very small inductances measured in nanoHenrys, which are a thousandth of a uH. 90007 90002 90007 90002 90007 90010 90003 Different Types of Inductors 90004 90013 90002 Now the μ in the above equation has some interesting implications. It suggests that the magnetic field inside the inductor can be manipulated.Like mentioned above, sometimes the magnetic field created even by a solenoid falls short of requirements sometimes. That is why in almost all cases you find inductors formed around a core material. 90007 90002 Cores are materials that support the creation of a magnetic field. They are generally made of iron and its compounds, such as ferrite (which is an oxide of iron). You can get a greater magnetic field using a core than without one. 90007 90002 90007 90122 90003 1. AIR CORE INDUCTORS: 90004 90125 90002 90007 90002 Like the name suggests, this kind of inductor has no core — the core material is air! Since air has a relatively low permeability, the inductance of air core inductors is quite low — rarely above 5uH.Since they have a low inductance, the rate of current rise is quite fast for an applied voltage and that makes them capable of handling high frequencies. They are mostly used in RF circuits. 90007 90002 90007 90122 90003 2. IRON CORE INDUCTORS 90004 90125 90002 90007 90002 Iron is perhaps the most recognizable magnetic material, which makes it an ideal choice for inductors. These take the form of iron-core inductors. They are usually used for low frequency line filtering, since they can be rather beefy and have large inductances.They are also used in audio equipment. 90007 90002 90007 90122 90003 3. FERRITE CORE INDUCTORS 90004 90125 90002 90007 90002 Ferrite is just a powder of oxides of iron. This powder is mixed with an epoxy resin and molded to form cores around which wires can be wound. 90003 Ferrite core inductors 90004 are easily the most recognizable because of their dull grey-black colour. They also are very brittle and break easily. They are the most widely used kinds of inductors, since the permeability can be finely controlled by controlling the ratio of ferrite to epoxy in the mix.90007 90002 90007 90010 90003 Inductors in Series and Parallel 90004 90013 90002 Inductors connected in series and parallel behave the exact opposite way to capacitors. 90007 90002 For example, to calculate the inductance of a group of inductors in series, you can simply sum up the values of the individual inductances. 90007 90002 90163 90007 90002 90003 L = L1 + L2 + … + Ln 90004 90007 90002 Where L is the total inductance and L1, L2 … Ln are the individual inductances.90007 90002 Suppose you have two inductors, one measuring 10uH and the other 15uH, then by putting them in series you obtain a total inductance of 25uH. 90007 90002 90174 90007 90002 Inductors in parallel behave the same way as resistors in parallel, the inductance is given by: 90007 90002 90003 1 / L = 1 / L1 + 1 / L2 + … + 1 / Ln 90004 90007 90002 Where L is the total inductance and L1, L2 … Ln are the individual inductances. 90007 90002 In this way if you connect two 10uH inductors in parallel, you’ll end up with an inductance of 5uH.90007 90002 90007 90010 90003 Useful Inductor Formulas 90004 90013 90122 90003 1. ENERGY STORED BY INDUCTORS: 90004 90125 90002 Inductors can store energy much like capacitors, but the energy is gone the moment you disconnect the power and the magnetic field collapses. In other words, an unpowered inductor can not sustain its magnetic field. 90007 90002 90003 E = ½ * L * I2 90004 90007 90002 Where E is the energy in Joules, L is the inductance in Henries and I is the current in amps.90007 90002 If you have an inductor of 20uH with a 5A current flowing through it, then the energy stored will be 0.00025J. In this aspect inductors too, like capacitors, hold very little energy. 90007 90122 90003 2. RATE OF CURRENT RISE 90004 90125 90002 This formula has already been discussed, but it is worth having a closer look. 90007 90002 90003 V / L = dI / dt 90004 90007 90002 Where V is the voltage applied across the inductor, L is the inductance, I is the current and t is the time.90007 90002 This states that when a constant voltage is applied across the inductor, the current rises in a linear slope. This can be useful in creating current ramps, just like the capacitor created voltage ramps at a constant current. 90007 90122 90003 3. IMPEDANCE 90004 90125 90002 Inductors have impedance that is related to the frequency by the formula: 90007 90002 90003 XL = 2π * f * L 90004 90007 90002 Where XL is the inductive impedance, f is the frequency in Hertz and L is the inductance in Henrys.90007 90002 90007 90010 90003 Inductor Behavior in Circuits 90004 90013 90002 Surprisingly, inductors are pretty much useless in DC circuits, since there is a constant current flowing and the inductor acts like a bit of wire. 90007 90002 They find most of their uses in AC circuits. Like mentioned above, they have an impedance, which makes them useful to limit current in an AC circuit, such as fluorescent lamp ballasts. 90007 90002 They can also be used to filter signals. 90007 90002 90007 90002 In the first case, the inductor allows all DC current to flow through it to ground, preventing all the low frequencies from reaching the output.At higher frequencies, the impedance of the inductor increases steadily, so the signal can pass through to the output, hence it is called a high pass filter. 90007 90002 In the second case, the inductor allows DC and low frequencies to pass through but blocks all high frequencies from the output and so it is called a low pass filter. 90007 90002 90007 90010 90003 Inductors in Real Life 90004 90013 90002 90257 90007 90002 Inductors, since they are made of copper wire and ferrite, tend to be expensive and find most of their uses in radios, power supplies and telecoms equipment.90007 90002 In power supplies, the property of an inductor to prevent sudden changes in current is used. Along with a capacitor, it acts to prevent sudden changes in the power supply output voltage and current. 90007 90002 RF circuits make use of an interesting LC circuit called a tank. The capacitor is charged and discharged into the inductor, which builds up its magnetic field. When the magnetic field collapses, a voltage is created and charges the capacitor. This creates periodic oscillations which can be used to generate high frequencies.90007 90002 The frequency can be calculated by the formula: 90007 90002 90268 90007 90002 Where f is the frequency in Hertz, L is the inductance in Henrys and C is the capacitance in Farads. 90007 90002 90007 90010 90003 Conclusion 90004 90013 90002 And that is all the practical knowledge you will require to work with inductors. They are intrinsically simple devices and are not as prevalent as their capacitor and resistor relatives, but are still very useful. 90007.90000 What is Inductor? — Definition & Types 90001 90002 90003 Definition: 90004 The inductor is a passive component which stores the electrical energy in the magnetic field when the electric current passes through it. Or we can say that the inductor is an electrical device which possesses the inductance. 90005 90002 The inductor is made of wire which has the property of inductance, i.e., opposes the flow of current. The inductance of wire increases by increasing the number of turns. The alphabet ‘L’ is used for representing the inductor, and it is measured in Henry.The inductance characterises the inductor. The figure below shows the symbolic representation of inductor. 90005 90002 90009 90005 90002 The electric current I flows through the coil generates the magnetic field around it. Consider the magnetic field generates the flux Φ when current flows through it. The ratio of the flux and the current gives inductances. 90012 90005 90002 The inductance of the circuit depends on the current paths and the magnetic permeability of the nearer material. The magnetic permeability shows the ability of the material to forms the magnetic field.90005 90016 Types of Inductor 90017 90002 The inductors are classified into two types. 90005 90002 90003 1. Air Cored Inductor (wound on non-ferrite material) 90004 — The inductor in which either the core is completely absent or ceramic material is used for making the core such type of inductor is known as the air-cored inductor. 90005 90002 90025 90005 90002 The ceramic material has the very low thermal coefficient of expansion. The low thermal coefficient of expansion means the shape of material remains same even with the rise of temperature.The ceramic material has no magnetic properties. The permeability of the inductor remains same due to the ceramic material. 90005 90002 In air core-inductor, the only work of the core is to give the coil a particular shape. The air cored structure has many advantages like they reduce the core losses and increases the quality factor. The air cored inductor is used for high-frequency applications work where low inductance is required. 90005 90002 90003 2. Iron Core Inductor (wound on ferrite core) 90004 — It is a fixed value inductor in which the iron core is kept between the coil.The iron-cored inductor is used in the filter circuit for smoothing out the ripple voltage, it is also used as a choke in fluorescent tube light, in industrial power supplies and inverter system etc. 90005 90002 90036 90005 90038 How Inductor Works? 90039 90002 The inductor is an electrical device used for storing the electrical energy in the form of the magnetic field. It is constructed by wounding the wire on the core. The cores are made of ceramic material, iron or by the air. The core may be toroidal or E- shaped.90005 90002 The coil-carrying the electric current induces the magnetic field around the conductor. The intensity of the magnetic field increases if the core is placed between the coil. The core provides the low reluctance path to the magnetic flux. 90005 90002 90045 90005 90002 The magnetic field induces the EMF in the coil which causes the current. And according to Lenz’s law, the causes always oppose the effect. Here, the current is the causes, and it is induced because of the voltage.Thus, the EMF oppose the change of current that changes the magnetic field. The current which reduces because of the inductance is known as the inductive reactance. The inductive reactance increases with the increase of the number of turn of coils. 90005 .