Последовательное и параллельное соединение резисторов тест
Тест для 10 класса по физике по теме «Последовательное и параллельное соединение проводников.» на два варианта, готовый к двухсторонней печати, + ответы для быстрой проверки. Тест составлены в программе Microsoft Office Word по сборнику Физика, 10 класс, Тесты, часть 2, Сычёв Ю.Н., 2012.
Идёт приём заявок
Подать заявку
Для учеников 1-11 классов и дошкольников
Тест по физике для 8 класса
Последовательное и параллельное соединение проводников
А1. Сопротивление в проводнике R 1 = 4 Ом. Какова сила тока в проводнике R 2, соединённым с ним последовательно?
А2. Сколько лампочек напряжением 6 В нужно взять для ёлочной гирлянды, чтобы её можно было включить в сеть напряжением 120 В?
А3. Каждый из двух нагревательных элементов кипятильника имеет силу тока 5 А. Определите силу тока в проводящих проводах, если элементы соединены последовательно.
А4. Проводники сопротивлением 2 Ом, 4 Ом и 6 Ом соединены последовательно и включены в сеть напряжением 36 В. Какова сила тока в проводниках?
А5. Вычислите сопротивление десяти последовательно соединённых одинаковых проводников сопротивлением по 10 Ом.
А6. Каким сопротивлением обладает электрическая цепь, состоящая из трёх ламп, соединённых параллельно, если сопротивление каждой из них 12 Ом?
А7. Электрические лампы сопротивлением 200 Ом и 300 Ом соединены параллельно. Вычислите их общее сопротивление.
А8. Сила тока в резисторах, соединённых параллельно, соответственно 2 А и 1 А. Найдите силу тока в неразветвлённой части цепи.
А9. Для освещения классной комнаты установлено 10 одинаковых ламп сопротивлением по 440 Ом каждая. Каково из общее сопротивление?
А10. При последовательном соединении проводников общее напряжение на всех проводниках …. на отдельных проводниках.
а) такое же, как и
б) равно сумме напряжений
Данный тест можно использовать в качестве контроля после прохождения темы «Соединение проводников».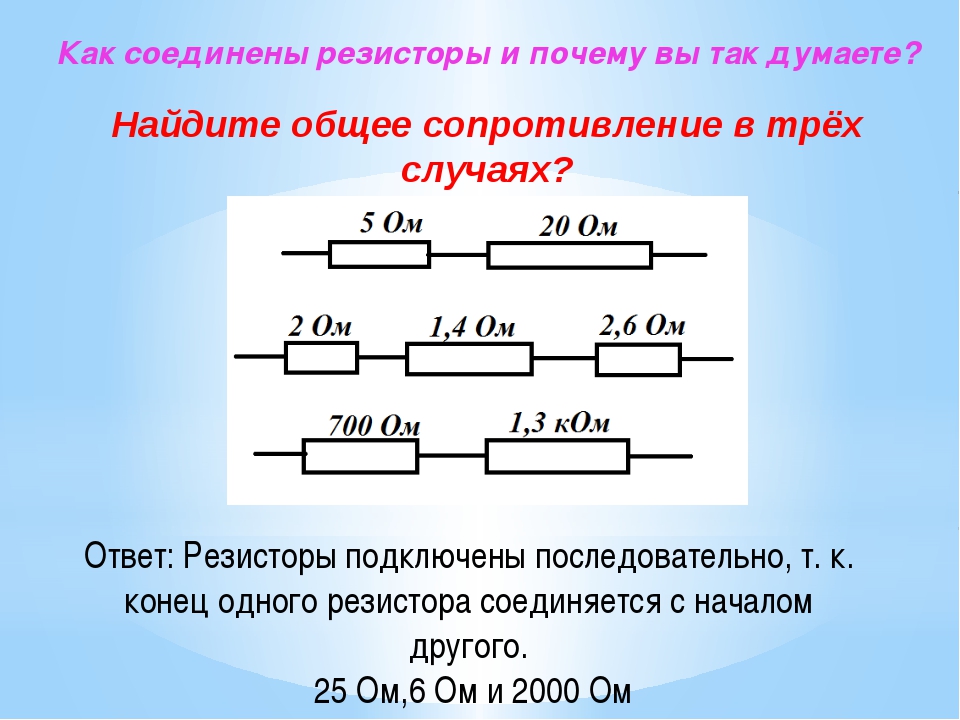 Он рассчитан на 20 минут. Задания не сложные, требуют знания основных законов последовательного и параллельного соединения проводников. Тест в одном варианте. Предложены ответы. Можно вывести их на доску и проверять, используя самоконтроль или взаимоконтроль.
Он рассчитан на 20 минут. Задания не сложные, требуют знания основных законов последовательного и параллельного соединения проводников. Тест в одном варианте. Предложены ответы. Можно вывести их на доску и проверять, используя самоконтроль или взаимоконтроль.
- Ефимова Татьяна ТерентьевнаНаписать 9628 05.03.2017
Номер материала: ДБ-246176
Не нашли то что искали?
Вам будут интересны эти курсы:
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Тест по физике Параллельное соединение проводников для учащихся 8 класса с ответами. Тест включает в себя 11 заданий с выбором ответа.
1. Какая схема из представленных на рисунке показывает параллельное соединение электроламп?
2. Каково соотношение напряжений на концах проводников, соединенных параллельно?
1) Напряжение на проводнике тем больше, чем больше его сопротивление
2) Напряжения на всех проводниках одинаковы
3) Напряжения на проводниках тем меньше, чем больше сопротивления
3. Каково соотношение сил токов в общей цепи и в параллельно соединенных проводниках?
1) Все силы токов одинаковы (I = I1 = I2)
2) В параллельно соединенных проводниках силы токов одинаковы и меньше силы тока в общей цепи
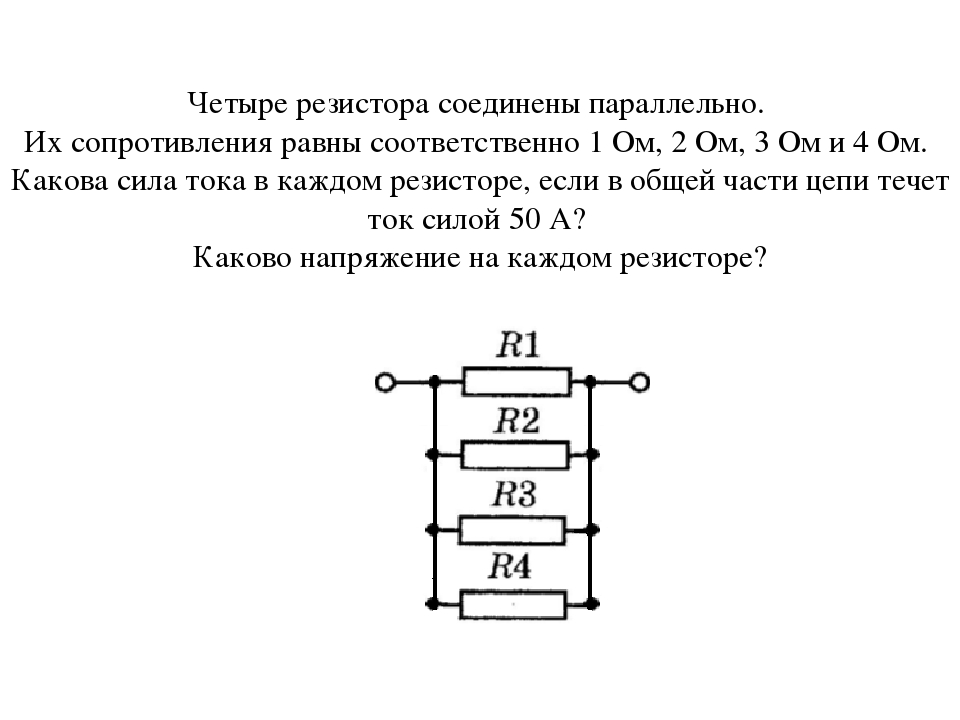
4. В цепь включены параллельно резисторы сопротивлением 5, 10, 15 и 20 Ом. Больше какого из этих значений сопротивление разветвленного участка цепи не может быть?
В цепь включены параллельно резисторы сопротивлением 5, 10, 15 и 20 Ом. Больше какого из этих значений сопротивление разветвленного участка цепи не может быть?
1) 20 Ом
2) 15 Ом
3) 10 Ом
4) 5 Ом
5. По какой формуле рассчитывается сопротивление участка цепи с параллельно соединенными проводниками?
6. Каково сопротивление участка цепи с проводниками сопротивлением 10 Ом и 40 Ом, соединенными параллельно?
1) 8 Ом
2) 30 Ом
3) 50 Ом
4) 400 Ом
7. Цепь имеет смешанное соединение электроприборов: через ключ к источнику тока присоединена лампа, а к ней — две такие же лампы, соединенные между собой параллельно. Какой из участков цепи — с одной лампой (№1) или двумя (№2) имеет меньшее сопротивление? В каком из них сила тока будет больше?
1) №2; №1
2) №1; №2
3) №2; силы тока будут одинаковы
4) Сопротивления равны; №1
8. Цепь собрана по схеме, показанной на рисунке.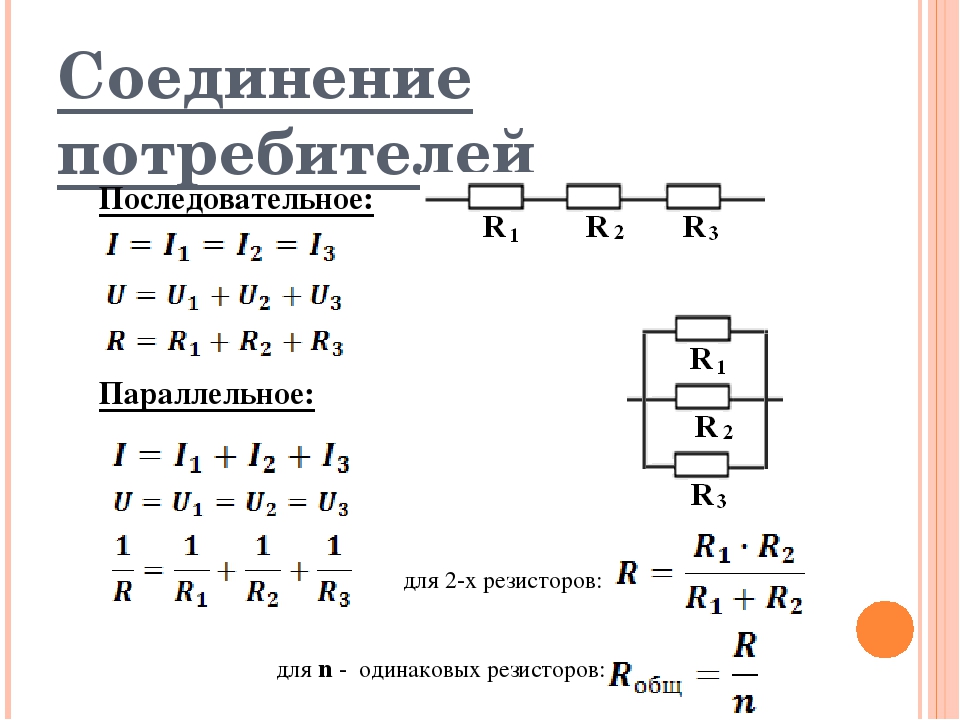 Напряжение на полюсах источника тока 10 В, амперметр фиксирует силу тока 2 А. Каково напряжение на лампе №2 и сила тока в лампе №1, если их сопротивления равны?
Напряжение на полюсах источника тока 10 В, амперметр фиксирует силу тока 2 А. Каково напряжение на лампе №2 и сила тока в лампе №1, если их сопротивления равны?
1) 5 В; 1 А
2) 5 В; 2 А
3) 10 B; 2 А
4) 10 В; 1 А
9. Два прибора, включенных параллельно в цепь с напряжением 320 В, имеют сопротивления 400 Ом и 800 Ом. Найдите силу тока в каждом из них и в общей цепи.
1) I1 = 0,8 A, I2 = 0,4 A, I = 1,2 A
2) I1 = 0,4 A, I2 = 0,2 A, I = 0,6 A
3) I1 = 0,8 A, I2 = 0,4 A, I = 0,4 A
4) I1 = 0,4 A, I2 = 0,2 A, I = 0,2 A
10. Сила тока в неразветвленной части цепи 0,6 А. На участке этой цепи, на концах которого напряжение 1,8 В, соединены между собой параллельно три одинаковых проводника. Какие значения сил токов зафиксируют амперметры в каждом из этих проводников? Каково сопротивление этого участка?
1) 0,2 А; 9 Ом
2) 0,2 А; 3 Ом
3) 0,6 А; 3 Ом
4) 0,2 А; 27 Ом
11. Сопротивление одной из трех одинаковых соединенных параллельно электроламп 300 Ом, а сила тока в ней 0,4 А. Определите напряжение на лампах и силу тока в неразветвленной части цепи.
Сопротивление одной из трех одинаковых соединенных параллельно электроламп 300 Ом, а сила тока в ней 0,4 А. Определите напряжение на лампах и силу тока в неразветвленной части цепи.
1) 120 В и 2,4 А
2) 120 В и 1,2 А
3) 40 В и 1,2 А
Ответы на тест по физике Параллельное соединение проводников
1-2
2-2
3-3
4-4
5-1
6-1
7-3
8-3
9-1
10-2
11-2
Тест по теме «Последовательное и параллельное соединение проводников» ( 8 класс)
Последовательное и параллельное соединение проводников вариант 1.
А1. Проводники сопротивлениями R1 = 4 Ом и R2=5 Ом соединены последовательно. Напряжение на концах первого проводника 4 В. Какова сила тока в проводнике R2?
a) 4 А б) 1 А в) 8 А
А2. Сколько лампочек напряжением 6 В нужно взять для ёлочной гирлянды, чтобы её можно было включить в сеть напряжением 120 В?
а) 8 б) 20 в) 30
А3. Проводники сопротивлениями R1 = 2 Ом и R2=4 Ом соединены
последовательно и включены в сеть напряжением 18 В. Какова сила тока в
проводниках?
Проводники сопротивлениями R1 = 2 Ом и R2=4 Ом соединены
последовательно и включены в сеть напряжением 18 В. Какова сила тока в
проводниках?
а) 3 А б) 1 А в) 8 А.
А4. Вычислите сопротивление десяти последовательно соединённых одинаковых проводников сопротивлением по 10 Ом.
а) 100 Ом б) 10 Ом в) 0,01 Ом
А5. Каким сопротивлением обладает электрическая цепь, состоящая из трёх ламп, соединённых параллельно, если сопротивление каждой из них 12 Ом?
а) 36 Ом б) 3 Ом в) 4 Ом
А1. Сила тока в резисторах, соединённых параллельно, соответственно 2 А и 1 А. Найдите силу тока в неразветвлённой части цепи.
а) 2 А б) 0,5 А в) 3 А
А2. Электрические лампы
сопротивлением 20 Ом и 30 Ом соединены параллельно.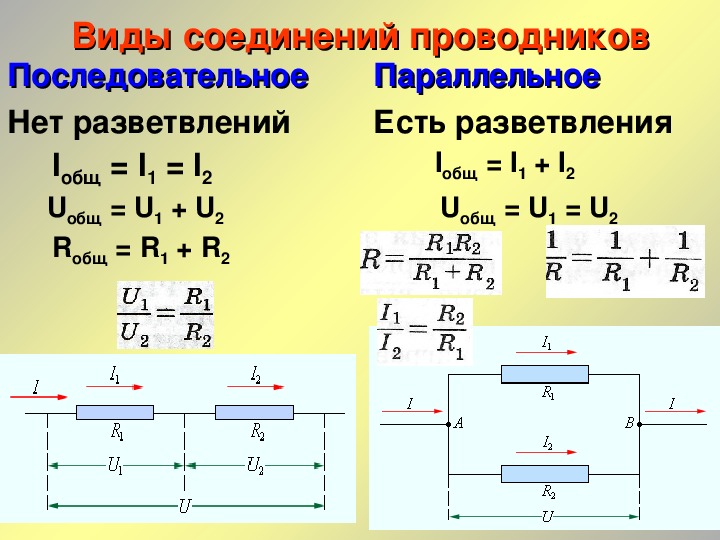 Вычислите их общее
сопротивление.
Вычислите их общее
сопротивление.
а) 12 Ом б) 50 Ом в) 25 Ом
А3. Проводники сопротивлением 2 Ом, 4 Ом и 6 Ом соединены последовательно и включены в сеть напряжением 36 В. Какова сила тока в проводниках?
а) 0,3 А б) 0,33 А в) 3 А
А4. Для освещения классной комнаты установлено 10 одинаковых ламп сопротивлением по 440 Ом каждая. Каково из общее сопротивление?
а) 44 Ом б) 4400 Ом в) 4,4 Ом
А5. В электрическую цепь последовательно включены 4 электроприбора, имеющие равные сопротивления (по 10 Ом). Сила тока в одном из них 1,5 А. Каково общее напряжение в этой цепи?
а) 15 В. б) 60 В в) 30 В.
Тест с ответами Соединение проводников (По какому признаку можно сразу определить …)
Рубрика: Физика
(правильные ответы отмечены плюсом)
1. По какому признаку можно сразу определить, последовательно или нет соединены потребители электрического тока:
а) по прекращению работы всей цепи при выключении какого-либо одного потребителя тока +
б) по одинаковости силы тока во всех проводниках
в) по зависимости напряжений на проводниках от их сопротивлений
2.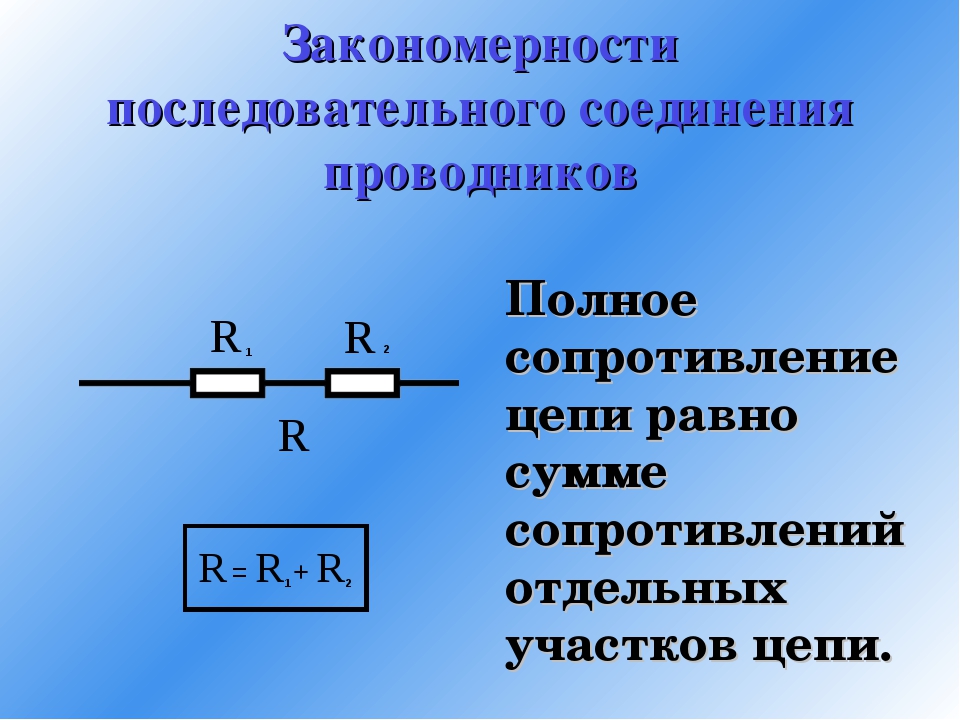 Чему равно общее сопротивление R цепи с последовательно включенными электроприборами:
Чему равно общее сопротивление R цепи с последовательно включенными электроприборами:
а) R = R1 − R2
б) R = R1 + R2 +
в) R = R1 ⋅ R2
3. Чему равно общее напряжение на последовательно соединенных участках цепи:
а) U = U1 ⋅ U2
б) U = U1 − U2
в) U = U1 + U2 +
4. В электрическую цепь последовательно включены 4 электроприбора, имеющие равные сопротивления (по 10 Ом). Сила тока в одном из них 1,5 А. Каково общее напряжение в этой цепи:
а) 60 В +
б) 15 В
в) 45 В
5. В цепи, состоящей из последовательно соединенных проводников сопротивлениями R1 = 15 Ом, R2 = 14 Ом, R3 = 11 Ом, сила тока равна 3 А. Каково общее напряжение в этой цепи и чему равно напряжение на первом проводнике:
а) U = 60 В; U1 = 5 В
б) U = 240 В; U1 = 150 В
в) U = 120 В; U1 = 45 В +
6. Напряжения на участках последовательной электрической цепи U1 = 100 В, U2 = 30 В, U3 = 75 В, U4 = 150 В. Какой из участков обладает наибольшим сопротивлением:
а) третий
б) четвертый +
в) второй
г) первый
7. Сила тока в цепи с последовательным соединением участков 0,2 А. Напряжения на участках таковы: U1 = 14 В, U2 = 16 В, U3 = 20 В. Определите общее сопротивление цепи (двумя способами):
Сила тока в цепи с последовательным соединением участков 0,2 А. Напряжения на участках таковы: U1 = 14 В, U2 = 16 В, U3 = 20 В. Определите общее сопротивление цепи (двумя способами):
а) 100 Ом
б) 300 Ом
в) 250 Ом +
8. Каково соотношение напряжений на концах проводников, соединенных параллельно:
а) напряжения на всех проводниках одинаковы +
б) напряжение на проводнике тем больше, чем больше его сопротивление
в) напряжения на проводниках тем меньше, чем больше сопротивления
9. Каково соотношение сил токов в общей цепи и в параллельно соединенных проводниках:
а) в параллельно соединенных проводниках силы токов одинаковы и меньше силы тока в общей цепи
б) все силы токов одинаковы
в) сумма сил токов в параллельно соединенных проводниках равна силе тока в неразветвленной части цепи +
10. В цепь включены параллельно резисторы сопротивлением 5, 10, 15 и 20 Ом. Больше какого из этих значений сопротивление разветвленного участка цепи не может быть:
а) 15 Ом
б) 5 Ом +
в) 50 Ом
11.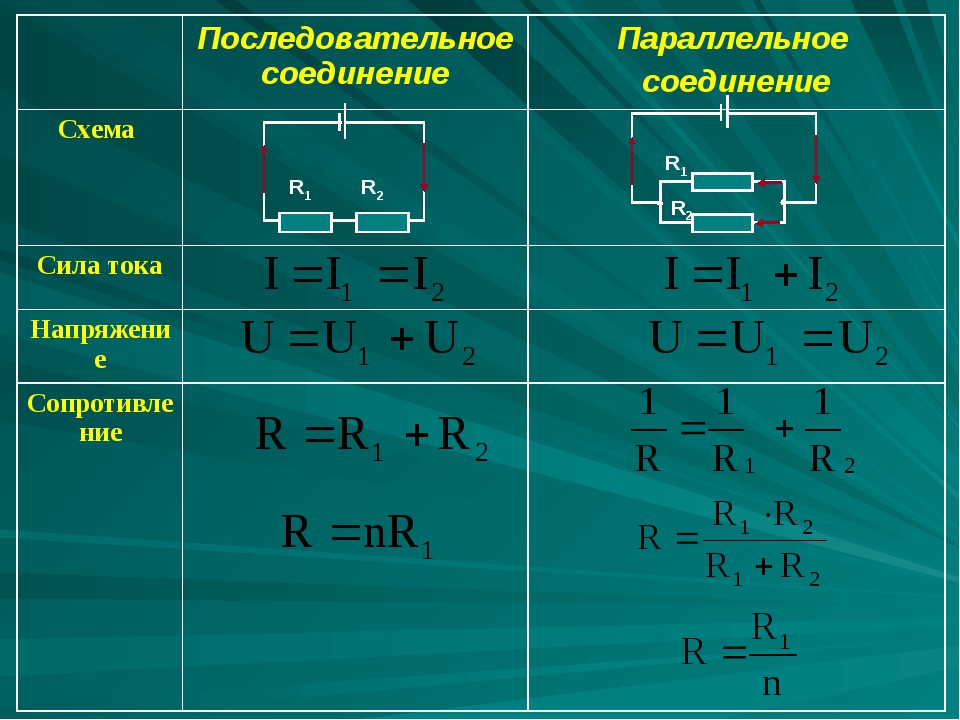 Каково соотношение напряжений на концах проводников, соединенных параллельно:
Каково соотношение напряжений на концах проводников, соединенных параллельно:
а) напряжения на всех проводниках одинаковы +
б) напряжение на проводнике тем больше, чем больше его сопротивление
в) напряжения на проводниках тем меньше, чем больше сопротивления
12. Каково соотношение сил токов в общей цепи и в параллельно соединенных проводниках:
а) все силы токов одинаковы (I = I1 = I2)
б) сумма сил токов в параллельно соединенных проводниках равна силе тока в неразветвленной части цепи +
в) в параллельно соединенных проводниках силы токов одинаковы и меньше силы тока в общей цепи
13. По какой формуле рассчитывается сопротивление участка цепи с параллельно соединенными проводниками:
а) 1/R = 1/R1 + 1/R2 +
б) 1/R = 1/R1 ⋅ 1/R2
в) 1/R = 1/R1 − 1/R2
14. Каково сопротивление участка цепи с проводниками сопротивлением 10 Ом и 40 Ом, соединенными параллельно:
а) 30 Ом
б) 50 Ом
в) 8 Ом +
15. Два прибора, включенных параллельно в цепь с напряжением 320 В, имеют сопротивления 400 Ом и 800 Ом.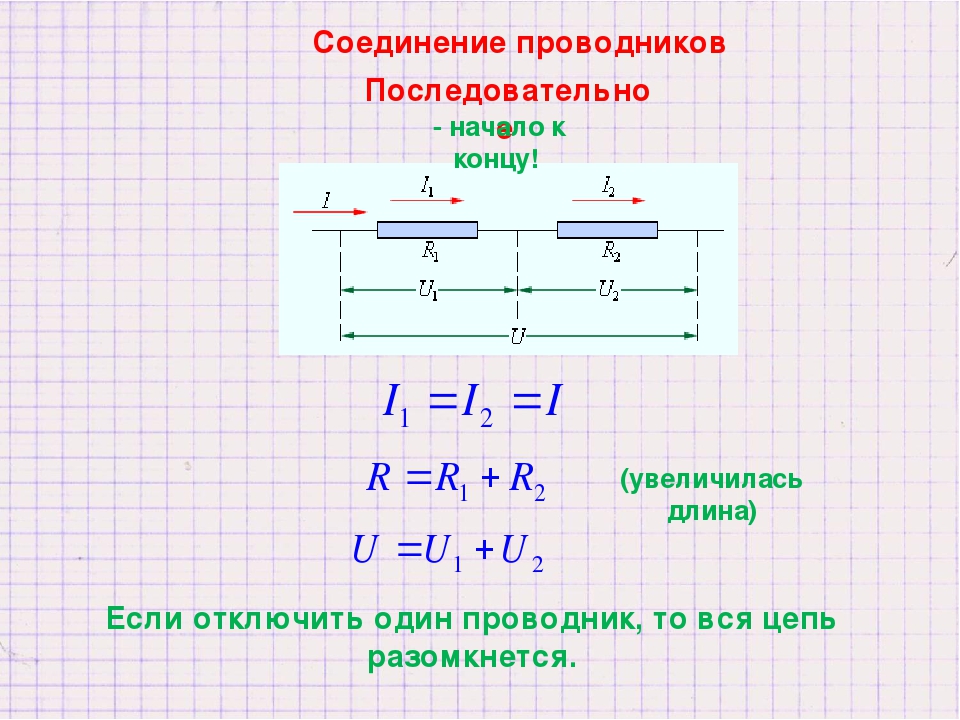 Найдите силу тока в каждом из них и в общей цепи:
Найдите силу тока в каждом из них и в общей цепи:
а) I1 = 0,8 A, I2 = 0,4 A, I = 1,2 A +
б) I1 = 0,4 A, I2 = 0,2 A, I = 0,6 A
в) I1 = 0,4 A, I2 = 0,2 A, I = 0,2 A
16. Сила тока в неразветвленной части цепи 0,6 А. На участке этой цепи, на концах которого напряжение 1,8 В, соединены между собой параллельно три одинаковых проводника. Какие значения сил токов зафиксируют амперметры в каждом из этих проводников? Каково сопротивление этого участка:
а) 0,6 А; 3 Ом
б) 0,2 А; 3 Ом +
в) 0,2 А; 27 Ом
17. Сопротивление одной из трех одинаковых соединенных параллельно электроламп 300 Ом, а сила тока в ней 0,4 А. Определите напряжение на лампах и силу тока в неразветвленной части цепи:
а) 120 В и 2,4 А
б) 40 В и 2,4 А
в) 120 В и 1,2 А +
18. Общее сопротивление при последовательном соединении является суммой всех отдельных:
а) напряжений
б) сопротивлений +
в) сил
19. Напряжение, которое таким образом рассчитано для участка цепи, называют … напряжения:
а) взлетом
б) скачком
в) падением +
20. Последовательно с потребителем в цепь включают:
Последовательно с потребителем в цепь включают:
а) конденсатор
б) электрический предохранитель +
в) резистор
21. При параллельном соединении общий ток является суммой токов, протекающих через … потребители:
а) отдельные +
б) общие
в) суммарные
22. Электрический кабель, который используется в электрической цепи квартиры, имеет три провода. Третий провод является:
а) вводом
б) заземлением +
в) выводом
23. При последовательном соединении все входящие в него проводники:
а) не соединяются между собой
б) одним своим концом присоединяются к одной точке цепи
в) соединяются друг за другом +
24. Полное напряжение в цепи при последовательном соединении равно … на отдельных участках цепи:
а) разности напряжений
б) сумме напряжений +
в) сумме сопротивлений
25. Сила тока в неразветвлённой части цепи равна … в отдельных параллельно соединённых проводниках:
а) сумме сил сопротивления
б) сумме сил напряжения
в) сумме сил тока +
26. Обратное значение общего сопротивления равно … отдельных проводников:
Обратное значение общего сопротивления равно … отдельных проводников:
а) сумме обратных значений напряжений
б) сумме обратных значений сопротивлений +
в) сумме обратных значений сил тока
27. Сопротивление в проводнике R1 = 4 Ом. Какова сила тока в проводнике R2, соединённым с ним последовательно:
а) 4 А +
б) 8 А
в) 2 А
28. Сколько лампочек напряжением 6 В нужно взять для ёлочной гирлянды, чтобы её можно было включить в сеть напряжением 120 В:
а) 2
б) 12
в) 20 +
29. Каждый из двух нагревательных элементов кипятильника имеет силу тока 5 А. Определите силу тока в проводящих проводах, если элементы соединены последовательно:
а) 5 А +
б) 25 А
в) 10 А
30. Проводники сопротивлением 2 Ом, 4 Ом и 6 Ом соединены последовательно и включены в сеть напряжением 36 В. Какова сила тока в проводниках:
а) 0,3 А
б) 3 А +
в) 0,33 А
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще.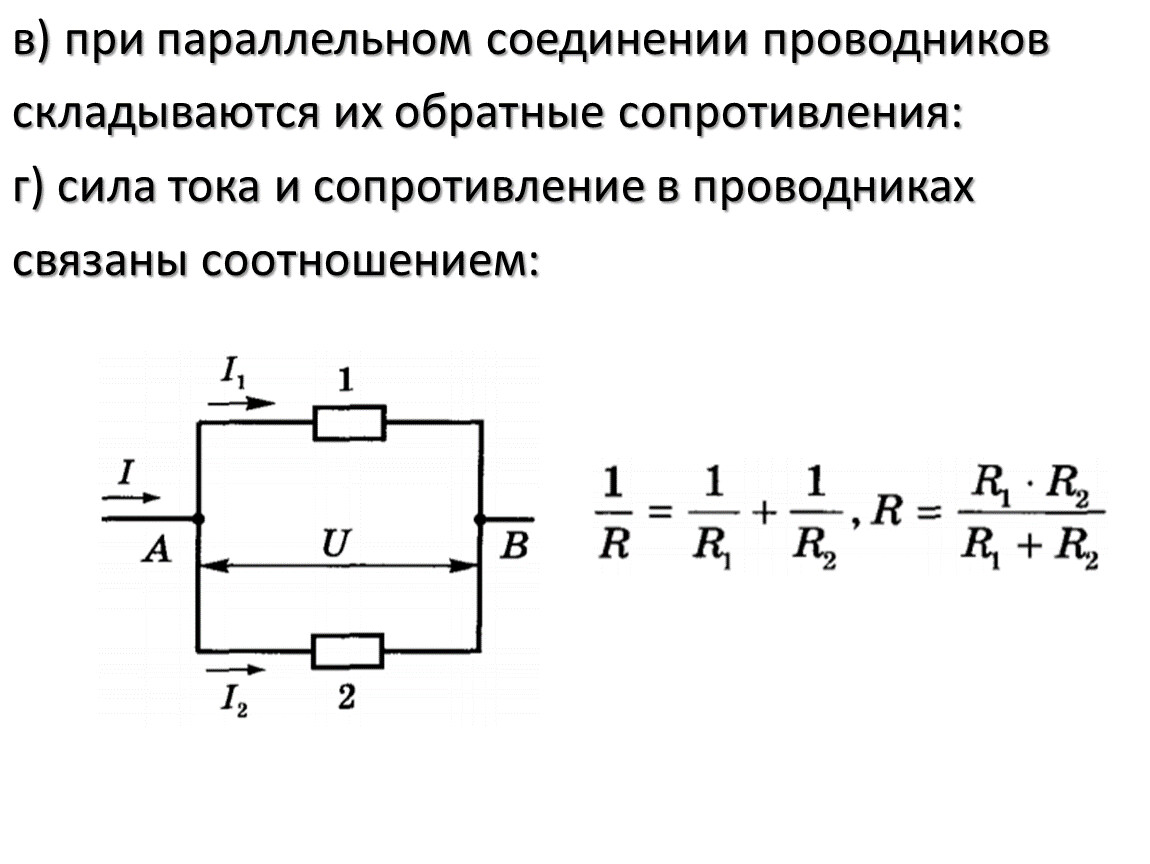 Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
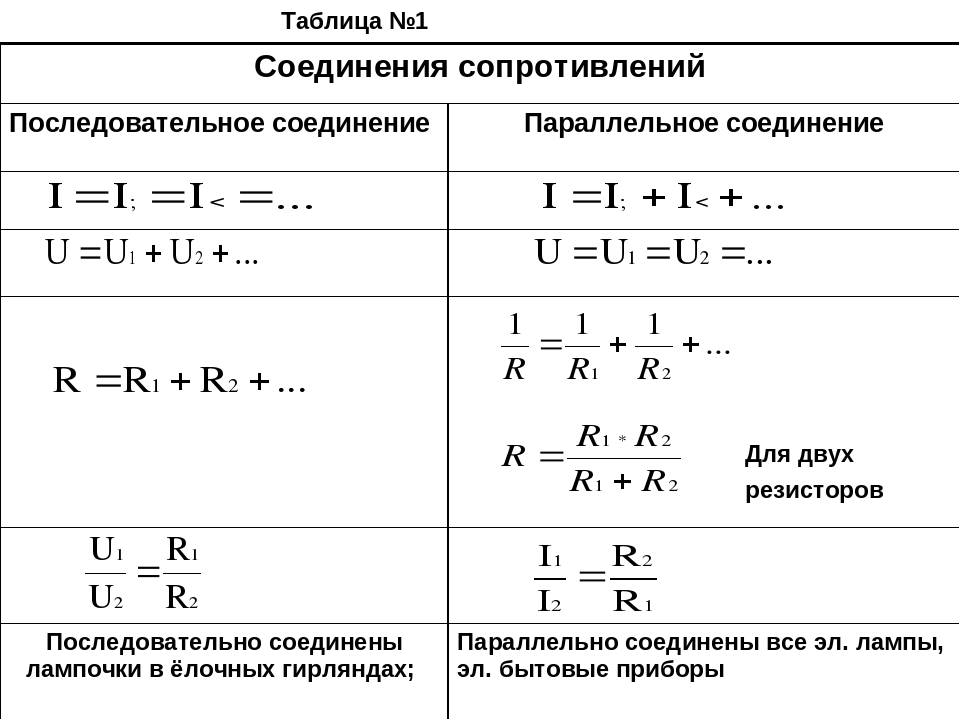
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
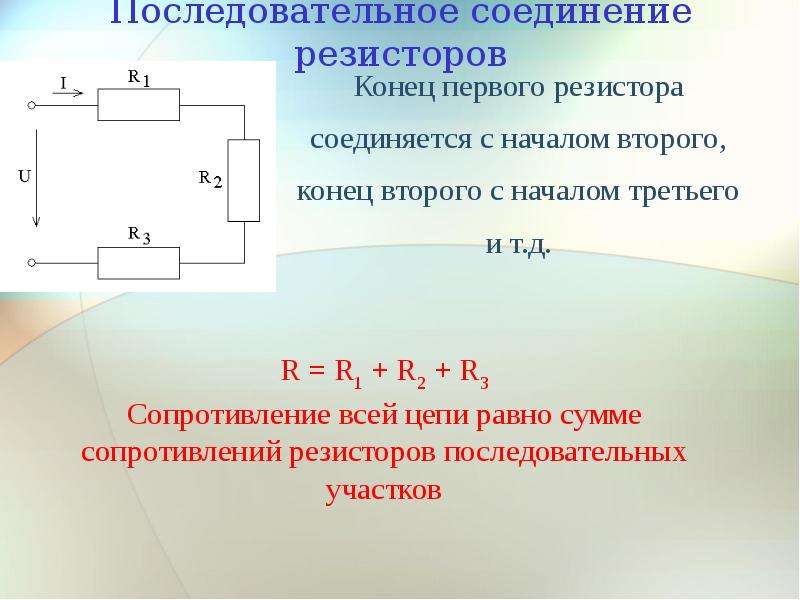
Последовательное соединение
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково.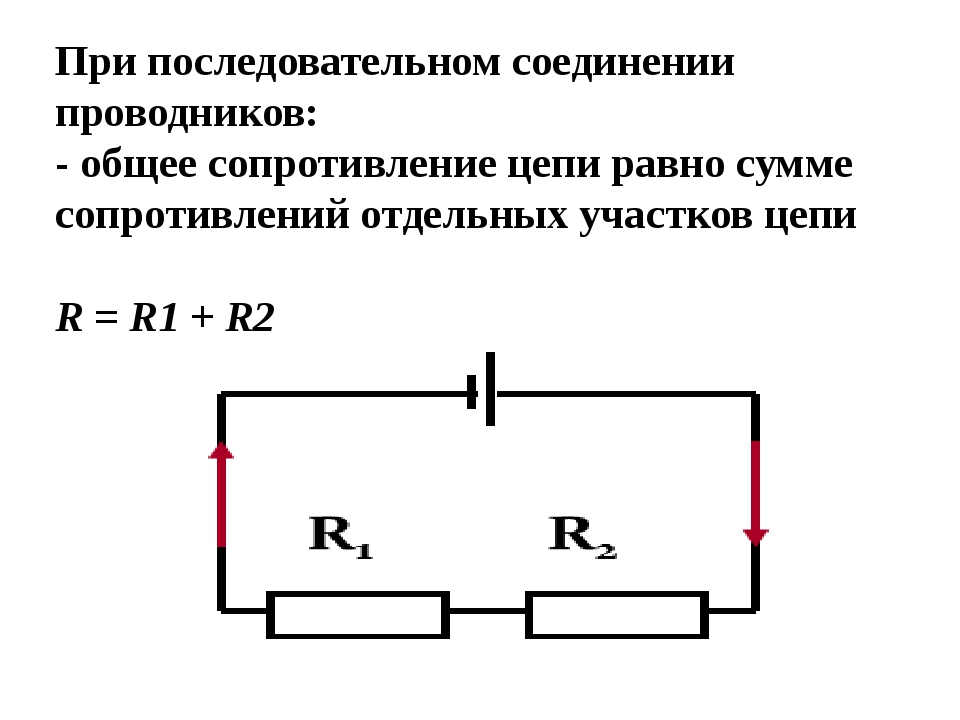 Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R3. Следует понимать, что после преобразования эквивалентное сопротивление R1R2 и резистор R3, соединены последовательно.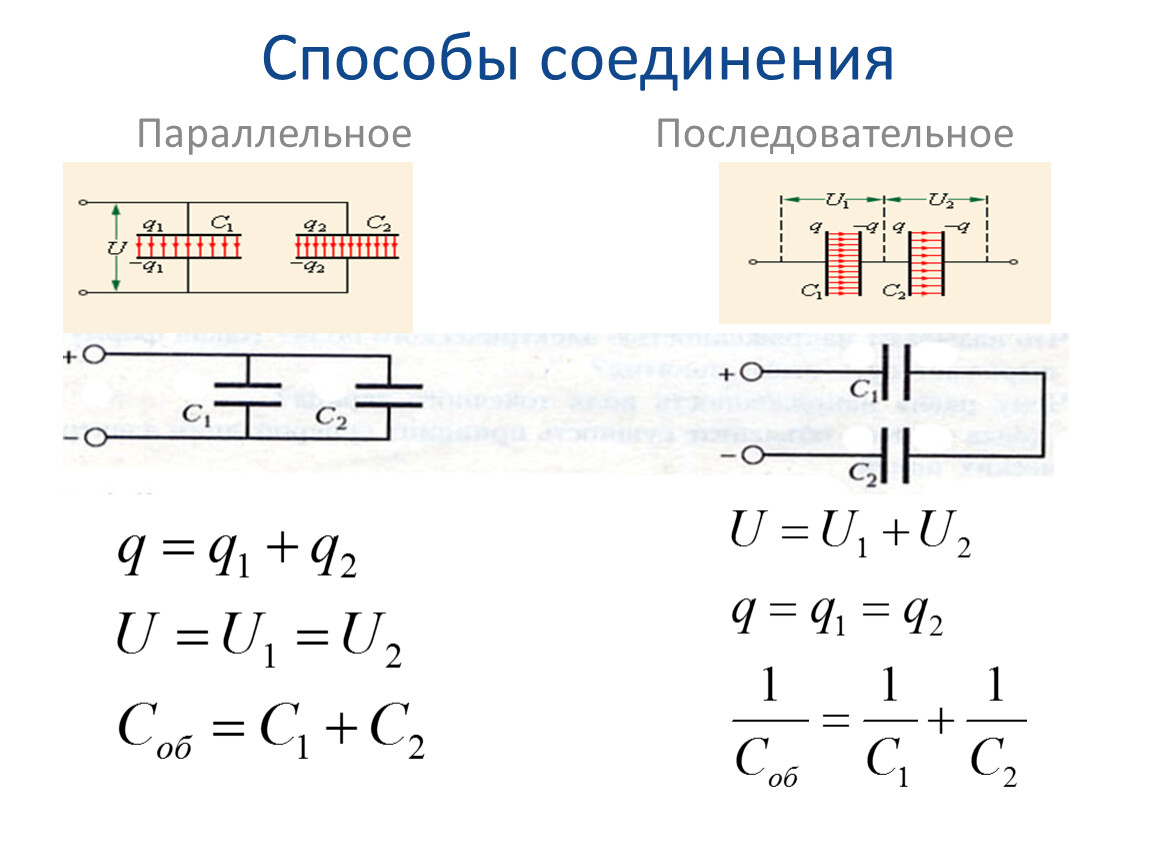
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R1, R2 и R3.
Затем находят общее эквивалентное сопротивление, учитывая, что резисторы R3,R4 и R5,R2 соединены между друг другом последовательно, а в парах параллельно.
Тест с ответами: “Параллельное соединение проводников”
1. При параллельном соединении общий ток является суммой токов, протекающих через … потребители:
а) отдельные +
б) общие
в) зависит от условий
2. Обратное значение общего сопротивления равно … отдельных проводников:
а) сумме обратных значений напряжений
б) сумме обратных значений сопротивлений +
в) сумме обратных значений сил тока
3. Каково сопротивление участка цепи с проводниками сопротивлением 10 Ом и 40 Ом, соединенными параллельно:
Каково сопротивление участка цепи с проводниками сопротивлением 10 Ом и 40 Ом, соединенными параллельно:
а) 30 Ом
б) 50 Ом
в) 8 Ом +
4. Два прибора, включенных параллельно в цепь с напряжением 320 В, имеют сопротивления 400 Ом и 800 Ом. Найдите силу тока в каждом из них и в общей цепи:
а) I1 = 0,8 A, I2 = 0,4 A, I = 1,2 A +
б) I1 = 0,4 A, I2 = 0,2 A, I = 0,6 A
в) I1 = 0,4 A, I2 = 0,2 A, I = 0,2 A
5. Сила тока в неразветвлённой части цепи равна … в отдельных параллельно соединённых проводниках:
а) сумме сил сопротивления
б) сумме сил напряжения
в) сумме сил тока +
6. Электрический кабель, который используется в электрической цепи квартиры, имеет три провода. Третий провод является:
а) вводом
б) заземлением +
в) выводом
7. Сопротивление одной из трех одинаковых соединенных параллельно электроламп 300 Ом, а сила тока в ней 0,4 А. Определите напряжение на лампах и силу тока в неразветвленной части цепи:
а) 120 В и 2,4 А
б) 40 В и 2,4 А
в) 120 В и 1,2 А +
8. По какой формуле рассчитывается сопротивление участка цепи с параллельно соединенными проводниками:
По какой формуле рассчитывается сопротивление участка цепи с параллельно соединенными проводниками:
а) 1/R = 1/R1 + 1/R2 +
б) 1/R = 1/R1 ⋅ 1/R2
в) 1/R = 1/R1 − 1/R2
9. Каково соотношение сил токов в общей цепи и в параллельно соединенных проводниках:
а) все силы токов одинаковы (I = I1 = I2)
б) сумма сил токов в параллельно соединенных проводниках равна силе тока в неразветвленной части цепи +
в) в параллельно соединенных проводниках силы токов одинаковы и меньше силы тока в общей цепи
10. Сила тока в неразветвленной части цепи 0,6 А. На участке этой цепи, на концах которого напряжение 1,8 В, соединены между собой параллельно три одинаковых проводника. Какие значения сил токов зафиксируют амперметры в каждом из этих проводников? Каково сопротивление этого участка:
а) 0,6 А; 3 Ом
б) 0,2 А; 3 Ом +
в) 0,2 А; 27 Ом
11. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи:
а) одинаково для всех элементов +
б) различны для всех элементов
в) зависит от условий
12. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям:
Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям:
а) последовательно включённых проводников
б) параллельно включённых проводников +
в) зависит от условий
13. Каково соотношение напряжений на концах проводников, соединенных параллельно:
а) напряжения на всех проводниках одинаковы +
б) напряжение на проводнике тем больше, чем больше его сопротивление
в) напряжения на проводниках тем меньше, чем больше сопротивления
14. Каково соотношение сил токов в общей цепи и в параллельно соединенных проводниках:
а) в параллельно соединенных проводниках силы токов одинаковы и меньше силы тока в общей цепи
б) все силы токов одинаковы
в) сумма сил токов в параллельно соединенных проводниках равна силе тока в неразветвленной части цепи +
15. Каково соотношение напряжений на концах проводников, соединенных параллельно:
а) напряжения на всех проводниках одинаковы +
б) напряжение на проводнике тем больше, чем больше его сопротивление
в) напряжения на проводниках тем меньше, чем больше сопротивления
16. Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников:
Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников:
а) различно
б) одно и то же +
в) зависит от условий
17. При параллельном соединении резисторов складываются величины:
а) прямо пропорциональные сопротивлению
б) параллельные сопротивлению
в) обратно пропорциональные сопротивлению +
18. В цепь включены параллельно резисторы сопротивлением 5, 10, 15 и 20 Ом. Больше какого из этих значений сопротивление разветвленного участка цепи не может быть:
а) 15 Ом
б) 5 Ом +
в) 50 Ом
19. Параллельным является соединение проводников, при котором проводники соединяются:
а) разными концами
б) односоставными концами
в) одноименными концами +
20. Параллельное соединение применяют для:
а) обозначения токов
б) деления токов +
в) оба варианта не верны
21. Что можно сказать о потребителях, включаемых параллельно в одну и ту же электрическую сеть:
а) они должны быть рассчитаны на одно и то же напряжение, равное напряжению в сети +
б) они могут быть рассчитаны на разные напряжения
в) они должны быть рассчитаны на одно и то же произвольное напряжение
22. Какое напряжение используется в бытовых сетях России:
Какое напряжение используется в бытовых сетях России:
а) 150 В
б) 220 В +
в) 330 В
23. Несколько потребителей соединены параллельно. Что произойдет с остальными , если один из потребителей отключить:
а) некоторые отключатся, некоторые будут продолжать работать
б) тоже отключатся
в) остальные будут продолжать работать +
24. Две лампочки , рассчитанные на напряжение 220В, включены параллельно в сеть с напряжением 120В. Какое напряжение будет на каждой лампочке:
а) 340В
б) 120В +
в) 220В
25. Два резистора соединены параллельно. Если к ним параллельно подсоединить еще один резистор, то сила тока в неразветвленной части цепи:
а) уменьшится
б) не изменится
в) увеличится +
26. Две лампочки соединены параллельно, их сопротивления соответственно равны 2(Ом) и 3(Ом). Определить общее сопротивление лампочек:
а) 1(Ом)
б) 1,2(Ом) +
в) 5(Ом)
27. При параллельном соединении проводников общее сопротивление цепи:
а) уменьшается +
б) увеличивается
в) не изменяется
28. Если параллельно соединить десять одинаковых резисторов R0, то общее сопротивление будет:
Если параллельно соединить десять одинаковых резисторов R0, то общее сопротивление будет:
а) в два раза больше, 2*R0
б) в сто раз больше, 100*R0
в) в десять раз меньше, R0\10 +
29. Соединение проводников, при котором часть соединена последовательно, а другая параллельно:
а) смешанное +
б) двойное
в) нестандартное
30. На основании какого закона рассчитываются сопротивления электрических цепей:
а) Кулона
б) Ома +
в) Джоуля-Ленца
Тест по физике Соединения проводников для 8 класса
Тест по физике Соединения проводников для 8 класса с ответами. Тест включает в себя 2 варианта, в каждом варианте 6 заданий.
1 вариант
A1. При параллельном соединении проводников
1) сила тока постоянна, напряжение постоянно на всех участках цепи
2) сила тока складывается из значений силы тока на отдельных участках цепи, напряжение постоянно на всех участках цепи
3) сила тока постоянна на всех участках цепи, напряжение складывается из значений напряжения на отдельных участках цепи
4) сила тока и напряжение складываются из соответствующих значений на отдельных участках цепи
А2. Два резистора 30 Ом и 40 Ом соединены в электрическую цепь, как показано на рисунке.
Два резистора 30 Ом и 40 Ом соединены в электрическую цепь, как показано на рисунке.
Сопротивление этого участка цепи равно
1) 0,04 Ом
2) 17 Ом
3) 20 Ом
4) 70 Oм
А3. Параллельно соединены 3 лампы. Сопротивление каждой лампы 420 Ом. Общее сопротивление участка цепи, состоящего из трёх ламп, равно
1) 140 Ом
2) 280 Ом
3) 840 Ом
4) 1260 Ом
А4. Два резистора 60 Ом и 80 Ом соединены в электрическую цепь, как показано на рисунке.
Сила тока I1, текущего через первый резистор,
1) равна силе тока I2, текущего через второй резистор
2) меньше силы тока I2, текущего через второй резистор
3) больше силы тока I2, текущего через второй резистор
4) меньше или равна силе тока I2, текущего через второй резистор
А5. Два резистора 40 Ом и 20 Ом соединены в электрическую цепь, как показано на рисунке.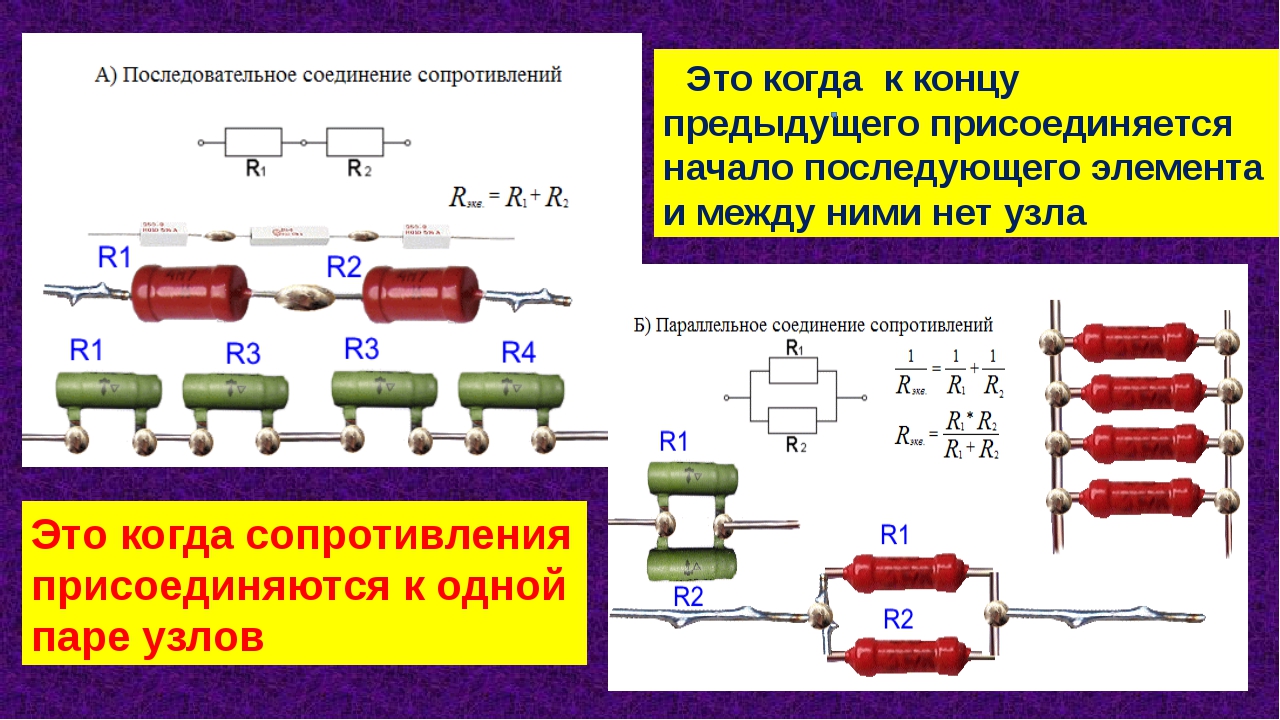
Напряжение U1 на первом резисторе,
1) равно напряжению U2 на втором резисторе
2) больше напряжения U2 на втором резисторе
3) меньше напряжения U2 на втором резисторе
4) меньше или равно напряжению U2 на втором резисторе
А6. На рисунке изображена электрическая цепь, состоящая из трёх ламп Л1, Л2, Л3 и источника тока.
Если перегорит лампа Л1, то
1) лампа Л2 продолжит гореть, лампа Л3 погаснет
2) лампа Л3 продолжит гореть, лампа Л2 погаснет
3) лампы Л2 и Л3 продолжат гореть
4) лампы Л2 и Л3 погаснут
2 вариант
A1. При последовательном соединении проводников
1) сила тока постоянна, напряжение постоянно на всех участках цепи
2) сила тока складывается из значений сил тока на отдельных участках цепи, напряжение постоянно на всех участках цепи
3) сила тока постоянна на всех участках цепи, напряжение складывается из значений напряжения на от дельных участках цепи
4) сила тока складывается из значений сил тока на отдельных участках цепи, напряжение постоянно на всех участках цепи
А2. Два резистора 30 Ом и 70 Ом соединены в электрическую цепь, как показано на рисунке.
Два резистора 30 Ом и 70 Ом соединены в электрическую цепь, как показано на рисунке.
Сопротивление этого участка цепи равно
1) 0,04 Ом
2) 21 Ом
3) 50 Ом
4) 100 Ом
А3. Последовательно соединены 3 лампы. Сопротивление каждой лампы 420 Ом. Общее сопротивление участка цепи, состоящего из трёх ламп, равно
1) 140 Ом
2) 280 Ом
3) 840 Ом
4) 1260 Ом
А4. Два резистора 20 Ом и 30 Ом соединены в электрическую цепь, как показано на рисунке.
Сила тока I1, текущего через первый резистор,
1) равна силе тока I2, текущего через второй резистор
2) меньше силы тока I2, текущего через второй резистор
3) больше силы тока I2, текущего через второй резистор
4) меньше или равна силе тока I2, текущего через второй резистор
А5. Два резистора 50 Ом и 30 Ом соединены в электрическую цепь, как показано на рисунке.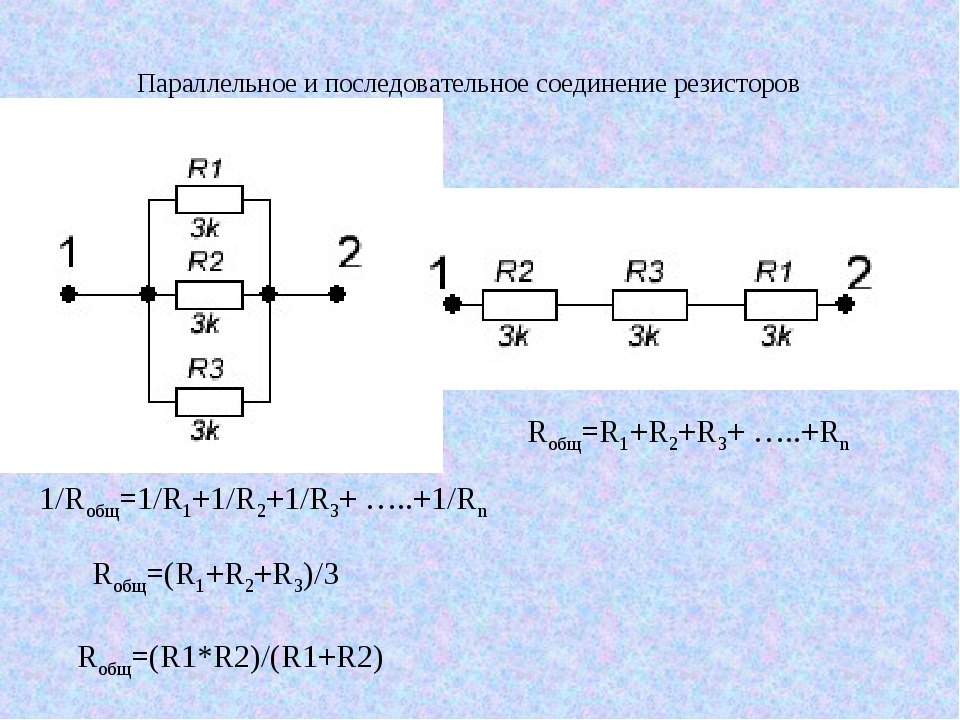
Напряжение U1 на первом резисторе,
1) больше напряжения U2 на втором резисторе
2) меньше напряжения U2 на втором резисторе
3) меньше или равно напряжению U2 на втором резисторе
4) равно напряжению U2 на втором резисторе
А6. На рисунке изображена электрическая цепь, состоящая из трёх ламп Л1, Л2, Л3 и источника тока.
Если перегорит лампа Л3, то
1) лампа Л2 продолжит гореть, лампа Л1 погаснет
2) лампа Л1 продолжит гореть, лампа Л2 погаснет
3) лампы Л1 и Л2 продолжат гореть
4) лампа Л1 и Л2 погаснут
Ответы на тест по физике Соединения проводников для 8 класса
1 вариант
А1-2
А2-4
А3-1
А4-3
А5-2
А6-4
2 вариант
А1-3
А2-2
А3-4
А4-1
А5-4
А6-3
Тест по физике. Последовательное соединение проводников.
 8 класс
8 классПросмотр содержимого документа
«Тест по физике. Последовательное соединение проводников. 8 класс»
Тест по физике. Последовательное соединение проводников. 8 класс
1. По какому признаку можно сразу определить, последовательно или нет соединены потребители электрического тока?
1) По одинаковости силы тока во всех проводниках
2) По тому, как соединены между собой все проводники
3) По прекращению работы всей цепи при выключении какого-либо одного потребителя тока
4) По зависимости напряжений на проводниках от их сопротивлений
2. Чему равно общее сопротивление R цепи с последовательно включенными электроприборами?
1) R = R1 + R2
2) R = R1 − R2
3) R = R2 − R1
4) R = R1 ⋅ R2
3.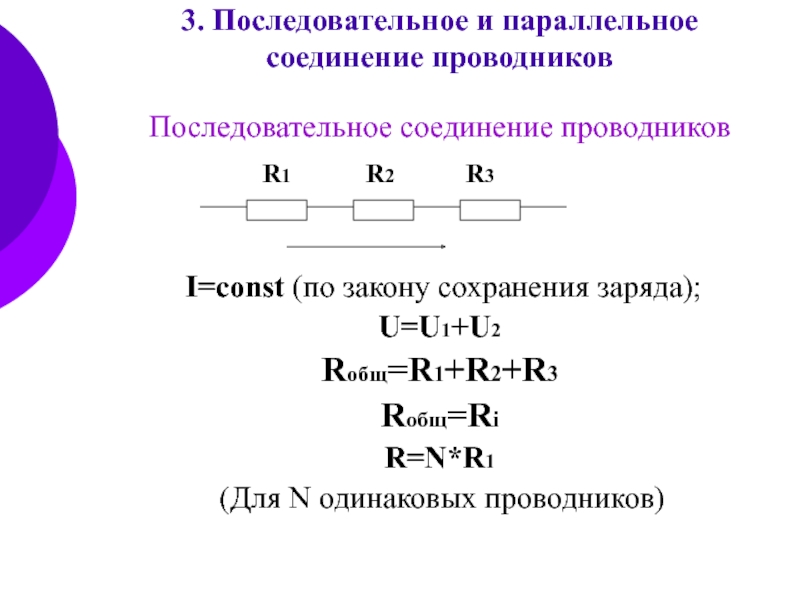 Чему равно общее напряжение на последовательно соединенных участках цепи?
Чему равно общее напряжение на последовательно соединенных участках цепи?
1) U = U1 = U2
2) U = U1 + U2
3) U = U1 − U2
4) U = U1 ⋅ U2
4. В электрическую цепь последовательно включены 4 электроприбора, имеющие равные сопротивления (по 10 Ом). Сила тока в одном из них 1,5 А. Каково общее напряжение в этой цепи?
1) 15 В
2) 60 В
3) 30 В
4) Решить нельзя, нет значений силы тока в других приборах
5. Напряжение на полюсах источника тока 12 В. Определите сопротивление проводника, если сила тока в цепи 0,8 А, а напряжение на лампе 4 В.
1) 15 Ом
2) 5 Ом
3) 10 Ом
4) 20 Ом
6. В цепи, состоящей из последовательно соединенных проводников сопротивлениями R1 = 15 Ом, R2 = 14 Ом, R3 = 11 Ом, сила тока равна 3 А. Каково общее напряжение в этой цепи и чему равно напряжение на первом проводнике?
1) U = 120 В; U1 = 45 В
2) U = 60 В; U1 = 5 В
3) U = 240 В; U1 = 150 В
4) U = 24 В; U1 = 15 В
7. Напряжения на участках последовательной электрической цепи U1 = 100 В, U2 = 30 В, U3 = 75 В, U4 = 150 В. Какой из участков обладает наибольшим сопротивлением?
Напряжения на участках последовательной электрической цепи U1 = 100 В, U2 = 30 В, U3 = 75 В, U4 = 150 В. Какой из участков обладает наибольшим сопротивлением?
1) Первый
2) Второй
3) Третий
4) Четвертый
8. Сила тока в цепи с последовательным соединением участков 0,2 А. Напряжения на участках таковы: U1 = 14 В, U2 = 16 В, U3 = 20 В. Определите общее сопротивление цепи (двумя способами).
1) 10 Ом
2) 100 Ом
3) 250 Ом
4) 300 Ом
9. Каково должно быть показание вольтметра, если в цепи, схема которой приведена на рисунке, лампа имеет сопротивление 25 Ом, резистор 35 Ом, а амперметр регистрирует силу тока 0,5А?
1) 12,5 Ом
2) 17,5 Ом
3) 20 В
4) 30 В
Ответы
1-3
2-1
3-2
4-2
5-3
6-1
7-4
8-3
9-4
Закон Ома для участка цепи.
 Последовательное и параллельное соединение проводников. 10 класс. Физика. — Объяснение нового материала.Комментарии преподавателяЗакон Ома для участка цепи
Последовательное и параллельное соединение проводников. 10 класс. Физика. — Объяснение нового материала.Комментарии преподавателяЗакон Ома для участка цепиСила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению участка.
Закон Ома оказался справедливым не только для металлов, но и для растворов электролитов. Сформулированный закон имеет место для так называемого однородного участка цепи – участка, не содержащего источников тока.
Математическая запись закона Ома проста, как и его формулировка, но экспериментально подтвердить эту зависимость очень трудно. Сила тока, протекающая по участку цепи, мала. Поэтому используют достаточно чувствительные приборы. Г. Ом изготовил чувствительный прибор для измерения силы тока, а в качестве источника тока использовал термопару. Действие амперметра и вольтметра основано на применение закона Ома для участка цепи. Угол поворота стрелки прибора пропорционален силе тока.
Угол поворота стрелки прибора пропорционален силе тока.
Из математической записи закона Ома:
можно выразить напряжение :
и сопротивление проводника:
.
Таким образом, закон Ома связывает три параметра, характеризующих постоянный электрический ток, проходящий по проводнику, и позволяет находить любой из них, если известны два других.
Закон Ома имеет границы применимости и выполняется только в том случае, когда при прохождении тока температура заметно не меняется. На вольт–амперной характеристике лампы накаливания видно, что график сильно искривляется при напряжении выше 10В, значит, закон Ома выше этого напряжения применять нельзя.
Также нельзя говорить, что сопротивление проводника зависит от напряжения и силы тока в цепи. Сопротивление участка цепи зависит от свойств проводника: длины, площади поперечного сечения и материала, из которого состоит проводник.
где l-длина проводника, s-его площадь поперечного сечения.
ρ –удельное сопротивление проводника – это физическая величина, характеризующая зависимость сопротивления проводника от материала, из которого он изготовлен.
Удельное сопротивление показывает, каким сопротивлением обладает сделанный из этого вещества проводник длиной 1м и площадью поперечного сечения 1м2 .
Из формулы видно, что единицей измерения в системе СИ является Ом·м. Но так как площадь поперечного сечения проводника достаточно мала, используют единицы измерения
при вычислении площадь поперечного сечения проводника следует выражать в мм2.
В заключении хочется заметить, что Ом начал свои опыты, когда был учителем физики в гимназии. В своих экспериментах Ом брал куски проволоки одинакового диаметра, но разного материала и изменял их длину таким образом, чтобы в цепи сила тока имела одинаковое значение. Находящаяся рядом магнитная стрелка отклонялась при прохождении тока в цепи. Установив связь между напряжением и силой тока, Г.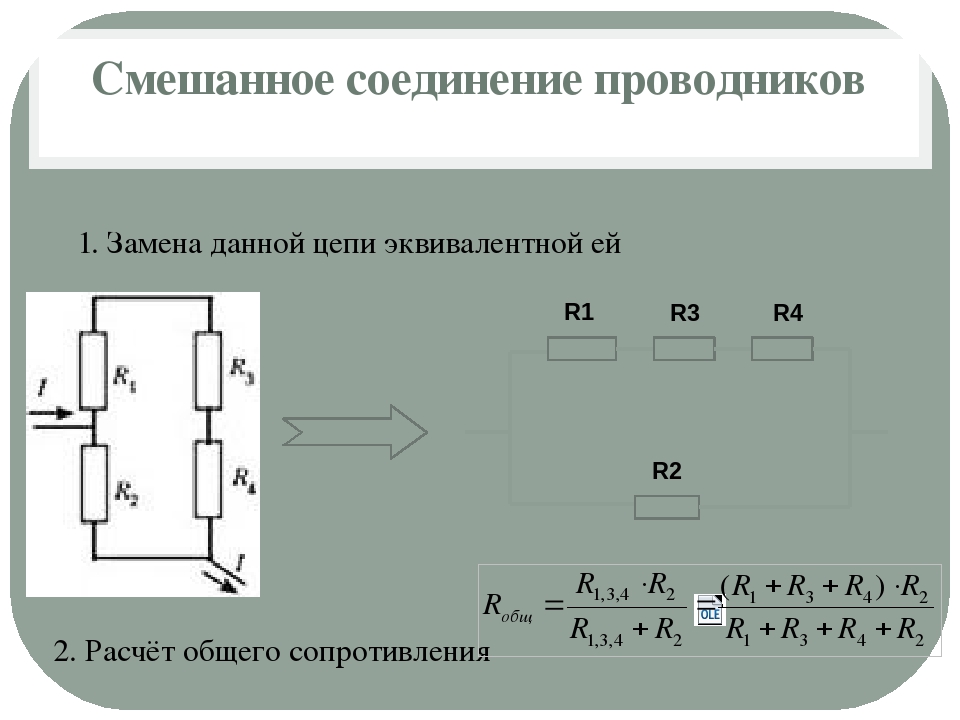 Ом вывел один из основных законов постоянного тока.
Ом вывел один из основных законов постоянного тока.
Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.
На рисунке а изображена цепь последовательного соединения двух электрических ламп, а на рисунке б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.
Рис. Последовательное включение лампочек и источников питания
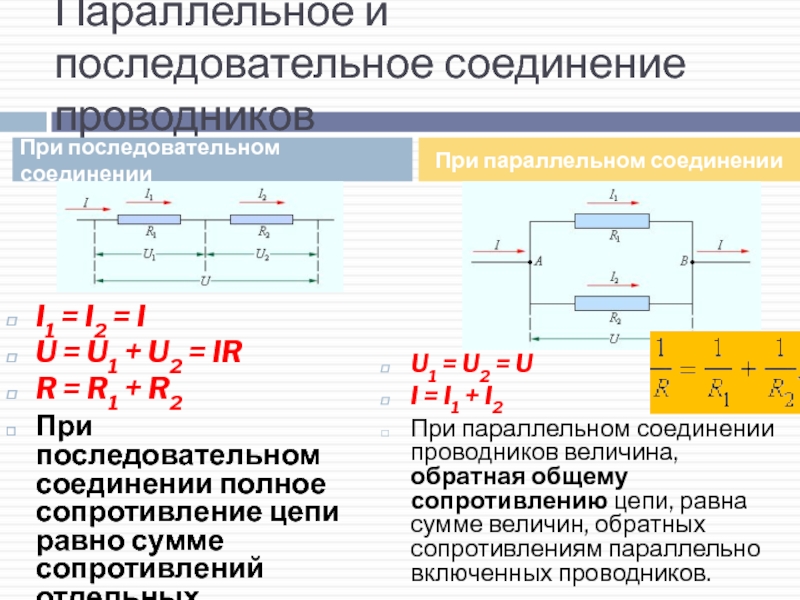
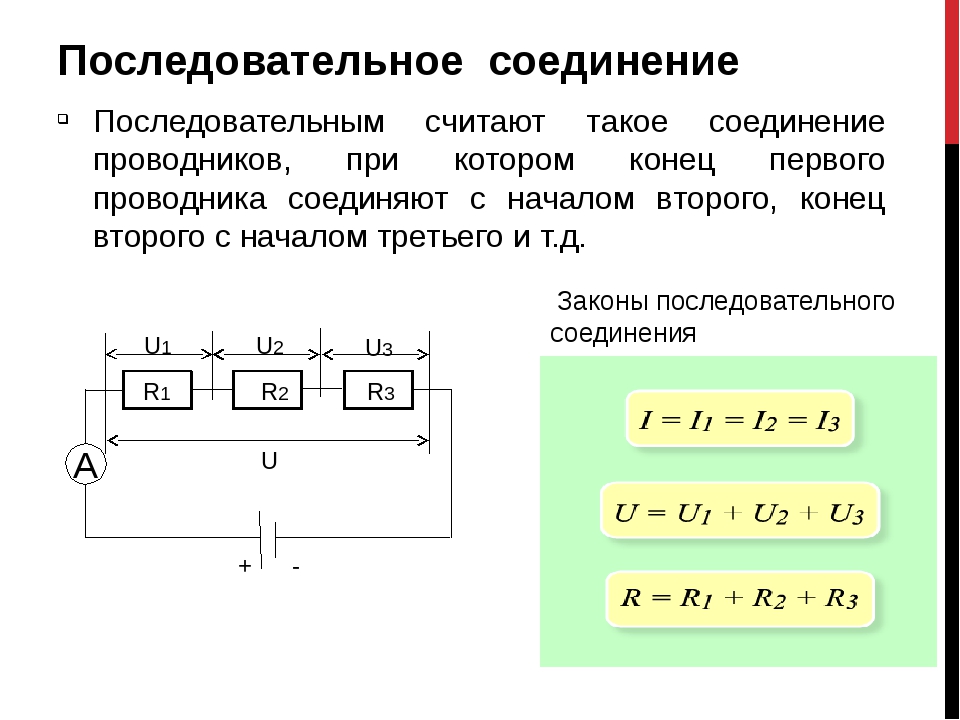
Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.
I = I1 = I2
А чему равно сопротивление последовательно соединённых проводников?
Соединяя проводники последовательно, мы как бы увеличиваем длину проводника.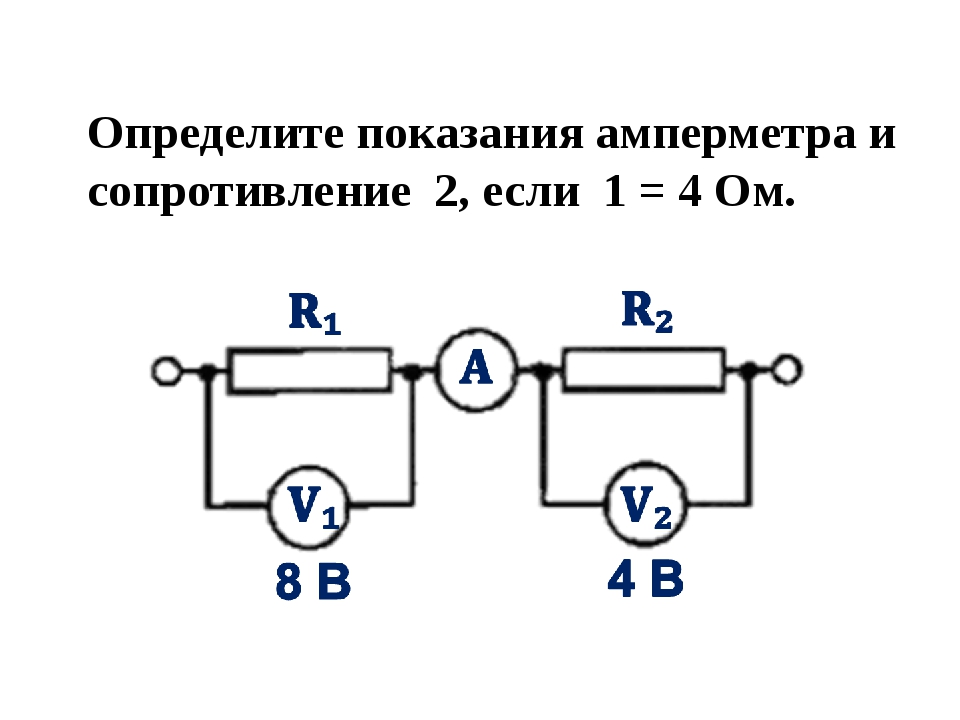 Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Последовательное соединение проводников
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
R = R1 + R2
Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:
U1 = IR1, U2 = IR2.
Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
U = U1 + U2.
Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.
Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.
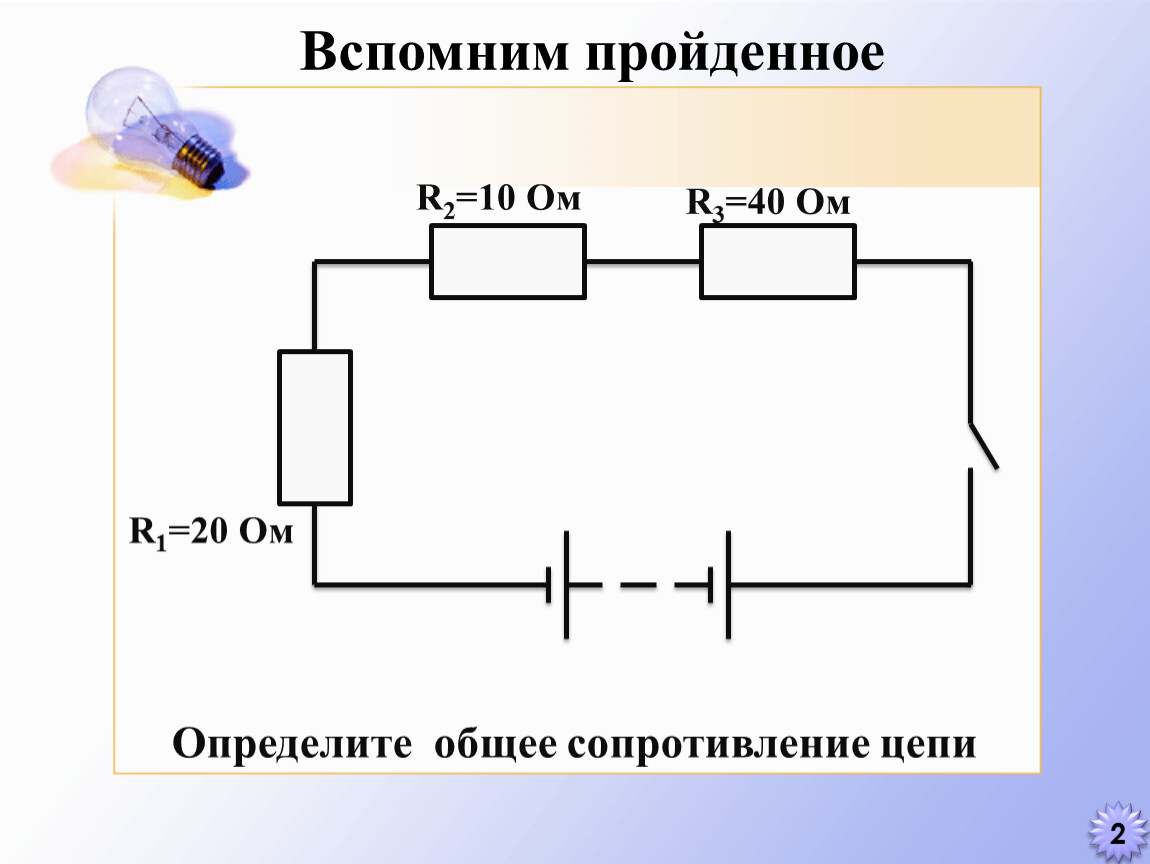
Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Запишем условие задачи и решим её.
Расчет параметров электрической цепи
при параллельном соединении сопротивлений:
1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках
2. напряжение на всех параллельно соединенных участках цепи одинаково
3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :
( R — сопротивление проводника,
1/R — электрическая проводимость проводника)
Если в цепь включены параллельно только два сопротивления, то:
( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )
4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
работа электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме работ на отдельных участках:
A=A1+A2
5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:
P=P1+P2
Для двух сопротивлений:
т.е. чем больше сопротивление, тем меньше в нём сила тока.
Домашняя работа.Задание 1. Ответить на вопросы.
- Какое соединение проводников называют последовательным? Изобразите его на схеме.
- Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
- Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
- Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
- Какое соединение проводников называют параллельным? Изобразите его на схеме.

- Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
- Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
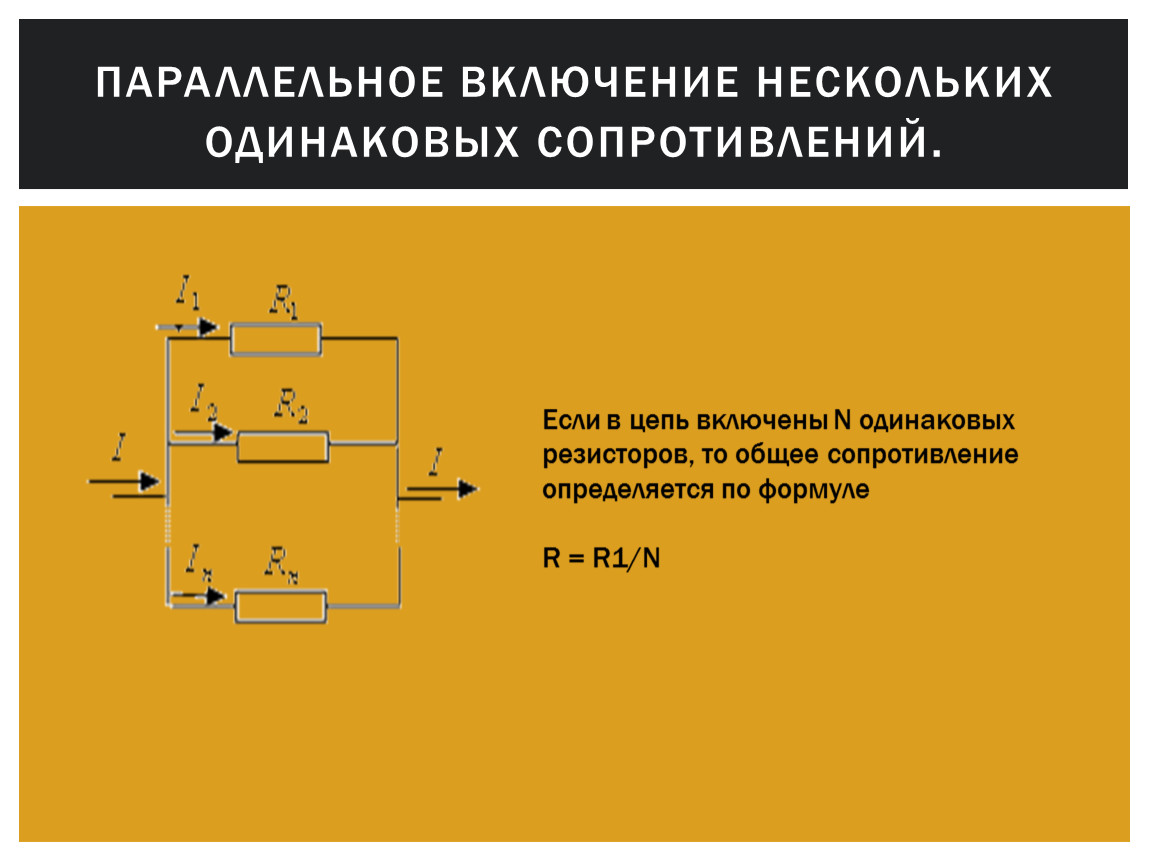
- Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
- Какое соединение проводников применяется в жилых помещениях? Какие напряжения используются для бытовых нужд?
Задание 2.Решите задачи.
1. Две лампочки соединены последовательно. Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на второй 4Ом.
2. Две лампочки соединены параллельно. Напряжение на второй лампочке10В. Найдите силу тока в цепи и на каждой из ламп, если сопротивление на первой лампе 1Ом, а на второй 2Ом.
К занятию прикреплен файл «Это интересно». Вы можете скачать файл в любое удобное для вас время.
Использованные источники:
- http://www.tepka.ru/
- http://class-fizika.narod.ru
- http://www.youtube.com/watch?v=cVKE9NItreo
- http://znaika.ru/catalog/10-klass/physics/
- http://www.youtube.com/watch?v=NB7hOVYe7h0
- https://www.youtube.com/watch?v=cVKE9NItreo
- https://www.youtube.com/watch?v=0hFWeR8ybxs
- http://www.youtube.com/watch?v=EDI8DzWSSWY
- http://www.youtube.com/watch?v=bH_-qGnjJqc
Серия
и параллельная — AP Physics 1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
10.3: Последовательные и параллельные резисторы
Цели обучения
К концу раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)).В последовательной схеме выходной ток первого резистора течет на вход второго резистора; следовательно, ток в каждом резисторе одинаков. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Рисунок \ (\ PageIndex {1} \): (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое.Резисторы серии
Считается, что резисторывключены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \).Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.На рисунке \ (\ PageIndex {2} \) ток, исходящий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор. Согласно закону Ома, падение потенциала \ (V \) на резисторе при протекании через него тока рассчитывается по формуле \ (V = IR \), где \ (I \) — ток в амперах (\ (A \)), а \ (R \) — сопротивление в Ом \ ((\ Omega) \).N V_i = 0. \]
Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе. Для рисунка \ (\ PageIndex {2} \) сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
\ [\ begin {align *} V — V_1 — V_2 — V_3 & = 0, \\ [4pt] V & = V_1 + V_2 + V_3, \\ [4pt] & = IR_1 + IR_2 + IR_3, \ end { выровнять *} \]
Решение для \ (I \)
\ [\ begin {align *} I & = \ frac {V} {R_1 + R_2 + R_3} \\ [4pt] & = \ frac {V} {R_ {S}}. N R_i.\ label {серия эквивалентных сопротивлений} \]
Одним из результатов включения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
- Рассчитайте эквивалентное сопротивление цепи.
- Рассчитайте ток через каждый резистор.
- Рассчитайте падение потенциала на каждом резисторе.
- Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Решение
- Эквивалентное сопротивление — это алгебраическая сумма сопротивлений (уравнение \ ref {серия эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 10 \, \ Омега = 90 \, \ Омега.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W. \ nonumber \]
Значение
Есть несколько причин, по которым мы использовали бы несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серии по девять луковиц.Если перегорает слишком много лампочек, в конечном итоге открываются шунты. Что вызывает это?
- Ответ
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление составит 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \). Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к сгоранию шунта.№ Р_и. \]
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке \ (\ PageIndex {4} \) показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Рисунок \ (\ PageIndex {4} \): Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.Ток, протекающий от источника напряжения на рисунке \ (\ PageIndex {4} \), зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы \ (R_1 \) и \ (R_2 \). По мере прохождения зарядов от батареи часть заряда проходит через резистор \ (R_1 \), а часть — через резистор \ (R_2 \).Сумма токов, протекающих в переходе, должна быть равна сумме токов, текущих из перехода:
\ [\ sum I_ {in} = \ sum I_ {out}. {- 1}.{-1}. \ label {10.3} \]
Это соотношение приводит к эквивалентному сопротивлению \ (R_ {P} \), которое меньше наименьшего из отдельных сопротивлений. Когда резисторы подключены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример \ (\ PageIndex {2} \): Анализ параллельной цепи
Три резистора \ (R_1 = 1,00 \, \ Omega \), \ (R_2 = 2,00 \, \ Omega \) и \ (R_3 = 2,00 \, \ Omega \) подключены параллельно.Параллельное соединение подключается к источнику напряжения \ (V = 3,00 \, V \).
- Какое эквивалентное сопротивление?
- Найдите ток, подаваемый источником в параллельную цепь.
- Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.
- Рассчитайте мощность, рассеиваемую каждым резистором.
- Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью уравнения \ ref {10.3}. (Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив \ (R_ {P} \) на полное сопротивление \ (I = \ frac {V} {R_ {P}} \).
(c) Отдельные токи легко вычислить по закону Ома \ (\ left (I_i = \ frac {V_i} {R_i} \ right) \), поскольку каждый резистор получает полное напряжение.{-1} = 0.50 \, \ Omega. \ Nonumber \] Общее сопротивление с правильным количеством значащих цифр равно \ (R_ {eq} = 0.50 \, \ Omega \). Как и предполагалось, \ (R_ {P} \) меньше наименьшего индивидуального сопротивления.
- Полный ток можно найти из закона Ома, заменив полное сопротивление \ (R_ {P} \). Это дает \ [I = \ frac {V} {R_ {P}} = \ frac {3.00 \, V} {0.50 \, \ Omega} = 6.00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
- Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом, \ [I_1 = \ frac {V} {R_1} = \ frac {3.00 \, V} {1.00 \, \ Omega} = 3.00 \, A. \ nonumber \] Аналогично, \ [I_2 = \ frac {V } {R_2} = \ frac {3.00 \, V} {2.00 \, \ Omega} = 1.50 \, A \ nonumber \] и \ [I_3 = \ frac {V} {R_3} = \ frac {3.00 \, V } {2.00 \, \ Omega} = 1.50 \, A. \ nonumber \] Полный ток — это сумма отдельных токов: \ [I_1 + I_2 + I_3 = 6.2} {2.00 \, \ Omega} = 4.50 \, W. \ nonumber \]
- Общую мощность также можно рассчитать несколькими способами. Выбор \ (P = IV \) и ввод общей текущей доходности \ [P = IV = (6.00 \, A) (3.00 \, V) = 18.00 \, W. \ nonumber \]
Значение
Общая мощность, рассеиваемая резисторами, также 18,00 Вт:
\ [P_1 + P_2 + P_3 = 9,00 \, W + 4,50 \, W + 4,50 \, W = 18,00 \, W. \ nonumber \]
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
Упражнение \ (\ PageIndex {2A} \)
Рассмотрим одну и ту же разность потенциалов \ ((V = 3,00 \, V) \), приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
- Раствор
Эквивалент последовательной схемы будет \ (R_ {eq} = 1.00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Упражнение \ (\ PageIndex {2B} \)
Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?
- Раствор
Река, текущая в горизонтальном направлении с постоянной скоростью, разделяется на две части и течет через два водопада. Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение — это потенциальная энергия на каждом резисторе.
При рассмотрении энергии аналогия быстро разрушается. В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
Суммируем основные характеристики резисторов параллельно:
- Эквивалентное сопротивление находится по формуле \ ref {10.3} и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Как вы помните, из раздела о емкости мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. Таблица \ (\ PageIndex {1} \) суммирует уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
Таблица \ (\ PageIndex {1} \): сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях Комбинация серий Параллельная комбинация Эквивалентная емкость \ [\ frac {1} {C_ {S}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +.N R_i \ nonumber \] \ [\ frac {1} {R_ {P}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +. . . \ nonumber \] Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учесть сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения можно уменьшить до одного эквивалентного сопротивления, используя метод, показанный на рисунке \ (\ PageIndex {5} \).Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Рисунок \ (\ PageIndex {5} \): (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, и эквивалентное сопротивление равно \ (R_ {34} = 10 \, \ Omega \). (c) Шаг 2: сокращенная схема показывает, что резисторы \ (R_2 \) и \ (R_ {34} \) включены параллельно, с эквивалентным сопротивлением \ (R_ {234} = 5 \, \ Omega \).(d) Шаг 3: сокращенная схема показывает, что \ (R_1 \) и \ (R_ {234} \) включены последовательно с эквивалентным сопротивлением \ (R_ {1234} = 12 \, \ Omega \), которое является эквивалентное сопротивление \ (R_ {eq} \). (e) Уменьшенная схема с источником напряжения \ (V = 24 \, V \) с эквивалентным сопротивлением \ (R_ {eq} = 12 \, \ Omega \). Это приводит к току \ (I = 2 \, A \) от источника напряжения.Обратите внимание, что резисторы \ (R_3 \) и \ (R_4 \) включены последовательно. Их можно объединить в одно эквивалентное сопротивление.Один из методов отслеживания процесса — включить резисторы в качестве индексов. {- 1} = 5 \, \ Omega.\ nonumber \]
Этот шаг процесса сокращает схему до двух резисторов, показанных на рисунке \ (\ PageIndex {5d} \). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
\ [R_ {eq} = R_ {1234} = R_1 + R_ {234} = 7 \, \ Omega + 5 \ Omega = 12 \, \ Omega. \ nonumber \]
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен \ (I = \ frac {V} {R_ {eq}} = \ frac {24 \, V} {12 \, \ Omega} = 2 \, A \). Этот ток проходит через резистор \ (R_1 \) и обозначается как \ (I_1 \). Падение потенциала на \ (R_1 \) можно найти с помощью закона Ома:
\ [V_1 = I_1R_1 = (2 \, A) (7 \, \ Omega) = 14 \, V. \ nonumber \]
Глядя на рисунок \ (\ PageIndex {5c} \), это оставляет \ (24 \, V — 14 \, V = 10 \, V \) отбрасывать через параллельную комбинацию \ (R_2 \) и \ ( R_ {34} \).Ток через \ (R_2 \) можно найти по закону Ома:
\ [I_2 = \ frac {V_2} {R_2} = \ frac {10 \, V} {10 \, \ Omega} = 1 \, A. \ nonumber \]
Резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, поэтому токи \ (I_3 \) и \ (I_4 \) равны
.\ [I_3 = I_4 = I — I_2 = 2 \, A — 1 \, A = 1 \, A. \ nonumber \]
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные капли равны \ (V_3 = I_3R_3 = 6 \, V \) и \ (V_4 = I_4R_4 = 4 \, V \).2 (4 \, \ Omega) = 4 \, W, \\ [4pt] P_ {рассеивается} & = P_1 + P_2 + P_3 + P_4 = 48 \, W. \ end {align *} \]
Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет
\ [\ begin {align *} P_s & = IV \\ [4pt] & = (2 \, A) (24 \, V) = 48 \, W \ end {align *} \]
Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
Пример \ (\ PageIndex {3} \): объединение последовательных и параллельных цепей
На рисунке \ (\ PageIndex {6} \) показаны резисторы, подключенные последовательно и параллельно.Мы можем считать \ (R_1 \) сопротивлением проводов, ведущих к \ (R_2 \) и \ (R_3 \).
- Найдите эквивалентное сопротивление цепи.
- Какое падение потенциала \ (V_1 \) на резисторе \ (R_1 \)?
- Найдите ток \ (I_2 \) через резистор \ (R_2 \).
- Какая мощность рассеивается \ (R_2 \)?
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения \ (R_2 \) и \ (R_3 \). Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с \ (R_1 \).
(b) Ток через \ (R_1 \) можно найти с помощью закона Ома и приложенного напряжения. Ток через \ (R_1 \) равен току от батареи. Падение потенциала \ (V_1 \) на резисторе \ (R_1 \) (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.{-1} = 5.10 \, \ Omega. \ Nonumber \] Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чисто параллельной (\ (20.0 \, \ Omega \) и \ (0.804 \, \ Omega \) ), соответственно).
- Ток через \ (R_1 \) равен току, обеспечиваемому батареей: \ [I_1 = I = \ frac {V} {R_ {eq}} = \ frac {12.0 \, V} {5.10 \, \ Omega} = 2.35 \, A. \ nonumber \] Напряжение на \ (R_1 \) равно \ [V_1 = I_1R_1 = (2.35 \, A) (1 \, \ Omega) = 2.35 \, V. \ nonumber \] Напряжение, приложенное к \ (R_2 \) и \ (R_3 \), меньше напряжения, подаваемого батареей, на величину \ (V_1 \).Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных \ (R_2 \) и \ (R_3 \).
- Чтобы найти ток через \ (R_2 \), мы должны сначала найти приложенное к нему напряжение. Напряжение на двух параллельных резисторах одинаковое: \ [V_2 = V_3 = V — V_1 = 12.0 \, V — 2.35 \, V = 9.65 \, V. \ nonumber \] Теперь мы можем найти ток \ (I_2 \) через сопротивление \ (R_2 \) по закону Ома: \ [I_2 = \ frac {V_2} {R_2} = \ frac {9.65 \, V} {6.00 \, \ Omega} = 1.2 (6.00 \, \ Omega) = 15.5 \, W. \ nonumber \]
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.
Упражнение \ (\ PageIndex {3} \)
Рассмотрите электрические цепи в вашем доме.Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
- Раствор
Все цепи верхнего освещения параллельны и подключены к основному питанию, поэтому при перегорании одной лампочки все верхнее освещение не гаснет. У каждого верхнего света будет по крайней мере один переключатель, включенный последовательно с источником света, поэтому вы можете включать и выключать его.
В холодильнике есть компрессор и лампа, которая загорается при открытии дверцы.Обычно у холодильника есть только один шнур для подключения к стене. Цепь, содержащая компрессор, и цепь, содержащая цепь освещения, параллельны, но есть переключатель, включенный последовательно со светом. Термостат управляет переключателем, который включен последовательно с компрессором, чтобы контролировать температуру холодильника.
Практическое значение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке \ (\ PageIndex {7} \). Устройство, обозначенное символом \ (R_3 \), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, обозначенных \ (R_1 \), уменьшая напряжение на лампочке (которое равно \ (R_2 \)), которое затем заметно гаснет.
Рисунок \ (\ PageIndex {7} \): Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей.
- Проверьте, являются ли ответы разумными и последовательными.
Пример \ (\ PageIndex {4} \): объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно \ ((R_1, \, R_2) \), соединены с двумя резисторами, включенными параллельно \ ((R_3, \, R_4) \).Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Через резистор \ (R_1 \) проходит ток 2,00 А. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
Рисунок \ (\ PageIndex {8} \): Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.- Нарисуйте четкую принципиальную схему (Рисунок \ (\ PageIndex {8} \)).
- Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы \ (R_1 \) и \ (R_2 \) включены последовательно, а резисторы \ (R_3 \) и \ (R_4 \) включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов \ (R_3 \) и \ (R_4 \) последовательно с последовательной конфигурацией резисторов \ (R_1 \) и \ (R_2 \).{-1} = 5,00 \, \ Омега. \ nonumber \] Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление схемы равно \ (R_ {eq} = R_1 + R_2 + R_ {34} = (25.00 \, \ Omega \). поэтому напряжение, подаваемое батареей, равно \ (V = IR_ {eq} = 2.00 \, A (25.00 \, \ Omega) = 50.00 \, V \).
- Один из способов проверить соответствие ваших результатов — это рассчитать мощность, потребляемую батареей, и мощность, рассеиваемую резисторами. Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
Поскольку мощность, рассеиваемая резисторами, равна мощности, обеспечиваемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При нахождении \ (R_ {eq} \) для параллельного соединения необходимо с осторожностью относиться к обратному. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Авторы и ссылки
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
и параллельные схемы — learn.sparkfun.com
Добавлено в избранное Любимый 53 Серияи параллельные схемы
Простые схемы (состоящие всего из нескольких компонентов) обычно довольно просты для понимания новичками.Но, когда на вечеринку приходят другие компоненты, все может запутаться. Куда идет ток? Что делает напряжение? Можно ли это упростить для облегчения понимания? Не бойся, бесстрашный читатель. Ценная информация приводится ниже.
В этом руководстве мы сначала обсудим разницу между последовательными и параллельными схемами, используя схемы, содержащие самые основные компоненты — резисторы и батареи, — чтобы показать разницу между двумя конфигурациями. Затем мы рассмотрим, что происходит в последовательных и параллельных цепях, когда вы комбинируете компоненты разных типов, например конденсаторы и катушки индуктивности.
рассматривается в этом учебном пособии
- Как выглядят конфигурации последовательной и параллельной цепей
- Как пассивные компоненты действуют в этих конфигурациях
- Как источник напряжения будет воздействовать на пассивные компоненты в этих конфигурациях
Рекомендуемая литература
Вы можете посетить эти учебные пособия по основным компонентам, прежде чем углубляться в построение схем в этом учебном пособии.
Видео
Цепи серииУзлы и текущий поток
Прежде чем мы углубимся в это, мы должны упомянуть, что такое узел .Ничего особенного, просто представление электрического соединения между двумя или более компонентами. Когда схема моделируется на схеме, эти узлы представляют собой провода между компонентами.
Пример схемы с четырьмя узлами уникального цвета.
Это полдела на пути к пониманию разницы между последовательным и параллельным. Нам также необходимо понять , как ток проходит через по цепи. Ток течет от высокого напряжения к более низкому напряжению в цепи.Некоторое количество тока будет проходить по каждому пути, который может пройти, чтобы добраться до точки с наименьшим напряжением (обычно называемой землей). Используя приведенную выше схему в качестве примера, вот как будет течь ток, когда он проходит от положительной клеммы аккумулятора к отрицательной:
Ток (обозначенный синей, оранжевой и розовой линиями), протекающий по той же примерной схеме, что и выше. Разные токи обозначены разными цветами.
Обратите внимание, что в некоторых узлах (например, между R 1 и R 2 ) ток на входе такой же, как на выходе.В других узлах (в частности, трехходовой переход между R 2 , R 3 и R 4 ) основной (синий) ток разделяется на два разных. Это ключевое различие между последовательным и параллельным подключением!
Определение цепей серииДва компонента соединены последовательно, если они имеют общий узел и если через них протекает один и тот же ток . Вот пример схемы с тремя последовательными резисторами:
В указанной выше цепи есть только один способ протекания тока.Начиная с положительной клеммы аккумулятора, ток сначала встречает R 1 . Оттуда ток будет течь прямо к R 2 , затем к R 3 и, наконец, обратно к отрицательной клемме батареи. Обратите внимание, что у текущего есть только один путь. Эти компоненты включены последовательно.
Параллельные схемы
Определение параллельных цепей
Если компоненты совместно используют два общих узла , они работают параллельно.Вот пример схемы трех резисторов, подключенных параллельно к батарее:
От положительной клеммы аккумуляторной батареи ток течет к R 1 … и R 2 , и R 3 . Узел, который подключает аккумулятор к R 1 , также подключен к другим резисторам. Другие концы этих резисторов аналогично связываются вместе, а затем снова подключаются к отрицательной клемме батареи. Существует три различных пути, по которым ток может пройти, прежде чем вернуться в батарею, и соответствующие резисторы считаются параллельными.
Если все последовательные компоненты имеют одинаковые токи, протекающие через них, все параллельные компоненты имеют одинаковое падение напряжения на них — series: current :: parallel: Voltage.
Совместная работа сериии параллельных цепей
Оттуда мы можем смешивать и сочетать. На следующем снимке мы снова видим три резистора и батарею. С положительной клеммы аккумуляторной батареи ток сначала достигает R 1 . Но на другой стороне R 1 узел разделяется, и ток может идти как на R 2 , так и на R 3 .Пути тока через R 2 и R 3 затем снова связываются вместе, и ток возвращается к отрицательному выводу батареи.
В этом примере R 2 и R 3 параллельны друг другу, а R 1 последовательно с параллельной комбинацией R 2 и R 3 .
Расчет эквивалентных сопротивлений в последовательных цепях
Вот некоторая информация, которая может оказаться для вас более полезной.Когда мы соединяем резисторы таким образом, последовательно и параллельно, мы меняем способ протекания тока через них. Например, если у нас есть питание 10 В через 10 кОм; резистора, закон Ома гласит, что у нас протекает ток 1 мА.
Если потом поставить еще 10к & ом; резистор, включенный последовательно с первым и оставив питание без изменений, мы сократили ток вдвое, потому что сопротивление увеличилось вдвое.
Другими словами, по-прежнему существует только один путь для прохождения тока, и мы только усложнили прохождение тока.Насколько сложнее? 10к & Ом; + 10к & Ом; = 20 кОм ;. Вот как мы рассчитываем последовательно включенные резисторы — просто складываем их значения .
Если выразить это уравнение в более общем виде: полное сопротивление Н. — произвольное количество резисторов — это их общая сумма.
Расчет эквивалентных сопротивлений в параллельных цепях
А как насчет параллельных резисторов? Это немного сложнее, но ненамного.Рассмотрим последний пример, в котором мы начали с источника питания 10 В и 10 кОм; резистор, но на этот раз мы добавляем еще 10кОм; параллельно, а не последовательно. Теперь у тока есть два пути. Поскольку напряжение питания не изменилось, закон Ома гласит, что первый резистор по-прежнему будет потреблять 1 мА. Но то же самое и со вторым резистором, и теперь у нас есть в общей сложности 2 мА, поступающие от источника питания, что вдвое превышает первоначальный 1 мА. Это означает, что мы уменьшили общее сопротивление вдвое.
Пока можно сказать, что 10к & ом; || 10к & Ом; = 5 кОм; («||» примерно переводится как «параллельно»), у нас не всегда будет 2 одинаковых резистора.Что тогда?
Уравнение для добавления произвольного количества резисторов параллельно:
Если обратные значения вам не подходят, мы также можем использовать метод, называемый «произведение на сумму», когда у нас есть два параллельных резистора:
Однако этот метод подходит только для двух резисторов в одном вычислении. Мы можем объединить более 2 резисторов этим методом, взяв результат R1 || R2 и вычисление этого значения параллельно с третьим резистором (снова как произведение на сумму), но обратный метод может быть меньше работы.
Время эксперимента — Часть 1
Что вам понадобится:
Давайте проведем простой эксперимент, чтобы доказать, что все работает именно так, как мы говорим.
Во-первых, мы собираемся подключить 10 кОм; последовательно подключите резисторы и наблюдайте, как они складываются самым необычным образом. Используя макетную плату, поместите один 10 кОм; резистор, как показано на рисунке, и измерьте его мультиметром. Да, мы уже знаем, что будет указано, что оно составляет 10 кОм, но это то, что мы в бизнесе называем «проверкой работоспособности».Убедившись, что мир существенно не изменился с тех пор, как мы в последний раз смотрели на него, поместите еще один аналогично, но с выводами каждого резистора, электрически подключенными через макетную плату, и снова произведите измерения. Теперь измеритель должен показывать что-то близкое к 20 кОм.
Вы можете заметить, что сопротивление, которое вы измеряете, может быть не совсем таким, как резистор должен быть. Резисторы имеют определенный допуск , что означает, что они могут быть отключены на определенный процент в любом направлении.Таким образом, вы можете прочитать 9.99k & ohm; или 10.01кОм. Пока оно близко к правильному значению, все должно работать нормально.
Читателю следует продолжать это упражнение до тех пор, пока он не убедится, что знает результат, прежде чем делать это снова, или у него закончатся резисторы, которые можно вставить в макет, в зависимости от того, что произойдет раньше.
Время эксперимента — Часть 2
Теперь давайте попробуем это с резисторами в конфигурации параллельно .Поместите один 10 кОм; резистор в макетной плате, как и раньше (мы полагаем, что читатель уже считает, что один резистор 10 кОм будет измерять на мультиметре что-то близкое к 10 кОм). Теперь поместите второй 10k & ohm; резистор рядом с первым, следя за тем, чтобы выводы каждого резистора находились в электрически соединенных рядах. Но перед тем, как измерить комбинацию, вычислите, используя метод «произведение над суммой» или «обратный», каким должно быть новое значение (подсказка: оно будет 5 кОм;).Затем измерьте. Это что-то близкое к 5к & ом ;? Если это не так, дважды проверьте отверстия, в которые вставлены резисторы.
Повторите упражнение с резисторами 3, 4 и 5. Расчетные / измеренные значения должны быть 3,33 кОм, 2,5 кОм; и 2кОм соответственно. Все ли получилось по плану? Если нет, вернитесь и проверьте свои соединения. Если это так, EXCELSIOR! Прежде чем продолжить, выпейте молочный коктейль. Ты заслужил это.
Практические правила для последовательных и параллельных резисторов
Есть несколько ситуаций, которые могут потребовать творческих комбинаций резисторов.Например, если мы пытаемся установить очень конкретное опорное напряжение, вам почти всегда потребуется очень конкретное соотношение резисторов, значения которых вряд ли будут «стандартными» значениями. И хотя мы можем получить очень высокую степень точности значений резисторов, мы, возможно, не захотим ждать X дней, необходимых для доставки чего-либо, или платить цену за нестандартные значения, отсутствующие на складе. Так что в крайнем случае мы всегда можем создать собственные номиналы резисторов.
Совет №1: Равнопараллельные резисторы
Добавление Н, резисторов с одинаковым номиналом R, , включенных параллельно, дает нам R / N Ом.Допустим, нам нужен 2,5 кОм; резистор, но все, что у нас есть, это ящик, полный 10 кОм. Объединение четырех из них параллельно дает нам 10 кОм / 4 = 2,5 кОм.
Совет № 2: Допуск
Знайте, какую терпимость вы можете терпеть. Например, если вам нужен 3.2k & ohm; резистор, можно было поставить 3 10кОм; резисторы параллельно. Это даст вам 3,3 кОм, что составляет около 4% отклонения от необходимого значения. Но если схема, которую вы строите, должна иметь допуск ближе, чем 4%, мы можем измерить наш запас в 10 кОм, чтобы увидеть, какие значения являются самыми низкими, потому что они также имеют допуск.По идее, если заначка 10к & ом; резисторы имеют допуск 1%, мы можем получить только 3,3 кОм. Но производители запчастей, как известно, допускают именно такого рода ошибки, поэтому стоит немного покопаться.
Совет № 3: Номинальная мощность при последовательном / параллельном подключении
Такая комбинация резисторов последовательно и параллельно работает и при номинальной мощности. Допустим, нам нужен 100 & Ом; резистор рассчитан на 2 Вт (Вт), но все, что у нас есть, это связка 1 кОм; резисторы на четверть ватта (Вт) (а сейчас 3 часа ночи, вся Mountain Dew исчезла, а кофе остыл).Вы можете объединить 10 из 1 кОм, чтобы получить 100 Ом; (1 кОм / 10 = 100 Ом), а номинальная мощность будет 10×0,25 Вт или 2,5 Вт. Не очень красиво, но это поможет нам завершить финальный проект и может даже принести нам дополнительные баллы за способность думать на ногах.
Нам нужно быть немного более осторожными, когда мы объединяем резисторы разных номиналов параллельно, когда речь идет об общем эквивалентном сопротивлении и номинальной мощности. Для читателя это должно быть совершенно очевидно, но …
Совет № 4: Разные резисторы параллельно
Суммарное сопротивление двух резисторов разного номинала всегда меньше, чем резистор наименьшего номинала.Читатель будет удивлен тем, сколько раз кто-то объединяет значения в своей голове и приходит к значению, которое находится посередине между двумя резисторами (1 кОм || 10 кОм; НЕ равняется чему-либо около 5 кОм ;!). Общее параллельное сопротивление всегда будет приближаться к резистору с наименьшим значением. Сделайте себе одолжение и прочитайте совет №4 10 раз.
Совет № 5: Параллельное рассеяние мощности
Мощность, рассеиваемая при параллельной комбинации резисторов разных номиналов, не распределяется между резисторами равномерно, поскольку токи не равны.Используя предыдущий пример (1k & ohm; || 10k & ohm;), мы видим, что 1k & ohm; будет потреблять в 10 раз больше тока 10 кОм. Поскольку закон Ома гласит, что мощность = напряжение x ток, отсюда следует, что 1 кОм; резистор рассеивает в 10 раз мощность, превышающую 10 кОм.
В конечном счете, уроки советов 4 и 5 заключаются в том, что мы должны уделять больше внимания тому, что мы делаем при параллельном соединении резисторов разного номинала. Но советы 1 и 3 предлагают несколько удобных ярлыков, когда значения совпадают.
Конденсаторы сериии параллельные
Объединение конденсаторов аналогично объединению резисторов … только наоборот. Как бы странно это ни звучало, это абсолютная правда. Почему это могло быть?
Конденсатор — это всего лишь две пластины, расположенные очень близко друг к другу, и его основная функция — удерживать целую группу электронов. Чем больше значение емкости, тем больше электронов она может удерживать. Если размер пластин увеличивается, емкость увеличивается, потому что физически больше места для электронов.А если пластины отодвинуть дальше друг от друга, емкость падает, потому что напряженность электрического поля между ними уменьшается с увеличением расстояния.
Теперь предположим, что у нас есть два конденсатора по 10 мкФ, соединенных последовательно, и предположим, что они оба заряжены и готовы к разрядке в друга, сидящего рядом с вами.
Помните, что в последовательной цепи есть только один путь для прохождения тока. Отсюда следует, что количество электронов, выходящих из колпачка внизу, будет таким же, как и количество электронов, выходящих из колпачка наверху.Значит, емкость не увеличилась?
На самом деле все еще хуже. Разместив конденсаторы последовательно, мы эффективно раздвинули пластины дальше друг от друга, потому что расстояние между пластинами двух конденсаторов складывается. Так что у нас нет 20 мкФ или даже 10 мкФ. У нас 5 мкФ. Результатом этого является то, что мы добавляем значения последовательного конденсатора так же, как мы добавляем значения параллельного резистора. И метод «произведение над суммой», и метод взаимности действительны для последовательного добавления конденсаторов.
Может показаться, что нет смысла добавлять конденсаторы последовательно. Но следует отметить, что мы получили вдвое большее напряжение (или номинальное напряжение). Как и в случае с батареями, когда мы соединяем конденсаторы последовательно, напряжения складываются.
Добавление конденсаторов параллельно похоже на добавление резисторов последовательно: значения просто складываются, никаких уловок. Почему это? Их параллельное расположение эффективно увеличивает размер пластин без увеличения расстояния между ними.Чем больше площадь, тем больше емкость. Простой.
Время эксперимента — часть 3
Что вам понадобится:
Давайте посмотрим, как работают последовательно и параллельно соединенные конденсаторы. Это будет немного сложнее, чем примеры резисторов, потому что измерить емкость напрямую мультиметром труднее.
Давайте сначала поговорим о том, что происходит, когда конденсатор заряжается с нуля вольт. Когда ток начинает идти в один из выводов, равное количество тока выходит из другого.А если последовательно с конденсатором нет сопротивления, может быть довольно большой ток. В любом случае ток течет до тех пор, пока конденсатор не начнет заряжаться до значения приложенного напряжения, и медленнее будет стекать до тех пор, пока напряжения не станут равными, когда ток полностью прекратится.
Как указано выше, потребляемый ток может быть довольно большим, если нет последовательного сопротивления конденсатора, а время зарядки может быть очень коротким (например, миллисекунды или меньше). Для этого эксперимента мы хотим иметь возможность наблюдать за зарядом конденсатора, поэтому мы собираемся использовать 10 кОм; резистор, включенный последовательно, чтобы замедлить действие до точки, где мы его легко увидим.Но сначала нам нужно поговорить о том, что такое постоянная времени RC.
В приведенном выше уравнении говорится, что одна постоянная времени в секундах (называемая тау) равна сопротивлению в омах, умноженному на емкость в фарадах. Простой? Нет? Продемонстрируем на следующей странице.
Время эксперимента — часть 3, продолжение …
В первой части этого эксперимента мы будем использовать один резистор 10 кОм и один резистор 100 мкФ (что равно 0,0001 фарад). Эти две части создают постоянную времени в 1 секунду:
При зарядке нашего конденсатора 100 мкФ через 10 кОм; резистора, мы можем ожидать, что напряжение на цоколе вырастет примерно до 63% от напряжения питания за 1 постоянную времени, которая составляет 1 секунду.После 5 постоянных времени (в данном случае 5 секунд) конденсатор заряжается примерно на 99% до напряжения питания, и он будет следовать кривой заряда, похожей на график ниже.
Теперь, когда мы это знаем, мы собираемся подключить схему, показанную на схеме (убедитесь, что полярность на этом конденсаторе правильная!).
С помощью нашего мультиметра, установленного для измерения вольт, проверьте выходное напряжение батареи при включенном переключателе. Это наше напряжение питания, и оно должно быть около 4.5В (будет немного больше, если батарейки новые). Теперь подключите схему, убедившись, что переключатель на батарейном блоке находится в положении «ВЫКЛ», прежде чем вставлять его в макетную плату. Также позаботьтесь о том, чтобы красный и черный провода были в нужных местах. Если это более удобно, вы можете использовать зажимы типа «крокодил», чтобы прикрепить измерительные щупы к ножкам конденсатора для измерения (вы также можете немного раздвинуть эти ножки, чтобы было легче).
Когда мы убедимся, что схема выглядит правильно, а наш счетчик включен и настроен на считывание вольт, переведите переключатель на батарейном блоке в положение «ВКЛ».Примерно через 5 секунд показания счетчика должны быть довольно близкими к напряжению аккумуляторной батареи, что демонстрирует, что уравнение верное, и мы знаем, что делаем. Теперь выключите выключатель. Он все еще довольно хорошо держит это напряжение, не так ли? Это потому, что у тока нет пути для разряда конденсатора; у нас разомкнутая цепь. Для разряда конденсатора можно использовать еще один резистор на 10 кОм параллельно. Примерно через 5 секунд он вернется к почти нулевому значению.
Experiment Time — Часть 3, и даже больше…
Теперь мы переходим к интересным моментам, начиная с подключения двух конденсаторов последовательно. Помните, что мы сказали, что результат будет аналогичен параллельному соединению двух резисторов. Если это правда, мы можем ожидать (используя произведение над суммой)
Что это будет делать с нашей постоянной времени?
Имея это в виду, подключите другой конденсатор последовательно с первым, убедитесь, что измеритель показывает ноль вольт (или около того), и переведите переключатель в положение «ON».Зарядка до напряжения аккумуляторной батареи занимала примерно половину времени? Это потому, что емкость вдвое меньше. Электронный бензобак стал меньше, поэтому на его зарядку уходит меньше времени. Для этого эксперимента предлагается третий конденсатор, просто чтобы доказать это, но мы держим пари, что читатель сможет увидеть надпись на стене.
Теперь мы попробуем подключить конденсаторы параллельно, не забывая о том, что мы говорили ранее, что это будет похоже на последовательное добавление резисторов. Если это правда, то мы можем ожидать 200 мкФ, верно? Тогда наша постоянная времени станет
.Это означает, что теперь потребуется около 10 секунд, чтобы увидеть, как параллельные конденсаторы заряжаются до напряжения питания 4.5В.
Для доказательства начнем с нашей исходной схемы на 10 кОм; последовательно подключены резистор и один конденсатор емкостью 100 мкФ, как показано на первой схеме этого эксперимента. Мы уже знаем, что конденсатор заряжается примерно за 5 секунд. Теперь подключите второй конденсатор параллельно. Убедитесь, что показания измерителя близки к нулю (разрядите через резистор, если он не показывает нулевое значение), и переведите переключатель на батарейном блоке в положение «ON». Нужно много времени, не правда ли? Разумеется, мы увеличили размер электронного бензобака, и теперь на его заполнение уходит больше времени.Чтобы убедиться в этом, попробуйте добавить третий конденсатор емкостью 100 мкФ и понаблюдайте, как он заряжается в течение долгого времени.
Дроссели сериии параллельные индукторы
Катушки индуктивности сериии параллельные
Случаи, когда катушки индуктивности должны быть добавлены последовательно или параллельно, довольно редки, но не редкость. В любом случае, давайте рассмотрим их для полноты картины.
Вкратце, они складываются так же, как и резисторы, то есть они складываются со знаком плюс, когда соединены последовательно, и с превышением произведения при параллельном соединении.Сложность возникает, когда они размещаются близко друг к другу, чтобы иметь взаимодействующие магнитные поля, намеренно или нет. По этой причине предпочтительнее иметь один компонент, чем два или более, хотя большинство индукторов экранированы для предотвращения взаимодействия магнитных полей.
В любом случае достаточно сказать, что они добавляют, как резисторы. Дополнительная информация о катушках индуктивности выходит далеко за рамки этого руководства.
Ресурсы и дальнейшее развитие
Теперь, когда вы знакомы с основами последовательных и параллельных цепей, почему бы не ознакомиться с некоторыми из этих руководств?
- Делители напряжения — одна из самых простых и повторяющихся схем — это делитель напряжения.Это схема, которая действительно основана на концепциях, рассмотренных в этом руководстве.
- Что такое Ардуино? — Теперь, когда у вас есть основы схем, вы можете перейти непосредственно к изучению микроконтроллеров с одной из самых популярных платформ: Arduino. Основы работы с коммутатором
- — В этом руководстве мы говорили о некоторых из наиболее основных элементов схемы, но это не был один из них. Переключатели являются важным компонентом практически в каждом электронном проекте.Узнайте все о переключателях в этом руководстве
- Шитье проводящей нитью — схемы не обязательно должны состоять из макетов и проводов. Электронный текстиль использует токопроводящую нить для вшивания светильников и другой электроники в одежду или другую ткань.
и параллельные [Analog Devices Wiki]
Цель:
Целью этой лабораторной работы является исследование последовательно и параллельно включенных резисторов.
Серияи параллельные схемы
Простые схемы, состоящие всего из нескольких компонентов, обычно просты для понимания новичками. Но все усложняется, когда в смесь входит большее количество компонентов. Куда идет ток? Что делают узловые напряжения? Можно ли упростить схему и облегчить понимание? Следующая информация должна помочь.
В этой лабораторной работе мы сначала обсудим разницу между последовательными цепями и параллельными цепями, используя цепи, содержащие самые основные компоненты, резисторы и батареи (или источники напряжения), чтобы показать разницу между двумя конфигурациями.
Прежде чем мы углубимся в объяснение, нам нужно определить, что такое узел схемы. Узел в цепи — это не что иное, как электрическое соединение между двумя или более компонентами. Когда схема изображена на схеме, такой как рисунок 1, узлы представлены проводами (линиями) между компонентами.
Рисунок 1, Пример схемы узла
На схеме изображена схема с 4 резисторами и источником напряжения. Также есть четыре уникальных узла.Цветные узлы (линии) Красный соединяет (+) конец источника напряжения с резистором R 1 , оранжевый соединяет R 1 и R 2 вместе, синий соединяет R 2 с R 3 и R 4 и зеленый соединяет (-) конец источника напряжения с R 3 и R 4 . Обратите внимание, что мы обычно определяем один узел как общий узел, на который ссылаются все остальные узлы, в данном случае это зеленый наземный узел.
Нам также необходимо понять, как ток течет по цепи.Обычный ток течет от более высокого или более положительного напряжения к более низкому или менее положительному напряжению в цепи. Некоторое количество тока будет проходить по каждому пути, который может пройти, чтобы добраться до точки с наименьшим напряжением, обычно называемой землей (0 вольт). Используя приведенную выше схему в качестве примера, вот как ток будет течь от положительной клеммы источника напряжения к отрицательной клемме.
Обратите внимание, что в некоторых узлах (например, между R 1 и R 2 ) ток на входе такой же, как на выходе.В других узлах (в частности, трехсторонний переход между R 2 , R 3 и R 4 ) основной (красный) ток разделяется на два разных: фиолетовый ток, текущий в R 3 и оранжевый ток протекает в R 4 . Также обратите внимание, что токи I R3 и I R4 рекомбинируют как зеленый ток. Это подчеркивает ключевое различие между последовательным и параллельным подключением.
Определение цепей серииКогда резисторы соединены последовательно (как показано на рисунке 2), вывод одного резистора подключается непосредственно к выводу следующего резистора, без каких-либо других возможных путей, так что весь ток в одном резисторе должен течь в следующий и скоро.
Когда резисторы включены последовательно, они могут быть объединены или объединены в один эквивалентный одиночный резистор с сопротивлением, равным сумме последовательных сопротивлений, , то есть ,
Рисунок 2: Последовательные резисторы, R СЕРИЯ = R 1 + R 2 + R 3 +…
Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление.Итак, для приведенной выше последовательной схемы:
Мы знаем, что все резисторы имеют одинаковый ток I S .
Аналогично для остальных трех резисторов так:
Или за вычетом I S :
Таким образом, полное эквивалентное сопротивление — это просто сумма их значений.
Определение параллельных цепей
Когда резисторы включены параллельно (как показано на рисунке 3), все их первые выводы соединены вместе, а все их вторые выводы соединены вместе.
Когда резисторы включены параллельно, они могут быть объединены или объединены в один эквивалентный одиночный резистор, значение которого определяется следующим уравнением:
Для двух параллельно подключенных резисторов это упрощает:
Рисунок 3: Параллельные резисторы
Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление. Итак, для вышеуказанной параллельной схемы:
Мы знаем, что все резисторы имеют одинаковое напряжение В S .
Ток, подаваемый источником напряжения В S , представляет собой сумму токов в резисторах.
Подставляя четыре резистора, получаем:
Или за вычетом V S :
Преобразуя сопротивление, получаем полное эквивалентное сопротивление:
Эксперименты
Материалы:
Аппаратный модуль ADALM1000
Макетная плата без пайки и перемычки
Резисторы 3 — 100 Ом
Резисторы 3 — 470 Омрезисторов в серии:
Поместите три резистора 100 Ом последовательно на беспаечную макетную плату, как показано на рисунке 4.Соедините с помощью перемычек, подключите вход CH A к левой стороне первого резистора, а вход CH B — к правой стороне того же резистора.
Рисунок 4, последовательно соединенные резисторы
Запустите прибор ALICE M1K Ohm Meter. Здесь показан экран. Программное обеспечение использует известный резистор для проверки неизвестного резистора. ADALM1000 имеет встроенный резистор 50 Ом, который можно использовать для этого. Убедитесь, что выбран параметр Int. Уровень напряжения, который используется для измерения резистора, может быть установлен.Тестирование при максимальном напряжении 5,0 В дает наилучшие результаты для большинства номиналов резисторов. Нажмите Run, и вы должны увидеть что-то подобное с единственным резистором 100 Ом.
Переместите перемычку CH B к правому концу второго резистора, как показано ниже.
Рисунок 5, два резистора последовательно
Омметр должен теперь показать значение для двух последовательно соединенных резисторов или около 200 Ом. Теперь переместите перемычку CH B к правому концу третьего резистора, как показано ниже.
Рисунок 6, три резистора последовательно
Омметр должен теперь показать значение трех последовательно соединенных резисторов или около 300 Ом.
Параллельно подключенных резисторов:
Теперь замените резисторы 100 Ом на резисторы 470 Ом, как показано на рисунке 7.
Измерение одного резистора 470 Ом
Омметр должен теперь показать значение одиночного резистора или около 470 Ом. Переместите средний резистор 470 Ом так, чтобы он был параллелен резистору справа, как показано ниже.
Измерение двух резисторов 470 Ом, включенных параллельно
Омметр должен теперь показать значение для двух резисторов 470 Ом, включенных параллельно. Соответствует ли измеренное значение формуле для параллельных резисторов?
Переместите третий резистор 470 Ом так, чтобы он был параллелен двум другим резисторам справа, как показано ниже.
Измерение трех резисторов 470 Ом, включенных параллельно
Омметр должен теперь показать значение для трех резисторов 470 Ом, включенных параллельно.Соответствует ли измеренное значение формуле для параллельных резисторов?
Поэкспериментируйте с другими комбинациями резисторов и номиналов, чтобы убедиться, что формулы верны для любого номинала резистора.
Комбинированные схемы
Более сложные соединения резисторов обычно представляют собой просто комбинации последовательного и параллельного соединения. Это часто встречается, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинированная схема может быть разбита на аналогичные части, которые являются последовательными или параллельными, как показано на рисунке 7. На рисунке общее сопротивление может быть вычислено путем соединения трех резисторов друг с другом как последовательно, так и параллельно.
Комбинированные последовательные и параллельные резисторы
R 2 и R 3 соединены параллельно друг другу, поэтому мы знаем, что для этих двух резисторов эквивалентное сопротивление будет:
Комбинированное сопротивление R 2 и R 3 последовательно с R1, поэтому общее эквивалентное сопротивление будет:
Для более сложных комбинированных схем различные части могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление.
Для дальнейшего изучения:
Академия Хана — Резисторные схемы
Безграничная физика
Последовательные и параллельные схемы (по физике)Вернуться к разделу «Введение в работу электротехнической лаборатории» Содержание
Учебное пособие по физике: Комбинированные схемы
Ранее в Уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь.Они могут быть соединены посредством последовательного или параллельного соединения. Когда все устройства в цепи соединены последовательными соединениями, тогда схема называется последовательной схемой. Когда все устройства в цепи соединены параллельными соединениями, тогда цепь называется параллельной цепью. Третий тип схемы предполагает двойное использование последовательного и параллельного соединений в схеме; такие схемы называются составными схемами или комбинированными схемами.Схема, изображенная справа, является примером использования как последовательного, так и параллельного соединения в одной и той же цепи. В этом случае лампочки A и B подключаются параллельно, а лампочки C и D подключаются последовательно. Это пример комбинированной схемы .
При анализе комбинированных цепей критически важно иметь твердое представление о концепциях, которые относятся как к последовательным цепям, так и к параллельным цепям.Поскольку оба типа соединений используются в комбинированных схемах, концепции, связанные с обоими типами схем, применяются к соответствующим частям схемы. Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.
Цепи серии - Ток одинаков на всех резисторах; этот ток равен току в батарее.
- Сумма падений напряжения на отдельных резисторах равна номинальному напряжению батареи.
- Общее сопротивление набора резисторов равно сумме отдельных значений сопротивлений,
Параллельные схемы - Падение напряжения одинаково на каждой параллельной ветви.
- Сумма тока в каждой отдельной ветви равна току вне ветвей.
- Эквивалентное или полное сопротивление набора резисторов определяется уравнением 1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 …
Каждое из вышеперечисленных понятий имеет математическое выражение. Комбинирование математических выражений вышеуказанных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной схемы.
Анализ комбинированных схемОсновная стратегия анализа комбинированных схем включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной схемы в последовательную. После преобразования в последовательную схему анализ можно проводить обычным образом. Ранее в Уроке 4 описывался метод определения эквивалентного параллельного сопротивления, затем общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
Этот метод соответствует формуле
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 + …, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, подключенных параллельно. Если два или более резистора, находящиеся в параллельных ветвях, не имеют одинакового сопротивления, необходимо использовать приведенную выше формулу.Пример этого метода был представлен в предыдущем разделе Урока 4.
Применяя свое понимание эквивалентного сопротивления параллельных ветвей к комбинированной цепи, комбинированную схему можно преобразовать в последовательную. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения общего сопротивления цепи. Рассмотрим следующие диаграммы ниже. Схема A представляет собой комбинированную схему с резисторами R 2 и R 3 , размещенными в параллельных ветвях.Два параллельных резистора 4 Ом эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы включены последовательно, можно использовать формулу для общего сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления составляет
. R до = R 1 + R 2 + R 3 + …Итак, на схеме B полное сопротивление цепи составляет 10 Ом.
После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже на двух примерах.
Пример 1:Первый пример — самый простой — резисторы, включенные параллельно, имеют одинаковое сопротивление. Цель анализа — определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательно подключенных резистора 8 Ом эквивалентны одному резистору 4 Ом. Таким образом, два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор 4 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
. R до = R 1 + 4 Ом + R 4 = 5 Ом + 4 Ом + 6 ОмR до = 15 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I tot = ΔV tot / R tot = (60 В) / (15 Ом)I до = 4 А
Расчет тока 4 А представляет собой ток в месте расположения батареи. При этом резисторы R 1 и R 4 включены последовательно, и ток в последовательно соединенных резисторах везде одинаков.Таким образом,
I до = I 1 = I 4 = 4 АДля параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно равняться 4 ампер. Существует бесконечное количество возможных значений I 2 и I 3 , которые удовлетворяют этому уравнению. Поскольку значения сопротивления равны, значения тока в этих двух резисторах также равны.Следовательно, ток в резисторах 2 и 3 равен 2 А.
I 2 = I 3 = 2 АТеперь, когда известен ток в каждом отдельном месте резистора, можно использовать уравнение закона Ома (ΔV = I • R) для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (4 А) • (5 Ом)
ΔV 1 = 20 В
ΔV 2 = I 2 • R 2 = (2 А) • (8 Ом)
ΔV 2 = 16 В
ΔV 3 = I 3 • R 3 = (2 А) • (8 Ом)
ΔV 3 = 16 В
ΔV 4 = I 4 • R 4 = (4 А) • (6 Ом)
ΔV 4 = 24 В
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Пример 2:Второй пример — более сложный — резисторы, включенные параллельно, имеют другое сопротивление. Цель анализа та же — определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением.Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить, используя обычную формулу для эквивалентного сопротивления параллельных ветвей:
1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 …1 / R экв. = 1 / (4 Ом) + 1 / (12 Ом)
1 / R экв. = 0,333 Ом -1
R экв = 1 / (0,333 Ом -1 )
R экв = 3.00 Ом
На основании этого расчета можно сказать, что два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 3 Ом. Этот резистор 3 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
. R до = R 1 + 3 Ом + R 4 = 5 Ом + 3 Ом + 8 ОмR до = 16 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I tot = ΔV tot / R tot = (24 В) / (16 Ом)I до = 1,5 А
Расчет тока 1,5 А представляет собой ток в месте расположения батареи. При этом резисторы R 1 и R 4 включены последовательно, и ток в последовательно соединенных резисторах везде одинаков.Таким образом,
I до = I 1 = I 4 = 1,5 АДля параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно быть равно 1,5 А. Существует бесконечное множество значений I 2 и I 3 , которые удовлетворяют этому уравнению. В предыдущем примере два параллельно включенных резистора имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями.В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Для определения силы тока потребуется использовать уравнение закона Ома. Но для его использования сначала необходимо знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от более простого случая, проиллюстрированного в предыдущем примере.
Чтобы определить падение напряжения на параллельных ветвях, сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R 1 и R 4 ).Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (1,5 А) • (5 Ом)
ΔV 1 = 7,5 В
ΔV 4 = I 4 • R 4 = (1,5 А) • (8 Ом)
ΔV 4 = 12 В
Эта схема питается от источника 24 В.Таким образом, совокупное падение напряжения заряда, проходящего по контуру цепи, составляет 24 вольта. Произойдет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R 1 и R 4 ). Падение напряжения на ответвлениях должно составлять 4,5 В, чтобы компенсировать разницу между общим значением 24 В и падением 19,5 В на R 1 и R 4 . Таким образом,
ΔV 2 = V 3 = 4,5 ВЗная падение напряжения на параллельно соединенных резисторах (R 1 и R 4 ), можно использовать уравнение закона Ома (ΔV = I • R) для определения тока в двух ветвях.
I 2 = ΔV 2 / R 2 = (4,5 В) / (4 Ом)
I 2 = 1,125 А
I 3 = ΔV 3 / R 3 = (4,5 В) / (12 Ом)
I 3 = 0,375 A
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Разработка стратегииДва приведенных выше примера иллюстрируют эффективную концептуально-ориентированную стратегию анализа комбинированных схем.Подход требовал твердого понимания концепций последовательностей и параллелей, обсуждавшихся ранее. Такие анализы часто проводятся, чтобы решить физическую проблему для указанного неизвестного. В таких ситуациях неизвестное обычно меняется от проблемы к проблеме. В одной задаче значения резистора могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче могут быть указаны ток в батарее и несколько значений резистора, и неизвестная величина становится сопротивлением одного из резисторов.Очевидно, что разные проблемные ситуации потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум приведенным выше примерам проблем.
Начинающему студенту предлагаются следующие предложения по решению задач комбинированной схемы:
- Если схематическая диаграмма не предоставлена, потратьте время на ее создание. Используйте условные обозначения, такие как те, что показаны в примере выше.
- При приближении к проблеме, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записав известные значения и приравняв их к символу, например, I — , I 1 , R 3 , ΔV 2 и т. Д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.
- Знать и использовать соответствующие формулы для эквивалентного сопротивления последовательно соединенных и параллельно соединенных резисторов. Использование неправильных формул гарантирует неудачу.
- Преобразуйте комбинированную схему в строго последовательную, заменив (по вашему мнению) параллельную секцию одним резистором, имеющим значение сопротивления, равное эквивалентному сопротивлению параллельной секции.
- Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будет определено с использованием этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при вычислении I 2 важно подставить в уравнение значения ΔV 2 и R 2 .
Для дальнейшей практики анализа комбинированных схем рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.
Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие — это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, расположить и подключить их так, как вам нужно. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).
Проверьте свое понимание1. Комбинированная схема показана на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы.
а. Ток в точке A равен _____ (больше, равен, меньше) ток в точке B.
г. Ток в точке B равен _____ (больше, равен, меньше) ток в точке E.
г. Ток в точке G равен _____ (больше, равен, меньше) ток в точке F.
г. Ток в точке E равен _____ (больше, равен, меньше) току в точке G.
e. Ток в точке B равен _____ (больше, равен, меньше) ток в точке F.
ф. Ток в точке A равен _____ (больше, равен, меньше) ток в точке L.
г. Ток в точке H равен _____ (больше, равен, меньше) ток в точке I.
2. Рассмотрим комбинированную схему на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы. (Предположим, что падение напряжения в самих проводах пренебрежимо мало.)
а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.
г. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
ф. Разность электрических потенциалов между точками L и A составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками B и K.
3.Используйте концепцию эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.
4. Проанализируйте следующую схему и определите значения общего сопротивления, общего тока, а также тока и падения напряжения на каждом отдельном резисторе.
5. Обращаясь к диаграмме в вопросе №4, определите …
а. … номинальная мощность резистора 4.
г. … скорость, с которой энергия потребляется резистором 3.
Последовательные и параллельные резисторы
Цели обучения
К концу этого раздела вы сможете:
- Нарисуйте схему с резисторами, включенными параллельно и последовательно.
- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Контраст — способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
- Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Рассчитайте общее сопротивление цепи, которая содержит смесь резисторов, включенных последовательно и параллельно.
Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи.Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Рис. 1. (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.
Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно.Например, если ток течет через человека, держащего отвертку, в землю, тогда R 1 на Рисунке 1 (a) может быть сопротивлением вала отвертки, R 2 сопротивлением ее ручки , R 3 сопротивление тела человека и R 4 сопротивление его обуви. На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно.(Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный шнур с высоким сопротивлением. прибор, уменьшающий рабочий ток.)
Рис. 2. Три резистора, подключенных последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения в каждом резисторе на Рисунке 2.Согласно закону Ома падение напряжения В на резисторе при протекании через него тока рассчитывается по формуле В = IR , где I равно току в амперах (A) и R — сопротивление в Ом (Ом). Другой способ представить это: В, — это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R 1 составляет В 1 = IR 1 , что на R 2 составляет В 2 = IR и 2 что для R 3 равно V 3 = IR 3 .Сумма этих напряжений равна выходному напряжению источника; то есть
V = V 1 + V 2 + V 3 .
Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV , где q — электрический заряд, а V — напряжение. Таким образом, энергия, поставляемая источником, составляет кв.кв. , а энергия, рассеиваемая резисторами, составляет
.qV 1 + qV 2 + qV 3 .
Установление связей: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые гласят, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии.Таким образом, qV = qV 1 + qV 2 + qV 3 . Плата q отменяется, давая V = V 1 + V 2 + V 3 , как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.) Теперь подстановка значений для отдельных напряжений дает
V = IR 1 + IR 2 + IR 3 = I ( R 1 + R 2 905 905 ).
Обратите внимание, что для эквивалентного сопротивления одной серии R с , мы имеем
V = IR с .
Это означает, что полное или эквивалентное последовательное сопротивление R с трех резисторов составляет R с = R 1 + R 2 + R 3 .Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление R с последовательного соединения составляет
R с = R 1 + R 2 + R 3 +…,
, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Пример 1. Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке 2 равно 12.0 В, а сопротивления равны R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите ток. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:
[латекс] \ begin {array} {lll} {R} _ {\ text {s}} & = & {R} _ {1} + {R} _ {2} + {R} _ {3} \ \ & = & 1.00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex].
Стратегия и решение для (b)Ток определяется по закону Ома, В = IR . Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
[латекс] I = \ frac {V} {{R} _ {\ text {s}}} = \ frac {12.0 \ text {V}} {20.0 \ text {} \ Omega} = 0.60 \ text {A }\\[/латекс].
Стратегия и решение для (c)Напряжение — или падение IR — на резисторе определяется законом Ома.Ввод значения тока и значения первого сопротивления дает
.В 1 = IR 1 = (0,600A) (1,0 Ом) = 0,600 В.
Аналогично
В 2 = IR 2 = (0,600 A) (6,0 Ом) = 3,60 В
и
V3 = IR 3 = (0,600 A) (13,0 Ом) = 7,80 В.
Обсуждение для (c)Три капли IR добавляют к 12.0 В, прогноз:
V 1 + V 2 + V 3 = (0,600 + 3,60 + 7,80) V = 12,0 В.
Стратегия и решение для (d)Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля , P = IV , где P — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток.Подставляя закон Ома V = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
P 1 = I 2 R 1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт
Аналогично
P 2 = I 2 R 2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт
и
P 3 = I 2 R 3 = (0.{2}} {R} \\ [/ latex], где В, — это падение напряжения на резисторе (а не полное напряжение источника). Будут получены те же значения.
Стратегия и решение для (e)Самый простой способ рассчитать выходную мощность источника — использовать P = IV , где В, — напряжение источника. Это дает
P = (0,600 A) (12,0 В) = 7,20 Вт.
Обсуждение для (e)Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
P 1 + P 2 + P 3 = (0,360 + 2,16 + 4,68) W = 7,20 Вт
Мощность — это энергия в единицу времени (ватты), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Последовательные сопротивления добавить: R с = R 1 + R 2 + R 3 +….
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
На рисунке 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника. Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)
Рис. 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)
Чтобы найти выражение для эквивалентного параллельного сопротивления R p , давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} \\ [/ latex] , [латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} \\ [/ latex] и [латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} \\ [/ латекс]. Сохранение заряда подразумевает, что полный ток I , производимый источником, является суммой этих токов:
I = I 1 + I 2 + I 3 .
Подстановка выражений для отдельных токов дает
[латекс] I = \ frac {V} {{R} _ {1}} + \ frac {V} {{R} _ {2}} + \ frac {V} {{R} _ {3}} = V \ left (\ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} \ справа) \\ [/ латекс].
Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает
[латекс] I = \ frac {V} {{R} _ {p}} = V \ left (\ frac {1} {{R} _ {p}} \ right) \\ [/ latex].
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая на любое количество резисторов, общее сопротивление R p параллельного соединения связано с отдельными сопротивлениями на
.[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ гидроразрыв {1} {{R} _ {\ text {.} 3}} + \ text {.} \ Text {…} \\ [/ latex]
Это соотношение приводит к общему сопротивлению R p , которое меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на Рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: В = 12.0 В, R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения.Ввод известных значений дает
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} = \ frac {1} {1 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {6 \ text {. } \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} \\ [/ latex].
Таким образом,
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1.00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.) Мы должны перевернуть это, чтобы найти полное сопротивление R p . Это дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {1 \ text {.} \ Text {2436}} \ text {} \ Omega = 0 \ text {.} \ Text { 8041} \ text {} \ Omega \\ [/ latex].
Общее сопротивление с правильным количеством значащих цифр составляет R p = 0,804 Ом
Обсуждение для (а)R p , как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)Полный ток можно найти из закона Ома, заменив полное сопротивление R p . Это дает
[латекс] I = \ frac {V} {{R} _ {\ text {p}}} = \ frac {\ text {12.0 V}} {0.8041 \ text {} \ Omega} = \ text {14} \ text {.} \ text {92 A} \\ [/ latex].
Обсуждение для (б)Ток I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,
[латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} = \ frac {12.0 \ text {V}} {1.00 \ text {} \ Omega} = 12.0 \ text {A} \\ [/ латекс].
Аналогично
[латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} = \ frac {12.0 \ text {V}} {6.00 \ text {} \ Omega} = 2 \ text {.} \ text {00} \ text {A} \\ [/ latex]
и
[латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} = \ frac {\ text {12} \ text {.} 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].
Обсуждение для (c)Общий ток складывается из отдельных токов:
I 1 + I 2 + I 3 = 14,92 A.
Это соответствует сохранению заряда.{2}} {13.0 \ text {} \ Omega} = 11.1 \ text {W} \\ [/ latex].
Обсуждение для (d)Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)Общую мощность также можно рассчитать несколькими способами. Выбрав P = IV и введя полный ток, получим
.P = IV = (14,92 A) (12,0 В) = 179 Вт.
Обсуждение для (e)Суммарная мощность, рассеиваемая резисторами, также 179 Вт:
P 1 + P 2 + P 3 = 144 Вт + 24,0 Вт + 11,1 Вт = 179 Вт
Это соответствует закону сохранения энергии.
Общее обсуждениеОбратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Основные характеристики параллельных резисторов- Параллельное сопротивление определяется из [latex] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {1}} + \ frac {1} { {R} _ {2}} + \ frac {1} {{R} _ {3}} + \ text {…} \\ [/ latex], и оно меньше любого отдельного сопротивления в комбинации.
- Каждый резистор, включенный параллельно, имеет то же полное напряжение, что и источник. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
- Параллельные резисторы не получают суммарный ток каждый; они делят это.
Сочетания последовательного и параллельного
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного подключения можно свести к одному эквивалентному сопротивлению, используя методику, показанную на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Рис. 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто единичное эквивалентное сопротивление.
Самая простая комбинация последовательного и параллельного сопротивления, показанная на рисунке 4, также является наиболее поучительной, поскольку она используется во многих приложениях.Например, R 1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые соединены параллельно. R 2 и R 3 могли быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 3. Расчет сопротивления,
IR Падение, ток и рассеиваемая мощность: объединение последовательных и параллельных цепейНа рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного подключения.Мы можем считать R 1 сопротивлением проводов, ведущих к R 2 и R 3 . (а) Найдите полное сопротивление. (b) Что такое падение IR в R 1 ? (c) Найдите текущие значения от I 2 от до R 2 . (d) Какую мощность рассеивает R 2 ?
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация включена последовательно с R 1 .
Стратегия и решение для (а)Чтобы найти полное сопротивление, отметим, что R 2 и R 3 находятся параллельно, и их комбинация R p последовательно с R 1 . Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет
.R до = R 1 + R p .
Сначала находим R p , используя уравнение для параллельных резисторов и вводя известные значения:
[латекс] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3 }} = \ frac {1} {6 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс].
Инвертирование дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {0,2436} \ text {} \ Omega = 4.11 \ text {} \ Omega \\ [/ latex].
Таким образом, общее сопротивление равно
.R до = R 1 + R p = 1,00 Ом + 4,11 Ом = 5,11 Ом.
Обсуждение для (а)Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чистой параллели (20.0 Ом и 0,804 Ом соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)Чтобы найти падение IR в R 1 , отметим, что полный ток I протекает через R 1 . Таким образом, его падение IR составляет
.В 1 = ИК 1
Мы должны найти I , прежде чем сможем вычислить V 1 .Полный ток I находится с помощью закона Ома для цепи. То есть
[латекс] I = \ frac {V} {{R} _ {\ text {tot}}} = \ frac {\ text {12.0} \ text {V}} {5.11 \ text {} \ Omega} = 2.35 \ text {A} \\ [/ latex].
Вводя это в выражение выше, мы получаем
В 1 = IR 1 = (2,35 А) (1,00 Ом) = 2,35 В.
Обсуждение для (б)Напряжение, приложенное к R 2 и R 3 меньше общего напряжения на величину В 1 .Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R 2 и R 3 .
Стратегия и решение для (c)Чтобы найти ток через R 2 , мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение В p , потому что оно приложено к параллельной комбинации резисторов. Напряжение, приложенное как к R 2 , так и к R 3 , уменьшается на величину В 1 , поэтому оно равно
V p = V — V 1 = 12.0 В — 2,35 В = 9,65 В.
Теперь ток I 2 через сопротивление R 2 находится по закону Ома:
[латекс] {I} _ {2} = \ frac {{V} _ {\ text {p}}} {{R} _ {2}} = \ frac {9.65 \ text {V}} {6.00 \ текст {} \ Omega} = 1,61 \ text {A} \\ [/ latex].
Обсуждение для (c)Ток меньше 2,00 А, который протекал через R 2 , когда он был подключен параллельно батарее в предыдущем примере параллельной цепи.
Стратегия и решение для (d)Мощность, рассеиваемая на R 2 определяется на
P 2 = ( I 2 ) 2 R 2 = (1,61 A) 2 (6,00 Ом) = 15,5 Вт
Обсуждение для (d)Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, обозначенное как R 3 , имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот повышенный ток вызывает большее падение IR в проводах, представленных R 1 , снижая напряжение на лампочке (которое составляет R 2 ), которое затем заметно тускнеет.
Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
Проверьте свое понимание
Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.
Решение Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы. В таких случаях правила Кирхгофа, которые будут включены в Правила Кирхгофа, позволят вам проанализировать схему. Стратегии решения проблем для последовательных и параллельных резисторов- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, уменьшайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при нахождении R необходимо соблюдать осторожность.
- Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Сводка раздела
Концептуальные вопросы
1. Переключатель имеет переменное сопротивление, которое почти равно нулю в замкнутом состоянии и очень велико в разомкнутом состоянии, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рис. 7 на ток в разомкнутом и замкнутом состоянии.
Рис. 7. Выключатель обычно включается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
2. Какое напряжение на разомкнутом переключателе на Рисунке 7?
3. На разомкнутом переключателе есть напряжение, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?
4. Почему мощность, рассеиваемая замкнутым переключателем, как на Рисунке 7, мала?
5. Студент в физической лаборатории по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рисунке 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и гаснет, когда он замкнут. (Не пытайтесь — батарея сильно разряжается!)
Рис. 8. Ошибка подключения. Включите этот переключатель параллельно устройству, обозначенному [латекс] R [/ латекс].(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
6. Зная, что сила электрического шока зависит от величины тока, протекающего через ваше тело, вы бы предпочли, чтобы он был включен последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он шокирован им? Объяснять.
7. Были бы ваши фары тусклыми при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.
8. Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкаются накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?
9.Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.
10. Предположим, вы проводите физическую лабораторию, в которой вас просят вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?
11. Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление.Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.
12. У некоторых лампочек есть три уровня мощности (не включая ноль), получаемые от нескольких нитей накала, которые индивидуально переключаются и соединяются параллельно. Какое минимальное количество нитей необходимо для трех режимов мощности?
Задачи и упражнения
Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.
1. (а) Каково сопротивление десяти последовательно соединенных резисторов сопротивлением 275 Ом? (б) Параллельно?
2. (a) Каково сопротивление последовательно соединенных резисторов 1,00 × 10 2 Ом, 2,50 кОм и 4,00 кОм? (б) Параллельно?
3. Какое наибольшее и наименьшее сопротивление можно получить, соединив резисторы на 36,0 Ом, 50,0 Ом и 700 Ом?
4. Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
5. Фара мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)
6.(a) Учитывая батарею на 48,0 В и резисторы на 24,0 и 96,0 Ом, найдите для каждого из них ток и мощность при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.
7. Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, вычислите I 3 двумя следующими способами: (a) по известным значениям I и I 2 ; (б) используя закон Ома для R 3 . В обеих частях явно показано, как вы следуете шагам, описанным в описании стратегии решения проблем для последовательных и параллельных резисторов выше.
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация включена последовательно с R 1 .
8. Ссылаясь на рисунок 5: (a) Вычислите P 3 и обратите внимание на его сравнение с P 3 , найденным в первых двух примерах задач в этом модуле. (b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.
9. См. Рисунок 6 и обсуждение затемнения света при включении тяжелого прибора. (a) Учитывая, что источник напряжения составляет 120 В, сопротивление провода составляет 0,400 Ом, а номинальная мощность лампы составляет 75,0 Вт, какая мощность будет рассеиваться лампой, если при включении двигателя через провода пройдет в общей сложности 15,0 А? Предположите незначительное изменение сопротивления лампы. б) Какая мощность потребляет двигатель?
Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
10. Линия электропередачи на 240 кВ, имеющая 5,00 × 10 2 , подвешена к заземленным металлическим опорам с помощью керамических изоляторов, каждый из которых имеет сопротивление 1,00 × 10 9 Ом (рис. 9 (а)). Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Ясно покажите, как вы следуете шагам, описанным выше в разделе «Стратегии решения проблем для последовательных и параллельных резисторов ».
Рис. 9. Высоковольтная (240 кВ) линия электропередачи 5,00 × 10 2 подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает сопротивление 1,00 × 10 9 Ом каждый.
11. Покажите, что если два резистора R 1 и R 2 объединены и один намного больше другого ( R 1 >> R 2 ): (a ) Их последовательное сопротивление почти равно большему сопротивлению R 1 .(b) Их параллельное сопротивление почти равно меньшему сопротивлению R 2 .
12. Необоснованные результаты Два резистора, один с сопротивлением 145 Ом, подключены параллельно, чтобы получить общее сопротивление 150 Ом. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
13. Необоснованные результаты Два резистора, один из которых имеет сопротивление 900 кОм, соединены последовательно, чтобы получить общее сопротивление 0.500 МОм. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Глоссарий
- серии:
- последовательность резисторов или других компонентов, включенных в цепь один за другим
- резистор:
- Компонент, обеспечивающий сопротивление току, протекающему по электрической цепи
- сопротивление:
- , вызывая потерю электроэнергии в цепи
- Закон Ома:
- соотношение между током, напряжением и сопротивлением в электрической цепи: В = IR
- напряжение:
- электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором
- падение напряжения:
- потеря электроэнергии при прохождении тока через резистор, провод или другой компонент
- ток:
- поток заряда через электрическую цепь мимо заданной точки измерения
- Закон Джоуля:
- соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое следующим образом: [latex] {P} _ {e} = \ text {IV} [/ latex]
- параллельно:
- подключение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
Избранные решения проблем и упражнения
1.(а) 2,75 кОм (б) 27,5 Ом
3. (а) 786 Ом (б) 20,3 Ом
5. 29,6 Вт
7. (а) 0,74 А (б) 0,742 А
9. (а) 60,8 Вт (б) 3,18 кВт
11. (a) [латекс] \ begin {array} {} {R} _ {\ text {s}} = {R} _ {1} + {R} _ {2} \\ \ Rightarrow {R} _ {\ text {s}} \ приблизительно {R} _ {1} \ left ({R} _ {1} \ text {>>} {R} _ {2} \ right) \ end {array} \\ [/ латекс]
(b) [латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2} } = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2}} \\ [/ latex],
, так что
[латекс] \ begin {array} {} {R} _ {p} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ приблизительно \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1}} = {R} _ {2} \ left ({R} _ {1 } \ text {>>} {R} _ {2} \ right) \ text {.} \ end {array} \\ [/ latex]
13. (a) –400 кОм (b) Сопротивление не может быть отрицательным. (c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.
Анализ последовательных и параллельных резисторов
Несколько резисторов подключаются одновременно, образуя цепь без ответвлений посередине, которая называется резистором в последовательной цепи. И цепь, которая соединяет два или более резистора между двумя точками в цепи с одинаковым напряжением на обоих концах резистора, называется резистором в параллельной цепи.Следующие разделы в основном посвящены схемам, методам расчета, характеристикам неисправностей и устранению неисправностей последовательно включенных и параллельных резисторов. И последняя часть вводит понятие — ESR, которое связано с последовательными резисторами и конденсаторами.
Каталог
I Резисторы в последовательной и параллельной цепях 1. Резисторы в последовательной цепиНесколько резисторов подключаются одновременно, образуя цепь без ответвлений посередине, которая называется резистором в последовательной цепи.На рисунке ниже показан резистор в последовательной цепи, состоящей из двух резисторов.
Резисторы в последовательной цепи
Характеристики последовательной цепи:
(1) Ток в последовательной цепи везде одинаков.
Если n резисторов соединены последовательно, то
(2) Общее напряжение в цепи равно сумме разделенных напряжений на последовательно соединенных резисторах.
(3) Общее сопротивление цепи равно сумме последовательного сопротивления.
R называется эквивалентным сопротивлением последовательно соединенных R1 и R2. После замены R1 и R2 на R это не влияет на ток и напряжение в цепи.
На рисунке 1 (b) — эквивалентная схема (a).
Если n резисторов подключены последовательно, то
(4) Взаимосвязь между распределением напряжения и распределением мощности в последовательных цепях.
Поскольку ток в последовательной цепи везде одинаков, поэтому
Две приведенные выше формулы показывают, что напряжение на каждом резисторе в последовательной цепи пропорционально сопротивлению каждого резистора. Мощность, потребляемая каждым резистором, также пропорциональна сопротивлению каждого резистора. Следовательно, когда последовательная цепь состоит из n резисторов, может быть получена формула деления напряжения последовательной цепи.
Совет: на практике резисторы часто подключаются последовательно, чтобы расширить диапазон измерения вольтметра.
2. Резисторы в параллельных цепяхЦепь, которая соединяет два или более резистора между двумя точками в цепи с одинаковым напряжением на обоих концах резистора, называется резистором в параллельной цепи.
Резисторы в параллельных цепях
Характеристики параллельной цепи:
(1) Напряжение на каждом резисторе в цепи одинаковое.
(2) Суммарный ток резисторов в параллельной цепи равен сумме токов ветвей.
(3) Обратное полное сопротивление параллельной цепи равно сумме обратных сопротивлений каждого параллельного резистора.
(4) Взаимосвязь между распределением тока и распределением мощности резисторов в параллельных цепях.
В параллельной цепи напряжения на параллельных резисторах одинаковы, поэтому
Приведенная выше формула показывает, что ток каждой ветви в параллельной цепи обратно пропорционален сопротивлению.И мощность, потребляемая резисторами каждой ветви, обратно пропорциональна сопротивлению.
Когда два резистора соединены параллельно, ток через каждый резистор можно рассчитать с помощью уравнения шунта. Формула шунта:
Приведенная выше формула показывает, что в резисторе в параллельной цепи ток ветви с малым сопротивлением велик, а ток ветви с большим сопротивлением мал.
Примечание : Резисторы в параллельных цепях широко используются в повседневной жизни.Например, электрические приборы в цепях освещения обычно подключаются параллельно. Только при параллельном использовании электроприборов другие электроприборы могут нормально работать, когда одно из электроприборов отключено, замкнуто или неисправно.
II C расчет S и P параллельно R esistanceОдин резистор может быть подключен вместе с множеством других резисторов последовательно и параллельно. образуют сложные резистивные цепи.
Если мы соединим различные резисторы параллельно и последовательно в одной цепи, как мы вычислим сумму сопротивления, тока и напряжения этих резисторов в цепи?
Резистивные цепи, в которых сочетаются последовательные и параллельные резисторы, обычно называются комбинациями резисторов или гибридными резисторными цепями. Метод расчета эквивалентного сопротивления цепи такой же, как и у любой одиночной последовательной или параллельной цепи. Теперь мы знаем, что последовательные резисторы имеют одинаковый ток, а параллельные резисторы имеют одинаковое напряжение.
1. Пример расчета 1Рассчитайте полный ток (IT), потребляемый от источника питания 12 В в следующей цепи.
На первый взгляд это может показаться сложной задачей, но если мы внимательно рассмотрим ее, то увидим, что два резистора, R 2 и R 3, на самом деле соединены вместе последовательно. Итак, мы можем сложить сопротивление. Таким образом, общее сопротивление этой комбинации составляет:
R2 + R3 = 8 Ом + 4 Ом = 12 Ом
Таким образом, мы можем заменить резисторы R2 и R3 на резистор 12 Ом
И теперь в схеме есть резистор RA и резистор. R4 подключены параллельно.Затем мы можем уменьшить эту параллельную комбинацию до единственного эквивалентного значения сопротивления R (комбинации), используя следующую формулу сопротивления.
В результате резистивная цепь теперь выглядит так:
Мы видим, что два оставшихся сопротивления, R1 и R (гребенчатый), соединены последовательно, и их можно снова сложить между точками. A и B.
R = R comb + R1 = 6 Ом + 6 Ом = 12 Ом
Один резистор 12 Ом может использоваться для замены четырех исходных резисторов, подключенных в исходной цепи.
Теперь, используя закон Ома, текущее значение (I) схемы просто рассчитывается следующим образом:
Следовательно, используя вышеуказанные шаги для замены всех резисторов, соединенных последовательно или параллельно, мы можем уменьшить любой сложный Схема резистора, состоящая из нескольких резисторов в простую единую схему с одним эквивалентным резистором.
Мы также можем получить два тока ответвления, I1 и I2, используя дополнительный метод Ом:
В (R1) = I * R1 = 1 * 6 = 6 В
В (RA) = VR4 = (12-VR1) = 6В
, следовательно:
I1 = 6В & делить; RA = 6 & делить; 12 = 0.5 А или 500 мА
I2 = 6 В и деление; R4 = 6 деление; 12 = 0,5 А или 500 мА
Поскольку сопротивления обеих ветвей равны 12 Ом, I1 и I2 равны 0,5 А (или 500 мА). Следовательно, общий ток питания IT = 0,5 + 0,5 = 1,0А.
После этих изменений иногда легче рисовать или перерисовывать новые схемы со сложными комбинациями резисторов и цепями резисторов, что становится наглядным пособием по математике. Затем продолжайте заменять любую последовательную или параллельную комбинацию, пока не найдете эквивалентное сопротивление R EQ .Давайте попробуем еще одну более сложную схему комбинации резисторов.
2. Пример расчета 2Чтобы найти эквивалентное сопротивление REQ, используемое в следующей схеме комбинации резисторов.
Опять же, эта схема лестничных резисторов может показаться очень сложной на первый взгляд, но, как и раньше, это просто комбинация последовательно соединенных между собой резисторов. Начиная с правой стороны и используя упрощенную формулу двух параллельных резисторов, мы можем найти эквивалентное сопротивление / комбинацию R8 и R10 и назвать это RA.
(Формула 4-1)
Следовательно, RA + R7 = 4 + 8 = 12 Ом
Сопротивление 12 Ом теперь параллельно R6, и общее сопротивление можно рассчитать как RB.
(Формула 4-2)
RB + R5 = 4 + 4 = 8 Ом
Значение сопротивления 8 Ом теперь параллельно с R4 и может быть рассчитано как RC, как показано.
(Формула 4-3)
RC подключен последовательно с R3, поэтому общее сопротивление RC + R3 = 8 Ом, что показано на рисунке.
Сопротивление 8 Ом параллельно R2, и его можно рассчитать как RD:
RD подключен последовательно с R1, поэтому общее сопротивление составляет RD + R1 = 4 + 6 = 10 Ом, как показано на фигура.
В конечном итоге, исходная сеть комплексных резисторов, которая включает десять независимых резисторов, соединенных последовательно и параллельно, может быть заменена эквивалентным сопротивлением REQ 10 Ом.
Когда мы сталкиваемся с любыми цепями, состоящими из последовательно включенных и параллельных резисторов, сначала нам нужно определить простое последовательное и параллельное сопротивление каждой ветви, а затем заменить их эквивалентным сопротивлением.
Это позволит нам снизить сложность схемы и поможет преобразовать сложные комбинированные резистивные схемы в один эквивалентный резистор.
Однако расчет более сложных Т-образных аттенюаторов и цепей резистивных мостов не может быть упрощен до простых параллельных или последовательных цепей с эквивалентным сопротивлением. Их необходимо решить, используя закон Кирхгофа и закон напряжения Кирхгофа.
III Fault C характеристики и T обработка R esistor s в S eries и параллельный1.
Особенности короткого замыкания и обрыва в последовательной цепи (1) Особенности короткого замыканияНа рисунке ниже показано короткое замыкание в последовательной цепи. В схеме резисторы R1 и R2 изначально были включены последовательно, но теперь резистор R2 закорочен. В это время в последовательной цепи произойдут следующие изменения.
Короткое замыкание в последовательной цепи
1) После короткого замыкания резистора R2 в последовательной цепи остается только резистор R1.В это время общее сопротивление цепи уменьшается, что равно сопротивлению резистора R1.
2) Поскольку рабочее напряжение постоянного тока + V в цепи не изменилось, а общее значение сопротивления последовательной цепи уменьшилось, ток последовательной цепи увеличится после короткого замыкания резистора R2.
Увеличение тока в цепи связано с сопротивлением сопротивления короткого замыкания R2. Если сопротивление R2 относительно велико, величина увеличения в последовательной цепи после короткого замыкания будет относительно большой, что вызовет перегрузку по току.Когда блок питания не выдерживает чрезмерного тока, он может сгореть. Так что короткие замыкания в последовательных цепях очень вредны.
3) В то же время, поскольку повышенный ток также течет через другие резисторы (например, R1) в последовательной цепи, он также вызовет перегрузку по току в других резисторах, что также приведет к их повреждению.
4) Если в последовательной цепи увеличивается ток, протекающий через определенный компонент, это указывает на короткое замыкание в цепи.Поскольку ток в последовательной цепи увеличивается после короткого замыкания, ток, протекающий через другие резисторы, также увеличивается, что также увеличивает падение напряжения на других резисторах.
5) Короткое замыкание в последовательной цепи относится к серьезной неисправности. Это может вызвать повреждение всех компонентов в последовательной цепи, поскольку ток, протекающий в последовательной цепи, увеличивается.
(2) Характеристики Разрыв цепи CКогда в резисторе в последовательной цепи происходит разрыв цепи, в цепи не будет протекать ток. какая часть последовательной цепи разомкнута.
Отказ обрыва цепи обычно не вредит последовательным цепям. Однако иногда из-за разомкнутой цепи напряжение цепи возбуждения нагрузки повышается, что приводит к ее выходу из строя.
Обрыв в последовательной цепи
2 . F ault A анализ серии R esist orsСледующая таблица представляет собой сводку анализа неисправностей последовательных цепей с резисторами R1 и R2.
3. Неисправность D обнаружение R esist или S eriesНазвание компонента
Тип неисправности
Анализ неисправностей
Анализ мыслей
9102000
000
000
Обрыв цепи
Нет тока через R1 и R2, и невозможно измерить напряжение на R1 и R2
Нет тока через резистор, поэтому нет напряжения.
Короткое замыкание
Ток, протекающий через R2, увеличивается, что может привести к сгоранию R2
Общее сопротивление уменьшается, что увеличивает общий ток. Если ток, протекающий через R2, слишком велик, он сожжет R2.
Сопротивление увеличилось
Ток, протекающий через R1 и R2, уменьшается, напряжение R1 увеличивается, а напряжение R2 уменьшается.
После того, как сопротивление R1 увеличивается, общее сопротивление увеличивается, общий ток уменьшается, а падение напряжения R2 уменьшается, поэтому напряжение R1 увеличивается.
Сопротивление уменьшилось
Ток, протекающий через R1 и R2, увеличивается, напряжение R1 уменьшается, а напряжение R2 увеличивается
После увеличения сопротивления R1 общее сопротивление уменьшается, и общий ток увеличивается, так что напряжение на R1 уменьшается.
Плохой контакт
Схема будет работать нормально в одном случае и ненормально в другом.
Схема работает нормально, когда контакт нормальный, цепь работает ненормально, когда контакт ненормальный
R2
Вышеупомянутые пять неисправностей
Анализ отказов такой же, как и выше (замените R1 с R2)
Аналитическое мышление такое же, как указано выше (замените R1 на R2)
Есть много способов проверить отказ резисторов в последовательной цепи.Например, значение сопротивления каждого резистора в цепи можно измерить с помощью диапазона Ом мультиметра. Однако при поиске и устранении неисправностей метод проверки часто выбирается гибко.
Структура мультиметра
(1) Метод обнаружения неисправности для Обрыв C СхемаЕсли устройство работает в цепи постоянного тока, используйте диапазон постоянного напряжения мультиметра для измерения напряжения на R1 (два измерительных провода соответственно подключены к двум контактам R1), тогда вы можете определить, есть ли в цепи обрыв цепи или нет.
Если устройство работает в цепи переменного тока, переменное напряжение мультиметра и диапазон переменного напряжения цифрового измерителя можно использовать для измерения переменного напряжения на R1.
(2) F ault I nspection Средство для короткого замыкания C цепиТеоретически вы также можете использовать описанный выше метод для измерения напряжения на R1 при проверке короткое замыкание резисторов в последовательной цепи.Если напряжение на R1 выше нормального значения, это можно объяснить коротким замыканием в цепи. Потому что только короткое замыкание в последовательной цепи увеличит ток и напряжение на R1.
Однако существует проблема с вышеупомянутым методом проверки короткого замыкания. Необходимо знать, каково нормальное напряжение на R1, иначе невозможно определить, увеличился ли ток в цепи.
4. F a ilure Testing параллельного R esist ors ( 1) F ault D etection M ethod для разомкнутой цепиКогда цепь отключена, используйте резистивный механизм мультиметра для измерения общего сопротивления параллельной цепи. В нормальных условиях измеренное значение общего сопротивления должно быть
Обнаружение обрыва цепи в параллельных цепях
Если измеренное значение сопротивления больше, чем R1 и R2, это означает, что R1 или R2 в цепи разомкнут. В частности, чтобы определить, какая цепь разомкнута, мы можем измерить ток каждой ветви сопротивления.
( 2) S hort C ircuit F ault D etection M etho dЕсли измеренное общее сопротивление ноль, это означает, что в параллельной цепи произошло короткое замыкание.Если вам нужно понять детальное положение и причину отказа, вам необходимо провести дальнейшие измерения. Это имеет большое значение для поиска и устранения неисправностей, которые определяют объем неисправной цепи и направление проверки.
IV E quivalent S eries R esistanceESR — это сокращение от эквивалентного последовательного сопротивления. Это эквивалентное «последовательное» сопротивление, означающее, что при последовательном подключении двух резисторов это значение будет увеличиваться, а при параллельном подключении — уменьшиться.
Появление ESR привело к отклонению поведения конденсаторов от его первоначального определения. Теоретически идеальный конденсатор сам по себе не вызывает никаких потерь энергии, но, поскольку материал, из которого изготовлен конденсатор, имеет сопротивление, а изоляционная среда имеет потери энергии, конденсатор становится несовершенным. Эти потери выглядят внешне так, как если бы резистор был подключен последовательно с конденсатором, поэтому они называются «эквивалентным последовательным сопротивлением».
Считаем, что резкое изменение напряжения на конденсаторе невозможно.Когда к конденсатору внезапно подается ток, напряжение конденсатора возрастает с 0 из-за его собственной зарядки. Но с ESR сам резистор генерирует падение напряжения, которое вызывает внезапное изменение напряжения на конденсаторе. Несомненно, это снизит фильтрующий эффект конденсатора, поэтому во многих высококачественных источниках питания используются конденсаторы с низким ESR.
Аналогичным образом, в случае колебательных контуров, ESR изменяет функцию контура, вызывая серьезные последствия, такие как отказ контура или даже повреждение.
Таким образом, в большинстве случаев конденсаторы с низким ESR работают лучше, чем конденсаторы с высоким ESR. Но есть исключения, и иногда ESR используется для чего-то полезного.
Например, в цепи стабилизации напряжения, когда нагрузка является переходной, конденсатор с определенным ESR немедленно генерирует колебания и запускает цепь обратной связи. Такой быстрый отклик достигается за счет определенных переходных характеристик. особенно когда скорость отклика силовой лампы низкая, а объем или емкость конденсатора строго ограничены.Такая ситуация наблюдается в некоторых трехконтактных регуляторах напряжения с трубками mos в качестве регуляторов или аналогичными схемами. В это время низкое ESR снизит общую производительность.
На самом деле, существует больше случаев, когда требуется более низкое ESR, а конденсаторы большой емкости с низким ESR относительно дороги. Поэтому во многих импульсных источниках питания принято параллельное соединение. Люди подключают несколько алюминиевых электролитических конденсаторов с относительно высоким ESR параллельно, чтобы сформировать конденсатор с низким ESR. Часто бывает выгодно пожертвовать определенным объемом места на печатной плате в обмен на снижение стоимости устройства.
Другой концепцией, аналогичной ESR, является ESL, что означает эквивалентную последовательную индуктивность. Ранние катаные конденсаторы часто имели очень высокий ESL, и чем больше емкость, тем больше ESL. ESL часто становится частью ESR, а также вызывает сбои некоторых цепей, например, последовательный резонанс. Однако с точки зрения емкости доля ESL слишком мала, и вероятность возникновения проблем очень мала. В дополнение к развитию процесса производства конденсаторов, ESL постепенно игнорируется, и ESR используется в качестве основного эталонного фактора помимо емкости.
Подавление ESL и ESR для конденсаторов
Кстати, емкость также имеет добротность Q, аналогичную индуктивности. Этот коэффициент обратно пропорционален ESR и связан с частотой. Также редко используется.
Отказы цепи, вызванные ESR, часто трудно обнаружить, а влияние ESR легко не заметить в процессе проектирования. Самый простой способ состоит в том, что во время моделирования, если вы не можете выбрать конкретные параметры конденсатора, вы можете попытаться искусственно подключить небольшой резистор последовательно с конденсатором, чтобы имитировать эффект ESR.Как правило, ESR танталовых конденсаторов обычно ниже 100 миллиом, а алюминиевые электролитические конденсаторы выше этого значения, а ESR некоторых типов конденсаторов может достигать даже нескольких Ом.
Типичное соотношение между ESR и частотой для танталовых конденсаторов
Связь между ESR и пульсационным напряжением можно выразить формулой:
V = R (ESR) × I
В этой формуле V равно пульсации напряжения, R — ESR конденсатора, I — ток.

