Ом кануны — Wikipedia

Wikipedia — ирекле энциклопедия проектыннан ([http://tt.wikipedia.org.ttcysuttlart1999.aylandirow.tmf.org.ru/wiki/Ом кануны latin yazuında])

Ом кануны шәкеле Ом кануны график күренештә

Ом кануны (tat.lat. Om qanunı) — физик канун, чыганакның Электр йөртү көче (Электр көчәнеше) Электр агымы һәм Электр каршылыгы арасында бәйләнешен билгели.

Шушы канун Георг Ом тәҗрибәләре нәтиҗәсендә 1826 елда ачылган.

Ом кануны тулы чылбыр өчен:

I=εR+r{\displaystyle I\!={\varepsilon \! \over {R+r}}}, (2)

биредә:

Ом канунының нәтиҗәләре:

• r<<R очракта электр агымы чылбырның каршылыгына кире пропорциональ
• r>>R агым тышкы каршылыгыннан бәйле булмый. Чыганак — электр агымы чыганагы булып исемләнә.

Ом кануны гади күренештә:

U=IR{\displaystyle U\!=IR}

U{\displaystyle U\!} — Электр көчәнеше

Электр йөртү көче йомык бүлемтек өчен:

ε=Ir+IR=U(r)+U(R){\displaystyle {\varepsilon \!}=Ir+IR=U(r)+U(R)}

j=σE{\displaystyle \mathbf {j} =\sigma \mathbf {E} }

биредә:

• j{\displaystyle \mathbf {j} } — электр агымы тыгызлыгы векторы,
• σ{\displaystyle \sigma \!} — электр үткәрүчәнлеге,
• E{\displaystyle \mathbf {E} } — Электр кыры көчәнешлелеге.

U=I⋅Z,{\displaystyle \mathbb {U} =\mathbb {I} \cdot Z,}

биредә:

= U₀eiωt — электр көчәнеше яки потенциаллар аермасы,

• I — электр агымы,
• Z

= Re⁻iδ — комплекс каршылык (импеданс),

= (R_a

² + R_r²)^1/2 — тулы каршылык,

= ωL − 1/(ωC) — реактив каршылык (индуктив һәм сыешлыклы каршылыклар аермасы),

• R_а — актив (омлы) каршылык, ешлыктан бәйле булмый,
• δ

= − arctg (R_r/R_a) — көчәнеш һәм агым фазалары аермасы.

Зурлыклар:

U=U0sin⁡(ωt+φ){\displaystyle U=U_{0}\sin(\omega t+\varphi )}

U=U0ei(ωt+φ),{\displaystyle \mathbb {U} =U_{0}e^{i(\omega t+\varphi )},} : Im⁡U=U.{\displaystyle \operatorname {Im} \mathbb {U} =U.}

Классик Друде теориясе буенча:

j→=n⋅e02⋅τm⋅E→=σ⋅E→{\displaystyle {\vec {j}}={\frac {n\cdot e_{0}^{2}\cdot \tau }{m}}\cdot {\vec {E}}=\sigma \cdot {\vec {E}}}

биредә:

tt.wikipedia.org

Закон Ома — Вікіпедія

Зако́н О́ма — це твердження про пропорційність сили струму в провіднику прикладеній напрузі.

Закон Ома справедливий для металів і напівпровідників при не надто великих прикладених напругах. Якщо для елемента електричного кола справедливий закон Ома, то говорять, що цей елемент має лінійну вольт-амперну характеристику.

Фізична природа закону[ред. | ред. код]

Закон Ома справедливий для провідників, виготовлених із матеріалів, у яких є вільні носії заряду: електрони провідності, дірки або іони. Якщо до таких провідників прикласти напругу, то в провідниках виникає електричне поле, що змушуватиме носії заряду рухатися. Під час цього руху носії заряду розганяються і збільшують свою кінетичну енергію. Проте зростання енергії носіїв заряду обмежене зіткненнями між собою, зі зміщеними з положень рівноваги, внаслідок теплового руху, атомами матеріалу. Під час таких зіткнень, надлишкова кінетична енергія носіїв струму передається коливанням кристалічної ґратки, та виділяється у вигляді тепла.

В середньому, носії заряду мають швидкість, яка визначається частотою зіткнень. Математичною характеристикою таких зіткнень є час розсіяння і зв’язана із ним довжина вільного пробігу носіїв заряду. Обчислення показують, що середня швидкість носіїв заряду пропорційна прикладеному електричному полю, а отже й напрузі.

Таким чином, у матеріалах із вільними носіями заряду сила струму пропорційна напруженості електричного поля. Проходження струму крізь матеріал супроводжується виділеннями тепла. Докладніше про це — у статті закон Джоуля-Ленца.

У сильних електричних полях закон Ома часто не справджується навіть для гарних провідників, оскільки фізична картина розсіювання носіїв заряду змінюється. Розігнаний до великої швидкості носій заряду може іонізувати нейтральний атом, породжуючи нові носії заряду, які теж у свою чергу вносять вклад в електричний струм. Електричний струм різко, іноді лавиноподібно, зростає.

У деяких матеріалах за низьких температур процеси розсіювання носіїв заряду гасяться завдяки особливій взаємодії між ними та коливаннями кристалічної ґратки — фононами. В такому разі виникає явище надпровідності.

Математичне формулювання[ред. | ред. код]

В електротехніці прийнято записувати закон Ома в інтегральному вигляді

U=I∗R{\displaystyle U=I*R}

де U — прикладена напруга, I — сила струму, R — електричний опір провідника.

I=U/R U=I×R R=U/I

Проте опір є характеристикою провідника, а не матеріалу, й залежить від довжини та поперечного перерізу провідника. Тому в фізиці застосовують закон Ома у диференціальному вигляді:

j=σ⋅E{\displaystyle \mathbf {j} =\sigma \cdot \mathbf {E} }

де j — густина струму, σ — питома провідність матеріалу, E — напруженість електричного поля.

Питома провідність залежить від кількості вільних носіїв заряду в провіднику і від їхньої рухливості.

Еквівалентність двох форм запису[ред. | ред. код]

Різниця потенціалів (напруга) на кінцях провідника довжиною l{\displaystyle l} з постійною напруженістю електричного поля E{\displaystyle E} дорівнює

U=Δφ=El{\displaystyle U=\Delta \varphi =El}

Якщо провідник має площу перерізу S, то сила струму в ньому зв’язана з густиною сили струму формулою:

I=jS{\displaystyle I=jS}.

Виходячи із закону Ома в формі

j=σE{\displaystyle j=\sigma E}

і, підставляючи значення j=I/S{\displaystyle j=I/S} та E=U/l{\displaystyle E=U/l}, отримуємо рівняння

IS=σUl{\displaystyle {\frac {I}{S}}=\sigma {\frac {U}{l}}},

або

U=lσSI=RI{\displaystyle U={\frac {l}{\sigma S}}I=RI},

де опір R{\displaystyle R} визначається через питому провідність формулою

R=lσS=ρlS{\displaystyle R={\frac {l}{\sigma S}}=\rho {\frac {l}{S}}}.

Тут ρ=1/σ{\displaystyle \rho =1/\sigma } — питомий опір.

У випадку змінного струму закон Ома можна розширити, включивши в розгляд також елементи електричного кола, які характеризуються ємністю й індуктивністю. Змінний струм проходить крізь конденсатор, та випереджає за фазою напругу. В індуктивності змінний струм відстає за фазою від напруги. Проте в обох випадках амплітуда змінного струму пропорційна амплітуді прикладеної змінної напруги. Математично це можна описати, ввівши комплексні опори (імпеданси).

Тоді можна записати

U=I⋅Z{\displaystyle U=I\cdot Z}

де U — амплітуда змінної напруги, I — амплітуда змінного струму, Z — імпеданс.

Закон Ома для повного кола[ред. | ред. код]

В повному колі окрім опору навантаження є ще джерело живлення, яке має власний внутрішній опір. Сила струму в ньому визначається формулою

I=ER+r{\displaystyle I={\frac {\mathcal {E}}{R+r}}}

де E{\displaystyle {\mathcal {E}}} — електрорушійна сила, R{\displaystyle R} — опір навантаження, r{\displaystyle r} — внутрішній опір джерела струму.

Георг Ом проводив дослідження протікання струму в електричному колі на початку XIX століття. На шляху до встановлення закономірності йому довелося подолати чимало перешкод. Для проведення досліджень і встановлення закономірності необхідно було мати вимірювальні прилади, джерела струму із стандартними властивостями, що не змінювалися б з часом, стандартні провідники. Усе це довелося створити або вдосконалити.

Було добре відомо, що магнітна дія струму змінюється при зміні елементів замкнутого кола: джерела електричного струму та провідників, які з’єднують полюси джерела. Чи існує закономірність, яка пов’язує магнітну дію струму з величинами, які характеризують елементи замкнутого кола? Мабуть, таке питання виникало у багатьох дослідників.

Легко уявити обставини, в яких почалися пошуки інтуїтивно відчуваної закономірності. Поняття напруги, спаду напруги, електрорушійної сили ще не були сформульовані. Точаться суперечки щодо механізму дії гальванічних елементів, незрозуміле взаємовідношення електростатичних сил та сил, які виникають при протіканні струму; нарешті невідомо що таке рухома електрика та електрика в спокої. Ом, наприклад, називає в своїх перших працях електричний струм «контактною електрикою».

Ом керувався наступною ідеєю. Якщо над провідником, яким проходить струм, підвісити на пружній нитці магнітну стрілку, то кут повороту стрілки дасть інформацію про струм, точніше про його зміни при варіаціях елементів замкнутого кола. Ом повернувся до ідеї Кулона й сконструював крутильні терези. Магнітна стрілка виявилась точним і чуттєвим гальванометром.

В перших дослідах, результати яких Ом опублікував у 1825 році, спостерігалась «втрата сили» (зменшення кута відхилення стрілки) із збільшенням довжини провідника, підключеного до полюсів вольтового стовпа (поперечний переріз провідника був постійним). Оскільки не було одиниць вимірювання, довелося вибрати еталон — «стандартний дріт». Як залежна змінна фігурувало зменшення сили, що діяла на магнітну стрілку. Досліди виявили закономірне зменшення цієї сили при збільшенні довжини провідника. Функція отримала аналітичний вираз, але Ом не претендував на встановлення закономірності тому, що гальванічний елемент не давав постійної електрорушійної сили (е.р.с.).

Ом ще не розумів значення внутрішнього опору джерела струму. Вольтів стовп, з яким він експериментував, мав внутрішній опір, який значно перевищував зовнішній. Щоб отримати показники, достатні для оцінки відхилення магнітної стрілки «гальванометра», звичайно ж доводилося зводити до мінімуму опір зовнішньої частини кола, який визначався, по суті, коротким відрізком металевого провідника. Зрозуміло, що в такій ситуації точність встановлення залежності сили струму від опору металевих провідників була недостатньою. До того ж внутрішній опір вольтового стовпа був далеко не постійним.

Звичайно ж потрібно дивуватися тому, що закономірність для описаної ситуації була отримана вірно, хоча б у першому наближенні. Проте до встановлення закону було ще далеко.

Успіх наступних експериментів Ома вирішило відкриття термоелектрики. Німецький фізик Томас Йоганн Зеєбек (1770 —†1831) брав участь у великій дискусії між прихильниками хімічної та контактної теорії. Він дотримувався думки Вольта, що е.р.с. виникає при контакті речовини незалежно від наявності хімічного реагенту, та шукав доказів. У 1822 році Зеебек виготовив спіраль з мідної смужки, всередині якої закріпив компас. Це був по-сучасному гальванометр з невеликим внутрішнім опором. Кінці спіралі приєднувались до різних металевих пластинок. Коли було взято бісмутовий диск і покладено на мідний, магнітна стрілка здригнулася. Ефекту не було, якщо диск брали не рукою, а за допомогою предмета, який мав кімнатну температуру.

Врешті-решт Зеебек з’ясував, що ефект пропорційний різниці температур двох контактів.

Одним з найважливіших чинників відкриття було те, що в руках експериментаторів з’явилося джерело, е.р.с. якого можна було плавно регулювати і підтримувати постійною.

Ом використав термопару бісмут-мідь, один спай поміщався в лід, інший — у окріп. Чутливість гальванометра довелося звичайно ж збільшити. Процес вимірів являв собою наступне : 8 експериментальних провідників почергово вмикалися в коло. В кожному випадку фіксувалося відхилення магнітної стрілки. Результат досліду Ом виразив такою формулою:

X=ab+x{\displaystyle X={\frac {a}{b+x}}}, де

• Х — сила магнітної дії провідника,
• а — стала, яка визначала е.р.с. термопари,
• х — довжина провідника.
• b — константа, яка визначала провідність всього кола.

Це був другий крок. Тут ще немає звичних нам понять сили струму, е.р.с., зовнішнього, внутрішнього опору. Вони відграняться поступово.

В наступній праці (1826 рік) Ом вводить поняття «електроскопічної сили», користується поняттям сили струму та записує закон для ділянки кола вже у формі, дуже близькій до сучасної:

X=kwal{\displaystyle X={\frac {kwa}{l}}}, де

• Х — сила струму,
• k — провідність,
• w — поперечний переріз провідника,
• а — електроскопічна сила,
• l — довжина провідника.

Незважаючи на переконливі дані експериментів та чіткі теоретичні основи, закон Ома протягом майже десяти років лишався маловідомим. Достатньо сказати, що Фарадей також не підозрював про існування закону; при описанні дослідів він був змушений звертатися до перечислення даних про елементи кола: кількість пластин в батареях, їхні розміри, склад електроліту, довжина, діаметр та матеріал дроту.

Омові довгий час безуспішно доводилося доводити місцевим вченим, що ним відкрито важливу істину. Ввести закон в фізику виявилося набагато складніше, ніж відкрити. І це закономірно. Фізичне мислення на той час було ще не готовим до сприйняття загальної закономірності (тим більше з рук провінційного вчителя).

Перевірка закону Ома тривала впродовж майже всього XIX століття. В 1876 році спеціальний комітет Британської асоціації провів точну перевірку, вказану Максвеллом. Справедливість закону Ома для рідких провідників було підтверджено Коном, Фітцтжеральдом та Троутоном.

• І.М. Кучерук, І.Т. Горбачук, П.П. Луцик (2006). Загальний курс фізики: Навчальний посібник у 3-х т. Т.2. Електрика і магнетизм. Київ: Техніка. 
• С.Е. Фріш і А.В. Тіморєва (1953). Курс загальної фізики. Том II. Електричні і електромагнітні явища. Київ: Радянська школа. 
• Сивухин Д.В. (1977). Общий курс физики. т III. Электричество. Москва: Наука. 

uk.wikipedia.org

Закон Ома в комплексной форме

Для анализа электрических цепей синусоидального тока удобнее применять закон Ома в комплексной форме. Цепи синусоидального тока – линейные цепи с установившимся режимом работы, когда после окончания в них переходных процессов, падения напряжений на участках, токи в ветвях и ЭДС источников являются синусоидальными функциями времени. В обратном случае закон в такой форме неприменим.

В отличие от обычной формы закона Ома, в комплексной форме напряжение, токи, сопротивления и ЭДС записываются как комплексные числа. Данное нововведение основано на том, что в цепях переменного тока существуют активные и реактивные значения напряжений, токов и сопротивлений, что требует определенных корректив.

Итак, вместо активного сопротивления R, которое используется в основном в цепях постоянного тока, запишем полное (комплексное) сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже становятся комплексными величинами. При практических расчетах удобнее пользоваться действующими значениями. Запишем формулу закона Ома в комплексной форме:

где

• Z – комплексное (полное) сопротивление,
• Y – комплексная (полная) проводимость.

где

• r – активное сопротивление,
• x – реактивное сопротивление,
• z – полное сопротивление,
• g – активная проводимость,
• b – реактивная проводимость,
• y – полная проводимость,
• j – комплексная единица, j=√(-1).

Решение задач

По заданной схеме определить полное сопротивление цепи, токи (I_1 ) ̇, (I_2 ) ̇, (I_3 ) ̇. U = 120 В, xC1 = 100 Ом, xL2 = 50 Ом, xC3 = 50 Ом, r1 = 25 Ом, r2 = 20 Ом.

Дано:	Решение:
U = 120 В xC1 = 100 Ом xL2 = 50 Ом xC3 = 50 Ом r1 = 25 Ом r2 = 20 Ом Z – ? I_1 – ? I_2 – ? I_3 – ?	Запишем формулу закона Ома в комплексной форме: — Найдем полное сопротивление цепи по формуле: Примем начальную фазу напряжения за нуль, тогда: По следствию из закона Ома ток распределяется обратно пропорционально сопротивлению ветвей, а значит

zakon-oma.ru

Закон на Ом – Уикипедия

Серия статии на тема Класическа електродинамика

Електричество Магнетизъм Електромагнетизъм Електродинамика Известни учени

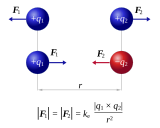
Законът на Ом е физичен закон, определящ зависимостта между напрежението, тока и съпротивлението на проводника в електрическа верига. Наречен е в чест на неговия откривател Георг Ом. Същността на закона е проста: създаваният от напрежението ток е обратно пропорционален на съпротивлението, което той трябва да преодолява, и е право пропорционален на пораждащото го напрежение.

Трябва също да се има предвид, че законът на Ом е фундаментален и може да се прилага към всяка физична система, в която действат някакви потоци енергия, преодоляващи съпротивление. Законът може да се прилага за изчисление на хидравлични, пневматични, магнитни, електрически, светлинни, топлинни потоци и т.н. (същото се отнася и за законите на Кирхоф), обаче такова приложение на тези закони става крайно рядко, само в рамките на тясно специализирани курсове.

Георг Симон Ом, провеждайки експерименти с различни проводници, установил, че силата на тока I{\displaystyle I} в даден проводник е пропорционална на напрежението U{\displaystyle U}, приложено към краищата му:

I=G⋅U{\displaystyle I=G\cdot U}

Коефициентът на пропорционалност G{\displaystyle G} се нарича електропроводимост, а величината R=1/G{\displaystyle R=1/G} е прието да се нарича електрическо съпротивление на проводника.

Законът на Ом за част от електрическата верига има вида:

• I=UR{\displaystyle \textstyle I={\frac {U}{R}}}, или
• U=R⋅I{\displaystyle \textstyle U=R\cdot I}, или

• R=UI{\displaystyle \textstyle R={\frac {U}{I}}},

където:

• U{\displaystyle \scriptstyle U} е напрежението или разликата между потенциалите,
• I{\displaystyle \scriptstyle I} е силата на тока,
• R{\displaystyle \scriptstyle R} е съпротивлението.

Законът на Ом се прилага също и към цялата верига, но в малко видоизменена форма:

I=ER+r{\displaystyle I={E \over {R+r}}},

където:

За по-лесно запомняне (в училище) законът на Ом се изобразява и като равностранен триъгълник с пресечна хоризонтална линия, под която има вертикална линия в средата. В горния малък триъгълник е U, под него са I и R. Лесно се помни и изглежда ето така:

U=I⋅R{\displaystyle \scriptstyle U=I\cdot R}, I=UR{\displaystyle \scriptstyle I={\frac {U}{R}}}, R=UI{\displaystyle \scriptstyle R={\frac {U}{I}}}.

                                  /\
                                 /  \
                                / U  \
                               /——————\
                              / I | R  \
                              ——————————

Съпротивлението R зависи както от материала на проводника, по който тече токът, така и от геометричните размери на проводника.

Полезно е да се запише законът на Ом в диференциална форма, при която зависимостта от геометричните размери изчезва и тогава законът на Ом описва само електропроводните свойства на материала. За изотропни материали:

j=σ⋅E{\displaystyle \mathbf {j} =\sigma \cdot \mathbf {E} },

където:

Всички величини, влизащи в това уравнение, са функции на координатите и в общия случай на времето. Ако материалът е анизотропен, то посоките на векторите на плътността на тока и на интензитета могат да не съвпадат. В този случай относителната проводимост е тензор от ранг (1, 1).

Разделът от физиката, изучаващ протичането на електрически ток в различни среди, се нарича електродинамика на непрекъснатите среди.

Ако веригата съдържа не само активни, но и реактивни елементи (капацитети, индуктивности), а токът е синусоидален с кръгова (ъглова) честота ω, то законът на Ом се обобщава, а участващите в него величини стават комплексни:

U˙=Z⋅I˙{\displaystyle {\dot {U}}=Z\cdot {\dot {I}}},

където:

• U˙=U⋅ejψu{\displaystyle \textstyle {\dot {U}}=U\cdot e^{j\psi _{u}}}

е комплексната ефективна стойност на напрежението; ψu{\displaystyle \textstyle \psi _{u}} е началната фаза на напрежението,

• I˙=I⋅ejψi{\displaystyle \textstyle {\dot {I}}=I\cdot e^{j\psi _{i}}}

е комплексната ефективна стойност на тока; ψi{\displaystyle \textstyle \psi _{i}} е началната фаза на тока,

• Z=z⋅ejφ{\displaystyle \textstyle Z=z\cdot e^{j\varphi }}

е комплексното пълно съпротивление (комплексният импеданс),

• z=R2+X2{\displaystyle \textstyle z={\sqrt {R^{2}+X^{2}}}}

е пълното съпротивление (импеданс),

Ако токът е периодична функция на времето, но не е синусоидален, то той може да представи като сума от синусоидални съставящи (хармонични) с честоти kω{\displaystyle \scriptstyle k\omega }, (k=1…∞{\displaystyle \scriptstyle k=1\ldots \infty }) чрез разлагане в ред на Фурие. За линейни вериги може да се счита, че тези съставящи от разлагането на тока в ред на Фурие действат независимо една от друга.

Трябва да се отбележи също, че законът на Ом във вида, представен по-горе, е в сила за линейни електрически вериги, т.е. такива вериги, в които параметрите R{\displaystyle \scriptstyle R}, L{\displaystyle \scriptstyle L} и C{\displaystyle \scriptstyle C} са константни величини, независещи от напрежението, тока и честотата. В практиката това означава, че законът на Ом важи в определени граници на изменение на честотата, напрежението или тока.

За описване на по-сложни (нелинейни) системи, когато не може да се пренебрегне зависимостта на съпротивлението от силата на тока, е прието да се разглежда тяхната волт-амперна характеристика. Отклонения от закона на Ом се наблюдават също и в случаите, когато скоростта на изменение на електрическото поле е толкова голяма, че не може да се пренебрегне инерционността на носителите на заряда.

• Фархи, С.Л., С.П.Папазов. Теоретична електротехника ч. I, София, 1999, Техника.
• Simonyi, K. Theoretische Elektrotechnik, Berlin, 1956, Deutscher Verlag der Wissenschaften.
• Нейман, Л. Р., К. С. Демирчян, Теоретические основы электротехники т. I, т. II, Ленинград, 1981, Энергоиздат.

bg.wikipedia.org

Георг Симон Ом биография, история жизни

Георг Симон Ом – немецкий учёный, известный всему миру своими научными достижениями в области физики. 16 марта 1787 года в городе Эрлаген немецкого королевства Бавария родился мальчик, которому суждено было стать одним из умнейших людей на нашей планете. Назвали младенца Георг Симон. Георг Симон Ом – немецкий учёный, известный всему миру своими научными достижениями в области физики.

Под родительским крылом

16 марта 1787 года в городе Эрлаген немецкого королевства Бавария родился мальчик, которому суждено было стать одним из умнейших людей на нашей планете. Назвали младенца Георг Симон.

История семьи

Георг Ом вырос в бедной семье. Отец физика Иоганн Вольфган Ом был родом из семьи слесаря, и всю жизнь продолжал заниматься потомственной профессией. Отец Георга не хотел быть безграмотным невежей, тяга к знаниям заставляла его заниматься по учебникам самостоятельно. Иоганн много читал, скрупулёзно изучал точные науки. Находясь в Берлине, занимался изучением технического рисования в специализированной школе. Благодаря тонкому уму, Иоганн Вольфган понимал, что заниматься собственным делом намного выгоднее, чем работать наёмным рабочим. Возвратившись в родной Эрлаген, он начал добиваться от властей разрешения работать самостоятельно. Его усилия были не напрасны, и в 1785 года отец Георга получил долгожданный патент. Не прошло и года, как Иоганн повстречал свою будущую жену, Марию Елизавету. Она была родом из семьи кузнеца Беккина. За совместную жизнь, Мария родила мужу 7 детей, четверо из которых умерло. Георг Ом трепетно любил свою мать, до конца дней своих считал её самой лучшей и нежной. Она умерла при родах, когда мальчику было всего 10 лет. У Георга остались ещё младшие брат и сестра.

Ранние годы

С раннего детства отец Георга прививал всем своим детям любовь к знаниям. Смерть жены не сломила его, оставшись с маленькими детьми на руках, он много работал. Днём и ночью Иоганн выполнял слесарные и кузнечные заказы, но всё свободное время посвящал обучению своих детей. Начинали своё обучение братья Георг и Мартин в довольно скромной школе, основателем и единственным учителем в ней был в прошлом представителем чулочной профессии. Чулочник не был профессиональным педагогом, его познания заключались в знании латыни и греческого языка. Природный талант педагога помог вложить в Георга достойные знания для дальнейшего обучения мальчика в эрлагенской гимназии. Иоганн Вольфган Ом математике и физике обучал сыновей самостоятельно. Он постоянно покупал новые книги, не жалея денег на образование детей. Георг рос очень способным мальчиком, преуспевал в различных направлениях. Хорошо изучив латынь, Георг перевёл учение Леонарда Эйлера «Интегральное исчисление» на немецкий язык. Отец со слов старшего сына записал его перевод с целью дальнейшего детального изучения трудов автора. Все эти старания приобщить детей к знаниям не пропали даром: оба мальчика приобрели статус профессора. Георг стал знаменитым физиком, а Мартин преуспевал в математике.

Отрочество

В 1798 году Георг Симон Ом начинает своё обучение в гимназии родного города. Продолжительность пребывания в учебном заведении составила 4 года, за которые, по мнению самого будущего учёного, он не узнал ничего нового. Тем временем отец Георга привлекал к дальнейшему развитию своих детей друзей, которые занимались профессорской деятельностью. Учёные с удовольствием просвещали способных братьев, восхищаясь их одарённостью. По достижению Георгом пятнадцатилетнего возраста, знаменитый профессор К. Е. Лангсдорф принимал у него экзамен по математике. Проверка знаний длилась в течение пяти часов, и Георг Ом выдержал её на отлично. Профессор задавал вопросы по пяти разделам математики, пятнадцатилетний юноша, не задумываясь, правильно отвечал на любые вопросы. Экзаменатор по достоинству оценил живой ум Георга и его брата, предрекая им блистательное будущее.

Студенческие годы

В 1805 году Георг Симон Ом успешно поступает в университет в родном городе. Блистательная подготовка позволила будущему учёному не прилагать никаких усилий при обучении в университете. Никакого дальнейшего развития в области физики мальчиком не наблюдалось, и у Георга появилось новое увлечение – спорт. Талантливый человек талантлив во всём. Он стал одним из лучших игроков в бильярд в университете, всерьёз занялся конькобежным спортом. Все эти увлечения отвлекали Георга от изучения точных наук, что вызывало у отца большое недовольство. Иоганн Ом всеми силами старался вернуть сына в нужное русло. На фоне этих событий у них случился первый и последний в их жизни разлад. Денег в семье всё чаще не хватало. На фоне всех этих событий Георг Ом принял решение покинуть университет и заняться преподавательской деятельностью в частной школе. Пройдя полтора года обучения, юноша покидает его.

Преподавательская деятельность

Частная школа, в которой юный Ом стал учителем математики, находилась в Швейцарии. Маленький городок Готтштадт встретил тёплым гостеприимством молодого педагога. Школа располагалась в большом старинном замке, единственной достопримечательности крошечного швейцарского городка. Очаровательная Швейцария, хорошая работа, достойная заработная плата – всё это безгранично радовало Георга. Он писал множество восторженных писем отцу, с надеждой получить его прощение и понимание. Иоганн не только не писал старшему сыну, но отказывался читать его письма. В душе отца Георга была пустота, он решил, что сын загубил свой талант, бросив учёбу. Время шло, и отец с сыном снова нашли взаимопонимание. Однообразная деятельность Георга в Готтштадте постепенно переставала радовать юношу, его живой ум тосковал по новым знаниям. В письмах на родину всё чаще стала проскальзывать нотка тоски по дому и обучению в университете.

Перемены

Вскоре Георгу пришлось покинуть место работы по причине приезда сына хозяина частной школы. Он был математиком, и занял преподавательское место Георга. Отправившись в другую школу, Георг Ом стал с жадностью изучать сложнейшие математические труды знаменитых учёных. Самообразованием Георг занялся по настоятельной рекомендации известного профессора К. Е. Лангсдорфа, который продолжал интересоваться судьбой юного дарования.

Возвращение на родину

Трудолюбие и самоотверженность в самообразовании дали положительные результаты. 1811 год становится очень плодотворным в жизни юноши. В этом году Георг Симон Ом возвращается в родной город. Проходит полное обучение в университете за год, после окончания курса обучения защищает диссертацию, становится профессором философии. После получения докторской степени, Ому предложено место доцента кафедры математики в Эрлагенском университете. Недолго пришлось занимать место доцента учёному, спустя полтора года он был вынужден искать другую работу из-за плачевного материального состояния.

Скитания

После долгих поисков в 1813 году Ом занял преподавательское место в школе города Бамберг. Ознакомившись с методическим образовательным процессом, Георга возмутился невежественностью системы преподавания. Педагог с учёной степенью не мог молчать, направив в Генеральный комиссариат письменное обращение с протестом. В результате школу в Бамберге расформировали, и Ом продолжил преподавательскую деятельность в местной подготовительной школе, условия преподавания и проживания в которой отличались в худшую сторону. Учёный Ом продолжал отстаивать свою точку зрения, разработав собственную методику обучения детей. Без устали, он продолжал посылать письма со своими трудами в школы и университеты, пытаясь добиться поддержки. К огромному сожалению, все старания были безрезультатны. В 1817 году в свет выходит большая заметка Ома, описывающая новую методику преподавания. Соображения Георга не были оценены по достоинству, наоборот, вызвали бурю негодования и протестов со стороны коллег. Небольшое количество сторонников молодого учёного поддерживали его взгляды. Знаменитому физику было уже 37 лет, когда его пригласили работать учителем физики и математики в город Кельн.

Годы достижений

В Кельне физика встретили с особой доброжелательностью. В его распоряжение были предоставлены все средства для научных разработок. Преподавательский график работы был построен так, чтобы учёный имел свободное время для научных достижений. Георг погружается в детальное изучение физики, отстранившись от математики. Прилежное трудолюбие и скрупулёзность обеспечивают успех в начинаниях. Знаменитый физик начинает заниматься своими первыми разработками по теме электрического тока и проводников. Тщательное изучение темы, частые эксперименты с детальным изучением результатов, тонкие мыслительные процессы, смелые предположения привели к революционным открытиям в области физики. В 1826 году выходит сенсационная научная статья физика Ома с описанием закона о проводимости металлами электрического тока. Опубликовал научную статью с результатами «Журнал физики и химии».

Научная деятельность

В первое время научные труды Ома не были оценены по достоинству, но этот факт совсем не огорчал Ома. В 1826 году учёный подаёт прошение о предоставлении ему отпуска на год с освобождением от профессиональной деятельности. После одобрения прошения, он отдаёт все силы для ведения научной деятельности. Георг переезжает к своему брату Мартину для дальнейшей работы над исследовательской работой в области электрических цепей. Уже через год, в 1827 году, в свет выходит научный труд Ома, размещённый на 245 страницах об исследовании электрических цепей.

Отзывы коллег

Уникальное научное учение с разработками и доказательствами вызвали чувство недовольства и протеста у физиков-современников Ома. Они не только всячески поносили его работы, но и старались помешать ему в его открытиях. Только знаменитый Фарадей выразил своё сожаление, что не имеет возможности детально изучить научные труды Ома из-за недостатка знаний в немецком языке. Непризнанного гения не останавливает осуждающие отзывы коллег, он продолжает продуктивно работать над новыми научными открытиями. Год за годом выдающийся учёный продолжает работать на благо науки, выходят публикации новых его работ. Признание учёного проходило постепенно, через 2 десятилетия учёного признали и на родине. В 1842 году Георгу Ому вручили высшую награду — золотую медаль Лондонского Королевского общества за научные достижения. 1845 год стал знаменателен назначением учёного членом Баварской АН. В 1849 году Ом был приглашён на должность экстраординарного профессора в Мюнхен. Там он плодотворно трудится и работает, следуя своим научным убеждениям.

Последние годы жизни

В 1852 году гениальный учёного назначают на должность ординарного профессора, он продолжает преподавать физику. В 1854 году у Ома ухудшается здоровье в связи с заболеванием сердца. Он больше не в силах читать лекции. 28 июня 1854 года король освободил Ома от лекций, а 10 июля знаменитого физика не станет в живых. Легендарный Георг Симон Ом увековечил память о себе в своих научных открытиях и акустических исследований в области физики. Любой современный ученик знает его имя из школьной программы, изучив закон об электрических цепях (закон Ома), в честь Георга названа единица сопротивления. Мемориал Славы в Мюнхене украшает бюст знаменитого физика, а один из университетов в Нюрнберге носит его имя, даже кратер на Луне назван нашими современниками в его честь. Биография Георга Ома является показательным примером самоотверженного посвящения себя науке.

Интересные факты из жизни

• 1789

  Родился Георг Симон Ом

• 1805

  Георг Ом поступил в Университет Эрлангена

• 1811

  Получил степень доктора философии в Университет Эрлангена

• 1812

  Королевским решением назначен учителем математики и физики школы в Бамберге.

• 1817

  Печатная публикация: «Наиболее оптимальный вариант преподавания геометрии в подготовительных классах»

• 1825

  Публикация статьи: «Предварительное сообщение о законе, по которому металлы проводят контактное электричество».

• 1826

  Написана статья в Журнале физики и химии: «Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата и мультипликатора Швейггера».

• 1827

  Публикация статьи: «Предварительное сообщение о законе, по которому металлы проводят контактное электричество».

• 1829

  Статья в Журнале физики и химии: «Экспериментальное исследование работы электромагнитного мультипликатора».

• 1830

  Исследование Ома: «Попытка создания приближенной теории униполярной проводимости».

• 1839

  Cформулирован акустический закон Ома

• 1842

  Лондонское Королевское общество наградило Ома золотой медалью и избрало своим членом.

• 1852

  Получил должность ординарного профессора.

• 1853

  Награжден орденом Максимилиана «за выдающиеся достижения в области науки»

• 1854

  6 июля Георг Ом ушел из жизни.

• 1881

zakon-oma.ru

Термодинамика — Википедия

Термодина́мика (юн. θέρμη — «гармӣ», δύναμις — «неру») — илмест дар бораи умумитарин хусусиятҳои системаҳои макроскопие, ки дар ҳолати мувозинати термодаиамикӣ мебошанд. Термодинамика равандҳои табдилиеро низ меомӯзад, ки байни ҳолатҳои мувозинати термодинамикӣ ба вуҷуд меоянд.

Дар нимаи дуюми асри 19 дар натиҷаи ташаккули назарияи мошинҳои ҳароратӣ (С. Карло) ва кашфи бақои энергия (10. Р. Майер, Ч. Ҷоул,Г. Гелмголц) ба пайдоиши термодинамика замина пайдо шуд. Дар инкишофи термодинамика Р. Клауаиус ва У. Томсол (шарҳи рукни дуюми термодинамика), Ҷ. Гиббс (усули потенциалҳои термодинамикӣ), В. Нернст (рукни сеюмн термодинамика) ва дигарон саҳми калон гузоштаанд.

Термодинамикаи физикӣ ё умумӣ, термодинамикаи химиявӣ (қонунҳои термодинамикаро ба процессҳои хммиявӣ ва физикию химиявӣ татбиқ мекунад), термодинамикаи техникӣ ва термодинамикаи процессҳои барнагарданда мавҷуданд.

Рукнҳои термодинамика[вироиш]

Термодинамика аз рукн (принцип) ҳои умдае иборат аст, ки дар натиҷаи ҷамъбасти мушоҳидаҳои зиёд ба даст омада, ба табиати конкретии ҷисмҳои системаро ташкилдиҳанда вобаста нестанд. Исботи қонунҳои термодинамика ва робитаи онҳо ба қонунҳои ҳаракати зарраҳое, ки ҷисмро ташкил медиҳанд, мавзӯи тадқиқоти физикаи статистикӣ мебошад.

Рукни якуми термодинамика[вироиш]

Рукни якуми термодинамика ифодаи қонуни бақои энергия барои системаҳое мебошад, ки дар онҳо процессҳои ҳароратӣ мавқеи муҳим доралд. Рукни якуми термодинамикаро олими немис Ю. Р. Майер таъриф додааст ва баъдтар Г. Гелмголц (1847) дар шакли мукаммали физикӣ баён кардааст. Бино ба рукни якуми термодинамика, системаи аз ҳисоби энергияи дохилии худ ё аз ҳисоби энергияи ягон манбаи беруна кор карда метавонад. Агар системаи териодинамикӣ миқдори муайяни гармӣ (Q) гирад, энергияи дохилии он қадре тағйир меёбад ва система кореро (А) ба ҷо меорад: (Q= u +А. Ин баробарӣ чӣ қадар тағйир ёфтани энергияи дохилии системаро нишон медиҳад. Ҳамин тариқ, u афзоиши бузургии u-ро мемонад, ки дар ҳар як ҳолат ба қимати муайян соҳиб аст, ё чӣ тавре ки мегӯянд, функцияи ҳолати система мебошад. Рукни якуми Термодинамика мавҷудиятиа муҳаррики абадии ҷинси аввалро инкор мекунад.

Рукни дуюми термодинамика[вироиш]

Рукни дуюми термодинамикаро физики немис Клаузиус (1850) чунин таъриф додааст: гармӣ худ аз худ аз системаи ҳарораташ паст ба системаи ҳарораташ баланд гузашта наметавонад. Ин қонун аз ҷиҳати математикӣ ба воситаи функцияи махсус — энтропия ифода меёбад Энтропия ҳолати ҳар як системаро муайян мекунад. Масалан, энтропия барои системаи якҷинса функцияи ду параметри мустақилест (фишор Р ва ҳарорат Термодинамика ё ҳарорат Термодинамика ва ҳаҷм V), ки ҳолати системаро муайян мекунанд. Энтропия ҳам монанди энергияи дохилӣ ба ҳолати система вобастабуда, пайваста ба ҳар як ҳолати система тағйир меёбад. Мувофиқи рукни дуюми Термодинамика, ягон мошин гармии қабулкардаашро пурра ба кор табдил дода наметавонад. Қисми муайяни гармӣ дар сардовак (хунуккунак) мемонад. Ин процесс ба воситаи теоремаи Карно аниқтар шарҳ ёфтааст. Мувофиқи теоремаи Карно ҳар як мошини ҳароратӣ аз цикли баргардандаи Карно зиёд буда наметавонад.

Рукни сеюми термодинамика[вироиш]

Рукни сеюми термодинамика қимати мутлақи энтропияро муайян мекунад. Онро инчунин қонуни ҳарорати Нернст меноманд.

Бино ба ин қонун, энтропияи осистемаи ихтиёрӣ 5 дар ҳарорат (S)-и дилхоҳӣ ба сифри мутлақ майлкунанда ба қимати ҳудудии соҳиб мегардад, ки он ба фишор ва зичӣ вобаста нест. Соли 1911 М. Планк рукни союми термодинамикаро ба таври зерин шарҳ дод: ҳангоми ба сифр майл кардани ҳарорати мутлақ энтропияи система ҳам ба сифр майл мекунад, яъне lim S = 0 аст. T – 0

• Адабиёт: Зомммерфелд А., Термодинамика и статистическая физика, Москва, 1955;
• Кубо Р., Термодинамика, Перевод с англ,, Москва, 1970.

Мақола дар асоси маводи Энсиклопедияи Советии Тоҷик навишта шудааст.

tg.wikipedia.org

Разрядлар неча хил булади?

Кафедра мудири: И.М.Коканбаев.

Тузувчи: Мелибоев М.

Разрядлар неча хил булади?	4	2	3	1
Куйидаги таърифлардан кайси бири Ленц коидасини ифодалайди?	Индукцион ток узини хосил килган магнит майдонига хамма вакт тескари таъсир килади	Индукцион ток магнит майдонига таъсир килмайди	Электр токи узини хосил килган магнит майдонига хама вакт реактив таъсир килади	Электр токи магнит майдонига таъсир килмайди
Ионланиш даражаси деб нимага айтилади?	Умумий атомлар сонини ионланган атомлар сонига нисбатига айтилади	Умумий атомлар сонини ионланмаган атомлар сонига нисбатига айтилади	Ионланган атомлар сонини ионланмаган атомлар сонига нисбатига айтилади	Ионланган атомлар сонини умумий атомлар сонига нисбатига айтилади
Электролиз деб нимага айтилади?	Электр майдон таъсирида электролитлардаги ионларни электродлардан ажралиш ходисаси.	Металл коришмаларини парчаланишига айтилади	Газларни ионланиш даражасига айтилади	Бир вактнинг узида молекулаларнинг электрон кобигидан бир ёки бир нечта электрон ажралиб чикишига айтилади.
Фарадейнинг 2-конуни ифодасини курсатинг
Фарадейнинг 1-конуни ифодасини курсатинг
Куйидагилардан кайси бири электролит учун Ом конуни хисобланади?
Электр майдон кучланганлиги формуласини топинг.
Тула кучланганлик окими формуласини курсатинг
Мухит учун Остраградский –Гаусс формуласини топинг
Суперпозиция принципини топинг.
Кулон конуни ифодасини топинг
Заряднинг сакланиш конуни кайси жавобда тугри берилган	Яккаланган системадаги зарядлар микдори вакт утиши билан узгармайди.	Нечта мусбат заряд ортса манфий заряд шунча камаяди.	Системадаги зарядлар микдори вакт утиши билан узгаради.	Нечта мусбат заряд ортса манфий заряд шунча ортади.
Конденсаторнинг параллел ва кетма –кет улаш кайси жавобда тугри берилган	;		;
Харакатланаётган заряд хосил килган магнит майдони индукциясини топинг.
Бир жинсли изотроп мухитда магнит ндукцияси билан магнит майдон кучланганлиги орасидаги богликлик кайси бирида тугри берилган
Электромагнит тулкинлар вакумдаги тезлиги нечага тенг?
Электромагнит тулкинлари кандай тулкинлардан иборат?	Кундаланг тулкинлардан	Буйлама тулкинлардан	Айланма тўлқинлардан	Сферик тўлқинлардан
Электромагнит тулкин узунлиги формуласини курсатинг
Куйидаги формулалардан кайси бири сигим каршилигини ифодалайди
Индуктив каршилик кайси жавобда тугри берилган?
Нуқтавий заряд электр майдон кучланганлиги формуласини кўрсатинг.
Потенциал билан кучланганлик орасидаги богланишни топинг
Электр майдон потенциали ифодасини топинг.
Токнинг йўналиши билан электронлар-нинг ҳаракат йўналиши қандай	Бир хил	қарама-қарши	перпендикуляр	Оғма
Куйилагилардан кайси бирида Кирхгофнинг биринчи конуни тугри ёзилган
Куйидагилардан Кирхгфнинг иккинчи конуни ифодасини топинг
R радиусли берк контур марказида магнит майдон индукция формуласи кайси?
Магнит майдонида бажарилган иш ифодаси?
Био –Савар –Лаплас конунининг формуласи кайси жавобда тугри берилган
Соленоид марказидаги магнит майдон индукцияси векторини топинг
Мажбурий тебранишнинг диффиренциал тенгламасини топинг.
Чикиш иши нималарда улчанади?	Амперметр	Милливольтметр	Электронвольтларда	Амперда
Чикиш иши кайси формула билан хисобланади
Электр диполи моменти формуласи кайси?
Конденсатор сигимини 2 марта ошириш учун унинг масофасини неча марта кичик килиш керак?	4	5	7	2
Индуктив галтак энергиясини 4 марта ошириш учун ундан утаётган ток неча марта катта булиши керак?	4	2	3	5
Магнит момент формуласи кўрсатинг?
Ом конунининг диффиренциал формуласи?
Якка заряд потенциал формуласи
Электр диполь моменти бирлиги нимада ўлчанади?
Заряд чизиқли зичлиги формуласини кўрсатинг.
Электр генератори қандай асбоб?	Электр энергиясини механик энергияга айлантирувчи қурилма.	Иссиқлик энергиясини доимий токка айлантирувчи қурилма.	Магнит майдон энергиясини электр энергиясига айлантирувчи қурилма	Механик энергияни электр энергияга айлантирувчи қурилма.
Заряд сирт зичлиги формуласи қайси.
Заряд ҳажм зичлиги формуласи қайси.
Электр заряди нима.	Электр майдонини ҳосил қилувчи манба.	Электр	Суюқ модда	Газсимон оқувчи материя
Магнит майдон хоссаси қандай	Уюрмавий	Потенциал	Суюқ	Қаттиқ
Электр майдон хоссаси қандай.	Уюрмавий	Потенциал	Суюқ	Қаттиқ
Шарнинг электр сиғими ифодасини топинг.
Ток утаётган берк ясси контурнинг магнит моментини топинг.
Кайси каторда Ампер конуни тугри курсатилган?
Электр майдон энергия зичлигини топинг.
Магнит майдон энергияси зичлигини топинг.
Тулкиндаги тула энергия зичлигини топинг.
Тула каршилик ифодаси тугри берилган жавобни топинг.
Трансформатор кандай асбоб?	Кучланишни ўзгартиради.	Токни ўзгартиради.	Ўзгармас токни ўзгартиради.	Ўзиндукция ходисаси асосида ўзгарувчан ток кучланиш ва кучини ўзгартириб бера оладиган қурилмага айтилади.
Магнит диполь неча қутбдан иборат.	5	4	3	2
Электр диполь неча қутбдан иборат.	5	4	2	1
Конденсатор электр майдонини …..	жамлайди	сочади	айлантиради	йўқотади
Куйидагилардан Жоуль –Ленц конуни ифодасини топинг.
Индуктив ғалтак магнит майдон энергиясини…….	Ютади	Тўплайди	Сочади	йўқотади
Қаршилик электр энергиясини	Сочади	Йиғади	Тўхтатади	Қотиради
Зарядларнинг неча тури бор.	Жуда кўп	3 та	7 та	2 та
Берк контурда бажарилган иш ифодаси кўрсатинг?
Амперметр ичида гальванометр ва шунт қандай уланади.	Параллел	Кетма – кет	Комбинатцион	Уланмаган
Тебраниш контури нимадан иборат	Сиғимдан	Индуктивлик	Қаршилик	Сиғим ва индуктивлик
Қаршилик бирлиги қайси бирликда ўлчанади?	Генри	Люкс	Ферми	Ом
Томсон формуласини ёзинг.
Термоэлектрон эмиссия ходисаси кандай ходиса?	Иссиклик остида металлардан электрон чикиши	Электр токини узидан яхши утказиш	Зарядланган зарраларнинг тартибла харакати	Иссиқлик остида ёруғлик чиқади
Ферромагнит моддалар учун магнит киритувчанлик кайси жавобда тугри берилган.
Кандай усул билан жисмларни электрлаш мумкин?	ишкалаш	тезланиш	таъсир	таъсир,ишкалаш,теккизиш
Заряднинг сакланиш формуласи кайси жавобда тўгри кўрсатилган?	Заряд сакланади
Индуктивлик бирлигини кўрсатинг.	Ом	Генри	Ампер	Сименс
Ярим ўтказгичларда қаршиликнинг термик коэфициянтини ишораси қандай бўлади.	Мусбат	Манфий	Ўзгариб туради	Ишорага эга эмас
Каршиликлар кетма –кет уланганда умумий каршилик нимага тенг?	айрим каршиликлар йигиндисига	хамма каршиликлар бир хил	айрим каршиликлар айирмасига тенг	токкучларининг йигиндисига тенг
Лоренц кучи кайси формулада ифодаланади?
Магнит майдон индукция бирлиги.	Тесла	Сименс	Ом	Генри
Электр сиғими қандай бирликда ўлчанади?	Ом	Фарада	Сименс	Генри
Куйидагилардан кайси бири сигим каршиликни ифодалайди?			R
Ясси конденсатор энергияси ифодасини топинг.
Электр майдони энергия зичлиги қандай бирликда ўлчанади.
Каршиликни хароратга богликлиги ифодаси?)
Суперпозиция принципи деб нимага айтилади?	Электр майдоннинг ихтиёрий бир нуктасида мусбат заряд барлигига тугри келган куч микдори.	Токнинг тармокланиш нуктасидаги ток кучларининг алгебраик йигиндиси	Яккаланган системадаги зарядлар микдори вакт утиши билан узгармаслиги	Натижавий кучлнганлик векторининг ташкил этувчи кучланганлик векторларининг геометрик йигиндисига тенг булиши
Электролит нима?	узидан электр токини утказувчи эритмалар.	узидан электр токини утазувчи газлар	электр майдон кучларганлиги бир бирликка тенг булгандаги токнинг тезлиги	электр токини утказмайдиган металлар
Термоэлектрон эмиссия сузининг маъноси?	Кириш	Бериш	Иссиклик остида чикиш	Олиш
Узиндукция ЭЮК ифодасини топинг
Актив қаршилик қандай бирликда ўлчанади.	Генри	Ом	Сименс	Ампер
Электр токини фойдали иш коэффициентини ифодасини кўрсатинг.
Вакуум деб нимага айтилади?	Газ мавжуд фазо	Вакуум мавжуд эмас	Суюқлик мавжуд бўлган фазо.	модда заррачалари бўлмаган фазо.
Диполь деб нимага айтилади?	Жсмга электр заряд берилганда юза бирлигига тугри келган электр микдори билан улчанадиган катталик	Бир –биридан жуда кичик масофада жойлашган бир хил заряд микдорига эга булган, карама –карши ишорали иккита нуктавий зарядлар системаси	Узунлик бирлигига тугри келган электр заряд микдори билан улчанадиган катталик	Электр майдоннинг ихтиёрий бир нуктасига мусбат заряд бирлигига тугри келган куч микдори билан улчаниб майдонни характерловчи физик катталик
Реактив қувват қандай бирликда ўлчанади?	Ампер.Вольт	Ватт	Ампер	Сименс
Узгарувчан токнинг иши ифодаси?
Электр резонанс ходисаси кандай ходиса?	Тебраниш кортурининг каршилиги катта булиб, электромагнит тебраниш булмасдан, ток жуда тез нолга тенг булиш ходисаси	Хусусий ва мажбурий тебранишлар частотаси тенглашганда ток кучининг ортиш ходисаси	Электр заряди, кучланиш, ток кучи, каршилик, электр ва магнит майдонларининг даврий равишда узгариб туриши	Тебраниш амплитудасининг камайиш тезлиги
Электр занжирда актив қувват бирлиги.	А.В	Ватт	Ампер	Сименс
Нуқтавий заряд 2 марта ошса унинг унинг кучланганлиги неча марта ошади.	2	8	4	16
Нуқтавий зарядлар орасидаги масофа 2 марта ошса ўзаро таъсир кучи қандай ўзгаради.	2 марта ортади	4 марта ортади	2 марта камаяди	4 марта камаяди
Конденсатор кучланиши икки марта ортса унинг энергияси қанчага ошади.	2	4	8	16
Ток иши қайси формулада берилган?
Ток зичлиги формуласини кўрсатинг?
Қаршилик формуласи қайси жавобда тўгри кўрсатилган?

uz.denemetr.com