Физический смысл первого закона кирхгофа: Первый закон Кирхгофа или первое правило Киргофа для расчета цепей постоянного тока

      Комментариев к записи Физический смысл первого закона кирхгофа: Первый закон Кирхгофа или первое правило Киргофа для расчета цепей постоянного тока нет

Содержание

Решение задач и курсовых по электротехнике Физический смысл первого и второго законов Кирхгофа — Сайт Электротехника и электроника на «пять»

Оба закона Кирхгофа формулируются достаточно понятно и имеют простой физический смысл. Первый закон Кирхгофа утверждает, что если рассматривать любой узел цепи (то есть место разветвления, где сходятся три или более проводника), то сумма поступающих в цепь электротоков будет равна сумме исходящих, что, в принципе, является следствием закона сохранения электрического заряда. Например, если у вас Т-образный узел электрической цепи и по двум проводам к нему подходят электрические токи, то по третьему проводу ток потечет в направлении от этого узла, и равен он будет сумме двух входящих токов. Физический принцип этого закона прост: если бы он не соблюдался, в узле непрерывно накапливался бы электрический заряд, а этого очевидно не происходит.

Второй закон не менее прост для понимания. Если мы имеем сложную, разветвленную цепь, ее можно представить в виде простых замкнутых контуров. Ток в цепи может различным образом перераспределяться по этим контурам, и труднее всего определить, по какому именно маршруту потекут токи в сложной цепи. В каждом из контуров электроны могут либо приобретать дополнительную энергию (например, от батареи), либо терять ее (например, на сопротивлении или ином элементе).

Второй закон Кирхгофа гласит, что чистое увеличение энергии электронов в любом замкнутом контуре цепи равно нулю. Этот закон также имеет простую физическую интерпретацию. Если бы это было не так, всякий раз, проходя через замкнутый контур, электроны приобретали или теряли бы энергию, и ток бы постоянно возрастал или убывал. В первом случае можно было бы получить вечный двигатель, а это запрещено законами термодинамики; во втором — любые токи в электрических цепях неизбежно затухали бы, а этого не наблюдается.

Формулировка и физический смысл закона утечки энергии в пределах замкнутой цепи

В 1845 г. Густав Кирхгоф, физик из Германии, вывел два правила, позволяющих рассматривать соответствия между разностью потенциалов и силой тока на участках электроцепи. Их ещё называют законами, но это скорее условия, которые позволяют составить систему уравнений. Решая подобные уравнения, рассчитывают любую самую сложную электрическую цепь.

Густав Роберт Кирхгоф – немецкий физик

Густав Роберт Кирхгоф – немецкий физик

Формулировка правил

Каждое правило Кирхгофа обладает универсальными свойствами. Как первое, так и второе, хоть и не относятся к фундаментальным законам, но твёрдо обоснованы.

Внимание! Правила Кирхгофа одинаково применимы к цепям любого рода тока.

Определения

Прежде, чем рассматривать простые принципы и смысл решения СУ (систем уравнений), нужно определиться с применяемыми формулировками. В типологии цепей пользуются следующими понятиями:

  • ветвь;
  • узел;
  • контур.

Всё это – элементы электрической цепи (ЭЦ).

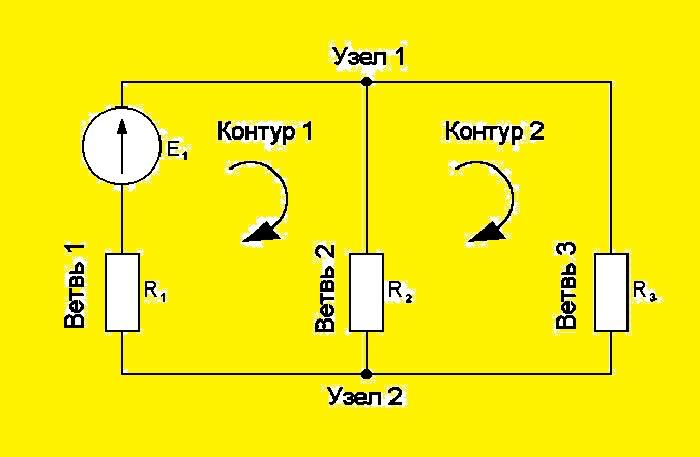
Элементы ЭЦ

Элементы ЭЦ

Часть электроцепи, через которую проходит электричество одной и той же величины, называется ветвью. Место, в котором соединяются три и более ветви, именуют узлом. Обычно на схемах узлы обозначаются крупными точками. Контуром называется путь, по которому протекает электрический ток, проходя через несколько участков ЭЦ, включающих в себя узлы и ветви.

Важно! Ток (I), выходя из одной точки контура и единожды проходя по разветвлениям и узлам, должен обязательно вернуться в начало. Контур – это замкнутая цепь.

Узлы и ветви, подлежащие изучаемому в определённый момент контуру, могут входить в состав других контуров: являться общими для нескольких замкнутых ЭЦ одновременно.

Первое правило

Первая закономерность Кирхгофа звучит так: «Сумма всех токов в узлах ЭЦ равна нулю». Если придать направление токам, текущим сквозь пересечения проводников, имеющих общий контакт (узел), то можно промаркировать стрелками, указывающими на узел, втекающие токи. Стрелками, имеющими направленность от узла, удобно отмечать вытекающие токи:

I1 + I2 – I3 – I4 – I5 = 0

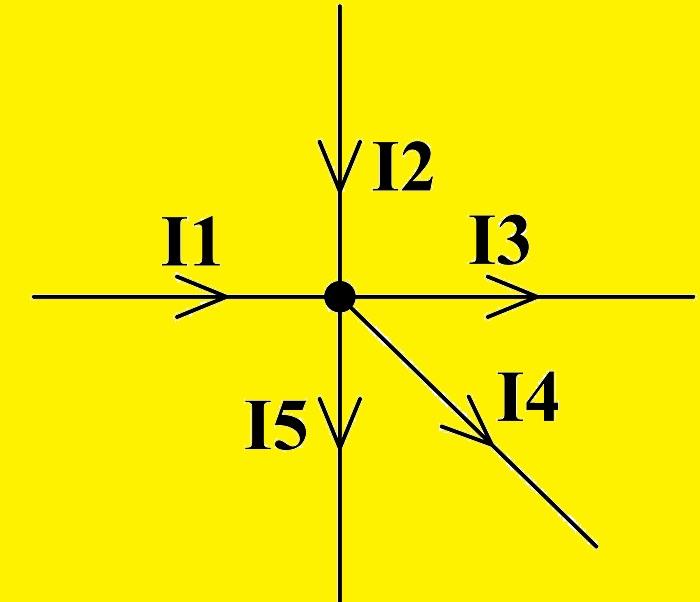
Изображение направления движения электричества

Изображение направления движения электричества

Условно считая, что входящие I имеют плюсовой знак, а выходящие – минусовой, можно перефразировать утверждение. Согласно закону сохранения заряда, алгебраические суммы входящих в узел и выходящих из него I по значению равны.

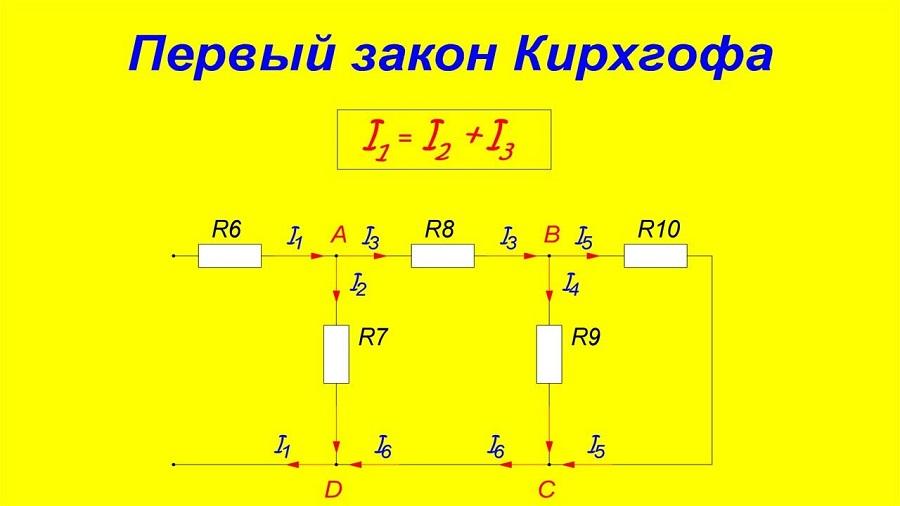
Первый закон

Первый закон

Убедиться в истинности первого правила можно, собрав смешанную схему включения резисторов, в качестве нагрузки, для источника питания U = 3 В.

Включенные в ветви амперметры позволяют визуально зафиксировать значения токов, входящих и выходящих из первого узла. Их алгебраическая сумма (учитывая знаки) будет равна нулю.

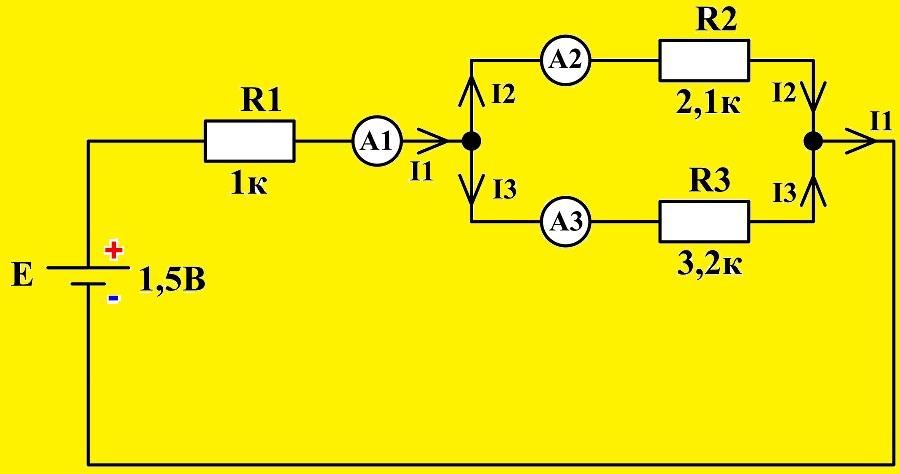
Схема цепи с установкой амперметров

Схема цепи с установкой амперметров

Второе правило

Его называют правилом напряжений, оно утверждает, что сумма всех E (ЭДС), входящих в контур, равняется сумме падений напряжений на резистивных элементах, при условии, что контур замкнутый:

ΣE = ΣI*R.

Например, для цепи с элементом питания и резистором напряжение на резисторе U = I*R будет равно ЭДС батарейки. По второму определению Кирхгофа выражение будет иметь вид:

E = I*R.

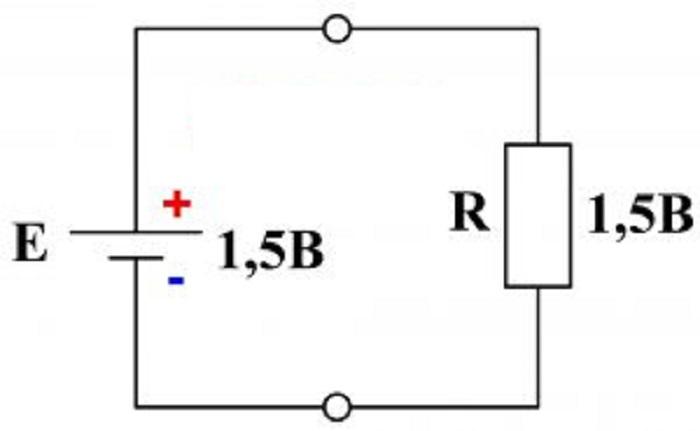
Схема с одной ЭДС и одним резистором

Схема с одной ЭДС и одним резистором

По аналогии, если количество резисторов увеличить, то падение напряжения на них распределится так, что в сумме они сравняются со значением ЭДС источника питания:

E = I*R1 + I*R2 + I*R.

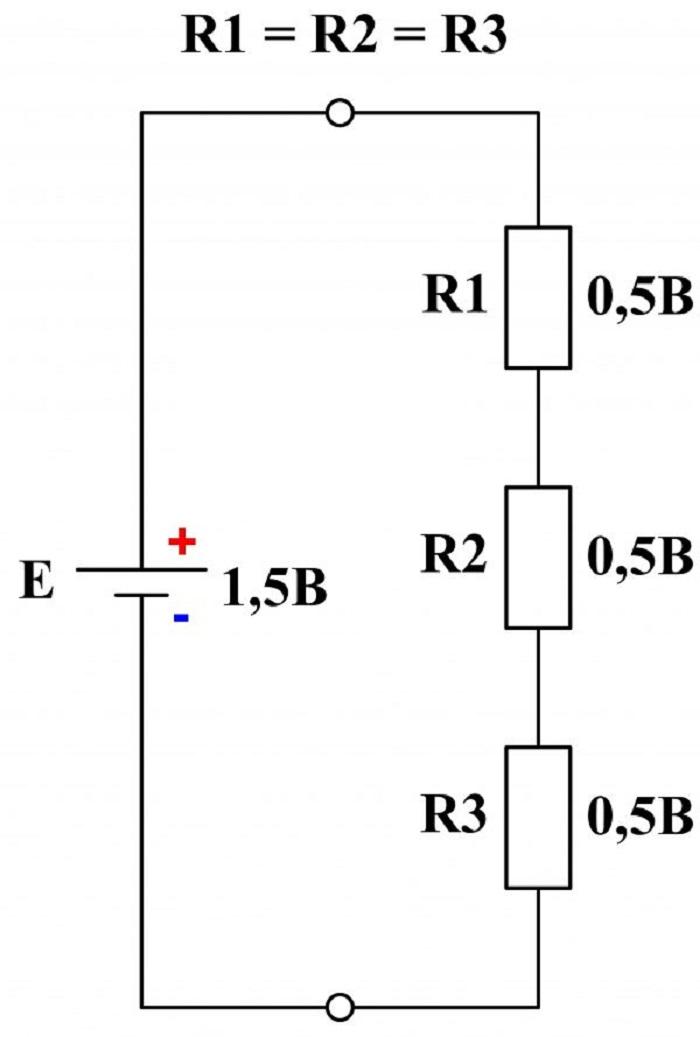
Включение одной ЭДС и трёх резисторов одного номинала

Включение одной ЭДС и трёх резисторов одного номинала

Объяснение было бы не полным, если не рассмотреть схему с несколькими ЭДС, входящими в контур.

В этом случае выражать равенство следует следующим образом:

E1 + E2 = I*R1 + I*R2 + I*R3.

К сведению. При подключении нескольких источников в один контур необходимо соблюдать полярность, выполняя последовательное соединение плюса одного источника с минусом другого, таким образом, значения ЭДС будут суммироваться.

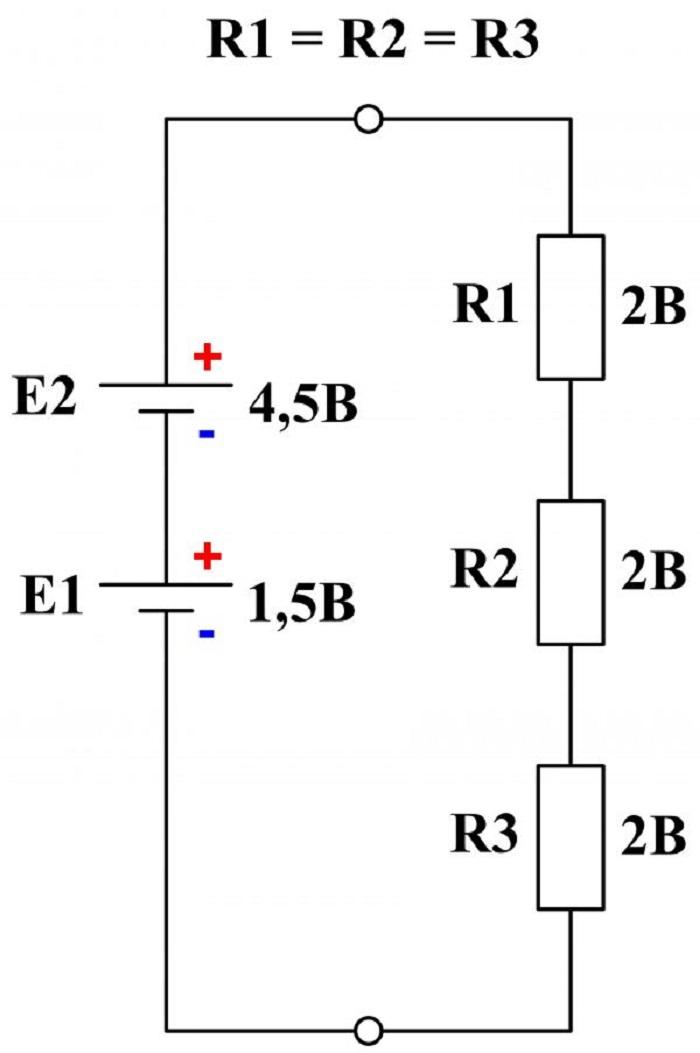
Включение двух источников в контур

Включение двух источников в контур

Расчеты электрических цепей с помощью законов Кирхгофа

Для выполнения подобных расчётов существует определённый алгоритм, при котором вычисляются токи для каждой ветви и напряжения на выводах всех элементов, включённых в ЭЦ.

Для того чтобы рассчитать любую схему, придерживаются следующего порядка:

  1. Разбивают ЭЦ на ветви, контуры и узлы.
  2. Стрелками намечают предполагаемые направления движения I в ветвях. Произвольно намечают направление, по которому при написании уравнений обходят контур.
  3. Пишут уравнения, применяя первое и второе правило Кирхгофа. При этом учитывают правила знаков, а именно:
  • «плюс» имеют токи, втекающие в узел, «минус» – токи, вытекающие из узла;
  • Е (ЭДС) и снижение напряжения на резисторах (R*I) обозначают знаком «плюс», если ток и обход совпадают по направлению, или «минус», если нет.
  1. Решая полученные уравнения, находят нужные величины токов и падения напряжений на резистивных элементах.

Информация. Независимыми узлами называют такие, которые отличаются от других как минимум одной новой веткой. Ветви, содержащие ЭДС именуют активными, без ЭДС – пассивными.

В качестве примера можно рассмотреть схему с двумя ЭДС и рассчитать токи.

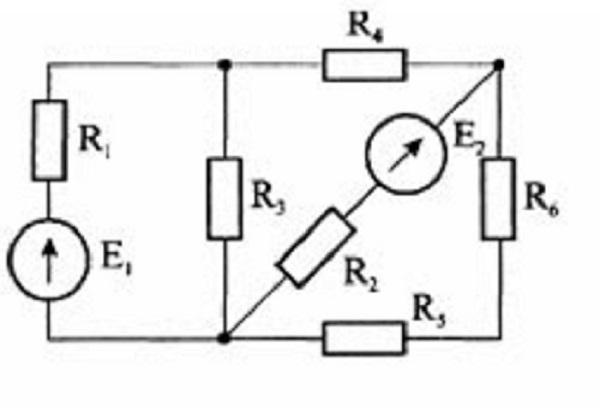
Пример схемы для расчёта с двумя E

Пример схемы для расчёта с двумя E

Произвольно выбирают направление токов и контурного обхода.

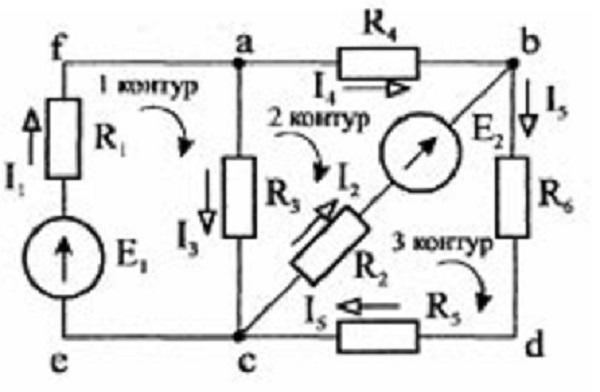
Намеченные направления на схеме

Намеченные направления на схеме

Составляются следующие уравнения с применением первого и второго закона Кирхгофа:

  • I1 – I3 – I4 = 0 – для узла a;
  • I2 + I4 – I5 = 0 – для узла b;
  • R1*I1 + R3*I3 = E1 – контур acef;
  • R4*I4 – R2*I2 – R3*I3 = – E2 – контур abc;
  • R6*I5 + R5*I5 + R2*I2 = E2 – контур bdc.

Уравнения решаются с помощью методов определителей или подстановки. Также можно использовать онлайн-калькуляторы.

О значении для электротехники

Кирхгоф вывел правила, носящие абсолютный прикладной характер для решения практических вопросов в электротехнике. Комплексные применения вместе с иными методами дают возможность рассчитывать участки схем любой сложности. Эти два закона можно употребить для нахождения электрических параметров линейной алгебры.

Законы Кирхгофа для магнитной цепи

Магнитная цепь (МЦ), как электрическая (ЭЦ), может быть рассчитана по данным правилам. По аналогии цепей можно выделить следующую связь:

  • магнитный поток – электрический ток;
  • МДС (магнитодвижущая сила) – ЭДС.

Первое правило для МЦ – магнитные потоки в узлах в алгебраической сумме дают ноль (ΣΦк= 0). Оно основано на физическом принципе непрерывности Φ.

Второе правило говорит о том, что падения магнитного напряжения (напряжённости) Uм в сомкнутом контуре в алгебраической сумме равны сумме МДС этого контура:

ΣUм = ΣI*ω, где:

  • I – ток, проходящий по проводнику;
  • ω – количество витков в обмотке.

Второй закон Кирхгофа – это по-другому записанная форма закона полного тока.

Внимание! Для магнитных цепей алгоритм составления уравнений тот же самый, как и для ЭЦ. Правила знаков действуют аналогично.

Закон излучения Кирхгофа

Когда электромагнитное излучение (ЭИ) падает на тело, то оно частично отражается, частично поглощается, какая-то доля проходит через него. Всё зависит от способности тела поглощать излучения. Чёрное тело (абсолютное) поглощает все попадающие на него световые волны.

Как гласит закон излучения, при определённых температуре и частоте величина, равная отношению излучательных r (ω, T) к поглощательным способностям a (ω, T), у всех тел одинаковая.

Формула имеет вид:

r(ω, T)/ a(ω, T) = f(ω,T),

где:

  • ω – частота;
  • T – температура.

Закон Кирхгофа в химии

Когда в ходе химреакции система меняет свою теплоёмкость, вместе с тем меняется и температурный коэффициент возникающего в результате этого процесса теплового эффекта. Применяя уравнение, вытекающее из этого закона, можно рассчитывать тепловые эффекты в любом диапазоне температур. Дифференциальная форма этого уравнения имеет вид:

∆Cp = d∆Q/dT,

где:

  • ∆Cp – температурный коэффициент;
  • d∆Q – изменение теплового эффекта;
  • dT – изменение температуры.

Важно! Коэффициент определяет, как изменится тепловой эффект при изменении температуры на 1 К (2730С).

Теорема Кирхгофа для термодинамики

Теорема Кирхгофа для термодинамики

Третье уравнения Максвелла, а также принцип сохранения зарядов позволили Густаву Кирхгофу создать два правила, которые применяются в электротехнике. Имея данные о значениях сопротивлений резисторов и ЭДС источников питания, можно рассчитывать протекающий I или приложенное U для любого элемента цепи.

Видео

Законы Кирхгофа • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Карьера Густава Кирхгофа во многом типична для немецкого физика XIX столетия. Германия позже своих западных соседей подошла к индустриальной революции и потому сильнее нуждалась в передовых технологиях, которые способствовали бы ускоренному развитию промышленности. В результате ученые, прежде всего естественники, ценились в Германии очень высоко. В год окончания университета Кирхгоф женился на дочери профессора, «соблюдя, тем самым, — как пишет один из его биографов, — два обязательных условия успешной академической карьеры». Но еще до этого, в возрасте двадцати одного года, он сформулировал основные законы для расчета токов и напряжений в электрических цепях, которые теперь носят его имя.

Середина XIX века как раз стала временем активных исследований свойств электрических цепей, и результаты этих исследований быстро находили практические применения. Базовые правила расчета простых цепей, такие как закон Ома, были уже достаточно хорошо проработаны. Проблема состояла в том, что из проводов и различных элементов электрических цепей технически уже можно было изготовлять весьма сложные и разветвленные сети — но никто не знал, как смоделировать их математически, чтобы рассчитать их свойства. Кирхгофу удалось сформулировать правила, позволяющие достаточно просто анализировать самые сложные цепи, и законы Кирхгофа до сих пор остаются важным рабочим инструментом специалистов в области электронной инженерии и электротехники.

Оба закона Кирхгофа формулируются достаточно просто и имеют понятную физическую интерпретацию. Первый закон гласит, что если рассмотреть любой узел цепи (то есть точку разветвления, где сходятся три или более проводов), то сумма поступающих в цепь электрических токов будет равна сумме исходящих, что, вообще говоря, является следствием закона сохранения электрического заряда. Например, если вы имеете Т-образный узел электрической цепи и по двум проводам к нему поступают электрические токи, то по третьему проводу ток потечет в направлении от этого узла, и равен он будет сумме двух поступающих токов. Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит.

Второй закон не менее прост. Если мы имеем сложную, разветвленную цепь, ее можно мысленно разбить на ряд простых замкнутых контуров. Ток в цепи может различным образом распределяться по этим контурам, и сложнее всего определить, по какому именно маршруту потекут токи в сложной цепи. В каждом из контуров электроны могут либо приобретать дополнительную энергию (например, от батареи), либо терять ее (например, на сопротивлении или ином элементе). Второй закон Кирхгофа гласит, что чистое приращение энергии электронов в любом замкнутом контуре цепи равно нулю. Этот закон также имеет простую физическую интерпретацию. Если бы это было не так, всякий раз, проходя через замкнутый контур, электроны приобретали или теряли бы энергию, и ток бы непрерывно возрастал или убывал. В первом случае можно было бы получить вечный двигатель, а это запрещено первым началом термодинамики; во втором — любые токи в электрических цепях неизбежно затухали бы, а этого мы не наблюдаем.

Самое распространенное применение законов Кирхгофа мы наблюдаем в так называемых последовательных и параллельных цепях. В последовательной цепи (яркий пример такой цепи — елочная гирлянда, состоящая из последовательно соединенных между собой лампочек) электроны от источника питания по серии проводов последовательно проходят через все лампочки, и на сопротивлении каждой из них напряжение падает согласно закону Ома.

В параллельной цепи провода, напротив, соединены таким образом, что на каждый элемент цепи подается равное напряжение от источника питания, а это означает, что в каждом элементе цепи сила тока своя, в зависимости от его сопротивления. Примером параллельной цепи является соединение ламп «лесенкой»: напряжение подается на шины, а лампы смонтированы на поперечинах. Токи, проходящие через каждый узел такой цепи, определяются по первому закону Кирхгофа.

Формулировка и физический смысл закона утечки энергии в пределах замкнутой цепи

Немецкий учёный Густав Роберт Кирхгоф является одним из великих физиков девятнадцатого века. Будучи отличным знатоком математики, он оставил богатейшее наследство из научных работ в области математической физики. Рядом с достижениями учёного в различных областях науки достойное место занимают первый и второй законы Кирхгофа.

Густав Роберт Кирхгоф

Термины, введённые в правила электротехники

Появление законов Кирхгофа дало возможность рассчитывать разнообразные электрические схемы. Для формулировки этих правил в электротехнике были введены конкретные термины:

  • ветвь;
  • узел;
  • контур.

Ветви

Ветви – это части электрических цепей, соединяющие соседние узлы. Ветвь – это отрезок, ограниченный двумя полюсами электрической системы.

Узел

Этим термином обозначают точки схождений нескольких разных проводников. Узлом может быть точка схождения трёх или нескольких ветвей.

Контур

Этим словом обозначают несколько ветвей, образующих замкнутую электрическую цепь. Замкнутая схема представляет систему, в которой однократное прохождение тока из определённой точки (узла) по всей схеме возвращается в исходный узел. Элементы этой системы определяются как единая схема – контур.

Обратите внимание! Ветви и узлы могут быть одновременно частями разных контуров.

Первый закон Кирхгофа

Принципы зависимости сил токов и величин напряжений, электродвижущей силы (ЭДС) и сопротивления всего контура, представляющего последовательные соединения источников и приёмников электричества, построены на основании закона Ома. Зачастую ЭДС из конкретной точки вхождения может проходить разными путями. В обособленной цепи ток не накапливается, иначе это может вызвать изменение значений потенциалов точек.

Действие закона Кирхгофа в разветвлённой цепи

В нижеприведённой схеме разветвлённой цепи можно увидеть, как действует первое правило Кирхгофа. В точке «А» провод разделяется на 4 проводника, сходящихся затем в узле «В».

На рисунке символы означают:

  • I – ток, входящий в точку А и одновременно выходящий из точки В;
  • I1, I2, I3, I4 – токи в ветвях.

Согласно правилу последовательного соединения сопротивлений (R), соотношение токов будет следующим:

I = I1 + I2 + I3 + I4.

Схематичное изображение первого правила Кирхгофа

Параллельное соединение сопротивлений (рис. выше) направляет ток по 4 веткам. Это понижает сопротивление всего контура и повышает общую проводимость. Она, на основании 1 закона Кирхгофа, составляет сложение проводимостей 4 веток. Применяя закон Ома, на всех участках силы тока можно обозначить следующим образом:

  • I = U/R;
  • I1 = U/R1;
  • I2 = U/R2;
  • I3 = U/R3;
  • I4 = U/R4.

Следовательно, можно записать следующее:

U/R = U/R1+U/R2+U/R3+U/R4.

Если исключить в обеих частях расчёта значение U, уравнение приобретёт простейшее выражение:

1/R = 1/R1+1/R2+1/R3+1/R4.

Для двух параллельных сопротивлений R1 и R2 получают такое выражение:

1/R =1/R1+1/R2.

Следовательно, сопротивление цепи будет таким:

R = R1 х R2/ R1 + R2.

В итоге учёный определил физический смысл первого закона Кирхгофа. Первый закон Кирхгофа гласит: «Сумма электрических зарядов, идущих в узел в течение определённого времени, равна сумме зарядов, уходящих из этой точки, за это же время.

Первое правило Кирхгофа

Второй закон Кирхгофа

Правило имеет второе название – закон напряжений. Второе правило Кирхгофа выражают в виде уравнения Кирхгофа:

Формула 2 закона Кирхгофа

Это означает, что в какой-либо замкнутой цепи падение напряжений равняется сумме ЭДС, находящихся в пределах этого контура.

Суть второго закона Кирхгофа можно выразить простыми словами: «При прохождении токов через все ветви контура падает потенциал. При их возвращении в исходный узел потенциал достигает своей первоначальной величины. То есть утечка потенциала (энергии) в пределах замкнутой электрической цепи равняется нулю».

Прежде, чем приступить к расчёту разветвленной схемы, подсчитывают необходимые уравнения, соответствующие 2 закону Кирхгофа. Количество уравнений равно разнице числа веток и числа узлов в контуре плюс единица.

При написании формул по закону Кирхгофа надо охватывать весь контур. Это даёт возможность определения токов и напряжений на всех участках закрытой системы. На плане указывают положительные движения токов. Одновременно обозначают направление обхода контура. Обычно обход производят по кругу движения стрелок часов.

Если в итоге вычислений ток получается отрицательным, то движение меняют в обратную сторону. При написании уравнений каждый раз включают последующую ветвь, не учтённую в предыдущих уравнениях.

Важно! Первый и второй закон Кирхгофа верны для всех нелинейных и линейных цепей. Абсолютно никакого значения не имеют перемены напряжений и токов в течение определённого времени.

На нижнем изображении приведён пример разветвлённой цепи для написания уравнений согласно теореме Кирхгофа.

Образец разветвлённой цепи

Согласно приведенной схеме, уравнения будут такими:

Значение законов Кирхгофа для мировой науки

Они на сегодняшний день сохранили своё актуальное значение для такой отрасли науки, как электротехника. Наряду с другими методиками расчётов, эти правила необходимы для разработки схем в области радиоэлектроники. Законы до сих пор не устарели и применяются для создания и развития новых компьютерных технологий.

Благодаря своим открытиям, немецкий учёный возглавил блестящую плеяду учёных-физиков второй половины девятнадцатого века. Его достижения в развитии науки пришлись по времени к началу индустриальной революции в промышленном развитии Германии. Основные правила законов электротехники легли в методику получения новейших технологий и способствовали появлению совершенно неизвестных ранее отраслей промышленности.

Середина 19 века ознаменовалась чередой открытий основных законов электричества, среди которых главенствующее положение заняли законы Кирхгофа. Именно они создали базу для математических расчётов электрических цепей.

Содержание обоих законов не составляет особых сложностей и вполне доступно для понимания широкому кругу людей.

Дополнительная информация. Прикладная природа правил вместе с другими методиками способствуют разрешению множества задач электротехники. Простая формулировка законов дала возможность применить методы линейной алгебры.

Во многих странах открытия учёного именуют по-разному. Большинство представителей научной общественности склонны к тому, что законы вернее называть правилами. В нашей стране приняты названия в обоих вариантах.

Видео

Оцените статью:

Законы Кирхгофа и их физический смысл. Расчет ЭЦ методом законов Кирхгофа. Баланс мощностей.


Элементы и структура ЭЦ. Режимы работы реального генератора ЭДС. Условие передачи максимальной мощности от генератора к нагрузке. Режим согласования. Замена реального генератора тока генератором ЭДС.

 

Электрическая цепь состоит из отдельных частей, выполняющих определенные функции и называемых элементами цепи. Основными элементами цепи являются источники и приемники электрической энергии. Электротехнические устройства, производящие электрическую энергию, называются генераторами или источниками электрической энергии, а устройства, потребляющие ее – приемниками электрической энергии.

Различают двух –и многополюсные элементы. Двухполюсники имеют два зажима. К ним относятся источники энергии, резисторы, катушки индуктивности, конденсаторы. Многополюсные элементы – это, например, триоды, трансформаторы, усилители и т.д.

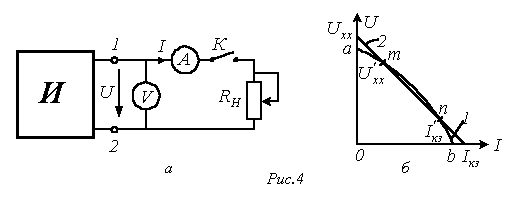
В общем случае внешней характеристикой источника (т.е. зависимость напряжения от тока) является нелинейной (кривая 1 на рис. 4,б). Она имеет две характерные точки, которые соответствуют:

а – режиму холостого хода .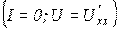

б –режиму короткого замыкания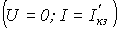

Прямая 2 на рис. 4,б описывается линейным уравнением

Кроме отмеченных режимов функционирования источника, на практике важное значение имеет согласованный режим работы, при котором нагрузкой RН от источника потребляется максимальная мощность

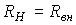
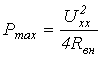
Условие такого режима

Разность потенциалов между двумя точками электрической цепи. Потенциальная диаграмма.

Разность потенциалов считается по формуле точке (б), идя от точки (а): fi(b)=fi(a)+R*I.

Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат — потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.

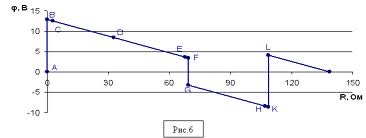
Преобразование пассивных ЭЦ (последовательное и параллельное соединение, треугольник-звезда и звезда-треугольник).

Параллельное: 1/R=1/R1+1/R2

Последовательное: R=R1+R2

 

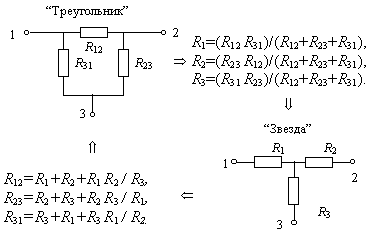
Законы Кирхгофа и их физический смысл. Расчет ЭЦ методом законов Кирхгофа. Баланс мощностей.

Первый закон Кирхгофа – алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю

Положительные направления токов каждой ветви произвольны. Токи направленные к узлу принимаются отрицательными, направленные от него – положительными (или наоборот).

Второй закон Кирхгофа – алгебраическая сумма ЭДС в любом замкнутом контуре равна алгебраической сумме падений напряжений в нем.

Направление обхода контура произвольно. При записи левой части равенства те ЭДС, направления которых совпадают с направлением обхода контура принимаются положительными; ЭДС, направленные против выбранного направления обхода – отрицательными. При записи правой части равенства со знаком плюс берутся падения напряжения на тех элементах rk через которые протекают токи ik, положительное направление которых совпадает c направлением обхода и со знаком минус – падения напряжения на тех элементах, через которые протекают токи, положительное направление которых противоположно направлению обхода.

Порядок анализа на основании законов Кирхгофа

1. Определить число неизвестных токов, равное NB — NJ . 2.Указать положительное направление тока в каждой ветви. 3. Составить N1 = N у — 1 независимых уравнений по первому закону Кирхгофа. 4. Составить N2 = NВ — NJ — (NУ — 1) независимых уравнений по второму закону Кирхгофа. При составлении уравнений по второму закону Кирхгофа следует выбирать лишь те контуры, которые не содержат ветвей с источниками тока. Указать направление обхода контуров. 5. Число уравнений равно числу неизвестных токов N1 + N2 = NВ — NJ.

Баланс мощностей можно сформулировать так: алгебраическая сумма мощностей источников, должна быть равна арифметической сумме мощностей нагрузок. Если направление ЭДС и направление тока ветви не совпадают, то составляющая мощности этого источника в балансе мощностей берется со знаком «минус».


Читайте также:


Рекомендуемые страницы:

Поиск по сайту

Первый закон Кирхгофа — Студопедия

Ток — это направленное движение эл. зарядов. Ток через какую-либо поверхность (например, через поперечное сечение провода) равен скорости переноса заряда через эту поверхность. На каждой ветви схемы эл. цепи указывается стрелка тока. Она имеет смысл направления вычисления тока. Ее еще называют условно-положительным направлением тока.

Ток в проводе будет положительным, если электроны перемещаются противоположно стрелке тока. Ток в проводе будет отрицательным, если электроны перемещаются в направлении стрелки тока. Направление стрелки тока может быть выбрано произвольно. Если его изменить, ток поменяет знак.

Сформулируем 1-й закон Кирхгофа: сумма токов, сходящихся в узле эл. цепи, равна нулю.

При этом токи, стрелка которых направлена к узлу, входят в сумму с дополнительным знаком минус:

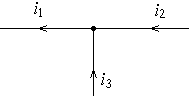Рис. 2.1.

.

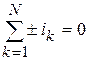Например, для узла на рис. 2.1 имеем:

.

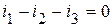Смысл 1-го закона Кирхгофа состоит в том, что сколько эл. заряда приходит к узлу эл. цепи, столько же и уходит из него.

Замечание 1: Первый закон Кирхгофа допускает обобщение: сумма токов, пересекающих любую замкнутую поверхность, равна нулю. В случае, когда такая поверхность охватывает узел эл. цепи, получаем приведенную выше формулировку закона.

Замечание 2: В первом законе Кирхгофа можно использовать и обратное правило знаков, суммируя выходящие из узла токи с дополнительным знаком «минус».

Замечание 3: Движение свободных эл. зарядов называется током проводимости. Существует еще ток смещения, обусловленный движением связанных зарядов и изменением электрического поля во времени.


Замечание 4: Строго говоря, 1-й закон Кирхгофа – это приближенное равенство. Он не учитывает перенос эл. заряда через изоляцию (токи утечки), а также токи, связанные с процессом накопления эл. заряда в области узла (токи смещения). Однако, по сравнению с токами в проводах, токи утечки и токи смещения обычно очень малы. Случаи, когда их приходится принимать во внимание, выходят за пределы теории эл. цепей.

Замечание 5: Гидравлическая аналогия позволяет уподобить поток электронов в проводах потоку несжимаемой жидкости, а провода и прочие элементы цепи – трубкам и сосудам, по которым эта жидкость течет. Ток утечки подобен просачиванию жидкости через мелкие трещины и поры трубок и сосудов; ток смещения – движению жидкости перпендикулярно стенкам трубок и сосудов, когда такое движение обусловлено их небольшим растяжением и сжатием. Если же трубки и сосуды без пор и трещин, и к тому же нерастяжимы, то сумма потоков жидкости в трубках, сходящихся в узле, равна нулю. Стрелка тока соответствует направлению вычисления потока жидкости.


Правило Прево. Законы Кирхгофа, Стефана-Больцмана, Вина

При тепловом равновесии выполняется правило Прево: если два тела поглощают разные количества энергии, то и излучение у них должно быть различным. Так, нагревая кристалл кварца и кусок стали до высокой температуры, наблюдаем яркое каление стали, кристалл же кварца совсем не светится. Таким образом, обнаруживается большая способность к излучению тел, хорошо поглощающих. 

Тогда закон Кирхгофа запишется в следующем виде:

1. Тепловое излучение является равновесным — сколько энергии излучается телом, столь ее им и поглощается. Для трех тел, находящихся в замкнутой полости можно записать:


2. Указанное соотношение будет верным и тогда, когда одно из тел будет АЧ:

 Т.к. для АЧТ  αλT=1

т.е. отношение излучательной способности тела к его поглощательной способности является одинаковым для всех тел.

Это закон Кирхгофа: отношение спектральной плотности энергетической светимости тела к его монохроматическому коэффициенту поглощения (при определенной температуре и для определенной длины волны) не зависит от природы тела и равно для всех тел спектральной плотности энергетической светимости при тех же самых температуре и длине волны.

Следствия из закона Кирхгофа:

1. Спектральная энергетическая светимость АЧТ является универсальной функцией длины волны и температуры тела.

2. Спектральная энергетическая светимость АЧТ наибольшая.

3. Спектральная энергетическая светимость произвольного тела равна произведению его коэффициента поглощения на спектральную энергетическую светимость абсолютно черного тела.

4. Любое тело при данной температуре излучает волны той же длины волны, которое оно поглощает при данной температуре.

 ε(λ,T)=rλТ  — физический смысл универсальной функции Кирхгофа — универсальная функция Кирхгофа — испускательная способность абсолютно черного тела. 

Систематическое изучение спектров ряда элементов позволило Кирхгофу и Бунзену установить однозначную связь между спектрами поглощения и излучения газов и индивидуальностью соответствующих атомов. Так был предложен спектральный анализ, с помощью которого можно выявить вещества, концентрация которых составляет 0,1*10-9

Закон Вина

Изучение распределения светимости для разных длин волн при разных температурах (рис 4) дало следующие результаты:

1. Спектр излучения сплошной 

2.Излучательная способность резче уменьшается в сторону коротких волн 

3.Максимум излучательной способности с ростом температуры  смещается в сторону более коротких волн.
4. Площадь, ограниченная каждой кривой и осью абсцисс, определяет полную энергию, испускаемую единицей поверхности за единицу времени, т.е. Rэ .

Тщательное количественное исследование кривых позволило установить соотношение 

  названное законом смещения Вина:  длина волны λmax, на которую приходиться максимум излучательной способности rλ , обратно пропорциональна его абсолютной температуре. По современным данным, постоянная Вина b = 2,898·10-3м·К.

Но все эти законы чисто эмпирические,следствия обобщения опытных данных, теоретическое обоснование было дано Планком.

Первый закон Кирхгофа — Правило перекрестка, Текущий закон, Правило узла

    • Классы
      • Класс 1-3
      • Класс 4-5
      • Класс 6-10
      • Класс 11-12
    • КОНКУРСНЫЙ ЭКЗАМЕН
      • BNAT 000 NC
        • 000 NC Книги
          • Книги NCERT для класса 5
          • Книги NCERT для класса 6
          • Книги NCERT для класса 7
          • Книги NCERT для класса 8
          • Книги NCERT для класса 9
          • Книги NCERT для класса 10
          • Книги NCERT для класса 11
          • Книги NCERT для класса 12
        • NCERT Exemplar
          • NCERT Exemplar Class 8
          • NCERT Exemplar Class 9
          • NCERT Exemplar Class 10
          • NCERT Exemplar Class 11
          • 9000 9000
          • NCERT Exemplar Class
            • Решения RS Aggarwal, класс 12
            • Решения RS Aggarwal, класс 11
            • Решения RS Aggarwal, класс 10
              • 90 003 Решения RS Aggarwal класса 9
            • Решения RS Aggarwal класса 8
            • Решения RS Aggarwal класса 7
            • Решения RS Aggarwal класса 6
          • Решения RD Sharma
            • RD Sharma Class 6 Решения
            • Решения RD Sharma
            • Решения RD Sharma класса 8
            • Решения RD Sharma класса 9
            • Решения RD Sharma класса 10
            • Решения RD Sharma класса 11
            • Решения RD Sharma класса 12
          • PHYSICS
            • Механика
            • Оптика
            • Термодинамика Электромагнетизм
          • ХИМИЯ
            • Органическая химия
            • Неорганическая химия
            • Периодическая таблица
          • MATHS
            • Теорема Пифагора
              • 0004
            • 000300030004
            • Простые числа
            • Взаимосвязи и функции
            • Последовательности и серии
            • Таблицы умножения
            • Детерминанты и матрицы
            • Прибыль и убыток
            • Полиномиальные уравнения
            • Деление фракций
          • 000
          • 000
          • 000
          • 000
          • 000
          • 000 Microology
          • 000
          • 000 Microology
          • 000 BIOG3000
              FORMULAS
              • Математические формулы
              • Алгебраические формулы
              • Тригонометрические формулы
              • Геометрические формулы
            • КАЛЬКУЛЯТОРЫ
              • Математические калькуляторы
              • 0003000 PBS4000
              • 000300030002 Примеры калькуляторов химии
                • Класс 6
              • Образцы бумаги CBSE для класса 7
              • Образцы бумаги CBSE для класса 8
              • Образцы бумаги CBSE для класса 9
              • Образцы бумаги CBSE для класса 10
              • Образцы бумаги CBSE для класса 11
              • Образцы бумаги CBSE чел. для класса 12
            • CBSE — вопросник за предыдущий год
              • CBSE — вопросник за предыдущий год, класс 10
              • CBSE — за предыдущий год — вопросник, класс 12
            • HC Verma Solutions
              • HC Verma Solutions Class 11 Physics
              • Решения HC Verma, класс 12, физика
            • Решения Лакмира Сингха
              • Решения Лакмира Сингха, класс 9
              • Решения Лакмира Сингха, класс 10
              • Решения Лакмира Сингха, класс 8
            • Заметки CBSE
            • , класс
                CBSE Notes
                  Примечания CBSE класса 7
                • Примечания CBSE класса 8
                • Примечания CBSE класса 9
                • Примечания CBSE класса 10
                • Примечания CBSE класса 11
                • Примечания CBSE класса 12
              • Примечания к редакции CBSE
                • Примечания к редакции
                • CBSE
                • Примечания к редакции класса 10 CBSE
                • Примечания к редакции класса 11 CBSE 9000 4
                • Примечания к редакции класса 12 CBSE
              • Дополнительные вопросы CBSE
                • Дополнительные вопросы по математике класса 8 CBSE
                • Дополнительные вопросы по науке 8 класса CBSE
                • Дополнительные вопросы по математике класса 9 CBSE
                • Дополнительные вопросы по науке класса 9 CBSE
                  • Дополнительные вопросы по математике для класса 10
                • Дополнительные вопросы по науке, класс 10 по CBSE
              • CBSE, класс
                • , класс 3
                • , класс 4
                • , класс 5
                • , класс 6
                • , класс 7
                • , класс 8
                • , класс 9 Класс 10
                • Класс 11
                • Класс 12
              • Учебные решения
            • Решения NCERT
              • Решения NCERT для класса 11
                • Решения NCERT для класса 11 по физике
                • Решения NCERT для класса 11 Химия
                  • Решения для биологии класса 11
                • Решения NCERT для математики класса 11
                  • 9 0003 NCERT Solutions Class 11 Accountancy
                • NCERT Solutions Class 11 Business Studies
                • NCERT Solutions Class 11 Economics
                • NCERT Solutions Class 11 Statistics
                • NCERT Solutions Class 11 Commerce
              • NCERT Solutions For Class 12
                • NCERT Solutions For Класс 12 по физике
                • Решения NCERT для химии класса 12
                • Решения NCERT для класса 12 по биологии
                • Решения NCERT для класса 12 по математике
                • Решения NCERT Класс 12 Бухгалтерия
                • Решения NCERT, класс 12, бизнес-исследования
                • Решения NCERT, класс 12 Экономика
                • NCERT Solutions Class 12 Accountancy Part 1
                • NCERT Solutions Class 12 Accountancy Part 2
                • NCERT Solutions Class 12 Micro-Economics
                • NCERT Solutions Class 12 Commerce
                • NCERT Solutions Class 12 Macro-Economics
              • NCERT Solutions For Класс 4
                • Решения NCERT для математики класса 4
                • Решения NCERT для класса 4 EVS
              • Решения NCERT для класса 5
                • Решения NCERT для математики класса 5
                • Решения NCERT для класса 5 EVS
              • Решения NCERT для класса 6
                • Решения NCERT для математики класса 6
                • Решения NCERT для науки класса 6
                • Решения NCERT для социальных наук класса 6
                • Решения NCERT для класса 6 Английский
              • Решения NCERT для класса 7
                • Решения NCERT для класса 7 Математика
                • Решения NCERT для класса 7 Наука
                • Решения NCERT для класса 7 по социальным наукам
                • Решения NCERT для класса 7 Английский
              • Решения NCERT для класса 8
                • Решения NCERT для класса 8 Математика
                • Решения NCERT для класса 8 Science
                • Решения NCERT для социальных наук 8 класса
                • Решение NCERT ns для класса 8 Английский
              • Решения NCERT для класса 9
                • Решения NCERT для социальных наук класса 9
              • Решения NCERT для математики класса 9
                • Решения NCERT для математики класса 9 Глава 1
                • Решения NCERT для Математика класса 9 Глава 2
                • Решения NCERT для математики класса 9 Глава 3
                • Решения NCERT для математики класса 9 Глава 4
                  • Решения NCERT
                • для математики класса 9 Глава 5
                • Решения NCERT для математики класса 9 Глава 6
                • Решения NCERT для Математика класса 9 Глава 7
                • Решения NCERT для математики класса 9 Глава 8
                  • Решения NCERT
                • для математики класса 9 Глава 9
                  • Решения NCERT
                • для математики класса 9 Глава 10
                • Решения NCERT для математики класса 9 Глава 11
                • Решения NCERT для Математика класса 9 Глава 12
                • Решения NCERT для математики класса 9 Глава 13
                  • Решения
                • NCERT для математики класса 9 Глава 14
                • Решения NCERT для математики класса 9 Глава 15
              • Решения NCERT для науки класса 9
                • Решения NCERT для науки класса 9 Глава 1
                • Решения NCERT для науки класса 9 Глава 2
                • Решения NCERT для класса 9 Наука Глава 3
                • Решения NCERT для Науки Класса 9 Глава 4
                • Решения NCERT для Науки Класса 9 Глава 5
                • Решения NCERT для Науки Класса 9 Глава 6
                • Решения NCERT для Науки Класса 9 Глава 7
                • Решения NCERT для Класса 9 Наука Глава 8
                • Решения NCERT для Науки Класса 9 Глава 9
                • Решения NCERT для Науки Класса 9 Глава 10
                • Решения NCERT для Науки Класса 9 Глава 12
                • Решения NCERT для Науки Класса 9 Глава 11
                • Решения NCERT для Класса 9 Наука Глава 13
                • Решения NCERT для класса 9 Наука Глава 14
                • Решения NCERT для класса 9 по науке Глава 15
              • Решения NCERT для класса 10
                • Решения NCERT для класса 10 по социальным наукам
              • Решения NCERT для математики класса 10
                • Решения NCERT для математики класса 10 Глава 1
                • Решения NCERT для математики класса 10 Глава 2
                • Решения NCERT для математики класса 10 Глава 3
                • Решения NCERT для математики класса 10 Глава 4
                • Решения NCERT для математики класса 10 Глава 5
                • Решения NCERT для математики класса 10 Глава 6
                • Решения NCERT для математики класса 10 Глава 7
                • Решения NCERT для математики класса 10 Глава 8
                • Решения NCERT для математики класса 10 Глава 9
                  • Решения NCERT
                • для математики класса 10 Глава 10
                  • Решения
                • NCERT для математики класса 10 Глава 11
                • Решения NCERT для математики класса 10 Глава 12
                • Решения NCERT для математики класса 10 Глава 13
                • NCERT Sol Решения NCERT для математики класса 10 Глава 14
                • Решения NCERT для математики класса 10 Глава 15
              • Решения NCERT для науки класса 10
                • Решения NCERT для науки класса 10 Глава 1
                • Решения NCERT для науки класса 10 Глава 2
                • Решения NCERT для науки 10 класса, глава 3
                • Решения NCERT для науки 10 класса, глава 4
                • Решения NCERT для науки класса 10 Глава 5
                • Решения NCERT для науки класса 10 Глава 6
                • Решения NCERT для науки класса 10 Глава 7
                • Решения NCERT для науки 10 класса, глава 8
                • Решения NCERT для науки класса 10 Глава 9
                • Решения NCERT для науки класса 10 Глава 10
                • Решения NCERT для науки класса 10 Глава 11
                • Решения NCERT для науки класса 10 Глава 12
                • Решения NCERT для науки 10 класса Глава 13
                • Решения NCERT для науки 10 класса Глава 14
                • Решения NCERT для науки класса 10 Глава 15
                  • Решения NCERT
                • для науки класса 10 Глава 16
              • Учебный план NCERT
              • NCERT
            • Commerce
              • Class 11 Commerce Syllabus
                  ancy Account
                • Программа обучения бизнесу 11 класса
        .

        Определение и примеры закона напряжения Кирхгофа

        Что такое закон напряжения Кирхгофа?

        Закон Кирхгофа по напряжению — это фундаментальный закон цепи, который утверждает, что алгебраическая сумма всех напряжений вокруг замкнутого пути равна нулю или, другими словами, сумма падений напряжения равна общему напряжению источника.

        Правило петли Кирхгофа

        В электрической цепи напряжения на резисторах (падения напряжения) всегда имеют полярность, противоположную полярности напряжения источника.Например, пройдите по круговой схеме по часовой стрелке и обратите внимание, что полярность источника — минус-плюс, а каждое падение напряжения — плюс-минус. Также обратите внимание, что напряжение падает на резисторах, обозначенных как В 1 , В 2 и т. Д.

        kvl

        Также обратите внимание, что ток выходит с положительной стороны источника и проходит через резисторы, как показано стрелками. Ток подается на положительную сторону каждого резистора и на отрицательную сторону.Падение уровня энергии на резисторе создает разность потенциалов или падение напряжения с полярностью плюс-минус в направлении тока.

        Обратите внимание, что напряжение от точки A до точки B в цепи равно напряжению источника V s . Кроме того, напряжение от A до B является суммой падений напряжения последовательного резистора. Следовательно, напряжение источника равно сумме трех падений напряжения.

        kirchoff

        Это обсуждение является примером закона напряжения Кирхгофа , который обычно формулируется следующим образом:

        Сумма всех напряжений вокруг одного замкнутого элемента в цепи равна общему напряжению источника в этом контуре. ,

        Другой способ сформулировать закон Кирхгофа о напряжении

        Если сложить все напряжения вокруг замкнутого контура, а затем вычесть эту сумму из напряжения источника, результат будет равен нулю. Этот результат возникает из-за того, что сумма падений напряжения всегда равна напряжению источника.

        Алгебраическая сумма всех напряжений (как источников, так и падений) вокруг замкнутого контура равна нулю.

        Следовательно, другой способ выразить закон напряжения Кирхгофа в виде уравнения:

        В с — В 1 — В 2 — В 3 -., , — V n = 0

        Вы можете проверить закон напряжения Кирхгофа, подключив цепь и измерив напряжение каждого резистора и напряжение источника. Когда напряжения резисторов складываются, их сумма будет равна напряжению источника. Можно добавить любое количество резисторов.

        Следующие три примера используют закон напряжения Кирхгофа для решения проблем цепи.

        k.voltage law

        Примеры закона напряжения Кирхгофа

        example of kvl

        Примеры kvl

        example of kvl

        Смотрите также:

        Что такое закон Кирхгофа по току?

        Вы узнали закон Кирхгофа, касающийся напряжений в замкнутой последовательной цепи.Теперь вы изучите текущий закон Кирхгофа, который касается токов в параллельной цепи.

        Соединение — это любая точка в цепи, в которой соединены два или более компонентов. Итак, в параллельной цепи соединение — это место, где сходятся параллельные ветви. Например, в схеме точка A — это одно соединение, а точка B — другое. Начнем с положительного вывода источника и проследим за током. Полный ток I T от источника идет в переход в точке A.В этот момент ток разделяется между тремя ветвями, как показано. Каждый из трех токов ответвления ( I 1 , I 2 , и I 3 ) находится вне соединения A. Закон Кирхгофа утверждает, что полный ток в переходе A равен полному току. вне соединения A.

        Формула закона Кирхгофа

        I T = I 1 + I 2 + I 3

        kcl

        Теперь, следуя токам через три ветви, вы видите, что они снова соединяются в точке B.В настоящее время I 1 , I 2 и I 3 находятся в соединении B, а I T находится вне соединения B. Таким образом, формула закона Кирхгофа в соединении B такая же, как и в соединении A. .

        I T = I 1 + I 2 + I 3

        Общая формула для текущего закона Кирхгофа

        В предыдущем обсуждении использовался конкретный пример для иллюстрированного текущего закона Кирхгофа. показывает обобщенное соединение цепи, где несколько ветвей подключены к точке в цепи.Ток I IN (I) от до I IN (n) входит в переход (n может быть любым числом). Ток I OUT (I) от до I out (m) не является переходом (m может быть любым числом, но не обязательно равным n). Согласно действующему закону Кирхгофа, сумма токов в переходе должна равняться сумме токов в переходе, которая должна равняться доле токов, исходящих из токов перехода.Со ссылкой на рисунок, общая формула текущего закона Кирхгофа:

        I IN (1) + I IN (2) +. , .I IN (n) = I OUT (1) I OUT (2) +. , , + I OUT (м)

        kirchoff

        Примеры действующего закона Кирхгофа

        example of kcl

        Смотрите также:

        .

        Закон Кирхгофа — Chemistry LibreTexts

        1. Последнее обновление
        2. Сохранить как PDF
        1. Введение
        2. Участники

        Закон Кирхгофа описывает энтальпию изменения реакции при изменении температуры.Как правило, энтальпия любого вещества увеличивается с температурой, что означает увеличение энтальпии продуктов и реагентов. Общая энтальпия реакции изменится, если увеличение энтальпии продуктов и реагентов будет другим.

        Введение

        При постоянном давлении теплоемкость равна изменению энтальпии, деленному на изменение температуры.

        \ [c_p = \ dfrac {\ Delta H} {\ Delta T} \ label {1} ​​\]

        Следовательно, если теплоемкости не меняются с температурой, то изменение энтальпии является функцией разницы в температуре и теплоемкости.{T_f} c_ {p} dT \ label {2} \]

        Если теплоемкость не зависит от температуры в диапазоне температур, то уравнение \ ref {1} можно приблизительно представить как

        \ [H_ {T_f} = H_ {T_i} + c_ {p} (T_ {f} -T_ {i}) \ label {3} \]

        с

        • \ (c_ {p} \) — (предполагаемая постоянная) теплоемкость, а
        • \ (H_ {T_ {i}} \) и \ (H_ {T_ {f}} \) — энтальпия при соответствующих температурах.

        Уравнение \ ref {3} может применяться только к небольшим изменениям температуры (<100 K), потому что при более значительном изменении температуры теплоемкость не является постоянной.Существует множество биохимических приложений, поскольку он позволяет нам прогнозировать изменения энтальпии при других температурах, используя стандартные данные энтальпии.

        Авторы

        • Янки Патель (UCD), Костя Маллей (UCD)
        ,

        Законы схем Кирхгофа — Простая английская Википедия, бесплатная энциклопедия

        В 1845 году немецкий физик Густав Кирхгоф описал два закона об электрических схемах. Эти законы являются обобщением закона Ома. Законы Кирхгофа для схем очень полезны при решении схемных задач.

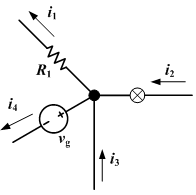
        Ток, входящий в любой переход, равен току, выходящему из этого перехода. i 1 + i 4 = i 2 + i 3

        Текущий закон Кирхгофа также известен как первый закон Кирхгофа и закон соединения Кирхгофа.Этот закон гласит, что «сумма тока в переходе равна сумме тока вне соединения». Это то же самое, что и закон Кирхгофа. В переходе действует закон сохранения суммы электрического заряда. Если входящее значение тока — это i2 и i3, этот ток разделяется на ток i1 и i4. Тогда уравнение (i1 + i4 = i2 + i3) выполняется. Правый рисунок дает пример. Первый закон Кирхгофа состоит в том, что заряд не разрушается и не создается в точке соединения.Это основано на законе сохранения электрического заряда.

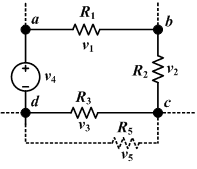        Сумма всех напряжений вокруг контура равна нулю. v 1 + v 2 + v 3 + v 4 = 0

        Закон напряжения Кирхгофа также известен как второй закон Кирхгофа, закон замкнутой цепи и закон петли Кирхгофа.

        Алгебраическая сумма разностей напряжений (потенциалов) в любом контуре должна равняться нулю (эта схема является замкнутой). Любую сложную схему можно разделить на множество замкнутых схем.Этот закон означает, что в цепи есть электрическая ячейка и электрическое сопротивление. Электрический элемент придает заряду электродвижущую силу, а затем электрическое сопротивление рассеивает эту силу. Но в электрическом сопротивлении, если направление противоположно направлению тока, это электрическое сопротивление добавляет электродвижущую силу. Этот второй закон Кирхгофа основан на законе сохранения потенциальной энергии.

        ,

        No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *