Закон Ома для участка цепи

В § 8-и мы начали знакомство с физической величиной «электрическое сопротивление». Продолжим его – проделаем опыт. Нам потребуются источник электроэнергии, амперметр, вольтметр, реостат и два резистора (две нихромовые спирали) с различными сопротивлениями.

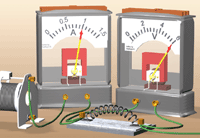Соберём цепь, как показано на рисунке слева или на схеме в конце параграфа. Перемещая движок реостата, поочерёдно установим значения силы тока 0,4 А, 0,6 А, 0,8 А, 1 А. Запишем показания амперметра и вольтметра в таблицу. Повторим опыт, заменив резистор, и дополним таблицу:

	Первый резистор				Второй резистор
I , A	0,4	0,6	0,8	1,0	0,4	0,6	0,8	1,0
U , В	1,6	2,4	3,2	4,0	2,4	3,6	4,8	6,0
Поделив напряжение на силу тока, обнаружим закономерность:
R = U/I	4	4	4	4	6	6	6	6

Закономерность в том, что вне зависимости от значений напряжения и силы тока их частное остаётся постоянным для каждого резистора. Проверьте: после деления каждого числа строки (U, В) на расположенное над ним число строки (I, А) получаются одинаковые результаты во всех колонках левой половины таблицы: 4 В/А и во всех колонках правой половины таблицы: 6 В/А. Это показывает, что величина R является характеристикой именно изучаемого участка цепи – резистора.

Заметим, что эта закономерность всегда справедлива для металлических проводников в твёрдом или жидком состоянии; для других проводников она справедлива не всегда. Однако величину R, равную отношению U/I, всегда называют электрическим сопротивлением проводника независимо от его материала и состояния, а 1 В/А называют 1 Ом. Следовательно, 1 Ом – сопротивление такого проводника, в котором возникнет ток 1 А, если на концах проводника напряжение 1 В.

Связь между величинами U, I, R обычно записывается в виде формулы, известной как закон Ома для участка цепи:

	I   =	U			I   – сила тока в участке цепи, А U – приложенное напряжение, В R – сопротивление участка цепи, Ом
		R

Чтобы выяснить, как следует прочитать эту формулу, вспомним знания по алгебре о видах пропорциональности величин.

прямая пропорциональность:	Y  =  k · X	→	I  =  1/R · U
обратная пропорциональность:	Y  =  k / X	→	I  =  U / R

Из первой строки следует: при постоянном сопротивлении величина ¹/_R тоже постоянна, поэтому сила тока прямо пропорциональна напряжению на концах участка цепи. Из второй строки: при постоянном напряжении сила тока обратно пропорциональна сопротивлению участка цепи. Объединяя это, получаем формулировку закона Ома для участка цепи: сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению этого участка.

Примечание. С точки зрения алгебры, формулу закона Ома можно записать в такой форме: U=I·R. Применим её для изучения цепи, изображённой на схеме. Допустим, клеммы A и B присоединены к источнику с напряжением 10 В, однако вольтметр позволяет измерить напряжение не более 6 В (см. рисунок в начале параграфа). Поэтому нам нужно создать падение напряжения на реостате на 4 В или более. Как это сделать? Чем правее мы смещаем движок, тем больше сопротивление реостата, и, согласно формуле U=I·R, больше напряжение на реостате, которое и называют падением напряжения. В результате на резисторе напряжение снижается и может стать менее 6 В, что нам и нужно.

ФИЗИКА: ЗАДАЧИ на Закон Ома с решениями

Задачи на Закон Ома с решениями

Формулы, используемые на уроках физики «Задачи на Закон Ома» в 8 классе, а также для подготовки к ОГЭ.

Название величины	Обозначение	Единица измерения	Формула
Сила тока	I	А	I = U / R
Напряжение	U	В	U = IR
Сопротивление	R	Ом	R = U/I

Решение задач на уроках физики в 10-11 классах и при подготовке к ЕГЭ смотрите в следующих конспектах:

ЕГЭ: Закон Ома для участка цепи  ЕГЭ: Закон Ома для всей цепи

---

Задачи на Закон Ома.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

---

Задача № 1.  Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?

---

Задача № 2.  Сопротивление проводника 6 Ом, а сила тока в нем 0,2 А. Определите напряжение на концах проводника.

---

Задача № 3.  Определите сопротивление проводника, если при напряжении 110 В сила тока в нем 2 А.

---

Задача № 4.  По графикам зависимости силы тока от напряжения определите сопротивление каждого проводника. 

Решение:

 

---

Задача № 5.  Чему равна сила тока в электрической лампе карманного фонаря, если сопротивление нити накала 16,6 Ом и лампа подключена к батарейке напряжением 2,5 В?

 

---

Задача № 6.  Электрический утюг включен в сеть с напряжением 220 В. Какова сила тока в нагревательном элементе утюга, если сопротивление его равно 48,4 Ом?

---

Задача № 7.  При напряжении 110 В, подведенном к резистору, сила тока в нем равна 5 А. Какова будет сила тока в резисторе, если напряжение на нем увеличить на 10 В?

---

Задача № 8.  Чему равно сопротивление спирали электрической лампы в рабочем состоянии, у которой на цоколе написано 6,3 В, 0,22 А?

---

Задача № 9.  Показание вольтметра, присоединенного к горящей электрической лампе накаливания, равно 120 В, а амперметра, измеряющего силу тока в лампе, 0,5 А. Чему равно сопротивление лампы? Начертите схему включения лампы, вольтметра и амперметра.

---

Задача № 10.   ОГЭ  Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения U_R на внешнем участке и падение напряжения U_r на внутреннем участке цепи.

 

---

Краткая теория для решения Задачи на Закон Ома.

 

---

Это конспект по теме «ЗАДАЧИ на Закон Ома». Выберите дальнейшие действия:

 

Простые примеры использования Закона Ома

Применение Закона Ома становится очевидным на простых электрических цепях, где имеется один источник тока (ЭДС).

Самый простая электрическая цепь — это такая цепь, которая содержит всего лишь два элемента, один из которых источник тока, а другой — резистивная нагрузка. В качестве источника может быть химический аккумулятор или гальваническая батарея. Для наглядности в качестве резистивной нагрузки может быть выбрана электрическая лампа накаливания, но вместо неё можно использовать любой нагревательный элемент, в том числе просто кусок провода.

Давайте посмотрим, как уравнения Закона Ома могут нам помочь анализировать простые схемы.

Рассмотрим схему нашей простейшей электрической цепи:

В приведённой выше схеме, есть только один источник напряжения (батареи, слева) и только одно сопротивление — резистивная нагрузка (лампы, справа). Для этой схемы достаточно легко применять Закон Ома. Если мы знаем значения любых двух из трёх величин (напряжение, ток и сопротивление) в этой схеме, тогда мы можем использовать Закон Ома для определения третьего.

В этом первом примере мы будем вычислять величину тока (I) в цепи, при заданных значениях напряжения ЭДС источника

(E) и сопротивления (R):

Чему равна величина тока (I) в этой схеме?

Во втором примере мы рассчитаем величину сопротивления (R), при заданных значений напряжения (E) и тока (I):

Чему равна величина сопротивления (R) лампы?

В последнем примере мы рассчитаем величину напряжения, выдаваемое батареей, для известных значений тока (I) и сопротивление (R):

Какова величина напряжения, которое выдаёт аккумуляторная батарея?

Закон Ома очень простой и полезный инструмент для анализа электрических цепей. Он используется так часто при изучении электротехники и электроники, что должен быть хорошо отложен в памяти каждого серьёзного студента. При работе в качестве электротехнического персонала (электромонтёром), применение

Закона Ома доводится до автоматизма, потому как очень часто используется.

Для тех, кто плохо знаком с алгеброй, есть хороший способ запомнить вариации применения Закона Ома. Для этого достаточно изобразить треугольник на листке бумаги, который будет разбит на три части. Вершина треугольника — это E, правый угол — это R, а левый угол — это I.

Для удобства полезно запомнить эту картинку:

Если вы знаете E и I, и желаете определить чему равно R, тогда нужно зачеркнуть на картинке неизвестное

R, и наглядно будет видно, что нужно сделать:

Если вам известны E и R, и вы желаете отыскать значение тока I, тогда выполняем подобное действие, но зачёркиваем неизвестное I. В итоге наглядно видим, что для отыскания I нужно напряжение делить на сопротивление R:

Если вы знаете I и R, и желаете определить Е, тогда зачеркните E и посмотрите, что получилось. Вам нужно умножить величину тока I, протекающего в электрической цепи (ветви), на величину сопротивления участка цепи. В итоге вы получите значение падения напряжения E на этом участке:

В конце концов, вы придёте к тому, что знание алгебры необходимо для глубокого изучения электротехники и электроники. Приведённый выше способ позволит вам легко выполнять свои первые расчёты электрических цепей. Если же вы знакомы с алгеброй, то вам достаточно помнить формулировку Закона Ома с тем, чтобы составить необходимую пропорцию и из неё получить все остальные формулы для нахождения неизвестных величин.

Дата: 24.06.2015

© Valentin Grigoryev (Валентин Григорьев)

Возможно Вам будут интересны следующие статьи из этого раздела:

Если Вы не нашли ничего интересного в этом разделе, тогда Вам следует воспользоваться левым вертикальным меню, чтобы попасть в интересующий Вас раздел сайта.

Есть ли отличия закона Ома для цепей переменного и постоянного напряжения?

Закон Ома является одним из основных законов электротехники. Он довольно прост и применяется при расчете практически любых электрических цепей. Но данный закон имеет некоторые особенности работы в цепях переменного и постоянного тока при наличии в цепи реактивных элементов. Эти особенности нужно помнить всегда.

Закон Ома для цепи постоянного тока

Классическая схема закона Ома выглядит так:

А звучит и того проще – ток, протекающей на участке цепи, будет равен отношению напряжения цепи к ее сопротивлению, что выражается формулой:

Но ведь мы знаем, что помимо активного сопротивления R, существует и реактивные сопротивления индуктивности Х_L и емкости X_C. А ведь согласитесь, что электрические схемы с чисто активным сопротивлением встречаются крайне редко. Давайте рассмотрим схему, в которой последовательно включена катушка индуктивности L, конденсатор С и резистор R:

Помимо чисто активного сопротивления R, индуктивность L и емкость С имеют и реактивные сопротивления  Х_L и X_C, которые выражены формулами:

Где ω это циклическая частота сети, равная ω = 2πf. f – частота сети в Гц.

Для постоянного тока частота равна нулю (f = 0), соответственно реактивное сопротивление индуктивности станет равным нулю (формула (1)), а емкости – бесконечности (2), что приведет к разрыву электрической цепи. Отсюда можно сделать вывод, что реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.

Закон Ома для цепи переменного тока

Если рассматривать классическую электрическую цепь и на переменном токе, то она практически ничем не будет отличаться от постоянного тока, только источником напряжения (вместо постоянного — переменное):

Соответственно и формула для такого контура останется прежней:

Но если мы усложним схему и добавим к ней реактивных элементов:

Ситуация изменится кардинально. Теперь f у нас не равна нулю, что сигнализирует о том, что помимо активного, в цепь вводится и реактивное сопротивление, которое также может влиять на величину тока, протекаемого в контуре и приводить к резонансу. Теперь полное сопротивление контура (обозначается как Z) и оно не равно активному Z ≠ R. Формула примет следующий вид:

Соответственно немного изменится и формула для закона Ома:

Почему это важно?

Знание этих нюансов позволит избежать серьезных проблем, которые могут возникнуть при неправильном подходе к решению некоторых электротехнических задач. Например, в контур переменного напряжения подключена катушка индуктивности со следующими параметрами: f_ном = 50 Гц, U_ном = 220 В, R = 0,01 Ома, L = 0,03 Гн. Ток, протекающий через данную катушку будет равен:

Где:

В случае, если подать на эту же катушку постоянное напряжение с таким же значением, получим:

Мы видим, что ток катушки возрастает в разы, что приводит к выходу из строя элементов контура.

Калькулятор закона

Ом

Укажите любые 2 значения и нажмите «Рассчитать», чтобы получить другие значения в уравнениях закона Ома V = I × R и P = V × I.

Связанный: калькулятор резистора

Закон Ома

Закон

Ома гласит, что ток через проводник между двумя точками прямо пропорционален напряжению. Это верно для многих материалов в широком диапазоне напряжений и токов, а сопротивление и проводимость электронных компонентов, изготовленных из этих материалов, остаются постоянными.Закон Ома верен для цепей, которые содержат только резистивные элементы (без конденсаторов или катушек индуктивности), независимо от того, является ли управляющее напряжение или ток постоянным (DC) или изменяющимся во времени (AC). Его можно выразить с помощью ряда уравнений, обычно всех трех вместе, как показано ниже.

Где:

В — напряжение в вольтах
R — сопротивление в Ом
Я ток в амперах

Электроэнергетика

Мощность — это скорость, с которой электрическая энергия передается по электрической цепи в единицу времени, обычно выражается в ваттах в Международной системе единиц (СИ).Электроэнергия обычно вырабатывается электрическими генераторами и поставляется предприятиям и домам через электроэнергетику, но также может поступать от электрических батарей или других источников.

В резистивных цепях закон Джоуля можно объединить с законом Ома для получения альтернативных выражений для количества рассеиваемой мощности, как показано ниже.

P = V × I
P =
P = I 2 × R

Где:

P — мощность в ваттах

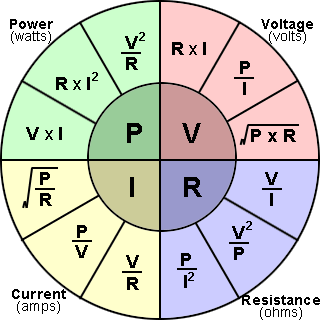
Колесо формулы закона Ома

Ниже приведено колесо формул для соотношений по закону Ома между P, I, V и R.По сути, это то, что делает калькулятор, и это просто представление алгебраической манипуляции с уравнениями выше. Чтобы использовать колесо, выберите переменную, которую нужно найти в середине колеса, затем используйте соотношение для двух известных переменных в поперечном сечении круга.

,Закон

Ома | Электрические цепи

Закон 11,2 Ома (ESBQ6)

Три основные величины для электрических цепей: ток, напряжение (разность потенциалов) и сопротивление . Резюме:

1. Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.

2. Разность потенциалов или напряжение \ (В \) — это количество энергии на единицу заряда, необходимое для перемещения этого заряда между двумя точками в цепи.

3. Сопротивление, \ (R \), является мерой того, насколько «трудно» протолкнуть ток через элемент схемы.

Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.

Важная взаимосвязь между током, напряжением и сопротивлением в цепи была обнаружена Георгом Симоном Омом и называется законом Ома .

Закон Ома

Величина электрического тока через металлический проводник при постоянной температуре в цепи пропорциональна напряжению на проводнике и может быть описана как

\ (I = \ frac {V} {R} \)

где \ (I \) — ток через проводник, \ (V \) — напряжение на проводнике, а \ (R \) — сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводника постоянно, независимо от приложенного к нему напряжения или проходящего через него тока.

Закон

Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий по проводнику, прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на ось X графика, а ток — на ось Y графика, мы получим прямую линию.

Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R}.\] С точки зрения постоянного сопротивления это можно изменить как: \ [R = \ frac {V} {I}. \]

Закон Ома

Цель

Для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов (напряжением) на том же резисторе.

Аппарат

4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода

Метод

Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное к резистору напряжение и измерять результирующий ток в цепи.Во второй части мы будем изменять ток в цепи и измерять результирующее напряжение на резисторе. После получения обоих наборов измерений мы исследуем взаимосвязь между током и напряжением на резисторе.

1. Изменение напряжения:

   1. Настройте схему в соответствии со схемой 1), начиная с одной ячейки.

   2. Нарисуйте следующую таблицу в своем лабораторном журнале.

      Количество ячеек	Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))
      \ (\ text {1} \)
      \ (\ text {2} \)
      \ (\ text {3} \)
      \ (\ text {4} \)

   3. Попросите учителя проверить электрическую цепь перед включением питания.

   4. Измерьте напряжение на резисторе с помощью вольтметра и ток в цепи с помощью амперметра.

   5. Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.

   6. Повторяйте, пока не получите четыре ячейки и не заполните таблицу.

2. Изменение тока:

   1. Настройте схему в соответствии со схемой 2), начиная с одного резистора в цепи.

   2. Нарисуйте следующую таблицу в своем лабораторном журнале.

      Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))

   3. Попросите учителя проверить вашу электрическую схему перед включением питания.

   4. Измерьте ток и напряжение на единственном резисторе.

   5. Теперь добавьте еще один резистор в цепь и снова измерьте ток и напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока у вас не будет четырех последовательно, но не забывайте каждый раз измерять напряжение только на исходном резисторе. Введите измеренные вами значения в таблицу.

Анализ и результаты

1. Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения.Поскольку напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная, которая будет отложена по оси \ (x \). Ток является зависимой переменной и должен быть нанесен на ось \ (y \).

2. Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом случае независимой переменной является ток, который должен быть нанесен на ось \ (x \), а напряжение является зависимой переменной и должно быть нанесено на ось \ (y \).

Выводы

1. Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?

2. Изучите график, который вы построили из второй таблицы. Что происходит с напряжением на резисторе, когда ток через резистор увеличивается? т.е. увеличивается или уменьшается?

3. Подтверждают ли результаты ваших экспериментов закон Ома? Объясните.

Вопросы и обсуждение

1. Для каждого из ваших графиков рассчитайте градиент и по нему определите сопротивление исходного резистора. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?

2. Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_0 \)?

Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.

Зарегистрируйтесь здесь

Закон Ома

Упражнение 11.1

Постройте график напряжения (по оси X) и тока (по оси Y).

Какой тип графика вы получите (прямолинейный, парабола, другая кривая)

прямая линия

Рассчитайте градиент графика.

Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжения:

\ Начать {*} Align m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\ & = \ текст {0,13} \ Конец {*} выравнивание

Подтверждают ли результаты ваших экспериментов закон Ома? Объясните.

Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.

Как вы можете определить сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_ {0} \)?

Вы начинаете с подключения известного резистора в цепь с источником питания. Теперь вы читаете напряжение источника питания и записываете его.

Затем вы последовательно подключаете два резистора.Теперь вы можете измерить напряжение на каждом из резисторов.

Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:

\ [V = IR \]

Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток везде одинаковый в цепи, мы можем найти неизвестное сопротивление.

\ Начать {*} Align V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ Конец {*} выравнивание

Омические и неомические проводники (ESBQ7)

Проводники, которые подчиняются закону Ома, имеют постоянное сопротивление, когда на них изменяется напряжение или увеличивается ток, проходящий через них.Эти проводники называются омическими проводниками, проводниками. График зависимости тока от напряжения на этих проводниках будет прямолинейным. Некоторые примеры омических проводников — резисторы цепи и нихромовая проволока.

Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводников называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка — распространенный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.

В лампочке сопротивление нити накала резко возрастает, когда она нагревается от комнатной до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, в результате этого увеличения тока произойдет повышение температуры нити накала, что приведет к увеличению ее сопротивления. Это эффективно ограничивает увеличение тока.В этом случае напряжение и ток не подчиняются закону Ома.

Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорировать. При применении металлических нитей накала ламп, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \) и начиная с комнатной температуры), изменение довольно велико.

В общем, для неомических проводников график зависимости напряжения от тока не будет прямолинейным, что указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.

Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определят, какой из них подчиняется закону Ома. Вам потребуются лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны обнаружить, что резистор подчиняется закону Ома, а лампочка — нет.

Омические и неомические проводники

Aim

Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома

Аппарат

4 ячейки, резистор, лампочка, провода соединительные, вольтметр, амперметр

Метод

Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во второй — лампочка.Настройте обе схемы выше, начиная с 1 ячейки. Для каждой цепи:

1. Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметра.

2. Измерьте ток в цепи с помощью амперметра.

3. Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.

Результаты

Нарисуйте в своей книге две таблицы, которые выглядят следующим образом.У вас должна быть одна таблица для измерений первой цепи с резистором и другая таблица для измерений второй цепи с лампочкой.

Количество ячеек	Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)

Анализ

Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs.\ (V \) (\ (x \) — ось), один для резистора и один для лампочки.

Вопросы и обсуждение

Внимательно изучите свои графики и ответьте на следующие вопросы:

1. Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?

2. Один или оба ваших графика выглядят так?

3. Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка закону Ома?

4. Имеет ли лампочка омический или неомический провод?

Использование закона Ома (ESBQ8)

Теперь мы готовы посмотреть, как закон Ома используется для анализа схем.

Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \), а напряжение на резисторе равно \ (\ text { 5} \) \ (\ text {V} \), то мы можем использовать закон Ома для расчета тока, протекающего через резистор. Наша первая задача — нарисовать принципиальную схему. Решая любую проблему с электрическими цепями, очень важно составить схему цепи, прежде чем производить какие-либо расчеты. Принципиальная схема этой проблемы выглядит следующим образом:

Уравнение закона Ома: \ [R = \ frac {V} {I} \]

, который можно преобразовать в: \ [I = \ frac {V} {R} \]

Ток, протекающий через резистор:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}

Рабочий пример 1: Закон Ома

Изучите принципиальную схему ниже:

Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор, равен \ (\ text {4} \) \ (\ text {A} \ ).Какова разность потенциалов (напряжение) на резисторе?

Определите, как подойти к проблеме

Нам задают сопротивление резистора и ток, проходящий через него, и просят вычислить напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]

Решить проблему

Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \). \ Начать {*} Align R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}

Напишите окончательный ответ

Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).

Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.

Зарегистрируйтесь здесь

Закон Ома

Упражнение 11.2

Вычислите сопротивление резистора с разностью потенциалов \ (\ text {8} \) \ (\ text {V} \) на нем, когда ток равен \ (\ text {2} \) \ (\ text {A} \) протекает через него. Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

. \ Начать {*} Align R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ Конец {*} выравнивание

Какой ток будет протекать через резистор \ (\ text {6} \) \ (\ text {Ω} \) при разности потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

. \ Начать {*} Align I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ Конец {*} выравнивание

Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет хоть это? Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

. \ Начать {*} Align V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ Конец {*} выравнивание

Резисторы последовательно и параллельно (ESBQ9)

В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы соединены последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. В параллельной цепи есть несколько путей, по которым течет ток.

Когда в цепи более одного резистора, мы обычно можем рассчитать общее суммарное сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .

Эквивалентное последовательное сопротивление

В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление — это просто сумма сопротивлений всех резисторов.

Эквивалентное сопротивление в последовательной цепи,

Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:

\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]

Применим это к следующей схеме.

Резисторы включены последовательно, следовательно:

\ Начать {*} Align R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {align *}

Эквивалентное параллельное сопротивление

В схеме, в которой резисторы включены параллельно, эквивалентное сопротивление определяется следующим определением.

Эквивалентное сопротивление в параллельной цепи

Для резисторов \ (n \), подключенных параллельно, эквивалентное сопротивление составляет:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]

Применим эту формулу к следующей схеме.

Какое полное (эквивалентное) сопротивление в цепи?

\ Начать {*} Align \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \право) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text { 1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text {Ω}} {\ text {10} \ text { Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {align *}

Последовательное и параллельное сопротивление

Упражнение 11.3

Два \ (\ text {10} \) \ (\ text {kΩ} \) резистора соединены последовательно. Рассчитайте эквивалентное сопротивление.

Поскольку резисторы включены последовательно, мы можем использовать:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ Начать {*} Align R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\ & = \ текст {20} \ текст {кОм} \ Конец {*} выравнивание

Два резистора соединены последовательно.Эквивалентное сопротивление равно \ (\ text {100} \) \ (\ text {Ω} \). Если один резистор равен \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.

Поскольку резисторы включены последовательно, мы можем использовать:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ Начать {*} Align R_ {s} & = R_ {1} + R_ {2} \\ R_ {2} & = R_ {s} — R_ {1} \\ & = \ text {100} \ text {Ω} — \ text {10} \ text {Ω} \\ & = \ текст {90} \ текст {Ω} \ Конец {*} выравнивание

Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитайте эквивалентное сопротивление.

Поскольку резисторы включены параллельно, мы можем использовать:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ Начать {*} Align \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\ & = \ frac {1 + 10} {\ text {100}} \\ & = \ frac {11} {\ text {100}} \\ R_ {p} & = \ text {9,09} \ text {kΩ} \ Конец {*} выравнивание

Два резистора подключены параллельно.Эквивалентное сопротивление равно \ (\ text {3,75} \) \ (\ text {Ω} \). Если сопротивление одного резистора равно \ (\ text {10} \) \ (\ text {Ω} \), каково сопротивление второго резистора?

Поскольку резисторы включены параллельно, мы можем использовать:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ Начать {*} Align \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} \\ & = \ frac {1} {\ text {3,75}} — \ frac {1} {\ text {10}} \\ & = \ frac {\ text {10} — \ text {3,75}} {\ text {37,5}} \\ & = \ frac {\ text {6,25}} {\ text {37,5}} \\ R_ {2} & = \ текст {6} \ текст {Ω} \ Конец {*} выравнивание

Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:

a) Резисторы включены параллельно, поэтому мы используем:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ Начать {*} Align \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\ & = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\ & = \ frac {\ text {5}} {\ text {6}} \\ R & = \ текст {1,2} \ текст {Ω} \ Конец {*} выравнивание

b) Резисторы включены параллельно, поэтому мы используем:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыва {1} {R_ {4}} \]

Эквивалентное сопротивление:

\ Начать {*} Align \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\ & = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\ & = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\ & = \ frac {\ text {25}} {\ text {12}} \\ R & = \ text {0,48} \ text {Ω} \ Конец {*} выравнивание

c) Резисторы включены последовательно, поэтому мы используем:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ Начать {*} Align R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\ & = \ текст {5} \ текст {Ω} \ Конец {*} выравнивание

d) Резисторы включены последовательно, поэтому мы используем:

\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]

Эквивалентное сопротивление:

\ Начать {*} Align R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ text {1} \ text {Ω} \\ & = \ текст {10} \ текст {Ω} \ Конец {*} выравнивание

Применение закона Ома в последовательных и параллельных цепях (ESBQB)

Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими установками.

Последовательные цепи

Рассмотрим схему, состоящую из трех резисторов и одного одиночная ячейка соединена последовательно.

Первый принцип, который нужно понять в отношении последовательных цепей, заключается в том, что величина тока одинакова через любой компонент в цепи. Это потому, что существует только один путь для движения электронов в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении будет течь ток. Мы знаем, что ток по условию течет от положительного к отрицательному.Обычный ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к A.

Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:

\ [I = I_ {1} = I_ {2} = I_ {3}. \]

Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений на всех трех резисторах. Итак, мы можем написать:

\ [V = V_ {1} + V_ {2} + V_ {3} \]

Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления последовательно включенных резисторов, мы можем решить некоторые проблемы схемы.

Рабочий пример 2: Закон Ома, последовательная цепь

Рассчитайте ток (I) в этой цепи, если оба резистора имеют омическую природу.

Определите, что требуется

Нам необходимо рассчитать ток, протекающий в цепи.

Определите, как подойти к проблеме

Поскольку резисторы по своей природе омические, мы можем использовать закон Ома. Однако в цепи два резистора, и нам нужно найти полное сопротивление.

Найдите полное сопротивление в цепи

Поскольку резисторы соединены последовательно, полное (эквивалентное) сопротивление R составляет:

\ [R = R_ {1} + R_ {2} \]

Следовательно,

\ Начать {*} Align R & = \ текст {2} + \ текст {4} \\ & = \ текст {6} \ текст {Ω} \ end {align *}

Примените закон Ома

\ begin {align *} R & = \ frac {V} {I} \\ R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\ I & = \ frac {V} {R} \\ & = \ frac {12} {6} \\ & = \ текст {2} \ текст {А} \ end {align *}

Напишите окончательный ответ

В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).

Рабочий пример 3: Закон Ома, последовательная цепь

Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найдите сопротивление \ (R_ {2} \), учитывая, что ток, текущий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ ( \ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ text {V} \). \ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).

Нарисуйте схему и введите все известные значения.

Определите, как подойти к проблеме.

Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление, используя:

\ [R = R_ {1} + R_ {2} \]

, потому что он находится в последовательной цепи.

Найдите полное сопротивление

\ Начать {*} Align R & = \ frac {V} {I} \\ & = \ frac {\ text {1,5}} {\ text {0,25}} \\ & = \ текст {6} \ текст {Ω} \ end {align *}

Найдите неизвестное сопротивление

Мы знаем, что:

\ [R = \ text {6} \ text {Ω} \]

и что

\ [R_ {1} = \ text {1} \ text {Ω} \]

с

\ [R = R_ {1} + R_ {2} \] \ [R_ {2} = R — R_ {1} \]

Следовательно,

\ [R_ {1} = \ text {5} \ text {Ω} \]

Рабочий пример 4: Закон Ома, последовательная цепь

Для следующей схемы рассчитайте:

1. падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \) и \ (R_3 \)

2. сопротивление \ (R_3 \).

Определите, как подойти к проблеме

Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета падения напряжения на известных резисторах. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \). Теперь мы можем использовать эту информацию, чтобы найти напряжение на неизвестном резисторе \ (R_3 \).

Рассчитать падение напряжения на \ (R_1 \)

Используя закон Ома: \ Начать {*} Align R_1 & = \ frac {V_1} {I} \\ I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\ V_1 & = {I} \ cdot {R_1} \\ & = 2 \ cdot 1 \\ V_1 & = \ текст {2} \ текст {V} \ end {align *}

Рассчитать падение напряжения на \ (R_2 \)

Снова используя закон Ома: \ Начать {*} Align R_2 & = \ frac {V_2} {I} \\ I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\ V_2 & = {I} \ cdot {R_2} \\ & = 2 \ cdot 3 \\ V_2 & = \ текст {6} \ текст {V} \ end {align *}

Рассчитать падение напряжения на \ (R_3 \)

Поскольку падение напряжения на всех резисторах вместе взятых должно быть таким же, как падение напряжения на ячейке в последовательной цепи, мы можем найти \ (V_3 \), используя: \ Начать {*} Align V & = V_1 + V_2 + V_3 \\ V_3 & = V — V_1 — V_2 \\ & = 18-2-6 \\ V_3 & am

.

Закон Ома для всей цепи

Закон Ома — один из основных постулатов физики. Общая формула, действующая как для всей цепи, так и для ее участка, указывает, что сила тока равна частичному значению, полученному в результате деления значения, выражающего напряжение в вольтах, на значение, выражающее ток в амперах. Эта зависимость показывает, что с уменьшением сопротивления ток увеличивается. Возникает вопрос: можно ли получить максимальную силу тока, снизив сопротивление до нуля? Практика показывает, что это невозможно.Закон Ома для всей цепи указывает, что напряжение следует разделить на полное, полное сопротивление, рассчитанное как сумма внешнего и внутреннего сопротивления, в зависимости от источника тока. Невозможно снизить внутреннее сопротивление системы до нуля. В противном случае очень высока вероятность взрыва аккумулятора.

Что такое внутреннее и внешнее сопротивление, согласно закону Ома для всей цепи? Если, например, в цепь подключен свет, то внешнее сопротивление этой лампочки.Внутреннее сопротивление всегда исходит от батареи, то есть формируется внутри самой системы. Если вместо батареи используется гальванический элемент, закон Ома для всей цепи учитывает сопротивление раствора электролита и электродов. Если внешнее сопротивление в несколько раз меньше внутреннего и цепь замкнута, по ней протекает ток короткого замыкания. Это максимальное значение тока, которое может пройти через эту цепь. Источники тока в автомобилях показывают значения силы тока короткого замыкания, критически опасные для жизни.В целях безопасности они подключаются к внешним аккумуляторным устройствам, которые обладают достаточным сопротивлением для предотвращения трагедии.

При последовательном подключении общее внутреннее сопротивление цепи рассчитывается путем сложения сопротивлений каждого из источников тока. При параллельном подключении напряжение на каждой из секций ответвления одинаково, а ток в неразветвленной цепи рассчитывается путем сложения значений, которые показывают амперметры на каждой из секций, соединенных параллельно.Источник тока на участке схемы не влияет на подключенный к нему параллельный участок.

Где применяются законы Ома для всей цепи? В основном они используются для расчета силы тока в линейных электрических цепях постоянного тока. Чтобы правильно производить расчеты, необходимо помнить постулаты Кихгофа. Во-первых, алгебраическая сумма текущих сил на сайте равна нулю. Во-вторых, произведение алгебраической суммы сил тока в любом замкнутом контуре разветвленной цепи на сопротивление участков данного контура всегда равно алгебраической сумме напряжений, находящихся в цепи.

При каких условиях, как и когда открылся закон на всю цепочку? Швейцарский исследователь Георг Симон Ом пришел к эмпирической формуле, известной сегодня всему миру. Он изучал магнитное действие тока и экспериментировал с различными генераторами, в своих экспериментах использовал проводники из разных металлов и сплавов. Ом был первым физиком, заметившим влияние температуры на проводники. Закон Ома для полной цепи был признан научным сообществом не сразу.Первыми учеными, которые оценили этот закон, были русские исследователи Якоби и Ленц. Американец Дж. Генри позже сравнил формулу, выражающую закон Ома для всей цепи, с молнией посреди безлюдной мрачной комнаты, а немецкий профессор Э. Ломмель назвал проем «ярким факелом в области электричества».

p >> ,

Согласно закону Ома, I V, но I ∝ 1 / V в уравнении мощности. Как?

In I = V / R, ток прямо пропорционален напряжению, но ток обратно пропорционален напряжению в P = VI?

Это еще один запутанный вопрос, который чаще всего задают на собеседованиях по электротехнике и электронике.

Согласно закону Ома, Ток увеличивается при увеличении напряжения (I = V / R), но Ток уменьшается при увеличении напряжения согласно формуле (P = VI).Как объяснить?

, т.е.

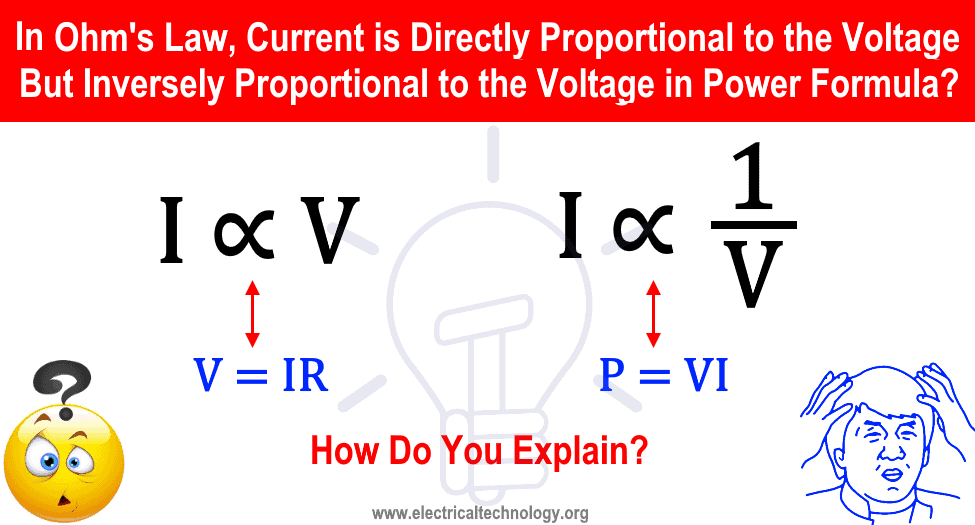
• Согласно закону Ома: I ∝ V (ток прямо пропорционален напряжению. I = V / R)
• Согласно формуле мощности: I 1 / V (ток обратно пропорционален напряжению. I = P / V)

Короче говоря, согласно закону Ома (V = IR или I = V / R), который показывает, что ток прямо пропорционален напряжению, но согласно P = VI или I = P / V , это показывает, что ток обратно пропорционален напряжению.

Давайте устраним путаницу, связанную с утверждением.

P = V x I

Фактически, это зависит от того, как вы увеличиваете параметры, то есть увеличиваете ли вы напряжение, сохраняя мощность источника постоянной или она меняется.

• Если мощность источника постоянная, ток будет уменьшаться при увеличении напряжения.
• Если вы не заботитесь о мощности и просто замените батарею на новую с более высокой номинальной мощностью, это может увеличить ток при повышении напряжения, поскольку мощность больше не постоянна i.е. мощность также была увеличена.

В случае трансформатора, когда напряжение увеличивается, ток уменьшается, потому что мощность остается постоянной, т.е. мощность на обеих сторонах равна P = VI (без учета коэффициента мощности: Cos θ).

В = I x R

По закону Ома ток (I) прямо пропорционален напряжению (В), если сопротивление (R) и температура остаются постоянными.

Согласно формуле мощности, она говорит, что ток обратно пропорционален напряжению, если мощность остается прежней.

Как мы уже знаем, в повышающем трансформаторе, если напряжение увеличивается, ток уменьшается там, где мощность такая же (поскольку трансформатор только повышает или понижает значение тока и напряжения и не меняет значение мощность). Точно так же напряжение уменьшается при увеличении тока в понижающем трансформаторе.

То же самое и с электростанцией, где выработка электроэнергии постоянна. Если мощность на стороне генерации улучшится, увеличатся как ток, так и напряжение.

Вкратце:

• Если мощность постоянная = Напряжение обратно пропорционально току , т.е. В 1 / I в P = VxI .
• Если сопротивление и температура постоянны: Напряжение прямо пропорционально току , т.е. В ∝ I в В = IxR .

Именно поэтому по закону Ома ток прямо пропорционален напряжению, но обратно пропорционален формуле напряжения в мощности.

Связанные вопросы / ответы:

.