формулировка закона, расчет теплоты по формуле i2rt

Одной из основополагающих, теоретически и практически значимых закономерностей физики можно смело назвать закон Джоуля Ленца, который англичанин Дж. Джоуль и россиянин Э.Х. Ленц вывели примерно в одно время (в 1840-1841 годах), однако при этом, не работая совместно.

Авторы закона: Джеймс Джоуль и Эмилий Ленц

Как был открыт закон

Оба физика проводили множество экспериментов, в которых главным действующим прибором был калориметр. Агрегат представлял собой устройство, изолированное от теплопотерь, у которого была измерена и зафиксирована теплоемкость. Калориметр был оснащен термометром, в него также вставлялся проводник с определенным электросопротивлением.

В результате опытов физики заметили, что при подключении проводника к электропитанию начинает выделяться тепло.

Воспроизведение опытов, с помощью которых была сформулирована закономерность Джоуля-Ленца

Джоуль проводил эти исследования в рамках изучения закона сохранения энергии. Он хотел оценить, какова величина механической энергии, давшей полученное количество теплоты. Для этого к динамо-машине, вращавшей ротор для выработки электричества, он привязывал некий груз и делал вывод, что разница между механической энергией груза в поле и вне поля тяготения и есть искомая величина. Англичанин доказал, что сделанные им выводы о преобразовании энергии применимы и для электролитических растворов.

Опыты Ленца более точные. Он определил, что открытая им закономерность не действует, если проводники двигаются, когда через них течет электроток (они называются проводники второго типа), такие как индуктивная катушка, находящаяся внутри электромотора.

Суть теплового закона

В проводнике, являющимся активным сопротивлением, по которому пропускается постоянное электричество, имеется электрическое поле, в котором упорядоченно протекают заряженные частицы. Электрофизические силы, присущие ему, оказывают воздействие на электроны, что имеет определение «работа тока» (Aэл. ). Та работа, которая замеряется в единицу времени (как правило, час), считается мощностью тока (Nэл.). Обозначенные электромеханические показатели измеряются при помощи приборов: амперметра, вольтметра и ваттметра. Эти 2 понятия: работа и мощность тока, формируют закон Джоуля Ленца.

Работа тока на подключенном участке преобразовывает электроэнергию во внутреннюю. Это происходит за счет того, что свободные электроны натыкаются на нейтральные молекулы (лишенные электронов) проводника, и присущая им механическая энергия превращается в тепловую. Она способствует увеличению температуры проводника. Согласуясь со всемирным законом сохранения энергии, тот объем тепла (q) приравнивается к работе тока.

Всякое преодоление сопротивления неизбежно сопровождается затратами энергии. Если, к слову, что-то тяжелое приходится тянуть, преодолевая силу трения, то работа по ее преодолению становится теплом. В случае с током и полупроводником электросопротивление выступает в роли трения.

Российский и английский ученые пришли к выводу, что количество теплоты q, получаемое в полупроводнике при прохождении постоянного тока, прямо пропорционально величине тока (I), возведенной во вторую степень, и тому времени (t), что ток пропускался по проводнику, испытывая сопротивление (R).

Знаменитый закон Лжоуля Ленца можно описать формулой:

Q =I2Rt.

Это закономерность – закон Джоуля-Ленца, применимый на однородном участке электроцепи. При этом количество тепла q может вычисляться в Джоулях (если сила тока равна 1) и в малых калориях (если сила тока 0,24). Малая калория – это количество тепла, расходуемое на нагрев 1 грамма воды на один градус.

Интегральная и дифференциальная формулы закона

Если обратить внимание на величину, представляющую разность внутренней энергии проводника за время прохождения по нему тока, можно заметить, что постепенно при нагревании эта энергия будет увеличиваться. Следуя закону Ньютона, можно предположить, что увеличится и мощность отдачи тепла q проводником. Через определенный промежуток времени температура полупроводника зафиксируется и перестанет расти. В это время внутренняя энергия перестанет меняться, и значение «дельта U» станет равно нулю. В таком равновесии формулировка 1-го термодинамического закона будет следующей:

A = – Q, т.е. работа тока полностью переходит в тепло.

Основываясь на этом выводе, можно представить тепловую закономерность Джоуля Ленца в несколько другом виде, а именно в ее интегральном и дифференциальном видах.

Закон Джоуля Ленца в интегральной и дифференциальной формах

Формула интегрального закона Джоуля-Ленца справедлива при любых данных, поэтому она считается законом. Другие же формулировки типа:

q=I*Ut и q=u2/R*t

работают лишь при определенных условиях, и их нельзя считать законом.

Дополнительная информация. Если углубляться в теорию и проводить дальнейшие расчеты, то можно вывести и другие формы данного теплового закона.

Теоретическая значимость

Открытие двух знаменитых физиков стало заметной вехой на пути к исследованию и всемирному принятию закона сохранения энергии. Благодаря ему, сегодня общеизвестно, что и тепло, и электроток, и движение механических частиц – есть формы материи, обладающие своей энергией, которую можно измерить. Закон Джоуля-Ленца (и последующие работы Джоуля) помогли установить соответствия для электрического, механического и теплового вида энергии и определить переводные соотношения между единицами различных видов (калории и джоули). Тепловая закономерность применяется и в разработке теории тока в металлах.

Обратите внимание! Поскольку тепло всегда вырабатывается в проводнике, находящемся под электрическим током, может случиться его перегрев и, как следствие, выход из строя электрических устройств. Особенно опасным явлением является короткое замыкание, когда сопротивление проводников стремится к нулю, ток становится очень сильным, соответственно, выделяется огромное количество тепла, приводящее к аварийным состояниям.

Чрезмерное выделение тепловой энергии при коротком замыкании

С помощью закона Джоуля-Ленца можно рассчитать оптимальную силу электротока, чтобы предотвратить перегрев проводников.

Попробуйте сформулируйте положение о том, как электричество переходит в тепло? Англичанину Джоулю и россиянину Ленцу это блестяще удалось: в открытом ими тепловом законе, гласящем, что электрический ток, проходящий по проводнику, выделяет тепло, равное работе электрических сил. Это наблюдение оказало большое влияние на дальнейшее развитие физики как науки.

Видео

Оцените статью:

Фізика закон джоуля-ленца — florstory.ru

Скачать фізика закон джоуля-ленца EPUB

Закон джоуля ленца формула и определение. Двигаясь в любом проводнике, электрический ток передает ему какую-то энергию, из-за чего проводник нагревается.

Энергетическая передача осуществляется на уровне молекул: в результате взаимодействия электронов тока с ионами или атомами проводника часть энергии остается у последнего.  Затем проводник отдает ее окружающим телам, то есть осуществляется теплопередача с нагреванием проводника.

Формула для расчета в этом случае следующая: A=U*I*t. Количество теплоты можно обозначить через Q. Тогда Q=A или Q=U*I*t. Зная, что U=IR, получается Q=I 2 *R*t, что и было сформулировано в законе Джоуля-Ленца. Знаменитый русский физик Ленц и английский физик Джоуль, проводя опыты по изучению тепловых действий электрического тока, независимо друг от друга вывели закон Джоуля-Ленца.

Данный закон отражает взаимосвязь количества теплоты, выделяемого в проводнике, и электрического тока, проходящего по этому проводнику в течение определенного периода времени. Содержание. Свойства электрического тока. Закон джоуля Ленца формула и определение.

Закон Джоуля-Ленца. Работа и мощность электрического тока.

Свойства электрического тока. Когда электрический ток проходит через металлический проводник, его электроны. Закон Джоуля-Ленца. Преодолевая сопротивление проводника, электрический ток выполняет работу, в процессе которой в проводнике выделяется тепло. Свободные электроны при своем движении сталкиваются с атомами и молекулами и при этих столкновениях механическая энергия движущихся электронов переходит в тепловую.

Зависимость тепловой энергии от силы тока в проводнике определяется по закону Джоуля-Ленца. При прохождении электрического тока по проводнику количество тепла, выделяемого током в проводнике, прямо пропорционально силе тока, взятой во второй степени, величине сопротивления проводника и врем. Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока.

Установлен в году Джеймсом Джоулем и независимо от него в году Эмилием Ленцем[1]. Закон Джоуля—Ленца». На одном из прошлых уроков мы с вами говорили о действиях электрического тока, которые он способен оказывать, протекая в различных средах: Также мы с вами говорили о том, что тепловое действие ток производит и любой среде: твёрдой, жидкой и газообразной.  Так, энергия электрического поля переходит во внутреннюю энергию проводника.

Обратимся теперь к количественной стороне вопроса: сколько теплоты выделяется при прохождении тока определённой силы в данном конкретном проводнике? Ответ на него мы найдём, применив закон сохранения энергии.

Открытие закона Джоуля-Ленца сулило огромные перспективы. Ведь, по сути, этот закон позволил создавать своего рода разные электронагревательные приборы и элементы. Например, чуть позже после открытия закона учёные заметили, что при нагревании определённых элементов они начинают светиться.

Они захотели поэкспериментировать с ними, используя разные проводники, и в году русский инженер Александр Николаевич Лодыгин изобрёл современную лампу накаливания, нить которой была сделана из вольфрама. Применяется закон Джоуля-Ленца и в электротехнике – например, при создании плавких предохранителей. Закон Джоуля-Ленца. Преодолевая сопротивление проводника, электрический ток выполняет работу, в процессе которой в проводнике выделяется тепло.

Свободные электроны при своем движении сталкиваются с атомами и молекулами и при этих столкновениях механическая энергия движущихся электронов переходит в тепловую. Зависимость тепловой энергии от силы тока в проводнике определяется по закону Джоуля-Ленца. При прохождении электрического тока по проводнику количество тепла, выделяемого током в проводнике, прямо пропорционально силе тока, взятой во второй степени, величине сопротивления проводника и врем.

Закон Джоуля-Ленца. Выделение тепла на проводниках – причина их перегорания, возникновения пожаров и других неполадок в электрооборудовании. Но это явление лежит также в основе электросварки и других технологий.  Какая-то ее часть может вносить вклад в общий нагрев проводника.

Таковы механизмы. Но закон Джоуля-Ленца носит качественный характер. Его выводили эмпирическим путем, постановкой опытов с разными проводниками различной длинны и площади сечения, с разными значениями силы тока. В ходе них были выявлены некоторые закономерности.

txt, txt, txt, doc

Похожее:

Новітня історія країн азії та африки читать онлайн

Презентація дитячі роки тараса шевченка

Гдз фізика 11 клас божинова каплун кірюхіна лабораторні

Біологія 6 класс читать онлайн

Презентація екологічна система

Закон Джоуля — Справочник химика 21

    Суммарную теплоемкость калориметрической системы определяют электрическим способом. Для этого к калориметрической системе подводят известное количество электрической энергии, превращающейся в тепло (З- Необходимо точно измерить время пропускания тока, ток и падение напряжения иа нагревателе.

Количество сообщенного системе тепла вычисляют по закону Джоуля [c.136]
    Количество теплоты прохождении тока, по закону Джоуля — Ленца равно  [c.83]

    Количество теплоты, сообщенной калориметру при пропускании постоянного тока, вычисляют, исходя из закона Джоуля — Ленца  [c.68]

    Это соотношение имеет кардинальное значение для экспериментального определения теплоемкостей и теплот процессов. Измерить теплоемкость можно, подводя к системе определенное количество теплоты. Это несложно сделать помещают в систему проводник определенного сопротивления R и пропускают через него ток» силой / в течение времени . По закону Джоуля — Ленца количество теплоты, выделившееся в проводнике и переданное системе, равно  

[c.188]

    Приведем пример использования вектора Пойнтинга в цепях постоян-10Г0 тока. Согласно закону Джоуля — Ленца =Q — есть количество еплоты, выделяющейся в единицу времени в единице объема проводника. Здесь / и е соответственно плотность тока и удельное электрическое со-фотивление вещества). Учитывая, что поток электромагнитной энергии Р=Е поступает через боковую поверхность проводника, заметим, что по /1ере проникновения в глубь вещества поток энергии постепенно ослабляет- я за счет превращения ее в теплоту, уменьшается вектор Пойнтинга и та юверхность, через которую проходит поток. 

[c.53]

    Если через проводник проходит электрический ток, то при этом происходит выделение тепла, т. е. нагревание проводника. По закону Джоуля количество тепла Q), которое развивает электрический ток в проводнике, будет зависеть от мощности тока и времени прохождения его через проводник, т. е. [c.256]

    Это тепло должно быть передано воде, греющей проволокой. Таким образом, последняя при прохождении через нее тока силой в 3 а должна выделить 30 000 кал в течение т сек. Согласно закону Джоуля 

[c. 257]

    Согласно закону Джоуля энтальпия и внутренняя энергия идеального газа при постоянной температуре не зависят от давления или объема. Следовательно, [c.78]

    В отличие от химической энергии электрическая энергия обладает способностью целиком превращаться п тепло. Это свойство электрической энергии известно под названием закона Джоуля—Ленца, являющегося частным случаем закона сохранения энергии  [c.202]

    По закону Джоуля — Ленца подведенное тепло равно А/У = = lut, где — продолжительность нагревания (200—300 с). При всех измерениях она должна быть одинаковой. Опыт состоит из измерения водяного числа калориметра и собственно теплоемкости исследуемой жидкости. Водяным числом Св называют теплоемкость всех частей калориметра без жидкости. 

[c.54]

    Закон Джоуля — Ленца  [c.511]

    Это свойство идеального газа было обнаружено английским физиком Джоулем и вошло в науку как закон Джоуля (1843)  [c.52]

    Количество теплоты q n, введенное в калориметрическую систему электрическим током, рассчитывается по закону Джоуля [c.128]

    Если реакция происходит между идеальными газами, то можно установить соотношение между р и используя следующее свойство, известное под названием закона Джоуля (который здесь не приводится) внутренняя энергия идеального газа зависит только от его температуры. 

[c.169]

    Внутренняя энергия продуктов, образующихся в ходе реакции при постоянном объеме, согласно закону Джоуля, равна внутренней энергии продуктов, образующихся в ходе реакции при постоянном давлении (если температура одна и та же). [c.170]

    Как уже указывалось, изменение внутренней энергии, сопровождающее изотермический процесс, в случае идеального газа равно нулю (закон Джоуля)  [c.192]

    Согласно закону Джоуля внутренняя энергия идеального газа зависит только от температуры.

Иначе говоря, внутренняя энергия продуктов, образующихся в ходе реакции при постоянном объеме, равна внутренней энергии продуктов, образующихся в ходе реакции при постоянных давлении и температуре. Отсюда следует, что Л 7″ = 0. [c.65]

    Электрические печи применяются в электротермических процессах, при которых высокие температуры (до 3500°С) создаются преобразованием электрической энергии в тепловую. В электрических печах используют главным образом переменный электрический ток напряжением 50—130 В. Количество выделяющейся теплоты (Дж) рассчитывают по закону Джоуля  [c.195]

    Инженерные расчеты. Использование электроэнергии в печах с электрообогревом основано на законе Джоуля—Ленца  [c.867]

    Б. Обычно для фракционирования белков сыворотки используют рекомендованное выше напряжение 110 В, при котором разделение длится от 14 до 16 ч, и охлаждения не требуется. Для особых целей напряжение может быть увеличено, но, согласно закону Джоуля, при этом соответственно увеличится теплообразование. Выделение тепла можно уменьшить, если снизить ионную силу раствора. При достаточной влажности фильтровальной бумаги, на которой ведут электрофорез, и не очень высокой температуре окружающего воздуха можно повысить напряжение на полоске до 250—300 В, не принимая специальных мер для охлаждения. Однако при дальнейшем увеличении напряжения требуются специальные приспособления для охлаждения. [c.52]

    Возникающее по закону Джоуля тепло увеличивает испаре- [c.52]

    Указание для ответа используйте дифференциальные формы термического и калорического уравнений состояния и закон Джоуля. [c.294]

    По закону Джоуля-Ленца мощность тепловой энергии, выделяющейся в проводнике с током, пропорциональна сопротивлению проводника и квадрату тока. Ухудшение электрического контакта вследствие окисления и уменьшения пло- [c.298]

    В электропечах сопротивления используются элементы активного электрического сопротивления, и теплота выделяется в соответствии с известным законом Джоуля — Ленца Q = и /К, [c. 286]

    Поскольку температурные сигналы зависят от тока нагрузки /, результаты измерений следует приводить к определенной силе тока, составляющей, как правило, 50 % от номинального значения. Формула пересчета значений ДГ вытекает из закона Джоуля-Ленца  [c.300]

    Каждое из выражений (5,4,7) является обычной формой закона Джоуля — Ленца. Из (5,4,7) в частности, следует, что если — бесконечно малая первого порядка, то теплота, выделяемая током за конечный промежуток времени, окажется бесконечно малой второго порядка этой теплотой можно пренебречь. [c.74]

    Ql), выделенное при прохождении тока, определяется законом Джоуля — Ленца  [c.100]

    Термопары применяются не только для непосредственного измерения температуры, но и для опосредованного измерения электрических величин по тепловому действию тока. Такое измерительное устройство принято называть термоэлектрическим преобразователем. Он состоит из двух основных частей — электрического нагревателя и термопары (или батареи термопар) [1]. Схема преобразователя для измерения электрических величин представлена на рис. 2. Связь между током /, подводимым к нагревателю, и термоЭДС Е, возникающей в термопаре, согласно закону Джоуля-Ленца может быть представлена в виде [c.129]

    В электротермических печах обычно используется переменный ток низкого напряжения. Количество выделяющегося тепла определяется по закону Джоуля [c.213]

    Каждое слагаемое правой части уравнения (11,7) зависит только от температуры. Поэтому внутренняя энергия идеального газа не зависит ни от объема, занимаемого газом, ни от давления, под которым находится газ, а является функцией только температуры (закон Джоуля). В случае одноатомных идеальных газов последнее слагаемое правой части уравнения (П,7) равно нулю, а второе слагаемое по сравнению с первым ничтожно мало. Поэтому внутренняя энергия таких систем определяется только кинетической энергией поступательного движения частиц (I/ = Е .  [c.60]

    Э. X. Ленц в числе других вопросов изучил тепловое действие тока. В 1843 г. он теоретически обосновал и сформулировал закон теплового действия тока, который независимо от него эмпирически был установлен английским физиком Джоулем этот закон известен теперь как закон Джоуля — Ленца. [c.10]

    При Т = onst изменение V вызывает изменение Р, поэтому не только ди дУ)т = 0, но и (ди/дР)т = 0. Следовательно, энергия идеального газа зависит только от температуры закон Джоуля, 1844 г.)  [c.126]

    При наложении электрического напряжения число столкновений возрастает в тем большей степени, чем больше ток, прохо-дяш ий через сопро1Тивление, и тем больше электрической энергии в соответствии с законом Джоуля-Ленца превращается в тепло [c.254]

    ИДЕАЛЬНЫЙ ГАЗ, теоретич. модель газа, в к-ром средняя кинетич. энергия частиц много больше средней потенц. энергии их взаимодействия. Частицы И. г. движутся независимо друг от друга, его энергия равна сумме энергий отд. частиц, а давление на ограждающую стенку — сумме импульсов, передаваемых частицами стенке в единицу времени. Термодинамич. состояние И. г. описывается ур-нием Клапейрона р = пкТ, где р — давл., п — число частиц в единицу объема, к — постоянная Больцмана, Т — термодинамич. т-ра. Внутр. энергия И. г. зависит только от Г (закон Джоуля). Распределение частиц И. г. по скоростям подчиняется закону Максвелла. Реальные газы хорошо описываются моделью И. г., если они достаточно разрежены. В химии часто рассматривают смесь химически реагирующих И. г.., в частности применяют модель идеального ассоцииров. газа. [c.207]

    По закону Джоуля количество выделенного тепла Q рав1Го  [c.209]

---

§15.Закон Джоуля-Ленца. Работа и мощность тока

Если между двумя точками с напряжением U перенести заряд

, то совершается работа . Сила тока , а значит И .

Работа тока

. (15.1)

Ток, проходя по проводнику, совершает работу (15. 1) в результате чего в проводнике выделяется тепло Джоуля-Ленца.

(15.2)

Мощность, развиваемая током

. (15.3)

В истории законом Джоуля-Ленца называют формулу (15.3), а не формулу (15.2). Закон был открыт в 1841 г. Дж. Джоулем (1818–1889) и в последующем подробно исследован Ленцем.

Применим закон Джоуля-Ленца к бесконечному круглому цилиндру сечением

.

Учитывая, что сопротивление бесконечно малого цилиндра равно

.

Из (15.3) можем получить, что

.

Введем объемную плотность тепловой мощности, выделяемой в проводнике:

. (15.4)

Формула (15.4) выражает закон Джона–Ленца в дифференциальной форме, поскольку все величины относятся к одной и той же точке.

Преобразуем (15.4):

. (15.5)

Любое из этих равенств является записью закона Джоуля–Ленца в дифференциальной форме.

Пример.

Рассмотрим замкнутую цепь, содержащую источник тока и нагрузку R. Энергия, вырабатываемая источником тока

Эта работа по закону Джоуля–Ленца ,Для мощности N существуют два тока

При той же полезной мощности меньшая энергия вырабатывается источником тока при меньшем токе. При этом и меньшие потери на источнике тока:

КПД

.

Переходные процессы.

Рассмотрим переходные процессы, которые могут происходить в цепи при ее замыкании и размыкании.

В некоторый момент времени t<0 подключили конденсатор к источнику постоянного напряжения и зарядили его, т. е. на конденсаторе имеется заряд

.

В момент t=0 замыкаем ключ k, тогда в цепи появляется ток

.

Напряжение

И , приравнивая правые части, получим, где (t-характерное время установление тока)

Количество теплоты

Интегрируя последнее соотношение, находим

При

вся энергия заряженного конденсатора превращается в теплоту, т. е. .

Изобретения России // Закон Джоуля — Ленца

       Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцом

       Закон Джоуля-Ленца определяет меру теплового действия электрического тока. Дело в том, что электрический ток представляет собой перемещение заряда под действием электрического поля. Отсюда следует, что электрическое поле совершает работу.

 

       dA = U dq = IU dt

 

       Заметим, что IU = P, т.е. мощность, значит P = dA/dt

       Теперь давайте подумаем. Если электрическое поле совершает работу и ток может обладать мощностью, то должна выделяться энергия. Каким образом и куда эта энергия уходит. Оказывается, если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на нагревание этого проводника.

 

       dQ = dA

 

       Другими словами, энергия переходит в другое качество, в тепловую энергию. Долго экспериментируя, независимо друг от друга Дж. Джоуль и Э. Х. Ленц пришли к единому выводу: количество теплоты, выделяющейся током в проводнике равно работе электрического поля по перемещению заряда за время t.

 

       Q = Ut = I2rt

 

       Это и есть закон Джоуля — Ленца.

       Теперь посмотрим еще на один очень важный момент. Если выделить в проводнике элементарный цилиндрический объем dV = dS dl (ось цилиндра совпадает с направлением тока), то его сопротивление будет равно R = ρ dl/dS. Тогда, по закону Джоуля — Ленца

 

       dQ = I2r dt = ρ dl/dS (jdS)2 dt = ρj2 dV dt

 

       Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока

 

       w = ρj2

 

       То же можно записать используя дифференциальную форму закона Ома

 

       W = jE = γE2

 

       Последние два выражения являются обобщенным выражением закона Джоуля — Ленца.

       Единица измерения количества теплоты — Джоуль (Дж). 1 кал = 4,1868 Дж 1Дж = 0,24 кал

Электрический ток — закон Ома

Категория:

   Электрическое оборудование

Публикация:

   Электрический ток — закон Ома — закон Джоуля-Ленца

Читать далее:

Электрический ток — закон Ома — закон Джоуля-Ленца

Каждый крановщик должен четко представлять работу всего электрооборудования мостовых кранов, а для этого знать основы электротехники, чтобы понимать процессы, протекающие в электрических машинах и аппаратах.

Электрический ток бывает двух видов: постоянный и переменный. При протекании по электрической цепи постоянный ток не изменяет своего направления, а переменный меняет направление и величину. На практике обычно пользуются синусоидальным переменным током, т. е. током, изменяющимся по закону синусоиды.

Промежуток времени, затрачиваемый на полный цикл изменений переменного тока, после чего направление тока и его мгновенные значения начинают повторяться, называется периодом. Число периодов в секунду представляет собой частоту переменного тока. В нашей стране все электростанции, питающие осветительные и промышленные установки, вырабатывают переменный ток частотой 50 периодов. Эта частота называется промышленной. Для специальных установок можно получить переменный ток любой частоты, но для питания осветительных ламп накаливания частота 50 периодов в секунду или 50 Гц (герц) вполне удовлетворительна и наиболее благоприятна для глаз. При излучении пульсирующего света частотой 15—20 Гц глаза будут раздражаться и болеть. Казалось бы, лампы накаливания дают непрерывный свет. На самом деле лампы мощностью до 100 Вт испускают пульсирующий свет и только лампы мощностью свыше 200 Вт, нить которых не успевает остынуть за время прохождения тока через нуль, излучают ровный свет. Надо сказать, что пульсация света маломощных ламп не заметна для3 глаз в отличие от пульсации люминисцентных ламп.

Рекламные предложения на основе ваших интересов:

Источник тока всегда обладает некоторым напряжением, и именно вследствие этого ток течет по электрической цепи. В то же время всякая электрическая цепь в той или иной мере препятствует протеканию тока. Это свойство цепи называется сопротивлением. Закон Ома устанавливает зависимость между такими тремя основными величинами электрической цепи, как напряжение U, ток / и сопротивление R:
I = U/R, (3.1)

т. е. сила тока (или ток) в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению этой цепи. За единицу электрического напряжения принят 1 В (вольт), за единицу силы тока — 1 А (ампер) и за единицу сопротивления — 1 Ом.

Из формулы 3.1 имеем: U = IR, R = U/T. Таким образом, зная две величины из трех, легко определить и третью. Вышеприведенная формула закона Ома справедлива для постоянного тока. При переменном токе полное сопротивление электрической цепи z будет являться геометрической суммой активного сопротивления цепи г и реактивного х.

При изменении температуры меняется сопротивление проводников. Изменение сопротивления на 1 Ом при изменении температуры на 1 °С называется температурным коэффициентом. У всех металлических проводников температурный коэффициент положительный — с увеличением температуры возрастает сопротивление проводника, а у электролитов и угля температурный коэффициент отрицательный, т. е. с ростом температуры сопротивление уменьшается, а при снижении температуры сопротивление увеличивается.

Из всех материалов, применяемых для изготовления проводов, меди свойственно наименьшее удельное сопротивление, а это значит, что при одинаковых длине и площади поперечного сечения медный провод обладает и наименьшим сопротивлением, что имеет большое значение при передаче электрической энергии. Если по проводнику идет ток /, А, а сопротивление проводника равно R, Ом, то по закону Ома падение напряжения в этом проводнике и = IR и действующее напряжение у зажимов потребителя будет уменьшено на величину и, т. е. составит U — и.

Принимая во внимание, что удельное сопротивление алюминия в 1,7 раза, а стали в 5—7 раз больше, чем у меди, площадь сечения алюминиевого проводника должна быть в 1,7 раза, а стального в 5—7 раз больше по сравнению с медным проводником. Практически площадь сечения алюминиевых проводников в 1,5 раза выше медных, а стальные проводники имеют ограниченное применение — в качестве троллейных проводов мостовых кранов, где увеличение площади сечения проводника не вызывает удорожания его стоимости, а возрастание его массы часто не имеет значения.

С падением напряжения ухудшается работа электроустановок, поэтому имеются ограничения, нормирующие допустимые колебания напряжения. Особенно чувствительны к колебаниям напряжения осветительные лампы накаливания, для них допускается колебание напряжения + 3 , а для электродвигателей +10.

Среди наиболее распространенных проводниковых материалов (табл. 3.1) наименьшим удельным сопротивлением обладает серебро, но из-за дороговизны его не применяют для изготовления проводниковых материалов, за исключением контактов различной электроаппаратуры: реле, пускателей, блок-контактов и т. п. В этих случаях серебро используют вследствие того, что его окислы так же хорошо проводят ток, как и сам металл.

Таблица 3.1
Проводниковые материалы

Медный контакт быстро покрывается тонкой пленкой окиси меди, которая очень плохо проводит электрический ток. В связи с этим поверхности медных контактов надо часто зачищать тонкой наждачной или крокусной бумагой. С появлением слоя окиси поверхностное сопротивление серебряных контактов почти не меняется. Но это не означает, что серебряные контакты не требуется чистить. Грязь и пыль с них надо счищать кисточкой или щеткой, смоченной винным спиртом. Нельзя чистить серебряные контакты бензином и ацетоном — на их поверхности появляется налет, плохо проводящий ток.

Количество теплоты в проводнике при протекании электрического тока прямо пропорционально сопротивлению этого проводника, квадрату силы тока и времени, в течение которого протекал ток. Из этого закона следует, что при увеличении сопротивления растет количество теплоты. Сопротивление переходных контактов (зажимов, кабельных наконечников и др.) должно быть очень малым. При неплотном контакте, слабо затянутых гайках переходное сопротивление значительно возрастает, контакт нагревается, что может привести к обгоранию контактных поверхностей или распайке кабельного наконечника. В связи с этим контактные поверхности должны быть гладкими, плотно соприкасающимися.

Из закона Джоуля — Ленца следует, что теплота выделяется как при передаче электроэнергии, когда сопротивление проводника должно быть наименьшим, так и в приемниках электрической энергии — осветительных лампах, нагревателях, двигателях, когда стремятся сделать сопротивление наибольшим.

Рекламные предложения:

Читать далее: Мощность и работа электрического тока в кране

Категория: — Электрическое оборудование

Главная → Справочник → Статьи → Форум

joule’s_laws

Законы Джоуля — это пара законов, касающихся тепла, выделяемого током, и зависимости энергии идеального газа от давления, объема и температуры соответственно.

Рекомендуемые дополнительные знания

Первый закон Джоуля , также известный как эффект Джоуля , представляет собой физический закон, выражающий соотношение между теплотой, генерируемой током, протекающим через проводник.Он назван в честь Джеймса Прескотта Джоуля, изучавшего это явление в 1840-х годах. Это выражается как:

Где Q — тепло, выделяемое постоянным током I , протекающим через проводник с электрическим сопротивлением R , в течение времени t . Когда ток, сопротивление и время выражаются в амперах, омах и секундах соответственно, единицей измерения Q является джоуль. Первый закон Джоуля иногда называют законом Джоуля-Ленца , поскольку позже он был независимо открыт Генрихом Ленцем.Эффект нагрева проводников, по которым протекает ток, известен как джоулев нагрев.

Первый закон Джоуля тесно связан с законом Ома и, таким образом, легко выводится из него. Ниже приведен краткий обзор того, как связаны эти два закона, для получения подробной информации см. Закон Ома.

Второй закон Джоуля гласит, что внутренняя энергия идеального газа не зависит от его объема и давления, а зависит только от его температуры.

Связь с законом Ома

Первый закон Джоуля тесно связан с законом Ома и, таким образом, легко выводится из него.Ниже приводится краткое описание взаимосвязи этих двух законов.

или

Закон Ома

Мощность, рассеиваемая на резисторе

Объединив два приведенных выше уравнения и представив их в терминах I и R:

Мощность, рассеиваемая в резисторе, выраженная в силе тока [ватт или джоуль / сек]

Для получения дополнительной информации о Power см. Power (физика). Наконец, количество мощности, рассеиваемой резистором, — это количество работы, проделанной на резисторе (т. Е.тепло, рассеиваемое в резисторе), деленное на время:

Что дает:

Обратите внимание, что первый закон Джоуля можно также записать в терминах напряжения на резисторе:

См. Также

ЭЛЕКТРИЧЕСКИЕ ЗАКОНЫ — E-knowledge.in

Если W — это работа, выполненная в системе, а Q — количество сердца, произведенное в результате этой работы, то

Выражение J говорит, что механический эквивалент тепла — это количество единиц работы, которое должно быть выполнено в системе для производства одной единицы тепла.

Эксперимент Джоуля

Для демонстрации его эксперимента мы сначала возьмем цилиндрический калориметр из меди. Мы будем использовать систему лопасть — лопасть, как показано выше.

Теперь заполним калориметр определенным количеством воды. Теперь мы прикрепим лопаточную систему к заполненному водой калориметру с помощью водонепроницаемой верхней крышки. Теперь мы прикрепим два груза известной и равной массы, как показано на рисунке выше, с помощью шкивов. Когда ручка системы вращается в любом направлении, оба груза поднимаются или опускаются вертикально в зависимости от направления вращения.

Прикрепляем две вертикальные шкалы для измерения вертикали; движения тяжестей. Мы также установили один термометр на верхней крышке системы, чтобы увидеть повышение температуры воды.

Теперь поднимем груз, вращая ручку. Подняв грузы на высоту h, мы позволяем им свободно опуститься в прежнее положение. Когда грузы падают, потенциальная энергия, накопленная в системе во время подъема грузов, высвобождается в виде кинетической энергии, которая вызывает вращение фургонов в воде.Эта работа, выполняемая в системе, приведет к выделению тепла в воде и повышению температуры воды. После того, как веса опустятся в исходное положение, мы снова поднимем их на ту же высоту h и позволим им свободно опускаться. Мы продолжаем делать это до тех пор, пока на термометре, установленном в системе, не появится измеримая разница температур. Теперь мы можем измерить проделанную работу, умножив общий вес на высоту движения гирь, количество повторений движений гири.Будем считать, что оба груза имеют одинаковую массу m. Итак, общая масса гирь составляет 2 метра. Таким образом, работа за счет падения груза по вертикали на h метров составляет 2 мгч. Теперь скажем, всего n повторений движений веса, сделанных до повышения температуры воды до ее измеренного значения. Следовательно, общая проделанная работа будет: Здесь все n, m, g и h известны, поэтому общую проделанную работу можно легко рассчитать.

Рассмотрим, M — масса воды в калориметре. W ‘- водный эквивалент калориметра.Таким образом, общее количество тепла, выделяемого из-за повышения температуры воды на θ, составляет Q = (M + W ‘) θ. Теперь, механический эквивалент тепла

После этого эксперимента, поместив все известные значения m, g, h, n, M, W ‘и θ, мы получим. Здесь в этом эксперименте потенциальная энергия падающей массы равна преобразуется в кинетическую энергию и, наконец, в тепловую энергию.

Эксперимент Фарадея

СВЯЗЬ МЕЖДУ ИНДУЦИРОВАННОЙ ЭДС И ПОТОКОМ В этом эксперименте Фарадей берет магнит и катушку и подключает гальванометр через катушку.При запуске магнит находится в состоянии покоя, поэтому гальванометр не прогибается, т.е. стрелка гальванометра находится в центральном или нулевом положении. Когда магнит перемещается к катушке, стрелка гальванометра отклоняется в одном направлении. Когда магнит удерживается в неподвижном положении в этом положении, стрелка гальванометра возвращается в нулевое положение. Теперь, когда магнит отодвигается от катушки, наблюдается некоторое отклонение стрелки, но в противоположном направлении, и снова, когда магнит становится неподвижным в этой точке относительно катушки, стрелка гальванометра возвращается в нулевое положение.Точно так же, если магнит удерживается в неподвижном состоянии, а катушка перемещается в сторону магнита, гальванометр показывает отклонение аналогичным образом. Также видно, что чем быстрее изменяется магнитное поле, тем больше будет наведенная ЭДС или напряжение в катушке.

Положение магнита	Отклонение гальванометра
Магнит в состоянии покоя	Отсутствие отклонения гальванометра
Магнит движется по направлению к катушке	Одностороннее отклонение магнита			в том же положении (рядом с катушкой)	Нет отклонения в гальванометре
Магнит движется от катушки	Отклонение в гальванометре, но в противоположном направлении
Магнит удерживается неподвижно в том же положении (вдали от катушки)	Отсутствие отклонения в гальванометре

Вывод: из этого эксперимента Фарадей пришел к выводу, что всякий раз, когда есть относительное движение между проводником и магнитным полем, магнитная связь с катушкой изменяется, и это изменение потока индуцирует напряжение на катушке.
Майкл Фарадей сформулировал два закона на основе вышеупомянутых экспериментов. Эти законы называются законами электромагнитной индукции Фарадея .

Законы Фарадея

Первый закон Фарадея

Любое изменение магнитного поля катушки с проволокой вызовет индукцию ЭДС в катушке. Эта индуцированная ЭДС называется индуцированной ЭДС, и если цепь проводника замкнута, ток также будет циркулировать по цепи, и этот ток называется индуцированным током.
Метод изменения магнитного поля:

1. Путем перемещения магнита по направлению к катушке или от нее.
2. Путем перемещения катушки в магнитное поле или из него.
3. Путем изменения площади катушки, помещенной в магнитное поле.
4. Путем вращения катушки относительно магнита.

Второй закон Фарадея

Он гласит, что величина ЭДС, индуцированная в катушке, равна скорости изменения магнитного потока, который связывается с катушкой. Магнитная связь катушки — это произведение количества витков в катушке и магнитного потока, связанного с катушкой.

Формула закона Фарадея

Рассмотрим, магнит приближается к катушке. Здесь мы рассматриваем два момента времени T ₁ и время T ₂ .Потоковая связь с катушкой во время, Потоковая связь с катушкой во время, Изменение в потокосцеплении, Пусть это изменение в потокосцеплении будет, Итак, Изменение в потокосцеплении Теперь скорость изменения потоковой связи Возьмите производную справа, мы будем get
Скорость изменения магнитной связи Но согласно закону электромагнитной индукции Фарадея скорость изменения магнитной индукции равна наведенной ЭДС. С учетом закона Ленца. Где, поток Φ в Wb = BA
B = напряженность магнитного поля
A = площадь катушки
КАК УВЕЛИЧИТЬ ЭДС, ИНДУЦИРОВАННУЮ В КАТУШКЕ

• Увеличивая количество витков в катушке i.e N, из приведенных выше формул легко увидеть, что если количество витков в катушке увеличивается, наведенная ЭДС также увеличивается.
• Путем увеличения напряженности магнитного поля, то есть B, окружающего катушку. Математически, если магнитное поле увеличивается, увеличивается поток, а если увеличивается поток, индуцированная ЭДС также увеличивается. Теоретически, если катушка проходит через более сильное магнитное поле, будет больше силовых линий, которые она может разрезать, и, следовательно, будет больше индуцированной ЭДС.
• За счет увеличения скорости относительного движения между катушкой и магнитом — Если относительная скорость между катушкой и магнитом увеличивается по сравнению с ее предыдущим значением, катушка будет обрезать линии потока с большей скоростью, поэтому больше индуцированной ЭДС будет произведено.

Применение закона Фарадея

Закон Фарадея — один из самых основных и важных законов электромагнетизма. Этот закон находит свое применение в большинстве электрических машин, промышленности, медицины и т. Д.

• Электрические трансформаторы работают по закону Фарадея
• Основным принципом работы электрического генератора является закон Фарадея о взаимной индукции.
• Индукционная плита — самый быстрый способ готовки. Он также работает по принципу взаимной индукции. Когда ток течет через катушку с медной проволокой, расположенную под посудой, он создает изменяющееся магнитное поле. Это переменное или изменяющееся магнитное поле индуцирует ЭДС и, следовательно, ток в проводящем контейнере, и мы знаем, что поток тока всегда выделяет в нем тепло.
• Электромагнитный расходомер используется для измерения скорости определенных жидкостей. Когда магнитное поле прикладывается к электрически изолированной трубе, по которой протекают токопроводящие жидкости, то, согласно закону Фарадея, в ней индуцируется электродвижущая сила. Эта индуцированная ЭДС пропорциональна скорости течения жидкости.
• Идея Фарадея о силовых линиях, являющаяся основой электромагнитной теории, используется в хорошо известных уравнениях Максвелла. Согласно закону Фарадея, изменение магнитного поля вызывает изменение электрического поля, и обратное этому используется в уравнениях Максвелла.
• Он также используется в музыкальных инструментах, таких как электрогитара, электрическая скрипка и т. Д.

Видео Презентация закона Фарадея

Закон Ленца назван в честь немецкого ученого Х.Ф. Ленца в 1834 году. Закон Ленца подчиняется третьему закону Ньютона. движение (т.е. на каждое действие всегда есть равная и противоположная реакция) и сохранение энергии (т.е. энергия не может быть ни создана, ни разрушена, и поэтому сумма всех энергий в системе является постоянной). Закон Ленца основан на законе индукции Фарадея, поэтому до понимания закона Ленца ; нужно знать, что такое закон индукции Фарадея? Когда изменяющееся магнитное поле связано с катушкой, в ней индуцируется ЭДС. Это изменение магнитного поля может быть вызвано изменением напряженности магнитного поля путем перемещения магнита по направлению к катушке или от нее или перемещением катушки в магнитное поле или из него по желанию. Или простыми словами, мы можем сказать, что величина ЭДС, индуцированная в цепи, пропорциональна скорости изменения магнитного потока.

Закон Ленца

Закон Ленца гласит, что, когда ЭДС генерируется изменением магнитного потока в соответствии с законом Фарадея, полярность индуцированной ЭДС такова, что она производит ток, магнитное поле которого противодействует изменению, которое его вызывает. .

Отрицательный знак, используемый в законе электромагнитной индукции Фарадея, указывает на то, что наведенная ЭДС (ε) и изменение магнитного потока (δΦ _B ) имеют противоположные знаки, где
ε = Индуцированная ЭДС
δΦ _B = изменение в магнитном потоке
N = Количество витков в катушке

Причина противодействия, причина индуцированного тока в

Законе Ленца ?

• Как указано выше, Закон Ленца подчиняется закону сохранения энергии, и если направление магнитного поля, которое создает ток, и магнитное поле тока в проводнике совпадают, то эти два магнитных поля суммируется и производит ток вдвое большей величины, а это, в свою очередь, создает большее магнитное поле, что вызывает увеличение тока, и этот процесс, продолжающийся и продолжающийся, приводит к нарушению закона сохранения энергии.
• Если индуцированный ток создает магнитное поле, которое равно и противоположно направлению магнитного поля, которое его создает, то только он может сопротивляться изменению магнитного поля в этой области, что соответствует третьему закону Ньютона. движение.

Объяснение закона Ленца

Для понимания закона Ленца рассмотрим два случая:
СЛУЧАЙ-I Когда магнит движется к катушке. Когда северный полюс магнита приближается к катушке, магнитный поток связывается с катушка увеличивается.Согласно закону электромагнитной индукции Фарадея, при изменении магнитного потока в катушке индуцируется ЭДС и, следовательно, ток, и этот ток создает собственное магнитное поле. Теперь, согласно закону Ленца , это созданное магнитное поле будет противодействовать своему собственному или, можно сказать, противодействовать увеличению потока через катушку, и это возможно только в том случае, если приближающаяся сторона катушки достигает северной полярности, поскольку мы знаем, что похожие полюса отталкиваются друг от друга. Как только мы узнаем магнитную полярность стороны катушки, мы можем легко определить направление индуцированного тока, применив правило правой руки.В этом случае ток течет против часовой стрелки.
CASE-II Когда магнит удаляется от катушки Когда северный полюс магнита удаляется от катушки, магнитный поток, связанный с катушкой, уменьшается. Согласно закону электромагнитной индукции Фарадея, в катушке индуцируется ЭДС и, следовательно, ток, и этот ток создает собственное магнитное поле. Теперь, согласно закону Ленца , это созданное магнитное поле будет противодействовать своему собственному или, можно сказать, противодействовать уменьшению потока через катушку, и это возможно только в том случае, если приближающаяся сторона катушки достигает южной полярности, поскольку мы знаем, что разные полюса притягиваются друг к другу.Как только мы узнаем магнитную полярность стороны катушки, мы можем легко определить направление индуцированного тока, применив правило правой руки. 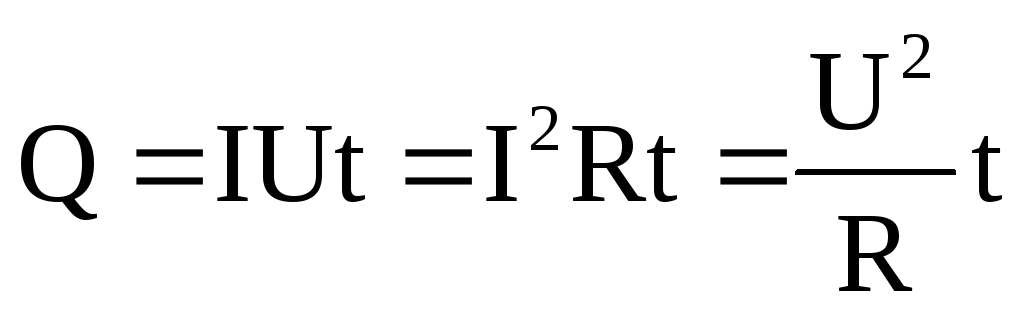В этом случае ток течет по часовой стрелке.

ПРИМЕЧАНИЕ: Для определения направления магнитного поля или тока используйте правило большого пальца правой руки, т.е. если пальцы правой руки расположены вокруг провода так, чтобы большой палец указывал в направлении потока тока, то будет видно изгибание пальцев. направление магнитного поля, создаваемого проволокой.Закон Ленца можно резюмировать следующим образом:

• Если магнитный поток Ф, соединяющий катушку, увеличивается, направление тока в катушке будет таким, что он будет противодействовать увеличению потока, и, следовательно, индуцированный ток будет вызывать его поток в направлении, как показано ниже (с использованием правила для большого пальца правой руки).
• Если магнитный поток Ф, соединяющий катушку, уменьшается, поток, создаваемый током в катушке, таков, что он поддерживает основной поток и, следовательно, направление тока такое, как показано ниже,

Применение закона Ленца

• Закон Ленца можно использовать для понимания концепции накопленной магнитной энергии в индукторе.Когда к индуктору подключен источник ЭДС, через него начинает течь ток. Противоэдс будет противодействовать этому увеличению тока через катушку индуктивности. Чтобы установить ток, внешний источник ЭДС должен проделать некоторую работу, чтобы преодолеть это противодействие. Эта работа может быть выполнена за счет того, что ЭДС сохраняется в катушке индуктивности, и ее можно восстановить после удаления внешнего источника ЭДС из цепи.
• Этот закон указывает на то, что индуцированная ЭДС и изменение потока имеют противоположные знаки, которые обеспечивают физическую интерпретацию. выбора знака в законе индукции Фарадея.
• Закон Ленца также применяется к электрическим генераторам. Когда в генераторе индуцируется ток, направление этого индуцированного тока таково, что он противодействует и вызывает вращение генератора (как в соответствии с законом Ленца ), и, следовательно, генератору требуется больше механической энергии. Он также обеспечивает обратную ЭДС в случае электродвигателей.

Закон Ленца также используется для электромагнитного торможения и индукционных варочных панелей.

Законы электролиза Фарадея

Прежде чем понять законы электролиза Фарадея , мы должны вспомнить процесс электролиза сульфата металла.
Когда электролит, такой как сульфат металла, разбавляется водой, его молекулы расщепляются на положительные и отрицательные ионы. Положительные ионы или ионы металлов перемещаются к электродам, соединенным с отрицательной клеммой батареи, где эти положительные ионы отбирают от нее электроны, становятся атомами чистого металла и осаждаются на электроде. В то время как отрицательные ионы или сульфионы перемещаются к электроду, соединенному с положительной клеммой батареи, где эти отрицательные ионы отдают свои лишние электроны и становятся радикалом SO ₄ .Поскольку SO ₄ не может существовать в электрически нейтральном состоянии, он атакует металлический положительный электрод и образует сульфат металла, который снова растворяется в воде. Законы электролиза Фарадея объединяют два закона, а именно:

Первый закон электролиза Фарадея

Из краткого объяснения выше ясно, что протекание тока через цепь внешней батареи полностью зависит от того, сколько электронов передается от отрицательного электрода. или катод на положительный металлический ион или катионы.Если катионы имеют валентность два, как Cu ⁺⁺ , то для каждого катиона будет два электрона, перенесенных с катода на катион. Мы знаем, что каждый электрон имеет отрицательный электрический заряд — 1,602 × 10 ^-19 кулонов, и скажем, что это — e. Таким образом, для размещения каждого атома Cu на катоде будет происходить передача заряда с катода на катион. Теперь предположим, что в течение t времени на катоде будет всего n атомов меди, поэтому общий переданный заряд будет равен -2.н.э. Кулоны. Очевидно, масса осажденной меди m зависит от числа нанесенных атомов. Таким образом, можно сделать вывод, что масса осажденной меди прямо пропорциональна количеству электрического заряда, проходящего через электролит. Следовательно, масса осажденной меди m Q количество электрического заряда проходит через электролит.
Первый закон электролиза Фарадея гласит только, что
Согласно этому закону химическое осаждение из-за протекания тока через электролит прямо пропорционально количеству электричества (кулонов), прошедшего через него., то есть масса химического осаждения, где Z — коэффициент пропорциональности, известный как электрохимический эквивалент вещества.
Если мы положим Q = 1 кулон в приведенное выше уравнение, мы получим Z = m, что означает, что электрохимический эквивалент любого вещества — это количество вещества, осажденного при прохождении 1 кулона через его раствор. Эта постоянная прохождения электрохимического эквивалента обычно выражается в миллиграммах на кулон или килограммах на кулон.

Второй закон электролиза Фарадея

До сих пор мы узнали, что масса химического вещества, отложившегося в результате электролиза, пропорциональна количеству электричества, которое проходит через электролит. Масса химического вещества, отложившегося в результате электролиза, не только пропорциональна количеству электричества, проходящего через электролит, но также зависит от некоторых других факторов. У каждого вещества будет свой атомный вес. Таким образом, при одинаковом количестве атомов разные вещества будут иметь разные массы.Опять же, количество атомов, нанесенных на электроды, также зависит от их валентности. Если валентность больше, то для того же количества электричества количество отложенных атомов будет меньше, тогда как если валентность меньше, то для того же количества электричества будет отложено большее количество атомов. Таким образом, при прохождении одного и того же количества электричества или заряда через разные электролиты масса нанесенного химического вещества прямо пропорциональна его атомному весу и обратно пропорциональна его валентности.
Второй закон электролиза Фарадея гласит, что, когда одно и то же количество электричества проходит через несколько электролитов, масса осажденных веществ пропорциональна их соответствующему химическому эквиваленту или эквивалентной массе.

Химический эквивалент или эквивалентный вес

Химический эквивалент или эквивалентный вес вещества может быть определен по законам электролиза Фарадея , и он определяется как вес той субаренды, которая будет сочетаться с водородом или замещать его. Таким образом, химический эквивалент водорода равен единице. Поскольку валентность вещества равна количеству атомов водорода, которые оно может заменить или с которыми оно может объединить, химический эквивалент вещества может быть определен как отношение его атомного веса к его валентности.Два французских физика, Жан Батист Био и Феликс Савар, в 1820 году вывели математическое выражение для плотности магнитного потока в точке из-за близлежащего проводника с током. Наблюдая за отклонением стрелки магнитного компаса, двое ученых пришли к выводу, что любой элемент тока создает магнитное поле. поле в пространстве.
После наблюдений и расчетов они вывели математическое выражение, которое показывает, что плотность магнитного потока, дБ, прямо пропорциональна длине элемента dl, току I, синусу угла и θ между направлением ток и вектор, соединяющий данную точку поля и текущий элемент, обратно пропорционален квадрату расстояния данной точки от текущего элемента, r.Это утверждение закона Био-Савара . Где k является константой, зависит от магнитных свойств среды и системы используемых единиц. В системе единиц СИ, следовательно, окончательный вывод закона Био-Савара таков: давайте рассмотрим длинный провод, по которому проходит ток I, а также точку p в пространстве. На рисунке ниже провод показан красным цветом. Рассмотрим также бесконечно малую длину провода dl на расстоянии r от точки P, как показано. Здесь r — вектор расстояния, который составляет угол θ с направлением тока в бесконечно малой части провода.

Если вы попытаетесь визуализировать состояние, вы легко сможете понять плотность магнитного поля в точке P, потому что бесконечно малая длина провода dl прямо пропорциональна току, протекающему по этой части провода.
Поскольку ток через эту бесконечно малую длину провода такой же, как ток, протекающий по самому проводу, мы можем написать: также очень естественно думать, что плотность магнитного поля в этой точке P из-за этой бесконечно малой длины провода dl обратно пропорциональна квадрату расстояния по прямой от точки P до центра dl.Математически мы можем записать это как: Наконец, плотность магнитного поля в этой точке P из-за того, что бесконечно малая часть провода также прямо пропорциональна фактической длине бесконечно малой длины провода dl. Поскольку θ — это угол между вектором расстояния r и направлением тока через этот бесконечно малый участок провода, компонент dl, обращенный непосредственно перпендикулярно точке P, равен dlsinθ. Теперь, объединив эти три утверждения, мы можем написать: Это основной форма Закон Био-Савара
Теперь, подставив значение константы k (которое мы уже ввели в начале этой статьи) в приведенное выше выражение, мы получаем Здесь μ ₀ , используемое в выражении константы k, является абсолютным проницаемость воздуха или вакуума и ее значение составляет 4π10 ^-7 W _b / Am в системе единиц СИ.μ _r выражения константы k — относительная проницаемость среды.
Теперь, плотность потока (B) в точке P, обусловленная общей длиной токопроводящего проводника или провода, может быть представлена ​​как: Если D — перпендикулярное расстояние точки P от провода, то теперь выражение плотности потока B в точке P можно переписать как, Как показано на рисунке выше, Наконец, выражение B выглядит так: Этот угол θ зависит от длины провода и положения точки P. Скажем, для определенной ограниченной длины провода, угол θ, как показано на рисунке выше, изменяется от θ ₁ до θ ₂ . Следовательно, плотность магнитного потока в точке P из-за общей длины проводника равна. Давайте представим, что провод бесконечно длинный, тогда θ будет варьироваться от 0 до π, то есть θ ₁ = 0 до θ ₂ = π. Помещая эти два значения в приведенное выше окончательное выражение закона Био-Савара , мы получаем

. Это не что иное, как выражение закона Ампера. Эта теорема утверждает, что полный электрический поток через любую замкнутую поверхность, окружающую заряд, равен чистому положительному заряду, заключенному на этой поверхности.

Предположим, что заряды Q ₁ , Q ₂ _ _ _ _Q _i , _ _ _ Q _n заключены в поверхность, тогда теорема может быть выражена математически через поверхностный интеграл как Где, D — поток плотность в кулонах / м ² и dS — вектор, направленный наружу.

Объяснение теоремы Гаусса

Для объяснения теоремы Гаусса лучше рассмотреть пример для правильного понимания.
Пусть Q будет зарядом в центре сферы, и поток, исходящий от заряда, перпендикулярен поверхности.Эта теорема утверждает, что полный поток, исходящий от заряда, будет равен Q кулонов, и это также можно доказать математически. Но что насчет того, когда заряд помещен не в центр, а в любую точку, кроме центра (как показано на рисунке). В это время силовые линии не перпендикулярны поверхности, окружающей заряд, тогда этот поток разрешается. на две составляющие, которые перпендикулярны друг другу, горизонтальная — это компонента sinθ, а вертикальная — компонента cosθ.Теперь, когда сумма этих компонентов берется для всех зарядов, тогда чистый результат равен полному заряду системы, что доказывает теорему Гаусса .

Доказательство теоремы Гаусса

Рассмотрим точечный заряд Q, расположенный в однородной изотропной среде с диэлектрической проницаемостью ε. Напряженность электрического поля в любой точке на расстоянии r от заряда равна.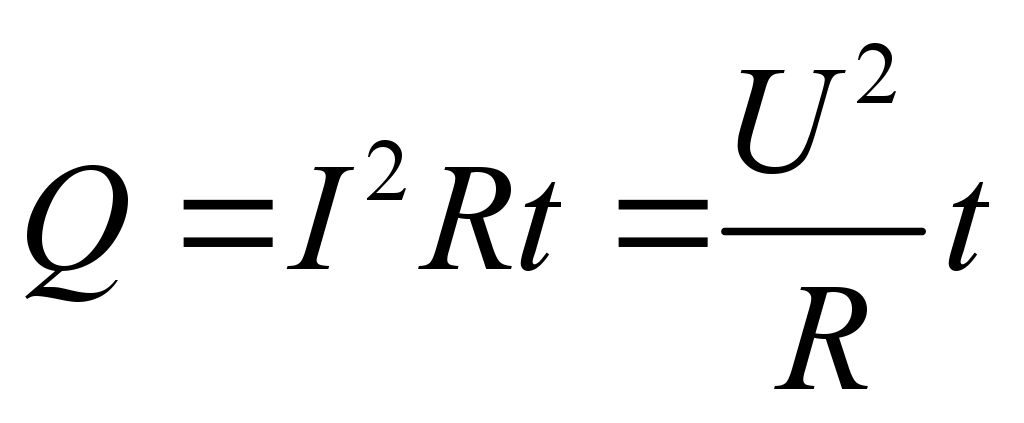 через область dSWhere, θ — угол между D и нормалью к dS
Теперь dScosθ — это проекция dS, перпендикулярная радиус-вектору.По определению телесного угла, где dΩ — телесный угол, стягиваемый в Q элементарной поверхностью dS. Итак, полное смещение потока по всей площади поверхности равно. Теперь мы знаем, что телесный угол, образуемый любой замкнутой поверхностью, составляет 4π стерадиана, поэтому полный электрический поток через всю поверхность равен. Это интегральная форма теоремы Гаусса . И, следовательно, эта теорема доказана: всякий раз, когда проводник с током попадает в магнитное поле, на проводник будет действовать сила, а, с другой стороны, если проводник с силой подвергнуть воздействию магнитного поля, будет индуцированное ток в этом проводнике.В обоих явлениях существует связь между магнитным полем, током и силой. Это отношение направленно определяется правилом для левой руки Флеминга и правилом для правой руки Флеминга соответственно. Направленный означает, что эти правила не показывают величину, но показывают направление любого из трех параметров (магнитное поле, ток, сила), если направление двух других известно. Правило левой руки Флеминга в основном применимо для электродвигателя, а правило Правило Флеминга применимо в основном для электрического генератора.В конце 19-го, ^-го, -го века, Джон Амброуз Флеминг ввел оба этих правила, и, согласно его имени, правила хорошо известны как правило для левой и правой руки Флеминга .

Правило левой руки Флеминга

Было обнаружено, что всякий раз, когда проводник с током помещается в магнитное поле, на проводник действует сила в направлении, перпендикулярном как направлению тока, так и магнитного поля. На рисунке показано, что часть проводника длиной L, помещенная вертикально в однородное горизонтальное магнитное поле H, создается двумя магнитными полюсами N и S.Если i — ток, протекающий через этот проводник, величина силы, действующей на проводник, равна: Вытяните левую руку указательным, вторым и большим пальцами под прямым углом друг к другу. Если указательный палец представляет направление поля, а второй — направление тока, то большой палец указывает направление силы.
В то время как ток течет по проводнику, вокруг него создается одно магнитное поле. Это можно представить, рассматривая количество замкнутых магнитных силовых линий вокруг проводника.Направление магнитных силовых линий может быть определено правилом штопора Максвелла или правилом правостороннего захвата. Согласно этим правилам направление магнитных силовых линий (или силовых линий) — по часовой стрелке, если ток течет от наблюдателя, то есть если направление тока через проводник направлено внутрь от плоскости отсчета, как показано на рисунке. фигура.

Теперь, если горизонтальное магнитное поле приложено извне к проводнику, эти два магнитных поля, то есть поле вокруг проводника из-за проходящего через него тока, и приложенное извне поле будут взаимодействовать друг с другом.На рисунке мы видим, что силовые линии внешнего магнитного поля проходят от северного к южному полюсу, то есть слева направо. Магнитные силовые линии внешнего магнитного поля и магнитные силовые линии, возникающие из-за тока в проводнике, находятся в одном направлении над проводником и в противоположном направлении под проводником. Следовательно, над проводником будет больше сонаправленных магнитных силовых линий, чем под проводником. Следовательно, в небольшом пространстве над проводником будет большая концентрация магнитных силовых линий.Поскольку магнитные силовые линии больше не являются прямыми линиями, они находятся под натяжением, как натянутые резиновые ленты. В результате возникнет сила, которая будет стремиться переместить проводник из более концентрированного магнитного поля в менее концентрированное магнитное поле, то есть из текущего положения вниз. Теперь, если вы заметите направление тока, силы и магнитного поля в приведенном выше объяснении, вы обнаружите, что направления соответствуют правилу левой руки Флеминга.

Правило Флеминга для правой руки

Согласно закону электромагнитной индукции Фарадея, всякий раз, когда проводник движется внутри магнитного поля, в нем будет индуцированный ток. Если этот проводник будет принудительно перемещен внутри магнитного поля, возникнет связь между направлением приложенной силы, магнитным полем и током. Это соотношение между этими тремя направлениями определяется правилом для правой руки Флеминга .

Эффект Зеебека

Он был открыт немецким физиком Томасом Зеебеком (1770-1831). Зеебек обнаружил это, наблюдая за стрелкой компаса, которая отклоняется, когда между этими двумя разными металлами или полупроводниками образуется замкнутая петля.Первоначально Зеебек считал, что это происходит из-за магнетизма, вызванного разницей температур, и назвал этот эффект термомагнитным эффектом. Однако датский физик Ганс Кристиан Орстед понял, что индуцируется электрический ток, который по закону Ампера отклоняет магнит.

Объяснение эффекта Зеебека

За это ответственны только валентные электроны в более теплой части металла, и причиной этого является тепловая энергия. Также из-за кинетической энергии этих электронов эти валентные электроны мигрируют быстрее к другому (более холодному) концу, по сравнению с более холодной частью электроны мигрируют к более теплой части.Концепция их движения:

• На горячей стороне распределение Ферми мягкое, то есть более высокая концентрация электронов выше энергии Ферми, но на холодной стороне распределение Ферми резкое, то есть у нас меньше электронов с энергией Ферми.
• Электроны идут туда, где энергия ниже, поэтому они будут перемещаться от более теплого конца к более холодному концу, что приводит к переносу энергии и, таким образом, к уравновешиванию температуры в конечном итоге

Или, простыми словами, мы можем прийти к выводу, что электроны на более теплом конце имеют высокий средний импульс по сравнению с более холодным.Следовательно, они будут брать с собой энергию (больше) по сравнению с другим.
Это движение приводит к более отрицательному заряду в более холодной части, чем в более теплой части, что приводит к генерации электрического потенциала. Если эта пара соединена через электрическую цепь. Это приводит к генерации постоянного тока. Однако создаваемое напряжение составляет несколько микровольт (10 ^-6 ) на разницу температур по Кельвину. Теперь мы все знаем, что напряжение увеличивается последовательно, а ток увеличивается параллельно.Помните об этом факте, если мы сможем подключить много таких устройств для увеличения напряжения (в случае последовательного соединения) или для увеличения максимального передаваемого тока (параллельно). Позаботьтесь только об одном, что для этого требуется большой перепад температур. Однако нужно иметь в виду одну вещь: мы должны поддерживать постоянную, но разную температуру, и поэтому распределение энергии на обоих концах будет различным, и, следовательно, это приводит к успешному упомянутому процессу.

Коэффициент Зеебека

Напряжение, возникающее между двумя точками на проводе, когда между ними поддерживается постоянная разница температур в 1 ^o Кельвина, называется коэффициентом Зеебека . Одна такая комбинация медного константана имеет коэффициент Зеебека , составляющий 41 микровольт на Кельвин при комнатной температуре.

Эффект Спина Зеебека

Однако в 2008 году было замечено, что когда тепло подается на намагниченный металл, его электрон перестраивается в соответствии с его спином.Однако эта перестановка не отвечает за выделение тепла. Этот эффект K / w как эффект Зеебека вращения. Этот эффект используется при разработке быстрых и эффективных микропереключателей.

Применение эффекта Зеебека

1. Этот эффект Зеебека обычно используется в термопарах для измерения разницы температур или для срабатывания электронных переключателей, которые могут включать или выключать систему. Обычно используемые комбинации металлов термопар включают константан / медь, константан / железо, константан / хромель и константан / алюмель.
2. Эффект Зеебека используется в термоэлектрическом генераторе, который работает как тепловая машина.
3. Они также используются на некоторых электростанциях для преобразования отработанного тепла в дополнительную энергию.
4. В автомобилях в качестве автомобильных термоэлектрических генераторов для повышения топливной экономичности.

Закон Видемана-Франца — это закон, который связывает теплопроводность (κ) и электропроводность (σ) материала, который состоит из несколько свободно движущихся в нем электронов.

• Теплопроводность (κ): Это степень (мера) способности материала проводить тепло.
• Электропроводность (σ): Это степень (мера) способности материала проводить электричество.

Металлы; когда температура увеличивается, скорость свободных электронов увеличивается, что приводит к увеличению теплопередачи, а также увеличивает столкновения между ионами решетки и свободными электронами. Это приводит к падению электропроводности.
Закон определяет отношение электронной роли теплопроводности материала к электропроводности материала (металла) непосредственно по отношению к температуре. Этот закон назван в честь Густава Видемана и Рудольфа Франца в 1853 году. сообщили, что соотношение имеет более или менее аналогичное значение для разнородного металла при той же температуре.

Вывод закона

Для этого мы должны предположить однородный изотропный материал. Затем этот материал подвергается воздействию температурного градиента.Направление теплового потока будет противоположным направлению температурного градиента на всем протяжении проводящей среды.
Тепло, протекающее через материал в единицу времени на единицу площади, является тепловым потоком. Он будет пропорционален градиенту температуры. K → Коэффициент теплопроводности (Вт / мK)
K = K _фонон + K _{электрон} ; так как передача тепла в твердых телах за счет фононов и электронов.
Теперь мы можем вывести выражение для коэффициента теплопроводности.
Для этого мы должны предположить, что поток тепла идет от более высокой температуры к более низкой температуре в металлической плите, которая имеет температурный градиент .c _v → Удельная теплоемкость
n → Количество частиц в единице объема
λ → среднее свободный пробег столкновений
v → скорость электронов
Сравнивая уравнения (1) и (2), мы получаем, что энергия свободных электронов равна. газ при постоянном объеме. Когда мы помещаем уравнение (8) в (6), мы получаем Далее, мы можем рассматривать плотность электрического тока металла с приложением электрического поля, E (рисунок 1)
J = σ E; Закон Ома Итак, правильная форма закона Ома дается формулой: существует длина свободного пробега и среднее время между столкновениями.e → Заряд электрона = 1,602 × 10 ^-9 C
τ → Время столкновения или среднее время: это среднее время, за которое электрон движется или перемещается до рассеяния.
v _d → Скорость дрейфа: Это стандартная скорость электрона во время столкновения.
Когда мы помещаем уравнение (11) в (10), мы получаем электрическую проводимость (проводимость Друде), поскольку рассмотрим электроны, которые движутся в металле без какого-либо приложения электрического поля. Тогда теорема о равнораспределении дается формулой Из уравнения (13) мы получаем m as Теперь мы помещаем уравнение (14) в (12) Таким образом, мы получили значения K и σ из уравнений (6) и (15).Теперь мы можем взять соотношение. Мы предполагаем, что v = v _d , тогда уравнение (16) становится Из этого мы можем сказать, что соотношение одинаково для всех металлов. Это также функция температуры. Этот закон известен как Закон Видемана-Франца Лоренца . Можно сделать вывод, что лучший проводник тепла будет лучшим проводником тепла.

Ограничения Закона Видемана Франца

• Значение L не одинаково для всех материалов.
• Этот закон не действует для промежуточной температуры.
• В чистых металлах как σ, так и κ возрастают с понижением температуры.

Закон Джоуля — эффект Джоуля или эффект нагрева тока

Закон Джоуля — эффект Джоуля или эффект нагрева тока и его приложения

Английский физик Джеймс Прескотт Джоуль открыл закон Джоуля (также известный как эффект Джоэля, Закон Джоуля-Ленца или первый закон Джоуля) в 1840-43 гг., Который показывает связь между током, теплотой и сопротивлением в определенное время i.е. когда через материал протекает ток, он выделяет в нем тепло.

Закон Джоуля

Закон Джоуля гласит, что «если через резистор« R »протекает ток« I »в течение« t »секунд, то объем выполненной работы (преобразование электрической энергии в тепловую) равен равно

Выполненная работа = Нагрев = I ² Rt… Джоулей

или

WD = Нагрев = VIt… Джоули… (∴ R = V / I)

или

WD = Нагрев = Wt… Джоули… (∴ W = VI)

или

WD = Тепло = V ² т / R… Джоули… (∴ I = V / R)

Выполненная работа — это количество тепловой энергии, преобразованной из электричества, которое рассеивается в воздухе.В этом случае количество произведенного тепла можно рассчитать, используя следующие формулы и уравнения.

Количество произведенного тепла = H = выполненная работа / Механический эквивалент тепла = WD / J

Где:

• J = 4187 джоулей / ккал = 4200 джоулей / ккал (прибл.)
• ∴ H = I ² Rt / 4200 ккал = VIt / 4200 ккал = Wt / 4200 ккал = V ² t / 4200 ккал

Одна килокалория (ккал) — это количество тепла, необходимое для повышения температуры на один килограмм (кг ) воды на один градус по Цельсию (1 ° C).

Похожие сообщения

Эффект нагрева от тока

Почти все мы испытали, что когда ток течет по проводнику или кабелю и проводу, он позже нагревается. Причина этой сцены в том, что когда ток течет по проводнику, приложенная электрическая энергия преобразуется в тепловую, что увеличивает температуру проводника.

Мы знаем, что поток электронов в веществе известен как электрический ток. Дрейфующие электроны в веществе сталкиваются друг с другом и с электронами атомов молекул вещества.Столкновение электронов производит тепло. Вот почему при прохождении электрического тока в веществе выделяется тепло. Этот эффект известен как эффект нагрева от тока.

Тепло, выделяемое электрическим током, зависит от силы тока и материала этого вещества. Например,

Электрический ток производит больше тепла в изоляторах (тех материалах, которые сильно препятствуют протеканию в нем тока, например, вольфрам, нихром), в то время как количество тепла, выделяемого протекающим током в проводниках (тех материалах, в которых ток течет очень легко из-за к меньшему или почти незначительному сопротивлению e.грамм. золото, медь, алюминий) меньше, чем у изоляторов).

Похожие сообщения:

Почему от тепла светится элемент обогревателя, а не шнур обогревателя?

Как правило, нагревательные элементы нагревателей изготавливаются из нихрома, который имеет очень высокое сопротивление. Когда напряжение питания подается на нагревательный элемент через провод, материал сильно противодействует потоку электронов в нем. Из-за дрейфа электронов внутри нагревающего материала электроны сталкиваются с электронами в атомах материала.Это непрерывное столкновение электронов нагревает и зажигает нагревательный элемент, который дополнительно обеспечивает тепловую энергию. Проще говоря, нагревательный элемент из нихрома преобразует электрическую энергию в тепловую. Весь этот процесс известен как эффект нагрева от тока.

С другой стороны, шнур, подключенный к нагревателю, сделан из проводника, по которому легко протекает ток без заметного сопротивления. Поэтому светится только нагревательный элемент, а не кабель нагревателя.

Похожие сообщения:

Решенный пример закона Джоуля для нагрева Эффект тока

Пример:

Электронагреватель содержит 1,6 кг воды при 20 ° C. Для повышения температуры до 100 ° C требуется 12 минут. Предположим, что потери из-за излучения и нагрева чайника составляют 10 кг калорий. Найдите номинальную мощность обогревателя.

Раствор

Тепло, необходимое для повышения температуры 1,6 кг воды до точки кипения = 1,6 x 100 x 1 x (100-20) кал.

= 128000 кал.

Потери тепла = 10 x 1000 = 10000 кал.

Всего тепла = 128000) + 10000 = 138000 кал.

Итак, произведенное тепло = Wt = (W x 12 x 60) / 4,2 кал.

Выработанное тепло = тепло, забираемое нагревателем, т.е.

= (W x 12 x 60) /4,2 = 138000

W = (138000 x 4,2) /) 12 x 60)

W = 805W = 0,8 кВт

Применение эффекта Джоуля или эффекта нагрева тока

Закон Джоуля или эффект нагрева электрическим током используются во многих домашних и промышленных приложениях.Ниже представлены приборы и устройства, использующие воздействие электрического тока.

• Электрические обогреватели, плиты, водонагреватели и нагревательные элементы
• Электрический утюг для одежды
• Электрическая плита
• Электросварка
• Пищевая промышленность
• Нить накаливания ламп накаливания и лампочек
• ИК-тепловизор (инфракрасная термография (IRT) ) лампочки
• Катушки резистивного нагрева, обогреватель помещения (электрический радиатор), погружные нагреватели PTC-нагреватели, картриджные нагреватели и тепловентиляторы
• Фены
• Паяльник
• Предохранители и плавкие элементы

Помимо этих полезных приложений Из-за теплового воздействия тока, есть некоторые недостатки, такие как потеря электроэнергии (I ² R) в линиях электропередачи и передачи HVAC (переменный ток высокого напряжения) из-за того, что существует некоторое сопротивление линий электропередачи материал.Более того, это приводит к серьезным проблемам с нагревом в электрических машинах и устройствах, таких как трансформатор, генератор, двигатели и т. Д.

Кроме того, термический КПД или эффективность нагрева тока вообще не могут использоваться, потому что есть некоторые потери тепла из-за излучение (передача тепла в виде волн нагрева) и конвекция (движение молекул в материале, используемом для передачи тепла).

Связанные сообщения:

Развитие сильно неоднородного температурного профиля в электрически нагреваемых щелочно-силикатных стеклах

Недавнее открытие EFIS стекла ^19,20,21 , настоящие наблюдения локального нагрева и теплового разгона (рис. 2–5) ), а моделирование методом МКЭ (рис. 5–8) ясно демонстрирует, что классический макромасштабный закон Джоуля для однородных образцов не применим к электрическому нагреву обычных стекол, даже любого ионопроводящего твердого тела, когда используются обычные металлические или графитовые электроды.О макромасштабной асимметрии изменения температуры сообщалось также во время мгновенного спекания кислород-анион-проводящей оксидной керамики, стабилизированной оксидом иттрия ^31,32 . Чтобы понять источник этого макромасштабного несоответствия, отметим случай простого резистивного нагрева, который обычно используется для плавления и очистки расплавов стекла ^33,34 . Этот метод зависит от удельного сопротивления стекла и его температурной зависимости как ионного проводника в расплавленной фазе ³⁵ .

В фазе жесткого стекла на макромасштабе закон Джоуля не применяется, потому что однородное стекло начинает изменяться при приложении к нему внешнего напряжения.В начале приложения напряжения однородное стекло подчиняется закону Джоуля ²⁶ . Однако подвижные ионы в стекле начинают мигрировать к противоположно заряженным электродам, образуя обедненный ионами щелочных металлов слой в стекле, ближайшем к аноду ²⁰ . Полученный тонкий слой имеет гораздо более высокое удельное сопротивление по сравнению с массивным стеклом, так что в течение одной минуты почти полное падение напряжения полирования происходит через этот слой в условиях термического полирования ^20,30 . Было рассчитано резкое падение напряжения на образце, которое видно на рис.6а для обедненного слоя 100 нм на анодной стороне модели при напряжении 200 В. При такой толщине внутреннее электрическое поле достигает ~ 1,9 × 10 ⁷ В / см, тогда как внешнее приложенное поле будет составлять 200 В / см, что делает внешнее поле макромасштабного уровня незначительным. Диэлектрическая прочность чистого кремнезема составляет 10 ⁷ В / см, и, следовательно, внутреннее электрическое поле достаточно велико, чтобы изменить потенциальный энергетический барьер для электронной проводимости внутри изоляционного материала ^36,37 .В этот момент может произойти пробой диэлектрика, увеличивая электронную проводимость до точки, когда рассеивание электрической энергии нагревает стекло до состояния теплового разгона. Таким образом, выделение тепла во время разгона может выдержать аварию. Альтернативная точка зрения состоит в том, что тепловыделение из-за сильно неоднородного джоулева нагрева вызывает тепловой разгон, который затем приводит к пробою диэлектрика. Настоящие результаты не могут полностью разрешить эту причинно-следственную дилемму между пробоем диэлектрика и тепловым разгоном.{{t} _ {f}} v \ ast i \, dt \, $$

(1)

, где Q — тепловая энергия из-за рассеивания мощности из-за электрических потерь [Дж], v — напряжение на образце [В], i — ток [A], t _с и t _f — время начала и окончания EFIS [s]. Это соотношение предполагает полное преобразование электрической энергии в тепловую без потерь.Затем тепловая энергия, оцененная по уравнению 1, может быть использована для расчета соответствующего повышения температуры в образце на основе простой теплопередачи со следующим соотношением:

$$ Q = m \ ast {C} _ {p} \ ast {\ Delta} T \, $$

(2)

где м — масса образца [г], C _p — удельная теплоемкость стекла [Дж / гК], а ΔT — изменение температуры от начальной до конечное значение [K].Этот расчет предполагает, что тепловыделение намного больше, чем тепловые потери, и что температура образца везде одинакова с постоянной теплоемкостью.

Очевидно, что очень высокие температуры могут быть реализованы в слое, обедненном щелочными ионами, рядом с анодом при одновременном приложении постоянного напряжения и нагрева печи — достаточно высоких, чтобы вызвать испарение и повторное осаждение стекловидного порошка, как показано на рис. 1a. ^30,38 . Например, рассмотрим стекло NS с напряжением 150 В постоянного тока, приложенное к печи T в диапазоне 350 ° C.Энергия, рассеиваемая внутри стекла во время такой обработки, была рассчитана на основе плотности мощности с использованием уравнения 1. На рис. 9 показаны временные рамки во время пробоя диэлектрика вместе с соответствующим увеличением температуры образца за пределами T _печи . Изменение температуры образца было аппроксимировано уравнением 2 с удельной теплоемкостью 1,15 Дж / г · К и массой 0,5921 г ³⁹ . На рис. 9 наблюдаются две важные особенности. Во-первых, диссипация энергии в начале пробоя диэлектрика увеличивается экспоненциально, что обозначено как «Thermal Runaway».Вторая особенность — линейное увеличение рассеиваемой энергии, которое является результатом ограничения тока, налагаемого силовым резистором, включенным последовательно с образцом. Рассеяние энергии в конечном итоге выравнивается из-за снятия приложенного напряжения. Это простое приближение дает ограничивающую оценку увеличения температуры образца на 2500 ° C после двух минут ограниченного током теплового неуправляемого нагрева. Этот интенсивный нагрев объясняет размягчение и последующее испарение стекла, оставляя отложения, богатые щелочью и кремнеземом, которые видны на рис.1.

Рисунок 9

Рассеяние энергии и соответствующее увеличение температуры образца (в пределе отсутствия тепловыделения) за пределами печи T для стекла NS при 150 В постоянного тока при 350 ° C. Диссипация энергии рассчитывается по формуле. 1 и повышение температуры по формуле. 2. Примечание. Красная пунктирная линия указывает на линейный режим ограничения тока из-за включенного последовательно включенного силового резистора.

Графики на рис. 9 основаны на простых приближениях, но они, кажется, правильно показывают величину температуры, при которой может происходить размягчение и испарение стекла.Большинство образцов размягчаются после ~ 30 с теплового разгона, и согласно рис. 9 однородная температура стекла будет порядка 1500 ° C. Чтобы оценить справедливость этого предположения, использовалось тепловизионное изображение для непосредственного измерения фактической температуры поверхности образца. Это также позволило детально наблюдать процесс теплового разгона, в том числе то, как соответствующее большое тепловложение распределяется в образце. Роль обедненного слоя вблизи анода наглядно показывает график профиля температуры на рис.3. Здесь в течение первых 20 с пробоя диэлектрика, вызванного протеканием большого тока, сильно локализованные области стекла вблизи анода нагреваются. Считается, что локализованный нагрев соответствует процессу термического пробоя диэлектрика, который, вероятно, инициируется на неровностях поверхности или диэлектрических неоднородностях, где напряженность электрического поля локально максимальна ¹¹ . Это могло бы объяснить неравномерный нагрев, наблюдаемый как на рисунках 2, так и на 3.

Различия в EFIS, наблюдаемые между приложенными напряжениями постоянного и переменного тока, как полагают, связаны с разницей в рассеиваемой мощности во время EFIS для двух случаев, что приводит к до самонагрева и теплового разгона ²¹ .Сравнение проводится для NS с 150 В постоянного тока на рис. 4 и 150 В переменного тока при 1 кГц на рис. 5. Обратите внимание, что образец на ИК-изображениях расположен в центре с анодом вверху и катодом внизу. для случая DC. На рисунке 4 сравнивается тот же образец NS с напряжением 150 В постоянного тока при двух значениях T _печи , 353,5 ° C и 363,6 ° C. Поскольку скорость нагрева печи составляла 10 ° C / мин, и два изображения были получены с интервалом в 40 секунд, огромная разница в температуре образца объясняется тепловым разгоном.Для случая постоянного тока на рис. 4 самая высокая температура была измерена на анодной стороне стекла, как и на рис. 2. В течение 40 секунд температура образца подскочила примерно на 1400 ° C и стала очень неоднородной. В случае переменного тока на рис. 5, два изображения были получены с интервалом примерно 270 с в печи T = 385,3 ° C и 428,6 ° C. Между двумя изображениями температура образца увеличилась с 500,8 ° C до 514,4 ° C, показывая, что изменение в печи T _{было больше, чем в стеклянном образце, скорее всего, из-за более однородного внутреннего поля и соответствующего распределения тепла под Переменного тока, чем в аналогичном случае постоянного тока.Очевидно, что резистивный нагрев в AC-EFIS может быть более управляемым по сравнению с резким тепловым разгоном DC-EFIS.}

Наблюдаемая разница в ИК-изображениях для полей постоянного и переменного тока подтверждается измеренной плотностью мощности на единицу объема. Мощность в DC-EFIS рассчитывалась по напряжению и току, а в AC-EFIS — по среднеквадратичному напряжению и току [Мощность, рассчитанная на основе среднеквадратичных значений напряжения и тока, включает ненагревающий компонент, в результате чего коэффициент мощности меньше чем один.Его значение трудно определить напрямую из-за постоянно меняющейся температуры и сопротивления обедненного слоя, но этот фактор не изменит настоящего вывода.]. Например, стекло NS, испытанное при 150 В постоянного тока, показало максимальную плотность мощности 91 мВт / мм ³ , тогда как при 150 В — 1 кГц переменного тока максимальная плотность мощности составила 55 мВт / мм ³ . Аналогичная тенденция была измерена с составом 5Л5НС при напряжении 150 В. При постоянном токе максимальная плотность мощности составляла 78 мВт / мм ³ , но при 150 В — 1 кГц переменного тока удельная мощность составляла 54 мВт / мм ³ .Следует отметить, что при постоянном токе рассеивание мощности намного более локально вблизи анода по сравнению со случаем переменного тока, что преувеличивает разницу в плотности мощности на единицу объема.

Самонагрев НЗ в переменном токе является равномерным, и самое горячее измерение было в центре образца между электродами. Этот профиль указывает на то, что резистивный джоулев нагрев, вероятно, является результатом колебательного напряжения, которое заставляет протекать ток и джоулева нагревание начинается и прекращается каждый полупериод частоты.Для сравнения, использование постоянного напряжения приводит к экстремальному локальному нагреву и размягчению стекла, в то время как переменный ток способствует равномерному нагреву и постепенному размягчению. Как обсуждалось в предыдущей работе AC-EFIS ²¹ , приложение переменного напряжения создает два процесса, которым подвергаются подвижные катионы. В первом полупериоде переменного напряжения электрод имеет временное положительное смещение, которое отводит подвижные катионы от границы раздела электрод / стекло в объем. Миграция ионов доминирует над диффузией в этом полупериоде.Во втором полупериоде смещение временно меняется на противоположное, теперь имеется большой градиент концентрации катионов, приводящий к диффузии катионов обратно к обедненному слою, и обратное смещение напряжения также вызывает обратную миграцию катионов. Этот процесс, вероятно, предотвращает пробой диэлектрика и интенсивный локальный нагрев, как измерено в DC-EFIS.

Экспоненциальный рост тока на рис. 7a показывает положительную обратную связь резистивного нагрева. Однако рост тока достигает асимптоты, демонстрирующей конкуренцию между тепловыделением за счет резистивного нагрева и тепловыми потерями из-за конвекции в электроды и излучения в окружающую печь.Расчетные температуры вместе с тепловым профилем хорошо согласуются с экспериментальными измерениями. Тепловидение показало, что температуры выше 1300 ° C (см. Рис. 2) часто достигаются при использовании постоянного напряжения. Максимальная температура 1868 ° C была измерена в NS около области обедненного слоя во время DC-EFIS при 150 В после ~ 30 с пробоя диэлектрика, как показано на рис. 4. Эти расчеты показывают, что размягчение стекла происходит от анода к катоду, как показано на рис. передача тепла от обедненного слоя в объем стеклянного образца.Это предположение подтверждается рис. 4б. Моделирование методом конечных элементов предсказывает общую температуру истощенного слоя около 1600 ° C, в то время как инфракрасное изображение измеряет около 1800 ° C. Расхождение в значениях могло быть результатом моделирования FEA образца как одномерного твердого тела, которое не учитывает накопление тепла в центре стекла с радиальным градиентом температуры. Модель также использовала для расчетов не зависящую от температуры теплопроводность.

В настройке модели FEA ограничение тока с помощью логического оператора было наложено на 0.3A, что было больше асимптоты, достигнутой во время FEA. Подобный максимум тока около 0,23 А был аналогичным образом измерен экспериментально во время EFIS, как показано на рис. 7a. Последовательный силовой резистор теоретически ограничивал максимальный ток до 0,5 А, но никогда не был полностью достигнут экспериментально ²⁰ . Сравнение теоретической и экспериментальной асимптот тока показывает, что процесс EFIS является самоподдерживающимся. Ток, протекающий через стекло, рассеивается в виде тепла, которое увеличивает температуру и увеличивает ионную миграцию и диффузию.Однако создание богатой диоксидом кремния области увеличивает сопротивление образца, предотвращая дальнейшее экспоненциальное увеличение тока. Это ограничение тепловыделения не соблюдалось во время AC-EFIS ²¹ . Рассеивание мощности постоянно увеличивалось во время AC-EFIS, но событие размягчения происходило при более низкой температуре печи. О последнем факте сообщалось в результате более равномерного нагрева и постепенного размягчения образца, в отличие от DC-EFIS, который был резким и резким ²¹ .В принципе, асимптотический ток будет наблюдаться также в AC-EFIS, если используется достаточно низкая частота, чтобы дать достаточно времени для образования слоя обеднения щелочными ионами и сохранения его стабильности на обоих электродах.

Для оптимизации тепловыделения моделирование профилей температуры методом FEA для различных значений δ выявляет проницательную тенденцию на рис.8. анод. Вместо этого в объеме стекла наблюдался равномерный джоулев нагрев.Тепло, которое генерировалось в обедненном слое 5 нм, могло быстро рассеиваться в электрод за счет теплопроводности. Максимальная температура, которую испытывал обедненный слой, приходилась на его толщину 100 нм. Значение δ выше 100 нм начинает ограничивать количество тока, который может проходить через образец из-за большего сопротивления обедненного слоя. В свою очередь, уменьшенный ток уменьшил сопутствующие эффекты джоулева нагрева, как показано на рис. 8. Следовательно, тепловой разгон либо расширяется до более длительного временного масштаба, либо подавляется до тех пор, пока теплопотери уже не являются незначительными по сравнению с тепловыделением и достигают устойчивое состояние.Это понимание, полученное с помощью теплового моделирования, объясняет динамический джоулев нагрев, наблюдаемый с помощью экспериментального тепловизора.

Видео тепловизоров показывают, что нагрев во время EFIS вблизи анода сильно локализован и неравномерен. Локализованная «горячая точка» также имеет тенденцию изгибаться в боковом направлении на границе раздела анод / стекло. Результаты модели FEA объясняют это наблюдение, когда интенсивный локализованный нагрев создает большое значение δ из-за термически усиленной миграции катионов. Затем δ может вырасти до порядка 50 мкм, как измерено с помощью линейных сканеров EDS ²¹ .При достижении относительно «толстого» обедненного слоя в 50 мкм тепловое бегство в этой локальной области подавляется ограниченным током через более резистивный слой. Этот процесс служит петлей отрицательной обратной связи способности диэлектрического материала поддерживать ток в этой локализованной области. Однако в области, прилегающей к локализованному нагреву, условия могут способствовать продолжению пробоя диэлектрика, переходя в боковом направлении в соседнюю область, которая была нагрета в результате близкого теплового разгона, но сохранила « оптимальное » значение δ на ~ 100 нм. .Процесс теплового разгона продолжается в этой новой области, пока он, в свою очередь, также не будет подавлен растущим обедняющим слоем, заставляя его снова перемещаться в соседнюю область и так далее. По мере того как соседние области «горячих точек» соединяются друг с другом, коллективное сопротивление расширенного обедненного слоя будет уменьшаться, и будет генерироваться достаточно тепла для инициирования EFIS. Таким образом, передача тепла из обедненного слоя в объемную часть в конечном итоге приведет к тому, что температура объемного образца достигнет температур размягчения, что позволит возникать вязкому течению.

Внешние силы

Силы неэлектростатического происхождения, действующие на заряды от источников тока, называются внешними силами.

Электродвижущая сила

Скалярная физическая величина, определяемая работой, совершаемой внешними силами при перемещении одиночного положительного заряда, называется электродвижущей силой (ЭДС), действующей в цепи или на ее части:.

Напряжение

Напряжение — — это физическая величина, определяемая работой, совершаемой общим электростатическим (кулоновским) полем и внешними силами при перемещении одиночного положительного заряда в данном участке цепи.

Разность потенциалов

Напряжение на неоднородном участке цепи (где есть внешние силы) равно сумме источника ЭДС и разности потенциалов в этой области:

Для однородного участка цепи там, где не действуют внешние силы,

Т.е. Напряжение совпадает с разностью потенциалов на концах цепочки .

Закон Ома для однородного участка Схема в интегральном и дифференциальном образуют .Сопротивление и его зависимость от температуры. Сверхпроводимость.

Закон Ома для однородного участка в интегральном и дифференциальном образуют

Закон Ома для однородной части цепи: n немецкий физик Георг Ом экспериментально установил, что ток в цепи прямо пропорционален приложенному напряжению и обратно пропорционален силе тока. сопротивление проводника:.

Закон Ома в дифференциальной форме (закон Ома для плотности тока).Закон Ома по форме распространяется на весь проводник. Представьте себе закон Ома в дифференциальной (т.е. относящийся к текущему элементу длиной дл а) форме. Некоторая точка внутри проводника характеризуется вектором плотности тока, напряженности электрического поля и свойствами материала проводника, то есть удельным сопротивлением. Выбираем мысленно небольшой объем возле рассматриваемой точки и подставляем закон Ома, получаем: , здесь — разность потенциалов между сечениями dS дальний dl .Как следствие,.

Учтем, что — напряженность электростатического поля; — плотность электрического поля; — удельная электропроводность.

Тогда из формулы (20) следует закон Ома в дифференциальной форме : .

Сопротивление и его зависимость от температуры

Температурную зависимость сопротивления можно представить как:,

Сверхпроводимость

Сверхпроводимость — некоторых проводников, которое заключается в том, что их электрическое сопротивление падает до нуля при охлаждении ниже определенной критической температуры T to, характерной для проводника.

16. Рабочий и силовой ток. Закон Джоуля-Ленца в интегрально-дифференциальной форме

Когда ток течет через однородный участок цепи, электрическое поле совершает работу. Во время Δ t А по цепи течет заряд. q = I Δ т . Электрическое поле на выделенном тесте делает свое дело

, выражающий закон Ома для однородного участка цепи с сопротивлением R , умножаем на I Δ t , получаем соотношение

Закон превращения тока в тепло независимо друг от друга экспериментально установлен Дж.Джоуля и Э. Ленивого и называется джоуль — Закон Ленца .

Мощность электрического тока равна отношению тока операции A к временному интервалу Δ t , за который выполнялась данная работа:

Работа электрического тока в СИ выражается в джоулях (Дж) мощность — в Вт (Вт)

Закон Джоуля-Ленца в дифференциальной форме — удельная мощность тока равна скалярному произведению векторов плотности тока и напряженности электрического поля:

,

где s — проводимость;

r — удельное сопротивление среды.

Закон Джоуля-Ленца в дифференциальной форме носит совершенно общий характер, то есть не зависит от природы сил, возбуждающих электричество. Закон Джоуля-Ленца, как показывает опыт, справедлив и для электролитов и полупроводников.

17 .. Обобщенный закон Ома для неоднородной части цепи в интегральной и дифференциальной форме. Анализ обобщенного закона Ома. Замкнутая электрическая цепь. Сопротивление подключения: последовательное и параллельное.

1

11 Сторонние электродвижущие силы.Закон Джоуля — Ленц

Согласно (11.4), ЭДС численно равна работе внешних сил, совершается при перемещении одиночного положительного заряда по замкнутой цепи.

Помимо внешних сил на заряд действуют силы. электростатическое поле, имеющее напряжение. Следовательно, результирующая сила, действующая на заряд в любой точке цепи, может быть записана в виде Это правило Кирхгофа является условием стационарности токов. В противном случае потенциал рассматриваемого узла со временем изменился бы, а это привело бы к изменению токов в цепи.

Второе правило Кирхгофа гласит, что алгебраическая сумма произведений сил токов в определенных участках произвольной замкнутой цепи на сопротивление этих участков равна алгебраической сумме ЭДС, действующей в этой цепи:

. (11.13)
Здесь и — сила тока и сопротивление для некоторого участка замкнутой цепи, — значение ЭДС. в той же цепочке.

Второе правило Кирхгофа является следствием закона Ома для замкнутой цепи.Направление обхода замкнутого контура и направление токов на всех участках контура выбираются произвольно. Сила тока фиксируется знаком «+», если его направление совпадает с направлением обхода замкнутого контура, и знаком «-» в противном случае. Величина ЭДС записывается со знаком «+», если при обходе замкнутого контура движение внутри источника идет от его отрицательного полюса к положительному, то есть совпадает по направлению с внутренним током источника.

Чтобы найти все неизвестные токи, необходимо решить систему независимых уравнений, в которой количество уравнений должно быть равно количеству неизвестных токов. В результате решения системы уравнений могут быть получены отрицательные значения силы тока. Это означает, что на рассматриваемом участке схемы реальный ток течет в обратном направлении относительно выбранного направления.

Например, в схеме, показанной на рисунке 16, можно выделить три замкнутых контура, для которых второе правило Кирхгофа —

.

(11.14)

Здесь записывается первое уравнение для контура.

, второе уравнение для контура

, третье уравнение для контура

. Эта система уравнений линейно зависима. Следовательно, для расчета неизвестных токов I 1 , г. I 2 I 3 необходимо использовать любые два из этих трех уравнений вместе с первым правилом Кирхгофа (11.12).

Рисунок 16. Пример разветвленной цепи постоянного тока
Используя правила Кирхгофа, можно вычислить, например, ЭДС. и внутреннее сопротивление батареи. Предположим, батарея состоит из нескольких источников постоянного напряжения, количество источников равно

, ЭДС каждого источника одинакова, внутреннее сопротивление равно и источники соединены последовательно. Тогда общая ЭДС. а общее внутреннее сопротивление батареи можно рассчитать следующим образом:

.Если в батарее источники соединены параллельно, то

.

Когда электрический ток проходит по цепи, выделяется тепло. Этот процесс можно охарактеризовать с помощью концепции тепловой мощности, тока

Тепловое воздействие тока можно описать на основе закона Закона Джоуля — Ленца . : тепловая мощность тока является произведением тока по напряжению на этом сайте:

.(11.16)
Используя закон Ома для участка цепи (10.10), выражение для тепловой мощности тока (11.16) можно представить в другом виде:

. (11.17)
Для переменного тока теплоемкость зависит от времени. Если ток изменяется относительно медленно, это называется квазистационарным. Условие квазистационарности будет сформулировано в разделе 30. В этом случае количество выделяемого тепла можно рассчитать следующим образом:

, (11.18)
Где и — начальный и конечный моменты времени.

Для постоянного тока тепловая мощность не зависит от времени, и интеграл в выражении (11.18) следует заменить произведением мощности и длительности рассматриваемого временного интервала.

Закон Джоуля — Ленц также может быть сформулирован как в дифференциальной форме. Для этого необходимо принять в расчет насыпную удельную тепловую мощность по току , то есть количество тепла, выделяемого в единицу времени в единице объема проводника

Используя соотношение (11.16) и (11.19), получаем локальную формулировку закона Джоуля-Ленца:

. (11.20)
Учитывая закон Ома (10.11), закон Джоуля-Ленца в дифференциальной форме также может быть записан как

. (11.21)
D Чтобы прояснить физический смысл формулы (11.20), введем в рассмотрение объемную плотность силы, действующей из электрического поля на свободные заряды

Смещение под действием электрического поля зарядов в проводнике всегда происходит таким образом, что электрическое поле в проводнике исчезает и ток прекращается.Чтобы ток протекал в течение длительного времени, силы, отличные от сил электростатического поля, должны действовать на заряды в электрической цепи, такие силы называются внешними силами.

Представьте внешнюю силу Fst, действующую на заряд q, в виде

Природа внешних сил может быть разной. Источники постоянного тока могут быть основаны на химическом (гальванические элементы и батареи) или тепловом (термопары) воздействии. В гальванических элементах внешние силы возникают из-за энергии химических реакций между электродами и электролитами.Гальванические элементы и батареи преобразуют химическую энергию в электрическую. В генераторе внешние силы образуются за счет механической энергии вращения ротора генератора и т. Д., Термопары преобразуют внутреннюю энергию в электрическую, а фотоэлементы преобразуют световую энергию в электрическую.

Электродвижущая сила (ЭДС) — скалярная физическая величина, которая характеризует работу внешних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока.В замкнутой проводящей цепи ЭДС равна работе этих сил по перемещению одного положительного заряда по всей цепи. По аналогии с электрическим полем они вводят понятие внешней силы \\ vec E_ (ex), которая понимается как векторная физическая величина, равная внешней силе, действующей на пробный электрический заряд на величину этого заряда. Тогда в замкнутом контуре L ЭДС будет равна:

Теория Бора была важным шагом в развитии атомной физики и важным шагом в создании квантовой механики.Однако эта теория имеет внутренние противоречия (с одной стороны, она применяет законы классической физики, а с другой — основана на квантовых постулатах). В теории Бора рассматриваются спектры атома водорода и водородоподобных систем и вычисляются частоты спектральных линий, но эта теория не могла объяснить интенсивности спектральных линий и ответить на вопрос: почему происходят определенные переходы? ? Серьезным недостатком теории Бора была невозможность с ее помощью описать спектр атома гелия — одного из простейших атомов, следующих сразу за атомом водорода.

Второй постулат Бора (правило частоты): когда электрон переходит с одной стационарной орбиты на другую, один фотон с энергией испускается (поглощается)

ч E E, ν = n — m (19,6)

равна разности энергий соответствующих стационарных состояний (Еn и Еm — соответственно энергии стационарных состояний атома до и после излучения (поглощения)). Когда Em … n — его поглощение (переходного атома в состояние с большей энергией, т.е.е. переход электрона на более орбитальную орбиту). Набор возможных дискретных частот квантовых переходов v = (En -Em) / h определяет линейчатый спектр атома.

Переменный ток (англ. Alternatingcurrent) — электрический ток, который изменяется со временем и величиной по направлению или, в конкретном случае, изменяется по величине, сохраняя свое направление в электрической цепи неизменным. Обозначение на электроприборах: \ Thicksim или \\ Thickapprox (знак синусоиды), либо латинскими буквами AC.

Период, обратный периоду, называется по частоте переменный ток:

частота переменного тока;

Период переменного тока.

Если создать разность потенциалов на концах любого провода AB (рис. 5.16), в нем возникнет электрическое поле E̅.

Под действием этого поля свободные заряженные частицы (в металлах это свободные электроны) будут двигаться в определенном направлении, не прекращая своего хаотического движения, создавая кратковременный ток.

Однако на практике в подавляющем большинстве случаев необходимо длительное время существования тока в проводниках. Для этого на концах провода разность потенциалов должна поддерживаться постоянной. Эту функцию в электрических цепях выполняют источники тока.

Любой источник тока имеет два полюса: положительный и отрицательный. Источник, как и любой другой проводник, имеет сопротивление r, , которое называется внутренним сопротивлением (рис.5.17).

На полюсах источника долгое время существует разность потенциалов. Но почему в этом случае ток не течет в самом источнике? На самом деле разность потенциалов существует на полюсах батареи для карманной лампы довольно долгое время, однако ток появляется только при подключении лампочки к полюсам батареи. Очевидно, что в источнике есть силы, которые пытаются поддерживать разность потенциалов на его полюсах, противодействуя электрическим силам, которые пытаются уравнять потенциалы на полюсах источника.Эти силы имеют неэлектрическое происхождение, поэтому их называют сторонними .

Рис. 5.17. Источник тока

Внешние силы определяют разделение противоположно заряженных частиц в источнике и поддерживают определенную разность потенциалов на его полюсах. В гальванических элементах разделение заряженных частиц осуществляется за счет химической энергии, в термогенераторах — за счет тепловой энергии и т. Д.

Таким образом, внешние силы внутри источника тока создают электрическое поле, которое называется полем внешних сил . Напряженность такого поля E ст. можно измерить силой, действующей на заряженные частицы с общим зарядом в одну единицу. Материал с сайта

E Арт. = F Арт. / q.

Очевидно, что напряженности поля сторонних сил и электрические силы в источнике имеют противоположные направления. Если внешняя часть цепи источника разомкнута, то силы обоих полей в источнике одинаковы, и в источнике нет тока.

Когда внешняя часть цепи источника разомкнута, напряженность поля внешних сил и электрические силы в источнике одинаковы по величине и противоположны по направлению, поэтому они компенсируют друг друга.

Таким образом, роль источника сводится к разделению противоположно заряженных частиц и их накоплению на полюсах источника.

Закон мощности и Джоуля

Автор: Э.Э. Кимберли Когда через сопротивление протекает непрерывный ток, скорость преобразования электрической энергии в тепловую прямо пропорциональна сопротивлению и квадрату тока. Этот закон был открыт Джоулем и носит его имя. По определению, скорость изменения энергии — это мощность. Следовательно, мощность сопротивления равна P = RI 2 (2-2) куда P = электрическая мощность в ваттах; R = сопротивление, Ом; I = ток в амперах. Сокращение для ватта — w. Поскольку R = V / I, или (2-3) , где V = электродвижущая сила в вольтах. Также (2-4) Ампер определяется в системе единиц cgs. Если проводник длиной 1 см будет перемещен со скоростью 10 8 см в секунду и перпендикулярно линиям потока магнитного поля, имеющего однородную напряженность 1 гаусс, будет генерироваться ЭДС 1 вольт. в проводнике (см. раздел «Электродвижущая сила, создаваемая движением»).Если в то же время в проводнике будет протекать ток в 1 ампер, сила реакции, против которой должен быть перемещен проводник, будет 1/10 дина (см. Закон Ленца). Электрическая мощность, генерируемая в проводнике, будет P = VI = 1 * 1 = 1 ватт Механическая мощность, подводимая к проводнику, будет куда P = механическая мощность, дин-сантиметр в секунду; F = сила, действующая на проводник, в динах; D = расстояние, на которое перемещается проводник, в сантиметрах; t = время в секундах. Таким образом, дин-см в секунду По закону сохранения мощности механическая мощность должна быть равна электрической мощности. Следовательно, 1 ватт = 10 7 дин-см в секунду Чаще всего используется единица измерения механической мощности в лошадиных силах. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт