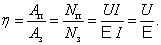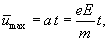открытие и основные физические величины, математическая запись и формулировка
 При протекании по проводнику электрический ток оказывает на него тепловое действие, во время которого выделяется определенное значение количества теплоты. Для его расчета применяется закон Джоуля-Ленца, который получил широкое применение при проектировании и изготовлении всех устройств, работающих от электричества.
При протекании по проводнику электрический ток оказывает на него тепловое действие, во время которого выделяется определенное значение количества теплоты. Для его расчета применяется закон Джоуля-Ленца, который получил широкое применение при проектировании и изготовлении всех устройств, работающих от электричества.
Общие сведения
В 1941 году английским физиком Джеймсом Джоулем и, независимо от него, в 1942 году русским ученым Эмилием Ленцем было открыто уравнение Джоуля-Ленца. Оно позволяет рассчитать по формуле количество теплоты в электрической цепи, выделяемое при прохождении электротока через проводник. Значение количества теплоты, выделяемое проводником при протекании тока через него, зависит от напряжения, времени, силы тока и сопротивления проводника. Открытие позволило точно рассчитывать схемы различных устройств при их проектировании.

Прежде чем сформулировать закон Джоуля-Ленца, следует рассмотреть и понять физический смысл основных и производных величин, от которых зависит, какое количество теплоты выделяет проводник при прохождении через него электротока.
Разность потенциалов
Научно доказано, что каждое вещество состоит из атомов, которые также состоят из элементарных или субатомных частиц. К ним относятся следующие: электроны, протоны и нейтроны. Атом в исходном состоянии имеет нейтральный заряд, поскольку количество протонов и электронов равны и, следовательно, справедливо равенство положительного и отрицательного зарядов, и они компенсируют друг друга.
 Однако возникают случаи «захвата» атомом электрона другого атома. Если атом захватывает электрон, то он называется отрицательным ионом, а при потере преобразовывается в положительный. В результате потери или притяжения субатомной отрицательно заряженной частицы образуется электромагнитное поле, составляющая которого зависит от заряда иона.
Однако возникают случаи «захвата» атомом электрона другого атома. Если атом захватывает электрон, то он называется отрицательным ионом, а при потере преобразовывается в положительный. В результате потери или притяжения субатомной отрицательно заряженной частицы образуется электромагнитное поле, составляющая которого зависит от заряда иона.
Разность между положительной и отрицательной составляющими является напряжением, единицей измерения которого является вольт (обозначение: В или V). Чем больше разница, тем больше напряжение. В некоторых источниках его еще называют разностью потенциалов, величину которой можно измерять при помощи вольтметра или рассчитать, используя формулы. При соединении потенциалов с противоположными знаками образуется электрический ток, который представляет упорядоченное движение заряженных частиц, под действием силы электромагнитного поля имеет векторное направление.
В научной литературе можно встретить такое определение: электрическим напряжением является работа, которая выполняется при перемещении точечного заряда. Таким образом, 1 В — это напряжение между двумя точечными положительным и отрицательным зарядами, равными 1 Кл, на перемещение которых тратится энергия электромагнитного поля 1 Дж. Вспомогательными единицами измерения являются следующие: 1 кВ = 1000 В, 1 МВ = 10
Сила тока
Сила тока (I) — величина, равная количеству заряженных частиц, которые проходят через проводник за единицу времени. Единица измерения — ампер (А), а с помощью амперметра можно измерять ее значение. Прибор подключается последовательно с потребителем в электрическую цепь. Если через площадь поперечного сечения проводника за 1 секунду проходит количество заряда, равное 1 Кл, то эта величина является силой тока в 1 А.
Математическая запись нахождения силы тока имеет вид: I = Qz / t, где Qz — значение заряда, а t — единица времени. Кроме того, существуют и дополнительные единицы измерения: 1 mА = 10^(-3) A, 1 кА = 1000 А и т. д. Электрический ток бывает следующих видов:
- Переменным.
- Постоянным.
 Переменный ток подчиняется определенному закону, который характеризует изменение амплитуды и направления протекания. Основной характеристикой является частота, согласно которой происходит разделение на синусоидальный и несинусоидальный токи. Графиком синусоидального типа тока является синусоида, формула которой зависит от максимальной амплитуды Imax и угловой частоты w. Она имеет следующий вид: i = Imax * sin (w * t).
Переменный ток подчиняется определенному закону, который характеризует изменение амплитуды и направления протекания. Основной характеристикой является частота, согласно которой происходит разделение на синусоидальный и несинусоидальный токи. Графиком синусоидального типа тока является синусоида, формула которой зависит от максимальной амплитуды Imax и угловой частоты w. Она имеет следующий вид: i = Imax * sin (w * t).
Для расчета значения угловой частоты необходимо значение частоты тока в сети (f), которое подставляется в формулу: w = 6,2832 * f. Постоянный ток не изменяет направление своего движения по проводнику, однако его значение может меняться.
Электрическое сопротивление
Вещества по проводимости электричества можно классифицировать на проводники, полупроводники и диэлектрики. К первому типу относятся все вещества, которые хорошо проводят ток. Эта особенность обуславливается наличием свободных носителей заряда, информацию о которых можно получить из электронной конфигурации элементов периодической системы Д. И. Менделеева.
 К проводникам относят следующие вещества: металлы, электролиты и ионизированный газ. В металлах электроны являются носителями заряда. В жидкостях (электролитах) носителями заряда являются анионы и катионы: первые обладают положительным зарядом, а вторые — отрицательным. При электролизе анионы притягиваются электродом, который является отрицательно заряженным (катодом), а на катионы действует положительный заряд анода. Функцию носителей заряда в газах выполняют отрицательно заряженные электроны и ионы.
К проводникам относят следующие вещества: металлы, электролиты и ионизированный газ. В металлах электроны являются носителями заряда. В жидкостях (электролитах) носителями заряда являются анионы и катионы: первые обладают положительным зарядом, а вторые — отрицательным. При электролизе анионы притягиваются электродом, который является отрицательно заряженным (катодом), а на катионы действует положительный заряд анода. Функцию носителей заряда в газах выполняют отрицательно заряженные электроны и ионы.
При повышении температуры проводника происходит взаимодействие атомов между собой, в результате которого разрушается кристаллическая решетка и появляются свободные носители заряда. При протекании тока происходит взаимодействие с узлами решетки и с электронами проводника, при котором движение упорядоченных заряженных частиц замедляется и выделяется тепловая энергия, а затем снова скорость их движения возвращается в исходное состояние, благодаря воздействию электромагнитного поля. Это физическое свойство называется электрическим сопротивлением проводника, при нагревании которого его величина возрастает.
Полупроводники — вещества, проводящие ток только при определенных условиях. Функцию носителей заряда выполняют электроны и дырки. При каком-либо воздействии внешней энергии (например, тепловой) происходит уменьшение силы притяжения между ядром и электронами, при котором некоторые из них «вырываются» и становятся свободным, а на их месте образуются дырки.
Происходит образование электромагнитного поля положительной составляющей и к ней притягивается соседняя субатомная частица с отрицательным зарядом. Этот процесс повторяется и приводит к движению дырок. Сопротивление вещества (проводника или полупроводника) зависит от следующих факторов:
- Температурных показателей.
- Типа вещества.
- Длины.
- Площади сечения.
- Значения силы тока и напряжения.
- Вида тока.

Диэлектрики — группа веществ, которые не могут проводить ток, поскольку в них отсутствуют какие-либо носители электрического заряда. Сопротивление или электропроводимость обозначается буквой R и является взаимодействием заряженных частиц, движущихся упорядочено, с узлами кристаллической решетки. Единицей его измерения является Ом.
Характеристика мощности
Мощностью электротока (P) называют количество работы, которое им совершается за единицу времени. Для постоянного и переменного токов мощность вычисляется по разным соотношениям. В цепи постоянного тока значения его силы (I) и напряжения (U) равны мгновенным значениям. Формула мощности записывается в следующем виде: P = U * I. Для цепи, в которой соблюдается закон Ома, формула принимает следующий вид: P = sqr (I) * R = sqr (U) / R.
 Для полной цепи формула включает значение электродвижущей силы (e): P = I * e. Если нужно учитывать значение внутреннего сопротивления источника питания (Rвн), то формулу нужно править при условии поглощения (использование в цепи электродвигателя или при зарядке аккумулятора) следующим образом: P = I * e — sqr (I) * Rвн = I * (e — (I * Rвн)).
Для полной цепи формула включает значение электродвижущей силы (e): P = I * e. Если нужно учитывать значение внутреннего сопротивления источника питания (Rвн), то формулу нужно править при условии поглощения (использование в цепи электродвигателя или при зарядке аккумулятора) следующим образом: P = I * e — sqr (I) * Rвн = I * (e — (I * Rвн)).
При наличии в цепи генератора или гальванического элемента (условие отдачи электроэнергии), формула принимает следующий вид: P = I * (e + (I * Rвн)). Однако эту формулу нельзя применять для расчета мощности переменного тока, поскольку он изменяется с течением времени.
- Активная определяется с учетом среднеквадратичных значений U и I, а также углом сдвига фаз (a): Pа = I * U * cos (a).
- Реактивная (Qр): Qp = U * I * sin (a).
- Полная (S): S = sqrt (sqr (Pа) + sqr (Qp)).
Значение Qp>0 при наличии в цепи индуктивной нагрузки, а при емкостной — Qp<0. Единицей измерения является ватт (Вт). Сила тока в 1 А при напряжении, равном 1 В, обладает мощностью 1 Вт.
Запись закона Джоуля-Ленца
Формулировка уравнения Джоуля-Ленца следующая: количество теплоты Q, которое выделилось за единицу времени t на участке цепи, прямо пропорционально произведению сопротивления R на квадрат силы тока I, протекающей через этот участок. Формула закона Джоуля-Ленца имеет вид: Q = a * sqr (I) * R * t. Литера «а» является температурным коэффициентом, который равен 1 при условии, что количество теплоты получается в джоулях. Если принять его равным 0,24, то результат будет измеряться в калориях. Поскольку а = 1, то формула Ленца будет выражаться кратко в таком виде: Q = sqr (I) * R * t.
При перегреве проводника может возникнуть короткое замыкание, которое приводит к выходу аппаратуры из строя. Оно может также быть причиной пожара. Для избежания таких ситуаций в электротехнике применяются плавкие предохранители, которые позволяют прекратить подачу электричества на устройство.

Закон позволяет найти необходимые параметры электрического тока, чтобы избежать перегрева и пожара. Основные соотношения для расчета составляющих величин закона в цепях постоянного тока следующие:
- Закон Ома для участка и полной цепи: I = U / R и i = e / (R + Rвн).
- Q = U * I * t.
- Q = e * i * t.
- Q = (t * sqr (U)) / R.
- Q = (t * sqr (e)) / (R + Rвн).
- Q = P * t.
Различие математической записи закона в цепях с переменным и постоянным токами обусловлено их свойствами и параметрами, а также появлением нагрузок активной и реактивной составляющей. Кроме того, ток переменной составляющей постоянно изменяется во времени. Основные соотношения:
- Закон Ома: i = U / Z, где Z — полное сопротивление цепи. Оно включает в себя активную, индуктивную и емкостную нагрузки.
- Q = S * t = t * [sqrt (sqr (Pа) + sqr (Qp))].
- Запись закона с учетом в электрической цепи активной и реактивной нагрузок: Q = sqr (i) * Z * t.

Примеров применения уравнения Джоуля-Ленца достаточно много, одним из которых является обыкновенная лампа накаливания с вольфрамовой нитью. Свечение происходит из-за высокого напряжения и материала, из которого изготовлена нить накаливания. Электродуговая сварка работает тоже по этому закону, поскольку ток проходит через электрод и оказывает на него тепловое действие, при котором образуется сварочная дуга. Благодаря закону, можно правильно рассчитать и сделать вывод о применении радиокомпонента в какой-либо схеме.
Таким образом, уравнение Джоуля-Ленца играет важную роль в электротехнике, поскольку позволяет произвести точные расчеты радиокомпонентов схемы, исключая перегрев деталей и пожар.
rusenergetics.ru
Закон Джоуля-Ленца | Практическая электроника
Электричество – неотъемлемый признак нашей эпохи. Абсолютно всё вокруг завязано на нём. Любой современный человек, даже без технического образования, знает, что электрический ток, текущий по проводам, способен в некоторых случаях нагревать их, зачастую до очень высоких температур. Казалось бы, это заведомо всем известно и не стоит упоминания. Однако, как объяснить это явление? Почему и как происходит нагрев проводника?
Опыты Ленца
Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.
Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать электрические цепи. В 1832 году Эмилий Ленц “застрял” с расчётами, так как параметры его смоделированной цепи “источник энергии – проводник – потребитель энергии” сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что существует некая зависимость между силой тока, электрическим сопротивлением и температурой проводника.

При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало – невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?
Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший “нагреватель” – стеклянная ёмкость, в которой находился спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся – тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.
Формула Джоуля-Ленца
В итоге, спустя десятилетие, в 1843 году Эмилий Ленц выставил на всеобщее обозрение научного сообщества результат своих опытов в виде закона. Однако, оказалось, что его опередили! Пару лет назад английский физик Джеймс Прескотт Джоуль уже проводил аналогичные опыты и также представил общественности свои результаты. Но, тщательно проверив все работы Джеймса Джоуля, русский учёный выяснил что собственные опыты гораздо точнее, наработан больший объём исследований, потому, русской науке есть чем дополнить английское открытие.
Научное сообщество рассмотрело оба результата исследований и объединила их в одно, тем самым закон Джоуля переименовали в закон Джоуля-Ленца. Закон утверждает, что количество теплоты, выделяемое проводником при протекании по нему электрического тока , равно произведению силы этого тока в квадрате, сопротивлению проводника и времени, за которое по проводнику течёт ток. Или формулой:
Q=I2Rt
где
Q — количество выделяемого тепла (Джоули)
I — сила тока, протекающего через проводник (Амперы)
R — сопротивление проводника (Омы)
t — время прохождения тока через проводник (Секунды)
Почему греется проводник
Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы “трётся”, соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.

Из формулы также следует – чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление 0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом – будет неравномерный нагрев в месте скрутки. В итоге – подгорание с последующим пропаданием контакта.
Применение закона Джоуля-Ленца в жизни
Открытие закона Джоуля-Ленца имело огромные последствия для практического применения электрического тока. Уже в 19 веке стало возможным создать более точные измерительные приборы, основанные на сокращении проволочной спирали при её нагреве протекающим током определённой величины – первые стрелочные вольтметры и амперметры. Появились первые прототипы электрических обогревателей, тостеров, плавильных печей – использовался проводник с высоким удельным сопротивлением, что позволяло получить довольно высокую температуру.
Были изобретены плавкие предохранители, биметаллические прерыватели цепи (аналоги современных тепловых реле защиты), основанные на разнице нагрева проводников с разным удельным сопротивлением. Ну и, конечно же, обнаружив что при определённой силе тока проводник с высоким удельным сопротивлением способен нагреться докрасна , данный эффект использовали в качестве источника света. Появились первые лампочки.
Проводник (угольная палочка, бамбуковая нить, платиновая проволока и т.д.) помещали в стеклянную колбу, откачивали воздух для замедления процесса окисления и получали незатухаемый, чистый и стабильный источник света – электрическую лампочку

Заключение
Таки образом, можно сказать что на законе Джоуля-Ленца держится чуть ли не вся электрика и электротехника. Открыв этот закон, появилась возможность уже заранее предсказать некоторые будущие проблемы в освоении электричества. Например, из-за нагрева проводника передача электрического тока на большое расстояние сопровождается потерями этого тока на тепло. Соответственно, чтобы компенсировать эти потери нужно занизить передаваемый ток, компенсируя это высоким напряжением. А уже на оконечном потребителе, понижать напряжение и получать более высокий ток.
Закон Джоуля-Ленца неотступно следует из одной эпохи технологического развития в другую. Даже сегодня мы постоянно наблюдаем его в быту – закон проявляется всюду, и не всегда люди ему рады. Сильно греющийся процессор персонального компьютера, пропадание света из-за обгоревшей скрутки «медь-алюминий»,выбитая вставка-предохранитель, выгоревшая из-за высокой нагрузки электропроводка – всё это тот самый закон Джоуля-Ленца.
www.ruselectronic.com
формула, применение на практике, вывод
В 1841 и 1842 года независимо друг от друга английский и русский физики установили зависимость количества тепла от протекания тока в проводнике. Эту зависимость назвали «Закон Джоуля-Ленца». Англичанин установил зависимость на год раньше, чем русский, но название закон получил от фамилий обоих ученных, потому как их исследования были независимы. Закон не носит теоретический характер, но имеет большое практическое значение. И так давайте кратко и понятно узнаем определение закона Джоуля-Ленца и где он применяется.
Формулировка
В реальном проводнике при протекании через него тока выполняется работа против сил трения. Электроны движутся через провод и сталкиваются с другими электронами, атомами и прочими частицами. В результате этого выделяется тепло. Закон Джоуля-Ленца описывает количество тепла, выделяемое при протекании тока через проводник. Оно прямо пропорционально зависит от силы тока, сопротивления и времени протекания.
В интегральной форме Закон Джоуля-Ленца выглядит так:

Сила тока обозначается буквой I и выражается в Амперах, Сопротивление — R в Омах, а время t — в секундах. Единица измерения теплоты Q — Джоуль, чтобы перевести в калории нужно умножить результат на 0,24. При этом 1 калория равна количеству теплоты, которое нужно подвести к чистой воде, чтобы увеличить её температуру на 1 градус.
Такая запись формулы справедлива для участка цепи при последовательном соединении проводников, когда в них протекает одна величина тока, но падает на концах различное напряжение. Произведение силы тока в квадрате на сопротивление равняется мощности. В то же время мощность прямо пропорциональна квадрату напряжения и обратно пропорциональна сопротивлению. Тогда для электрической цепи при параллельном соединении можно Закон Джоуля-Ленца можно записать в виде:

В дифференциальной форме он выглядит следующим образом:

Где j — плотность тока А/см2, E — напряженность электрического поля, сигма — удельное сопротивление проводника.
Стоит отметить что для однородного участка цепи сопротивление элементов будет одинаковым. Если в цепи присутствуют проводники с разным сопротивлением возникает ситуация, когда максимальное количество тепла выделяется на том, который имеет самое большое сопротивление, о чем можно сделать вывод, проанализировав формулу Закона Джоуля-Ленца.
Частые вопросы
Как найти время? Здесь имеется в виду период протекания тока через проводник, то есть когда цепь замкнута.
Как найти сопротивление проводника? Для определения сопротивления используют формулу, которую часто называют “рельс”, то есть:

Здесь буквой «Ро» обозначается удельное сопротивление, оно измеряется в Ом*м/см2, l и S это длина и площадь поперечного сечения. При вычислениях метры и сантиметры квадратные сокращаются и остаются Омы.
Удельное сопротивление — это табличная величина и для каждого металла она своя. У меди на порядки меньше, чем у высокоомных сплавов типа вольфрама или нихрома. Для чего это применяется мы рассмотрим ниже.

Перейдем к практике
Закон Джоуля-Ленца имеет большое значение для электротехнических расчетов. В первую очередь вы можете его применить при расчете нагревательных приборов. В качестве нагревательного элемента чаще всего применяется проводник, но не простой (типа меди), а с высоким сопротивлением. Чаще всего это нихром или кантал, фехраль.

Они имеют большое удельное сопротивление. Вы можете использовать и медь, но тогда вы потратите очень много кабеля (сарказм, медь не используют в этих целях). Чтобы рассчитать мощность тепла для нагревательного прибора вам нужно определится, какое тело и в каких объемах вам нужно нагреть, учесть количество требуемой теплоты и за какое время её нужно передать телу. После расчетов и преобразований вы получите сопротивление и силу тока в этой цепи. На основании полученных данных по удельному сопротивлению подбираете материал проводника, его сечение и длину.
Закон Джоуля-Ленца при передаче электричества на расстояние
При передаче электроэнергии на расстояния возникает существенная проблема — потери на линиях передачи (ЛЭП). Закон Джоуля-Ленца описывает количество тепла, выделенного проводником при протекании тока. ЛЭП питают целые предприятия и города, а для этого нужна большая мощность, как следствие большой ток. Так как количество теплоты зависит от сопротивления проводника и тока, чтобы кабеля не грелись нужно уменьшить количество тепла. Увеличить сечение проводов не всегда можно, т.к. это затратно в плане стоимости самой меди и веса кабеля, что влечет за собой удорожание несущей конструкции. Высоковольтные линии электропередач изображены ниже. Это массивные металлоконструкции, созданные чтобы поднять кабеля на безопасную высоту над землей, с целью избежания поражения электрическим током.

Поэтому нужно снизить ток, чтобы это сделать повышают напряжение. Между городами линии электропередач обычно имеют напряжение 220 или 110 кВ, а у потребителя понижается до нужной величины с помощью трансформаторных подстанций (КТП) или целым рядом КТП постепенно понижая до более безопасных для передачи величин, например 6 кВ.
Таким образом при той же потребляемой мощности при напряжении в 380/220 В ток снизится в сотни и тысячи раз ниже. А по закону Джоуля-Ленца количество тепла в этом случае определяется мощностью, которая теряется на кабеле.
Плавкие вставки и предохранители
Закон Джоуля-Ленца применяется при расчете плавких предохранителей. Это такие элементы, которые защищают электрическое или электронное устройство от чрезмерных для него токов, которые могут возникнуть в следствии скачка питающего напряжения, короткого замыкания на плате или обмотках (в случае двигателей) для защиты от дальнейших разрушений электрической системы в целом и пожара. Они состоят из корпуса, изолятора и тонкой проволоки. Проволока подбирается таким сечением, чтобы номинальный ток через нее протекал, а при его превышении количество выделяемого тепла при этом пережигало её.
В результате выше описанного сделаем вывод, что Закон Джоуля-Ленца нашел широчайшее применение и очень важен для электротехники. Благодаря информации о количеству теплоты, которую даёт выполнение расчетов по формулам указанным выше, мы можем узнать о режимах работы устройств, подобрать необходимые материалы и сечение для повышения безопасности, надежности и долговечности прибора или цепи в целом.
На этом мы и заканчиваем нашу статью. Надеемся, предоставленная информация была для вас полезной и интересной. Напоследок рекомендуем просмотреть видео, на котором более подробно рассматривается данный вопрос:
Наверняка вы не знаете:
samelectrik.ru
Закон Джоуля – Ленца в физике
При течении электрического тока по проводнику выделяется энергия. Она зависит от рода физических факторов, которые вызывают падение потенциала. Если потенциал изменяется на сопротивлении проводника, то прохождение тока вызывает выделение тепла. Закон был открыт в 1841 г. Джоулем, Ленц провел его исследования.
Формулировка закона Джоуля – Ленца в интегральной форме
Если проводники в цепи не движутся, сила тока является постоянной величиной, то количество тепла (Q), которое выделяется на проводнике за счет тока пропорционально величине силы этого тока (I), времени его течения (t) и падению напряжения (U). В интегральной форме Закон Джоуля — Ленца записывают как:
где — напряжение на концах проводника.
Этот же закон, применяя закон Ома для участка цепи можно записать в виде:
В том случае, если сила тока в проводнике является переменной, то закон Джоуля — Ленца применяют, разбивая отрезок времени наблюдения на малые части (), когда силу тока можно считать постоянной величиной:
Формулировка закона Джоуля – Ленца в дифференциальной форме
Плотность тепловой мощности тока () (или удельное количество тепла или удельная мощность тепловыделения) равна произведению квадрата плотности тока () на удельное сопротивление проводника (). В математическом виде закон Джоуля — Ленца в дифференциальной форме запишем как:
где — тепло, которое выделяется в единице объема проводника в единицу времени.
В дифференциальной форме (4) закон Джоуля — Ленца не зависит от рода сил, которые вызывают ток, следовательно, это наиболее общий закон. Если сила, действующая на заряженные частицы, имеет только электрическую природу, то выражение (4) можно представить как:
где — удельная проводимость вещества, — вектор напряженности в данной точке поля.
Примеры решения задач
ru.solverbook.com
Закон Джоуля-Ленца в интегральной и дифференциальной формах
Теперь подробнее обсудим величину DU (которая представляет в расчетах изменение внутренней энергии) применительно к проводнику, по которому начинает течь ток.
Постепенно, выбранный проводник будет нагреваться, а это значит, что будет увеличиваться его внутренняя энергия. По мере нагрева разность между температурой проводника и окружающей его среды будет увеличиваться. Согласно закономерности Ньютона, вместе с этим возрастать будет и мощность теплоотдачи проводника. Таким образом, через какое-то время температура проводника, достигнув определенного значения, перестанет увеличиваться. В этот момент величина DU будет равной нулю, и перестанет изменяться внутренняя энергия проводника.
Тогда для этого состояния первый закон термодинамики будет выглядеть так: A = – Q. То есть когда не меняется внутренняя энергия проводника, работа тока целиком превращается в теплоту. Используя этот вывод, можем записать все три рассмотренные формулы для расчета работы тока в несколько ином виде, в конечном итоге получаем закон Джоуля-Ленца в интегральной форме:
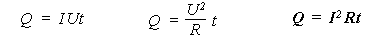 На
первый взгляд все формулы могут считаться
равноправными, однако только последняя
справедлива всегда, поэтому она и
считается законом. А вот остальные две
справедливы только при определенных
условиях, поэтому законом считаться не
могут.
На
первый взгляд все формулы могут считаться
равноправными, однако только последняя
справедлива всегда, поэтому она и
считается законом. А вот остальные две
справедливы только при определенных
условиях, поэтому законом считаться не
могут.
Закон Джоуля-Ленца в дифференциальной форме выглядит совершенно по-иному, мы рассмотрим только общий вариант, без дополнительных выведений и вычислений, который выглядит так:
 Где:
Где:
 —
является мощностью тепла, выделяемого
в единице объёма;
—
является мощностью тепла, выделяемого
в единице объёма; —
плотность электрического тока;
—
плотность электрического тока; —
это напряжённость электрического поля;
—
это напряжённость электрического поля; —
проводимость выбранной среды.
—
проводимость выбранной среды.
Так в общих чертах выглядит закон Джоуля-Ленца и его интегральная и дифференциальная формы. Хотя, если проводить дальнейшие вычисления, то закон может принимать и другие формы.
21. Закон Ома для неоднородного участка цепи (обобщенный закон Ома). Закон Ома для замкнутой цепи.
Участок цепи, содержащий источник ЭДС, называется неоднородным(рис.5.11). Всякий источник ЭДС характеризуется величиной ЭДС ε ивнутренним сопротивлением r.

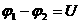 —
напряжение на концах участка цепи.
—
напряжение на концах участка цепи.
Рис.5.11. Неоднородный участок цепи.
Закон Ома для неоднородного участка цепи имеет вид:

При
соединении концов неоднородного участка
цепи идеальнымпроводником
образуется замкнутая цепь, в
которой потенциалы φ1 иφ2 выравниваются
и мы приходим к закону
Ома для замкнутой (или полной) цепи:
потенциалы φ1 иφ2 выравниваются
и мы приходим к закону
Ома для замкнутой (или полной) цепи:
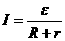
Если
сопротивление внешней цепи  ,
то имеем случай короткого
замыкания.
В этом случае в цепи течетмаксимальный ток:
,
то имеем случай короткого
замыкания.
В этом случае в цепи течетмаксимальный ток:
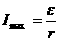
При  имеем разомкнутую цепь.
В этом случае ток в цепи равен
нулю:
имеем разомкнутую цепь.
В этом случае ток в цепи равен
нулю:
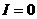
22. Правила Кирхгофа для разветвленных цепей постоянного тока
Правило 1: в любом узле сумма входящих токов и выходящих равна нулю. Оно учитывает закон сохранения электрического заряда.
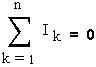
При этом токи, идущие к узлу, и токи, исходящие из узла, следует считать величинами разных знаков.
Правило 2: алгебраическая сумма произведений сил токов на сопротивления при обходе контура равна сумме ЭДС в контуре. Учитывается закон сохранения энергии.
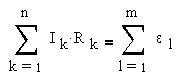
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.
В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
|
Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3,I4 < 0 |
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
|
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
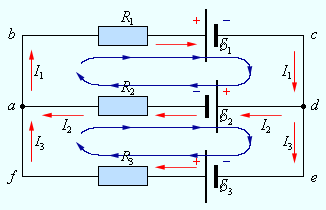
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).
|
Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef) |
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома.
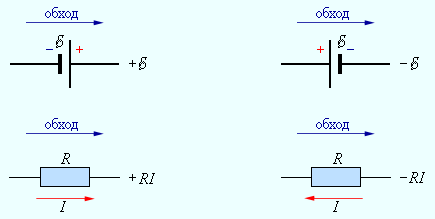
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
|
Рисунок 1.10.3. «Правила знаков» |
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для
участка bc: I1R1 = Δφbc – 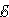 1.
1.
Для
участка da: I2R2 = Δφda – 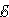 2.
2.
Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:
I1R1 + I2R2 = Δφbc + Δφda – |
Аналогично, для контура adef можно записать:
– I2R2 + I3R3 = |
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:
I1R1 + I2R2 = – |
– I2R2 + I3R3 = |
– I1 + I2 + I3 = 0 |
23. Работа и мощность постоянного электрического тока. КПД источника тока.
Работа А электрического тока на участке цепи с электрическим сопротивлением R за время D t равна:
A = I · U · ? t = I2 · R · ? t
Мощность P электрического тока равна отношению работы А тока ко времени D t, за которое эта работа совершена:
P = A / ? t = I · U = I2 R = U2 / R.
Работа А электрического тока равна количеству теплоты Q, выделяемому проводником (если не совершается механическая работа и не происходят химические реакции):
Q = I2 · R · ? t
Этот закон был экспериментально установлен английским ученым Джеймсом Джоулем (1818-1889) и русским ученым Эмилием Ленцем (1804-1865) и поэтому носит название закона Джоуля — Ленца.
Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением R (рис. 7.5).
КПД всегда определяем как отношение полезной работы к затраченной:
| | (7.8.1) |
|
Полезная
работа –
мощность, выделяемая на внешнем
сопротивлении Rв
единицу времени. По закону Ома
имеем: 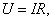 а
а 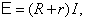 тогда
тогда
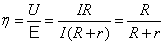 .
.
24. Вывод закона Ома из классической теории электропроводимости металлов.
Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное

и к концу пробега скорость упорядоченного движения достигнет значения
| (18.2) |
где
t — среднее время между двумя последовательными
соударениями электрона с ионами решетки.
Друде не учитывал распределение
электронов по скоростям и приписывал
всем электронам одинаковое значение
средней скорости  .
В этом приближении
.
В этом приближении  ,
где
,
где 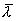 —
среднее значение длины свободного
пробега,
—
среднее значение длины свободного
пробега,  —
скорость теплового движения электронов.
Подставим это значение t в формулу (18.2)
—
скорость теплового движения электронов.
Подставим это значение t в формулу (18.2)
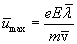
Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального
Подставив это выражение в
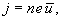
получим
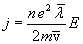
Плотность
тока оказалась пропорциональной
напряженности поля. Следовательно, мы
получили закон Ома. Согласно  коэффициент
пропорциональности между j и Е представляет
собой проводимость
коэффициент
пропорциональности между j и Е представляет
собой проводимость
| (18.3) |
Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.
Вывод закона Джоуля-Ленца из классической теории электропроводности металлов. Затруднения этой теории.
К
концу свободного пробега электрон
приобретает скорость 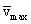 ,
и, следовательно, дополнительную
кинетическую энергию, средняя величина
которой
,
и, следовательно, дополнительную
кинетическую энергию, средняя величина
которой
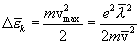
Столкнувшись
с ионом, электрон по предположению
полностью теряет приобретенную им за
время пробега скорость, и передает
энергию кристаллической решетке. Эта
энергия идет на увеличение внутренней
энергии металла, проявляющееся в его
нагревании. Каждый электрон претерпевает
за секунду в среднем 1/t соударений,
сообщая всякий раз решетке энергию 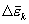 .
Следовательно, в единице объема за
единицу времени должно выделяться тепло
.
Следовательно, в единице объема за
единицу времени должно выделяться тепло
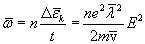
где
n — число электронов проводимости в
единице объема. Величина 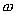 есть
не что иное, как удельная мощность тока.
Множитель при
есть
не что иное, как удельная мощность тока.
Множитель при 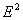 совпадает
со значением
совпадает
со значением 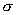 (18.3)
для закона Ома. Таким образом. Мы пришли
к выражению закона Джоуля-Ленца в
дифференциальной форме.
(18.3)
для закона Ома. Таким образом. Мы пришли
к выражению закона Джоуля-Ленца в
дифференциальной форме.

Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3R. Учтем, что теплоемкость одноатомного электронного газа равна 3/2R. Тогда атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой. Поэтому объяснить затруднения элементарной классической теории электропроводности металлов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой теорией простой и наглядной.
Несамостоятельный и самостоятельный газовые разряды.
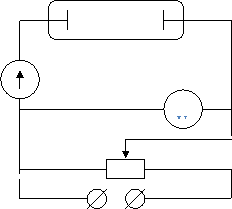
Несамостоятельный газовый разряд. Процесс прохождения электрического тока через газ называется газовым разрядом. Если электропроводность газа создается внешними ионизаторами, то электрический ток, возникающий в нем, называется несамостоятельным газовым разрядом. С прекращением действия внешних ионизаторов несамостоятельный разряд прекращается. Несамостоятельный газовый разряд не сопровождается свечением газа. Ниже изображен график зависимости силы тока от напряжения при несамостоятельном разряде в газе. Для построения графика использовалась стеклянная трубка с двумя впаянными в стекло металлическими электродами. Цепь собрана как показано на рисунке ниже.
|
+ —
Самостоятельный
газовый разряд.
Электрический разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом. Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды. Основным источником их возникновения является ударная ионизация молекул газа.
Если после достижения насыщения продолжать увеличивать разность потенциалов между электродами, то сила тока при достаточно большом напряжении станет резко возрастать (график 2).
Это означает, что в газе появляются дополнительные ионы, которые образуются за счет действия ионизатора. Сила тока может возрасти в сотни и тысячи раз, а число заряженных частиц, возникающих в процессе разряда, может стать таким большим, что внешний ионизатор будет уже не нужен для поддержания разряда. Поэтому ионизатор теперь можно убрать.

I
|
27. Магнитное поле, Магнитная индукция. Принцип суперпозиции магнитных полей. Закон Ампера.
Зако́н
Ампе́ра —
закон взаимодействия электрических
токов.
Впервые был установлен Андре
Мари Ампером в 1820 для
постоянного тока. Из закона Ампера
следует, что параллельные проводники с
электрическими токами, текущими в одном
направлении, притягиваются, а в
противоположных — отталкиваются.
Законом Ампера называется также закон,
определяющий силу, с которой магнитное
поле действует
на малый отрезок проводника с током.
Сила 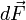 ,
с которой магнитное поле действует на
элемент объёма
,
с которой магнитное поле действует на
элемент объёма 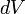 проводника
с током плотности
проводника
с током плотности 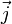 ,
находящегося в магнитном поле с
индукцией
,
находящегося в магнитном поле с
индукцией 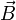 :
:
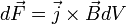 .
.
Модуль силы Ампера можно найти по формуле:
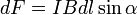 ,
,
где 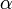 —
угол между векторами магнитной индукции
и тока.
—
угол между векторами магнитной индукции
и тока.
Сила 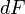 максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции (
максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции (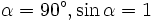 ):
):
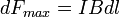 .
.
Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2]
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Магни́тная
инду́кция 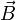 — векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой
— векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой 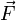 магнитное
поле действует на заряд
магнитное
поле действует на заряд 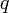 ,
движущийся со скоростью
,
движущийся со скоростью 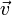 .
.
Более
конкретно, 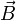 —
это такой вектор, что сила
Лоренца
—
это такой вектор, что сила
Лоренца 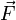 ,
действующая со стороны магнитного
поля[1] на
заряд
,
действующая со стороны магнитного
поля[1] на
заряд 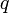 ,
движущийся со скоростью
,
движущийся со скоростью 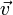 ,
равна
,
равна
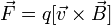
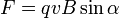
где
косым крестом обозначено векторное
произведение,
α — угол между векторами скорости и
магнитной индукции (направление
вектора  перпендикулярно
им обоим и направлено по правилу
буравчика).
перпендикулярно
им обоим и направлено по правилу
буравчика).
studfile.net
ДЖОУЛЯ-ЛЕНЦА ЗАКОН — это… Что такое ДЖОУЛЯ-ЛЕНЦА ЗАКОН?
- ДЖОУЛЯ-ЛЕНЦА ЗАКОН
(по имени англ. физика Дж. П. Джоуля и рус. физика Э. X. Ленца) — закон, характеризующий тепловое действие электрич. тока. Согласно Д. — Л. э., кол-во теплоты О. выделяющейся в проводнике при прохождении по нему пост. электрич. тока, зависит от силы тока I, сопротивления проводника R и времени прохождения тока t:О = I*Rt.
Большой энциклопедический политехнический словарь. 2004.
- ДЖОУЛЬ
- ДЖОУЛЯ-ТОМСОНА ЭФФЕКТ
Смотреть что такое «ДЖОУЛЯ-ЛЕНЦА ЗАКОН» в других словарях:
ДЖОУЛЯ — ЛЕНЦА ЗАКОН — определяет кол во теплоты Q, выделяющееся в проводнике с сопротивлением Л за время t при прохождении через него тока I: Q=aI2Rt. Коэфф. пропорциональности а зависит от выбора ед. измерений: если I измеряется в амперах, R в омах, t в секундах, то… … Физическая энциклопедия
ДЖОУЛЯ — ЛЕНЦА ЗАКОН — ДЖОУЛЯ ЛЕНЦА ЗАКОН, определяет количество теплоты Q, выделяемой в проводнике при прохождении через него электрического тока: Q прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Открыт Дж. Джоулем и Э.… … Энциклопедический словарь
Джоуля — Ленца закон — определяет количество тепла Q, выделяющегося в проводнике при прохождении через него электрического тока: Q пропорционально сопротивлению R проводника, квадрату силы тока I в цепи и времени прохождения тока t, Q = aI2Rt. Здесь а… … Большая советская энциклопедия
Джоуля-Ленца закон — определяет количество теплоты Q, выделяемой в проводнике при прохождении через него электрического тока: Q прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Открыт Дж. П. Джоулем и Э. Х. Ленцем в… … Энциклопедический словарь
ДЖОУЛЯ — ЛЕНЦА ЗАКОН — определяет кол во теплоты Q, выделяемой в проводнике при прохождении через него электрич. тока: Q прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Открыт Дж. П. Джоулем и Э. X. Ленцем в нач. 40 х гг.… … Естествознание. Энциклопедический словарь
Закон Джоуля — Ленца — Закон Джоуля Ленца физический закон, дающий количественную оценку теплового действия электрического тока. Открыт в 1840 году независимо Джеймса Джоуля и Эмилия Ленца. В словесной формулировке звучит следующим образом[1] Мощность тепла … Википедия
ЗАКОН ДЖОУЛЯ-ЛЕНЦА — закон, определяющий тепловое действие электрического тока; согласно этому закону количество теплоты Q, выделяющееся в проводнике при прохождении по нему постоянного электрического тока, равно произведению квадрата силы тока I, сопротивления… … Большая политехническая энциклопедия
Закон Джоуля-Ленца — (по имени английского физика Джеймса Джоуля и русского физика Эмилия Ленца, одновременно, но независимо друг от друга открывших его в 1840г) закон, дающий количественную оценку теплового действия электрического тока. При протекании тока по… … Википедия
Закон Джоуля — Ленца — (по имени английского физика Джеймса Джоуля и русского физика Эмилия Ленца, одновременно, но независимо друг от друга открывших его в 1840г) закон, дающий количественную оценку теплового действия электрического тока. При протекании тока по… … Википедия
закон Джоуля-Ленца — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN Joule Lenz s lawJoule s law … Справочник технического переводчика
dic.academic.ru
Закон Джоуля Ленца | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Закон Джоуля Ленца — Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка
![Rendered by QuickLaTeX.com \[\Large Q=A=Uq=UIt=I^2Rt=\frac{U^2}{R}t\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-6a6eabf3da22b482bb7a800abd10b0e0_l3.png)
Закон Джоуля Ленца в интегральной форме в тонких проводах:
![Rendered by QuickLaTeX.com \[\Large Q=\int_{0}^{t}{RI^2 dt} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-7d6d1bed8eeef43d667afd6dae4f451f_l3.png)
Если сила тока изменяется со временем, проводник неподвижен и химических превращений в нем нет, то в проводнике выделяется тепло.
Закон Джоуля Ленца — Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля
![Rendered by QuickLaTeX.com \[\large w = \vec j \cdot \vec E = \sigma E^2\! \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-071e6142baa693ecc8225c5fa31ebc88_l3.png)
Закон Джоуля Ленца
Преобразование электрической энергии в тепловую широко используется в электрических печах и различных электронагревательных приборах. Тот же эффект в электрических машинах и аппаратах приводит к непроизвольным затратам энергии (потере энергии и снижении КПД). Тепло, вызывая нагрев этих устройств, ограничивает их нагрузку; при перегрузке повышение температуры может вызвать повреждение изоляции или сокращение срока службы установки.
В формуле мы использовали :
Q — Количество теплоты
q — Заряд
A — Работа тока
U — Напряжение в проводнике
I — Сила тока в проводнике
t — Время
![Rendered by QuickLaTeX.com \[dt\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-0048980e400a2ca326f64541d0122046_l3.png)
— Промежуток времени
R — Сопротивление
w — Мощность выделения тепла в единице объёма
![Rendered by QuickLaTeX.com \[\vec j\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-7256661f02f793ea66978537d08d5360_l3.png)
— Плотность электрического тока
![Rendered by QuickLaTeX.com \[\vec E\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8f259ddd80f58c17bbbe9fdad894c880_l3.png)
— Напряжённость электрического поля
![Rendered by QuickLaTeX.com \[\sigma \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-3fe4953c4956464b56b17998bb55c72e_l3.png)
— Проводимость среды
xn—-ctbjzeloexg6f.xn--p1ai

 —
является мощностью тепла, выделяемого
в единице объёма;
—
является мощностью тепла, выделяемого
в единице объёма;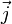 —
плотность электрического тока;
—
плотность электрического тока;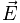 —
это напряжённость электрического поля;
—
это напряжённость электрического поля;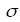 —
проводимость выбранной среды.
—
проводимость выбранной среды.
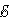 1 +
1 + 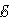 2 = –
2 = –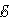 1 –
1 – 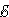 2.
2.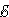 2 +
2 + 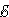 3.
3.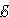 1 –
1 – 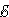 2,
2, 2 +
2 +  3,
3,