Закон Ома кратко и понятно для чайников
Закон Ома является одним из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Его важно знать и понимать. Понятное объяснение вы найдёте в статье.
Закон Ома официально и абсолютно оправдано можно отнести к ряду основополагающих в физике по нескольким признакам. Данный закон объясняют в школе на базовом уровне, а после, более углубленно, в учреждениях, специализирующихся на изучении технических аспектов технологий.
Закон Ома – определение
Впервые данный закон был официально зафиксирован и сформулирован в восемнадцатом веке, благодаря сделанному сейчас уже широко известным всем Георгом Симоном Омом открытию. Благодаря данному закону получило грамотное и исчерпывающее объяснение наличие количественной связи между тремя фигурирующими в определении параметрами. Зависимость рассматривается как пропорциональная. Когда данное явление только было выявлено, закон несколько раз формулировали. В итоге сейчас всем известно данное определение: «величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению».
Для лучшего понимания разделим определение на две части и разберём отдельно более понятным языком смысл каждой.
- Первая часть определения указывает на то, что если на определенной отрезке цепи происходит количественный скачок напряжения, то величина тока также увеличивается на данном участке. Важно упомянуть, что становится больше и величина тока на заданном участке цепи.
- Концовка определения расшифровывается также просто. Выше напряжение – меньше сила тока.
Закон Ома – формула

 Иллюстрация связи сопротивления
Иллюстрация связи сопротивленияРисунок наглядно демонстрирует связь фигурирующих в понятии «участников». Таким образом, вытекают простые выводы:
1. При данных условиях: на конкретном отрезке увеличивается напряжение, но при том сопротивление остаётся прежним, ток резко возрастает;
2. Иная ситуация: наоборот, изменяется сопротивление, а точнее возрастает, при том что уровень напряжения не меняется вовсе, тока становится меньше.
В итоге в законе Ома участвуют всего три величины.
Готовая формула выглядит так:
I = U/R
Фигурируют и другие две переменные, их также можно вычислить, при условии, что другие два значения известны. Видоизменив формулу, получим:
| Формула сопротивления | R = U/I |
| Формула напряжения | U = I × R |
| Формула силы тока | I = U/R |
Важно!

 Шпаргалка для закона Ома
Шпаргалка для закона ОмаНа начальном этапе, когда составлять формулы ещё сложно, можно воспользоваться небольшой шпаргалкой.
На треугольнике просто нужно закрыть то значение, которое необходимо найти.
Закон Ома для участка цепи
Итоговая формула не видоизменяется вовсе. Обычно сопротивление в данном законе является явной характеристикой проводника, потому что это значение не постоянная величина: в зависимости от материала и других параметров число может увеличиваться или уменьшаться. Закон применим как при расчёте с использованием металлов, так и растворов электролитов, однако существует важный нюанс: в цепи не должно быть реального источника тока, или же источник должен быть идеальным, то есть он не должен создавать дополнительное сопротивление.

 Шпаргалка для использования закона Ома
Шпаргалка для использования закона ОмаС ЭДС
Обобщённый закон Ома формулируется так:
I = (Uab+E)/R
Также формулу можно выразить через проводимость:
I = (Uab + E) × G, как понятно, G – проводимость участка электрической цепи. Эти формулы можно использовать, если сохраняются условия, зафиксированные на рисунке.

 Участок цепи с ЭДС
Участок цепи с ЭДСБез ЭДС
Для начала определим, что положительное направление – это то, что слева направо. Только в этом случае напряжение на участке будет равняться разности потенциалов.

 Разность потенциалов
Разность потенциаловЕсли сохраняется условие и потенциал конечный меньше потенциала начального, то напряжение будет больше нуля. Значит, как и полагается, направление линий напряженности в проводнике будет от начала к концу, следовательно, направление тока будет идентичным. Именно такое направление тока принято считать положительным, I > O. Данный вариант самый простой для расчётов. Формула действительна с любыми числами.
Закон Ома для полной (замкнутой) цепи
При данной вариации закона выявляется значение тока при реальных условиях, то есть в настоящей полной цепи. Важно учитывать то, что получившееся в результате расчетов число зависит от нескольких параметров, а не только от сопротивления нагрузки.
Сопротивление нагрузки – внешнее сопротивление, а сопротивление самого источника тока – внутреннее сопротивление (обозначается маленькой r).
Вывод формулы закона Ома для замкнутой цепи
Если к цепи подключено напряжение и в цепи замечено напряжение (ток), то, чтобы поддержать его во внешней цепи, необходимо создать условия, при которых между её концами возникнет разность потенциалов. Это число будет равняться I × R. Однако важно помнить о том, что вышеупомянутый ток будет и во внутренней цепи и его также необходимо поддерживать, поэтому нужно создать разность потенциалов между концами сопротивления r. Эта разность равняется I × r.
Чтобы поддержать ток в цепи, электродвижущая сила (ЭДС) аккумулятора должна иметь величину:
E = I × r + I × R
Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:
E = I(r + R)
или
I = E / (r + R)
Две последние формулы выражают закона Ома для полной цепи.
Закон Ома в дифференциальной форме

 Дифференциальная форма закона Ома
Дифференциальная форма закона ОмаЗакон можно представить таким образом, чтобы он не был привязан к размерам проводника. Для этого выделим участок проводника Δl, на концах которой расположены ф1 и ф2. Среднюю площадь проводника обозначают ΔS , а плотность тока j, при таких условиях сила тока будет равняться:
I = jΔS = (ф1- ф2) / R = -(((ф1 — ф2)ΔS) / pΔl , отсюда следует, что j = -y × (Δф/Δl)
При условии, что Δl будет равен 0, то, взяв предел отношения:
lim (-(Δф/Δl)) = -(dф/dl) = Е,
окончательное выражение будет выглядеть так:
j = yE
Данное выражение закона находит силу тока в произвольной точке проводника в зависимости от его свойств и электрического состояния.
Закон Ома в интегральной форме
В данной интерпретации закона не содержится в условиях ЭДС, то есть формула выглядит так:
I = U/R
Чтобы найти значение для однородного линейного проводника, выразим R через p и получим:
R = p (l/S), где за р принимаем удельное объёмное сопротивление.
Линией тока принято называть кривую, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. При таких условиях вектор плотности находится из отношения J = jt, где t – это единичный вектор касательной к линии тока.
Для лучшего понимания предположим, что удельное сопротивление, а также напряженность поля движущих сил на поперечном сечении проводника однородны. При таком условии Е однородна, а значит, и j также однородная величина. Примем произвольное значение поперечного сечения цепи S, тогда pl/s = E. Получившееся равенство умножим на dl. Тогда Edl = (Е эл.ст.+Е стор.) dl = Е эл.ст. dl + Е стор. dl = -dф + dE. Отсюда получим (pI/S) dl = -dф + dE. Возьмём в учёт, что p/s dl = dR и запишем закон Ома в интегральной форме:
IdR = -dф + dE.
Закон Ома в комплексной форме
Чтобы провести анализ электрических цепей синусоидального тока, комфортнее использовать закон Ома в комплексной форме. Для лучшего понимания введем основное понятие, фигурирующее в данной интерпретации закона: синусоидальный ток – это линейные цепи с установившимся режимом работы, после того, как переходные процессы в них завершены, уровень напряжения резко уменьшается на конкретной дистанции, токи в ветвях и ЭДС источников являются синусоидальными функциями времени. В противном случае, когда данные параметры не соблюдаются, закон не может быть применим. Чем отличается эта форма от обычной? Ответ прост: токи, сопротивление и ЭДС фиксируются как комплексные числа. Это обусловлено тем, что существуют как активные так и реактивные значения напряжений, токов и сопротивлений, а в результате этого требуется внесение определенных коррективов.
Вместо активного сопротивления используется полное, то есть комплексное сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже превращаются в комплексные величины. При реальных расчетах лучше и удобнее применять действующие значения. Итак, закон в комплексной форме выглядит так:
i = U/Z, i = UY
В данной формуле Z – комплексное сопротивление, Y – комплексная проводимость.
Чтобы выявить эти величины, выведены формулы. Пропустим шаги их создания и приведем готовые формулы:
Z = ze = z cosф + jz sinф = r + jx
Y = 1/ ze = ye = y cos ф — jy sin ф = g + jb
Закон Ома для переменного тока
После того как Фарадей открыл электромагнитную индукцию, стали активно использовать генераторы сперва постоянного, а после и переменного тока.
Используется уже известная формула:
I = U/Z
Полное сопротивление тока – это совокупность активного, а также индуктивного и емкостного сопротивлений. Проще говоря, ток в цепи переменного тока зависит от многих параметров, в том числе от величины ёмкости и индуктивности. Полное сопротивление вычисляется по формуле.

 Формула полного сопротивления
Формула полного сопротивленияПолное сопротивление можно изобразить как гипотенузу прямоугольного треугольника, катетами которого является активное и индуктивное сопротивление.

 Треугольник полного сопротивления
Треугольник полного сопротивленияИтак, формула амплитудного значения силы тока будет выглядеть так:
Im = Um/ ((R^2 + (ωL — (1/ωC)^2

 Цепь
ЦепьВ такой цепи колебания тока и напряжения разные по фазе, а разность фаз зависит от индуктивности катушки и ёмкости конденсатора:
U = Um sin (ωt)
I = Im sin (ωt + ф)
Закон Ома для постоянного тока
В данном случае частота будет равняться нулевому значению, поэтому остальные показатели также будут нулевыми соответственно, в то время как значение ёмкости достигнет бесконечности. Цепь разорвётся. Поэтому отсюда вытекает логичный вывод: реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.
Закон Ома для однородного участка цепи
Формула выглядит уже известным образом:
I = U/R
В данном случае главной характеристикой проводника остаётся сопротивление. От того, как выглядит проводник, зависит количество узлов кристаллической решётки и атомов примесей. Поэтому электроны могут замедляться или ускоряться.
Сопротивление будет зависеть от вида проводника, а именно от его сечения, материала и длины:
R = p (L/S)
Закон Ома для неоднородного участка цепи
При решении задачи становится понятным, что для того, чтобы поддерживался стабильный ток в замкнутой цепи, нужны силы совершенной другой природы, а не кулоновские. В этом случае можно заметить такую закономерность: заряды, которые никак не соприкасаются друг с другом, выступают в двух ролях одновременно, то есть они являются силами электрического поля и силами иного вида – сторонними в это же время. Участок, на котором замечена данная закономерность, называется неоднородным.

 Неоднородный участок цепи
Неоднородный участок цепиФормула принимает вид:
E = Eq + Est
Закон Ома в данном подразделе был сформулирован таким образом: сила тока прямо пропорциональна напряжению на данном участке и обратно пропорциональна его полному сопротивлению.
Итак, готовая формула:
I = U12/R, где U12
Закон Ома для магнитной цепи
В каждом электромагните совмещены несколько важных элементов: стальной сердечник и катушка. По последней протекает ток. При совмещении нескольких участков образуется магнитная цепь.
При кольцевом магнитопроводе все поле находится внутри кольца. Тогда поток в магнитопроводе равен:
Ф = Вср S = μHср S
Формула закона для магнитной цепи:

 Формула закона ома для магнитной цепи
Формула закона ома для магнитной цепиЗадачи с решениями на закон Ома
Задача №1
Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 127 В. Определить силу тока в проволоке.
Дано:
- l = 120 м,
- S = 0,5 мм,
- U = 127 В,
- p = 1,1 Ом*мм2 /м.
Найти: I — ?
Решение:
- R = p * l / S,
- R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
- I = 127 В : 264 Ом = 0,48 А.
Ответ: I = 0,48 Ом
Задача №2
Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 220 В. Определить силу тока в проволоке.
Дано:
- l = 120 м,
- S = 0,5 мм,
- U = 220 В,
- p = 1,1 Ом*мм2 /м.
Найти: I — ?
Решение:
- R = p * l / S,
- R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
- I = 220 В : 264 Ом = 0,83 А.
Ответ: I = 0,83 Ом
Задача №3
Дано:
- U = 15 В,
- R1 = 3 Ом,
- R2 = R3 = 4 Ом.
Найти: I — ?
Решение:
- R2 и R3 соединены параллельно R2 = R3, R2.3 = R2 / 2 = 2 Ом, составим эквивалентную схему:


- R = R1 + R2,3
- R = 3 Ом + 2 Ом = 5 Ом
- Найдем силу тока на участке цепи по закону Ома I = U / R
- I = 15 В / 5 Ом = 3 А
Ответ: I = 3 A.
Закон Ома для участка цепи, пример расчета.
21 Января 2017
1950
Всем привет.
В предыдущей статье мы собрали простую замкнутую цепь, состоящий из источника питания, проводников по которым протекает ток и нагрузки. Выяснили, что такое сопротивление проводника и сопротивление нагрузки. Так же рассмотрели взаимосвязь между напряжением тока, силой тока и сопротивлением на разных участках цепи (проводника и нагрузки). Все эти отношения установлены в основном законе электротехники – в законе Ома.
В этой статье, мы рассмотрим Закон Ома для участка цепи.
Закон Ома для участка цепи
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.
Давайте рассмотрим этот закон на примере. Соберем следующую схему:

Так как сопротивление проводников близко к нулю, будем считать, что они равны нулю. В нашу электрическую цепь, кроме нагрузки, мы еще добавили два прибора.
Амперметр – прибор для измерения силы тока, или другими словами измеряет сколько потребляет нагрузка, так легче запомнить. Соединяется последовательно с нагрузкой.
Вольтметр – прибор для измерения напряжения тока, при подключении к нагрузке, показывает сколько падает напряжение на нагрузку. Соединятся параллельно с нагрузкой.
Давайте нагрузку поставим сопротивлением равной 100 Ом, с источника питания пустим напряжение 5 В (вольт). Снимем показания с приборов. Нас интересует показатель амперметра. Амперметр показывает — 0,05 А (ампер) для удобства можно перевести в миллиамперы – 50 мА (миллиампер).


наведите или кликните мышкой, для анимации
Теперь поменяем напряжение тока, вместо 5 В установим 10 В. Снимем показатель амперметра. Амперметр показывает — 0,1 А переводим в миллиамперы – 100 мА. Сразу отметим для себя — с увеличением напряжения увеличилась сила тока.


Теперь вернемся к первому опыту, то есть установим напряжение обратно на значение 5 В. Попробуем изменить сопротивление нагрузки.
Поменяем нагрузку со значение сопротивления 200 Ом. Снимем показатели с амперметра и сравним с показателями первого опыта. Амперметр показывает — 0,025 А переводим в миллиамперы – 25 мА. Таким образом увеличение сопротивления нагрузки, уменьшило силу тока.
В законе ома: «сила тока в участке цепи … обратно пропорциональна электрическому сопротивлению».


наведите или кликните мышкой, для анимации
Закон Ома для участка цепи записывается следующей формулой:
I = U/R
Как нам уже известно:
I = сила тока
U = напряжение тока
R = сопротивление (сопротивление нагрузки)

Так же эту формулу можно преобразовывать для определения напряжения тока или сопротивления нагрузки. Что бы легче запомнить формулы, надо запомнить треугольник Ома, который изображен выше. Закрывая искомую величину пальцем, можно увидеть формулу для нее.
Формула для определения напряжения:

Формула для определения сопротивления:

Рассмотрим простой пример расчета используя закон Ома для участка цепи. Если в примере выше, мы бы не использовали амперметр, зная напряжение тока 5 В (U) и сопротивление нагрузки 100 Ом (R). Использую следующую формулу I = U/R, мы бы получили результат: 5/100 = 0,05. Ответ 0,05 А = 50 мА.
Мы разобрали закон Ома для участка цепи, ознакомились с формулами для определения силы тока, напряжение тока и сопротивления. Так же хочу добавить, при расчетах, необходимо переводить единицы измерения в систему СИ. В примерах выше для демонстраций замкнутой цепи, я использовал программу — Electronics Workbench. Программа предназначена для моделирования и анализа электронных схем.
Электротехника. Основы. Закон Ома
В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.
Закон Ома
Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.
Закон Ома для участка цепи без ЭДС
Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:
\begin{equation} I = {U_{ab}\over R}; \end{equation}- I — ток через участок ab электрической цепи;
- Uab — напряжение на участке ab электрической цепи;
- R — сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation} I = U_{ab} × G; \end{equation}Где:
- G — проводимость участка ab электрической цепи.
Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.
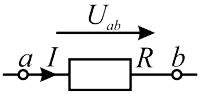
Рисунок 1 — Участок цепи без ЭДС
Закон Ома для участка цепи содержащего ЭДС
Где:
- I — ток через участок ac электрической цепи;
- Uab — напряжение на участке ab электрической цепи;
- E — ЭДС на участке bс электрической цепи;
- R — сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation} I = {(U_{ab} + E) × G}; \end{equation}Где:
- G — проводимость участка ab электрической цепи.
Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.
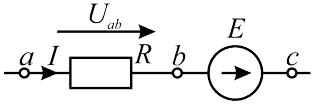
Рисунок 2 — Участок цепи содержащий ЭДС
Закон Ома для полной цепи
Закон формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation} I = {E\over {R + r}}; \end{equation}Где:
- I — ток в электрической цепи;
- E — ЭДС электрической цепи;
- R — сопротивление электрической цепи;
- r — внутреннее сопротивление источника ЭДС.
Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).
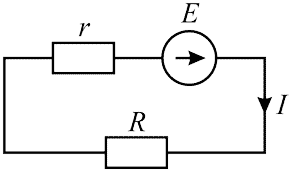
Рисунок 3 — Полная цепь
На схеме видно, что R и r соединены последовательно, а в формуле это отражено как сумма R (сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на Rп
\begin{equation} I = {E\over R_п}; \end{equation}Где:
- Rп — полное сопротивление электрической цепи (включая сопротивление источника ЭДС).
Закон Ома в дифференциальной форме
Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].
\begin{equation} \vec E = {ρ × \vec\jmath}; \end{equation}- \(\vec\jmath\) — плотность тока;
- ρ — удельное сопротивление;
- \(\vec E\) — напряжённость электрического поля.
Примеры применения
Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.
Пример 1
Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.
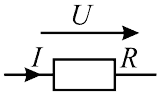
Рисунок 4 — Схема к 1 и 2-му примеру
Для решения задания воспользуемся выражением (1):
\begin{equation} I = {U\over R} = {26\over 5,2} = {5 \ А;} \end{equation}Пример 2
Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.
Для решения задания преобразуем выражение (2) относительно G:
\begin{equation} I = {U × G} \ \Rightarrow \ G = {I\over U} = {1,5\over 24} = {0,0625 \ См;} \end{equation}Пример 3
Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.

Рисунок 5 — Схема к 3-му примеру
Для решения задания преобразуем выражение (3) относительно E:
\begin{equation} I = {U — E\over R} \ \Rightarrow \ {I × R} = {U — E} \ \Rightarrow \ E = {U — I × R}; \end{equation}Подставим в выражение (10) известные величины:
\begin{equation} E = {U — I × R} = {220 — 0,5 × 140} = {150 \ В;} \end{equation}
Пример 4
Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь — 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.
Преобразуем выражение (5) относительно r:
\begin{equation} I = {E\over {R + r}} \ \Rightarrow \ {I × (R + r)} = E \ \Rightarrow \ {I × r} = {E — I × R} \ \Rightarrow \ r = {E — I × R\over I}; \end{equation}Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:
\begin{equation} r = {E — I × R\over I} = {9 — 0,72 × 12\over 0,72} = {0,36\over 0,72} = {0,5 \ Ом;} \end{equation}
Использованные термины
Электрический потенциал точки:
Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.
Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.
Электрическое напряжение:
Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: Uab = φa — φb.
Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение — скалярная величина, но на электрических схемах указывают его положительное направление.
Электродвижущая сила (ЭДС):
Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.
ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС — скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.
Электрическое ток:
Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление — направленное движение заряженных частиц.
Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11].
Плотность тока:
Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.
Плотность тока обозначается буквой \(\vec\jmath\) латинского алфавита и измеряется в амперах на метр квадратный (А/м2). Плотность тока — векторная величина [4].
Электрическое сопротивление:
Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.
Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление — скалярная величина.
Электрическая проводимость:
Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.
Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость — скалярная величина.
Удельное сопротивление:
Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м2.
Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].
В дальнейшем при использовании вышеперечисленных терминов слово «электрический» будет упускаться.
Список использованных источников
- Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов — Москва: Высшая школа, 1996. — 623 с.
- Иванова, С.Г. Теоретические основы электротехники: Версия 1.0 [Электронный ресурс] : учеб. пособие / С. Г. Иванова, В. В. Новиков – Красноярск: ИПК СФУ, 2008. — 318 с.
- Википедия — Удельное электрическое сопротивление [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление
- Википедия — Плотность тока [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Плотность_тока
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток: |
| Последовательное соединение.
1. Сила тока во всех последовательно соединенных участках цепи одинакова: I1=I2=I3=…=In=… 2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке: U=U1+U2+…+Un+… 3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка: R=R1+R2+…+Rn+… Если все сопротивления в цепи одинаковы, то: R=R1. N При последовательном соединении общее сопротивление увеличивается (больше большего). | Параллельное соединение. 1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках. I=I1+I2+…+In+… |
| 2. Напряжение на всех параллельно соединенных участках цепи одинаково: U1=U2=U3=…=Un=… 3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению):
Если все сопротивления в цепи одинаковы, то: При параллельном соединении общее сопротивление уменьшается (меньше меньшего). | 4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. A=I2Rt=I2(R1+R2+…+Rn+…)t. 5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. силы тока во всех участках одинаковы, то: U1:U2:…:Un:… = R1:R2:…:Rn:… Для двух резисторов: | 4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к.
5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. напряжения на всех участках одинаковы, то: I1R1= I2R2=…= I3R3=… Для двух резисторов: |
Закон Ома для участка цепи
Скажу сразу, что закон Ома – основной закон электротехники и применяется для расчета таких величин, как: ток, напряжение и сопротивление в цепи.
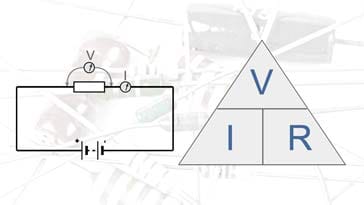
Рассмотрим электрическую цепь, приведенную на рисунке 1.
Рисунок 1. Простейшая цепь, поясняющея закон Ома.
Мы знаем, что электрический ток, то есть поток электронов, возникает в цепи между двумя точками (на рисунке А и Б) с разными потенциалами. Тогда следует считать, что чем больше разность потенциалов, тем большее количество электронов переместятся из точки с низким потенциалом (Б) в точку с высоким потенциалом (А). Количественно ток выражается суммой зарядов прошедших через заданную точку и увеличение разности потенциалов, то есть приложенного напряжения к резистору R, приведет к увеличению тока через резистор.
С другой стороны сопротивление резистора противодействует электрическому току. Тогда следует сказать, что чем больше сопротивление резистора, тем меньше будет средняя скорость электронов в цепи, а это ведет к уменьшению тока через резистор.
Совокупность двух этих зависимостей (тока от напряжения и сопротивления) известна как закон Ома для участка цепи и записывается в следующем виде:
I=U/R
Это выражение читается следующим образом: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Следует знать что:
I – величина тока, протекающего через участок цепи;
U – величина приложенного напряжения к участку цепи;
R – величина сопротивления рассматриваемого участка цепи.
При помощи закона Ома для участка цепи можно вычислить приложенное напряжение к участку цепи (рисунок 1), либо напряжение на входных зажимах цепи (рисунок 2).
Рисунок 2. Последовательная цепь, поясняющая расчет напряжения на зажимах цепи.
В этом случае формула (1) примет следующий вид:
U = I *R
Но при этом необходимо знать ток и сопротивление участка цепи.
Третий вариант закона Ома для участка цепи, позволяющий рассчитать сопротивление участка цепи по известным значениям тока и напряжения имеет следующий вид:
R =U/I
Как запомнить закон Ома: маленькая хитрость!
Для того, что бы быстро переводить соотношение, которое называется закон Ома, не путаться, когда необходимо делить, а когда умножать входящие в формулу закона Ома величины, поступайте следующим образом. Напишите на листе бумаги величины, которые входят в закон Ома, так как показано на рисунке 3.
Рисунок 3. Как запомнить закон Ома.
Теперь закройте пальцем, ту величину, которую необходимо найти. Тогда относительное расположение оставшихся незакрытыми величин подскажет, какое действие необходимо совершить для вычисления неизвестной величины.
Подробнее можно узнать в мультимедийном учебнике по основам электротехники и электроники.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Физика, 10 класс
Урок 29. Закон Ома для участка цепи. Соединения проводников
Перечень вопросов, рассматриваемых на уроке:
- условия, необходимые для существования электрического тока;
- постоянный электрический ток;
- закон Ома для участка цепи;
- формула расчета сопротивления проводника с учетом свойств материала проводника и его геометрических размеров;
- типы соединений проводников и формулы расчета параметров электрической цепи для каждого типа.
Глоссарий по теме.
Сила тока I — скалярная величина, равная отношению заряда q, прошедшего через поперечное сечение проводника, к промежутку времени t, в течение которого шёл ток.
Постоянный ток — электрический ток, не изменяющийся со временем.
Последовательное соединение проводников. При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом.
Параллельное соединение проводников. При параллельном соединении концы проводников присоединены к одной и той же паре точек.
Смешанное соединение проводников — это такое соединение, когда в цепи присутствует и последовательное, и параллельное соединение.
Узел – это точка электрической цепи, где сходится не менее трех ветвей.
Свойство проводника ограничивать силу тока в цепи, то есть противодействовать электрическому току, называют электрическим сопротивлением проводника.
Резистор или проводник — элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления.
Основная и дополнительная литература по теме урока:
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 335 – 340.
2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009. – С. 105 – 109.
3. Элементарный учебник физики. Учебное пособие в 3 томах под редакцией академика Ландсберга Г.С.: Т.2. Электричество и магнетизм. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 110 – 115.
4. Тульчинский М.Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 83 – 87.
5. Савельев И.В. Курс общей физики, том II. Электричество. М.: Изд. «Наука», 1970 г. С. 108.
Открытые электронные ресурсы:
http://kvant.mccme.ru/1979/02/elektrichestvo_ie_temperatura.htm
Теоретический материал для дополнительного изучения
Сложно представить нашу жизнь без электрического тока. Каждый день, не задумываясь, мы используем различные электрические приборы, в основе работы которых лежат простые и сложные электрические цепи. Какому закону подчиняются основные параметры электрических цепей? Как рассчитать эти цепи, чтобы приборы работали исправно?
Вы уже знаете, электрическим током называют упорядоченное (направленное) движение заряженных частиц.
Для возникновения и существования электрического тока в проводнике необходимо:
- наличие свободных заряженных частиц;
- сила, действующая на них в определённом направлении, то есть наличие электрического поля в проводнике.
Различают следующие действия электрического тока:
- тепловое ;
- химическое ;
- магнитное .
Постоянный ток — электрический ток, у которого сила тока и направление не изменяются со временем.
Сила тока I равна отношению электрического заряда q, прошедшего через поперечное сечение проводника, ко времени его прохождения t:

За направление электрического тока условно выбрано направление движения положительно заряженных частиц, то есть в сторону, противоположную направлению движения электронов.

Для каждого проводника – твердого, жидкого и газообразного – существует определённая зависимость силы тока от приложенной разности потенциалов (напряжения) на концах проводника. Эту зависимость выражает, так называемая, вольт-амперная характеристика проводника.

Для широкого класса проводников (в т. ч. металлов ) при неизменной температуре справедлив закон Ома для участка цепи:
Сила тока на участке цепи прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению этого участка цепи:

Закон имеет простую форму, но доказать экспериментально его справедливость довольно трудно.
Закон Ома является основой всей электротехники постоянных токов. Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно.
Основная электрическая характеристика проводника – сопротивление. От этой величины зависит сила тока в проводнике при заданном напряжении. Причиной электрического сопротивления является взаимодействие электронов при их движении по проводнику с ионами кристаллической решетки. Сопротивление проводника зависит от свойств материала проводника и его геометрических размеров.

Электрическое сопротивление металлов прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения:

где величина ρ – удельное сопротивление проводника — величина, зависящая от рода вещества и его состояния (от температуры в первую очередь). Удельное сопротивление веществ приводятся в справочных таблицах.
Омметр – прибор для измерения сопротивления.
От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию. Для этого составляют электрические цепи различной сложности. Различают последовательное, параллельное, смешанное соединения проводников.
Последовательное соединение проводников. При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом. Главная особенность последовательного соединения заключается в том, что через все проводники протекает одинаковый ток. Если через один проводник протекает ток определенной величины, то такой же ток протекает и через все остальные. Если хотя бы в одном проводнике отсутствует ток, то он обязательно отсутствует и во всех остальных. Напряжение на концах последовательно соединенных проводников складывается. Полное сопротивление всего участка цепи при последовательном соединении равно сумме сопротивлений всех проводников.

Последовательное соединение | |
Физическая величина | Формула |
Сила тока | I = I1 = I2 |
Напряжение | U = U1 + U2 |
Сопротивление | R = R1 + R2 |
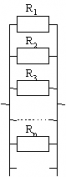
Параллельное соединение проводников. При параллельном соединении концы проводников присоединены к одной и той же паре точек.

Параллельное соединение | |
Физическая величина | Формула |
Сила тока | I = I1 + I2 |
Напряжение | U = U1 = U2 |
Сопротивление |
|
Узел – это точка электрической цепи, где сходится не менее трех ветвей.
Узел обозначается на схеме жирной точкой в том месте, где ветви соединяются между собой.
Смешанное соединение проводников.
Смешанным соединением проводников называют такое соединение, при котором в цепи присутствует и последовательное, и параллельное соединение.

Метод эквивалентных преобразований заключается в том, что электрическую цепь или ее часть заменяют более простой по структуре электрической цепью. При этом токи и напряжения в непреобразованной части цепи должны оставаться неизменными, т.е. такими, какими они были до преобразования. В результате преобразований расчет цепи упрощается и часто сводится к элементарным арифметическим операциям.
Расчет сопротивления сложной цепи:

Рези́стор или проводник — пассивный элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления.

Примеры и разбор решения заданий
1. Выберите один из 3 вариантов ответа:
При параллельном соединении проводников…
1) напряжение зависит от сопротивления на данном участке цепи
2) напряжение везде разное
3) напряжение везде одинаковое
Ответ: 3) напряжение везде одинаковое.
2. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно 24 Ом. Чему равно полное сопротивление участка при замкнутом ключе К?

Решение.
После замыкания ключа схема будет представлять собой параллельное соединение резистора с двумя последовательно соединенными резисторами.

Полное сопротивление участка при замкнутом ключе равно
(R+R)R/((R+R) + R) = 2R/3 = 16 Ом.
Ответ: 16 Ом.
Закон Ома для участка цепи
Пожалуй, закон Ома для участка цепи является основой электротехники и электроники. Любое Пособие по физике для поступающих в вузы описывает Закон Ома и любой инженер должен его знать. Этот закон настолько прост, что его, по идее, должен знать и понимать каждый школьник. Однако я встречал людей с высшим техническим образованием, которые не знали как рассчитать простейшую электрическую цепь из двух резисторов. И это не шутка. Именно поэтому я решил написать небольшую статью, посвящённую Закону Ома для участка цепи. Постараюсь сделать это понятными словами.Закон Ома для участка цепи определяет зависимость между силой тока в проводнике и напряжением (разностью потенциалов) между двумя точками этого проводника. Эти точки ещё называют сечениями. Почему? Проводник, каким бы он ни был (круглым, квадратным или любой другой формы) можно мысленно рассечь (см. рис. 1). Это и будет сечение. А ещё есть понятие площадь поперечного сечения (обычно, когда говорят «сечение» по отношению к проводнику, то как раз и подразумевают площадь поперечного сечения, но это уже другая тема).
Рис. 1. Сечение проводника.
В 1826 г. немецким учёным Георгом Омом (1787-1854) было замечено, что отношение разности потенциалов (напряжения) на концах металлического проводника к силе тока является величиной постоянной, то есть:
U/I = R = constЭта величина зависит от геометрических свойств проводника (то есть от его размеров, в частности, от площади поперечного сечения), а также от его электрических свойств и температуры. Эта величина называется омическим (активным) сопротивлением, или просто сопротивлением.
Определение закона Ома для участка цепи следующее
Сила тока прямо пропорциональна разности потенциалов (напряжению) на концах участка
цепи и обратно пропорциональна сопротивлению этого участка:I = U/R
|
Единица измерения омического сопротивления в СИ – ом (Ом). Проводник имеет сопротивление 1 Ом, если при силе тока в этом проводнике 1 А разность потенциалов (напряжение) на его концах равна 1 В, то есть
1 Ом = 1 В / 1 АИными словами, если взять проводник, по которому течёт ток силой 1 А, отмерить отрезок этого проводника таким образом, чтобы напряжение на концах этого отрезка было равно 1 В, то сопротивление этого отрезка будет 1 Ом (рис. 2).
Рис. 2. Сопротивление проводника.
Как говаривал один известный товарищ – теория без практики мертва. Надеюсь, что всё прочитанное выше вы поняли. Но остался один вопрос – зачем это надо? Где можно применить полученные знания на практике? Приведу два простых примера, которые, однако, используются очень часто в электронике.Делитель напряжения
Довольно часто приходится сталкиваться с необходимостью понизить напряжение, например, с 12 до 3 вольт. Сделать это можно с помощью двух резисторов (см. рис. 3). Если вы не знаете, что такое резисторы, то советую ознакомиться со статьёй РЕЗИСТОРЫ. Ну а если знаете, то дальше можете прочитать о том, как это сделать.Задача, в общем-то, не сложная. Требуется подобрать два резистора таким образом, чтобы падение напряжения на одном из них составляло 3 вольта, а на втором – (12 – 3) = 9 вольт (для нашего примера). Кроме того, необходимо знать ток, который должен протекать в цепи. Допустим, что в нашем случае ток должен быть равен 50 мА (0,05 А). Тогда, используя закон Ома для участка цепи, вычислим полное сопротивление цепи, то есть общее сопротивление резисторов R1 и R2:
R = U/I = 12 В / 0,05 А = 240 ОмНапомню, что все единицы измерения должны соответствовать принятым в СИ, то есть напряжение измеряется в ВОЛЬТАХ, ток – в АМПЕРАХ, а сопротивление – в ОМАХ.
Поскольку на любом участке цепи из последовательно включенных элементов ток одинаков, то вычислить сопротивление резисторов R2 и R1 не составит труда:
R1 = U1 / I = 9 / 0,05 = 180 Ом R2 = U2 / I = 3 / 0,05 = 60 ОмНу вот и всё. Задача решена. Однако использовать такой делитель нужно с умом. Ведь любая нагрузка имеет своё сопротивление, которое называется входным сопротивлением. Это значит, что, подключив нагрузку к выходу делителя, мы тем самым уменьшим сопротивление цепи, а это, в свою очередь, увеличит ток в цепи и падение напряжения на резисторе R1 увеличится, а на нагрузке, соответственно, уменьшится. Что из этого следует? А следует из этого тот печальный факт, что сколь-нибудь мощную нагрузку подключать к выходу делителя нецелесообразно. Поэтому такие делители используются в основном, в электронных схемах, где протекают относительно небольшие токи.
Если интересно, то вы можете немного поэкспериментировать с делителем напряжения при помощи представленного ниже флэш-ролика (рис. 3). Для изменения входного напряжения и сопротивления резисторов воспользуйтесь соответственными «ползунками» или непосредственно введите данные в поля жёлтого цвета. Если флэш-ролик не отображается или не работает, то вам придётся настроить (или заменить) ваш браузер и/или установить (обновить) флэш-плеер.
Рис. 3. Делитель напряжения.
Как зажечь (но не сжечь) светодиод?
Светодиоды в наше время применяются очень широко – от простых устройств индикации до автомобильных фонарей и светофоров. Возможно, у вас возникала мысль поменять лампочки в автомобиле на светодиоды. Как бывалый автомобилист я вам этого делать не советую – возни много, а смысла мало. А вот как электронщик – помогу разобраться в премудростях включения светодиодов в электрическую цепь. Дело это несложное, но многие просто понятия не имеют, что и здесь нужно всё делать «по науке». А потом говорят, что светодиоды – вещь ненадёжная, хотя, как правило, выходят из строя светодиоды при правильной эксплуатации очень и очень редко. А вот при неправильной – ещё как. При желании сжечь светодиод можно моментально.Надо сказать, что сейчас в магазинах довольно много разных «мигающих» и прочих светодиодов, которые на самом деле являются электронными устройствами, встроенными в корпус светодиодов. Такие устройства можно подключать непосредственно к источнику питания, без гасящего резистора. Однако мы здесь будем говорить об обычных светодиодах.
Схема включения светодиода показана на рис. 4. При включении светодиода в цепь постоянного тока необходимо соблюдать полярность (см. документацию на светодиод).
Итак, главное, что нам нужно знать:
- Максимальное напряжение
- Максимально допустимый ток светодиода
Итак, допустим, что мы зачем-то хотим установить светодиод на автомобиль. Напряжение бортовой сети автомобиля при исправном оборудовании не может превышать 15 В. На это напряжение и будем рассчитывать. Допустим, что максимальный ток нашего светодиода составляет 20 мА (0,02 А). Далее нам необходимо учесть тот факт, что на любом полупроводнике (коим является и светодиод) падает какое-то напряжение. Для светодиодов это обычно 1,5…2 В. Примем его для нашего случая равным 2 В.
Поскольку резистор и светодиод будут подключены последовательно, то максимально возможное напряжение на резисторе для нашего примера будет
U1 = U – Ud = 15 – 2 = 13
- Где
- U1 – напряжение на гасящем резисторе R1
- U – входное напряжение
- Ud – напряжение, падающее на светодиоде
- U – входное напряжение
R = U1 / I = 13 / 0,02 = 650 ОмНу вот и всё. Задача решена – для включения светодиода с заданными характеристиками нам потребуется резистор сопротивлением 650 Ом. Однако сопротивление – это не единственный параметр резистора. Резистор ещё должен иметь подходящую мощность. Кроме того, промышленностью не выпускаются резисторы сопротивлением 650 Ом (точнее, выпускаются, но для особых случаев). Но это уже другая история. Хотите знать больше? Читайте статью РЕЗИСТОРЫ.
Ну и кроме того предоставлю вам возможность закрепить полученный материал с помощью флэш-ролика (рис. 4).
Рис. 4. Подключение светодиода.
См. также:
Закон
Ом • Закон Ома
ЗаконОм объясняет связь между напряжением и током, протекающим через резисторы.
Закон Ом : Ток, протекающий через любой резистор, прямо пропорционален напряжению, приложенному к его концам.
Математически закон Ома дается V = IR
, где
В = Напряжение,
I = ток,
R = сопротивление
ЗаконОма широко используется в электротехнике для решения цепей.Схема — это комбинация источника напряжения и резисторов, образующих замкнутый контур (как показано выше).
Утверждение закона Ома является экспериментально полученным утверждением. Джордж выполнил различные эксперименты на резисторе 1 кОм и, наконец, опубликовал трактат в 1827 году.
Основы закона Ома: напряжение, ток и сопротивление
ЗаконОма касается трех основных электрических свойств: напряжения, тока и сопротивления. Давайте разберемся с ними индивидуально.
Напряжение: Мы все знаем о магните, который притягивает железо к себе.Магнит делает это, потому что у него есть магнитное поле, которое сильнее в непосредственной близости и которое становится слабее с увеличением расстояния. Подобно магнитному полю, подобное электрическое поле существует в природе. Технически это электрическое поле называется электрическим потенциалом. Разность напряжений или потенциалов — это измерение напряженности электрического поля между двумя точками.
Ток: металлический проводник имеет большое количество свободных валентных электронов, которые непрерывно движутся внутри него.Источник напряжения, подключенный к проводнику, заставляет эти электроны течь от отрицательной клеммы батареи к положительной клемме. Электрический ток является мерой потока заряда.
Сопротивление: хотя электрический проводник несет большое количество свободных электронов, он также содержит атомы и другие связанные электроны. Во время своего движения свободные электроны также сталкиваются со связанными электронами и атомами. При этом они теряют свою энергию. Сопротивление — это измерение этого противодействия, с помощью которого связанные электроны и атомы сопротивляются движению свободных электронов.
Зачем вам нужен закон Ома?
Поскольку мы практически изучаем закон, важно ответить на BIG WHY. Мы уже знаем, что ток, напряжение и сопротивление являются тремя основными электрическими свойствами. Давайте посмотрим, как мы можем применить отношения Ома (V = IR) в реальной жизни.
Электронагреватель
Рассмотрим нагреватель, подключенный к настенной розетке 220 В переменного тока с сопротивлением 20 Ом.Если мы хотим узнать ток, протекающий через нагреватель, мы можем легко сделать это, используя уравнение: V = IR,
I = V / R = 220 В переменного тока / 50 Ом = 4,4 A
найти неизвестный резистор
Рассмотрим неизвестный резистор, к которому приложено 120 вольт. Ток равен 6 А. Опять же, изменив исходное уравнение, мы можем вычислить неизвестное сопротивление, то есть
.R = V / I = 120 В / 12 A = 10 Ом
Чтобы узнать, сколько входных напряжений предоставляется
Рассмотрим третий случай, когда резистивный элемент 35 Ом подключен к неизвестному источнику напряжения.В то время как ток, протекающий через цепь, составляет 10 А, мы заинтересованы в поиске вольт, связанных с источником входного сигнала. К счастью, мы можем использовать исходное утверждение, чтобы найти это, V = IR = 10 A * 35 Ω = 350 В
Роль метрических префиксов в законе Ома
Метрические префиксы — это буквы, которые используются вместе с цифрами. В настоящее время на практике применяются 21 метрический префикс (приблизительно). Каждый префикс представляет конкретное число. Наличие метрических префиксов помогает нам выражать очень меньшее и очень большое число.Давайте сначала посмотрим на метрические префиксы:
- йокто = 10 -24 = 0 000 000 000 000 000 000 000 001
- zepto = 10 -21 = 0 000 000 000 000 000 000 001
- atto = 10 -18 = 0 000 000 000 000 000 001
- фемто = 10 -15 = 0 000 000 000 000 001
- пико = 10 -12 = 0 000 000 000 001
- нано = 10 -9 = 0 000 000 001
- микро = 10 -6 = 0.000 001
- милли = 10 -3 = 0,001
- сенти = 10 -2 = 0,01
- деци = 10 -1 = 0,1
- ед. = 10 0 = 1
- дека = 10 1 = 1 0
- гекто = 10 2 = 1 00
- кг = 10 3 = 1 000
- мега = 10 6 = 1 000 000
- гигабайт = 10 9 = 1 000 000 000
- тера = 10 12 = 1 000 000 000 000
- peta = 10 15 = 1 000 000 000 000 000
- экз = 10 18 = 1 000 000 000 000 000 000
- дзета = 10 21 = 1 000 000 000 000 000 000 000
- йота = 10 24 = 1 000 000 000 000 000 000 000 000
Допустим, вы измеряете ток со значением 0.000 001 A. Написание такого числа является трудной задачей, а упоминание нулей кому-то еще более утомительно. Знание метрического префикса пригодится здесь, и вы можете просто выразить 0. 000 001 1 микроампер. Из всех 21 ряда есть несколько значений, которые вы должны держать под рукой:
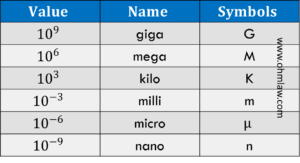
Почему они важны?
- Часто резисторов рассчитаны на в кОм (кОм) и мОм (МОм) .
- Ток рассчитан на миллиампер (мА), и микроампер (мкА) .
Как мы используем их в наших омических цепях?
Рассмотрим резистор 5 кОм (5000 Ом), подключенный к источнику 12 В. Давайте используем наше уравнение I = V / R, чтобы найти ток, протекающий по цепи.
I = V / R = 12 В / 5000 Ом = 0,0024 A = 2,4 * 10-3 A = 20,4 мА
Приведенный выше расчет довольно утомителен. Для сложных расчетов это может оказаться проблематичным.
Существует альтернативный способ обработки префиксов. В то время как мА представляет собой 0,001, оно обратно пропорционально кА.1 мА = (1 / кА). Мы можем использовать эту обратную методику:
- милли = 1 / кило
- микро = 1 / Мега
- нано = 1 / гига
Давайте применим это правило к предыдущему случаю:
I = V / R = 12 В / 5 кОм = (12 В / 5 Ом) m = 20,4 мА
Начинающий может запутать эти вычисления. Тем не менее, вы можете освоить их после некоторой практики.
закон Ома и сила
Хотя напряжение, ток и сопротивление являются тремя основными электрическими свойствами, четвертый игрок — это сила.
Как мы можем связать власть с тремя другими свойствами? Первый закон Джоуля ответит на это.
Джеймс Прескотт Джоул провел различные эксперименты на проводниках и обнаружил, что количество тепла, генерируемого в проводниках, прямо пропорционально квадрату тока, умноженному на сопротивление.
Математически,
P = I 2 R
Мы можем использовать другие уравнения закона, чтобы получить 12 различных формул.
Давайте подведем итоги вышеприведенного обсуждения в инфографику:

Ом
ЗаконОма показывает линейную зависимость между напряжением и током в электрической цепи.
Падение напряжения и сопротивление резистора задают постоянный ток, протекающий через резистор.
По аналогии с потоком воды мы можем представить электрический ток как ток воды через трубу, резистор как тонкую трубу, которая ограничивает поток воды, напряжение как перепад высот воды, который обеспечивает поток воды.
формула закона Ома
Ток I резистора в амперах (A) равен сопротивлению резистора напряжение V в вольтах (В), деленное на сопротивление R в омах (Ом):
В — падение напряжения на резисторе, измеренное в вольтах (В).В некоторых случаях закон Ома использует букву E для обозначения напряжения. E обозначает электродвижущую силу.
I — электрический ток, протекающий через резистор, измеренный в амперах (A)
R — сопротивление резистора, измеряется в Ом (Ω)
Расчет напряжения
Когда мы знаем ток и сопротивление, мы можем рассчитать напряжение.
Напряжение V в вольтах (В) равно току I в амперах (A), умноженному на сопротивление R в омах (Ом):
Расчет сопротивления
Когда мы знаем напряжение и ток, мы можем рассчитать сопротивление.
Сопротивление R в омах (Ом) равно напряжению V в вольтах (В), деленному на ток I в амперах (A):
Поскольку ток определяется значениями напряжения и сопротивления, формула закона Ома может показать, что:
- Если мы увеличим напряжение, ток увеличится.
- Если мы увеличим сопротивление, ток уменьшится.
Пример №1
Найти ток электрической цепи с сопротивлением 50 Ом и напряжением питания 5 Вольт.
Решение:
В = 5 В
R = 50Ω
I = В / R = 5 В / 50 Ом = 0,1 А = 100 мА
Пример №2
Найти сопротивление электрической цепи, которая имеет напряжение питания 10 Вольт и ток 5 мА.
Решение:
В = 10 В
I = 5 мА = 0,005A
R = В / I = 10 В / 0,005 А = 2000 Ом = 2 кОм
ЗаконОм для цепи переменного тока
Ток нагрузки I в амперах (A) равен напряжению нагрузки V Z = V в вольтах (В), деленному на полное сопротивление Z в омах (Ом):
В — падение напряжения на нагрузке, измеряется в Вольтах (В)
I — электрический ток, измеренный в амперах (A)
Z — полное сопротивление нагрузки, измеряется в Ом (Ω)
Пример № 3
Найти ток в цепи переменного тока с напряжением питания 110 В ± 70 ° и нагрузкой 0.5kΩ∟20 °.
Решение:
В = 110 В∟70 °
Z = 0,5 кОм20 ° = 500 кОм20 °
I = В / Z = 110 В ~ 70 ° / 500 Ом ~ 20 ° = (110 В / 500 Ом) ∟ (70 ° -20 °) = 0,22 А ~ 50 °
Закон закона Ома (краткая форма)
Ом закон калькулятора: рассчитывает соотношение между напряжением, током и сопротивлением.
Введите 2 значений, чтобы получить третье значение, и нажмите кнопку Рассчитать :
закон закона Ома II ►
См. Также
,Закон Ома является одним из самых фундаментальных законов в теории электричества. Формула или уравнение закона Ома связывает напряжение и ток со свойствами проводника, то есть его сопротивления в цепи.
Сопротивление Учебник включает в себя:
Что такое сопротивление
Закон Ома
удельное сопротивление
Таблица удельного сопротивления для обычных материалов
Температурный коэффициент сопротивления
Электрическая проводимость
Последовательные и параллельные резисторы
Таблица параллельных резисторов
Параллельный калькулятор резисторов
Закон Ома
является одним из наиболее фундаментальных и важных законов, регулирующих электрические и электронные схемы.Он связывает ток, напряжение и сопротивление для линейного устройства, так что если два известны, третий может быть рассчитан.
Учитывая то, что ток, напряжение и сопротивление являются тремя основными величинами цепи, это означает, что закон Ома также очень важен.
Закон Омаиспользуется во всех отраслях электротехники и электроники. Он используется для расчета значения резисторов, требуемых в цепях, и также может использоваться для определения тока, протекающего в цепи, где напряжение можно легко измерить через известный резистор, но более того, закон Ома используется в огромное количество вычислений во всех формах электрических и электронных схем — фактически везде, где течет ток.
Открытие закона Ома
Существует математическая зависимость, которая связывает ток, напряжение и сопротивление. Немецкий ученый по имени Георг Ом провел много экспериментов, чтобы показать связь между ними. В те дни, когда он проводил свои эксперименты, метров не было, как мы их знаем сегодня.
Только после значительных усилий и со второй попытки ему удалось придумать то, что мы знаем сегодня как Закон Ома.
Примечание по Георгу Ом:
Георг Ом, родившийся в Эрлангене, примерно в 50 милях к северу от Мюнхена в 1879 году, стал одним из тех, кто много исследовал новую науку, связанную с электричеством, обнаружив связь между напряжением и током в проводнике — этот закон сейчас назвал закон Ома, чтя работу, которую он сделал.
Подробнее о Георг Ом.
Что такое закон Ома?
ЗаконОма описывает, как ток протекает через материал, когда применяются различные уровни напряжения. Некоторые материалы, такие как электрические провода, имеют небольшое сопротивление току, и этот тип материала называется проводником. Следовательно, если этот проводник расположен, например, непосредственно через батарею, большой ток будет течь.
В других случаях другой материал может препятствовать протеканию тока, но, тем не менее, допускает его использование. В электрических цепях эти компоненты часто называют резисторами. Тем не менее, другие материалы практически не пропускают ток, и эти материалы называются изоляторами.
Ом посмотрел, как течет ток в различных материалах, и он смог разработать свой закон, который мы теперь называем Законом Ома.
Чтобы получить первое представление о происходящем, можно сравнить электрическую ситуацию с течением воды в трубе.Напряжение представлено давлением воды в трубе, ток — количеством воды, протекающей по трубе, и, наконец, сопротивление эквивалентно размеру трубы.
Можно представить, что чем шире труба, тем больше воды будет течь. Причина этого в том, что больше воды протекает через более широкую трубу, чем более узкую — более узкая обеспечивает большее сопротивление потоку воды. Кроме того, если в трубе больше давления, то для той же трубы будет течь больше воды.
Ом определили, что для обычных материалов удвоение напряжения удваивает поток тока для данного компонента. Различные материалы или одинаковые материалы с различными формами будут иметь разные уровни сопротивления течению тока.
Закон определения Ома
Закон Ом гласит, что ток, протекающий в цепи, прямо пропорционален приложенной разности потенциалов и обратно пропорционален сопротивлению в цепи.
Другими словами, удваивая напряжение на цепи, ток также удваивается. Однако, если сопротивление удвоится, ток упадет вдвое.
В этом математическом соотношении единица сопротивления измеряется в Омах.

Формула закона Ома
Формула или уравнение закона Ома очень просты.
Закон Омаможно выразить в математической форме:
Где:В = напряжение, выраженное в вольтах.
I = ток, выраженный в амперах.
R = сопротивление, выраженное в Ом.
закон закона треугольника
Чтобы вспомнить формулу, можно использовать треугольник с одной горизонтальной стороной и вершиной сверху, как пирамиду. Это иногда называют законом треугольника Ома.
В верхнем углу треугольника закона Ом находится буква V, в левом углу — буква I, а в правом нижнем углу — R.

Чтобы использовать треугольник, прикрыть неизвестное количество, а затем, а затем вычислить его из двух других.Если они находятся на одной линии, они умножаются, но если одна находится над другой, их следует разделить. Другими словами, если нужно рассчитать ток, напряжение делится на сопротивление, то есть V / R и так далее.

Если необходимо рассчитать напряжение, то оно определяется путем умножения тока на сопротивление, т. Е. I x R.
Пример расчета закона вОм
Если на резистор 500 Ом подается напряжение 10 В, определите величину тока, который будет течь.

Глядя на треугольник закона Ома, ток является неизвестным, оставляя в качестве известных значений напряжение и сопротивление.

Таким образом, ток определяется путем деления напряжения на сопротивление.
я знак равно В р знак равно 10 500 знак равно 0.02 знак равно 20 м
Пример 2
Аналогичным образом можно использовать закон Ома, чтобы найти сопротивление, если известны ток и напряжение.Взять, к примеру, напряжение 10 вольт и ток 0,1А. Используя треугольник закона Ома, можно увидеть, что:
р знак равно В я знак равно 10 0,1 знак равно 100 Ω
Пример 3
Наконец, другая комбинация состоит в том, что сопротивление и ток известны, тогда можно рассчитать ожидаемое напряжение на сопротивлении. Возьмите пример расстояния 250 Ом, которое имеет ток 0.Через него протекает 1 А, тогда напряжение можно рассчитать, как показано ниже:
В знак равно я р знак равно 0,1 × 250 знак равно 25 вольт
Линейный график
Можно видеть, что если бы напряжение и ток были построены для фиксированного резистора или длины провода и т. Д., Была бы линейная кривая.
 График напряжения и тока для линейного сопротивления
График напряжения и тока для линейного сопротивленияВидно, что удвоение напряжения удваивает ток, который проходит через конкретный элемент схемы.
На графике есть две линии, одна для более высокого сопротивления — эта требует больше напряжения, чтобы быть приложенным для данного текущего тока. Соответственно это должно иметь более высокое сопротивление. Наоборот, кривая для более низкого сопротивления показывает компонент, который требует применения более низкого напряжения для данного тока.
Нелинейные компоненты
ЗаконОм в его основной форме, где удвоение напряжения приводит к удвоению тока, применяется к линейным компонентам, таким как обычные резисторы.Некоторые компоненты, такие как диоды, имеют нелинейные кривые, на которые сопротивление влияет приложенным напряжением.
Закон Омаявляется одним из самых основных понятий в области электротехники и электроники. Концепция элемента, имеющего определенное сопротивление, которое определяет величину тока, протекающего через него при определенном напряжении, является ключом к работе практически всех цепей.
Более основные понятия:
Напряжение
Текущий
сопротивление
емкость
Мощность
трансформеры
РЧ шум
Децибел, дБ
Q, добротность
Возврат в меню основных концепций., ,
CQ-Calling All
Хамса! Рекламная информация | Основной закон Ома закон Ома может быть очень трудно понять любому, у кого никогда не было базовое понимание или обучение основам электричества.Мы примем что у вас есть кое-какие знания об основах электричества. Мы объясним это в условия потока воды! НЕ ПОЛУЧИТЬ ВЛАСТЬ! Что такое Ома Закон: Закон Ома сделан из 3 математических уравнений , которые показывают соотношение между электрическими напряжением , , текущий и сопротивление . Что такое напряжение? An анология будет огромный резервуар для воды заполнен с тысячами галлонов воды высоко на холме.Разница между давлением воды в резервуаре и водой, которая выходит из труба, соединенная снизу, ведущая к крану, определяется Размер трубы и размер выходного отверстия крана. Эта разница давления между двумя можно рассматривать как потенциальное напряжение. Какой ток? Аналогия будет количество потока определяется давлением (напряжением) воды через трубы , ведущие к крану.Семестр ток относится к количеству, объему или интенсивности электрического потока, как в противоположность напряжению, которое относится к силе или «давлению», вызывающему текущий потокЧто такое сопротивление? Аналогия будет размер водопроводных труб и размер крана. чем больше труба и кран (меньше сопротивление), тем больше воды поступает вне! Чем меньше труба и кран (больше сопротивления), тем меньше воды это выходит! Это можно рассматривать как сопротивление потоку течение воды. Все три из них: напряжение, ток и сопротивление напрямую взаимодействовать в законе Ома. Измените любые два из них, и вы эффект третий. Информация: Закон Ома был назван в честь Баварского математик и физик Георг Ом . Закон Ома может быть
заявлено как математических уравнений , все получены из I измеряется током в ампер (связано с давлением (Напряжение) воды через трубы и кран) иR — измеренное сопротивление в Ом в зависимости от размера труб и крана:V = I x R (напряжение = ток, умноженный на Сопротивление) R = В / I (Сопротивление = Напряжение, деленное на Текущий) I = В / Р (ток = Напряжение, деленное на сопротивление) Зная любые два значения схемы , можно определить (вычислить) , третье, , используя ом Закон. Например, чтобы найти напряжение в схема:Если цепь имеет ток 2 А, и сопротивление 1 Ом, (<это два «известных»), затем в соответствии с законом Ом и приведенными выше формулами напряжение равно току умноженное на сопротивление: (V = 2 А х 1 Ом = 2
вольт). В этом третьем примере мы знаем ток (2 А) и
напряжение (2 вольт) …. какое сопротивление? Иногда очень полезно
Связать эти формулы визуально. Закон Ома «колеса» и графика
ниже может быть очень полезным инструментом, чтобы подтолкнуть вашу память и помочь вам
понять их отношения. колесо выше разделен на три секции: Вольт
V (сверху разделительной линии) Для использования, просто покрыть неизвестное количество, которое вам нужно, своим глазом и тем, что осталось это формула, чтобы найти неизвестное. Пример: Чтобы найти
ток цепи (I), просто накрыть раздел I или Amps в ваших шахтах
глаз, и что остается, это V вольт над разделительной линией и R
Ом (сопротивление) ниже. Теперь подставим известные значения. Просто
разделил известные вольты на известное сопротивление. Вот другой пример: Вы знаете ток и сопротивление в цепи, но вы хотите узнать напряжение. Just
покрыть раздел напряжения с вашими глазами … то, что осталось, это I X R
разделы. Просто умножьте значение I на значение R, чтобы получить ответ!
Тренируйтесь с колесом, и вы будете удивлены, насколько хорошо он работает
поможет вам запомнить формулы, не пытаясь! Вы будете должны вставить X между I и R на рисунке и представить горизонтальная линия деления, но основной является только тем же. в вышеуказанном
Законное колесо Ома, которое вы заметите, имеет дополнительный раздел (P) для силы
и буква E * была использована вместо буквы V для
напряжение. Допустим, вы знаете мощность и ток в цепи и хотите знать напряжение. Найди свой неизвестное значение в желтых областях (V или E * в этом колесе) и просто посмотрите наружу и выберите ценности, которые вы знаете.Это будет P и I. Подставьте свои значения в формулу, (P, деленное на I) сделайте математика, и у вас есть свой ответ! Информация: Как правило, закон Ома применяется только к
Цепи постоянного тока, а не переменный ток
схемы . |

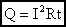

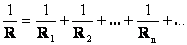
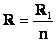
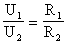 — чем больше сопротивление, тем больше напряжение.
— чем больше сопротивление, тем больше напряжение.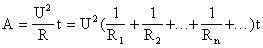 .
.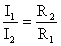 — чем больше сопротивление, тем меньше сила тока.
— чем больше сопротивление, тем меньше сила тока.