Репетитор-онлайн — подготовка к ЦТ
Пример 11. Шесть одинаковых резисторов по 20 Ом каждый и два конденсатора с электроемкостями 15 и 25 мкФ соединены в цепь так, как показано на рисунке. К концам участка подключают источник с ЭДС, равной 0,23 кВ, и внутренним сопротивлением 3,5 Ом. Найти разность потенциалов между обкладками второго конденсатора.
Решение. Между точками A и Б ток не протекает, так как между этими точками в схему включены конденсаторы. Для определения разности потенциалов между указанными точками упростим схему, исключив из рассмотрения участок АБ.
На рис. а показана схема упрощенной цепи.
Ток течет через резисторы R 1, R 2, R 3, R 4 и R 6, соединенные последовательно. Общее сопротивление такой цепи:
R общ = R 1 + R 2 + R 3 + R 4 + R 6
где R 1 = R 2 = R 3 = R 4 = R 6 = R.
Сила тока I определяется законом Ома для полной цепи:
I=ℰRобщ+r=ℰ5R+r,
где ℰ — ЭДС источника тока, ℰ = 0,23 кВ; r — внутреннее сопротивление источника тока, r = 3,5 Ом; R общ — общее сопротивление цепи, R общ = 5R.
Рассчитаем падение напряжения между точками А и Б.
Между точками А и Б находятся резисторы сопротивлениями R 2, R 3 и R 4, соединенные между собой последовательно, как показано на рис. б.
Их общее сопротивление
R
общ1 = R
Падение напряжения на указанных резисторах определяется формулой
U АБ = IR общ1,
или в явном виде, —
UАБ=3ℰR5R+r.
Между точками А и Б включена батарея конденсаторов C 1 и C 2, соединенных между собой последовательно, как показано на рис. в.
Их общая электроемкость
Cобщ=C1C2C1+C2,
где C 1 — электроемкость первого конденсатора, C 1 = 15 мкФ; C 2 — электроемкость второго конденсатора, C 2 = 25 мкФ.
Разность потенциалов на обкладках батареи:
Uобщ=qCобщ,
где q — заряд на обкладках каждого из конденсаторов (совпадает с зарядом батареи при последовательном соединении конденсаторов), q = = C 1U 1 = C 2U 2; U 1 — разность потенциалов между обкладками первого конденсатора; U 2 — разность потенциалов между обкладками второго конденсатора (искомая величина).
В явном виде разность потенциалов между обкладками конденсаторов определяется формулой
Uобщ=C2U2Cобщ=(C1+C2)U2C1.
Падение напряжения на резисторах между точками А и Б совпадает с разностью потенциалов на батарее конденсаторов, подключенной к указанным точкам:
U АБ = U общ.
Данное равенство, записанное в явном виде
3ℰR5R+r=(C1+C2)U2C1,
позволяет получить выражение для искомой величины:
U2=3ℰRC1(5R+r)(C1+C2).
Произведем вычисление:
U2=3⋅0,23⋅103⋅20⋅15⋅10−6(5⋅20+3,5)(15+25)⋅10−6=50 В.
Между обкладками второго конденсатора разность потенциалов составляет 50 В.
vedy.by
Закон Ома для неоднородного участка цепи
Один из основных законов электродинамики был открыт в 1826 г. немецким учителем физики Георгом Омом. Он установил, что сила тока в проводнике пропорциональна разности потенциалов:
.
| Георг Симон Ом (1787 – 1854) – немецкий физик. В 1826 г. Ом открыл свой основной закон электрической цепи. Этот закон не сразу нашел признание в науке, а лишь после того, как Э. X. Ленц, Б. С. Якоби, К. Гаусс, Г. Кирхгоф и другие ученые положили его в основу своих исследований. В 1881 г. на Международном конгрессе электриков именем Ома была названа единица электрического сопротивления (Ом). Последние годы своей жизни Ом посвятил исследованиям в области акустики. Акустический закон Ома был положен затем немецким ученым Г. Гельмгольцем в основу резонансной теории слуха. Ом вел также исследования и в области оптики и кристаллооптики. |
Рассмотрим неоднородный участок цепи, участок, содержащий источник ЭДС (т.е. участок, где действуют неэлектрические силы). Напряженность поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил, т.е.
Величина, численно равная работе по переносу единичного положительного заряда суммарным полем кулоновских и сторонних сил на участке цепи (1 – 2), называется напряжением
Рис. 7.4
| . | (7.5.1) |
т.к. , или , тогда
| (7.5.2) |
Напряжение на концах участка цепи совпадает с разностью потенциалов только в случае, если на этом участке нет ЭДС, т.е. на однородном участке цепи. Запишем обобщенный закон Ома для участка цепи содержащей источник ЭДС:
| (7.5.3) |
Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для пассивных участков (не содержащих ЭДС), так и для активных.
В электротехнике часто используют термин падение напряжения – изменение напряжения вследствие переноса заряда через сопротивление
| (7.5.4) |
В замкнутой цепи: ;
или
где ; r – внутреннее сопротивление активного участка цепи (рис. 7.5).
Тогда закон Ома для замкнутого участка цепи, содержащего источник ЭДС запишется в виде
| (7.5.5) |
Рис. 7.5
7.5. Закон Ома для неоднородного участка цепи.
Рис. 3 Перемещение заряда на этих участках возможно лишь с помощью сил
неэлектрического происхождения (сторонних сил): химические процессы, диффузия носителей заряда, вихревые электрические поля. Аналогия: насос, качающий воду в водонапорную башню, действует за счет негравитационных сил (электромотор).
Сторонние силы можно характеризовать работой, которую они совершают над перемещающимися зарядами.
Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой. Э.Д.С. действующей в цепи.
ε = | A |
| Дж | =[В]; |
| |
| ; |
|
| (7.4.1) | ||
q |
| |||||
|
| Кл |
|
| ||
Ясно, что размерность Э.Д.С. совпадает с размерностью потенциала, т.е. измеряется в вольтах.
Стороннюю силу, действующую на заряд, можно представить в виде:
r | Fст. = Eст.q , | (7.4.2) |
Eст. | – напряженность поля сторонних сил. |
|
| Работа сторонних сил на участке 1 – 2 |
|
| 2 r | r | 2 | r | r |
| ||
A12 | = ∫Fст.dl | = q∫Eст.dl , | (7.4.3) | |||||
| 1 |
| 1 |
|
|
| ||
|
|
|
| A12 |
| 2 r | r |
|
тогда | ε12 | = |
|
| = ∫Eст.dl . | (7.4.4) | ||
| q | |||||||
|
|
|
| 1 |
|
| ||
Для замкнутой цепи: ε = ∑εi | = ∫Eст.dl . | (7.4.5) | ||||||
Циркуляция вектора напряженности сторонних сил равна Э.Д.С., действующей в замкнутой цепи (алгебраической сумме Э.Д.С.).
При этом необходимо помнить, что поле сторонних сил не является потенциальным, и к нему нельзя применять термин – разность потенциалов или напряжение.
Рассмотрим неоднородный участок цепи, участок, содержащий источник Э.Д.С.
(т.е. участок, – где действуют неэлектрические силы). Напряженность E поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил, т.е.
E = Eq +Eст. .
67

Величина, численно равная работе по переносу единичного положительного заряда суммарным полем кулоновских и сторонних сил на участке цепи (1 – 2), называется напряжением на этом участке U12 (Рис. 4)
| Рис. 4 |
|
| ||
| 2 r r | 2 | r | r |
|
| U12 = ∫Eq dl + | ∫Eст.dl ; | (7.5.1) | ||
| 1 | 1 |
|
|
|
| 2 | r | r |
|
|
т. к. | Eq dl = −dφ и ∫Eq dl | = φ1 −φ2 ; | (7.5.2) | ||
| 1 |
|
|
|
|
тогда | U12 = (φ1 – φ2) + ε12 | (7.5.3) | |||
Напряжение на концах участка цепи совпадает с разностью потенциалов только в | |||||
случае, если на этом участке нет Э.Д.С., т.е. на однородном участке цепи. |
| ||||
| I·R12 = (φ1 – φ2) + ε12 | (7.5.4) | |||
Это обобщенный закон Ома. Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для пассивных участков (не содержащих Э.Д.С.), так и для активных.
В электротехнике часто используют термин падения напряжения – изменение напряжения вследствие переноса заряда через сопротивление
U = I R |
| (7.5.5) | |||
В замкнутой цепи: φ1 = φ2 ; |
|
| ε |
| |
I RΣ= ε | или | I = | |||
R∑ | |||||
|
|
| |||
Где R Σ =R + r; r – внутреннее сопротивление активного участка цепи (Рис. 5).
Тогда закон Ома для замкнутого участка цепи, содержащего Э.Д.С. запишется в
виде:
I = | ε | ; | (7.5.6) | |
R + r | ||||
|
|
|
Рис. 5
7.6. Закон Ома в дифференциальной форме.
Закон Ома в интегральной форме для однородного участка цепи (не содержащего Э.Д.С.)
I = U | ; |
| (7.6.1) | ||
R |
|
|
| ||
Для однородного линейного проводника выразим R через ρ |
| ||||
R = ρ | l |
| ; | (7.6.2) | |
S | |||||
|
|
| |||
ρ – удельное объемное сопротивление; [ρ] = [Ом м].
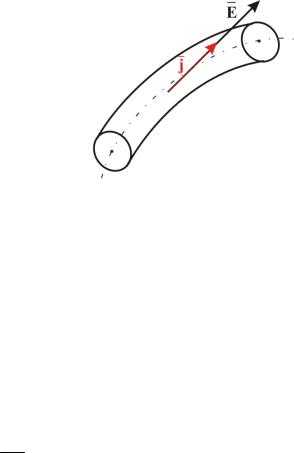
Найдем связь между j и E в бесконечно малом объеме проводника – закон Ома в
дифференциальной форме.
В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов (Рис.6) движутся в направлении действия силы, т.е. плотность тока
j ↑↑ E , следовательно, векторы коллинеарны.
|
|
|
|
|
|
| Рис. 6 |
|
| |||||||
|
|
|
| I = | U |
| = |
| Edl |
| = | EdS | ; | |||
|
|
|
| R |
| ρ |
| dl |
| ρ | ||||||
|
|
|
|
| r | dS |
| |||||||||
|
|
|
|
|
|
|
|
|
| |||||||
| dI |
| 1 |
|
|
|
|
| 1 r |
|
| |||||
А мы знаем что: j = |
| = |
| E , т.е. | j = |
|
|
| E j или |
| ||||||
dS | ρ |
| ρ |
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
| j = σE |
|
|
|
|
|
|
| (7.6.3) | ||||
это запись закона Ома в дифференциальной форме.
Здесь σ – удельная электропроводность. Размерность j – [ Oм−1 м−1 ]; Плотность тока можно выразить через заряд, n и vrдр. .
j = envrдр.
r
обозначим: b = vEдр. , то vrдр. = bE ;
j = enbE ,
а если σ = enb,
где n – число пар ионов, b – расстояние. j = jE
– закон Ома в дифференциальной форме.

7.7. Работа и мощность тока. Закон Джоуля — Ленца.
Рассмотрим произвольный участок цепи, к концам которого приложено напряжение U. За время dt через каждое сечение проводника проходит заряд
dq = I dt | (7.7.1) |
При этом силы электрического поля, действующего на данном участке совершают | |
работу: |
|
dA = U dq = U I dt | (7.7.2) |
Разделив работу на время, получим выражение для мощности: |
|
N = dA =UI | (7.7.3) |
dt |
|
Полезно вспомнить и другие формулы для мощности и работы:
| N = RI2 | (7.7.4) |
| A = RI2t | (7.7.5) |
| В 1841г. Английский физик Джеймс Джоуль и русский физик | |
| Эмилий Ленц установили закон теплового действия электрического | |
| тока. |
|
| ДЖОУЛЬ Джеймс Пресскотт (Рис. 6) |
|
| (24.12.1818 – 11. 10.1889) – английский физик, один |
|
| из первооткрывателей закона сохранения энергии. |
|
| Первые уроки по физике ему давал Дж. Дальтон, под |
|
| влиянием которого Джоуль начал свои эксперименты. |
|
| Работы посвящены электромагнетизму, кинетической |
|
Рис. 6 | теории газов. |
|
ЛЕНЦ Эмилий Христианович (Рис. 7) (24.2.1804 |
| |
|
| |
– 10.2.1865) – русский физик. Основные работы в области |
| |
электромагнетизма. В 1833 установил правило определения | Рис. 7 | |
электродвижущей силы индукции (закон Ленца), а в 1842 (независимо | ||
от Дж. Джоуля) – закон теплового действия электрического тока (закон Джоуля — Ленца). Открыл обратимость электрических машин. Изучал зависимость сопротивление металлов от температуры. Работы относятся также к геофизике.
Независимо друг от друга Джоуль и Ленц показали, что при протекании тока в проводнике выделится количество теплоты:
Q = RI2t | (7.7.6) | |
Если ток изменяется со временем, то |
| |
Q = ∫2 | RI 2dt ; | (7.7.7) |
1
(7.7.7) это закон Джоуля – Ленца в интегральной форме.
Следовательно, нагревание происходит за счет работы, совершаемой силами поля над зарядом (мощность выделения тепла N = RI2).
Получим закон Джоуля – Ленца в дифференциальной форме.
dQ = RI 2dt = ρ dSdl (jdS )2 dt = ρj2dldSdt = ρj2dldSdt = ρj2 dVdt,
где dV = dl dS – элементарный объем. |
|
Количество тепла выделяющегося в единицу объема в единицу времени |
|
Q уд = ρj2 | (7.7.8) |
studfile.net
Закон Ома для неоднородного участка цепи
В простейшем варианте для расчета электрических параметров подразумевают воздействие кулоновских сил, которые обеспечивают перемещение зарядов. Закон Ома для неоднородного участка цепи позволяет учесть дополнительные факторы. Его применение помогает повысить точность вычислений.
Закон Ома для участка цепи
Неоднородный участок цепи постоянного тока
Определение основных параметров и процессов:
- перемещение зарядов (q) характеризуется плотностью, которая зависит от площади поперечного сечения (S) и силы тока;
- при концентрации (n) можно подсчитать количество единичных зарядов (q0), перемещенных за единицу времени;
- эту величину можно изобразить в виде цилиндрического участка проводника с объемом (V):
q = q0*n*V.
Если подключить клеммы аккумулятора к проводнику, источник питания разрядится. Для длительного поддержания процесса перемещения зарядов можно создать замкнутый в кольцо путь. Однако и в этом случае свободный дрейф электронов ограничивают совместные столкновения, противодействие зарядов молекулярной решетки материала. Чтобы компенсировать сопротивление, необходимо приложение дополнительных «сторонних» сил.
Пример неоднородного участка цепи
Рисунок демонстрирует факторы, которые следует принять во внимание. Для вычисления напряженности в любой точке этой схемы нужно суммировать векторные составляющие Eq и Est (кулоновских и сторонних сил, соответственно). Приведенный закон Ома для неоднородного участка определяет, что сила тока (I12) = напряжение на данном участке (U12) / полное электрическое сопротивление (R).
Чтобы перенести единичный заряд q из точки «1» в точку «2», необходимо выполнить работу A12. Для этого понадобится создание определенной разницы потенциалов (ϕ1- ϕ2). Источник постоянного тока создает электродвижущую силу (ЭДС), которая способна переместить заряд по цепи. Общее напряжение будет содержать сумму перечисленных сил.
Ниже приведены формулы, характеризующие рассмотренный пример:
- A12/q = ϕ1 – ϕ2;
- Ast/q = E12;
- U = A12/q + Ast/q = ϕ1 – ϕ2 + E12;
- I = (ϕ1 – ϕ2 + E12)/ R.
Интегральный вариант представления рассматриваемых процессов даст аналогичный результат.
К сведению. При выполнении расчетов следует учитывать действительную полярность источника постоянного тока. В зависимости от подключения соответствующая ЭДС будет способствовать или препятствовать перемещению заряда.
Следующий пример демонстрирует решение практической задачи. Необходимо рассчитать ток в цепи, которая составлена из источника питания с ЭДС=40V и проводки с электрическим сопротивлением R=5Ом. На выходе измерены потенциалы:
ϕ1= 20V; ϕ2=10V.
Подставив значения в формулу, можно получить нужный результат:
(20-10+40)/5 = +10А.
Знак «плюс» означает, что ток идет по направлению от точки «1» к «2».
Если рассматривать процесс в дифференциальной форме, можно представить «облако», созданное из определенного количества (N) зарядов. Оно перемещается в проводнике с определенной скоростью дрейфа (Vдр). На него действуют три вида сил:
- кулоновские – Fкул;
- сторонние – Fc;
- сопротивления кристаллической решетки – Fсп.
Последний показатель будет зависеть от особенностей материала. Он может выражаться удельной проводимостью. Вектор плотности тока будет равен сумме векторов ЭДС (кулоновской и сторонней природы), деленной на удельное сопротивление.
Закон Ома для замкнутой цепи
В реальной ситуации следует учитывать электрические сопротивления нагрузки (Rн) и самого источника питания (Rи). Классическую формулу дополняют следующим образом:
I = E/(Rн+Rи).
Если в рассмотренный выше пример добавить Rи=1Ом, получится I = (ϕ1 – ϕ2 + E12)/(Rн+Rи) = (20-10+40)/(5+1) = +8,33А. Видно уменьшение силы тока в цепи, обусловленное увеличением общего электрического сопротивления. Чтобы компенсировать потери для подключения более мощной нагрузки, необходимо увеличить ЭДС источника.
Классическая формулировка
Для участка цепи без источника ЭДС достаточно использовать классический закон Ома:
I (сила тока) = U (напряжение) /R (электрическое сопротивление).
Данное соотношение было установлено экспериментальным путем в начале 19 века. В названии сохранена фамилия немецкого ученого, который сделал открытие. Напряжение определяют по разнице потенциалов на концах проводника:
U = ϕ1 – ϕ2.
Элементарные вычисления показывают взаимные зависимости перечисленных параметров:
- I1 = 24/6 = 4А;
- I2 = 60/6 = 10А.
Увеличив разницу потенциалов, при неизменном сопротивлении получают большую силу тока:
I2 > I1.
Чтобы уменьшить ток до нужного уровня, при работе с определенным источником питания изменяют сопротивление:
- I1 = 24/4 = 6А;
- I2 = 24/12 = 2А.
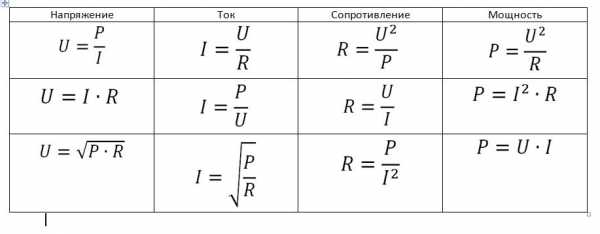
Основные формулы
Для запоминания правил пользуются такой картинкой. Чтобы вычислить определенный параметр, закрывают соответствующий сегмент. Взаимное расположение оставшихся компонентов условно изобразит необходимую формулу.
Ток, напряжение и сопротивление
Эта картинка наглядно демонстрирует взаимное влияние тех основных электрических параметров. С ее помощью можно пояснить особенности практического применения на примере типового проекта домашней сети питания.
В современных жилых объектах часто используют кондиционеры, духовые шкафы, другую технику с большой мощностью потребления. Для нормального функционирования требуется увеличивать ток, потому что напряжение ограничено стандартами. Повышающие трансформаторы в данном случае не пригодятся, так как серийные изделия рассчитаны на подключение к сети 220 (380) V.
При увеличении силы тока понадобятся проводники с достаточно большим поперечным сечением. В противном случае концентрация зарядов на единицу объема повысится до критичной величины. Воздействие на кристаллическую решетку повысит температуру металла вплоть до механического разрушения проводки.
Чтобы исключить проблемы, кроме кабельной продукции, тщательно выбирают защитные автоматы. Для создания проекта электроснабжения и перечня подходящих функциональных компонентов пользуются представленными выше формулами.
Видео
amperof.ru
22) Закон Ома для однородного и неоднородного участка цепи.
Законы Ома.
Закон Ома для однородного участка цепи.
Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении.
где U — напряжение на участке, R — сопротивление участка.
Закон Ома для произвольного участка цепи, содержащего источник постоянного тока.
где φ1 — φ2 + ε = U напряжение на заданном участке цепи, R — электрическое сопротивление заданного участка цепи.
Закон Ома для полной цепи.
Сила тока в полной цепи равна отношению электродвижущей силы источника к сумме сопротивлений внешнего и внутреннего участка цепи.
где R — электрическое сопротивление внешнего участка цепи, r — электрическое сопротивление внутреннего участка цепи.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
it-iatu.ru
Закон Ома для электрической цепи
 Электрический ток, как и любое другое физическое явление подчиняется определенным законам. Так, в 1826 году, Георг Ом вывел эмпирический закон, который способен объяснить зависимость силы тока, напряжения, а также особенностей проводника в электроцепи. В дальнейшем вносились определенные изменения, сам закон Ома для электрической цепи модифицировался, и на данный момент ученые его интерпретируют в четырех вариантах, которые мы и рассмотрим.
Электрический ток, как и любое другое физическое явление подчиняется определенным законам. Так, в 1826 году, Георг Ом вывел эмпирический закон, который способен объяснить зависимость силы тока, напряжения, а также особенностей проводника в электроцепи. В дальнейшем вносились определенные изменения, сам закон Ома для электрической цепи модифицировался, и на данный момент ученые его интерпретируют в четырех вариантах, которые мы и рассмотрим.
В ходе практических исследований, на их базе, ученый смог определить зависимость силы тока и напряжения от специфики проводника, по которому протекает ток. Если быть точнее, то каждый материал имеет определенное сопротивление и на определенном участке цепи, сила тока вычисляется отношением напряжения и сопротивления.
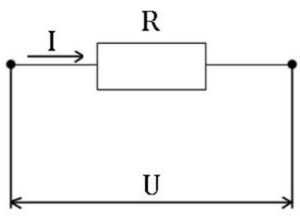
I = U/ R,
где I – сила тока, U – напряжение, R – сопротивление проводника.
Фактически, этот закон аналогичен прохождению воды по трубам: чем больше диаметр трубы и напор, тем больше ее выльется в конечной точке.
Закон Ома для замкнутой цепи
Подобная интерпретация подразумевает наличие источника питания, а также проводника, по которому протекает ток. В этом случае, помимо сопротивления на отдельно взятом участке следует учитывать и то, которое возникает в ИП. Учитывая эти факторы, можно сказать, что сила тока будет равна отношению электродвижущей силы к сумме сопротивлений.
I = E/ Rвн+r,
где Е – ЭДС, Rвн – внешнее сопротивление, а r соответственно внутреннее.
Закон Ома для замкнутой цепи можно объяснить доступным языком. Электродвижущая сила по определению должна полноценно обеспечивать постоянную разницу потенциалов, и эта сила может иметь неприродное происхождение: химическое, если в качестве источника используется батарейка или механическая, в случае подключения к электрической цепи генератора. При подключении медной проволоки с идентичным сечением к батарейке и аккумулятору. Эффект должен быть таким, что по этому проводнику, в котором сопротивление практически отсутствует, должен пойти ток с величиной, стремящейся к бесконечности. Однако этого не происходит и разница в показателях будет существенной, а во втором случае, проволока и вовсе может перегореть. Именно поэтому в расчет берется внутреннее сопротивление источника питания, чтобы описать подобное явление.
Закон ома для неоднородного участка цепи
Перед тем, как записать формулу для подобной интерпретации закона, следует разобраться в таких понятиях, как линейные и нелинейные участки цепи.
Если сопротивление никаким образом не зависит от тока и подаваемого напряжения, то с ростом второго параметра, первый будет прямо пропорционально возрастать и наоборот, то есть зависимость можно описать прямой линией. Подобная зависимость относится к линейным участкам цепи и сопротивление имеет аналогичное название.
Однако вышеизложенный вариант считается идеальным и его можно смоделировать лишь в идеальных условиях, что фактически невозможно, ведь, как минимум, окружающая среда вносит свои коррективы. В этом случае, рост напряжения не будет прямо пропорциональным силе тока и на графике зависимость будет изображаться в виде кривой.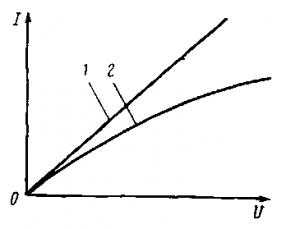
На рисунке изображено два графика, первый из которых описывает линейную зависимость, а второй нелинейную.
Чтобы отчетливо понимать разницу между этими понятиями, рассмотрим принцип работы обычной электрической лампы накаливания. При прохождении тока по нити, температура в значительной степени повышается, что приводит к заметному росту сопротивления. Соответственно, при возрастании напряжения, сила тока будет увеличиваться медленнее, то есть не линейно.
Примечание: в некоторых ситуациях, некоторыми внешними факторами пренебрегают по причине того, что они очень незначительны и в числовом эквиваленте никоим образом не могут повлиять на общую картину. Это значит, что нелинейная зависимость на графике фактически совпадает с линейной.
Учитывая вышесказанное, можно установить следующую зависимость:
I = U/ R = (f1 – f2) + E/ R,
Где f1 и f2 – потенциалы (соответственно f1 – f2 называется разницей потенциалов), E – ЭДС неоднородного участка цепи, а R – суммарное сопротивление на этом же участке.
Нужно упомянуть и о том, что электродвижущая сила не всегда в этом случае будет иметь положительное значение. Если направление тока источника будет аналогичным с направлением в электрической сети, протонов будет больше, чем электронов (положительных и отрицательных частиц), то в этом случае величина E будет иметь значение со знаком «+», в иной ситуации, этот параметр будет со знаком «-».
Закон Ома для переменного тока
Если в электроцепи имеется емкость или инертность, то этот факт следует однозначно учитывать при расчётах силы тока. Они имеют собственные показатели сопротивления, что приводит к ситуации, которая будет иметь переменный характер. В случае Закона Ома для переменного тока формула записывается следующим образом:
I = U/ Z, где
I – сила тока, U – напряжение, а Z – суммарное значение сопротивления на всех участках электрической цепи (этот параметр именуется еще, как импеданс).
Как говорилось изначально, закон Ома считается эмпирическим. Это обозначает то, что он может не всегда работать и выполнять вычисления на его основе не представляется возможным. Подобная ситуация может сложиться в нескольких случаях:
- в ситуации, когда электросеть имеет высокую частоту и электромагнитное поле может сильно изменяться за короткие промежутки времени;
- при наличии проводников, которые обладают свойствами сверхпроводимости, расположенных в условиях низких температурных показателей;
- при перегреве проводника под воздействием проходящего по нему тока, отношение напряжения и сопротивления может носить переменный, неоднородный характер;
- если проводник (диэлектрик) находится под высоким напряжением;
- светодиодных лампах;
- в полупроводниках и аналогичных устройствах.
На основе этого закона, можно произвести вывод некоторых формул математическим путем. С их помощью можно производить разнообразные расчеты.
Поделиться ссылкой:
Похожее
uelektrika.ru
Закон Ома в интегральной форме
Для того, чтобы перейти к интегральной форме записи закона Ома для участка проводника, на котором действуют две силы, введем понятие линии тока.
Линия тока – кривая, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. В этом случае вектор плотности находится из соотношения:
где τ ⃗ – единичный вектор касательной к линии тока.
Предположим, что удельное сопротивление (r) и напряженность поля движущих сил (E ⃗) на поперечном сечении проводника однородны, т.к. E ⃗ однородна, то j ⃗ так же однородная величина. Возьмем произвольное значение поперечного сечения цепи – S. Тогда:
, а значитПоследнее равенство до множим на dl (элементарное перемещение вдоль вектора плотности тока):
где- dφ – элементарный сброс потенциала электростатического поля,
- dε – элементарная работа сторонних сил по перемещению единичного положительного заряда (ЭДС).
Учитывая, что ρ/S dl=dR (элементарное сопротивление), запишем закон Ома в интегральной форме:
Закон Ома в интегральной форме для неоднородного участка цепи
Проинтегрируем получившееся соотношение на конкретном участке цепи постоянного тока между поперечными сечениями S1 и S2:
интегральный закон Ома для участка цепи
где:
- – сопротивление участка,
- – работа сторонних сил на перемещении единичного положительного заряда по данному участку цепи ЭДС участка,
- – работа электростатических сил на перемещении единичного положительного заряда по данному участку цепи (напряжение участка),
- – абсолютная величина работы сил сопротивления на перемещении единичного положительного заряда по данному участку цепи (падение напряжения участка).
Запишем значение напряжения при постоянном токе:
Отсюда запишем закон Ома:
Таким образом закон Ома в интегральной форме – это закон изменения механической энергии единичного положительного заряда на этом участке. В арифметическом виде этот закон можно записать так:
Решение задач
Какой будет плотность тока в металлическом проводнике с удельным сопротивлением ρ постоянного сечения, имеющем длину l, если напряжение, которое приложено к проводу равно U?
| Дано: | Решение: |
|---|---|
|
| Дано: | Решение: |
|---|---|
|
|
zakon-oma.ru