Правила Кирхгофа — Википедия

Пра́вила Кирхго́фа (часто в технической литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.

Решения систем линейных уравнений, составленных на основе правил Кирхгофа, позволяют найти все токи и напряжения в электрических цепях постоянного, переменного и квазистационарного тока^[1].

Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.

Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений и, соответственно, при решении этой системы найти значения токов на всех ветвях цепи и все межузловые напряжения.

Сформулированы Густавом Кирхгофом в 1845 году^[2].

Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.

Определения[править | править код]

Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R₁, I₁ есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин

замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило[править | править код]

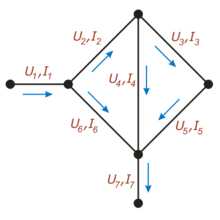
Сколько тока втекает в узел, столько из него и вытекает.
i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.

∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило[править | править код]

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}

для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Особенности составления уравнений для расчёта токов и напряжений[править | править код]

Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.

• Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
• Перед тем, как составить уравнения, нужно произвольно выбрать:
  • положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
  • положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
• Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
• При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
• В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.

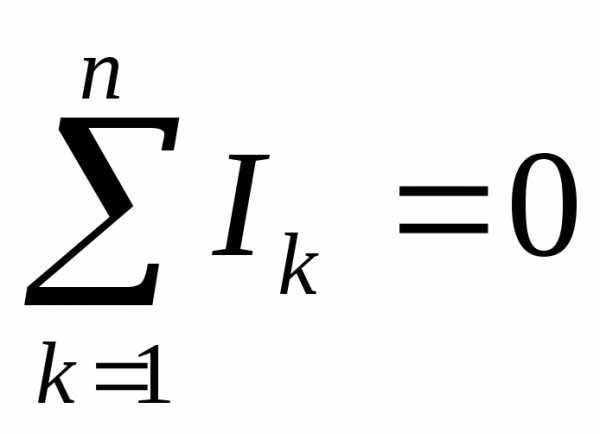На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)

Количество узлов: 3.

p−1=2{\displaystyle p-1=2}

Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.

m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}

Количество контуров: 2.

Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:

{I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть

методом контурных токов.

В соответствии со вторым правилом, справедливы соотношения:

{U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}

Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Первое правило Кирхгофа может быть сформулировано в матричном виде. Именно, пусть электрическая цепь состоит из n{\displaystyle n} узлов. Составим матрицу A={aij}i,j=1n{\displaystyle A=\{a_{ij}\}_{i,j=1}^{n}}, где aij{\displaystyle a_{ij}} при i≠j{\displaystyle i\neq j} есть проводимость ветви, соединяющеей узлы с номерами i{\displaystyle i} и j{\displaystyle j} (если они не соединены, можно мысленно соединить их ветвью нулевой проводимости). Величины aii{\displaystyle a_{ii}} положим равными ∑i=1, i≠jn(−aij){\displaystyle \sum _{i=1,~i\neq j}^{n}(-a_{ij})}. Пусть U{\displaystyle U} — потенциал, который мы рассматриваем как функцию, определённую на множестве узлов (или, что то же самое, вектор u=(U1,U2,…,Un){\displaystyle \mathbf {u} =(U_{1},U_{2},\dots ,U_{n})} в n{\displaystyle n}-мерном пространстве Rn{\displaystyle \mathbb {R} ^{n}}). Тогда по определению проводимости имеем Iij=aij(Uj−Ui){\displaystyle I_{ij}=a_{ij}(U_{j}-U_{i})}, где Iij{\displaystyle I_{ij}} — ток в ветви, идущей из вершины i{\displaystyle i} в вершину j{\displaystyle j}. Стало быть, первое правило Кирхгофа для j{\displaystyle j}-того узла можно записать как ∑i=1, i≠jnIij=∑i=1, i≠jnaij(Uj−Ui)=0{\displaystyle \sum _{i=1,~i\neq j}^{n}I_{ij}=\sum _{i=1,~i\neq j}^{n}a_{ij}(U_{j}-U_{i})=0}, или же ∑i=1, i≠jnaijUj+(∑i=1, i≠jn(−aij))Ui=0{\displaystyle \sum _{i=1,~i\neq j}^{n}a_{ij}U_{j}+\left(\sum _{i=1,~i\neq j}^{n}(-a_{ij})\right)U_{i}=0}, или же, учитывая определение диагональных элементов матрицы, как ∑i=1naijUj=0{\displaystyle \sum _{i=1}^{n}a_{ij}U_{j}=0}. В левой части равенства легко узнать координату произведения матрицы

ru.wikipedia.org

первый и второй закон для тока и напряжения

В статье мы расскажем про законы Кирхгофа с иллюстрацией и формулой. Первый и второй закон Густава Кирхгофа.

Вступление

Закон Ома является одним из самых фундаментальных законов электрической науки, но из-за своей простоты он может быть не очень полезен при решении вопросов, касающихся сложных электрических цепей. Закон Кирхгофа, сформулированный немецким физиком Густавом Кирхгофом (1824-1887) в 1847 году, представляет собой инструмент для анализа как простых, так и очень сложных электрических цепей. Эти законы позволяют определить значения и направление токов, протекающих по электрической цепи, а также разность потенциалов (напряжений) между выбранной парой точек в цепи. В основном они являются законами сохранения заряда и электрической энергии применительно к электрическим цепям и описываются следующим образом.

Первый закон Кирхгофа для тока

Также известный под другими именами, такими как Закон Кирхгофа для тока, это закон сохранения заряда. В нем просто говорится, что в любой точке или соединении в электрической цепи общая величина тока, поступающего в это соединение, равна общей величине тока, который покидает это соединение.

Предположим, что есть электрическая цепь, которая имеет точку, обозначенную на рисунке 1, показанном ниже. Точка соединения действует как точка встречи для четырех проводников, каждый из которых проводит ток в направлении, указанном черными наконечниками стрел. Согласно закону Кирхгофа общая сумма тока, входящего в соединение, должна быть равна току, выходящему из него. Это может быть математически представлено следующим образом

Ia = Ib + Ic + Id

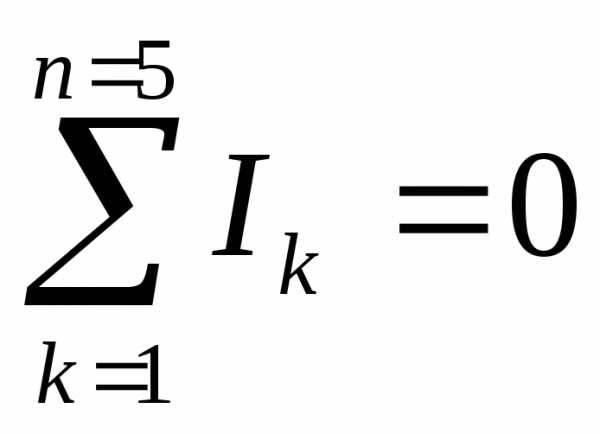
Где I — ток в каждом из проводников a, b, c и d соответственно.

В этой точке также следует отметить, что конденсатор представляет собой устройство, которое используется для накопления заряда в виде электростатической силы в диэлектрическом материале, окруженном пластинами проводника с обеих сторон. Есть некоторые исключения из первого правила Кирхгофа, если конденсатор присутствовал в каком-либо из узлов, но лучше не вдаваться в такие детали на этом базовом уровне. Следовательно, для всех практических целей в других ситуациях применяется закон Кирхгофа.

Первый закон Кирхгофа — применение

Чтобы продемонстрировать, как правильно применять первый закон Кирхгофа, мы будем использовать простой пример. На рисунке ниже показана электрическая цепь, состоящая из превосходного источника электродвижущей силы и двух резисторов с сопротивлениями R₁ и R₂.

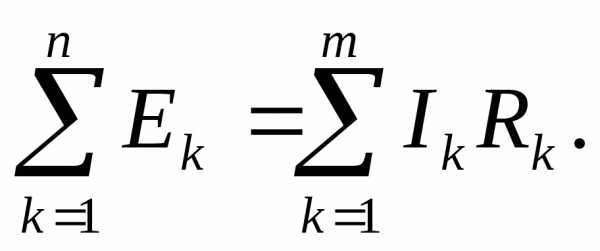Простая электрическая цепь, состоящая из двух узлов (точки B и D), трех ветвей, соединяющих узлы — левого (BAD), центрального (BD) и правого (BCD) и трех ячеек, образующих комбинацию ветвей, образующих замкнутый контур — слева (BADB), справа (BCDB) и большое ушко (ABCDA).

Ток интенсивности I, исходящий из источника ЭДС, имеет то же значение в левой ветви (BAD), ток I ₁ — в средней ветви (BD), а ток I ₂ — в правой ветви (BCD). Сосредоточим внимание на узле B: электрический заряд поступает в этот узел от источника ЭДС вместе с током I и течет с токами I ₁ и I ₂ , протекающими через резисторы R ₁ и R ₂соответственно, Общий заряд в узле B не изменяется, поэтому в соответствии с первым законом Кирхгофа сумма токов, протекающих в этот узел, должна быть равна сумме токов, протекающих из этого узла, которые мы можем записать так: 

I=I ₁ + I ₂

Точно такое же выражение, как и выше для узла B, получаем узел D. В узел D влияют токи I ₁ и I ₂ , и ток протекает с интенсивностью I, являющейся суммой этих двух токов: 

I ₁ + I ₂ = I

чтобы вычислить, сколько стоят значения этих токов, мы будем использовать второй закон Кирхгофа.

Второй закон Кирхгофа для напряжения

Алгебраическая сумма потенциальных изменений в замкнутой электрической цепи равна нулю.

Этот закон применяется, когда используется напряжениями вместо тока в отличие от первого закона и, следовательно, также известен как Закон Кирхгофа для напряжения. В нем говорится, что в замкнутой цепи алгебраическая сумма произведений токов и сопротивлений всех проводников плюс алгебраическая сумма ЭДС равна нулю. Пожалуйста, обратите внимание на слово «алгебраическая», которое просто означает, что значение имеет не только количество этих токов и напряжений, но и их направление. Это приводит нас к следующему вопросу, касающемуся определения знака напряжений и тока в замкнутой цепи, который объясняется следующим образом.

Напряжение — в случае ЭДС батареи повышение напряжения обозначается знаком + ve, а падение напряжения — знаком -ve. Этот знак не зависит от направления тока в этой конкретной ветви. Напротив, падение ИК-сопротивления на резисторе зависит исключительно от направления тока независимо от любой ЭДС, присутствующей в ветви.

Ток — выбор направления тока для целей расчета с использованием закона Кирхгофа в основном является делом удобства и может осуществляться как по часовой стрелке, так и против часовой стрелки, НО после выбора направления его необходимо придерживаться, в противном случае это приведет к путанице и неправильному расчеты.

Второй закон Кирхгофа — применение

Теперь давайте поговорим о практическом применении второго закона Кирхгофа, а именно об определении токов I , I ₁ и I _2, протекающих через электрическую цепь, показанную на рисунке выше. Предположим, что ЭДС источника составляет ε = 12 В, а сопротивление (сопротивление) резисторов равно R ₁ = 10 Ом и R _2.= 20 Ом. Для начала давайте проанализируем ситуацию еще раз: источник ЭДС «прокачивает» электрические заряды между отрицательным и положительным полюсами. Направление движения этих носителей и, следовательно, направление тока определяется стрелкой, направленной от отрицательного полюса к положительному полюсу, поэтому в случае нашей схемы это по часовой стрелке. Этот ток, обозначенный I , после подачи на узел B делится на ток I ₁ , который протекает через резистор R _1, и на ток I ₂ , который протекает через резистор R ₂, Эти резисторы соединены параллельно, то есть их начало и конец соединены вместе с помощью одних и тех же проводов, к которым одинаковая разность потенциалов равна ЭДС источника ε. Чтобы упростить эту схему, мы заменим резисторы R ₁ и R ₂ эквивалентным резистором R ₁₂ , что позволит нам определить ток I, генерируемый источником ЭДС (определение этого тока возможно, потому что этот ток не разветвляется на другие токи в цепи),

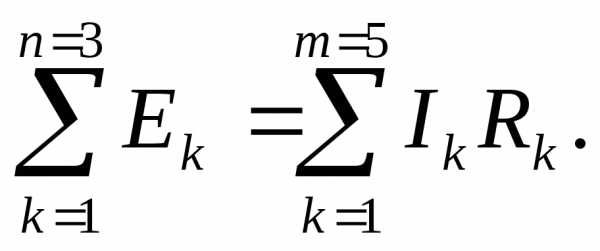Эквивалентная электрическая цепь, в которой резисторы R ₁ и R ₂ параллельно заменены резистором R ₁₂.

Сопротивление R заменителя резистора ₁₂ стоимость , используя следующее уравнение (см последовательно и параллельно, соединяющие резисторы ) 

Следующим шагом является применение второй закон Кирхгофа к такой упрощенной электрической цепи. Правильное использование этого закона состоит в обходе всего контура в направлении или против часовой стрелки (выбор за нами), уделяя пристальное внимание потенциальным изменениям, встречающимся на этом пути. На данный момент мы должны сохранить два основных правила для анализа электрических цепей:

1. Когда мы анализируем цепь в направлении протекания тока, изменение потенциала источника ЭДС составляет + ε. В противном случае, т.е. когда мы анализируем цепь в направлении, противоположном направлению потока тока, изменение потенциала источника равно -ε.
2. Когда мы анализируем цепь в направлении протекания тока, изменение потенциала при прохождении через резистор составляет -IR. В противном случае потенциальное изменение равно + IR.

Изменение потенциала при прохождении через резистор, равное ± ИК, вытекает из определения электрического сопротивления: R = U / I. Отметим, что согласно рисунку выше положительный полюс источника ЭДС подключен к верхнему концу резистора R _12, а отрицательный полюс — к его нижнему концу. Это означает, что верхний конец резистора имеет более высокий потенциал, чем его нижний конец, и поэтому изменение потенциала при прохождении через резистор от конца с более высоким потенциалом к ​​концу с более низким потенциалом равно -IR (имеется уменьшение потенциала). В противном случае, то есть, когда движение нагрузок происходит от отрицательного полюса к положительному полюсу, изменение потенциала равно + IR, поскольку происходит увеличение электрического потенциала.

Используя эту информацию, давайте воспользуемся вторым законом Кирхгофа, минуя цепь в направлении потока тока, то есть по часовой стрелке, начиная с точки A: 

начиная и заканчивая анализ цепи в точке A, мы, конечно, должны получить тот же потенциал V _A (мы вернемся к этому та же точка), что подтверждается приведенной выше формулой. После уменьшения величины V _A мы получим: 

где из преобразования из тока я получаю: 

(полностью равное значение тока, которое я получу после прохождения этой цепи в направлении против часовой стрелки) 

Зная значение тока I мы можем вернуться к первой цепи с двумя параллельно подключенными резисторами, чтобы вычислить ток I₁ и I₂. Записав второе право Кирхгофа для левой сетки (BADB) и начав анализ в точке A, двигаясь в направлении потока тока, мы получим: 

где из преобразования мы получим значение тока I ₁ : 

чтобы найти ток I _{2, мы} будем использовать первый закон Кирхгофа. Мы знаем, что ток интенсивности I после подачи в узел B делится на ток I ₁ и I ₂ , таким образом:

meanders.ru

Первый и второй законы Кирхгофа

В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта http://www.sxemotehnika.ru.

 

Пример сложной электрической цепи вы можете посмотреть на рисунке 1.

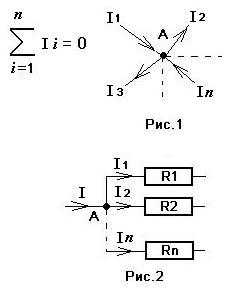
Рисунок 1. Сложная электрическая цепь.

Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.

Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.

Первый закон Кирхгофа

Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.

Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.

Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.

Здесь ток I₁— ток, втекающий в узел , а токи I₂ и I₃ — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:

I₁ = I₂ + I₃  (1)

Что бы подтвердить справедливость формулировки №2, перенесем токи I₂ и I₃ в левую часть выражения (1), тем самым получим:

I₁ — I₂ — I₃ = 0   (2)

Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.

Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).

Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.

Второй закон Кирхгофа.

Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.

Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».

— напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».

Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.

E₁— Е₂ = -UR₁ — UR₂ или E₁ = Е₂ — UR₁ — UR₂   (3)

Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).

Расчеты электрических цепей с помощью законов Кирхгофа.

Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.

Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E₁=12 в и E₂=5 в , с внутренним сопротивлением источников r₁=r₂=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

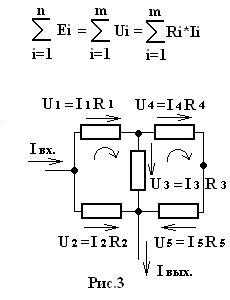
Рисунок 4. Пример расчета сложной электрической цепи.

Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:

I = I₁ + I₂,

так как I₁ и I₂ втекают в узел А, а ток I вытекает из него.

Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.

Для внешнего контура:

E₁-E₂ = Ur₁ – Ur₂ или E₁-E₂ = I₁*r₁ – I₂*r₂

Для внутреннего левого контура:

E₁ = Ur₁ + UR или E₁ = I₁*r₁ + I*R

Итак, у нас получилась система их трех уравнений с тремя неизвестными:

I = I₁ + I₂;

E

1-E₂ = I₁*r₁ – I₂*r₂;

E₁ = I₁*r₁ + I*R.

Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:

I = I₁ + I₂;

7 = 0,1I₁ – 0,1I₂;

12 = 0,1I₁ +2I.

Далее из первого и второго уравнения выразим ток I₂

I₂=I — I₁;

I₂ = I₁ – 70;

12 = 0,1I₁ + 2I.

Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:

I — I₁= I₁ – 70;

12 = 0,1I₁ + 2I.

Выражаем из первого уравнения значение I

I = 2I₁– 70;

И подставляем его значение во второе уравнение

12 = 0,1I₁ + 2(2I₁ – 70).

Решаем полученное уравнение

12 = 0,1I₁ + 4I₁ – 140.

12 + 140= 4,1I₁

I₁=152/4,1

I₁=37,073 (А)

Теперь в выражение I = 2I₁– 70 подставим значение

I₁=37,073 (А) и получим:

I = 2*37,073 – 70 = 4,146 А

Ну, а согласно первому закона Кирхгофа ток I₂=I — I₁

I₂=4,146 — 37,073 = -32,927

Знак «минус» для тока I₂ означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I₂ вытекает из узла А.

Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.

Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.

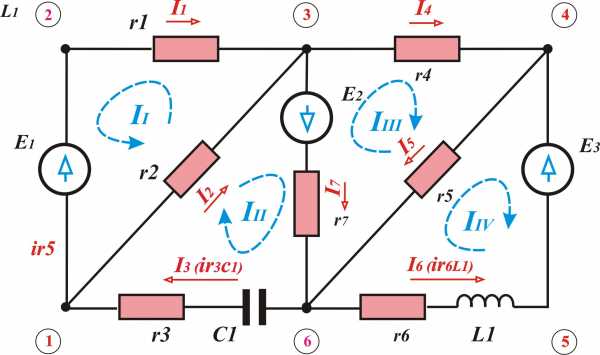 Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.

Для закрепления результатата предлагаю посмотреть подготовленное мной видео:

www.sxemotehnika.ru

Законы Кирхгофа для электрической и магнитной цепи

Для расчетов задач по электротехнике в физике есть ряд правил, часто используют первый и второй закон Кирхгофа, а также закон Ома. Немецкий ученый Густав Кирхгоф имел достижения не только в физике, но и в химии, теоретической механике, термодинамике. В электротехнике используется закономерность, которую он установил для электрической цепи, из двух соотношений. Законы Кирхгофа (также их называют правилами) описывают распределение токов в узлах и падений напряжений на элементах контура. Далее мы попытаемся объяснить простым языком, как применять соотношения Кирхгофа для решения задач.

Первый закон Кирхгофа

Определение первого закона звучит так: «Алгебраическая сума токов, протекающих через узел, равна нулю». Можно сказать немного в другой форме: «Сколько токов втекло в узел, столько же и вытекло, что говорит о постоянстве тока».

Узлом цепи называют точку соединения трех и больше ветвей. Токи в таком случае распределяются пропорционально сопротивлениям каждой ветви.

I₁=I₂+I₃

Такая форма записи справедлива для цепей постоянного тока. Если использовать первый закон Кирхгофа для цепи переменного тока, то используются мгновенные значения напряжений, обозначаются буквой İ и записывается в комплексной форме, а метод расчета остаётся прежним:

Комплексная форма учитывает и активную и реактивную составляющие.

Второй закон Кирхгофа

Если первый описывает распределение токов в ветвях, то второй закон Кирхгофа звучит так: «Сумма падений напряжений в контуре равна сумме всех ЭДС». Простыми словами формулировка звучит так: «ЭДС, приложенное к участку цепи, распределится по элементам данной цепи пропорционально сопротивлениям, т.е. по закону Ома».

Тогда как для переменного тока это звучит так: «Сумма амплитуд комплексных ЭДС равняется сумме комплексных падений напряжений на элементах».

Z – это полное сопротивление или комплексное сопротивление, в него входит и резистивная часть и реактивная (индуктивность и ёмкость), которая зависит от частоты переменного тока (в постоянном токе есть только активное сопротивление). Ниже представлены формулы комплексного сопротивления конденсатора и индуктивности:

Вот картинка, иллюстрирующая вышесказанное:

Тогда:

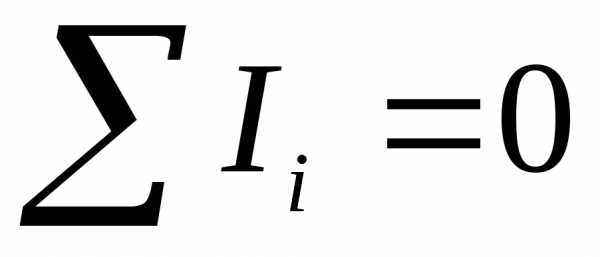
Методы расчетов по первому и второму законам Кирхгофа

Давайте приступим к применению на практике теоретического материала. Чтобы правильно расставить знаки в уравнениях, нужно выбрать направление обхода контура. Посмотрите на схему:

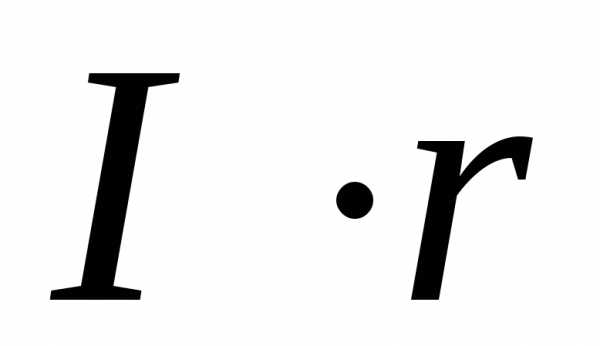
Предлагаем выбрать направление по часовой стрелке и обозначить его на рисунке:

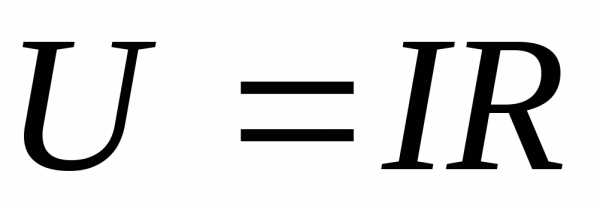
Штрих-пунктирной линией обозначено, как идти по контуру при составлении уравнений.

Следующий шаг – составить уравнения по законам Кирхгофа. Используем сначала второй. Знаки расставляем так: перед электродвижущей силой ставится минус, если она направлена против движения часовой стрелки (выбранное нами в предыдущем шаге направление), тогда для ЭДС направленного по часовой стрелке – ставим минус. Составляем для каждого контура с учетом знаков.

Для первого смотрим направление ЭДС, оно совпадает со штрих-пунтирной линией, ставим E1 плюс E2:

Для второго:

Для третьего:

Знаки у IR (напряжения) зависят от направлением контурных токов. Здесь правило знаков такое же, как и в предыдущем случае.

IR пишется с положительным знаком, если ток протекает в сторону направления обхода контура. А со знаком «–», если ток течет против направления обхода контура.

Направление обхода контура — это условная величина. Нужна она только для расстановки знаков в уравнениях, выбирается произвольно и на правильность расчётов не влияет. В отдельных случаях неудачно выбранное направление обхода может усложнить расчёт, но это не критично.

Рассмотрим еще одну цепь:

Здесь целых четыре источника ЭДС, но порядок расчета тот же, сначала выбираем направление для составления уравнений.

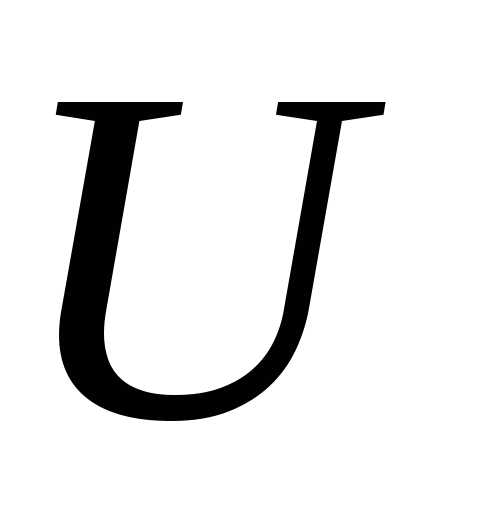
Теперь нужно составить уравнения согласно первому закону Кирхгофа. Для первого узла (слева на схеме цифра 1):

I₃ втекает, а I₁, I₄ вытекает, отсюда и знаки. Для второго:

Для третьего:

Вопрос: «Узла четыре, а уравнения всего три, почему?». Дело в том, что число уравнений первого правила Кирхгофа равно:

N_{уравнений}=n_узлов-1

Т.е. уравнений всего на 1 меньше, чем узлов, т.к. этого достаточно, чтобы описать токи во всех ветвях, советую еще раз подняться к схеме и проверить, все ли токи записаны в уравнениях.

Теперь перейдем к построению уравнений по второму правилу. Для первого контура:

Для второго контура:

Для третьего контура:

Если подставить значения реальных напряжений и сопротивлений, тогда выяснится, что первый и второй законы справедливы и выполняются. Это простые примеры, на практике приходится решать гораздо более объёмные задачи.

Вывод. Главное при расчётах с помощью первого и второго законов Кирхгофа – соблюдения правила составления уравнений, т.е. учитывать направления протекания токов и обхода контура для правильной расстановки знаков для каждого элемента цепи.

Законы Кирхгофа для магнитной цепи

В электротехнике также важны и расчёты магнитных цепей, оба закона нашли своё применение и здесь. Суть остаётся той же, но вид и величины изменяются, давайте рассмотрим этот вопрос подробнее. Сначала нужно разобраться с понятиями.

Магнитодвижущая сила (МДС) определяется произведением количества витков катушки, на ток через неё:

F=w*I

Магнитное напряжение – это произведение напряженности магнитного поля на ток, через участок, измеряется в Амперах:

U_m=H*I

Или магнитный поток через магнитное сопротивление:

U_m=Ф*R_m

L – средняя длина участка, μ_r и μ₀ – относительная и абсолютная магнитная проницаемость.

Проводя аналогии запишем первый закон Кирхгофа для магнитной цепи:

То есть сумма всех магнитных потоков через узел равна нулю. Вы заметили, что звучит почти так же, как и для электрической цепи?

Тогда второй закон Кирхгофа звучит, как «Сумма МДС в магнитном контуре равна сумме U_{M­­ ­­}(магнитных напряжений).

Магнитный поток равен:

Для переменного магнитного поля:

Он зависит только от напряжения на обмотке, но не от параметров магнитной цепи.

В качестве примера рассмотрим такой контур:

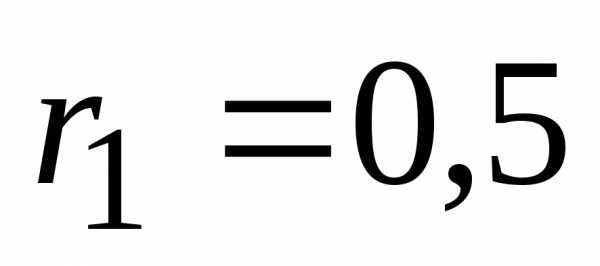
Тогда для ABCD получится такая формула:

Для контуров с воздушным зазором выполняются следующие соотношения:

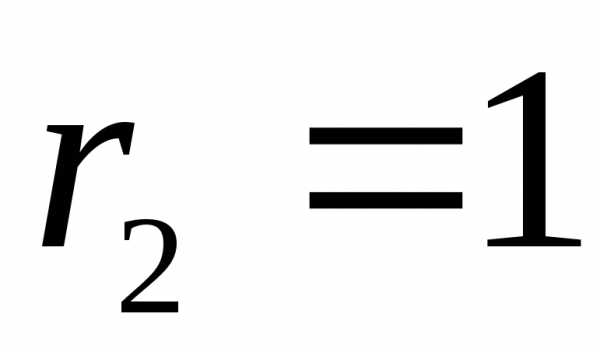
Сопротивление магнитопровода:

А сопротивление воздушного зазора (справа на сердечнике):

Где S — это площадь сердечника.

Чтобы полностью усвоить материал и наглядно просмотреть некоторые нюансы использования правил, рекомендуем ознакомиться с лекциями, которые предоставлены на видео:

Открытия Густава Кирхгофа внесли весомый вклад в развитие науки, в особенности электротехники. С их помощью довольно просто рассчитать любой электрический или магнитный контур, токи в нём и напряжения. Надеемся, теперь вам стали более понятны правила Кирхгофа для электрической и магнитной цепи.

Похожие материалы:

samelectrik.ru

Второй закон Кирхгофа

Господа, всем привет!

Сегодня мы рассмотрим второй закон Кирхгофа. Он чуть сложнее, чем первый закон Кирхгофа, который мы уже рассматривали ранее, поэтому я сперва дам общую формулировку, а потом мы постараемся аккуратно разобраться во всем этом деле. 

Итак, второй закон Кирхгофа гласит, что алгебраическая сумма ЭДС, действующих в контуре равна алгебраической сумме падений напряжения в ветвях контура. Может быть сложновато для восприятия, если вы читаете это в первый раз, не спорю. Но сейчас попробуем разобраться более детально во всем этом. Для начала давайте определим, что же такое контур электрической цепи, где эти самые ЭДС действуют. Пожалуй, это тот случай, когда проще нарисовать картинку, чем объяснять словами. Взглянем на рисунок 1.

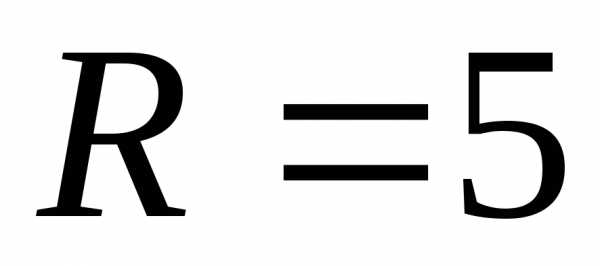
Рисунок 1 – Контура в схеме

На нем мы можем видеть три контура: я обозначил их красным, оранжевым и синим цветами. То есть контур –  это некоторая замкнутая часть электрической цепи, состоящая из нескольких ветвей.

То есть что говорит второй закон Кирхгофа? У нас есть большая и сложная электрическая схема. В ней много различных контуров. Будем рассматривать подробно один из этих контуров, любой на выбор. И вот если мы в этом контуре сложим ЭДС всех источников, какие там есть, то их сумма будет равна сумме падений напряжения на всех сопротивлениях этого контура. И это верно для любого контура в нашей схеме. Довольно интересный факт. И если про первый закон Кирхгофа можно говорить, что он интуитивно очевиден, то здесь, вообще говоря, это не совсем так. А поскольку он не очевиден на первый взгляд, тем больше поводов показать его верность математически.

Господа, прошу обратить внимание на рисунок 2. На нем изображен один из контуров какой-то сложной электрической схемы.

Рисунок 2 – Контур схемы

Почему он именно такой, можете вы спросить? Да просто так! Я рисовал его так, как подскажет фантазия в тот момент. Вы можете смело заявить, что ваша фантазия лучше и нарисовать какой-либо другой контур с другими компонентами. Потом повторите все действия, которые я буду производить над этим контуром, и в конечном счете у вас должен получиться точно такой же результат, как и у меня.

Первым делом давайте зададимся направлением обхода контура. Это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода контура у нас по часовой стрелке, и я показал его синей стрелочкой на рисунке 2.

Следующим шагом нам надо расставить предполагаемое направление токов в каждой ветви. Тут опять же все целиком отдается вашей фантазии. На данном этапе можно рисовать любое направление токов. Если мы угадали – отлично, если нет – в конце всех расчетов получим ток с другим знаком. Я расставил на рисунке 2 все токи черными стрелками и рядом с ними подписал их величины (I₁…I₄).

А теперь внимание, господа. Пришло время вспомнить то выражение, ради получения которого я написал предыдущую статью. На всякий случай, если вдруг кто забыл, напоминаю его

Оно означает, что если потенциалы на концах ветви равны φ₁ и φ₂, то их разность равна ЭДС источника в ветви минус произведение тока в ветви на сопротивление в ветви.

Применим это выражение для каждой ветви нашего контура, изображенного на рисунке 2. Поскольку у нас в контуре четыре ветви, то всего мы получим четыре уравнения. Резонный вопрос – а как быть со знаками при записи этих уравнений? Правила тут два.

• Если направление работы источника напряжения совпадает с направлением обхода контура, то берем его со знаком плюс. Если не совпадает – со знаком минус. Совсем просто: если стрелка в источнике напряжения совпадает со стрелкой обхода, то Е в уравнении пишется без изменения знака, если стрелки в разные стороны – то надо поставить минус перед E.
• Если направление тока, которое мы сами выбрали чуть раньше, совпадает с направлением обхода, то в нашем уравнении перед произведением тока на сопротивление так и остается знак минус. Если они направлены в разные стороны, то знак минус меняем на плюс.

Пользуясь этими простыми правилами, запишем уравнения для каждой ветви.

Очевидно, что если в цепи нет источника ЭДС, то у нас не будет первого слагаемого в правой части. А если нет сопротивления, то не будет второго слагаемого в правой части. Собственно, это и видно из составленных уравнений.

Господа, надеюсь вы помните, что с уравнениями в одной системе можно творить всякие интересные штуки? Например, можно все их сложить между собой (правые и левые части). Легко заметить, что при сложении всех этих четырех уравнений в левой части будет нолик, то есть все потенциалы волшебным образом самоликвидируются. Сделаем это! Получим

А теперь давайте перенесем все слагаемые с ЭДС в одну сторону, а с током и сопротивлением – в другую. Имеем

А имеем мы, собственно, второй закон Кирхгофа. Все честно, как я и писал в начале – алгебраическая сумма ЭДС, действующих в контуре равна алгебраической сумме падений напряжения в ветвях контура. Надеюсь, господа, после статьи про закон Ома у вас не возникает вопросов, почему произведение тока на сопротивление – это падение напряжения на сопротивлении?  Если возникает – срочно, очень срочно, прямо сейчас пройдитесь по этой ссылке и разрешите эти вопросы!

А что же все-таки тут понимается под словом алгебраическая сумма? Это словосочетание нам уже встречалось. Это значит, что складывать надо с учетом знака. А как выбирать правильно этот самый знак? Господа, взгляните еще разок на рисунок 2. Там у нас задано направление обхода контура и направление токов. Все это мы выбирали (я бы даже сказал придумывали) сами. Ну и направление работы источника еще видно по его графическому изображению.

Так вот, если направление работы источника ЭДС совпадает с направлением обхода контура, то мы ему приписываем знак плюс, а если не совпадает – минус. Аналогично и для правой части. Если направление тока совпадет с направлением обхода, то мы пишем произведение тока на сопротивление со знаком плюс. Иначе – со знаком минус.

Специально для труЪ-математиков привожу запись второго закона Кирхгофа с использованием хитрых значков суммирования. Вне всякого сомнения, если вы будете использовать эту запись, то произведете впечатление человека, который шарит в теме!

Здесь у нас N источников c ЭДС E_i и M ветвей с сопротивлениями R_j и токами I_j. Разумеется, суммирование идет все так же с учетом знаков.

Может возникнуть резонный вопрос: «Как же так? Получается, я сам все придумываю: и направление обхода, и направление токов и это значит, что знак может получиться любой. Поверну стрелку тока в другую сторону и сразу знак у слагаемого поменяется! Но ведь в реальной схеме токи всегда текут в своем направлении вне зависимости от того, что я там нарисую на листочке! Какое-то противоречие!» Господа, вопрос весьма справедливый. Но предлагаю разобраться в нем в следующей статье. Сохраним некоторую интригу на текущий момент, как принято во всяких этих сериальчиках . А сейчас – спасибо, что прочитали статью, огромной вам всем удачи, и пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

myelectronix.ru

Законы Кирхгофа

Законы Кирхгофа – правила, которые показывают, как соотносятся токи и напряжения в электрических цепях. Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.

Первый закон Кирхгофа – сумма токов сходящихся в узле равна нулю. 

Давайте разбираться. Узел это точка, соединяющая ветви. Ветвью называется участок цепи между узлами. На рисунке видно, что ток i входит в узел, а из узла выходят токи i₁ и i₂. Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i₁-i₂=0. Ток i как бы растекается на два тока поменьше и равен сумме токов i₁ и i₂ i=i₁+i₂. Но если бы, например, ток i₂ входил в узел, тогда бы ток I определялся как i=i₁-i₂. Важно учитывать знаки при составлении уравнения.

Первый закон Кирхгофа это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла, т.е. электрический заряд в узле не накапливается и не исчезает.

Второй закон Кирхгофа – алгебраическая сумма ЭДС, действующая в замкнутом контуре, равна алгебраической сумме падений напряжения в этом контуре. 

 Напряжение выражено как произведение тока на сопротивление (по закону Ома). 

 

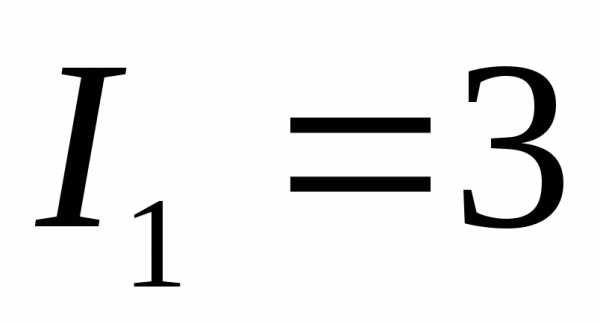
В этом законе тоже существуют свои правила по применению. Для начала нужно задать стрелкой направление обхода контура. Затем просуммировать ЭДС и напряжения соответственно, беря со знаком плюс, если величина совпадает с направлением обхода и минус, если не совпадает. Составим уравнение по второму закону Кирхгофа, для нашей схемы. Смотрим на нашу стрелку, E₂ и Е₃ совпадают с ней по направлению, значит знак плюс, а Е₁ направлено в противоположную сторону, значит знак минус. Теперь смотрим на напряжения, ток I₁ совпадает по направлению со стрелкой, а токи I₂ и I₃ направлены противоположно. Следовательно:

              -E₁+E₂+E₃=I₁R₁-I₂R₂-I₃R₃

На основании законов Кирхгофа составлены методы анализа цепей переменного синусоидального тока. Метод контурных токов – метод основанный на применении второго закона Кирхгофа и метод узловых потенциалов основанный на применении первого закона Кирхгофа.

Читайте также — Примеры решения задач на законы Кирхгофа

Просмотров: 11560

electroandi.ru

Закон кирхгофа для электрической цепи для чайников

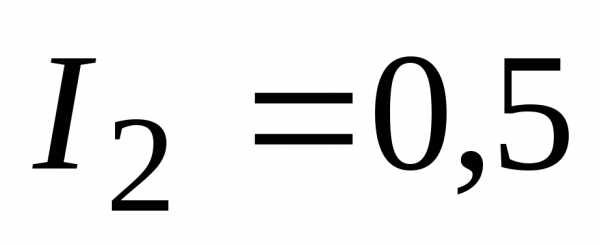
По каждому проводнику, составляющему электрическую цепь, течет ток. В точке, где проводники сходятся, называемой узлом, справедливо правило: ток суммарный, подтекающий к нему, равняется сумме, оттекающих.

{ ArticleToC: enabled=yes }

Законы кирхгофа

Другими словами – сколько зарядов подтечет к этой точке за единицу времени, столько же оттечет. Если принять, что приходящий будет «+», а оттекающий – «-», то суммарная его величина будет нулевой.

Это и есть Первый закон кирхгофа для электрической цепи. Смысл его в том состоит, что заряд не накапливается.

Закон Второй, применим к цепи электрической разветвленной.

Эти универсальные законы Кирхгофа применяют очень широко, поскольку позволяют решить множество задач. Большим их достоинство считают простую и понятную всем формулировку, несложные вычисления.

История

Пополнил ряды немецких ученых Кирхгоф в девятнадцатом столетии, когда в стране, находившаяся на пороге революции индустриальной, требовались новейших технологии. Ученые занимались поиском решений, которые могли бы ускорить развитие промышленности.

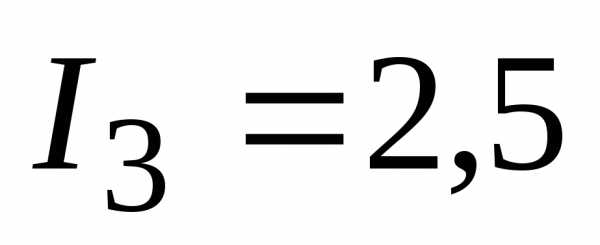
Активно занимались исследованиями в области электричества, поскольку понимали, что в будущем оно будет широко использоваться. Проблема состояла на тот момент не в том, как составлять электрические цепи из возможных элементов, а в проведении математических вычислений. Тут и появились законы, сформулированные физиком. Они очень помогли.

Алгебраическая сумма приходящих к узлам токов и исходящих из него равна нулю. Эта одновременно вытекает из другого закона — постоянства энергии.

К узлу подходят 2 провода, а отходит один. Значение тока, текущего от узла, такое же, как сумма его, протекающего по двум остальным проводникам, т.е. идущим к нему. Правило Кирхгофа объясняет, что, при ином раскладе, накапливался бы заряд, но такого не бывает. Все знают, что всякую сложную цепь легко разделить на отдельные участки.

Но, при этом непросто определить путь, по которому он проходит. Тем более, что на различных участках сопротивления не одинаковы, поэтому и распределение энергии не будет равномерным.

В соответствие со Вторым правилом Кирхгофа, энергия электронов на каждом из замкнутых участков электрической цепи равняется нулю – нулю равняется всегда в таком контуре суммарное значение напряжений. Если бы нарушилось данное правило, энергия электронов при прохождении определенных участков, уменьшалась бы или увеличивалась. Но, этого не наблюдается.

Применение

Таким образом, благодаря этим двум, выдвинутым Кирхгофом утверждениям, установлено зависимость токов от напряжений в разветвленных участках.

Формула Первого закона такова:

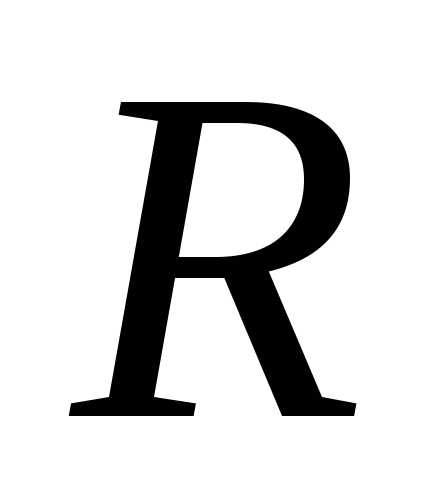
Для схемы, приведенной ниже, справедливо:

I1 — I2 + I3 — I4 + I5 = 0

Плюсовые — это токи, идущие к точке, а те, что выходят из нее «-».

Записывается это так:

• k — количество ЭДС источников;
• m – ветви замкнутого контура;
• Ii,Ri – их сопротивление i-й и ток.

В данной схеме: Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4.

• ЭДС принимается «+» при совпадении ее направления с выбранным направлением обхода.
• При совпадении направления тока и обхода на резисторе, с плюсом будет также напряжение.

Расчет цепи

Способ заключается в умении составления систем уравнений, а также решении их, для нахождения токов в каждой ветви (b), а уже, зная их, умении нахождения величины напряжений.

Проще говоря, количество ветвей совпадать должно с неизвестными величинами в системе. Вначале записывают их, исходя из первого правила: число их идентично с количеством узлов.

Но, независимыми будут (y – 1) выражений. Обеспечивается это выбором, а происходит он так, чтобы разнились они (последующий со смежными) минимум одной ветвью.

Далее, составляются уравнения с использованием второго закона: b — (y — 1) = b — y +1.

Независимым считают контур, содержащий одну (или больше) ветвь, которая в другие не входит.

В качестве примера можно рассмотреть такую схему:

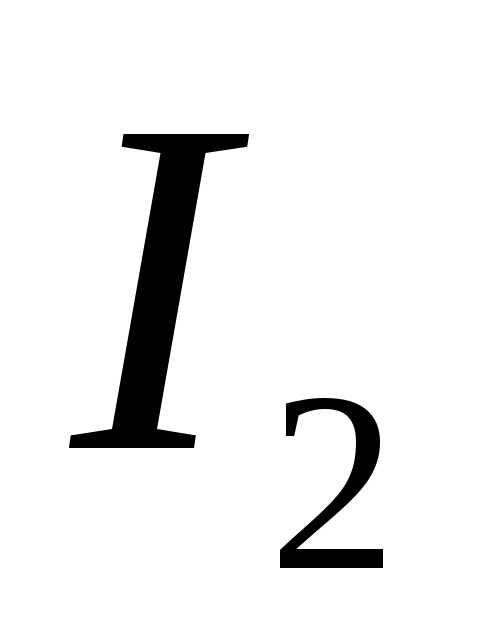
Сдержит она:

узлов – 4;

ветвей –6.

По Первому закону записывают три выражения, т.е. y — 1 = 4 – 1=3.

И столько же на основании Второго, поскольку b — y + 1 = 6 — 4 + 1 = 3.

В ветвях выбирают плюсовое направление и путь обхода (у нас — по стрелке часовой).

Получается:

Осталось относительно токов решить получившуюся систему, понимая, что, когда в процессе решения он получается отрицательным, это свидетельствует о том, что направлен он будет в противоположную сторону.

Правило Кирхгофа применительно к синусоидальным токам

Правила для синусоидального, такие же, как для тока постоянного. Правда, учитываются величины напряжений с комплексными токами.

Первое звучит: «в электрической цепи нулю равна сумма алгебраическая комплексных токов в узле».

Второе правило выглядит так: «алгебраическая сумма ЭДС комплексных в контуре замкнутом равняется сумме алгебраической значений комплексных напряжений, имеющихся на пассивных составляющих данного контура.

Видео: Законы Кирхгофа

motocarrello.ru