Закон кирхгофа 1 и 2 простыми словами

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0

В этом уравнении токи, направленные к узлу, приняты положительными.

Физически первый закон Кирхгофа – это закон непрерывности электрического тока.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветви.

Так, для замкнутого контура схемы (рис. 2 ) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4

Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;

2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа

Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.

Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.

Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b — (y — 1) = b — y +1 .

Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.

Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и шесть ветвей.

Поэтому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3 , также три уравнения.

Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.

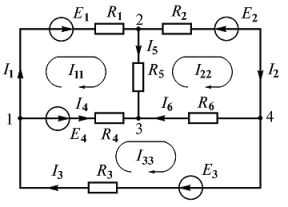
Составляем необходимое число уравнений по первому и второму законам Кирхгофа

Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.
Потенциальная диаграмма – это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях. Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми.

Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.

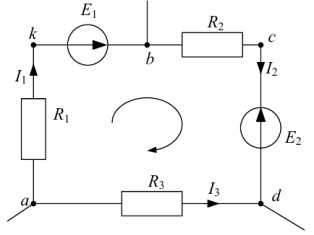
Рис. 4. Контур для построения потенциальной диаграммы

Потенциал любого узла принимаем равным нулю (например, ?а= 0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а — I1R1 , ? b = ? к + Е1, ?с = ? b — I2R2 , ? d = ?c — Е2, ? a = ?d + I3R3 = 0

При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5 ).

Рис. 5. Потенциальная диаграмма

Законы Кирхгофа в комплексной форме

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.

Первый закон Кирхгофа : «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»

Второй закон Кирхгофа : «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».

Законы Кирхгофа (более корректно — правила Киргхгофа) применяются при расчете сложных (разветвленных) электрических цепей. Предлагаю рассмотреть их по очереди и начать, естественно, с первого.

Здесь:

• I i — ток в узле,
• n — число проводников, сходящихся в узле,
• токи, втекающие в узел ( I₁, In ) считаются положительными,
• вытекающие токи ( I₂, I₃ ) — отрицательными.

В таком виде этот закон звучит и выглядит, наверное, очень академично, поэтому предлагаю все несколько упростить.

Нарисуем разветвленную электрическую цепь в более привычном виде (рис.2) и дадим такую формулировку:

Сумма токов втекающих в узел равна сумме токов, вытекающих из узла.

Для этого случая формула первого закона Кирхгофа примет вид: I= I

1+I₂+. +In , что для повседневных вычислений гораздо удобнее.

ВТОРОЙ ЗАКОН КИРХГОФА

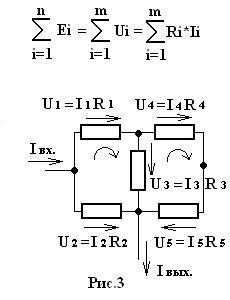Второй закон Кирхгофа определяет зависимость между падениями напряжений и ЭДС в замкнутых контурах и имеет следующий вид (рис.3) и определение:

При отсутствии в контуре ЭДС сумма падений напряжений равна 0.

Теперь несколько пояснений по практическому применению этого правила Кирхгофа:

• поскольку, алгебраическая сумма требует учета знака следует выбрать направление обхода контура ( на рис.3 — по часовой стреклке), токи и напряжения, совпадающие с этим направлением считать положительными, иные — отрицательными. При затруднении в определении направления тока, возьмите произвольное, если в результате вычислений получите результат со знаком «-«, поменяйте выбранное направление на противоположенное.
• для нашего примера можно записать:
  U₁+U₃-U₂=0
  U₄+U₅-U₃=0
• кроме того, руководствуясь первым правилом Кирхгофа :
  I_вх — I₁ — I₂ = 0
  I₁ — I₃ — I₄=0
  I₄ — I₅=0
  I₂ + I₃ + I₅ — I_вых=0 ,

получаем систему из 6 уравнений, полностью описывающую рассматриваемую электрическую цепь.

© 2012-2019 г. Все права защищены.

Все представленные на этом сайте материалы имеют исключительно информационный характер и не могут быть использованы в качестве руководящих и нормативных документов

В статье мы расскажем про законы Кирхгофа с иллюстрацией и формулой. Первый и второй закон Густава Кирхгофа.

Вступление

Закон Ома является одним из самых фундаментальных законов электрической науки, но из-за своей простоты он может быть не очень полезен при решении вопросов, касающихся сложных электрических цепей. Закон Кирхгофа, сформулированный немецким физиком Густавом Кирхгофом (1824-1887) в 1847 году, представляет собой инструмент для анализа как простых, так и очень сложных электрических цепей. Эти законы позволяют определить значения и направление токов, протекающих по электрической цепи, а также разность потенциалов (напряжений) между выбранной парой точек в цепи. В основном они являются законами сохранения заряда и электрической энергии применительно к электрическим цепям и описываются следующим образом.

Первый закон Кирхгофа для тока

Также известный под другими именами, такими как Закон Кирхгофа для тока, это закон сохранения заряда. В нем просто говорится, что в любой точке или соединении в электрической цепи общая величина тока, поступающего в это соединение, равна общей величине тока, который покидает это соединение.

Предположим, что есть электрическая цепь, которая имеет точку, обозначенную на рисунке 1, показанном ниже. Точка соединения действует как точка встречи для четырех проводников, каждый из которых проводит ток в направлении, указанном черными наконечниками стрел. Согласно закону Кирхгофа общая сумма тока, входящего в соединение, должна быть равна току, выходящему из него. Это может быть математически представлено следующим образом

Ia = Ib + Ic + Id

Где I — ток в каждом из проводников a, b, c и d соответственно.

В этой точке также следует отметить, что конденсатор представляет собой устройство, которое используется для накопления заряда в виде электростатической силы в диэлектрическом материале, окруженном пластинами проводника с обеих сторон

. Есть некоторые исключения из первого правила Кирхгофа, если конденсатор присутствовал в каком-либо из узлов, но лучше не вдаваться в такие детали на этом базовом уровне. Следовательно, для всех практических целей в других ситуациях применяется закон Кирхгофа.

Первый закон Кирхгофа — применение

Чтобы продемонстрировать, как правильно применять первый закон Кирхгофа, мы будем использовать простой пример. На рисунке ниже показана электрическая цепь, состоящая из превосходного источника электродвижущей силы и двух резисторов с сопротивлениями R₁ и R₂.

Ток интенсивности I, исходящий из источника ЭДС, имеет то же значение в левой ветви (BAD), ток I ₁ — в средней ветви (BD), а ток I ₂ — в правой ветви (BCD). Сосредоточим внимание на узле B: электрический заряд поступает в этот узел от источника ЭДС вместе с током I и течет с токами I ₁ и I ₂ , протекающими через резисторы R ₁ и R ₂соответственно, Общий заряд в узле B не изменяется, поэтому в соответствии с первым законом Кирхгофа сумма токов, протекающих в этот узел, должна быть равна сумме токов, протекающих из этого узла, которые мы можем записать так:

Точно такое же выражение, как и выше для узла B, получаем узел D. В узел D влияют токи I ₁ и I ₂ , и ток протекает с интенсивностью I, являющейся суммой этих двух токов:

чтобы вычислить, сколько стоят значения этих токов, мы будем использовать второй закон Кирхгофа.

Второй закон Кирхгофа для напряжения

Алгебраическая сумма потенциальных изменений в замкнутой электрической цепи равна нулю.

Этот закон применяется, когда используется напряжениями вместо тока в отличие от первого закона и, следовательно, также известен как Закон Кирхгофа для напряжения. В нем говорится, что в замкнутой цепи алгебраическая сумма произведений токов и сопротивлений всех проводников плюс алгебраическая сумма ЭДС равна нулю. Пожалуйста, обратите внимание на слово «алгебраическая», которое просто означает, что значение имеет не только количество этих токов и напряжений, но и их направление. Это приводит нас к следующему вопросу, касающемуся определения знака напряжений и тока в замкнутой цепи, который объясняется следующим образом.

Напряжение — в случае ЭДС батареи повышение напряжения обозначается знаком + ve, а падение напряжения — знаком -ve. Этот знак не зависит от направления тока в этой конкретной ветви. Напротив, падение ИК-сопротивления на резисторе зависит исключительно от направления тока независимо от любой ЭДС, присутствующей в ветви.

Ток — выбор направления тока для целей расчета с использованием закона Кирхгофа в основном является делом удобства и может осуществляться как по часовой стрелке, так и против часовой стрелки, НО после выбора направления его необходимо придерживаться, в противном случае это приведет к путанице и неправильному расчеты.

Второй закон Кирхгофа — применение

Теперь давайте поговорим о практическом применении второго закона Кирхгофа, а именно об определении токов I , I ₁ и I _2, протекающих через электрическую цепь, показанную на рисунке выше. Предположим, что ЭДС источника составляет ε = 12 В, а сопротивление (сопротивление) резисторов равно R ₁ = 10 Ом и R _2.= 20 Ом. Для начала давайте проанализируем ситуацию еще раз: источник ЭДС «прокачивает» электрические заряды между отрицательным и положительным полюсами. Направление движения этих носителей и, следовательно, направление тока определяется стрелкой, направленной от отрицательного полюса к положительному полюсу, поэтому в случае нашей схемы это по часовой стрелке. Этот ток, обозначенный I , после подачи на узел B делится на ток I ₁ , который протекает через резистор R _1, и на ток I ₂ , который протекает через резистор R ₂, Эти резисторы соединены параллельно, то есть их начало и конец соединены вместе с помощью одних и тех же проводов, к которым одинаковая разность потенциалов равна ЭДС источника ε. Чтобы упростить эту схему, мы заменим резисторы R ₁ и R ₂ эквивалентным резистором R ₁₂ , что позволит нам определить ток I, генерируемый источником ЭДС (определение этого тока возможно, потому что этот ток не разветвляется на другие токи в цепи),

Сопротивление R заменителя резистора ₁₂ стоимость , используя следующее уравнение (см последовательно и параллельно, соединяющие резисторы )

Следующим шагом является применение второй закон Кирхгофа к такой упрощенной электрической цепи. Правильное использование этого закона состоит в обходе всего контура в направлении или против часовой стрелки (выбор за нами), уделяя пристальное внимание потенциальным изменениям, встречающимся на этом пути. На данный момент мы должны сохранить два основных правила для анализа электрических цепей:

1. Когда мы анализируем цепь в направлении протекания тока, изменение потенциала источника ЭДС составляет + ε. В противном случае, т.е. когда мы анализируем цепь в направлении, противоположном направлению потока тока, изменение потенциала источника равно -ε.
2. Когда мы анализируем цепь в направлении протекания тока, изменение потенциала при прохождении через резистор составляет -IR. В противном случае потенциальное изменение равно + IR.

Изменение потенциала при прохождении через резистор, равное ± ИК, вытекает из определения электрического сопротивления: R = U / I. Отметим, что согласно рисунку выше положительный полюс источника ЭДС подключен к верхнему концу резистора R _12, а отрицательный полюс — к его нижнему концу. Это означает, что верхний конец резистора имеет более высокий потенциал, чем его нижний конец, и поэтому изменение потенциала при прохождении через резистор от конца с более высоким потенциалом к ​​концу с более низким потенциалом равно -IR (имеется уменьшение потенциала). В противном случае, то есть, когда движение нагрузок происходит от отрицательного полюса к положительному полюсу, изменение потенциала равно + IR, поскольку происходит увеличение электрического потенциала.

Используя эту информацию, давайте воспользуемся вторым законом Кирхгофа, минуя цепь в направлении потока тока, то есть по часовой стрелке, начиная с точки A:

начиная и заканчивая анализ цепи в точке A, мы, конечно, должны получить тот же потенциал V _A (мы вернемся к этому та же точка), что подтверждается приведенной выше формулой. После уменьшения величины V _A мы получим:

где из преобразования из тока я получаю:

(полностью равное значение тока, которое я получу после прохождения этой цепи в направлении против часовой стрелки)

Зная значение тока I мы можем вернуться к первой цепи с двумя параллельно подключенными резисторами, чтобы вычислить ток I₁ и I₂. Записав второе право Кирхгофа для левой сетки (BADB) и начав анализ в точке A, двигаясь в направлении потока тока, мы получим:

где из преобразования мы получим значение тока I ₁ :

чтобы найти ток I _{2, мы} будем использовать первый закон Кирхгофа. Мы знаем, что ток интенсивности I после подачи в узел B делится на ток I ₁ и I ₂ , таким образом:

Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ

crast.ru

Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Понятия и формулы для электричества и магнетизма.  / / Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения. Поделиться:    Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения. Kirchhoff current (или «first») rule (или «law») & Kirchhohh loop (или «mesh», или «second») rule (или «law»). узлы — точки соединения трёх и более проводников контуры — ЗАМКНУТЫЕ пути из проводников. При этом каждый проводник может входить в несколько контуров. ветви — последовательное соединение элементов между двумя ближайшими узлами Закон токов Кирхгофа (Правило токов Кирхгофа, ЗТК, ПТК, Первый закон Кирхгофа, Первое правило Кирхгофа ). Закон напряжений Кирхгофа (Правило напряжений Кирхгофа, ЗНК, ПТК, Второй закон Кирхгофа, Второе правило Кирхгофа). Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере временной зависимости токов и напряжений. Алгебраическая сумма токов в любой точке любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком)  ΣIi = I1+I2+ …+In = 0   Иными словами, сколько тока втекает в точку цепи ( на прак

dpva.ru

Законы Кирхгофа простыми словами, теория и примеры

Два приема, которые применяют для упрощения процесса составления уравнений, необходимых при расчетах сложных разветвленных цепей постоянного тока называют законами (вернее было бы сказать правилами) Кирхгофа. Прежде чем перейти к самим правила Кирхгофа введем два необходимых определения.

Разветвлёнными цепями названы цепи, которые имеют несколько замкнутых контуров, несколько источников электродвижущей силы (ЭДС).

Узлом разветвлённой цепи называют точку, в которой сходятся три или более проводников с токами.

Первый закон (правило) Кирхгофа, простыми словами

Первое правило Кирхгофа называют правилом узлов, так как оно касается сил токов в узах цепи. Словесно первый закон Кирхгофа формулируют следующим образом: Алгебраическая сумма сил токов в узле равна нулю. В виде формулы это правило запишем как:

   

С каким знаком сила тока будет входить в сумму (1), зависит от произвольного выбора. Но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Пусть все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными. Если направления токов изначально не заданы, то их задают произвольно. Если при расчетах получено, что сила тока отрицательна, значит, что верное направление тока является противоположным тому, которое предполагали.

Первый закон Кирхгофа является следствием закона сохранения заряда. Если в цепи текут только постоянные токи, то нет в этой цепи точек, которые накапливали бы заряд. Иначе токи не были бы постоянными.

Первый закон Кирхгофа дает возможность составить независимое уравнение, при наличии в цепи k узлов.

Второй закон (правило) Кирхгофа, простыми словами

Второй закон Кирхгофа относят к замкнутым контурам, поэтому его называют правилом контуров. Согласно этому правилу суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних ЭДС (), входящих в рассматриваемый контур. В виде формулы второй закон Кирхгофа запишем как:

   

где величину часто называют падением напряжения; N – число рассматриваемых участков избранного контура. При использовании второго правила Кирхгофа важно помнить о направлении обхода контура. Как это делается? Произвольно выберем направление обхода рассматриваемого в задаче контура (по часовой стрелке или против нее). В случае совпадения направления обхода контура с направлением силы тока в рассматриваемом элементе, величина входит в (2) со знаком плюс. ЭДС войдет в сумму правой части выражения (2) со знаком плюс, если при движении вдоль контура, в соответствии с избранным направлением обхода первым мы встречаем отрицательный полюс источника ЭДС.

Используя второе правило Кирхгофа можно получить независимые уравнения для тех контуров цепи, которые не получены наложением уже описанных контуров. Количестов независимых контуров (n) равно:

   

где p – количество ветвей в цепи; k – число узлов.

Количество независимых уравнений, которые дадут оба правила Кирхгофа равно (s):

   

Делаем вывод о том, что число независимых уравнений будет равно числу разных токов в исследуемой цепи.

Второе правило Кирхгофа — следствие закона Ома. В принципе любую цепь можно рассчитать, применяя только закон Ома и закон сохранения заряда. Правила Кирхгофа являются всего лишь упрощающими приемами для решения задач, рассматривающих цепи постоянного тока.

Используя правила Кирхгофа для составления уравнений необходимо внимательно следить за расстановкой знаков токов и ЭДС.

Первое и второе правила Кирхгофа дают метод расчета цепи, то есть используя их можно найти все токи в цепи, если известны все ЭДС и сопротивления, в том числе и внутренние сопротивления источников.

Примеры решения задач

ru.solverbook.com

Первый закон Кирхгофа: определение, формулы, физический смысл

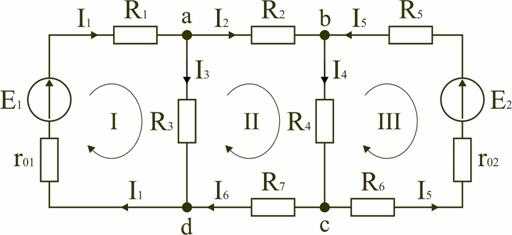
Первый закон Кирхгофа основан на принципе непрерывности и применим к узлу электроцепи.

Первый закон Кирхгофа определяет взаимосвязь между суммой токов, сходящихся в одном узле, и формулируется следующим образом:

Алгебраическая сумма величин токов Ik, сходящихся в любой точке (узле) электроцепи, равна нулю в любой момент времени

∑ Ik = 0,

при этом k — количество ветвей, сходящихся в узле цепи;

Ik – мгновенная величина тока для k-й ветви.

Физически Первый закона Кирхгофа означает: движение электрических зарядов осуществляется таким образом, что ни в одном из участков цепи он не имеет тенденцию к накоплению.

Отсюда, вытекает еще одна формулировка закона: в любом узле электроцепи сумма токов направленных к узлу оказывается равной сумме токов, направленных от этого узла, или:

∑ Ik = ∑ Im,

при этом k — количество ветвей, втекающих в узел;

m- — количество ветвей, вытекающих из узла.

Узлом электрической цепи принято называть точку подключения 3-х и более ветвей. ток принимается со знаком «+», если он втекает в узел, и со знаком «-», если вытекает.

К примеру, рассмотрим баланс токов на примере схемы:

I1 + I2 + I3 – I4 – I5 = 0, либо

I1 + I2 + I3 = I4 + I5.

Очевидным фактом, является то, что формулировка формы записи может иметь различный характер. Существенным является лишь принимаемая договоренность о знаке токов: нельзя использовать разнонаправленное направление в пределах одной электрической цепи для одного или нескольких узлов.

Направление тока для каждой цепи определяют произвольно. При этом нет необходимости стремиться, чтобы для всех узлов использовались токи различных направлений. Также может иметь место ситуация, что в каком-то узле все токи будут направлены от узла или к нему, что тем самым нарушает принцип непрерывности. Но в такой ситуации в процессе определения значений токов один или несколько будут отрицательными, что будет служить признаком об их протекании в противоположном направлении от принятого.

При расчете разветвленных электроцепей используются второй закон Кирхгофа. Они были сформулированы в 1945г. великим физиком 19 в. Густавом Робертом Кирхгофом.

pue8.ru

1.4. Законы Ома и Кирхгофа

1.4. Законы Ома и Кирхгофа

Закон Ома для всей цепи выражает соотношение между электродвижущей силой (ЭДС), сопротивлением и током. Согласно этому закону ток в замкнутой цепи равен ЭДС источника деленной на сопротивление всей цепи:

 

,                                                  (1.19)

где I – ток, протекающий по цепи;

E – ЭДС, генератора, подключенного к электрической цепи;

Rг – сопротивление генератора;

Rц – сопротивление цепи.

Закон Ома для участка цепи. Ток на участке цепи прямо пропорционален напряжению между началом и концом  участка и обратно пропорционален сопротивлению участка. Аналитически закон выражается в следующем виде:

,                                                                  (1.20)

где I – ток, протекающий на участке цепи;

R – сопротивление участка цепи;

U – напряжение на участке цепи.

Обобщенный закон Ома. Сила тока  в контуре цепи прямо пропорциональна алгебраической сумме ЭДС всех источников цепи и обратно пропорциональна арифметической сумме всех активных сопротивлений цепи.

,                                                          (1.21)

где m и n – количество источников и резисторов в контуре цепи.

При алгебраическом суммировании со знаком “плюс” берутся те ЭДС, направление которых совпадает с направлением тока, а со знаком “минус”– те ЭДС, направление которых не совпадает с направлением тока.

Первый закон Кирхгофа. Электрические цепи подразделяют на неразветвленные и разветвленные. На рис. 1.10 представлена простейшая разветвленная цепь.

Рис. 1.10 Схема разветвленной цепи.

Разветвленной называется такая электрическая цепь, в которой ток от какого-либо источника может идти по различным путям и, в которой, следовательно, имеются точки, где сходятся два и более проводников. Эти точки называютузлами. Токи, текущие к узлу считаются имеющими один знак, а от узла – другой.

Учитывая это правило для схемы, изображенной на рис. 1.11,а можно записать

или

.

Для цепи, имеющей n ветвей, сходящихся в одном узле, имеем:

,                                                          (1.22)

т.е. алгебраическая сумма токов ветвей, сходящихся в любом узле, равна

нулю.

Рис. 1.11 Схема поясняющая законы Кирхгофа.

Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.

Второй закон Кирхгофа устанавливает связь между ЭДС, токами и сопротивлениями в любом замкнутом контуре, который можно выделить в рассматриваемой цепи.

В соответствии со вторым законом Кирхгофа алгебраическая сумма ЭДС, действующих в любом контуре разветвленной электрической цепи, равна алгебраической сумме падений напряжений на всех сопротивлениях контура

,                                                  (1.23)

Рассмотрим электрическую цепь, изображенную на рис. 1.11,б. Обозначим стрелкой направление обхода контура. При составлении уравнений будем брать со знаком “плюс” те ЭДС и падения напряжений, направления которых совпадают с направлением обхода контура и со знаком “минус” те, которые направлены против обхода. Для цепи, изображенной на рис. 1.11,б второй закон Кирхгофа запишется в следующем виде:

.

support17.com

2. Второй закон Кирхгофа | 5. Схемы делителей и законы Кирхгофа | Часть1

2. Второй закон Кирхгофа

Второй закон Кирхгофа

Давайте посмотрим на нашу последовательную схему с другой стороны. На этот раз мы пронумеруем все точки схемы, чтобы к ним можно было привязать напряжения:

Если мы подключим вольтметр к точкам 1 и 2 (красный щуп к точке 2, а черный — к точке 1), то он зарегистрирует напряжение +45 В. Обычно дисплей цифрового электроизмерительного прибора знак «+» не показывает, но так как в рамках нашей статьи полярность напряжения имеет очень важное значение, мы будем  показывать положительные числа с этим знаком:

 

 

Когда рядом с напряжением указываются два символа (символы «2-1» в обозначении U_2-1), это означает, что напряжение в первой точке (2) измеряется по отношению ко второй точке (1). Напряжение обозначенное как «U_cd» скажет нам о том, что красный щуп измерительного прибора подсоединяется к точке «с», а черный — к точке «d», то есть это напряжение измеряется в точке «c» относительно точки «d»:

 

 

Если мы теперь возьмем тот же самый вольтметр и измерим напряжения на каждом резисторе цепи, обходя ее по часовой стрелке (подсоединяя при этом красный щуп к первой точке, а черный — ко второй), то получим следующие показания:

 

 

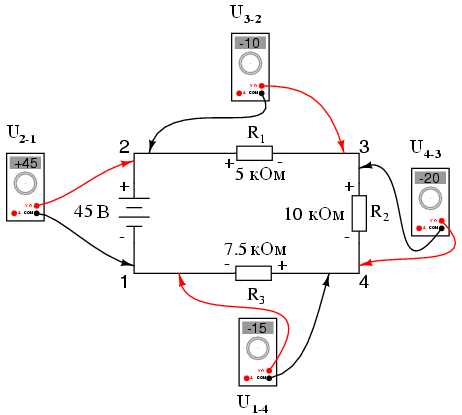
Ранее вы познакомились с одним из принципов последовательной цепи, который гласит что общее напряжение такой цепи складывается из напряжений ее отдельных участков. Но, если при измерении напряжения мы будем учитывать его полярность (математический знак), то пред нами откроется новый аспект этого принципа — суммарное напряжение цепи будет равно нулю:

 

 

Этот принцип известен как Второй Закон Кирхгофа или Закон напряжений Кирхгофа (открыт в 1847 году немецким физиком Густавом Кирхгофом), и гласит он следующее:

«Алгебраическая сумма всех напряжений любой замкнутой цепи должна равняться нулю» 

Здесь под словом «алгебраическая» понимается учет математического знака (полярности) напряжения, а под словом «замкнутой цепи» — понимается последовательный путь, проложенный вокруг этой цепи из одной ее точки к другим точкам, и обратно к первой точке. В приведенном выше примере замкнутая цепь сформирована последовательностью точек 1-2-3-4-1. Не имеет абсолютно никакого значения с какой точки мы начнем и в каком направлении мы будем двигаться; сумма напряжений все равно будет равняться нулю. В качестве еще одного примера можно подсчитать напряжение в последовательности точек 3-2-1-4-3 этой же схемы:

 

 

Все это будет более понятно, если перерисовать нашу последовательную цепь таким образом, чтобы все ее компоненты находились на одной линии:

 

 

Перед вами все та же последовательная цепь, только ее компоненты расположены иным способом. Обратите внимание на полярность напряжений резисторов относительно батареи: напряжение последней отрицательно слева и положительно справа, тогда как напряжения на всех резисторах ориентированы в другую сторону (положительны слева и отрицательны справа). Различия в полярности обусловлены тем, что резисторы сопротивляются потоку электронов, производимому батареей.

На следующем рисунке вы можете увидеть показания цифровых вольтметров на каждом компоненте этой цепи:

 

 

Если мы произведем замеры напряжения на группах компонентов, начиная с левой стороны цепи (с резистора R₁), то увидим, что напряжения складываются алгебраически (к нулевому результату):

 

 

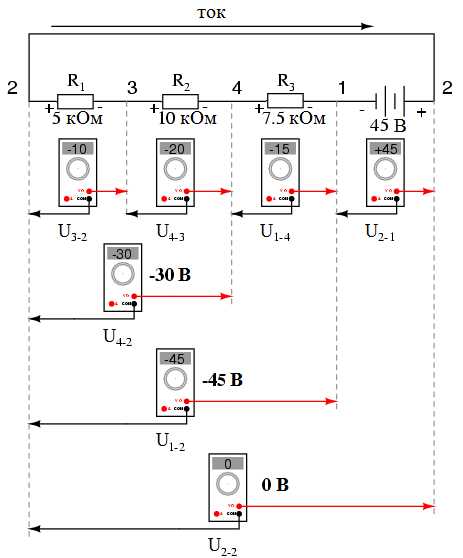
То, что напряжения последовательной цепи складываются, является очевидным фактом, и в этом сложении очень важную роль играет полярность напряжения. Измеряя напряжение на резисторах R₁, R₁—R₂, R₁—R₂—R₃ (символ двойного тире «—» используется для того, чтобы показать последовательное соединение между резисторами R₁, R₂, и R₃) мы видим, что его величина (хоть и отрицательная) последовательно увеличивается от начальной точки к каждому последующему резистору. Такое увеличение является следствием одинаковой ориентации (полярности) напряжения на всех резисторах («+» слева, «-» справа).  Сумма напряжений на резисторах R₁, R₂, и R₃ нашей схемы будет равна 45 вольт, что аналогично напряжению на выводах батареи, за тем исключением, что полярность батареи («-» слева, «+» справа) противоположна полярности суммарного напряжения резисторов. Таким образом, общее напряжение на всей линейке компонентов схемы будет равно нулю (45В + (-45В) = 0).

Полученное в результате суммирования итоговое напряжение, величиной 0 вольт, вполне закономерно. Посмотрев на схему можно увидеть, что ее крайняя левая точка (точка № 2 слева от резистора R₁) непосредственно связана с крайней правой точкой (точкой № 2 справа от батареи). Поскольку непосредственно связанные точки являются электрически общими по отношению друг к другу, напряжение между ними должно быть равно нулю.

Второй закон Кирхгофа будет работать не только на последовательной конфигурации цепи, но и на любой другой. Посмотрите как он работает на следующей параллельной цепи:

 

 

В параллельной цепи, как вы знаете, напряжение на каждом резисторе равно напряжению батареи, которое в нашем случае составляет 6 вольт. Подсчитав напряжение в последовательности точек 2-3-4-5-6-7-2, мы получим:

 

 

Обратите внимание, суммарное напряжение мы обозначили как U_2-2. А обозначили мы его так из за того, что начали измерения в точке 2, и закончили в этой же точке. Алгебраическая сумма напряжений в этом случае будет равна напряжению между точками 2-2, которое конечно-же равно нулю.

Тот факт, что эта цепь параллельная а не последовательная, никак не влияет на справедливость второго закона Кирхгофа. Любая схема вообще может быть «черным ящиком», а ее конфигурация может быть полностью скрыта от нашего взгляда. При этом, если контрольные точки этой схемы будут открыты, то замеры напряжения между ними подтвердят верность данного закона:

Попробуйте в вышеприведенной схеме измерить напряжения любой последовательностью шагов между любыми ее точками (возвращаясь при этом в исходную точку), и вы увидите, что алгебраическая сумма напряжений всегда равна нулю.

Последовательность точек, к которой можно применить закон, не обязательно должна соответствовать реальному потоку электронов. Единственным условием, которое необходимо выполнить, является то, что последовательность должна начинаться и заканчиваться в одной точке цепи, при этом полярность при проведении замеров должна неукоснительно соблюдаться. Давайте рассмотрим абсурдный пример, замерив напряжения в последовательности точек 2-3-6-3-2 этой же цепи:

 

 

 

Второй закон Кирхгофа можно использовать для определения неизвестного напряжения сложной цепи, в которой остальные напряжения выбранной последовательности точек известны. Возьмем в качестве примера следующую сложную цепь (представляющую две последовательные цепи, основания которых соединены проводом):

 

 

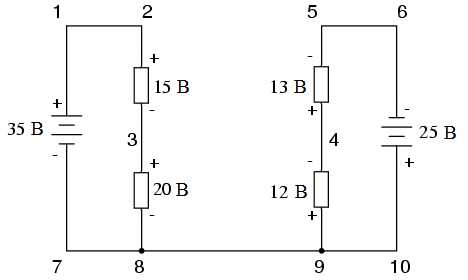
Для упрощения задачи мы опустим значения сопротивлений, оставив только значения напряжений на каждом резисторе. Так как две изображенные на рисунке последовательные схемы имеют общий провод (провод 7-8-9-10), у нас появляется возможность измерить между ними напряжение. Если мы хотим определить напряжение между точками 4 и 3, то его нужно подставить в уравнение Второго закона Кирхгофа как неизвестное:

 

 

 

 

 

 

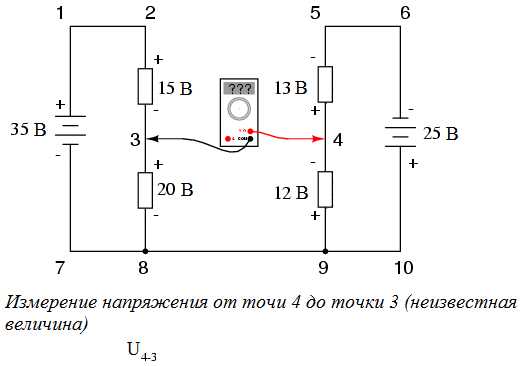
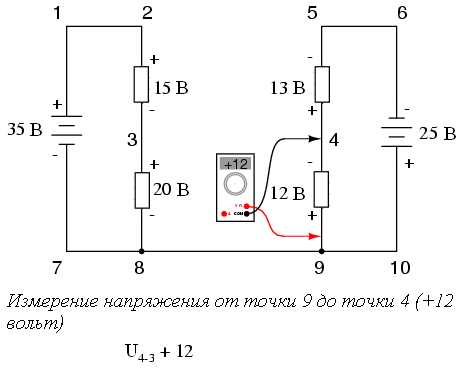
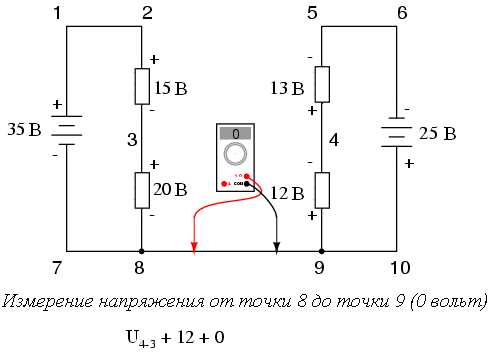
В ходе измерения напряжений в последовательности точек 3-4-9-8-3 мы записывали числа так, как их отображал цифровой вольтметр. При этом красный щуп прибора подсоединялся к первой точке, а черный — ко второй. Таким образом, напряжение от точки 9 до точки 4 оказалось положительным +12 вольт, так как красный щуп подключался к точке 9, а черный — к точке 4. Напряжение от точки 3 до точки 8 так же положительно + 20 вольт (красный щуп к точке 3, черный — к точке 8). И напряжение от точки 8 до точки 9 имеет нулевое значение, потому что эти две точки являются электрически общими.

Итак, окончательным ответом для напряжения от точки 4 до точки 3 будет  -32 вольта. Именно такое напряжение покажет вольтметр, если мы подключим его красный щуп к точке 4, а черный — к точке 3:

 

 

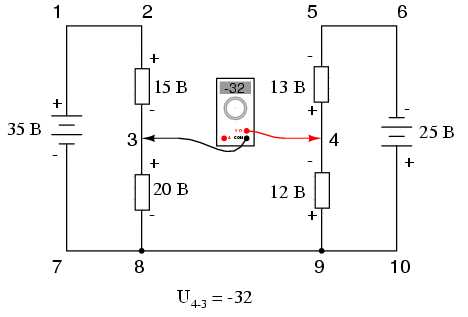
Если бы наше уравнение начиналось с U_3-4 вместо U_4-3, то последовательность измерений проводилась бы при противоположной ориентации тестовых проводов мультиметра. В этом случае окончательный ответ был бы следующим — U_3-4=+32 В:

 

 

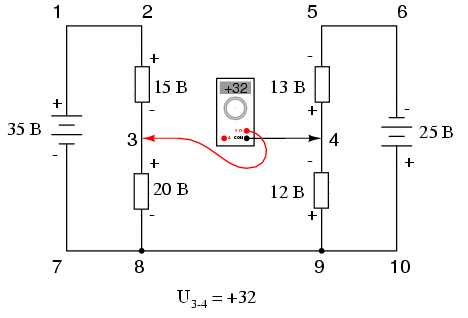
Здесь важно понять, что оба подхода являются правильными. В обоих случаях мы достигаем правильной оценки напряжения между точками 3 и 4.

www.radiomexanik.spb.ru

Каждый закон Кирхгофа прост и понятен :: SYL.ru

Густав-Роберт Киргоф, выдающийся немецкий физик и математик позапрошлого века, открыл и сформулировал два электротехнических закона, названных в его честь.

Открытия Кирхгоффа

При всей видимой простоте и понятности, законы Кирхгофа стали фундаментальными основами современной науки и базой для методов схематических расчетов. Их практическое значение трудно переоценить. Базой для научных изысканий профессора Кирхгофа стали законы сохранения заряда и энергии, открытые ранее. Некоторые специалисты считают, что правильнее называть описанные Кирхгоффом закономерности правилами, чтобы не путать их с другими замечательными открытиями этого физика, касающимися способностей тел излучать и поглощать энергию, а также зависимости скорости протекания химических реакций от температуры. Однако в научной и технической литературе принято все же пользоваться термином «закон Кирхгофа», тем самым подчеркивая заслуги этого великого ученого в области электротехники. Итак, их два.

1. Закон Кирхгофа о токах в узлах

Узлами в электротехнике называют точки соединения проводников в количестве не менее трех. Для того чтобы понять действие Первого закона Киргофа, достаточно представить себе обычный водопроводный тройник. Если в одну из труб подается вода, то в две остальные она вытекает. Возможен и другой вариант, когда отводная труба одна, а приточных две, но в любом случае, сколько воды в тройник затечет, столько же и вытечет. Теперь задачу можно усложнить, допустив, что количество входов и выходов в узле сколь угодно большое. Однако результат будет тот же, количество поступающей и уходящей жидкости будет равным, то есть, говоря языком математики, алгебраическая сумма расходов равна нулю. Первый закон Кирхгофа рассматривает электрические токи в узлах, которые ведут себя так же, как и вода в тройнике. Если есть входящие и выходящие токи, то их сумма с учетом знака будет нулевой. При этом величина входящих токов обозначается положительным знаком «плюс», а выходящих – отрицательным «минус». Математическая формула выглядит примерно так:

∑(I вх., … I вых.) = 0

где I вх. — величины входящих токов со знаком «+»;

I вых. — величины выходящих токов со знаком «-».

2. Закон Кирхгофа о сумме падений напряжений

Второй закон Кирхгофа понять несколько сложнее, у него нет столь прямых и наглядных ассоциаций как у первого, тем не менее, он тоже несложен. Для начала следует представить себе замкнутую простейшую электрическую цепь, состоящую из источника питания и активной нагрузки в виде сопротивления. При замыкании клемм выключателя через резистор пойдет ток, и все подаваемое напряжение на нем же упадет. Задача вновь усложняется, и количество сопротивлений изменяется. Теперь их много, и у всех разная величина. При прохождении через них электрического тока он будет в цепи одинаковым и, согласно закону Ома, равен напряжению источника, поделенному на сумму всех сопротивлений. На каждом из них будет падать его часть. Так вот, Второй закон Кирхгофа гласит, что общая сумма падений напряжений на каждом из участков цепи равна величине напряжения питания. Говоря иными словами, общая алгебраическая сумма вместе с источником равна нулю.

Простейшая математическая формула описывает Второй закон Кирхгофа следующим образом:

∑U ц = 0

где U ц – падения напряжений на разных участках замкнутой электрической цепи (контура).

www.syl.ru