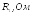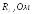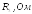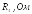1) Записать уравнения по законам Кирхгофа в дифференциальной и комплексной формах.
Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра теоретических основ электротехники

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2
По дисциплине «Основы теории цепей»
На тему «Расчёт разветвлённых линейных электрических цепей однофазного синусоидального тока»
Специальность «Информационные системы»
Выполнил Ануарбеков Шыңғыс Группа ИС-16-2
Принял доцент каф. ТОЭ Айтжанов Н.М.
_________ «____»____________2017г.
Алматы 2017
Содержание
Введение…………………………………………………………………………………………………….3
Задание………………………………………………………………………………………………………4
Расчетная часть…………………………………………………………………………………………..6
Уравнения по законам Кирхгофа в двух формах…………………………………..6
Методы контурных токов и узловых потенциалов………………………………..8
Свод результатов расчетов в таблицу…………………………………………………13
Метод эквивалентного генератора……………………………………………………..13
Баланс комплексных мощностей……………………………………………………….17
Мгновенные значения токов и график тока…………………………………………17
Заключение……………………………………………………………………………………………….19
Список литературы……………………………………………………………………………………20
Введение
Цель работы: умение составлять систему уравнения по законам Кирхгофа для разветвлённых электрических цепей однофазного синусоидального тока, рассчитывать токи методом контурных токов, методом узловых потенциалов в комплексной форме, методом эквивалентного генератора.
Дана
электрическая цепь, в которой действуют
источники синусоидальной ЭДС 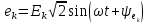 и синусоидального тока
и синусоидального тока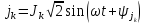 (см. рисунок 2.1-2.10). Действующие значения
ЭДС
(см. рисунок 2.1-2.10). Действующие значения
ЭДС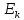
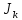 , а также начальные фазы
, а также начальные фазы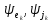 приведены в таблице 2.2. Параметры
электрической цепи приведены в таблицах
2.1, 2.3.
приведены в таблице 2.2. Параметры
электрической цепи приведены в таблицах
2.1, 2.3.Таблица 2.1
Год поступления | Первая буква фамилии | |||||||||
Четный | А БВ | ГДЕ | ЖЗИ | КЛ | МН | ОПР | СТ У | ФХЦ | ЧШ Щ | ЭЮ Я |
Нечетный | КЛ | ОПР | СТ У | ФХЦ | АБ В | Е | ЖЗИ | МН | ЭЮ Я | ЧШЩ |
№ схемы | 3.1 | 3.2 | 3.3 | 3.4 | 3.5 | 3.6 | 3.7 | 3.8 | 3.9 | 3.10 |
| 3 | 10 | 20 | 10 | 40 | 10 | 40 | 20 | 10 | 40 |
| 5 | 2 | 30 | 20 | 16 | 20 | 10 | 60 | 20 | 5 |
| 8 | 6 | 25 | 5 | 20 | 40 | 30 | 50 | 12 | |
| 2 | 16 | 65 | 25 | 15 | 100 | 50 | 40 | 40 | 18 |
| 4 | 25 | 20 | 10 | 8 | 10 | 10 | 10 | 30 | 30 |
| 10 | 10 | 15 | 30 | 15 | 25 | 40 | 5 | 60 | 40 |
| 6 | 5 | 20 | 8 | 5 | 20 | 20 | 18 | 40 | |
| 18 | 10 | 30 | 20 | 8 | 50 | 30 | 10 | 20 | 30 |
Таблица 2.2
поступления | Последняя цифра студенческого билета | |||||||||
Четный | 0 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Нечетный | 2 | 5 | 6 | 1 | 3 | 4 | 7 | 8 | 9 | 0 |
| 10 | 20 | 15 | 30 | 25 | 16 | 12 | 30 | 40 | 18 |
| 20 | 12 | 18 | 28 | 30 | 35 | 40 | 15 | 8 | 25 |
| 30 | 15 | 20 | 10 | 16 | 15 | 45 | 50 | 30 | 20 |
| 35 | 20 | 15 | 25 | 10 | 18 | 32 | 40 | 42 | 35 |
| 10 | 15 | 8 | 5 | 20 | 10 | 6 | 12 | 3 | 4 |
, град | 30 | 40 | 25 | 45 | -40 | 60 | 0 | 35 | 50 | 70 |
| 120 | 80 | 90 | -30 | -60 | —40 | 30 | -10 | -20 | -90 |
| 130 | 150 | 180 | -45 | -30 | -60 | -90 | 40 | 15 | 20 |
| 0 | 20 | 90 | -60 | -45 | -50 | 45 | 70 | 30 | 120 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 2.3
Год поступления | Предпоследняя цифра студенческого билета | |||||||||
Четный | 2 | 3 | 4 | 8 | 0 | 1 | 5 | 7 | 6 | 9 |
Нечетный | 8 | 2 | 0 | 7 | 6 | 4 | 3 | 5 | 9 | 1 |
| 60 | 100 | 40 | 50 | 80 | 20 | 15 | 25 | 30 | 12 |
| 50 | 45 | 90 | 40 | 30 | 25 | 10 | 20 | 18 | 6 |
| 6 | 10 | 8 | 15 | 20 | 30 | 25 | 40 | 60 | 10 |
| 120 | 100 | 80 | 60 | 40 | 20 | 10 | 8 | 15 | 45 |
МЭГ, График тока | i4 | i1 | i2 | i3 | i4 | i1 | i2 | i3 | i4 | i1 |
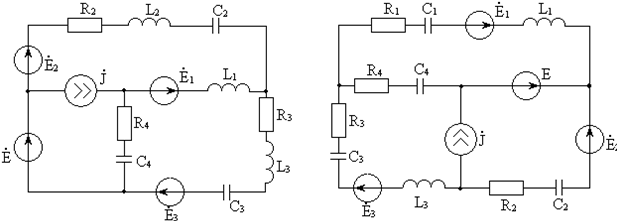
Рисунок 2.1
Задание:
1) Записать уравнения по законам Кирхгофа в дифференциальной и комплексной формах.
2) Определить комплексные действующие значения токов во всех ветвях методом контурных токов и методом узловых потенциалов. Свести результаты расчетов в одну таблицу.
3) Определить комплекс действующего значения требуемого тока (см. таблицу 2.3) методом эквивалентного генератора.
4) Проверить баланс комплексных мощностей в цепи.
5)
Записать мгновенные значения токов
всех ветвей и построить график одного
из токов i(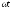 )
(см. таблицу 2.3).
)
(см. таблицу 2.3).
Расчетная часть
Законы Кирхгофа в дифференциальной форме. Законы Кирхгофа в дифференциальной форме записываются для мгновенных значений переменных токов и напряжений.
Первый
закон Кирхгофа: алгебраическая сумма
мгновенных значений токов в узле схемы
равна нулю: 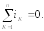 Со знаком «+» записываются токиік,
положительные направления которых
направлены к рассматриваемому узлу, со
знаком «-» записываются токи ік,
положительные направления которых
направлены от данного узла (или наоборот).
Число
уравнений, составляемых по первому
закону Кирхгофа, равно
Со знаком «+» записываются токиік,
положительные направления которых
направлены к рассматриваемому узлу, со
знаком «-» записываются токи ік,
положительные направления которых
направлены от данного узла (или наоборот).
Число
уравнений, составляемых по первому
закону Кирхгофа, равно 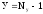 ,
где
,
где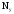 —
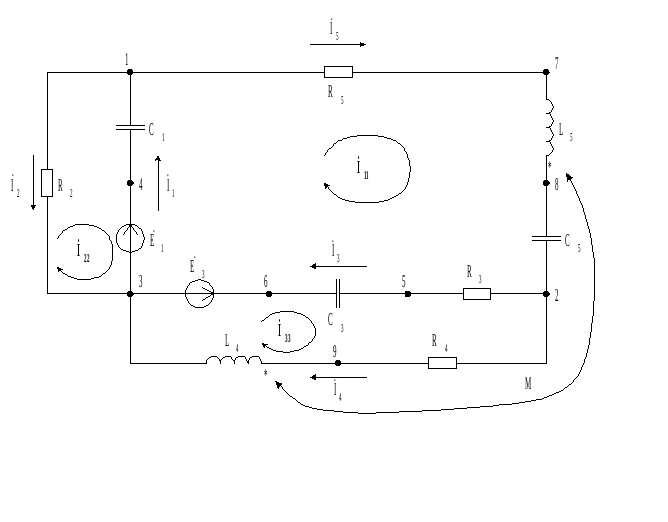
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений поI
закону Кирхгофа). Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3:
—
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений поI
закону Кирхгофа). Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3:
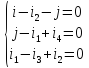
Второй закон Кирхгофа: алгебраическая сумма мгновенных ЭДС всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме мгновенных напряжений на всех остальных элементах того же контура:
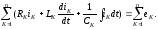
Второй
закон Кирхгофа записывается для
независимых контуров схемы, независимые
контура выбираются так же, как и для
цепей постоянного тока. Со знаком «+»
записываются мгновенные напряжения,
если положительные направления токов ік и направление обхода контура совпадают,
в противном случае напряжения записываются
со знаком «-». Мгновенные ЭДС ек записываются со знаком «+», если
положительные направления ек и направление обхода контура совпадают.
Число уравнений, составляемых по второму
закону Кирхгофа, равно: 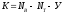 ,
где
,
где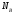 — число ветвей,
— число ветвей,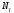 — число источников тока. Исходя из этого,
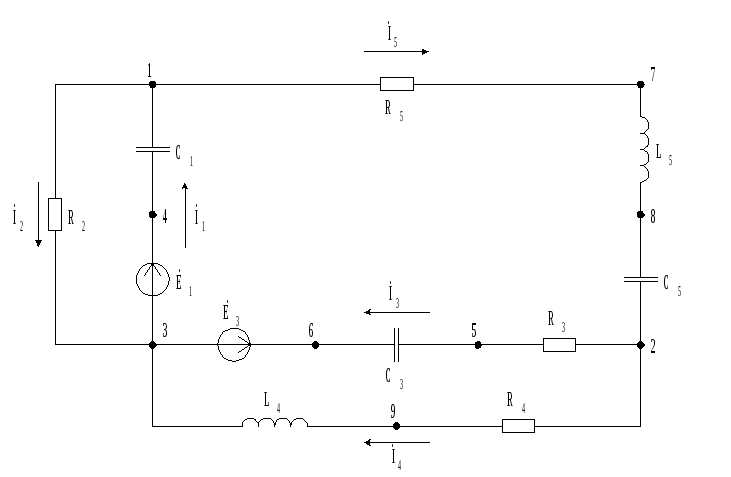
в цепи (рис 2.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 2.1). И для
каждого контура (внешний контур и контур
2342) запишем уравнение поII
закону Кирхгофа:
— число источников тока. Исходя из этого,
в цепи (рис 2.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 2.1). И для
каждого контура (внешний контур и контур
2342) запишем уравнение поII
закону Кирхгофа:
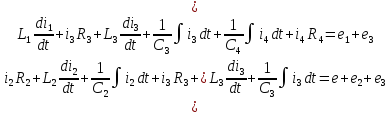
Общая система уравнений по законам Кирхгофа в дифференциальной форме будет выглядеть следующим образом:
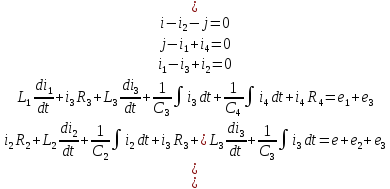
Законы Кирхгофа в комплексной форме.
Для узла электрической цепи переменного тока по первому закону Кирхгофа сумма мгновенных значений токов, направленных к узлу, равна сумме мгновенных значений токов, направленных от узла. То же самое правило справедливо и при записи токов в комплексной форме. Запишем уравнения для 1, 2, 3 узлов:
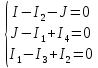
Для замкнутого контура электрической цепи переменного тока по второму закону Кирхгофа алгебраическая сумма мгновенных значений ЭДС, действующих в контуре, равна алгебраической сумме мгновенных значений падений напряжения на отдельных его участках. Приписав ЭДС и токам, совпадающим по направлению с направлением обхода контура, знак плюс, а несовпадающим – минус, получим при комплексной записи для любого замкнутого контура:
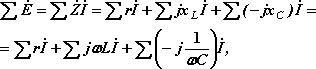
Таким образом, для всякого замкнутого контура алгебраическая сумма комплексных ЭДС источников питания равна алгебраической сумме комплексных падений напряжений. Выбираем два независимых контура, не имеющих источника тока, затем произвольно выбираем обход контура (рис 2.1). И для каждого контура (внешний контур и контур 2-3-4-2(узлы)) запишем уравнение по II закону Кирхгофа:
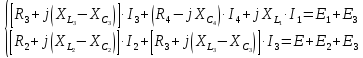
Общая система уравнений по законам Кирхгофа в комплексной форме будет выглядеть следующим образом:
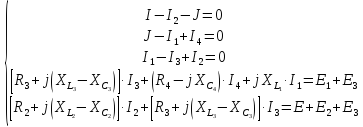
50. Законы Ома, Кирхгофа и Джоуля-Ленца в дифференциальной форме.
Выделим в проводящей среде небольшой параллелепипед объемом V (рис. 16.1).
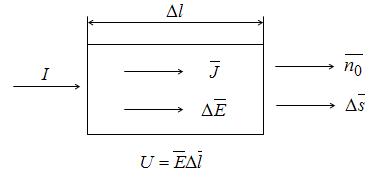
Рис. 16.1. Параллелепипед в проводящей среде
Длина ребер параллелепипеда Δl, площадь поперечного сечения Δs.
Расположим его так, чтобы напряженность поля была в нем направлена параллельно ребру. В силу малости объема можно считать, что напряженность поля одна и та же во всем элементарном объеме:
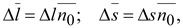
где 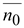 –
единичный вектор по направлению
–
единичный вектор по направлению 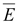
Ток:
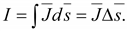 (16.2)
(16.2)
Напряжение на элементе объема:
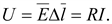 (16.3)
(16.3)
Сопротивление элемента объема:
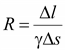 ,
(16.4)
,
(16.4)
где γ – удельная проводимость среды.
Поставив в (16.3) выражения (16.2) и (16.4) получим:
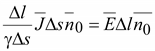 ,
,
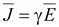 .
(16.5)
.
(16.5)
Выражение (16.5) называют законом Ома в дифференциальной форме. Это уравнение справедливо для областей вне источников ЭДС. В областях, занятых источниками ЭДС, существует также так называемое стороннее электрическое поле, обеспечивающее непрерывное движение зарядов в электрической цепи. Это поле обусловлено химическими, электрохимическими, тепловыми и термоэлектрическими процессами. Закон Ома в дифференциальной форме для областей, занятых источниками ЭДС
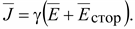 (16.6)
(16.6)
Уравнение (16.6) называется обобщенным законом Ома. Если от обеих частей взять интеграл по замкнутому контуру, то получим второй закон Кирхгофа в дифференциальной форме.
Если в проводящей среде выделить некоторый объем, по которому протекает постоянный, не изменяющийся во времени ток, то можно сказать, что ток, входящий в объем, равняется току, выходящему из объема, иначе в этом объеме происходило бы накопление электрических зарядов, что опыт не подтверждает. Математически это записывают так:
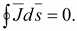 (16.7)
(16.7)
Разделим правую и левую часть уравнения (16.7) на объем и возьмем предел в случае, когда объем стремится к нулю
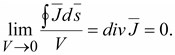 (16.8)
(16.8)
Соотношение
(16.8) называется первым законом Кирхгофа
в дифференциальной форме. Он гласит,
что в установившемся режиме (при
постоянном токе) в любой точке тока нет
ни истока, ни стока линий тока
проводимости 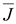 .
.
Из курса физики известно, что при протекании постоянного тока по проводнику в нём выделяется в виде тепла мощность
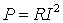 .
.
Найдём мощность, выделяющуюся в единице объема:
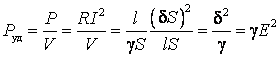 .
.
Таким образом:
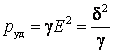 .
(1.44)
.
(1.44)
Это и есть закон Джоуля – Ленца в дифференциальной форме.
В общем случае мощность, выделяющаяся в виде тепла в проводнике, может быть рассчитана согласно выражению:
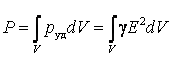 .
(1.45)
.
(1.45)
51.Уравнение Лапласа
Так же, как и в электростатическом поле, напряженность электрического поля в проводящей среде:
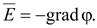
В неизменном во времени поле:
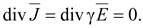
Если среда однородна и изотропна, т.е. γ = const, то можно записать:
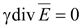 или
или 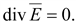
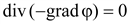
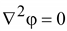 (16.9)
(16.9)
Поле в однородной проводящей среде подчиняется уравнению Лапласа.
Это
поле является потенциальным, в нем в
областях, не занятых источниками 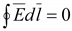 .
.
52.Граничные условия для электрического поля постоянного тока.
На поверхности раздела сред, где γ , Eс и 𝛿 изменяются скачком, справедливы следующие соотношения:
E1t — E2t = E1сt — E2сt
т.е. скачок тангенциальной составляющей вектора напряженности электрического поля равен скачку сторонней тангенциальной составляющей вектора напряженности электрического поля. Если Eс = 0, то тангенциальная составляющая векторного поля E непрерывна на любой поверхности раздела сред.
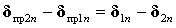
т.е. скачок нормальной составляющей плотности тока проводимости равен скачку нормальной составляющей сторонней плотности тока с противоположным знаком. Если 𝛿 = 0, то нормальная составляющая плотности тока проводимости непрерывна на любой поверхности раздела сред.
§ 20.3. Первый закон Кирхгофа в дифференциальной форме.
Если в проводящей среде выделить,некоторый объём, по которому, про-, текает постоянный, не изменяющийся во времени ток, тс можно сказать, что ток, который войдет в объем, должен равняться току, вышедшему из него,..иначе в этом объеме происходило бы накопление электрических зарядов, что опыт не подтверждает. Сумму входящего в объем и выходящего из объема токов записывают так:
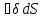 =
0. (20.4)
=
0. (20.4)
Если разделить и левую и правую части (20.4) на одно и то же числа (на объем, о котором шла речь), то равенство останется справедливым:
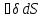
——— = 0
V
Очевидно, что последнее соотношение будет справедливо и в том случае, если объему находящийся внутри замкнутой поверхности, устремим к нулю:,
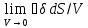 =
div
=
div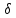 = 0.
= 0.
Таким образом, для постоянного, неизменного во времени поля в проводящей среде:
div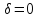 (20.5)
(20.5)
Это
соотношение называют первым
законом Кирхгофа в дифференциальной
форме. Оно
означает, что в установившемся режиме
(при постоянном
токе) в любой точке поля нет ни истока,
ни стока линий тока
проводимости 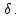
72
§ 20.4. Дифференциальная форма закона Джоуля — Ленца. В гл. 1
отмечалось, что если по какому либо проводнику сопротивлением R протекает постоянный ток I, то в единицу времени (в секунду) в нем
выделяется энергия, равная I 2R. Определим энергию, выделяющуюся в единицу времени в единице объема, проводящей среды (с этой целью
воспользуемся рис. 20.1, a):
Следовательно, в единице объема проводящей среды в единицу времени выделяется энергия, численно равная уЕг.
§ 20.5. Уравнение Лапласа для электрического поля в проводящей среде. Так же как и в электростатическом поле, напряженностьэлектрического поля в проводящей среде Е = —grad φ. В неизменном во времени поле
div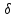 =
div𝛶E=
0. (20.7)
=
div𝛶E=
0. (20.7)
Если 𝛶 среды не изменяется от точки к точке, т. ё. если, среда однородна и изотропна, то у как постоянную..величину можно вынести за знак дивергенции и, следовательно, вместо div𝛶E = 0 можно написать 𝛶 div E ==0 или
divE = 0, (20.8) —
т.е ‘■»■» ‘■
div(—grad φ)=0 ;
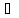 2φ=0 (20..9)
2φ=0 (20..9)
Таким образом, поле в однородной проводящей среде подчиняется уравнению Лапласа. Поле постоянного тока в проводящей среде является полем потенциальным. В нем, в областях, незанятых источниками,
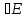 dl = 0. ‘ ■
‘ —
dl = 0. ‘ ■
‘ —
§ 20.6. Переход
тока из среды с проводимостью у1 в среду
с проводимостью γ2.Граничные
условия.
Выясним, какие граничныеусловия выполняются
при переходе тока из среды с одной
проводимостью в среду с, другой
проводимостью.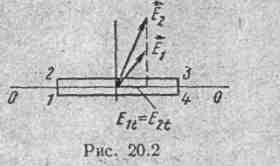
контура равно нулю,
73
На рис. 20.2 линия 00 есть граница раздела сред. Возьмем на границе плоский замкнутый контур 1234. Составим циркуляцию: вдоль этого контура. Стороны 12 и 34 его весьма малы по сравнению со сторонами 23 и 41 (длину последних обозначим dl).
Так как  Edl вдоль любого
замкнутого равно нулю и для контура 1234.
Edl вдоль любого
замкнутого равно нулю и для контура 1234.
В силу малости отрезков 12 и 34 пренебрежем составляющими интеграла вдоль этих путей и тогда:»
Eltdl-E2tdl = 0 или Elt = E2t (20.10)
Это соотношение совпадает с соотношением (19.34).
На границе раздела равны нормальные составляющие плотностей токов. Докажем это.
На границе раздела выделим сплющенный параллелепипед (рис. 20.3, а). Поток вектора б, втекающий в объем через нижнюю грань.
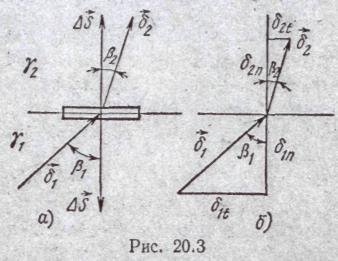
равен
—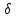 1n
1n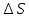 ;
поток вектора,вытекающий
из объема через верхнюю
грань,
;
поток вектора,вытекающий
из объема через верхнюю
грань, 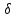 2n
2n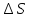 . Так
как
. Так
как 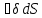 = 0, то:
= 0, то:
—2n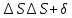 2n
2n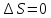 ; (20.11)
; (20.11)
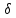 1n=
1n= 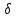 2n
2n
Следовательно, при переходе тока из среды с одной проводимостью в среду с другой проводимостью непрерывна тангенциальная составляющая вектора Е, т. e E1t= E2t
(но Е1п =Е2п), и непрерывна
нормальная составляющая плотности
тока 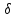 1п.==
1п.== 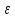 2л (но
2л (но 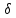 1t
1t 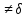 2t).
2t).
Отсюда
следует, что полные значения вектора
E и вектора 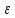 в общем
случае меняются скачком на границе
раздела.
в общем
случае меняются скачком на границе
раздела.
Найдем связь между углом падения β1 и углом преломления β2. В соответствии с рис. 20.3, б:
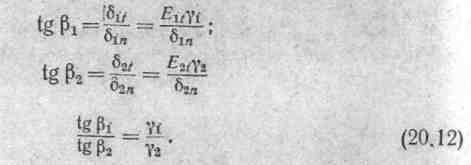
или
Если
ток переходит из среды с большой
проводимостью (например,
из металла) в среду с малой проводимостью
(например, в землю),то
тангенс угла преломления tg
β2 = tgβ1 Υ 2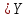 1меньше
тангенса углападения
и, следовательно, угол β2 будет меньше угла β1.Если у2 весьма
мало, то угол β2
1меньше
тангенса углападения
и, следовательно, угол β2 будет меньше угла β1.Если у2 весьма
мало, то угол β2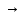 0. ,
0. ,
§ 20.7, Аналогия между полем в проводящей среде и электростатическим полем. По своей природе поле электростатическое и поле постоянного тока в проводящей среде различны. Электростатическое поле создается электрическими зарядами, неизменными во времени и неподвижными в пространстве, тогда как электрическое поле
74
в проводящей среде — это поле, в котором электрические заряды имеют упорядоченное движение под действием внешнего источника.
Тем не менее между двумя полями может быть проведена определенная формальная аналогия.
Действительно,
электростатическое поле в областях,
не, занятых зарядами, удовлетворяет
уравнению Лапласа. Электрическое Поле
постоянного тока в проводящей среде
вне сторонних источников также
ему удовлетворяет. В обоих полях имеют
дело с вектором напряженности
поля Е. С
вектором электрического смещения D= εаE
можно сопоставить вектор плотности,
тока 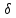 =уЕ. С
потоком вектора D (обозначим
его буквой
=уЕ. С
потоком вектора D (обозначим
его буквой 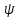 ) ψ
= ∫
) ψ
= ∫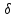 ds можно
сопоставить поток вектора плотности
электрического тока I =∫
ds можно
сопоставить поток вектора плотности
электрического тока I =∫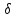 dS.
dS.
Граничные условия на поверхности раздела двух диэлектриков: E1t = E2t и D1n = D2n.
Граничные условия
на поверхности раздела двух сред с
различной проводимостью E1t = E2t и 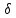 1n =
1n = 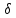 2n
2n
Но если два поля
удовлетворяют одному и тому же уравнению 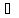 2φ
= 0 и в них выполняются тождественные
граничные условия для сходных
величин, то при однаковой форме граничных
поверхностей на основании теоремы
единственности можно сказать, что
совокупность
силовых и эквипотенциальных линий в
этих двух полях (т. е. картина
поля) будет одинаковой.
2φ
= 0 и в них выполняются тождественные
граничные условия для сходных
величин, то при однаковой форме граничных
поверхностей на основании теоремы
единственности можно сказать, что
совокупность
силовых и эквипотенциальных линий в
этих двух полях (т. е. картина
поля) будет одинаковой.
Эта формальная аналогия широко используется на практике. Так, например, если какое-либо электростатическое поле уже изучено, то все сведения о нем могут быть перенесены и на геометрически подобное поле в проводящей среде. Справедливо и обратное заключение.
Тепловой эффект. Уравнение Кирхгофа
Так, получаем:
\[E=Q’+\tilde{A}\ \left(2\right).\]Можно записать, что $E=-Q$, где $Q$ — количество теплоты, подведенное к системе, тогда в соответствии с первым началом термодинамики, получим:
\[E=-\triangle U-\int\limits^2_1{pdV\left(3\right),}\]где $\triangle U=U_2-U_1$ — изменение внутренней энергии системы, $p$ — давление, $V$ — объем.
Понятие теплового эффекта часто применяется в термохимии. Тепловым эффектом химической реакции является количество тепла, которое выделяется в ходе этой реакции. Если тепло выделяется, то реакция называется экзотермической, если поглощается — эндотермической. Принято считать, что в экзотермической реакции $E>0$, в эндотермической — $E
Предположим, что химическая реакция протекает при $V=const$. В таком случае тепловой эффект реакции $E_V$ рассчитывается как:
\[E_V=U_1-U_2\left(4\right).\]В том случае, если реакция проходит при постоянном давлении, то выражение для теплового эффекта (3) удобнее записать, используя тепловую функцию (энтальпию — H):
Так как:
\[H=U+pV\left(5\right),\] \[E=H_1-H_2+\int\limits^2_1{Vdp\left(6\right).}\]В таком случае тепловой эффект реакции при $p=const$ равен:
\[E_p=H_1-H_2\left(7\right).\]Уравнения (4) и (5) показывают нам, что тепловой эффект реакции при изохорном и изобарном процессах не зависит от хода (промежуточных стадий) реакции, а определяется начальным и конечным состояниями системы. Это формулировка закона Гесса — первый закон термохимии. Если начальные и конечные продукты реакции — твердые или жидкие, то $E_p$ и $E_V$ почти не отличаются друг от друга. Это происходит из-за неизменности объема системы. В реакциях с газообразными составляющими в виду существенной переменности объема тепловые эффекты $E_p$ и $E_V$ существенно отличаются, чаще всего рассматривают тепловой эффект при постоянном давлении. При заданной температуре тепловой эффект реакции $E_p$ практически (а в идеальном газе совсем) не зависит от внешнего давления (которое поддерживают постоянным). Тепловой эффект определённый при t=250C и p=760 мм рт.ст. считается стандартным.
Из закона Гесса вытекают следствия, которые упрощают расчет химических реакций, в системе при $p=const$ или $V=const$:
- тепловой эффект реакции разложения химического соединения численно равен и противоположен по знаку тепловому эффекту реакции синтеза этого соединения из продуктов разложения;
- разность тепловых эффектов двух реакций, приводящих из разных состояний к одинаковым конечным состояниям, равна тепловому эффекту реакции перехода из одного начального состояния в другое;
- разность тепловых эффектов двух реакций, приводящих из одного исходного состояния к разным конечным состояниям, равна тепловому эффекту реакции перехода из одного конечного состояния в другое.
Закон Гесса позволяет оперировать термохимическими уравнениями, как алгебраическими. Зависимость количества теплоты, выделяющейся в реакции (E) от теплового эффекта реакции (Eo) и количества вещества (nb) одного из участников реакции (вещества b — исходного вещества или продукта реакции), выражается уравнением:
\[E=\frac{n_b}{{\nu }_b}E_0,(8)\]Здесь $\ {\nu }_b$— количество вещества b, задаваемое коэффициентом перед формулой вещества b в термохимическом уравнении.
Уравнение Кирхгофа
Большинство термохимических данных в справочниках приведено при температуре 298К. Для расчета тепловых эффектов при других температурах используют уравнения Кирхгофа. Уравнения Кирхгофа записываются для изохорного $(E_V)$ и изобарного ${(E}_p)$ тепловых эффектов. В дифференциальной форме они имеют вид:
\[{\left(\frac{\partial E_V}{\partial T}\right)}_V={\left(\frac{\partial U_1}{\partial T}\right)}_V-{\left(\frac{\partial U_2}{\partial T}\right)}_V=C_{V_1}-C_{V_2}=-\triangle C_V\left(9\right),\] \[{\left(\frac{\partial E_p}{\partial T}\right)}_p={\left(\frac{\partial H_1}{\partial T}\right)}_p-{\left(\frac{\partial H_2}{\partial T}\right)}_p=C_{p_1}-C_{p_2}=-\triangle C_p\left(10\right),\]В уравнениях (10) и (9) $C_V$, $C_p$- теплоемкости вещества при соответствующих процессах (изобарном и изохорном).
В интегральной форме уравнение Кирхгофа для энтальпии имеет вид:
\[H_{T_2}=H_{T_1}+\int\limits^{T_2}_{T_1}{\triangle C_p\left(T\right)dT}\left(11\right),\]где $\triangle C_p=\sum\limits_j{{\nu }_jC_p(B_j})-\sum\limits_i{{\nu }_iC_p(A_i})$ — разность изобарных теплоемкостей продуктов реакции и исходных веществ. Уравнением (11) в химии пользуются чаще всего.
Пример 2
Задание: По приведенным ниже химическим уравнениям вычислите тепловой эффект реакции (E) образования 1 моль ${Fe}_2O_{3\ }$при стандартных условиях из $Fe$ и $O_2$.
- $2Fe+O_2=2FeO,\ H\left(298K,\ 1\right)=-529,6\ кДж$
- $4FeO+O_2=2{Fe}_2O_3,\ H\left(298K,\ 2\right)=-585,2\ кДж$
Решение:
Таким образом, необходимо рассчитать тепловой эффект образования 1 моль оксида железа (${Fe}_2O_3$) в реакции:
- $2Fe+{1,5O}_2={Fe}_2O_3\ \left(2.1\right)$.
Получается, что из двух реакций, приведенных в условиях задачи, необходимо сформировать реакцию (2.1). Для этого разделим коэффициенты в реакции (2) на 2 и сложим с химическим уравнением (1), таким образом, получим:
\[2Fe+O_2+2FeO+{0,5O}_2=2FeO+{Fe}_2O_3\ \left(2.2\right).\]Проведем сокращения, получим уравнение реакции:
\[2Fe+1,5O_2={Fe}_2O_3\ \]Мы получили уравнение (2.1)
Так как приведенная выше последовательность манипуляций с химическими уравнениями 1 и 2 из условий задачи привела нас к требуемому уравнению (2.1), то проведя аналогичную схему действий с тепловыми эффектами, мы получим тепловой эффект реакции (2.1). Мы помним, что все процессы протекают в стандартных условиях, то есть при T=298K. Таким образом, получаем:
\[E\left(3\right)=H\left(1\right)+0,5H\left(2\right)\left(2.3\right),\]где цифры в скобках обозначают номер химической реакции. Проведем расчет:
\[E\left(3\right)=-529,6+0,5\cdot \left(-585,2\right)=-822,2\ \left(кДж\right).\]Ответ: Тепловой эффект реакции -822, 2 кДж.
RGR2
Уфимский государственный авиационный технический университет
Кафедра ТОЭ
Расчетно-графическая работа №2
Анализ электрической цепи переменного тока
Выполнил:
Проверил:
Уфа 2001
Порядок выполнения работы:
Анализ электрической цепи синусоидального тока.
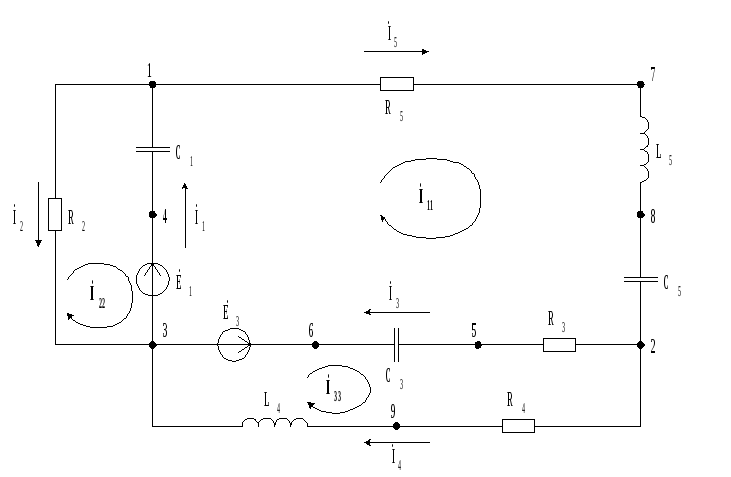
Согласно индивидуальному заданию, составить схему электрической цепи, обозначить все элементы, задать направления токов. В распечатке исходных данных сопротивления даны в омах, индуктивности – в миллигенри, емкости – в микрофарадах, модули комплексов ЭДС – в вольтах, аргументы комплексов ЭЖС – в градусах, частота основной гармоники ЭДС (частота синусоидального ЭДС) – 50 герц.
Составить систему уравнений по законам Кирхгофа в дифференциальной и комплексной форме.
Определить токи в ветвях схемы методом контурных токов.
Записать мгновенные значения токов.
Проверить правильность расчетов по законам Кирхгофа.
Составить баланс активных и реактивных мощностей.
Составить топографическую диаграмму напряжений, совместив ее с векторной диаграммой токов ветвей схемы.
Определить токи в ветвях цепи при введении индуктивной связи между двумя индуктивностями.
Анализ электрической цепи синусоидального тока.
Определить для исходной схемы мгновенные значения токов в ветвях при замене синусоидальных источников напряжений на периодические несинусоидальные.
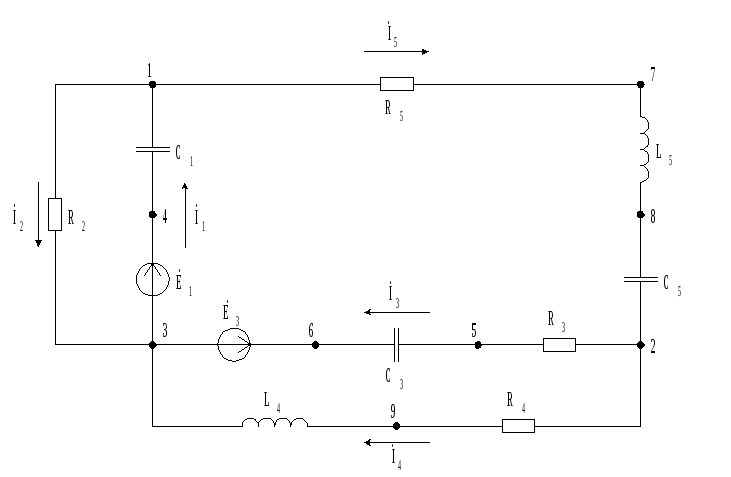
E1 = E3-4 = 50 310 В = 50*cos310 + j50*sin310 = 32,1394 – j38,3022 В
E3 = E3-6 = 20 320 В = 20*cos320 + j20*sin320 = 15,3209 – j12,8558 В
R2 = R1-3 = 80 Ом
R3 = R2-5 = 70 Ом
R4 = R2-9 = 40 Ом
R5 = R1-7 = 30 Ом
L4 = L9-3 = 200*10-3 Гн
L5 = L7-8 = 180*10-3 Гн
C1 = C1-4 = 140*10-6 Ф
C3 = C5-6 = 260*10-6 Ф
С5 = C8-2 = 300*10-6 Ф
Система уравнений в дифференциальной форме:
по первому закону Кирхгофа:
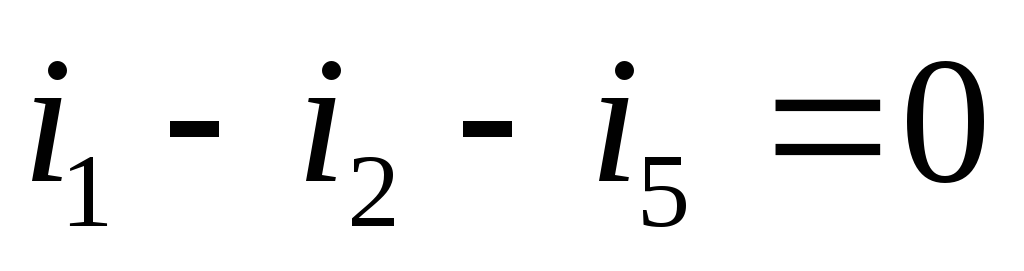
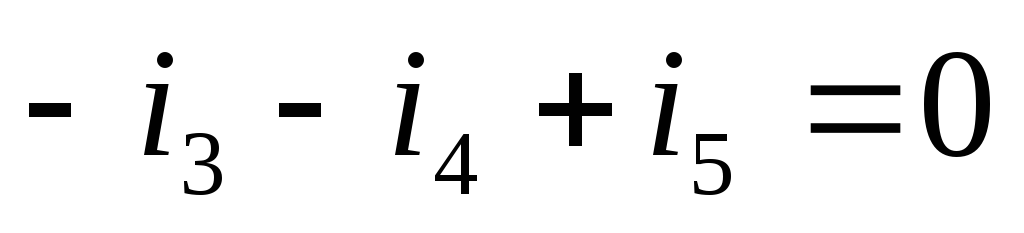
по второму закону Кирхгофа:
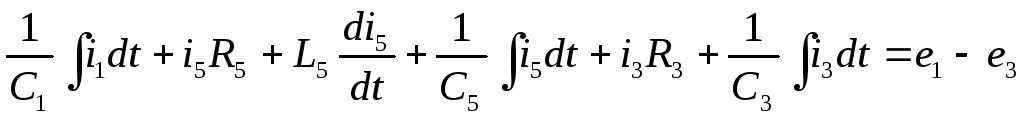
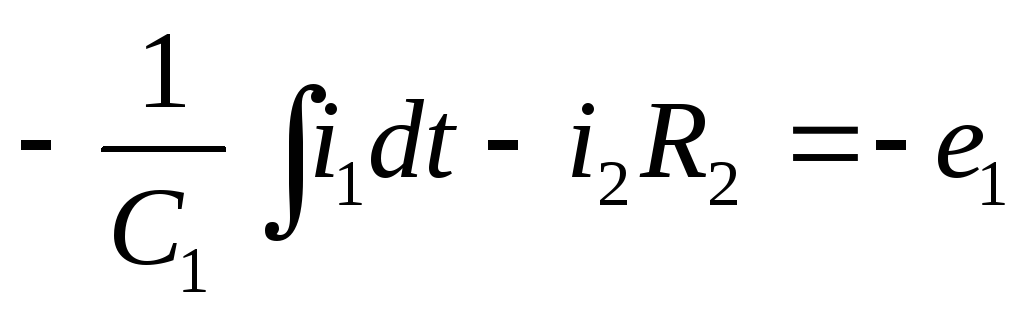
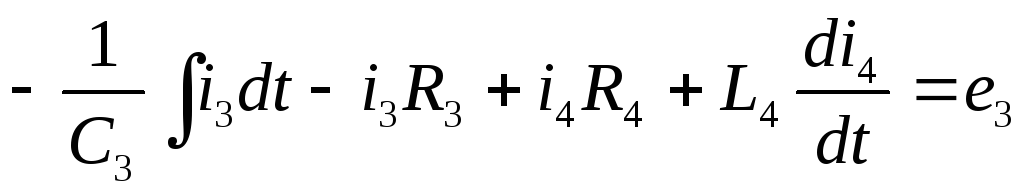
Система уравнений в комплексной форме:
по первому закону Кирхгофа:
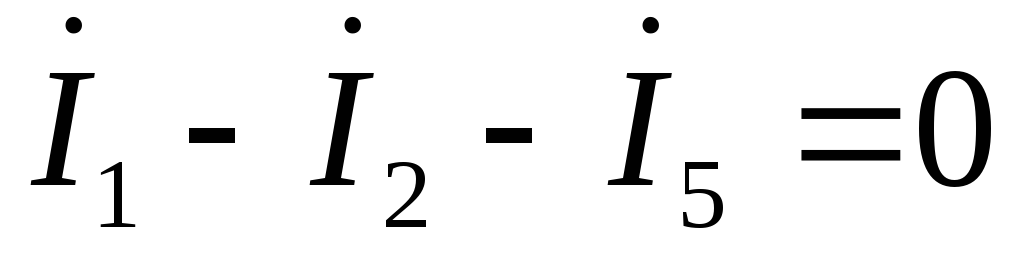
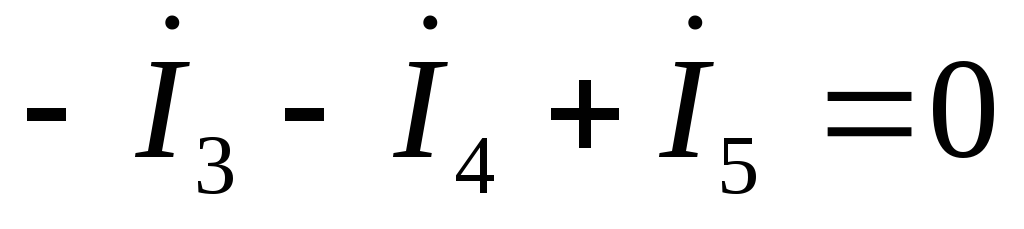
по второму закону Кирхгофа:
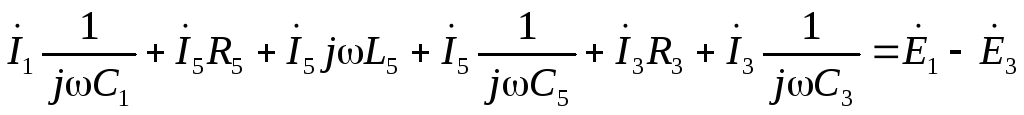

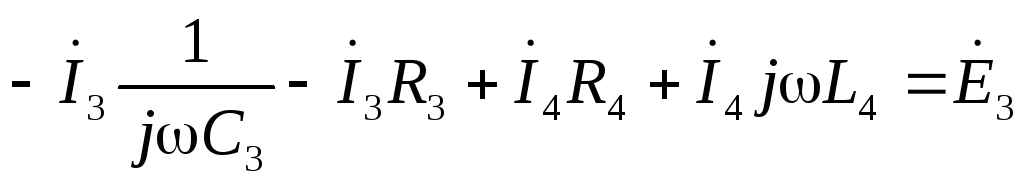
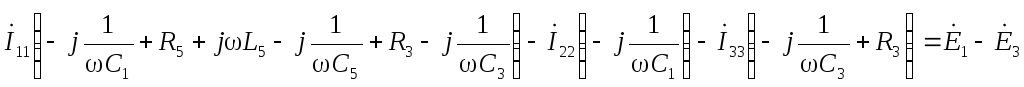
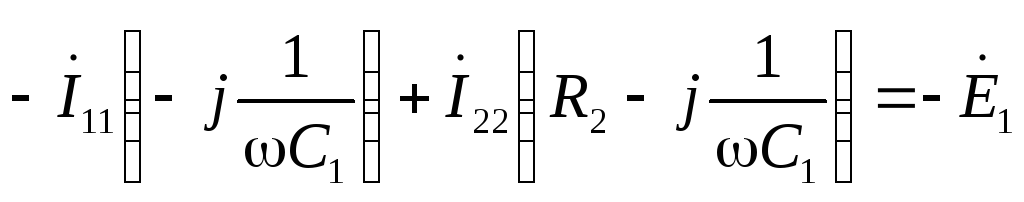
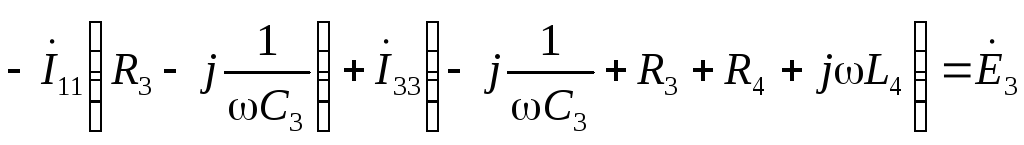
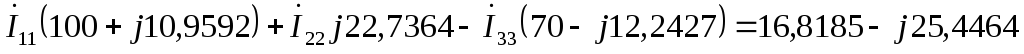
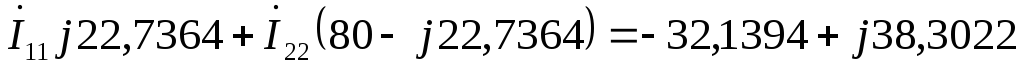
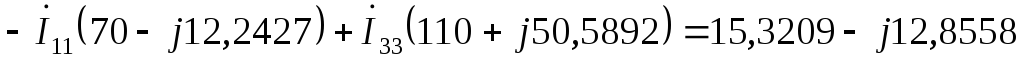
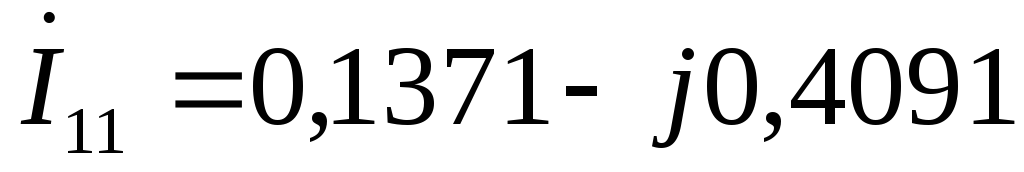 А
А 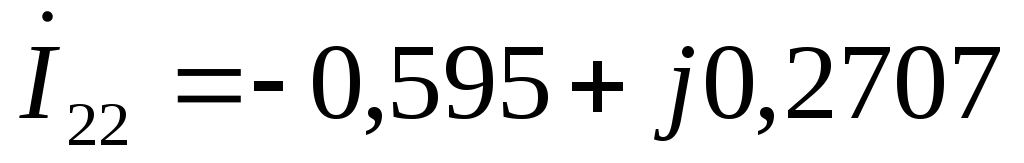 А
А 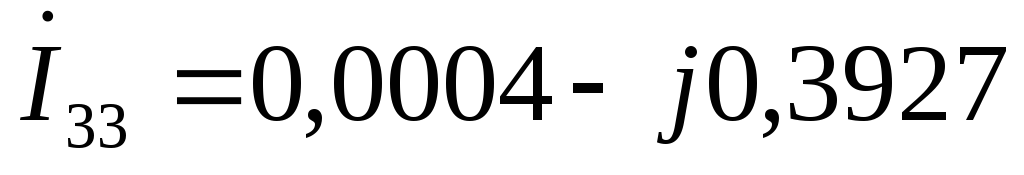 А
А
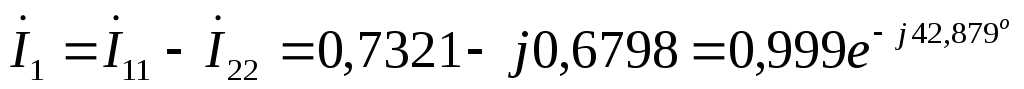 А
А 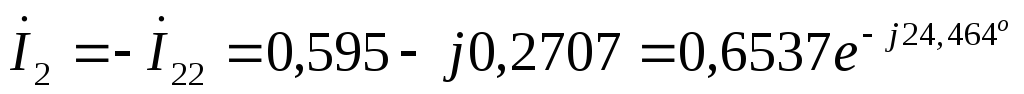 А
А 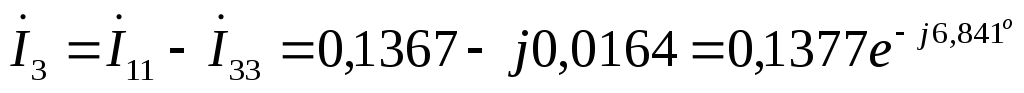 А
А 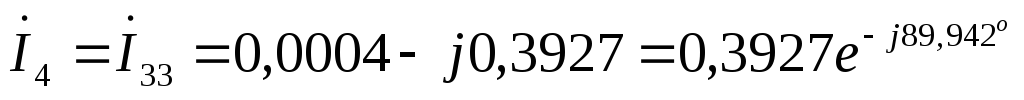 А
А 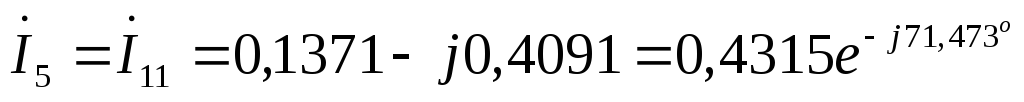 А
А
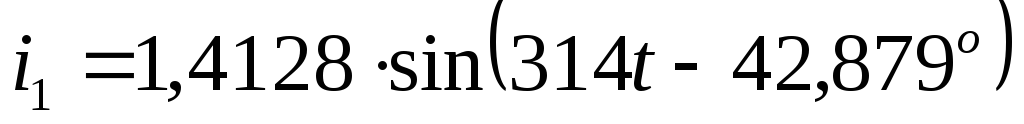
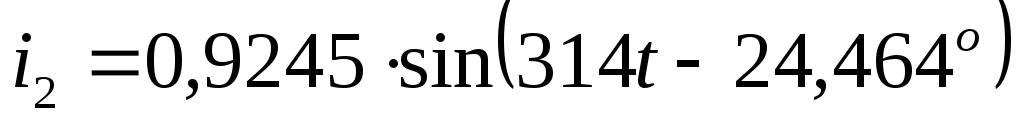
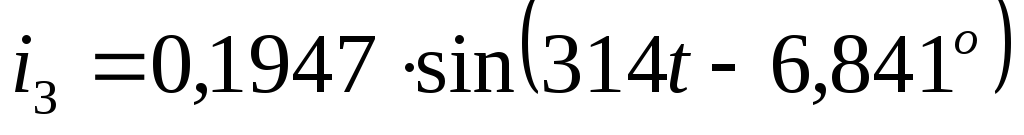
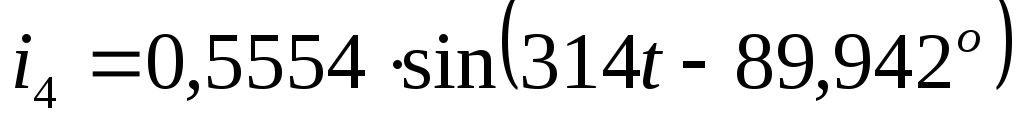
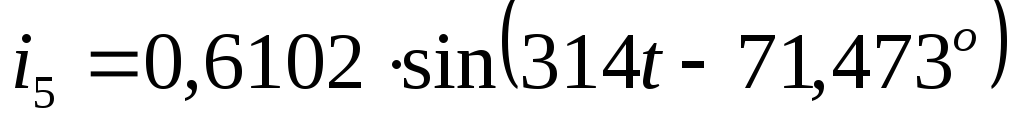
по первому закону Кирхгофа:
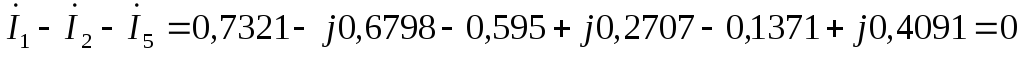
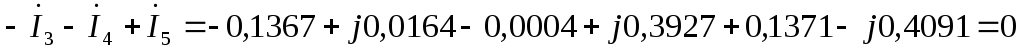
по второму закону Кирхгофа:
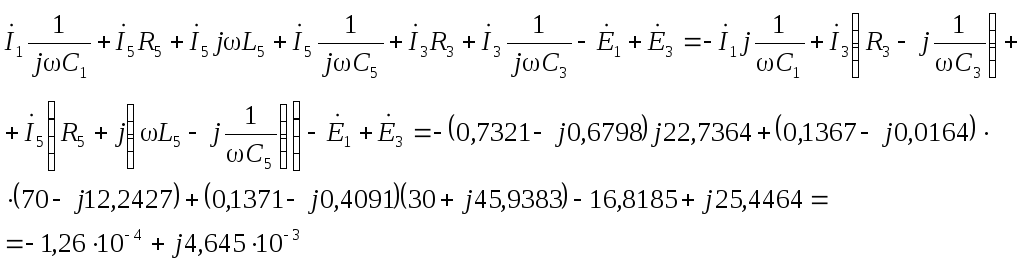

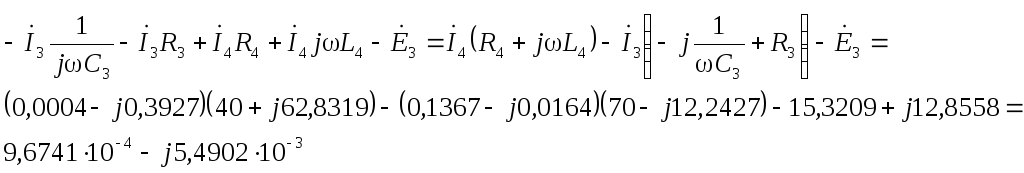
Проверки на законы Кирхгофа показали, что расчеты выполнены верно.
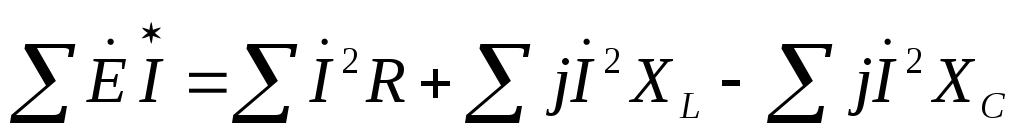
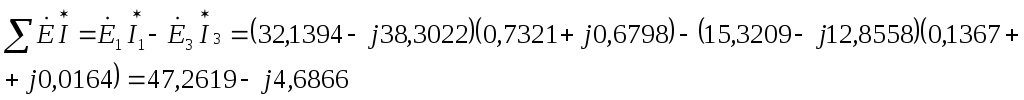
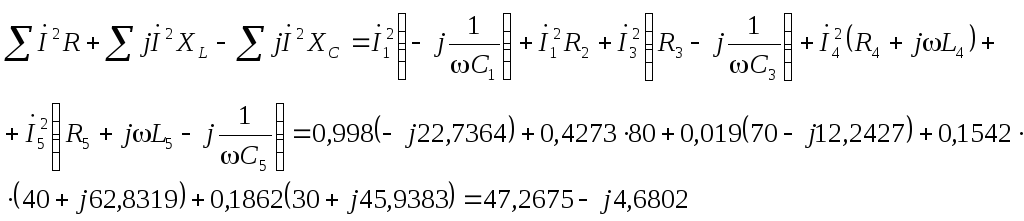
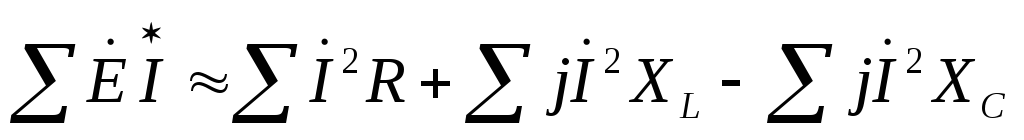
Баланс мощностей сошелся (почти).
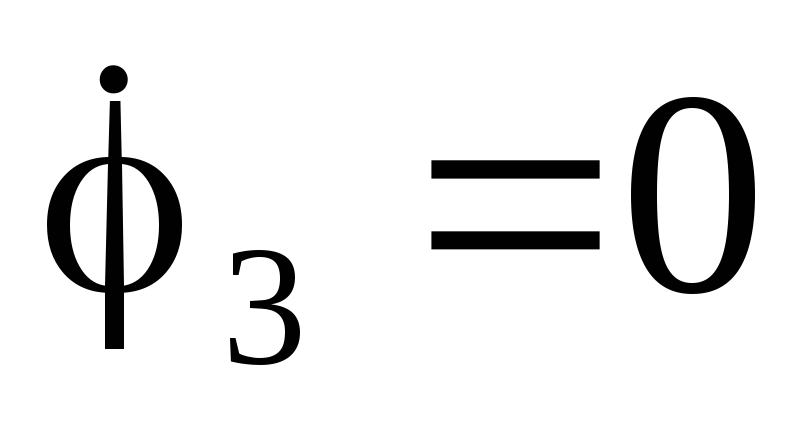 В
В 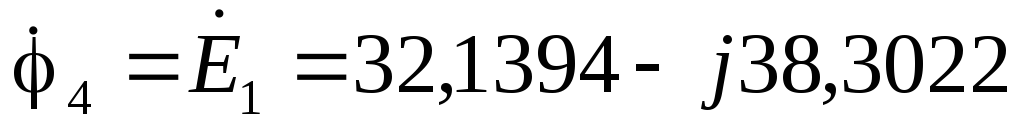 В
В 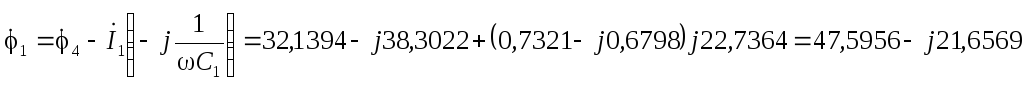
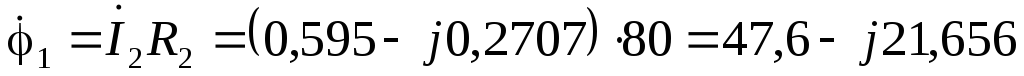 В
В 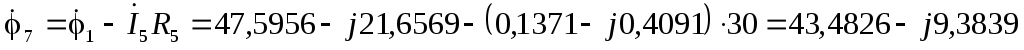 В
В 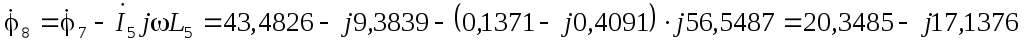 В
В 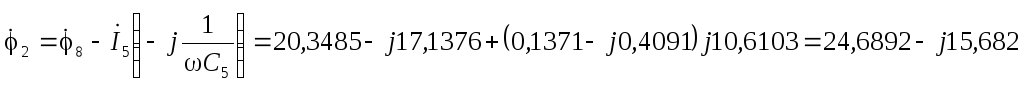 В
В 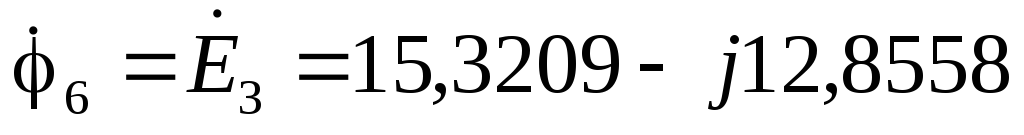 В
В 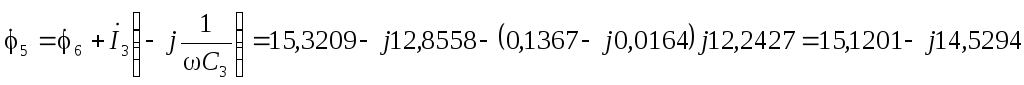 В
В 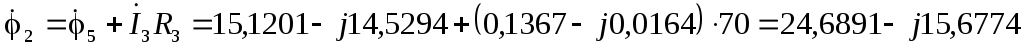 В
В 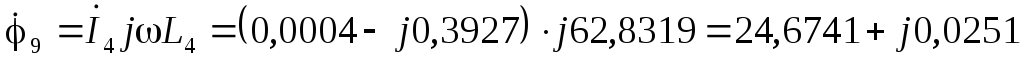 В
В 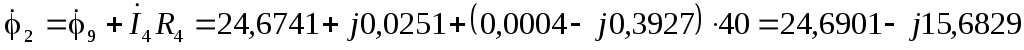 В
В
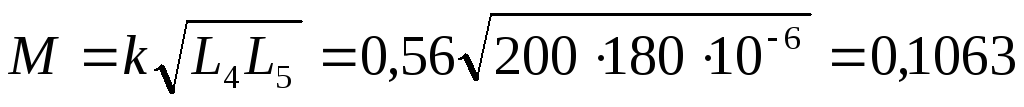
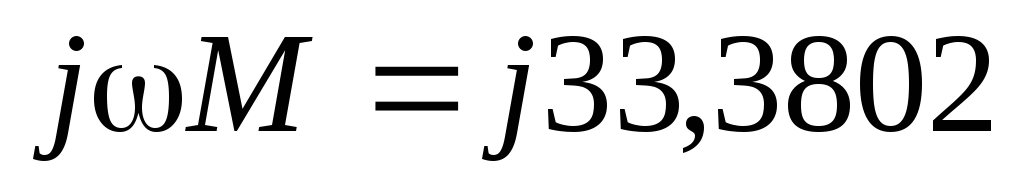
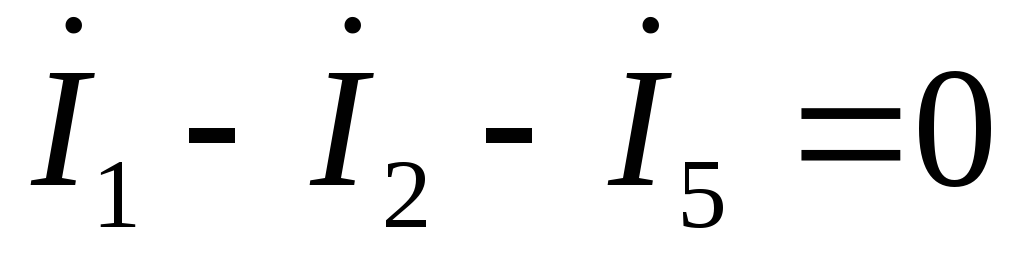
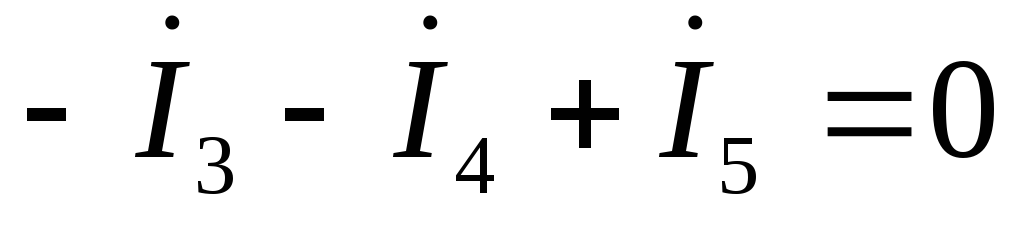
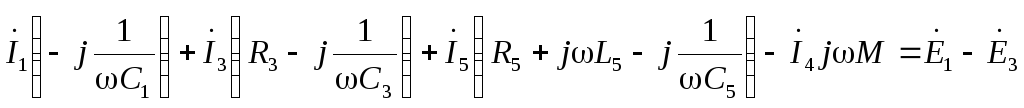
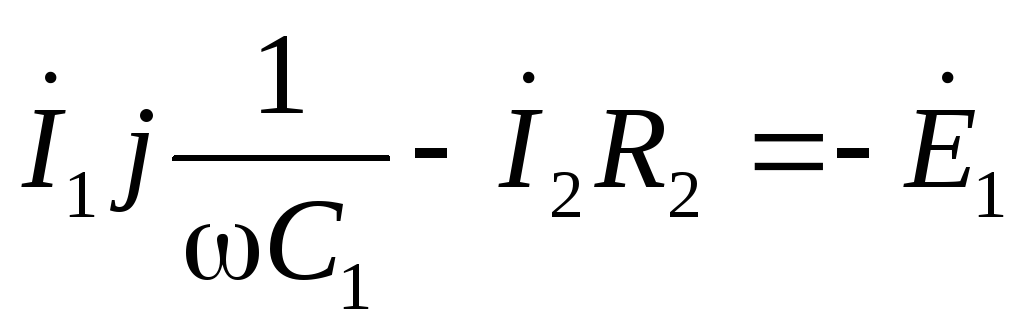
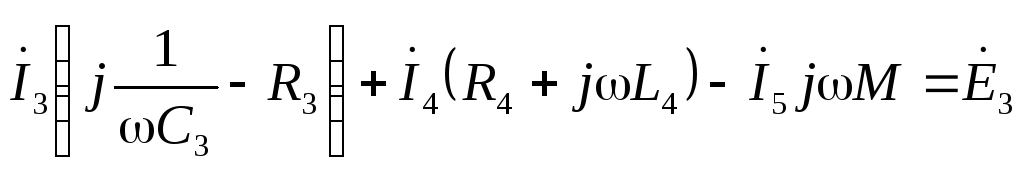
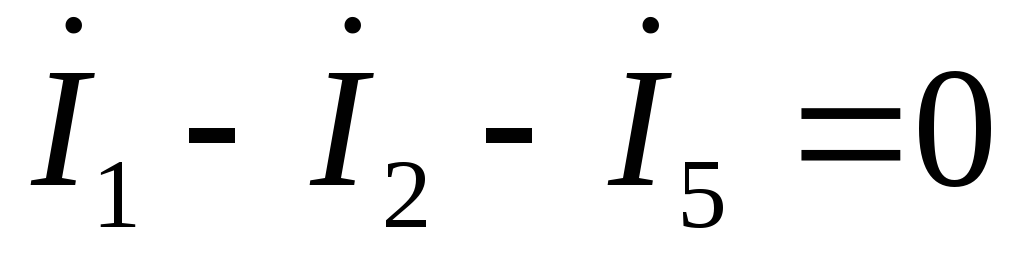
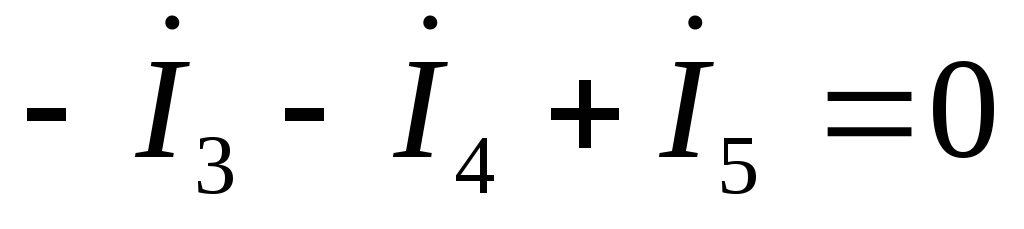
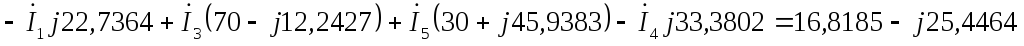
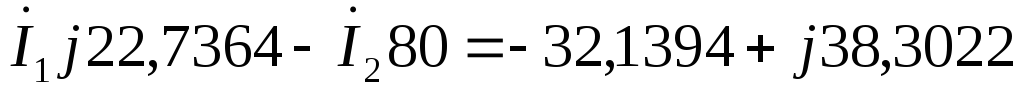
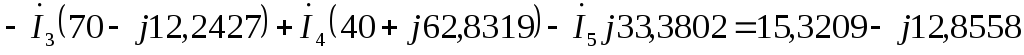
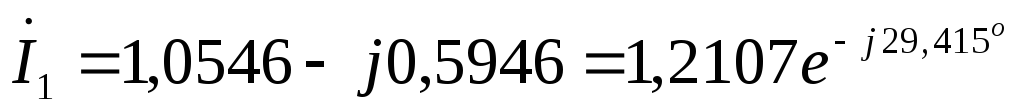 А
А 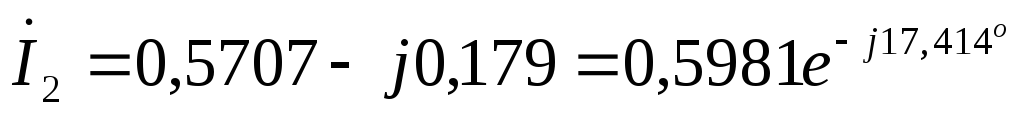 А
А 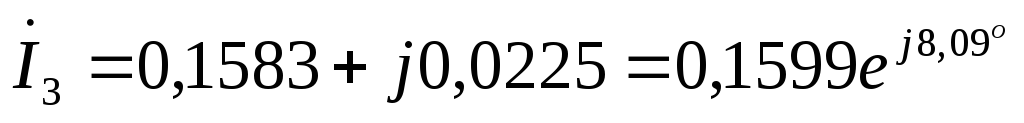 А
А 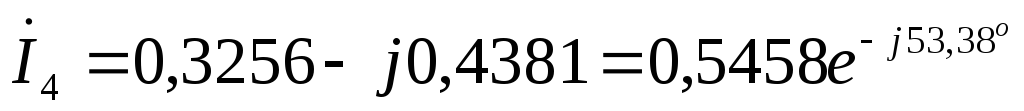 А
А 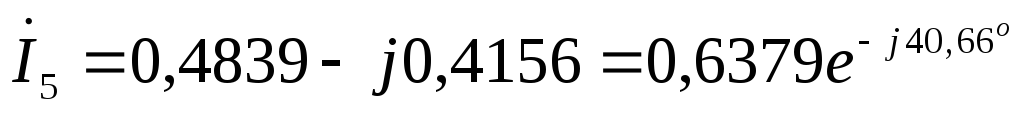 А
А
E1 = E3-4 = (40; 50 310; 40 70) В
E3 = E3-6 = (30; 20 320; 10 100) В
Нулевая гармоника:
Отсутствует частота, следовательно сопротивления в емкостях равны бесконечности, а в индуктивностях – нулю. Схема принимает вид:
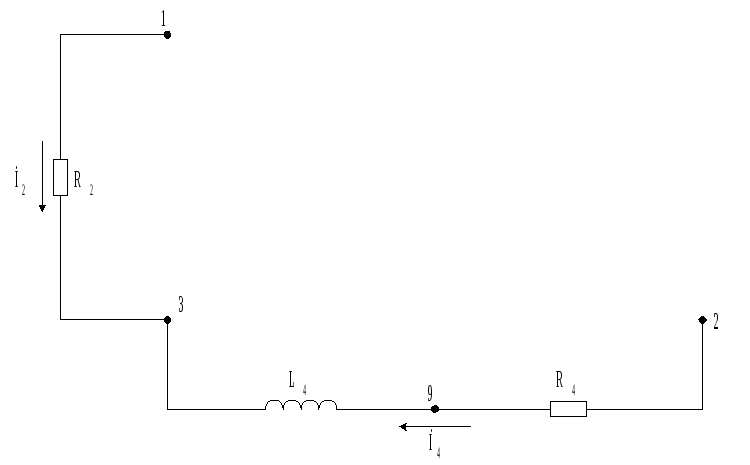
Поскольку не имеется ни одного замкнутого контура, то нулевая гармоника тока не создает.
Первая гармоника:
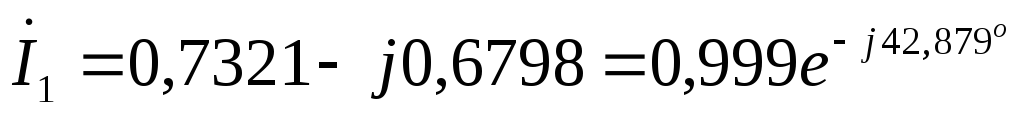 А
А  А
А 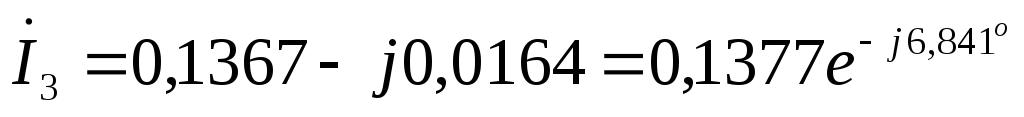 А
А 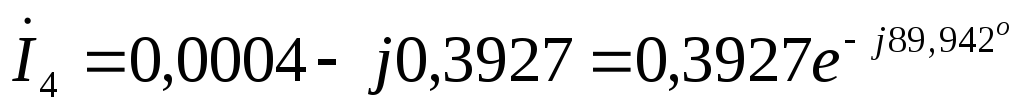 А
А 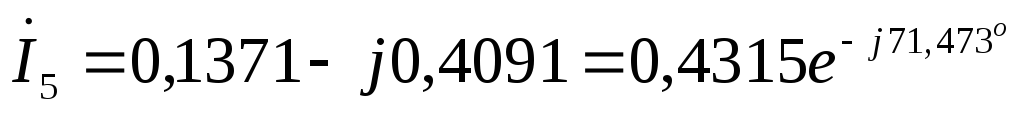 А
А
Третья гармоника:
E1 = E3-4 = 40 70 = 40*cos70 + j40*sin70 = 13,6808 + j37,5877 В
E3 = E3-6 = 10 100 = 10*cos100 + j10*sin100 = –1,7365 + j9,8481 В
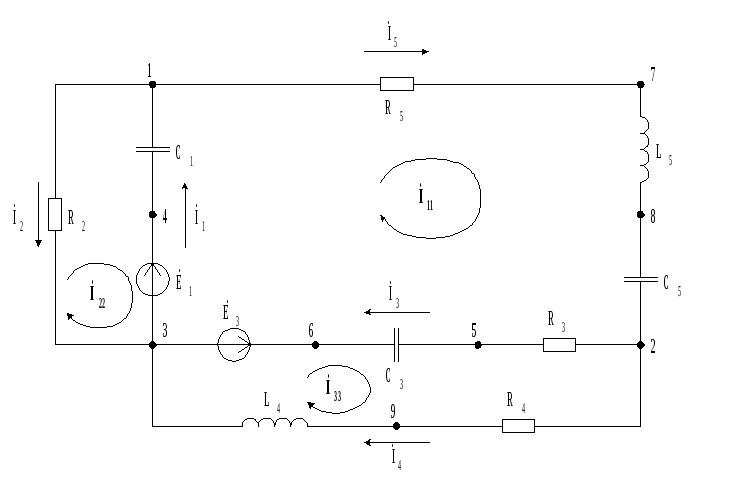
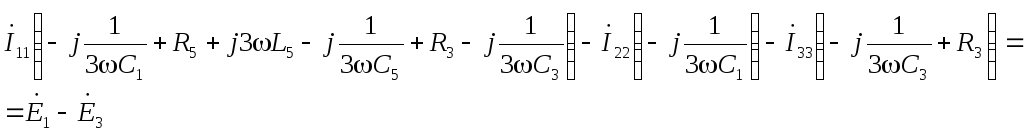
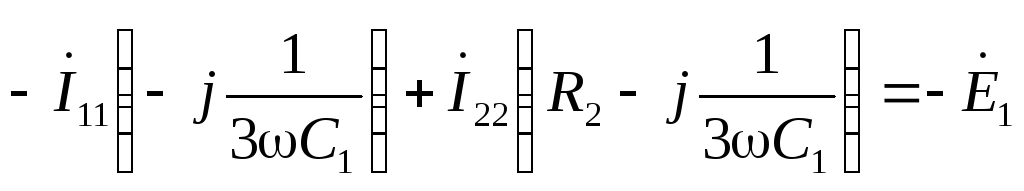
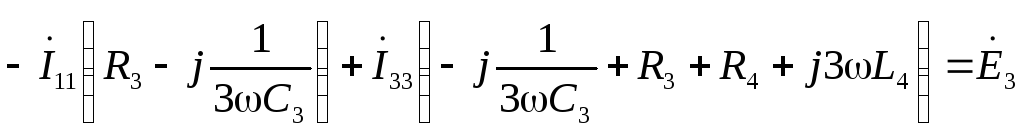
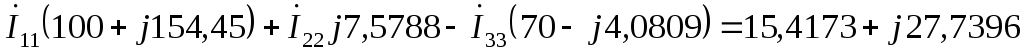
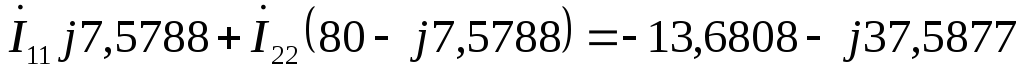
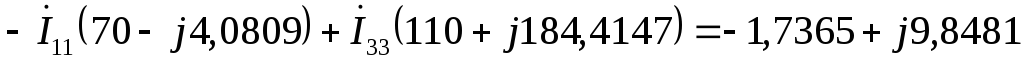
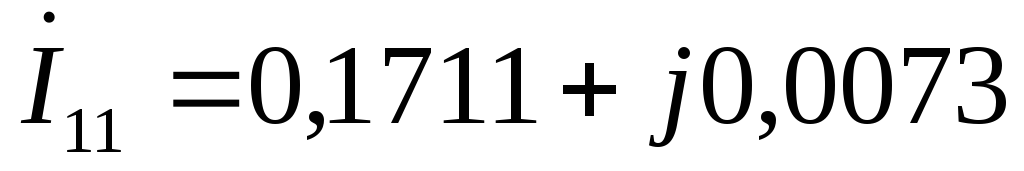 А
А 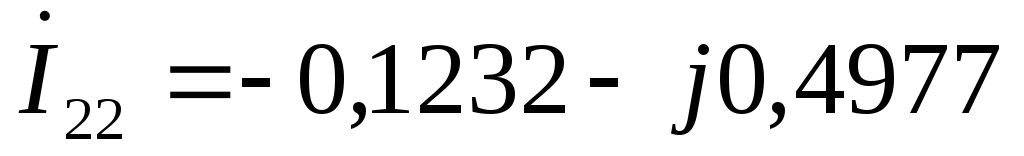 А
А 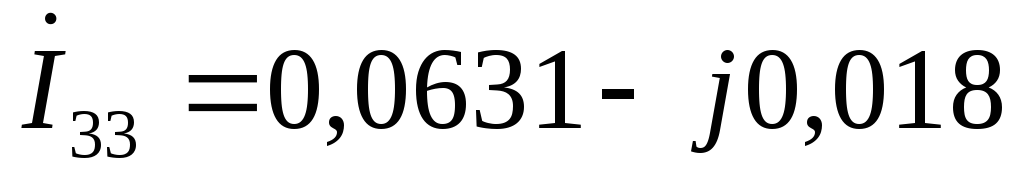 А
А
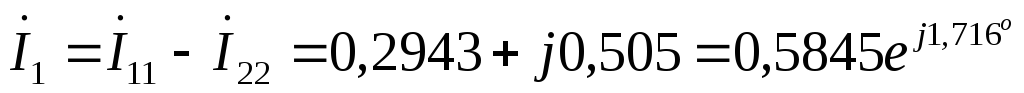 А
А 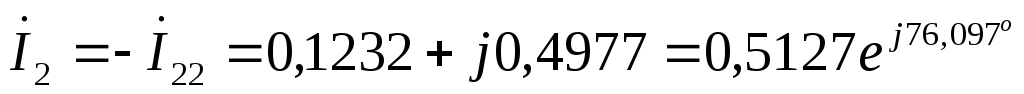 А
А 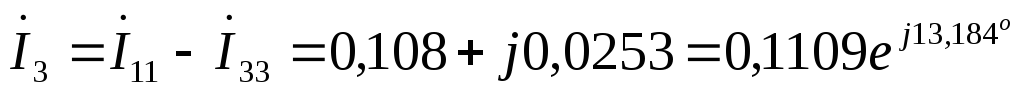 А
А 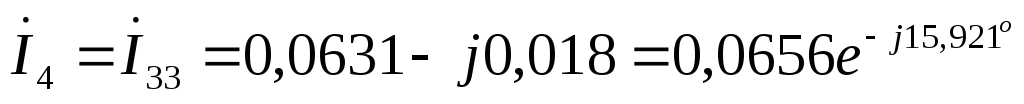 А
А 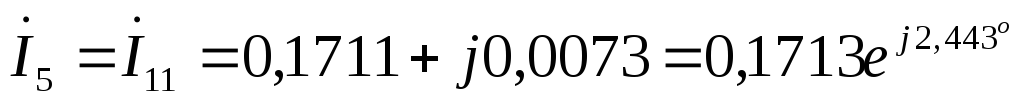 А
А
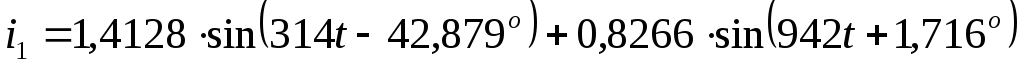 А
А 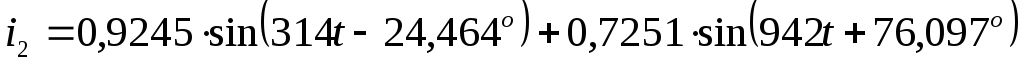 А
А 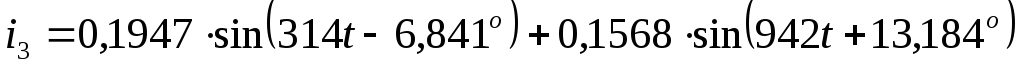 А
А 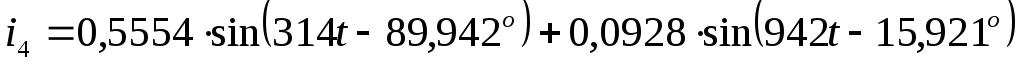 А
А 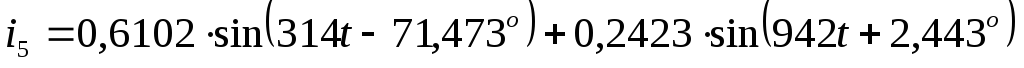 А
А
12
made by avengerЗакон Джоуля – Ленца в дифференциальной форме — Студопедия
Мощность тепловых потерь в проводнике равна произведению тока и напряжения P = IU.
Если рассмотреть в проводящей среде элемент объема dV, то мощность тепловых потерь
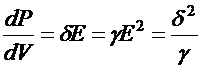
| (42.4) |
Формула (42.4) является дифференциальной формой закона Джоуля – Ленца. Мощность тепловых потерь в объеме V можно выразить следующим образом:
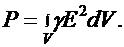
| (42.5) |
Первый закон Кирхгофа в дифференциальной форме
Если в проводящей среде выделить некоторый объем, по которому протекает постоянный, не изменяющийся во времени ток, то можно сказать, что ток, который войдет в объем, должен равняться току, вышедшему из него, иначе в этом объеме происходило бы накопление зарядов, что не подтверждается опытом. Сумму входящего в объем и выходящего из объема токов записывают так:
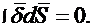
Равенство останется справедливым, если обе его части разделить на объем:

Очевидно, что последнее соотношение будет справедливо и в том случае, если объем, находящийся внутри замкнутой поверхности, устремить к нулю:
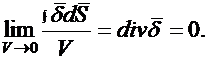
Таким образом, для постоянного, неизменного во времени поля в проводящей среде
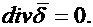
| (42.6) |
Это соотношение называют первым законом Кирхгофа в дифференциальной форме. Оно означает, что в установившемся режиме в любой точке поля нет ни истока, ни стока линий тока проводимости.
Уравнение Лапласа для электрического поля в
Проводящей среде
Напряженность электрического поля в проводящей среде, как и в электростатическом поле, 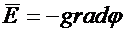 .
.
В неизменном во времени поле
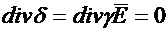
| (42.7) |
Если среда однородна и изотропна (γ=const), то 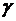 можно вынести за знак дивиргенции и, следовательно,
можно вынести за знак дивиргенции и, следовательно,
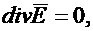
| (42.8) |
или
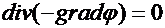 . .
| (42.9) |
Таким образом, поле в однородной проводящей среде подчиняется уравнению Лапласа. Поле постоянного тока в проводящей среде является полем потенциальным. В нем, в областях, не занятых источниками, 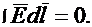
6. Переход тока из среды с проводимостью γ1 в среду с
проводимостью γ2. Граничные условия
Выясним, какие граничные условия выполняются при переходе тока из среды с одной проводимостью в среду с другой проводимостью.
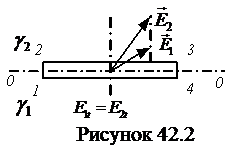 Возьмем на границе раздела сред – линия 00 (рис. 42.2) замкнутый контур 1234. Составим циркуляцию вектора
Возьмем на границе раздела сред – линия 00 (рис. 42.2) замкнутый контур 1234. Составим циркуляцию вектора 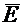 вдоль этого контура. Стороны 12 и 34 его весьма малы по сравнению со сторонами 23 и 41 (длину последних обозначим dl).
вдоль этого контура. Стороны 12 и 34 его весьма малы по сравнению со сторонами 23 и 41 (длину последних обозначим dl).
Так как 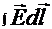 вдоль любого замкнутого контура равен нулю, то он равен нулю и для контура 12341.
вдоль любого замкнутого контура равен нулю, то он равен нулю и для контура 12341.
В силу малости отрезков 12 и 34 пренебрежем составляющими интеграла вдоль этих путей и тогда
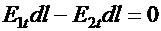 или или 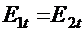 , ,
| (42.10) |
т.е. на границе раздела равны тангенциальные составляющие напряженности поля.
На границе раздела равны нормальные составляющие плотностей токов. Докажем это.
 |
На границе раздела выделим сплющенный параллелепипед (рис. 42.3,а). Поток вектора
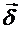 , втекающий в объем через нижнюю грань, равен
, втекающий в объем через нижнюю грань, равен 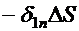 ; поток вектора
; поток вектора 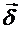 , вытекающий из объема через верхнюю грань
, вытекающий из объема через верхнюю грань 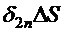 . Так как
. Так как 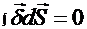 , то
, тоСледовательно, при переходе тока из среды с одной проводимостью в среду с другой проводимостью непрерывна тангенциальная составляющая вектора 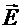 , то есть
, то есть 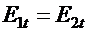 (но
(но 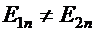 ), и непрерывна нормальная составляющая плотности тока
), и непрерывна нормальная составляющая плотности тока 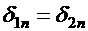 (но
(но 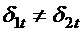 ).
).
Отсюда следует, что полные значения вектора 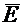 и вектора
и вектора 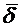 в общем случае меняются скачком на границе раздела.
в общем случае меняются скачком на границе раздела.
Найдем связь между углом падения 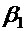 и углом преломления
и углом преломления 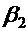 . В соответствии с рис. 42.3,б:
. В соответствии с рис. 42.3,б:
Если ток переходит из среды с большой проводимостью (например, из металла) в среду с малой (например, в землю), то тангенс угла преломления 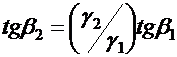 меньше тангенса угла падения и, следовательно, угол
меньше тангенса угла падения и, следовательно, угол 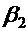 меньше угла
меньше угла 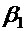 . Если
. Если 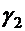 весьма мало, то угол
весьма мало, то угол 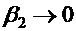 .
.
Вопросы для самоконтроля
1. Какой ток называют током проводимости , а какой – током смещения?
2. Как связаны вектор плотности тока и ток?
3. Проделайте вывод закона Ома в дифференциальной форме.
4. Что понимают под сторонней напряженностью электрического поля?
5. Почему уравнение 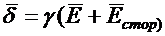 называют обобщенным законом Ома, а также вторым законом Кирхгофа?
называют обобщенным законом Ома, а также вторым законом Кирхгофа?
6. Проделайте вывод первого закона Кирхгофа в дифференциальной форме и поясните его физический смысл.
7. Получите выражение для закона Джоуля-Ленца в дифференциальной форме.
8. Докажите, что электрическое поле в проводящей среде подчиняется уравнению Лапласа.
9. Сформулируйте условия на границе раздела двух сред с разной удельной проводимостью.
закон Кирхгофа в дифференциальной форме — со всех языков на русский
См. также в других словарях:
Закон Ома для полной цепи — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия
Закон Ома — Классическая электродинамика … Википедия
Закон сохранения электрического заряда — гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется. Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме… … Википедия
Закон сохранения заряда — Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется. Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение объясняют следствием принципа… … Википедия
Закон индукции Фарадея — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия
Закон магнитоэлектрической индукции — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия
Ома закон — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия
ОМА ЗАКОН — устанавливает зависимость между силой тока I в проводнике и разностью потенциалов (напряжением) U между двумя фиксиров. точками (сечениями) этого проводника: U=rI. (1) Коэфф. пропорциональности r, зависящий от геом. и электрич. св в проводника и… … Физическая энциклопедия
Ома закон — для участка электрической цепи (проводника), не содержащего источников эдс, устанавливает связь между силой тока в проводнике и разностью потенциалов (напряжением) на его концах: сила тока прямо пропорциональна напряжению и обратно… … Энциклопедический словарь
Магнитный закон Гаусса — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия
Ома закон — устанавливает, что сила постоянного электрического тока I в проводнике прямо пропорциональна разности потенциалов (напряжению) U между двумя фиксированными точками (сечениями) этого проводника: RI = U. (1) Коэффициент… … Большая советская энциклопедия
Закон Кирхгофа — Учебный материал для IIT JEE

- Полный курс физики — 11 класс
ПРЕДЛАГАЕМАЯ ЦЕНА: рупий.2 968
- Просмотр подробностей
Ток и напряжение
Прежде чем перейти к законам Кирхгофа, давайте обсудим ток и напряжение в сети, поскольку закон касается как напряжения, так и тока.
В металлах электроны на внешней орбите не связаны прочно, и поэтому эти электроны покидают соответствующий атом и плавают вокруг. Эти электроны называются свободными электронами. Таким образом, электропроводность — это поток этих свободных электронов. Проводники, такие как медь, серебро, позволяют свободно перемещаться крайним электронам от одного атома к другому. Изоляторы, такие как дерево и резина, не позволяют электронам перемещаться между атомами, поскольку они прочно удерживаются внутри атомов.Направление электрического тока будет противоположным направлению потока электронов.
Электрический ток — это скорость, с которой электрический заряд проходит через точку. Это поток положительных зарядов. Через материал протекает электрический ток в один ампер, если один кулон заряда проходит через проводник за одну секунду. Единица измерения тока в системе СИ — амперы. Чем выше скорость, с которой электроны текут в цепи, тем выше ток.
Электрический ток течет из-за разницы потенциалов между двумя точками.Потенциальная разница — это изменение количества отрицательных зарядов, вызывающих поток электронов. Отрицательный потенциал — это точка с большим количеством электронов, а положительный потенциал — это точка с меньшим количеством электронов. Таким образом, электроны текут от отрицательного потенциала к положительному. Таким образом, ток течет от конца положительного потенциала к концу отрицательного потенциала, когда будет разность потенциалов. Эта разность потенциалов упоминается как напряжение в цепи. Напряжение определяется как энергия, необходимая для перемещения единичного заряда из одной точки в другую.Единица измерения напряжения — вольт. Один джоуль на кулон называется вольт.
Сила тока в цепи определяется разницей в напряжении. Например, , когда через лампочку не проходит ток, это означает, что напряжение на обеих сторонах лампы одинаковое. Разность потенциалов обычно обеспечивается батареями. Рассмотрим несколько лампочек, которые подключены к батарее параллельно. Напряжение на каждой лампочке будет равно напряжению, производимому батареей.В этом случае общий ток, снимаемый с батареи, равен сумме всех токов, потребляемых каждой лампочкой. Когда лампочки соединены последовательно, ток, проходящий через каждую лампочку, одинаков, и поэтому свет не будет таким ярким.
Густав Роберт Кирхгоф
Густав Роберт Кирхгоф был ученым девятнадцатого века, внесшим большой вклад в теорию цепей. Таким образом он мог лучше понять электрические цепи.Он обнаружил, что по проводнику электрический ток течет со скоростью света.
Законы Кирхгофа
Густав Кирхгоф разработал свод законов, касающихся сохранения тока и энергии в электрических цепях. Это KCL (Закон Кирхгофа) , который касается тока, протекающего в цепи, и KVL (Закон напряжения Кирхгофа) , который касается источника напряжения, присутствующего в цепи. Его открытия также проложили путь к квантовой теории электромагнитной индукции Макса Планка.Большинство его открытий и исследований касалось электрического тока. Среди них закон цепей Кирхгофа является наиболее важным.
Мы знаем, что Георг Симон Ом показал взаимосвязь между напряжением, током и сопротивлением и сформулировал закон Ома. Этот закон — основа электричества. Закон гласит, что V = I R, где напряжение V выражено в вольтах, ток I — в амперах, а сопротивление R — в омах. Таким образом, I = V / R и R = V / I. Но в сложных схемах трудно определить напряжение и ток в цепи, используя закон Ома.Следовательно, для сложных схем закон схем Кирхгофа помогает нам найти значения напряжения и тока, протекающие в цепи.
Условия схемы
Цепь — это замкнутая цепь, по которой протекает ток. Путь — это одна линия, состоящая из элементов схемы и источников. Узел определяется как терминал или соединение, в котором два или более элемента будут соединены вместе и, таким образом, будут иметь общую точку для более чем одной ветви. Ветвь состоит из элементов, таких как резисторы и источники, подключенные между двумя узлами.Цикл — это замкнутый путь, в котором элементы учитываются только один раз. Сетка — это открытый контур и открытый путь без элементов в нем. Если элементы соединены последовательно, ток, протекающий через каждый из них, будет одинаковым. Если элементы соединены параллельно, напряжение на каждом компоненте остается неизменным.
Первый закон — Действующий закон Кирхгофа
Этот закон касается тока, протекающего в цепи. Он утверждает, что алгебраическая сумма всех токов, встречающихся в точке, равна нулю.Полный ток, входящий в узел или соединение, равен общему току или заряду, выходящему из узла. Это также известно как Conservation of Charge .
Рассмотрим узел, и здесь три тока входят в узел, а три тока выходят из узла. Токи, входящие в узел, считаются положительными, а ток, выходящий из узла, считается отрицательным. Закон гласит, что суммарный ток, входящий в узел, плюс общие токи, выходящие из узла, равны нулю.

Действующий закон Кирхгофа
Таким образом, I 1 — I 2 — I 3 + I 4 + I 5 — I 6 = 0 или I 1 + I 4 + I 5 = I 2 + I 3 + I 6. Это правило соединения.
Итак, токи, входящие в узел, = токи, выходящие из узла.
Второй закон — Закон Кирхгофа о напряжении
Когда ток проходит по цепи, величина тока изменяется в зависимости от произведения тока и сопротивления или ЭДС, включенных в цепь.Таким образом, закон гласит, что алгебраическая сумма всех напряжений в контуре будет равна нулю. Это также известно как Сохранение энергии . Здесь сумма падений напряжения равна сумме подъемов напряжения. Рассмотрим три напряжения V 1 , V 2 , V 3 , которые включены в цепь.

Закон Кирхгофа о напряжении
Уравнение по закону записывается как V 1 + V 2 + V 3 = 0.
Направление тока может быть как по часовой стрелке, так и против часовой стрелки. После выбора направления тока нам необходимо поддерживать одно и то же направление по всей цепи. Если окончательное значение положительное, очевидно, что предполагаемое направление тока правильное. Если окончательное значение, которое мы получаем, является отрицательным, это говорит о том, что текущее направление, которое мы приняли, было обратным. Падение напряжения на резисторах, когда ток течет по часовой стрелке n по часовой стрелке, считается положительным падением.Падение напряжения на резисторах при протекании тока против часовой стрелки считается отрицательным. Это также известно как Loop , Rule .
Анализ цепей
Здесь мы решаем приведенную ниже схему, используя закон Кирхгофа по току и закон Кирхгофа по напряжению. Рассмотрим схему с резисторами R 1 , R 2 и R 3 , значения которых составляют 5 Ом, 10 Ом и 5 Ом соответственно.Две ячейки E 1 и E 2 подключены в цепи, значения которых составляют 10 В и 5 В соответственно.

Решение схемы по KCL и KVL
Учитывайте направление тока, указанное стрелками на схеме. Теперь применим текущий закон Кирхгофа к перекресткам B и E.
Так ток в сетке EAB = i 1.
Ток в сетке BE = i 2.
Таким образом, ток в сетке BCDE = i 1 — i 2.
Далее мы применяем закон напряжения Кирхгофа к сетке EAB. Здесь 10 В считается по часовой стрелке.
5 i 1 + 10 i 2 = 10. Пусть это будет первое уравнение.
Рассмотрим следующую сетку EBCD, в которой снова 5 В по часовой стрелке.
5 (i 1 — i 2 ) — 10 i 2 = 5
5 i 1 — 5 i 2 — 10 i 2 = 5
5 i 1 — 15 i 2 = 5
Решая два уравнения, получаем
5 i 1 + 10 i 2 = 10 —
5 i 1 — 15 i 2 = 5
Тогда 10 i 2 — (- 15i 2 ) = 5
10 я 2 + 15 я 2 = 5
Таким образом, 25 i 2 = 5
и 2 = 5/25 = 0.2 А
Подставляем это значение в уравнение 1, получаем 5 i 1 + 10 (0,2) = 10
5 i 1 + 2 = 10
5 и 1 = 8
i 1 = 8/5 = 1,6 А
Таким образом, i 1 = 1,6 A и i 2 = 0,2 A
1,6 A — это ток, протекающий через сетку EAB с сопротивлением 5 Ом. 0,2 А — это ток, протекающий через 10 Ом
i 1 — i 2 = 1,6 — 0,2 = 1.4 А — это ток, протекающий в сетке BCDE с сопротивлением 5 Ом.
Определение внутреннего сопротивления и ЭДС ячеек по закону Кирхгофа
ЭДС или электродвижущая сила — это разность потенциалов, которая возникает между двумя выводами батареи в разомкнутой цепи. Внутреннее сопротивление — это сопротивление, которое обеспечивают электролит и электроды, присутствующие в элементе. Таким образом, внутреннее сопротивление обеспечивается электродами и электролитом, которые препятствуют прохождению тока внутри ячейки.

Найти внутреннее сопротивление
Мы знаем, что общее количество энергии в цепи равно общему количеству потребляемой энергии. Итак, энергия на входе = энергия на выходе. Мы также знаем, что согласно закону Ома V = I R, где I — ток, а R — сопротивление.
20 В = (0,5 * 5) + (0,5 * 10) + (0,5 * r)
= 2,5 + 5 + 0,5 г
= 7,5 + 0,5 г
20 — 7,5 = 0,5 г
0.5 р = 12,5
г = 12,5 / 0,5
= 25 Ом
Таким образом, мы смогли найти внутреннее сопротивление ячейки.
Далее мы собираемся найти ЭДС схемы, приведенной ниже. Из второго закона мы можем записать уравнение как 1,5 * 5 + 1,5 * 2 + 1,5 * 3 = ЭДС
Таким образом, ЭДС = 7,5 + 3 + 4,5
= 15 В

Найти ЭДС
ЭДС батареи, которая заставляет ток течь по часовой стрелке, будет положительной, а ЭДС батареи, которая заставляет ток течь в направлении против часовой стрелки, отрицательна.
Применение закона Кирхгофа
Мы поняли, что закон Кирхгофа используется для определения значений текущего напряжения и внутреннего сопротивления в цепях постоянного тока. Таким образом, мы можем обнаружить неизвестные значения в сложных сетях и схемах. Мост Уитстона — важное приложение закона Кирхгофа. Он используется при анализе сетки и узлов.
Ограничения закона Кирхгофа
И закон KCL, и KVL не подходят для цепей переменного тока высокой частоты.Текущие законы применимы только тогда, когда электрический заряд в цепи постоянный. KVL применяется в предположении, что магнитные поля не изменяются в замкнутой цепи. Таким образом, мы не можем применять KVL, когда магнитное поле изменяется внутри цепи.
Сводка
Густав Кирхгоф дал лучшее понимание электрических цепей.
Первый закон Кирхгофа гласит, что полный ток, который входит в узел или переход, равен общему току или заряду, выходящему из узла.Он известен как Conservation of Charge . Это правило пересечения.
Второй закон Кирхгофа гласит, что сумма падений напряжения равна сумме повышений напряжения. Он известен как Conservation of Energy . Это правило цикла.
Посмотрите это видео, чтобы получить дополнительную информацию
Дополнительная информация
Закон Кирхгофа

Особенности курса
- 101 Видеолекция
- Примечания к редакции
- Документы за предыдущий год
- Ментальная карта
- Планировщик обучения
- Решения NCERT
- Обсуждение Форум
- Тестовая бумага с видео-решением
.
Закон Кирхгофа для сложных схем | ОРЕЛ
ЗаконОма — ваш золотой билет для расчета напряжения, тока или сопротивления в простой последовательной или параллельной цепи, но что происходит, когда ваша схема более сложная? Возможно, вы разрабатываете электронику, которая имеет как параллельное, так и последовательное сопротивление, и закон Ома начинает падать. Или что, если у вас нет источника постоянного тока? В таких ситуациях, когда нельзя использовать только V = IR, пора встать на плечи Ома и применить закон Кирхгофа.Здесь мы рассмотрим, что такое Закон Кирхгофа и как его использовать для анализа напряжения и тока сложных электрических цепей.
Что такое Окружной закон Кирхгофа?
Когда вы строите сложную схему, включающую мосты или Т-сети, вы не можете полагаться исключительно на закон Ома, чтобы найти напряжение или ток. Здесь пригодится закон Кирхгофа, который позволяет рассчитывать как ток, так и напряжение для сложных цепей с помощью системы линейных уравнений.Существует два варианта закона Кирхгофа, в том числе:
- Текущий закон Кирхгофа: Для анализа полного тока сложной цепи
- Закон Кирхгофа о напряжении : для анализа полного напряжения сложной цепи
- Когда вы объединяете эти два закона, вы получаете Окружной закон Кирхгофа
Как любой другой научный или математический закон, названный в честь их создателя, Закон Кирхгофа был изобретен немецким физиком Густавом Кирхгофом.Густав был известен многими достижениями при жизни, в том числе теорией спектрального анализа, которая доказала, что элементы излучают уникальный световой узор при нагревании. Когда Кирхгоф и химик Роберт Бунзен проанализировали эти световые узоры через призму, они обнаружили, что каждый элемент периодической таблицы имеет свою уникальную длину волны. Открытие этого паттерна позволило дуэту открыть два новых элемента, цезий и рубидий.

Густав Кирхгоф (слева) и Роберт Бунзен (справа)
Кирхгоф позже применил свою теорию спектрального анализа для изучения состава Солнца, где он обнаружил множество темных линий в спектре длин волн Солнца.Это было вызвано тем, что газ Солнца поглощает световые волны определенной длины, и это открытие ознаменовало начало новой эры исследований и исследований в области астрономии.
Немного ближе к дому в мире электроники, Кирхгоф объявил свой свод законов для анализа тока и напряжения в электрических цепях в 1845 году, известный сегодня как Закон Кирхгофа о цепях. Эта работа строится на основе, изложенной в законе Ома, и помогла проложить путь к сложному анализу схем, на который мы полагаемся сегодня.
Первый закон — Действующий закон Кирхгофа
Закон Кирхгофа по току гласит, что величина тока, поступающего в узел, равна величине тока, выходящего из узла. Почему? Потому что, когда ток входит в узел, ему некуда идти, кроме выхода. То, что входит, должно выйти. Вы можете определить узел, в котором два или более пути соединены общей точкой. На схеме это будет точка соединения, соединяющая две пересекающиеся сетевые соединения.
Взгляните на изображение ниже, чтобы визуально понять этот Закон.Здесь у нас есть два тока, входящие в узел, и три тока, выходящие из узла. Согласно закону Кирхгофа, взаимосвязь между этими токами, входящими в узел и выходящими из него, может быть представлена как I 1 + I 2 = I 3 + I 4 + I 5 .

Текущий закон Кирхгофа, ток на входе должен равняться току на выходе. (Источник изображения)
Когда вы уравновешиваете это уравнение как алгебраическое выражение, вы делаете вывод, что ток на входе и выходе из узла всегда будет равен 0, или I 1 + I 2 + (-I 3 + -I 4 + -I 5 ) = 0 Все должно уравновешиваться, и Кирхгоф назвал этот принцип Сохранением заряда .
Давайте посмотрим на пример схемы, чтобы увидеть, как это работает. Ниже у нас есть схема с четырьмя узлами: A, C, E и F. Сначала ток течет от источника напряжения и разделяется на узле A, а затем протекает через резисторы R1 и R2. Оттуда ток рекомбинирует в узле C и снова разделяется, чтобы течь через резисторы R3, R4 и R5, где он встречается с узлом E и узлом F.

(Источник изображения)
Чтобы подтвердить закон Кирхгофа в этой цепи, нам необходимо предпринять следующие шаги:
- Рассчитать полный ток цепи
- Рассчитать ток, протекающий через каждый узел
- Сравните входные и выходные токи в определенных узлах, чтобы подтвердить текущий закон Кирхгофа.
1. Рассчитайте общий ток
Здесь мы используем закон Ома, чтобы получить полный ток нашей цепи с I = V / R . У нас уже есть общее напряжение 132 В, и теперь нам просто нужно найти общее сопротивление во всех наших узлах. Для этого требуется простой метод расчета общего сопротивления резисторов, подключенных параллельно, которое составляет:

Начиная с узла AC, получаем следующее сопротивление для параллельных резисторов R1 и R2:

И переходя к узлу CEF, мы получаем следующее сопротивление для параллельных резисторов R3, R4 и R5:

Теперь у нас есть общее сопротивление 11 Ом для всей цепи, которое мы можем затем подключить к закону Ома I = V / R , чтобы получить общий ток в нашей цепи:

2.Расчет узловых токов
Теперь, когда мы знаем, что через нашу цепь выходит 12 ампер, мы можем рассчитать ток в каждом наборе узлов. Мы снова воспользуемся помощью закона Ома в форме I = V / R , чтобы получить ток для каждой ветви узла.
Во-первых, нам нужны напряжения для узловых ветвей AC и CF:

Затем мы можем рассчитать ток для каждой ветви узла:

3. Подтвердите действующий закон Кирхгофа
После вычисления тока для каждой ветви узла у нас теперь есть две отдельные контрольные точки, которые мы можем использовать для сравнения наших входных и выходных токов.Это позволит нам проанализировать нашу схему и подтвердить текущий закон Кирхгофа следующим образом:

Второй закон — Закон Кирхгофа о напряжении
Закон Кирхгофа о напряжении гласит, что в любой цепи с замкнутым контуром полное напряжение всегда будет равно сумме всех падений напряжения в контуре. Вы обнаружите, что при протекании тока через пассивный компонент, такой как резистор, происходит падение напряжения, и Кирхгоф назвал этот закон Сохранением энергии .Опять же, то, что входит, должно выходить наружу.
Взгляните на изображение ниже, чтобы понять это визуально. В этой схеме у нас есть источник напряжения и четыре области в цепи, где напряжение встретит пассивный компонент, что вызовет заметное падение напряжения.

Поскольку эти пассивные компоненты соединены последовательно, вы можете просто сложить общие падения напряжения и сравнить их с общим напряжением, чтобы получить соотношение, которое выглядит следующим образом:

Давайте начнем с простой схемы, чтобы продемонстрировать, как это работает.В приведенном ниже примере у нас есть две известные переменные: полное напряжение и падение напряжения на R1.

(Источник изображения)
Что нам нужно выяснить, так это падение напряжения на R2, и мы можем использовать закон Кирхгофа, чтобы выяснить это со следующей зависимостью:

Поскольку полное падение напряжения в цепи должно равняться общему напряжению источника, это обеспечивает простой способ вычисления нашей недостающей переменной. Если бы вы хотели выразить это соотношение в виде правильного алгебраического выражения, вы бы получили сумму всех падений напряжения и общее напряжение, равное нулю, как показано здесь:

Давайте посмотрим на другой пример.В схеме ниже у нас есть три резистора, подключенных последовательно к батарее на 12 В.

Чтобы проверить закон напряжения Кирхгофа в этой цепи, нам необходимо предпринять следующие шаги:
- Вычислить общее сопротивление цепи
- Вычислить полный ток цепи
- Рассчитайте ток через каждого резистора
- Рассчитайте падение напряжения на на каждом резисторе
Сравните источник напряжения с общим падением напряжения , чтобы подтвердить закон Кирхгофа о напряжении
1.Рассчитайте общее сопротивление
Поскольку все наши резисторы соединены последовательно, мы можем легко найти общее сопротивление, просто сложив все значения сопротивления вместе:

2. Рассчитайте общий ток
Теперь, когда мы знаем наше полное сопротивление, мы снова можем использовать закон Ома, чтобы получить полный ток нашей цепи в виде I = V / R, , который выглядит так:

3. Рассчитайте ток через каждый резистор
Поскольку все наши резисторы соединены последовательно, через них будет проходить одинаковый ток, который можно выразить как:

4.Рассчитайте падение напряжения на каждом резисторе
.В нашем окончательном расчете мы снова будем использовать закон Ома, чтобы получить полное падение напряжения для каждого резистора в виде В = IR , которое выглядит следующим образом:

5. Подтвердите закон Кирхгофа о напряжении
Теперь у нас есть все необходимые данные, включая полное напряжение нашей цепи, а также каждое падение напряжения на каждом из наших резисторов. Собирая все это вместе, мы можем легко проверить закон напряжения Кирхгофа с помощью следующего соотношения:

Это также можно выразить как:

Как видите, полное напряжение равно общему падению напряжения в нашей цепи.То, что входит, должно выйти наружу, и закон Кирхгофа снова работает!
Процесс использования закона Кирхгофа о схемах
Понимая, как работает закон Кирхгофа, в вашем наборе инструментов теперь есть новый инструмент для анализа напряжения и тока в полных цепях. При использовании этих Законов в дикой природе рассмотрите возможность использования следующего пошагового процесса:
- Во-первых, начните с маркировки всех известных напряжений и сопротивлений на вашей цепи.
- Затем назовите каждую ветвь в вашей цепи текущей меткой, например I1, I2, I3 и т. Д.Ветвь — это один или группа компонентов, соединенных между двумя узлами.
- Затем найдите текущий закон Кирхгофа для каждого узла в вашей цепи.
- Затем найдите закон напряжения Кирхгофа для каждой из независимых петель в вашей цепи.
После расчета законов Кирхгофа по току и напряжению вы можете использовать свои уравнения, чтобы найти недостающие токи. Готовы попробовать это самостоятельно? Взгляните на схему ниже и посмотрите, сможете ли вы проверить закон тока Кирхгофа и закон напряжения с небольшой помощью Ома!

Напишите свои ответы в комментариях ниже!
Стоя на плечах Ома
Имея в руках Закон Кирхгофа о цепях, теперь у вас есть все инструменты, необходимые для анализа напряжения и тока в сложных цепях.Как и многие другие научные и математические принципы, закон Кирхгофа стоит на плечах того, что было раньше — закона Ома. Вы обнаружите, что используете закон Ома для расчета отдельных сопротивлений, напряжений или токов, а затем, основываясь на этих расчетах с законом Кирхгофа, убедитесь, что ваша схема соответствует этим принципам тока и напряжения.
Готовы применить закон Кирхгофа в своем собственном проекте электронного дизайна? Попробуйте Autodesk EAGLE бесплатно сегодня!
.Закон Фурье — формула, вывод, определение, уравнение
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma класса 8
- Решения RD Sharma класса 9
- Решения RD Sharma класса 10
- Решения RD Sharma класса 11
- Решения RD Sharma класса 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- BNAT 000 NC
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образцы документов CBSE чел для класса 12
- Классы
- CBSE Контрольный документ за предыдущий год
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- , класс
- CBSE Notes
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции
- CBSE Class
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE
Дополнительные вопросы по математике для класса 10
- CBSE Class
- Дополнительные вопросы по науке, класс 10 по CBSE
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions For Класс 12 по физике
- Решения NCERT для химии класса 12
- Решения NCERT для класса 12 по биологии
- Решения NCERT для класса 12 по математике
- Решения NCERT Класс 12 Бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- Решения NCERT, класс 12 Экономика
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для социальных наук класса 6
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для класса 7 Наука
- Решения NCERT для класса 7 по социальным наукам
- Решения NCERT для класса 7 Английский
- Решения NCERT для класса 8 Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для социальных наук 8 класса
- Решение NCERT ns для класса 8 Английский
- Решения NCERT для социальных наук класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для Математика класса 9 Глава 2
- Решения NCERT для математики класса 9 Глава 3
- Решения NCERT для математики класса 9 Глава 4 Решения NCERT
- для математики класса 9 Глава 5
- Решения NCERT для математики класса 9 Глава 6
- Решения NCERT для Математика класса 9 Глава 7
- Решения NCERT для математики класса 9 Глава 8 Решения NCERT
- для математики класса 9 Глава 9 Решения NCERT
- для математики класса 9 Глава 10
- Решения NCERT для математики класса 9 Глава 11
- Решения NCERT для Математика класса 9 Глава 12
- Решения NCERT для математики класса 9 Глава 13 Решения
- NCERT для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для Науки Класса 9 Глава 4
- Решения NCERT для Науки Класса 9 Глава 5
- Решения NCERT для Науки Класса 9 Глава 6
- Решения NCERT для Науки Класса 9 Глава 7
- Решения NCERT для Класса 9 Наука Глава 8
- Решения NCERT для Науки Класса 9 Глава 9
- Решения NCERT для Науки Класса 9 Глава 10
- Решения NCERT для Науки Класса 9 Глава 12
- Решения NCERT для Науки Класса 9 Глава 11
- Решения NCERT для Класса 9 Наука Глава 13
- Решения NCERT для класса 9 Наука Глава 14
- Решения NCERT для класса 9 по науке Глава 15
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- Решения NCERT для математики класса 10 Глава 3
- Решения NCERT для математики класса 10 Глава 4
- Решения NCERT для математики класса 10 Глава 5
- Решения NCERT для математики класса 10 Глава 6
- Решения NCERT для математики класса 10 Глава 7
- Решения NCERT для математики класса 10 Глава 8
- Решения NCERT для математики класса 10 Глава 9 Решения NCERT
- для математики класса 10 Глава 10 Решения
- NCERT для математики класса 10 Глава 11
- Решения NCERT для математики класса 10 Глава 12
- Решения NCERT для математики класса 10 Глава 13
- NCERT Sol Решения NCERT для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки класса 10 Глава 1
- Решения NCERT для науки класса 10 Глава 2
- Решения NCERT для науки класса 10, глава 3
- Решения NCERT для науки класса 10, глава 4
- Решения NCERT для науки класса 10, глава 5
- Решения NCERT для науки класса 10, глава 6
- Решения NCERT для науки класса 10, глава 7
- Решения NCERT для науки 10 класса, глава 8
- Решения NCERT для науки класса 10 Глава 9
- Решения NCERT для науки класса 10 Глава 10
- Решения NCERT для науки класса 10 Глава 11
- Решения NCERT для науки класса 10 Глава 12
- Решения NCERT для науки 10 класса Глава 13
- Решения NCERT для науки 10 класса Глава 14
- Решения NCERT для науки 10 класса Глава 15
- Решения NCERT для науки 10 класса Глава 16
- Class 11 Commerce Syllabus
- ancy Account
- Учебный план по бизнесу, класс 11
- Учебный план по экономике, класс 11
- Учебный план по коммерции, класс 12
- Учебный план по бухгалтерии, класс 12
- Учебный план по бизнесу, класс 12
- Учебный план по экономике, класс 12 9000 9000
- Образцы документов по коммерции класса 11
- Образцы документов по коммерции класса 12
- TS Grewal Solutions
- TS Grewal Solutions Class 12 Accountancy
- TS Grewal Solutions Class 11 Accountancy
- Отчет о движении денежных средств
- Что такое Entry eurship
- Защита прав потребителей
- Что такое основной актив
- Что такое баланс
- Формат баланса
- Что такое акции
- Разница между продажами и маркетингом
- ICSE
- Документы
- ICSE
- Вопросы ICSE
- ML Aggarwal Solutions
- ML Aggarwal Solutions Class 10 Maths
- ML Aggarwal Solutions Class 9 Maths
- ML Aggarwal Solutions Class 8 Maths
- ML Aggarwal Solutions Class 7 Maths
- ML 6 Maths
- ML 6 Maths
- Selina Solutions
- Selina Solutions для класса 8
- Selina Solutions для Class 10
- Selina Solutions для Class 9
- Frank Solutions
- Frank Solutions для математики класса 10
- Frank Solutions для математики класса 9
- Класс ICSE 9000 2
- ICSE Class 6
- ICSE Class 7
- ICSE Class 8
- ICSE Class 9
- ICSE Class 10
- ISC Class 11
- ISC Class 12
- Exam
- IAS
- Civil
- Сервисный экзамен
- Программа UPSC
- Бесплатная подготовка к IAS
- Текущие события
- Список статей IAS
- Пробный тест IAS 2019
- Пробный тест IAS 2019 1
- Пробный тест IAS 2019 2
- Экзамен KPSC KAS
- Экзамен UPPSC PCS
- Экзамен MPSC
- Экзамен RPSC RAS
- TNPSC Group 1
- APPSC Group 1
- Экзамен BPSC
- WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
- Ключ ответов UPSC 2019
- IA S Coaching Бангалор
- IAS Coaching Дели
- IAS Coaching Ченнаи
- IAS Coaching Хайдарабад
- IAS Coaching Mumbai
- BYJU’SEE
- 9000 JEE 9000 Основной документ JEE 9000 JEE 9000
- Вопросник JEE
- Биномиальная теорема
- Статьи JEE
- Квадратичное уравнение
- Программа BYJU NEET
- NEET 2020
- NEET Приемлемость 9000 Критерии 9000 NEET4 9000 Пример 9000 NEET 9000 9000 NEET
- Поддержка
- Разрешение жалоб
- Служба поддержки
- Центр поддержки
- GSEB
- GSEB Syllabus
- GSEB4
- GSEB3 Образец статьи GSEB3
004 - MSBSHSE
- MSBSHSE Syllabus
- MSBSHSE Учебники
- Образцы статей MSBSHSE
- Вопросники MSBSHSE
- AP Board
- APSCERT
- Syll
- AP 9000SC4
- Syll
- AP
- Syll 9000SC4
- Syll
- Syll
- MP Board
- MP Board Syllabus
- MP Board Образцы документов
- Учебники MP Board
- Assam Board
- Assam Board Syllabus
- Assam Board Учебники 9000 9000 Board4 BSEB
- Bihar Board Syllabus
- Bihar Board Учебники
- Bihar Board Question Papers
- Bihar Board Model Papers
- BSE Odisha
- Odisha Board Syllabus
- Odisha Board Syllabus
- Odisha Board Syllabus
- Программа PSEB
- Учебники PSEB
- Вопросы PSEB
- RBSE
- Rajasthan Board Syllabus
- RBSE Учебники
- RBSE Question Papers
- HPBOSE
- HPBOSE
- HPBOSE
- JKBOSE
- Программа обучения JKBOSE
- Образцы документов JKBOSE
- Шаблон экзамена JKBOSE
- TN Board
- TN Board Syllabus
- TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 9000 Paper Papers 9000 TN Board 9000 4 JAC
- Программа JAC
- Учебники JAC
- Вопросники JAC
- Telangana Board
- Telangana Board Syllabus
- Telangana Board Учебники
- Papers Telangana Board Учебники
- Учебный план KSEEB
- Типовой вопросник KSEEB
- KBPE
- Учебный план KBPE
- Учебники KBPE
- Документы по KBPE
- 9000 Доска UPMSP 9000 Доска UPMSP 9000 Доска UPMSP 9000
- Совет по Западной Бенгалии
- Учебный план Совета по Западной Бенгалии
- Учебники для Совета по Западной Бенгалии
- Вопросы для Совета по Западной Бенгалии
- UBSE
- TBSE
- Гоа Совет
- 000
- NBSE0003 Board
- Manipur Board
- Haryana Board
- Государственные экзамены
- Банковские экзамены
- Экзамены SBI
- Экзамены IBPS
- Экзамены RBI
- IBPS
03
- Экзамены SSC
9SC2 - SSC GD
- SSC CPO 900 04
- SSC CHSL
- SSC CGL
- Экзамены RRB
- RRB JE
- RRB NTPC
- RRB ALP
- O Экзамены на страхование
- LIC4
- LIC4 9000 ADF UPSC CAPF
- Список статей государственных экзаменов
- Банковские экзамены
- Обучение детей
- Класс 1
- Класс 2
- Класс 3
- Академические вопросы
- Вопросы по физике
- Вопросы по химии
- Вопросы по химии
- Вопросы
- Вопросы по науке
- Вопросы GK
- Онлайн-обучение
Закон цепи тока в дифференциальной форме
Что такое закон Ампера?
Согласно закону Ампера «Линейный интеграл магнитного поля B вдоль замкнутого пути из-за тока равен произведению проницаемости свободного пространства и тока, заключенного в замкнутом пути».
Математически это выражается как:

Где
μ 0 = проницаемость свободного пространства
i = ток, текущий через проводник.
Проба: 
Рассмотрим прямой проводник, по которому протекает ток i. Ток создает магнитное поле B вокруг проводника. Силовые линии магнитного поля имеют форму концентрических кругов.
Ампера показал, что плотность потока B в любой точке вблизи проводника прямо пропорциональна току i и обратно пропорциональна расстоянию r от проводника, поэтому: 

Где — длина пути, называемого окружность круга?
Разделите круг, представляющий силовую линию магнитного поля, на большое количество маленьких элементов, каждый длиной dl.Величина B.dl рассчитывается для каждого элемента по следующей формуле:
B.dl = Bdlcos = Bdlcos0 = Bdl
Для полного круга:

Интегральная форма закона контура тока

Дифференциальная форма закона тока
Поскольку интегральная форма закона Ампера имеет вид:

Вышеупомянутое соотношение известно как дифференциальная форма закона оборота Ампера.
Применение закона цепи тока
Рассмотрим соленоид, имеющий n витков на единицу длины.Когда ток проходит через соленоид, внутри соленоида создается магнитное поле, направленное вдоль оси соленоида. Магнитное поле в космосе снаружи настолько слабое, что считается нулевым.

Чтобы вычислить значение магнитного поля B внутри соленоида по закону Ампера, мы рассмотрим замкнутый путь abcda в форме прямоугольника. Этот замкнутый путь известен как амперовский путь, как показано на рисунке.
Пусть этот путь разделен на четыре элемента длины как:
ab = L1
bc = L2
cd = L3
da = L4
Таким образом, что сумма точек Произведение магнитного поля на длину элемента составляет:
∑ B.ΔL = BL1 Cos θ1 + BL2 Cos θ2 + BL3 Cos θ3 + BL4 Cos θ4 ………. (1)
Поскольку L1 параллельно силовым линиям магнитного поля внутри соленоида, θ = 0 °
BL1 Cos θ1 = BL1
L2 и L4 перпендикулярны магнитному полю, т.е. θ2 = 90 ° и θ4 = 90 °
BL2 Cos θ2 = 0
BL4 Cos θ4 = 0
Линии и L3 вне соленоида, где поле слабее, то есть B = 0
или BL3 Cos θ3 = 0
Подставив все эти значения в уравнение (1), мы получим:
∑ B.ΔL = BL1 + 0 + 0 + 0
∑ B.ΔL = BL1 ………… .. (2)
По закону Ампера
∑ B.ΔL = μ0I ……… (3)
Если N — количество витков катушки, тогда
Ток = NI
И если «n» — количество витков на единицу длины, то
n = N / L1
N = nL1
Ток = n L1I
∑ B.ΔL = μ0n L1I ………… (4)
Сравнивая уравнения (2) и (4), мы получаем
μ0n L1I = BL1
B = μ0nI
Связанные темы на нашем сайте:

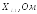
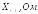
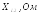
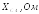
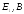
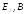
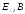

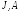
 ,
град
,
град ,
град
,
град ,
град
,
град ,
град
,
град