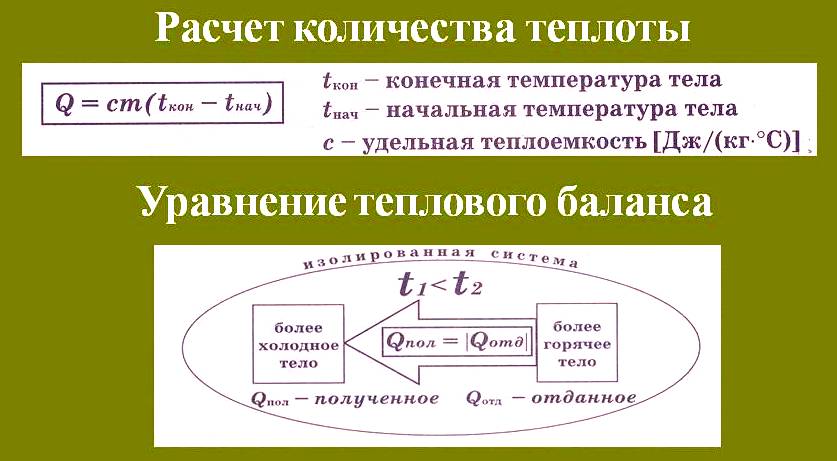
Формула количества теплоты
Здесь – количество теплоты, – удельная теплоёмкость вещества, из которого состоит тело, – масса тела, – разность температур.
Единица измерения количества теплоты — Дж (Джоуль) или кал (калория).
По сути тепловая энергия – это внутренняя энергия тела, значит потеря тепла – это уменьшение внутренней энергии тела, а нагревание – увеличение. Удельная теплоёмкость – это характеристика вещества, обозначающая его способность накапливать в себе внутреннюю (тепловую) энергию. Чем она меньше, тем легче вещество нагреть или охладить. Она не пропорциональна плотности, то есть более плотное вещество не обязательно будет нагреваться легче, чем менее плотное. Одно из веществ с большой теплоёмкостью – вода ( Дж/(кг * К)).
Примеры решения задач по теме «Количество теплоты»
Формула количества теплоты в физике
Определение и формула количества теплоты
Внутреннюю энергию термодинамической системы можно изменить двумя способами:
- совершая над системой работу,
- при помощи теплового взаимодействия.
Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем, что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии, которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.
Теплотой называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой). Обозначается теплота, обычно буквой Q.
Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики. Говорят, что теплота – это энергия в форме молекулярного движения.
Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.
Формула расчета теплоты при изменении температуры
Элементарное количество теплоты обозначим как . Обратим внимание, что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом. Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.
Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:
где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:
где – удельная теплоемкость тела, m – масса тела, — молярная теплоемкость, – молярная масса вещества, – число молей вещества.
Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты (), которое получает тело при увеличении его температуры на величину можно вычислить как:
где t2, t1 температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности () в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.
Формула количества теплоты при фазовых переходах
Переход от одной фазы вещества в другую сопровождается поглощением или выделением некоторого количества теплоты, которая носит название теплоты фазового перехода.
Так, для перевода элемента вещества из состояния твердого тела в жидкость ему следует сообщить количество теплоты () равное:
где – удельная теплота плавления, dm – элемент массы тела. При этом следует учесть, что тело должно иметь температуру, равную температуре плавления рассматриваемого вещества. При кристаллизации происходит выделение тепла равного (4).
Количество теплоты (теплота испарения), которое необходимо для перевода жидкости в пар можно найти как:
где r – удельная теплота испарения. При конденсации пара теплота выделяется. Теплота испарения равна теплоте конденсации одинаковых масс вещества.
Единицы измерения количества теплоты
Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж
Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.
Примеры решения задач
ПримерЗадание. Какие объемы воды следует смешать, чтобы получить 200 л воды при температуре t=40С, если температура одной массы воды t1=10С, второй массы воды t2=60С?
Решение. Запишем уравнение теплового баланса в виде:
где Q=cmt – количество теплоты приготовленной после смешивания воды; Q
Из уравнения (1.1) следует:
При объединении холодной (V1) и горячей (V2) частей воды в единый объем (V) можно принять то, что:
Так, мы получаем систему уравнений:
Решив ее получим:
Проведем вычисления (это можно сделать, не переходя в систему СИ):
(л)
(л)
Ответ.
Задание. Теплоемкость тела изменяется по линейному закону (рис.1) в зависимости от абсолютной температуры в рассматриваемом интервале . Какое количество теплоты получает тело, если T1=300 К, T2=400 К.
Решение. Исследуя график функции теплоемкости (C(T)) (рис.1) запишем его аналитическое выр
«Количество теплоты. Удельная теплоёмкость»
Количество теплоты
Изменение внутренней энергии путём совершения работы характеризуется величиной работы, т.е. работа является мерой изменения внутренней энергии в данном процессе. Изменение внутренней энергии тела при теплопередаче характеризуется величиной, называемой количествоv теплоты.
Количество теплоты – это изменение внутренней энергии тела в процессе теплопередачи без совершения работы. Количество теплоты обозначают буквой Q.
Работа, внутренняя энергия и количество теплоты измеряются в одних и тех же единицах — джоулях (Дж), как и всякий вид энергии.
В тепловых измерениях в качестве единицы количества теплоты раньше использовалась особая единица энергии — калория (
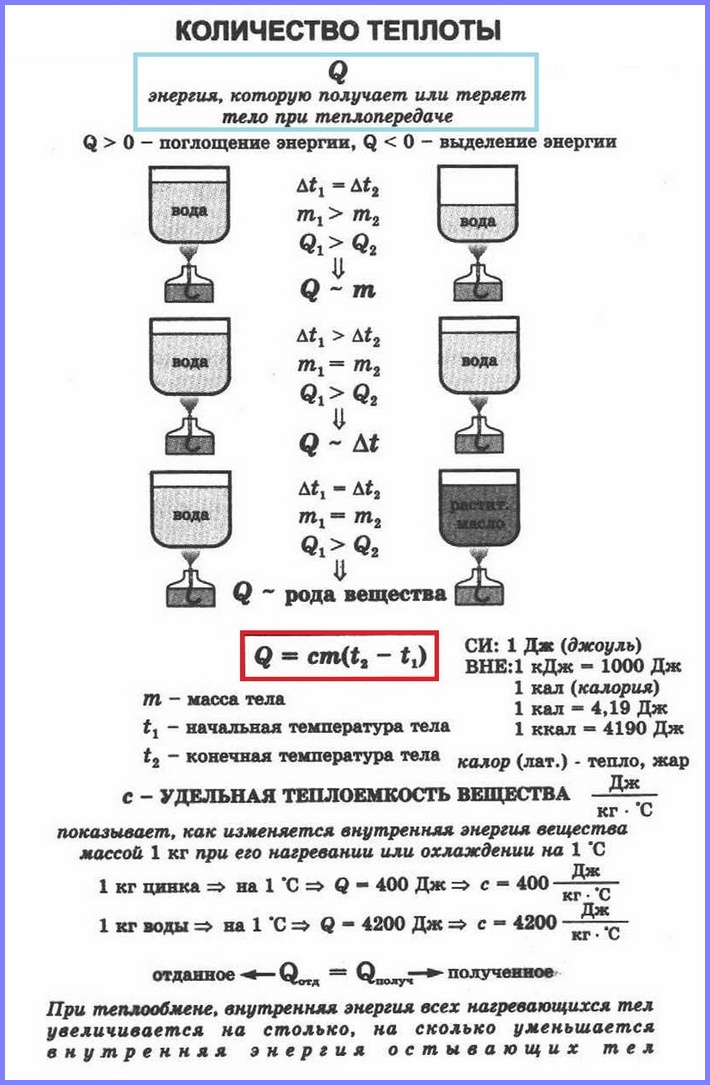
При передаче телу некоторого количества теплоты без совершения работы его внутренняя энергия увеличивается, если тело отдаёт какое-то количество теплоты, то его внутренняя энергия уменьшается.
Если в два одинаковых сосуда налить в один 100 г воды, а в другой 400 г при одной и той же температуре и поставить их на одинаковые горелки, то раньше закипит вода в первом сосуде. Таким образом, чем больше масса тела, тем большее количество тепла требуется ему для нагревания. То же самое и с охлаждением.

Количество теплоты, необходимое для нагревания тела зависит еще и от рода вещества, из которого это тело сделано. Эта зависимость количества теплоты, необходимого для нагревания тела, от рода вещества характеризуется физической величиной, называемой удельной теплоёмкостью
Удельная теплоёмкость
Удельная теплоёмкость – это физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания его на 1 °С (или на 1 К). Такое же количество теплоты 1 кг вещества отдаёт при охлаждении на 1 °С.
Удельная теплоёмкость обозначается буквой с. Единицей удельной теплоёмкости является 1 Дж/кг °С или 1 Дж/кг °К.
Значения удельной теплоёмкости веществ определяют экспериментально. Жидкости имеют большую удельную теплоёмкость, чем металлы; самую большую удельную теплоёмкость имеет вода, очень маленькую удельную теплоёмкость имеет золото.
Поскольку кол-во теплоты равно изменению внутренней энергии тела, то можно сказать, что удельная теплоёмкость показывает, на сколько изменяется внутренняя энергия
Количество теплоты Q, необходимое для нагревания тела массой m от температуры t1°С до температуры t2°С, равно произведению удельной теплоёмкости вещества, массы тела и разности конечной и начальной температур, т.е.
Q = c ∙ m (t2 — t1)
По этой же формуле вычисляется и количество теплоты, которое тело отдаёт при охлаждении. Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.

Это конспект по теме «Количество теплоты. Удельная теплоёмкость». Выберите дальнейшие действия:
Проходя по проводнику, ток может оказывать некоторые действия: тепловое, химическое и магнитное (подробно об этом можно почитать в \(7\) теме). Вспомним, с чем связано тепловое действие тока. Оно объясняется тем, что свободные электроны в металлах или ионы в растворах солей, кислот, щелочей, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества проводника и передают им свою энергию. В результате работы электрического тока внутренняя энергия проводника увеличивается. Например, спираль лампочки раскаляется до такой температуры, что начинает излучать свет.

Нагретый проводник отдаёт полученную энергию окружающим телам путём теплопередачи. Значит, количество теплоты, выделяемое проводником, по которому течёт ток, равно работе тока, т.е. Q = A, где \(А\) — работа тока, \(Q\) — количество теплоты.
Работу тока рассчитывают по формуле: A = U⋅I⋅t. Тогда количество теплоты будет определяться по такой же формуле: Q = U⋅I⋅t.
Пользуясь законом Ома, можно количество теплоты, выделяемое проводником с током, выразить через силу тока \(I\), сопротивление участка цепи \(R\) и время \(t\). Зная, что напряжение U = IR, получим: Q = I2⋅R⋅t.
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени.
К такому же выводу на основании опытов пришли независимо друг от друга английский учёный Джеймс Джоуль и русский учёный Эмилий Христианович Ленц. Поэтому сформулированный выше вывод называется законом Джоуля—Ленца.

Джоуль Джеймс Прескотт (\(1818—1889\)) — английский физик, член Лондонского королевского общества. Он внёс значительный вклад в исследование электромагнетизма и тепловых явлений, в создание физики низких температур, в обоснование закона сохранения и превращения энергии. Именем Джоуля назвали единицу измерения работы и энергии в системе СИ.

Эмилий Христианович Ленц (\(1804—1865\)) — российский физик и электротехник, академик Петербургской АН (\(1830\)), ректор Санкт-Петербургского университета (с \(1863\)) — один из основоположников электротехники. С его именем связано открытие закона, определяющего тепловые действия тока, и закона, определяющего направление индукционного тока.
Преобразование электрической энергии в тепловую широко используется в электрических печах и различных электронагревательных приборах.
Состояние сети, когда по проводам и приборам проходит ток больше допустимого значения, называется перегрузкой. Опасность этого явления в тепловом действии тока, ведь при большой перегрузке изоляция проводников легко воспламеняется. Перегрузка может возникнуть при подключении устройств большой мощности через удлинитель (смотри рисунок и никогда так не делай!).

Для примера, перегрузка проводов на \(25\)% приводит к сокращению срока их службы где-то с \(20\) лет до \(3—5\) месяцев, а перегрузка проводов на \(50\)% — до нескольких часов.
Источники:
Пёрышкин А.В. Физика, 8 класс// ДРОФА, 2013.
http://www.myshared.ru/slide/93472/
http://electricalschool.info/main/osnovy/1090-zakon-dzhoulja-lenca.html
http://class-fizika.narod.ru/10_7.htm
http://уроки.мирфизики.рф/%d0%b7%d0%b0%d0%ba%d0%be%d0%bd-%d0%b4%d0%b6%d0%be%d1%83%d0%bb%d1%8f-%d0%bb%d0%b5%d0%bd%d1%86%d0%b0/
http://www.nscience.ru/chemistry/physical/thermodynamics/what_does_thermidynamics_research/
http://energetika.in.ua/ru/books/book-2/part-2/section-1/1-2
http://to-name.ru/biography/emilij-lenc.htm
http://mistroim.ru/remont-pomesheniy/elektrichestvo/kakie-neispravnosti-v-elektroseti-mogut-vozniknut/
http://frutmrut.ru/zakon-dzhoulya-lenca
На практике часто приходится проводить различные тепловые расчёты. Например, при строительстве зданий необходимо учитывать, какое количество теплоты должна отдавать зданию вся система отопления, и какое количество теплоты будет уходить в окружающее пространство через окна, стены, двери.
Выведем формулу для расчёта количества теплоты, необходимого для нагревания некоторого вещества массой m на разность температур Δt=tконечная−tначальная.
Чтобы нагреть некоторое вещество массой \(1\) кг на \(1\)°C, необходимо затратить количество теплоты, равное удельной теплоёмкости \(с\) данного вещества, то есть в данном случае:
Q=c.
Если масса нагреваемого вещества в m раз больше, то и необходимое количество теплоты также в m раз больше:
Q=cm.
Аналогично, если разность температур вещества не \(1\)°C, а в Δt=tконечная−tначальная раз больше, то и теплоты понадобится в Δt=tконечная−tначальная раз больше.
Количество теплоты, получаемое веществом при нагревании, прямо пропорционально удельной теплоёмкости вещества, его массе и разности температур, то есть:
Q=cmΔt
или
Q=cmtкон−tнач.
Обрати внимание!
Данная формула даёт возможность найти и выделяемую при охлаждении вещества теплоту.
Чтобы рассчитать количество теплоты, необходимое для нагревания вещества (или выделяемое им при охлаждении), следует удельную теплоёмкость вещества умножить на его массу и на разность между конечной и начальной температурой вещества.
Так как конечная температура остывающего вещества меньше его начальной температуры:
tкон<tнач,
то изменение температуры оказывается отрицательным числом:
tкон−tнач<0.
Значит, и выделяемое веществом количество теплоты выражается отрицательным числом:
Qотданное<0.
Последний факт обозначает не рост, а убыль внутренней энергии вещества.
Источники:
Пёрышкин А.В. Физика, 8 кл.: учебник. — М.: Дрофа, 2013. — 237 с.
Исаченкова Л.А. Физика, 8 кл.: учебник. — Мн.: Народная асвета, 2015. — 183 с.
Опубликовано 13 Окт 2013
Рубрика: Теплотехника | 93 комментария
Человечеству известно немного видов энергии – механическая энергия (кинетическая и потенциальная), внутренняя энергия (тепловая), энергия полей (гравитационная, электромагнитная и ядерная), химическая. Отдельно стоит выделить энергию взрыва,…
…энергию вакуума и еще существующую только в теории – темную энергию. В этой статье, первой в рубрике «Теплотехника», я попытаюсь на простом и доступном языке, используя практический пример, рассказать о важнейшем виде энергии в жизни людей — о тепловой энергии и о рождающей ее во времени тепловой мощности.
Несколько слов для понимания места теплотехники, как раздела науки о получении, передаче и применении тепловой энергии. Современная теплотехника выделилась из общей термодинамики, которая в свою очередь является одним из разделов физики. Термодинамика – это дословно «теплый» плюс «силовой». Таким образом, термодинамика – это наука об «изменении температуры» системы.
Воздействие на систему извне, при котором изменяется ее внутренняя энергия, может являться результатом теплообмена. Тепловая энергия, которая приобретается или теряется системой в результате такого взаимодействия с окружающей средой, называется количеством теплоты и измеряется в системе СИ в Джоулях.
Если вы не инженер-теплотехник, и ежедневно не занимаетесь теплотехническими вопросами, то вам, столкнувшись с ними, иногда без опыта бывает очень трудно быстро в них разобраться. Трудно без наличия опыта представить даже размерность искомых значений количества теплоты и тепловой мощности. Сколько Джоулей энергии необходимо чтобы нагреть 1000 метров кубических воздуха от температуры -37˚С до +18˚С?.. Какая нужна мощность источника тепла, чтобы сделать это за 1 час?.. На эти не самые сложные вопросы способны сегодня ответить «сходу» далеко не все инженеры. Иногда специалисты даже помнят формулы, но применить их на практике могут лишь единицы!
Прочитав до конца эту статью, вы сможете легко решать реальные производственные и бытовые задачи, связанные с нагревом и охлаждением различных материалов. Понимание физической сути процессов теплопередачи и знание простых основных формул – это главные блоки в фундаменте знаний по теплотехнике!
Количество теплоты при различных физических процессах.
Большинство известных веществ могут при разных температуре и давлении находиться в твердом, жидком, газообразном или плазменном состояниях. Переход из одного агрегатного состояния в другое происходит при постоянной температуре (при условии, что не меняются давление и другие параметры окружающей среды) и сопровождается поглощением или выделением тепловой энергии. Не смотря на то, что во Вселенной 99% вещества находится в состоянии плазмы, мы в этой статье не будем рассматривать это агрегатное состояние.
Рассмотрим график, представленный на рисунке. На нем изображена зависимость температуры вещества Т от количества теплоты Q, подведенного к некой закрытой системе, содержащей определенную массу какого-то конкретного вещества.
1. Твердое тело, имеющее температуру T1, нагреваем до температуры Tпл, затрачивая на этот процесс количество теплоты равное Q1.
2. Далее начинается процесс плавления, который происходит при постоянной температуре Тпл (температуре плавления). Для расплавления всей массы твердого тела необходимо затратить тепловой энергии в количестве Q2— Q1.
3. Далее жидкость, получившаяся в результате плавления твердого тела, нагреваем до температуры кипения (газообразования) Ткп, затрачивая на это количество теплоты равное Q3—Q2.
4. Теперь при неизменной температуре кипения Ткп жидкость кипит и испаряется, превращаясь в газ. Для перехода всей массы жидкости в газ необходимо затратить тепловую энергию в количестве Q4—Q3.
5. На последнем этапе происходит нагрев газа от температуры Ткп до некоторой температуры Т2. При этом затраты количества теплоты составят Q5—Q4. (Если нагреем газ до температуры ионизации, то газ превратится в плазму.)
Таким образом, нагревая исходное твердое тело от температуры Т1 до температуры Т2 мы затратили тепловую энергию в количестве Q5, переводя вещество через три агрегатных состояния.
Двигаясь в обратном направлении, мы отведем от вещества то же количество тепла Q5, пройдя этапы конденсации, кристаллизации и остывания от температуры Т2 до температуры Т1. Разумеется, мы рассматриваем замкнутую систему без потерь энергии во внешнюю среду.
Заметим, что возможен переход из твердого состояния в газообразное состояние, минуя жидкую фазу. Такой процесс именуется возгонкой, а обратный ему процесс – десублимацией.
Итак, уяснили, что процессы переходов между агрегатными состояниями вещества характеризуются потреблением энергии при неизменной температуре. При нагреве вещества, находящегося в одном неизменном агрегатном состоянии, повышается температура и также расходуется тепловая энергия.
Главные формулы теплопередачи.
Формулы очень просты.
Количество теплоты Q в Дж рассчитывается по формулам:
1. Со стороны потребления тепла, то есть со стороны нагрузки:
1.1. При нагревании (охлаждении):
Q=m*c*(Т2-Т1)
Здесь и далее:
m – масса вещества в кг
с – удельная теплоемкость вещества в Дж/(кг*К)
1.2. При плавлении (замерзании):
Q=m*λ
λ – удельная теплота плавления и кристаллизации вещества в Дж/кг
1.3. При кипении, испарении (конденсации):
Q=m*r
r – удельная теплота газообразования и конденсации вещества в Дж/кг
2. Со стороны производства тепла, то есть со стороны источника:
2.1. При сгорании топлива:
Q=m*q
q – удельная теплота сгорания топлива в Дж/кг
2.2. При превращении электроэнергии в тепловую энергию (закон Джоуля — Ленца):
Q=t*I*U=t*R*I^2=(t/R)*U^2
t – время в с
I – действующее значение тока в А
U – действующее значение напряжения в В
R – сопротивление нагрузки в Ом
Делаем вывод – количество теплоты прямо пропорционально массе вещества при всех фазовых превращениях и при нагреве дополнительно прямо пропорционально разности температур. Коэффициенты пропорциональности (c, λ, r, q) для каждого вещества имеют свои значения и определены опытным путем (берутся из справочников).
Тепловая мощность N в Вт – это количество теплоты переданное системе за определенное время:
N=Q/t
Чем быстрее мы хотим нагреть тело до определенной температуры, тем большей мощности должен быть источник тепловой энергии – все логично.
Расчет в Excel прикладной задачи.
В жизни бывает часто необходимо сделать быстрый оценочный расчет, чтобы понять – имеет ли смысл продолжать изучение темы, делая проект и развернутые точные трудоемкие расчеты. Сделав за несколько минут расчет даже с точностью ±30%, можно принять важное управленческое решение, которое будет в 100 раз более дешевым и в 1000 раз более оперативным и в итоге в 100000 раз более эффективным, чем выполнение точного расчета в течение недели, а то и месяца, группой дорогостоящих специалистов…
Условия задачи:
В помещение цеха подготовки металлопроката размерами 24м х 15м х 7м завозим со склада на улице металлопрокат в количестве 3т. На металлопрокате есть лед общей массой 20кг. На улице -37˚С. Какое количество теплоты необходимо, чтобы нагреть металл до +18˚С; нагреть лед, растопить его и нагреть воду до +18˚С; нагреть весь объем воздуха в помещении, если предположить, что до этого отопление было полностью отключено? Какую мощность должна иметь система отопления, если все вышесказанное необходимо выполнить за 1час? (Очень жесткие и почти не реальные условия – особенно касающиеся воздуха!)
Расчет выполним в программе MS Excel или в программе OOo Calc.
С цветовым форматированием ячеек и шрифтов ознакомьтесь на странице «О блоге».
Исходные данные:
1. Названия веществ пишем:
в ячейку D3: Сталь
в ячейку E3: Лед
в ячейку F3: Лед/вода
в ячейку G3: Вода
в ячейку G3: Воздух
2. Названия процессов заносим:
в ячейки D4, E4, G4, G4: нагрев
в ячейку F4: таяние
3. Удельную теплоемкость веществ c в Дж/(кг*К) пишем для стали, льда, воды и воздуха соответственно
в ячейку D5: 460
в ячейку E5: 2110
в ячейку G5: 4190
в ячейку H5: 1005
4. Удельную теплоту плавления льда λ в Дж/кг вписываем
в ячейку F6: 330000
5. Массу веществ m в кг вписываем соответственно для стали и льда
в ячейку D7: 3000
в ячейку E7: 20
Так как при превращении льда в воду масса не изменяется, то
в ячейках F7 и G7: =E7=20
Массу воздуха находим произведением объема помещения на удельный вес
в ячейке H7: =24*15*7*1,23=3100
6. Время процессов t в мин пишем только один раз для стали
в ячейку D8: 60
Значения времени для нагрева льда, его плавления и нагрева получившейся воды рассчитываются из условия, что все эти три процесса должны уложиться в сумме за такое же время, какое отведено на нагрев металла. Считываем соответственно
в ячейке E8: =E12/(($E$12+$F$12+$G$12)/D8)=9,7
в ячейке F8: =F12/(($E$12+$F$12+$G$12)/D8)=41,0
в ячейке G8: =G12/(($E$12+$F$12+$G$12)/D8)=9,4
Воздух также должен прогреться за это же самое отведенное время, читаем
в ячейке H8: =D8=60,0
7. Начальную температуру всех веществ T1 в ˚C заносим
в ячейку D9: -37
в ячейку E9: -37
в ячейку F9: 0
в ячейку G9: 0
в ячейку H9: -37
8. Конечную температуру всех веществ T2 в ˚C заносим
в ячейку D10: 18
в ячейку E10: 0
в ячейку F10: 0
в ячейку G10: 18
в ячейку h20: 18
Думаю, вопросов по п.7 и п.8 быть недолжно.
Результаты расчетов:
9. Количество теплоты Q в КДж, необходимое для каждого из процессов рассчитываем
для нагрева стали в ячейке D12: =D7*D5*(D10-D9)/1000=75900
для нагрева льда в ячейке E12: =E7*E5*(E10-E9)/1000= 1561
для плавления льда в ячейке F12: =F7*F6/1000= 6600
для нагрева воды в ячейке G12: =G7*G5*(G10-G9)/1000= 1508
для нагрева воздуха в ячейке h22: =H7*H5*(h20-H9)/1000= 171330
Общее количество необходимой для всех процессов тепловой энергии считываем
в объединенной ячейке D13E13F13G13h23: =СУММ(D12:h22) = 256900
В ячейках D14, E14, F14, G14, h24, и объединенной ячейке D15E15F15G15h25 количество теплоты приведено в дугой единице измерения – в ГКал (в гигакалориях).
10. Тепловая мощность N в КВт, необходимая для каждого из процессов рассчитывается
для нагрева стали в ячейке D16: =D12/(D8*60)=21,083
для нагрева льда в ячейке E16: =E12/(E8*60)= 2,686
для плавления льда в ячейке F16: =F12/(F8*60)= 2,686
для нагрева воды в ячейке G16: =G12/(G8*60)= 2,686
для нагрева воздуха в ячейке h26: =h22/(H8*60)= 47,592
Суммарная тепловая мощность необходимая для выполнения всех процессов за время t рассчитывается
в объединенной ячейке D17E17F17G17h27: =D13/(D8*60) = 71,361
В ячейках D18, E18, F18, G18, h28, и объединенной ячейке D19E19F19G19h29 тепловая мощность приведена в дугой единице измерения – в Гкал/час.
На этом расчет в Excel завершен.
Выводы:
Обратите внимание, что для нагрева воздуха необходимо более чем в два раза больше затратить энергии, чем для нагрева такой же массы стали.
При нагреве воды затраты энергии в два раза больше, чем при нагреве льда. Процесс плавления многократно больше потребляет энергии, чем процесс нагрева (при небольшой разности температур).
Нагрев воды в десять раз затрачивает больше тепловой энергии, чем нагрев стали и в четыре раза больше, чем нагрев воздуха.
Для получения информации о выходе новых статей и для скачивания рабочих файлов программ прошу вас подписаться на анонсы в окне, расположенном в конце статьи или в окне вверху страницы.
После ввода адреса своей электронной почты и нажатия на кнопку «Получать анонсы статей» НЕ ЗАБУДЬТЕ ПОДТВЕРДИТЬ ПОДПИСКУ кликом по ссылке в письме, которое тут же придет к вам на указанную почту (иногда — в папку «Спам»)!
Мы вспомнили понятия «количество теплоты» и «тепловая мощность», рассмотрели фундаментальные формулы теплопередачи, разобрали практический пример. Надеюсь, что мой язык был прост, понятен и интересен.
Жду вопросы и комментарии на статью!
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
Ссылка на скачивание файла: raschet-teplovoy-moshchnosti (xls 19,5KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Количество теплоты
Количество теплоты — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основных термодинамических величин. Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.
Внутренняя энергия тела может изменяться за счет работы внешних сил. Для характеристики изменения внутренней энергии при теплообмене вводится величина, называемая количеством теплоты и обозначаемая Q. В международной системе единицей количества теплоты, также как работы и энергии, является джоуль: [Q] = [A] = [E] = 1 Дж. На практике еще иногда применяется внесистемная единица количества теплоты – калория. 1 кал. = 4,2 Дж.
Количество теплоты, передаваемое от одного тела к другому, может идти на нагревание тела, плавление, парообразование, либо выделяться при противоположных процессах – остывании тела, кристаллизации, конденсации. Теплота выделяется при сгорании топлива. Между массой вещества и количеством теплоты, необходимым для его нагревания, существует прямая пропорциональная зависимость.
- Количество теплоты, необходимое для нагревания тела или выделяющееся при его охлаждении, прямо пропорционально массе тела и изменению его температуры:
Q = cmΔT, где с — удельная теплоемкость [Дж/кг·К], m — масса тела [кг], ΔT — изменение температуры [К]
- Количество теплоты, необходимое для превращения жидкости в пар или выделяющееся при его конденсации, прямо пропорционально массе жидкости: Q = Lm, где L — удельная теплота парообразования [Дж/кг], m — масса тела [кг]
- Количество теплоты, необходимое для плавления тела или выделяющееся при его кристаллизации, прямо пропорционально массе этого тела: Q = λm, где λ (лямбда) — удельная теплота плавления [Дж/кг], m — масса тела [кг]
- Количество теплоты, выделяющееся при сгорании топлива, прямо пропорционально его массе: Q = qm, где q — удельная теплота сгорания [Дж/кг], m — масса тела [кг]
Удельная теплоемкость вещества показывает, чему равно количество теплоты, необходимое для нагревания или выделяющееся при охлаждении 1 кг вещества на 1 К.
Удельные теплоты парообразования, плавления, сгорания показывают, какое количество теплоты требуется для парообразования, плавления или выделяется при конденсации, кристаллизации, сгорании 1 кг вещества.
Другие заметки по физике
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса 9
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agard Agard Agard Agard Agulis Class 12- Классы
- RS Решения Aggarwal класса 10
- RS Решения Aggarwal класса 11
- RS Решения Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Предыдущий год Вопросник
- CBSE Предыдущий год Вопросники Класс 10
- CBSE Предыдущий год Вопросник класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы по CBSE 8 класса
- Дополнительные вопросы по CBSE 8 по естествознанию
- CBSE 9 Дополнительные вопросы по математике
- CBSE 9 по дополнительным вопросам по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для 11 класса Физика
- Решения NCERT для класса 11 Химия
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса 9
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agard Agard Agard Agard Agulis Class 12- Классы
- RS Решения Aggarwal класса 10
- RS Решения Aggarwal класса 11
- RS Решения Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Предыдущий год Вопросник
- CBSE Предыдущий год Вопросники Класс 10
- CBSE Предыдущий год Вопросник класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Maths
- Решения NCERT для класса 6 Science
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Класс 11 Бизнес-программы Syllabus
- Класс 11 Экономика Syllabus
Формула тепловых потерь теплопроводности
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса 9
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agard Agard Agard Agard Agulis Class 12- Классы
- RS Решения Aggarwal класса 10
- RS Решения Aggarwal класса 11
- RS Решения Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Предыдущий год Вопросник
- CBSE Предыдущий год Вопросники Класс 10
- CBSE Предыдущий год Вопросник класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Maths
- Решения NCERT для класса 6 Science
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Учебный курс по бизнес-классу 11000
- Учебная программа по экономическому классу
- Учебная программа по 12 классу
- Учебная программа по 12 классу
- Учебная программа по экономическому классу
- Решения TS Grewal Класс 12 Бухгалтерский учет
- Решения TS Grewal Класс 11 Бухгалтерский учет
- ML Решения Aggarwal Class 10 Maths
- ML Решения Aggarwal Class 9 Математика
- ML Решения Aggarwal Class 8 Maths
- ML Решения Aggarwal Class 7 Математические решения
- ML 6 0004
- ML 6
- Selina Solution для класса 8
- Selina Solutions для класса 10
- Selina Solution для класса 9
- ICSE класс 6
- ICSE класс 7
- ICSE
- ICSE
- ICSE Class 9
- ICSE Class 10
- ISC C lass 11
- ISC Class 1
— концепция — видео по химии от Brightstorm
Хорошо, давайте поговорим о удельной теплоемкости, удельной теплоемкости, которую мы будем обозначать буквой с. Это количество тепла, необходимое для повышения температуры 1 грамма вещества на 1 градус Цельсия или 1 Кельвин. Причина, по которой они могут быть взаимозаменяемыми, заключается в том, что они имеют одинаковые инкрементные значения, с которыми они могут переключаться. Итак, когда мы говорим о тепле, мы фактически измеряем тепло и энергию, и давайте поговорим о числах, которые вы на самом деле будете видеть в единицах, поэтому мы измеряем энергию в калориях или джоулях.Таким образом, 1 калория равна 4,184 джоуля, но это не та калория, которую вы видите на обратной стороне пищевой этикетки, это фактически калория с большой буквы C, которая фактически составляет 1 килограмм калорий, и те, которые равны тысяче калорий или 4,184 джоуля. Итак, понимая, что означают эти цифры, говоря о тепле, давайте вернемся к разговору об удельной теплоемкости, которая измеряется в джоулях на грамм градусов Цельсия.
Давайте поговорим об удельной теплоемкости воды, удельная теплоемкость воды составляет 4,184 джоулей на грамм градусов Цельсия, и что это значит? Это означает, что на каждый грамм воды, который вы хотите поднять на 1 градус Цельсия, требуется 4.184 Дж энергии. Это на самом деле относительно высоко по сравнению с остальными вещами в этой таблице и большинством веществ на самом деле. Это потому, что для нагревания воды требуется много энергии, если вы думаете о том, когда кипятите воду на плите или о чем-то, для чего на самом деле требуется много времени и много тепла для того, чтобы он действительно поднялся, перешел из жидкого состояния вверх когда оно достигает газообразного состояния. Лед в удельной теплоемкости фактически отличается для каждого состояния вещества, поэтому для того, чтобы лед повысил температуру льда, потребуется всего 2.03 Дж тепла, чтобы поднять 1 грамм вещества на 1 градус Цельсия.
И пар — это то же самое, для этого требуется всего 2,01, поэтому вдвое меньше энергии, чтобы поднять температуру льда или пара по сравнению с водой. Алюминий также относительно высок по сравнению с другими металлами. Металлы обычно имеют очень низкую удельную теплоемкость. Но алюминий на самом деле довольно высок — 0,897 Дж на грамм градуса Цельсия, поэтому чем меньше это значение, тем легче ему нагреваться. Хорошо, когда мы используем это в реальных формулах и на самом деле говорим о количестве необходимого тепла или о том, сколько температурных сдвигов или сколько массы нам нужно для определенных веществ.Итак, мы собираемся использовать эту формулу q равно mc дельта t или q равно m cad. q, когда мы говорим о тепле, является символом тепла и обычно измеряется в джоулях, может измеряться в килоджоулях или калориях, что не имеет значения, но это q представляет количество необходимого тепла или требуемого тепла или энергия.
м — наш символ для массы, обычно измеряется в граммах, c — наша удельная теплоемкость этого конкретного вещества, а дельта — это изменение, которое может быть снова, оно может быть в градусах Кельвина или градусах Цельсия, это не имеет значения потому что это изменение тепла.Теперь поговорим о том, как это влияет на диаграмму изменения фазы. Хорошо, это диаграмма изменения фазы для воды, позвольте мне записать это. Итак, обратите внимание, если вы посмотрите на склоны для изменения энергии как повышенную температуру твердого вещества по сравнению с жидкостью. Обратите внимание, что твердое тело имеет более крутой уклон, чем жидкое, потому что жидкости требуется больше энергии для повышения температуры в граммах, чем в случае твердого тела или газа. Они на самом деле круче на склонах, чем для жидкости, так что это фактически влияет на диаграмму изменения фазы, и это из-за удельной теплоемкости.
Давайте вместе решим проблему и выясним, как это на самом деле влияет на другие вещи. Итак, у нас есть архитектор, и он действительно заинтересован в устойчивой энергетике. Таким образом, архитектор проектирует дом, который частично нагревается от солнечной энергии, тепло от солнца будет храниться в солнечном пруду, как и в этом другом бассейне. Итак, у нас есть этот пруд, с которым мы имеем дело. Он состоит из 14 500 кг гранитной породы, а затем в нем содержится 22 500 кг воды.Хорошо вместе гранит и вода поглощают тепло в течение дня и выпускают его ночью, а затем выделяют ночью в дом, обогревая дом ночью. Архитектор обнаружил, что солнечный пруд увеличивается на 22 градуса Цельсия днем и понижается на 22 градуса Цельсия ночью. Так сколько энергии он выделяет и поглощает в течение дня? Итак, давайте подчеркнем, что мы, информация, которая у нас есть.
Давайте начнем с воды, так как у нас есть 2 вещества — гранит и вода, количество энергии, которое на самом деле требуется, общее количество энергии будет равно q гранита плюс q h3O плюс, причем q, которое мы знаем, равно Mc Delta T.Итак, давайте сначала разберемся с водой, хорошо, хорошо, вода хорошо вода, у нас есть масса 22 500 кг, и мы хотим, чтобы это было в граммах. Итак, мы собираемся сделать это 2,25 раза от 10 до седьмого грамма в порядке. C воды или удельная теплоемкость воды составляет 4,184 Дж на грамм градусов Цельсия. Теперь причина, по которой я хотел этого даже в граммах, и я не мог использовать килограммы, заключается в том, что в моем аппарате для измерения удельного веса были граммы. Итак, я хочу убедиться, что эти единицы одинаковы, хорошо. Итак, мы собираемся, мы знаем, что это меняет температуру, увеличивается и понижается до 22 градусов Цельсия.Таким образом, наше изменение температуры составляет 22 градуса по Цельсию.
Хорошо, поэтому, когда я умножаю их все вместе, я получаю количество энергии, которое требуется или которое поглощается водой из солнечного пруда [IB], которая находится в солнечном пруду. И поэтому мы умножаем их вместе, и мы получаем 2.1 в 10 раз с точностью до девятых джоулей, и причина в том, что снова удельная теплоемкость измеряется в джоулях, или это q измеряется в джоулях. Хорошо, давайте поговорим о q для гранита, потому что бассейн состоит из воды и гранита. Масса воды — 14, извините, масса гранита — 14 500 кг, что равно 1.45 раз от 10 до седьмого грамма. Значение q для гранита, если вы посмотрите на нашу таблицу, составляет 0,803, и опять-таки, это меняется на 22 градуса Цельсия. И я просто не ставлю единицы, потому что хочу сэкономить место. Хорошо, когда я умножаю все это вместе, я получаю 2,4 извините, это не правда, я сожалею о том, что я получаю 2,6 раза 10 с восьмым джоулем. Итак, общее количество энергии, которое получает этот реальный солнечный бассейн за день, равно 2. Мы собираемся добавить это 2,4 раза 10 к девятым джоулям энергии.Так что это на самом деле экономит нам много энергии, когда мы имеем дело, когда мы на самом деле собираемся нагреть или охладить наш дом. Таким образом, мы экономим много денег на устойчивой энергии, используя солнечный бассейн. Так что удельная теплоемкость на самом деле говорит нам много разных вещей, и она уникальна для каждого конкретного вещества, и это количество энергии, необходимое для поднятия 1 грамма вещества, 1 градус Цельсия.
