Основы электротехники и электроники: Курс лекций, страница 3

При свертке параллельных ветвей эквивалентное сопротивление всегда меньше наименьшего из сворачиваемых.

Если параллельно соединены n одинаковых сопротивлений (Рис. 3.3), эквивалентное сопротивление в n раз меньше сопротивления любой из ветвей.

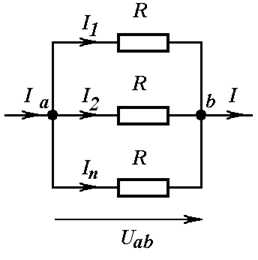
Рис. 3.3

Если на участке цепи параллельно соединены лишь два элемента (Рис. 3.4), выражение (3.2) упрощается. В этом случае эквивалентное сопротивление можно определить как отношение произведения двух сопротивлений к их сумме:

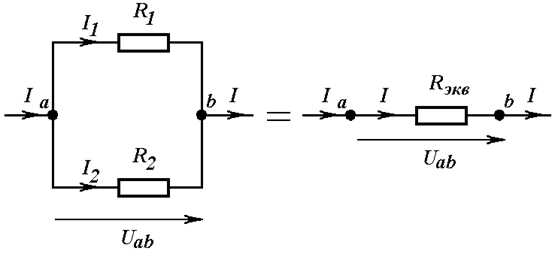
Рис. 3.4

4. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

К основным законам электрических цепей относятся закон Ома и законы Кирхгофа.

Закон Ома

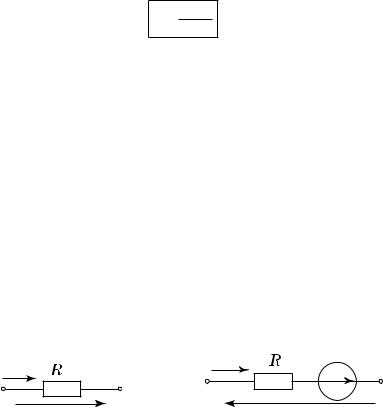
Если в ветви не содержится ЭДС, к ней применим уже известный закон Ома для пассивного участка цепи (1.1). Его можно сформулировать и следующим образом. Ток в ветви, не содержащей ЭДС, равен падению напряжения в ветви, деленному на сопротивление ветви (Рис. 4.1):

Рис. 4.1

Закон Ома для ветви, содержащей ЭДС, позволяет найти ток этой ветви по известной разности потенциалов на концах ветви. Ток в ветви, содержащей ЭДС, равен дроби, знаменатель которой – это сопротивление ветви. В числителе дроби – напряжение на концах ветви плюс алгебраическая сумма ЭДС, заключенных между концами ветви. С плюсом берутся напряжения и ЭДС, направление которых совпадает с направлением тока, с минусом – противоположные.

В частности, ток в ветви, изображенной на Рис. 4.2, равен:

.

Рис. 4.2

Первый закон Кирхгофа

В любом узле цепи алгебраическая сумма токов равна нулю. При этом, токи, направленные к узлу, принято считать положительными, токи, направленные от узла, принято считать отрицательными (Рис. 4.3).

Рис. 4.3

По первому закону Кирхгофа можно написать столько уравнений, сколько узлов содержит схема. Но не все они будут независимыми. Если схема содержит  узлов, независимыми будут  уравнений. Оставшееся уравнение будет являться следствием всех предыдущих.

Второй закон Кирхгофа

В любом замкнутом контуре цепи алгебраическая сумма напряжений равна алгебраической сумме ЭДС, включенных в контур.

При этом, положительными считаются те напряжения и ЭДС, которые совпадают с направлением обхода контура, отрицательными считаются напряжения и ЭДС, которые противоположны направлению обхода контура. Направление обхода контура можно выбирать произвольно.

Алгоритм составления уравнения по второму закону Кирхгофа для замкнутого контура цепи

Для заданного контура (Рис. 4.4 а) уравнение по второму закону Кирхгофа составляется в следующем порядке:

Рис. 4.4 а

1. Задается направление токов в ветвях (Рис. 4.4 б).

Рис. 4.4 б

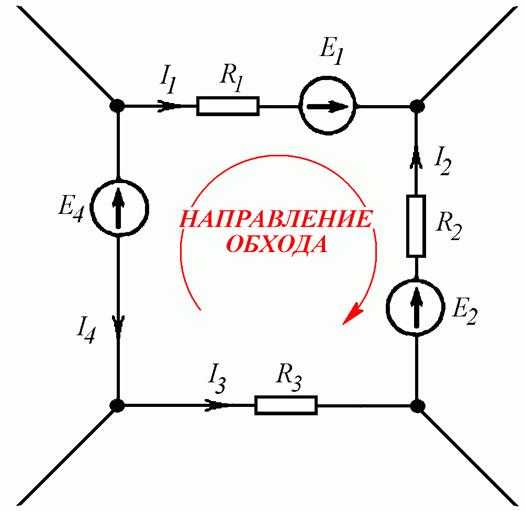
2. Выбирается направление обхода контура ( Рис. 4.4 в).

Рис. 4.4 в

3. Записывается уравнение, в левой части которого – сумма падений напряжений на сопротивлениях ветвей. В правой части – сумма ЭДС контура.

Примечание: Падение напряжения на сопротивлении ветви записывается в соответствии с известным уже законом Ома (1.1):

Применение второго закона Кирхгофа для незамкнутого участка цепи

Второй закон Кирхгофа справедлив только для замкнутого контура. При этом, любой незамкнутый участок цепи можно дополнить до замкнутого контура с помощью напряжения в разрыве незамкнутого участка.

Пример 4.1:

Незамкнутый участок цепи abcd изображен на Рис. 4.5 а.

а)

б)

Рис. 4.5

Дополняем участок до замкнутого контура, добавляя напряжение между незамкнутыми точками c и d (Рис. 4.5 б). Теперь для контура abcd можно записать второй закон Корхгофа:

Применение законов Кирхгофа при наличии в цепи источника тока

Источник тока имеет бесконечно большое сопротивление, поэтому не образует замкнутого контура и не может входить в уравнения второго закона Кирхгофа. Однако, в уравнениях первого закона Кирхгофа источник тока должен содержаться обязательно.

При необходимости записать уравнение по второму закону Кирхгофа для контура, содержащего источник тока, его заменяют напряжением на выводах источника тока.

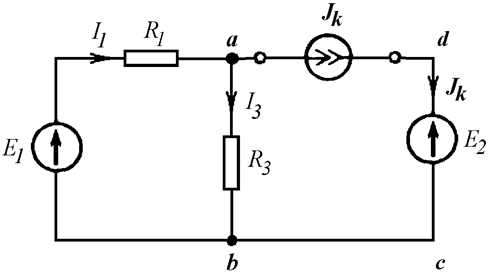
Пример 4.2:

Написать уравнение по первому закону Кирхгофа для узла a и уравнение по второму закону Кирхгофа для контура abcd (Рис. 4.6 а).

а)

б)

Рис. 4.6

Уравнение по первому закону Кирхгофа для узла a содержит источник тока и имеет вид:

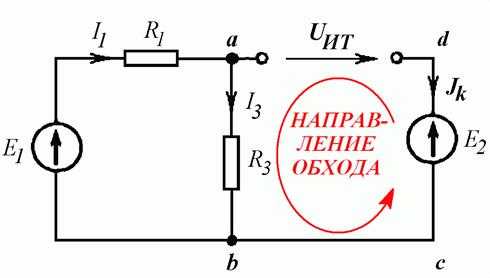
Для того чтобы написать уравнение по второму закону Кирхгофа для контура abcd, заменяем источник тока напряжением на его выводах (Рис. 4.6 б), задаем направление обхода контура против часовой стрелки и получаем:

Для упрощения расчетов источник тока с параллельным сопротивлением можно заменить на эквивалентный источник ЭДС (Рис. 4.7). После расчета необходимо обязательно вернуться к исходной схеме.

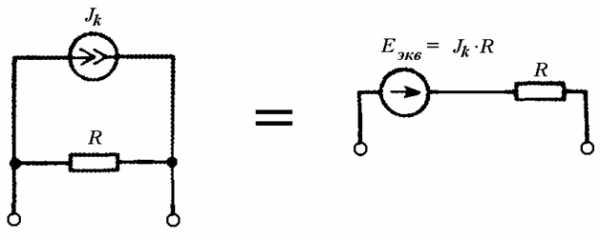
Рис. 4.7

Независимый контур цепи

В принципе, по второму закону Кирхгофа можно составить столько уравнений, сколько контуров содержит цепь. Но не все эти уравнения будут независимыми. Для определения независимости уравнений по второму закону Кирхгофа вводится такое понятие как независимый контур цепи.

Независимый контур цепи – это такой контур, который содержит хотя бы одну новую ветвь, не вошедшую в другие контуры цепи.

Независимые контуры в общем случае выбираются произвольно, но проще всего выбирать их так, чтобы они совпадали с ячейками цепи (Рис. 4.8 б).

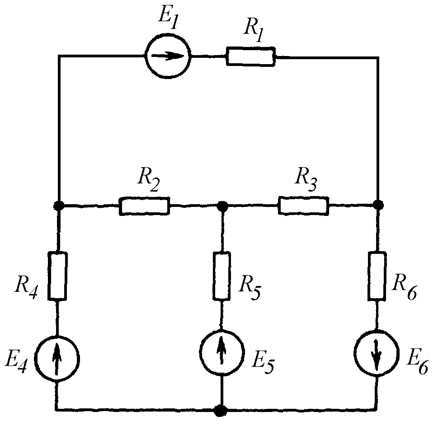
а)

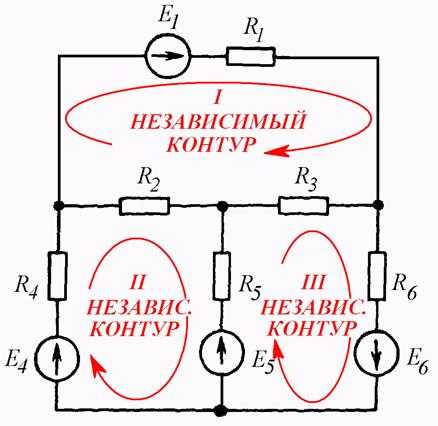
б)

Рис. 4.8

Если схема содержит  ветвей и  узлов, число независимых контуров равно

.

Схема на Рис. 4.8 б содержит три независимых контура.

5. СИСТЕМА УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА ДЛЯ РАСЧЕТА ТОКОВ ЦЕПИ

Законы Кирхгофа можно использовать для расчета токов в ветвях цепи. Главное требование при этом – получение системы независимых уравнений, в которой число неизвестных равно количеству токов, подлежащих определению.

Алгоритм составления системы уравнений по законам Кирхгофа

vunivere.ru

Закон кирхгофа с источником постоянного тока решение. Закон кирхгофа простыми словами

В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, ЭДС и сопротивлением всей цепи или, между напряжением и сопротивлением на каком-либо участке цепи определяется законом Ома .

На практике в цепях, токи, от какой-либо точки, идут по разным путям.
Точки, где сходятся несколько проводников, называются узлами, а участки цепи, соединяющие два соседних узла, ветвями.

В замкнутой электрической цепи ни в одной ее точке не могут скапливаться электрические заряды так, как это вызвало бы изменение потенциалов точек цепи. Поэтому электрические заряды притекающие к какому-либо узлу в единицу времени, равны зарядам, утекающим от этого узла за ту же единицу.
Разветвлённая цепь.
В узлеА цепь разветвляется на четыре ветви, которые сходятся в узел В

.

Обозначим токи в неразветвленной части цепи —I , а в ветвях соответственно

I1 , I2 , I3 , I4 .

У этих токов в такой цепи будет соотношение:

I = I1+I2+I3+I4;

Cумма токов, подходящих к узловой точке электрической цепи,
равна сумме токов, уходящих от этого узла.

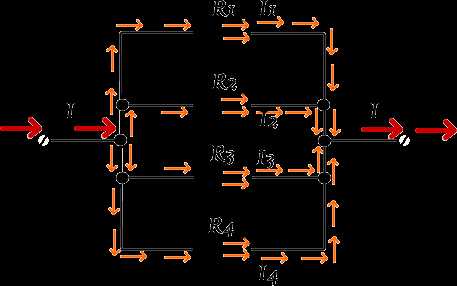
При параллельном соединении резисторов ток проходит по четырем направлениям, что уменьшает общее сопротивление или увеличивает общую проводимость цепи, которая равна сумме проводимостей ветвей.

Обозначим силу тока в неразветвленной ветви буквойI .
Силу тока в отдельных ветвях соответственно I1 , I2 , I3 и I4 .
Напряжение между точками A и B — U .
Общее сопротивление между этими точками — R .

По закону Ома напишем:

I = U/R ; I1 = U/R1 ; I2 = U/R2 ; I3 = U/R3 ; I4 = U/R4 ;

Согласно первому закону Кирхгофа:

I = I1+I2+I3+I4 ; или U/R = U/R1+U/R2+U/R3+U/R4 .

Сократив обе части полученного выражения на U получим:

1/R = 1/R1+1/R2+1/R3+1/R4 , что и требовалось доказать.

Cоотношение для любого числа параллельно соединенных резисторов.
В случае, если в цепи содержится два параллельно соединенных резистора
R1 и R2 , то можно написать равенство:

1/R =1/R1+1/R2 ;

Из этого равенства найдем сопротивление R , которым можно заменить два параллельно соединенных резистора:

Полученное выражение имеет большое практическое применение.
Благодаря этому закону производятся расчёты электрических цепей.

Второй закон Кирхгофа

В замкнутом контуре электрической цепи сумма всех эдс равна
сумме падения напряжения в сопротивлениях того же контура.

E1 + E2 + E3 +…+ En = I1R1 + I2R2 + I3R3 +…+ InRn . При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.

Если в электрической цепи включены два источника энергии, эдс которых совпадают по направлению, т. е. согласно изо1, то эдс всей цепи равна сумме эдс этих источников,
т. е.
E = E1+E2 .

Если же в цепь включено два источника, эдс которых имеют противоположные направления, т. е. включены встречно изо2, то общая эдс цепи равна разности эдс этих источников
Е = Е1-Е2 .

Благодаря этим законам производятся расчёты электрических цепей.
Существует несколько методов расчёта, один из них «Метод узловых напряжений»

Два приема, которые применяют для упрощения процесса составления уравнений, необходимых при расчетах сложных разветвленных цепей постоянного тока называют законами (вернее было бы сказать правилами) Кирхгофа. Прежде чем перейти к самим правила Кирхгофа введем два необходимых определения.

Разветвлёнными цепями названы цепи, которые имеют несколько замкнутых контуров, несколько источников электродвижущей силы (ЭДС).

Узлом разветвлённой цепи называют точку, в которой сходятся три или более проводников с токами.

Первый закон (правило) Кирхгофа, простыми словами

Первое правило Кирхгофа называют правилом узлов, так как оно касается сил токов в узах цепи. Словесно первый закон Кирхгофа формулируют следующим образом: Алгебраическая сумма сил токов в узле равна нулю. В виде формулы это правило запишем как:

С каким знаком сила тока будет входить в сумму (1), зависит от произвольного выбора. Но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Пусть все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными. Если направления токов изначально не заданы, то их задают произвольно. Если при расчетах получено, что сила тока отрицательна, значит, что верное направление тока является противоположным тому, которое предполагали.

Первый закон Кирхгофа является следствием закона сохранения заряда. Если в цепи текут только постоянные токи, то нет в этой цепи точек, которые накапливали бы заряд. Иначе токи не были бы постоянными.

Первый закон Кирхгофа дает возможность составить независимое уравнение, при наличии в цепи k узлов.

Второй закон (правило) Кирхгофа, простыми словами

Второй закон Кирхгофа относят к замкнутым контурам, поэтому его называют правилом контуров. Согласно этому правилу суммы произведений алгебраических величин сил тока на внешние и

les74.ru

Постоянный ток: законы Кирхгофа

При решении задач на законы Кирхгофа лучше придерживаться определенного алгоритма: 1. определить число неизвестных токов – столько уравнений должно быть в системе ; 2. определить количество узлов – уравнений по первому закону тогда нужно составить на одно меньше; 3. проложить контуры и записать для них уравнения по второму закону. Кто хочет разобраться досконально – есть видео.

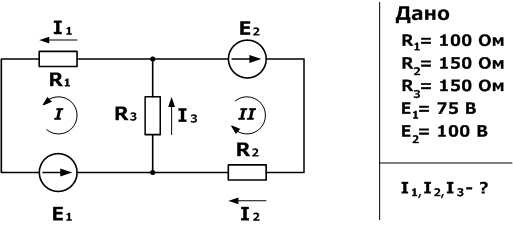
Задача 1. Два элемента с В и В соединены по схеме, показанной на рисунке . Сопротивление Ом. Внутреннее сопротивление элементов одинаково Ом. Определить силу тока, идущего через сопротивление .

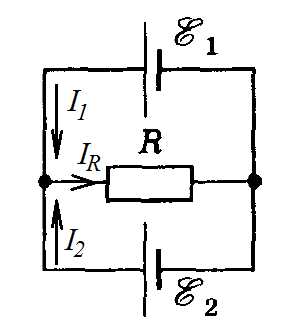
К задаче 1

Обозначим токи в ветвях произвольно. По первому закону Кирхгофа сумма токов, сходящихся в узле, равна 0:

   

Будем обходить верхний контур против часовой стрелки. По второму закону Кирхгофа сумма падений напряжений в контуре равна сумме ЭДС:

   

   

Будем обходить второй контур по часовой стрелке:

   

   

Неизвестных токов – три, мы составили три уравнения. Этого достаточно, чтобы найти токи:

   

Выразим из второго уравнения, а – из третьего:

   

   

Подставим эти выражения в первое уравнение:

   

   

   

   

   

Тогда токи и

   

   

Ответ: A, A, A.
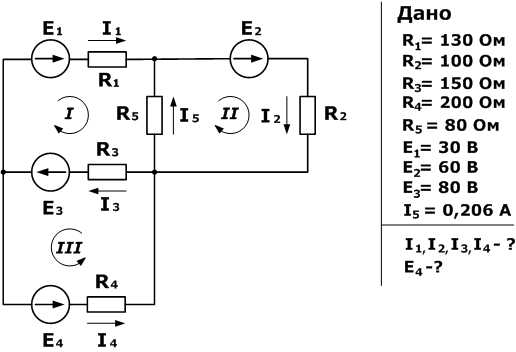
Задача 2. Найти силу тока на всех участках цепи‚ если В, В‚ В, Ом‚ Ом‚ Ом‚ Ом‚  Ом, Ом.

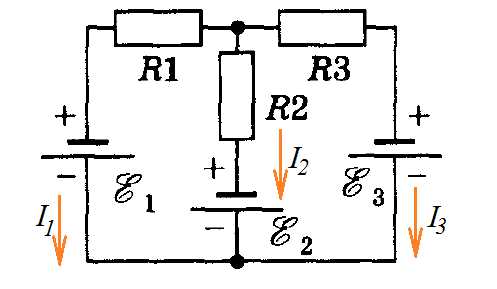
К задаче 2

Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас два узла, поэтому уравнение будет одно.  Затем, обходя контуры, составим два уравнения по второму закону: их нужно составить два, так как неизвестных токов в цепи три.

   

Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора):  , , .

Ответ: , , .

 

Задача 3. В схеме, показанной на рисунке, найти силу тока через гальванометр, если В, кОм; В, кОм.  Сопротивлением гальванометра пренебречь.

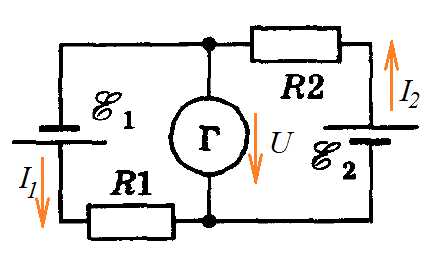
К задаче 3

Нам неизвестно сопротивление гальванометра, запишем для напряжения на нем два уравнения:

   

   

Приравнивая, получим

   

Заметим, что, если  , то равенство будет выполнено. Таким образом, ток через гальванометр не течет.

Ответ: .

Задача 4. В цепи   В‚ В, Ом,  Ом. Найти распределение токов в цепи. Внутреннее сопротивление источников тока не учитывать.

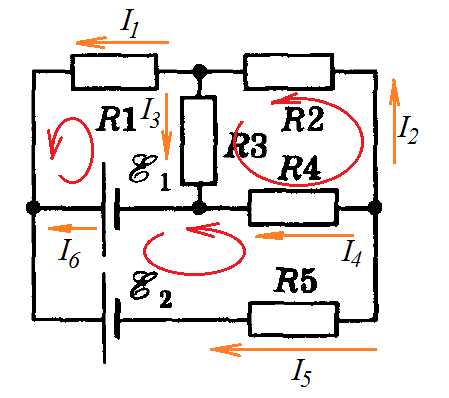
К задаче 4

Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас три узла, поэтому уравнений будет два.  Затем, обходя контуры, составим три уравнения по второму закону: их нужно составить именно три, так как неизвестных токов в цепи шесть.

   

Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора):  , , , , , .

Ответ: , , , , , .
Задача 5. Какую силу тока покажет амперметр в схеме, изображенной на рисунке? Сопротивлением амперметра пренебречь.

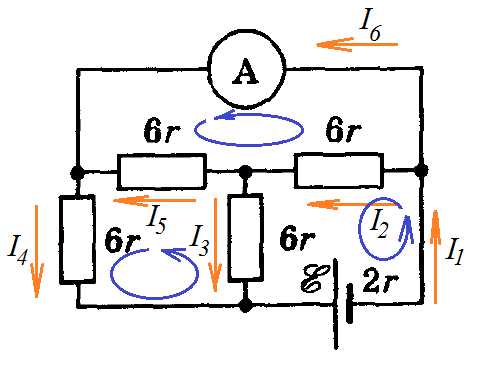
К задаче 5

Обозначим токи в цепи произвольно. Обозначим направления обхода контуров. Запишем систему уравнений: составим три уравнения по первому закону (на одно меньше, чем количество узлов) и три уравнения по второму закону, так как неизвестных токов шесть и система должна состоять из шести уравнений.

   

Чтобы воспользоваться калькулятором, я задала Ом и В.  В итоге получилось: , , , , , .

Минусы свидетельствуют о противоположном направлении тока в этой ветви тому, что мы нарисовали.

easy-physic.ru

Примеры решения задач на законы Кирхгофа

Рассмотрим на примерах как можно использовать законы Кирхгофа при решении задач.

Задача 1

Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа.

 

Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение.

Напомним, что по первому закону, сумма токов сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи 

Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС.

На примере первого контура – ток I₁ и I₃ совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс.

Уравнения для первого и второго контуров по второму закону будут: 

Все эти три уравнения образуют систему

Подставив известные значения и решив данную линейную систему уравнений, найдем токи в ветвях (способ решения может быть любым). 

Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей.

Задача 2

Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.

 

Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2 

Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче. 

На основании этих уравнений составляем систему с 5-ью неизвестными 

Решив эту систему любым удобным способом, найдем неизвестные величины 

Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками. 

Баланс мощностей сошелся, а значит токи и ЭДС найдены верно. 

Читайте также — расчет простых цепей постоянного тока

Просмотров: 43832

electroandi.ru

Электротехника: Второй закон Кирхгофа.

  Второй закон (правило) Кирхгофа — алгебраическая сумма напряжений на элементах контура электрической цепи равна нулю.
Контур электрической цепи — замкнутый проводящий ток путь образованный элементами электрической цепи.
Рассмотрим схему на рисунке 1:

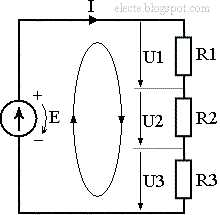
Рисунок 1 — Схема с одним контуром

В этой схеме присутствуют: источник ЭДС и резисторы R1, R2 и R3; эти элементы образуют замкнутый путь проводящий ток т.е. контур. Напряжение на источнике ЭДС равно E и направлено так как показано на рисунке 1 стрелочкой справа от источника. Стрелка на условном обозначении источника направлена в сторону противоположную направлению напряжения на источнике ЭДС (иногда это запутывает при расчёте схем но так принято обозначать источник ЭДС). Направления падений напряжений на резисторах указаны стрелками (рис. 1). Для составления уравнения, по второму закону Кирхгофа, необходимо выбрать направление обхода контура (по часовой стрелке или против). В схеме на рисунке показано направление по часовой стрелке. Запишем уравнение по второму закону Кирхгофа:

Напряжения резисторов вошли в левую часть уравнения со знаком плюс т.к. направление обхода контура совпадает с направлениями напряжений на резисторах. Напряжение источника ЭДС E вошло в правую часть со знаком плюс т.к. направление обхода контура не совпадает с направлением напряжения источника. Можно также записать напряжение источника в левой части уравнения со знаком минус (что, в принципе, тоже самое):

Уравнение (2) больше подходит для определения второго закона Кирхгофа приведенного выше.

Напряжения совпадающие по направлению с обходом контура записаны со знаком плюс а напряжение источника не совпадающее с обходом контура — со знаком минус и вся эта алгебраическая сумма равна нулю. Теперь, из выражения (2), зная три каких либо напряжения можно найти четвёртое. Обычно расчёт цепи сводится к нахождению токов во всех ветвях или потенциалов всех узлов т.к. зная эти величины (токи ветвей или потенциалы узлов), сопротивления всех элементов и напряжения источников ЭДС (и токи всех источников тока) можно найти напряжение на любом элементе и ток любого элемента. В схеме на рисунке 1 для определения напряжений U1, U2 и U3 достаточно знать ток I т.к. он одинаков для всех элементов цепи (R1, R2, R3, E). Умножением тока I на сопротивление R1 находится напряжение U1, умножением тока I на сопротивление R2 находится напряжение U2, умножением тока I на сопротивление R3 находится напряжение U3. Учитывая это можно привести уравнение (1) к виду:

Из уравнения (3) можно найти ток I. Т.к. контур один то и ток в уравнении один но если схема содержит больше одно контура то и токов будет больше. Вынеся ток I за скобки и поделив обе части уравнения на сумму сопротивлений R1, R2 и R3 получаем уравнение для нахождения тока I, но этот ток можно найти и другим способом например заменой последовательного соединения резисторов R1, R2 и R3 одним резистором R123 и делением напряжения E на сопротивление резистора R123.

Сопротивление резистора R123 равно сумме сопротивлений резисторов R1, R2 и R3. Ток находится из уравнения:

     Если в контуре содержится больше одного источника ЭДС то уравнение, по второму закону (правилу) Кирхгофа, составляется аналогично.

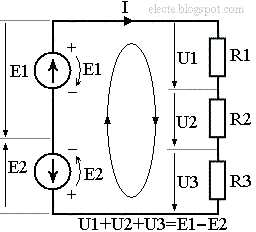
Рисунок 2 — Схема с двумя источниками ЭДС

Запишем уравнение, по второму закону Кирхгофа, для контура в схеме на рисунке 2:

Напряжение E2 источника E2 записано в правой части уравнения со знаком минус т.к. оно совпадает по направлению с обходом контура. Заменяя напряжения на резисторах произведениями тока I на сопротивления резисторов получим уравнение:

Из уравнения (6) может быть найден ток I.

Если схема имеет больше одного контура то Закон (правило) Кирхгофа все равно выполняется для всех контуров. Уравнения по второму закону Кирхгофа, в таком случае, составляются аналогично тому как в примерах выше. Отличие будет только в том что необязательно для всех элементов будет один и тот же ток. В случае если схема имеет больше одного контура можно считать что через каждый элемент течет свой ток. Напряжение на элементе, в таком случае, находится умножением сопротивления этого элемента (если этот элемент например резистор) на ток данного элемента.

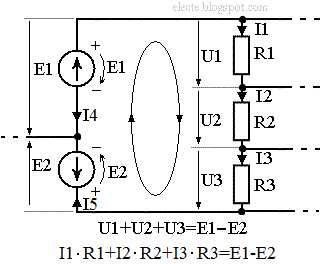
Рисунок 3 — Часть схемы имеющей больше одного контура

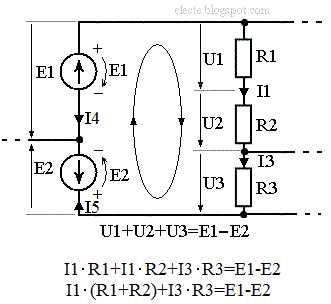
Рисунок 4 — Часть схемы имеющей больше одного контура и ветвь из двух элементов

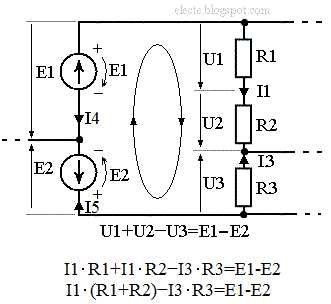
Рисунок 4 — Часть схемы имеющей больше одного контура, ветвь из двух элементов и элементы напряжения на на которых имеют направления не совпадающие с выбранным направлением обхода контура

При составлении уравнений по второму закону Кирхгофа не стоит слишком много времени уделять выбору направлений обходов контуров и направлений токов (они (направления обходов и токов) выбираются произвольно) так как реальные направления токов определяются при решении этих уравнений.

Пример:

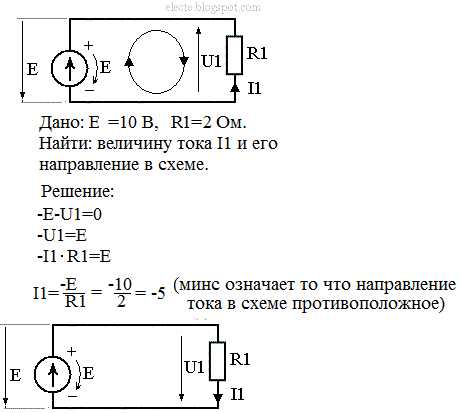
Направление напряжения на элементе R1 такое же как и направление тока этого элемента по тому что принято считать что ток течёт от большего потенциала к меньшему а напряжение направлено также (от большего потенциала к меньшему).

electe.blogspot.com

2.5.1. Метод непосредственного применения законов Кирхгофа

Пример . Методом непосредственного применения законов Кирхгофа рассчитать токи в схеме на рис.

Число ветвей обозначим m, а число узлов n. Произвольно выбираем положительные направления токов в ветвях и направления обхода контуров. Поскольку в каждой ветви протекает свой ток, то число токов, которое следует определить, а следовательно, и число уравнений, которое нужно составить, равно m. По первому закону Кирхгофа составляем n-1 уравнений. Недостающие m-(n-1) уравнений следует составить по второму закону Кирхгофа для взаимно независимых контуров.

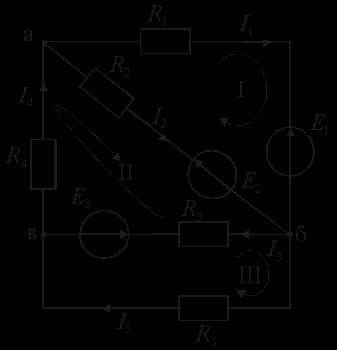Рис. 2.20. Схема замещения сложной электрической цепи с несколькими источниками энергии: I, II, III – номера контуров

1. Проводим топологический анализ.

Она содержит пять ветвей и три узла, m = 5, n = 3. Составляем два уравнения по первому закону Кирхгофу, т. к. n – 1 = 2 (например, для узлов а и б).

2. Составляем уравнения по певому и второму законам Кирхгофа

Для узла «а» — I₁ — I₂ + I₄ = 0.

Для узла «б» — I₁ + I₂ — I₃ — I₅ = 0.

Остальные m — (n — 1) = 3 уравнения составляем по второму закону Кирхгофа.

Для контура I — R₁·I₁ — R₂·I₂ = — E₁ + E₂.

Для контура II — R₂·I₂ + R₃·I₃ + R₄·I₄ = — E₂ — E₃.

Для контура III — — R₃·I₃ + R₅·I₅ = E₃.

Решив систему, состоящую из пяти уравнений, находим пять неизвестных токов. Если какие-либо значения токов оказались отрицательными, то это означает, что действительные направления этих токов противоположны первоначально выбранным.

При расчётах сложных цепей с использованием ЭВМ удобна матричная форма записи. Уравнения, составленные по законам Кирхгофа, запишем в виде

— I₁ — I₂ + 0 + I₄ + 0 = 0

I₁ + I₂ — I₃ + 0 — I₅ = 0

R₁·I₁ — R₂·I₂ + 0 + 0 + 0 = — E₁ + E₂

0 + R₂·I₂ + R₃·I₃ + R₄·I₄ + 0 = — E₂ — E₃

0 + 0 + — R₃·I₃ + 0 + R₅·I₅ = E₃.

В матричной форме

или [R]·[I] = [Е],

где [R] – квадратная (5 х 5) матрица, элементами которой являются коэффициенты при неизвестных токах в исходных уравнениях;

[I] – матрица — столбец неизвестных токов;

[E] – матрица — столбец, элементами которой могут быть алгебраическая сумма ЭДС.

Решение матричного уравнения ищут в виде

[I] = [R]^-1·[E],

где [R]^-1 – матрица, обратная матрице [R].

Рассмотренный метод расчета неудобен, если в цепи имеется большое количество узлов и контуров, поскольку потребуется решать громоздкую систему уравнений. В таких случаях рекомендуется применять метод контурных токов, позволяющий значительно сократить число расчетных уравнений 2.

Метод контурных токов

Метод основан на 2-м законе Кирхгофа. При его использовании в составе анализируемой схемы выбирают независимые контуры и предполагают, что в каждом из контуров течет свой контурный ток. Для каждого из независимых контуров составляют уравнение по 2-му закону Кирхгофа и их решают. Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих по данной ветви.

Все источники сигналов, представленные источниками тока, заменяют источниками ЭДС (рис. 4.29).

Эта схема эквивалентна, если

а)E = IZ_i^I;

б) Z_i^II = Z_i^I.

1) Топологический анализ схемы.

а) Как и в предыдущем методе, определяют число ветвей b.

б) Определяют число узлов у.

в) Подсчитывают число независимых контуров N_k = b – y + 1.

Все независимые контуры обозначены дугами со стрелками на них, которые показывают положительное направление обхода.

Все контуры нумеруют и каждому контуру присваивают свой контурный ток: I_k1; I_k2;I_kNk.

За положительное направление контурного тока принимают положительное направление обхода контура.

2) По второму закону Кирхгофа относительно контурных токов записывают уравнения, которые после приведения подобных членов образуют систему линейных уравнений N_k = N_kпорядка:

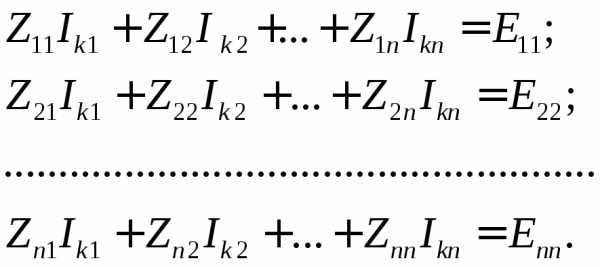
где I_ki– контурный токi-го контура;

Z_ii– собственное сопротивлениеi-го контура и равно алгебраической сумме сопротивлений, входящих вi-й контур;

Z_ji– сопротивление смежных ветвей междуi-м иj-м контурами. Оно представляет собой алгебраическую сумму, причем ее члены берутся со знаком «+», если контурные токи направлены одинаково, и со знаком «–», если они направлены встречно;

E_ki– контурная ЭДСi-ого контура. Она равна алгебраической сумме ЭДС, входящих вi-й контур. Контурная ЭДСE_kiберется со знаком «+», когда направление источника ЭДС и направление тока совпадают, и со знаком «–», если они направлены встречно.

3) По правилу Крамера находят контурные токиI_ki=.

4) Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих через данную ветвь. В алгебраической сумме контурные токи берутся со знаком «+» , если ток ветви и совпадает с контурным током и «–» если не совпадает.

Если токи ветви оказались положительными, то выбранное направление тока совпадает с истинным и наоборот.

Пример.Дана комплексная схема замещения электрической цепи (рис. 4.30). Определить токи во всех ветвях.

1. Проводим топологический анализ

а) b= 6; б)y= 4;в)N_k= 6 – 4 + 1=3.

2) Составим систему уравнений по методу МКТ

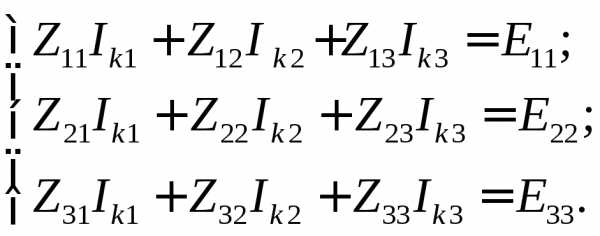
где: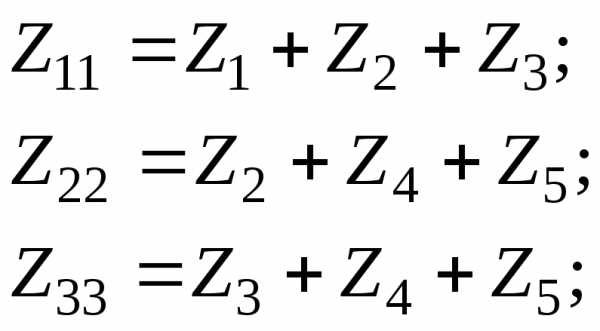

E₁₁= E₁; E₂₂ = 0;E₃₃ = 0.

3) По методу Крамера находим контурные токи I_ki = .

4) Находим токи в ветвях: I₁ = I_k1; I₂ = = I_k1 – I_k2; I₃ = I_k1 – I_k3; I₄ = –I_k2 + I_k3; I₅ = I_k2; I₆ = I_k3.

Пример 2. Рассмотрим электрической цепи постоянного тока, рис. 2.21.

1. Проводим топологический анализ

а) b= 5; б)y= 3;в)N_k= 5 – 3 + 1=3.

2) Для каждого контура записывают уравнение второго закона Кирхгофа,

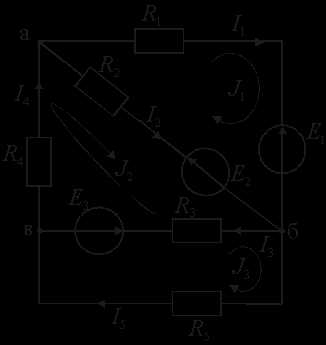Рис. 2.21. – Расчетная схема для метода контурных токов

В каждом из трех контуров протекает свой контурный ток J₁, J₂, J₃. Произвольно выбираем направление этих токов, например, по часовой стрелке. Составляем уравнения по второму закону Кирхгофа для каждого контура с учетом соседних контурных токов, протекающих по смежным ветвям

(R₁ + R₂)·J₁ — R₂·J₂ = E₂ — E₁

— R₂·J₁ + (R₂ + R₃ + R₄)·J₂ — R₃·J₃ = — E₂ — E₃

— R₃·J₂ + (R₃ + R₅)·J₃ = E₃.

Решив систему уравнений, находят контурные токи J₁, J₂, J₃. Затем определяют реальные токи в ветвях, причем токи во внешних ветвях равны контурным, а в смежных – алгебраической сумме 2-х контурных токов, протекающих в данной ветви

I₁ = J₁; I₂ = J₂ — J₁; I₃ = J₂ — J₃; I₄ = J₂; I₅ = J₃.

Исходная система уравнений в матричной форме

или

[R]·[J] = [E],

где [R] – квадратная матрица коэффициентов контурных токов;

[J] – матрица – столбец контурных токов; [E] – матрица – столбец ЭДС.

Решением матричного уравнения является матрица

[J] = [R]^-1 ·[E],

где [R]^-1 – матрица, обратная матрице [R]

• Пример 3. Для электрической цепи, схема которой приведена на рис. 1.1, получим следующие уравнения:

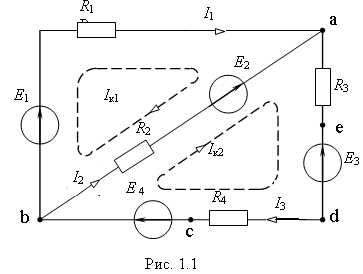
получим следующие уравнения:

По методу Крамера найдем контурные токи:

Действительные токи в ветвях: I1 = Ik1; I2 = Ik2 – Ik1; I3 = Ik2.

Пример 4. Расчет цепи методом контурных токов на рис. 2.22.

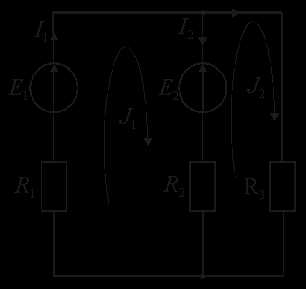Рис. 2.22. – Расчет цепи методом контурных токов

Для схемы замещения электрической цепи, показанной на рис. 2.22, задано: E₁ = 30 B; E₂ = 10 В; R₁ = 8 Ом; R₂ = 15 Ом; R₃ = 36 Ом. Требуется определить токи в ветвях методом контурных токов. Составить баланс мощности.

Схема содержит три ветви (m = 3), два узла (n = 2). Выбираем положительные направления токов в ветвях произвольно. Число уравнений, составленных по методу контурных токов, равно m — (n — 1) = 2. Задаем направление контурных токов (например, по часовой стрелке) и составляем систему уравнений

(R₁ + R₂)·J₁ — R₂·J₂ = E₁ — E₂

— R₂·J₁ + (R₂ + R₃)·J₂ = E₂.

Подставляя численные значения сопротивлений резисторов и ЭДС в приведённые уравнения, находим контурные токи J₁, J₂ (Например, методом определителей)

20 = 23·J₁ – 15·J₂

10 = — 15·J₁ + 51·J₂

Токи в ветвях

I₁ = J₁ = 1,23 А; I₂ = — J₂ + J₁ = 1,23 — 0,56 = 0,67 А; I₃ = J₂ = 0,56 А.

Составляем баланс мощностей.

Мощность генераторов (источников)

Р_И = Е₁·I₁ — Е₂·I₂ = 30·1,23 – 10·0,67 = 30,2 Вт,

где произведение Е₂·I₂ имеет знак минус (ток через источник не совпадает с ЭДС, значит источник ЭДС работает в режиме потребителя электрической энергии).

Мощность, потребляемая нагрузкой, составляет

Р_Н = R₁·I₁² + R₂·I₂² + R₃·I₃² = 8·1,23² + 15·0,56² + 36·0,56² = 30,13 Вт.

Погрешность

составляет менее 1%, т. е. токи найдены верно.

Метод узловых потенциалов (МУП)

Метод основан на применении первого закона Кирхгофа. В нем за неизвестные величины принимают потенциалы узлов. По закону Ома определяют токи во всех ветвях схемы.

Все источники ЭДС, имеющиеся в схеме, заменяют источниками тока (рис. 4.31).

а) I = E/Z_i^I;

б) Z_i^II = Z_i^I.

1) Топологический анализ.

а) Подсчитывают число ветвей bи число узловy.Определяется количество независимых узловN_y =y – 1.

б) Нумеруют все узлы. Один из узлов, к которому сходится наибольшее число ветвей, считают нулевым, где 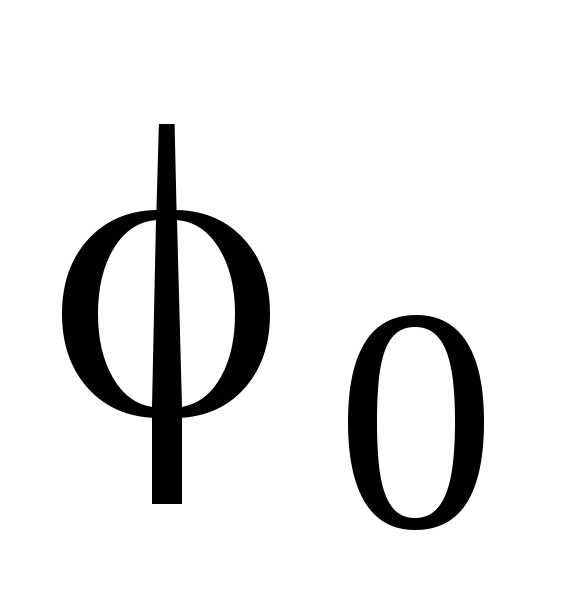– потенциал нулевого узла.

2) По 1-му закону Кирхгофа составляют уравнения для Nузлов схемы и решают их относительно потенциалов узлов:

,

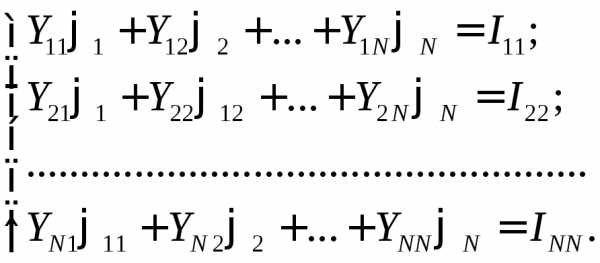где Y_ii– собственная узловая проводимость. Она равна сумме проводимостей всех ветвей, сходящихся вi-м узле, все они берутся со знаком «+»;

Y_ij– межузловая проводимость междуi-м иj-м узлами. Проводимости всех узлов берутся со знаком «–»;

I_ii– алгебраическая сумма токов источников тока, сходящихся вi-м узле. Втекающие токи записываются в эту сумму со знаком «+», а вытекающие – со знаком «–».

3) Потенциалы узлов находят по формуле Крамера

.

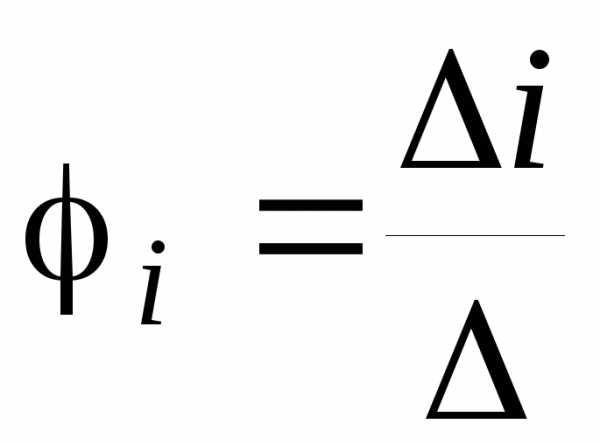4) Токи в ветвях находят по закону Ома

I= (₁ –₂)/Z.

Пример.Дана электрическая цепь (рис. 4.32). Рассчитать токи во всех ветвях.

П

I₂

Z₂

редварительно преобразуем все источники напряжения (рис. 4.32) в источники тока (рис. 4.33).

Z₁

Z₂

Z₃

Z₄

E₁

E₂

I

I₁

I₂

I₄

I

I₃

I₁

Z₁

Z₃

Z₄

Рис. 4.32 Рис. 4.33

Проведем топологический анализ.

а) число ветвей b= 4;

б) число независимых узлов N_у= 2, их потенциалы: φ₁и φ₂(рис. 4.33).

Составим систему уравнений по методу узловых потенциалов:

;

.

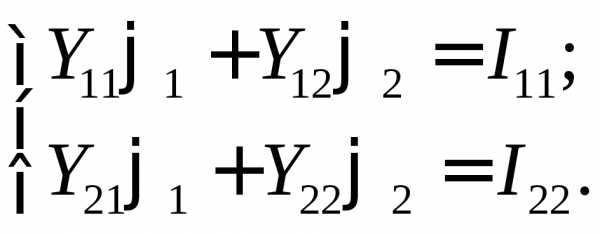
По методу Крамера найдем потенциалы узлов .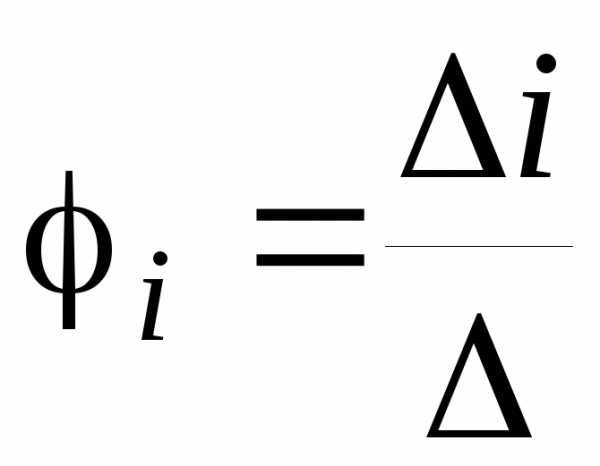

По закону Ома найдем токи во всех ветвях схемы:

.

1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ по теме цепи переменного тока

studfile.net

Законы Кирхгофа

30	1. Основные положения

Если в электрической цепи (или на её участке, для которого производится расчёт), помимо пассивных элементов, присутствуют источники ЭДС, то их необходимо учитывать при расчёте по закону Ома. Знаки ЭДС и напряжения определяются относительно направления тока: если направления ЭДС или напряжения совпадают с направлением тока, то напряжение и ЭДС берутся со знаком «+», иначе –– со знаком «−».

Закон Ома для активного участка цепи (или, как его ещё называют, Закон Ома для полной цепи), имеет следующий вид (для цепи, приведённой на рис. 1.19):

i = e − u R

Следует понимать, что закон Ома задаёт линейную зависимость между током и напряжением, следовательно, если цепь будет иметь нелинейный характер, закон Ома выполняться не будет.

1.3.2.1. Первый закон Кирхгофа

Законы Кирхгофа были теоретически обоснованы выдающимся немецким физиком, профессором Берлинского университета Густавом Робертом Кирхгофом (1824 –– 1887 гг.) в 1845 г.

Согласно определению, электрический ток это направленное движение зарядов, таким образом, в части ветвей, входящих в узел электрической цепи, заряды будут двигаться к узлу, а в остальных ветвях данного узла –– от него. При этом общая сумма зарядов направленных к узлу и от узла будет равна нулю, т. к. в противном случае заряды

Рис. 1.18. Пассивный участок цепи Рис. 1.19. Активный участок цепи

1.3. Законы Кирхгофа и Ома

31

будут либо пропадать (или накапливаться в узле), либо браться ниоткуда, что противоречит законам сохранения4.

Таким образом, мы получим первый закон Кирхгофа:

Алгебраическая сумма токов в узле электрической цепи равна нулю:

X

i = 0

При составление уравнений по первому закону Кирхгофа находится алгебраическая сумма5 токов, протекающих во всех ветвях, сходящихся в данном узле.

Обычно, для удобства расчётов, токи входящие в узел берутся со знаком «−», а токи исходящие из узла берутся со знаком «+» (при необходимости это правило можно поменять на противоположное).

Для схемы, приведённой на рис. 1.20, выражение по первому закону Кирхгофа будет иметь следующий вид:

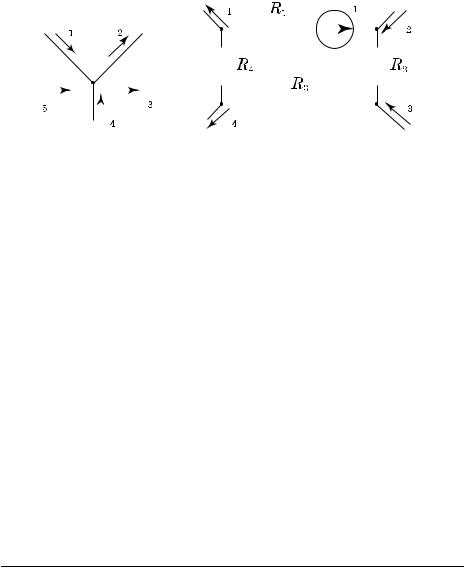
−i1 + i2 + i3 − i4 − i5 = 0.

Следует отметить, что первый закон Кирхгофа может применяться не только к узлам электрической цепи, но и к её отдельным частям (рис. 1.21).

1.3.2.2. Второй закон Кирхгофа

Электрический ток в цепи характеризуется переносом электрических зарядов, который осуществляется за счёт энергии электрического поля, являющегося потенциальным. Как известно из курса физики, работа по замкнутому контуру в потенциальном поле равна нулю, таким образом работа по переносу электрического заряда в замкнутом контуре электрической цепи будет равно нулю. Согласно определению

4Строгое доказательство первого закона Кирхгофа даётся на основе принципа непрерывности электрического тока.

5Алгебраическая сумма –– это сумма с учётом знака.

32

1. Основные положения

i

e

i

i

i

i

i

i

i

i

Рис. 1.20. Первый закон

Рис. 1.21. Первый закон Кирхгофа

Кирхгофа для узла

для участка цепи

−i1 + i2 + i3 − i4 − i5 = 0

i1 − i2 − i3 + i4 = 0

(стр. 9) работу по переносу заряда равна разности потенциалов (падению напряжению), следовательно, сумма падений напряжений на всех элементах замкнутого контура (как пассивных, так и активных), будет равна нулю.

Полученный вывод соответствует обобщённой форме Второго за-

кона Кирхгофа:	X u = 0
Алгебраическая сумма падений напряжений в контуре
	электрической цепи равна нулю.

Знак, с которым берётся напряжение при суммировании, определяется в соответствие с произвольно выбранным направлением обхода контура: если условно–положительное направление тока или напряжения совпадает с направлением обхода, то ставится знак плюс, в противном случае –– минус.

В электротехнических расчётах удобно разделять активные и пассивные элементы, поэтому большее применение нашла другая форма второго закона Кирхгофа, в которой в левой части равенства собраны падения напряжения, а в правой –– ЭДС:

Алгебраическая сумма падений напряжений в контуре электрической цепи равна алгебраической сумме ЭДС в этом же контуре:

1.3. Законы Кирхгофа и Ома

33

XX

Ri = e

При составлении уравнения по второму закону Кирхгофа, со знаком «+» берутся падения напряжения на элементах, условно–поло- жительное направление тока в которых совпадает с произвольно выбранным направлением обхода контура. В противном случае падение напряжения берётся со знаком «−». Знаки ЭДС определяются аналогично относительно направления обхода. Если в электрической цепи имеются источники тока, то для удобства составления выражений по второму закону Кирхгофа их необходимо преобразовать в источники напряжения (эти преобразования рассмотрены в § 1.4.3 на стр. 36).

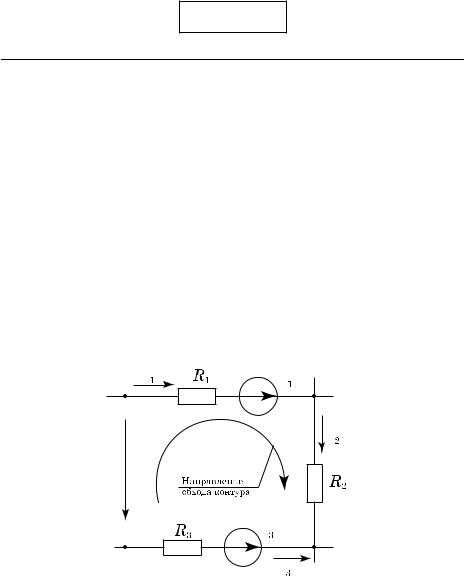
Выражение по Второму закону Кирхгофа, для схемы, приведённой на рис. 1.22, будет иметь следующий вид:

−u + i1R1 + i2R2 − i3R3 = e1 − e3

i

u

e

i

Рис. 1.22. Второй закон Кирхгофа i1R1 + i2R2 − i3R3 − u = e1 − e3

studfile.net