его формулировка и применение. Выбор проводов для цепей
Задача по теме «Законы постоянного тока». Задача может быть интересна учащимся 10-х классов и выпускникам для подготовки к ЕГЭ. Кстати, подобного рода задача была на ЕГЭ в части 1 с несколько иным вопросом (необходимо было найти отношение количеств теплоты, выделяющихся на резисторах).
На каком из резисторов выделится наибольшее (наименьшее) количество теплоты? R1 = R4 = 4 Ом, R2 = 3 Ом, R3 = 2Ом. Дать решение. Чтобы ответить на вопрос задачи, необходимо сравнить количество теплоты, выделяющееся на каждом их резисторов. Для этого воспользуемся формулой закона Джоуля — Ленца. То есть основной задачей будет являться определение силы тока (или сравнение), протекающей через каждый резистор.
Согласно законам последовательного соединения, сила тока, протекающая через резисторы R1 и R2, и R3 и R4, одинаковая.Чтобы определить силу тока в верхней и в нижней ветвях, воспользуемся законом параллельного соединения, согласно которому, напряжение на этих ветвях одинаковое.
Вы можете оставить комментарий, или поставить трэкбек со своего сайта.
Написать комментарий
fizika-doma.ru
Тепловая мощность — формула расчета
С теплотехническими расчётами приходится сталкиваться владельцам частных домов, квартир или любых других объектов. Это основа основ проектирования зданий.
Понять суть этих расчётов в официальных бумагах, не так сложно, как кажется.
Для себя также можно научиться выполнять вычисления, чтобы решить, какой утеплитель применять, какой толщины он должен быть, какой мощности приобретать котёл и достаточно ли имеющихся радиаторов на данную площадь.
Ответы на эти и многие другие вопросы можно найти, если понять, что такое тепловая мощность. Формула, определение и сферы применения – читайте в статье.
Что такое тепловой расчет?
Если говорить просто, тепловой расчёт помогает точно узнать, сколько тепла хранит и теряет здание, и сколько энергии должно вырабатывать отопление, чтобы поддерживать в жилье комфортные условия.
Оценивая теплопотери и степень теплоснабжения, учитываются следующие факторы:
- Какой это объект: сколько в нём этажей, наличие угловых комнат, жилой он или производственный и т. д.
- Сколько человек будет «обитать» в здании.
- Важная деталь — это площадь остекления. И размеры кровли, стен, пола, дверей, высота потолков и т. д.
- Какова продолжительность отопительного сезона, климатические характеристики региона.
- По СНиПам определяют нормы температур, которые должны быть в помещениях.
- Толщина стен, перекрытий, выбранные теплоизоляторы и их свойства.

Могут учитываться и другие условия и особенности, например, для производственных объектов считаются рабочие и выходные дни, мощность и тип вентиляции, ориентация жилья по сторонам света и др.
Для чего нужен тепловой расчет?
Как умудрялись обходиться без тепловых расчётов строители прошлого?
Сохранившиеся купеческие дома показывают, что всё делалось просто с запасом: окна поменьше, стены — потолще. Получалось тепло, но экономически не выгодно.
Теплотехнический расчёт позволяет строить наиболее оптимально. Материалов берётся ни больше — ни меньше, а ровно столько, сколько нужно. Сокращаются габариты строения и расходы на его возведение.
Вычисление точки росы позволяет строить так, чтобы материалы не портились как можно дольше.
Для определения необходимой мощности котла также не обойтись без расчётов. Суммарная мощность его складывается из затрат энергии на обогрев комнат, нагрев горячей воды для хозяйственных нужд, и способности перекрывать теплопотери от вентиляции и кондиционирования. Прибавляется запас мощности, на время пиковых холодов.
Прибавляется запас мощности, на время пиковых холодов.
При газификации объекта требуется согласование со службами. Рассчитывается годовой расход газа на отопление и общая мощность тепловых источников в гигакалориях.
Нужны расчёты при подборе элементов отопительной системы. Обсчитывается система труб и радиаторов – можно узнать, какова должна быть их протяжённость, площадь поверхности. Учитывается потеря мощности при поворотах трубопровода, на стыках и прохождении арматуры.
При расчетах затрат тепловой энергии могут пригодиться знания, как перевести Гкал в Квт и обратно. В следующей статье подробно рассмотрена эта тема с примерами расчета.
Полный расчет теплого водяного пола приведен в этом примере.
Знаете ли вы, что количество секций радиаторов отопления не берется «с потолка»? Слишком малое их количество приведет к тому, что в доме будет холодно, а чрезмерно больше создаст жару и приведет к чрезмерной сухости воздуха. По ссылке http://microklimat.pro/sistemy-otopleniya/raschet-sistem-otopleniya/kolichestva-sekcij-radiatorov.
Расчет тепловой мощности: формула
Рассмотрим формулу и приведем примеры, как произвести расчет для зданий с разным коэффициентом рассеивания.
Vx(дельта)TxK= ккал/ч (тепловая мощность), где:
- Первый показатель «V» – объем рассчитываемого помещения;
- Дельта «Т» — разница температур – это та величина, которая показывает насколько градусов внутри помещения теплее, чем снаружи;
- «К» — коэффициент рассеивания (его еще называют «коэффициент пропускания тепла»). Величина берется из таблицы. Обычно цифра колеблется от 4 до 0,6.
Примерные величины коэффициента рассеивания для упрощенного расчёта
- Если это неутепленный металлопрофиль или доска то «К» будет = 3 – 4 единицы.
- Одинарная кирпичная кладка и минимальное утепление – «К» = от 2 до 3-ёх.
- Стена в два кирпича, стандартное перекрытие, окна и
- двери – «К» = от 1 до 2.
- Самый теплый вариант.

Более точный расчет можно произвести, высчитывая точные размеры отличающихся по свойствам поверхностей дома в м2 (окна, двери и т. д.), производя расчёт для них отдельно и складывая получившиеся показатели.
Пример расчета тепловой мощности
Возьмем некое помещение 80 м2 с высотой потолков 2,5 м и посчитаем, какой мощности котел нам потребуется для его отопления.
Вначале высчитываем кубатуру: 80 х 2,5 = 200 м3. Дом у нас утеплен, но недостаточно – коэффициент рассеивания 1,2.
Морозы бывают до -40 °C, а в помещении хочется иметь комфортные +22 градуса, разница температур (дельта «Т») получается 62 °C.
Подставляем в формулу мощности тепловых потерь цифры и перемножаем:
200 х 62 х 1,2 = 14880 ккал/ч.
Полученные килокалории переводим в киловатты, пользуясь конвертером:
- 1 кВт = 860 ккал;
- 14880 ккал = 17302,3 Вт.
Округляем в большую сторону с запасом, и понимаем, что в самый сильный мороз -40 градусов нам потребуется 18 кВт энергии в час.
Умножаем периметр дома на высоту стен:
(8 + 10) х 2 х 2,5 = 90 м2 поверхности стены + 80 м2 потолок = 170 м2 поверхности, контактирующей с холодом. Теплопотери, высчитанные нами выше, составили 18 кВт/ч, делим поверхность дома на расчетную израсходованную энергию получаем, что 1 м2 теряет примерно 0,1 кВт или 100 Вт ежечасно при температуре на улице -40 °C, а в помещении +22 °С.
Эти данные могут стать основой для расчёта требуемой толщины утеплителя на стены.
Приведем другой пример расчета, он в некоторых моментах сложнее, но более точный.
Формула:
Q = S x (дельта)T / R:
- Q– искомая величина теплопотерь дома в Вт;
- S– площадь охлаждающих поверхностей в м2;
- T– разница температур в градусах Цельсия;
- R– тепловое сопротивление материала (м2 х К/Вт) (Метры квадратные умноженные на Кельвин и делёный на Ватт).
Итак, чтобы найти «Q» того же дома, что и в примере выше, подсчитаем площадь его поверхностей «S» (пол и окна считать не будем).
- «S» в нашем случае = 170 м2, из них 80 м2 потолок и 90 м2 — стены;
- T = 62 °С;
- R– тепловое сопротивление.
Ищем «R» по таблице тепловых сопротивлений или по формуле. Формула для расчета по коэффициенту теплопроводности такая:
R= H/ К.Т. (Н – толщина материала в метрах, К.Т. – коэффициент теплопроводности).
В этом случае, дом у нас имеет стены в два кирпича обшитые пенопластом толщиной 10 см. Потолок засыпан опилками толщиной 30 см.
Отопительную систему частного дома нужно устраивать с учетом экономии средств на энергоносители. Расчет системы отопления частного дома, а также рекомендации по выбору котлов и радиаторов — читайте внимательно.
Чем и как утеплить деревянный дом изнутри, вы узнаете, прочитав эту информацию. Выбор утеплителя и технология утепления.
Из таблицы коэффициентов теплопроводности (измеряется Вт / (м2 х К) Ватт делёный на произведение метра квадратного на Кельвин). Находим значения для каждого материала, они будут:
- кирпич — 0,67;
- пенопласт – 0,037;
- опилки – 0,065.

- R (потолка 30 см толщиной) = 0,3 / 0,065 = 4,6 (м2 х К) / Вт;
- R (кирпичной стены 50 см) = 0,5 / 0,67 = 0,7 (м2 х К) / Вт;
- R (пенопласт 10 см) = 0,1 / 0,037 = 2,7 (м2 х К) / Вт;
- R (стен) = R(кирпич) + R(пенопласт) = 0,7 + 2,7 = 3,4 (м2 х К) / Вт.
Теперь можем приступить к расчету теплопотерь «Q»:
- Q для потолка = 80 х 62 / 4,6 = 1078,2 Вт.
- Q стен = 90 х 62 / 3,4 = 1641,1 Вт.
- Остается сложить 1078,2 + 1641,1 и перевести в кВт, получается (если сразу округлить) 2,7 кВт энергии за 1 час.
Всё дело в степени утомлённости домов (хотя, конечно, данные могли быть и иными, если бы мы рассчитывали пол и окна).
Заключение
Приведённые формулы и примеры показываю, что при теплотехнических расчётах очень важно учитывать как можно больше факторов, влияющих на теплопотери. Сюда входит и вентиляция, и площадь окон, степень их утомлённости и т. д.
Сюда входит и вентиляция, и площадь окон, степень их утомлённости и т. д.
А подход, когда на 10 м2 дома берётся 1 кВт мощности котла – слишком приблизительный, чтобы всерьёз опираться на него.
Видео на тему
microklimat.pro
13 Тепловой расчет
10. Тепловой расчет.
Конструкция ИМС должна быть такой, чтобы теплота, выделяющаяся при ее функционировании, не приводила в наиболее неблагоприятных условиях эксплуатации к отказам элементов в результате перегрева. К основным тепловыделяющим элементам следует отнести, прежде всего, резисторы, активные элементы и компоненты. Мощности, рассеиваемые конденсаторами и индуктивностями, невелики. Пленочная коммутация ИМС, благодаря малому электрическому сопротивлению и высокой теплопроводности металлических пленок, способствует отводу теплоты от наиболее нагретых элементов и выравниванию температуры платы ГИС и кристалла полупроводниковой ИМС.
Рис. 10.1. Вариант крепления платы на корпус.
Тепловой расчёт резисторов.
Тепловое сопротивление резистора вычислим по формуле (10.1)
п = 0.03 [Вт/см °С] — коэффициент теплопроводности материала подложки;
δп = 0.06 см – толщина платы.
RT=0.06/0.03=2 см2∙°С/Вт
Рассчитаем температуру пленочных резисторов по формуле
PR – мощность, выделяемая на резисторе;
SR – площадь, занимаемая резистором на плате;
P0 – суммарная мощность, выделяемая всеми компонентами микросхемы;
Sп – площадь платы.
PR = 0.43 мВт – мощность выделяемая на резисторе;
SR = 0.426мм2 – площадь занимаемая резистором;
Sn = 80 мм2 – площадь платы;
RT = 2 см2∙°С/Вт – тепловое сопротивление резистора;
Токр.ср = 40С – максимальная температура окружающей среды;
T = 125С = максимально допустимая температура пленочных резисторов.
TR=(0.43∙10-3∙200)/0.426+(24.82∙10-3∙200)/80+40=40.26 С
Температура остальных резисторов рассчитывается аналогично с помощью программы MathCad. Результаты расчётов представлены в Таблице10. 1
1
Таблица. 10.1
Из таблицы видно, что для всех пленочных резисторов заданный тепловой режим соблюдается.
Тепловой расчет для навесного элемента.
Тепловое сопротивление будет вычисляться по формуле:
k = 0.003 [Вт/см °С] — коэффициент теплопроводности клея;
δк1 = 0.01 см – толщина клея.
Rт=(0.06/0.03)+(0.01/0.003)=5.33 см2∙°С/Вт
Рассчитаем температуру навесного элемента по формуле:
Расчет транзистор КТ202А, VT14
Pнэ = 2,6 мВт – мощность выделяемая на транзисторе;
Sнэ = 0,49 мм2 – площадь занимаемая транзистором;
P0 = 24.82 мВт – мощность выделяемая всеми компонентами платы;
Sn = 80 мм2 – площадь платы;
Т0С = 40С – максимальная температура окружающей среды;
T = 85С = максимально допустимая температура транзистора.
Tнэ=(2.6∙10-3∙533)/0.49+(24.82∙10-3∙533)/80+40=42.99С
Следовательно заданный тепловой режим соблюдается.
Температура остальных транзисторов рассчитывается аналогично с помощью программы MathCad. Результаты расчётов представлены в Таблице10.2
Результаты расчётов представлены в Таблице10.2
Таблица 10.2
Из таблицы видно, что для всех транзисторов заданный тепловой режим соблюдается. Следовательно и тепловые условия для всей схемы выполняются.
studfiles.net
Тепловая мощность электрического тока и ее практическое применение
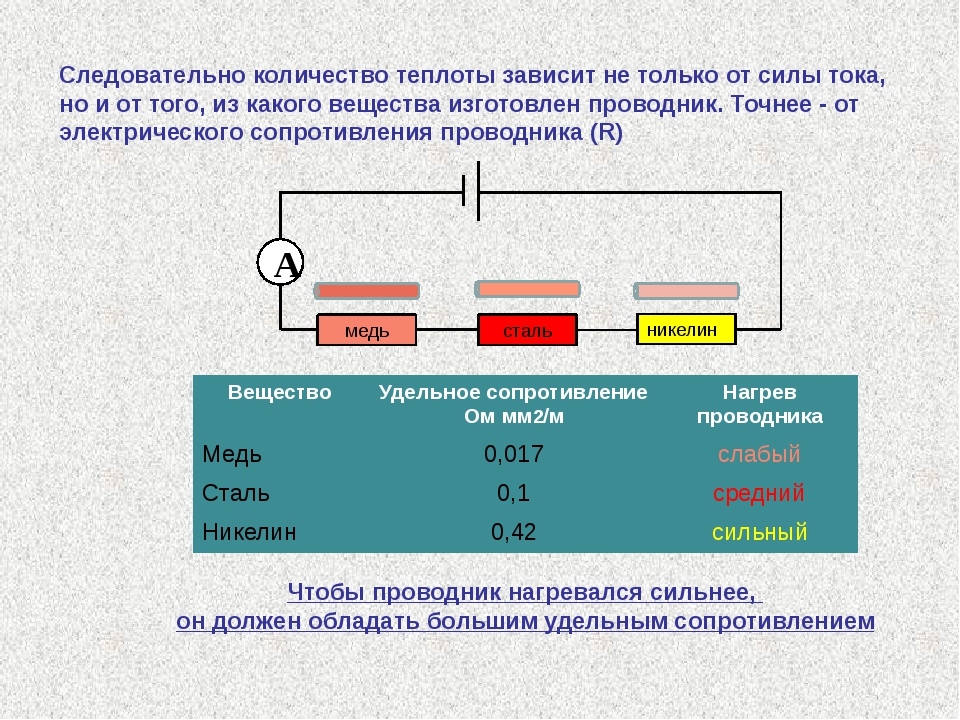
Причина нагревания проводника кроется в том, что энергия движущихся в нем электронов (иными словами, энергия тока) при последовательном столкновении частиц с ионами молекулярной решётки металлического элемента преобразуется в тёплый тип энергии, или Q, так образуется понятие «тепловая мощность».
Работу тока измеряют с помощью международной системы единиц СИ, применяя к ней джоули (Дж), мощность тока определяют как «ватт» (Вт). Отступая от системы на практике, могут применять в том числе и внесистемные единицы, измеряющие работу тока. Среди них ватт-час (Вт × ч), киловатт-час (сокращённо кВт × ч). Например, 1 Вт × ч обозначает работу тока с удельной мощностью 1 ватт и длительностью времени на один час.
Если электроны движутся по неподвижному проводнику из металла, в этом случае вся полезная работа вырабатываемого тока распределяется на нагревание металлической конструкции, и, исходя из положений закона сохранения энергии, это можно описать формулой Q=A=IUt=I2Rt=(U2/R)*t. Такие соотношения с точностью выражают известный закон Джоуля-Ленца. Исторически он впервые был определён опытным путём учёным Д. Джоулем в середине 19-го века, и в то же время независимо от него ещё одним учёным — Э.Ленцем. Практическое применение тепловая мощность нашла в техническом исполнении с изобретения в 1873 году русским инженером А. Ладыгиным обыкновенной лампы накаливании.
Тепловая мощность тока задействуется в целом ряде электрических приборов и промышленных установок, а именно, в тепловых измерительных приборах, нагревательного типа электрических печках, электросварочной и инвенторной аппаратуре, очень распространены бытовые приборы на электрическом нагревательном эффекте – кипятильники, паяльники, чайники, утюги.
Находит себя тепловой эффект и в пищевой промышленности. С высокой долей использования применяется возможность электроконтактного нагрева, что гарантирует тепловая мощность. Он обуславливается тем, что ток и его тепловая мощность, оказывая влияние на пищевой продукт, который обладает определённой степенью сопротивления, вызывает в нем равномерное разогревание. Можно привести в пример то, как производятся колбасные изделия: через специальный дозатор мясной фарш поступает в металлические формы, стенки которых одновременно служат электродами. Здесь обеспечивается постоянная равномерность нагрева по всей площади и объёму продукта, поддерживается заданная температура, сохраняется оптимальная биологическая ценность пищевого продукта, вместе с этими факторами длительность технологических работ и расход энергии остаются наименьшими.
Удельная тепловая мощность электрического тока (ω), иными словами — количество теплоты, что выделяется в единице объёма за определённую единицу времени, рассчитывается следующим образом. Элементарный цилиндрический объём проводника (dV), с поперечным проводниковым сечением dS, длиной dl, параллельной направлению тока, и сопротивлением составляют уравнения R=p(dl/dS), dV=dSdl.
Элементарный цилиндрический объём проводника (dV), с поперечным проводниковым сечением dS, длиной dl, параллельной направлению тока, и сопротивлением составляют уравнения R=p(dl/dS), dV=dSdl.
Согласно определениям закона Джоуля-Ленца, за отведённое время (dt) во взятом нами объёме выделится уровень теплоты, равный dQ=I2Rdt=p(dl/dS)(jdS)2dt=pj2dVdt. В таком случае ω=(dQ)/(dVdt)=pj2 и, применяя здесь закон Ома для установления плотности тока j=γE и соотношение p=1/γ, мы сразу получаем выражение ω=jE= γE2. Оно в дифференциальной форме даёт понятие о законе Джоуля-Ленца.
fb.ru
Страничка эмбеддера » Тепловые расчеты
Все электронные компоненты выделяют тепло, поэтому умение рассчитывать радиаторы так, чтобы не пролетать в прикидках на пару порядков очень полезно любому электронщику.
Тепловые расчеты очень просты и имеют очень много общего с расчетами электронных схем. Вот, посмотрите на обычную задачу теплового расчета, с которой я только что столкнулся
Задача
Нужно выбрать радиатор для 5-вольтового линейного стабилизатора, который питается от 12вольт максимум и выдает 0. 5А. Максимальная выделяемая мощность получается (12-5)*0.5 = 3.5Вт
5А. Максимальная выделяемая мощность получается (12-5)*0.5 = 3.5Вт
Погружение в теорию
Для того, чтобы не плодить сущностей, люди почесали тыковку и поняли, что тепло очень похоже на электрической ток, и для тепловых расчетов можно использовать обычный закон Ома, только
Напряжение (U) заменяется температурой (T)
Ток (I) заменяется мощностью (P)
Сопротивление заменяется тепловым сопротивлением. Обычное сопротивление имеет размерность Вольт/Ампер, а тепловое – °C/Ватт
В итоге, закон Ома заменяется на свой тепловой аналог:
Небольшой замечание – для того, чтобы обозначить, что имеется ввиду тепловое (а не электрическое) сопротивление, к букве R, дописывают букву тэта:на клавиатуре у меня такой буквы нет, а копировать из таблицы символов лень, поэтому я буду пользоваться просто буквой R.
Продолжаем
Тепло выделяется в кристалле стабилизатора, а наша цель – не допустить его перегрева (не допустить перегрева именно кристалла, а не корпуса, это важно!).
До какой температуры можно нагревать кристалл, написано в даташите:
Обычно, предельную температуру кристалла называют Tj (j = junction = переход – термочувствительные внутренности микросхем в основном состоят из pn переходов. Можно считать, что температура переходов равна температуре кристалла)
Без радиатора
Тепловая схема выглядит очень просто:
Специально для случаев использования корпуса без радиатора, в даташитах пишут тепловое сопротивление кристалл-атмосфера (Rj-a) (что такое j вы уже в курсе, a = ambient = окружающая среда)
Заметьте, что температура “земли” не нулевая, а равняется температуре окружающего воздуха (Ta). Температура воздуха зависит от того, в каких условиях находится радиатор Если стоит на открытом воздухе, то можно положить Ta = 40 °C, а вот, если в закрытой коробке, то температура может быть значительно выше!
Записываем тепловой закон Ома: Tj = P*Rj-a + Ta. Подставляем P = 3.5, Rj-a = 65, получаем Tj = 227. 5 + 40 = 267.5 °C. Многовато, однако!
5 + 40 = 267.5 °C. Многовато, однако!
Цепляем радиатор
Тепловая схема нашего примера со стабилизатором на радиаторе становится вот такой:
- Rj-c – сопротивление от кристалла до теплоотвода корпуса (c = case = корпус). Дается в даташите. В нашем случае – 5 °C/Вт – из даташита
- Rc-r – сопротивление корпус-радиатор. Тут не все так просто. Это сопротивление зависит от того, что находится между корпусом и радиатором. К примеру, силиконовая прокладка имеет коэффициент теплопроводности 1-2 Вт/(м*°C), а паста КПТ-8 – 0.75Вт/(м*°C). Тепловое сопротивление можно получить из коэффициента теплопроводности по формуле:
R = толщина прокладки/(коэффициент теплопроводности * площадь одной стороны прокладки)
Часто Rc-r вообще можно игнорировать. К примеру, в нашем случае (используем корпус TO220, с пастой КПТ-8, средняя глубина пасты, взятая с потолка – 0.05мм). Итого, Rc-r = 0.5 °C/Вт. При мощности 3.5вт, разница температур корпуса стабилизатора и радиатора — 1.
 75градуса. Это – не много. Для нашего примера, возьмем Rc-r = 2 °C/Вт
75градуса. Это – не много. Для нашего примера, возьмем Rc-r = 2 °C/Вт
Rr-a – тепловое сопротивление между радиатором и атмосферой. Определяется геометрией радиатора, наличием обдува, и кучей других факторов. Этот параметр намного проще измерить, чем посчитать (см в конце статьи). Для примера — Rr-c = 12.5 °C/Вт
Ta = 40°C – тут мы прикинули, что атмосферная температура редко выше, можно взять и 50 градусов, чтобы уж точно было.
Подставляем все эти данные в закон Ома, и получаем Tj = 3.5*(5+2+12.5) + 40 = 108.25 °C
Это значительно меньше, чем предельные 150 °C. Такой радиатор можно использовать. При этом, корпус радиатора будет греться до Tc = 3.5*12.5 + 40 = 83.75 °C. Такая температура уже способна размягчить некоторые пластики, поэтому нужно быть осторожным.
Измерение сопротивления радиатор-атмосфера.
Скорее-всего, у вас уже валяется куча радиаторов, которые можно задействовать. Тепловое сопротивление измеряется очень легко. Это этого нужно сопротивление и источник питания.
Лепим сопротивление на радиатор, используя термопасту:
Подключаем источник питания, и выставляем напряжение так, чтобы на сопротивлении выделялась некая мощность. Лучше, конечно, нагревать радиатор той мощностью, которую он будет рассеивать в конечном устройстве (и в том положении, в котором он будет находиться, это важно!). Я обычно оставляю такую конструкцию на пол часа, чтобы она хорошо прогрелась.
После того, как измерили температуру, можно рассчитать тепловое сопротивление
Rr-a = (T-Ta)/P. К примеру, у меня радиатор нагрелся до 81 градуса, а температура воздуха – 31 градус. таким образом, Rr-a = 50/4 = 12.5 °C/Вт.
Прикидка площади радиатора
В древнем справочнике радиолюбителя приводился график, по которому можно прикинуть площадь радиатора. Вот он:
Работать с ним очень просто. Выбираем перегрев, который хочется получить и смотрим, какая площадь соответствует необходимой мощности при таком перегреве.
К примеру, при мощности 4вт и перегреве 20 градусов, понадобится 250см^2 радиатора. Этот график дает завышенную оценку площади, и не учитывает кучу факторов как то принудительный обдув, геометрия ребер, итп.
Этот график дает завышенную оценку площади, и не учитывает кучу факторов как то принудительный обдув, геометрия ребер, итп.
bsvi.ru
Закон Джоуля – Ленца – закон физики, определяющий количественную меру теплового действия электрического тока. Сформулирован этот закон был в 1841 году английским учёным Д. Джоулем и совершенно отдельно от него в 1842 году известным русским физиком Э. Ленцем. Поэтому он получил своё двойное название — закон Джоуля – Ленца.
Определение закона и формула
Словесная формулировка имеет следующий вид: мощность тепла, выделяемого в проводнике при протекании сквозь него , пропорционально произведению значения плотности электрического поля на значение напряженности.
Математически закон Джоуля — Ленца выражается следующим образом:
ω = j E = ϭ E²,
где ω — количество тепла, выделяемого в ед. объема;
E и j – напряжённость и плотность, соответственно, электрического полей;
σ — проводимость среды.
Физический смысл закона Джоуля – Ленца
Закон можно объяснить следующим образом: ток, протекая по проводнику, представляет собой перемещение электрического заряда под воздействием . Таким образом, электрическое поле совершает некоторую работу. Эта работа расходуется на нагрев проводника.
Другими словами, энергия переходит в другое свое качество – тепло.
Но чрезмерный нагрев проводников с током и электрооборудования допускать нельзя, поскольку это может привести к их повреждению. Опасен сильный перегрев при проводов, когда по проводниках могут протекать достаточно большие токи.
В интегральной форме для тонких проводников закон Джоуля – Ленца звучит следующим образом: количество теплоты, которое выделяется в единицу времени в рассматриваемом участке цепи, определяется как произведение квадрата силы тока на сопротивление участка.
Математически эта формулировка выражается следующим образом:
Q = ∫ k I² R t,
при этом Q – количество выделившейся теплоты;
I – величина тока;
R — активное сопротивление проводников;
t – время воздействия.
Значение параметра k принято называть тепловым эквивалентом работы. Величина этого параметра определяется в зависимости от разрядности единиц, в которых выполняются измерения значений, используемых в формуле.
Закон Джоуля-Ленца имеет достаточно общий характер, поскольку не имеет зависимости от природы сил, генерирующих ток.
Из практики можно утверждать, что он справедлив, как для электролитов, так проводников и полупроводников.
Область применения
Областей применения в быту закона Джоуля Ленца – огромное количество. К примеру, вольфрамовая нить в лампе накаливания, дуга в электросварке, нагревательная нить в электрообогревателе и мн. др. Это наиболее широко распространенный физический закон в повседневной жизни.
Содержание:Знаменитый русский физик Ленц и английский физик Джоуль, проводя опыты по изучению тепловых действий электрического тока, независимо друг от друга вывели закон Джоуля-Ленца. Данный закон отражает взаимосвязь количества теплоты, выделяемого в проводнике, и электрического тока, проходящего по этому проводнику в течение определенного периода времени.
Свойства электрического тока
Когда электрический ток проходит через металлический проводник, его электроны постоянно сталкиваются с различными посторонними частицами. Это могут быть обычные нейтральные молекулы или молекулы, потерявшие электроны. Электрон в процессе движения может отщепить от нейтральной молекулы еще один электрон. В результате, его кинетическая энергия теряется, а вместо молекулы происходит образование положительного иона. В других случаях электрон, наоборот, соединиться с положительным ионом и образовать нейтральную молекулу.
В процессе столкновений электронов и молекул происходит расход энергии, в дальнейшем превращающейся в тепло. Затраты определенного количества энергии связаны со всеми движениями, во время которых приходится преодолевать сопротивление. В это время происходит превращение работы, затраченной на преодоление сопротивления трения, в тепловую энергию.
Закон джоуля Ленца формула и определение
Согласно закону джоуля Ленца, электрический ток, проходящий по проводнику, сопровождается количеством теплоты, прямо пропорциональным квадрату тока и сопротивлению, а также времени течения этого тока по проводнику.
В виде формулы закон Джоуля-Ленца выражается следующим образом: Q = I 2 Rt, в которой Q отображает количество выделенной теплоты, I — , R — сопротивление проводника, t — период времени. Величина «к» представляет собой тепловой эквивалент работы и применяется в тех случаях, когда количество теплоты измеряется в калориях, сила тока — , сопротивление — в Омах, а время — в секундах. Численное значение величины к составляет 0,24, что соответствует току в 1 ампер, который при сопротивлении проводника в 1 Ом, выделяет в течение 1 секунды количество теплоты, равное 0,24 ккал. Поэтому для расчетов количества выделенной теплоты в калориях применяется формула Q = 0,24I 2 Rt.
При использовании системы единиц СИ измерение количества теплоты производится в джоулях, поэтому величина «к», применительно к закону Джоуля-Ленца, будет равна 1, а формула будет выглядеть: Q = I 2 Rt. В соответствии с I = U/R. Если это значение силы тока подставить в основную формулу, она приобретет следующий вид: Q = (U 2 /R)t.
Основная формула Q = I 2 Rt очень удобна для использования при расчетах количества теплоты, которое выделяется в случае последовательного соединения. Сила тока во всех проводниках будет одинаковая. При последовательном соединении сразу нескольких проводников, каждый из них выделит столько теплоты, которое будет пропорционально сопротивлению проводника. Если последовательно соединить три одинаковые проволочки из меди, железа и никелина, то максимальное количество теплоты будет выделено последней. Это связано с наибольшим удельным сопротивлением никелина и более сильным нагревом этой проволочки.
При параллельном соединении этих же проводников, значение электрического тока в каждом из них будет различным, а напряжение на концах — одинаковым. В этом случае для расчетов больше подойдет формула Q = (U 2 /R)t. Количество теплоты, выделяемое проводником, будет обратно пропорционально его проводимости. Таким образом, закон Джоуля — Ленца широко используется для расчетов установок электрического освещения, различных отопительных и нагревательных приборов, а также других устройств, связанных с преобразованием электрической энергии в тепловую.
Закон Джоуля-Ленца. Работа и мощность электрического тока
Джеймс Прескотт Джоуль (слева) и Эмилий Христианович Ленц (справа)
Электрические нагреватели всевозможных типов используются человечеством уже столетия, благодаря свойству электрического тока выделять тепло при прохождении через проводник. У этого явления есть и негативный фактор – перегретая электропроводка из-за слишком большого тока часто становилась причиной короткого замыкания и возникновения пожаров. Выделение тепла от работы электрического тока изучалось в школьном курсе физики, но многие позабыли эти знания.
Впервые зависимость выделения теплоты от силы электрического тока была сформулирована и математически определена Джеймсом Джоулем в 1841 году, и чуть позже, в 1842 г., независимо от него, Эмилем Ленцем. В честь этих физиков и был назван закон Джоуля-Ленца, по которому рассчитывают мощность электронагревателей и потери на тепловыделение в линиях электропередач.
Определение закона Джоуля – Ленца
В словесном определении, согласно исследований Джоуля и Ленца закон звучит так:
Количество теплоты, выделяемой в определенном объеме проводника при протекании электрического тока прямо пропорционально умножению плотности электрического тока и величины напряженности электрического поля
В виде формулы данный закон выглядит следующим образом:
Выражение закона Джоуля — Ленца
Поскольку описанные выше параметры редко применяются в обыденной жизни, и, учитывая, что почти все бытовые расчеты выделения теплоты от работы электрического тока касаются тонких проводников (кабели, провода, нити накаливания, шнуры питания, токопроводящие дорожки на плате и т. п.), используют закон Джоуля Ленца с формулой, представленной в интегральном виде:
п.), используют закон Джоуля Ленца с формулой, представленной в интегральном виде:
Интегральная форма закона
В словесном определении закон Джоуля Ленца звучит так:
Словесное определение закона Джоуля — Ленца
Если принять, что сила тока и сопротивление проводника не меняется в течение времени, то закон Джоуля — Ленца можно записать в упрощенном виде:
Применив закон Ома и алгебраические преобразования, получаем приведенные ниже эквивалентные формулы:
Эквивалентные выражения теплоты согласно закона Ома
Применение и практическое значение закона Джоуля – Ленца
Исследования Джоуля и Ленца в области тепловыделения от работы электрического тока существенно продвинули научное понимание физических процессов, а выведенные основные формулы не претерпели изменений и используются по сей день в различных отраслях науки и техники. В сфере электротехники можно выделить несколько технических задач, где количество выделяемой при протекании тока теплоты имеет критически важное значение при расчете таких параметров:
- теплопотери в линиях электропередач;
- характеристики проводов сетей электропроводки;
- тепловая мощность (количество теплоты) электронагревателей;
- температура срабатывания автоматических выключателей;
- температура плавления плавких предохранителей;
- тепловыделение различных электротехнических аппаратов и элементов радиотехники.

Электроприборы, в которых используется тепловая работа тока
Тепловое действие электрического тока в проводах линий электропередач (ЛЭП) является нежелательным из-за существенных потерь электроэнергии на тепловыделение.
По различным данным в линиях электропередач теряется до 40% всей производимой электрической энергии в мире. Для уменьшения потерь при передаче электроэнергии на большие расстояния, поднимают напряжение в ЛЭП, производя расчеты по производным формулам закона Джоуля – Ленца.
Диаграмма всевозможных потерь электроэнергии, среди которых теплопотери на воздушных линиях составляют львиную долю (64%)
Очень упрощенно тепловую работу тока можно описать следующим образом: двигаются электроны между молекулами, и время от времени сталкиваются с ними, отчего их тепловые колебания становятся более интенсивными. Наглядная демонстрация тепловой работы тока и ассоциативные пояснения процессов показаны на видео ниже:
Расчеты потерь электроэнергии в линиях электропередач
В качестве примера можно взять гипотетический участок линии электропередач от электростанции до трансформаторной подстанции. Поскольку провода ЛЭП и потребитель электроэнергии (трансформаторная подстанция) соединены последовательно , то через них течет один и тот же ток I. Согласно рассматриваемому тут закону Джоуля – Ленца количество выделяемой на проводах теплоты Q w (теплопотерь) рассчитывается по формуле:
Поскольку провода ЛЭП и потребитель электроэнергии (трансформаторная подстанция) соединены последовательно , то через них течет один и тот же ток I. Согласно рассматриваемому тут закону Джоуля – Ленца количество выделяемой на проводах теплоты Q w (теплопотерь) рассчитывается по формуле:
Производимая электрическим током мощность (Q c) в нагрузке рассчитывается согласно закону Ома:
Таким образом, при равенстве токов, в первую формулу можно вставить вместо I выражение Q c /U c , поскольку I = Q c /U c:
Если проигнорировать зависимость сопротивления проводников от изменения температуры, то можно считать R w неизменным (константой). Таким образом, при стабильном энергопотреблении потребителя (трансформаторной подстанции), тепловыделение в проводах ЛЭП будет обратно пропорционально квадрату напряжения в конечной точке линии. Другими словами, чем больше напряжение электропередачи, тем меньше потери электроэнергии.
Для передачи электроэнергии высокого напряжения требуются большие опоры ЛЭП
Работа закона Джоуля – Ленца в быту
Данные расчеты справедливы также и в быту при передаче электроэнергии на малые расстояния – например, от ветрогенератора до инвертора. При автономном энергоснабжении ценится каждый Ватт выработанной низковольтным ветряком энергии, и возможно, будет выгодней поднять напряжение трансформатором прямо у ветрогенератора, чем тратиться на большое сечение кабеля, чтобы уменьшить потери электроэнергии при передаче.
При автономном энергоснабжении ценится каждый Ватт выработанной низковольтным ветряком энергии, и возможно, будет выгодней поднять напряжение трансформатором прямо у ветрогенератора, чем тратиться на большое сечение кабеля, чтобы уменьшить потери электроэнергии при передаче.
При значительном удалении низковольтного ветрогенератора переменного тока для уменьшения потерь электроэнергии будет выгодней подключение через повышающий трансформатор
В бытовых сетях электропроводки расстояния крайне малы, чтобы уменьшения тепловых потерь поднимать напряжение, поэтому при расчете проводки учитывается тепловая работа тока, согласно закону Джоуля – Ленца при выборе поперечного сечения проводов, чтобы их тепловой нагрев не привел к оплавлению и возгоранию изоляции и окружающих материалов. Выбор кабеля по мощности и электропроводки проводятся согласно таблиц и нормативных документов ПУЭ, и подробно описаны на других страницах данного ресурса.
Соотношения силы тока и поперечного сечения проводников
При расчете температуры нагрева радиотехнических элементов, биметаллической пластины автоматического выключателя или плавкого предохранителя используется закон Джоуля – Ленца в интегральной форме, так как при росте температуры изменяется сопротивление данных материалов.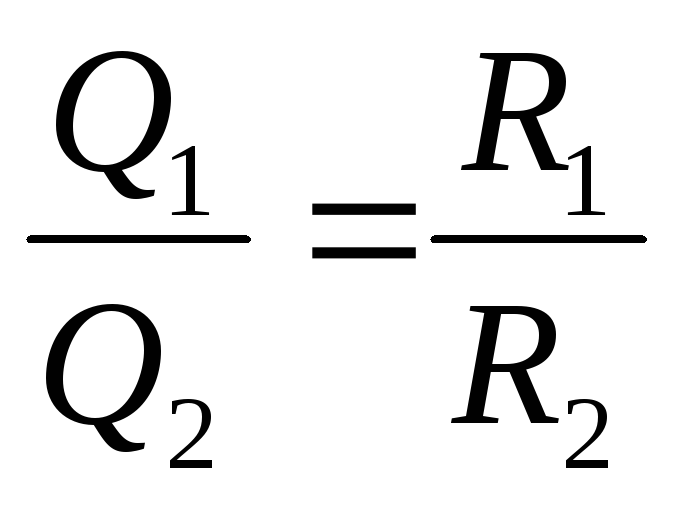 При данных сложных расчетах также учитываются теплоотдача, нагрев от других источников тепла, собственная теплоемкость и множество других факторов.
При данных сложных расчетах также учитываются теплоотдача, нагрев от других источников тепла, собственная теплоемкость и множество других факторов.
Программное моделирование тепловыделения полупроводникового прибора
Полезная тепловая работа электрического тока
Тепловыделяющая работа электрического тока широко применяется в электронагревателях, в которых используется последовательное соединение проводников с различным сопротивлением. Данный принцип работает следующим образом: в соединенных последовательно проводниках течет одинаковый ток, значит, согласно закону Джоуля – Ленца, тепла выделится больше у материала проводника с большим сопротивлением.
Спираль с повышенным сопротивлением накаляется, но питающие провода остаются холодными
Таким образом, шнур питания и подводящие провода электроплитки остаются относительно холодными, в то время как нагревательный элемент нагревается до температуры красного свечения. В качестве материала для проводников нагревательных элементов используются сплавы с повышенным (относительно меди и алюминия электропроводки) удельным сопротивлением — нихром, константан, вольфрам и другие.
Нить лампы накаливания изготовляют из тугоплавких вольфрамовых сплавов
При параллельном соединении проводников тепловыделение будет больше на нагревательном элементе с меньшим сопротивлением, так как при его уменьшении возрастает ток относительного соседнего компонента цепи. В качестве примера можно привести очевидный пример свечения двух лампочек накаливания различной мощности – у более мощной лампы тепловыделение и световой поток больше.
Если прозвонить омметром лампочки, то окажется, что у более мощной лампы сопротивление меньше. На видео ниже автор демонстрирует последовательное и параллельное подключение, но к сожалению, он ошибся в комментарии — будет ярче светить лампа с большим сопротивлением, а не наоборот.
Задачи по физике и математике с решениями и ответами
Задача по физике — 13878
В схеме, изображенной на рисунке, сверхпроводящие катушки с индуктивностями $L_{1}$ и $L_{2}$ соединены последовательно с конденсатором емкостью $C$. В начальный момент ключи $K_{1}$ и $K_{2}$ разомкнуты, а конденсатор заряжен до напряжения $U_{0}$. Сначала замыкают ключ $K_{1}$, а после того, как напряжение на конденсаторе станет равным нулю, замыкают ключ $K_{2}$. Через некоторое время после замыкания ключа $K_{2}$ конденсатор перезарядится до некоторого максимального напряжения $U_{m}$. Найдите ток через катушки индуктивности непосредственно перед замыканием ключа $K_{2}$. Найдите также напряжение $U_{m}$.
В начальный момент ключи $K_{1}$ и $K_{2}$ разомкнуты, а конденсатор заряжен до напряжения $U_{0}$. Сначала замыкают ключ $K_{1}$, а после того, как напряжение на конденсаторе станет равным нулю, замыкают ключ $K_{2}$. Через некоторое время после замыкания ключа $K_{2}$ конденсатор перезарядится до некоторого максимального напряжения $U_{m}$. Найдите ток через катушки индуктивности непосредственно перед замыканием ключа $K_{2}$. Найдите также напряжение $U_{m}$. Подробнее
Задача по физике — 13879
В цепи, состоящей из источника тока с ЭДС $\mathcal{E}$, конденсатора емкостью $C$, катушки индуктивностью $L$ и идеального диода D, ключ K первоначально разомкнут (рис.). Определите напряжение, до которого зарядится конденсатор после замыкания ключа. Диод считается идеальным, если его сопротивление в прямом направлении бесконечно мало, а в обратном направлении — бесконечно велико. {-5} Ф$, сопротивления резисторов $R_{0} = 10 Ом, R = 15 Ом$, ЭДС источника $\mathcal{E} = 450 В$.
{-5} Ф$, сопротивления резисторов $R_{0} = 10 Ом, R = 15 Ом$, ЭДС источника $\mathcal{E} = 450 В$. Подробнее
Задача по физике — 13881
В колебательном контуре (рис.) происходят колебания. Максимальное напряжение на конденсаторе емкостью $C = 40 мкФ$ равно $U_{0} = 2 В$. Параллельно конденсатору подсоединены через ключ (изначально разомкнутый) параллельно соединенные резистор и катушка с индуктивностью, в $k = 3$ раза меньшей индуктивности катушки колебательного контура. Ключ замыкают в момент, когда напряжение на конденсаторе становится в $n = 2$ раза меньше своего максимального значения. Какое количество теплоты выделится в резисторе после замыкания ключа? Омическим сопротивлением катушек и сопротивлением соединительных проводов пренебречь.Подробнее
Задача по физике — 13882
В схеме, изображенной на рисунке, конденсатор емкостью $C$ заряжен до напряжения $U_{0}$, конденсатор емкостью $2C$ не заряжен, ключи разомкнуты.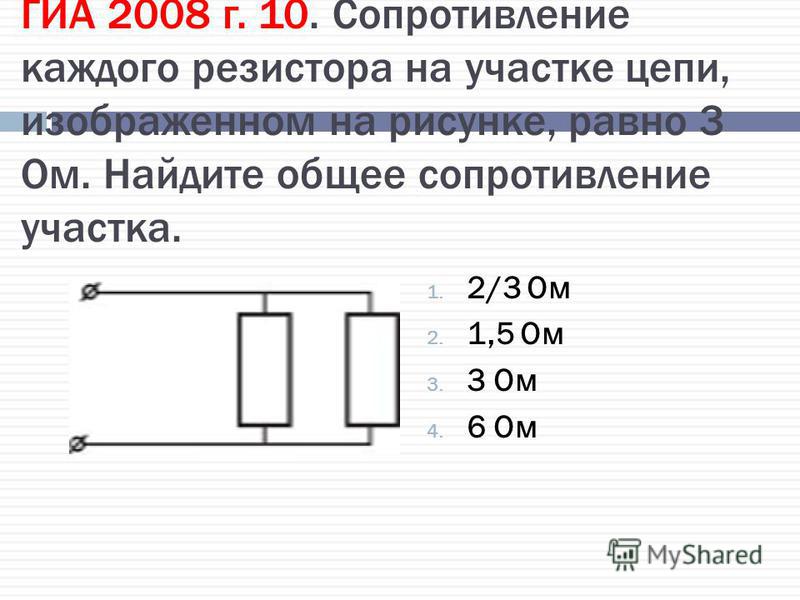 Ключ K замыкают. Когда ток в катушке индуктивностью $L$ достигает максимального значения, замыкают ключ $K_{2}$. Какое количество теплоты выделится на резисторе сопротивлением $R$? Параметры схемы указаны на рисунке. Считайте, что сопротивления катушек, подводящих проводов и ключей пренебрежимо малы.
Ключ K замыкают. Когда ток в катушке индуктивностью $L$ достигает максимального значения, замыкают ключ $K_{2}$. Какое количество теплоты выделится на резисторе сопротивлением $R$? Параметры схемы указаны на рисунке. Считайте, что сопротивления катушек, подводящих проводов и ключей пренебрежимо малы. Подробнее
Задача по физике — 13887
Экспериментатор Глюк сконструировал источник тока с регулируемым на выходе напряжением. В прибор он встроил миникомпьютер, показывающий протекший через источник заряд и среднюю силу тока (отношение всего протекшего заряда ко времени работы источника). Глюк присоединил к источнику резистор и, включив установку, начал регулировать напряжение. В результате ему удалось снять зависимость средней силы тока через резистор от времени (рис.). Однако в процессе эксперимента компьютер дал сбой, и зависимость протекшего заряда от времени оказалась утерянной.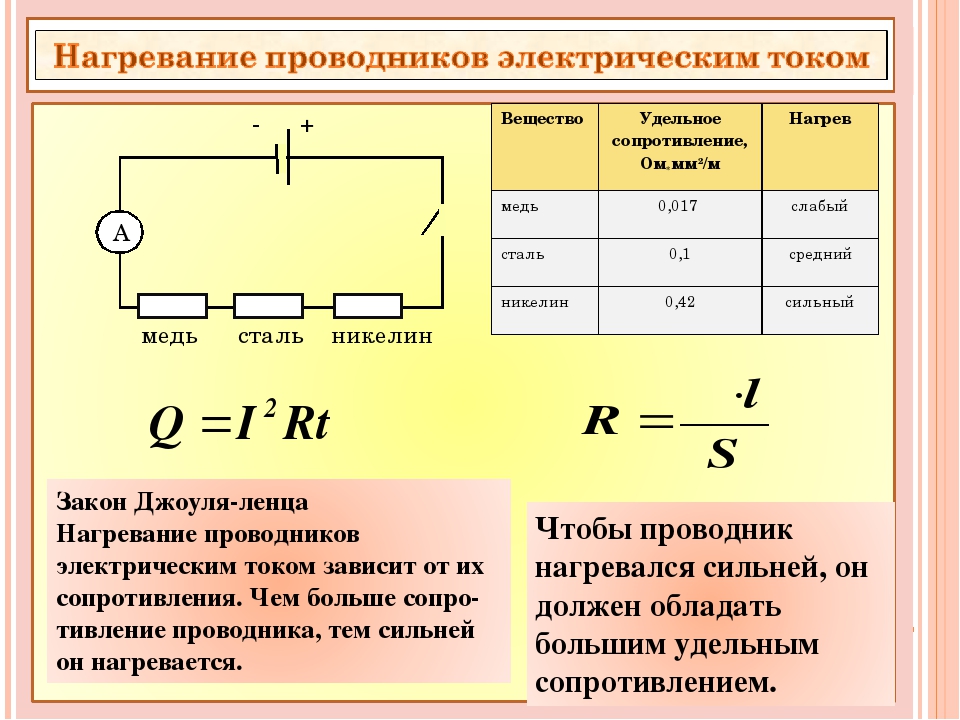
1) Восстановите зависимость протекшего через источник заряда от времени $q(t)$ и постройте на миллиметровой бумаге ее график.
2) Определите сопротивление $R$ резистора, если известно, что в точке А на нем выделялась мощность $P_{A} = 0,16 Вт$.
3) Определите максимальную мощность, выделявшуюся на резисторе во время эксперимента. Подробнее
Задача по физике — 13891
Стабилизированный источник тока способен выдавать постоянный ток $I_{0}$ независимо от подключенной к нему нагрузки. Источник включен в цепь, показанную на рисунке. Все элементы цепи можно считать идеальными, их параметры указаны на рисунке. До замыкания ключа конденсатор не был заряжен. В некоторый момент времени ключ замкнули. Какое количество теплоты $Q$ выделилось на резисторе сопротивлением $R$ после замыкания ключа?Подробнее
Задача по физике — 13892
Две материальные точки с массами $m$ и $M$ ($M > m$) и одинаковыми положительными зарядами $q$ находятся на расстоянии $l$ друг от друга в однородном электрическом поле $\vec{E}$, направленном от $m$ к $M$ (рис. {6} B$.
{6} B$. Подробнее
Задача по физике — 13900
Источник тока с ЭДС $\mathcal{E}$ и внутренним сопротивлением $r$ замыкают на реостат. При каком сопротивлении реостата на нем будет выделяться максимальная мощность? Чему она равна? ПодробнееЗадача по физике — 13913
Из сплава с линейно изменяющимся с расстоянием удельным сопротивлением изготовлены два тонких проводника одинаковой длины с вдвое отличающейся площадью сечения. Удельное сопротивление с одного конца каждого из проводников $\rho_{1}$, а с другого $\rho_{2}$. Проводники соединили параллельно и подключили к идеальному источнику с напряжением $U$, а к их серединам — точкам $a$ и $b$ — подсоединили идеальный вольтметр (рис.). Найдите показание вольтметра.
Подробнее
Задача по физике — 13916
Три одинаковых конденсатора емкостью $C$ каждый, резистор сопротивлением $R$ и диод D включены в схему (рис.). Вольт-амперная характеристика диода представлена на рисунке. Первоначально левый конденсатор заряжен до напряжения $U_{0}$, при этом заряд его верхней пластины положительный. Два других конденсатора не заряжены, ключ разомкнут. Затем ключ замыкают. Определите:1) напряжения на конденсаторах через большой промежуток времени после замыкания ключа;
2) количество теплоты, которое выделится в схеме к этому моменту времени;
3) количество теплоты, выделившееся к этому моменту на диоде;
4) количество теплоты, выделившееся к этому моменту на резисторе.
Подробнее
Задача по физике — 13926
Построите график зависимости сопротивления цепи, изображенной на рисунке, от сопротивления $r$ каждого из одной пары резисторов.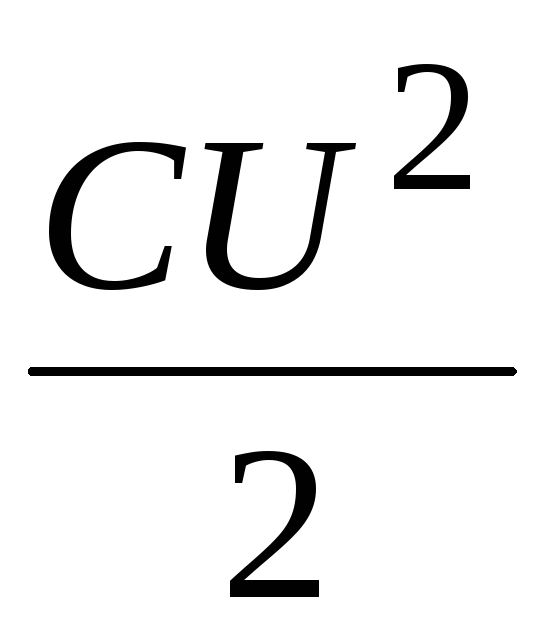 Сопротивление другой пары резисторов неизменно и равно $R = 50 Ом$ у каждого. Диод считайте идеальным, т.е. его сопротивление в прямом направлении пренебрежимо мало, а в обратном — очень велико.
Сопротивление другой пары резисторов неизменно и равно $R = 50 Ом$ у каждого. Диод считайте идеальным, т.е. его сопротивление в прямом направлении пренебрежимо мало, а в обратном — очень велико. Подробнее
Задача по физике — 13929
Протон, ускоренный разностью потенциалов $U = 500 кВ$, пролетает сквозь поперечное однородное магнитное поле с индукцией $B = 0,51 Тл$ (рис.). Толщина области с полем $d = 10 см$. Найдите смещение и угол отклонения скорости протона от первоначального направления на выходе из этой области.Подробнее
Задача по физике — 13937
В идеальном колебательном контуре, состоящем из плоского конденсатора и катушки индуктивности, происходят собственные незатухающие колебания. Пластины конденсатора равномерно и очень медленно раздвинули так, что частота колебаний увеличилась в $n$ раз. Во сколько раз изменилась при этом энергия колебаний? Подробнее
Пластины конденсатора равномерно и очень медленно раздвинули так, что частота колебаний увеличилась в $n$ раз. Во сколько раз изменилась при этом энергия колебаний? Подробнее Разряд конденсатора с выделением тепла
Переходные процессы – сложная тема, сложная даже для студентов, тем более – для школьников. Помните: постоянный ток не протекает через конденсатор. Напряжение на конденсаторе определяется его подключением: если параллельно резистору – то напряжение такое же, как на резисторе, если последовательно с источником – то конденсатор зарядится до ЭДС источника, после чего ток исчезнет. Если дать конденсатору возможность разрядиться – то энергия, запасенная в нем, превратится в тепло на резисторе.
Задача 1. Источник постоянного тока с ЭДС В и внутренним сопротивлением Ом подсоединен к параллельно соединенным резисторам Ом, Ом и конденсатору. Определите емкость конденсатора С, если энергия электрического поля конденсатора равна мкДж.
К задаче 1
Определить емкость легко из энергии конденсатора, только надо знать напряжение:
Объединим резисторы в один:
Ток в неразветвленной части цепи равен
Напряжение на внутреннем сопротивлении тогда равно
Тогда на резисторах и конденсаторе напряжение
Емкость равна
Ответ: мкФ.
Задача 2. Источник постоянного напряжения с ЭДС 100 В подключен через резистор к конденсатору переменной емкости, расстояние между пластинами которого можно изменять (см. рис.). Пластины медленно раздвинули. Какая работа была совершена против сил притяжения пластин, если за время движения пластин на резисторе выделилось количество теплоты 10 мкДж и заряд конденсатора изменился на 1 мкКл?
К задаче 2
У конденсатора была энергия до того, как пластины раздвинули – пусть . И после тоже была – пусть . В процессе раздвижения пластин совершили работу (которую надо найти), и, так как заряд уменьшился (а он именно уменьшился, так как напряжение осталось тем же), то источник тоже совершил работу. Поэтому закон сохранения энергии запишется так:
Поэтому закон сохранения энергии запишется так:
Заряд на конденсаторе сначала: , потом – . Тогда изменение заряда равно
Работа источника
Тогда наш закон сохранения можно переписать:
Ответ: 60 мкДж
Задача 3. Заряженный конденсатор мкФ включен в последовательную цепь из резистора Ом, незаряженного конденсатора мкФ и разомкнутого ключа К (см. рис.). После замыкания ключа в цепи выделяется количество теплоты мДж. Чему равно первоначальное напряжение на конденсаторе ?
К задаче 3
Первоначально на конденсаторе есть заряд:
После замыкания ключа заряд разделится:
Но напряжение на конденсаторах одно и то же:
Тогда
Откуда:
Энергия до замыкания, запасенная в конденсаторе , сохраняется:
Ответ:
Задача 4. В электрической схеме, показанной на рисунке, ключ К замкнут. ЭДС батарейки В, сопротивление резистора Ом, заряд конденсатора 2 мкКл. После размыкания ключа К в результате разряда конденсатора на резисторе выделяется количество теплоты 20 мкДж. Найдите внутреннее сопротивление батарейки .
В электрической схеме, показанной на рисунке, ключ К замкнут. ЭДС батарейки В, сопротивление резистора Ом, заряд конденсатора 2 мкКл. После размыкания ключа К в результате разряда конденсатора на резисторе выделяется количество теплоты 20 мкДж. Найдите внутреннее сопротивление батарейки .
К задаче 4
Сначала на конденсаторе напряжение такое же, как на резисторе (потому что они включены параллельно):
Определим ток. Он замыкается в контуре , потому что постоянный ток не течет через конденсатор:
Тогда напряжение на резисторе и конденсаторе:
С другой стороны, когда ключ разомкнется, вся энергия, запасенная в конденсаторе, рассеется в виде тепла через резистор:
То есть
Приравняем:
А внутреннее сопротивление равно
Ответ:
ФИЗИКА: ЗАДАЧИ на Закон Джоуля-Ленца
Задачи на Закон Джоуля-Ленца с решениямиФормулы, используемые на уроках «Задачи на Закон Джоуля-Ленца»
| Название величины | Обозначение | Единица измерения | Формула |
| Сила тока | I | А | I = U / R |
| Напряжение | U | В | U = IR |
| Время | t | с | t = Q / I2R |
| Количество теплоты | Q | Дж | Q = I2Rt |
1 мин = 60 с; 1 ч = 60 мин; 1 ч = 3600 с.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Какое количество теплоты выделит за 20 мин спираль электроплитки сопротивлением 25 Ом, если сила тока в цепи 1,2 А?
Задача № 2. Какое количество теплоты выделит за 30 мин спираль электроплитки, если сила тока в цепи 2 А, а напряжение 220 В?
Задача № 3. Сколько времени нагревалась проволока сопротивлением 20 Ом, если при силе тока 1 А в ней выделилось 6 кДж теплоты.
Задача № 4. Электрическая плитка при силе тока 5 А за 30 мин потребляет 1080 кДж энергии. Рассчитайте сопротивление плитки.
Задача № 5. Какое количество теплоты выделится за 25 мин в обмотке электродвигателя, если ее активное сопротивление равно 125 Ом, а сила тока, протекающего в ней, равна 1,2 А?
Краткая теория для решения Задачи на Закон Джоуля-Ленца.

Это конспект по теме «ЗАДАЧИ на Закон Джоуля-Ленца». Выберите дальнейшие действия:
Билеты для переводного экзамена по физике
Билеты для переводного экзамена по физике 8 класс
Билет 1
Строение вещества. Тепловое движение. Диффузия. Взаимодействие частиц вещества.
Лабораторная работа: Определение зависимости сопротивления проводника от силы тока.
1. Нарисуйте схему цепи, состоящей из источника тока, ключа, реостата, вольтметра и амперметра.
2. Соберите цепь.
3. Проведите измерения силы тока и напряжения при двух различных положениях движка реостата.
4. Рассчитайте сопротивления реостата в этих положениях. Запишите формулу для расчета.
5. Занесите результаты измерений и расчетов в таблицу. Сделайте вывод.
Сделайте вывод.
Задача на расчет выталкивающей силы.
Билет 2
Давление жидкостей и газов. Закон Паскаля. Сообщающиеся сосуды.
Лабораторная работа: Проверьте предположение, что при последовательном соединении проводников общее напряжение равно сумме напряжений на каждом резисторе.
1. Нарисуйте схему цепи, состоящей из источника тока, ключа, двух резисторов, вольтметра и амперметра.
2. Соберите цепь.
3. Проведите измерения напряжения на первом резисторе, на втором и на двух вместе.
4. Занесите результаты измерений в таблицу. Сделайте вывод.
Задача на расчет количества теплоты при агрегатных переходах.
Билет 3
Сообщающиеся сосуды. Гидравлическая машина. Атмосферное давление
Лабораторная работа: Определите силу тока в резисторе и напряжение на его концах.
1. Нарисуйте схему цепи, состоящей из источника тока, ключа, резистора, вольтметра и амперметра.
2. Соберите цепь.
3. Проведите измерения силы тока и напряжения.
4. Запишите результаты измерений. Сделайте вывод.
Задача на расчет количества теплоты при агрегатных переходах.
Билет 4
Действие жидкости и газа на погруженное в них тело.
Лабораторная работа: Определите мощность электрического тока в резисторе.
1. Нарисуйте схему цепи, состоящей из источника тока, ключа, резистора, вольтметра и амперметра.
2. Соберите цепь.
3. Проведите измерения силы тока и напряжения.
4. Запишите формулу для расчета мощности тока. Рассчитайте мощность.
5. Запишите результаты измерений и расчетов в таблицу. Сделайте вывод.
Задача на расчет количества теплоты при плавлении.
Билет 5
Внутренняя энергия тела. Способы изменения внутренней энергии тела.
Способы изменения внутренней энергии тела.
Лабораторная работа: Проверьте на опыте: как зависит выталкивающая сила, действующая на цилиндр от плотности жидкости, в которую он погружен.
1. Измерьте вес тела в воздухе, затем, полностью погрузив его в воду, вес тела в воде.
2. Рассчитайте выталкивающую силу.
3. Повторите измерения для соленой воды, плотность которой больше, чем пресной.
4. Запишите формулы для расчета, результаты измерений и расчетов.
5. Сделайте вывод.
Задача на расчет общего сопротивления при смешанном соединении проводников.
Билет 6
Виды теплопередачи: теплопроводность, конвенция, излучение. Количество теплоты.
Лабораторная работа: Постройте график зависимости массы тела от его объема и найдите плотность вещества, из которого это тело изготовлено.
1. Возьмите три тела, сделанных из одного материала, имеющих разные размеры. Взвесьте их на рычажных весах.
Взвесьте их на рычажных весах.
2. Определите объемы этих тел путем погружения в мензурку с водой.
3. Занесите результаты в таблицу. Постройте график получившейся зависимости.
4. По среднему значению с графика определите плотность вещества.
5. Сделайте вывод.
Задача на расчет силы тока в проводнике.
Билет 7
Количество теплоты. Удельная теплоемкость вещества. Удельная теплота сгорания. Удельная теплота парообразования. Удельная теплота плавления.
Лабораторная работа: Определите плотность вещества, из которого изготовлен цилиндр.
1. Взвесьте тело на рычажных весах.
2. Определите объем тела путем погружения в мензурку с водой.
3. Запишите формулу для расчета плотности и результаты измерений. Рассчитайте плотность вещества.
4. Сделайте вывод.
Задача на расчет работы и мощности электрического тока.
Билет 8
Принципы работы тепловых двигателей. Двигатель внутреннего сгорания. КПД тепловых двигателей.
Лабораторная работа: Определите работу, совершаемую электрическим током за 5 минут.
1. Нарисуйте схему цепи, состоящей из источника тока, ключа, резистора, вольтметра и амперметра.
2. Соберите цепь.
3. Проведите измерения силы тока и напряжения.
4. Запишите формулу для расчета работы тока. Рассчитайте работу.
5. Запишите результаты измерений и расчетов в таблицу. Сделайте вывод.
Задача на сообщающиеся сосуды .
Билет 9
Электрический заряд. Электрическое взаимодействие. Электризация тел. Строение атома.
Лабораторная работа: Определите влажность воздуха в помещении. Рассчитайте давление водяных паров.
1. Измерьте температуру воздуха в помещении с помощью сухого и влажного термометров. По психрометрической таблице определите относительную влажность воздуха.
По психрометрической таблице определите относительную влажность воздуха.
2. Запишите формулу для расчета относительной влажности воздуха, результаты измерений.
3. Рассчитайте давление водяного пара в воздухе, пользуясь справочной таблицей для определения давления насыщенного пара при данной температуре.
4. Сделайте вывод.
Задача на расчет количества теплоты при плавлении.
Билет 10
Электрическое поле. Проводники и диэлектрики.
Лабораторная работа: Определите выталкивающую силу, действующую на тело, погруженное в воду.
1. Измерьте вес тела в воздухе, затем, полностью погрузив его в воду, вес тела в воде.
2. Рассчитайте выталкивающую силу.
3. Запишите формулы для расчета, результаты измерений и расчетов.
4. Сделайте вывод.
Задача на определение относительной влажности.
Билет 11
Электрический ток.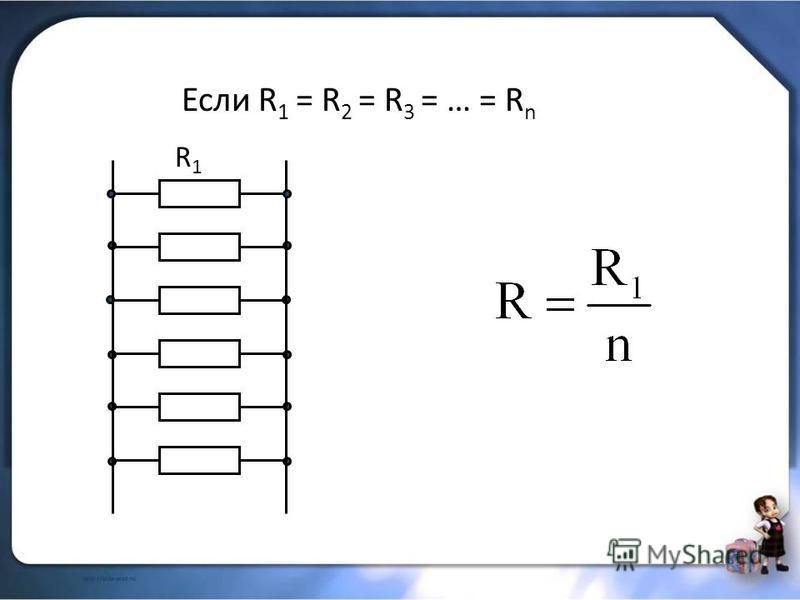 Источники тока. Действия электрического тока.
Источники тока. Действия электрического тока.
Лабораторная работа: Проверьте предположение, что сила тока в цепи с последовательным соединением проводников одинакова в различных местах цепи.
1. Нарисуйте схему цепи, состоящей из источника тока, ключа, резистора и амперметра.
2. Соберите цепь.
3. Проведите измерения силы тока при трех различных положениях амперметра.
4. Занесите результаты измерений в таблицу. Сделайте вывод.
Задача на расчет количества теплоты при нагревании тела.
Билет 12
Электрическая цепь. Сила тока. Амперметр.
Лабораторная работа: Проверьте предположение, что при последовательном соединении проводников общее напряжение равно сумме напряжений на каждом резисторе.
1. Нарисуйте схему цепи, состоящей из источника тока, ключа, двух резисторов, вольтметра и амперметра.
2. Соберите цепь.
3. Проведите измерения напряжения на первом резисторе, на втором и на двух вместе.
4. Занесите результаты измерений в таблицу. Сделайте вывод.
Задача на расчет количества теплоты при сгорании топлива.
Билет 13
Электрический ток. Напряжение. Работа тока.
Лабораторная работа: Определите удельную теплоемкость вещества цилиндра.
1. Возьмите стакан с водой комнатной температуры (измерьте температуру и массу воды). Опустите в него нагретое тело (измерьте температуру воды, в которую было погружено тело и его массу).
2. Когда температура воды перестанет увеличиваться, измерьте температуру воды.
3. Запишите формулу для расчета количества теплоты, полученного водой при остывании тела и результаты измерений. Произведите расчет.
4. Запишите формулу для расчета удельной теплоемкости тела.
5. Сделайте вывод. Определите, из какого вещества сделано тело.
Задача на расчет количества теплоты при парообразовании.
Билет 14
Сопротивление проводника. Закон Ома для участка цепи.
Лабораторная работа: Определите количество теплоты, полученное телом при нагревании.
1. Возьмите стакан с водой комнатной температуры (измерьте температуру и массу воды). Опустите в него нагретое тело (измерьте температуру воды, в которую было погружено тело).
2. Когда температура воды перестанет увеличиваться, измерьте температуру воды.
3. Запишите формулу для расчета количества теплоты, полученного водой при остывании тела и результаты измерений. Произведите расчет.
4. Сделайте вывод. Объясните, почему для измерения количества теплоты, полученного телом, вы определяли количество теплоты, полученное водой.
Задача на расчет силы Кулона.
Билет 15
Последовательное и параллельное соединение проводников.
Лабораторная работа: Проверьте на опыте: как зависит выталкивающая сила, действующая на цилиндр от плотности жидкости, в которую он погружен.
1. Измерьте вес тела в воздухе, затем, полностью погрузив его в воду, вес тела в воде.
2. Рассчитайте выталкивающую силу.
3. Повторите измерения для соленой воды, плотность которой больше, чем пресной.
4. Запишите формулы для расчета, результаты измерений и расчетов.
5. Сделайте вывод.
Задача на расчет количества теплоты при агрегатных переходах.
Билет 16
Работа и мощность электрического тока. Закон Джоуля-Ленца.
Лабораторная работа: Постройте график зависимости массы тела от его объема и найдите плотность вещества, из которого это тело изготовлено.
1. Возьмите три тела, сделанных из одного материала, имеющих разные размеры. Взвесьте их на рычажных весах.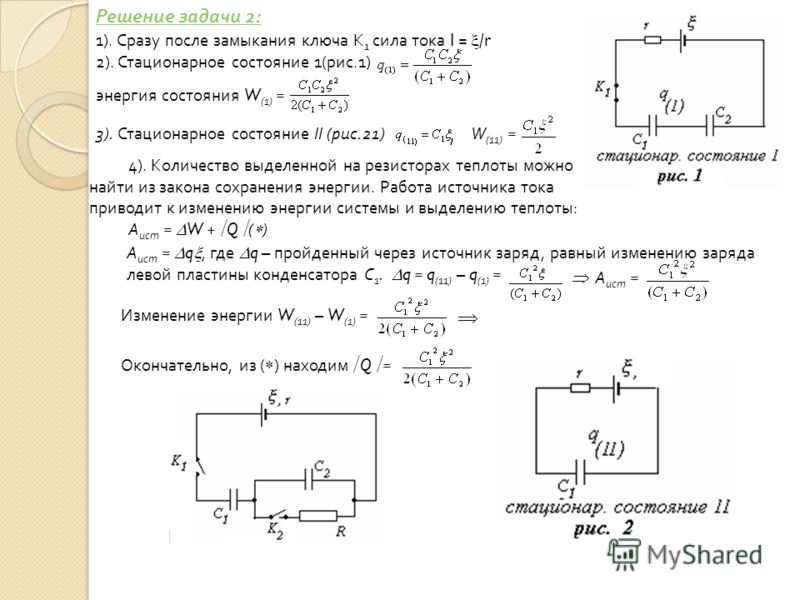
2. Определите объемы этих тел путем погружения в мензурку с водой.
3. Занесите результаты в таблицу. Постройте график получившейся зависимости.
4. По среднему значению с графика определите плотность вещества.
5. Сделайте вывод.
Задача на расчет количества теплоты при нагревании тела.
A. Закон Джоуля—Ленца — PhysBook
Закон Джоуля—Ленца
В электрической цепи при прохождении тока происходит ряд превращений энергии. Во внешнем участке цепи работу по перемещению заряда совершают силы стационарного электрического поля и энергия этого поля превращается в другие виды: механическую, тепловую, химическую, в энергию электромагнитного излучения. Следовательно, полная работа тока на внешнем участке цепи
\(~A_0 = W_{meh} + A_{him} + W_{izl} + Q .\)Если же на участке цепи под действием электрического поля не совершается механическая работа и не происходят химические превращения, то работа электрического тока приводит только к нагреванию проводника.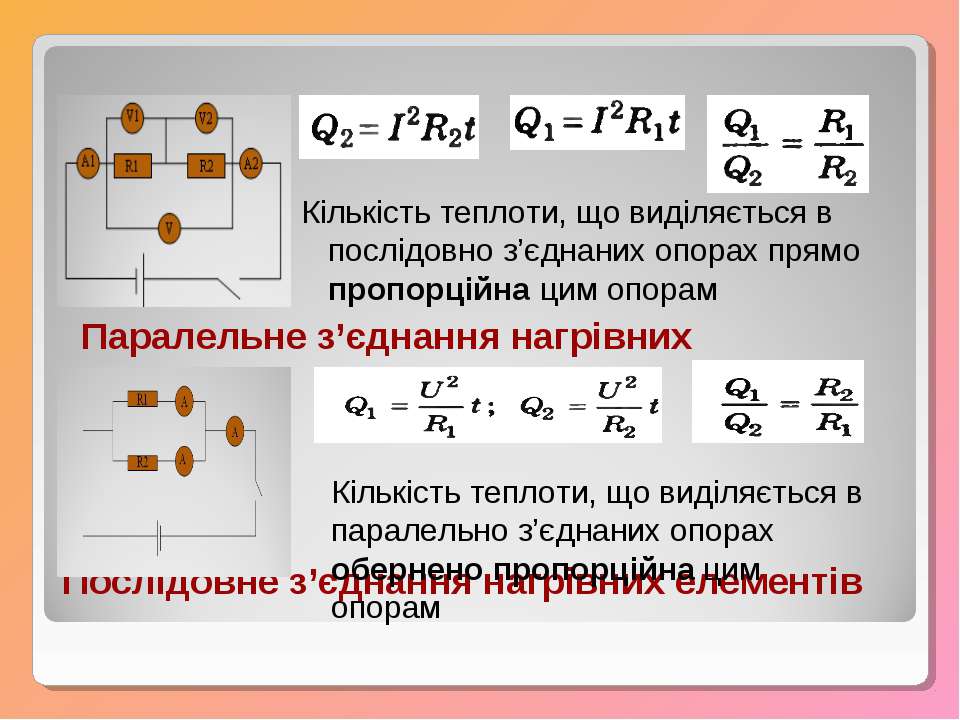 2Rt\).
2Rt\).
Эта формула выражает закон Джоуля—Ленца, установленный опытным путем в XIX в. двумя учеными (английским — Дж. Джоулем и русским Э. X. Ленцем).
При прохождении электрического тока по проводнику количество теплоты, выделяющейся в проводнике, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока.
На законе Джоуля Ленца основано действие многих электронагревательных приборов. Это утюги, электроплиты, электрочайники, кипятильники, паяльники, электрокамины и т.д.
Основной частью любого электронагревательного прибора является нагревательный элемент (проводник с большим удельным сопротивлением наматывается на пластинку из жаростойкого материала: слюды, керамики).
Вышеприведенную формулу закона Джоуля—Ленца удобно применять при последовательном соединении резисторов, так как сила тока во всех участках последовательно соединенной цепи одинакова. Если последовательно соединены два резистора с сопротивлениями R1 и R2, то \(~Q_1 = I^2R_1t\), \(~Q_2 = I^2R_2t\) , откуда \(~\frac{Q_1}{Q_2} = \frac{R_1}{R_2}\) , т. 2}{R_2} t\), откуда
2}{R_2} t\), откуда
т.е. количество теплоты, выделяемой током в ветвях параллельно соединенной цепи, обратно пропорционально сопротивлениям резисторов, включенных в эти ветви.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 269-270.
Работа и мощность тока | Физика
1. Работа тока. Закон Джоуля-Ленца
Работа тока
Работу электрического поля по перемещению свободных зарядов в проводнике называют работой тока. При перемещении заряда q вдоль проводника поле совершает работу A = qU (см. § 53), где U – разность потенциалов на концах проводника. Поскольку q = It, работу тока можно записать в виде
A = UIt.
Закон Джоуля-Ленца
Рассмотрим практически важный случай, когда основным действием тока является тепловое действие. В таком случае согласно закону сохранения энергии количество теплоты, выделившееся в проводнике, равно работе тока: Q = A. Поэтому
В таком случае согласно закону сохранения энергии количество теплоты, выделившееся в проводнике, равно работе тока: Q = A. Поэтому
Q = IUt. (1)
? 1. Докажите, что количество теплоты Q, выделившееся в проводнике с током, выражается также формулами
Q = I2Rt, (2)
Q = (U2/R)t. (3)
Подсказка. Воспользуйтесь формулой (1) и законом Ома для участка цепи.
Мы вывели формулы (1) – (3), используя закон сохранения энергии, но исторически соотношение Q = I2Rt независимо друг от друга установили на опыте российский ученый Эмилий Христианович Ленц и английский ученый Дж. Джоуль за несколько лет до открытия закона сохранения энергии.
Закон Джоуля – Ленца: количество теплоты, выделившееся за время t в проводнике сопротивлением R, сила тока в котором равна I, выражается формулой
Q = I2Rt.
Применение закона Джоуля – Ленца к последовательно и параллельно соединенным проводникам
Выясним, в каких случаях для сравнения количества теплоты, выделившейся в проводниках, удобнее пользоваться формулой (2), а в каких случаях – формулой (3).
Формулу Q = I2Rt удобно применять, когда сила тока в проводниках одинакова, то есть когда они соединены последовательно (рис. 58.1).
Из этой формулы видно, что при последовательном соединении проводников большее количество теплоты выделяется в проводнике, сопротивление которого больше. При этом
Q1/Q2 = R1/R2.
Формулу Q = (U2/R)t удобно применять, когда напряжение на концах проводников одинаково, то есть когда они соединены параллельно (рис. 58.2).
Из этой формулы видно, что при параллельном соединении проводников большее количество теплоты выделяется в проводнике, сопротивление которого меньше. При этом
Q1/Q2 = R2/R1.
? 2. При последовательном соединении в первом проводнике выделилось в 3 раза большее количество теплоты, чем во втором. В каком проводнике выделится большее количество теплоты при их параллельном соединении? Во сколько раз большее?
? 3. Имеются два проводника сопротивлением R1 = 1 Ом и R2 = 2 Ом. Их подключают к источнику напряжения 6 В. Какое количество теплоты выделится за 10 с, если:
Имеются два проводника сопротивлением R1 = 1 Ом и R2 = 2 Ом. Их подключают к источнику напряжения 6 В. Какое количество теплоты выделится за 10 с, если:
а) подключить только первый проводник?
б) подключить только второй проводник?
в) подключить оба проводника последовательно?
г) подключить оба проводника параллельно?
д) чему равно отношение значений количества теплоты Q1/Q2, если проводники включены последовательно? Параллельно?
Поставим опыт
Будем включать в сеть две лампы накаливания с разными сопротивлениями нити накала параллельно и последовательно (рис. 58.3, а, б). Мы увидим, что при параллельном соединении ламп ярче светит одна лампа, а при последовательном – другая.
? 4. У какой из ламп (1 или 2) сопротивление больше? Поясните ваш ответ.
? 5. Объясните, почему при последовательном соединении накал нити каждой лампы меньше, чем накал этой же лампы при параллельном соединении.
? 6. Почему при включении лампы в осветительную сеть нить накала раскаляется добела, а последовательно соединенные в нею соединительные провода почти не нагреваются?
2.
 Мощность тока
Мощность токаМощностью тока P называют отношение работы тока A к промежутку времени t, в течение которого эта работа совершена:
P = A/t. (4)
Единица мощности – ватт (Вт). Мощность тока равна Вт, если совершаемая током за 1 с работа равна 1 Дж. Часто используют производные единицы, например киловатт (кВт).
? 7. Докажите, что мощность тока можно выразить формулами
P = IU, (5)
P = I2R, (6)
P = U2/R. (7)
Подсказка. Воспользуйтесь формулой (4) и законом Ома для участка цепи.
? 8. Какой из формул (5) – (7) удобнее пользоваться при сравнении мощности тока:
а) в последовательно соединенных проводниках?
б) в параллельно соединенных проводниках?
? 9. Имеются проводники сопротивлением R1 и R2. Объясните, почему при последовательном соединении этих проводников
P1/P2 = R1/R2,
а при параллельном
P1/P2 = R2/R1.
? 10. Сопротивление первого резистора 100 Ом, а второго – 400 Ом. В каком резисторе мощность тока будет больше и во сколько раз больше, если включить их в цепь с заданным напряжением:
а) последовательно?
б) параллельно?
в) Чему будет равна мощность тока в каждом резисторе при параллельном соединении, если напряжение в цепи 200 В?
г) Чему при том же напряжении цепи равна суммарная мощность тока в двух резисторах, если они соединены: последовательно? параллельно?
Мощностью электроприбора называют мощность тока в этом приборе. Так, мощность электрочайника – примерно 2 кВт.
Обычно мощность прибора указывают на самом приборе.
Ниже приведены примерные значения мощности некоторых приборов.
Лампа карманного фонарика: около 1 Вт
Лампы осветительные энергосберегающие: 9-20 Вт
Лампы накаливания осветительные: 25-150 Вт
Электронагреватель: 200-1000 Вт
Электрочайник: до 2000 Вт
Все электроприборы в квартире включаются параллельно, поэтому напряжение на них одинакова.
? 11. В сеть напряжением 220 В включен электрочайник мощностью 2 кВт.
а) Чему равно сопротивление нагревательного элемента в рабочем режиме (когда чайник включен)?
б) Чему равна при этом сила тока?
? 12. На цоколе первой лампы написано «40 Вт», а на цоколе второй – «100 Вт». Это – значения мощности ламп в рабочем режиме (при раскаленной нити накала).
а) Чему равно сопротивление нити накала каждой лампы в рабочем режиме, если напряжение в цепи 220 В?
б) Какая из ламп будет светить ярче, если соединить эти лампы последовательно и подключить к той же сети? Будет ли эта лампа светить так же ярко, как и при параллельном подключении?
? 13. В электронагревателе имеются два нагревательных элемента сопротивлением R1 и R2, причем R1 > R2. Используя переключатель, элементы нагревателя можно включать в сеть по отдельности, а также последовательно или параллельно. Напряжение в сети равно U.
а) При каком включении элементов мощность нагревателя будет максимальной? Чему она при этом будет равна?
б) При каком включении элементов мощность нагревателя будет минимальной (но не равной нулю)? Чему она при этом будет равна?
в) Чему равно отношение R1/R2, если максимальная мощность в 4,5 раза больше минимальной?
Дополнительные вопросы и задания
14. На рисунке 58.4 изображена электрическая схема участка цепи, состоящего из четырех одинаковых резисторов. Напряжение на всем участке цепи постоянно. Примите, что зависимостью сопротивления резистора от температуры можно пренебречь.
На рисунке 58.4 изображена электрическая схема участка цепи, состоящего из четырех одинаковых резисторов. Напряжение на всем участке цепи постоянно. Примите, что зависимостью сопротивления резистора от температуры можно пренебречь.
а) На каком резисторе напряжение самое большое? самое маленькое?
б) В каком резисторе сила тока самая большая? самая маленькая?
в) В каком резисторе выделяется самое большое количество теплоты? самое маленькое количество теплоты?
г) Как изменится количество теплоты, выделяемое в каждом из резисторов 2, 3, 4, если резистор 1 замкнуть накоротко (то есть заменить проводником с очень малым сопротивлением)?
д) Как изменится количество теплоты, выделяемое в каждом из резисторов 2, 3, 4, если отсоединить провод от резистора 1 (то есть заменить этот резистор проводником с очень большим сопротивлением)?
Мощность и энергия
- Изучив этот раздел, вы сможете:
- Выполнять расчеты мощности, напряжения, тока и сопротивления.

- • с использованием соответствующих единиц и подразделов.
- Различайте мощность и энергию в электрических цепях.
Мощность резисторов
Когда через резистор протекает ток, электрическая энергия преобразуется в ТЕПЛОВУЮ энергию.Тепло, генерируемое в компонентах схемы, каждый из которых обладает хотя бы некоторым сопротивлением, рассеивается в воздухе вокруг компонентов. Скорость рассеивания тепла называется МОЩНОСТЬЮ, обозначается буквой P и измеряется в ваттах (Вт).
Количество рассеиваемой мощности может быть вычислено с использованием любых двух величин, используемых в расчетах по закону Ома. Помните, что, как и в любой формуле, в формуле должны использоваться ОСНОВНЫЕ КОЛИЧЕСТВА, то есть ВОЛЬТЫ, ОМЫ и АМПЕРЫ (не милли, мег и т. Д.).
Чтобы найти мощность P, используя V и I
Чтобы найти мощность P, используя V и R
Чтобы найти мощность P, используя I и R
Перед тем, как начать, подумайте об этих нескольких советах, они облегчат задачу, если следовать им.
1. Разработайте ответы, используя карандаш и бумагу; в противном случае легко запутаться на полпути и получить неправильный ответ.
2.Конечно, ответ — это не просто число, это будет определенное количество ватт (или несколько или несколько единиц ватт). Не забудьте указать правильную единицу измерения (например, Вт или мВт и т. Д.), А также число, иначе ответ не имеет смысла.
3. Преобразуйте все вспомогательные единицы, такие как мВ или кОм, в ватты, указав их в соответствующей формуле. Ошибка здесь даст действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.
4. Хотя структура этих формул мощности кажется очень похожей на формулы закона Ома, есть небольшая разница — они содержат некоторые квадраты (I 2 и V 2 ).Будьте очень осторожны при использовании трюка с треугольником для транспонирования этих формул. Если вам нужно связать мощность с сопротивлением, то I или V необходимо возвести в квадрат (умножить на себя). Однако вы можете построить треугольник, который соответствует любой из формул для получения R, как показано ниже.
Однако вы можете построить треугольник, который соответствует любой из формул для получения R, как показано ниже.
Не забудьте загрузить нашу брошюру «Подсказки по математике», в которой показано, как использовать калькулятор с показателями степени и инженерной нотацией, чтобы иметь дело с этими частями и каждый раз получать правильный ответ.
Нет научного калькулятора? Буклет «Подсказки по математике» объясняет, что вам нужно (и что вам не нужно, чтобы не тратить деньги без надобности). Если вы не хотите покупать научный калькулятор, вы всегда можете получить его бесплатно в сети. Пользователи ПК могут попробовать Calc98 на сайте www.calculator.org/download.html. Какой бы калькулятор вы ни выбрали, прочтите инструкции, чтобы ознакомиться с методами работы, которые вам следует использовать, поскольку они варьируются от калькулятора к калькулятору.
Важно знать о влиянии рассеивания мощности в компонентах: чем больше мощность, тем больше тепла должно рассеиваться компонентом. Обычно это означает, что компоненты, рассеивающие большое количество энергии, нагреваются, а также они будут значительно больше по размеру, чем типы с низким энергопотреблением. Если компоненту требуется рассеивать больше энергии, чем он предназначен, он не сможет достаточно быстро избавиться от выделяемого тепла. Его температура повысится, и перегрев может вызвать полный выход из строя компонента и, возможно, повреждение других компонентов и самой печатной платы (PCB).В качестве меры предосторожности резисторы большой мощности часто устанавливают вне печатной платы с использованием более длинных выводных проводов, заключенных в керамические гильзы. Резисторы с проволочной обмоткой большой мощности могут быть даже заключены в металлический радиатор и прикреплены болтами к большой металлической поверхности, такой как корпус оборудования, чтобы избавиться от нежелательного тепла. Примеры резисторов большой мощности показаны на странице конструкции резистора.
Обычно это означает, что компоненты, рассеивающие большое количество энергии, нагреваются, а также они будут значительно больше по размеру, чем типы с низким энергопотреблением. Если компоненту требуется рассеивать больше энергии, чем он предназначен, он не сможет достаточно быстро избавиться от выделяемого тепла. Его температура повысится, и перегрев может вызвать полный выход из строя компонента и, возможно, повреждение других компонентов и самой печатной платы (PCB).В качестве меры предосторожности резисторы большой мощности часто устанавливают вне печатной платы с использованием более длинных выводных проводов, заключенных в керамические гильзы. Резисторы с проволочной обмоткой большой мощности могут быть даже заключены в металлический радиатор и прикреплены болтами к большой металлической поверхности, такой как корпус оборудования, чтобы избавиться от нежелательного тепла. Примеры резисторов большой мощности показаны на странице конструкции резистора.
Такие компоненты, как резисторы, имеют конкретную номинальную мощность, указанную производителем (в ваттах или милливаттах). Этот рейтинг (параметр) необходимо проверить при замене компонента, чтобы не произошло завышения рейтинга. Это важный фактор безопасности при обслуживании электронного оборудования.
Этот рейтинг (параметр) необходимо проверить при замене компонента, чтобы не произошло завышения рейтинга. Это важный фактор безопасности при обслуживании электронного оборудования.
TIP
Тепло, выделяемое резисторами большой мощности, является основной причиной преждевременного выхода из строя многих цепей. Либо сам резистор выходит из строя из-за «разомкнутой цепи», особенно в резисторах с проволочной обмоткой. В резисторах из углеродного состава перегрев в течение длительного периода может вызвать изменение значения. Это может увеличиваться в типах с высоким сопротивлением или более опасно уменьшаться (позволяя увеличить ток) в типах с низким сопротивлением.Увеличение тока, вызванное уменьшением сопротивления, только ускоряет процесс, и в конечном итоге резистор (а иногда и другие связанные компоненты) сгорает!
Энергия в резисторах
Если определенное количество мощности рассеивается в течение заданного времени, то ЭНЕРГИЯ рассеивается. Энергия (мощность x время) измеряется в Джоулях, и, включив время (t) в формулы мощности, можно рассчитать энергию, рассеиваемую компонентом или схемой.
Рассеиваемая энергия = Pt или VIt или V 2 t / R или даже I 2 Rt Джоули
Обратите внимание, что в формулах для энергии такие величины, как мощность, время, сопротивление, ток и напряжение, должны быть преобразованы в их основные единицы, например.г. Ватты, секунды, Ом, Амперы, Вольт и т. Д. Никаких дополнительных единиц или нескольких единиц! Как описано в буклете «Советы по математике».
Все вышеперечисленные единицы являются частью интегрированной системы международно стандартизированных единиц; Система S.I. (Système International d´Unités). Эта система устанавливает основные единицы для любых электрических, механических и физических свойств и их отношения друг к другу. Он также включает стандартную форму кратных и долей кратных, описанную в буклете «Подсказки по математике».{2} \ tau}) \ frac {L} {a}, V = I (ne2τm) aL,
, где mmm и eee — масса и заряд электрона соответственно, LLL и aaa — длина и площадь проводящего материала, составляющего резистор, nnn — плотность носителей заряда, а τ \ tau τ — интервал времени между два столкновения электронов в резисторе. Сопротивление также можно расширить до:
Сопротивление также можно расширить до:
R = ρLA, R = \ frac {\ rho L} {A}, R = AρL,
, где ρ \ rhoρ — это удельное сопротивление , — свойство материала резистора, а LLL и AAA — длина и площадь поперечного сечения резистора соответственно.
Неупругие столкновения электронов, движущихся по проводнику, являются причиной сопротивления. Кристаллическая структура атомов металла в проводнике препятствует прохождению через него электронов. В любой данный момент электроны имеют определенную вероятность неупругого рассеяния от металлической решетки, передавая часть своей энергии решетке в виде кинетической энергии, то есть тепла. Это рассеяние тепла в решетке, называемое Джоулевым нагревом , является источником рассеивания мощности в резисторе.Обратите внимание, что хотя межэлектронные столкновения могут давать свою собственную связанную тепловую энергию движения, эта энергия остается внутренней по отношению к системе до тех пор, пока она не рассеивается в металлической решетке, которая не переносит ток.
Расчет среднего времени свободного пробега электронов, движущихся через проводник, показывает, что электроны проходят через большое количество узлов решетки, прежде чем вступить в существенное взаимодействие с катионами металлов. Объяснение этому факту исходит из квантовой механики и дуальности волна-частица.Из-за волновой природы электрона электроны могут распространяться без неупругого рассеяния на большее расстояние через решетку, чем ожидалось, и вероятность рассеяния гораздо более чувствительна к дефектам решетки, чем плотность решетки.
Можно ли подсчитать, сколько тепла и повышения температуры произойдет в резисторе
Мощность, подаваемая на резистор, и вся она преобразуется в тепло, — это напряжение на нем, умноженное на проходящий через него ток:
P = IV
Где P — мощность, I — ток, а V — напряжение.Ток через резистор зависит от напряжения на нем и сопротивления:
I = V / R
где R — сопротивление. С помощью этого дополнительного соотношения вы можете изменить приведенные выше уравнения, чтобы мощность была прямой функцией напряжения или тока:
P = V 2 / R
P = I 2 R
Так получилось, что если вы придерживаетесь единиц измерения вольт, ампер, ватт и ом, никаких дополнительных констант преобразования не требуется.
В вашем случае у вас есть 20 В на резисторе 1 кОм:
(20 В) 2 / (1 кОм) = 400 мВт
Вот сколько мощности будет рассеивать резистор.
Первый шаг к решению этой проблемы — убедиться, что резистор рассчитан на такую большую мощность. Очевидно, резистор ¼ Вт не подойдет. Следующий распространенный размер — «½ Вт», который теоретически может выдержать такую мощность при соблюдении всех соответствующих условий. Внимательно прочтите техническое описание, чтобы узнать, при каких условиях ваш резистор ½ Вт может рассеивать ½ Вт.В нем может быть указано, что температура окружающей среды должна быть 20 ° C или менее при определенной вентиляции. Если этот резистор находится на плате, которая находится в коробке с чем-то другим, рассеивающим мощность, например, источником питания, температура окружающей среды может быть значительно выше 20 ° C. В этом случае резистор «½ Вт» действительно не может выдержать ½ Вт, если, возможно, нет воздуха от вентилятора, активно дующего через его верх.
Чтобы узнать, насколько температура резистора превысит температуру окружающей среды, вам понадобится еще одна цифра — тепловое сопротивление резистора окружающей среде.Это будет примерно то же самое для тех же типов корпусов, но истинный ответ доступен только из таблицы данных резистора.
Скажем, просто выберите число (из воздуха, я ничего не нашел, только пример), что резистор с подходящими медными контактными площадками имеет тепловое сопротивление 200 ° C / Вт. Резистор рассеивает 400 мВт, поэтому его повышение температуры будет примерно (400 мВт) (200 ° C / Вт) = 80 ° C. Если он находится на открытой плате на вашем столе, вы, вероятно, можете рассчитать максимальную температуру окружающей среды 25 ° C, поэтому резистор может нагреться до 105 ° C.Учтите, что он достаточно горячий, чтобы вскипятить воду, но с большинством резисторов при этой температуре подойдет. Просто держи палец подальше. Если это на плате в коробке с источником питания, который повышает температуру в коробке на 30 ° C от окружающей среды, тогда температура резистора может достигать (25 ° C) + (30 ° C) + (80 ° C) = 135 ° С. Это нормально? Не спрашивайте меня, проверьте таблицу данных.
Это нормально? Не спрашивайте меня, проверьте таблицу данных.
НАГРЕВАТЕЛЬНЫЙ ЭФФЕКТ ЭЛЕКТРИЧЕСКОГО ТОКА
Введение
Когда ток течет по проводнику, в проводнике генерируется тепловая энергия.Нагревательный эффект электрического тока зависит от трех факторов:
- Сопротивление R проводника. Чем выше сопротивление, тем больше тепла.
- Время t, в течение которого течет ток. Чем дольше время, тем больше выделяется тепла
- Величина тока I. Чем выше сила тока, тем больше выделяется тепла.
Следовательно, эффект нагрева, производимый электрическим током I, проходящим через проводник сопротивления, R в течение некоторого времени, t определяется как H = I 2 Rt.Это уравнение называется уравнением Джоуля электрического нагрева.
Электроэнергия и мощность
Работа, выполняемая при проталкивании заряда по электрической цепи, определяется как w.d = VIt
Так что мощность, P = w. d / t = VI
d / t = VI
Электроэнергия, потребляемая электроприбором, определяется как P = VI = I 2 R = V 2 / R
Пример
- Электрическая лампочка имеет маркировку 100 Вт, 240 В.Вычислить:
б) Сопротивление нити накала, используемой в лампе.
Решение
- I = P / V = 100/240 = 0,4167A
- R = P / I 2 = 100 / 0,4167 2 = 576,04 Ом или R = V 2 / P = 240 2 /100 = 576 Ом
- Найдите энергию, рассеиваемую за 5 минут электрической лампочкой с нитью накала 500 Ом, подключенной к источнику питания 240 В.{ ANS. 34,560J }
Решение
E = Pt = V2 / R * t = (240 2 * 5 * 60) / 500 = 34,560 Дж
- Для нагрева воды используется погружной нагреватель мощностью 2,5 кВт. Вычислить:
- Рабочее напряжение нагревателя при сопротивлении 24 Ом
- Электрическая энергия, преобразованная в тепловую за 2 часа.

{ анс. 244,9488 В, 1,8 * 10 7 Дж }
Решение
- P = VI = I 2 R
I = (2500/24) 1/2 = 10.2062A
В = ИК = 10,2062 * 24 = 244,9488 В
- E = VIt = Pt = 2500 * 2 * 60 * 60 = 1,8 * 10 7 Дж
ИЛИ E = VIt = 244,9488 * 10,2062 * 2 * 60 * 60 = 1,8 * 10 7 Дж
Электрическая лампочка имеет маркировку 100W, 240V. Вычислить:Ток через нить накала
Сопротивление нити накала, используемой в лампочке.
Решение
P = VI I = P / V = 100/240 = 0,4167AСогласно закону Ома, V = IR R = V / I = 240 / 0,4167 = 575,95 Ом
Применение нагревающего эффекта электрического тока
Большинство бытовых электроприборов таким образом преобразуют электрическую энергию в тепло.К ним относятся лампы накаливания, электрический нагреватель, электрический утюг, электрический чайник и т. Д.
Д.
В осветительных приборах
- Лампы накаливания — изготовлены из вольфрамовой проволоки, заключенной в стеклянную колбу, из которой удален воздух. Это происходит потому, что воздух окисляет нить. Нить нагревается до высокой температуры и становится раскаленной добела. Вольфрам используется из-за его высокой температуры плавления; 3400 0 Колба заполнена неактивным газом, например аргон или азот при низком давлении, что снижает испарение вольфрамовой проволоки.Однако одним из недостатков инертного газа является то, что он вызывает конвекционные токи, которые охлаждают нить накала. Эта проблема сводится к минимуму за счет наматывания проволоки таким образом, чтобы она занимала меньшую площадь, что снижает потери тепла за счет конвекции.
- Люминесцентные лампы — эти лампы более эффективны по сравнению с лампами накаливания и служат намного дольше. У них есть пары ртути в стеклянной трубке, которая при включении испускает ультрафиолетовое излучение.
 Это излучение заставляет порошок в трубке светиться (флуоресцировать) i.е. излучает видимый свет. Из разных порошков получаются разные цвета. Обратите внимание, что люминесцентные лампы дороги в установке, но их эксплуатационные расходы намного меньше.
Это излучение заставляет порошок в трубке светиться (флуоресцировать) i.е. излучает видимый свет. Из разных порошков получаются разные цвета. Обратите внимание, что люминесцентные лампы дороги в установке, но их эксплуатационные расходы намного меньше.
В электронагревателе
- Электрические плиты — электрические плиты раскалены докрасна, и произведенная тепловая энергия поглощается кастрюлей за счет теплопроводности.
- Электрические обогреватели — лучистые обогреватели становятся красными при температуре около 900 0 C, а испускаемое излучение направляется в комнату с помощью полированных отражателей.
- Электрочайники — нагревательный элемент ставится на дно чайника так, чтобы нагреваемая жидкость покрывала его. Затем тепло поглощается водой и распределяется по всей жидкости за счет конвекции.
- Электрические утюги — когда через нагревательный элемент протекает ток, выделяемая тепловая энергия передается на основание из тяжелого металла, повышая его температуру.
 Затем эта энергия используется для прессования одежды. Температуру утюга можно контролировать с помощью термостата (биметаллической планки).
Затем эта энергия используется для прессования одежды. Температуру утюга можно контролировать с помощью термостата (биметаллической планки).
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что Вы ищете? Увидеть больше результатов
Предложения или отзывы?
Основы: Рассеивание мощности и электронные компоненты
Постоянно существующей проблемой в проектировании электронных схем является выбор подходящих компонентов, которые не только выполняют поставленную задачу, но и выживут в предсказуемых условиях эксплуатации. Большая часть этого процесса — убедиться, что ваши компоненты будут оставаться в пределах своих безопасных рабочих ограничений с точки зрения тока, напряжения и мощности. Из этих трех «силовая» часть часто бывает самой сложной (как для новичков, так и для экспертов), потому что безопасная рабочая зона может очень сильно зависеть от деталей ситуации.
Большая часть этого процесса — убедиться, что ваши компоненты будут оставаться в пределах своих безопасных рабочих ограничений с точки зрения тока, напряжения и мощности. Из этих трех «силовая» часть часто бывает самой сложной (как для новичков, так и для экспертов), потому что безопасная рабочая зона может очень сильно зависеть от деталей ситуации.
Далее мы познакомим вас с некоторыми из основных концепций рассеяния мощности в электронных компонентах, чтобы понять, как выбирать компоненты для простых схем с учетом ограничений мощности.
— НАЧАЛО ПРОСТОГО —
Давайте начнем с одной из самых простых схем, которую только можно вообразить: батарея, подключенная к единственному резистору:
Здесь у нас одна батарея на 9 В и одна батарея на 100? (100 Ом) резистор, соединенный проводами для образования полной цепи.
Достаточно просто, правда? Но теперь вопрос: если вы действительно хотите построить эту схему, насколько «большой» из 100? резистор нужно ли использовать, чтобы убедиться, что он не перегревается? Другими словами, можем ли мы просто использовать «обычный» резистор ¼ W, как показано ниже, или нам нужно увеличить?
Чтобы это выяснить, нам необходимо рассчитать мощность, рассеиваемую резистором.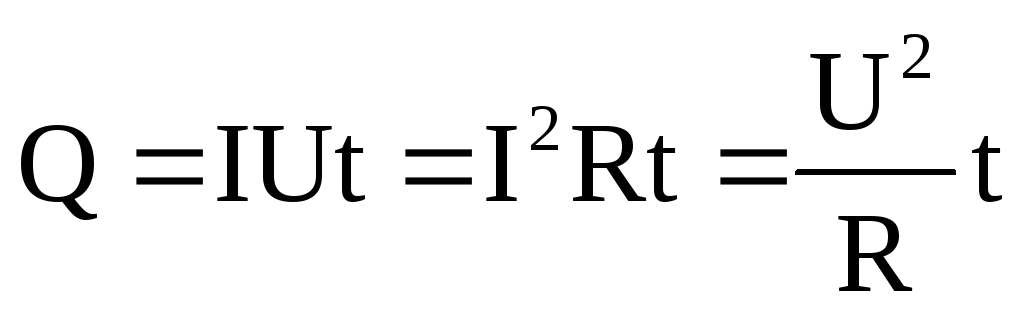
Вот общее правило расчета рассеиваемой мощности:
Правило питания: P = I × В
Если ток I протекает через данный элемент в вашей цепи, теряя при этом напряжение В , то мощность, рассеиваемая этой цепью Элемент является произведением этого тока и напряжения: P = I × V .
В сторону :
Каким образом ток, умноженный на напряжение, может дать нам измерение «мощности»?
Чтобы понять это, нам нужно помнить, что физически представляют ток и напряжение.
Электрический ток — это скорость прохождения электрического заряда через цепь, обычно выражаемая в амперах, где 1 ампер = 1 кулон в секунду. (Кулон — это единица измерения электрического заряда в системе СИ.)
Напряжение или, более формально, электрический потенциал — это потенциальная энергия на единицу электрического заряда в рассматриваемом элементе схемы. В большинстве случаев вы можете думать об этом как о количестве энергии, которое «расходуется» в элементе на единицу проходящего заряда. Электрический потенциал обычно измеряется в вольтах, где 1 вольт = 1 джоуль на кулон. (Джоуль — единица энергии в системе СИ.)
Электрический потенциал обычно измеряется в вольтах, где 1 вольт = 1 джоуль на кулон. (Джоуль — единица энергии в системе СИ.)
Итак, если мы возьмем ток, умноженный на напряжение, это даст нам количество энергии, которое «израсходовано» в элементе на единицу заряда, умноженное на , количество этих единиц заряда, проходящих через элемент в секунду. :
1 ампер × 1 вольт =
1 (кулон / секунда) × 1 (джоуль / кулон) =
1 джоуль / секунда
Результирующая величина выражается в единицах один джоуль в секунду: скорость потока энергии, более известная как мощность.Единица измерения мощности в системе СИ — ватт, где 1 ватт = 1 джоуль в секунду.
Итак, у нас есть
1 ампер × 1 вольт = 1 ватт
Вернемся к нашей трассе! Чтобы использовать правило мощности ( P = I × V ), нам нужно знать как ток через резистор, так и напряжение на резисторе.
Во-первых, мы используем закон Ома ( В = I × R ), чтобы найти ток через резистор.
• Напряжение на резисторе В = 9 В.
• Сопротивление резистора R = 100 Ом.
Следовательно, ток через резистор равен:
I = В / R = 9 В / 100? = 90 мА
Затем мы можем использовать правило мощности ( P = I × V ), чтобы найти мощность, рассеиваемую резистором.
• Ток через резистор I = 90 мА.
• Напряжение на резисторе В = 9 В.
Следовательно, мощность, рассеиваемая на резисторе, составляет:
P = I × В = 90 мА × 9 В = 0,81 Вт
Так вы можете использовать резистор на 1/4 Вт?
Нет, потому что он, скорее всего, выйдет из строя из-за перегрева.
100? резистор в этой схеме должен быть рассчитан не менее чем на 0,81 Вт. Обычно выбирается следующий больший доступный размер, в данном случае 1 Вт.
Резистор мощностью 1 Вт обычно поставляется в гораздо более крупном физическом корпусе, как показано здесь:
(резистор 1 Вт, 51 Ом, для сравнения размеров. )
)
Поскольку резистор на 1 Вт физически намного больше, он должен быть в состоянии справиться с рассеиванием большей мощности за счет большей площади поверхности и более широких выводов. (Он все еще может сильно нагреваться на ощупь, но не должен нагреваться настолько, чтобы выйти из строя.)
Вот альтернативное расположение, которое работает с четырьмя 25? резисторы в серии (а в сумме все равно 100?).В этом случае ток через каждый резистор по-прежнему составляет 90 мА. Но, поскольку на каждом резисторе имеется только четверть напряжения, на каждом резисторе рассеивается только четверть меньшей мощности. Для этого достаточно, чтобы четыре резистора были рассчитаны на 1/4 Вт.
В сторону: прорабатываем этот пример.
Поскольку четыре резистора включены последовательно, мы можем сложить их значения, чтобы получить их общее сопротивление, равное 100 Ом. Использование закона Ома с этим общим сопротивлением снова дает нам ток 90 мА. И снова, поскольку резисторы включены последовательно, одинаковый ток (90 мА) должен протекать через каждый обратно к батарее. Напряжение через каждые 25? резистор тогда В = I × R , или 90 мА × 25? = 2,25 В. (Чтобы еще раз убедиться, что это разумно, обратите внимание, что суммарные напряжения на четырех резисторах составляют 4 × 2,25 В = 9 В.)
И снова, поскольку резисторы включены последовательно, одинаковый ток (90 мА) должен протекать через каждый обратно к батарее. Напряжение через каждые 25? резистор тогда В = I × R , или 90 мА × 25? = 2,25 В. (Чтобы еще раз убедиться, что это разумно, обратите внимание, что суммарные напряжения на четырех резисторах составляют 4 × 2,25 В = 9 В.)
Сила на каждого человека 25? резистор P = I × В = 90 мА × 2,25 В? 0,20 Вт, безопасный уровень для использования с резистором 1/4 Вт.Интуитивно понятно, что если разделить 100? резистор на четыре равные части, каждая из которых должна рассеивать четверть всей мощности.
— ЗА РЕЗИСТОРАМИ —
В качестве следующего примера рассмотрим следующую ситуацию: предположим, что у вас есть схема, которая принимает входной сигнал от источника питания 9 В и имеет встроенный линейный стабилизатор для понижения напряжения до 5 В, где все работает. Ваша нагрузка на конце 5 В может достигать 1 А.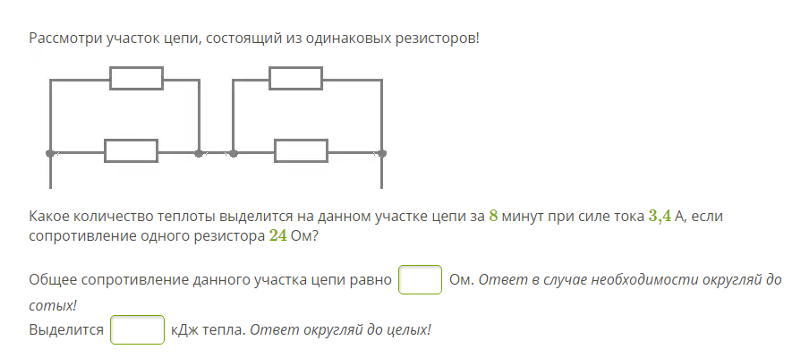
Как выглядит мощность в этой ситуации?
Регулятор, по сути, действует как большой переменный резистор, который регулирует свое сопротивление по мере необходимости для поддержания постоянного выходного напряжения 5 В. Когда выходная нагрузка составляет 1 А, выходная мощность, выдаваемая регулятором, составляет 5 В × 1 А = 5 Вт, а мощность, потребляемая в цепи источником питания 9 В, составляет 9 Вт. Падение напряжения на стабилизаторе. составляет 4 В, а при 1 А, это означает, что 4 Вт рассеивается линейным регулятором — также разница между входной и выходной мощностью.
В каждой части этой схемы соотношение мощности задается формулой P = I × V . Две части — регулятор и нагрузка — это места, где рассеивается мощность. А в части цепи, подключенной к источнику питания, P = I × V описывает мощность , вводимую в систему — напряжение увеличивается на по мере прохождения тока по источнику питания.
Кроме того, стоит отметить, что мы, , не сказали , какая нагрузка тянет этот 1 А. Энергия потребляется, но это не обязательно означает, что она преобразуется в (просто) тепловую энергию — это может быть питание двигателя или, например, набора зарядных устройств для аккумуляторов.
Энергия потребляется, но это не обязательно означает, что она преобразуется в (просто) тепловую энергию — это может быть питание двигателя или, например, набора зарядных устройств для аккумуляторов.
Кроме того:
В то время как линейный регулятор напряжения, подобный этой, представляет собой обычную установку для электроники , стоит отметить, что это также невероятно неэффективная схема : 4/9 входной мощности просто сгорает как тепло, даже при работе на более низких токах.
— КОГДА НЕТ ПРОСТОЙ СПЕЦИФИКАЦИИ «МОЩНОСТЬ» —
Далее, немного более сложная часть: убедиться, что ваш регулятор может справиться с мощностью. На резисторах четко указана их мощность, а на линейных регуляторах это не всегда. В приведенном выше примере регулятора предположим, что мы используем регулятор L7805ABV от ST (техническое описание здесь).
(Фото: типичный корпус TO-220, тип, обычно используемый для линейных регуляторов средней мощности)
L7805ABV — это линейный стабилизатор 5 В в корпусе TO-220 (аналогичный показанному выше), рассчитанный на 1. Выходной ток 5 А и входное напряжение до 35 В.
Выходной ток 5 А и входное напряжение до 35 В.
Наивно, вы можете предположить, что вы можете подключить это прямо к входу 35 В и рассчитывать на выход 1,5 А, а это означает, что регулятор будет излучать мощность 30 В * 1,5 А = 45 Вт. Но это крошечный пластиковый пакет; на самом деле он не может справиться с такой большой мощностью. Если вы посмотрите таблицу данных в разделе «Абсолютные максимальные характеристики», чтобы попытаться определить, с какой мощностью он может справиться, все, что там написано, является «внутренне ограниченным», что само по себе далеко не ясно.
Оказывается, существует фактическая номинальная мощность, но обычно она несколько «скрыта» в таблице данных. Вы можете понять это, взглянув на пару связанных спецификаций:
• T OP , Диапазон рабочих температур перехода: от -40 до 125 ° C
• R thJA , Термическое сопротивление переход-окружающая среда: 50 ° C / Вт
• R thJC , Тепловое сопротивление переходного корпуса: 5 ° C / Вт
Рабочий диапазон температур перехода, T OP , определяет, насколько горячим может быть «переход» — активная часть интегральной схемы регулятора, прежде чем он перейдет в режим теплового отключения. (Тепловое отключение — это внутренний предел, который делает мощность регулятора «внутренне ограниченной».) Для нас это максимум 125 ° C.
(Тепловое отключение — это внутренний предел, который делает мощность регулятора «внутренне ограниченной».) Для нас это максимум 125 ° C.
Тепловое сопротивление переход-окружающая среда R thJA (часто обозначается как? JA ), сообщает нам, насколько нагревается переход, когда (1) регулятор рассеивает заданное количество мощности и (2) регулятор находится внутри на открытом воздухе при заданной температуре окружающей среды. Предположим, нам нужно спроектировать наш регулятор для работы только в скромных коммерческих условиях, температура которых не превышает 60 ° C.Если нам нужно поддерживать температуру перехода ниже 125 ° C, то максимальное повышение температуры, которое мы можем допустить, составляет 65 ° C. Если у нас есть R thJA 50 ° C / Вт, то максимальная рассеиваемая мощность, которую мы можем допустить, составляет 65/50 = 1,3 Вт, если мы хотим предотвратить переход регулятора в состояние теплового отключения. Это значительно ниже 4 Вт, которых можно было бы ожидать при токе нагрузки 1 А. Фактически, мы можем выдержать только 1,3 Вт / 4 В = 325 мА среднего выходного тока, не отправляя регулятор в состояние теплового отключения.
Фактически, мы можем выдержать только 1,3 Вт / 4 В = 325 мА среднего выходного тока, не отправляя регулятор в состояние теплового отключения.
Это, однако, относится к случаю, когда TO-220 излучает в окружающий воздух — почти наихудшая ситуация. Если мы сможем добавить радиатор или иным образом охладить регулятор, мы сможем добиться большего.
Противоположный конец спектра представлен другой термической спецификацией: корпус с термическим сопротивлением, R thJC . Это определяет, какую разницу температур можно ожидать между переходом и внешней стороной корпуса TO-220: всего 5 ° C / Вт. Это соответствующий номер , если вы можете быстро отвести тепло от корпуса, например, если у вас есть очень хороший радиатор, подключенный к внешней стороне корпуса TO-220.С большим радиатором и идеальным соединением с этим радиатором при 4 Вт температура перехода повысится всего на 20 ° C по сравнению с температурой вашего радиатора. Это представляет собой абсолютный минимум нагрева, который можно ожидать в идеальных условиях.
В зависимости от технических требований, вы можете начать с этого момента, чтобы построить полный бюджет мощности, чтобы учесть теплопроводность каждого элемента вашей системы, от самого регулятора до термоинтерфейсной площадки между ним и радиатором, к тепловой связи радиатора с окружающим воздухом.Затем вы можете проверить соединения и относительную температуру каждого компонента с помощью бесконтактного инфракрасного термометра с точечным считыванием. Но часто бывает лучше переоценить ситуацию и посмотреть, есть ли лучший способ сделать это.
В данной ситуации можно подумать о переходе на стабилизатор для поверхностного монтажа, который обеспечивает лучшую управляемую мощность (за счет использования печатной платы в качестве радиатора), или, возможно, стоит подумать о добавлении силового резистора (или стабилитрона) до Регулятор понижает большую часть напряжения за пределами блока регулятора , уменьшая нагрузку на него.Или, что еще лучше, посмотрите, есть ли способ построить вашу схему без каскада линейного регулятора с потерями.
— ПОСЛЕ СЛОВА —
Мы рассмотрели основы понимания рассеяния мощности в нескольких простых цепях постоянного тока.
Принципы, которые мы рассмотрели, являются довольно общими, и их можно использовать для понимания энергопотребления в большинстве типов пассивных элементов и даже в большинстве типов интегральных схем. Однако существуют реальные ограничения, и можно потратить всю жизнь на изучение нюансов энергопотребления, особенно при более низких токах или высоких частотах, когда небольшие потери, которыми мы пренебрегли, становятся важными.
В цепях переменного тока многие вещи ведут себя по-разному, но правило мощности все еще сохраняется в большинстве случаев: P (t) = I (t) × В (t) для изменяющихся во времени тока и напряжения. И не все регуляторы работают с потерями: импульсные источники питания могут преобразовывать (например) 9 В постоянного тока в 5 В постоянного тока с КПД 90% или выше — это означает, что при хорошем дизайне может потребоваться всего около 0,6 А при 9 В для производят 5 В при 1 А. Но это уже отдельная история.
Но это уже отдельная история.
Сопротивление | Электрические схемы | Siyavula
Сопротивление — это мера того, «насколько сложно» «протолкнуть» электричество через элемент цепи.Сопротивление также может применяться ко всей цепи.
Что вызывает сопротивление? (ESAFH)
На микроскопическом уровне электроны, движущиеся по проводнику, сталкиваются (или взаимодействуют) с частицами, из которых состоит проводник (металл). Когда они сталкиваются, они передают кинетическую энергию. Таким образом, электроны теряют кинетическую энергию и замедляются. Это приводит к сопротивлению. Передаваемая энергия вызывает нагрев резистора. Вы можете почувствовать это напрямую, если прикоснетесь к зарядному устройству мобильного телефона во время зарядки мобильного телефона — зарядное устройство нагревается, потому что в его цепях есть резисторы!
Примеры резисторов
Фотография oskay на Flickr.com
- Сопротивление
Сопротивление замедляет прохождение заряда в цепи.
 Единицей измерения сопротивления является ом (Ом), который определяется как вольт на ампер тока.
Единицей измерения сопротивления является ом (Ом), который определяется как вольт на ампер тока.Количество: Сопротивление R Единица: Ом Обозначение единицы: ω
В люминесцентных лампах не используются тонкие провода; они используют тот факт, что некоторые газы светятся, когда через них протекает ток.Они намного эффективнее (гораздо меньше сопротивления), чем лампочки.
Лампа накаливания
Фотография clagnut на Flickr.com
Все проводники имеют некоторое сопротивление. Например, кусок провода имеет меньшее сопротивление, чем лампочка, но оба имеют сопротивление.
Лампочка — это очень тонкий провод, окруженный стеклянным корпусом. Высокое сопротивление небольшого провода (нити) в лампочке заставляет электроны передавать большую часть своей кинетической энергии в виде тепла.Тепловой энергии достаточно, чтобы нить накала стала раскаленной добела, что дает свет.
Провода, соединяющие лампу с элементом или батареей, почти не нагреваются при одинаковом токе. Это связано с их гораздо меньшим сопротивлением из-за большего поперечного сечения (они толще).
Важным действием резистора является то, что он преобразует электрической энергии в другие формы тепловой энергии . Light энергия является побочным продуктом производимого тепла.
Существует особый тип проводника, называемый сверхпроводником , который не имеет сопротивления, но материалы, из которых состоят все известные сверхпроводники, становятся сверхпроводниками только при очень низких температурах. «Самым высокотемпературным» сверхпроводником является оксид ртути, бария, кальция, меди \ ((\ text {HgBa} _ {2} \ text {Ca} _ {2} \ text {Cu} _ {3} \ text {O} _ {\ text {x}}) \), который является сверхпроводящим для температур \ (- \ text {140} \) \ (\ text {℃} \) и ниже.
Физические атрибуты, влияющие на сопротивление [НЕ ЗАГЛАВНЫМИ БУКВАМИ]
Физические характеристики резистора влияют на его общее сопротивление.
Длина : при увеличении длины резистора увеличивается его сопротивление. Обычно, если вы увеличиваете длину резистора в определенном разы, вы увеличиваете сопротивление во столько же раз.
Ширина и высота или площадь поперечного сечения : если резистор обеспечивает больший путь за счет расширения или расширения, то через него может протекать больший ток. Если общая площадь поверхности, через которую протекает ток (площадь поперечного сечения), увеличивается в раз, сопротивление обычно уменьшается в такой же раз.
Расширение: Для одиночного резистора это можно обозначить как
\ [R \ propto \ frac {L} {A} \]где \ (L \) — длина, а \ (A \) — площадь поперечного сечения.
Почему разряжаются батареи?
Аккумулятор хранит потенциальную химическую энергию. Когда он включен в цепь, внутри батареи происходит химическая реакция, которая преобразует химическую потенциальную энергию в электрическую энергию, которая заставляет электроны двигаться по цепи.




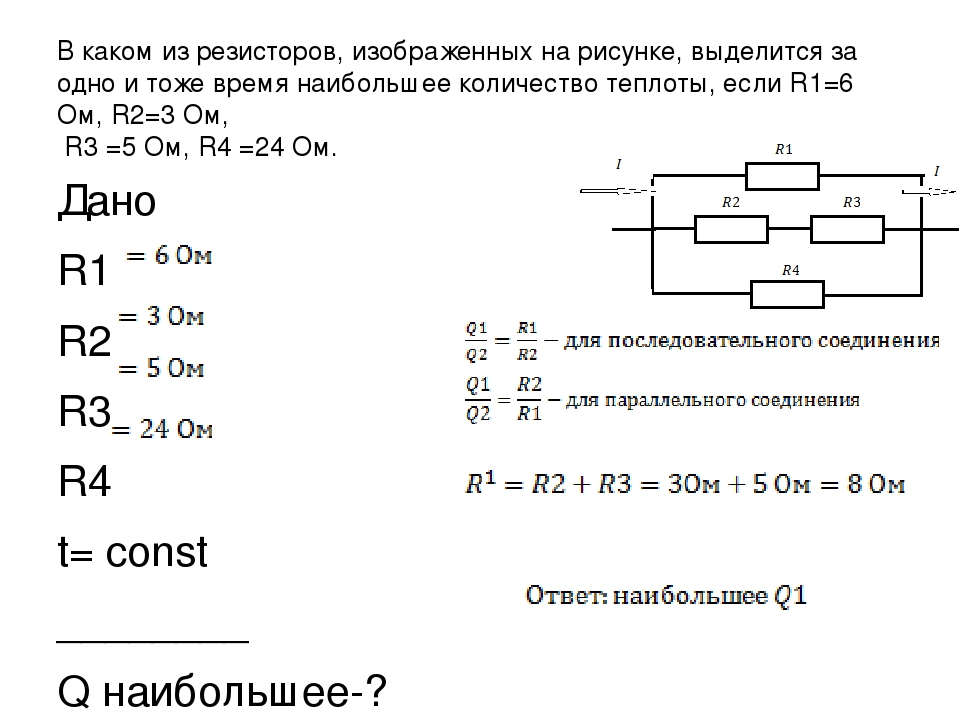 75градуса. Это – не много. Для нашего примера, возьмем Rc-r = 2 °C/Вт
75градуса. Это – не много. Для нашего примера, возьмем Rc-r = 2 °C/Вт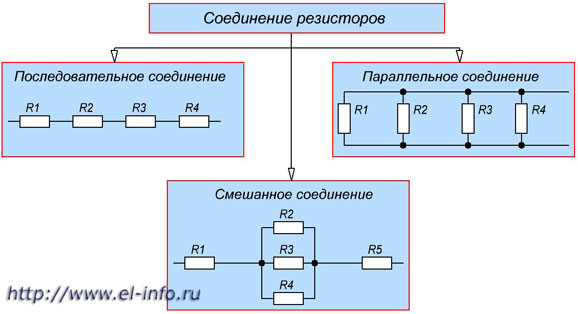


 Это излучение заставляет порошок в трубке светиться (флуоресцировать) i.е. излучает видимый свет. Из разных порошков получаются разные цвета. Обратите внимание, что люминесцентные лампы дороги в установке, но их эксплуатационные расходы намного меньше.
Это излучение заставляет порошок в трубке светиться (флуоресцировать) i.е. излучает видимый свет. Из разных порошков получаются разные цвета. Обратите внимание, что люминесцентные лампы дороги в установке, но их эксплуатационные расходы намного меньше. Затем эта энергия используется для прессования одежды. Температуру утюга можно контролировать с помощью термостата (биметаллической планки).
Затем эта энергия используется для прессования одежды. Температуру утюга можно контролировать с помощью термостата (биметаллической планки). Единицей измерения сопротивления является ом (Ом), который определяется как вольт на ампер тока.
Единицей измерения сопротивления является ом (Ом), который определяется как вольт на ампер тока.