Системы счисления. Перевод из одной системы в другую.

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):

0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):

0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

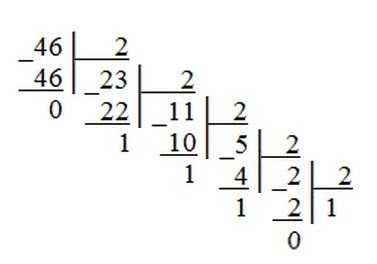
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

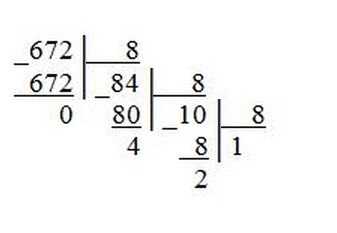
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т.е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т.е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Переводы из различных систем счисления. Таблица соответствия систем.

Перевод из десятичной в двоичную систему счисления.

[youtube fLv4gs9EnJs nolink]

Перевод из двоичной в десятичную систему счисления и наоборот.

[youtube C0ai9-3GHJY nolink]

Перевод чисел из двоичной системы счисления в восьмеричную и наоборот.

[youtube x1bx7o2uESg nolink]

Перевод чисел из двоичной системы счисления в шестнадцатеричную. Сложение двоичных чисел.

[youtube rToqA6rEUQ8 nolink]

Перевод чисел в десятичную систему счисления. Полиномы.

[youtube eSviqB6Db7A nolink]

Краткая таблица соответствия — двоичная система в восьмеричную (8СС) и шестнадцатеричная (16СС) системы:

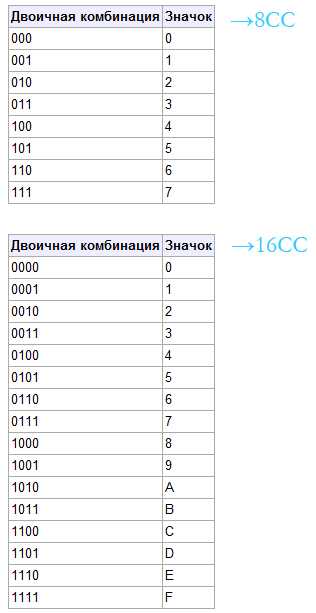
Таблица соответствия десятеричного от 1 до 255 (Decimal), двоичного (Binary) и шестнадцатеричного (Hexadecimal) представлений чисел.

Dec — десятеричная система;

Hex

— шестнадцатеричная система;

Bin — двоичная система.

Dec	Hex	Bin	Dec	Hex	Bin	Dec	Hex	Bin	Dec	Hex	Bin
0	0	0	64	40	1000000	128	80	10000000	192	c0	11000000
1	1	1	65	41	1000001	129	81	10000001	193	c1	11000001
2	2	10	66	42	1000010	130	82	10000010	194	c2	11000010
3	3	11	67	43	1000011	131	83	10000011	195	c3	11000011
4	4	100	68	44	1000100	132	84	10000100	196	c4	11000100
5	5	101	69	45	1000101	133	85	10000101	197	c5	11000101
6	6	110	70	46	1000110	134	86	10000110	198	c6	11000110
7	7	111	71	47	1000111	135	87	10000111	199	c7	11000111
8	8	1000	72	48	1001000	136	88	10001000	200	c8	11001000
9	9	1001	73	49	1001001	137	89	10001001	201	c9	11001001
10	a	1010	74	4a	1001010	138	8a	10001010	202	ca	11001010
11	b	1011	75	4b	1001011	139	8b	10001011	203	cb	11001011
12	c	1100	76	4c	1001100	140	8c	10001100	204	cc	11001100
13	d	1101	77	4d	1001101	141	8d	10001101	205	cd	11001101
14	e	1110	78	4e	1001110	142	8e	10001110	206	ce	11001110
15	f	1111	79	4f	1001111	143	8f	10001111	207	cf	11001111
16	10	10000	80	50	1010000	144	90	10010000	208	d0	11010000
17	11	10001	81	51	1010001	145	91	10010001	209	d1	11010001
18	12	10010	82	52	1010010	146	92	10010010	210	d2	11010010
19	13	10011	83	53	1010011	147	93	10010011	211	d3	11010011
20	14	10100	84	54	1010100	148	94	10010100	212	d4	11010100
21	15	10101	85	55	1010101	149	95	10010101	213	d5	11010101
22	16	10110	86	56	1010110	150	96	10010110	214	d6	11010110
23	17	10111	87	57	1010111	151	97	10010111	215	d7	11010111
24	18	11000	88	58	1011000	152	98	10011000	216	d8	11011000
25	19	11001	89	59	1011001	153	99	10011001	217	d9	11011001
26	1a	11010	90	5a	1011010	154	9a	10011010	218	da	11011010
27	1b	11011	91	5b	1011011	155	9b	10011011	219	db	11011011
28	1c	11100	92	5c	1011100	156	9c	10011100	220	dc	11011100
29	1d	11101	93	5d	1011101	157	9d	10011101	221	dd	11011101
30	1e	11110	94	5e	1011110	158	9e	10011110	222	de	11011110
31	1f	11111	95	5f	1011111	159	9f	10011111	223	df	11011111
32	20	100000	96	60	1100000	160	a0	10100000	224	e0	11100000
33	21	100001	97	61	1100001	161	a1	10100001	225	e1	11100001
34	22	100010	98	62	1100010	162	a2	10100010	226	e2	11100010
35	23	100011	99	63	1100011	163	a3	10100011	227	e3	11100011
36	24	100100	100	64	1100100	164	a4	10100100	228	e4	11100100
37	25	100101	101	65	1100101	165	a5	10100101	229	e5	11100101
38	26	100110	102	66	1100110	166	a6	10100110	230	e6	11100110
39	27	100111	103	67	1100111	167	a7	10100111	231	e7	11100111
40	28	101000	104	68	1101000	168	a8	10101000	232	e8	11101000
41	29	101001	105	69	1101001	169	a9	10101001	233	e9	11101001
42	2a	101010	106	6a	1101010	170	aa	10101010	234	ea	11101010
43	2b	101011	107	6b	1101011	171	ab	10101011	235	eb	11101011
44	2c	101100	108	6c	1101100	172	ac	10101100	236	ec	11101100
45	2d	101101	109	6d	1101101	173	ad	10101101	237	ed	11101101
46	2e	101110	110	6e	1101110	174	ae	10101110	238	ee	11101110
47	2f	101111	111	6f	1101111	175	af	10101111	239	ef	11101111
48	30	110000	112	70	1110000	176	b0	10110000	240	f0	11110000
49	31	110001	113	71	1110001	177	b1	10110001	241	f1	11110001
50	32	110010	114	72	1110010	178	b2	10110010	242	f2	11110010
51	33	110011	115	73	1110011	179	b3	10110011	243	f3	11110011
52	34	110100	116	74	1110100	180	b4	10110100	244	f4	11110100
53	35	110101	117	75	1110101	181	b5	10110101	245	f5	11110101
54	36	110110	118	76	1110110	182	b6	10110110	246	f6	11110110
55	37	110111	119	77	1110111	183	b7	10110111	247	f7	11110111
56	38	111000	120	78	1111000	184	b8	10111000	248	f8	11111000
57	39	111001	121	79	1111001	185	b9	10111001	249	f9	11111001
58	3a	111010	122	7a	1111010	186	ba	10111010	250	fa	11111010
59	3b	111011	123	7b	1111011	187	bb	10111011	251	fb	11111011
60	3c	111100	124	7c	1111100	188	bc	10111100	252	fc	11111100
61	3d	111101	125	7d	1111101	189	bd	10111101	253	fd	11111101
62	3e	111110	126	7e	1111110	190	be	10111110	254	fe	11111110
63	3f	111111	127	7f	1111111	191	bf	10111111	255	ff	11111111

 

И, напоследок — удобный online-калькулятор систем счисления тут>>>.

Раздел: HOWTO’s Разное

rtfm.co.ua

Таблица чисел в системах счисления

Таблица умножения чисел в шестнадцатеричной системе счисления

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	0	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E
3	0	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D
4	0	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C
5	0	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B
6	0	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A
7	0	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69
8	0	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78
9	0	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87
A	0	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96
B	0	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	9A	A5
C	0	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4
D	0	D	1A	27	34	41	4E	5B	68	75	82	8F	9C	A9	B6	C3
E	0	E	1C	2A	38	46	54	62	70	7E	8C	9A	A8	B6	C4	D2
F	0	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1

Таблица сложения чисел в шестнадцатеричной системе счисления

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
1	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
2	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11
3	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11	12
4	4	5	6	7	8	9	A	B	C	D	E	F	10	11	12	13
5	5	6	7	8	9	A	B	C	D	E	F	10	11	12	13	14
6	6	7	8	9	A	B	C	D	E	F	10	11	12	13	14	15
7	7	8	9	A	B	C	D	E	F	10	11	12	13	14	15	16
8	8	9	A	B	C	D	E	F	10	11	12	13	14	15	16	17
9	9	A	B	C	D	E	F	10	11	12	13	14	15	16	17	18
A	A	B	C	D	E	F	10	11	12	13	14	15	16	17	18	19
B	B	C	D	E	F	10	11	12	13	14	15	16	17	18	19	1A
C	C	D	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B
D	D	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C
E	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D
F	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D	1E

Таблица сложения чисел в восьмеричной системе счисления

	0	1	2	3	4	5	6	7
0	0	1	2	3	4	5	6	7
1	1	2	3	4	5	6	7	10
2	2	3	4	5	6	7	10	11
3	3	4	5	6	7	10	11	12
4	4	5	6	7	10	11	12	13
5	5	6	7	10	11	12	13	14
6	6	7	10	11	12	13	14	15
7	7	10	11	12	13	14	15	16

Таблица умножения чисел в восьмеричной системе счисления

	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7
2	0	2	4	6	10	12	14	16
3	0	3	6	11	14	17	22	25
4	0	4	10	14	20	24	30	34
5	0	5	12	17	24	31	36	43
6	0	6	14	22	30	36	44	52
7	0	7	16	25	34	43	52	61

studfile.net

Методическая разработка по информатике и икт (10 класс) по теме: Таблица перевода из одной системы счисления в другую

По теме: методические разработки, презентации и конспекты

«Способы перевода из одной системы счисления в другую»

конспект и презентация…

Системы счисления. Перевод из одной системы счисления в другую.

Разработка урока «Системы счисления. Перевод из одной системы счисления в другую «…

Кодирование информации. Системы счисления. Перевод из одной системы счисления в другую.

В архиве приложены скриншоты презентации.Файл с презентацией полностью можно скачать по ссылке http://ultrashare.net/hosting/fl/7a2929007…

Системы счисления. Перевод чисел из одной системы счисления в другую систему счисления.

План-конспект урока с использованием ЭОР «Системы счисления. Перевод чисел из одной системы счисления в другую систему счисления»….

Урок-игра по информатике и ИКТ в 8 классе по теме: «Системы счисления. Перевод из одной системы счисления в другие, арифметические операции в двоичной системе счисления»

Урок-игра по информатике и ИКТ в 8 классе по теме: «Системы счисления. Перевод из одной системы счисления в другие, арифметические операции в двоичной системе счисления»…

«Системы счисления. Перевод из одной системы счисления в другие, арифметические операции в двоичной системе счисления»

систематизировать знания учащихся по теме «Системы счисления. Перевод из одной системы счисления в другие, арифметические операции в двоичной системе счисления»…

Открытый урок «Перевод из одной системы счисления в другую»

открытый урок по информатике для 9 класса…

nsportal.ru

Справочный материал по теме «Системы счисления»

Позиционные системы счисления

Система счисления

Основание

Алфавит

Десятичная

10

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Двоичная

2

0, 1

Троичная

3

0, 1, 2

Восьмеричная

8

0, 1, 2, 3, 4, 5, 6, 7

Шестнадцатеричная

16

0, 1, 2, 3, 4, 5, 6, 7, 8, 9,

А, B, C, D, E, F

10 11 12 13 14 15

Правила перевода чисел

1. Перевод целых чисел из ПСС с основанием q в 10-ю СС.

Чтобы перевести целое число из любой ПСС с основанием q в 10-ую СС, необходимо представить его в развёрнутом виде (составить сумму степенного ряда с основанием системы, в которой записано число), а затем выполнить арифметические действия. Например: перевод двоичного числа:

2. Перевод целых чисел из 10-ой СС в ПСС с основанием q.

Чтобы перевести целое 10-ое число в другую СС, необходимо осуществлять последовательное деление 10-ого числа и затем получаемых целых частных на основание той системы, в которую оно переводится, до тех пор, пока не получится частное, меньшее делителя. Число в новой системе записывается в виде остатков от деления, начиная с последнего частного.

Таблица степеней

Степень

0

1

2

3

4

5

6

7

8

9

10

2

1

2

4

8

16

32

64

128

256

512

1024

8

1

8

64

512

4096

16

1

16

256

4096

Двоичная арифметика

+

0

1

х

0

1

0

0

1

0

0

0

1

1

10

1

0

1

Связь родственных систем

Из 2-ичной в 8-ричную: 011 101  000 ₂

3 5 0 ₈

Из 2-ичной в 16-ричную: 1110 1000 ₂

Е 8 ₁₆

Из 8-ричной в 2-ичную: 3 5 0 ₈

011 101  000 ₂

Из 16-ричной в 2-ичную: Е 8 ₁₆

1110 1000 ₂

Таблица родственных систем счисления:

10-тичная

2-ичная

8-ричная

16-ричная

0

0

0

0

1

1

1

1

2

10

2

2

3

11

3

3

4

100

4

4

5

101

5

5

6

110

6

6

7

111

7

7

8

1000

10

8

9

1001

11

9

10

1010

12

A

11

1011

13

B

12

1100

14

C

13

1101

15

D

14

1110

16

E

15

1111

17

F

16

10000

20

10

infourok.ru

Перевод чисел из одной системы счисления в другую онлайн

С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.

 Результат уже получен!

Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения

Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:

число	6	3	7	2
позиция	3	2	1	0

Тогда число 6372 можно представить в следующем виде:

6372=6000+300+70+2 =6·10³+3·10²+7·10¹+2·10⁰.

Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.

Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:

число	1	2	8	7	.	9	2	3
позиция	3	2	1	0		-1	-2	-3

Тогда число 1287.923 можно представить в виде:

1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10³ +2·10² +8·10¹+7·10⁰+9·10^-1+2·10^-2+3·10^-3.

В общем случае формулу можно представить в следующем виде:

Ц_n·sⁿ+Ц_n-1·s^n-1+…+Ц₁·s¹+Ц₀·s⁰+Д_-1·s^-1+Д_-2·s^-2+…+Д_-k·s^-k

(1)

где Ц_n-целое число в позиции n, Д_-k— дробное число в позиции (-k), s — система счисления.

Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.

В таблице Таб.1 представлены числа в разных системах счисления.

Таблица 1
Система счисления
10	2	8	16
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

 

Перевод чисел из одной системы счисления в другую

Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.

Перевод чисел из любой системы счисления в десятичную систему счисления

С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.

Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:

1·2⁶+0·2⁵+1·2⁴+1·2³+1·2² +0·2¹+1·2⁰+0·2^-1+0·2^-2+1·2^-3 =64+16+8+4+1+1/8=93.125

Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:

Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:

Здесь A -заменен на 10, B — на 11, C— на 12, F — на 15.

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.

Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.

Пример 4. Переведем число 159 из десятичной СС в двоичную СС:

159	2
158	79	2
1	78	39	2
	1	38	19	2
		1	18	9	2
			1	8	4	2
				1	4	2	2
					0	2	1
						0

Рис. 1

Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:

159₁₀=10011111₂.

Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.

615	8
608	76	8
7	72	9	8
	4	8	1
		1

Рис. 2

При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:

615₁₀=1147₈.

Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.

19673	16
19664	1229	16
9	1216	76	16
	13	64	4
		12

Рис. 3

Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.

Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.

Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).

Рассмотрим вышеизложенное на примерах.

Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.

		0.214
	x	2
0		0.428
	x	2
0		0.856
	x	2
1		0.712
	x	2
1		0.424
	x	2
0		0.848
	x	2
1		0.696
	x	2
1		0.392

Рис. 4

Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.

Следовательно можно записать:

0.214₁₀=0.0011011₂.

Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.

		0.125
	x	2
0		0.25
	x	2
0		0.5
	x	2
1		0.0

Рис. 5

Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:

0.125₁₀=0.001₂.

Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.

		0.214
	x	16
3		0.424
	x	16
6		0.784
	x	16
12		0.544
	x	16
8		0.704
	x	16
11		0.264
	x	16
4		0.224

Рис. 6

Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:

0.214₁₀=0.36C8B4₁₆.

Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.

		0.512
	x	8
4		0.096
	x	8
0		0.768
	x	8
6		0.144
	x	8
1		0.152
	x	8
1		0.216
	x	8
1		0.728

Рис. 7

Получили:

0.512₁₀=0.406111₈.

Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:

159.125₁₀=10011111.001₂.

Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:

19673.214₁₀=4CD9.36C8B4₁₆.

matworld.ru

двоичная, восьмеричная, шестнадцатеричная — урок. Информатика, 8 класс.

Для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.

Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую  информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.

Двоичной системой счисления называется позиционная система счисления с основанием \(2\).

Для записи чисел в ней использовали только две цифры:  \(0\) и \(1\).

Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 110112 —  число в двоичной системе счисления.

 

Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием \(2\), например:

 

1012=1 ·22+0 ·21+1 ·20.

 

В десятичной системе счисления это число будет выглядеть так:

 

1012=4+0+1=5.

 

Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на \(2\) до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём десятичное число \(13\) в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

 

 

Получили 1310=11012.

Пример:

Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:

 

\(224\)	\(112\)	\(56\)	\(28\)	\(14\)	\(7\)	\(3\)	\(1\)
\(0\)	\(0\)	\(0\)	\(0\)	\(0\)	\(1\)	\(1\)	\(1\)

 

22410=111000002.

Восьмеричной системой счисления называется позиционная система счисления с основанием \(8\).

 

Для записи чисел в восьмеричной системе счисления используются цифры:  \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\).

Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.

Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём восьмеричное число  154368 в десятичную систему счисления.

154368=1 ·84+5 ·83+4 ·82+3 ·81+6 ·80=694210

Пример:

Переведём десятичное число \(94\) в восьмеричную систему счисления.

 

 

9410=1368

Шестнадцатеричной системой счисления называется позиционная система счисления с основанием \(16\).

 

Для записи чисел в шестнадцатеричной системе счисления используются цифры:  \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\) и латинские буквы A, B, C, D, E, F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510.

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Для перевода целого десятичного числа в шестнадцатеричную  систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на \(16\) до тех пор, пока не получим частное, равное нулю. Исходное число в системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём шестнадцатеричное число \(2\)\(A7\) в десятичное. В соответствии с вышеуказанными правилом представим его в виде суммы степеней с основанием \(16\):

2A716=2 ·162+10 ·161+7 ·160=512+160+7=679.

Пример:

Переведём десятичное число \(158\) в шестнадцатеричную систему счисления.

 

 

15810=9E16.

Для перевода числа из любой позиционной системы счисления в десятичную необходима использовать развернутую формулу числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами.

Для перевода целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы счисление, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

www.yaklass.ru

No related posts.