Закон Ома — онлайн калькулятор

Чтобы посчитать Закон Ома воспользуйтесь нашим очень удобным онлайн калькулятором:

Закон Ома для участка цепи

Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).

Онлайн калькулятор

Найти силу тока

Формула

I = ^U/_R

Пример

Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:

Сила тока на этом участке I = ¹²/₂= 6 А

Найти напряжение

Формула

U = I ⋅ R

Пример

Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:

Напряжение

на этом участке U = 6⋅2 = 12 В

Найти сопротивление

Формула

R = ^U/_I

Пример

Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:

Электрическое сопротивление на этом участке R = ¹²/₆ = 2 Ом

Закон Ома для полной цепи

Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Онлайн калькулятор

Найти силу тока

Формула

I = ^ε/_R+r

Пример

Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:

Сила тока I = ¹²/₄₊₂ = 2 А

Найти ЭДС

Формула

ε = I ⋅ (R+r)

Пример

Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:

ЭДС ε = 2 ⋅ (4+2) = 12 В

Найти внутреннее сопротивление источника напряжения

Формула

r = ^ε/_I— R

Пример

Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:

Внутреннее сопротивление источника напряжения r = 12/2 — 4 = 2 Ом

Найти сопротивление всех внешних элементов цепи

Формула

R = ^ε/_I— r

Пример

Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:

Сопротивление всех внешних элементов цепи: R = 12/2 — 2 = 4 Ом

См. также

poschitat.online

Онлайн калькулятор — закон Ома (ток, напряжение, сопротивление) + Мощность :: АвтоМотоГараж

Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.

В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.

Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению

Так записывается основная формула:

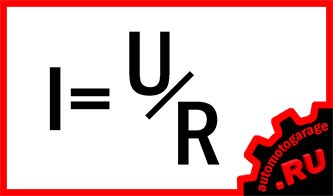
Путем преобразования основной формулы можно найти и другие две величины:

      

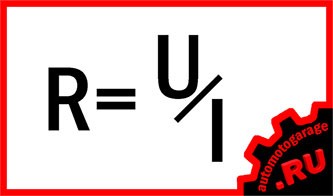
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

Формула мгновенной электрической мощности:

Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.

 

 

Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.

 

Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.

Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.

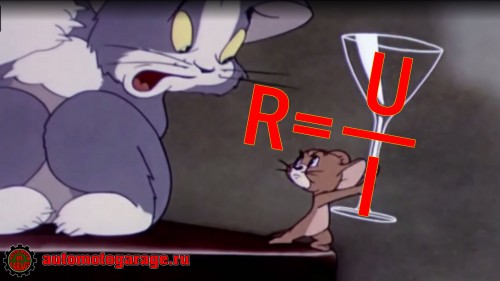
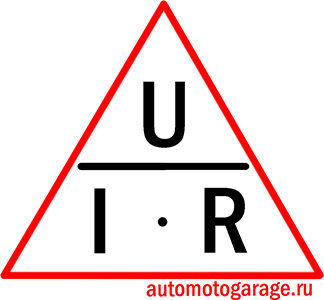
Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.

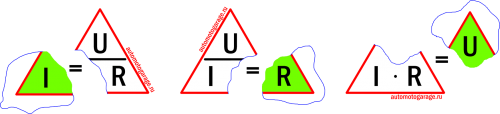
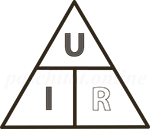
Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.

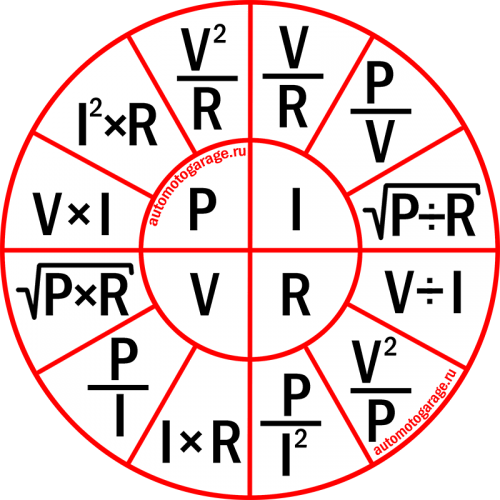
Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.

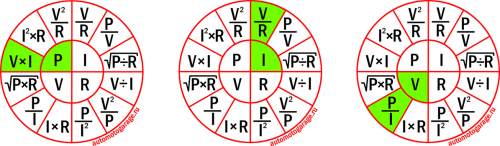
Этот круг также, как и треугольник можно назвать магическим.

 

automotogarage.ru

Закон Ома. Онлайн расчёт для постоянного и переменного тока.

Онлайн расчёт электрических величин напряжения, тока и мощности для:

участка цепи, полной цепи с резистивными, ёмкостными и индуктивными
элементами.

— А любите ли Вы закон Ома так, как люблю его я? — спросил учитель физики стоящего рядом с щитком и разглядывающего свой обугленный палец электрика, — Всеми силами души Вашей, со всем энтузиазмом и исступлением, к которому только способна пылкая молодость, — никак не угомонялся он, сверкая из-под очков пытливым взглядом.
— Мужик, ты что, дурак? – вежливо поинтересовался обиженный противоестественным вопросом электрик и пошёл, насвистывая «Калинку-Малинку» в направлении ближайшего супермаркета — не ради пьянства окаянного, а дабы залечить свой увечный палец.

А тем временем, закон Ома является в электротехнике основным законом, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R,

где
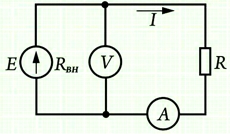
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеряемая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.

Зная любые два из трёх приведённых параметров можно легко произвести расчёт и величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:

P_(Вт) = U_(В)×I_(А) = I²_(А)×R_(Ом) = U²_(В)/R_(Ом)

Можно, конечно, описывая закон Ома обойтись и вообще без формул, а вместо них пользоваться словами или картинками:

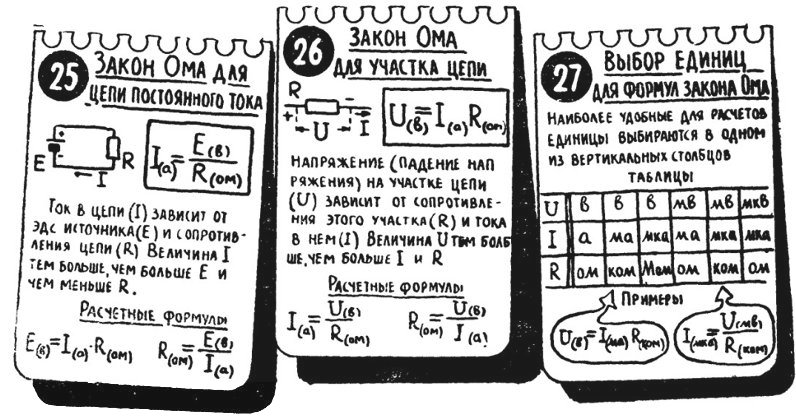
С другой стороны, формулы настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Калькулятор Вам в помощь, дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:
1В=1000мВ=1000000мкВ;
1А=1000мА=1000000мкА;
1Ом=0.001кОм=0.000001МОм;
1Вт=1000мВт=100000мкВт.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.

ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.

Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.

Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения r_внутр.
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = R_внешн + r_внутр , после чего закон приобретает солидное название — закон Ома для полной цепи:
I=U/(R+r) .

Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду: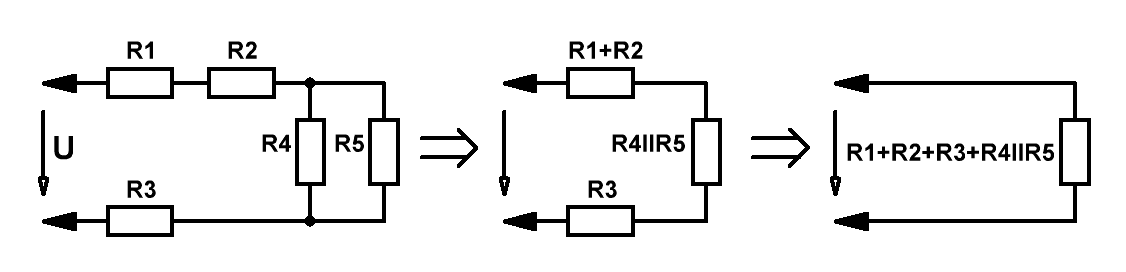

Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/R_ll = 1/R₄+1/R₅.
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока — под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.

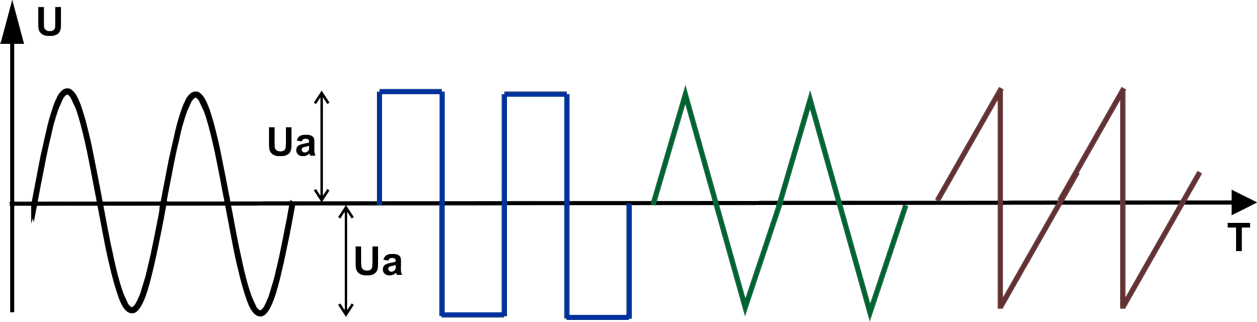
Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.

С этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае смотреться это будет так:

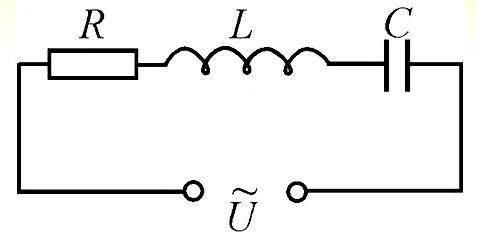
А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид:
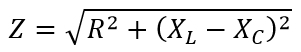
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: X_C = 1/(2πƒС) ,   X_L = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента — необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.

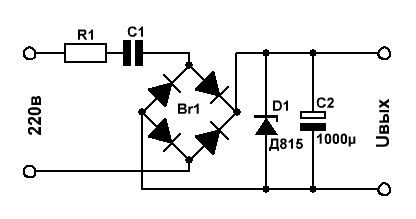
Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом — 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в — 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки.
Зададимся номиналами R1 — 30 Ом, С1 — 1 Мкф, частотой сети f — 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет — надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости — 3,18 Мкф, при котором Z = 1,04кОм.

Всё — закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!

 

vpayaem.ru

Закон Ома | Мозган калькулятор онлайн

На данной странице калькулятор поможет рассчитать сопротивление, напряжение или силу тока по закону Ома онлайн.

Закон Ома — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

Как найти сопротивление

---

---

Электрическое сопротивление определяет силу тока, текущего по цепи при заданном напряжении.

Под Электрическим сопротивлением R понимают отношение напряжения на концах проводника к силе тока, текущего по проводнику.

Формула для нахождения сопротивления по закону Ома:

U — напряжение; I — сила тока.

Как найти силу тока

---

---

Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

Формула для нахождения силы тока по закону Ома:

U — напряжение; R — сопротивление.

Как найти напряжение

---

---

Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.

Формула для нахождения напряжения по закону Ома:

I — сила тока; R — сопротивление.

www.mozgan.ru

Закон Ома

Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“

Единицы измерения в электронике. Закон Ома.

Единицы измерения в электронике

Единицы измерения служат для количественного определения какой-либо физической величины. К примеру, покупая яблоки, вы измеряете их вес в килограммах. Аналогично мультиметр измеряет сопротивление элементов в омах, напряжение — в вольтах, а ток — в амперах. В табл. 1.1 показаны общепринятые единицы измерения и их аббревиатуры для физических величин, которые используются в электронике.

Физическая величина	Аббревиатура	Единицы измерения	Символ единиц измерения
Сопротивление	R	ом	Ом, ?
Емкость	С	фарад	Ф
Индуктивность	L	генри	Гн
Напряжение	U (V или Е)	вольт	В
Ток	I	ампер	А
Мощность	Р	ватт	Вт
Частота	f	герц	Гц

Таблица 1.1. Единицы измерения, используемые в электронике

Переход к большим или меньшим величинам. При измерении веса яблок очень даже можно столкнуться с малым количеством яблока (или его кусочка), а можно измерять и центнерами, не так ли? Диапазон измерения физических величин в электронике еще шире. В одной схеме вы можете иметь сопротивление в миллионы ом, тогда как в другой протекающий ток будет меньше одной тысячной ампера. Говоря о подобных величинах — как громадных, так и предельно малых, — приходится иметь дело со специальной терминологией. Чтобы показывать очень большие и очень малые числа, в электронике применяют специальные префиксы, или приставки, и экспоненциальное представление. В табл. 1.2 показаны самые широко используемые префиксы и тип записи числовых величин.

Тблица 1.2. Приставки, используемые в электронике

Число	Название	Экспоненциальное представление	Префикс	Аббревиатура
1000000000	1 миллиард	109	Гига	Г
1000000	1 миллион	106	Мега	м
1000	1 тысяча	103	кило	к
100	1 сотня	102
10	1 десяток	101
1	один	100
0,1	1 десятая	10-1
0,01	1 сотая	10-2
0,001	1 тысячная	10-3	милли	м
0,000001	1 миллионная	10-6	микро	мк
0,000000001	1 миллиардная	10-9	нано	н
0,000000000001	1триллионная	10-12	пико	п

Как же правильно прочитать число, записанное как 10⁶ или 10^-6? Экспоненциальное представление представляет собой наиболее удобный способ указания того, сколько нулей нужно добавить к числу в десятичной системе счисления, т.е. основанной на степени числа 10. Например, верхний индекс “6” в записи 10⁶ означает, что точка, разделяющая целую и дробную части числа, должна находиться на шесть разрядов правее, а в записи 10^-6 — что эту точку нужно сдвинуть на шесть разрядов левее. Таким образом, в числе 1 х 10⁶ разделитель разрядов сдвигается на шесть мест вправо, и мы получаем в результате число 1 000 000 (1 миллион). В числе же 1 х 10^-6 разделитель разрядов сдвигается на столько же мест влево, и результатом является 0,000001, или одна миллионная. 3,21 х 10⁴ можно записать, сдвинув запятую на 4 знака вправо: 32100.

Префиксы + единицы измерения = ?

В предыдущих абзацах вы увидели как для обозначения физических величин и единиц их измерения используются аббревиатуры. В этом разделе мы научимся объединять их и использовать очень краткую запись. Например, ток 5 миллиампер можно записать в виде 5 мА, а частоту 3 мегагерца — как 3 МГц.

Кроме того, так же, как при измерении яблок удобнее всего пользоваться килограммами, а при строительстве загородного офиса большой компании вес стальных конструкций определенно будут измерять не иначе как в тоннах, в электронике тоже существуют такие физические величины, для измерения которых пользуются большими числами, и такие, которые измеряются малыми. Это значит, что чаще всего вам придется иметь дело с одним и тем же набором приставок для каждой физической величины. Ниже приведены такие комбинации величин и единиц их измерения.

> Ток: пА, нА, мкА, мА, А.

> Индуктивность: нГн, мГн, мкГн, Гн.

> Емкость: пФ, нФ, мкФ, мФ, Ф.

> Напряжение: мкВ, мВ, В, кВ.

> Сопротивление: Ом, кОм, МОм.

> Частота: Гц, кГц, МГц, ГГц.

Использование некоторых новых терминов

Хотя ранее мы уже рассматривали такие понятия, как сопротивление, напряжение и ток, есть еще некоторые термины, которые могут оказаться для вас внове.

Емкость представляет собой способность накапливать заряд под воздействием электрического поля. Такой накопленный заряд может повышать или понижать напряжение более плавно, чем в отсутствие емкости. Для применения данного свойства на практике используется такой компонент, как конденсатор.

Частотой переменного тока называется мера повторяемости сигнала. Например, напряжение в настенной розетке совершает один полный цикл изменения 50 раз в секунду.

Индуктивность – это способность запасать энергию в магнитном поле; эта накопленная энергия препятствует изменению тока точно так же, как энергия, накопленная конденсатором, препятствует резким изменениям напряжения. Для использования данного свойства на практике в электронике применяются катушки индуктивности, или дроссели.

Мощность служит мерой количества работы, которую электрический ток совершает при протекании через элементы схемы. К примеру, если приложить к электрической лампе напряжение, подведя ток при помощи проводов, то на нагрев этих проводов будет затрачивться какая-то работа. В данном случае мощность можно вычислить, перемножив приложенное к лампе напряжение на ток, протекающий по проводам.

Используя информацию, приведенную в табл. 1.1 и 1.2, вы уже можете перевести экспоненциальную запись числа или аббревиатуру физической величины на человеческий язык. Ниже дано несколько примеров:

> мА: миллиампер, или 1 тысячная ампера;

> мкВ: микровольт, или 1 миллионная вольта;

> нФ: нанофарада, или 1 миллиардная фарады;

> кВ: киловольт, или 1 тысяча вольт;

> МОм: мегаом, или 1 миллион ом;

> ГГц: гигагерц, или 1 миллиард герц.

В аббревиатурах префиксов, которые представляют числа, превышающие 1, такие как М (для приставки Мега), используют прописные буквы. Аббревиатуры приставок, которые меньше 1, пишутся со строчной буквы — как, например, в слове милли. Единственным исключением из этого правила является приставка к для обозначения префикса кило-, которая также записывается с маленькой буквы.

Иногда все же для обозначения тысяч используют и прописную литеру К — а именно при записи килоом; если вы увидите запись вида 3,3 К, то это будет значить 3,3 килоома.

Вы должны научиться преобразовывать любое число к экспоненциальному виду, чтобы затем нормально проводить расчеты. Убедиться в этом вы сможете уже в следующем разделе.

---

Понятие о законе Ома

Итак, давайте предположим, что вы собрали свою первую схему. Вы знаете величину тока, которую компонент схемы может выдержать, не выходя из строя, и напряжение, выдаваемое источником питания. Следовательно, вам нужно рассчитать сопротивление, которое не позволит току в цепи превысить пороговое значение.

В начале 1800-х годов Георг Ом опубликовал уравнение, названное впоследствии законом Ома, которое позволяет выполнить такой расчет. Закон Ома гласит: напряжение равняется произведению тока на сопротивление, или (в стандартной математической записи):

U = I x R

Выводы из закона Ома

Помните ли вы из школы основы алгебры? Давайте еще раз вспомним вместе: если в уравнении с тремя величинами известны две, то достаточно легко рассчитать третью неизвестную величину. Закон Ома основывается именно на таком уравнении; члены уравнения можно переставлять как угодно, но зная любые два, всегда можно вычислить третий. Например, можно сказать, что ток является частным от деления напряжения на сопротивление:

 I = U / R

Наконец, можно рассчитать сопротивление при известных токе и напряжении, переставив члены того же уравнения:

R = U / I

Итак, пока вроде бы все ясно. Теперь давайте попробуем проверить наши знания на практике: пусть есть схема, питающаяся от 12-вольтовой батареи, и электрическая лампа (скажем, большой фонарик). Перед установкой лампочки в фонарик вы измерили сопротивление схемы мультиметром и нашли, что оно равно 9 Ом. Вот формула для расчета электрического тока по закону Ома:

 I = U / R = 12  вольт / 9 Ом = 1,3 A

Ну, а что, если вы обнаружили, что лампочка светит чересчур уж ярко? Яркость можно изменить, уменьшив ток, т.е. просто добавив в схему резистор. Изначально мы имели сопротивление схемы 9 Ом; добавив 5-омный резистор в схему, мы повысим ее сопротивление до 14 Ом. В этом случае ток будет равен:

I = U / R = 12 вольт / 14 Ом = 0,9 А

Расчеты с применением больших и малых величин

Предположим, что у вас есть схема с небольшой сиреной, которая имеет сопротивление 2 килоома, а также 12-вольтовая батарея. Для того чтобы рассчитать ток, вам нужно выразить сопротивление цепи не в килоомах, а в базовых единицах — омах, не используя приставку “кило”. В нашем случае это значит, что нужно разделить напряжение на 2000 Ом:

I = U / R = 12 вольт / 2000 Ом = 0,006 A

В результате мы получили ток, записанный как доля 1 А. После окончания расчета будет удобнее вновь использовать префикс, чтобы дать ответ в более лаконичном виде: 0,006 А = 6 мА

Подводя итоги, можно сказать: для проведения расчетов необходимо все исходные величины преобразовать к базовым единицам счисления.

Мощность и закон Ома

Георг Ом (вот уж поистине, наш пострел везде поспел!) также нашел выражение для мощности, вычисляемое при известных напряжении и токе:

Р = U х I; или Мощность = напряжение умноженное на силу тока.

Это уравнение можно использовать для расчета мощности, потребляемой сиреной из предыдущего примера:

Р = 12 В х 0,006 А = 0,072 Вт, или 72 мВт.

Ладно, а что же делать, если напряжение на сирене нам не известно? Вы можете заняться простейшим преобразованием формулы для мощности, используя школьные знания (а вы-то думали, что зря протираете штаны на уроках физики!). Поскольку U = I х R, можно подставить это выражение в формулу для мощности, получив

Р = I2 х R; или Мощность = сила тока в квадрате умноженная на сопротивление.

Вы также можете использовать алгебраические преобразования, чтобы самостоятельно прикинуть, как можно рассчитать сопротивление, напряжение или ток, зная мощность и любой другой из этих же параметров.

---

---

radio-stv.ru

Закон Ома — это… Что такое Закон Ома?

V — напряжение,
I — сила тока,
R — сопротивление.

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде : ,

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r^[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

Из закона Ома для полной цепи вытекают следствия:

• При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
• При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто^[2] выражение:

(3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

(4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

(5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

(6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо^[3], впоследствии переименованный в Си́менс (обозначение: См, S).

Мнемоническая диаграмма для Закона

Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

В соответствии с этой диаграммой формально может быть записано выражение:

(7)

Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

(8)

где:

•  — удельное сопротивление материала, из которого сделан проводник,
•  — его длина
•  — площадь его поперечного сечения

Закон Ома и ЛЭП

Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением:

= (9)

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома в дифференциальной форме

Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.

Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re^−iδ — комплексное сопротивление (импеданс),
• R = (R_a² + R_r²)^1/2 — полное сопротивление,
• R_r = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = − arctg (R_r/R_a) — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Трактовка закона Ома

Закон Ома можно просто объяснить при помощи теории Друде:

Здесь:

См. также

Примечания

Ссылки

dal.academic.ru

No related posts.