Последовательное и параллельное соединение проводников — урок. Физика, 8 класс.

В быту и в промышленности в электрическую цепь соединяются сразу несколько потребителей электрической энергии. Различают три вида соединения сопротивлений (резисторов):

1. последовательное соединение проводников
2. параллельное соединение проводников
3. смешанное соединение проводников

Последовательное соединение проводников

Схема соединения выглядит следующим образом:

 

 

Обрати внимание!

При последовательном соединении все входящие в него проводники соединяются друг за другом, т.е. конец первого проводника соединяется с началом второго.

 

 

Опыт показывает:

Сила тока в любых частях цепи одна и та же (об этом свидетельствуют показания амперметров): I=I1=I2.

Если выкрутить одну лампу, то цепь разомкнётся, а другая лампа тоже погаснет.

 

Опыт показывает следующее: 

При последовательном соединении сопротивлений результирующее напряжение равно сумме напряжений на участках: U=U1+U2.

 

 

Результирующее сопротивление последовательно соединённых потребителей равно сумме сопротивлений потребителей: R=R1+R2.

Для проверки данного утверждения можно использовать омметр. При подключении омметра ключ должен быть разомкнут!

 

Омметр подключают по очереди к каждому потребителю, а потом к обоим одновременно.

 

Сопротивление цепи \(R\), состоящей из \(n\) одинаковых ламп, сопротивлением R1 каждая, в \(n\) раз больше сопротивления одной лампы: \(R\) = R1* \(n\).

 

Параллельное соединение проводников

Схема соединения выглядит следующим образом:

 

 

Обрати внимание!

При параллельном соединении все входящие в него проводники одним своим концом присоединяются к одной точке цепи А, а вторым концом — к другой точке В.

 

 

Опыт доказывает:

Сила тока в неразветвлённой части цепи равна сумме сил тока в отдельных параллельно соединённых проводниках.

Об этом свидетельствуют показания амперметров: I=I1+I2.

 

 

Если выкрутить одну лампу, то другая лампа продолжает гореть. Это свойство используют для подключения бытовых приборов в помещении.

 

Опыт свидетельствует, что:

Напряжение на участке цепи АВ и на концах всех параллельно соединённых проводников одно и то же.

Об этом свидетельствуют показания вольтметров:

U=U1=U2.

 

 

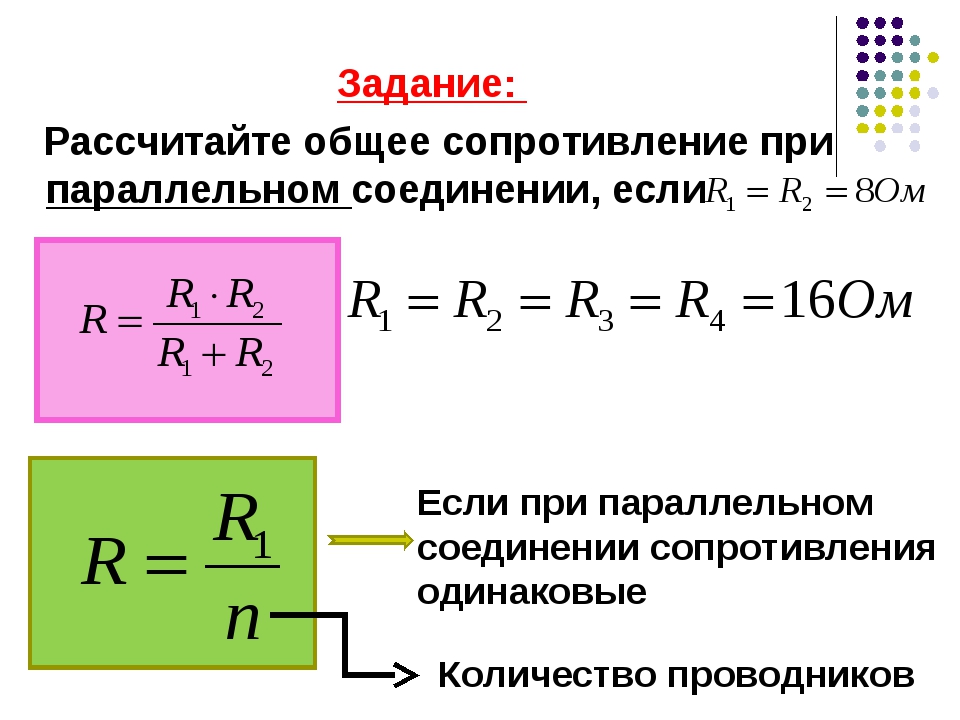
Общее сопротивление цепи при параллельном соединении проводников определяется по формуле:

 

1R=1R1+1R2.

 

Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников.

Для проверки формулы можно использовать омметр. При подключении омметра ключ должен быть разомкнут!

 

Сопротивление цепи \(R\), состоящей из \(n\) одинаковых ламп, сопротивлением R1 каждая, в \(n\) раз меньше сопротивления одной лампы: \(R\) = R1/ \(n\).

Источники:

http://files.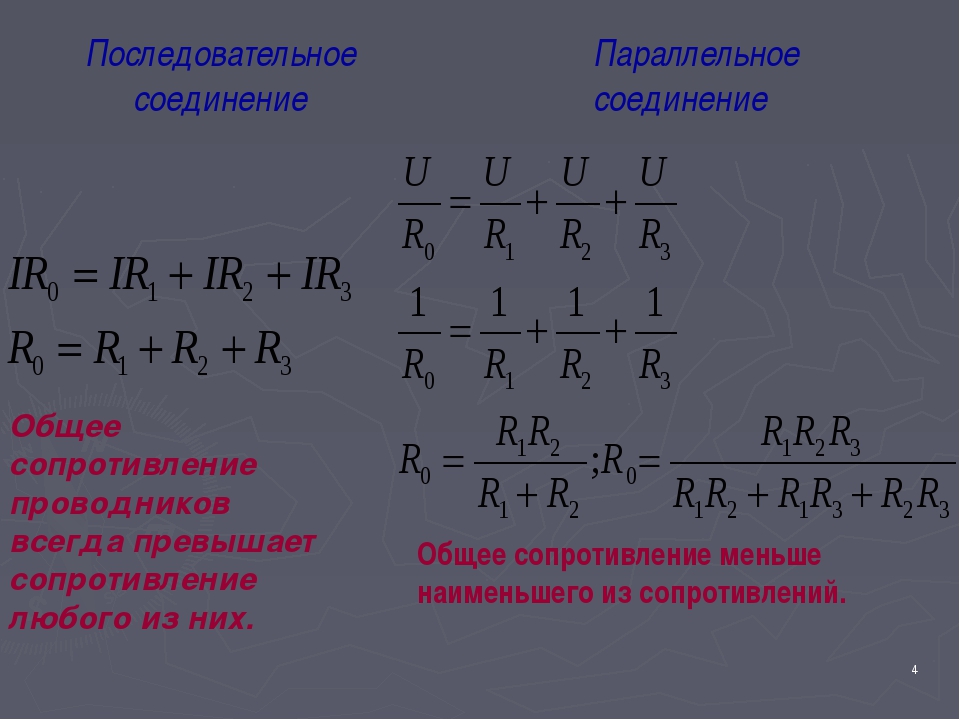 school-collection.edu.ru/dlrstore/669ba073-e921-11dc-95ff-0800200c9a66/3_17.swf
http://files.school-collection.edu.ru/dlrstore/669ba074-e921-11dc-95ff-0800200c9a66/3_18.swf

http://class-fizika.narod.ru/8_33.htm

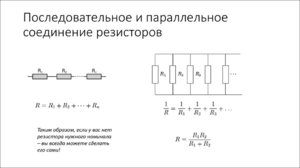
Последовательное и параллельное соединение резисторов

Последовательное соединение резисторов

Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле:
R = R1 + R2.
Это справедливо и для большего количества соединённых последовательно резисторов:
R = R1 + R2 + R3 + R4 + … + Rn.

 

Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.

При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.

Параллельное соединение резисторов (формула)

Параллельное соединение резисторов

необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.

Расчет параллельного сопротивления

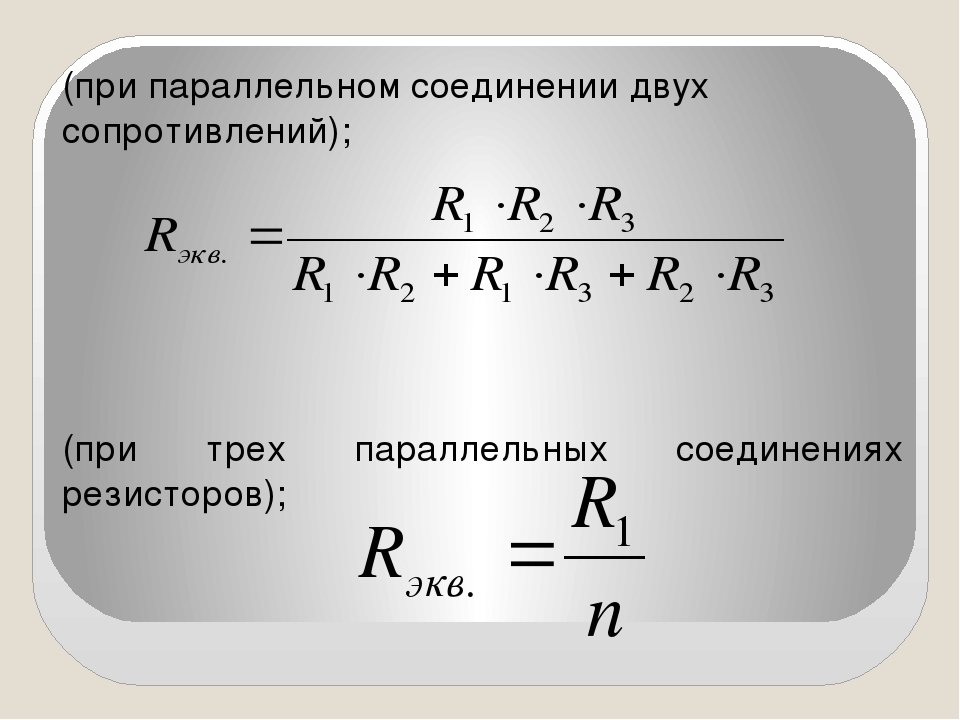
Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:

 

Сопротивление из двух резисторов:	R =	R1 × R2
		R1 + R2

Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:

Сопротивление параллельных резисторов

1	=	1	+	1	+	1	+ . ..
R		R1		R2		R3

Как видно, вычислить сопротивление двух параллельных резисторов значительно удобнее.

Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.

Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.

Например: десять резисторов номиналом 1 КОм и мощностью 1 Вт каждый, соединённые параллельно будут иметь общее сопротивление 100 Ом и мощность 10 Вт.
При последовательном соединении мощность резисторов также складывается. Т.е. в том же примере, но при последовательном соединении, общее сопротивление будет равно 10 КОм и мощность 10 Вт.

Суммарное сопротивление при последовательном соединении. Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов. Сопротивление параллельной цепи

Содержание:

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи.

Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.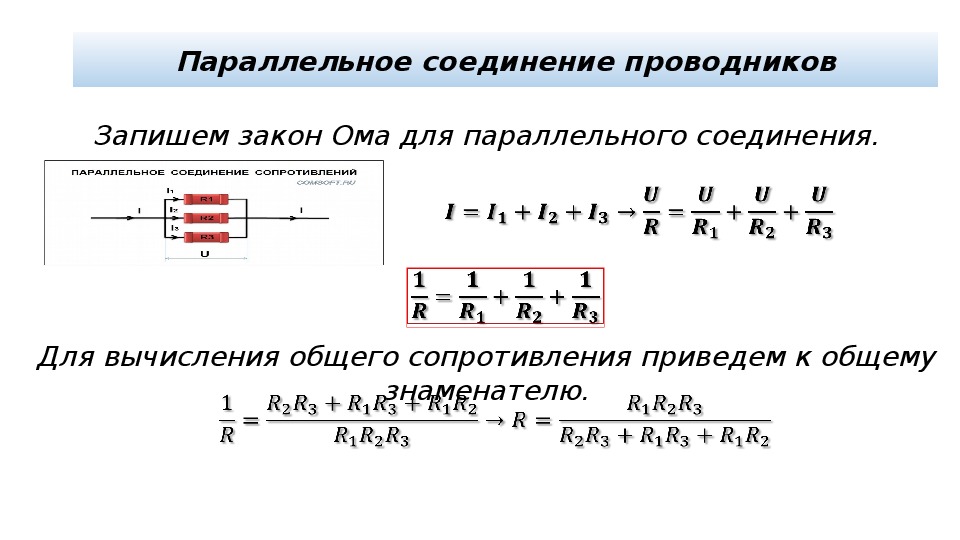

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.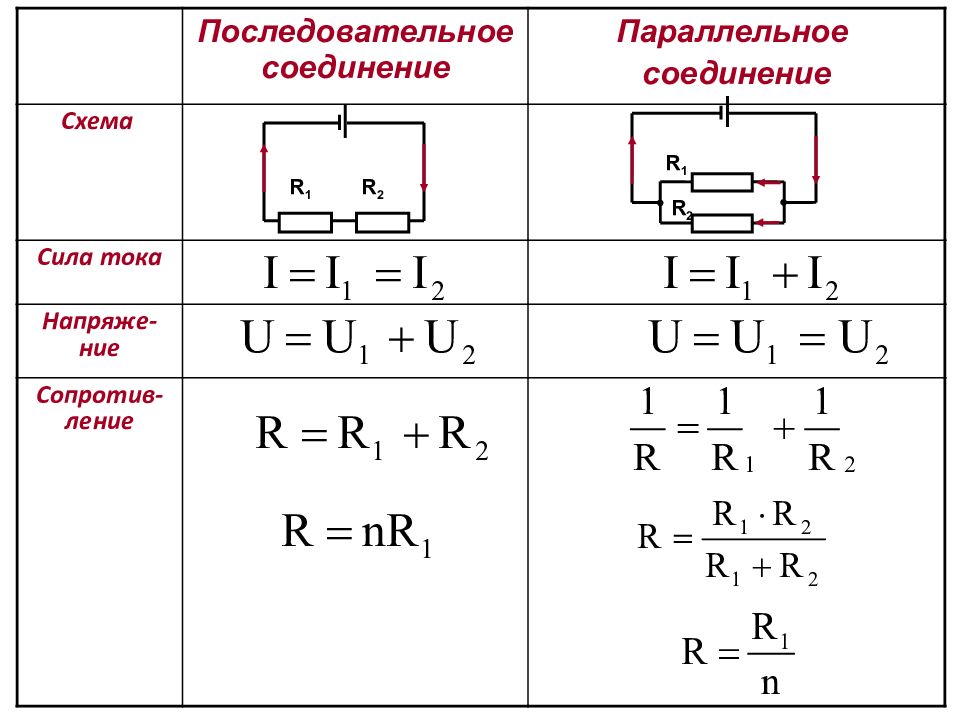

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт .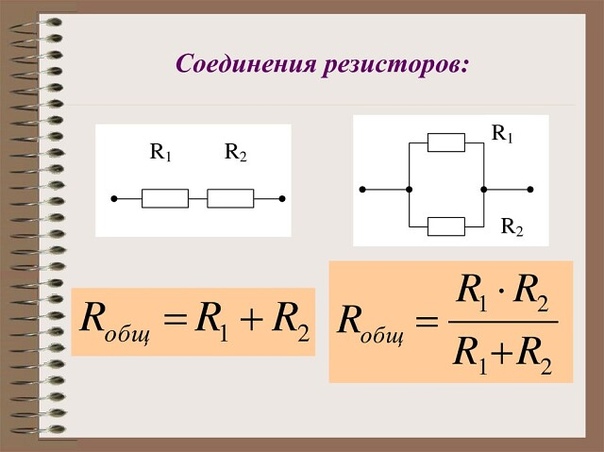 В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Темы кодификатора ЕГЭ : параллельное и последовательное соединение проводников, смешанное соединение проводников.

Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.

Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.

Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис.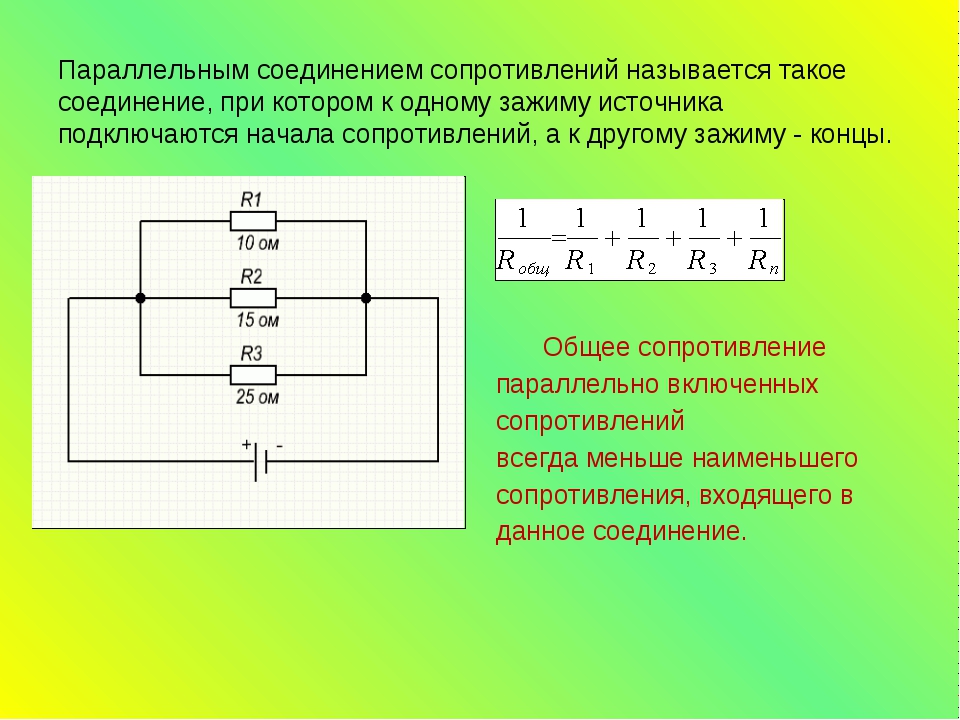 1 ):

Рис. 1. Резистор

Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.

Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.

Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2 ):

Рис. 2.

Стационарное поле совершает при этом положительную работу .

Так как alt=»q > 0″> и alt=»A > 0″> , то и alt=»\varphi_a — \varphi_b > 0″> , т. е. alt=»\varphi_a > \varphi_b»> .

Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .

Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3 ):

Рис. 3.

Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным . В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.

Последовательное соединение

При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.

Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4 ). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

Рис. 4. Последовательное соединение

Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.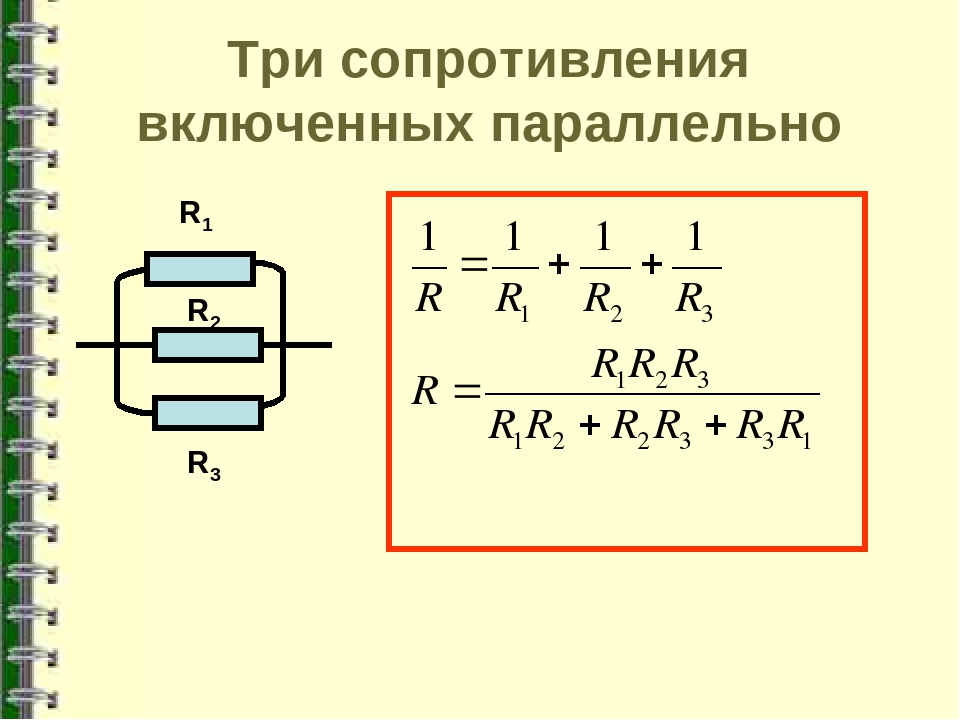

1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.

2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике .

Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:

Можно и более формально, без всяких словесных объяснений:

3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.

Пусть — сопротивление участка .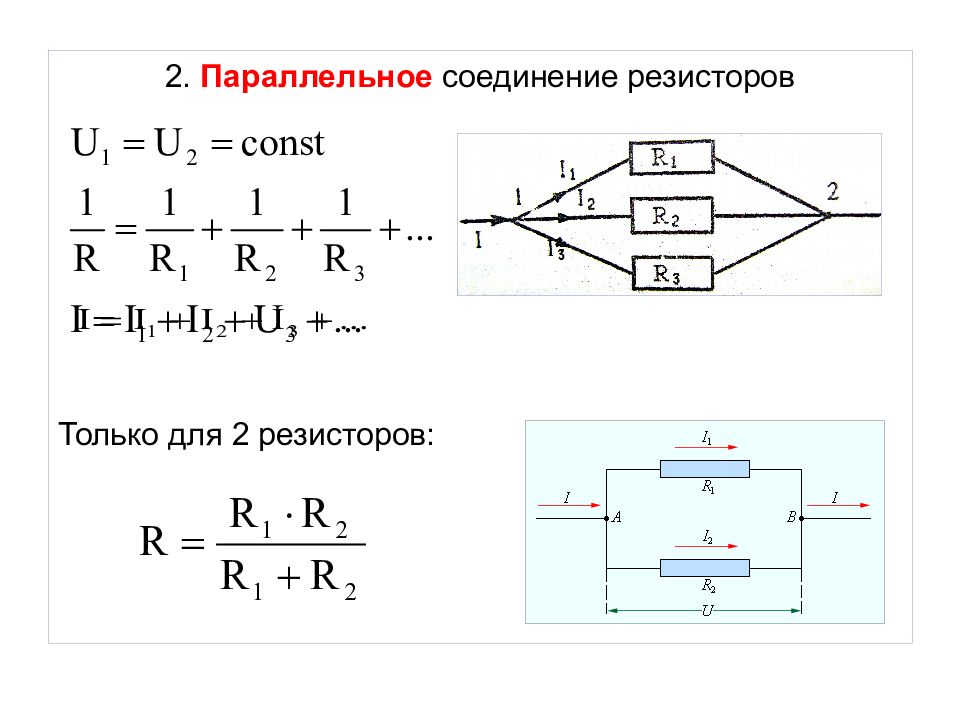 По закону Ома имеем:

что и требовалось.

Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .

Сопротивления проводников равны:

Эти два проводника образуют единый проводник длиной и сопротивлением

Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.

Параллельное соединение

При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.

Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5 ).

Рис. 5. Параллельное соединение

Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями ; участок от к (по направлению тока) называется неразветвлённой частью цепи.

Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.

1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:

Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.

2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .

Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:

что и требовалось.

3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:

Сокращая на , получим:

(1)

что и требовалось.

Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:

Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.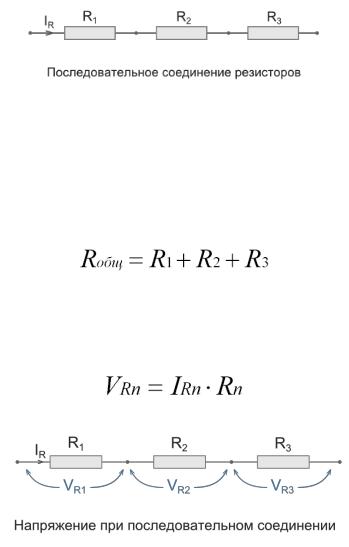

Из соотношения (1) можно найти :

(2)

К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением

(3)

Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:

Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.

Смешанное соединение

Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.

Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.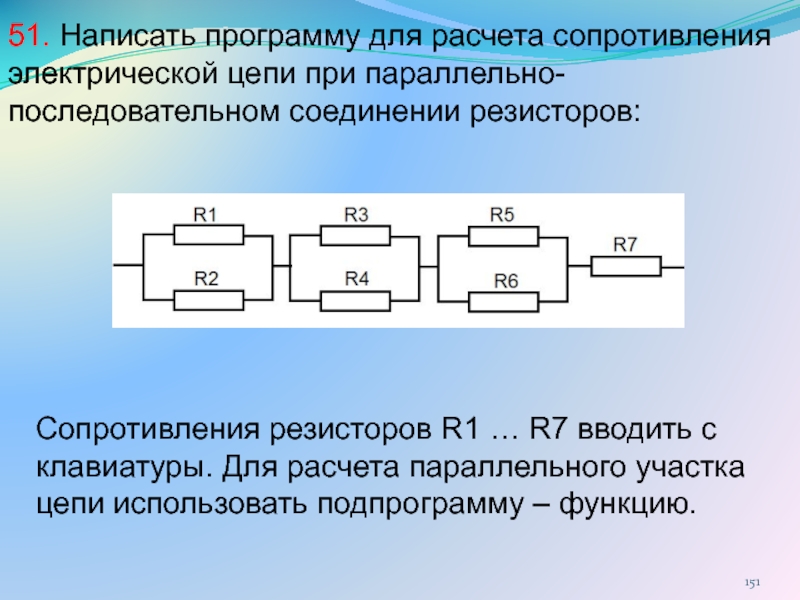

Рассмотрим пример смешанного соединения проводников (рис. 6 ).

Рис. 6. Смешанное соединение

Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.

Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :

Ом.

Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:

Ом.

Сопротивление цепи:

Ом.

Теперь находим силу тока в цепи:

Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:

(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)

Оба резистора и находятся под напряжением , поэтому:

(В сумме имеем А, как и должно быть при параллельном соединении.)

Сила тока в резисторах и одинакова, так как они соединены последовательно:

Стало быть, через резистор течёт ток A.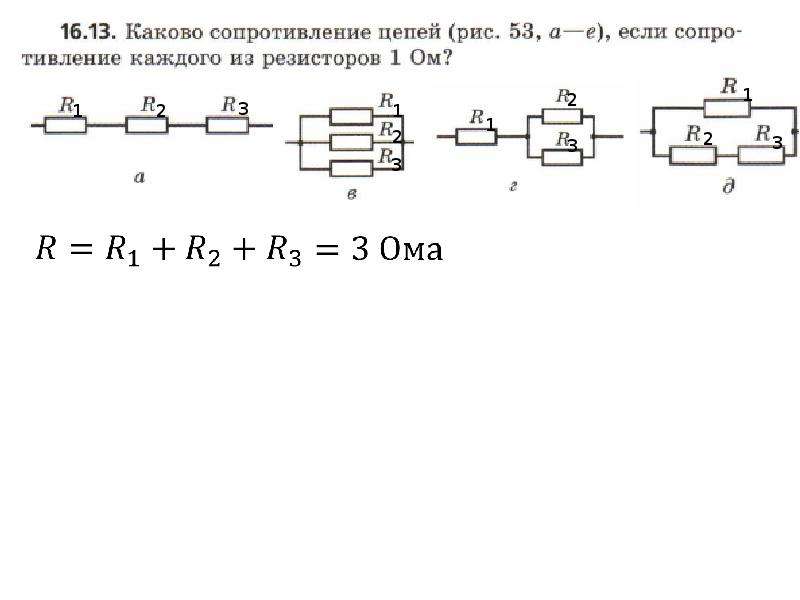

Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому

Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A 0).

Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам М и N напряжение U. Вольтметры показывают, что при последовательном соединении напряжение U равно сумме напряжений на отдельных участках цепи:

Применяя закон Ома для каждого участка цепи, получим:

где R — общее сопротивление последовательно соединенной цепи. Подставляя U, U 1 , U 2 в формулу (1), имеем

Сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме сопротивлений этих резисторов:

Если сопротивления отдельных резисторов равны между собой, т. е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .

При последовательном соединении резисторов справедливо соотношение

т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.

Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам М и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:

Амперметр показывает, что сила тока I в неразветвленной части цепи равна сумме сил токов I 1 и I 2 в параллельно соединенных проводниках R 1 и R 2:

Это вытекает и из закона сохранения электрического заряда. Применим закон Ома для отдельных участков цепи и всей цепи с общим сопротивлением R:

Подставляя I, I 1 и I 2 в формулу (2), получим.

Содержание:

Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.

Напряжение при последовательном соединении

При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке.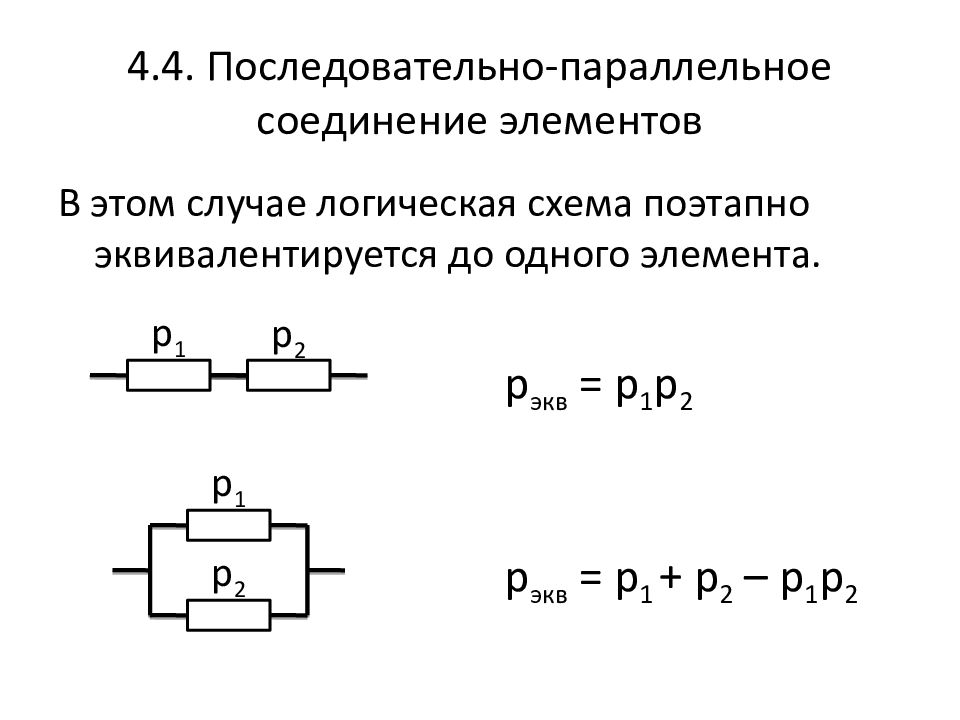 Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.

Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .

Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.

Напряжение при параллельном соединении

При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.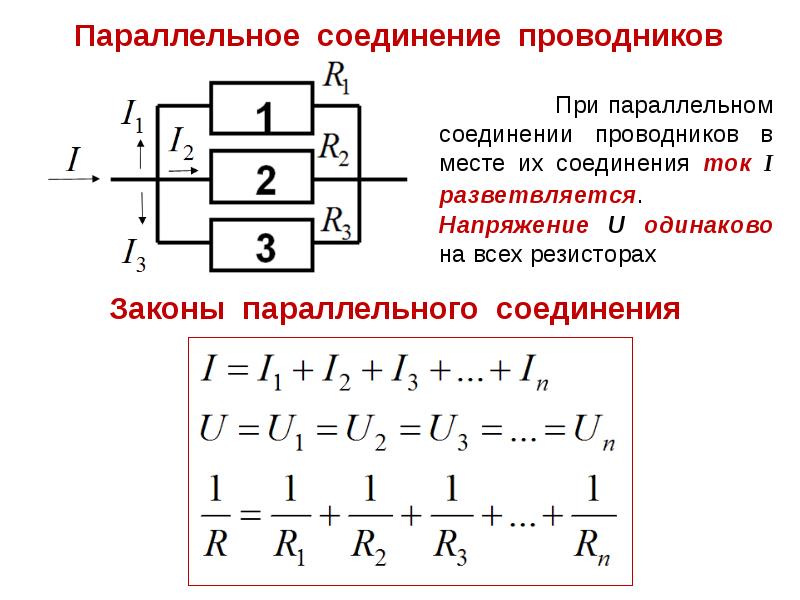

Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.

На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.

В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.

Параллельное и последовательное соединение резисторов (сопротивлений)

Все разнообразие схем построено на двух типах соединения — параллельном и последовательном. Для разных соединений действуют разные законы, что и дает возможность создания устройств с различными характеристиками. Рассмотрим последовательное и параллельное соединение резисторов.

Содержание статьи

Что такое резистор и для чего он нужен

Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.

Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.

Для чего нужны резисторы: для подстройки параметров питания

Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.

Так выглядят переменные и постоянные резисторы

Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.

Последовательное соединение сопротивлений

Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.

Лампы накаливания соединенные последовательно, можно рассматривать как сопротивления

Теоретическая часть

Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).

Последовательно соединенные сопротивления. I1 — ток протекающий через резистор R1, I2 — ток протекающий через резистор R2

Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов.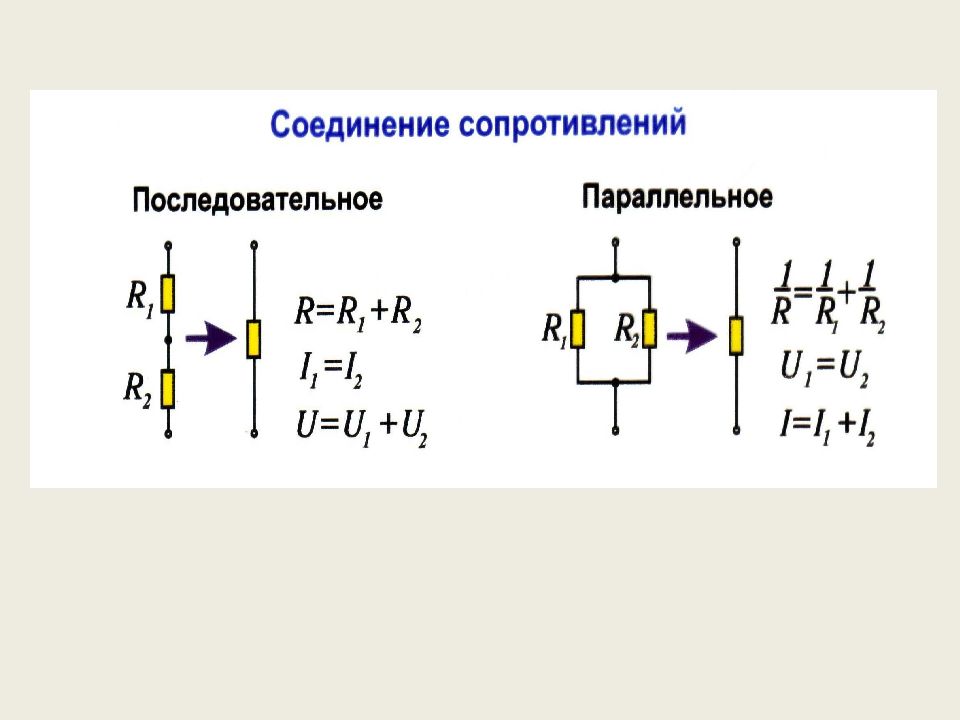 То есть, номиналы складывают.

R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.

Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.

Примеры расчета

Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:

• U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
• U2 = R2 * I = 800 Ом * 2А = 1600 В.

Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В.

Так понятнее, что такое последовательное соединение

Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток.    R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2  А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.

А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором  — 1600 В.  При этом напряжение источника питания — 4000 В.

Параллельное соединение резисторов

Параллельное соединение — это когда входы нескольких деталей соединяются в одной точке. Точно так же — в одну точку — соединяют их выходы.

Так выглядит параллельное соединение на схеме и в реальности

Теория и законы параллельного соединения

Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение. То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение.

U = U1 = U2 = U3.

Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

Так выглядит параллельное соединение резисторов на схеме

Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле:

1/R = 1/R1 + 1/R + 1/R3+…

Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.

Формулы расчета сопротивления при параллельном подключении двух и трех резисторов

Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала.

Примеры расчета параллельного соединения сопротивлений

Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

• Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
• Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.

Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Как высчитывать сопротивление составных резисторов

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше.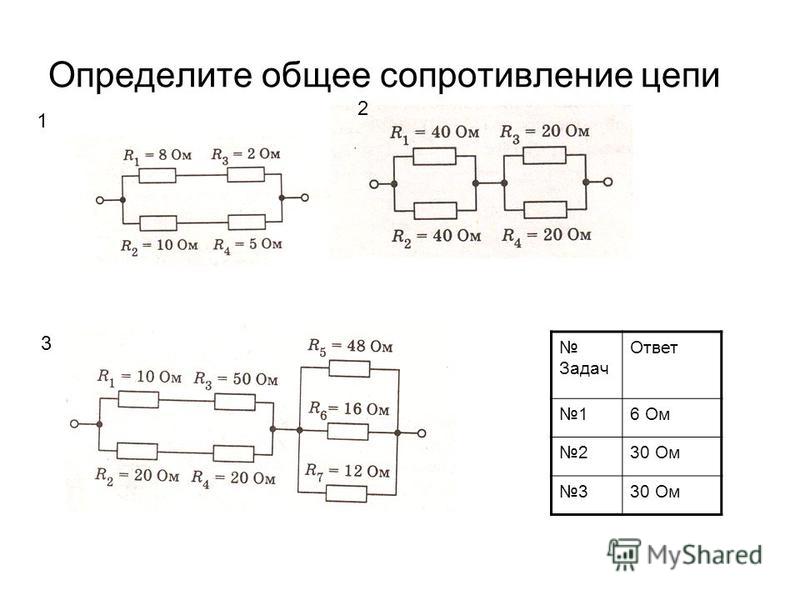 Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.

Еще один пример с лампочками

При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее. Но картина не отличается:

• Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом.
• Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом.

Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.

Смешанное соединение

Как быть, если в схеме есть и параллельное, и последовательное соединение резисторов? В таком случае считают общее сопротивление по участкам. Можно при этом перерисовывать схему, заменяя составные сопротивления на один «прямоугольник», но проставляя над ним высчитанный результат.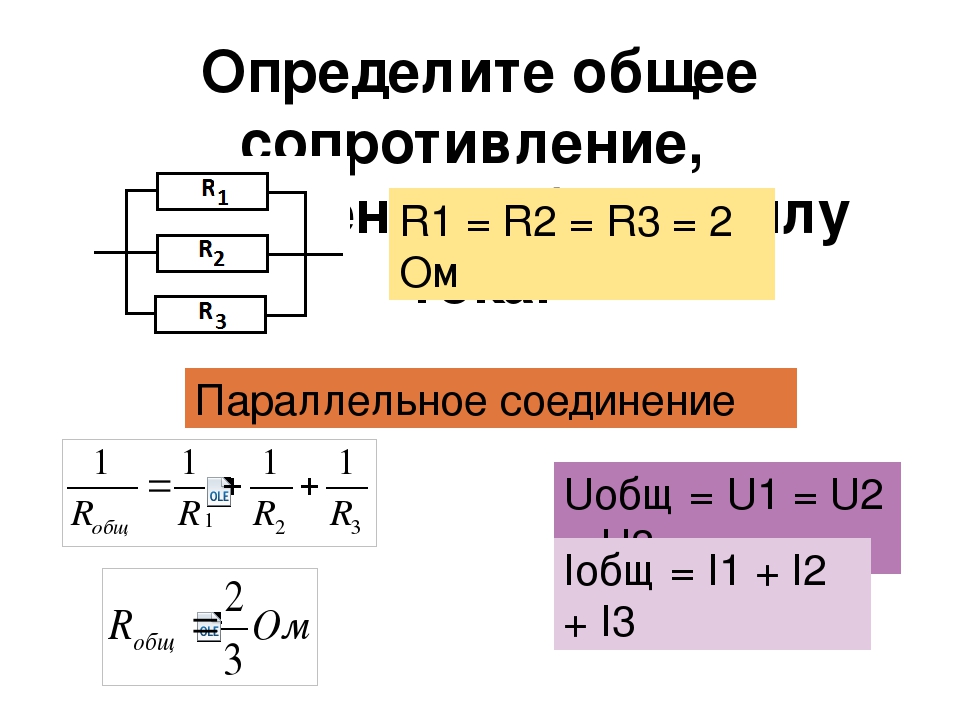

Пример расчета сопротивления при смешанном соединении резисторов. Рассматриваем исходную схему как совокупность параллельных и последовательных соединений

Шаг 1. Нашли общее сопротивление последовательно соединенных резисторов R3 и R4:

R3-4 = 3 кОм + 3 кОм = 6 кОм;

Шаг 2. Рассчитали сопротивление параллельно соединенных резисторов R2 и R3-4:

R2-4 = 3 кОм * 6 кОм / (3 кОм + 6 кОм) = 18 кОм/9 кОм = 2 кОм;

Шаг 3. Рассчитали общее сопротивление последовательно соединенных резисторов R1 и R2-4:

R1-4 = R1 + R2-4 = 1 кОм + 2 кОм = 3 кОм.

Практическое применение параллельного и последовательного соединения резисторов

Для чего практически можно использовать параллельное и последовательное соединение резисторов? Случается, что при ремонте электронной аппаратуры, не всегда в наличии сопротивление нужного номинала. Ехать в магазин за одним копеечным элементом — накладно. Вот тут и могут пригодиться составные резисторы. Просто надо последовательно или параллельно соединить их, подобрав требуемый номинал.

Последовательное и параллельное соединение резисторов применяют для подбора требуемого номинала. Контролировать точное значение получившегося сопротивления можно при помощи цифрового мультиметра

При соединении резисторов, их ножки первоначально скручивают. Какой стороной разворачивать сопротивление — неважно (в отличие от диодов, резисторы одинаково пропускают ток в обоих направлениях). На концах скрутку слегка обжимают плоскогубцами, затем пропаивают. Следите за тем, чтобы корпуса были друг от друга подальше — так они будут лучше охлаждаться при работе.

Последовательное и параллельное соединение. Применение и схемы

В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.

Последовательное соединение

При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого.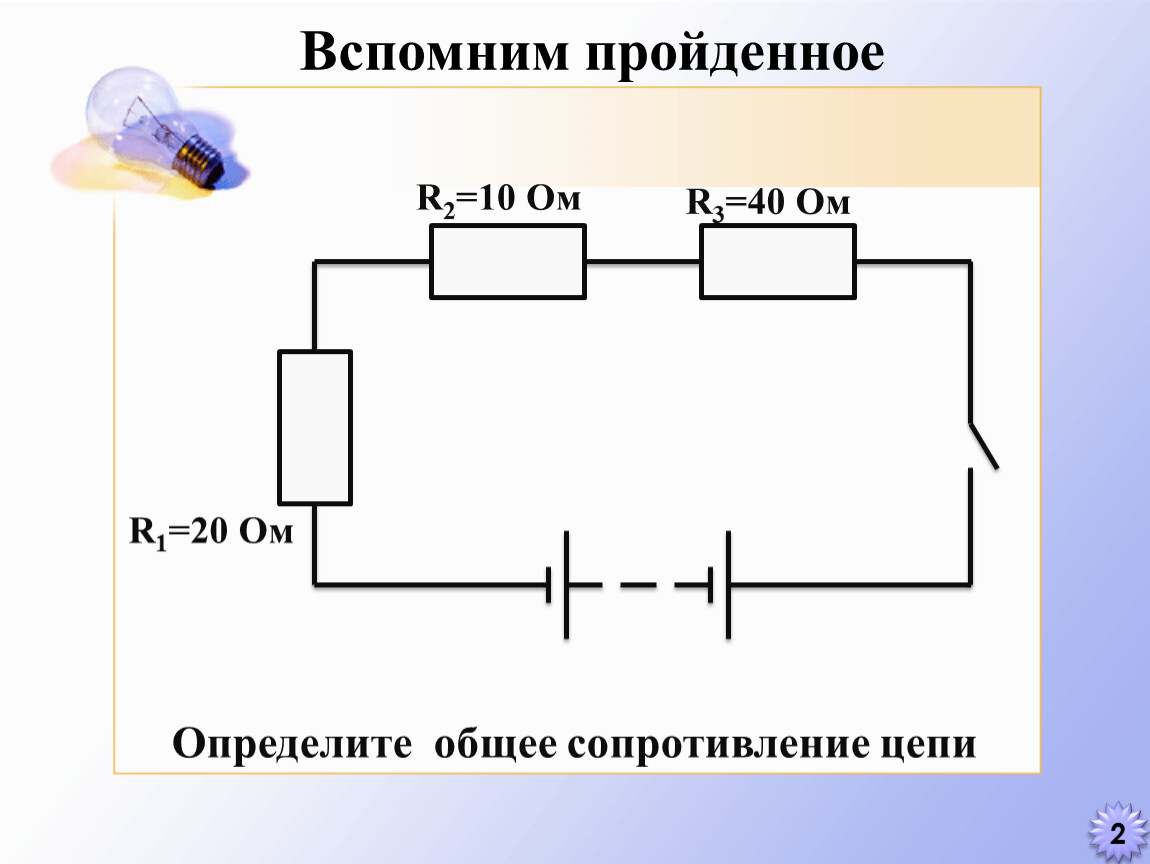 Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.

Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.

Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений.

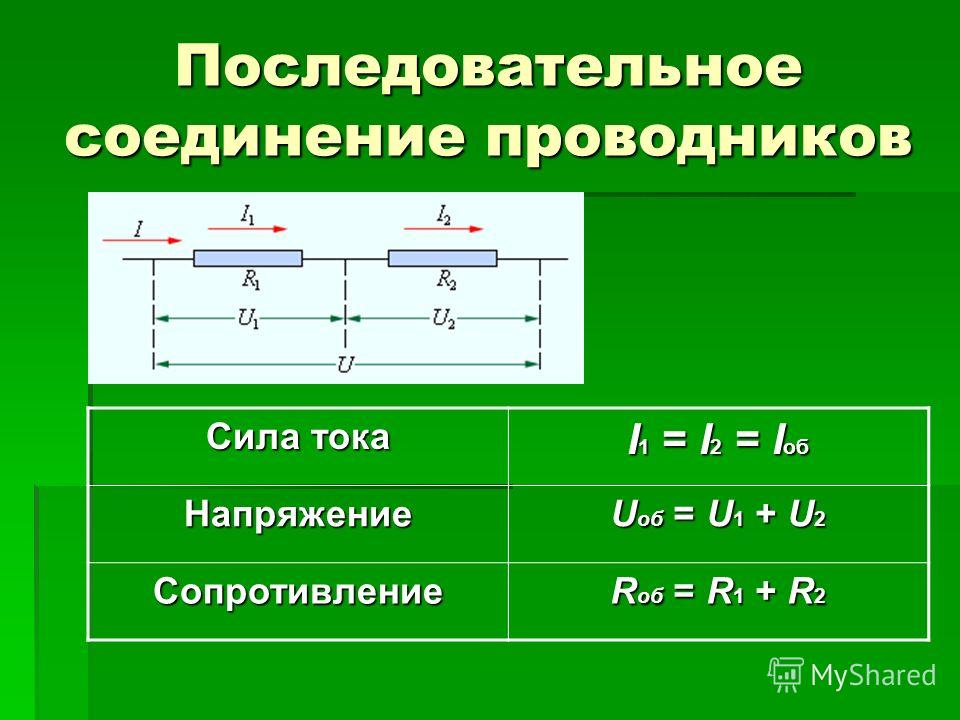Следствием первых двух правил будет являться третье правило.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.

Параллельное соединение

В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.

Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.

Применение

Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.

Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.

Работа тока

Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:

А = I х U х t, где А – работа тока, t – время течения по проводнику.

Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.

Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:

Р=Р1 + Р2

Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.

Влияние схемы соединения на новогоднюю гирлянду

После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:

С= q/(U1 + U2 + U3)

Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.

Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.

Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.

Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.

Теперь используем формулу расчета сопротивления:

• Первая формула для последовательного вида соединения.
• Далее, для параллельной схемы.
• И окончательно для последовательной схемы.

Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.

Похожие темы:

параллельных цепей — базовое электричество

Параллельная схема, вероятно, является наиболее распространенным типом схемы, с которой вы столкнетесь. Нагрузки в системах распределения электроэнергии в большинстве случаев так или иначе подключаются параллельно друг другу.

Построение параллельной цепи

Параллельная цепь создается путем соединения клемм всех отдельных устройств нагрузки так, чтобы на каждом компоненте появлялось одинаковое значение напряжения.

Рисунок 19.Параллельная схема

• Напряжение на каждой ветви одинаковое.
• Существует три отдельных пути (ответвления) для прохождения тока, каждый из которых покидает отрицательную клемму и возвращается к положительной клемме.

В отличие от последовательной цепи, ток все еще течет к остальным устройствам в цепи, если какая-либо одна ветвь или компонент в параллельной цепи разомкнута.

Три закона параллельной цепи

Существует три основных соотношения, касающихся напряжения, тока и сопротивления во всех параллельных цепях.

Напряжение

В параллельной цепи каждый нагрузочный резистор действует как независимая ответвленная цепь, и поэтому каждая ветвь «видит» все напряжение источника питания.

Полное напряжение параллельной цепи имеет то же значение, что и напряжение на каждой ветви.

Это соотношение может быть выражено как:

ET = E1 = E2 = E3…

Рисунок 20. Ток в параллельной цепи

В приведенной выше схеме напряжение в каждой ветви составляет 120 В.

Текущая

Параллельная цепь имеет более одного пути для прохождения тока. Количество путей тока определяется количеством резисторов нагрузки, подключенных параллельно.

Полный ток в параллельной цепи — это сумма токов отдельных ветвей.

Это соотношение в параллельной цепи выражается как:

IT = I1 + I2 + I3…

Чтобы вычислить общий ток, необходимо сначала определить токи отдельных ответвлений, используя закон Ома:

I1 = 120 В / 20 Ом = 6 А

I2 = 120 В / 40 Ом = 3 А

I3 = 120 В / 60 Ом = 2 А

IT = 6 A + 3 A + 2 A = 11 A

Сопротивление

Чем больше сопротивлений подключается параллельно, тем меньше общее сопротивление цепи.

Общее сопротивление параллельной цепи всегда меньше любого из отдельных значений сопротивления.

Общее сопротивление обычно определяется с помощью обратного уравнения:

1 / RT = 1 / R1 + 1 / R2 + 1 / R3…

Использование обратной кнопки калькулятора может упростить определение общего сопротивления.

параллельных резисторов

Обзор

Резисторы в цепи могут быть подключены последовательно или параллельно.Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.

Параллельные резисторы

Сопротивления параллельны, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.

Параллельные резисторы

Параллельное соединение резисторов.

Каждый резистор потребляет такой же ток, как если бы он был единственным резистором, подключенным к источнику напряжения.Это верно для схем в доме или квартире. Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.

Закон Ома и параллельные резисторы

Каждый резистор в цепи имеет полное напряжение. Согласно закону Ома токи, протекающие через отдельные резисторы, равны $ I_1 = \ frac {V} {R_1} $, $ I_2 = \ frac {V} {R_2} $ и $ I_3 = \ frac {V} {R_3 } $. Сохранение заряда подразумевает, что полный ток является суммой этих токов:

Резисторы параллельные

Три резистора, подключенных параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление.

$ I = I_1 + I_2 + I_3. $

Подстановка выражений для отдельных токов дает:

$ I = \ frac {V} {R_1} + \ frac {V} {R_2} + \ frac {V} {R_3} $

или

$ I = V (\ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3}) $

Это означает, что полное сопротивление в параллельной цепи равно сумме инверсии каждого отдельного сопротивления. Следовательно, для каждой цепи с числом $ n $ или параллельно подключенными резисторами

$ R_ {n \; (parallel)} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3}… + \ frac {1} {R_n}. $

Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений. Когда резисторы подключены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.

Каждый резистор, включенный параллельно, имеет одинаковое полное напряжение источника, приложенного к нему, но делит общий ток между ними. Примером может служить соединение двух лампочек в параллельную цепь с 1.Аккумулятор 5 В. В последовательной цепи две лампочки будут вдвое менее тусклыми при подключении к одному источнику батареи. Однако, если бы две лампочки были подключены параллельно, они были бы столь же яркими, как если бы они были подключены к батарее по отдельности. Поскольку к обеим лампочкам подается одинаковое полное напряжение, батарея также разряжается быстрее, поскольку она по существу обеспечивает полную энергию для обеих лампочек. В последовательной цепи батарея будет работать столько же, сколько и с одной лампочкой, только тогда яркость будет разделена между лампочками.

Серия

и параллельные схемы — learn.sparkfun.com

Добавлено в избранное Любимый 54 Серия

и параллельные схемы

Простые схемы (состоящие всего из нескольких компонентов) обычно довольно просты для понимания новичками. Но, когда на вечеринку приходят другие компоненты, все может запутаться. Куда идет ток? Что делает напряжение? Можно ли это упростить для облегчения понимания? Не бойся, бесстрашный читатель.Ценная информация приводится ниже.

В этом руководстве мы сначала обсудим разницу между последовательными и параллельными схемами, используя схемы, содержащие самые основные компоненты — резисторы и батареи, — чтобы показать разницу между двумя конфигурациями. Затем мы рассмотрим, что происходит в последовательных и параллельных цепях, когда вы комбинируете компоненты разных типов, например конденсаторы и катушки индуктивности.

рассматривается в этом учебном пособии

• Как выглядят конфигурации последовательной и параллельной цепей
• Как пассивные компоненты действуют в этих конфигурациях
• Как источник напряжения будет воздействовать на пассивные компоненты в этих конфигурациях

Рекомендуемая литература

Вы можете посетить эти учебные пособия по основным компонентам, прежде чем углубляться в построение схем в этом учебном пособии.

Видео

Цепи серии

Узлы и текущий поток

Прежде чем мы углубимся в это, мы должны упомянуть, что такое узел . Ничего особенного, просто представление электрического соединения между двумя или более компонентами. Когда схема моделируется на схеме, эти узлы представляют собой провода между компонентами.

Пример схемы с четырьмя узлами уникального цвета.

Это полдела на пути к пониманию разницы между последовательным и параллельным. Нам также нужно понять , как ток течет по цепи. Ток течет от высокого напряжения к более низкому напряжению в цепи. Некоторое количество тока будет проходить по каждому пути, который может пройти, чтобы добраться до точки с наименьшим напряжением (обычно называемой землей). Используя приведенную выше схему в качестве примера, вот как будет течь ток, когда он проходит от положительной клеммы аккумулятора к отрицательной:

Ток (обозначенный синей, оранжевой и розовой линиями), протекающий по той же схеме, что и выше.Разные токи обозначены разными цветами.

Обратите внимание, что в некоторых узлах (например, между R ₁ и R ₂ ) ток на входе такой же, как на выходе. В других узлах (в частности, трехходовой переход между R ₂ , R ₃ и R ₄ ) основной (синий) ток разделяется на два разных. Это ключевое различие между последовательным и параллельным подключением!

Определение цепей серии

Два компонента соединены последовательно, если они имеют общий узел и если через них протекает один и тот же ток .Вот пример схемы с тремя последовательными резисторами:

В указанной выше цепи есть только один способ протекания тока. Начиная с положительной клеммы аккумулятора, ток сначала встречает R ₁ . Оттуда ток будет течь прямо к R ₂ , затем к R ₃ и, наконец, обратно к отрицательной клемме батареи. Обратите внимание, что у текущего есть только один путь. Эти компоненты включены последовательно.

Параллельные схемы

Определение параллельных цепей

Если компоненты совместно используют два общих узла , они работают параллельно.Вот пример схемы трех резисторов, подключенных параллельно к батарее:

От положительной клеммы аккумуляторной батареи ток течет к R ₁ … и R ₂ , и R ₃ . Узел, который подключает аккумулятор к R ₁ , также подключен к другим резисторам. Другие концы этих резисторов аналогично связываются вместе, а затем снова подключаются к отрицательной клемме батареи. Существует три различных пути, по которым ток может пройти перед возвращением в батарею, и соответствующие резисторы считаются параллельными.

Если все последовательные компоненты имеют одинаковые токи, протекающие через них, все параллельные компоненты имеют одинаковое падение напряжения на них — series: current :: parallel: Voltage.

Совместная работа серии

и параллельных цепей

Оттуда мы можем смешивать и сочетать. На следующем снимке мы снова видим три резистора и батарею. С положительной клеммы аккумуляторной батареи ток сначала достигает R ₁ . Но на другой стороне R ₁ узел разделяется, и ток может идти как на R ₂ , так и на R ₃ .Затем пути тока через R ₂ и R ₃ снова связываются вместе, и ток возвращается к отрицательному выводу батареи.

В этом примере R ₂ и R ₃ параллельны друг другу, а R ₁ последовательно с параллельной комбинацией R ₂ и R ₃ .

Расчет эквивалентных сопротивлений в последовательных цепях

Вот некоторая информация, которая может оказаться для вас более полезной.Когда мы соединяем резисторы таким образом, последовательно и параллельно, мы меняем способ протекания тока через них. Например, если у нас есть питание 10 В через 10 кОм; резистора, закон Ома гласит, что у нас протекает ток 1 мА.

Если потом поставить еще 10к & ом; резистор, включенный последовательно с первым и оставив питание без изменений, мы сократили ток вдвое, потому что сопротивление увеличилось вдвое.

Другими словами, по-прежнему существует только один путь для прохождения тока, и мы только усложнили прохождение тока.Насколько сложнее? 10к & Ом; + 10к & Ом; = 20 кОм ;. Вот как мы рассчитываем последовательно подключенные резисторы — всего складываем их значения .

Если выразить это уравнение в более общем виде: полное сопротивление Н, — произвольное количество резисторов — это их общая сумма.

Расчет эквивалентных сопротивлений в параллельных цепях

А как насчет параллельных резисторов? Это немного сложнее, но ненамного.Рассмотрим последний пример, в котором мы начали с источника питания 10 В и 10 кОм; резистор, но на этот раз мы добавляем еще 10кОм; параллельно, а не последовательно. Теперь у тока есть два пути. Поскольку напряжение питания не изменилось, закон Ома гласит, что первый резистор по-прежнему будет потреблять 1 мА. Но то же самое и со вторым резистором, и теперь у нас есть в общей сложности 2 мА, поступающие от источника питания, что вдвое превышает первоначальный 1 мА. Это означает, что мы уменьшили общее сопротивление вдвое.

Пока можно сказать, что 10к & ом; || 10к & Ом; = 5 кОм; («||» примерно переводится как «параллельно»), у нас не всегда будет 2 одинаковых резистора.Что тогда?

Уравнение для добавления произвольного количества резисторов параллельно:

Если обратные значения вам не подходят, мы также можем использовать метод, называемый «произведение на сумму», когда у нас есть два резистора параллельно:

Однако этот метод подходит только для двух резисторов в одном вычислении. Мы можем объединить более 2 резисторов этим методом, взяв результат R1 || R2 и вычисление этого значения параллельно с третьим резистором (снова как произведение на сумму), но обратный метод может быть меньше работы.

Время эксперимента — Часть 1

Что вам понадобится:

Давайте проведем простой эксперимент, чтобы доказать, что все работает именно так, как мы говорим.

Во-первых, мы собираемся подключить 10 кОм; последовательно подключите резисторы и наблюдайте, как они складываются самым необычным образом. Используя макетную плату, поместите один 10 кОм; резистор, как показано на рисунке, и измерьте его мультиметром. Да, мы уже знаем, что будет указано, что оно составляет 10 кОм, но это то, что мы в бизнесе называем «проверкой работоспособности».Убедившись, что мир существенно не изменился с тех пор, как мы в последний раз смотрели на него, поместите еще один аналогично, но с выводами каждого резистора, электрически подключенными через макетную плату, и снова произведите измерения. Теперь измеритель должен показывать что-то близкое к 20 кОм.

Вы можете заметить, что сопротивление, которое вы измеряете, может быть не совсем таким, как резистор должен быть. Резисторы имеют определенное значение , допуск , что означает, что они могут быть отключены на определенный процент в любом направлении.Таким образом, вы можете прочитать 9.99k & ohm; или 10.01кОм. Пока оно близко к правильному значению, все должно работать нормально.

Читателю следует продолжать это упражнение до тех пор, пока он не убедится, что знает, что будет в результате, прежде чем делать это снова, или у него закончатся резисторы, которые можно вставить в макет, в зависимости от того, что наступит раньше.

Время эксперимента — Часть 2

Теперь давайте попробуем это с резисторами в конфигурации параллельно .Поместите один 10 кОм; резистор в макетной плате, как и раньше (мы полагаем, что читатель уже считает, что один резистор 10 кОм будет измерять на мультиметре что-то близкое к 10 кОм). Теперь поместите второй 10k & ohm; резистор рядом с первым, следя за тем, чтобы выводы каждого резистора находились в электрически соединенных рядах. Но перед тем, как измерить комбинацию, вычислите, используя метод «произведение над суммой» или обратный метод, каким должно быть новое значение (подсказка: оно будет 5 кОм;).Затем измерьте. Это что-то близкое к 5к & ом ;? Если это не так, дважды проверьте отверстия, в которые вставлены резисторы.

Повторите упражнение с резисторами 3, 4 и 5. Расчетные / измеренные значения должны быть 3,33 кОм, 2,5 кОм; и 2кОм соответственно. Все ли получилось по плану? Если нет, вернитесь и проверьте свои соединения. Если это так, EXCELSIOR! Прежде чем продолжить, выпейте молочный коктейль. Ты заслужил это.

Практические правила для последовательных и параллельных резисторов

Есть несколько ситуаций, которые могут потребовать творческих комбинаций резисторов.Например, если мы пытаемся установить очень конкретное опорное напряжение, вам почти всегда потребуется очень определенное соотношение резисторов, значения которых вряд ли будут «стандартными» значениями. И хотя мы можем получить очень высокую степень точности значений резисторов, мы, возможно, не захотим ждать X дней, необходимых для доставки чего-либо, или платить цену за нестандартные значения, отсутствующие на складе. Так что в крайнем случае мы всегда можем создать собственные номиналы резисторов.

Совет №1: Равнопараллельные резисторы

Добавление Н, резисторов с одинаковым номиналом R , включенных параллельно, дает нам R / N Ом.Допустим, нам нужен 2,5 кОм; резистор, но все, что у нас есть, это ящик, полный 10 кОм. Объединение четырех из них параллельно дает нам 10 кОм / 4 = 2,5 кОм.

Совет № 2: Допуск

Знайте, какую терпимость вы можете терпеть. Например, если вам нужен 3.2k & ohm; резистор, можно было поставить 3 10кОм; резисторы параллельно. Это даст вам 3,3 кОм, что составляет около 4% отклонения от необходимого значения. Но если схема, которую вы строите, должна иметь допуск ближе, чем 4%, мы можем измерить наш запас в 10 кОм, чтобы увидеть, какие из них являются самыми низкими значениями, потому что они также имеют допуск.По идее, если заначка 10к & ом; резисторы имеют допуск 1%, мы можем получить только 3,3 кОм. Но производители запчастей, как известно, допускают именно такого рода ошибки, поэтому стоит немного покопаться.

Совет № 3: Номинальная мощность при последовательном / параллельном подключении

Такая комбинация резисторов последовательно и параллельно работает и с номинальной мощностью. Допустим, нам нужен 100 & Ом; резистор рассчитан на 2 Вт (Вт), но все, что у нас есть, это связка 1 кОм; резисторы на четверть ватта (Вт) (а сейчас 3 часа ночи, вся Mountain Dew исчезла, а кофе остыл).Вы можете объединить 10 из 1 кОм, чтобы получить 100 Ом; (1 кОм / 10 = 100 Ом), а номинальная мощность будет 10×0,25 Вт или 2,5 Вт. Не очень красиво, но это поможет нам завершить финальный проект и даже может принести нам дополнительные баллы за способность думать на ногах.

Нам нужно быть немного более осторожными, когда мы объединяем резисторы разных номиналов параллельно, когда речь идет об общем эквивалентном сопротивлении и номинальной мощности. Для читателя это должно быть совершенно очевидно, но …

Совет № 4: Разные резисторы параллельно

Суммарное сопротивление двух резисторов разного номинала всегда меньше, чем резистор наименьшего номинала.Читатель будет поражен тем, сколько раз кто-то объединяет значения в своей голове и приходит к значению, которое находится посередине между двумя резисторами (1 кОм || 10 кОм; НЕ равняется чему-либо около 5 кОм ;!). Общее параллельное сопротивление всегда будет приближаться к резистору с наименьшим значением. Сделайте себе одолжение и прочитайте совет №4 10 раз.

Совет № 5: Параллельное рассеяние мощности

Мощность, рассеиваемая при параллельной комбинации резисторов разного номинала, не распределяется между резисторами равномерно, поскольку токи не равны.Используя предыдущий пример (1k & ohm; || 10k & ohm;), мы видим, что 1k & ohm; будет потреблять в 10 раз больше тока 10 кОм. Поскольку закон Ома гласит, что мощность = напряжение x ток, отсюда следует, что 1 кОм; резистор рассеивает в 10 раз мощность, превышающую 10 кОм.

В конечном счете, уроки советов 4 и 5 заключаются в том, что мы должны уделять больше внимания тому, что мы делаем при параллельном соединении резисторов разного номинала. Но советы 1 и 3 предлагают несколько удобных ярлыков, когда значения совпадают.

Конденсаторы серии

и параллельные

Объединение конденсаторов аналогично объединению резисторов … только наоборот. Как бы странно это ни звучало, это абсолютная правда. Почему это могло быть?

Конденсатор — это всего лишь две пластины, расположенные очень близко друг к другу, и его основная функция — удерживать целую группу электронов. Чем больше значение емкости, тем больше электронов она может удерживать. Если размер пластин увеличивается, емкость увеличивается, потому что физически больше места для электронов.А если пластины отодвинуть дальше друг от друга, емкость падает, потому что напряженность электрического поля между ними уменьшается с увеличением расстояния.

Теперь предположим, что у нас есть два конденсатора по 10 мкФ, соединенных последовательно, и предположим, что они оба заряжены и готовы к разряду в друга, сидящего рядом с вами.

Помните, что в последовательной цепи есть только один путь для прохождения тока. Отсюда следует, что количество электронов, выходящих из колпачка внизу, будет таким же, как и количество электронов, выходящих из колпачка наверху.Значит, емкость не увеличилась?

На самом деле все еще хуже. Разместив конденсаторы последовательно, мы эффективно раздвинули пластины дальше друг от друга, потому что расстояние между пластинами двух конденсаторов складывается. Так что у нас нет 20 мкФ или даже 10 мкФ. У нас 5 мкФ. Результатом этого является то, что мы добавляем значения последовательного конденсатора так же, как мы добавляем значения параллельного резистора. И метод «произведение над суммой», и метод взаимности действительны для последовательного добавления конденсаторов.

Может показаться, что нет смысла добавлять конденсаторы последовательно. Но следует отметить, что мы получили вдвое большее напряжение (или номинальное напряжение). Как и в случае с батареями, когда мы соединяем конденсаторы последовательно, напряжения складываются.

Добавление конденсаторов параллельно похоже на последовательное добавление резисторов: значения просто складываются, никаких уловок. Почему это? Их параллельное расположение эффективно увеличивает размер пластин без увеличения расстояния между ними.Чем больше площадь, тем больше емкость. Простой.

Время эксперимента — Часть 3

Что вам понадобится:

Давайте посмотрим, как работают конденсаторы, соединенные последовательно и параллельно. Это будет немного сложнее, чем примеры резисторов, потому что измерить емкость напрямую мультиметром труднее.

Давайте сначала поговорим о том, что происходит, когда конденсатор заряжается с нуля вольт. Когда ток начинает идти в один из выводов, равное количество тока выходит из другого.А если последовательно с конденсатором нет сопротивления, может быть довольно большой ток. В любом случае ток течет до тех пор, пока конденсатор не начнет заряжаться до значения приложенного напряжения, и медленнее будет стекать до тех пор, пока напряжения не станут равными, когда ток полностью прекратится.

Как указано выше, потребляемый ток может быть довольно большим, если нет сопротивления последовательно с конденсатором, а время зарядки может быть очень коротким (например, миллисекунды или меньше). Для этого эксперимента мы хотим иметь возможность наблюдать за зарядом конденсатора, поэтому мы собираемся использовать 10 кОм; резистор, включенный последовательно, чтобы замедлить действие до точки, где мы его легко увидим.Но сначала нам нужно поговорить о том, что такое постоянная времени RC.

В приведенном выше уравнении говорится, что одна постоянная времени в секундах (называемая тау) равна сопротивлению в омах, умноженному на емкость в фарадах. Простой? Нет? Продемонстрируем на следующей странице.

Время эксперимента — часть 3, продолжение …

В первой части этого эксперимента мы будем использовать один резистор 10 кОм и один резистор 100 мкФ (что равно 0,0001 фарад). Эти две части создают постоянную времени в 1 секунду:

При зарядке нашего конденсатора 100 мкФ через 10 кОм; резистора, мы можем ожидать, что напряжение на цоколе вырастет примерно до 63% от напряжения питания за 1 постоянную времени, которая составляет 1 секунду.После 5 постоянных времени (в данном случае 5 секунд) конденсатор заряжается примерно на 99% до напряжения питания, и он будет следовать кривой заряда, похожей на график ниже.

Теперь, когда мы это знаем, мы собираемся подключить схему, показанную на схеме (убедитесь, что полярность на этом конденсаторе правильная!).

С помощью нашего мультиметра, установленного для измерения вольт, проверьте выходное напряжение батареи при включенном переключателе. Это наше напряжение питания, и оно должно быть около 4.5В (будет немного больше, если батарейки новые). Теперь подключите схему, убедившись, что переключатель на батарейном блоке находится в положении «ВЫКЛ», прежде чем вставлять его в макетную плату. Также позаботьтесь о том, чтобы красный и черный провода были в нужных местах. Если это более удобно, вы можете использовать зажимы типа «крокодил», чтобы прикрепить измерительные щупы к ножкам конденсатора для измерения (вы также можете немного раздвинуть эти ножки, чтобы упростить задачу).

Когда мы убедимся, что схема выглядит правильно, а наш счетчик включен и настроен на считывание вольт, переведите переключатель на батарейном блоке в положение «ВКЛ».Примерно через 5 секунд показания счетчика должны быть довольно близкими к напряжению аккумуляторной батареи, что демонстрирует, что уравнение верное, и мы знаем, что делаем. Теперь выключите выключатель. Он все еще довольно хорошо держит это напряжение, не так ли? Это потому, что ток не может разрядить конденсатор; у нас разомкнутая цепь. Для разряда конденсатора можно использовать еще один резистор на 10 кОм параллельно. Примерно через 5 секунд он вернется к почти нулевому значению.

Experiment Time — Часть 3, и даже больше…

Теперь мы переходим к интересным моментам, начиная с последовательного соединения двух конденсаторов. Помните, что мы сказали, что результат будет аналогичен параллельному соединению двух резисторов. Если это правда, мы можем ожидать (используя произведение над суммой)

Что это будет делать с нашей постоянной времени?

Имея это в виду, подключите другой конденсатор последовательно с первым, убедитесь, что измеритель показывает ноль вольт (или около того), и переведите переключатель в положение «ON».Зарядка до напряжения аккумуляторной батареи занимала примерно половину времени? Это потому, что емкость вдвое меньше. Электронный бензобак стал меньше, поэтому на его зарядку уходит меньше времени. Для этого эксперимента предлагается третий конденсатор, просто чтобы доказать это, но мы держим пари, что читатель сможет увидеть надпись на стене.

Теперь мы попробуем подключить конденсаторы параллельно, помня, что мы говорили ранее, что это будет похоже на последовательное добавление резисторов. Если это правда, то мы можем ожидать 200 мкФ, верно? Тогда наша постоянная времени станет

.

Это означает, что теперь потребуется около 10 секунд, чтобы увидеть, как параллельные конденсаторы заряжаются до напряжения питания 4.5В.

Для доказательства начнем с нашей исходной схемы из одного 10 кОм; последовательно подключены резистор и один конденсатор емкостью 100 мкФ, как показано на первой схеме этого эксперимента. Мы уже знаем, что конденсатор заряжается примерно за 5 секунд. Теперь подключите второй конденсатор параллельно. Убедитесь, что показания измерителя близки к нулю (разрядите через резистор, если он не показывает нулевое значение), и переведите переключатель на батарейном блоке в положение «ON». Нужно много времени, не правда ли? Разумеется, мы увеличили размер электронного бензобака, и теперь на его заполнение уходит больше времени.Чтобы убедиться в этом, попробуйте добавить третий конденсатор емкостью 100 мкФ и понаблюдайте, как он заряжается в течение долгого времени.

Катушки индуктивности серии

и параллельные

Катушки индуктивности серии

и параллельные

Случаи, когда индукторы необходимо добавлять последовательно или параллельно, довольно редки, но не редкость. В любом случае, давайте рассмотрим их, чтобы быть полными.

Вкратце, они складываются так же, как и резисторы, то есть они складываются со знаком плюс, когда соединены последовательно, и с превышением произведения при параллельном соединении.Сложность возникает, когда они размещаются близко друг к другу, чтобы иметь взаимодействующие магнитные поля, намеренно или нет. По этой причине предпочтительнее иметь один компонент, чем два или более, хотя большинство индукторов экранированы для предотвращения взаимодействия магнитных полей.

В любом случае достаточно сказать, что они добавляют, как резисторы. Дополнительная информация о катушках индуктивности выходит далеко за рамки этого руководства.

ресурсов и дальнейшее развитие

Теперь, когда вы знакомы с основами последовательных и параллельных цепей, почему бы не ознакомиться с некоторыми из этих руководств?

• Делители напряжения — Одна из самых простых и повторяющихся схем — это делитель напряжения.Это схема, которая действительно основана на концепциях, рассмотренных в этом руководстве.
• Что такое Ардуино? — Теперь, когда у вас есть основы схемотехники, вы можете перейти непосредственно к изучению микроконтроллеров с одной из самых популярных платформ: Arduino.
Основы работы с коммутатором
• — В этом руководстве мы говорили о некоторых наиболее основных элементах схемы, но это не был один из них. Переключатели являются важным компонентом практически в каждом электронном проекте.Узнайте все о переключателях в этом руководстве
• Шитье проводящей нитью — схемы не обязательно должны состоять из макетов и проводов. Электронный текстиль использует токопроводящую нить для вшивания светильников и другой электроники в одежду или другую ткань.

Резисторы

в схемах — Практика — Физический гипертекст

Давайте начнем процесс с комбинирования резисторов. В этой схеме четыре последовательных пары.

слева

R s = 3 Ом + 1 Ом R s = 4 Ом R s = 4 Ом + 2 Ом R s = 6 Ом

правый

R s = 2 Ом + 3 Ом R s = 5 Ом R s = 1 Ом + 4 Ом R s = 5 Ом

Эти пары образуют две параллельные цепи, одну слева и одну справа.

слева

1 = 1 + 1 R p 4 Ом 6 Ом

R p = 12 Ом = 2.4 Ом 5

правый

1 = 1 + 1 R p 5 Ом 5 Ом

R p = 5 Ом = 2.5 Ом 2

Каждый набор из четырех резисторов включен последовательно с другим.

слева

R с = 2,4 Ом + 0,6 Ом R с = 3 Ом

правый

R с = 2,5 Ом + 0,5 Ом R с = 3 Ом

Левая и правая половины цепи параллельны друг другу и батарее.

1 = 1 + 1 = 2 R p 3 Ом 3 Ом 3 Ом

R p = 3 Ом = 1.5 Ом 2

Теперь, когда у нас есть эффективное сопротивление всей цепи, давайте определим ток от источника питания, используя закон Ома.

I итого =	V всего	+	24 В	= 16 А
	R итого		1.5 Ом

Теперь пройдите по цепи (не буквально, конечно). На каждом соединении ток будет делиться: больше по пути с меньшим сопротивлением и меньше по пути с большим сопротивлением. Поскольку заряд не протекает нигде в полной цепи, ток будет одинаковым для всех элементов, последовательно соединенных друг с другом.

Левая и правая половины схемы идентичны по общему сопротивлению, что означает, что ток будет равномерно делиться между ними.

8 A для резистора 0,6 Ом на левом .

8 A для резистора 0,5 Ом на правой стороне .

С каждой стороны ток снова делится на две параллельные ветви.

Ветви на слева имеют сопротивления в соотношении…

R 1 и 3 = 4 Ом + 2 R 2 и 4 6 Ом 3

что означает, что токи разделятся в соотношении…

для резисторов 1 Ом и 3 Ом на слева .

для резисторов 2 Ом и 4 Ом на слева .

Ветви на правом идентичны, поэтому ток разделяется на две равные половины.

☟

☟

☟

☟

☟

для резисторов 2 Ом и 3 Ом на правой стороне .

для резисторов 1 Ом и 4 Ом на правой стороне .

Комбинированные последовательные / параллельные схемы — Устранение неисправностей двигателей и органов управления

Кен Диксон-Селф

В простых последовательных цепях все компоненты соединены встык, образуя только один путь для прохождения электронов по цепи:

В простых параллельных цепях все компоненты подключаются между одними и теми же двумя наборами электрически общих точек, создавая несколько путей для прохождения электронов от одного конца батареи к другому:

Для каждой из этих двух базовых конфигураций схемы у нас есть определенные наборы правил, описывающих отношения напряжения, тока и сопротивления.

• Цепи серии :
• Падения напряжения прибавляются к общему напряжению.
• Все компоненты имеют одинаковый (равный) ток.
• Сопротивления добавляют к равному общему сопротивлению.

• Параллельные цепи:
• Все компоненты имеют одинаковое (равное) напряжение.
• Токи ответвления добавляются к равному общему току.
• Сопротивления уменьшаются до полного сопротивления.

Однако, если компоненты схемы соединены последовательно в одних частях и параллельно в других, мы не сможем применить единый набор правил для каждой части этой цепи.Вместо этого нам придется определить, какие части этой цепи являются последовательными, а какие — параллельными, а затем выборочно применять правила последовательного и параллельного подключения, если это необходимо, чтобы определить, что происходит. Возьмем, к примеру, следующую схему:

Эта схема не является ни простой последовательной, ни простой параллельной. Скорее, он содержит элементы обоих. Ток выходит из нижней части батареи, разделяется, чтобы пройти через R ₃ и R ₄ , снова присоединяется, затем снова разделяется, чтобы пройти через R ₁ и R ₂ , затем снова присоединяется, чтобы вернуться к верх аккумуляторной батареи.Существует более одного пути для прохождения тока (не последовательно), но в цепи более двух наборов электрически общих точек (не параллельных).

Поскольку схема представляет собой комбинацию как последовательной, так и параллельной, мы не можем применять правила для напряжения, тока и сопротивления «поперек стола», чтобы начать анализ, как мы могли бы, когда цепи были в том или ином положении. Например, если бы вышеуказанная схема была простой последовательной, мы могли бы просто сложить R ₁ через R ₄ , чтобы получить общее сопротивление, вычислить общий ток, а затем вычислить все падения напряжения.Аналогичным образом, если бы вышеуказанная схема была простой параллельной, мы могли бы просто решить для токов ответвления, сложить токи ответвления, чтобы вычислить общий ток, а затем вычислить общее сопротивление из общего напряжения и общего тока. Однако решение этой схемы будет более сложным.

Таблица по-прежнему поможет нам управлять различными значениями для последовательно-параллельных комбинированных цепей, но мы должны быть осторожны, как и где применять разные правила для последовательного и параллельного подключения. Закон Ома, конечно, по-прежнему работает точно так же для определения значений в вертикальном столбце таблицы.

Если мы можем определить, какие части схемы являются последовательными, а какие — параллельными, мы можем анализировать это поэтапно, подходя к каждой части по очереди, используя соответствующие правила для определения отношений напряжения, тока и сопротивления. . Остальная часть этой главы будет посвящена демонстрации техник для этого.

Процесс анализа последовательно-параллельной цепи резисторов

Целью анализа последовательно-параллельной цепи резисторов является определение всех падений напряжения, токов и рассеиваемой мощности в цепи.Общая стратегия достижения этой цели следующая:

• Шаг 1. Определите, какие резисторы в цепи соединены вместе простым последовательным или простым параллельным соединением.
• Шаг 2: Изобразите схему заново, заменив каждую из комбинаций последовательных или параллельных резисторов, определенных на шаге 1, одним резистором эквивалентного номинала. При использовании таблицы для управления переменными создайте новый столбец таблицы для каждого эквивалента сопротивления.
• Шаг 3: Повторяйте шаги 1 и 2, пока вся схема не будет уменьшена до одного эквивалентного резистора.
• Шаг 4: Рассчитайте общий ток из общего напряжения и общего сопротивления (I = E / R).
• Шаг 5: Взяв значения общего напряжения и полного тока, вернитесь к последнему шагу в процессе сокращения цепи и вставьте эти значения, где это возможно.
• Шаг 6: Из известных значений сопротивления и значений полного напряжения / полного тока из шага 5 используйте закон Ома для вычисления неизвестных значений (напряжения или тока) (E = IR или I = E / R).
• Шаг 7: Повторяйте шаги 5 и 6, пока все значения напряжения и тока не будут известны в исходной конфигурации схемы.По сути, вы будете шаг за шагом переходить от упрощенной версии схемы к ее исходной сложной форме, вводя значения напряжения и тока там, где это необходимо, до тех пор, пока не будут известны все значения напряжения и тока.
• Шаг 8: Рассчитайте рассеиваемую мощность на основе известных значений напряжения, тока и / или сопротивления.

Это может показаться пугающим процессом, но его гораздо легче понять на примере, чем через описание.

В приведенном выше примере схемы R ₁ и R ₂ соединены простым параллельным расположением, как и R ₃ и R ₄ .После идентификации эти секции необходимо преобразовать в эквивалентные одиночные резисторы и заново нарисовать схему:

Символы двойной косой черты (//) обозначают «параллельность», чтобы показать, что эквивалентные значения резисторов были рассчитаны по формуле 1 / (1 / R). Резистор 71,429 Ом в верхней части схемы эквивалентен R ₁ и R ₂ , включенным параллельно друг другу. Резистор 127,27 Ом внизу эквивалентен R ₃ и R ₄ , включенным параллельно друг другу.

Наша таблица может быть расширена, чтобы включить эти эквиваленты резисторов в отдельные столбцы:

Теперь должно быть очевидно, что схема была уменьшена до простой последовательной конфигурации только с двумя (эквивалентными) сопротивлениями. Последний шаг в уменьшении — сложить эти два сопротивления, чтобы получить общее сопротивление цепи. Когда мы складываем эти два эквивалентных сопротивления, мы получаем сопротивление 198,70 Ом. Теперь мы можем перерисовать схему как единое эквивалентное сопротивление и добавить значение общего сопротивления в крайний правый столбец нашей таблицы.Обратите внимание, что столбец «Итого» был переименован (R ₁ // R ₂ —R ₃ // R ₄ ), чтобы указать, как он электрически связан с другими столбцами цифр. Символ «-» здесь используется для обозначения «серии», так же как символ «//» используется для обозначения «параллельности».

Теперь общий ток цепи можно определить, применив закон Ома (I = E / R) к столбцу «Всего» в таблице:

Вернемся к нашему рисунку эквивалентной схемы, наше общее текущее значение 120.Здесь показан только ток 78 миллиампер:

Теперь мы начинаем работать в обратном направлении в нашей прогрессии переделки схем до исходной конфигурации. Следующий шаг — перейти к схеме, в которой последовательно соединены R ₁ // R ₂ и R ₃ // R ₄ :

Поскольку R ₁ // R ₂ и R ₃ // R ₄ включены последовательно друг с другом, ток через эти два набора эквивалентных сопротивлений должен быть одинаковым.Кроме того, ток через них должен быть таким же, как и полный ток, поэтому мы можем заполнить нашу таблицу соответствующими значениями тока, просто скопировав текущую цифру из столбца Total в R ₁ // R ₂ и R ₃ // R ₄ столбцов:

Теперь, зная ток через эквивалентные резисторы R ₁ // R ₂ и R ₃ // R ₄ , мы можем применить закон Ома (E = IR) к двум правым вертикальным столбцам, чтобы найти падение напряжения на них:

Поскольку мы знаем, что R ₁ // R ₂ и R ₃ // R ₄ являются эквивалентами параллельных резисторов, и мы знаем, что падения напряжения в параллельных цепях одинаковы, мы можем передавать соответствующие падения напряжения в соответствующие столбцы таблицы для этих отдельных резисторов.Другими словами, мы делаем еще один шаг назад в нашей последовательности рисования к исходной конфигурации и заполняем таблицу соответствующим образом:

Наконец, исходный раздел таблицы (столбцы с R ₁ по R ₄ ) заполнен достаточным количеством значений для завершения. Применяя закон Ома к остальным вертикальным столбцам (I = E / R), мы можем определить токи через R ₁ , R ₂ , R ₃ и R ₄ по отдельности:

Размещение значений напряжения и тока на диаграммах

Найдя все значения напряжения и тока для этой цепи, мы можем показать эти значения на принципиальной схеме как таковые:

В качестве последней проверки нашей работы мы можем увидеть, складываются ли рассчитанные текущие значения должным образом в общую сумму.Поскольку R ₁ и R ₂ подключены параллельно, их комбинированные токи в сумме должны составить 120,78 мА. Аналогичным образом, поскольку R ₃ и R ₄ подключены параллельно, их комбинированные токи в сумме также должны составлять 120,78 мА. Вы можете проверить сами, чтобы убедиться, что эти цифры складываются так, как ожидалось.

Эта глава является адаптацией книги Lessons in Electric Circuits Тони Р. Купхальда (на allaboutcircuits.com) и используется по лицензии Design Science License.

Параллельные резисторы | Электрические цепи

17,5 Резисторы параллельные (ЭСАФК)

Когда мы добавляем резисторы параллельно цепи:

• Есть больше путей для прохождения тока, что обеспечивает разделение тока по различным путям .

• Напряжение на резисторах то же . Напряжение на батарее в цепи равно напряжению на каждом из параллельных резисторов:

  \ [{V} _ {\ text {battery}} = {V} _ {1} = {V} _ {2} = {V} _ {3} \ ldots \]

• Сопротивление току уменьшается .Общее сопротивление \ ({R} _ {P} \) дается выражением:

  \ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]

При параллельном подключении резисторов начальная и конечная точки для всех резисторов одинаковы. Эти точки имеют одинаковую потенциальную энергию, поэтому разность потенциалов между ними одинакова, независимо от того, что между ними вставлено. Между двумя точками может быть один, два или несколько резисторов, разность потенциалов не изменится.Вы можете игнорировать любые компоненты, находящиеся между двумя точками в цепи, при вычислении разницы между двумя точками.

Посмотрите на следующие принципиальные схемы. Батарея во всех случаях одна и та же, меняется только добавление резисторов между точками, отмеченными черными точками. Если бы мы измерили разность потенциалов между двумя точками в этих схемах, мы бы получили одинаковый ответ для всех трех случаев.

Давайте посмотрим на два параллельно подключенных резистора более внимательно.Когда вы создаете схему, вы используете провода, и вы можете подумать, что измерение напряжения в разных местах на проводах будет иметь значение. Это неправда. Измерение разности потенциалов или напряжения будет отличаться только в том случае, если вы измеряете другой набор компонентов. Все точки на проводах, между которыми нет компонентов схемы, дадут вам одинаковые измерения.

Все три измерения, показанные на рисунке ниже (т. Е. A – B, C – D и E – F), дадут вам одинаковое напряжение.Различные точки измерения слева не имеют компонентов между собой, поэтому нет изменений в потенциальной энергии. То же самое относится и к разным точкам справа. Когда вы измеряете разность потенциалов между точками слева и справа, вы получите одинаковый ответ.

Рабочий пример 7: Напряжения I

Рассмотрим принципиальную схему:

Какое напряжение на резисторе в показанной цепи?

Проверьте, что у вас есть и единицы

У нас есть схема с батареей и одним резистором.Нам известно напряжение на батарее. Мы хотим найти это напряжение на резисторе.

\ [{V} _ {\ text {battery}} = \ text {2} \ text {V} \]

Применимые принципы

Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех других компонентах схемы.

\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]

Есть только один другой компонент схемы — резистор.

\ [{V} _ {\ text {total}} = {V} _ {1} \]

Это означает, что напряжение на батарее равно напряжению на резисторе.

\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} = {V} _ {1} \\ {V} _ {1} & = \ text {2} \ text {V} \ end {align *}

Рабочий пример 8: Напряжения II

Рассмотрим эту схему:

Какое напряжение на неизвестном резисторе в показанной цепи?

Проверьте, что у вас есть и единицы

У нас есть схема с батареей и двумя резисторами. Нам известно напряжение на батарее и на одном из резисторов.Мы хотим найти это напряжение на резисторе.

\ begin {align *} {V} _ {\ text {battery}} & = \ text {2} \ text {V} \\ {V} _ {B} & = \ text {1} \ text {V} \ end {align *}

Применимые принципы

Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех других компонентах схемы, включенных последовательно.

\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]

Общее напряжение в цепи — это сумма напряжений на отдельных резисторах

\ [{V} _ {\ text {total}} = {V} _ {A} + {V} _ {B} \]

Использование зависимости между напряжением на батарее и общим напряжением на резисторах

\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\\\ {V} _ {\ text {battery}} & = {V} _ {1} + {V} _ {\ text {resistor}} \\ \ text {2} \ text {V} & = {V} _ {1} + \ text {1} \ text {V} \\ {V} _ {1} & = \ text {1} \ text {V} \ end {align *}

Рабочий пример 9: Напряжения III

Рассмотрим принципиальную схему:

Какое напряжение на неизвестном резисторе в показанной цепи?

Проверьте, что у вас есть и единицы

У нас есть схема с батареей и тремя резисторами.Нам известно напряжение на батарее и двух резисторах. Мы хотим найти это напряжение на неизвестном резисторе.

\ begin {align *} {V} _ {\ text {battery}} & = \ text {7} \ text {V} \\ {V} _ {\ text {известное}} & = {V} _ {A} + {V} _ {C} \\ & = \ текст {1} \ текст {V} + \ текст {4} \ текст {V} \ end {align *}

Применимые принципы

Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех других компонентах схемы, включенных последовательно.

\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]

Общее напряжение в цепи — это сумма напряжений на отдельных резисторах

\ [{V} _ {\ text {total}} = {V} _ {B} + {V} _ {\ text {known}} \]

Использование зависимости между напряжением на батарее и общим напряжением на резисторах

\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\ {V} _ {\ text {battery}} & = {V} _ {B} + {V} _ {\ text {known}} \\ \ text {7} \ text {V} & = {V} _ {B} + \ text {5} \ text {V} \\ {V} _ {B} & = \ text {2} \ text {V} \ end {align *}

Рабочий пример 10: Напряжения IV

Рассмотрим принципиальную схему:

Какое напряжение на параллельной комбинации резисторов в показанной цепи? Подсказка: остальная часть схемы такая же, как и в предыдущей задаче.

Быстрый ответ

Схема такая же, как и в предыдущем примере, и мы знаем, что разница напряжений между двумя точками в цепи не зависит от того, что между ними, поэтому ответ такой же, как и выше \ ({V} _ {\ text {parallel }} = \ текст {2} \ текст {V} \).

Проверьте, что у вас есть и единицы — длинный ответ

У нас есть схема с батареей и пятью резисторами (два последовательно и три параллельно). Нам известно напряжение на батарее и двух резисторах.Мы хотим найти это напряжение на параллельных резисторах \ ({V} _ {\ text {parallel}} \).

\ begin {align *} {V} _ {\ text {battery}} = \ text {7} \ text {V} \\ {V} _ {\ text {известное}} = \ text {1} \ text {V} + \ text {4} \ text {V} \ end {align *}

Применимые принципы

Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех других компонентах схемы.

\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]

Напряжения складываются только алгебраически для последовательно соединенных компонентов.Параллельно подключенные резисторы можно рассматривать как единый компонент, который включен последовательно с другими компонентами, а затем можно складывать напряжения.

\ [{V} _ {\ text {total}} = {V} _ {\ text {parallel}} + {V} _ {\ text {known}} \]

Использование зависимости между напряжением на батарее и общим напряжением на резисторах

\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\ {V} _ {\ text {battery}} & = {V} _ {\ text {parallel}} + {V} _ {\ text {known}} \\ \ text {7} \ text {V} & = {V} _ {\ text {parallel}} + \ text {5} \ text {V} \\ {V} _ {\ text {parallel}} & = \ text {2} \ text {V} \ end {align *}

В отличие от последовательного случая, когда мы добавляем резисторы параллельно, мы создаем еще путей , по которым может течь ток.Таким образом мы уменьшаем на общее сопротивление цепи на !

Взгляните на диаграмму ниже. Слева у нас та же схема, что и в предыдущем разделе, с батареей и резистором. Амперметр показывает ток \ (\ text {1} \) \ (\ text {A} \). Справа мы добавили второй резистор параллельно первому. Это увеличило количество путей (ответвлений), по которым заряд может проходить через цепь — общее сопротивление уменьшилось. Вы можете видеть, что ток в цепи увеличился.Также обратите внимание, что ток в разных ветвях может быть разным.

Общее сопротивление ряда параллельных резисторов НЕ является суммой отдельных сопротивлений, поскольку общее сопротивление уменьшается с увеличением количества путей прохождения тока. Общее сопротивление для параллельных резисторов равно:

. \ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]

Давайте рассмотрим случай, когда у нас есть два резистора, включенных параллельно, и выясним, каким будет конечное сопротивление.Эта ситуация показана на диаграмме ниже:

Применяя формулу для общего сопротивления, получаем:

\ begin {align *} \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \\ & \ text {Резисторов всего два} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} \\ & \ text {Добавить дроби} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} \ times \ frac {{R} _ {2}} {{R} _ {2 }} + \ frac {1} {{R} _ {2}} \ times \ frac {{R} _ {1}} {{R} _ {1}} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2}} {{R} _ {1} {R} _ {2}} + \ frac {{R} _ {1}} {{R} _ {1} {R} _ {2}} \\ & \ text {Переставить} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} + {R} _ {1}} {{R} _ {1} {R} _ {2} } \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2} } \\ {R} _ {P} & = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ end {выровнять *}

Для любых двух параллельно включенных резисторов мы теперь знаем, что

\ [{R} _ {P} = \ frac {\ text {произведение сопротивлений}} {\ text {сумма сопротивлений}} = \ frac {{R} _ {1} {R} _ {2}} { {R} _ {1} + {R} _ {2}} \]

Делители тока

Цель

Проверьте, что происходит с током и напряжением в последовательных цепях при добавлении дополнительных резисторов.

Аппарат

• Аккумулятор

• Вольтметр

• Амперметр

• Провода

• Резисторы

Метод

• Подключите каждую цепь, показанную ниже

• Измерьте напряжение на каждом резисторе в цепи.

• Измерьте ток до и после каждого резистора в цепи, а также до и после параллельных ветвей.

Результаты и выводы

• Сравните токи через отдельные резисторы между собой.

• Сравните сумму токов через отдельные резисторы с током до параллельных ветвей.

• Сравните различные измерения напряжения на параллельных резисторах.

Рабочий пример 11: Параллельные резисторы I

Цепь содержит два параллельно включенных резистора. Резисторы имеют значения сопротивления \ (\ text {15} \) \ (\ text {Ω} \) и \ (\ text {7} \) \ (\ text {Ω} \).

Какое полное сопротивление в цепи?

Проанализировать вопрос

Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общее сопротивление.Значения двух резисторов указаны в правильных единицах, Ом.

Применять соответствующие принципы

Было показано, что полное сопротивление резисторов, включенных параллельно, является произведением сопротивлений, разделенных на сумму. Мы можем использовать

\ [{R} _ {P} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \]

У нас всего два резистора, и теперь мы резисторы. В данном случае это:

\ begin {align *} {R} _ {P} & = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \\ & = \ frac {\ left (\ text {15} \ text {Ω} \ right) \ left (\ text {7} \ text {Ω} \ right)} {\ text {15} \ text {Ω} + \ text {7} \ text {Ω}} \\ & = \ frac {105 {\ Omega} ^ {2}} {\ text {22} \ text {Ω}} \\ & = \ текст {4,77} \ текст {Ω} \ end {align *}

Цитировать окончательный результат

Полное сопротивление параллельно включенных резисторов \ (\ text {4,77} \) \ (\ text {Ω} \)

Рабочий пример 12: Параллельные резисторы II

Мы добавляем третий параллельный резистор в конфигурацию (настройку) в предыдущем примере.Дополнительный резистор имеет сопротивление \ (\ text {3} \) \ (\ text {Ω} \).

Какое полное сопротивление в цепи?

Проанализировать вопрос

Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общее сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.

Применять соответствующие принципы

Общее сопротивление резисторов, включенных параллельно, составляет

. \ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]

У нас есть три резистора, и теперь мы резисторы.В данном случае это:

\ begin {align *} \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \\ & \ text {есть три резистора} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1 } {{R} _ {3}} \\ & \ text {добавить дроби} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} \ times \ frac {{R} _ {2} {R} _ {3}} {{R} _ {2} {R} _ {3}} + \ frac {1} {{R} _ {2}} \ times \ frac {{R} _ {1} {R} _ {3} } {{R} _ {1} {R} _ {3}} + \ frac {1} {{R} _ {3}} \ times \ frac {{R} _ {1} {R} _ {2 }} {{R} _ {1} {R} _ {2}} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} {R} _ {3}} {{R} _ {1} {R} _ {2} { R} _ {3}} + \ frac {{R} _ {1} {R} _ {3}} {{R} _ {1} {R} _ {2} {R} _ {3}} + \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} {R} _ {2} {R} _ {3}} \\ & \ text {переставить} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} {R} _ {3} + {R} _ {1} {R} _ {3} + { R} _ {2} {R} _ {3}} {{R} _ {1} {R} _ {2} {R} _ {3}} \\ {R} _ {P} & = \ frac {{R} _ {1} {R} _ {2} {R} _ {3}} {{R} _ {2} {R} _ {3} + {R} _ {1} {R} _ {3} + {R} _ {2} {R} _ {3}} \\ {R} _ {P} & = \ frac {\ left (\ text {15} \ text {Ω} \ right) \ left (\ text {7} \ text {Ω} \ right) \ left (\ text { 3} \ text {Ω} \ right)} {\ left (\ text {7} \ text {Ω} \ right) \ left (\ text {3} \ text {Ω} \ right) + \ left (\ text {15} \ text {Ω} \ right) \ left (\ text {3} \ text {Ω} \ right) + \ left (\ text {7} \ text {Ω} \ right) \ left (\ text { 15} \ text {Ω} \ right)} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {21 {\ Omega} ^ {2} + 45 {\ Omega} ^ {2} + 105 {\ Omega} ^ { 2}} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {171 {\ Omega} ^ {2}} \\ {R} _ {P} & = \ text {1,84} \ text {Ω} \ end {align *}

Цитировать окончательный результат

Полное сопротивление параллельно включенных резисторов \ (\ text {1,84} \) \ (\ text {Ω} \)

При расчете сопротивления для сложных конфигураций резисторов вы можете начать с любой комбинации двух резисторов (последовательно или параллельно) и рассчитать их общее сопротивление.Затем вы можете заменить их одним резистором с рассчитанным вами общим сопротивлением. Теперь используйте этот новый резистор в сочетании с любым другим резистором и повторяйте процесс, пока не останется только один резистор. В приведенном выше примере мы могли бы просто использовать ответ из первого примера параллельно с новым резистором, и мы получили бы тот же ответ.

Рабочий пример 13: Параллельные резисторы III

Мы добавляем третий параллельный резистор к первой конфигурации (настройке), работающей параллельно.Дополнительный резистор имеет сопротивление \ (\ text {3} \) \ (\ text {Ω} \)

Какое полное сопротивление в цепи?

Проанализировать вопрос

Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общее сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.

Применять соответствующие принципы

Мы можем поменять местами резисторы, не меняя схему:

Мы уже рассчитали, что полное сопротивление двух резисторов в пунктирной рамке равно \ (\ text {4,77} \) \ (\ text {Ω} \). {2}} {\ text {11,77} \ Omega} \\ & = \ текст {1,84} \ текст {Ω} \ end {align *}

Цитировать окончательный результат

Полное сопротивление параллельно включенных резисторов равно \ (\ text {1,84} \) \ (\ text {Ω} \).Это тот же результат, что и при одновременном сложении всех трех резисторов.

Siyavula Practice дает вам доступ к неограниченному количеству вопросов с ответами, которые помогут вам в обучении. Тренируйтесь где угодно, когда угодно и на любом устройстве!

Зарегистрируйтесь, чтобы потренироваться сейчас

Сопротивление

Упражнение 17.1

Как называется единица сопротивления и каков ее символ?

Решение пока недоступно

Объясните, что происходит с общим сопротивлением цепи, когда резисторы добавляются последовательно?

Решение пока недоступно

Объясните, что происходит с общим сопротивлением цепи, когда резисторы добавляются параллельно?

Решение пока недоступно

Почему батарейки разряжаются?

Решение еще не доступно

Цепь параллельных резисторов и простая схема делителя тока

Формула для параллельного резистора будет нашей основной темой здесь.После обсуждения последовательного резистора и делителя напряжения давайте узнаем о параллельных резисторах и делении тока. Параллельный резистор относится к одному из пассивных элементов.

Вы узнаете, включены ли резисторы параллельно или последовательно, просто по их клеммному соединению. Мы называем резисторы подключенными параллельно, если их выводы соединены вместе, соответственно, от резистора к резистору.

Определение параллельной цепи

Этот параллельный резистор отличается от последовательного резистора, в котором есть только один прямой путь, проходящий через резисторы.В параллельном резисторе будет много путей от головы к голове и от хвоста к хвосту. Исходя из этого термина, параллельный резистор используется как делитель тока, а последовательный резистор — как делитель напряжения.

Поскольку ток разделяется на несколько путей или ответвлений, ток для каждой ветви может отличаться друг от друга. Но падение напряжения на каждом резисторе будет одинаковым для каждого другого. Отсюда следует вывод, что для резисторов, включенных параллельно, они могут иметь разный ток через каждый из них, но всегда иметь одинаковое падение напряжения на каждом из них.

Зачем нам нужно изучать формулу для параллельного резистора? Вы должны знать, прочитав этот пост, пока не закончите.

Определение параллельных резисторов — это резистивная схема, в которой резисторы подключены вместе к одним и тем же узлам и образуют более одного пути тока, подключенного к одному источнику напряжения. Если вы все еще не понимаете, как мы делаем параллельную резистивную схему, мы можем найти ее ниже.

Схема параллельной цепи

Пример ниже представляет собой простой параллельный резистор в цепи.Мы используем три резистора R ₁ , R ₂ и R ₃ . Из объяснения выше, падение напряжения на резисторах при параллельном подключении будет одинаковым для друг друга и равным источнику напряжения.

Следовательно,

Все три резистора соединены между собой между A и B.

В отличие от последовательных резистивных цепей, где эквивалентное сопротивление является суммой всех резисторов, параллельный резистор рассчитывается по-другому.Мы используем величину, обратную сопротивлению (1 / R) для каждого сложенного резистора.

Формула для параллельного резистора

Как мы уже упоминали выше, эквивалентное сопротивление параллельных резисторов является суммой, обратной величине каждого резистора. Если резисторы, соединенные параллельно, имеют одинаковое значение, это будет очень просто.

Как мы уже упоминали выше, мы можем посмотреть на пример ниже:

Если два резистора, подключенных параллельно, имеют одинаковое сопротивление, то эквивалентное сопротивление, R _T — это половина сопротивления одного резистора. резистор.Следовательно, эквивалентное сопротивление двух резисторов, соединенных параллельно, если они имеют одинаковое сопротивление, равно R / 2. Если параллельно подключено три резистора, эквивалентное сопротивление равно R / 3 и так далее.

Помимо последовательных резисторов, этот тип цепи является наиболее распространенным типом электрических цепей. Для анализа цепи параллельного резистора мы можем использовать тот же метод для последовательного резистора, используя законы Кирхгофа и закон Ома.

Рассмотрим схему на рисунке (1),

на рисунке 1.Параллельное соединение резисторов

, при котором два резистора соединены параллельно и, следовательно, имеют одинаковое напряжение на них.

Из закона Ома

(1)

Применение KCL в узле a дает полный ток i как

(2)

Подставляя уравнение (1) в (2), мы получаем

(3)

, где R _eq — эквивалентное сопротивление резисторов, включенных параллельно:

(4)

или

(5)

Следовательно,

Эквивалентное сопротивление двух параллельных резисторов равно произведение их сопротивлений, деленное на их сумму.

Выше представлено простейшее уравнение параллельного резистора, которое мы можем использовать каждый раз, когда нам это нужно.

Следует отметить, что уравнение (5) работает только для двух параллельно подключенных резисторов.

Мы можем расширить уравнение параллельного резистора в уравнении (4) до общего случая цепи с N резисторами, включенными параллельно. Эквивалентное сопротивление составляет

(6)

Обратите внимание, что R _eq всегда меньше, чем сопротивление наименьшего резистора в параллельном соединении.Если R ₁ = R ₂ =… = R _N = R , то

(7)

Например, если 4 резистора с сопротивлением 100 Ом подключены параллельно, их эквивалентное сопротивление составляет 25 Ом.

Имейте в виду, что,

Эквивалентное сопротивление параллельных резисторов всегда меньше, чем сопротивление наименьшего резистора, подключенного к этой сети. Следовательно, эквивалентное сопротивление RT будет уменьшаться каждый раз, когда у нас будут дополнительные параллельные резисторы.

Формула проводимости для параллельной цепи

Из-за этого простого, но сложного уравнения параллельного резистора для эквивалентного сопротивления мы узнаем о новом значении, известном как проводимость (G), измеренном в Сименсах (S). Проводимость обратно пропорциональна сопротивлению, где G = 1 / R. После того, как мы получим проводимость, мы преобразуем ее обратно обратно, чтобы получить эквивалентное сопротивление R _T параллельных резисторов.

При параллельном подключении резисторов легче использовать проводимость, чем сопротивление.

Из уравнения (6) эквивалентная проводимость для резисторов N составляет

(8)

, где:

Уравнение. (8) утверждает:

Эквивалентная проводимость резисторов, подключенных параллельно, равна сумме их индивидуальная проводимость.

Это означает, что мы можем перерисовать рисунок (1) на (2), где мы заменим сопротивления на проводимости.

Эквивалентные проводимости параллельных резисторов получаются таким же образом, как эквивалентные сопротивления последовательных резисторов.

Напротив, эквивалентные сопротивления последовательных резисторов получаются таким же образом, как эквивалентные сопротивления параллельных резисторов.

Рисунок 2. Эквивалентное сопротивление или проводимость

Следовательно, эквивалентная проводимость G _eq последовательно соединенных резисторов N составляет

(9)

Учитывая общий ток i, входящий в узел a на рисунке. (1) с одинаковые значения напряжения, получаем

(10)

Мы определяем параллельные резисторы как резисторы, соединенные между собой между одними и теми же двумя точками.Сам параллельный резистор имеет различные схемы.

Как найти ток в параллельной цепи

Поскольку ток в параллельной цепи зависит от ее сопротивления, теперь мы узнаем, как найти ток в параллельной цепи. Токи I ₁ , I ₂ ,…, I _n , входящие в параллельный путь резисторов, зависят от сопротивления этой ветви. Полный ток I _T представляет собой сумму токов в параллельных ветвях.Если сопротивление между ветвями равно, то токи также будут разделены поровну.

Если R ₁ = R ₂ , то I ₁ = I ₂ = 0,5 I _T . Это означает, что общий ток I _T делится поровну на две ветви. Если сопротивление R ₁ отличается от сопротивления R ₂ , тогда нам нужно рассчитать I ₁ и I ₂ по-разному.Даже если напряжения на ветвях равны, ток может отличаться по закону Ома.

Для примера параллельной схемы давайте посмотрим на схему ниже и попытаемся найти все токи,

Поскольку R ₁ и R ₂ имеют разные значения, тогда токи I ₁ и I ₂ гарантированно имеют разные значения. Помните один из законов Кирхгофа?

Текущие законы Кирхгофа гласят:

Общий ток, выходящий из узла, равен току, входящему в тот же самый узел.

Следовательно,
Полный ток в цепи может быть выражен как:

После этого мы будем использовать закон Ома для расчета тока, поступающего в каждую ветвь через резисторы. I ₁ — это входящий ток R ₁ , а I ₂ — это ток, входящий R ₂ . Источник напряжения В _с имеет 12 В, и мы получаем:

И получаем полный ток,

Чтобы прояснить это, мы используем закон Ома для вычисления I _T из В _с и R _T .
Суммарное сопротивление R _T составляет

Тогда полный ток I _T равен

Таким образом, это проясняет наши расчеты.

Мы заключаем, что

Уравнение делителя тока

Комбинируя уравнения. (1) и (10) мы получаем уравнение текущего делителя.

(11)

, который показывает, что полный ток i распределяется между резисторами обратно пропорционально их сопротивлениям.

Это известно как принцип деления тока , а схема на рисунке (1) известна как делитель тока .

Обратите внимание, что больший ток проходит через меньшее сопротивление.

Рисунок 3. Короткое замыкание и разрыв в параллельном соединении

Предположим, что один из резисторов на рисунке (1) равен нулю, скажем, R ₂ = 0; поэтому R ₂ — это короткое замыкание, как видно на рисунке. (3a).

Из уравнения.(11), R ₂ = 0 означает, что i ₁ = 0, i ₂ = i . Это означает, что весь ток i обходит R ₁ и протекает через короткое замыкание R ₂ = 0, путь с наименьшим сопротивлением.
Когда цепь закорочена, как показано на рисунке (3a), обратите внимание, что:

1. Эквивалентное сопротивление R _экв. = 0
2. Весь ток протекает через короткое замыкание.

Для другого крайнего примера, где R ₂ = ∞, то есть R ₂ — это разомкнутая цепь, как показано на рисунке. (3b).
Ток по-прежнему течет по пути с наименьшим сопротивлением, R ₁ .
Уравнение (11) преобразуется в

(12)

В общем, если делитель тока имеет N проводников, параллельных току источника i , N -й проводник будет иметь ток

(13)

Очень удобно комбинировать резисторы последовательно и параллельно в одно эквивалентное сопротивление R _eq .

Такое эквивалентное сопротивление должно иметь те же значения тока и напряжения, что и исходная сеть на выводе.

Примеры параллельного резистора

Давайте рассмотрим приведенный ниже пример для лучшего понимания
Найдите R _eq для схемы на рисунке.