1.2 Правила Кирхгофа — Законы постоянного тока
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.
В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рисунок 1.1) Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
Рисунок 1.1
Узел электрической цепи. I1, I2 > 0; I3,I4 < 0
В узлах цепи постоянного тока не может происходить накопление зарядов.
Первое правило Кирхгофа:
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
I1 + I2 + I3 + … + In = 0.
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называютсямконтурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).
На разных участках выделенного контура могут протекать различные токи. На рис. 1.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).
Рисунок 1.2
Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef)
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома.
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.3.
1.3.
Рисунок 1.3.
«Правила знаков»
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для участка bc: I1R1 = Δφbc – 1.
Для участка da: I2R2 = Δφda – 2.
Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:
I1R1 + I2R2 = Δφbc + Δφda – 1 + 2 = –1 – 2.
Аналогично, для контура adef можно записать:
– I2R2 + I3R3 = 2 + 3.
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:
I1R1 + I2R2 = – 1 – 2,
– I2R2 + I3R3 = 2 + 3,
– I1 + I2 + I3 = 0.
Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.
Модель. Цепи постоянного тока
Модель. Конденсаторы в цепях постоянного тока
ИЗУЧЕНИЕ ПРАВИЛ КИРХГОФА Цель работы
ЛАБОРАТОРНАЯ РАБОТА № 6
ИЗУЧЕНИЕ ПРАВИЛ КИРХГОФА
Цель работы: изучение правил Кирхгофа.
Приборы и оборудование: источник тока, три амперметра, три вольтметра, два магазина сопротивлений, реостат, ключ, соединительные провода.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Расчёт простейших схем ни у кого не вызывает затруднений (простейшие — это такие, в которых проводники, резисторы, «;нагрузки»; могут соединяться последовательно или параллельно). Не вызовут также затруднения задачи с симметрией. Но к расчёту разветвлённых цепей постоянного тока, если сопротивления разные, метод симметрии не подходит. Некоторые схемы разветвлённых цепей можно упростить. Если же упрощение цепи невозможно, то расчет такой электрической цепи удобно проводить, пользуясь двумя правилами Кирхгофа.
Не вызовут также затруднения задачи с симметрией. Но к расчёту разветвлённых цепей постоянного тока, если сопротивления разные, метод симметрии не подходит. Некоторые схемы разветвлённых цепей можно упростить. Если же упрощение цепи невозможно, то расчет такой электрической цепи удобно проводить, пользуясь двумя правилами Кирхгофа.
Рассмотрим произвольную разветвленную цепь, часть которой изображена на рис. 1.
Первое правило Кирхгофа относится к узлам, т.е. точкам, в которых сходится не менее трех проводников. Вследствие закона сохранения заряда в любой точке цепи, в том числе и в любом узле, при прохождении постоянного тока не должно происходить накопления электрического заряда. Поэтому сумма притекающих к узлу токов должна равняться сумме утекающих. Если условиться считать подходящие к узлу токи положительными, а исходящие из узла – отрицательными, то можно сказать, что алгебраическая сумма сил токов в узле равна нулю:
, (1)
где n обозначает число проводов, сходящихся в узле.
Второе правило Кирхгофа относится к произвольным замкнутым контурам, которые можно выделить в рассматриваемой замкнутой цепи. Рассмотрим контур ABCA на рис. 1. Поскольку при расчете мы будем использовать закон Ома для неоднородного участка цепи, то, как мы видели, направление токов в неразветвленных участках можно задать произвольно, например, так как на рис. 1. ( Напомним, что если в результате расчета какой – либо из токов окажется отрицательным, то это означает, что в действительности ток на этом участке течет в противоположную сторону.) Запишем закон Ома для каждого участка контура ABCA. Обозначив потенциалы узлов через и , получим:
(2)
В этих формулах через обозначено полное сопротивление участка, по которому течет ток . Легко заметить, что если первое уравнение системы умножить на (-1) и затем сложить почленно все три уравнения, то потенциалы узлов выпадут:
(3)
Глядя на полученную формулу, нетрудно сформулировать правило, с помощью которого можно было бы непосредственно получить это равенство: нужно выбрать определенное направление обхода замкнутого контура (например, по часовой стрелке) и приравнять алгебраическую сумму произведений сил токов на сопротивления соответствующих участков алгебраической сумме ЭДС, встречающихся в этом контуре. При этом ток считается положительным, если его направление совпадает с направлением обхода контура, и отрицательным в противоположном случае; ЭДС берется со знаком «+», если она повышает потенциал в цепи в направлении обхода контура, и со знаком «-», если понижает. Это и есть второе правило Кирхгофа, которое можно коротко записать так:
При этом ток считается положительным, если его направление совпадает с направлением обхода контура, и отрицательным в противоположном случае; ЭДС берется со знаком «+», если она повышает потенциал в цепи в направлении обхода контура, и со знаком «-», если понижает. Это и есть второе правило Кирхгофа, которое можно коротко записать так:
(5)
где n – число неразветвленных участков в рассматриваемом контуре (совпадающее с числом встречающихся в этом контуре узлов) а m – число ЭДС действующих в контуре.
Теперь можно сформулировать общие правила расчета произвольных разветвленных цепей постоянного тока с использованием правил Кирхгофа.
Обозначить на схеме токи во всех неразветвленных участках, произвольно задавая им направление.
Согласно первому правилу Кирхгофа написать уравнения для всех узлов, кроме одного (уравнение для последнего узла писать не нужно, так как оно является следствием предыдущих).
Согласно второму правилу Кирхгофа составить уравнения для всех простых контуров, которые можно выделить в данной цепи и которые не получаются наложением уже рассмотренных.
 Простым считается такой контур, при обходе которого мы побываем в каждой точке только по одному разу. В правильно выбранной системе контуров каждый участок цепи должен фигурировать по крайней мере в одном из контуров.
Простым считается такой контур, при обходе которого мы побываем в каждой точке только по одному разу. В правильно выбранной системе контуров каждый участок цепи должен фигурировать по крайней мере в одном из контуров.Если в результате решения получившейся системы уравнений какие – либо токи окажутся отрицательными, то в действительности их направление противоположно выбранному на схеме.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
ИЗУЧЕНИЕ ПЕРВОГО ПРАВИЛА КИРХГОФА
1. Собрать электрическую цепь по схеме, изображенной на рис. 2. В качестве R1 и R2 используются магазины сопротивлений.
2. Определить цену деления, предел измерения и класс точности приборов, используемых в схеме (рис.2).
3. С помощью магазинов сопротивлений три раза меняют сопротивление в цепи (значения сопротивлений задаются преподавателем). Снимают показания с амперметров и заносят их в таблицу №1.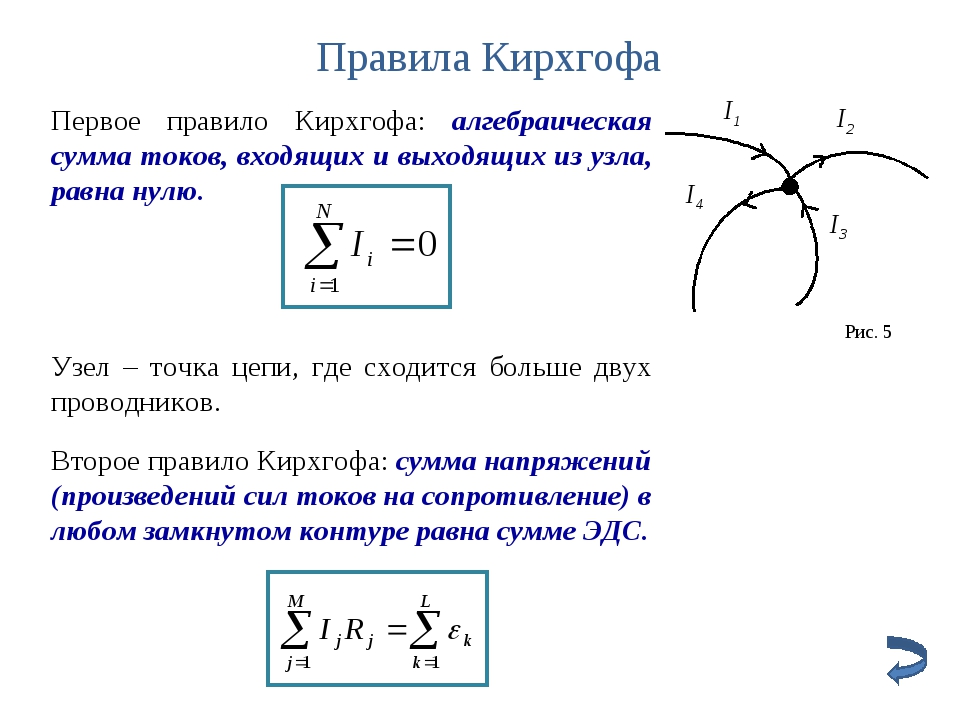
Рис. 2.
Таблица 1
№ опыта | I1, А | I2, А | I3, А | (I1+ I2), А |
1 | ||||
2 | ||||
3 |
Оценить погрешность результатов измерений
Сделать выводы
ИЗУЧЕНИЕ ВТОРОГО ПРАВИЛА КИРХГОФА
1. Собрать электрическую цепь по схеме, изображенной на рис. 3.
Рис. 3.
2. Определить цену деления, предел измерения и класс точности приборов, используемых в схеме (рис.3).
3. При трех различных положениях движка реостата произвести измерения напряжений. Результаты измерений занести в таблицу №2. Проверить, выполняется ли второе правило Кирхгофа. Сделать выводы.
Таблица № 2
№ опыта | U0, В | U1, В | U2, В | (U1 +U2), В |
1 | ||||
2 | ||||
3 |
4. Оценить погрешность результатов измерений.
5. Сделать выводы
КОНТРОЛЬНЫЕ ВОПРОСЫ
Что называют разветвленной электрической цепью?
Что называют узлом электрической цепи?
Что называют ветвью электрической цепи?
Сформулируйте первое правило Кирхгофа.
Сформулируйте второе правило Кирхгофа.
Какова методика применения правил Кирхгофа при расчете разветвленной электрической цепи?
Для электрических цепей, схемы которых показаны на рисунке, записать необходимое количество уравнений для расчета цепей с помощью правил Кирхгофа.
а) б)
в) г)
ЛИТЕРАТУРА
Трофимова Т.И. Курс физики/Т.И. Трофимова.- М.: Высшая школа, 1990
Детлаф А.А. Курс физики/ А.
 А. Детлаф, Б.М. Яворский. – М.: Высшая школа, 1999
А. Детлаф, Б.М. Яворский. – М.: Высшая школа, 1999Лаврова И.В. Курс физики. – М.,: Просвещение, 1981.
Айзенцон А.Е. Курс физики /А.Е. Айзенцон. – М.: Высшая школа, 1996
Калашников С.Г. Электричество /С.Г. Калашников. –М.: Наука, 1985
Расчеты электрических цепей по правилам Кирхгофа | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Правила Кирхгофа, разработанные в 1847 году, устанавливают соотношение сил тока и напряжений в разветвленных электрических цепях постоянного тока и переменных токов небольших частот, например тока промышленной частоты.
На рис. 5.26, а показаны детали разветвленной электрической цепи. Точки разветвления A, B, C называются узлами цепи. На рис. 5.26, б показана схема узла, где сходятся три тока, силы которых I1, I2 и I3. Токи, приходящие к узлу (I1 и I2 в нашем случае), считаются положительными, а токи, выходящие из узла, — отрицательными.
Токи, приходящие к узлу (I1 и I2 в нашем случае), считаются положительными, а токи, выходящие из узла, — отрицательными.
Первое правило Кирхгофа является следствием закона сохранения заряда: какой заряд приносят свободные носители заряда к узлу за единицу времени, такой и должен выноситься из узла.
Первое правило Кирхгофа. Алгебраическая сумма токов в узле равна нулю.
I1 + I2 + I3 = 0, или Σni=1 Ii = 0.
Второе правило Кирхгофа касается любого замкнутого контура в разветвленной цепи (например, ABCA на рис. 5.26, а). В таком контуре алгебраическая сумма всех падений напряжений на отдельных участках контура равна алгебраической сумме электродвижущих сил действующих в этом контуре
Σni=1 I
Второе правило Кирхгофа. В любом замкнутом контуре в электрической цепи алгебраическая сумма всех падений напряжений I / R, на всех участках контура равна алгебраической сумме электродвижущих сил, действующих в этом контуре.
| Рис. 5.26, а. Разветвления в электрической цепи |
| Рис. 5.26, б. Узел в электрической цепи |
При применении второго правила Кирхгофа следует договориться, какие из токов считаются положительными, а какие — отрицательными. Предположим, что положительными являются токи, направления которых совпадают с направлением движения часовой стрелки, а отрицательными — направления которых противоположные направлению движения часовой стрелки.
Положительными будем считать такие электродвижущие силы, которые повышают потенциал полюсов источника тока в направлении обхода контура (рис.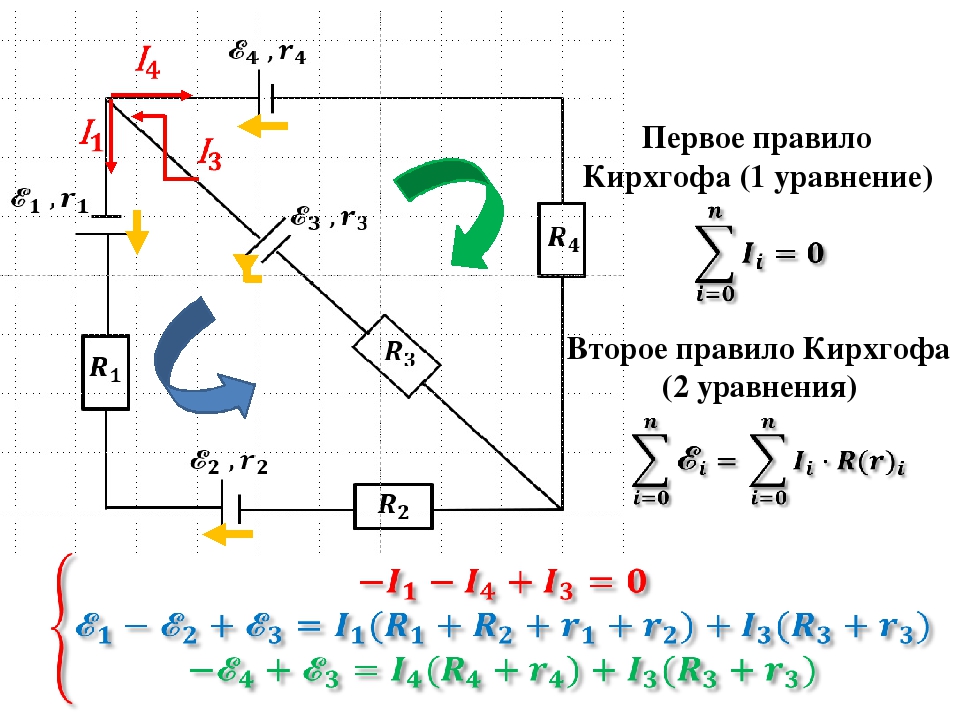
| Рис. 5.27, а. Электродвижущая сила считается положительной |
| Рис. 5.27, б. Электродвижущая сила считается отрицательной |
Пусть в контуре ABCA (рис.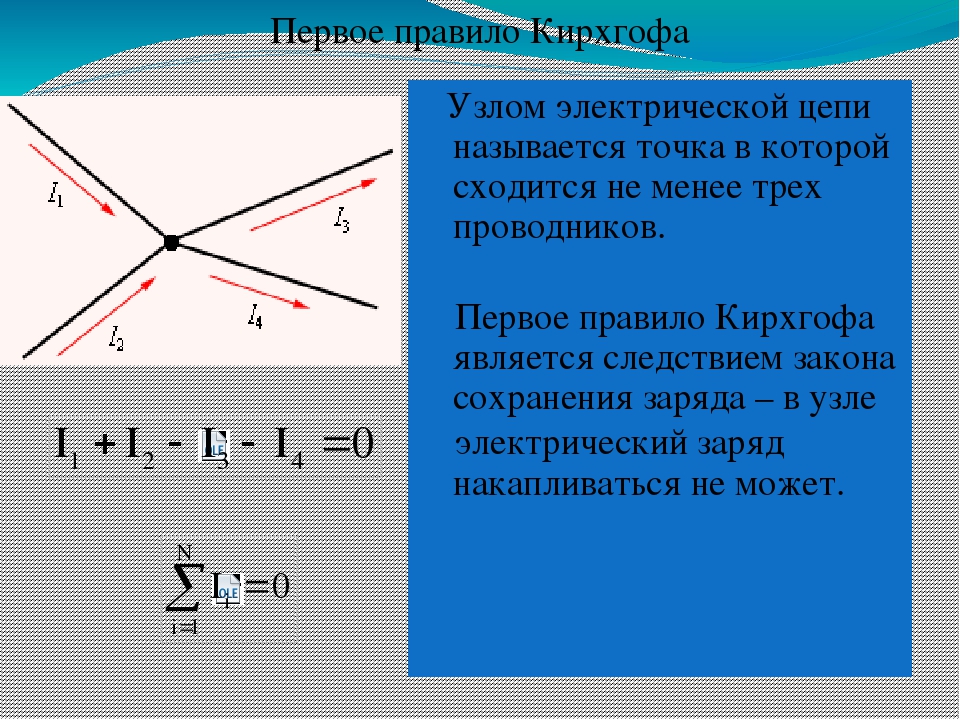 5.26, а) обход осуществляется по часовой стрелке и направления тока выбраны так, как показано на рисунке. В этом случае все произведения I
5.26, а) обход осуществляется по часовой стрелке и направления тока выбраны так, как показано на рисунке. В этом случае все произведения I
Для этого случая второе правило Кирхгофа записывается в таком виде
I1R1 + I3R3 + I2R2 = Ɛ1 — Ɛ3.
Понятно, что не всегда можно точно установить настоящие направления токов или электродвижущих сил. Тогда в ответах решенных задач эти величины получатся со знаком минус.
Что считается узлами разветвленной электрической цепи? Проиллюстрируйте ответ схемами электрических цепей или их частей.
Закон кергофа второе правило сокращенно
Правила кирхгофа кратко
Расчет электрической цепи школьный материал
Киркгоф гравитация
В каких устройствах встречается смешанное соединение проводников
Какие токи в узлах можно считать положительными, а какие — отрицательными?
На каких закономерностях основывается первое правило Кирхгофа?
Сформулируйте первое правило Кирхгофа.
Как определяются замкнутые контуры в разветвленных электрических кругах?
Что такое падение напряжения на участке цепи?
Какой ток в контуре считают положительным, а какой — отрицательным?
Какие электродвижущие силы в контурах считают положительными, а какие — отрицательными?
Сформулируйте второе правило Кирхгофа.

Если в решении задачи ток оказывается отрицательным, то что это значит?
Методическая разработка занятия «Решение задач на разветвлённые цепи постоянного тока с использованием правил Кирхгофа»
преподаватель физики
ГБПОУ КО «Калужский колледж народного хозяйства и природообустройства»
город Калуга, Россия
Методическая разработка занятия по дисциплине «Физика» для повышения познавательной активности способных студентов 1 курсов по теме: «Решение задач на разветвлённые цепи постоянного тока с использованием правил Кирхгофа».
Дата проведения занятия: 24 апреля 2014 года.
Эпиграф к уроку:
«При изучении наук примеры не менее
поучительны, нежели правила»
И. Ньютон.
Ньютон.
Актуальность темы: на практике часто приходиться рассчитывать сложные разветвлённые электрические цепи, содержащие узлы. Непосредственное применение закона Ома для полной цепи обычно затруднительно и приводит к ошибкам в расчёте.
Трудности при решении подобных задач упрощаются, если применять правила Кирхгофа.
Цели урока:
обобщить и оценить знания студентов по данной теме;
проверить умения учащихся применять правила Кирхгофа при расчёте разветвлённой цепи постоянного тока;
развивать мышление, речь, умение комментировать, тренировать память;
прививать интерес к дисциплине, путём понимания её актуальности в развитии практических компетенций.
Методы и приёмы: словестный, наглядный.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: интерактивная доска, «Листы учёта знаний», содержащие вопросы и задания.
План урока:
1. Повторение основных понятий разветвлённых электрических цепей.
Повторение основных понятий разветвлённых электрических цепей.
2.Повторение закона Ома для полной цепи и правил Кирхгофа.
3.По данной схеме восстановить последовательность использования правил Кирхгофа
при расчёте сложной разветвлённой электрической цепи.
4.Расчёт электрической цепи, изображённой на схеме.
Ход урока:
1этап.
1.Организационный момент: студенты занимают свои места, готовят необходимые принадлежности для урока, проверка присутствующих.
2.Оглашение темы урока: преподаватель объявляет тему уроку, зачитываетэпиграф, план урока; учащиеся записывают тему и план в рабочую тетрадь.
3. Получение необходимой информации: преподаватель раздаёт учащимся «Листы учёта знаний», предлагает записать на них свои фамилии и напоминает правила их заполнения.
«Лист учёта знаний» для группы №1.
Фамилии студентов:
№ | Формулировка задания | Возможное количество баллов | Набранное количество баллов | Примечание |
1. | Что называют узлом в разветвлённой электрической цепи? | 1 | ||
2. | Сформулируйте закон Ома для полной цепи и запишите его математическую формулу. | 2 | ||
3. | Что означает, если при решении задачи значение какого-нибудь тока получится отрицательным? | 1 | ||
4. | Как выбрать направление обхода замкнутого контура (по часовой или против часовой стрелки)? | 1 | ||
5. | Работа у доски. Составление уравнений по правилам Кирхгофа в общем виде для данной схемы. | 1 | ||
6. | Дополнение ответов — каждое | 1 | ||
7. | Итого: |
«Лист учёта знаний» для группы №2.
Фамилии студентов:
№ | Формулировка задания | Возможное количество баллов | Набранное количество баллов | Примечание |
1. | Что называют ветвью в разветвлённой электрической цепи? | 1 | ||
2. | Сформулируйте первое правило Кирхгофа и запишите его математическую формулу. | 2 | ||
3. | В каком случае перед Э.Д.С. ставится знак «+», если идти от отрицательного полюса к положительному или от положительного к отрицательному? | 1 | ||
4. | В одной ветке цепи (участок между узлами) сколько значений и сколько направлений может иметь ток? | 1 | ||
5. | Работа у доски. Составление уравнений по правилам Кирхгофа в общем виде для данной схемы. | 1 | ||
6. | Дополнение ответов — каждое | 1 | ||
7. | Итого: |
«Лист учёта знаний» для группы №3.
Фамилии студентов:
№ | Формулировка задания | Возможное количество баллов | Набранное количество баллов | Примечание |
1. | Что называют замкнутым контуром в разветвлённой электрической цепи? | 1 | ||
2. | Сформулируйте второе правило Кирхгофа и запишите его математическую формулу. | 2 | ||
3. | Токи, подходящие к узлу, считаются положительными или отрицательными? | 1 | ||
4. | Как выбрать на всех участках цепи направления токов? | 1 | ||
5. | Работа у доски. Составление уравнений по правилам Кирхгофа в общем виде для данной схемы. | 1 | ||
6. | Дополнение ответов — каждое | 1 | ||
7. | Итого: |
2этап.
Воспроизведение основных структурных блоков темы:
а) теоретическая часть.
1) Каждой группе студентов предлагается ответить на 4 вопроса, сформулированные в «Листе учёта знаний». Представители от каждого стола зачитывают последовательно свои ответы. Учащиеся за другими столами следят за правильностью ответов и при необходимости делают замечание, дополнение и получают за это дополнительные баллы. После каждого ответа появляется на доске слайд с правильным ответом.
По итогам работы студенты проставляют в «Лист учёта знаний» баллы, заработанные ими на этом этапе.
2) Работа у доски по схеме.
На доске появляется слайд с изображением схемы разветвлённой электрической цепи.
Учитель с помощью студентов выясняет из каких элементов состоит электрическая цепь, сколько она содержит узлов, ветвей, контуров и задаёт обход контуров и направления токов.
Группа №1 записывает уравнения для узла А и узла F. Группа №2 записывает уравнение для контура ВАКFВ. Группа №3 записывает уравнение для контура ВFDCВ.
Студенты каждой группы внимательно следят за работой своего представителя и могут подкорректировать его запись, если он где-то ошибся.
По окончании этой работы студенты выполняют проверку:
У первой группы работу проверяют студенты второй группы; у второй группы – студенты третьей группы; у третьей группы – студенты первой группы.
1 балл –записаны правильно уравнения для узлов;
1 балл – записаны правильно уравнения для контуров.
Заработанные баллы за это задание студенты каждой группы проставляют в «Лист учёта знаний».
б) выполнение практического задания.
На доске появляется схема электрической цепи.
Преподаватель диктует условие задачи и открывает слайд с данными условия задачи, учащиеся перерисовывают схему и записывают данные задачи в тетрадь.
Задача.
Определить силу токов, текущих в ветвях, если ξ1 = 2,1 В, ξ2 =1,9 В, внешние сопротивления
R1=45 Ом, R2 =10 Ом, R3 =10 Ом. Внутренним сопротивлением элементов пренебречь.
Дано:
ξ1 = 2,1В
ξ2 =1,9 В
R1=45 Ом
R2 =10 Ом
R3 =10 Ом
r1= r2=0
I1 =?, I2 = ?,I3=?
Решение:
1). Выберем направление обхода контура по часовой стрелке.
2). Выберем и обозначим на схеме стрелками направления токов на всех участках цепи.
(Помним, что в пределах одной ветки ток имеет одно значение и одно направление).
3). По первому правилу Кирхгофа составим уравнение для узла А. Пусть ток I2входит в узел А, а
токи I1иI3 выходят из узла А.
(Если в цепи kузлов, то достаточно составить k – 1 уравнений).
В нашей цепи 2 узла А и С, поэтому достаточно составить одно уравнение:
I2 —I1 —I3=0 (для узла А) или I1 + I3 — I2 = 0 (для узла С)
4). Составим уравнения для замкнутых линейно не зависимых контуров данной цепи по второму
правилу Кирхгофа:
Замкнутых контуров в нашей цепи три –АВСА, АСDА и АВСD, но контур АВСD линейно и
зависим, поэтому достаточно составить два уравнения:
I3R3—I1R1=ξ1 (для контура АВСА)
I1R1 + I2R2 = — ξ2 (для контураАСDА).
5). Составим систему уравнений, подставим данные из условий задачи:
— I1 + I2 -I3= 0
-R1 I1+ 0+ R3I3= ξ1
R1 I1+R2I2 + 0 = —ξ2
— I1 + I2 — I3 = 0
-45I1 + 0+ 10I3 = 2,1
45I1+ 10 I2 + 0 = — 1,9 (можно решить систему формулами Крамера)
Обозначим I1= х1; I2 = х2; I3= х3
Получили: I1 = — 0,04 А; I2 = — 0,01А; I3= 0,03А
Отрицательные значения токов I1 и I2 означают, что надо изменить первоначально выбранные направления этих токов на схеме, а значения токов взять без минуса.
Проверка: в уравнение— I1 + I2 — I3 = 0 подставим полученные значения токов
-(-0,04) + (-0,01) – 0,03 =0
Ответ: I1 = 0,04 А; I2 = 0,01А; I3= 0,03А
3этап.Формулировка домашнего задания.
Решить задачу, текст которой студенты записывают в тетрадь.
Задача.
Определить силу токов, текущих в ветвях, если ξ1 = 10 В, ξ2 = 24 В, внутренние сопротивления источников r1 = 2 Ом, r2 = 6 Ом, внешнее сопротивление R =16 Ом.
Дано:
ξ1 = 10 В
ξ2 = 24 В
r1 = 2 Ом
r2 = 6 Ом
R =16 Ом
Определить:
I1 =?, I2 = ?,I=?
4 этап. Подведение итогов урока.
Подведение итогов урока.
1). Самооценка работы учащимися:
— подсчёт количества выполненных заданий и заработанных баллов;
— какие работы вызвали затруднения и требуют повторения?
2). Оценка работы студентов преподавателем. Сбор «Листов учёта знаний» и выставление
оценок.
Итоговая оценка за урок выставляется с учётом набранных баллов по «Листу учёта знаний» и индивидуальной работы каждого студента.
Структура урока обобщения и систематизации знаний.
Этап урока | Время | Методическая цель | Развитие компетенций |
1 | 2 | 3 | 4 |
Первый этап Организационный момент Оглашение темы и задача урока Получение необходимой информации | 2 мин. 5мин. 5 мин. | готовность к уроку обеспечить понимание учащихся их деятельности, чего они должны достигнуть в результате урока инструктаж студентов для выполнения задания | |
Второй этап Воспроизведение основных структурных блоков темы: а) теоретическая часть; б) выполнение практического задания | 33 мин. 35 мин. | установление уровня овладения студентами теоретических знаний проверка и оценка умений обучающихся | ОК 6 ОК7 ОК6 |
Третий этап Домашнее задание | 5 мин. | закрепление пройденного материала | |
Четвёртый этап Подведение итогов | 5 мин. | а) самооценка работы студентами (подсчёт баллов) б) оценка работы студентов преподавателем |
При проведении занятий по физике для всех специальностей большое значение уделяется практическим занятиям – решению задач.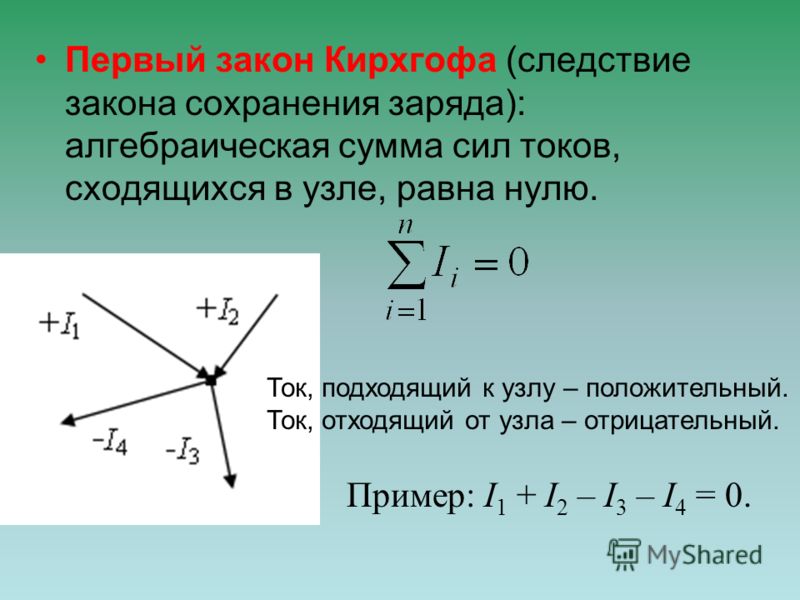 {н}ох{Эй}это{Дж}=0}. В левой части равенства легко научиться координировать работы матрицы i = 1 n a i j U j = 0 (я = 1 н а я и Ю и j = 0) {\свойства стиль отображения значение A вектор-столбца A} {\свойства стиль отображения значение \mathbf u. поэтому первое правило Кирхгофа в матричной форме, гласит: {u} } {\свойства стиль отображения значение а\mathbf A u = 0.
{н}ох{Эй}это{Дж}=0}. В левой части равенства легко научиться координировать работы матрицы i = 1 n a i j U j = 0 (я = 1 н а я и Ю и j = 0) {\свойства стиль отображения значение A вектор-столбца A} {\свойства стиль отображения значение \mathbf u. поэтому первое правило Кирхгофа в матричной форме, гласит: {u} } {\свойства стиль отображения значение а\mathbf A u = 0.
В таком виде она допускает обобщение на токопроводящие поверхности. Искривленную поверхность проводимость зависит не только от точки, но и направление. другими словами, проводимость является функцией на касательные векторы к поверхности. если мы предположим, что касательное пространство это хорошо приближается к положительно определенной квадратичной форме, мы можем говорить о нем, как в Римановой метрики {u} =0} {\свойства стиль отображения значение g отличается от расстояния на поверхности в геометрической форме с учетом анизотропии электрических свойств. каждая точка поверхности может служить узел, и, следовательно, емкость будет не вектор, а функция g} {\свойства стиль отображения значение u на поверхности. аналог матрицы проводимостей является оператором Лапласа — Бельтрами ∆ u} {\свойства стиль отображения значение \компании Delta _{г}} метрики-проводимость, которая действует на пространстве гладких функций. первое правило Кирхгофа к поверхности читает точно так же: Δ g {\свойства стиль отображения значение \компании Delta _{г}У=0}. другими словами, потенциал есть гармоническая функция.
аналог матрицы проводимостей является оператором Лапласа — Бельтрами ∆ u} {\свойства стиль отображения значение \компании Delta _{г}} метрики-проводимость, которая действует на пространстве гладких функций. первое правило Кирхгофа к поверхности читает точно так же: Δ g {\свойства стиль отображения значение \компании Delta _{г}У=0}. другими словами, потенциал есть гармоническая функция.
В этой связи, матрица g u = 0 (г У = 0) {\свойства стиль отображения значение A, который сопоставляет произвольной взвешенного графа, за исключением диагонали равен матрицы смежности, иногда называют дискретного лапласиана. аналоги теорем о гармонических функций, таких как наличие гармонических функций в области с области с заданным значением по краю, в результате свертки с некоторой ядра есть место для дискретных гармонических функций. назад проводящей поверхности можно аппроксимировать сетки резисторов, и дискретной гармонической функции на сетке аппроксимации гармонических функций на соответствующей поверхности. в этом случае компания интегратор gershgorina, аналоговые вычислительная машина, используемая для решения уравнения Лапласа в A} — 30-х лет 70-х века.
в этом случае компания интегратор gershgorina, аналоговые вычислительная машина, используемая для решения уравнения Лапласа в A} — 30-х лет 70-х века.
В случае проводящей поверхности, а не разность потенциалов, имеет смысл говорить о XX 1-форме {\свойства стиль отображения значение d u (д). связанные с показателями проводимости векторного поля du} {\свойства стиль отображения значение \mathrm g r a d g u (г р А Д Г) — это электрический ток на поверхности. первое правило Кирхгофа, это {grad} _{g}u} ({деления} _{г}у}) также гармоничный, который лежит в ядре Йыгева лапласиана определены дифференциальные формы. он дает подсказку, как правильно сформулировать закон Кирхгофа для случая, когда поле не потенциально, то есть 1-форма в результате нынешнего, рассматривается как векторное поле, используя проводимость, рассматриваемых как римановы метрики, должен быть гармоничным. зная ЭДС вокруг каждого топологически нетривиальные петли на поверхности, можно восстановить силу и направление течения в каждой точке, кроме того, единственный способ. В частности, измерение всевозможных ток, равный размерности пространства топологически нетривиальные контуры. это было одним из оснований для открытия Пуанкаре двойственность, тот факт, что электродвижущие силы, однозначно определить гармонический ток 1-форма, является частным случаем теории Ходжа для 1-форму.
В частности, измерение всевозможных ток, равный размерности пространства топологически нетривиальные контуры. это было одним из оснований для открытия Пуанкаре двойственность, тот факт, что электродвижущие силы, однозначно определить гармонический ток 1-форма, является частным случаем теории Ходжа для 1-форму.
Правило соединения — первый закон Кирхгофа
Физика > Правило соединения
Рассмотрите первый закон Кирхгофа – правило соединения и сохранения электрического заряда: уравнение первого правила Кирхгофа, схема электрической цепи.
Правило соединения Кирхгофа: при любом соединении схемы сумма токов, протекающих из перехода и в него, равняется.
Задача обучения
- Сформулируйте правило соединения и опишите ограничение.
Основные пункты
- Правило соединения – использование принципа сбережения электрического заряда. Ток – поток заряда за временной промежуток.
 Поток, протекающий в точку, должен равняться тому, что получаем на выходе из нее.
Поток, протекающий в точку, должен равняться тому, что получаем на выходе из нее. - В виде формулы: (Ik – ток k, а n – общее количество проводов, проходящих в/из рассматриваемого перехода).
- Закон ограничивается применимостью к участкам, где плотность заряда не способна оставаться стабильной.
Термины
- Электрический заряд – квантовое число, характеризующее электромагнитные контакты некоторых субатомных частичек.
- Поток – скорость перемещения электрического заряда.
Первым законом Кирхгофа для электрической цепи выступает правило соединения, нацеленное на сбережение электрического заряда. Согласно ему, в любом соединении в пределах электрической цепи сумма потоков, протекающих в переход, равна той, что получится на выходе. То есть, ток будет положительным или отрицательным, основываясь на том, перемещается к переходу или от него. Алгебраическое суммирование токов сети проводников, сталкивающихся в токе, приравнивается к нулю.
Закон соединения показан как токи, проходящие в проход и из него
В математическом виде первое правило Кирхгофа для разветвленных цепей:
(n – общее количество проводов, передающих ток в узел или из него).
Первый закон Кирхгофа основывается на сбережении заряда.
Ограничения
Этот закон имеет ограничения на использования. Он пригодится в ситуациях, где общий электрический заряд (Q) выступает постоянным в исследуемом участке. Это практически всегда работает для конкретной точки. Но если мы смотрим более масштабно, то плотность заряда не может оставаться стабильной. Тогда заряд сохраняется за счет потока через границу области, что нарушает правило.
Цепи постоянного тока — Физика
ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ (СИЛЫ) ТОКА .
ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ: величина (сила) тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике , где R — сопротивление проводника.
РЕЗИСТОРОМ называется устройство, обладающее заданным постоянным сопротивлением.
НАПРЯЖЕНИЕ НА РЕЗИСТОРЕ .
ЗАКОН ОМА ДЛЯ НЕОДНОРОДНОГО УЧАСТКА ЦЕПИ
, где j1 и j2 — потенциалы концов участка Е12 — э.д.с., действующая на данном участке цепи.
ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ , где Е — суммарная э.д.с., действующая в цепи, R — суммарное сопротивление всей цепи.
РАЗВЕТВЛЕННОЙ ЦЕПЬЮ называется электрическая цепь, имеющая узлы.
УЗЛОМ называется точка, в которой сходится более чем два проводника. Ток, текущий к узлу, принято считать положительным, а ток, текущий от узла, считается отрицательным.
ПЕРВОЕ ПРАВИЛО КИРХГОФА: алгебраическая сумма токов, сходящихся в узле, равна нулю = 0.
ВТОРОЕ ПРАВИЛО КИРХГОФА: в каждом из замкнутых контуров, которые можно мысленно выделить в данной разветвленной цепи, алгебраическая сумма падений напряжения равна алгебраической сумме э. д.с.
д.с.
.
При анализе разветвленной цепи следует обозначать с одним индексом ток, протекающий по всем последовательно соединенным элементам от одного узла до другого. Направление каждого тока выбирается произвольно.
При составлении уравнений второго правила Кирхгофа токам и э.д.с. нужно приписывать знаки в соответствии с выбранным (как вам удобно) НАПРАВЛЕНИЕМ ОБХОДА:
- ток принято считать положительным, если он совпадает с направлением обхода, и отрицательным, если он направлен против этого направления;
- э.д.с. считается положительной, если ее действие (создаваемый ею ток) совпадает с направлением обхода.
КОЛИЧЕСТВО УРАВНЕНИЙ первого правила Кирхгофа должно быть на одно меньше количества узлов в данной цепи. Количество независимых уравнений второго правила Кирхгофа должно быть таким, чтобы общее количество уравнений оказалось равным количеству различных токов. Каждый новый контур при этом должен содержать хотя бы один участок цепи, не вошедший в уже рассмотренные контуры.
МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ
В данной лабораторной работе исследуется модель простейшей разветвленной электрической цепи, состоящей из трех источников э.д.с., подключенных параллельно к одному резистору (нагрузке).
Закройте окно теории. Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы и зарисуйте их в конспект.
Нарисуйте в конспекте эквивалентную схему цепи, расположив источники один под другим и учитывая наличие внутреннего сопротивления у каждого источника. Укажите знаки э.д.с., направления токов в каждом участке и направления обхода каждого замкнутого контура. Составьте систему уравнений для нахождения токов в каждом участке.
ИЗМЕРЕНИЯ
Соберите на экране заданную эквивалентную цепь. Для этого сначала щелкните левой кнопкой мыши над кнопкой э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Ориентируйтесь на рисунок схемы в описании к данной ЛР. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен первый источник э. д.с. Переместите маркер мыши вниз на одну клетку и снова щелкните левой кнопкой под тем местом, где расположился первый источник. Там появится второй источник э.д.с. Аналогично разместите и третий источник.
д.с. Переместите маркер мыши вниз на одну клетку и снова щелкните левой кнопкой под тем местом, где расположился первый источник. Там появится второй источник э.д.с. Аналогично разместите и третий источник.
Разместите далее последовательно с каждым источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку R в нижней части экрана) и амперметр (кнопка А там же). Затем расположите резистор нагрузки и последовательно соединенный с ним амперметр. Под нагрузкой расположите вольтметр, измеряющий напряжение на нагрузке.
Подключите соединительные провода. Для этого нажмите кнопку провода внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкните левой кнопкой мыши в точке, где проходит провод.
Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, равное взятому из таблицы 1 для вашего варианта.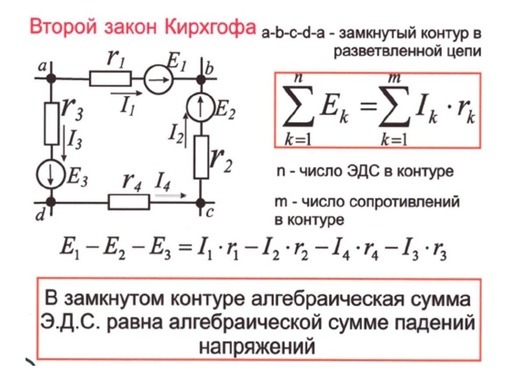
Установите сопротивления резистора нагрузки R = 1 Ом. Измерьте значения всех токов и напряжения на нагрузке (щелкнув мышью по кнопке «Счет») и запишите их в таблицу 2. Меняя сопротивление R, повторите измерения параметров и заполните таблицу 2.
Таблица 1. Значения э.д.с. и внутреннего сопротивления источников (не перерисовывать)
|
Вариат |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Е1,Е2,Е3 [В] |
3,7,-2 |
4,-3,-8 |
3,6,-4 |
6,-2,-8 |
-6,5,8 |
5,8,-4 |
-4,6,-7 |
8,-4,6 |
|
R1,R2,R3 [Ом] |
2,1,1 |
1,3,1 |
2,1,2 |
1,1,2 |
2,1,1 |
1,2,1 |
1,1,2 |
1,3,1 |
|
Таблица 2. |
Таблица 3. Результаты расчета |
||||||||||
|
R[Ом] |
I1 [A] |
I2 [A] |
I3 [A] |
I [A] |
U [В] |
I1 [A] |
I2 [A] |
I3 [A] |
I [A] |
||
|
1 |
|||||||||||
|
2 |
|||||||||||
|
3 |
|||||||||||
|
4 |
|||||||||||
|
5 |
|||||||||||
|
6 |
|||||||||||
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА
Запишите для вашей цепи решение системы уравнений для всех токов в общем виде.
Рассчитайте значения всех токов для каждого сопротивления нагрузки и запишите в таблицу 3.
Постройте график экспериментальной зависимости падения напряжения на нагрузке U от тока I через нее.
Сформулируйте выводы по графику.
Вопросы и задания для самоконтроля
- Что такое электрический ток?
- Дайте определение величины (силы) тока.
- Дайте определение разности потенциалов (напряжения).
- Напишите формулу, связывающую приращение потенциалов и напряжение.
- Что такое резистор?
- Напишите формулу для сопротивления последовательно соединенных резисторов.
- Напишите формулу для сопротивления параллельно соединенных резисторов.
- Напишите закон Ома для участка цепи. Сравните его с законом Ома в дифференциальной (локальной) форме.
- Какой участок цепи называется неоднородным?
- Запишите закон Ома для неоднородного участка цепи.
- Какими характеристиками описывается источник ЭДС?
- Сформулируйте первый закон Кирхгофа.
 Какое свойство заряда он отражает?
Какое свойство заряда он отражает? - Запишите формулу для первого закона Кирхгофа.
- Сформулируйте второй закон Кирхгофа.
- Запишите формулу для второго закона Кирхгофа.
- Что такое узел электрической цепи?
- Что такое полная электрическая цепь?
правил Кирхгофа | Безграничная физика
Введение и значение
Законы цепи Кирхгофа — это два уравнения, которые касаются сохранения энергии и заряда в контексте электрических цепей.
Цели обучения
Опишите взаимосвязь между законами цепи Кирхгофа и энергией и зарядом в электрических цепях.
Основные выводы
Ключевые моменты
- Кирхгоф использовал работу Георга Ома в качестве основы для создания закона Кирхгофа (KCL) и закона напряжения Кирхгофа (KVL) в 1845 году.Их можно вывести из уравнений Максвелла, которые появились 16-17 лет спустя.
- Невозможно проанализировать некоторые схемы с обратной связью путем упрощения в виде суммы и / или ряда компонентов.
 В этих случаях можно использовать законы Кирхгофа.
В этих случаях можно использовать законы Кирхгофа. - Законы Кирхгофа — частные случаи сохранения энергии и заряда.
Ключевые термины
- резистор : Электрический компонент, который передает ток прямо пропорционально напряжению на нем.
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея.Она измеряется в вольтах (не в ньютонах, Н; ЭДС — это не сила).
- конденсатор : Электронный компонент, состоящий из двух проводящих пластин, разделенных пустым пространством (иногда вместо этого между пластинами помещается диэлектрический материал), и способный хранить определенное количество заряда.
Введение в законы Кирхгофа
Законы цепи Кирхгофа — это два уравнения, впервые опубликованные Густавом Кирхгофом в 1845 году. По сути, они касаются сохранения энергии и заряда в контексте электрических цепей.
Хотя законы Кирхгофа можно вывести из уравнений Джеймса Клерка Максвелла, Максвелл не публиковал свою систему дифференциальных уравнений (которые составляют основу классической электродинамики, оптики и электрических цепей) до 1861 и 1862 годов. Кирхгоф, скорее, использовал Георга. Работа Ома как основа для текущего закона Кирхгофа (KCL) и закона напряжения Кирхгофа (KVL) .
Законы Кирхгофа чрезвычайно важны для анализа замкнутых цепей.Рассмотрим, например, схему, показанную на рисунке ниже, состоящую из пяти резисторов, соединенных последовательно и параллельно. Упрощение этой схемы до комбинации последовательного и параллельного включения невозможно. Однако, используя правила Кирхгофа, можно проанализировать схему, чтобы определить параметры этой схемы, используя номиналы резисторов (R 1 , R 2 , R 3 , r 1 и r 2 ). . Также важно в этом примере то, что значения E 1 и E 2 представляют источники напряжения (например.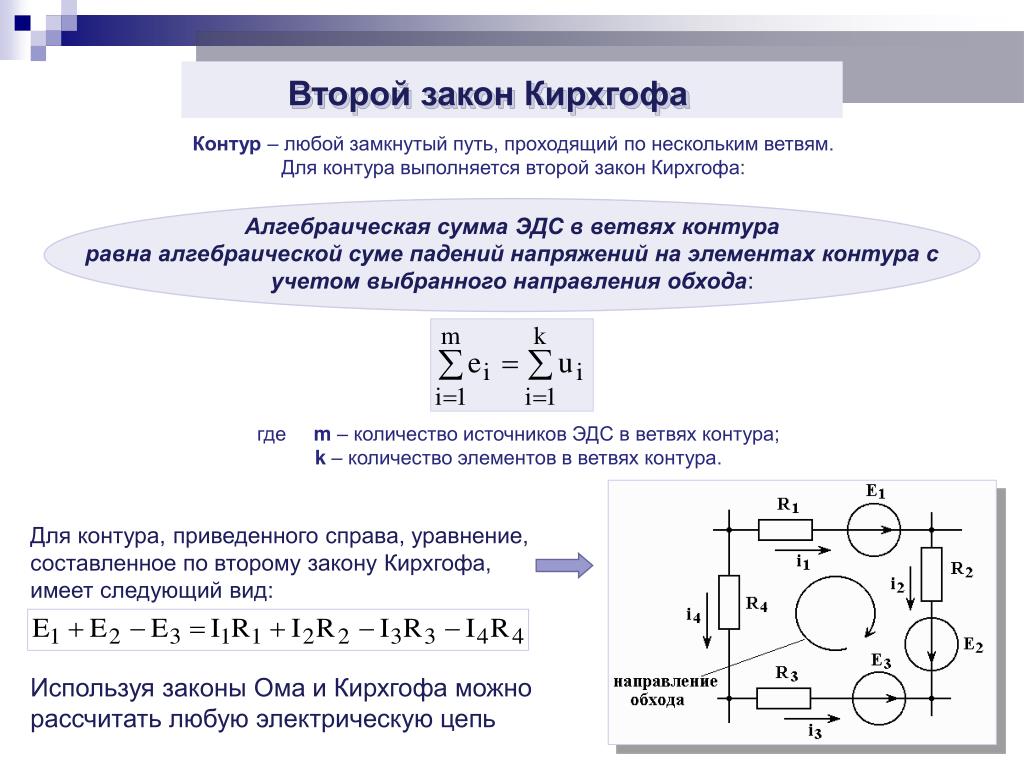 г., батарейки).
г., батарейки).
Замкнутая цепь : Чтобы определить все переменные (т. Е. Падение тока и напряжения на различных резисторах) в этой цепи, необходимо применить правила Кирхгофа.
В заключение, законы Кирхгофа зависят от определенных условий. Закон напряжения является упрощением закона индукции Фарадея и основан на предположении, что в замкнутом контуре нет флуктуирующего магнитного поля. Таким образом, хотя этот закон может быть применен к схемам, содержащим резисторы и конденсаторы (а также другие элементы схемы), его можно использовать только как приближение к поведению схемы при изменении тока и, следовательно, магнитного поля.
Правило пересечения
Правило соединений Кирхгофа гласит, что в любом соединении цепи сумма токов, текущих в это соединение и из него, равна.
Цели обучения
Сформулируйте правило пересечения Кирхгофа и опишите его ограничения
Основные выводы
Ключевые моменты
- Правило соединения Кирхгофа — это применение принципа сохранения электрического заряда: ток — это поток заряда за время, и если ток постоянный, то, что течет в точку в цепи, должно быть равно тому, что вытекает из нее.
 {\ text {n}} \ text {I} _ \ text {k} = 0 [/ latex], где I k — ток k, а n — общее количество проводов, входящих и выходящих из соединения. с учетом.
{\ text {n}} \ text {I} _ \ text {k} = 0 [/ latex], где I k — ток k, а n — общее количество проводов, входящих и выходящих из соединения. с учетом. - Закон перехода Кирхгофа ограничен в его применимости в регионах, в которых плотность заряда может быть непостоянной. Поскольку заряд сохраняется, это возможно только при наличии потока заряда через границу области. Этот поток был бы током, нарушая закон.
Ключевые термины
- электрический заряд : квантовое число, определяющее электромагнитные взаимодействия некоторых субатомных частиц; По соглашению, электрон имеет электрический заряд -1, а протон +1, а кварки имеют дробный заряд.
- ток : временная скорость протекания электрического заряда.
Правило соединения Кирхгофа, также известное как текущий закон Кирхгофа (KCL), первый закон Кирхгофа, правило точки Кирхгофа и узловое правило Кирхгофа, является применением принципа сохранения электрического заряда.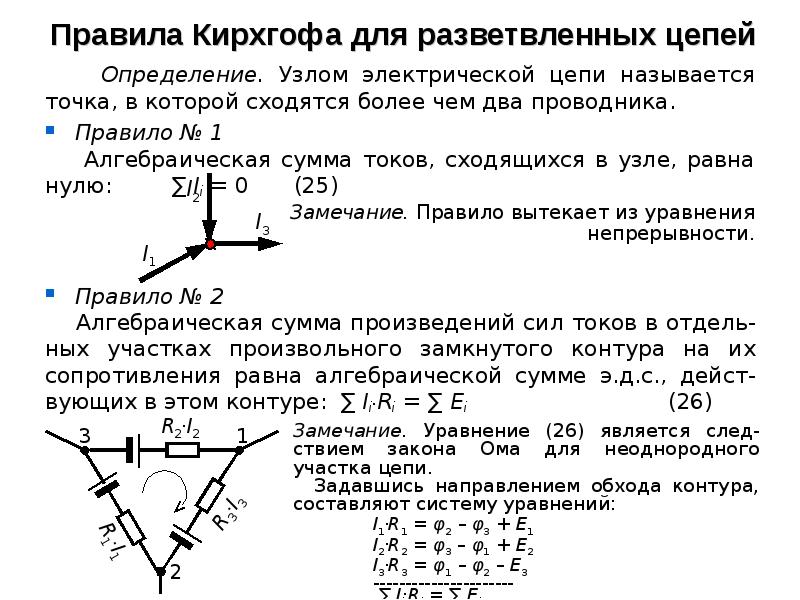
Правило соединений Кирхгофа гласит, что в любом соединении (узле) в электрической цепи сумма токов, протекающих в этом соединении, равна сумме токов, вытекающих из этого соединения.Другими словами, при условии, что ток будет положительным или отрицательным в зависимости от того, течет он к стыку или от него, алгебраическая сумма токов в сети проводников, встречающихся в одной точке, равна нулю. Визуальное представление можно увидеть на.
Закон соединения Кирхгофа : Закон соединения Кирхгофа, проиллюстрированный как токи, текущие в соединение и выходящие из него.
Теория правил Кирхгофа петли и соединений : Мы оправдываем правила Кирхгофа, исходя из сохранения энергии.{\ text {n}} \ text {I} _ \ text {k} = 0 [/ latex]
, где n — общее количество ветвей, по которым ток идет к узлу или от него.
Этот закон основан на сохранении заряда (измеряемого в кулонах), который является произведением силы тока (в амперах) и времени (в секундах).
Ограничение
Применимость закона Кирхгофа ограничена. Это справедливо для всех случаев, когда полный электрический заряд (Q) постоянен в рассматриваемой области. На практике это всегда так, если закон применяется к определенной точке.Однако в определенной области плотность заряда может быть непостоянной. Поскольку заряд сохраняется, это возможно только при наличии потока заряда через границу области. Этот поток был бы током, что нарушало бы закон Кирхгофа.
Правило цикла
Правило петли Кирхгофа гласит, что сумма значений ЭДС в любом замкнутом контуре равна сумме падений потенциала в этом контуре.
Цели обучения
Сформулируйте правило петли Кирхгофа, учитывая его допущения.
Основные выводы
Ключевые моменты
- Правило петли Кирхгофа — это правило, относящееся к схемам, основанное на принципе сохранения энергии.
 \ text {n} \ text {V} _ \ text {k} = 0 [/ latex].
\ text {n} \ text {V} _ \ text {k} = 0 [/ latex]. - Правило петли Кирхгофа является упрощением закона индукции Фарадея и выполняется при предположении, что нет флуктуирующего магнитного поля, связывающего замкнутый контур.
Ключевые термины
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
- резистор : Электрический компонент, который передает ток прямо пропорционально напряжению на нем.
Правило петли Кирхгофа (также известное как закон напряжения Кирхгофа (KVL), правило сетки Кирхгофа, второй закон Кирхгофа, или второе правило Кирхгофа ) является правилом, относящимся к схемам, и основано на принципе сохранения энергия.
Сохранение энергии — принцип, согласно которому энергия не создается и не разрушается — широко используется во многих исследованиях в области физики, включая электрические схемы. Применительно к схемотехнике подразумевается, что направленная сумма разностей электрических потенциалов (напряжений) вокруг любой замкнутой сети равна нулю.Другими словами, сумма значений электродвижущей силы (ЭДС) в любом замкнутом контуре равна сумме падений потенциала в этом контуре (которые могут исходить от резисторов).
Применительно к схемотехнике подразумевается, что направленная сумма разностей электрических потенциалов (напряжений) вокруг любой замкнутой сети равна нулю.Другими словами, сумма значений электродвижущей силы (ЭДС) в любом замкнутом контуре равна сумме падений потенциала в этом контуре (которые могут исходить от резисторов).
Другое эквивалентное утверждение состоит в том, что алгебраическая сумма произведений сопротивлений проводников (и токов в них) в замкнутом контуре равна общей электродвижущей силе, доступной в этом контуре. Математически правило петли Кирхгофа можно представить как сумму напряжений в цепи, которая приравнивается к нулю:
Теория правил Кирхгофа петли и соединений : Мы оправдываем правила Кирхгофа, исходя из сохранения энергии. \ text {n} \ text {V} _ \ text {k} = 0 [/ latex].
\ text {n} \ text {V} _ \ text {k} = 0 [/ latex].
Здесь V k — это напряжение на элементе k, а n — общее количество элементов в замкнутой цепи. Иллюстрация такой схемы показана на. В этом примере сумма v 1 , v 2 , v 3 и v 4 (и v 5 , если она включена) равна нуль.
Правило петли Кирхгофа : Правило петли Кирхгофа гласит, что сумма всех напряжений вокруг петли равна нулю: v1 + v2 + v3 — v4 = 0.
Учитывая, что напряжение является мерой энергии на единицу заряда, правило петли Кирхгофа основано на законе сохранения энергии, который гласит: общая энергия, полученная на единицу заряда, должна равняться количеству энергии, потерянной на единицу заряда .
Пример
иллюстрирует изменения потенциала в простой петле последовательной цепи. Второе правило Кирхгофа требует, чтобы ЭДС-Ir-IR 1 -IR 2 = 0. В перестановке это ЭДС = Ir + IR 1 + IR 2 , что означает, что ЭДС равна сумме падений IR (напряжения) в контуре.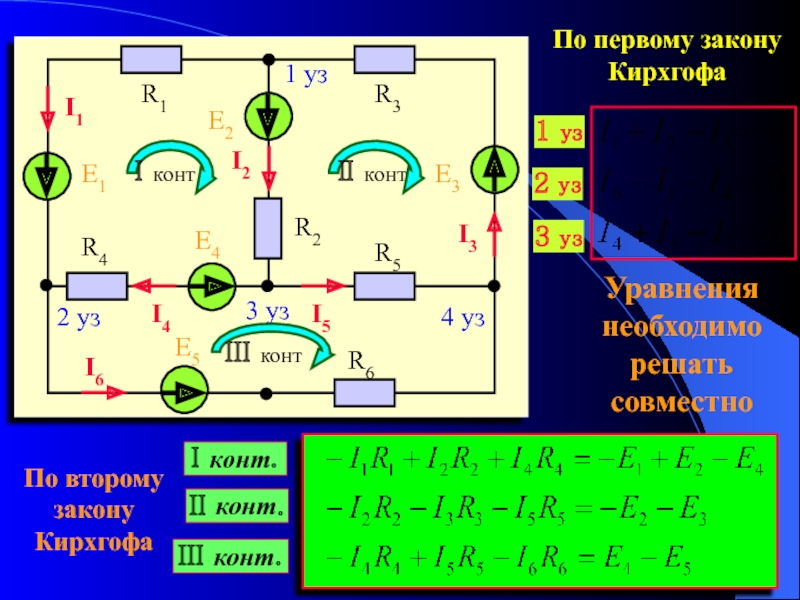 ЭДС подает 18 В, которое уменьшается до нуля из-за сопротивления, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, всего 18 В.
ЭДС подает 18 В, которое уменьшается до нуля из-за сопротивления, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, всего 18 В.
Правило цикла : пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) В этой стандартной схеме простой последовательной цепи ЭДС подает 18 В, которое снижается до нуля из-за сопротивлений, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки для всего 18 В.(b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и понижается за счет сопротивлений. (Обратите внимание, что сценарий E означает ЭДС.)
Ограничение
Правило петли Кирхгофа является упрощением закона индукции Фарадея и выполняется при предположении, что нет флуктуирующего магнитного поля, связывающего замкнутый контур. В присутствии переменного магнитного поля могут индуцироваться электрические поля и возникать ЭДС, и в этом случае правило петли Кирхгофа нарушается.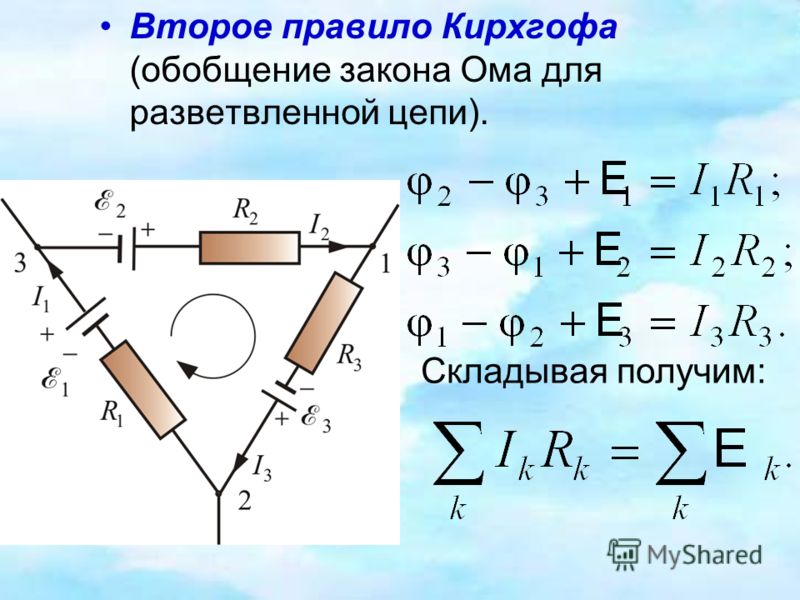
Приложения
Правила Кирхгофа можно использовать для анализа любой схемы и модифицировать для схем с ЭДС, резисторами, конденсаторами и т. Д.
Цели обучения
Опишите условия, при которых полезно применять правила Кирхгофа.
Основные выводы
Ключевые моменты
- Правила Кирхгофа применимы к любой цепи, независимо от ее состава и структуры.
- Поскольку часто легко комбинировать элементы параллельно и последовательно, не всегда удобно применять правила Кирхгофа.
- Для определения тока в цепи можно применить правила петли и соединения. Как только все токи связаны правилом соединения, можно использовать правило петли для получения нескольких уравнений, которые будут использоваться в качестве системы для нахождения каждого значения тока в терминах других токов. Их можно решить как систему.
Ключевые термины
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея.
 Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
Обзор
ПравилаКирхгофа можно использовать для анализа любой цепи, изменяя их для этих цепей с электродвижущими силами, резисторами, конденсаторами и т. Д. Однако с практической точки зрения правила полезны только для характеристики тех цепей, которые нельзя упростить, комбинируя элементы последовательно и параллельно.
Последовательные и параллельные комбинации, как правило, намного проще выполнить, чем применение любого из правил Кирхгофа, но правила Кирхгофа применимы более широко и должны использоваться для решения проблем, связанных со сложными схемами, которые нельзя упростить, комбинируя элементы схемы последовательно или параллельно.
Пример правил Кирхгофа
показывает очень сложную схему, но можно применить правила Кирхгофа для петель и соединений. Чтобы решить схему для токов I 1 , I 2 и I 3 , необходимы оба правила.
Правила Кирхгофа: пример задачи : На этом изображении показана очень сложная схема, которую можно сократить и решить с помощью правил Кирхгофа.
Применяя правило Кирхгофа в точке a, находим:
[латекс] \ text {I} _1 = \ text {I} _2 + \ text {I} _3 [/ latex]
, потому что I 1 течет в точку a, а I 2 и I3 вытекает.То же самое можно найти в точке e. Теперь мы должны решить это уравнение для каждой из трех неизвестных переменных, что потребует трех разных уравнений.
Учитывая цикл abcdea, мы можем использовать правило цикла Кирхгофа:
[латекс] — \ text {I} _2 \ text {R} _2 + \ mathrm {\ text {emf}} _ 1- \ text {I} _2 \ text {r} _1- \ text {I} _1 \ text { R} _1 = — \ text {I} _2 (\ text {R} _2) + \ text {r} _1) + \ mathrm {\ text {emf}} _ 1- \ text {I} _1 \ text {R} _1 = 0 [/ латекс]
Подставляя значения сопротивления и ЭДС из рисунка на диаграмме и отменяя единицу измерения ампер, получаем:
[латекс] -3 \ text {I} _2 + 18-6 \ text {I} _1 = 0 [/ латекс]
Это вторая часть системы трех уравнений, которую мы можем использовать, чтобы найти все три текущих значения. Последнюю можно найти, применив правило цикла к циклу aefgha, которое дает:
Последнюю можно найти, применив правило цикла к циклу aefgha, которое дает:
[латекс] \ text {I} _1 \ text {R} _1 + \ text {I} _3 \ text {R} _3 + \ text {I} _3 \ text {r} _2- \ mathrm {\ text {emf}} _2 = \ text {I} _1 \ text {R} _1 + \ text {I} _3 (\ text {R} _3 + \ text {r} _2) — \ mathrm {\ text {emf}} _ 2 = 0 [/ латекс ]
Используя замену и упрощение, это становится:
[латекс] 6 \ text {I} _1 + 2 \ text {I} _3-45 = 0 [/ латекс]
В этом случае знаки поменялись местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении.
Теперь у нас есть три уравнения, которые можно использовать в системе. Второй будет использоваться для определения I 2 и может быть изменен на:
[латекс] \ text {I} _2 = 6-2 \ text {I} _1 [/ латекс]
Третье уравнение может использоваться для определения I 3 и может быть преобразовано в:
[латекс] \ text {I} _3 = 22,5-3 \ text {I} _1 [/ латекс]
Подставляя новые определения I 2 и I 3 (которые являются общими терминами I 1 ) в первое уравнение (I 1 = I 2 + I 3 ), получаем:
[латекс] \ text {I} _1 = (6-2 \ text {I} _1) + (22. 5-3 \ text {I} _1) = 28,5-5 \ text {I} _1 [/ latex]
5-3 \ text {I} _1) = 28,5-5 \ text {I} _1 [/ latex]
Упрощая, получаем, что I 1 = 4,75 A. Подставляя это значение в два других уравнения, мы находим, что I 2 = -3,50 A и I 3 = 8,25 A.
10.3 Правила Кирхгофа — Университетская физика, Том 2
Цели обучения
К концу раздела вы сможете:- Государственное правило Кирхгофа
- Государственное правило петли Кирхгофа
- Анализировать сложные схемы по правилам Кирхгофа
Мы только что видели, что некоторые схемы можно проанализировать, сведя схему к одному источнику напряжения и эквивалентному сопротивлению.Многие сложные схемы не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в предыдущих разделах. В этом разделе мы подробно рассмотрим использование правил Кирхгофа для анализа более сложных схем. Например, схема на рис. 10.19 известна как многоконтурная схема, состоящая из переходов.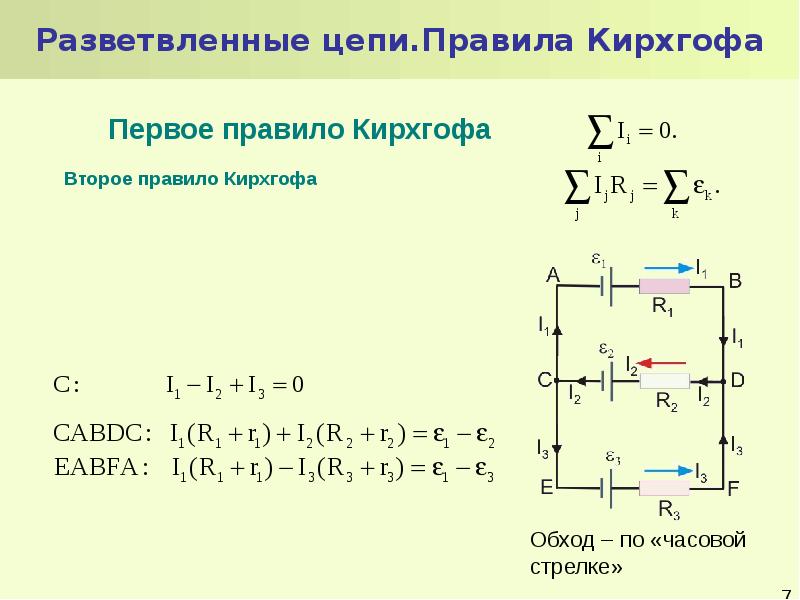 Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы имеют четкую последовательную или параллельную конфигурацию, которую можно уменьшить.Попробуйте. Резисторы R1R1 и R2R2 включены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое и с резисторами R4R4 и R5R5. Но что же тогда делать?
Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы имеют четкую последовательную или параллельную конфигурацию, которую можно уменьшить.Попробуйте. Резисторы R1R1 и R2R2 включены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое и с резисторами R4R4 и R5R5. Но что же тогда делать?
Несмотря на то, что эта схема не может быть проанализирована с помощью уже изученных методов, два правила анализа схемы могут использоваться для анализа любой схемы, простой или сложной. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).
Рисунок 10.19 Эта схема не может быть сведена к комбинации последовательного и параллельного соединения.Однако мы можем использовать правила Кирхгофа для его анализа.
Правила Кирхгофа
- Первое правило Кирхгофа — правило соединения.
 Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения:
∑Iin = ∑Iout.∑Iin = ∑Iout.
Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения:
∑Iin = ∑Iout.∑Iin = ∑Iout.10,4
- Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любого пути (контура) замкнутой цепи должна быть равна нулю:
Теперь мы даем объяснения этих двух правил, за которыми следуют советы по их применению и рабочий пример, в котором они используются.
Первое правило Кирхгофа
Первое правило Кирхгофа (правило соединения) применяется к заряду, входящему в соединение и выходящему из него (рис. 10.20). Как указывалось ранее, соединение или узел — это соединение трех или более проводов. Ток — это поток заряда, и заряд сохраняется; таким образом, любой заряд, попадающий в переход, должен вытекать.
Рисунок 10.20 Заряд должен сохраняться, поэтому сумма токов в переходе должна быть равна сумме токов на выходе.
Хотя это чрезмерное упрощение, можно провести аналогию с водопроводными трубами, соединенными в водопроводной разводке. Если провода на рис. 10.20 были заменены водопроводными трубами и вода считалась несжимаемой, объем воды, текущей в соединение, должен быть равен объему воды, вытекающей из соединения.
Если провода на рис. 10.20 были заменены водопроводными трубами и вода считалась несжимаемой, объем воды, текущей в соединение, должен быть равен объему воды, вытекающей из соединения.
Второе правило Кирхгофа
Второе правило Кирхгофа (правило петли) применяется к разности потенциалов. Правило петли сформулировано в терминах потенциала В , а не потенциальной энергии, но они связаны между собой, поскольку U = qV.U = qV. В замкнутом контуре, какая бы энергия ни поступала от источника напряжения, энергия должна быть передана в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжение, подаваемое источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простую петлю без стыков, как на рис. 10.21.
Рисунок 10.21 Простая петля без стыков. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.
Правило петли Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.
Схема состоит из источника напряжения и трех внешних нагрузочных резисторов. Этикетки a , b , c и d служат в качестве ссылок и не имеют другого значения. Скоро станет очевидна полезность этих этикеток. Цепь обозначается как Loop abcda , и метки помогают отслеживать разницу напряжений при перемещении по цепи.Начните с точки a и двигайтесь к точке b . Напряжение источника напряжения добавляется к уравнению и вычитается падение потенциала резистора R1R1. От точки b до c вычитается падение потенциала на R2R2. От c до d вычитается потенциальное падение на R3R3. От точек d до a ничего не делается, потому что нет компонентов.
От точек d до a ничего не делается, потому что нет компонентов.
На рис. 10.22 показан график напряжения при перемещении по контуру.Напряжение увеличивается при прохождении через батарею, тогда как напряжение уменьшается при прохождении через резистор. Падение потенциала или изменение электрического потенциала равно току через резистор, умноженному на сопротивление резистора. Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
Рисунок 10.22 График напряжения при движении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор.Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
Тогда правило петли Кирхгофа утверждает
V-IR1-IR2-IR3 = 0. V-IR1-IR2-IR3 = 0.
Уравнение контура можно использовать для определения тока в контуре:
I = VR1 + R2 + R2 = 12,00 В, 1,00 Ом + 2,00 Ом + 3,00 Ом = 2,00 А. I = VR1 + R2 + R2 = 12,00 В, 1,00 Ом + 2,00 Ом + 3,00 Ом = 2,00 А.Этот цикл можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем мощь метода Кирхгофа в следующем разделе.
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы генерируем набор линейных уравнений, которые позволяют нам находить неизвестные значения в схемах. Это могут быть токи, напряжения или сопротивления. Каждый раз, когда применяется правило, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то проблема может быть решена.
Использование метода анализа Кирхгофа требует нескольких шагов, перечисленных в следующей процедуре.
Стратегия решения проблем
Правила Кирхгофа
- Обозначьте точки на принципиальной схеме строчными буквами a , b , c ,….
 Эти ярлыки просто помогают сориентироваться.
Эти ярлыки просто помогают сориентироваться. - Найдите соединения в цепи. Соединения — это точки, в которых соединяются три или более проводов. Обозначьте каждое соединение токами и направлениями в него и из него. Убедитесь, что по крайней мере один ток направлен на соединение, а по крайней мере один ток выходит из соединения.
- Выбрать петли в схеме. Каждый компонент должен содержаться хотя бы в одном цикле, но компонент может содержаться более чем в одном цикле.
- Примените правило соединения.Опять же, некоторые стыки не следует включать в анализ. Вам нужно использовать достаточно узлов только для включения каждого тока.
- Примените правило цикла. Используйте карту на рисунке 10.23.
Рисунок 10.23 Каждый из этих резисторов и источников напряжения проходит от до до на . (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном току, добавьте падение потенциала.(c) При перемещении источника напряжения от отрицательного вывода к положительному, добавьте падение потенциала. (d) При перемещении через источник напряжения от положительной клеммы к отрицательной вычтите падение потенциала.
(b) При перемещении через резистор в направлении, противоположном току, добавьте падение потенциала.(c) При перемещении источника напряжения от отрицательного вывода к положительному, добавьте падение потенциала. (d) При перемещении через источник напряжения от положительной клеммы к отрицательной вычтите падение потенциала.
Давайте рассмотрим некоторые этапы этой процедуры более подробно. При размещении переходов в цепи не обращайте внимания на направление токов. Если направление потока тока неочевидно, выбора любого направления достаточно, если хотя бы один ток направлен в соединение и хотя бы один ток выходит из соединения.Если стрелка находится в направлении, противоположном обычному течению тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.
Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.
Рассмотрим рисунок 10.24. В этой цепи два перехода: переход b и переход e .Точки a , c , d и f не являются перекрестками, потому что стык должен иметь три или более соединений. Уравнение для перехода b : I1 = I2 + I3I1 = I2 + I3, а уравнение для перехода e — I2 + I3 = I1I2 + I3 = I1. Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.
Рис. 10.24 На первый взгляд, эта схема содержит два соединения, соединение b и соединение e , но следует рассматривать только один, поскольку их уравнения соединения эквивалентны.
При выборе петель в схеме вам необходимо достаточное количество петель, чтобы каждый компонент был покрыт один раз, без повторения петель. На рис. 10.25 показаны четыре варианта петель для решения типовой схемы; варианты (a), (b) и (c) имеют достаточное количество циклов для полного решения схемы. Вариант (d) отражает больше петель, чем необходимо для решения схемы.
На рис. 10.25 показаны четыре варианта петель для решения типовой схемы; варианты (a), (b) и (c) имеют достаточное количество циклов для полного решения схемы. Вариант (d) отражает больше петель, чем необходимо для решения схемы.
Рисунок 10.25 Панели (a) — (c) достаточно для анализа схемы. В каждом случае два показанных контура содержат все элементы схемы, необходимые для полного решения схемы.На панели (d) показаны три использованных контура, что больше, чем необходимо. Любые две петли в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла дает избыточную информацию.
Рассмотрим схему на рисунке 10.26 (а). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала промаркируйте схему, как показано в части (b).
Рисунок 10.26 (a) Многоконтурная схема. (b) Пометьте цепь, чтобы облегчить ориентацию.
Далее определяем перекрестки.В этой схеме точки b и e имеют по три соединенных провода, что делает их соединениями.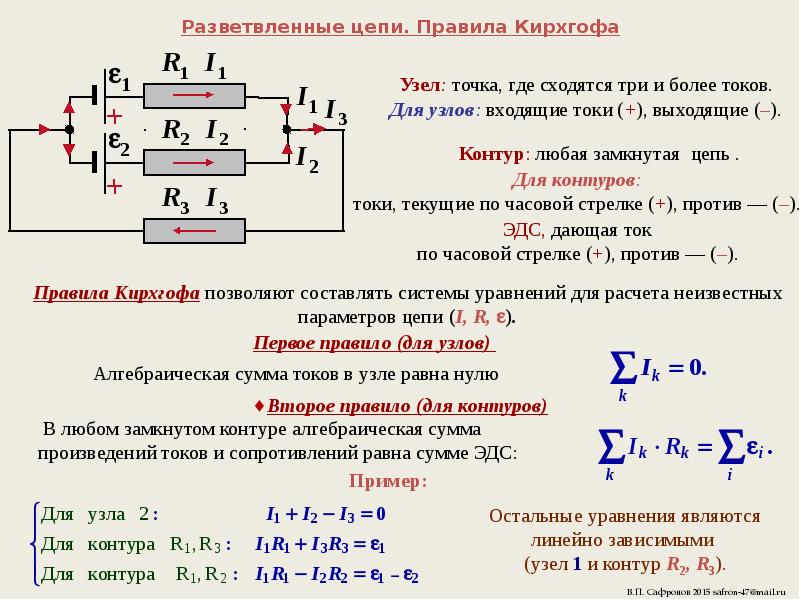 Начните применять правило соединения Кирхгофа (∑Iin = ∑Iout) (∑Iin = ∑Iout), нарисовав стрелки, представляющие токи, и пометив каждую стрелку, как показано на рисунке 10.27 (b). Соединение b показывает, что I1 = I2 + I3I1 = I2 + I3, а соединение e показывает, что I2 + I3 = I1I2 + I3 = I1. Поскольку соединение e дает ту же информацию, что и соединение b , ее можно не принимать во внимание.Эта схема имеет три неизвестных, поэтому для ее анализа нам понадобятся три линейно независимых уравнения.
Начните применять правило соединения Кирхгофа (∑Iin = ∑Iout) (∑Iin = ∑Iout), нарисовав стрелки, представляющие токи, и пометив каждую стрелку, как показано на рисунке 10.27 (b). Соединение b показывает, что I1 = I2 + I3I1 = I2 + I3, а соединение e показывает, что I2 + I3 = I1I2 + I3 = I1. Поскольку соединение e дает ту же информацию, что и соединение b , ее можно не принимать во внимание.Эта схема имеет три неизвестных, поэтому для ее анализа нам понадобятся три линейно независимых уравнения.
Рис. 10.27 (a) Эта схема имеет два соединения, обозначенных b и e , но в анализе используется только узел b . (b) Обозначенные стрелки представляют токи в переходах и на выходе из них.
Далее нам нужно выбрать петли. На рисунке 10.28 контур abefa включает в себя источник напряжения V1V1 и резисторы R1R1 и R2R2. Цикл начинается в точке a , затем проходит через точки b , e и f , а затем возвращается к точке a .Второй контур, контур ebcde , начинается в точке e и включает резисторы R2R2 и R3R3, а также источник напряжения V2V2.
Цикл начинается в точке a , затем проходит через точки b , e и f , а затем возвращается к точке a .Второй контур, контур ebcde , начинается в точке e и включает резисторы R2R2 и R3R3, а также источник напряжения V2V2.
Рисунок 10.28 Выберите петли в схеме.
Теперь мы можем применить правило цикла Кирхгофа, используя карту на рисунке 10.23. Начиная с точки a и двигаясь к точке b , резистор R1R1 пересекается в том же направлении, что и ток I1I1, поэтому падение потенциала I1R1I1R1 вычитается. Двигаясь от точки b к точке e , резистор R2R2 пересекается в том же направлении, что и ток I2I2, поэтому падение потенциала I2R2I2R2 вычитается. Двигаясь от точки e к точке f , источник напряжения V1V1 пересекается от отрицательной клеммы к положительной клемме, поэтому добавляется V1V1. Между точками f и a нет компонентов. Сумма разностей напряжений должна равняться нулю:
Двигаясь от точки e к точке f , источник напряжения V1V1 пересекается от отрицательной клеммы к положительной клемме, поэтому добавляется V1V1. Между точками f и a нет компонентов. Сумма разностей напряжений должна равняться нулю:
Наконец, мы проверяем цикл ebcde . Мы начинаем с точки e и переходим к точке b , пересекая R2R2 в направлении, противоположном течению тока I2I2.Добавляется падение потенциала I2R2I2R2. Затем мы пересекаем R3R3 и R4R4 в том же направлении, что и ток I3I3, и вычитаем падения потенциала I3R3I3R3 и I3R4.I3R4. Обратите внимание, что ток через резисторы R3R3 и R4R4 одинаковый, потому что они соединены последовательно. Наконец, источник напряжения пересекается с положительной клеммы на отрицательную, а источник напряжения V2V2 вычитается. Сумма этих разностей напряжений равна нулю и дает уравнение контура
Сумма этих разностей напряжений равна нулю и дает уравнение контура
Теперь у нас есть три уравнения, которые мы можем решить относительно трех неизвестных.
(1) Узел b: I1 − I2 − I3 = 0. (2) Петля: I1R1 + I2R2 = V1. (3) Узел b: I2R2 − I3 (R3 + R4) = V2. (1) Узел b: I1 − I2 − I3 = 0. (2) Цикл: I1R1 + I2R2 = V1. (3) Цикл: I2R2-I3 (R3 + R4) = V2.Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока I2I2. Сначала добавьте уравнение. (1) умножить на R2R2 по формуле. (2). Результат обозначен как уравнение. (4):
(R1 + R2) I1 − R2I3 = V1. (4) 6ΩI1−3ΩI3 = 24 В. (R1 + R2) I1 − R2I3 = V1.(4) 6ΩI1−3ΩI3 = 24В.Затем вычтите уравнение. (3) из уравнения. (2). Результат обозначен как уравнение. (5):
I1R1 + I3 (R3 + R4) = V1 − V2. (5) 3ΩI1 + 7ΩI3 = −5V. I1R1 + I3 (R3 + R4) = V1 − V2. (5) 3ΩI1 + 7ΩI3 = −5V. Мы можем решить уравнения. (4) и (5) для тока I1I1. Сложив в семь раз уравнение. (4) и троекратное уравнение. (5) дает 51 Ом I1 = 153 В, 51 Ом I1 = 153 В или I1 = 3,00 А. I1 = 3,00 А. Используя уравнение. (4) дает I3 = −2,00 A. I3 = −2,00 A. Наконец, уравнение. (1) дает I2 = I1 − I3 = 5,00 A. I2 = I1 − I3 = 5,00 A. Один из способов проверить соответствие решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:
(4) и троекратное уравнение. (5) дает 51 Ом I1 = 153 В, 51 Ом I1 = 153 В или I1 = 3,00 А. I1 = 3,00 А. Используя уравнение. (4) дает I3 = −2,00 A. I3 = −2,00 A. Наконец, уравнение. (1) дает I2 = I1 − I3 = 5,00 A. I2 = I1 − I3 = 5,00 A. Один из способов проверить соответствие решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:
Обратите внимание, что решение для тока I3I3 отрицательное. Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединений, имеет направление, противоположное направлению обычного тока. Мощность, отдаваемая вторым источником напряжения, составляет 58 Вт, а не −58 Вт.
Пример 10.6
Расчет тока по правилам Кирхгофа
Найдите токи, протекающие в цепи на рисунке 10.29. Рисунок 10.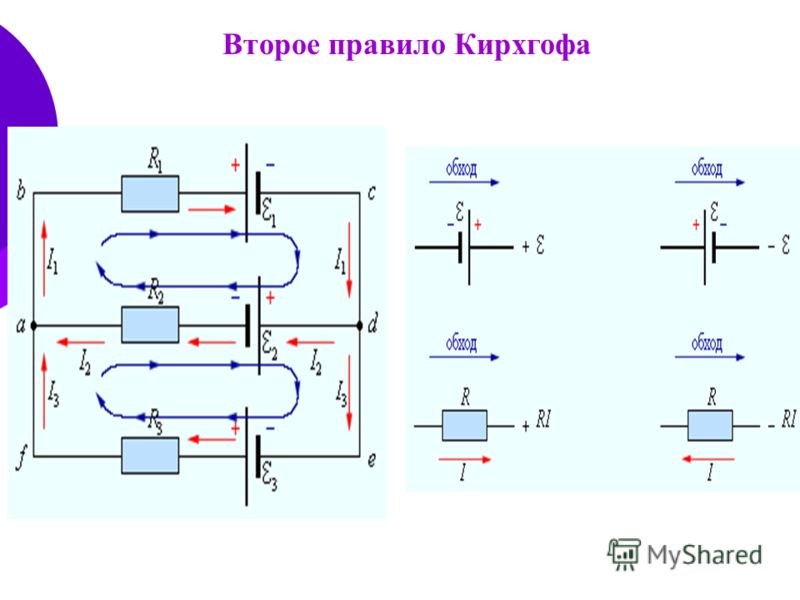 29 Эта схема представляет собой комбинацию последовательной и параллельной конфигураций резисторов и источников напряжения. Эта схема не может быть проанализирована с использованием методов, обсуждаемых в «Электродвижущей силе», но может быть проанализирована с использованием правил Кирхгофа.
29 Эта схема представляет собой комбинацию последовательной и параллельной конфигураций резисторов и источников напряжения. Эта схема не может быть проанализирована с использованием методов, обсуждаемых в «Электродвижущей силе», но может быть проанализирована с использованием правил Кирхгофа.Стратегия
Эта схема достаточно сложна, чтобы токи нельзя было найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены как I1, I1, I2, I2 и I3I3, и были сделаны предположения об их направлениях.Места на схеме обозначены буквами от до до h . В решении мы применяем правила перехода и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.Решение
Применение правил соединения и петли дает следующие три уравнения. У нас есть три неизвестных, поэтому требуется три уравнения.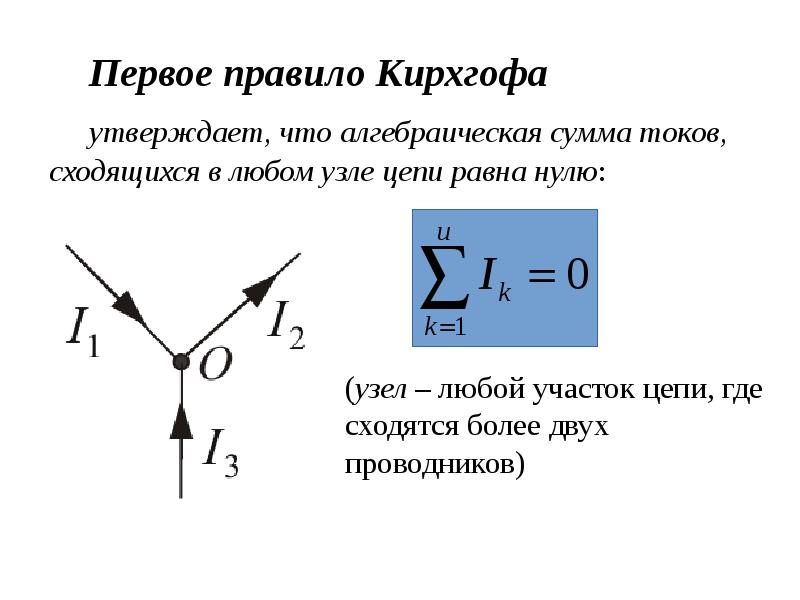 Соединениеc: I1 + I2 = I3.Loopabcdefa: I1 (R1 + R4) −I2 (R2 + R5 + R6) = V1-V3.Loopcdefc: I2 (R2 + R5 + R6) + I3R3 = V2 + V3. Соединениеc: I1 + I2 = I3.Loopabcdefa: I1 (R1 + R4) −I2 (R2 + R5 + R6) = V1 − V3. Loopcdefc: I2 (R2 + R5 + R6) + I3R3 = V2 + V3.
Соединениеc: I1 + I2 = I3.Loopabcdefa: I1 (R1 + R4) −I2 (R2 + R5 + R6) = V1-V3.Loopcdefc: I2 (R2 + R5 + R6) + I3R3 = V2 + V3. Соединениеc: I1 + I2 = I3.Loopabcdefa: I1 (R1 + R4) −I2 (R2 + R5 + R6) = V1 − V3. Loopcdefc: I2 (R2 + R5 + R6) + I3R3 = V2 + V3.Упростите уравнения, поместив неизвестные в одну сторону уравнений.
Соединениеc: I1 + I2-I3 = 0, замкнутый контур: I1 (3 Ом) -I2 (8 Ом) = 0,5 В-2,30 В. Замкнутый контур: I2 (8 Ом) + I3 (1 Ом) = 0,6 В + 2,30 В. Соединение c: I1 + I2 − I3 = 0, loopabcdefa: I1 (3Ω) −I2 (8Ω) = 0.5V − 2.30V. Loopcdefc: I2 (8Ω) + I3 (1Ω) = 0.6V + 2.30V.Упростите уравнения. Уравнение первого цикла можно упростить, разделив обе части на 3,00. Второе уравнение петли можно упростить, разделив обе части на 6.00.
Переход c: I1 + I2 − I3 = 0 .Loopabcdefa: I1 (3 Ом) −I2 (8 Ом) = — 1,8 В. Loopcdefc: I2 (8 Ом) + I3 (1 Ом) = 2,9 В.Результатов:
I1 = 0,20 A, I2 = 0,30 A, I3 = 0,50 A. I1 = 0,20 A, I2 = 0,30 A, I3 = 0,50 A.Значение
Метод проверки расчетов заключается в вычислении мощности, рассеиваемой резисторами, и мощности, подаваемой источниками напряжения: PR1 = I12R1 = 0,04 Вт. PR2 = I22R2 = 0,45 Вт. PR3 = I32R3 = 0,25 Вт. PR4 = I12R4 = 0,08 Вт. PR5 = I22R5 = 0,09 Вт.PR6 = I22R6 = 0,18 Вт. Рассеиваемое = 1,09 Вт. Psource = I1V1 + I2V3 + I3V2 = 0,10 Вт + 0,69 Вт + 0,30 Вт = 1,09 Вт. PR1 = I12R1 = 0,04 Вт. PR2 = I22R2 = 0,45 Вт. PR3 = I32R3 = 0,25 Вт. PR4 = I12R4 = 0,08 Вт. PR5 = I22R5 = 0,09 Вт. PR6 = I22R6 = 0,18 Вт. Рассеиваемая мощность = 1,09 Вт. Источник = I1V1 + I2V3 + I3V2 = 0,10 Вт + 0,69 Вт + 0,30 Вт = 1,09 Вт.
PR2 = I22R2 = 0,45 Вт. PR3 = I32R3 = 0,25 Вт. PR4 = I12R4 = 0,08 Вт. PR5 = I22R5 = 0,09 Вт.PR6 = I22R6 = 0,18 Вт. Рассеиваемое = 1,09 Вт. Psource = I1V1 + I2V3 + I3V2 = 0,10 Вт + 0,69 Вт + 0,30 Вт = 1,09 Вт. PR1 = I12R1 = 0,04 Вт. PR2 = I22R2 = 0,45 Вт. PR3 = I32R3 = 0,25 Вт. PR4 = I12R4 = 0,08 Вт. PR5 = I22R5 = 0,09 Вт. PR6 = I22R6 = 0,18 Вт. Рассеиваемая мощность = 1,09 Вт. Источник = I1V1 + I2V3 + I3V2 = 0,10 Вт + 0,69 Вт + 0,30 Вт = 1,09 Вт.Подаваемая мощность равна мощности, рассеиваемой резисторами.
Проверьте свое понимание 10.6
При рассмотрении следующей схемы и мощности, подаваемой и потребляемой схемой, будет ли источник напряжения всегда обеспечивать питание схемы или может ли источник напряжения потреблять энергию?
Пример 10.7
Расчет тока по правилам Кирхгофа
Найдите ток, протекающий в цепи на рисунке 10.30. Рисунок 10.30 Эта схема состоит из трех последовательно соединенных резисторов и двух батарей. Обратите внимание, что батареи подключены с противоположной полярностью.
Обратите внимание, что батареи подключены с противоположной полярностью.
Стратегия
Эту схему можно проанализировать с помощью правил Кирхгофа. Есть только один цикл и нет узлов. Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки a к точке b .Рассмотрим цикл abcda и воспользуемся рисунком 10.23, чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку 10.23, батарея V1V1 будет добавлена, а батарея V2V2 вычтена.Решение
Применение правила соединения дает следующие три уравнения. У нас есть одно неизвестное, поэтому требуется одно уравнение: Loopabcda: -IR1-V1-IR2 + V2-IR3 = 0. Loopabcda: -IR1-V1-IR2 + V2-IR3 = 0.Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.
I (R1 + R2 + R3) = V2-V1.I = V2-V1R1 + R2 + R3 = 24V-12V 10. 0Ω + 30.0Ω + 10.0Ω = 0.20AI (R1 + R2 + R3) = V2 − V1.I = V2 − V1R1 + R2 + R3 = 24 В − 12 В 10,0 Ом + 30,0 Ом + 10,0 Ом = 0,20 А.
0Ω + 30.0Ω + 10.0Ω = 0.20AI (R1 + R2 + R3) = V2 − V1.I = V2 − V1R1 + R2 + R3 = 24 В − 12 В 10,0 Ом + 30,0 Ом + 10,0 Ом = 0,20 А.Значение
Мощность, рассеиваемая или потребляемая схемой, равна мощности, подаваемой в схему, но обратите внимание, что ток в батарее V1V1 протекает через батарею от положительной клеммы к отрицательной клемме и потребляет мощность. PR1 = I2R1 = 0.40WPR2 = I2R2 = 1.20WPR3 = I2R3 = 0.80WPV1 = IV1 = 2.40WPdissipated = 4.80WPsource = IV2 = 4.80WPR1 = I2R1 = 0.40WPR2 = I2R2 = 1.20WPR3 = I2R3 = 0.80WPV1 = IV1 = 2.40WPdissipated = 4.80WPsource = IV2 = 4.80WПодаваемая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей V1.V1.
Проверьте свое понимание 10,7
При использовании законов Кирхгофа вам необходимо решить, какие петли использовать, и направление тока, протекающего через каждую петлю. При анализе схемы в Примере 10.7 направление тока было выбрано по часовой стрелке от точки a до точки b . Как бы изменились результаты, если бы направление тока было выбрано против часовой стрелки, от точки b до точки a ?
Как бы изменились результаты, если бы направление тока было выбрано против часовой стрелки, от точки b до точки a ?
Несколько источников напряжения
Для многих устройств требуется более одной батареи. Несколько источников напряжения, таких как батареи, могут быть подключены в последовательной конфигурации, параллельной конфигурации или их комбинации.
Последовательно положительная клемма одной батареи соединена с отрицательной клеммой другой батареи.Любое количество источников напряжения, в том числе аккумуляторы, можно подключать последовательно. Две последовательно соединенные батареи показаны на рисунке 10.31. Использование правила петли Кирхгофа для схемы в части (b) дает результат
ε1 − Ir1 + ε2 − Ir2 − IR = 0, [(ε1 + ε2) −I (r1 + r2)] — IR = 0. ε1 − Ir1 + ε2 − Ir2 − IR = 0, [(ε1 + ε2) — I (r1 + r2)] — IR = 0. Рисунок 10.31 (a) Две батареи, подключенные последовательно через нагрузочный резистор. (b) Принципиальная схема двух батарей и нагрузочного резистора, каждая из которых моделируется как идеализированный источник ЭДС и внутреннее сопротивление.
(b) Принципиальная схема двух батарей и нагрузочного резистора, каждая из которых моделируется как идеализированный источник ЭДС и внутреннее сопротивление.
Когда источники напряжения включены последовательно, их внутренние сопротивления можно складывать вместе, а их ЭДС можно складывать вместе, чтобы получить общие значения. Последовательное соединение источников напряжения является обычным явлением, например, в фонариках, игрушках и других приборах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС. На рисунке 10.31 напряжение на клеммах равно
. Vterminal = (ε1 − Ir1) + (ε2 − Ir2) = [(ε1 + ε2) −I (r1 + r2)] = (ε1 + ε2) + Ireq.Vterminal = (ε1 − Ir1) + (ε2 − Ir2) = [(ε1 + ε2) −I (r1 + r2)] = (ε1 + ε2) + Ireq. Обратите внимание, что одинаковый ток I присутствует в каждой батарее, потому что они соединены последовательно. Недостаток последовательного соединения ячеек в том, что их внутренние сопротивления складываются.
Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь. Например, светодиодный фонарик может иметь две батарейки типа AAA, каждая с напряжением на клеммах 1,5 В, чтобы обеспечить 3,0 В для фонарика.
Любое количество аккумуляторов может быть подключено последовательно.Для последовательно включенных аккумуляторов N напряжение на зажимах равно
Vterminal = (ε1 + ε2 + ⋯ + εN − 1 + εN) −I (r1 + r2 + ⋯ + rN − 1 + rN) = ∑i = 1Nεi − IreqVterminal = (ε1 + ε2 + ⋯ + εN − 1 + εN) −I (r1 + r2 + ⋯ + rN − 1 + rN) = ∑i = 1Nεi − Ireq10,6
, где эквивалентное сопротивление req = ∑i = 1Nrireq = ∑i = 1Nri.
Когда нагрузка подключается к источникам напряжения последовательно, как показано на рисунке 10.32, мы можем найти ток:
(ε1 − Ir1) + (ε2 − Ir2) = IR, Ir1 + Ir2 + IR = ε1 + ε2, I = ε1 + ε2r1 + r2 + R. (ε1 − Ir1) + (ε2 − Ir2) = IR, Ir1 + Ir2 + IR = ε1 + ε2, I = ε1 + ε2r1 + r2 + R. Как и ожидалось, внутренние сопротивления увеличивают эквивалентное сопротивление.
Рисунок 10.32 Две батареи подключаются последовательно к светодиодной лампе, как в фонарике.
Источники напряжения, такие как батареи, также можно подключать параллельно. На рисунке 10.33 показаны две батареи с одинаковыми ЭДС, включенные параллельно и подключенные к сопротивлению нагрузки. Когда батареи подключаются параллельно, положительные клеммы соединяются вместе, а отрицательные клеммы соединяются вместе, а сопротивление нагрузки подключается к положительной и отрицательной клеммам.Обычно источники напряжения, включенные параллельно, имеют идентичные ЭДС. В этом простом случае, поскольку источники напряжения подключены параллельно, общая ЭДС равна индивидуальной ЭДС каждой батареи.
Рисунок 10.33 (a) Две батареи подключаются параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея как источник ЭДС и внутренний резистор. Два источника ЭДС имеют идентичные ЭДС (каждый из которых обозначен εε), соединенные параллельно, которые создают одинаковую ЭДС.
Рассмотрим анализ Кирхгофа схемы на рисунке 10.33 (б). Есть две петли и узел в точке b и ε = ε1 = ε2ε = ε1 = ε2.
Узел b : I1 + I2-I = 0I1 + I2-I = 0.
Цикл abcfa : ε − I1r1 + I2r2 − ε = 0, I1r1 = I2r2.ε − I1r1 + I2r2 − ε = 0, I1r1 = I2r2.
Петля fcdef : ε2-I2r2-IR = 0, ε-I2r2-IR = 0. ε2-I2r2-IR = 0, ε-I2r2-IR = 0.
Решение для тока через резистор нагрузки приводит к I = εreq + RI = εreq + R, где req = (1r1 + 1r2) −1req = (1r1 + 1r2) −1. Напряжение на клеммах равно падению потенциала на нагрузочном резисторе IR = (εreq + R) IR = (εreq + R).Параллельное соединение снижает внутреннее сопротивление и, таким образом, может производить больший ток.
Параллельно можно подключить любое количество батарей. Для параллельно включенных аккумуляторов N напряжение на зажимах равно
Vterminal = ε − I (1r1 + 1r2 + ⋯ + 1rN − 1 + 1rN) −1 = ε − IreqVterminal = ε − I (1r1 + 1r2 + ⋯ + 1rN − 1 + 1rN) −1 = ε − Ireq10,7
, где эквивалентное сопротивление равно req = (∑i = 1N1ri) −1req = (∑i = 1N1ri) −1.
Например, в некоторых грузовиках с дизельным двигателем параллельно используются две батареи на 12 В; они производят полную ЭДС 12 В, но могут обеспечивать больший ток, необходимый для запуска дизельного двигателя.
Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме индивидуальных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют равные ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше, чем отдельные внутренние сопротивления. Аккумуляторы подключаются последовательно для увеличения напряжения на клеммах нагрузки.Аккумуляторы подключаются параллельно для увеличения тока нагрузки.
Массив солнечных батарей
Другой пример, имеющий дело с несколькими источниками напряжения, — это комбинация солнечных элементов, соединенных как последовательно, так и параллельно, чтобы обеспечить желаемое напряжение и ток. Фотогальваническая генерация, которая представляет собой преобразование солнечного света непосредственно в электричество, основана на фотоэлектрическом эффекте. Фотоэлектрический эффект выходит за рамки этой главы и рассматривается в книге «Фотоны и волны материи», но, как правило, фотоны, ударяясь о поверхность солнечного элемента, создают в нем электрический ток.
Фотогальваническая генерация, которая представляет собой преобразование солнечного света непосредственно в электричество, основана на фотоэлектрическом эффекте. Фотоэлектрический эффект выходит за рамки этой главы и рассматривается в книге «Фотоны и волны материи», но, как правило, фотоны, ударяясь о поверхность солнечного элемента, создают в нем электрический ток.
Большинство солнечных элементов изготовлено из чистого кремния. Большинство отдельных элементов имеют выходное напряжение около 0,5 В, в то время как выходной ток зависит от количества солнечного света, падающего на элемент (падающее солнечное излучение, известное как инсоляция). При ярком полуденном солнечном свете типичные монокристаллические элементы вырабатывают ток на единицу площади около 100 мА / см 2100 мА / см 2 площади поверхности ячейки.
Отдельные солнечные элементы электрически соединены в модули для удовлетворения потребностей в электроэнергии.Их можно соединить последовательно или параллельно — как батареи, о которых говорилось ранее. Группа или модуль солнечных элементов обычно состоит из 36-72 элементов с выходной мощностью от 50 до 140 Вт.
Группа или модуль солнечных элементов обычно состоит из 36-72 элементов с выходной мощностью от 50 до 140 Вт.
Солнечные элементы, как и батареи, вырабатывают напряжение постоянного тока. Ток от источника постоянного напряжения однонаправлен. Для большинства бытовых приборов требуется напряжение переменного тока.
21.3 Правила Кирхгофа — Колледж Физики, главы 1-17
Применяя правила Кирхгофа, мы генерируем уравнения, которые позволяют нам находить неизвестные в схемах.Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то проблема может быть решена. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете в результате применения правил.
Рисунок 4 и следующие пункты помогут правильно определить знаки плюса и минуса при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах потребуется построить более одного контура. Проходя каждый цикл, нужно быть последовательным в отношении знака изменения потенциала. (См. Пример 1.)
Во многих схемах потребуется построить более одного контура. Проходя каждый цикл, нужно быть последовательным в отношении знака изменения потенциала. (См. Пример 1.)
Пример 1: Расчет силы тока: с использованием правил Кирхгофа
Найдите токи, протекающие в цепи, показанной на Рисунке 5.
Рис. 5. Эта схема похожа на схему на Рис. 1, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви отмечены и предполагается, что они движутся в показанных направлениях.В этом примере для нахождения токов используются правила Кирхгофа.Стратегия
Эта схема достаточно сложна, поэтому токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены [латекс] \ boldsymbol {I_1} [/ latex], [latex] \ boldsymbol {I_2} [/ latex] и [latex] \ boldsymbol {I_3} [/ latex]. сделал о своих направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.
В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.
Решение
Начнем с применения правила Кирхгофа первого или перекрестка в точке а. Это дает
[латекс] \ boldsymbol {I_1 = I_2 + I_3}, [/ латекс]
, поскольку [latex] \ boldsymbol {I_1} [/ latex] течет в соединение, а [latex] \ boldsymbol {I_2} [/ latex] и [latex] \ boldsymbol {I_3} [/ latex] вытекает. Применение правила соединения в e дает точно такое же уравнение, так что новая информация не получается.Это одно уравнение с тремя неизвестными — необходимы три независимых уравнения, поэтому необходимо применять правило цикла.
Теперь рассмотрим цикл abcdea. Переходя от a к b, мы пересекаем [латекс] \ boldsymbol {R_2} [/ latex] в том же (предполагаемом) направлении, что и текущий [латекс] \ boldsymbol {I_2} [/ latex], и поэтому изменение потенциала [латекс] \ boldsymbol {-I_2R_2} [/ латекс]. Затем, переходя от b к c, мы переходим от — к +, так что изменение потенциала составляет [latex] \ boldsymbol {+ \ textbf {emf} _1} [/ latex]. Если пересечь внутреннее сопротивление [латекс] \ boldsymbol {r_1} [/ latex] от c до d, получим [латекс] \ boldsymbol {-I_2r_1} [/ latex]. Завершение цикла путем перехода от d к a снова проходит через резистор в том же направлении, что и его ток, давая изменение потенциала [latex] \ boldsymbol {-I_1R_1} [/ latex].
Если пересечь внутреннее сопротивление [латекс] \ boldsymbol {r_1} [/ latex] от c до d, получим [латекс] \ boldsymbol {-I_2r_1} [/ latex]. Завершение цикла путем перехода от d к a снова проходит через резистор в том же направлении, что и его ток, давая изменение потенциала [latex] \ boldsymbol {-I_1R_1} [/ latex].
Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,
[латекс] \ boldsymbol {-I_2R_2 + \ textbf {emf} _1 — I_2r_1 — I_1R_1 = -I_2 (R_2 + r_1) + \ textbf {emf} _1 — I_1R_1 = 0}.[/ латекс]
Подставляя значения из принципиальной схемы для сопротивлений и ЭДС и отменяя единицу измерения ампер, получаем
[латекс] \ boldsymbol {-3I_2 + 18 -6I_1 = 0}. [/ Латекс]
Теперь, применяя правило цикла к aefgha (мы могли бы также выбрать abcdefgha), аналогично дает
[латекс] \ boldsymbol {+ I_1R_1 + I_3R_3 + I_3r_2 — \ textbf {emf} _2 = + I_1R_1 + I_3 (R_3 + r_2) — \ textbf {emf} _2 = 0}. [/ Латекс]
Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении. С введенными значениями это становится
С введенными значениями это становится
[латекс] \ boldsymbol {+ 6I_1 + 2I_3 — 45 = 0}. [/ Latex]
Этих трех уравнений достаточно для решения трех неизвестных токов. Сначала решите второе уравнение для [латекса] \ boldsymbol {I_2} [/ latex]:
[латекс] \ boldsymbol {I_2 = 6 — 2I_1}. [/ Латекс]
Теперь решите третье уравнение для [латекса] \ boldsymbol {I_3} [/ latex]:
[латекс] \ boldsymbol {I_3 = 22,5 — 3I_1}. [/ Latex]
Подстановка этих двух новых уравнений в первое позволяет нам найти значение для [latex] \ boldsymbol {I_1} [/ latex]:
[латекс] \ boldsymbol {I_1 = I_2 + I_3 = (6 — 2I_1) + (22.5 — 3I_1) = 28,5 — 5I_1}. [/ Latex]
Объединение терминов дает
[латекс] \ boldsymbol {6I_1 = 28,5} [/ латекс] и
[латекс] \ boldsymbol {I_1 = 4.75 \; \ textbf {A}}. [/ Latex]
Подставляя это значение вместо [latex] \ boldsymbol {I_1} [/ latex] обратно в четвертое уравнение, получаем
[латекс] \ boldsymbol {I_2 = 6 — 2I_1 = 6 — 9,50} [/ латекс]
[латекс] \ boldsymbol {I_2 = -3,50 \; \ textbf {A}}.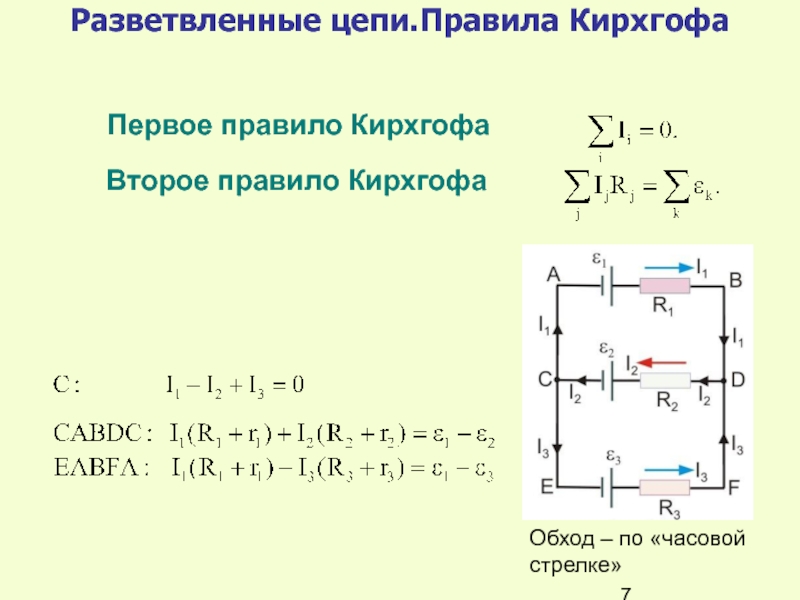 [/ Latex]
[/ Latex]
Знак минус означает, что [латекс] \ boldsymbol {I_2} [/ latex] течет в направлении, противоположном предполагаемому на рисунке 5.
Наконец, подстановка значения [latex] \ boldsymbol {I_1} [/ latex] в пятое уравнение дает
[латекс] \ boldsymbol {I_3 = 22,5 — 3I_1 = 22,5 — 14,25} [/ латекс]
[латекс] \ boldsymbol {I_3 = 8.25 \; \ textbf {A}}. [/ Latex]
Обсуждение
Для проверки отметим, что действительно [латекс] \ boldsymbol {I_1 = I_2 + I_3} [/ latex]. Результаты также можно было проверить, введя все значения в уравнение для цикла abcdefgha.
Материал в этом разделе теоретически верен. Мы сможем проверить это, измерив ток и напряжение. Фактически, некоторые из устройств, используемых для таких измерений, представляют собой прямое применение принципов, рассмотренных до сих пор, и будут исследованы в следующих модулях. Как мы увидим, результат очень основного, даже глубокого факта — выполнение измерения изменяет измеряемую величину.
Законы Кирхгофа (ток и напряжение): что это такое и почему это важно?
Обновлено 28 декабря 2020 г.
Автор: GAYLE TOWELL
По мере того, как электрические цепи становятся все более сложными с множеством ветвей и элементов, становится все сложнее определить, какой ток может протекать через любую данную ветвь, и как это настроить.Полезно иметь систематический способ анализа цепей.
Важные определения
Чтобы понять законы Кирхгофа, необходимо несколько определений:
- Напряжение В — это разность потенциалов на элементе схемы. Он измеряется в вольтах (В).
- Ток I — это мера скорости прохождения заряда через точку в цепи. Он измеряется в амперах (А).
- Сопротивление R — это мера сопротивления элемента схемы протеканию тока.Он измеряется в омах (Ом).
- Закон Ома связывает эти три величины следующим уравнением: V = IR.
Что такое законы Кирхгофа?
В 1845 году немецкий физик Густав Кирхгоф формализовал следующие два правила о схемах:
1. Правило соединения (также известное как закон Кирхгофа или KCL): Сумма всех токов, протекающих в переходе в цепи. цепь должна равняться общему току, вытекающему из перехода.
Правило соединения (также известное как закон Кирхгофа или KCL): Сумма всех токов, протекающих в переходе в цепи. цепь должна равняться общему току, вытекающему из перехода.
Другой способ выражения этого закона состоит в том, что алгебраическая сумма токов, текущих в переход, равна 0. Это означало бы рассматривать любые токи, протекающие в переход, как положительные, а любые текущие — как отрицательные. Поскольку общий приток должен равняться общему оттоку, это эквивалентно утверждению, что суммы будут равны 0, поскольку это равносильно перемещению оттекающих на другую сторону уравнения с отрицательным знаком.
Этот закон выполняется при простом применении сохранения заряда.Все, что входит, должно равняться тому, что вытекает. Представьте, что водопроводные трубы соединяются и разветвляются подобным образом. Точно так же, как вы ожидаете, что общая вода, текущая в переход, будет равна общему количеству воды, вытекающей из перехода, так и с текущими электронами.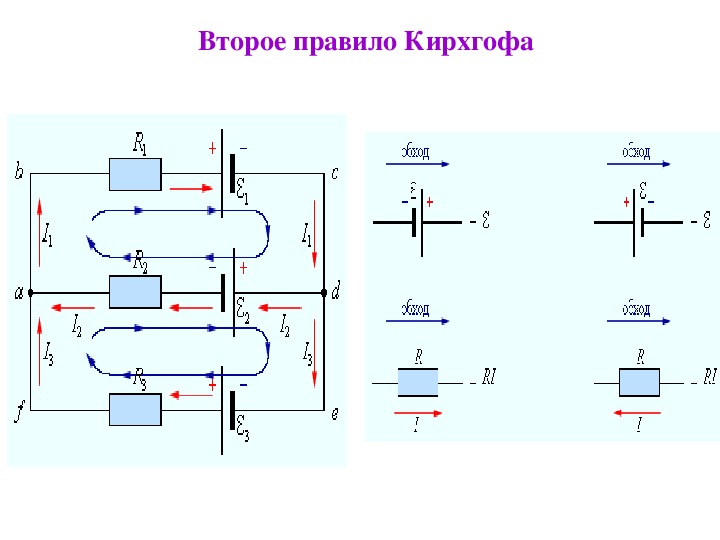
2. Правило цикла (также известное как закон напряжения Кирхгофа или KVL): Сумма разностей потенциалов (напряжений) вокруг замкнутого контура в цепи должна равняться 0.
Чтобы понять второй закон Кирхгофа, представьте себе что бы случилось, если бы это было неправдой.Рассмотрим одноконтурный контур, в котором есть несколько батарей и резисторов. Представьте, что вы начинаете с точки A и двигаетесь по петле по часовой стрелке. Вы набираете напряжение, когда идете через батарею, а затем падаете, когда вы проходите через резистор и так далее.
Обойдя весь круг, вы снова окажетесь в точке A . Сумма всех разностей потенциалов при обходе контура должна тогда равняться разнице потенциалов между точкой A и самой собой.Что ж, одна точка не может иметь два разных значения потенциала, поэтому эта сумма должна быть 0.
В качестве аналогии рассмотрим, что произойдет, если вы пойдете по круговой пешеходной тропе. Предположим, вы начинаете с точки A и начинаете поход.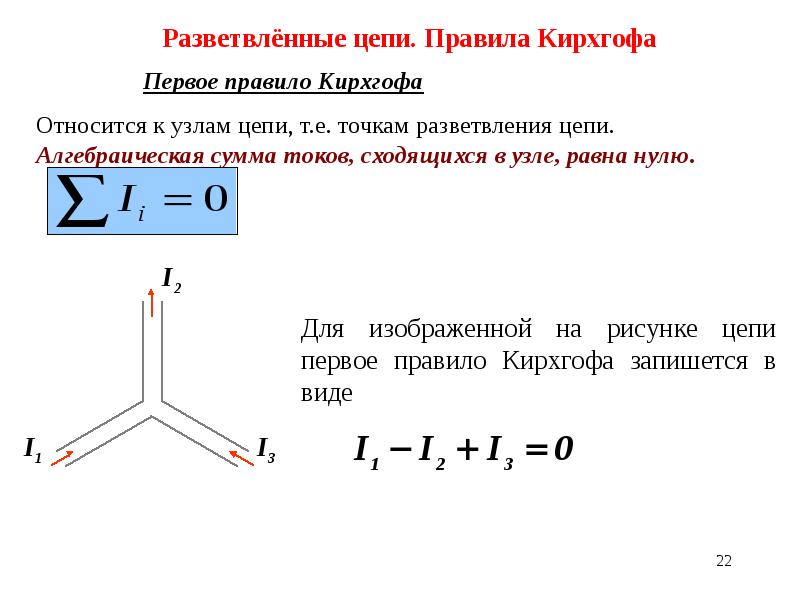 Часть похода ведет в гору, часть — под гору и так далее. После завершения цикла вы снова вернетесь в точку A . Это обязательно тот случай, когда сумма ваших приростов и перепадов высоты в этом замкнутом контуре должна быть равна 0 именно потому, что высота в точке A должна равняться сама себе.
Часть похода ведет в гору, часть — под гору и так далее. После завершения цикла вы снова вернетесь в точку A . Это обязательно тот случай, когда сумма ваших приростов и перепадов высоты в этом замкнутом контуре должна быть равна 0 именно потому, что высота в точке A должна равняться сама себе.
Почему важны законы Кирхгофа?
При работе с простой последовательной цепью определение тока в контуре требует только знания приложенного напряжения и суммы сопротивлений в контуре (с последующим применением закона Ома).
В параллельных цепях и электрических цепях с комбинациями Однако для последовательных и параллельных элементов задача определения тока, протекающего через каждую ветвь, быстро усложняется. Ток, входящий в соединение, будет разделяться по мере того, как он входит в разные части цепи, и не очевидно, сколько будет проходить в каждую сторону без тщательного анализа.
Два правила Кирхгофа позволяют анализировать все более сложные схемы. Хотя требуемые алгебраические шаги по-прежнему довольно сложны, сам процесс прост. Эти законы широко используются в области электротехники.
Хотя требуемые алгебраические шаги по-прежнему довольно сложны, сам процесс прост. Эти законы широко используются в области электротехники.
Возможность анализировать схемы важна для предотвращения перегрузки элементов схемы. Если вы не знаете, какой ток будет протекать через устройство или какое напряжение упадет на нем, вы не будете знать, какой будет выходная мощность, и все это имеет значение для функционирования устройства.
Как применять законы Кирхгофа
Правила Кирхгофа можно применить для анализа принципиальной схемы, выполнив следующие шаги:
- Если ток проходит в положительном направлении через источник напряжения, это положительное значение напряжения. Если ток проходит через источник напряжения в отрицательном направлении, напряжение должно иметь отрицательный знак.
- Если ток проходит в положительном направлении через резистивный элемент, то вы используете закон Ома и добавляете -I i × R (падение напряжения на этом резисторе) для этого элемента. Если ток проходит в отрицательном направлении через резистивный элемент, вы добавляете + I i × R для этого элемента.
- После того, как вы обошли контур, установите эту сумму всех напряжений равной 0. Повторите для всех контуров в цепи.

Для каждой ветви, i , цепи, пометьте неизвестный ток, текущий через нее I i и выберите направление для этого тока. (Направление не обязательно должно быть правильным. Если окажется, что этот ток на самом деле течет в противоположном направлении, то вы просто получите отрицательное значение при решении для этого тока позже.)
Для каждой петли в цепи выберите направление. (Это произвольно. Вы можете выбрать против часовой стрелки или по часовой стрелке. Это не имеет значения.)
(Это произвольно. Вы можете выбрать против часовой стрелки или по часовой стрелке. Это не имеет значения.)
Для каждого цикла начните с одной точки и двигайтесь в выбранном направлении, складывая разности потенциалов по каждому элементу. Эти разности потенциалов можно определить следующим образом:
Для каждого перехода сумма токов, протекающих в этом переходе, должна равняться сумме токов, вытекающих из этого перехода.Запишите это в виде уравнения.
Теперь у вас должен быть набор одновременных уравнений, который позволит вам определять ток (или другие неизвестные величины) во всех ветвях цепи. Последний шаг — решить эту систему алгебраически.
Примеры
Пример 1: Рассмотрим следующую схему:
Применяя шаг 1, для каждой ветви мы маркируем неизвестные токи.
••• na
Применяя Шаг 2, мы выбираем направление для каждой петли в схеме следующим образом:
••• na
Теперь мы применяем Шаг 3: Для каждой петли, начиная с одной точки и обходя в выбранном направлении складываем разности потенциалов по каждому элементу и устанавливаем сумму равной 0.
Для цикла 1 на диаграмме мы получаем:
-I_1 \ times 40 — I_3 \ times 100 + 3 = 0
Для цикла 2 на диаграмме получаем:
-I_2 \ times 75-2 + I_3 \ times 100 = 0
Для шага 4 мы применяем правило соединения. На нашей диаграмме есть два соединения, но оба они дают эквивалентные уравнения. А именно:
На нашей диаграмме есть два соединения, но оба они дают эквивалентные уравнения. А именно:
I_1 = I_2 + I_3
Наконец, на шаге 5 мы используем алгебру для решения системы уравнений для неизвестных токов:
Используйте уравнение соединения, чтобы подставить в уравнение первого контура:
— (I_2 + I_3) \ times 40 — I_3 \ times 100 + 3 = -40I_2 — 140I_3 + 3 = 0
Решите это уравнение для I 2 :
I_2 = \ frac {3-140I_3} {40}
Подставьте это в уравнение второго цикла:
— [(3-140I_3) / 40] \ times 75-2 + 100I_3 = 0
-3 \ times 75/40 + (140 \ times 75/40) I_3 — 2 + 100I_3 = 0 \\ \ подразумевает I_3 = (2 + 3 \ times 75/40) / (140 \ times 75/40 + 100) = 0.021 \ text {A}
Используйте значение I 3 , чтобы найти I 2 :
I_2 = (3-140 \ times (0,021)) / 40 = 0,0015 \ text {A}
I_1 = I_2 + I_3 = 0,021 + 0,0015 = 0,0225 \ text {A}
Итак, окончательный результат таков: I 1 = 0,0225 A, I 2 = 0,0015 A и I 3 = 0,021 A.
Подстановка этих текущих значений в исходные уравнения проверяет правильность, поэтому мы можем быть достаточно уверены в результате!
Попробуйте повторить эту же задачу еще раз, но сделайте другой выбор для ваших текущих меток и направлений петли.Если все будет сделано осторожно, вы должны получить тот же результат, показывая, что первоначальный выбор действительно произвольный.
(Обратите внимание, что если вы выберете разные направления для обозначенных токов, тогда ваши ответы для них будут отличаться знаком минус; однако результаты все равно будут соответствовать тому же направлению и величине тока в цепи.)
Пример 2: Какова электродвижущая сила (ЭДС) ε батареи в следующей цепи? Какой ток в каждой ветке?
••• na
Сначала мы маркируем все неизвестные токи.Пусть I 2 = ток вниз через среднюю ветвь и I 1 = ток вниз через крайнюю правую ветвь. Изображение уже показывает текущий I в крайнем левом ответвлении с маркировкой.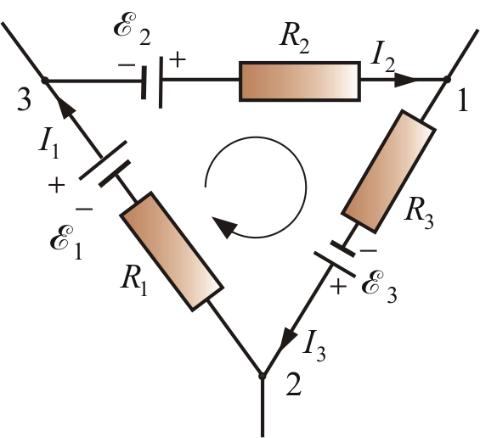
Выбор направления по часовой стрелке для каждого контура и применение законов схемы Кирхгофа дает следующую систему уравнений:
\ begin {align} & I_1 = I-I_2 \\ & \ varepsilon — 4I — 6I_2 + 8 = 0 \\ & — 12I_1 — 8 + 6I_2 = 0 \ end {align}
Для решения замените I — I 2 на I 1 в третьем уравнении, а затем подставьте данное значение для I и решите это уравнение относительно I 2 .Когда вы знаете I 2 , вы можете подставить I и I 2 в первое уравнение, чтобы получить I 1 . Затем вы можете решить второе уравнение относительно ε . Следуя этим шагам, вы получите окончательное решение:
\ begin {align} & I_2 = 16/9 = 1,78 \ text {A} \\ & I_1 = 2/9 = 0,22 \ text {A} \\ & \ varepsilon = 32/3 = 10.67 \ text {V} \ end {align}
Опять же, вы всегда должны проверять свои окончательные результаты, вставляя их в исходные уравнения. Совершать простые алгебраические ошибки очень легко!
Совершать простые алгебраические ошибки очень легко!
электричество | Определение, факты и типы
Электростатика — это изучение электромагнитных явлений, которые происходят при отсутствии движущихся зарядов, то есть после установления статического равновесия. Заряды быстро достигают положения равновесия, потому что электрическая сила чрезвычайно велика. Математические методы электростатики позволяют рассчитывать распределения электрического поля и электрического потенциала по известной конфигурации зарядов, проводников и изоляторов.И наоборот, имея набор проводников с известными потенциалами, можно рассчитать электрические поля в областях между проводниками и определить распределение заряда на поверхности проводников. Электрическую энергию набора зарядов в состоянии покоя можно рассматривать с точки зрения работы, необходимой для сборки зарядов; в качестве альтернативы, можно также считать, что энергия находится в электрическом поле, создаваемом этой сборкой зарядов. Наконец, энергия может храниться в конденсаторе; энергия, необходимая для зарядки такого устройства, хранится в нем как электростатическая энергия электрического поля.
Статическое электричество — это знакомое электрическое явление, при котором заряженные частицы передаются от одного тела к другому. Например, если два предмета трутся друг о друга, особенно если они являются изоляторами, а окружающий воздух сухой, предметы приобретают равные и противоположные заряды, и между ними возникает сила притяжения. Объект, теряющий электроны, становится заряженным положительно, а другой — отрицательно. Сила — это просто притяжение между зарядами противоположного знака.Свойства этой силы описаны выше; они включены в математическое соотношение, известное как закон Кулона. Электрическая сила, действующая на заряд Q 1 в этих условиях, вызванная зарядом Q 2 на расстоянии r , определяется законом Кулона
Жирным шрифтом в уравнении обозначается вектор характер силы, а единичный вектор r̂ — это вектор, который имеет размер один и указывает от заряда Q 2 до заряда Q 1 .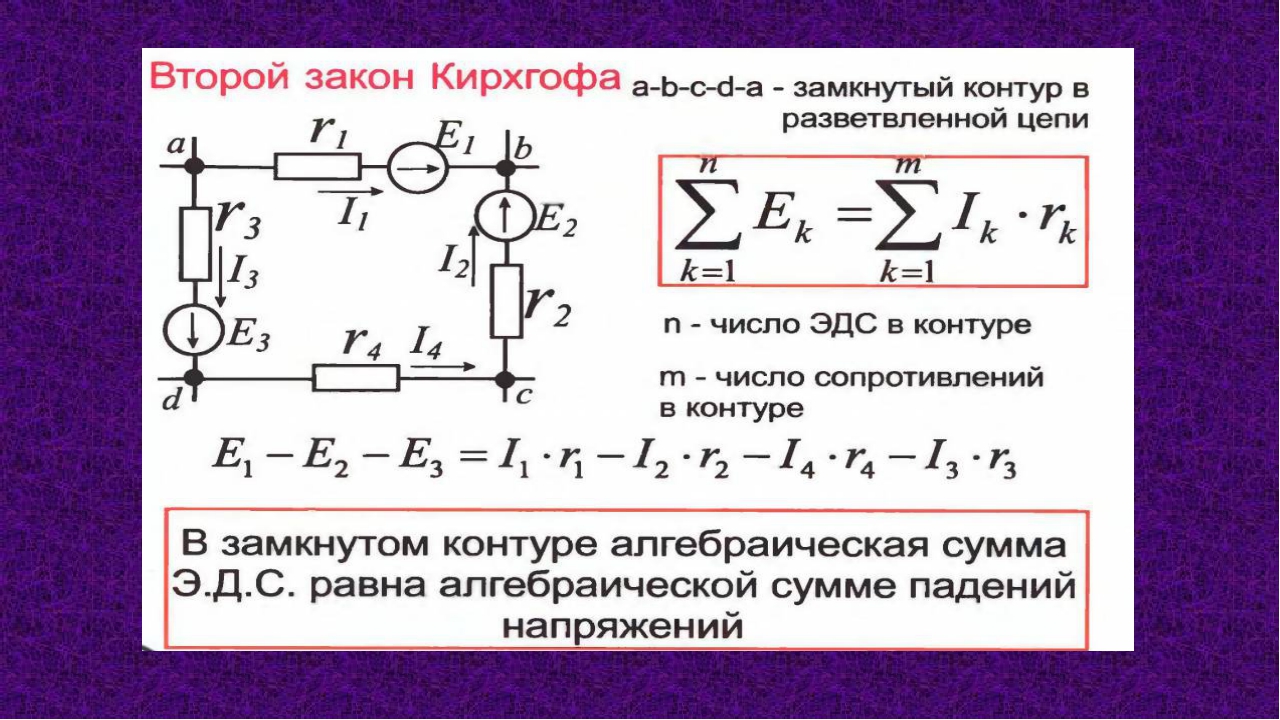 Константа пропорциональности k равна 10 −7 c 2 , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10 9 ньютон-квадратный метр на квадратный кулон (Нм 2 / C 2 ). На рисунке 1 показано усилие, действующее на Q 1 из-за Q 2 . Числовой пример поможет проиллюстрировать эту силу. И Q 1 , и Q 2 выбраны произвольно в качестве положительных зарядов, каждый с величиной 10 −6 кулонов.Заряд Q 1 расположен в координатах x , y , z со значениями 0,03, 0, 0 соответственно, а Q 2 имеет координаты 0, 0,04, 0. Все координаты даны в метрах. Таким образом, расстояние между Q 1 и Q 2 составляет 0,05 метра.
Константа пропорциональности k равна 10 −7 c 2 , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10 9 ньютон-квадратный метр на квадратный кулон (Нм 2 / C 2 ). На рисунке 1 показано усилие, действующее на Q 1 из-за Q 2 . Числовой пример поможет проиллюстрировать эту силу. И Q 1 , и Q 2 выбраны произвольно в качестве положительных зарядов, каждый с величиной 10 −6 кулонов.Заряд Q 1 расположен в координатах x , y , z со значениями 0,03, 0, 0 соответственно, а Q 2 имеет координаты 0, 0,04, 0. Все координаты даны в метрах. Таким образом, расстояние между Q 1 и Q 2 составляет 0,05 метра.
 Подпишись сейчас
Подпишись сейчас Величина силы F на заряде Q 1 , рассчитанная по уравнению (1), равна 3.6 ньютонов; его направление показано на рисунке 1. Сила, действующая на Q 2 из-за Q 1 , составляет — F , что также имеет величину 3,6 ньютона; его направление, однако, противоположно направлению F . Сила F может быть выражена через ее компоненты по осям x и y , поскольку вектор силы лежит в плоскости x y . Это делается с помощью элементарной тригонометрии из геометрии рисунка 1, а результаты показаны на рисунке 2.Таким образом, в ньютонах. Закон Кулона математически описывает свойства электрической силы между зарядами в состоянии покоя. Если заряды имеют противоположные знаки, сила будет притягивающей; притяжение было бы указано в уравнении (1) отрицательным коэффициентом единичного вектора r̂. Таким образом, электрическая сила на Q 1 будет иметь направление, противоположное единичному вектору r̂ , и будет направлена от Q 1 к Q 2 .В декартовых координатах это привело бы к изменению знаков компонентов силы x и y в уравнении (2).
Таким образом, электрическая сила на Q 1 будет иметь направление, противоположное единичному вектору r̂ , и будет направлена от Q 1 к Q 2 .В декартовых координатах это привело бы к изменению знаков компонентов силы x и y в уравнении (2).
Рисунок 2: Составляющие x и y силы F на рисунке 4 (см. Текст).
Предоставлено Департаментом физики и астрономии Университета штата Мичиган Как можно понять эту электрическую силу на Q 1 ? По сути, сила возникает из-за наличия электрического поля в позиции Q 1 .Поле создается вторым зарядом Q 2 и имеет величину, пропорциональную размеру Q 2 . При взаимодействии с этим полем первый заряд на некотором расстоянии либо притягивается, либо отталкивается от второго заряда, в зависимости от знака первого заряда.
Законы Кирхгофа для тока и напряжения
В 1845 году немецкий физик Густав Кирхгоф впервые описал два закона, которые стали центральными в электротехнике.Текущий закон Кирхгофа, также известный как закон соединения Кирхгофа и первый закон Кирхгофа, определяют способ распределения электрического тока, когда он проходит через соединение — точку, где встречаются три или более проводника. Другими словами, законы Кирхгофа гласят, что сумма всех токов, покидающих узел в электрической сети, всегда равна нулю.
Эти законы чрезвычайно полезны в реальной жизни, поскольку они описывают соотношение значений токов, протекающих через точку соединения, и напряжений в контуре электрической цепи.Они описывают, как электрический ток течет во всех миллиардах электроприборов и устройств, а также во всех домах и на предприятиях, которые постоянно используются на Земле.
Законы Кирхгофа: основы
В частности, в законах говорится:
Алгебраическая сумма тока в любом соединении равна нулю.
Поскольку ток — это поток электронов через проводник, он не может накапливаться на стыке, а это означает, что ток сохраняется: то, что входит, должно выходить.Представьте себе хорошо известный пример соединения: распределительную коробку. Эти ящики устанавливаются в большинстве домов. Это коробки, в которых проложена проводка, по которой должно протекать все электричество в доме.
При выполнении расчетов ток, текущий в переход и выходящий из него, обычно имеет противоположные знаки. Вы также можете сформулировать Действующий закон Кирхгофа следующим образом:
Сумма тока в соединении равна сумме тока вне соединения.
Вы можете более конкретно разбить два закона.
Действующий закон Кирхгофа
На картинке показано место соединения четырех проводов (проводов). В стык текут токи v 2 и v 3 , а из него вытекают токи v 1 и v 4 . В этом примере правило соединения Кирхгофа дает следующее уравнение:
В этом примере правило соединения Кирхгофа дает следующее уравнение:
v 2 + v 3 = v 1 + v 4
Закон Кирхгофа о напряжении
Закон Кирхгофа о напряжении описывает распределение электрического напряжения в петле или замкнутом проводящем пути электрической цепи.Закон Кирхгофа о напряжении гласит, что:
Алгебраическая сумма разностей напряжений (потенциалов) в любом контуре должна равняться нулю.
Различия в напряжении включают в себя те, которые связаны с электромагнитными полями (ЭМП) и резистивными элементами, такими как резисторы, источники питания (например, батареи) или устройства — лампы, телевизоры и блендеры, подключенные к цепи. Представьте себе, что напряжение растет и падает по мере того, как вы двигаетесь по любой из отдельных петель в цепи.
Закон Кирхгофа о напряжении возникает потому, что электростатическое поле в электрической цепи является консервативным силовым полем. Напряжение представляет собой электрическую энергию в системе, поэтому рассматривайте его как особый случай сохранения энергии. Когда вы идете по циклу, когда вы прибываете в начальную точку, имеет тот же потенциал, что и в начале, поэтому любые увеличения и уменьшения по циклу должны отменяться, чтобы общее изменение было нулевым. В противном случае потенциал в начальной / конечной точке имел бы два разных значения.
Напряжение представляет собой электрическую энергию в системе, поэтому рассматривайте его как особый случай сохранения энергии. Когда вы идете по циклу, когда вы прибываете в начальную точку, имеет тот же потенциал, что и в начале, поэтому любые увеличения и уменьшения по циклу должны отменяться, чтобы общее изменение было нулевым. В противном случае потенциал в начальной / конечной точке имел бы два разных значения.
Положительные и отрицательные признаки в законе напряжения Кирхгофа
Использование правила напряжения требует некоторых условных обозначений, которые не обязательно так ясны, как в правиле тока. Выберите направление (по часовой стрелке или против часовой стрелки), в котором будет проходить петля. При переходе от положительного к отрицательному (+ к -) в ЭДС (источнике питания) напряжение падает, поэтому значение становится отрицательным. При переходе от отрицательного к положительному (- к +) напряжение возрастает, поэтому значение будет положительным.
Помните, что, путешествуя по цепи для применения закона Кирхгофа, убедитесь, что вы всегда движетесь в одном и том же направлении (по часовой стрелке или против часовой стрелки), чтобы определить, представляет ли данный элемент увеличение или уменьшение напряжения.Если вы начнете прыгать, двигаться в разных направлениях, ваше уравнение будет неверным.
При переходе через резистор изменение напряжения определяется по формуле:
I * R
где I — значение тока, а R — сопротивление резистора. Пересечение в том же направлении, что и ток, означает, что напряжение падает, поэтому его значение отрицательное. При пересечении резистора в направлении, противоположном току, значение напряжения положительное, поэтому оно увеличивается.
Применение закона Кирхгофа о напряжении
Самые основные применения законов Кирхгофа относятся к электрическим цепям. Вы, возможно, помните из физики средней школы, что электричество в цепи должно течь в одном непрерывном направлении. Если, например, вы щелкнете выключателем света, вы нарушите цепь и, следовательно, выключите свет. Как только вы снова щелкнете выключателем, вы снова включите цепь, и снова загорится свет.
Если, например, вы щелкнете выключателем света, вы нарушите цепь и, следовательно, выключите свет. Как только вы снова щелкнете выключателем, вы снова включите цепь, и снова загорится свет.
Или подумайте о том, как повесить огни на свой дом или рождественскую елку.Если перегорает только одна лампочка, гаснет вся цепочка огней. Это потому, что электричеству, остановленному разбитым светом, некуда деться. Это то же самое, что выключить свет и разорвать цепь. Другой аспект этого в отношении законов Кирхгофа состоит в том, что сумма всего электричества, входящего и вытекающего из соединения, должна быть равна нулю. Электричество, поступающее в соединение (и протекающее по цепи), должно равняться нулю, потому что электричество, которое входит в него, также должно выходить.
Итак, в следующий раз, когда вы будете работать над своей распределительной коробкой или наблюдать за тем, как это делает электрик, натягивая электрические праздничные огни, или включаете или выключаете телевизор или компьютер, помните, что Кирхгоф сначала описал, как все это работает, тем самым открывая век электричество.
Действующий закон Кирхгофа (KCL) | Делительные схемы и законы Кирхгофа
Что такое действующий закон Кирхгофа?
Закон Кирхгофа о течениях, часто сокращаемый до KCL, гласит, что «алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю.”
Этот закон используется для описания того, как заряд входит и покидает точку соединения или узел на проводе.
Вооружившись этой информацией, давайте теперь рассмотрим пример применения закона на практике, почему он важен и как он был получен.
Обзор параллельной цепиДавайте внимательнее рассмотрим эту последнюю параллельную схему примера:
Решение для всех значений напряжения и тока в этой цепи:
На данный момент мы знаем значение тока каждой ветви и полного тока в цепи.Мы знаем, что полный ток в параллельной цепи должен равняться сумме токов ответвления, но в этой цепи происходит нечто большее, чем просто это. Взглянув на токи в каждой точке соединения проводов (узле) в цепи, мы должны увидеть кое-что еще:
Токи, входящие в узел и выходящие из него
В каждом узле положительной «шины» (провода 1-2-3-4) у нас есть разделение тока от основного потока к каждому последующему резистору ответвления.В каждом узле на отрицательной «шине» (провод 8-7-6-5) у нас есть ток, сливающийся вместе, чтобы сформировать основной поток от каждого последовательного резистора ответвления. Этот факт должен быть довольно очевиден, если вы подумаете об аналогии контура водопровода с каждым ответвлением, действующим как тройник, разделением или слиянием водяного потока с основным трубопроводом, когда он движется от выхода водяного насоса к обратной резервуар или отстойник.
Если мы внимательно рассмотрим один конкретный узел «тройник», такой как узел 6, мы увидим, что ток, входящий в узел, равен по величине току, выходящему из узла:
Сверху и справа у нас есть два тока, входящие в соединение проводов, обозначенное как узел 6.Слева у нас есть единственный ток, выходящий из узла, равный по величине сумме двух входящих токов. Обратимся к аналогии с водопроводом: пока в трубопроводе нет утечек, поток, поступающий в фитинг, должен также выходить из фитинга. Это верно для любого узла («подгонки»), независимо от того, сколько потоков входит или выходит. Математически мы можем выразить это общее соотношение как таковое:
Действующий закон Кирхгофа
Г-н Кирхгоф решил выразить это в несколько иной форме (хотя и математически эквивалентной), назвав ее Текущий закон Кирхгофа (KCL):
Текущий закон Кирхгофа, кратко изложенный в одной фразе, гласит:
«Алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю»
То есть, если мы присвоим каждому току математический знак (полярность), обозначающий, входят ли они (+) или выходят (-) из узла, мы можем сложить их вместе, чтобы получить гарантированно нулевое значение.
Взяв наш пример узла (номер 6), мы можем определить величину тока, выходящего слева, задав уравнение KCL с этим током в качестве неизвестного значения:
Отрицательный (-) знак на значении 5 миллиампер говорит нам, что ток на выходе из узла, в отличие от токов 2 миллиампер и 3 миллиампер, которые оба должны быть положительными (и, следовательно, входит в узел) . Независимо от того, обозначает ли отрицательное или положительное значение текущий вход или выход, совершенно произвольно, если они являются противоположными знаками для противоположных направлений и мы остаемся последовательными в наших обозначениях, KCL будет работать.
Вместе законы напряжения и тока Кирхгофа представляют собой замечательную пару инструментов, полезных при анализе электрических цепей. Их полезность станет еще более очевидной в следующей главе («Сетевой анализ»), но достаточно сказать, что эти законы заслуживают того, чтобы их запомнил изучающий электронику не меньше, чем закон Ома.
ОБЗОР:
- Текущий закон Кирхгофа (KCL): «Алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю»
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
.
 Простым считается такой контур, при обходе которого мы побываем в каждой точке только по одному разу. В правильно выбранной системе контуров каждый участок цепи должен фигурировать по крайней мере в одном из контуров.
Простым считается такой контур, при обходе которого мы побываем в каждой точке только по одному разу. В правильно выбранной системе контуров каждый участок цепи должен фигурировать по крайней мере в одном из контуров. А. Детлаф, Б.М. Яворский. – М.: Высшая школа, 1999
А. Детлаф, Б.М. Яворский. – М.: Высшая школа, 1999






 Поток, протекающий в точку, должен равняться тому, что получаем на выходе из нее.
Поток, протекающий в точку, должен равняться тому, что получаем на выходе из нее. Результаты измерений
Результаты измерений Какое свойство заряда он отражает?
Какое свойство заряда он отражает? В этих случаях можно использовать законы Кирхгофа.
В этих случаях можно использовать законы Кирхгофа. {\ text {n}} \ text {I} _ \ text {k} = 0 [/ latex], где I k — ток k, а n — общее количество проводов, входящих и выходящих из соединения. с учетом.
{\ text {n}} \ text {I} _ \ text {k} = 0 [/ latex], где I k — ток k, а n — общее количество проводов, входящих и выходящих из соединения. с учетом. \ text {n} \ text {V} _ \ text {k} = 0 [/ latex].
\ text {n} \ text {V} _ \ text {k} = 0 [/ latex]. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.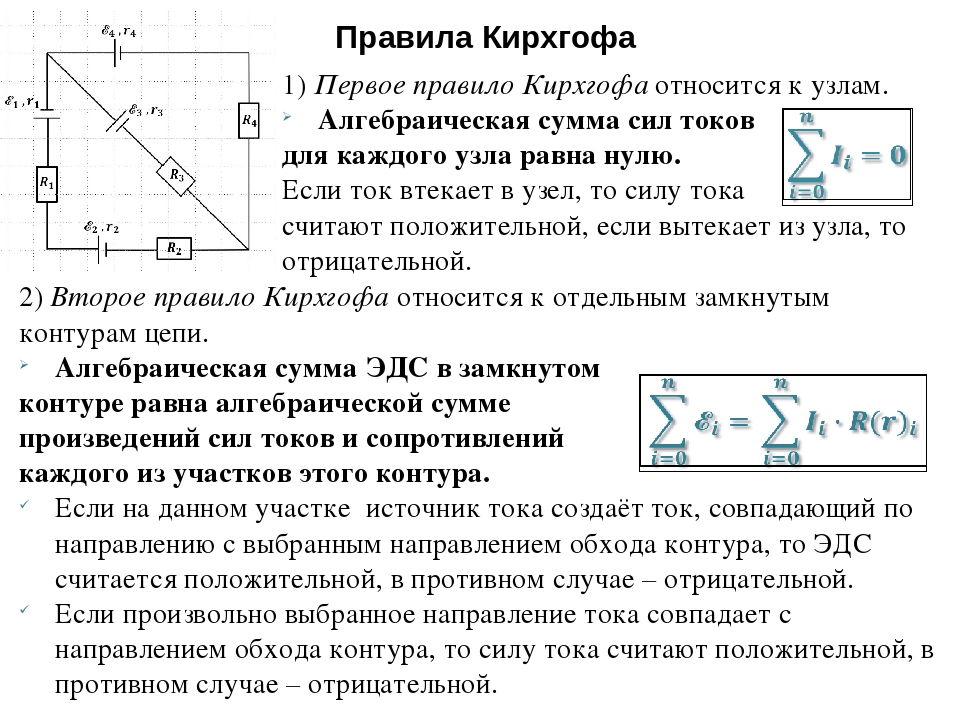 Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения:
∑Iin = ∑Iout.∑Iin = ∑Iout.
Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения:
∑Iin = ∑Iout.∑Iin = ∑Iout. Эти ярлыки просто помогают сориентироваться.
Эти ярлыки просто помогают сориентироваться.
