Сопротивление. Омы. Резистор.

Еще со школы мы сталкиваемся с таким термином как сопротивление. В курсе физики для 8-го класса эта тема рассматривается вместе с изучение закона Ома. Понимание теории позволяет посчитать какая мощность выделяется в резисторе, какое общее сопротивление последовательно или параллельно соединенных резисторов. Сложно представить современную электронику без резисторов, а тем более понять как работает тот или иной узел.

Что такое напряжение и ток?

Для полного понимания изложенного материала не помешает ознакомится с такими величины как напряжение и ток. Напряжение — это разница потенциалов. Если взять батарейку то на ее клеммах будет присутствовать разность потенциалов. То есть на одном выводе электронов будет больше, чем на другом. Если соединить две клеммы вместе, то электроны начнут течь от клеммы, на которой есть их избыток, к клемме с дефицитом электронов. Величина которая показывает сколько электронов пройдет за единицу времени и называется током. Не сложно заметить что напряжение и ток величины зависимые. Зависимость эта выражается законом ома:

I = U/R

U и I обозначают напряжение и ток соответственно, а величина R называется сопротивлением и измеряется в Омах [Ом].

Типы резисторов. Обозначение резисторов на схеме.

На схемах резисторы обозначается следующим образом:

1 — это постоянный резистор. 2, 3 и 4 — переменного сопротивления. Рисунком под номером 2 обычно обозначают подстроечный резистор (сопротивление которого может изменяться в процессе наладки схемы). 3 — потенциометр (осуществляет регулировку напряжения), 4 — реостат (регулирует ток).

Последовательно соединенные резисторы. Делитель напряжения.

Если резисторы соединены последовательно, то их общее сопротивление равняется сумме сопротивлений каждого резистора. Рассмотрим схему:

Пусть сопротивление R1 — 20 Ом, а сопротивление R2 — 10 Ом. Напряжение источника питания U — 3В. Как найти напряжения U1 и U2 на резисторах? Все проще, чем может показаться на первый взгляд, давайте вспомнит вышеупомянутый закон Ома I = U/R. R в данном случае суммарное сопротивление резисторов. Так как они соединены последовательно, то R = 20 + 10 = 30 Ом. Находим I = 3/30 = 0,1 А. Именно такой ток протекает через каждый резистор цепи. Немного изменив формулу получив выражение напряжения через сопротивление и ток: U = IR. Подставив значения в выражение получаем U1=20*0,1=2В, U2=10*0,1=1В.

Рассмотренная схема называется делителем напряжения. Внимательный читатель мог заметить что выше я называл потенциометр регулятором напряжения. Все верно — потенциометр делает ничто иное, как «разделяем» своим бегунком один резистор на два.

Параллельное соединение резисторов.

Если сопротивление последовательно соединенных резисторов считать довольно просто, то с резисторами соединенными параллельно дело обстоит немного сложнее. Давайте выведем формулу по которой считается общее сопротивление. Рассмотрим следующую схему:

Пусть R1 = 10 Ом, R2 = 20 Ом, R3=15 Ом, U = 5В. Тогда I1 = U/R1 = 5/10 = 0,5А. I2 = U/R2. I3 = U/R3. R = U/I = U / (U/R1 + U/R2 + U/R3) = U*R1*R2*R3/ ( U*R2*R1 + U*R1*R3 + U*R2*R3) = R1*R2*R3/(R1*R3+R2*R3 + R1*R2) = 10*15*20*/(10*15 + 20*15 + 10*20) = 4,615… Ом.

На первый взгляд, вывод очень сложный, но запоминать формулу не понимая откуда берется каждый ее член еще сложнее. На практике редко приходиться считать общее сопротивление более чем двух параллельно соединенных резисторов. Да и для этих случаев есть специализированный софт.

Мощность резистора.

Мощность выделяющаяся на резисторе зависит от тока, который через него протекает. Узнать необходимую мощность можно воспользовавшись формулой P = I*I*R. Если известно напряжения, то P = U*U/R. Данные формулы следуют из закона Ома и формулы для определения мощности P = U*I.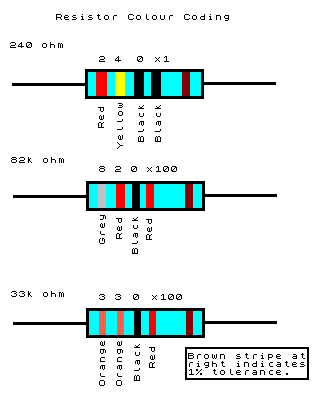

Закон Ома (страница 3)

Решение:
Падения напряжения на резисторах R₁ и R₂, а также на резисторах 2R₁ и 2R₂ пропорциональны их сопротивлениям. Поэтому падение напряжения на резисторе R равно нулю и ток через него не проходит. Через резистор R₂ течет ток


18 Один полюс источника тока с э. д. с. ε = 1400 В и внутренним сопротивлением r = 2,2 Ом подключен к центральной алюминиевой жиле кабеля (диаметр жилы D₁ = 8мм), другой — к его свинцовой оболочке (наружный диаметр D₂ =18 мм, внутренний — d₂ = 16 мм). На каком расстоянии l от источника кабель порвался и произошло замыкание жилы с оболочкой, если начальный ток короткого замыкания I=120 А? Удельные сопротивления алюминия и свинца ρ₁ =0,03 мкОм·м и ρ₂ = 0,2 мкОм·м.

Решение:
Полное сопротивление цепи R= R₁ + R₂ + r, где сопротивления жилы и оболочки до места замыкания

Ток в цепи I= e/R; отсюда

19 Найти ток I, текущий через резистор с сопротивлением R₁ в схеме, параметры которой даны на рис. 107, в первый момент после замыкания ключа, если до этого напряжение на конденсаторе было постоянным.

Решение:
Напряжение на конденсаторе V=ε. Это же напряжение будет в первый момент после замыкания ключа на резисторе R₁. Поэтому текущий через него в этот момент ток I=ε/R₁.

20 Найти напряжения V₁ и V₂ на конденсаторах с емкостями С₁ и С₂ в схеме, параметры которой даны на рис. 108.

Решение:
После включения источника тока с э. д. с. ε конденсаторы зарядятся, и, когда ток прекратится, все их обкладки, соединенные с резистором R, будут иметь одинаковый потенциал. Конденсаторы с емкостями С+С₁ и С+С₂ включены последовательно с источником тока. Общее напряжение на них V₁+V₂ =ε, а заряд на них

отсюда

21 Найти заряды q₁, q₂ и q₃ на каждом из конденсаторов в схеме, параметры которой даны на рис. 109.

Решение:
Обкладки конденсатора C₁ замкнуты через резисторы R₁ и R₂. Поэтому заряд на этом конденсаторе q₁=0 (после прекращения зарядки конденсаторов С₂ и С₃). Так как после зарядки конденсаторов токи в схеме не протекают, то напряжения на конденсаторах С₂ и С₃ равны ε. Следовательно,

22 В цепь, питаемую источником тока с внутренним сопротивлением r = 3 Ом, входят два резистора с одинаковыми сопротивлениями R₁ = R₂ = 28 Ом, включенные параллельно, и резистор с сопротивлением R₃ = 40 Ом (рис.110). Параллельно резистору R₃ подключен конденсатор емкости С=5 мкФ, заряд которого q=4,2 Кл. Найти э. д. с. ε источника.

Решение:
Падение напряжения на резисторе R₃ будет V=q/C=IR₃; отсюда ток, текущий через этот резистор, I=q/CR₃. Полное сопротивление цепи и э. д. с. источника тока


23 Два резистора с одинаковыми сопротивлениями R₁ =25 Ом и резистор с сопротивлением R₂ = 50 Ом подключены к источнику тока по схеме, изображенной на рис. 111. К участку ab подключен конденсатор емкости С = 5 мкФ. Найти э. д. с. ε источника тока, если заряд на конденсаторе q = 0,11 мКл.

Решение:


24 Найти заряд на конденсаторе емкости С в схеме, параметры которой даны на рис. 112.

Решение:
Сопротивление конденсатора постоянному току бесконечно велико. Поэтому после зарядки конденсатора по резистору R₃ ток протекать не будет. Не будет и падения напряжения на этом резисторе. Следовательно, точка а и верхняя обкладка конденсатора будут иметь одинаковый потенциал. Потенциал же точки b будет равен потенциалу нижней обкладки конденсатора. Таким образом, напряжение на конденсаторе будет равно падению напряжения на резисторе R₂. Ток в цепи

отсюда заряд на конденсаторе

25 Найти напряжение на конденсаторе емкости в схеме, параметры которой даны на рис. 113.

Решение:


26 Источник тока с внутренним сопротивлением r=10м замкнут на резистор с сопротивлением R. Вольтметр, подключенный к зажимам источника, показывает напряжение V₁=20 B. Когда параллельно резистору с сопротивлением R присоединен резистор с таким же сопротивлением R, показание вольтметра уменьшается до V₂ = 15 B. Найти сопротивление резистора R, если сопротивление вольтметра велико по сравнению с R.

Решение:
Напряжения на зажимах источника тока в первом и во втором случаях V₁=I₁R и V₂=I₂R/2. Токи в общей цепи в этих случаях

отсюда


27 К источнику тока с э. д. с. ε = 200 В и внутренним сопротивлением r = 0,5 Ом подключены последовательно два резистора с сопротивлениями R₁ = 100Ом и R₂ = 500 Ом. К концам резистора R₂ подключен вольтметр. Найти сопротивление R вольтметра, если он показывает напряжение V=160 В.

Решение:
Падение напряжения на резисторе R₂ (и на вольтметре) V=IRо (рис. 358), где R₀ = R₂R/(R₂ + R)-сопротивление параллельно включенных вольтметра и резистора R₂. Ток в общей цепи равен

Решая совместно эти уравнения, получим

Тот же результат можно получить, решая систему уравнений

28 Проволока из нихрома изогнута в виде кольца радиуса а=1 м (рис.114). В центре кольца помещен гальванический элемент с э. д. с. ε = 2 В и внутренним сопротивлением r=1,5 0м. Элемент соединен с точками с и d кольца по диаметру с помощью такой же нихромовой проволоки. Найти разность потенциалов между точками cad. Удельное сопротивление нихрома ρ=1,1мкОм⋅м, площадь сечения проволоки S= 1 мм².

Решение:
В эквивалентной схеме резисторы R₁ соответствуют проволокам, соединяющим элемент с кольцом, а резисторы R₂-двум половинам кольца (рис. 359). Полное внешнее сопротивление цепи

Ток в общей цепи

Разность потенциалов между точками с и d


29 К источнику тока с внутренним сопротивлением r = 1 Ом подключены два параллельно соединенных резистора с сопротивлениями R₁ = 10 Ом и R₂ = 2 Ом. Найти отношение токов, протекающих через резистор R₁ до и после обрыва в цепи резистора R₂.

Решение:


30 Два резистора с сопротивлениями R₁ = R₂ = 1 Ом и реостат, имеющий полное сопротивление R₃ = 2 Ом, присоединены к источнику тока с внутренним сопротивлением r = 0,5 Ом (рис. 115). К разветвленному участку цепи подключен вольтметр. Когда движок реостата находится на его середине (точка а), вольтметр показывает напряжение V_a=13 В. Каково будет показание вольтметра, если движок передвинуть в крайнее правое положение на реостате? Сопротивление вольтметра велико по сравнению с R₁ и R₂.

Решение:


31 Шесть проводников с одинаковыми сопротивлениями R₀ = 2 Ом соединены попарно параллельно. Все три пары соединены последовательно и подключены к источнику тока с внутренним сопротивлением r=1 Ом. При этом по каждому проводнику течет ток I₀ = 2,5А. Какой ток будет течь по каждому проводнику, если один из них удалить?

Решение:
Сопротивление каждой пары проводников равно R₀/2. Полное внешнее сопротивление цепи до удаления одного из проводников R₁=3R₀/2. По закону Ома для полной цепи

отсюда э. д. с. источника тока

После удаления одного из проводников полное внешнее сопротивление цепи

Ток в общей цепи

Через проводник, оставшийся без пары, будет идти ток

а через остальные проводники будут идти токи I₂/2 = 2 А.

32 Источник тока с э. д. с. ε = 100 В и внутренним сопротивлением r = 0,2 Ом и три резистора с сопротивлениями R₁ = 3 Ом, R₂ = 2 Ом и R₃ = 18,8 Ом включены по схеме, изображенной на рис. 116. Найти токи, текущие через резисторы R₁ и R₂.

Решение:


33 К источнику тока с э. д. с. e=120 В и внутренним сопротивлением r=10 Ом подключены два параллельных провода с сопротивлениями R₁ =20 Ом. Свободные концы проводов и их середины соединены друг с другом через две лампы с сопротивлениями R₂ = 200 Ом. Найти ток, текущий через источник тока.

Решение:
Верхняя лампа и провода, идущие к ней, начиная от места присоединения нижней лампы (рис. 360), образуют последовательную цепочку с сопротивлением R₃=R₁+R₂. Эта цепочка соединена параллельно с нижней лампой и вместе с ней образует сопротивление

Полное внешнее сопротивление цепи

Через источник тока течет ток


34 При замыкании источника тока на резистор с сопротивлением R₁=5 Ом в цепи идет ток I₁ = 5 А, а при замыкании на резистор с сопротивлением R₂ = 2 Ом идет ток I₂ = 8 А. Найти внутреннее сопротивление r и э. д. с. источника тока ε.

Решение:
Если ε и r — э. д. с. и внутреннее сопротивление источника тока, то

Из этих уравнений имеем


35 При замыкании источника тока на резистор с сопротивлением R₁ = 14 Ом напряжение на зажимах источника V₁ = 28 В, а при замыкании на резистор с сопротивлением R₂ = 29 Ом напряжение на зажимах V₂ = 29 В. Найти внутреннее сопротивление r источника.

Решение:


36 Амперметр с сопротивлением R₁ = 2 Ом, подключенный к источнику тока, показывает ток I₁ = 5 А. Вольтметр с сопротивлением R₂ = 150 Ом, подключенный к такому же источнику тока, показывает напряжение V=12B. Найти ток короткого замыкания I_к источника.

Решение:
При подключении к источнику тока амперметра через него течет I₁=ε/(R1+r), где ε — э. д. с. батареи, а r — ее внутреннее сопротивление; при подключении к источнику тока вольтметра через него течет ток I₂=ε/(R₂+r), и вольтметр показывает напряжение

отсюда

Ток короткого замыкания (при равном нулю внешнем сопротивлении)

37 Два параллельно соединенных резистора с сопротивлениями R₁=40 Ом и R₂ = 10 Ом подключены к источнику тока с э. д. с. ε=10 В. Ток в цепи I=1 А. Найти внутреннее сопротивление источника и ток короткого замыкания.

Решение:


38 Аккумулятор с э. д. с. ε = 25 В и внутренним сопротивлением r = 1 Ом заряжается от сети с напряжением V=40 В через сопротивление R = 5 Ом. Найти напряжение V_а на зажимах аккумулятора.

Решение:
При зарядке аккумулятор включается навстречу источнику тока. Во время зарядки ток внутри аккумулятора течет от положительного полюса к отрицательному. Напряжение сети V=ε+I(R+r), где I-ток зарядки; отсюда I=(V-ε)/(R+r). Напряжение на зажимах аккумулятора

Какой формулой рассчитать мощность резисторов

Резисторы применяются практически во всех электросхемах. Это наиболее простой компонент, в основном, служащий для ограничения или регулирования тока, благодаря наличию сопротивления при его протекании.

Резисторы

Виды резисторов

Внутреннее устройство детали может быть различным, но преимущественно это изолятор цилиндрической формы, с нанесённым на его внешнюю поверхность слоем либо несколькими витками тонкой проволоки, проводящими ток и рассчитанными на заданное значение сопротивления, измеряемое в омах.

Существующие разновидности резисторов:

1. Постоянные. Имеют неизменное сопротивление. Применяются, когда определенный участок электроцепи требует установки заданного уровня по току или напряжению. Такие компоненты необходимо рассчитывать и подбирать по параметрам;
2. Переменные. Оснащены несколькими выводными контактами. Их сопротивление поддается регулировке, которая может быть плавной и ступенчатой. Пример использования – контроль громкости в аудиоаппаратуре;
3. Подстроечные – представляют собой вариант переменных. Разница в том, что регулировка подстроечных резисторов производится очень редко;
4. Есть еще резисторы с нелинейными характеристиками – варисторы, терморезисторы, фоторезисторы, сопротивление которых меняется под воздействием освещения, температурных колебаний, механического давления.

Важно! Материалом для изготовления практически всех нелинейных деталей, кроме угольных варисторов, применяемых в стабилизаторах напряжения, являются полупроводники.

Параметры резисторного элемента

1. Для резисторов применяется понятие мощности. При прохождении через них электротока происходит выделение тепловой энергии, рассеиваемой в окружающее пространство. Мощность детали является параметром, который показывает, сколько энергии она может выделить в виде тепла, оставаясь работоспособной. Мощность зависит от габаритов детали, поэтому у маленьких зарубежных резисторов ее определяют на глаз, сравнивая с российскими, технические характеристики которых известны;

Важно! Импортные резисторные элементы идентичной мощности имеют несколько меньшие размеры, так как российские производятся с некоторым запасом по этому показателю.

На схеме мощность показана следующим образом.

Условное обозначение мощности

2. Второй параметр – сопротивление элемента. На российских деталях типа МЛТ и крупных импортных образцах оба параметра указываются на корпусе (мощность – Вт, сопротивление – Ом, кОм, мОм). Для визуального определения сопротивления миниатюрных импортных элементов применяется система условных обозначений с помощью цветных полосок;

Цветовая маркировка резисторов

3. Допуски. Невозможно изготовить деталь с номинальным сопротивлением, в точности соответствующим заявленному значению. Поэтому всегда указываются границы погрешности, называемые допуском. Его величина – 0,5-20%;
4. ТКС – коэффициент температуры. Показывает, как варьируется сопротивление при изменении внешней температуры на 1°С. Желательно, но не обязательно подбирать элементы с близким или идентичным значением этого показателя для одной цепи.

Расчет резисторов

Для расчета сопротивления резистора формула применяемая в первую очередь – это закон Ома:

I = U/R.

Исходя из этой формулы, можно вывести выражение для сопротивления:

R = U/I,

где U – разность потенциалов на выводных контактах резистора.

Пример. Необходимо провести зарядку аккумулятора 2,4 В зарядным током 50 мА от автомобильной 12-вольтовой батареи. Прямое соединение сделать нельзя из-за слишком высоких показателей по току и напряжению. Но возможно поставить в схему сопротивление, которое обеспечит нужные параметры.

Предварительно нужно рассчитать резистор:

• Расчет начинается с определения падения напряжения, которое должен обеспечить резисторный элемент:

U = 12-2,4 = 9,6 B

• Протекающий по детали ток – 50 мА. Следовательно, R = 9,6/0,05 = 192 Ом

Теперь можно уже подобрать нужный резистор по одному показателю.

Если рассчитанной детали не нашлось, можно применить соединение из нескольких резисторных элементов, установив их последовательно или параллельно. Расчет сопротивлений при этом имеет свои особенности.

Последовательное соединение

Последовательно соединенные сопротивления складываются:

R = R1+ R2.

Если нужно получить общий результат 200 Ом, и имеется один резистор на 120 Ом, то расчет другого:

R2 = R-R1 = 200-120 = 80 Ом.

Последовательное соединение

Параллельное соединение

При параллельной схеме другая зависимость:

1/R = 1/R1 + 1/R2.

Или преобразованный вариант:

R = (R1 x R2)/ (R1 + R2).

Важно! Параллельное соединение можно использовать, когда в наличии детали с большим сопротивлением, чем требуется, последовательное наоборот.

Пример. Необходимо сопротивление 200 Ом. Имеется деталь R2 на 360 Ом. Какое сопротивление подобрать еще? R1 = R2/(R2/R-1) = 360/(360/200-1) = 450 Ом.

Параллельное соединение

Смешанное соединение

В смешанных схемах присутствуют последовательно-параллельные комбинации. Расчет таких схем сводится к их упрощению путем преобразований. На рисунке ниже представлено, как упростить схему, рассчитывая общий показатель для шести резисторов с учетом их соединения.

Расчет сопротивления в смешанной схеме

Мощность

Определив сопротивление, еще нельзя выбрать деталь. Чтобы обеспечить надежную работу схемы, необходимо найти и другой параметр – мощность. Для этого надо знать, как рассчитать мощность резисторного элемента.

Формулы, по которым можно рассчитать мощность резистора:

Пример. I = 50 мА; R = 200 Ом. Тогда P = I² x R = 0,05² x 200 = 0,5 Вт.

Если не учитывать значение тока, расчет мощности резистора ведется по другой формуле.

Пример. U = 9,6 В, R = 200 Ом. P = U²/R = 9,6²/200 = 0,46 Вт. Получился тот же результат.

Теперь, зная точные параметры рассчитываемого резисторного элемента, подберем радиодеталь.

Важно! При выборе деталей возможно их заменить на резисторы с мощностью, больше рассчитанной, но обратный вариант не подходит.

Это основные формулы для расчета резисторных деталей, на основании которых производится анализ узлов схемы, где главным является определение токов и напряжений, протекающих через конкретный элемент.

Видео

Оцените статью:

Резистор | Все своими руками

Здравствуйте уважаемый читатель блога Моя лаборатория радиолюбителя.

В сегодняшнем материале хотелось бы освятить довольно таки нужную тему о резисторах, в особенности вопрос о том, что такое резистор, возникает у новичков радиолюбителей. В этой обширной статейке я довольно таки подробно постараюсь объяснить, что такое резистор, как он выглядит и где применяется.

И так начнем повествование о резисторах, поэтому усаживаемся поудобнее за нашими мониторами, желательно сделать себе кофе и погрузиться в мир радиоэлектроники 🙂

Для более таки удобной навигации, вот менюшка разделов статьи
— Что такое резистор?
— Маркировка резисторов
— Мощность резисторов и рассеиваемая мощность
— Последовательное и параллельное соединение резисторов
— Делитель напряжения на резисторе
— Делитель тока на резисторе

—Что такое резистор?

Резистор – это пассивный элемент электрической схемы, создающий сопротивление электрическому току.
Где применяются резисторы? Применяются резисторы во всех схемах, и чаще, в количественном отношении, чем другие элементы схемы. С помощью резисторов регулируют значения тока и напряжения.
Единица измерения сопротивления – Ом. Измерения записываются в сторону увеличения: Ом, кОм(1000Ом)-килоом, мОм(1.000.000Ом)-мегаом и Гом(1.000.000.000Ом)-гигаом.

Типы резисторов:

Постоянные резисторы – это резисторы имеющие постоянное, неизменное, сопротивление независимое от воздействия окружающих воздействий, таких как свет, температура.

— так обозначаются на схемах постоянные резисторы и подписываются буквой R

Так и не только так выглядят резисторы в жизни

Переменные резисторы — это резисторы меняющее свое сопротивление в зависимости от положения движка переменного резистора.

— так обозначаются переменные резисторы в схемах

Переменный резистор
Ползунковый переменный резистор

Такие переменные резисторы используются в многой бытовой технике вокруг нас, старые телевизоры, где звук регулировали крутя ручку звука и подобные

Подстроечные резисторы — это те же самые переменные резисторы, но используемые для точных настроек токов и напряжений схем. Устанавливаются преимущественно на самих печатных платах.
— обозначение подстроечных резисторов на схемах

Подстроечные резисторы в жизни

Фоторезисторы – это резисторы меняющие свое сопротивление под действием света.
— обозначение фоторезистора на схеме

Фоторезисторы

Терморезисторы – резисторы меняющие свое сопротивление в зависимости от температуры, приложенной к нему
— схематическое обозначение терморезистор

Пример терморезисторов

— Маркировка резисторов:

Маркировка по ГОСТу номинальный ряд
Все резисторы, выпускаемые нашей промышленностью, имеют свою особую сокращенную маркировку, дабы было удобно читать номинал на маленьких резисторах. Для сокращения используют буквы указывающие единицу измерения
E и R – единица Ома
К – единица кОм
M- мОм
А вот сотни единиц, обозначаются буквами, стоящими перед цифрами.
Например: 0,33Ом -E33, 33Ом-33E, 33кОм-33K, 330кОм-M33, 33мОм-33M.

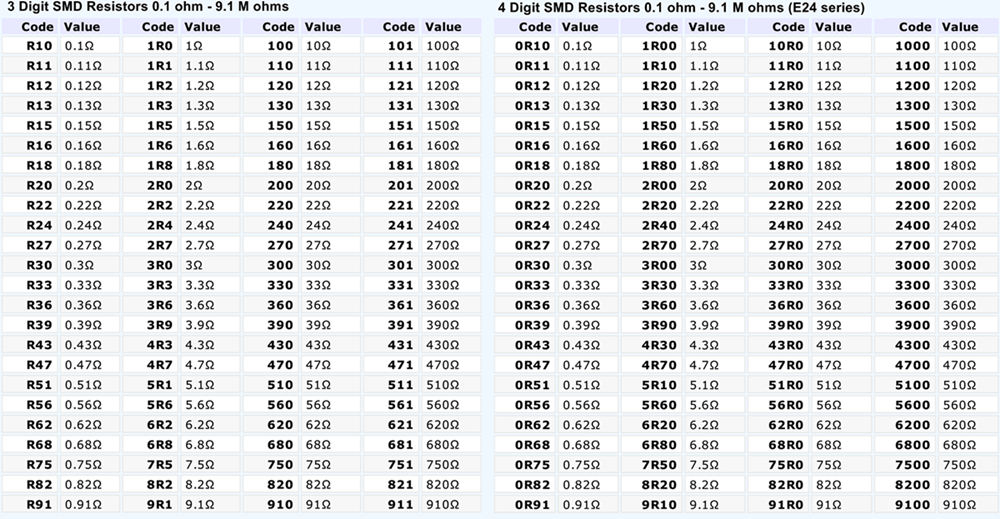
Заграничный ГОСТ
Тут немного проще. По американским стандартам маркируются резисторы 3 буквами, две первые указывающие номинал, а третья — количество нулей добавляемых к номиналу

Например: 0,33Ом –R33, 33Ом-330, 33кОм-333, 330кОм-334, 33мОм-336.

Цветовая маркировка резисторов
На мой взгляд самая удобная и простая в использовании. Обозначается она разноцветными полосками на резисторе. Полосок бывает 4 и 5. Научится читать резисторы цветной маркировки очень просто:

-Первые две полосы указывают номинал резистора.

-Третья полоска, у резисторов с 4 полосами, указывает множитель, а у резисторов с 5 полосами, указывает третью цифру номинала.

-Четвертая полоса в 4 полосной маркировке говорит о точности номинала, а в 5 полосной указывает на множитель номинала.

-Пятая полоса указывает на точность

Что бы удобно было ориентироваться, вот табличка с цветовой кодировкой резисторов

Цвет	Число	Множитель	Точность
Черный	0	1	—
Коричневый	1	10	1 %
Красный	2	100	2 %
Оранжевый	3	1 000	—
Желтый	4	10 000	—
Зеленый	5	100 000	0,5 %
Синий	6	1 000 000	0,25 %
Фиолетовый	7	10 000 000	0,1 %
Серый	8	100 000 000	—
Белый	9	1 000 000 000	—
Серебристый	—	0,01	10 %
Золотой	—	0,1	5 %

К примеру, резистор номиналом 1 кОм с погрешностью 1% будет иметь код — коричневый черный красный коричневый

— Мощность резисторов и рассеиваемая мощность

Каждый резистор, пропуская через себя напряжение, создает определенное падение напряжение, что обусловлено законом Ома (R=U\I). 2/R

Для примера нам нужно рассчитать балластный резистор для блока питания 5В с током нагрузки 0,1А. Сначала по закону Ома рассчитаем, какое сопротивление резистора нам нужно R=5/0.1=50(Ом). Имея сопротивления резистора, рассчитываем мощность резистора P=5*0.1=0.5Вт.

То есть наш балластный резистор должен быть сопротивлением 50Ом и рассеиваемой мощностью 1ВТ, а 1 Вт — потому что всегда нужно брать резисторы с запасом в 1.5-2 раза, что бы небыло ситуаций как на этой очень удачно подобранной картинке 🙂

Сгоревший резистор

Поэтому запоминаем, что необходимо брать мощность резистора в 2 раза большей от расчетной!

Мощность резисторов на схемах указываются так:
— мощностью рассеивания 0,125 Вт
— мощностью рассеивания 0,25 Вт
— мощностью рассеивания 0,5 Вт
— мощностью рассеивания 1 Вт
— мощностью рассеивания 2 Вт
— мощностью рассеивания 5 Вт

Есть и далее продолжение маркировки, но это уже не обязательно, потому что это саамы ходовые мощности и больше редко используются в схемах

— Последовательное и параллельное соединение резисторов
Так же для достижения нужного нам сопротивления мы можем подключать последовательно резисторы

, где общее сопротивление будет равно сумме всех сопротивлений и считается по формуле R=R1+R2+R3
И подключать резисторы параллельно

, где общее сопротивление будет равно сумме величин, обратно пропорциональных сопротивлению 1/R=1/R1+1/R2+1/R3. А при параллельном соединении 2-х резисторов удобно пользоваться этой формулой R=R1*R2/(R1+R2)

— Делитель напряжения на резисторе

Делитель напряжения на резисторах часто используется в схемах для получения нужного напряжениях в отдельных цепях схемы.
Делитель напряжение, это два последовательно подключенные резистора. В нем выходное напряжение напрямую зависит от номиналов сопротивлений и питающего напряжения. Переменные резисторы так же являются делителями напряжения.

И прежде чем мы начнем рассматривать формулы, давайте выясним один очень важный момент.
Что бы четко рассчитывать нужное нам напряжение на выходе, используйте R2 сопротивлением в 100 раз меньше сопротивления нагрузки подключенной к выходу делителя

Рассмотрим самые нужные формулы для расчета делителя:

1. Нам известно входящее напряжение Uвх и сопротивление R1 и R2.
Uвых=Uвх*R2/(R1+R2)
Например, входящее напряжение 12В, резисторы R1=2.2к и R2=1к. Uвых=12В*1000Ом/3200Ом=3.75В

2. Известно нужное Uвых и сопротивление R1 и R2.
Uвх=Uвых*(R1+R2)/R2
Например, нам нужно получить 5 вольт для питания, резисторы R1=2.2к и R2=1к. Uвх=5В*3200Ом/1000Ом=16В

3. Определим значение R1 при известном Uвх, Uвых
R1=Uвх*R2/Uвых-R2
Например, входящее напряжение 12 вольт, выходящее напряжение 5В, значение R2=1к
R1= 12В*1000Ом/5В – 1000Ом=1400Ом

4. Определим значения R1 и R2, зная их суммарное сопротивление Rобщ и Uвх и Uвых
R2=Uвых*Rобщ/Uвх, R1= Rобщ-R2
Например R2=5В*3200Ом/12В=1333Ом, R1= 3200-1333=1867(Ом)

Это самые ходовый формулы, которые я использую уже около года, с тех пор, как только узнал о них

— Делитель тока на резисторе

Делитель тока на резисторах необходим для того, что бы определенную нужную часть тока перевести в другое плече делителя и после вернуть его обратно.

Делитель тока это параллельно соединенные резисторы, делящие между собой протекаемый ток.

Применяют делители тока для измерительных приборов, когда основной ток проходит через шунтирующий резистор, а малая часть тока проходит через катушки измерительного прибора, которая является вторым сопротивлением в схеме. Так же применяется для усиления тока, когда одного резистора не хватает

Формула расчета шунта для измерительных приборов R2 =I1*R1/(Iобщ-I1),где R1 это сопротивление прибора, а I1 это ток отклонения катушки прибора. 2*R. P1=3.33*3.33*0.1=1.1(Вт), P2=1.66*1.66*0.2=0.55Вт

И на этой ноте можно заканчивать материал. Изучайте, понимайте, задавайте вопросы.
С ув. Admin-чек

Похожие материалы: Загрузка…

Что такое резистор, классификация резисторов и их обозначения на схемах

Резистор (англ. resistor от лат. resisto — сопротивляюсь) —один из самых распространенных радиоэлементов. Даже в простом транзисторном приемнике число резисторов достигает нескольких десятков, а в современном теле-иизоре их не менее двух-трех сотен.

Резисторы используют в качестве нагрузочных и токоограничительных элементов, делителей напряжения, добавочных сопротивлений и шунтов в измерительных цепях и т. д.

Основным параметром резистора является сопротивление, характеризующее его способность препятствовать протеканию электрического тока. Сопротивление измеряется в омах, килоомах (тысяча Ом) и мегаомах (1 000000 Ом).

Постоянные резисторы

Вначале резисторы изображали на схемах в виде ломаной линии — меандра (рис. 1,а, б), которая обозначала высокоомный прокол, намотанный на изоляционный каркас. По мере усложнения радиоприборов число резисторов в них увеличивалось, и, чтобы облегчить начертание, их с шли изображать на схемах в виде зубчатой линии (рис. 1,в).

На смену этому символу пришел символ в виде прямоугольника (рис. 1,г), который стали применять для обозначения любого резистора, независимо от его конструкции и особенностей.

Рис. 1. Постойнные резисторы и их обозначение.

Постоянные резисторы могут иметь один или несколько отводов от резистивного элемента. На условном обозначении такого резиетора дополнительные выводы изображают в том же порядке, как это имеет место в самом резисторе (рис. 2). При большом числе отводов длину символа допускается увеличивать.

   Рис. 2. Постоянные резисторы с отводами — обозначение.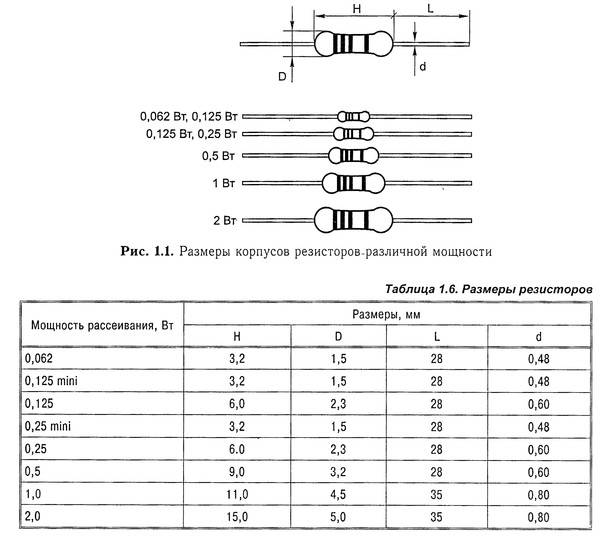

Сопротивление постоянного резистора, как говорит само название, изменить невозможно. Поэтому, если в цепи требуется установить определенный ток или напряжение, то для этого приходится подбирать отдельные элементы цепи, которыми часто являются резисторы. Возле символов этих элементов на схемах ставят звездочку * — знак, говорящий о необходимости их подбора при настройке или регулировке.

Обозначение сопротивления резисторов

Нимннальную мощность рассеяния резистора (от 0,05 до 5 Вт) обозначают специальными знаками, помещаемыми внутри символа (рис. 3). Заметим, мм ни таки не должны касаться контура условного обозначения резистора.

Рис. 3. Обозначение мощности резисторов.

На принципиальной схеме номинальное сопротивление резистора указывают рядом с условным обозначением (рис. 4). Согласно ГОСТ 2.702—7S сопротивлении от 0 до 999 Ом указывают числом без единицы измерения (2,2; 33, 120…), от 1 до 999 кОм — числом с бумвой к (47 к, 220 к, 910к и т. д.),свыше 1 мегаома — числом с буквой М (1 М, 3,6М и т. д.).

   Рис. 4. Обозначение сопротивления для резисторов на схемах.

На резисторах отечественного производства номинальное сопротивление, допускаемое отклонение от него, а если позволяют размеры, и номинальную мощность рассеяния указывают в виде полного или сокращенного (кодированного) обозначения.

Согласно ГОСТ 11076—69 единицы сопротивления в кодированной системе обозначают буквами Е (ом), К (килоом) и М (мегаом). Так, резисторы сопротивлением 47 Ом маркируют 47Е, 75 Ом —75Е, 12 кОм — 12К, 82 кОм —82К и т. д.

Сопротивления от 100 до 1000 Ом и от 100 до 1000 кОм выражают в долях килоома и мегаома соответственно, причем на месте нуля и запятой ставят соответствующую единицу измерения:

• 180 Ом = 0,18 кОм = К18;
• 910 Ом = 0,91 кОм = К91;
• 150 к0м = 0,15 МОм = М15;
• 680 к0м = 0,68 МОм = М68 и т. д.

Если же номинальное сопротивление выражено целым числом с дробью, то единицу измерения ставят на месте запятой: 2,2 Ом — 2Е2; 5,1 кОм —5К1; 3,3 МОм — ЗМЗ и т. д.

Кодированные буквенные обозначения установлены и для допускаемых отклонений сопротивления от номинального. Допускаемому отклонению ±1% -соответствует буква Р, ±2%—Л, ±5%—И, ±10% —С, ±20%—В. Таким образом, надпись на корпусе резистора К75И обозначает номинальное сопротивление 750 Ом с допускаемым отклонением ±5%; надпись МЗЗВ — 330 кОм ±20% и т. д.

Переменные резисторы

Переменные резисторы, как правило, имеют минимум три вывода: от концов токопроводящего элемента и от щеточного контакта, который может перемещаться по нему. С целью уменьшения размеров и упрощения конструкции токопроводящий элемент обычно выполняют в виде незамкнутого кольца, а щеточный контакт закрепляют на валике, ось которого проходит через его центр.

Таким образом, при вращении валика контакт перемещается по поверхности токопроводящего элемента, в результате сопротивление между ним и крайними выводами изменяется.

В непроволочных переменных резисторах обладающий сопротивлением то-копроводящий слой нанесен на подковообразную пластинку из гетинакса или текстолита (резисторы СП, СПЗ-4) или впрессован в дугообразную канавку керамического основания (резисторы СПО).

В проволочных резисторах сопротивление создается высокоомным проводом, намотанным в один слой на кольцеобразном каркасе. Для надежного соединения между обмоткой и подвижным контактом провод зачищают на глубину до четверти его диаметра, а в некоторых случаях и полируют.

Существуют две схемы включения переменных резисторов в электрическую цепь. В одном случае их используют для регулирования тока в цепи, и тогда регулируемый резистор называют реостатом, в другом — для регулирования напряжения, тогда его называют потенциометром. Показанное на рис. 5 условное графическое обозначение используют, когда необходимо изобразить реостат в общем виде.

Для регулирования тока в цепи переменный резистор можно включить диумя выводами: от щеточного контакта и одного из концов токопроводящего элемента (рис. 6,а). Однако такое включение не всегда допустимо.

Рис. 5. Реостаты и переменные резисторы — условное обозначение.

Если, например, в процессе регулирования случайно нарушится соединение щеточного контакта с токопроводящим элементом, электрическая цепь ока-1 жется разомкнутой, а это может явиться причиной повреждения при

бора. Чтобы исключить такую возможность, второй вывод токопроводящего элемента соединяют с выводом щеточного контакта (рис. 6,б). В этом случае даже при нарушении соединения электрическая цепь не будет разомкнута.

Общее обозначение потенциометра (рис. 6,в) отличается от символа реостата без разрыва цепи только отсутствием соединения выводов между собой.

Рис. 6. Обозначение потенциометра на принципиальных схемах.

К переменным резисторам, применяемым в радиоэлектронной аппаратуре, часто предъявляются требования по характеру изменения сопротивления при повороте их оси.

Так, для регулирования громкости в звуковоспроизводящей аппаратуре необходимо, чтобы сопротивление между выводом щеточного контакта и правым (если смотреть со стороны этого контакта) выводом токопроводящего элемента изменялось по показательному (обратному логарифмическому) закону.

Только в этом случае наше ухо воспринимает равномерное увеличение громкости при малых и больших уровнях сигнала. В измерительных генераторах сигналов звуковой частоты, где в качестве частотозадающих элементов часто используют переменные резисторы, также желательно, чтобы их сопротивление изменялось по логарифмическому или показательному закону.

Если это условие не выполнить, шкала генератора получается неравномерной, что затрудняет точную установку частоты.

Промышленность выпускает непроволочные переменные резисторы, в основном, трех групп:

• А — с линейной,
• Б — с логарифмической,
• В — с обратно-логарифмической зависимостью сопротивления между правым и средним выводами от угла поворота оси ф (рис. 47,а).

Резисторы группы А используют в радиотехнике наиболее широко, поэтому характеристику изменения их сопротивления на схемах обычно не указывают. Если же переменный резистор нелинейный (например, логарифмический) и это необходимо указать на схеме, символ резистора перечеркивают знаком нелинейного регулирования, возле которого (внизу) помещают соответствующую математическую запись закона изменения.

Рис. 7. Переменный резистор с обратно-логарифмической зависимостью сопротивления.

Резисторы групп Б и В конструктивно отличаются от резисторов группы А только токопроводящим элементом: на подковку таких резисторов наносят токопроводящий слой с удельным сопротивлением, меняющимся по ее длине. В проволочных резисторах форму каркаса выбирают такой, чтобы длина витка высокоомного провода менялась по соответствующему закону (рис. 7,6).

Регулируемые резисторы

Регулируемые резисторы — резисторы, сопротивление которых можно изменять в определенных пределах, применяют в качестве регуляторов усиления, громкости, тембра и т. д. Общее обозначение такого резистора состоит из базового символа и знака регулирования, причем независимо от положения символа на схеме стрелку, обозначающую регулирование, проводят в направлении снизу вверх под углом 45 градусов.

Регулируемые резисторы имеют относительно невысокую надежность и ограниченный срок службы. Кому из владельцев радиоприемника или магнитофона не приходилось после двух-трех лет эксплуатации слышать шорохи п треоки из громкоговорителя при регулировании громкости.

Причина этого неприятного явления — в нарушении контакта щетки с токопроводящим слоем или износ последнего. Поэтому, если основным требованием к переменному резистору является повышенная надежность, применяют резисторы со ступенчатым регулированием.

Такой резистор может быть выполнен на базе переключателя на несколько положений, к контактам которого подключены ре-, зисторы постоянного сопротивления.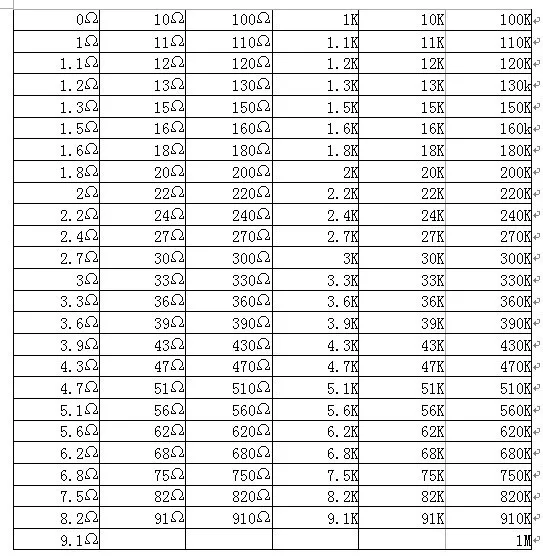 На схемах эти подробности не показывают, ограничиваясь изображением символа регулируемого резистора со знаком ступенчатого регулирования, а если необходимо, указывают и число ступеней (рис. 8).

Рис. 8. Изображение символа регулируемого резистора со знаком ступенчатого регулирования.

Некоторые переменные резисторы изготовляют с одним, двумя и даже с тремя отводами. Такие резисторы применяют, например, в тонкомпенсиро-ванных регуляторах громкости, используемых в высококачественной звуковоспроизводящей аппаратуре. Отводы изображают в виде линий, отходящих от длинной стороны основного символа (рис. 9).

Рис. 9. Обозначение переменного резистора с отводами.

Для регулирования громкости, тембра, уровня записи в стереофонической аппаратуре, частоты в измерительных генераторах сигналов и т. д. применяют сдвоенные переменные резисторы, сопротивления которых изменяются одновременно при повороте общей оси (или перемещении движка). На схемах символы входящих в них резисторов стараются расположить возможно ближе друг к другу, а механическую связь показывают либо двумя сплошными линиями, либо одной штриховой (рис. 10,а).

   Рис. 10. Внешний вид и обозначение блоков с переменными резисторами.

Если же сделать этого не удается, т. е. символы резисторов оказываются на большом удалении один от другого, механическую связь изображают отрезками штриховой линии (рис. 10,6). Принадлежность резисторов к одному сдвоенному блоку показывают в этом случае и в позиционном обозначении (R1.1—первый — по схеме — резистор сдвоенного переменного резистора R1, R1.2 — второй).

Встречаются и такие сдвоенные переменные резисторы, в которых каждым резистором можно управлять отдельно (ось одного проходит внутри трубчатой оси другого). Механической связи, обеспечивающей одновременное изменение сопротивлений обоих резисторов, в этом случае нет, поэтому и на схемах ее не показывают (принадлежность к сдвоенному резистору указывают только в позиционном обозначении).

В бытовой радиоаппаратуре часто применяют переменные резисторы, объединенные с одним или двумя выключателями. Символы их контактов размещают на схемах рядом с обозначением переменного резистора и соединяют штриховой линией с жирной точкой, которую изображают с той стороны прямоугольника, при перемещении к которой узел щеточного контакта (движок) воздействует на выключатель (рис. 11,а).

Рис. 11. Обозначение переменного резистора совмещенного с переключателем.

При этом имеется в виду, что контакты замыкаются при движении от точки, а размыкаются при движении к ней. В случае, если символы резистора и выключателя удалены один от другого, механическую связь показывают отрезками штриховых линий (рис. 11,6).

Подстроечные резисторы

Подстроечные резисторы — разновидность переменных. Узел щеточного контакта таких резисторов приспособлен для управления отверткой. Условное обозначение подстроечного резистора (рис. 12) наглядно отражает его назначение: это, по сути, постоянный резистор с отводом, положение которого можно изменять.

Рис. 12. Внешний вид и обозначение подстроечных резисторов.

Общее обозначение подстроечного резистора отличается тем, что вместо знака регулирования использован знак подстроечного регулирования.

Нелинейные резисторы

В радиотехнике, электронике и автоматике находят применение нелинейные саморегулирующиеся резисторы, изменяющие свое сопротивление поя действием внешних электричеоких или неэлектрических факторов: угольные столбы, варисторы, терморезисторы и tj д.

Угольный столб, представляющий собой пакет угольных шайб, изменяет свое сопротивление под действием механического усилия.

Рис. 13. Вид и обозначение нелинейных саморегулирующихся резисторов.

Для сжатия шайб обычно используют электромагнит. Изменяя напряжение на его обмйтке, можно в больших пределах изменять степень сжатия шайб и, следовательно, сопротивление угольного столба.

Используют такие резисторы в стабилизаторах и регуляторах напряжения. Условное обозначение угольного столба состоит из ба-зовцго символа резистора и знака нелинейного саморегулирования с буквой Р, которая символизирует механическое усилие — давление (рис. 13,а).

Терморезисторы, как говорит само название, характеризуются тем, что их сопротивление изменяется под действием температуры. Токопроводящие элементы этих резисторов изготовляют из полупроводниковых материалов.

Сопротивление терморезистора прямого подогрева изменяется за счет выделяющейся в нем мощности или при изменении температуры окружающей среды, а терморезистора косвенного подогрева — под действием тепла, выделяемого специальным подогревателем.

Зависимость сопротивления терморезисторов от температуры имеет нелинейный характер, поэтому на схемах их изображают в виде нелинейного резистора со знаком температуры —1° (рис. 13,6, в).

Знак температурного коэффициента сопротивления (положительный, если с увеличением температуры сопротивление терморезистора возрастает, и отрицательный, если оно уменьшается) указывают только в том случае, если он отрицательный (рис. 13,в).

В условное обозначение терморезистора косвенного подогрева кроме знака нелинейного регулирования входит символ подогревателя, напоминающий перевернутую латинскую букву U (рис. 13,г).

Нелинейные полупроводниковые резисторы, известные под названием варисторов, изменяют свое сопротивление при изменении приложенного к ним напряжения.

Существуют варисторы, у которых увеличение напряжения всего в 2—3 раза сопровождается уменьшением сопротивления в несколько десятков раз. На схемах их обозначают в виде нелинейного саморегулирующегося резистора с латинской буквой U (напряжение) у излома знака саморегулирования (рис. 13,3).

В системах автоматики широко используют фоторезисторы — полупроводниковые резисторы, изменяющие свое сопротивление под действием света. Условное графическое обозначение такого резистора состоит из базового символа, помещенного в круг (символ корпуса полупроводникового прибора), и знака фотоэлектрического эффекта — двух наклонных параллельных стрелок.

Литература: В.В. Фролов, Язык радиосхем, Москва, 1998.

Калькулятор соединения резисторов онлайн. Параллельное соединение резисторов

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.

Параллельное соединение: общая информация

Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление , используя нижеописанные формулы.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Расчет сопротивления

В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

• R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

R(общ)=R1*R2/R1+R2.

• R(общ) – суммарное сопротивление;
• R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Видео: Пример расчёта сопротивления

Универсальная схема расчета

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

• R(общ) – суммарное значение сопротивления;
• R – номинал резистора, подсоединенного по параллельной схеме;
• n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.

Пример расчёта

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

R(общ)=1/(1/100+1/150+1/30)=

1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Видео: Правильное подключение светодиодов

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом.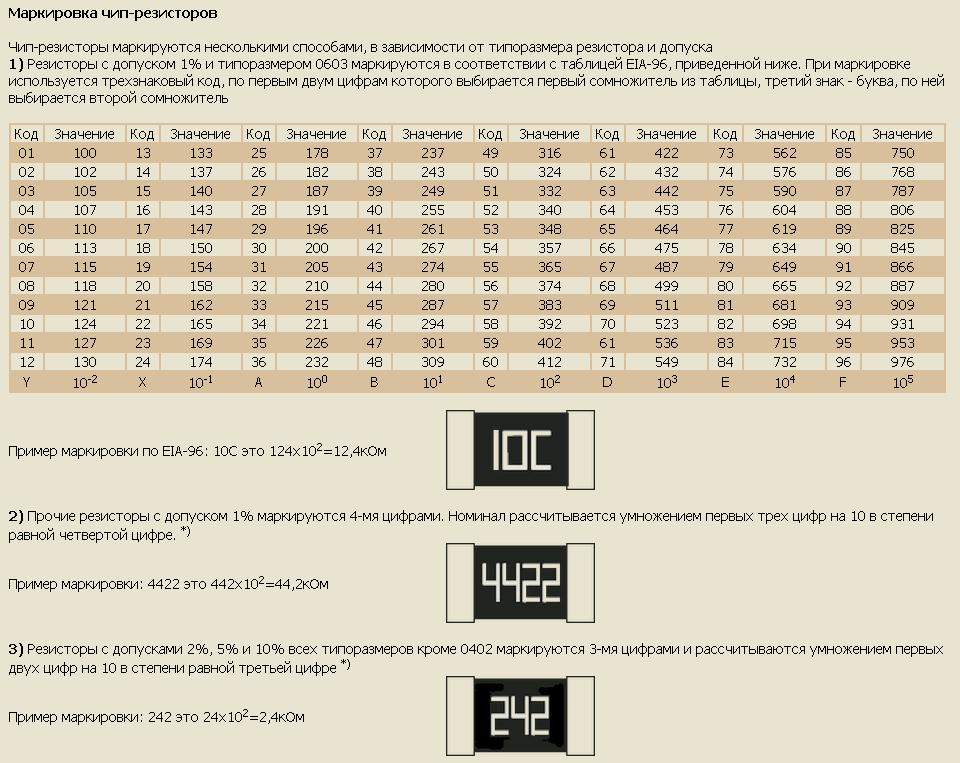 Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.

Эквивалентное сопротивление R eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.

Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:

Эта формула для R eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:

Если параллельно соединены только два резистора, формула упрощается:

Если имеется n соединенных параллельно одинаковых резисторов R , то их эквивалентное сопротивление будет равно

Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.

Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.

При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства . Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи. Во втором варианте все элементы установлены последовательно: конец одного элемента соединен с началом следующего. В такой схеме сила тока на всех элементах одинаковая, а падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подсоединены начала всех элементов, а ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль. Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.

Расчет общего сопротивления при параллельном соединении резисторов

В отличие от последовательного соединения, где для нахождения общего сопротивления достаточно сложить значение каждого элемента, для параллельного то же самое будет справедливо для проводимости. А так как она обратно пропорциональна сопротивлению, получим формулу, представленную вместе со схемой на следующем рисунке:

Необходимо отметить одну важную особенность расчета параллельного соединения резисторов: общее значение будет всегда меньше, чем самое маленькое из них. Для резисторов справедливо как для постоянного, так и для переменного тока. Катушки и конденсаторы имеют свои особенности.

Сила тока и напряжение

При расчете параллельного сопротивления резисторов необходимо знать, как рассчитать напряжение и силу тока. В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.

Исходя из первой формулировки закона Кирхгофа, получим, что сумма сходящихся в одном узле токов равна нулю. Направление выбираем по направлению протекания тока. Таким образом, положительным направлением для первого узла можно считать входящий ток от источника питания. А отрицательными будут отходящие из каждого резистора. Для второго узла картина противоположна. Исходя из формулировки закона, получим, что суммарный ток равен сумме токов, проходящих через каждый параллельно соединенный резистор.

Итоговое напряжение же определяется по второму закону Кирхгофа. Оно одинаково для каждого резистора и равно общему. Эта особенность используется для подключения розеток и освещения в квартирах.

Пример расчета

В качестве первого примера приведем расчет сопротивления при параллельном соединении одинаковых резисторов. Сила тока, протекающая через них, будет одинаковой. Пример расчета сопротивления выглядит так:

По этому примеру прекрасно видно, что общее сопротивление ниже в два раза, чем каждое из них. Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного. А также прекрасно соотносится с увеличением проводимости в два раза.

Второй пример

Рассмотрим пример параллельного соединения трех резисторов. Для расчета используем стандартную формулу:

Похожим образом рассчитываются схемы с большим количеством параллельно соединенных резисторов.

Пример смешанного соединения

Для смешанного соединения, например, представленного ниже, расчет будет производиться в несколько этапов.

Для начала последовательные элементы можно условно заменить одним резистором, обладающим сопротивлением, равным сумме двух заменяемых. Далее общее сопротивление считаем тем же способом, что и для предыдущего примера. Данный метод подойдет и для других более сложных схем. Последовательно упрощая схему, можно получить необходимое значение.

Например, если вместо резистора R3 будут подключены два параллельных, потребуется сначала рассчитать их сопротивление, заменив их эквивалентным. А далее то же самое, что и в примере выше.

Применение параллельной схемы

Параллельное соединение резисторов находит свое применение во многих случаях. Последовательное подключение увеличивает сопротивление, а для нашего случая оно уменьшится. Например, для электрической цепи требуется сопротивление в 5 Ом, но есть только резисторы на 10 Ом и выше. Из первого примера мы знаем, что можно получить в два раза меньшее значение сопротивления, если установить два одинаковых резистора параллельно друг другу.

Уменьшить сопротивление можно еще больше, например, если две пары параллельно соединенных резисторов соединить параллельно относительно друг друга. Можно уменьшить сопротивление еще в два раза, если резисторы имеют одинаковое сопротивление. Комбинируя с последовательным соединением, можно получить любое значение.

Второй пример — это использование параллельного подключения для освещения и розеток в квартирах. Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.

Еще один пример использования параллельного подключения — это защитное заземление электрооборудования. Например, если человек касается металлического корпуса прибора, на который произойдет пробой, получится параллельное соединения его и защитного проводника. Первым узлом будет место прикосновения, а вторым нулевая точка трансформатора. По проводнику и человеку будет течь разный ток. Величину сопротивления последнего принимают за 1000 Ом, хотя реальное значение зачастую гораздо больше. Если бы не было заземления, весь ток, протекающий в схеме, пошел бы через человека, так как он был бы единственным проводником.

Параллельное соединение может использоваться и для батарей. Напряжение при этом остается прежним, однако в два раза возрастает их емкость.

Итог

При подключении резисторов параллельно, напряжение на них будет одинаковым, а ток равен сумме протекающих через каждый резистор. Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.

Необходимо учитывать при расчете параллельного соединения резисторов то, что итоговое сопротивление будет всегда меньше самого маленького. Это также можно объяснить суммированием проводимости резисторов. Последняя будет возрастать при добавлении новых элементов, соответственно и проводимость будет уменьшаться.

Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях — Help for engineer

Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях

Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений. Состоит он из двух и более элементов (резисторов, реактивных сопротивлений). Элементарный делитель можно представить как два участка цепи, называемые плечами. Участок между положительным напряжением и нулевой точкой – верхнее плечо, между нулевой и минусом – нижнее плечо.

Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений. Применяется для низкого напряжения и не предназначен для питания мощных машин. Простейший делитель состоит из двух последовательно соединенных резисторов:

На резистивный делитель напряжения подается напряжение питающей сети U, на каждом из сопротивлений R1 и R2 происходит падение напряжения. Сумма U1 и U2 и будет равна значению U.

В соответствии с законом Ома (1):

Падение напряжения будет прямо пропорционально значению сопротивления и величине тока. Согласно первому закону Кирхгофа, величина тока, протекающего через сопротивления одинакова. С чего следует, что падение напряжения на каждом резисторе (2,3):

Тогда напряжение на всем участке цепи (4):

Отсюда определим, чему равно значение тока без включения нагрузки (5):

Если подставить данное выражение в (2 и 3), то получим формулы расчета падения напряжения для делителя напряжения на резисторах (6, 7):

Необходимо упомянуть, что значения сопротивлений делителя должны быть на порядок или два (все зависит от требуемой точности питания) меньше, чем сопротивление нагрузки. Если же это условие не выполняется, то при приведенном расчете подаваемое напряжение будет посчитано очень грубо.

Для повышения точности необходимо сопротивление нагрузки принять как параллельно подсоединенный резистор к делителю. А также использовать прецизионные (высокоточные) сопротивления.

Онлайн подбор сопротивлений для делителя

Пусть источник питания выдает 24 В постоянного напряжения, примем, что величина сопротивления нагрузки переменная, но минимальное значение равно 15 кОм. Необходимо рассчитать параметры резисторов для делителя, выходное напряжение которого равно 6 В.

Таким образом, напряжения: U=24 B, U₂=6 В; сопротивление резисторов не должно превышать 1,5 кОм (в десять раз меньше значения нагрузки). Принимаем R1=1000 Ом, тогда используя формулу (7) получим:

выразим отсюда R₂:

Зная величины сопротивления обоих резисторов, найдем падение напряжения на первом плече (6):

Ток, который протекает через делитель, находится по формуле (5):

Схема делителя напряжения на резисторах рассчитана выше и промоделирована:

Использование делителя напряжения очень неэкономичный, затратный способ понижения величины напряжения, так как неиспользуемая энергия рассеивается на сопротивлении (превращается в тепловую энергию). КПД очень низкий, а потери мощности на резисторах вычисляются формулами (8,9):

По заданным условиям, для реализации схемы делителя напряжения необходимы два резистора:

		1. R1=1 кОм, P1=0,324 Вт.
		2. R2=333,3 Ом, P2=0,108 Вт.

Полная мощность, которая потеряется:

---

Делитель напряжения на конденсаторах применяется в схемах высокого переменного напряжения, в данном случае имеет место реактивное сопротивление.

Сопротивление конденсатора рассчитывается по формуле (10):

		где С – ёмкость конденсатора, Ф;
		f – частота сети, Гц.

Исходя из формулы (10), видно, что сопротивление конденсатора зависит от двух параметров: С и f. Чем больше ёмкость конденсатора, тем сопротивление его ниже (обратная пропорциональность). Для ёмкостного делителя расчет имеет такой вид (11, 12):

Еще один делитель напряжения на реактивных элементах – индуктивный, который нашел применение в измерительной технике. Сопротивление индуктивного элемента при переменном напряжении прямо пропорционально величине индуктивности (13):

где L – индуктивность, Гн.

Падение напряжения на индуктивностях (14,15):

Недостаточно прав для комментирования

Калькулятор параллельных резисторов

R1 + R2 = эквивалентный резистор R схема сопротивления, эквивалентная общая сумма резисторов, упрощенная комбинация = параллельная

параллельная калькуляция резисторов R1 + R2 = эквивалентный резистор R эквивалентная схема сопротивления, полная поисковая система резисторов, упрощенная совмещенная = параллельная — sengpielaudio Sengpiel Berlin

R всего

Формула: R всего = R1 × R2 / (R1 + R2)

Введите , два значения резистора , будет рассчитано третье значение параллельной цепи.
Вы даже можете ввести общее сопротивление R _всего и одно известное сопротивление R ₁ или R ₂ .

Формула (уравнение) для расчета двух сопротивлений R ₁ и R ₂ , соединенных параллельно:

Расчет необходимого параллельного резистора R ₂ , при R ₁ и суммарное сопротивление R _{дается всего} :

Решение формулы R итого = ( R 1 × R 2 ) / ( R 1 + R 2 ) для R 1 : Первый шаг — очистить все дроби, умножив на наименьшего числа. общий знаменатель, то есть R t × R 1 × R 2 … Итак, получаем: 1/ R всего = 1/ R 1 + 1/ R 2 R всего × R 1 × R 2 [1/ R всего = 1/ R 1 + 1/ R 2 ] R 1 × R 2 = R всего × R 2 + R всего × R 1 затем соберите члены с R 1 и решите R 1 × R 2 — R всего × R 1 = R всего × R 2 R 1 ( R 2 — R всего ) = R 2 × R всего 9000 9 Последний шаг: R 1 = R 2 × R всего / ( R 2 — R всего ) или: R 2 = R 1 × R всего / ( R 1 — R всего )

Примечание: Этот калькулятор также может решать другие математические задачи. Расчет резисторов параллельно
точно так же, как вычисления, необходимые для параллельных катушек индуктивности или для конденсаторов, включенных последовательно.

Два резистора, включенных параллельно, и результирующее общее сопротивление: Два одинаковых значения, также покажите уравнение, что результаты всегда равны половине. Это упрощает, когда проектирование схем или прототипирование. С кепками всегда вдвое больше, потом с кепками всего просто сложите параллельно.

• Поисковые сопротивления R ₁ и R ₂ , когда известно целевое сопротивление (эквивалентное сопротивление) •

Расчет: пары резисторов — калькулятор с обратной конструкцией
Поиск R ₁ и R ₂ с известным целевым сопротивлением

● Рассчитать несколько резисторов параллельно ●

Этот калькулятор определяет сопротивление от до 10 резисторов, включенных параллельно . Введите значения сопротивления в поля ниже и после ввода всех значений . нажмите кнопку «рассчитать», и результат появится в поле под этой кнопкой. В качестве теста, если мы введем сопротивления 4, 6 и 12 Ом, ответ должен быть 2 Ом. Примечание. При снятии флажков вручную сохраненные значения не сбрасываются. Воспользуйтесь «сбросом».

Закон Ома — калькулятор и формулы

Два резистора, включенных параллельно, и результирующее общее сопротивление
Сопротивление в диапазоне от 1 Ом до 100 Ом

R2	R1
	1	1. 5	2,2	3,3	4,7	6,8	10	15	22	33	47	68
1	0,5	0,6	0,69	0.77	0,83	0,87	0,91	0,93	0,95	0,97	0,98	0,99
1,5	0,6	0,75	0,89	1.03	1,14	1,22	1,30	1,36	1,40	1,43	1.45	1,46
2,2	0,69	0,89	1,1	1,32	1,50	1,66	1,82	1,92	2,0	2,06	2,10	2,13
3,3	0,77	1.03	1,32	1.65	1,94	2,22	2,48	2,70	2,87	3,00	3,08	3,14
4,7	0,83	1,14	1,50	1,94	2,35	2,78	3,20	3,58	3,87	4,12	4.27	4,39
6,8	0,87	1,22	1,66	2,22	2,78	3,40	4,05	4,68	5,19	5,64	5,94	6,18
10	0,91	1,30	1,82	2.48	3,20	4,05	5,0	6,0	6,9	7,7	8,3	8,7
15	0,93	1,36	1,92	2,70	3,58	4,68	6,0	7,50	8,9	10,3	11,4	12. 2
22	0,95	1,40	2,00	2,87	3,87	5,19	6,9	8,9	11,0	13,2	15,0	16,6
33	0,97	1,43	2,06	3,0	4.12	5,64	7,7	10,3	13,2	16,5	19,4	22,2
47	0,98	1,45	2,1	3,08	4,27	5,94	8,3	11,4	15,0	19,4	23,5	27.8
68	0,99	1,46	2,13	3,14	4,39	6,18	8,7	12,2	16,6	22,2	27,8	34,0

Примечание: Этот калькулятор также может решать другие математические задачи. Расчет резисторов параллельно
точно так же, как вычисления, необходимые для параллельных катушек индуктивности или для конденсаторов, включенных последовательно.

Мощность, рассеиваемая в резисторе: P = В × I , P = В 2 / R , P = I 2 × R .

Примечание: Для последовательно соединенных резисторов ток одинаков для каждого резистора, а для резисторов, включенных параллельно, напряжение одинаково для каждого резистора.

Резисторы — learn.sparkfun.com

Добавлено в избранное Любимый 48

Возьмите стойку, стойку сопротивления

Резисторы

— самые распространенные электронные компоненты. Они являются важной частью практически каждой цепи. И они играют важную роль в нашем любимом уравнении — законе Ома.

В этом разделе résistance мы рассмотрим:

• Что такое резистор ?!
• Блоки резисторов
• Обозначение цепи резистора
• Последовательные и параллельные резисторы
• Различные варианты резисторов
• Цветовое кодирование декодирование
• Расшифровка резистора для поверхностного монтажа
• Пример применения резистора

Считайте чтение…

Некоторые концепции в этом руководстве основаны на предыдущих знаниях в области электроники. Прежде чем переходить к этому руководству, подумайте о том, чтобы сначала прочитать (хотя бы бегло просмотр) эти:

---

Хотите попробовать резисторы?

и nbsp

и nbsp

Основы резистора

Резисторы — это электронные компоненты, которые обладают постоянным постоянным электрическим сопротивлением. Сопротивление резистора ограничивает поток электронов через цепь.

Это пассивных компонента , то есть они только потребляют энергию (и не могут ее генерировать). Резисторы обычно добавляются в схемы, где они дополняют активных компонентов , таких как операционные усилители, микроконтроллеры и другие интегральные схемы. Обычно резисторы используются для ограничения тока, деления напряжений и подтягивания линий ввода / вывода.

Блоки резисторы

Электрическое сопротивление резистора измеряется в Ом . Символ ома — греческая заглавная буква омега: & ohm ;.(Несколько окольным) определение 1 & ohm; — это сопротивление между двумя точками, где 1 вольт (1 В) приложенной потенциальной энергии будет подталкивать 1 ампер (1 А) тока.

В единицах СИ большие или меньшие значения Ом могут быть сопоставлены с префиксом, например, кило-, мега- или гига-, чтобы облегчить чтение больших значений. Очень часто можно увидеть резисторы в килоомах (кОм;) и мегаомах (МОм;) (гораздо реже можно увидеть резисторы в миллиомах (м & ом;)). Например, 4,700 Ом; резистор эквивалентен 4.7к & Ом; резистор и 5,600,000 Ом; резистор можно записать как 5,600 кОм; или (чаще) 5.6M & ohm ;.

Схематическое обозначение

Все резисторы имеют две клеммы , по одной клемме на каждом конце резистора. При моделировании на схеме резистор отображается как один из этих двух символов:

Два общих условных обозначения резистора. R1 — это 1 кОм в американском стиле; резистор, а R2 — международный 47кОм; резистор.

Выводы резистора — это каждая из линий, идущих от волнистой линии (или прямоугольника). Это то, что подключается к остальной части схемы.

Обозначения схемы резистора обычно дополняются значением сопротивления и именем. Значение, отображаемое в омах, очевидно, имеет решающее значение как для оценки, так и для фактического построения схемы. Название резистора обычно — R перед числом. Каждый резистор в цепи должен иметь уникальное имя / номер.Например, вот несколько резисторов в цепи таймера 555:

В этой схеме резисторы играют ключевую роль в установке частоты на выходе таймера 555. Другой резистор (R3) ограничивает ток через светодиод.

---

Типы резисторов

Резисторы

бывают разных форм и размеров. Они могут быть сквозными или поверхностными. Это может быть стандартный статический резистор, набор резисторов или специальный переменный резистор.

Прерывание и монтаж

Резисторы

могут быть одного из двух типов: для монтажа в сквозное отверстие или для поверхностного монтажа. Эти типы резисторов обычно обозначаются аббревиатурой PTH (сквозное отверстие с металлическим покрытием) или SMD / SMT (технология или устройство для поверхностного монтажа).

Резисторы со сквозным отверстием поставляются с длинными гибкими выводами, которые можно вставить в макетную плату или вручную припаять к макетной плате или печатной плате (PCB). Эти резисторы обычно более полезны при макетировании, прототипировании или в любом другом случае, когда вы не хотите паять крошечные, маленькие 0.Резисторы SMD длиной 6 мм. Длинные выводы обычно требуют обрезки, и эти резисторы неизбежно занимают гораздо больше места, чем их аналоги для поверхностного монтажа.

Наиболее распространенные сквозные резисторы поставляются в аксиальном корпусе. Размер осевого резистора зависит от его номинальной мощности. Обычный резистор ½ Вт имеет диаметр около 9,2 мм, тогда как резистор меньшей Вт имеет длину около 6,3 мм.

Резистор мощностью полуватта (½Вт) (вверху) мощностью до четверти ватта (Вт).

Резисторы для поверхностного монтажа обычно представляют собой крошечные черные прямоугольники, оканчивающиеся с обеих сторон еще меньшими, блестящими, серебряными проводящими краями.Эти резисторы предназначены для установки на печатных платах, где они припаяны к ответным посадочным площадкам. Поскольку эти резисторы настолько малы, их обычно устанавливает робот и отправляет через печь, где припой плавится и удерживает их на месте.

Крошечный 0603 330 & Ом; резистор, парящий над блестящим носом Джорджа Вашингтона на вершине [США квартал] (http://en.wikipedia.org/wiki/Quarter_ (United_States_coin).

Резисторы SMD

бывают стандартных размеров; обычно либо 0805 (0.08 «в длину на 0,05» в ширину), 0603 или 0402. Они отлично подходят для массового производства печатных плат или в конструкциях, где пространство является драгоценным товаром. Однако для ручной пайки им нужна твердая и точная рука!

Состав резистора

Резисторы

могут быть изготовлены из различных материалов. Чаще всего современные резисторы изготавливаются из углеродной, металлической или металлооксидной пленки . В этих резисторах тонкая пленка проводящего (но все же резистивного) материала намотана спиралью вокруг и покрыта изоляционным материалом.Большинство стандартных простых сквозных резисторов имеют углеродную или металлическую пленку.

Загляните внутрь нескольких резисторов из углеродной пленки. Значения сопротивления сверху вниз: 27 Ом, 330 Ом; и 3,3 МОм. Внутри резистора углеродная пленка обернута вокруг изолятора. Чем больше обертываний, тем выше сопротивление. Довольно аккуратно!

Другие сквозные резисторы могут быть намотаны проволокой или изготовлены из сверхтонкой металлической фольги.Эти резисторы обычно являются более дорогими, более дорогими компонентами, специально выбранными из-за их уникальных характеристик, таких как более высокая номинальная мощность или максимальный температурный диапазон.

Резисторы

для поверхностного монтажа обычно бывают толстыми или тонкопленочными . Толстая пленка обычно дешевле, но менее точна, чем тонкая. В обоих типах резисторов небольшая пленка из резистивного металлического сплава помещается между керамической основой и стеклом / эпоксидным покрытием, а затем соединяется с концевыми токопроводящими краями.

Пакеты специальных резисторов

Существует множество других резисторов специального назначения. Резисторы могут поставляться в предварительно смонтированных пакетах из пяти или около того резисторных матриц. Резисторы в этих массивах могут иметь общий вывод или быть настроены как делители напряжения.

Массив из пяти 330 Ом; резисторы, соединенные вместе на одном конце.

Переменные резисторы (например, потенциометры)

Резисторы

также не обязательно должны быть статическими. Переменные резисторы, известные как реостаты , представляют собой резисторы, которые можно регулировать в определенном диапазоне значений.Аналогичен реостату потенциометр . Горшки соединяют два резистора внутри последовательно, и регулируют центральный отвод между ними, создавая регулируемый делитель напряжения. Эти переменные резисторы часто используются для входов, например регуляторов громкости, которые необходимо регулировать.

---

Расшифровка маркировки резисторов

Хотя они могут не отображать свое значение сразу, большинство резисторов имеют маркировку, показывающую их сопротивление. Резисторы PTH используют систему цветовой кодировки (которая действительно добавляет немного изюминки схемам), а резисторы SMD имеют свою собственную систему маркировки значений.

Расшифровка цветовых полос

Осевые резисторы, проходящие через отверстие, обычно используют систему цветных полос для отображения своего значения. Большинство из этих резисторов будут иметь четыре цветных полосы, окружающие резистор, хотя вы также найдете пять полосных и шесть полосных резисторов.

Четырехполосные резисторы

В стандартных четырехполосных резисторах первые две полосы обозначают две старшие цифры номинала резистора. Третья полоса — это значение веса, которое умножает двух значащих цифр на десять.

Последняя полоса указывает допуск резистора. Допуск объясняет, насколько более или менее фактическое сопротивление резистора можно сравнить с его номинальным значением. Ни один резистор не может быть доведен до совершенства, и различные производственные процессы приводят к лучшим или худшим допускам. Например, 1 кОм; резистор с допуском 5% на самом деле может быть где-то между 0,95 кОм; и 1.05кОм ;.

Как определить, какая группа первая и последняя? Последний диапазон допусков часто четко отделен от диапазонов значений, и обычно это либо серебро, либо золото.

Пяти- и шестиполосные резисторы

Пять полосных резисторов имеют третью полосу значащих цифр между первыми двумя полосами и полосой умножителя . Пятиполосные резисторы также имеют более широкий диапазон допусков.

Шестиполосные резисторы — это, по сути, пятиполосные резисторы с дополнительной полосой на конце, которая указывает температурный коэффициент. Это указывает на ожидаемое изменение номинала резистора при изменении температуры в градусах Цельсия. Обычно эти значения температурного коэффициента чрезвычайно малы, в диапазоне ppm.

Цветовые полосы резистора декодирования

При расшифровке цветовых полос резисторов обратитесь к таблице цветовых кодов резисторов, подобной приведенной ниже. Для первых двух полос найдите соответствующее цифровое значение этого цвета. 4,7 кОм; Резистор, показанный здесь, имеет в начале цветные полосы желтого и фиолетового цветов, которые имеют числовые значения 4 и 7 (47). Третья полоса 4,7 кОм; красный, что означает, что 47 следует умножить на 10 ² (или 100). 47 умножить на 100 — это 4700!

4.7к & Ом; резистор с четырьмя цветными полосами

Если вы пытаетесь сохранить код цветовой полосы в памяти, может помочь мнемоническое устройство. Существует несколько (иногда сомнительных) мнемоник, которые помогают запомнить цветовую кодировку резистора. Хороший пример, который показывает разницу между b Отсутствие и b rown:

« B ig b rown r abbits o ften y ield g reat b IG v ocal g roans w hen g igly s napped .«

Или, если вы помните «ROY G. BIV», вычтите индиго (бедный индиго, никто не помнит индиго) и добавьте черный и коричневый к передней части и серый и белый к задней части классической цветовой схемы радуги. .

Таблица цветов резистора

Проблемы со зрением? Щелкните изображение для лучшего просмотра!

Калькулятор цветового кода резистора

Если вы предпочитаете пропустить математику (мы не будем судить!) И просто воспользуетесь удобным калькулятором, попробуйте один из них!

Четырехполосные резисторы

Диапазон 1	Диапазон 2	Диапазон 3		Диапазон 4
Значение 1 (MSV)	Значение 2	Вес		Допуск
Черный (0) Коричневый (1) Красный (2) Оранжевый (3) Желтый (4) Зеленый (5) Синий (6) Фиолетовый (7) Серый (8) Белый (9)	Черный (0) Коричневый (1) Красный (2) Оранжевый (3) Желтый (4) Зеленый (5) Синий (6) Фиолетовый (7) Серый (8) Белый (9)	Черный (1) Коричневый (10) Красный (100) Оранжевый (1k) Желтый (10k) Зеленый (100k) Синий (1M) Фиолетовый (10M) Серый (100M) Белый (1G)		Золото (± 5%) Серебро (± 10%)

Сопротивление: 1 кОм; ± 5%

Пяти- и шестиполосные резисторы

Примечание: Рассчитайте здесь свой шестиполосный резистор, но не забудьте добавить температурный коэффициент к окончательному значению резистора.

Диапазон 1	Диапазон 2	Диапазон 3	Диапазон 4		Диапазон 5
Значение 1 (MSV)	Значение 2	Значение 3	Вес		Допуск
Черный (0) Коричневый (1) Красный (2) Оранжевый (3) Желтый (4) Зеленый (5) Синий (6) Фиолетовый (7) Серый (8) Белый (9)	Черный (0) Коричневый (1) Красный (2) Оранжевый (3) Желтый (4) Зеленый (5) Синий (6) Фиолетовый (7) Серый (8) Белый (9)	Черный (0) Коричневый (1) Красный (2) Оранжевый (3) Желтый (4) Зеленый (5) Синий (6) Фиолетовый (7) Серый (8) Белый (9)	Черный (1) Коричневый (10) Красный (100) Оранжевый (1k) Желтый (10k) Зеленый (100k) Синий (1M) Фиолетовый (10M) Серый (100M) Белый (1G)		Золото (± 5%) Серебро (± 10%) Коричневый (± 1%) Красный (± 2%) Зеленый (± 0.5%) Синий (± 0,25%) Фиолетовый (± 0,1%) Серый (± 0,05%)

Сопротивление: 1 кОм; ± 5%

Расшифровка маркировки для поверхностного монтажа

Резисторы SMD

, как и в корпусах 0603 или 0805, имеют собственный способ отображения своего значения. Есть несколько распространенных методов маркировки этих резисторов. Обычно на корпусе печатается от трех до четырех символов — цифр или букв.

Если три символа, которые вы видите, это все числа , вы, вероятно, смотрите на резистор с маркировкой E24 .Эти маркировки на самом деле имеют некоторое сходство с системой цветных полос, используемой на резисторах PTH. Первые два числа представляют собой первые две наиболее значимые цифры значения, последнее число представляет величину.

На приведенном выше примере резисторы обозначены 104 , 105 , 205 , 751 и 754 . Резистор с маркировкой 104 должен быть 100 кОм; (10×10 ⁴ ), 105 будет 1 МОм & Ом; (10×10 ⁵ ) и 205 составляет 2M & Ом; (20х10 ⁵ ). 751 — 750 Ом; (75×10 ¹ ) и 754 составляет 750 кОм; (75×10 ⁴ ).

Другая распространенная система кодирования — E96 , и она самая загадочная из всех. Резисторы E96 будут обозначены тремя символами — двумя цифрами в начале и буквой в конце. Два числа сообщают вам первые , три цифры значения, соответствующие одному из не столь очевидных значений в этой поисковой таблице.

931 9001 1205

Код	Значение			Код значения		Значение	Код	Значение	Код	Значение	Код		Значение		Код	Значение		Код	Значение
01	100		17	147		17	147	1	49	316		65	464		81	681
02	102		18	150		34	221		50	324		66	475		82	698
03	105		19	154		35	226			332		67	487		83	715
04	107		20	158		36	232		52	340		68	499		84	732
05	110		21	162		37	237			53	348		69	511 90 010		85	750
06	113		22	165		38	243		54	357			523		86	768
07	115		23	169		39	249		55	3652		71	536		87	787
08	118		24	174		40	255		56	37		72	549		88	8 06
09	121		25	178		41	261		57	383		73	562		89	825
10	124		26	182		42	267		58	392		74	576	90	845
11	127		27	187		43	274		59	402		75 590		91	866
12	130		28	191		44 ​​	280		60	412		76	604		92	887
133		29	196		45	287		61	422		77	619		93	909
14	137		30	200		46	294		62	432		78	634		94
15	140		31		47	301		63	442		79	649		95	953
16	143
16	143	9	32	210		48	309		64	453		80	665		96	976

Буква в конце представляет множитель, соответствующий чему-то в этой таблице:

11 900

1

Letter	Множитель		Letter	Множитель		Letter	Множитель
	A	1		D	1000
Y или R	0,01		B или H	10		E	10000
X или S	0,1		C	100		F	100000

Итак, резистор 01C — наш хороший друг, 10 кОм; (100×100), 01B составляет 1 кОм; (100×10), а 01D — 100 кОм.Это просто, другие коды могут быть не такими. 85A с рисунка выше составляет 750 Ом; (750×1) и 30C на самом деле 20 кОм.

---

Номинальная мощность

Номинальная мощность резистора — одна из наиболее скрытых величин. Тем не менее это может быть важно, и это тема, которая возникает при выборе типа резистора.

Мощность — это скорость, с которой энергия преобразуется во что-то другое. Он рассчитывается путем умножения разности напряжений в двух точках на ток, протекающий между ними, и измеряется в ваттах (Вт).Лампочки, например, превращают электричество в свет. Но резистор может превратить только электрическую энергию, проходящую через него, в тепла . Хит обычно не лучший товарищ по играм с электроникой; слишком много тепла приводит к дыму, искрам и пожару!

Каждый резистор имеет определенную максимальную номинальную мощность. Чтобы резистор не перегревался слишком сильно, важно убедиться, что мощность на резисторе не превышает его максимального значения. Номинальная мощность резистора измеряется в ваттах и ​​обычно находится между & frac18; Вт (0.125 Вт) и 1 Вт. Резисторы с номинальной мощностью более 1 Вт обычно называют силовыми резисторами и используются специально из-за их способности рассеивать мощность.

Определение номинальной мощности резистора

Номинальную мощность резистора обычно можно определить, наблюдая за размером его корпуса. Стандартные сквозные резисторы обычно имеют номинальную мощность ¼ или ½ Вт. Силовые резисторы более специального назначения могут указывать свою номинальную мощность на резисторе.

Эти силовые резисторы могут выдерживать гораздо большую мощность, прежде чем они сработают.Сверху справа и снизу слева приведены примеры резисторов 25 Вт, 5 Вт и 3 Вт со значениями 2 Ом, 3 Ом; 0,1 & Ом; и 22к & Ом. Меньшие силовые резисторы часто используются для измерения тока.

О номинальной мощности резисторов для поверхностного монтажа обычно можно судить также по их размеру. Резисторы типоразмера 0402 и 0603 обычно рассчитаны на 1/16 Вт, а резисторы 0805 могут потреблять 1/10 Вт.

Измерение мощности на резисторе

Мощность обычно рассчитывается путем умножения напряжения на ток (P = IV).Но, применяя закон Ома, мы также можем использовать значение сопротивления при расчете мощности. Если нам известен ток, протекающий через резистор, мы можем рассчитать мощность как:

Или, если нам известно напряжение на резисторе, мощность можно рассчитать как:

---

Резисторы серии

и параллельные

Резисторы постоянно соединяются вместе в электронике, обычно в последовательной или параллельной схеме. Когда резисторы объединяются последовательно или параллельно, они создают общее сопротивление , которое можно рассчитать с помощью одного из двух уравнений.Знание того, как сочетаются значения резисторов, пригодится, если вам нужно создать конкретное значение резистора.

Резисторы серии

При последовательном подключении значения резисторов просто складываются.

Резисторы Н. последовательно. Общее сопротивление — это сумма всех последовательных резисторов.

Так, например, если у вас всего , вам нужно , 12,33 кОм; резистор, найдите некоторые из наиболее распространенных номиналов резисторов 12 кОм; и 330 Ом, и соединить их последовательно.

Резисторы параллельные

Найти сопротивление резисторов, включенных параллельно, не так-то просто. Общее сопротивление параллельно включенных резисторов N является обратной суммой всех обратных сопротивлений. Это уравнение может иметь больше смысла, чем последнее предложение:

Резисторы Н, включенные параллельно. Чтобы найти общее сопротивление, инвертируйте каждое значение сопротивления, сложите их, а затем инвертируйте.

(Сопротивление, обратное сопротивлению, на самом деле называется проводимостью , так что короче: проводимость параллельных резисторов является суммой каждой из их проводимостей).

В качестве частного случая этого уравнения: если у вас есть только два резистора , подключенных параллельно, их полное сопротивление можно рассчитать с помощью этого чуть менее инвертированного уравнения:

В качестве даже более особого случая этого уравнения, если у вас есть два параллельных резистора с равным значением , общее сопротивление составляет половину их значения. Например, если два 10k & ohm; резисторы включены параллельно, их полное сопротивление 5кОм.

Сокращенно сказать, что два резистора включены параллельно, можно с помощью оператора параллельности: || .Например, если R ₁ идет параллельно с R ₂ , концептуальное уравнение может быть записано как R ₁ || R ₂ . Намного чище и скрывает все эти неприятные фракции!

Резисторные сети

В качестве специального введения в вычисление полного сопротивления учителя электроники просто любят подвергать своих учеников поиску сумасшедших, замысловатых резисторных сетей.

Приручить резисторный сетевой вопрос может быть что-то вроде: «какое сопротивление между выводами A, и B в этой цепи?»

Чтобы решить такую ​​проблему, начните с задней части схемы и упростите ее к двум клеммам.В этом случае ₇ рандов, ₈ рандов и ₉ рандов идут последовательно и могут складываться вместе. Эти три резистора подключены параллельно с R ₆ , поэтому эти четыре резистора можно превратить в один с сопротивлением ₆ || (R ₇ + R ₈ + R ₉ ). Делаем нашу схему:

Теперь четыре крайних правых резистора можно упростить еще больше. R ₄ , R ₅ и наша конгломерация R ₆ — R ₉ все находятся в серии и могут быть добавлены.Тогда все эти последовательные резисторы подключены параллельно с R ₃ .

И это всего лишь три резистора между клеммами A и B . Добавьте их! Таким образом, общее сопротивление этой цепи составляет: ₁ + ₂ + ₃ || ( ₄ + ₅ + ₆ || ( ₇ + _{) 8} + Р ₉ )).

---

Примеры приложений

Резисторы

присутствуют практически во всех электронных схемах.Вот несколько примеров схем, которые сильно зависят от наших друзей-резисторов.

Резисторы

— это ключ к тому, чтобы светодиоды не взорвались при подаче питания. Посредством соединения резистора последовательно со светодиодом ток, протекающий через два компонента, может быть ограничен до безопасного значения.

При выборе токоограничивающего резистора обратите внимание на два характерных значения светодиода: типичное прямое напряжение и максимальный прямой ток .Типичное прямое напряжение — это напряжение, необходимое для включения светодиода, и оно варьируется (обычно где-то между 1,7 В и 3,4 В) в зависимости от цвета светодиода. Максимальный прямой ток обычно составляет около 20 мА для основных светодиодов; непрерывный ток через светодиод всегда должен быть равен или меньше этого номинального тока.

После того, как вы получили эти два значения, вы можете подобрать токоограничивающий резистор по следующему уравнению:

В _S — это напряжение источника — обычно напряжение батареи или источника питания.V _F и I _F — это прямое напряжение светодиода и желаемый ток, который проходит через него.

Например, предположим, что у вас есть батарея на 9 В для питания светодиода. Если ваш светодиод красный, то прямое напряжение может быть около 1,8 В. Если вы хотите ограничить ток до 10 мА, используйте последовательный резистор примерно 720 Ом.

Делители напряжения

Делитель напряжения представляет собой схему резистора, которая преобразует большое напряжение в меньшее. Используя всего два последовательно подключенных резистора, можно создать выходное напряжение, составляющее часть входного напряжения.

Вот схема делителя напряжения:

Два резистора, R ₁ и R ₂ , соединены последовательно, и источник напряжения (V _в ) подключен через них. Напряжение от _{В до} на GND можно рассчитать как:

Например, если R ₁ было 1,7 кОм; и R ₂ составлял 3,3 кОм, входное напряжение 5 В можно было преобразовать в 3,3 В на выводе V _out .

Делители напряжения

очень удобны для считывания показаний резистивных датчиков, таких как фотоэлементы, гибкие датчики и силочувствительные резисторы.Одна половина делителя напряжения — это датчик, а часть — статический резистор. Выходное напряжение между двумя компонентами подается на аналого-цифровой преобразователь на микроконтроллере (MCU) для считывания значения датчика.

Здесь резистор R ₁ и фотоэлемент создают делитель напряжения для создания переменного выходного напряжения.

Подтягивающие резисторы

Подтягивающий резистор используется, когда вам нужно смещать входной вывод микроконтроллера в известное состояние.Один конец резистора подключен к выводу MCU, а другой конец подключен к высокому напряжению (обычно 5 В или 3,3 В).

Без подтягивающего резистора входы на MCU можно оставить плавающими . Нет гарантии, что на плавающем контакте высокий (5 В) или низкий (0 В) вывод.

Подтягивающие резисторы часто используются при взаимодействии с входом кнопки или переключателя. Подтягивающий резистор может смещать входной контакт, когда переключатель разомкнут. И это защитит цепь от короткого замыкания при замкнутом переключателе.

В приведенной выше схеме, когда переключатель разомкнут, входной вывод MCU подключен через резистор к 5 В. Когда переключатель замыкается, входной контакт подключается непосредственно к GND.

Обычно значение подтягивающего резистора не обязательно должно быть каким-либо конкретным. Но он должен быть достаточно высоким, чтобы не терять слишком много мощности, если к нему приложить 5 В или около того. Обычно значения около 10 кОм; работать хорошо.

---

Покупка резисторов

Не ограничивайте количество резисторов.У нас есть наборы, пакеты, отдельные детали и инструменты, которым вы просто не можете противостоять , .

Наши рекомендации:

Щелкните здесь, чтобы просмотреть больше резисторов в каталоге

инструментов:

Цифровой мультиметр — базовый

В наличии TOL-12966

Цифровой мультиметр (DMM) — незаменимый инструмент в арсенале каждого энтузиаста электроники.Цифровой мультиметр SparkFun, h…

21 год

Инструмент для гибки выводов резистора

В наличии ТОЛ-13114

Этот маленький кусочек пластика с зазубринами — инструмент для гибки выводов резистора. Иногда этот маленький…

3

---

Ресурсы и дальнейшее развитие

Теперь, когда вы начинающий эксперт по резисторам, как насчет изучения некоторых более фундаментальных концепций электроники! Резисторы, конечно, не единственный базовый компонент, который мы используем в электронике, есть еще:

Или, может быть, вы хотите подробнее изучить применение резисторов?

резисторов параллельно

Электрические цепи используются в авиакосмической технике, от систем управления полетом до приборов в кабине и двигателей системы управления, чтобы аэродинамическая труба приборостроение и эксплуатация.Самая простая схема включает один резистор и источник электрического потенциала или напряжения . Электроны проходят через схема, производящая ток и электроэнергии. Сопротивление, напряжение и ток связаны друг с другом соотношением Закон Ома. Обычно в практической схеме используется более одного резистора. При анализе сложной схемы мы часто можем группировать компоненты вместе и разработать схему замещения .При анализе схем с несколько резисторов, мы должны определить, подвержены ли резисторы какое-то напряжение или такой же ток. Несколько резисторов в параллельной цепи подвергаются одинаковому напряжению. Несколько резисторов в последовательная цепь подвергаются одинаковому току. На этой странице мы обсуждаем эквивалентную схему для резисторов параллельно.

На рисунке изображена схема, состоящая из источника питания и трех резисторов. подключены параллельно.Если обозначить сопротивление R , ток и , а напряжение В , то закон Ома гласит, что для каждого резистора в цепи:

V = i R

я = V / R

Если рассматривать каждый резистор по отдельности, каждый резистор имеет свой ток. ( i1 , i2 и i3 ), сопротивление ( R1 , R2 и R3 ), и напряжение ( V1 , V2 и V3 ).Поскольку резисторы подключены параллельно друг другу, напряжение на каждый резистор одинаковый:

V = V1 = V2 = V3

Ток через каждый резистор определяется законом Ома:

i1 = V / R1

i2 = V / R2

i3 = V / R3

Если обозначить пересечение проводов, соединяющих резисторы, как узлов , В нашей схеме с тремя резисторами шесть узлов.На рисунке мы помечаем два узлы в правом верхнем углу схемы. В каждом узле ток, поступающий в узел должен равняться току, выходящему из узла, согласно закону Фарадея . Для узлов, расположенных выше и ниже резистора R2 , ток ib вход в узел определяется:

ib = i2 + i3

Аналогично для узлов сверху и снизу резистор R1 , текущий ia вход в узел определяется:

ia = i1 + ib = i1 + i2 + i3

Теперь мы знаем напряжение, сопротивление и ток в каждой части цепи.

Если бы мы построили эквивалентную схему, как показано в нижнем левом углу, мы бы иметь одинаковое напряжение В , такой же ток от источника питания ie = ia , и один эквивалентный резистор Re . Для нашей эквивалентной схемы закон Ома указывает, что:

ie = V / Re

Мы можем определить значение Re , используя небольшую алгебру:

V / Re = ie = i1 + i2 + i3

V / Re = V / R1 + V / R2 + V / R3

1 / Re = 1 / R1 + 1 / R2 + 1 / R3

1 / Re = (R2 R3 + R1 R3 + R1 R2 / (R1 R2 R3)

Re = (R1 R2 R3) / (R2 R3 + R1 R3 + R1 R2).

Мы можем использовать эти знания о схеме параллельного резистора для анализа Мост Уитстона схема, которая используется для контроля температуры в аэродинамической трубе баланс сил используя электронные тензодатчики.

---

Навигация ..

Руководство для начинающих Домашняя страница

Последовательные и параллельные резисторы

Цели обучения

К концу этого раздела вы сможете:

• Нарисуйте цепь с резисторами, включенными параллельно и последовательно.
• Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
• Сравните способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
• Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
• Рассчитайте общее сопротивление цепи, которая содержит смесь резисторов, включенных последовательно и параллельно.

Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на Рисунке 1.Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.

Рис. 1. (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.

Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то R ₁ на Рисунке 1 (a) может быть сопротивлением вала отвертки, R ₂ сопротивлением ее ручки , R ₃ сопротивление тела человека и R ₄ сопротивление его обуви.На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. Это могло бы стать недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением. прибор, уменьшающий рабочий ток.)

Рис. 2. Три резистора, подключенных последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).

Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе на рисунке 2. Согласно закону Ома, падение напряжения В на резистор, когда через него протекает ток, рассчитывается по формуле V = IR , где I равно току в амперах (A), а R — сопротивление в омах (Ω).Другой способ представить это: В, — это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R ₁ составляет В ₁ = IR ₁ , что на R ₂ составляет В ₂ = IR ₂ и 2 что через R ₃ это V ₃ = IR ₃ .Сумма этих напряжений равна выходному напряжению источника; то есть

V = V ₁ + V ₂ + V ₃ .

Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV , где q — электрический заряд, а V — напряжение. Таким образом, энергия, поставляемая источником, составляет кв , а энергия, рассеиваемая резисторами, равна

.

qV ₁ + qV ₂ + qV ₃ .

Установление связей: законы сохранения

Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые гласят, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.

Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии.Таким образом, qV = qV ₁ + qV ₂ + qV ₃ . Плата q отменяется, давая V = V ₁ + V ₂ + V ₃ , как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.) Теперь подстановка значений для отдельных напряжений дает

V = IR ₁ + IR ₂ + IR ₃ = I ( R ₁ + R _{2 5 909 ).}

Обратите внимание, что для эквивалентного сопротивления одной серии R _с , мы имеем

V = IR _с .

Это означает, что полное или эквивалентное последовательное сопротивление R _с трех резисторов составляет R _с = R ₁ + R ₂ + R ₃ .Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, общее сопротивление R _с последовательного соединения составляет

R _с = R ₁ + R ₂ + R ₃ +…,

, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.

Пример 1. Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи

Предположим, что выходное напряжение батареи на Рисунке 2 равно 12.0 В, а сопротивления равны R ₁ = 1,00 Ом, R ₂ = 6,00 Ом и R ₃ = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите ток. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)

Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:

[латекс] \ begin {array} {lll} {R} _ {\ text {s}} & = & {R} _ {1} + {R} _ {2} + {R} _ {3} \ \ & = & 1.00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex].

Стратегия и решение для (b)

Ток определяется по закону Ома, В = IR . Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:

[латекс] I = \ frac {V} {{R} _ {\ text {s}}} = \ frac {12.0 \ text {V}} {20.0 \ text {} \ Omega} = 0.60 \ text {A }\\[/латекс].

Стратегия и решение для (c)

Напряжение — или IR падение — в резисторе определяется законом Ома.Ввод значения тока и значения первого сопротивления дает

.

В ₁ = IR ₁ = (0,600A) (1,0 Ом) = 0,600 В.

Аналогично

В ₂ = IR ₂ = (0,600A) (6,0 Ом) = 3,60 В

и

V3 = IR ₃ = (0,600 A) (13,0 Ом) = 7,80 В.

Обсуждение для (c)

Три капли IR добавляют к 12.0 В, прогноз:

V ₁ + V ₂ + V ₃ = (0,600 + 3,60 + 7,80) V = 12,0 В.

Стратегия и решение для (d)

Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля , P = IV , где P — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток.Подставляя закон Ома V = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как

P ₁ = I ² R ₁ = (0,600 A) ² (1,00 Ом) = 0,360 Вт.

Аналогично

P ₂ = I ² R ₂ = (0,600 A) ² (6,00 Ом) = 2,16 Вт.

и

P ₃ = I ² R ₃ = (0.{2}} {R} \\ [/ latex], где В — это падение напряжения на резисторе (а не полное напряжение источника). Получатся те же значения.

Стратегия и решение для (e)

Самый простой способ рассчитать выходную мощность источника — использовать P = IV , где В — напряжение источника. Это дает

P = (0,600 A) (12,0 В) = 7,20 Вт.

Обсуждение для (e)

Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть

P ₁ + P ₂ + P ₃ = (0,360 + 2,16 + 4,68) W = 7,20 Вт.

Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.

Основные характеристики резисторов серии

1. Последовательные сопротивления добавить: R _с = R ₁ + R ₂ + R ₃ +….
2. Один и тот же ток последовательно проходит через каждый резистор.
3. Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.

На рисунке 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника. Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)

Рис. 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)

Чтобы найти выражение для эквивалентного параллельного сопротивления R _p , давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} \\ [/ latex] , [латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} \\ [/ latex] и [латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} \\ [/ латекс]. Сохранение заряда подразумевает, что полный ток I , производимый источником, является суммой этих токов:

I = I ₁ + I ₂ + I ₃ .

Подстановка выражений для отдельных токов дает

[латекс] I = \ frac {V} {{R} _ {1}} + \ frac {V} {{R} _ {2}} + \ frac {V} {{R} _ {3}} = V \ left (\ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} \ справа) \\ [/ латекс].

Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает

[латекс] I = \ frac {V} {{R} _ {p}} = V \ left (\ frac {1} {{R} _ {p}} \ right) \\ [/ latex].

Члены в круглых скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление R _p параллельного соединения связано с отдельными сопротивлениями на

[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ гидроразрыв {1} {{R} _ {\ text {.} 3}} + \ text {.} \ Text {…} \\ [/ latex]

Это соотношение приводит к общему сопротивлению R _p , которое меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.

Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи

Пусть выходное напряжение батареи и сопротивления в параллельном соединении на Рисунке 3 будут такими же, как в ранее рассмотренном последовательном соединении: В = 12.0 В, R ₁ = 1,00 Ом, R ₂ = 6,00 Ом и R ₃ = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)

Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения.Ввод известных значений дает

[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} = \ frac {1} {1 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {6 \ text {. } \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} \\ [/ latex].

Таким образом,

[латекс] \ frac {1} {{R} _ {p}} = \ frac {1.00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].

(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.) Мы должны перевернуть это, чтобы найти полное сопротивление R _p . Это дает

[латекс] {R} _ {\ text {p}} = \ frac {1} {1 \ text {.} \ Text {2436}} \ text {} \ Omega = 0 \ text {.} \ Text { 8041} \ text {} \ Omega \\ [/ latex].

Общее сопротивление с правильным количеством значащих цифр составляет R _p = 0,804 Ом

Обсуждение для (а)

R _p , как и предполагалось, меньше наименьшего индивидуального сопротивления.

Стратегия и решение для (b)

Полный ток можно найти из закона Ома, заменив полное сопротивление R _p . Это дает

[латекс] I = \ frac {V} {{R} _ {\ text {p}}} = \ frac {\ text {12.0 V}} {0.8041 \ text {} \ Omega} = \ text {14} \ text {.} \ text {92 A} \\ [/ latex].

Обсуждение для (б)

Ток I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.

Стратегия и решение для (c)

Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,

[латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} = \ frac {12.0 \ text {V}} {1.00 \ text {} \ Omega} = 12.0 \ text {A} \\ [/ латекс].

Аналогично

[латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} = \ frac {12.0 \ text {V}} {6.00 \ text {} \ Omega} = 2 \ text {.} \ text {00} \ text {A} \\ [/ latex]

и

[латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} = \ frac {\ text {12} \ text {.} 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].

Обсуждение для (c)

Полный ток складывается из отдельных токов:

I ₁ + I ₂ + I ₃ = 14,92 A.

Это соответствует сохранению заряда.{2}} {13.0 \ text {} \ Omega} = 11.1 \ text {W} \\ [/ latex].

Обсуждение для (д)

Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.

Стратегия и решение для (e)

Общую мощность также можно рассчитать несколькими способами. Выбрав P = IV и введя полный ток, получим

P = IV = (14,92 A) (12,0 В) = 179 Вт.

Обсуждение для (e)

Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт:

P ₁ + P ₂ + P ₃ = 144 Вт + 24,0 Вт + 11,1 Вт = 179 Вт

Это соответствует закону сохранения энергии.

Общее обсуждение

Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.

Основные характеристики резисторов, подключенных параллельно

1. Параллельное сопротивление определяется из [latex] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {1}} + \ frac {1} { {R} _ {2}} + \ frac {1} {{R} _ {3}} + \ text {…} \\ [/ latex], и оно меньше любого отдельного сопротивления в комбинации.
2. Каждый резистор, включенный параллельно, имеет такое же полное напряжение, что и источник. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
3. Параллельные резисторы не получают суммарный ток каждый; они делят это.

Сочетания последовательного и параллельного

Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они обычно встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного соединения можно свести к одному эквивалентному сопротивлению, используя метод, показанный на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.

Рис. 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто единичное эквивалентное сопротивление.

Простейшая комбинация последовательного и параллельного сопротивления, показанная на рисунке 4, также является наиболее поучительной, поскольку она используется во многих приложениях.Например, R ₁ может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. R ₂ и R ₃ может быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.

Пример 3. Расчет сопротивления,

IR Падение, ток и рассеиваемая мощность: объединение последовательных и параллельных цепей

На рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного подключения.Мы можем рассматривать R ₁ как сопротивление проводов, ведущих к R ₂ и R ₃ . (а) Найдите полное сопротивление. (b) Что такое падение IR в R ₁ ? (c) Найдите текущие значения от I ₂ до R ₂ . (d) Какую мощность рассеивает R ₂ ?

Рисунок 5. Эти три резистора подключены к источнику напряжения, так что R ₂ и R ₃ параллельны друг другу, и эта комбинация последовательно с R ₁ .

Стратегия и решение для (а)

Чтобы найти полное сопротивление, отметим, что R ₂ и R ₃ находятся параллельно, и их комбинация R _p находится последовательно с R ₁ . Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет

.

R _Tot = R ₁ + R _p .

Сначала мы находим R _p , используя уравнение для параллельных резисторов и вводя известные значения:

[латекс] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3 }} = \ frac {1} {6 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс].

Инвертирование дает

[латекс] {R} _ {\ text {p}} = \ frac {1} {0,2436} \ text {} \ Omega = 4.11 \ text {} \ Omega \\ [/ latex].

Итак, общее сопротивление

R _tot = R ₁ + R _p = 1,00 Ом + 4,11 Ом = 5,11 Ом.

Обсуждение для (а)

Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чистой параллели (20.0 Ом и 0,804 Ом соответственно), найденные для тех же резисторов в двух предыдущих примерах.

Стратегия и решение для (b)

Чтобы найти падение IR в R ₁ , отметим, что полный ток I протекает через R ₁ . Таким образом, его IR падение составляет

В ₁ = ИК ₁

Мы должны найти I , прежде чем сможем вычислить V ₁ .Полный ток I находится с помощью закона Ома для схемы. То есть

[латекс] I = \ frac {V} {{R} _ {\ text {tot}}} = \ frac {\ text {12.0} \ text {V}} {5.11 \ text {} \ Omega} = 2.35 \ text {A} \\ [/ latex].

Вводя это в выражение выше, мы получаем

В ₁ = IR ₁ = (2,35 A) (1,00 Ом) = 2,35 В.

Обсуждение для (б)

Напряжение, приложенное к R ₂ и R ₃ , меньше общего напряжения на величину В ₁ .Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R ₂ и R ₃ .

Стратегия и решение для (c)

Чтобы найти ток через R ₂ , мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение В _p , потому что оно приложено к параллельной комбинации резисторов. Напряжение, приложенное как к R ₂ , так и к R ₃ , уменьшается на величину В ₁ , и поэтому оно составляет

V _p = V — V ₁ = 12.0 В — 2,35 В = 9,65 В.

Теперь ток I ₂ через сопротивление R ₂ находится по закону Ома:

[латекс] {I} _ {2} = \ frac {{V} _ {\ text {p}}} {{R} _ {2}} = \ frac {9.65 \ text {V}} {6.00 \ текст {} \ Omega} = 1,61 \ text {A} \\ [/ latex].

Обсуждение для (c)

Ток меньше, чем 2,00 А, которые проходили через R ₂ , когда он был подключен параллельно к батарее в предыдущем примере параллельной цепи.

Стратегия и решение для (d)

Мощность, рассеиваемая R ₂ определяется

P ₂ = ( I ₂ ) ² R ₂ = (1,61 A) ² (6,00 Ом) = 15,5 Вт

Обсуждение для (д)

Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.

Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным.

Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).

То, что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, обозначенное как R ₃ , имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот повышенный ток вызывает большее падение IR в проводах, представленных R ₁ , снижая напряжение на лампочке (которое составляет R ₂ ), которое затем заметно тускнеет.

Рис. 6. Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.

Проверьте свое понимание

Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.

Решение Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы. В таких случаях правила Кирхгофа, которые будут включены в Правила Кирхгофа, позволят вам проанализировать схему.

Стратегии решения проблем для последовательных и параллельных резисторов

1. Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
2. Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
3. Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
4. Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, уменьшайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при нахождении R необходимо соблюдать осторожность.
5. Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и так далее.

Сводка раздела

Концептуальные вопросы

1. Переключатель имеет переменное сопротивление, которое почти равно нулю в замкнутом состоянии и очень велико в разомкнутом состоянии, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рис. 7 на ток в разомкнутом и замкнутом состоянии.

Рис. 7. Выключатель обычно включается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)

2. Какое напряжение на разомкнутом переключателе на Рисунке 7?

3. На разомкнутом переключателе есть напряжение, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?

4. Почему мощность, рассеиваемая замкнутым переключателем, как на рис. 7, мала?

5. Студент в физической лаборатории по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рисунке 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и гаснет, когда он замкнут. (Не пытайтесь — батарея сильно разряжается!)

Рис. 8. Ошибка подключения. Включите этот переключатель параллельно устройству, обозначенному [латекс] R [/ латекс].(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)

6. Зная, что сила электрического шока зависит от величины тока, проходящего через ваше тело, вы бы предпочли, чтобы он был включен последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он шокирован им? Объяснять.

7. Были бы ваши фары тусклыми при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.

8. Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкаются накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?

9.Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.

10. Предположим, вы проводите физическую лабораторию, в которой вас просят вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?

11. Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление.Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.

12. У некоторых лампочек есть три уровня мощности (не включая ноль), получаемые от нескольких нитей накала, которые индивидуально переключаются и соединяются параллельно. Какое минимальное количество нитей нити необходимо для трех режимов мощности?

Задачи и упражнения

Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.

1. (a) Каково сопротивление десяти последовательно соединенных резисторов сопротивлением 275 Ом? (б) Параллельно?

2. (a) Каково сопротивление последовательно соединенных резисторов 1,00 × 10 ² Ом, 2,50 кОм и 4,00 кОм? (б) Параллельно?

3. Какое наибольшее и наименьшее сопротивление можно получить, соединив резисторы на 36,0 Ом, 50,0 Ом и 700 Ом?

4. Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?

5. Фара мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)

6.(a) Учитывая батарею на 48,0 В и резисторы на 24,0 и 96,0 Ом, найдите для каждого из них ток и мощность при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.

7. Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, вычислите I ₃ двумя следующими способами: (a) по известным значениям I и I ₂ ; (б) используя закон Ома для R ₃ . В обеих частях явно показано, как вы выполняете шаги, указанные в описании стратегии решения проблем для последовательных и параллельных резисторов выше.

Рисунок 5. Эти три резистора подключены к источнику напряжения, так что R ₂ и R ₃ параллельны друг другу, и эта комбинация последовательно с R ₁ .

8. Ссылаясь на рисунок 5: (a) Вычислите P ₃ и обратите внимание на его сравнение с P ₃ , найденным в первых двух примерах задач в этом модуле. (b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.

9. См. Рисунок 6 и обсуждение затемнения света при включении тяжелого прибора. (a) Учитывая, что источник напряжения составляет 120 В, сопротивление провода составляет 0,400 Ом, а номинальная мощность лампы составляет 75,0 Вт, какая мощность будет рассеиваться лампой, если при включении двигателя через провода пройдет в общей сложности 15,0 А? Предположите незначительное изменение сопротивления лампы. б) Какая мощность потребляет двигатель?

Рис. 6. Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.

10. Линия электропередачи на 240 кВ с 5,00 × 10 ² подвешена к заземленным металлическим опорам с помощью керамических изоляторов, каждый из которых имеет сопротивление 1,00 × 10 ⁹ Ом (рис. 9 (а)). Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Ясно покажите, как вы выполняете шаги, указанные в описании стратегии решения проблем для последовательных и параллельных резисторов выше.

Рис. 9. Высоковольтная линия электропередачи (240 кВ) 5,00 × 10 ² подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает сопротивление 1,00 × 10 ⁹ Ом каждый.

11. Покажите, что если два резистора R ₁ и R ₂ объединены, и один из них намного больше другого ( R ₁ >> R ₂ ): (a ) Их последовательное сопротивление почти равно большему сопротивлению R ₁ .(b) Их параллельное сопротивление почти равно меньшему сопротивлению R ₂ .

12. Необоснованные результаты Два резистора, один из которых имеет сопротивление 145 Ом, подключены параллельно, чтобы получить общее сопротивление 150 Ом. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

13. Необоснованные результаты Два резистора, один из которых имеет сопротивление 900 кОм, соединены последовательно, чтобы получить общее сопротивление 0.500 МОм. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

Глоссарий

серия:

последовательность резисторов или других компонентов, включенных в цепь один за другим

резистор:

компонент, обеспечивающий сопротивление току, протекающему по электрической цепи

сопротивление:

вызывает потерю электроэнергии в цепи

Закон Ома:

соотношение между током, напряжением и сопротивлением в электрической цепи: В = IR

напряжение:

электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором

падение напряжения:

потеря электроэнергии при прохождении тока через резистор, провод или другой компонент

текущий:

поток заряда через электрическую цепь мимо заданной точки измерения

Закон Джоуля:

соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое следующим образом: [latex] {P} _ {e} = \ text {IV} [/ latex]

параллельно:

разводку резисторов или других компонентов в электрической цепи, так что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы

Избранные решения проблем и упражнения

1.(а) 2,75 кОм (б) 27,5 Ом

3. (а) 786 Ом (б) 20,3 Ом

5. 29,6 Вт

7. (а) 0,74 А (б) 0,742 А

9. (а) 60,8 Вт (б) 3,18 кВт

11. (a) [латекс] \ begin {array} {} {R} _ {\ text {s}} = {R} _ {1} + {R} _ {2} \\ \ Rightarrow {R} _ {\ text {s}} \ приблизительно {R} _ {1} \ left ({R} _ {1} \ text {>>} {R} _ {2} \ right) \ end {array} \\ [/ латекс]

(b) [латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2} } = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2}} \\ [/ latex],

так что

[латекс] \ begin {array} {} {R} _ {p} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ приблизительно \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1}} = {R} _ {2} \ left ({R} _ {1 } \ text {>>} {R} _ {2} \ right) \ text {.} \ end {array} \\ [/ latex]

13. (a) –400 кОм (b) Сопротивление не может быть отрицательным. (c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.

Калькулятор параллельного сопротивления

— Инструменты для электротехники и электроники

С легкостью рассчитайте общее сопротивление параллельно включенных резисторов!

Как рассчитать полное сопротивление резисторов, включенных параллельно

Расчет эквивалентного сопротивления (R _EQ ) параллельно включенных резисторов вручную может быть утомительным.Этот инструмент был разработан, чтобы помочь вам быстро рассчитать эквивалентное сопротивление, независимо от того, подключены ли у вас два или десять резисторов параллельно. Чтобы использовать его, просто укажите количество параллельных резисторов и значение сопротивления для каждого из них.

Вы можете легко вычислить эквивалентное сопротивление, когда у вас есть два идентичных резистора, подключенных параллельно: это половина отдельного сопротивления. Это удобно, когда вам нужно определенное значение сопротивления, а подходящей детали нет в наличии. Например, если вы знаете, что вам нужно около 500 Ом, чтобы получить желаемую яркость светодиодной цепи, вы можете использовать два резистора 1 кОм параллельно.

Имейте в виду, что ток через отдельный резистор не изменяется, когда вы добавляете резисторы параллельно, потому что добавление резисторов параллельно не влияет на напряжение на выводах резисторов. Изменяется общий ток, подаваемый источником питания, а не ток через один конкретный резистор.

Уравнения

$$ \ frac {1} {R_ {EQ}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + … + \ frac {1} {R_ {N}} $$

Когда у вас есть только два параллельно подключенных резистора: $$ R_ {EQ} = \ frac {R_1 \ times R_2} {R_1 + R_2} $$

Приложения

Последовательные резисторы эквивалентны одному резистору, сопротивление которого является суммой каждого отдельного резистора.С другой стороны, параллельное соединение резисторов дает эквивалентное сопротивление, которое всегда ниже, чем у каждого отдельного резистора. Если подумать, это имеет смысл: если вы подаете напряжение на резистор, протекает определенное количество тока. Если вы добавите еще один резистор параллельно первому, вы, по сути, откроете новый канал, по которому может течь больше тока. Независимо от того, насколько велик второй резистор, общий ток, протекающий от источника питания, будет, по крайней мере, немного выше, чем ток через единственный резистор.А если общий ток выше, общее сопротивление должно быть ниже.

Дополнительная литература

резисторов параллельно | Формула эквивалентного сопротивления

Введение

Два резистора считаются подключенными параллельно, если оба вывода резистора подключены к каждому соответствующему выводу другого резистора. В сети параллельных резисторов ток может проходить по нескольким путям, в отличие от сети с последовательными резисторами, поскольку существует несколько путей для прохождения тока.Следовательно, параллельные резистивные цепи являются делителями тока.

Параллельные резисторы

Если два или более резистора подключены параллельно, то разность потенциалов на каждом резисторе будет одинаковой. При параллельном соединении резисторы подключаются к одним и тем же узлам. Это можно определить по наличию более чем одного пути прохождения тока. Например, приведенная ниже схема представляет собой параллельное соединение резисторов. Разность потенциалов на резисторе R1 такая же, как и на резисторе R2, который равен потенциалу питания V _AB .

Если V _AB — это подаваемый потенциал, тогда

V _R1 = V _R2 = V _AB

В следующей схеме резисторы R1, R2 и R3 подключены параллельно комбинация.

Здесь потенциал питания составляет V _AB между точками A и B. Поскольку резисторы R1, R2 и R3 соединены параллельно, разность потенциалов на каждом резисторе такая же, как и у источника питания.Следовательно, V _AB = V _R1 = V _R2 = V _R3 .

Где

В _R1 — потенциал на резисторе R1.

В _R2 — это потенциал на резисторе R2.

В _R3 — потенциал на резисторе R3.

Но ток, протекающий через эти три резистора, разный. Если I — это ток, покидающий узел A, то он имеет три пути, чтобы достичь узла B. Ток, протекающий через каждый резистор, зависит от его сопротивления.Следовательно, в случае параллельных резистивных цепей ток во всех резисторах неодинаков. Если I1 — это ток, протекающий через резистор R1, I2 — это ток, протекающий через резистор R2, а I3 — это ток, протекающий через резистор R3, тогда токи I, I1, I2 и I3 могут быть связаны с помощью закона тока Кирхгофа. . Согласно текущему закону Кирхгофа, «сумма токов, входящих в узел, равна сумме токов, выходящих из узла».

Следовательно,

I = I1 + I2 + I3.

Формула эквивалентного сопротивления

Любое количество резисторов, включенных в параллельную комбинацию, может быть заменено одним резистором с сопротивлением, равным эквивалентному сопротивлению резисторов параллельной комбинации.

Было установлено, что напряжение на каждом резисторе в параллельной комбинации одинаково, а общий ток равен сумме отдельных токов. Рассмотрим следующую схему.

Здесь I = I1 + I2 + I3

I1 = V / R1

I2 = V / R2

I3 = V / R3

Если R _T — полное сопротивление цепи, то

I = V / R _T

Следовательно V / R _T = V / R ₁ + V / R ₂ + V / R ₃

1 / R _T = 1 / R ₁ + 1 / R ₂ + 1 / R ₃

Если R _eq является эквивалентным сопротивлением цепи, то оно рассчитывается путем сложения обратных значений отдельных сопротивлений (1 / R).Обратная величина этой алгебраической суммы даст эквивалентное сопротивление. Уравнение эквивалентного сопротивления R _eq показано ниже для параллельной резистивной цепи из n резисторов.

(1 / R _экв ) = (1 / R1) + (1 / R2) + (1 / R3) + ……… + (1 / Rn)

Из приведенного выше уравнения можно сделать вывод, что эквивалентное сопротивление резисторов, соединенных параллельно, всегда меньше, чем сопротивление самого маленького резистора.

Если два резистора подключены параллельно, то эквивалентное сопротивление будет

(1 / R _eq ) = (1 / R1) + (1 / R2)

R _EQ = R ₁ * R ₁ / (R ₁ + R ₂ )

Если два резистора равного сопротивления R соединены параллельно, то эквивалентное сопротивление комбинации будет R / 2.

Аналогично, если три резистора равного сопротивления R соединены в параллельном соединении, тогда эквивалентное сопротивление комбинации будет R / 3.

Параллельное соединение резисторов дает значение проводимости. Проводимость — это величина, обратная сопротивлению. Обычно он обозначается символом G. Единицы проводимости — Сименс, представленные символом S. Ранее единицами проводимости были Mho (℧), что означает обратное написание Ом, а символ — перевернутое представление Ω.

Несмотря на то, что параллельные резисторы подключены между двумя узлами, представление этого подключения может иметь любую из следующих форм.

Все вышеупомянутые комбинации представляют собой параллельные резистивные схемы, и все правила параллельных резисторов применимы и к вышеупомянутым комбинациям.

Расчет тока

Ток в каждой ветви параллельной резистивной цепи отличается от другой. Поскольку напряжение на каждом резисторе одинаково, ток, протекающий через каждый резистор, зависит от сопротивления этого резистора.Следовательно, если значение сопротивления в одной ветви отличается от другой, тогда ток в этих ветвях будет другим. Величину этого тока можно определить с помощью закона Ома.

Рассмотрим параллельную сеть из двух резисторов с напряжением питания V между двумя точками A и B.

Пусть I будет полным током в следующей цепи.

Пусть ток, протекающий через резистор R ₁ , равен I _R1 , а ток, протекающий через резистор R ₂ , равен I _R2 .

Тогда, согласно закону Кирхгофа, «полный ток, входящий в цепь, равен току, выходящему из цепи».

Если I _T — это общий ток, тогда

I _T = I _R1 + I _R2

Поскольку падение напряжения на каждом резисторе одинаково

I _R1 = V / R ₁

And I _R2 = V / R ₂

Если рассматривать параллельную резистивную цепь, состоящую из n резисторов, то общий ток в цепи составляет

I _Total = I _R1 + Я _R2 +….+ I _Rn

Если последовательные резистивные цепи называются цепями делителя напряжения, то аналогично параллельные резистивные цепи называются цепями делителя тока.

Если рассматривается параллельная резистивная цепь из n резисторов с разным сопротивлением, то можно иметь n разных путей для протекания тока и n разных значений тока через эти пути. Резисторы в параллельной комбинации можно менять местами, не влияя на общий ток и эквивалентное сопротивление.

Пример параллельного подключения резисторов

1. Рассмотрим следующую схему, в которой четыре резистора R1, R2, R3 и R4 подключены параллельно.

Значения сопротивления каждого резистора:

R1 = 10 Ом

R2 = 20 Ом

R3 = 30 Ом

R4 = 40 Ом

Напряжение питания V = 24 В

Общий ток в схеме можно рассчитать двумя способами.

Первый метод — вычислить отдельные токи, протекающие через каждый резистор.

Если I1 — это ток, протекающий через резистор R1, то согласно закону Ома

I1 = V / R ₁ = 24/10 = 2,4 A

Аналогично, если I2 — это ток, протекающий через резистор R2, то согласно по закону Ома

I2 = V / R ₂ = 24/20 = 1,2 A

Если I3 — это ток, протекающий через резистор R3, то по закону Ома

I3 = V / R ₃ = 24 / 30 = 0,8 А

А если I4 — ток, протекающий через резистор R4, то по закону Ома

I4 = V / R ₄ = 24/40 = 0.6 A

Если I _ИТОГО — это полный ток в цепи, то согласно закону Кирхгофа

I _ИТОГО = I1 + I2 + I3 + I4 = 2,4 + 1,2 + 0,8 + 0,6 = 5A

Второй метод расчета тока — это определение эквивалентного сопротивления цепи.

Эквивалентное сопротивление цепи

1 / R _EQ = (1 / R ₁ ) + (1 / R ₂ ) + (1 / R ₃ ) + (1 / R ₄ )

1 / R _EQ = (1/10) + (1/20) + (1/30) + (1/40)

R _EQ = 1/2.083 = 4,8 Ом

Этот единственный резистор можно использовать для замены всех резисторов в параллельной комбинации.

∴ I _ИТОГО = V / R _EQ = 24 / 4,8 = 5A.

Рассмотрим следующую схему, в которой три резистора R1, R2 и R3 соединены параллельно.

Ток, протекающий через R1, равен I1 = 6A

Ток, протекающий через R2, равен I2 = 4A

Ток, протекающий через R3, равен I3 = 2A

В параллельных резистивных цепях напряжение на каждом резисторе одинаково и равно напряжению питания.

Здесь напряжение питания V = 12 В.

Если V1 — это напряжение на резисторе R1, V2 — это напряжение на резисторе R2, а V3 — это напряжение на резисторе R3, тогда

V = V1 = V2 = V3 = 12 В

Тогда по закону Ома

R1 = V ₁ / I ₁

R1 = 12/6

R1 = 2 Ом

R2 = V ₂ / I ₂

R2 = 12/4

R2 = 3 Ом

R3 = V ₃ / I ₃

R3 = 12/2

R3 = 6 Ом

Применения

Концепция резисторов в parallel используется при анализе мостовой схемы Уитстона.Параллельно соединенные резисторы действуют как цепь делителя тока. Эта текущая концепция делителя используется в таких приложениях, как аналого-цифровые преобразователи и цифро-аналоговые преобразователи.

Как рассчитать резисторы, включенные последовательно и параллельно — Kitronik Ltd

Резисторы

серии

Когда резисторы подключаются друг за другом, это называется последовательным соединением. Это показано ниже. Чтобы рассчитать общее полное сопротивление ряда резисторов, подключенных таким образом, вы складываете отдельные сопротивления.Это делается по следующей формуле: Rtotal = R1 + R2 + R3 и так далее. Пример: чтобы рассчитать общее сопротивление для этих трех последовательно соединенных резисторов.

Rtotal = R1 + R2 + R3 = 100 + 82 + 1 Ом = 183 Ом

---

Задача 1:

Рассчитайте общее сопротивление следующего последовательно включенного резистора.

	Rtotal	= _______________
		= _______________

	Rtotal	= _______________
		= _______________

	Rtotal	= _______________
		= _______________

Параллельные резисторы

Когда резисторы подключаются друг к другу (бок о бок), это называется параллельным подключением.Это показано ниже.

Два параллельных резистора

Для расчета общего полного сопротивления a двух резисторов, подключенных таким образом, вы можете использовать следующую формулу:

Пример: чтобы рассчитать полное сопротивление для этих двух резисторов, включенных параллельно.

---

Задача 2:

Рассчитайте полное сопротивление следующего резистора, включенного параллельно.

Три или более резистора, включенных параллельно

Чтобы рассчитать общее общее сопротивление ряда из трех или более резисторов, подключенных таким образом, вы можете использовать следующую формулу: Пример: Чтобы вычислить общее сопротивление для этих трех резисторов, подключенных параллельно

---

Задача 3:

Рассчитайте полное сопротивление следующего резистора, включенного параллельно.

---

ответы

Задача 1

1 = 1492 Ом 2 = 2242 Ом 3 = 4847 Ом

Задача 2

1 = 5 Ом 2 = 9,57 Ом 3 = 248,12 Ом

Задача 3

1 = 5,95 Ом 2 = 23,76 Ом Загрузите pdf-версию этой страницы здесь. Подробнее об авторе подробнее »

© Kitronik Ltd — Вы можете распечатать эту страницу и ссылку на нее, но не должны копировать страницу или ее часть без предварительного письменного согласия Kitronik.

.

No related posts.