Последовательное и параллельное соединение резисторов
Последовательное и параллельное соединение резисторов в схемах являются самыми распространенными, также – это база для расчета более сложных схем.
Последовательное подключение
Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше.
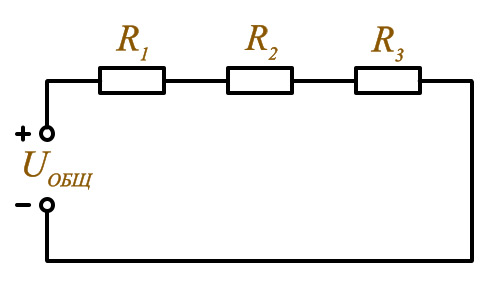
Рис. Последовательное подключение.Обозначение:
Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим. Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях – складываем, в параллельных – это обратно пропорциональная величина.
Параллельное соединение
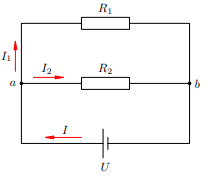
Рис. Параллельное подключение.Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах – //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле.
Более наглядно это можно представить в виде формул:
1. Каждый вид соединения находится под одинаковым напряжением:
U = U1 = U2;
2. Суммарная сила тока равняется суммарному значению тока каждого участка
I = I1 + I2;
3. Сопротивление цепи равно сумме величина обратных сопротивлению участка:
1/R = 1/R1 + 17R2 + . . . + 1/Rn;
4. Сила тока пропорциональна сопротивлению каждого участка
I1/I2=R2/R1.
Далее рассмотрим схему как работает не только последовательное параллельное, но и смешанное соединение резисторов.
Смешанное подключение
Рис. Смешанное подключение резисторовВ электрических схемах используются не только типовые схемы, но и смешанное, созданное из критерий определенных требований. Чаще всего в схемах встречается третий вариант, представляющий набор из элементарных типов схем. В смешанных участках учитываются не только элементы, но и направления движения тока.
При вычислении мощности резисторов смешанного подключения используются формулы для параллельного и последовательного соединения резисторов, формула также является составной.
Основные законы электротехники, наиболее часто используемые для расчетов
Рассмотрим основные законы электротехники и свойства последовательного и параллельного соединения резисторов для участка цепи
Закон Ома
Напряжение находится по закону Ома по формуле I=U/R – чем больше сопротивление, тем меньше ток. Напряжение можно найти из этой же формулы. U=R*I, ток умножается на сопротивление. Запишем эту формулу для каждого участка U1=R1· I1, Un=Rn · In.
Законы Кирхгофа
Первый закон
Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два.
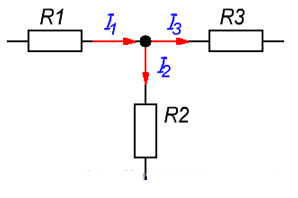
Рис. иллюстрация к пояснению действия первого закона Кирхгофа.Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю.
Если посмотреть на схему, I1 – это ток, который заходит в узел, I2 и I3 – это электроны, которые вытекают из него.
Применяя формулировку первого закона можно записать формулу по-другому:
I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.
Второй закон Кирхгофа.
Рис. иллюстрация к пояснению действия второго закона Кирхгофа.Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре.
E1- Е2 = – UR1 – UR2 или E1 = Е2 – UR1 – UR2.
Параллельное и последовательное соединение резисторов, решение задач
Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно.
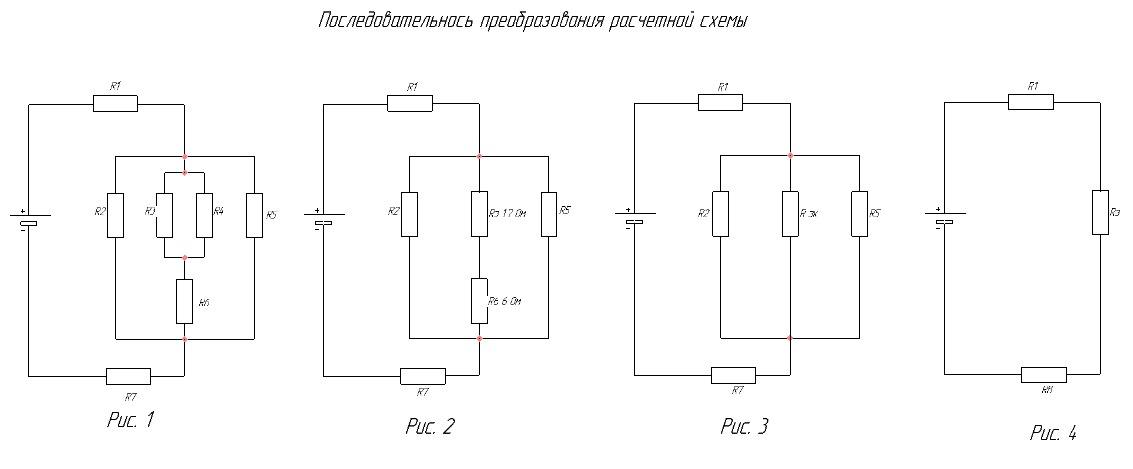
Рис. Порядок замещения при расчете сложных позиций более простыми.Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. Рассмотрим схему №1 на рис.
На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?
Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.
Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.
Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше (рис 3).
Теперь образовалась ситуация – включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех.
Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.
Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.
Схема с подключением сопротивлений «треугольником»
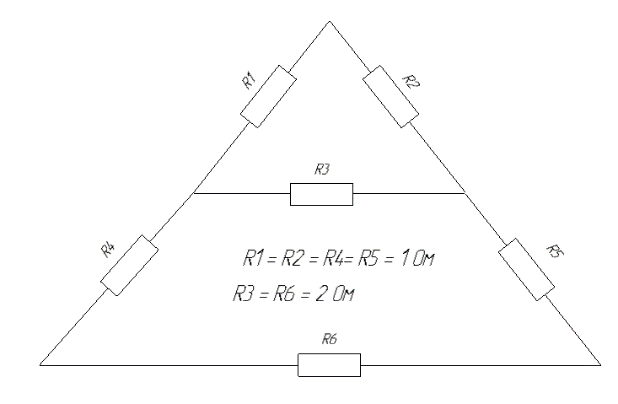
Рис. Расчетная схема соединения резисторов в треугольник.Иногда некоторые затруднения возникают при разборе схемы соединения в треугольник.
Рассмотрим на примере рисунка расчет резисторов по этому подключению.
Из схемы видно, что R1 и R2 соединены последовательно Rэ12 будет соединяться R3 последовательно.
Затем Rэ123 соединяется с сопротивлением R4, R5 в последовательную цепь. Затем все это объединяется с Rэ в //.
Проведем несложные вычисления учитывая, что
R1, R2, R4, R5 равняется 1 Ом. R3, R7 – 2 Ом.
RЭ1,2 = R1+R2 = 1+1=2 Ом.
Вычисляем параллельное подключение: Rэ 12 с R3. Rэ1,3 = (Rэ12*R3) /(Rэ12+R3) = (2*2) /(2+2) = 1Ом.
Далее мы видим последовательное: RЭ123 + R4 + R5 = 1+1+1 = 3 Ом.
И последнее – Rэ123 4 5 с R6 – параллельное.
Общее сопротивление цепи Rц = Rоб = (RЭ1,2,3,4,5 *R6) /(RЭ1,2,3,4,5+R6) = (3 * 2) / (3+2) = 1,2 Ом. Как видно, что расчет подобного варианта также не сложный.
Расчет последовательного и параллельного подключения резисторов онлайн
Подсчитать значение мощность и сопротивлений подставляя их в формулы можно только в учебных целях, или, когда объемы не очень большие. Наиболее практичный вариант расчета является онлайн калькуляторы, которые расположены на многочисленных интернет ресурсах. Для расчёта любой сложности нужно правильно определить тип соединения резисторов последовательное или параллельное и внести данные для расчета в поля калькулятора.
Также такая форма расчета подойдет и для проверки результатов решения учебных задач.
Последовательное и параллельное соединение резисторов и конденсаторов
Электрические цепи состоят не только из резисторов, в них применяется большое количество различных деталей, например, конденсатор, которые подключаются в последовательное, // и смешанное соединение.
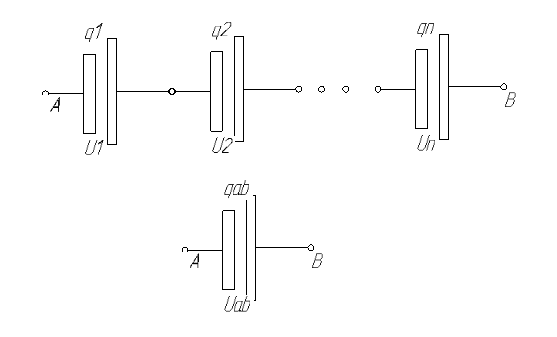
Рис. Замещения последовательно включенных элементов.Определение этому элементу можно дать следующее: Конденсатор – это совокупность проводящих тел служащий для накопления электрического заряда.
Элементарный конденсатор имеет две пластины, форма этих пластин может быть различной: сферической, круглой, цилиндрической, прямоугольной – по форме пластин разделяется и тип конденсатора.
Важное свойство. Одно из важных свойств конденсатора: если заряжается одна пластина конденсатора, то благодаря явлению электростатической индукции заряжается и вторая половина, но с противоположным знаком.
Устройство конденсатора
Плоский конденсатор состоит из двух плоских пластин отстоящих друг от друга на маленькое расстояние. У конденсатора к двум пластинам припаивается вывод всего их получается два.
Типовые схемы подключения конденсаторов
Рассмотрим различные виды подключения конденсатора.
Последовательное
Первый вид — это последовательное соединение.
Предположим, что емкость этих конденсаторов будут равны. Тогда заряды также будут равны: q1=q2=q3, как и в примере с резисторами, сложный тип позиций с конденсатором можно упростить, заменив несколько элементов одним. У элементов соединенных друг за другом, общая емкость будет обратно пропорциональная всем имеющимся элементам. То есть: Rэк будет равняться 1/С1 + 1/С2 +…. 1/Сn/
Напряжение складывается, U эк = U1 + U2+ … Un.
Параллельное
Второй тип подключения конденсаторов – это соединение в паралель
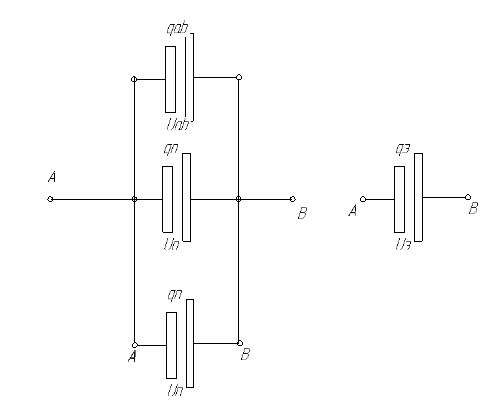
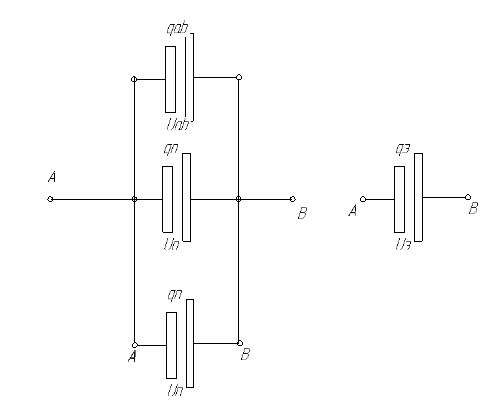Рис. Схема замещения элементов, включенных в параллель.Соответственно эти конденсаторов обозначены C1, C2, … Cn заряды: Q1, Q2, … Qn и напряжение: U1, U2, … Un.
У элементов в // емкость складывается Сэ = C1 + C2 + … C n.
Напряжение Un на каждом конденсаторе будет равно напряжению на эквивалентном
Uэ = U1 = U2 =… = Un – это особенность параллельного подсоединения всех элементов цепи.
Емкость будет складываться из суммы отдельных элементов Сэ =С1 + С2 + … Сп.
Рис. Расчетные позиции элементов при различном включении.Простая позиция, которая не требует преобразования №1 – последовательное подключение. По известной формуле для этих поз. запишем 1/Сэ = 1/С1 +1/С2 +1/С3, подставив формулу значения, которые даны в условии задачи, получим 1/Сэ = 1/С1 +1/С2 +1/С3 = 59 мФ.
Не требует преобразования и 2 схема: емкость общего конденсатора будет равняться сумме конденсаторов которые включены в параллельной цепи: Сэ =С1 +С2 +С3
Сэ = 100 + 200 + 500 = 800 мФ.
Рассмотрев рис. №3 видно, что пара конденсаторов включена параллельно и один последовательно. Алгоритм преобразования таких цепей мы уже рассматривали, поэтому: сразу же находим емкость конденсатора Сэ соединения: Сэ = С1+С2 = 200+500 = 700 мФ.
Теперь находим общие эквивалентную емкость элементов с последовательным подключением 1/Сэ = 1/С2,3 +1/ С1 = 89 мф.
Практическая задача решена.
Вконтакте
Google+
Внимание покупателей подшипников  Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас: +7(499)403 39 91
Доставка подшипников по РФ и зарубежью. Каталог подшипников на сайте themechanic.ru
|
Внимание покупателей подшипников
Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 646 00 12
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте
Внимание покупателей подшипников
Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 646 00 12
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте
последовательное и параллельное соединение, токоограничивающие и подтягивающие сопротивления [Амперка / Вики]
Резистор (сопротивление) — один из наиболее распространённых компонентов в электронике. Его назначение — простое: сопротивляться течению тока, преобразовывая его часть в тепло.
Основной характеристикой резистора является сопротивление. Единица измерения сопротивления — Ом (Ohm, Ω). Чем больше сопротивление, тем большая часть тока рассеивается в тепло. В схемах, питаемых небольшим напряжением (5 – 12 В), наиболее распространены резисторы номиналом от 100 Ом до 100 кОм.
Закон Ома
Закон Ома позволяет на заданном участке цепи определить одну из величин: силу тока I, напряжение U, сопротивление R, если известны две остальные:
Для обозначения напряжения наряду с символом U используется V.
Рассмотрим простую цепь
Расчитаем силу тока, проходящего через резистор R1 и, соответственно, затем через лампу L1. Для простоты будем предполагать, что сама лампа обладает нулевым собственным сопротивлением.
Аналогично, если бы у нас был источник питания на 5 В и лампа, которая по документации должна работать при токе 20 мА, нам нужно бы было выбрать резистор подходящего номинала.
В данном случае, разница в 10 Ом между идеальным номиналом и имеющимся не играет большого значения: можно смело брать стандартный номинал — 240 или 220 Ом.
Аналогично, мы могли бы расчитать требуемое напряжение, если бы оно было не известно, а на руках были значения сопротивления и желаемая сила тока.
Соединение резисторов
При последовательном соединении резисторов, их сопротивление суммируется:
При параллельном соединении, итоговое сопротивление расчитывается по формуле:
Если резистора всего два, то:
В частном случае двух одинаковых резисторов, итоговое сопротивление при параллельном соединении равно половине сопротивления каждого из них.
Таким образом можно получать новые номиналы из имеющихся в наличии.
Применеие на практике
Среди ролей, которые может выполнять резистор в схеме можно выделить следующие:
Токоограничивающий резистор (current-limiting resistor)
Стягивающий, подтягивающий резистор (pull-down / pull-up resistor)
Делитель напряжения (voltage divider)
Токоограничивающий резистор
Пример, на котором рассматривался Закон Ома представляет собой также пример токоограничевающего резистора: у нас есть компонент, который расчитан на работу при определённом токе — резистор снижает силу тока до нужного уровня.
В случае с Ардуино следует ограничивать ток, поступающий с выходных контактов (output pins). Напряжение, в состоянии, когда контакт включен (high) составляет 5 В. Исходя из документации, ток не должен превышать 40 мА. Таким образом, чтобы безопасно увести ток с контакта в землю понадобится резистор номиналом R = U / I = 5 В / 0.04 А = 125 Ом или более.
Стягивающие и подтягивающие резисторы
Стягивающие (pull-down) и подтягивающие (pull-up) резисторы используются в схемах рядом со входными контактами логических компонентов, которым важен только факт: подаётся ноль вольт (логический ноль) или не ноль (логическая единица). Примером являются цифровые входы Ардуино. Резисторы нужны, чтобы не оставить вход в «подвешенном» состоянии. Возьмём такую схему
Мы хотим, чтобы когда кнопка не нажата (цепь разомкнута), вход фиксировал отсутствие напряжения. Но в данном случае вход находится в «никаком» состоянии. Он может срабатывать и не срабатывать хаотично, непредсказуемым образом. Причина тому — шумы, образующиеся вокруг: провода действуют как маленькие антенны и производят электричество из электромагнитных волн среды. Чтобы гарантировать отсутствие напряжения при разомкнутой цепи, рядом с входом ставится стягивающий резистор:
Теперь нежелательный ток будет уходить через резистор в землю. Для стягивания используются резисторы больших сопротивлений (10 кОм и более). В моменты, когда цепь замкнута, большое сопротивление резистора не даёт большей части тока идти в землю: сигнал пойдёт к входному контакту. Если бы сопротивление резистора было мало (единицы Ом), при замкнутой цепи произошло бы короткое замыкание.
Аналогично, подтягивающий резистор удерживает вход в состоянии логической единицы, пока внешняя цепь разомкнута:
То же самое: используются резисторы больших номиналов (10 кОм и более), чтобы минимизировать потери энергии при замкнутой цепи и предотвратить короткое замыкание при разомкнутой.
Делитель напряжения
Делитель напряжения (voltage divider) используется для того, чтобы получить из исходного напряжения лишь его часть. Например, из 9 В получить 5. Он подробно описан в отдельной статье.
Мощность резисторов
Резисторы помимо сопротивления обладают ещё характеристикой мощности. Она определяет нагрузку, которую способен выдержать резистор. Среди обычных керамических резисторов наиболее распространены показатели 0.25 Вт, 0.5 Вт и 1 Вт. Для расчёта нагрузки, действующей на резистор, используйте формулу:
При превышении допустимой нагрузки, резистор будет греться и его срок службы может сильно сократиться. При сильном превышении — резистор может начать плавиться и вызвать воспламенение. Будьте осторожны!
Соединения проводников — материалы для подготовки к ЕГЭ по Физике
Темы кодификатора ЕГЭ: параллельное и последовательное соединение проводников, смешанное соединение проводников.
Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.
Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.
Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1):
Рис. 1. Резистор
Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2):
Рис. 2.
Стационарное поле совершает при этом положительную работу .
Так как и , то и , т. е. .
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3):
Рис. 3.
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.
1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике.
Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть — сопротивление участка . По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).
Рис. 5. Параллельное соединение
Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от к (по направлению тока) называется неразветвлённой частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.
1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .
Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:
Сокращая на , получим:
(1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти :
(2)
К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
(3)
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:
откуда
Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис. 6).
Рис. 6. Смешанное соединение
Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :
Ом.
Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:
Ом.
Сопротивление цепи:
Ом.
Теперь находим силу тока в цепи:
A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
B;
B.
(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора и находятся под напряжением , поэтому:
A;
A.
(В сумме имеем А, как и должно быть при параллельном соединении.)
Сила тока в резисторах и одинакова, так как они соединены последовательно:
А.
Стало быть, через резистор течёт ток A.
Последовательное соединение резисторов — Студопедия
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
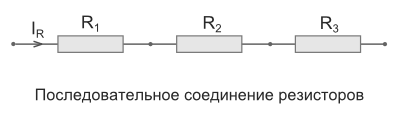
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
2) Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
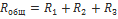
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
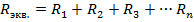
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
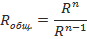
3)Электропроводность, электрическая проводимость, проводимость, способность тела пропускать электрический ток под воздействием электрического поля, а также физическая величина, количественно характеризующая эту способность. Тела, проводящие электрический ток, называются проводниками, в отличие от изоляторов.. .
Основная единица измерения сопротивления — Ом. Удельная проводимость — величина обратная сопротивлению, она измеряется в Сименсах, ранее назывшихся mho. Применительно к сыпучим веществам удобнее говорить об особой проводимости, обычно называемой удельной проводимостью.
Удельная проводимость — это проводимость, измеренная между противоположными сторонами куба вещества со стороной 1 см. Единицей данного типа измерений является Сименс/см. При измерении проводимости воды чаще используются более точные мкС/см (микросименс) и мС/см (миллисименс) .
Соответствующие единицы измерения сопротивления (или удельного сопротивления) — Ом/см, МегаОм/см и килоОм/см. При измерении сверхчистой воды чаще используют МегаОм/см, так как это дает более точные результаты. Сопротивление менее чистой воды, как например, водопроводной, измеряют в килоОм/см.
4) Общее сопротивление при последовательном соединении равно сумме сопротивлений Rсумм=R1+R2+R3…
Ток через все сопротивления протекает один ( I ). Поэтому ток вычисляешь как Отношение напряжения источника U к Rсумм.
I=U/Rсумм
Мощность
P=U*I или P=I*I*R (так как U=I*R).
тогда,
P1=I*I*R1
P2=I*I*R2
P3=I*I*R3
5) мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:
P=P1+P2
При параллельном соединении каждая лампа подсоединяется на своё номинальное напряжение 220 В. при этом в каждой лампе появляется свой номинальный ток, обеспечивающий заданное свечение в соответствии с номинальной мощностью. мощность зависит от сопротивления нити накаливания. чем больше сопротивление нити, тем меньше ток и соответственно меньше номинальная мощность.
при последовательном соединении ток идёт один и тот же в каждой лампе. а напряжение распределяется в зависимости от доли сопротивления каждой лампы по отношению к сопротивлению всей цепи.
для цепи из двух ламп общее напряжение делится.
напряжение на лампе 40 Вт будет 220Х60:(40+60)=132; В.
напряжение на лампе 60 Вт будет 220Х40:(40+60)=80; В.
ФИЗИКА: ЗАДАЧИ на Последовательное соединение
Задачи на Последовательное соединение
проводников с решениями
Формулы, используемые на уроках «Задачи на Последовательное соединение проводников»
Название величины | Обозначение | Единица измерения | Формула |
Сила тока | I | А | I = U / R |
Напряжение | U | В | U = IR |
Сопротивление | R | Ом | R = U/I |
Сила тока на участке цепи | I | A | I = I1 = I2 |
Напряжение на концах участка | U | B | U = U1 + U2 |
Сопротивление участка цепи | R | Ом | R = R1 + R2 |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Два проводника сопротивлением 2 Ом и 3 Ом соединены последовательно. Сила тока в цепи 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение.
Задача № 2. Два проводника сопротивлением 20 Ом и 30 Ом соединены последовательно. Напряжение на концах первого проводника 12 В. Определить сопротивление цепи, силу тока в цепи, напряжение на втором проводнике и полное напряжение.
Задача № 3. Два резистора соединены последовательно. Сопротивление первого 12 Ом, полное сопротивление 30 Ом. Сила тока в цепи 2 А. Определить сопротивление первого резистора, напряжение на каждом проводнике и полное напряжение.
Задача № 4. В каких пределах можно менять сопротивление в цепи, если сопротивление реостата R имеет пределы 0…10 Ом? Сопротивление резистора R1 равно 20 Ом.
Ответ: Сопротивления R и R1 соединены параллельны. Сопротивление цепи будет изменяться в пределах от 20 до 30 Ом.
Задача № 5. Последовательно с нитью накала радиолампы сопротивлением 3,9 Ом включен резистор, сопротивление которого 2,41 Ом. Определите их общее сопротивление.
Задача № 6. Общее сопротивление последовательно включенных двух ламп сопротивлением 15 Ом каждая и реостата равно 54 Ом. Определите сопротивление реостата.
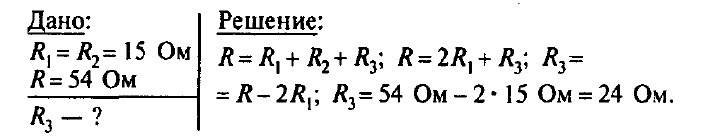
Задача № 7. Два резистора сопротивлением 8 и 1 кОм соединены последовательно. Определите показание вольтметра, подключенного между точками А и С, если сила тока в цепи равна 3 мА. Что будет показывать вольтметр, подключенный между точками А и В, В и С?
Задача № 8. В цепь включены последовательно три проводника сопротивлениями: R1=5 Ом, R2=6 Ом, R3= 12 Ом. Какую силу тока показывает амперметр и каково напряжение между точками А и В, если показание вольтметра 1,2 В?
Задача № 9. Последовательно с электрической лампой включен реостат. Начертите схему цепи и определите сопротивление реостата и лампы, если напряжение на зажимах цепи 12 В. Вольтметр, подключенный к реостату, показывает 8 В. Сила тока в цепи 80 мА.
Краткая теория для решения Задачи на Последовательное соединение проводников.
Это конспект по теме «ЗАДАЧИ на Последовательное соединение проводников». Выберите дальнейшие действия:
Лекция по основам электротехники «Соединение резисторов. Закон Ома»
ТЕМА: Соединения резисторов. Законы Ома.
План
Последовательное соединение резисторов.
Параллельное соединение резисторов.
Смешанное соединение резисторов.
Законы Ома.
Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.
Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов.
Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.
Рисунок 1. Соединение резисторов
Последовательное соединение резисторов
Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).
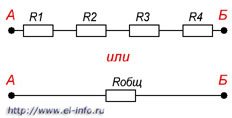
Рисунок 2. Последовательное соединение резисторов
То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток.
Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.
Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает.
Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле:
Rобщ = R1 + R2 + R3+…+ Rn.
Где можно наблюдать последовательное соединение сопротивлений? — Да допустим в той же самой новогодней гирлянде. Каждая лампочка в новогодней гирлянде, как правило, обладает одинаковым сопротивлением. При последовательном соединении, если перегорает одна лампочка, то в электрической цепи будет наблюдаться разрыв и соответственно, в этом случае, новогодняя гирлянда не будет гореть полностью.
Параллельное соединение резисторов
Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).
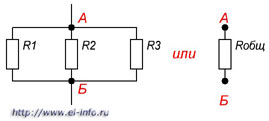
Рисунок 3. Параллельное соединение резисторов
При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением:
1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn
Следует отметить, что здесь действует правило «меньше — меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.
Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле:
Rобщ= R1*R2/R1+R2
Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них.
В этой теме можно привести множество примеров из нашей повседневной жизни, касающихся параллельного подключения сопротивлений. Параллельное соединение одинаковых сопротивлений — это наглядный пример подключения люстры с n-ым количеством ламп и с одинаковым сопротивлением для каждой лампы \рис.1\.
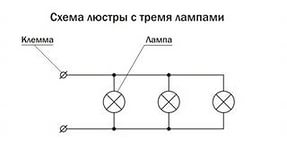
рис.1
Если допустим в люстре состоящей из нескольких ламп \с одинаковым сопротивлением\ перегорела одна лампа и была произведена замена на лампочку другой мощности, — в этом случае, подключение люстры будет выглядеть как параллельное подключение с разным сопротивлением.
Какие еще можно привести примеры из практики — при параллельном подключении сопротивлений? Допустим, Вы подключили в своей квартире через удлинитель три бытовых электроприбора:
электроплиту;
стиральную машину;
телевизор.
Характер такого подключения примет значение как для параллельного подключения сопротивлений, разных по величине. То-есть, для каждого электроприбора, сопротивление имеет свое значение.
Смешанное соединение резисторов
Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением.
На рисунке 4 показан простейший пример смешанного соединения резисторов.
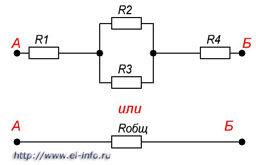
Рисунок 4. Смешанное соединение резисторов
На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.
Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:
1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
4. Рассчитывают сопротивления полученной схемы.
Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.
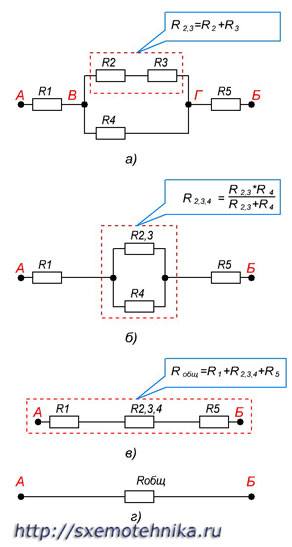
Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов
Закон Ома для участка цепи
Скажу сразу, что закон Ома – основной закон электротехники и применяется для расчета таких величин, как: ток, напряжение и сопротивление в цепи.
Рассмотрим электрическую цепь, приведенную на рисунке 1.
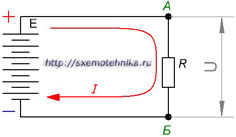
Рисунок 1. Простейшая цепь, поясняющея закон Ома
Мы знаем, что электрический ток, то есть поток электронов, возникает в цепи между двумя точками (на рисунке А и Б) с разными потенциалами. Тогда следует считать, что чем больше разность потенциалов, тем большее количество электронов переместятся из точки с низким потенциалом (Б) в точку с высоким потенциалом (А). Количественно ток выражается суммой зарядов прошедших через заданную точку и увеличение разности потенциалов, то есть приложенного напряжения к резистору R, приведет к увеличению тока через резистор.
С другой стороны сопротивление резистора противодействует электрическому току. Тогда следует сказать, что чем больше сопротивление резистора, тем меньше будет средняя скорость электронов в цепи, а это ведет к уменьшению тока через резистор.
Совокупность двух этих зависимостей (тока от напряжения и сопротивления) известна как закон Ома для участка цепи и записывается в следующем виде:
I=U/R
Это выражение читается следующим образом: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Следует знать что:
I – величина тока, протекающего через участок цепи;
U – величина приложенного напряжения к участку цепи;
R – величина сопротивления рассматриваемого участка цепи.
При помощи закона Ома для участка цепи можно вычислить приложенное напряжение к участку цепи (рисунок 1), либо напряжение на входных зажимах цепи (рисунок 2).
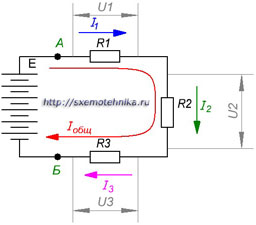
Рисунок 2. Последовательная цепь, поясняющая расчет напряжения на зажимах цепи.
В этом случае формула (1) примет следующий вид:
U = I *R
Но при этом необходимо знать ток и сопротивление участка цепи.
Третий вариант закона Ома для участка цепи, позволяющий рассчитать сопротивление участка цепи по известным значениям тока и напряжения имеет следующий вид:
R =U/I
Как запомнить закон Ома: маленькая хитрость!
Для того, что бы быстро переводить соотношение, которое называется закон Ома, не путаться, когда необходимо делить, а когда умножать входящие в формулу закона Ома величины, поступайте следующим образом. Напишите на листе бумаги величины, которые входят в закон Ома, так как показано на рисунке 3.
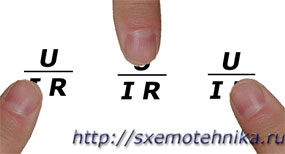
Рисунок 3. Как запомнить закон Ома.
Теперь закройте пальцем, ту величину, которую необходимо найти. Тогда относительное расположение оставшихся незакрытыми величин подскажет, какое действие необходимо совершить для вычисления неизвестной величины.
Закон Ома для полной цепи определяет значение тока в реальной цепи, который зависит не только от сопротивления нагрузки, но и от сопротивления самого источника тока. Другое название этого закона — закон Ома для замкнутой цепи. Рассмотрим смысл закона Ома для полной цепи более подробно.
Потребители электрического тока (например, электрические лампы) вместе с источником тока образуют замкнутую электрическую цепь. На рисунке 1 показана замкнутая электрическая цепь, состоящая из автомобильного аккумулятора и лампочки.
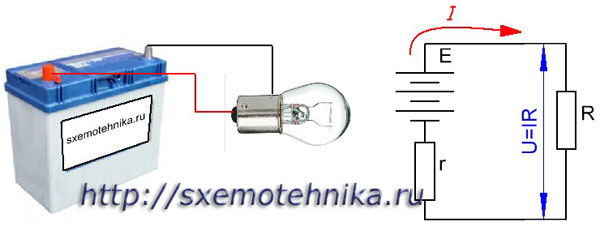
Рисунок 1. Замкнутая цепь, поясняющея закон Ома для полной цепи.
Ток, проходящий через лампочку, проходит также и через источник тока. Следовательно, проходя по цепи, ток кроме сопротивления проводника встретит еще и то сопротивление, которое ему будет оказывать сам источник тока (сопротивление электролита между пластинами и сопротивление пограничных слоев электролита и пластин). Следовательно, общее сопротивление замкнутой цепи будет складываться из сопротивления лампочки и сопротивления источника тока.
Сопротивление нагрузки, присоединенной к источнику тока, принято называть внешним сопротивлением, а сопротивление самого источника тока — внутренним сопротивлением. Внутреннее сопротивление обозначается буквой r.
Если по цепи, изображенной на рисунке 1, протекает ток I, то для поддержания этого тока во внешней цепи согласно закону Ома между ее концами должна существовать разность потенциалов, равная I*R. Но этот же ток I протекает и по внутренней цепи. Следовательно, для поддержания тока во внутренней цепи, также необходимо существование разности потенциалов между концами сопротивления r. Эта разность потенциалов па закону Ома должна быть равна I*r.
Поэтому для поддержания тока в цепи электродвижущая сила (ЭДС) аккумулятора должна иметь величину:
E=I*r+I*R
Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:
E=I(r+R)
или
I=E/(r+R)
Две последние формулы выражают закона Ома для полной цепи.
Закон Ома для полной замкнутой цепи формулируется так: сила тока в замкнутой цепи прямо пропорциональна ЭДС в цепи и обратно пропорциональна общему сопротивлению цепи.
Под общим сопротивлением подразумевается сумма внешнего и внутреннего сопротивлений.
Физика для науки и техники II
из отдела академических технологий на Vimeo.
Пример — последовательное и параллельное соединение сопротивлений
Хорошо. Давайте рассмотрим пример, связанный с подключением сопротивлений. Предположим, у нас есть несколько сопротивлений, которые соединены таким образом. Сюда подключается R 1, R 2, а здесь подключается R 3. Здесь R, 4, а здесь сопротивление R 6, которое в конечном итоге подключено к сопротивлению R 7 здесь.Затем, допустим, мы применяем разность потенциалов ко всей комбинации, соединив концы этих соединений с выводами электродвижущей силы, которая генерирует ε вольт.
Давайте посмотрим, вопрос в том, какая мощность рассеивается через каждое сопротивление? Теперь, чтобы иметь возможность определить мощность, если вы помните, что она была равна рассеиваемой мощности — давайте использовать индекс рассеиваемой мощности — была равна i в 2 раза больше сопротивления R . Квадрат тока, проходящего через сопротивление, умноженный на значение сопротивления этого резистора, даст нам, сколько энергии преобразуется в тепло за каждую секунду.
Ну, очевидно, что числовые значения наших сопротивлений даны. Допустим, R 1 равно 2 Ом, R 2 равно 6 Ом и R 3 равно 12 Ом. R 4 равно 4 Ом, R 6 равно 10 Ом и, наконец, R 7 равно 3 Ом. Итак, зная числовые значения этих сопротивлений, поэтому, если мы сможем определить количество тока, протекающего через каждый резистор, то мы сможем определить мощность, рассеиваемую через каждый резистор.
Хорошо. Чтобы сделать это, сначала мы попытаемся определить эквивалентное сопротивление цепи, а затем проследим его обратно, чтобы определить ток, протекающий через каждое сопротивление. Если мы вспомним закон Ома, который был просто равен, из определения сопротивления, и это было равно отношению разности потенциалов между двумя точками к величине тока, проходящего через эти точки.
Когда мы смотрим на этот закон, мы видим, что для определения любой из этих величин, напряжения, тока, сопротивления, нам необходимо знать две другие из этих величин.Итак, мы собираемся попытаться определить эти величины, поскольку сопротивления даны, мы попытаемся определить ток, и, чтобы иметь возможность сделать это, нам нужно определить разность потенциалов на каждом резисторе. Таким образом, применяя свойства, связанные с параллельным и последовательным подключением, мы определим эти величины, следовательно, в конечном итоге ток через каждое сопротивление, и как только мы это определим, мы сможем вычислить рассеиваемую мощность.
Хорошо.Если мы посмотрим на нашу схему, мы увидим, что сначала эти три сопротивления R 2, R 3 и R 4 соединены параллельно. Сначала отметим точки соединения. Это точки, в которых мы заканчиваем с разными ветвями для протекания тока. Когда мы смотрим здесь, на схему, мы видим, что у нас есть точка соединения здесь, еще одна здесь, еще одна там и еще одна здесь. Таким образом, мы можем легко увидеть, что эти три сопротивления подключены параллельно.
Другими словами, я могу перерисовать эту схему в таком виде. Это R 1, и теперь из этой точки соединения я могу перерисовать его как R 2, R 3 и R 4, которые связаны через эти точки соединения, которые я также могу нарисовать таким образом. . У нас есть R 6, а затем у нас есть этот сегмент провода, просто провод, и мы подключаем его параллельно, который в конечном итоге таким образом подключается к R 7. Следовательно, ток можно перерисовать в этой форме, чтобы четко видеть соединения, и это эквивалентно нашей исходной схеме.
Итак, мы перерисовываем схему, чтобы четко видеть соединения, и мы можем легко увидеть, что эти три сопротивления теперь подключены параллельно. Поэтому сначала мы заменим их эквивалентами. По мере того, как мы это делаем, мы перерисовываем схему, и вот электродвижущая сила, сопротивление R 1. Мы собираемся заменить это на, назовем это как R eq 1 и давайте просто сконцентрируемся. об этом параллельном подключении здесь.Когда мы смотрим на этот сегмент схемы, следующий за током, выходящим из источника питания, который будет разделен на три ветви, проходя через R 2, R 3 и R 4, и он присоединится, и тогда снова будет и .
Теперь, когда ток доходит до этой точки, заряды будут видеть два доступных пути. Один из них — это, а другой — это. Таким образом, когда они попытаются пройти через эти две ветви, они увидят, что вдоль этой ветви есть сопротивление R 6, тогда как вдоль этой ветви сопротивления нет.Поэтому, естественно, заряды выберут путь, по которому нет сопротивления. Другими словами, они будут проходить прямо по этому пути, и никакой ток не пройдет через сопротивление R 6. Следовательно, как эквивалент этого сегмента здесь, мы можем просто записать или заменить его простым проводом без сопротивления на все, а затем мы получим следующее сопротивление, которое будет последовательно подключено к этому сопротивлению R 7. Таким образом, схема будет приведена к этой упрощенной форме.
Теперь давайте продолжим и вычислим R eq 1, поскольку это эквивалент параллельного соединения R 2, R 3, R 4. 1 больше R eq 1 будет равно 1 более R 2 плюс 1 более R 3 плюс 1 более R 4, исходя из свойств параллельного соединения сопротивлений. Двигаясь дальше, 1 больше R eq 1 будет равно, R 2 будет 6 Ом, 1 больше 6, плюс R 3 будет 12 Ом, 1 больше 12, плюс R 4 будет 4 Ом, так что здесь будет 1 на 4.Теперь, если у вас есть общие знаменатели, то мы должны умножить это соотношение, числитель и знаменатель, на 2, это только на 1, а это на 3, потому что у них будет общий знаменатель 12.
Двигаясь дальше, 1 больше R экв 1 будет равно 2 плюс 1 плюс 3 больше 12, что будет равно 6 больше 12, и будет равно 1 больше R экв 1 Чтобы получить R eq 1, мы возьмем обратное значение, которое будет равно 12 на 6, и это даст нам 2 Ом.Следовательно, значение R экв 1 будет равно 2 Ом. Другими словами, если мы просто вытащим этот параллельный блок и разместим здесь сопротивление 2 Ом, он будет выполнять ту же работу, что и эти три при параллельном подключении.
Теперь мы сделаем еще один шаг и найдем эквивалент этих трех последовательно соединенных сопротивлений. Прежде чем мы это сделаем, позвольте мне показать вам также, почему у нас не будет тока, протекающего через R 6. Опять же, если мы просто подумаем об этом как о параллельном соединении сопротивлений и попытаемся вычислить эквивалентное сопротивление этого устройства — давайте назовите его как 1 по сравнению с R eq 2 — эквивалентное сопротивление этого устройства здесь будет равно 1 по сравнению с R 6 плюс 1 по сравнению с сопротивлением этого сегмента.Мы собираемся предположить, что сопротивление провода намного, намного меньше, чем сопротивление этого резистора, поэтому мы предположим, что оно почти 0. Другими словами, у нас будет 1 больше 0 или 1 больше очень , очень маленькое число, поэтому, если мы разделим 1 на очень маленькое число, которое стремится к бесконечности, то получится 1 на 6 плюс бесконечность. Конечно, тогда весь этот член уйдет в бесконечность, потому что не имеет значения, прибавляем ли мы число к очень большому числу или вычитаем его.
Отсюда, если мы решим для R eq 2, это будет обратным этому. Другими словами, число, деленное на бесконечность, будет равно 0, потому что, если мы разделим 1 на очень большое число, мы получим очень маленькое число. Следовательно, эквивалентное сопротивление всего этого блока будет равно 0. Это означает, что через это сопротивление не будет протекать ток. Весь ток предпочтет проходить по гораздо менее резистивному пути, другими словами, почти нулевому резистивному пути.
Хорошо. Теперь, когда мы выяснили, что весь ток проходит через эту ветвь, мы можем легко вычислить эквивалентное сопротивление всех этих трех сопротивлений при последовательном соединении. Это будет равно эквивалентному сопротивлению всей цепи. Приведем также числовое значение этой электродвижущей силы. Предположим, что эта величина также указана и равна 7 вольт. Таким образом, здесь мы можем вычислить эквивалентное сопротивление всей цепи, которое будет равно эквиваленту всех этих трех сопротивлений, а именно: R 1 плюс R экв 1 плюс R 7.Подставив числовые значения, эквивалентное сопротивление окажется равным R 1 2 Ом, плюс R eq 1 также 2 Ом, плюс R 7 3 Ом, и в сумме будет 7. Ом. Следовательно, эквивалентное сопротивление всей цепи составляет 7 Ом.
Теперь, когда мы определим эквивалентное сопротивление, мы сможем определить, какой ток будет протекать через эту цепь, другими словами, сколько тока потребляется от электродвижущей силы в 7 вольт.Для этого мы применим закон Ома, поскольку мы знаем, что R eq будет равно разности потенциалов на резисторе, которая будет равна разности потенциалов, подаваемой источником питания, и что составляет ε вольт, деленное на величину тока, протекающего через этот резистор, и это составляет i . Решив для i , у нас будет ε вместо R eq . ε составляет 7 вольт, а R eq — 7 Ом, поэтому это будет равно 1 ампер.Следовательно, через эту цепь будет протекать ток 1 ампер.
Как только мы это определили, мы проследим наши цепи в обратном направлении, поэтому мы перейдем к этой цепи. Теперь, когда мы идем туда, мы знаем, что, поскольку R eq выполняет работу, которую эти три сопротивления выполняют в цепи, и источник питания такой же, поэтому ток и будет протекать через эта схема. Поскольку все эти три сопротивления соединены последовательно, то ток, протекающий через каждое из них, будет одним и тем же током, который равен и , или, другими словами, 1 ампер.
Теперь мы знаем, что ток 1 А протекает через R 1, через R eq 1 и через R 7. Таким образом, мы можем легко вычислить мощность, рассеиваемую через каждое из этих сопротивлений. Что ж, давайте назовем первого как P1. P1 будет равно i 12 умножить на R 1, но i 12 будет равно i , так что это будет i 2 R 1. i 2 равно 1 A. умноженное на R 1 и R 1 составило 2 Ом, следовательно, это будет равно 2 Вт мощности, рассеиваемой через сопротивление R 1.
Точно так же мы можем рассчитать мощность, рассеиваемую через R 7, поскольку мы знаем ток, протекающий через R 7. Это будет равно i 72 умножить на R 7, но i 7 равно и . i 2 умножить на R 7, и это снова будет равно 1 А в квадрате, умноженном на R 7, и R 7 было 3 Ом, что даст нам 3 Вт мощности, рассеиваемой как ток. протекает через сопротивление R 7.
Хорошо. Мы определили мощность, рассеиваемую через два сопротивления. Теперь мы пойдем дальше, проследим его до первого контура. Мы видим, что R eq 1 является эквивалентом этих трех сопротивлений, и они подключены параллельно. Мы знаем, что при параллельном подключении разность потенциалов во всей комбинации равна разности потенциалов на каждом резисторе, подключенном параллельно. Следовательно, если мы найдем разность потенциалов на R eq 1, давайте назовем это одним V eq 1, это будет такая же разность потенциалов на каждом резисторе при параллельном подключении.Таким образом, все эти три сопротивления будут иметь одинаковую разность потенциалов В экв 1.
Это легко посчитать. Поскольку мы знаем сопротивление, мы знаем и ток. Тогда мы знаем две из этих величин, сопротивление и ток, поэтому мы можем легко вычислить разность потенциалов. В этом случае V eq 1 будет равно i умножить на R eq 1, что будет равно 1 A умножить на R eq 1, позвольте мне рассчитать это, составляет +2 Ом.Следовательно, 1 умноженное на 2 равно 2 вольтам — это разность потенциалов на сопротивлении R eq 1. Теперь, когда мы проследим его до исходной схемы здесь, то для всех R 2, R 3 и R 4 разность потенциалов между их концами будет одинаковой, и они будут быть равно В экв 1.
В этом случае теперь мы знаем разность потенциалов и сопротивление. Таким образом, мы можем вычислить, сколько тока проходит через каждое из этих сопротивлений, потому что, как вы можете видеть, как только ток и достигает этой точки соединения, некоторая часть проходит через R 2.Назовем его, например, i 2. Некоторая часть пройдет через R 3 как i 3, а затем оставшаяся часть пройдет через R 4 как i 4. Таким образом, зная разность потенциалов, а также значение сопротивления, мы можем вычислить i 2, i 3 и i 4.
Опять же, вспоминая закон Ома, ток будет равен В по R , поэтому i 2 будет равен В 2 по R 2, но В 2 будет равно V eq 1, и подставив числовые значения, V eq 1 составляет 2 вольта, разделенных на R 2, и числовое значение R 2 составляет 6 Ом, и это даст us 1 более 3 ампер.
i 3 будет равно V 3 по R 3, что будет равно V eq 1 по R 3, потому что разность потенциалов на R 3 равна до V eq 1. Опять же, V eq 1 составляет 2 вольта, а R 3 — 12 Ом. Это будет равно 1 на 6 ампер.
Наконец, i 4 будет равно V 4 по сравнению с R 4, что будет равно V eq 1 по R 4.Это даст нам 2 вольта, разделенные на R 4, и R 4 будет равно 4 Ом. Это даст нам от 1 до 2 ампер. Итак, это токи, протекающие через R 2, R 3 и R 4.
Зная эти значения тока, мы можем вычислить мощность, рассеиваемую через эти резисторы, и поэтому P 2 будет равно i 22 раза R 2 более 32 раз R 2 и R 2 было 6 Ом. , который будет равен 1 в 9 умноженном на 6.Опять же, мы можем упростить это как 2 и 3, поэтому ответ будет 2 на 3 Вт. Это количество мощности, рассеиваемой через сопротивление R 2.
Точно так же P 3 будет равно i 3 в квадрате R 3 и i 3 будет 1 на 6, поэтому 1 на 6 умножить на R 3, и это будет 12 Ом, равняется 1 на 36 умножить на 12. Опять же, мы можем сделать здесь упрощение, которое даст нам всего 1 на 3 Вт.Наконец, мощность, рассеиваемая через R 4, будет равна i 42, умноженным на R 4, и i 4 была равна 1 на 2 ампера, поэтому возьмем квадрат, умноженный на R 4. 4 Ом, что будет равно 1 в 4 умножить на 4, и это даст нам просто 1 ватт.
Таким образом, при выполнении этих вычислений мы определили, сколько мощности рассеивается через каждое из этих сопротивлений. Давайте посчитаем общую рассеиваемую мощность.Он будет равен сумме мощности, рассеиваемой через каждое сопротивление, поэтому P 1 плюс P 2 плюс P 3 плюс P 4 плюс P 5 плюс P 6 плюс P 7. То есть через P 1 мы нашли 2 Вт, плюс через P 2, через 2 более 3 Вт, через P 3, 1 более 3 Вт и через P 4 мы нашли 1 ватт, и через P 5 я фактически пропустил P 5 и обозначил это как R 6, поэтому давайте удалим P 5 из наших уравнений.Оказалось, что я пропустил один из них численно. Ладно.
Через P 6 мы обнаружили, что ток не течет через R 6, следовательно, нет рассеивания мощности, так как i составляет от 0 до P 6, и это было 0. Через P 7 мы имеем обнаружено, что рассеивается мощность 3 Вт. Таким образом, общая рассеиваемая мощность будет равна, здесь у нас будет 2 больше 3 плюс 1 больше 3, даст нам 3 больше 3, так что будет 1. 1 плюс 1 равно 2, плюс 3 равно 5 плюс 2 — это 7 Вт.Рассеивается 7 Вт мощности. Другими словами, это количество энергии каждую секунду преобразуется в тепло.
Давайте также посчитаем подводимую мощность. Подаваемая мощность, по определению, равна величине тока, потребляемого от источника питания, а это –, умноженное на разность потенциалов между выводами источника питания, и это составляет ε вольт. Как вы помните, мы обнаружили, что ток, потребляемый электродвижущей силой, составлял 1 ампер, а разность потенциалов между выводами источника питания составляла 7 вольт.Таким образом, это будет равно 7 Вт.
Это подтверждает правильность наших расчетов, и когда мы сравниваем рассеиваемую мощность с подаваемой мощностью, мы видим, что эти две величины равны друг другу. Это хорошая контрольная точка, потому что мы знаем из принципа сохранения энергии, что эти две величины должны быть равны друг другу. Если они не были равны, мы должны были вернуться и проверить наши численные расчеты и посмотреть, где была ошибка. Следовательно, это хорошая контрольная точка, когда вы имеете дело с подобными проблемами цепи.
.Серия— Параллельные схемы | Кафедра химической инженерии и биотехнологии
Введение
В этом разделе мы рассмотрим, как анализировать схемы, содержащие резисторы, включенные последовательно и параллельно.
Определение и анализ параллельных цепей
На рисунке ниже показана базовая схема, содержащая последовательно-параллельную комбинацию резисторов. Сопротивление от точки A, к точке B составляет R1 , сопротивление от B до C представляет собой комбинацию параллельных R2 и R3 .Общее сопротивление цепи (от точки A, до C, ) составляет последовательный резистор R1 в сочетании с параллельными компонентами.
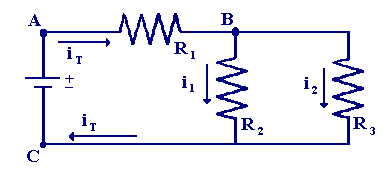
Более сложный пример последовательно-параллельной схемы резистора показан ниже
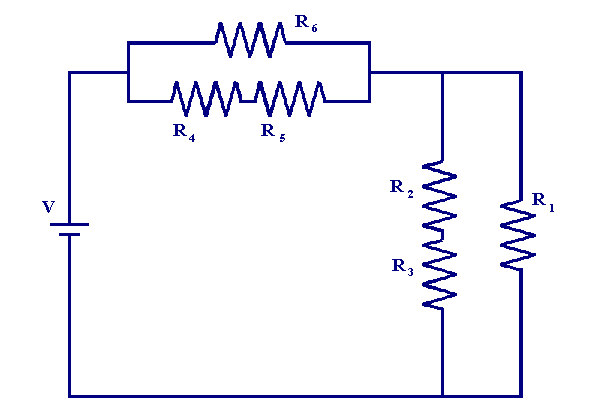
здесь резистор R6 параллелен резисторам R4 и R5 . Также резисторы R3 , R2 и R1 образуют параллельную комбинацию.Также ясно, что две параллельные комбинации идут последовательно друг с другом. Чтобы вычислить полное сопротивление последовательно-параллельной цепи, мы используем методы, разработанные в двух предыдущих разделах. Чтобы проиллюстрировать основные процедуры анализа, мы воспользуемся парой примеров. Сначала рассмотрим схему ниже
и хотите рассчитать полное сопротивление цепи. Очевидно, что ток будет проходить через резистор 80 Ом перед разделением на две составляющие в параллельной комбинации, в точке A, параллельные токи ответвления будут рекомбинировать и течь к положительному выводу.Чтобы рассчитать полное сопротивление цепи, сначала мы вычисляем эффективное сопротивление параллельной комбинации, используя метод из предыдущего раздела.
| R Параллельно = 1 / (1/100 + 1/50) = 33,3 Ом |
Используя этот результат, мы можем перерисовать приведенную выше схему следующим образом:
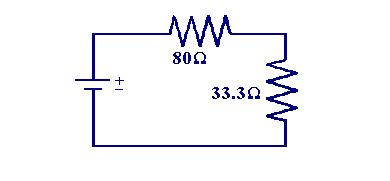
Теперь можно рассчитать полное сопротивление цепи, суммируя два последовательных сопротивления.
| РТ = 80 + 33.3 = 113,3 Ом |
Далее мы рассмотрим чуть более сложную схему ниже.
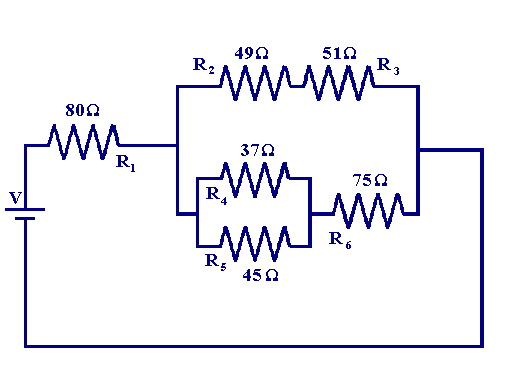
Используя ту же процедуру, что и выше, мы сначала вычисляем эквивалентное сопротивление каждой из параллельных комбинаций, чтобы получить эффективное сопротивление последовательно с R1 . Начнем с резисторов R4 и R5
| R5-4 = 1 / (1/37 + 1/45) = 20.3 Ом |
Теперь прорабатываем сопротивление в каждой из параллельных ветвей. Для верхней ветви сопротивление равно сумме резисторов R2 и R3
.| R3-2 = 49 + 51 = 100 Ом |
для нижнего ответвления он равен сумме резисторов R6 и R5-4
| R6-5-4 = 75 + 20.3 = 95,3 Ом |
Теперь у нас осталась схема, эквивалентная рисунку ниже
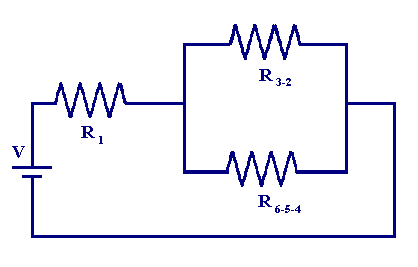
Итак, все, что осталось, это вычислить эффективное сопротивление параллельной комбинации R6-5-4 и R3-2
| R6-5-4-3-2 = 1 / (1/100 + 1 / 95,3) = 48,8 Ом |
Таким образом, полное сопротивление цепи равно
| RT = 80 + 48.8 = 128,8 Ом |
Системный подход, который мы представили выше, может быть использован для расчета эффективного сопротивления любой конкретной цепи. Однако, если мы знаем характеристики напряжения или тока схемы, мы можем использовать тот же подход для вычисления неизвестных. В следующем разделе анализа цепей переменного тока мы рассмотрим цепи, содержащие резисторы, конденсаторы и катушки индуктивности, и будем использовать очень похожую стратегию для анализа отклика цепей этих систем.
.