Репетитор-онлайн — подготовка к ЦТ
Пример 12. Батарею с ЭДС 20 В и внутренним сопротивлением 20 мОм необходимо получить соединением одинаковых гальванических элементов. Каждый элемент имеет ЭДС 2,0 В и внутреннее сопротивление 0,20 Ом. Сколько понадобится гальванических элементов с указанными характеристиками?
Решение. Для получения батареи с заданными значениями ЭДС и внутреннего сопротивления необходимо использовать как последовательное, так и параллельное соединение гальванических элементов.
1. Последовательное соединение блоков, состоящих из параллельно соединенных источников, внутреннее сопротивление каждого их которых r 1, а ЭДС — ℰ1, в количестве n 1 штук показано на рисунке.
ЭДС всей батареи, составленной из указанных блоков, определяется формулой
ℰ2 = n 1ℰ1
и должно составлять ℰ2 = 20 В.
Внутреннее сопротивление всей батареи, составленной из указанных блоков, определяется произведением
r 2 = n 1r 1
и должно составлять r
2 = 20 мОм.
2. Параллельное соединение гальванических элементов с заданными в условии характеристиками (r 0 = 0,20 Ом и ℰ0 = 2,0 В) в пределах одного блока в количестве n 2 штук показано на рисунке.
Внутреннее сопротивление блока определяется отношением
r1=r0n2,
а ЭДС блока совпадает с ЭДС одного элемента:
ℰ1 = ℰ0.
Записанные уравнения образуют систему, позволяющую определить количество элементов в каждом блоке n
ℰ2=n1ℰ1,r2=n1r1,r1=r0n2,ℰ1=ℰ0.}
Для решения системы подставим последнее уравнение в первое и найдем n 1:
n1=ℰ2ℰ0=202,0=10.
Третье уравнение системы подставим во второе и найдем n 2:
n2=r0n1r2=0,20⋅1020⋅10−3=100.
Общее количество гальванических элементов, необходимых для составления батареи с указанными характеристиками, равно произведению
N = n
1n
2 = 10 ⋅ 100 = 1000 штук.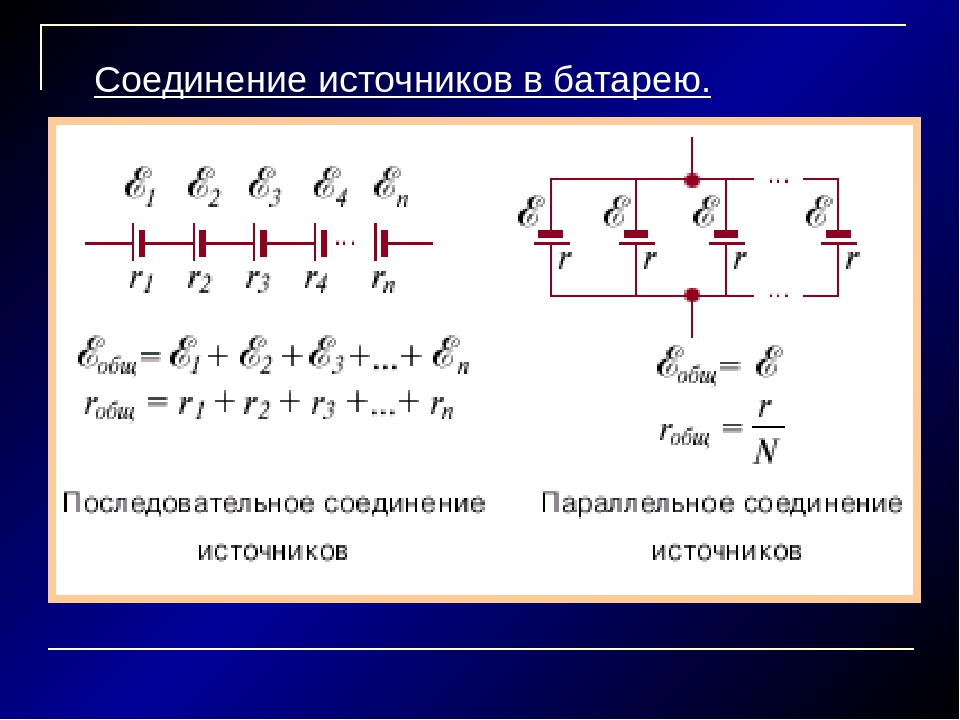
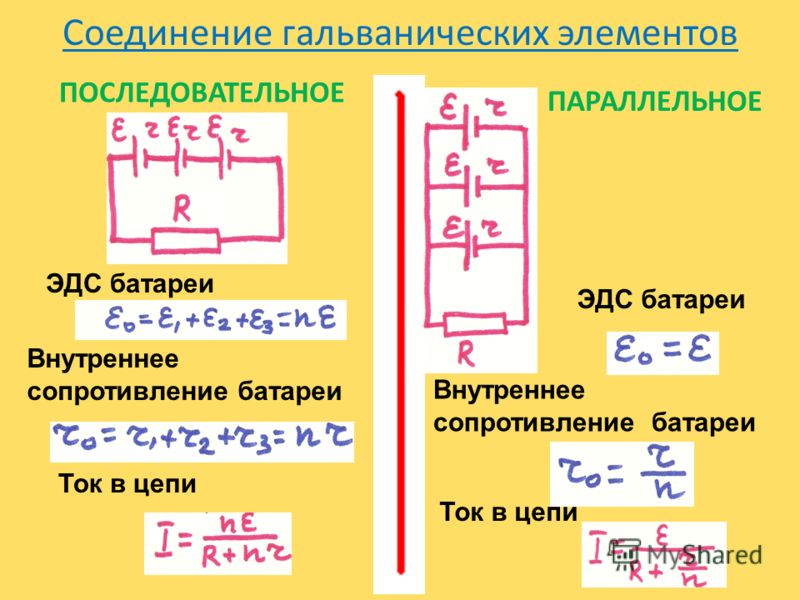
1. При последовательном соединении источников:
εпосл = ε·n,
rпосл = r·n,
где ε – ЭДС одного источника,
r – сопротивление одного источника,
n – число источников.
2. При параллельном соединении n одинаковых источников:
εпар = ε,
Элементы электрических цепей и сами электрические цепи изображают схематически следующим образом:
– внешнее сопротивление проводника (участок электрической цепи без ЭДС) | |
– амперметр и его включение в цепь; | |
– вольтметр и его включение в цепь; | |
– источник
тока (источник ЭДС) с внутренним
сопротивлением. | |
– последовательное соединение сопротивлений и источников тока. | |
– параллельное соединение сопротивлений и источников тока. | |
– полная электрическая цепь. |
Для решения задач по расчету электрических цепей используется закон Ома:
1. Закон Ома для участка цепи (без эдс):
или ,
где – удельная проводимость проводника,
Е – напряженность электрического поля в проводнике.
2. Закон Ома для полной цепи:
где R – внешнее сопротивление цепи,
r – внутреннее сопротивление источника тока,
R
+ r –
называется полным сопротивлением цепи.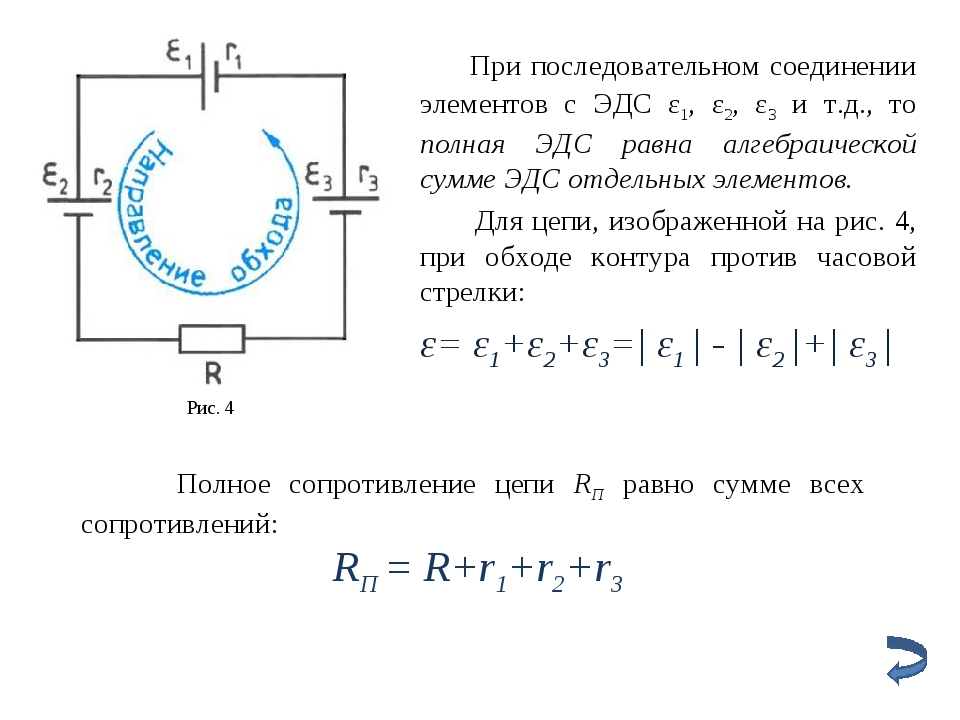
Следствия:
а) если R → 0, источник замкнут накоротко:
где Iкз – ток короткого замыкания;
б) если R → ∞, цепь разомкнута:
I = 0; U = ε,
т.е. ЭДС источника численно равна напряжению на его зажимах при разомкнутой внешней цепи.
Для расчетов полных электрических цепей полезно знать следующие величины:
а) полная мощность, развиваемая источником:
б) полезная мощность (выделяемая на внешнем сопротивлении):
в) мощность потерь: Pпотерь = Pu – Pn = I2·r;
г) КПД источника:
Электрический ток I, проходя по участку цепи без ЭДС с сопротивлением R, совершает работу А по перемещению электрических зарядов, которую можно рассчитать по формуле:
,
где U – напряжение на участке цепи,
t –
время пропускания тока.
Мощность N тока, согласно определения, равна:
При протекании тока по проводнику он нагревается и в нем выделяется количество теплоты Q, которое без учета потерь рассчитывается по закону Джоуля-Ленца:
Электрический ток – это проходящие через проводник электроны, несущие отрицательный заряд. Объем этого заряда или, иными словами, количество электричества характеризует силу тока. Мы знаем, что сила тока одинакова во всех местах цепи.
Электроны не могут исчезать или «спрыгивать» с проводов и нагрузки. Поэтому, силу тока мы можем измерить в любом местеэлектрической цепи. Однако, будет ли одинаковымдействие тока на разные участки этой цепи? Давайте разберемся.
Проходя
по проводам, ток лишь слегка их нагревает,
однако не совершает при этом большой
работы. Проходя же через спираль
электрической лампочки, ток не просто
сильно нагревает ее, он нагревает ее до
такой степени, что она, раскаляясь,
начинает светиться.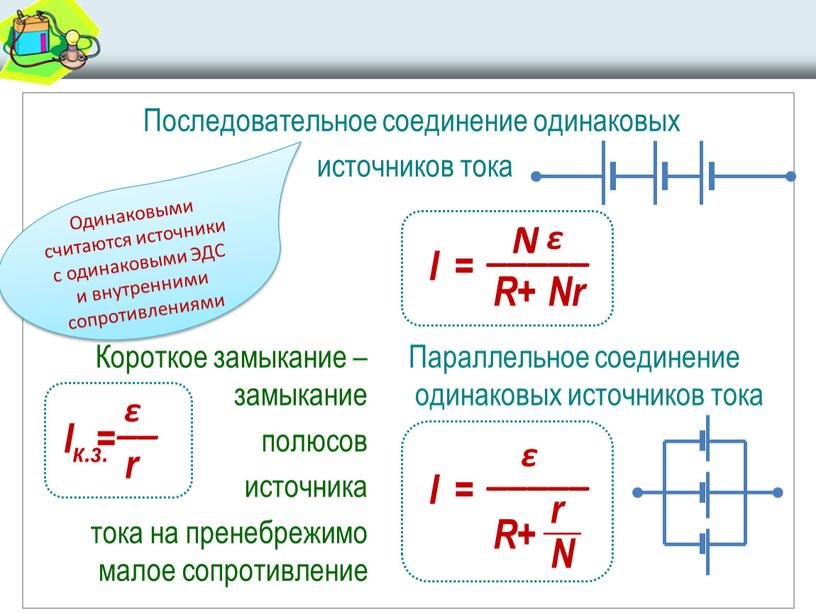
Определение электрического напряжения
То есть электрическое поле должно было «протащить» электроны через нагрузку, и энергия, которая при этом израсходовалась, характеризуется величиной, называемой электрическим напряжением. Эта же энергия потратилась на какое-то изменение состояния вещества нагрузки. Энергия, как мы знаем, не пропадает в никуда и не появляется из ниоткуда. Об этом гласит Закон сохранения энергии. То есть, если ток потратил энергию на прохождение через нагрузку, эту энергию приобрела нагрузка и, например, нагрелась.
То
есть, приходим к определению: напряжение
электрического тока – это величина,
показывающая, какую работу совершило
поле при перемещении заряда от одной
точки до другой. Напряжение в разных
участках цепи будет различным.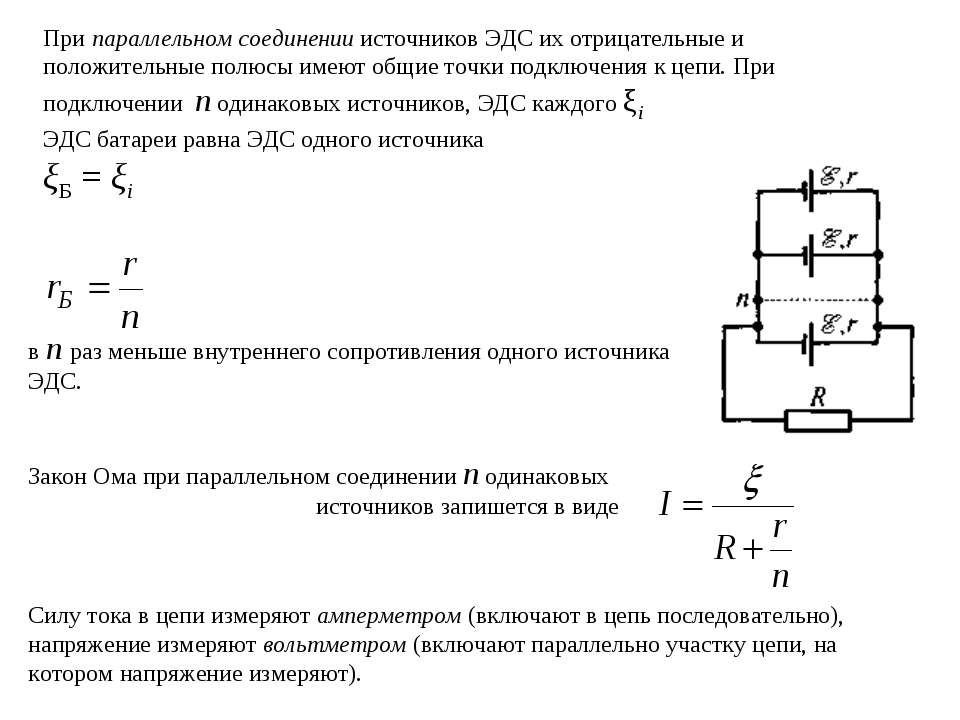 Напряжение
на участке пустого провода будет совсем
небольшим, а напряжение на участке с
какой-либо нагрузкой будет гораздо
большим, и зависеть величина напряжения
будет от величины работы, произведенной
током. Измеряют напряжение в вольтах
(1 В). Для определения напряжения существует
формула:
Напряжение
на участке пустого провода будет совсем
небольшим, а напряжение на участке с
какой-либо нагрузкой будет гораздо
большим, и зависеть величина напряжения
будет от величины работы, произведенной
током. Измеряют напряжение в вольтах
(1 В). Для определения напряжения существует
формула:
U=A/q,
где U — напряжение,A – работа, совершенная током по перемещению заряда q на некий участок цепи.
Напряжение на полюсах источника тока
Что касается напряжения на участке цепи – все понятно. А что же тогда означает напряжение на полюсах источника тока? Вданном случае это напряжение означает потенциальную величину энергии, которую может источник придать току. Это как давление воды в трубах. Эта величина энергии, которая будет израсходована, если к источнику подключить некую нагрузку. Поэтому, чем большее напряжение у источника тока, тем большую работу может совершить ток.
2. Последовательное соединение элементов
где ЕЭ– ЭДС;U– напряжение; rЭ– внутреннеесопротивление элемента |
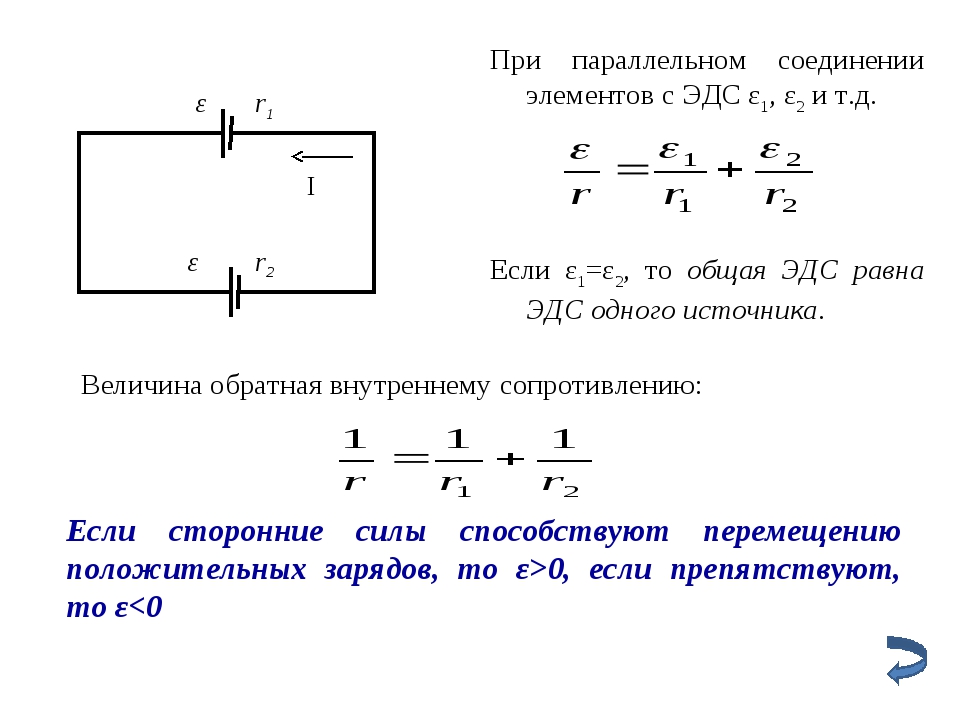
3. Параллельное соединение элементов
В тех случаях, когда номинальное напряжение приемника энергии равно напряжению одного элемента, а его ток больше допустимого разрядного тока одного элемента, применяют параллельное соединение элементов.
При параллельном соединении увеличиваются разрядный ток и емкость батареи. Все параллельно соединенные элементы должны иметь одинаковые ЭДС и внутренне сопротивление.
4. Смешанное соединение элементов
Смешанное соединение элементов применяется для увеличения напряжения и емкости батареи.
где n – число элементов одной ветви батареи, соединенных последовательно; m – число ветвей батареи. |
Нагревание проводов током
Закон Джоуля-Ленца
Количество электрический энергии, преобразуемой в проводнике в тепловую энергию, прямо пропорционально квадрату тока, эл. сопротивлению проводника и времени прохождения тока:
Количество тепла Q, выделяемого в проводнике, будет определяться по той же формуле:
При протекании тока в проводнике количество выделяемого тепла, а следовательно, и температура проводника увеличивается. При некоторой температуре количество тепла, выделяемого во внешнюю среду, и тепла, выделяемого проводником, уравновесят друг друга. Такая температура называется установившейся.
Нагрев проводов допускается до 65 – 800С. Ток, при котором нагревание достигает допустимой температуры, называетсяноминальным током.
Значения номинальных
токов для различных потребителей и
сечений даются в справочниках.
Короткое замыкание. Предохранители
Расчет проводов по допустимой потере напряжения:
Разница между напряжением в начале и в конце называется потерей напряжения. При заданномможно определить сечение провода:
Часто потери напряжения задают в процентах от , обозначаются буквой:
Регистр устанавливает нормы падения напряжения для судовой электросети:
1. силовая сеть и нагревательные приборы ;
2. осветительная сеть напряжением 110 В и выше ;
3. осветительная сеть напряжением 36 В и ниже ;
4. слаботочные сети и телефонные
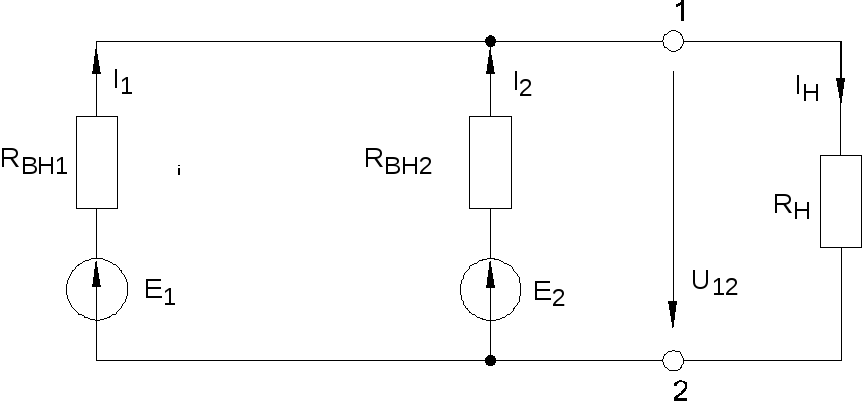
Электрическая цепь (неразветвленная) с несколькими источниками эдс
Если ЭДС источника
совпадают по направлению, то такое
включение называется согласным.
Если же ЭДС источника не совпадают по направлению, то такое включение называется встречным.
Если источники включены согласно, то результирующая ЭДС равна сумме ЭДС источника.
Если источники включены встречно, то ток в цепи будет направлен в сторону большей ЭДС. Допустим, тогда. Источник ЭДСпри встречном включении является потребителей электроэнергии.
Таким образом, источник электроэнергии может работать в режиме генератора (отдавая электроэнергию) и в режиме потребителя (потребляя электроэнергию).
Если источник работает в режиме генератора, то направление тока и ЭДС в нем совпадают. Напряжения на его зажимах будет равно:
— уравнение равновесия ЭДС для генератора
Если источник
работает в режиме потребителя, то токи
ЭДС в нем направлены встречно. И напряжение на его зажимах будет равно:
И напряжение на его зажимах будет равно:
— уравнение равновесия ЭДС для источника в режиме потребителя (двигателя)
ЭДС источника в режиме потребителя называется противо ЭДС.
Последовательное, параллельное и смешанное соединения электрических сопротивлений и источников э. д. с.
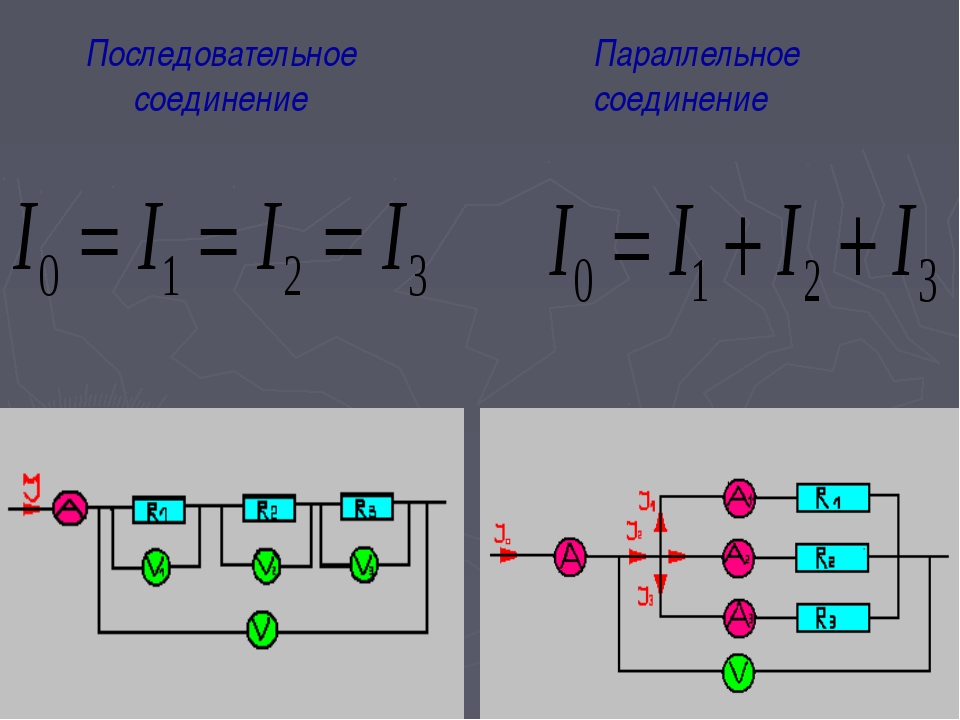
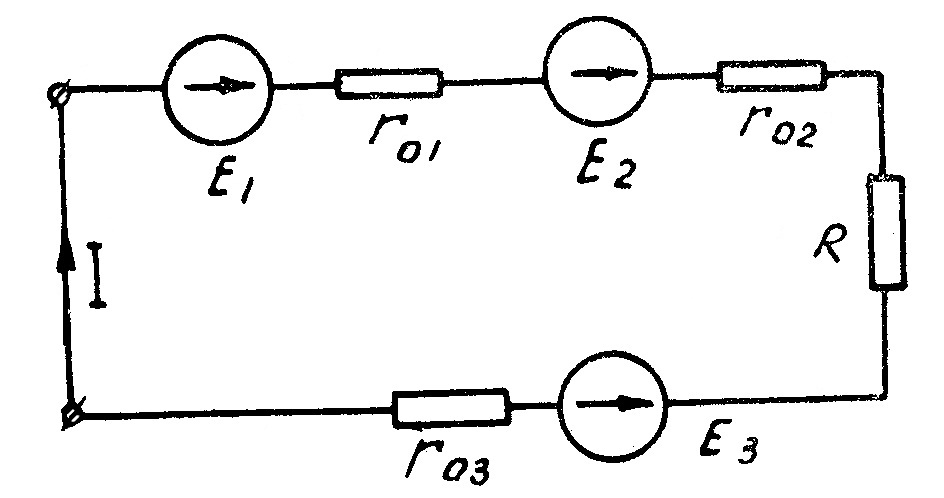
Различают последовательное, параллельное и смешанное соединения электрических сопротивлений и других потребителей электрической энергии.На рис. 1 показано последовательное соединение генератора Г и трех электрических сопротивлений (r1, r2, r3).
При последовательном соединении электрических сопротивлений во всех сопротивлениях проходит один и тот же ток, так как сопротивления включаются одно за другим.
Рис.1. Последовательное соединение генератора Г и трех электрических сопротивлений
На рис.
 2 изображено параллельное соединение трех электрических ламп с сопротивлениями r1, r2, r3 и одного реостата, сопротивление которого r4; соединение изображено упрощенной (слева) и развернутой (справа) схемами.
2 изображено параллельное соединение трех электрических ламп с сопротивлениями r1, r2, r3 и одного реостата, сопротивление которого r4; соединение изображено упрощенной (слева) и развернутой (справа) схемами.Рис.2.Параллельное соединение трех электрических ламп и одного реостата
При параллельном соединении сопротивлений падение напряжения во всех сопротивлениях одинаково, а ток в каждом сопротивлении (ветви) определяется только величиной сопротивления данной ветви.
Смешанным называется соединение сопротивлений, в котором имеются сопротивления, включенные последовательно и параллельно друг другу.
В схеме, показанной на рис. 3, группа, состоящая из трех параллельно включенных сопротивлений (r1, r2, r3), соединена последовательно с группой, состоящей из двух параллельно включенных сопротивлений (r4 и r5).
Рис.3.Группа из трех параллельно включенных сопротивлений соединена последовательно с группой из двух параллельно включенных сопротивлений.
Группу сопротивлений, образующую последовательное, параллельное или смешанное соединение, при расчетах заменяют эквивалентным сопротивлением.
 Величина этого сопротивления выбирается такой, что ток во всех остальных элементах схемы (сопротивлениях, генераторах и т. д.), не входящих в это соединение, остается неизменным.
Величина этого сопротивления выбирается такой, что ток во всех остальных элементах схемы (сопротивлениях, генераторах и т. д.), не входящих в это соединение, остается неизменным.Эквивалентное сопротивление последовательного соединения равно сумме всех сопротивлений, входящих в соединение. Это очевидно, так как включая последовательно сопротивления, мы тем самым затрудняем прохождение электрического тока в цепи.
Определим эквивалентное сопротивление параллельно включенных сопротивлений. Так как каждая новая параллельная ветвь создает для тока дополнительный путь, то тем самым электрическая проводимость будет увеличиваться по мере присоединения новых ветвей, и чем больше будет отдельных ветвей, тем больше будет электрическая проводимость соединения.Эквивалентная электрическая проводимость параллельного соединения сопротивления равна сумме электрических проводимостей каждой ветви
Если все ветви соединения имеют сопротивления одинаковой величины rn, а число ветвей равно n, то в соответствии с последней формулой имеем Последовательным соединением нескольких источников э. д. с., например, гальванических элементов или генераторов, называется такое соединение, при котором положительный полюс первого соединяют с отрицательным полюсом второго, положительный полюс второго — с отрицательным полюсом третьего и т. д. (рис. 4).
д. с., например, гальванических элементов или генераторов, называется такое соединение, при котором положительный полюс первого соединяют с отрицательным полюсом второго, положительный полюс второго — с отрицательным полюсом третьего и т. д. (рис. 4).Электродвижущая сила батареи последовательно соединенных элементов равна сумме электродвижущих сил отдельных элементов, а эквивалентное внутреннее сопротивление равно сумме их внутренних сопротивлений.
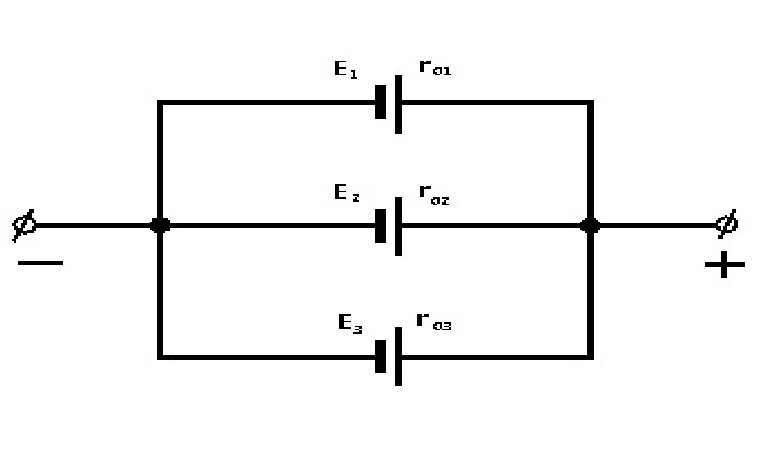
Параллельным соединением нескольких источников э. д. с. (например, гальванических элементов) называется такое, при ко-тором соединяют в один общий полюс все положительные полюсы элементов, а в другой — все отрицательные.
Соединять параллельно можно только элементы (или другие источники э. д. с.) с одинаковыми электродвижущими силами, так как неравенство последних приводит к возникновению токов, идущих от элементов с большой электродвижущей силой к элементам с меньшей электродвижущей силой. Эти токи не поступают во внешнюю цепь, т. е. связанная с ними энергия расходуется только на нагрев элементов и соединяющих элементы проводов.
е. связанная с ними энергия расходуется только на нагрев элементов и соединяющих элементы проводов.
На рис. 5 показано параллельное соединение трех элементов. Стрелками обозначено направление токов в каждом элементе и в общей (внешней) цепи.
Эквивалентное внутреннее сопротивление батареи элементов (или других источников тока) рассчитывается по тем же формулам, что и эквивалентное сопротивление соединенных параллельно сопротивлений.
Возможно и смешанное соединение источников э. д. с. Соединяя источники э. д. с. параллельно друг другу и соединяя образовавшиеся группы последовательно, можно получить соединение, обладающее любой электродвижущей силой при любом значении эквивалентного внутреннего сопротивления.
Рис. 6
При замене одного источника несколькими такими же, включенными параллельно, напряжение на нагрузке меньше зависит от сопротивления нагрузки. Отсюда следует, например, что если яркость свечения ламп при одном источнике э. д. с. будет сильно колебаться при изменении числа ламп, включенных в сеть (параллельно), то при включении достаточного числа источников э.
 д. с. параллельно друг другу яркость включенных в сеть ламп практически не будет зависеть от числа ламп. ⇓ДОБАВИТЬ В ЗАКЛАДКИ⇓
д. с. параллельно друг другу яркость включенных в сеть ламп практически не будет зависеть от числа ламп. ⇓ДОБАВИТЬ В ЗАКЛАДКИ⇓⇒ВНИМАНИЕ⇐
- Материал на блоге⇒ Весь материал предоставляется исключительно в ознакомительных целях! При распространении материала используйте пожалуйста ссылку на наш блог!
- Ошибки⇒ Если вы обнаружили ошибки в статье, то сообщите нам через контакты или в комментариях к статье. Мы будем очень признательны!
- Файлообменники⇒ Если Вам не удалось скачать материал по причине нерабочих ссылок или отсутствующих файлов на файлообменниках, то сообщите нам через контакты или в комментариях к статье.
- Правообладателям⇒ Администрация блога отрицательно относится к нарушению авторских прав на www.electroengineer.ru. Поэтому, если Вы являетесь правообладателем исключительных прав на любой материал, предоставленный на ресурсе, то сообщите нам через контакты и мы моментально примем все действия для удаления Вашего материала.

⇓ОБСУДИТЬ СТАТЬЮ⇓
Эквивалентные преобразования в электрических цепях
При расчёте электрических цепей грамотно проведённые преобразования позволяют уменьшить число уравнений, описывающих работу схемы. Далее приведены основные эквивалентные преобразования.
Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.Последовательное соединение пассивных элементов
Пример схемы приведён на рис. 1.
Рис. 1. Преобразование последовательно соединённых элементов
Эквивалентное сопротивление определяется по формуле
$$ \underline{Z}={{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}. $$
В общем случае при последовательном соединении N элементов
$$ \underline{Z}=\sum\limits_{i=1}^{N}{{{\underline{Z}}_{i}}}. {N}{\frac{1}{{{\underline{Z}}_{i}}}}}. $$
{N}{\frac{1}{{{\underline{Z}}_{i}}}}}. $$
Преобразование источника ЭДС в источник тока
Пример схемы приведён на рис. 5.
Рис. 5. Преобразование источника ЭДС в источник тока
Сила тока источника тока определяется по формуле
$$ \underline{J}=\frac{\underline{E}}{\underline{Z}}. $$
Проводимость ветви, параллельной источнику току, определяется по формуле
$$ \underline{Y}=\frac{1}{\underline{Z}}. $$
Преобразование источника тока в источник ЭДС
Пример схемы приведён на рис. 6.
Рис. 6. Преобразование источника тока в источник ЭДС
ЭДС определяется по формуле
$$ \underline{E}=\frac{\underline{J}}{\underline{Y}}. $$
Сопротивление определяется по формуле
$$ \underline{Z}=\frac{1}{\underline{Y}}. $$
Преобразование звезды сопротивлений в треугольник
Пример схемы приведён на рис. 7.
Рис. 7. Преобразование звезды в треугольник
Сопротивления треугольника определяются по формулам
$$ {{\underline{Z}}_{12}}={{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}+\frac{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{2}}}{{{\underline{Z}}_{3}}}, $$
$$ {{\underline{Z}}_{23}}={{\underline{Z}}_{2}}+{{\underline{Z}}_{3}}+\frac{{{\underline{Z}}_{2}}\cdot {{\underline{Z}}_{3}}}{{{\underline{Z}}_{1}}}, $$
$$ {{\underline{Z}}_{31}}={{\underline{Z}}_{1}}+{{\underline{Z}}_{3}}+\frac{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{3}}}{{{\underline{Z}}_{2}}}.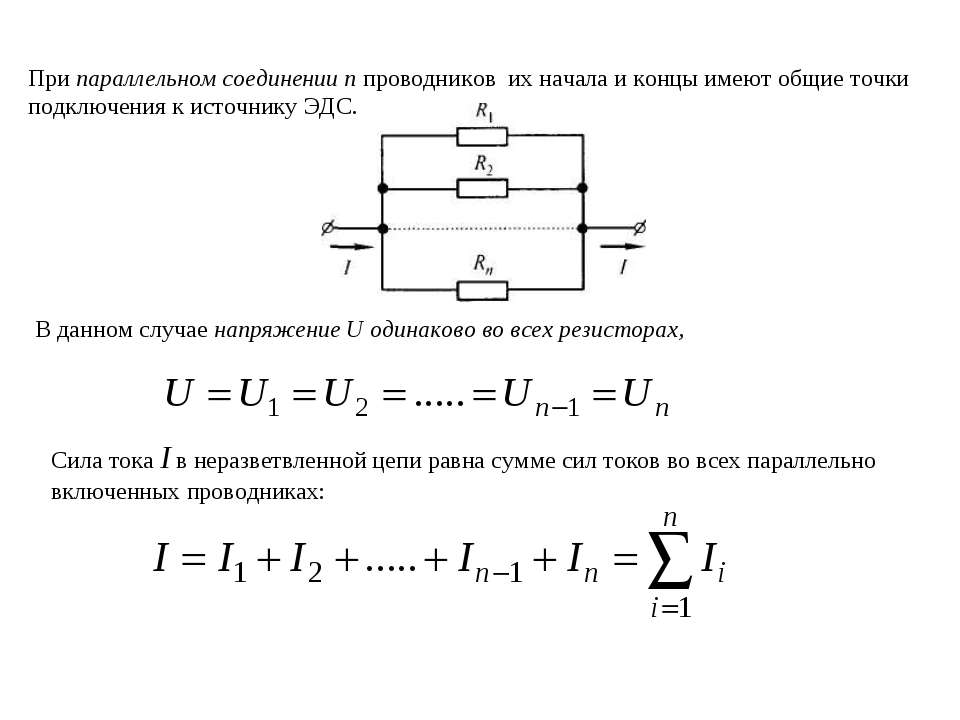 $$
$$
Калькулятор преобразования звезды сопротивлений в треугольник
$ \underline{Z}_1 = $ $ \textrm{Ом} $
$ \underline{Z}_2 = $ $ \textrm{Ом} $
$ \underline{Z}_3 = $ $ \textrm{Ом} $
Рассчитать
Преобразование треугольника сопротивлений в звезду
Пример схемы приведён на рис. 8.
Рис. 8. Преобразование треугольника в звезду
Сопротивления звезды определяются по формулам
$$ {{\underline{Z}}_{1}}=\frac{{{\underline{Z}}_{31}}\cdot {{\underline{Z}}_{12}}}{{{\underline{Z}}_{12}}+{{\underline{Z}}_{31}}+{{\underline{Z}}_{23}}}, $$
$$ {{\underline{Z}}_{2}}=\frac{{{\underline{Z}}_{23}}\cdot {{\underline{Z}}_{12}}}{{{\underline{Z}}_{12}}+{{\underline{Z}}_{31}}+{{\underline{Z}}_{23}}}, $$
$$ {{\underline{Z}}_{3}}=\frac{{{\underline{Z}}_{31}}\cdot {{\underline{Z}}_{23}}}{{{\underline{Z}}_{12}}+{{\underline{Z}}_{31}}+{{\underline{Z}}_{23}}}. $$
Калькулятор преобразования треугольника сопротивлений в звезду
$ \underline{Z}_{12} = $ $ \textrm{Ом} $
$ \underline{Z}_{23} = $ $ \textrm{Ом} $
$ \underline{Z}_{31} = $ $ \textrm{Ом} $
Рассчитать
Список использованной литературы
- Зевеке Г.
 В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Рекомендуемые записи
Несколько последовательно соединенных источников. Последовательное и параллельное соединения источников тока
Основы > Задачи и ответы > Постоянный электрический ток
Последовательное и параллельное соединения источников тока
Правило Кирхгофа
1
Найти разность потенциалов между точками а и
b
в схеме, изображенной на рис. 118. Э. д. с. источников тока
e
1
=
1
В и
e
2
=1,3 В, сопротивления резисторов
R
1 = 10
Ом и
R
2 = 5 Ом.
Решение:
Поскольку
e
2
>
e
1
то ток I будет идти в направлении, указанном на рис. 118, при этом разность потенциалов между точками а и b
2
Два элемента с э. д. с.
e
1
=
1
,5
B и
e
2
r1
=0,6
Ом и
r
2 = 0,4 Ом соединены по схеме, изображенной на рис. 119. Какую разность потенциалов между точками а и b покажет вольтметр, если сопротивление вольтметра велико по сравнению с внутренними сопротивлениями элементов?
Решение:
Поскольку
e
2
>
e
1
, то ток I будет идти в направлении, указанном на рис. 119. Током через вольтметр пренебрегаем ввиду
119. Током через вольтметр пренебрегаем ввиду
того, что его сопротивление велико по сравнению с внутренними сопротивлениями элементов. Падение напряжения на внутренних сопротивлениях элементов должно равняться разности э. д. с. элементов, так как они включены навстречу друг другу:
отсюда
Разность потенциалов между точками а и b (показание вольтметра)
3
Два элемента с э. д. с.
e
1
=1.4B и
e
2
= 1,1 В и внутренними сопротивлениями
r
=0,3 Ом и
r
2 = 0,2 Ом замкнуты разноименными полюсами (рис. 120). Найти напряжение на зажимах элементов. При каких условиях разность потенциалов между точками а и
b
равна нулю?
Решение:
4 Два источника тока с одинаковыми э. д. с. e = 2 В и внутренними сопротивлениями r1 =0,4 Ом и r 2 = 0,2 Ом соединены последовательно. При каком внешнем сопротивлении цепи R напряжение на зажимах одного из источников будет равным нулю?
Решение:
Ток в цепи
(рис.361). Напряжения на зажимах источников тока
Решая первые два уравнения при условии V1=0, получим
Условие V2=0 неосуществимо, так как совместное решение первого и третьего уравнений приводит к значению R
5
Найти внутреннее сопротивление
r1
первого элемента в схеме, изображенной на рис. 121, если напряжение на его зажимах равно нулю. Сопротивления резисторов
R
1 = ЗОм,
R
2 = 6 0м, внутреннее сопротивление второго элемента
r
2 = 0,4 Ом, э. д. с. элементов одинаковы.
121, если напряжение на его зажимах равно нулю. Сопротивления резисторов
R
1 = ЗОм,
R
2 = 6 0м, внутреннее сопротивление второго элемента
r
2 = 0,4 Ом, э. д. с. элементов одинаковы.
Решение:
Ток в общей цепи
По условию задачи напряжение на зажимах первого элемента
отсюда
6
При каком соотношении между сопротивлениями резисторов R
1
, R2, R3 и внутренними сопротивлениями элементов
r1,
r2
(рис. 122) напряжение
на зажимах одного из элементов будет равно нулю? Э. д. с. элементов одинаковы.
Решение:
7
Два генератора с одинаковыми э. д. с.
e
= 6 В и внутренними сопротивлениями
r1
=0,5 Ом и
r2
= 0,38 Ом включены по схеме, изображенной на рис. 123. Сопротивления резисторов R
1
= 2 Ом, R2 = 4 Ом,
R3
= 7 Ом. Найти напряжения V
1
и V2 на зажимах генераторов.
Решение:
Ток в общей цепи
где внешнее сопротивление цепи
Напряжения на зажимах первого и второго генератора
напряжение на зажимах второго генератора
8
Три элемента с э. д. с.
e
1
= 2,2 В,
e
2
=
1
,1 В и
e
3
= 0,9 В и внутренними сопротивлениями r
1
= 0,2 Ом,
r
2 = 0,4 Ом и
r
з = 0,5 Ом включены в цепь последовательно. Внешнее сопротивление цепи R=
1
Ом. Найти напряжение на зажимах каждого элемента.
д. с.
e
1
= 2,2 В,
e
2
=
1
,1 В и
e
3
= 0,9 В и внутренними сопротивлениями r
1
= 0,2 Ом,
r
2 = 0,4 Ом и
r
з = 0,5 Ом включены в цепь последовательно. Внешнее сопротивление цепи R=
1
Ом. Найти напряжение на зажимах каждого элемента.
Решение:
По закону Ома для полной цепи ток
Напряжение на зажимах каждого элемента равно разности э. д. с. и падения напряжения на внутреннем сопротивлении элемента:
Напряжение на зажимах батареи элементов равно падению напряжения на внешнем сопротивлении цепи:
Напряжение на зажимах третьего элемента оказалось отрицательным, так как ток определяется всеми сопротивлениями цепи и суммарной э.д.с, а падение напряжения на внутреннем сопротивлении r3 больше, чем э.д.с.
e
3
.
9
Батарея из четырех последовательно включенных в цепь элементов с э. д. с.
e
= 1,25 В и внутренним сопротивлением
r
= 0,1 Ом питает два параллельно соединенных проводника с сопротивлениями
R1
= 50 Ом и
R
2 = 200 Ом. Найти напряжение на зажимах батареи.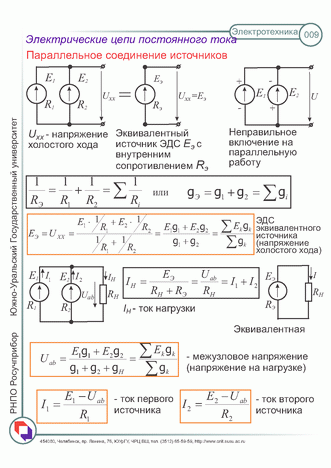
Решение:
10 Сколько одинаковых аккумуляторов с э. д. с. e = 1 ,25B и внутренним сопротивлением r = 0,004 Ом нужно взять, чтобы составить батарею, которая давала бы на зажимах напряжение V= 11 5 В при токе I =25 А?
Решение:
Напряжение на зажимах батареи
Следовательно,
11 Батарея из n = 40 последовательно включенных в цепь аккумуляторов с э. д. с. e = 2,5 В и внутренним сопротивлением r = 0,2 Ом заряжается от сети с напряжением V=121 В. Найти зарядный ток, если последовательно в цепь введен проводник с сопротивлением R = 2 Ом.
Решение:
12
Два элемента с э. д. с.
e
1
= 1,25 В и
e
2
= 1,5 В и одинаковыми внутренними сопротивлениями
r
= 0,4 Ом соединены параллельно (рис. 124). Сопротивление резистора
R
= 10 Ом. Найти токи, текущие через резистор и каждый элемент.
Решение:
Падение напряжения на резисторе, если токи текут в направлениях, указанных на рис. 124,
Учитывая, что I=I1+I2, находим
Заметим, что I1
13
Два элемента с э.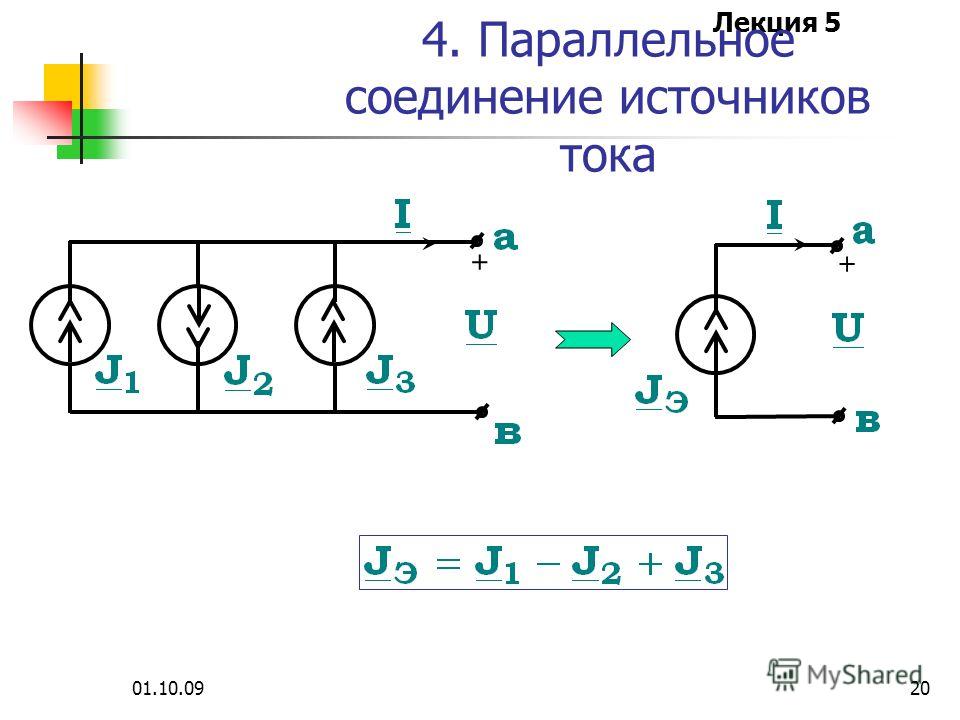 д. с.
e
1
=6 В и
e
2
= 5 В и внутренними сопротивлениями
r1
= 1 Ом и
r2
= 20м
соединены по схеме, изображенной на рис. 125. Найти ток, текущий через резистор с сопротивлением
R
= 10 Ом.
д. с.
e
1
=6 В и
e
2
= 5 В и внутренними сопротивлениями
r1
= 1 Ом и
r2
= 20м
соединены по схеме, изображенной на рис. 125. Найти ток, текущий через резистор с сопротивлением
R
= 10 Ом.
Решение:
Выбрав направления токов, указанные на рис. 362, составим уравнения Кирхгофа. Для узла b имеем I1+I2-I=0; для контура abef (обход по часовой стрелке)
и для контура bcde (обход против часовой стрелки)
Из этих уравнений найдем
14
Три одинаковых элемента с э. д. с.
e
= 1,6 В и внутренним сопротивлением
r
=0,8 Ом включены в цепь по схеме, изображенной на рис. 126. Миллиамперметр показывает ток
I
=100 мА. Сопротивления резисторов
R
1 = 10Ом и
R2
= 15 0м, сопротивление резистора
R
неизвестно. Какое напряжение V показывает вольтметр? Сопротивление вольтметра очень велико, сопротивление миллиамперметра пренебрежимо мало.
Решение:
Внутреннее сопротивление элементов
Сопротивление параллельно включенных резисторов
Общая э. д. с. элементов
e
0
=2
e
Согласно закону Ома для полной цепи
д. с. элементов
e
0
=2
e
Согласно закону Ома для полной цепи
15
Сопротивления резисторов R
1
и
R
2 и э. д. с.
e
1
и
e
2
источников тока в схеме, изображенной на рис. 127, известны. При какой э.д.с.
e
3
третьего источника ток через резистор R3 не течет?
Решение:
Выберем направления токов I1, I2 и I3 через резисторы R1, R2 и R3, указанные на рис. 363. Тогда I3=I1+I2. Разность потенциалов между точками а и b будет равна
Если
Исключая I1 находим
16
Цепь из трех одинаковых последовательно соединенных элементов с э.д.с.
e
и внутренним сопротивлением
r
замкнута накоротко (рис. 128). Какое
напряжение покажет вольтметр, подключенный к зажимам одного из элементов?
Решение:
Рассмотрим ту же схему без вольтметра (рис. 364). Из закона Ома для полной цепи находим
Из закона Ома для участка цепи между точками а и b получим
Подключение вольтметра к точкам, разность потенциалов между которыми равна нулю, ничего не может изменить в цепи. Поэтому вольтметр будет показывать напряжение, равное нулю.
Поэтому вольтметр будет показывать напряжение, равное нулю.
17
Источник тока с э.д.с.
e
0
включен в схему, параметры которой даны на рис. 129. Найти э.д.с.
e
источника тока и направление его подключения
к выводам а и
b
, при которых ток через резистор с сопротивлением R2 не идет.
Решение:
Подключим источник тока к выводам а и b и выберем направления токов, указанные на рис. 365. Для узла е имеем I=I0+I2. При обходе контуров aefb и ecdf по часовой стрелке получим
Используя условие I2 = 0, находим
Знак минус показывает, что полюсы источника тока на рис. 365 нужно поменять местами.
18
Два элемента с одинаковыми э.д.с.
e
включены в цепь последовательно. Внешнее сопротивление цепи R = 5 Ом. Отношение напряжения на зажимах первого элемента к напряжению на зажимах второго элемента
равно 2/3. Найти внутренние сопротивления элементов
r1
и
r
2, если
r
1=2
r
2.
Решение:
19
Два одинаковых элемента с э.д.с.
e
=
1
,5 В
и внутренним сопротивлением
r
= 0,2 Ом замкнуты на
резистор, сопротивление которого составляет в одном
случае R1=0,2
Oм, В другом —
R
2 = 20
Ом.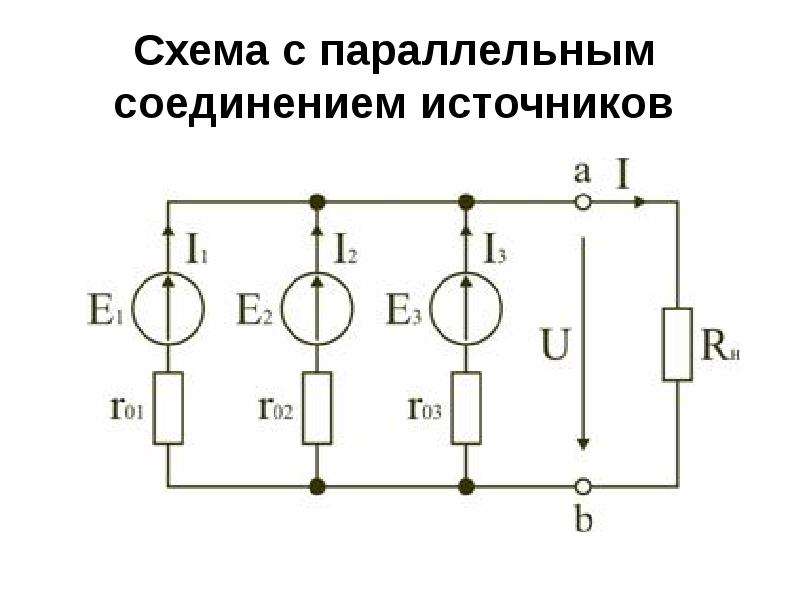 Как нужно
соединить элементы (последовательно или параллельно) в первом и во втором случаях, чтобы получить наибольший ток в цепи?
Как нужно
соединить элементы (последовательно или параллельно) в первом и во втором случаях, чтобы получить наибольший ток в цепи?
Решение:
При параллельном соединении двух элементов внутреннее сопротивление и э.д.с. равны r/2 и
e
при последовательном соединении они равны 2r и 2
e
. Через резистор R при этом текут токи
Отсюда видно, что I2>I1, если R/2+rr. Поэтому ток больше при последовательном соединении.
20
Два элемента с э.д.с.
e
1
=4В и
e
2
= 2В
и внутренними сопротивлениями
r1
= 0,25 Ом
и
r
2 = 0,75 Ом включены в схему, изображенную на
рис. 130. Сопротивления резисторов
R1
= 1 Ом и R2 = 3 Ом, емкость конденсатора С=2 мкФ.
Найти заряд на конденсаторе.
Решение:
21
К батарее из двух параллельно включенных элементов
с э.д.с.
e
1
и
e
2
и внутренними
сопротивлениями
r1
и
r
2 подключен резистор с сопротивлением R. Найти ток
I
, текущий через резистор R, и токи
I1
и
I
2 в первом и втором элементах. При каких
условиях токи в отдельных цепях могут быть равными
нулю или изменять свое направление на обратное?
Решение:
Выберем направления токов, указанные на рис.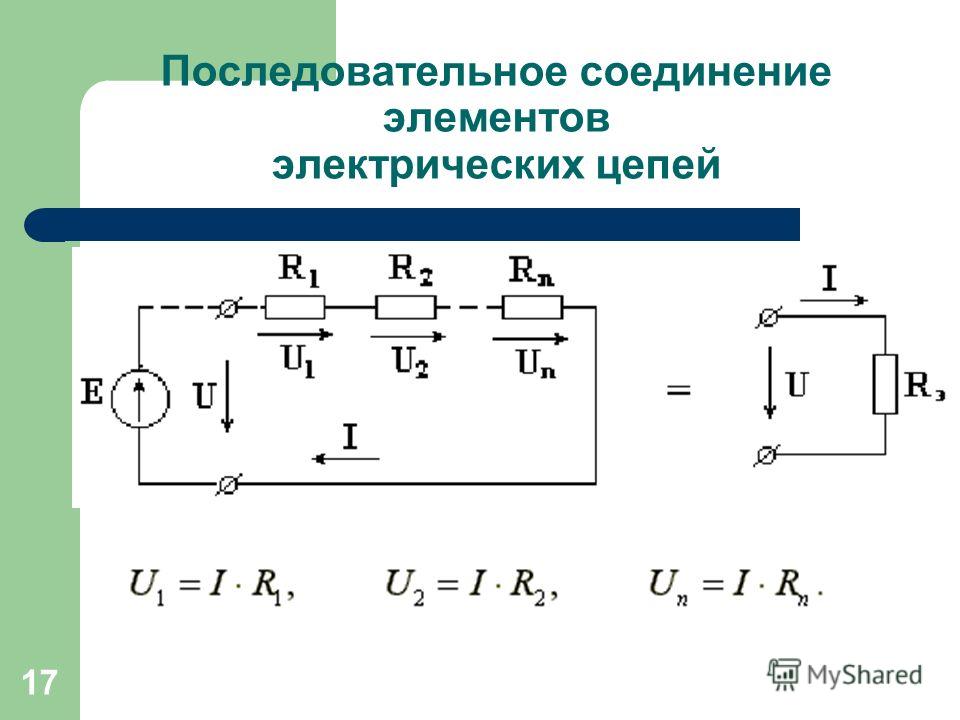 366. Для узла b имеем I-I1-I2=0. При обходе контуров abef и bcde по часовой стрелке получим
366. Для узла b имеем I-I1-I2=0. При обходе контуров abef и bcde по часовой стрелке получим
Из этих уравнений находим
Ток I=0 тогда, когда изменена полярность включения одного из элементов и, кроме того, выполнено условие
Ток I1=0 при
а ток I2 = 0 при
Токи I1 и I2 имеют направления, указанные на рис.366, если
Они меняют свое направление при
22 Батарея из n одинаковых аккумуляторов, соединенных в одном случае последовательно, в другом- параллельно, замыкается на резистор с сопротивлением R. При каких условиях ток, текущий через резистор, в обоих случаях будет один и тот же?
Решение:
При n(R-r) = R-r. Если R=r, то число элементов произвольно; если R
№
r, задача не имеет решения (n
=1).
23
Батарея из
n
= 4 одинаковых элементов с внутренним сопротивлением
r
=2 Ом, соединенных в одном случае
последовательно, в другом — параллельно, замыкается на резистор с сопротивлением
R
=10Ом. Во сколько раз показание вольтметра н одном случае отличается от показания вольтметра в другом случае? Сопротивление вольтметра велико по сравнению с
R
и
r.
Решение:
где V1 — показание вольтметра при последовательном соединении элементов, V2-при параллельном.
24
Как изменится ток, текущий через резистор с сопротивлением R = 2 Ом, если
n
=10 одинаковых элементов, соединенных последовательно с этим резистором, включить параллельно ему? Э.д.с. элемента
e
= 2 В, его внутреннее сопротивление
r
= 0,2 Ом.
Решение:
25
Батарея составлена из N=600 одинаковых
элементов так, что п групп соединены последовательно
и в каждой из них содержится т элементов, соединенных параллельно. Э.д.с. каждого элемента
e
= 2 В, его
внутреннее сопротивление
r
= 0,4 Ом. При каких значениях
n
и
m
батарея, будучи замкнута на внешнее
сопротивление R = 0,6 Ом, отдаст во внешнюю цепь
максимальную мощность? Найти при этом ток, текущий
через сопротивление R.
Решение:
Общее число элементов N=nm (рис. 367). Ток во внешней цепи
где r/
m
— внутреннее сопротивление группы из т параллельно соединенных элементов, а
n
r/
m
— внутреннее сопротивление
n
групп, соединенных последовательно.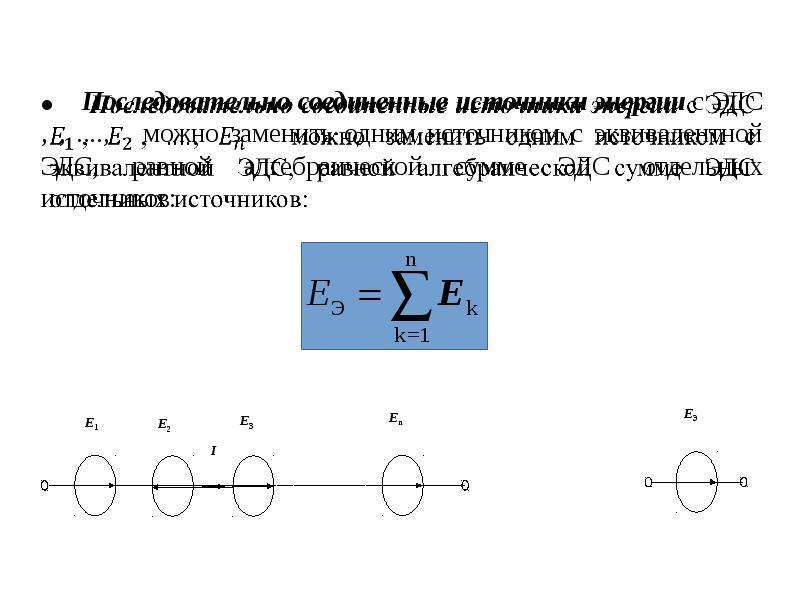 Максимальная мощность (см. задачу 848) отдается во внешнюю цепь при равенстве сопротивления R внутреннему сопротивлению батареи элементов
n
r/
m
, т. е.
Максимальная мощность (см. задачу 848) отдается во внешнюю цепь при равенстве сопротивления R внутреннему сопротивлению батареи элементов
n
r/
m
, т. е.
При этом через сопротивление R течет точек I=46 А.
26 Емкость аккумулятора =80 А Ч ч. Найти емкость батареи из n = 3 таких аккумуляторов, включенных последовательно и параллельно.
Решение:
При последовательном соединении через все аккумуляторы батареи течет один и тот же ток, поэтому все они разрядятся в течение одного и того же времени. Следовательно, емкость батареи будет равна емкости каждого аккумулятора:
При параллельном соединении
n
аккумуляторов через каждый из них течет 1/n часть общего тока; поэтому при том же разрядном токе в общей цепи батареи будет разряжаться в
n
раз дольше, чем один аккумулятор, т. е. емкость батареи в п раз больше емкости отдельного аккумулятора:
Заметим, однако, что энергия
отдаваемая батареей в цепь, и при последовательном и при параллельном соединении
n
аккумуляторов в
n
раз больше энергии, отдаваемой одним аккумулятором. Это происходит потому, что при последовательном соединении э. д. с. батареи в
n
раз больше э. д. с. одного аккумулятора, а при параллельном соединении э.д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в
n
раз.
Это происходит потому, что при последовательном соединении э. д. с. батареи в
n
раз больше э. д. с. одного аккумулятора, а при параллельном соединении э.д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в
n
раз.
27
Найти емкость батареи аккумуляторов, включенных по схеме, изображенной на рис.131. Емкость каждого аккумулятора
Qo
=64
А
Ч
ч
.
Решение:
Каждая группа из пяти аккумуляторов, включенных последовательно, имеет емкость
Три параллельно включенные группы дают общую емкость батареи
28
Мост для измерения сопротивлений сбалансирован так, что ток через гальванометр не идет (рис. 132). Ток в правой ветви
I
=0,2 А. Найти напряжение V на зажимах источника тока. Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 1 Ом.
Решение:
29
Найти токи, протекающие в каждой ветви цепи, изображенной на рис. 133. Э.д.с. источников тока
e
1
= 6,5 В и
e
2
= 3,9 В. Сопротивления резисторов R1=R2=R3=R4=R5=R6=R=10 Ом.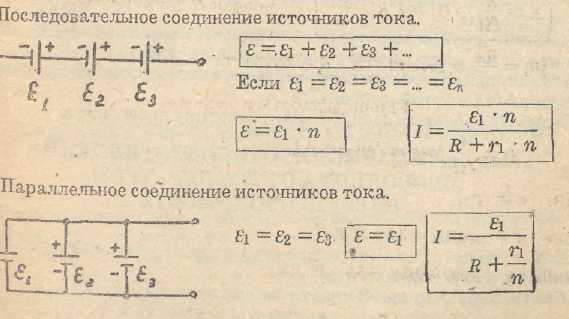
Решение:
Составляем уравнения Кирхгофа в соответствии с направлениями токов, указанными на рис. 133: I1 + I2 — I3 = 0 для узла b;
I3 — I4 — I5 =0 для узла h; I5 — I1 — I6 = 0 для узла f: при этом | Электромашины | Оборудование | Нормы |
3.5. Эквивалентные преобразования схем
Эквивалентными называются такие преобразования схем, при которых остаются неизменными токи и напряжения в части схемы, не затронутой преобразованием.
3.5.1. Последовательное соединение двухполюсников
Последовательным называется такое соединение двухполюсников, при котором по всем двухполюсникам протекает один и тот же ток (рис. 3.13).
По второму закону Кирхгофа .
Здесь , то есть эквивалентное сопротивление ветви равно сумме сопротивлений, включенных последовательно.
Частный случай :при окажется .
Для схемы рис. 3.14 по второму закону
Кирхгофа имеем:
. Значит, эквивалентная ЭДС равна алгебраической сумме
ЭДС источников, включенных последовательно. C
о знаком «плюс» в этой сумме учитываются
те из них, чьи стрелки направлены по отношению к узлам так же, как стрелка
Значит, эквивалентная ЭДС равна алгебраической сумме
ЭДС источников, включенных последовательно. C
о знаком «плюс» в этой сумме учитываются
те из них, чьи стрелки направлены по отношению к узлам так же, как стрелка
Последовательное соединение идеальных источников тока с разными задающими токами не имеет физического смысла.
3.5.2. Параллельное соединение двухполюсников
Параллельным называется такое соединение двухполюсников, при котором все они находятся под одним и тем же напряжением (иными словами, каждый из них подключен к одной и той же паре узлов, как на рис. 3.15).
По первому закону Кирхгофа
Отсюда . Значит, эквивалентная проводимость равна сумме проводимостей параллельных ветвей.
Частный случай : при окажется
Еще один частный случай (схема рис. 3.16):
Здесь же
По аналогии .
Ток
в одной из двух параллельных пассивных ветвей равен произведению тока в неразветвленной
части на сопротивление другой ветви, отнесенному к сумме сопротивлений обеих ветвей («правило параллельных ветвей »).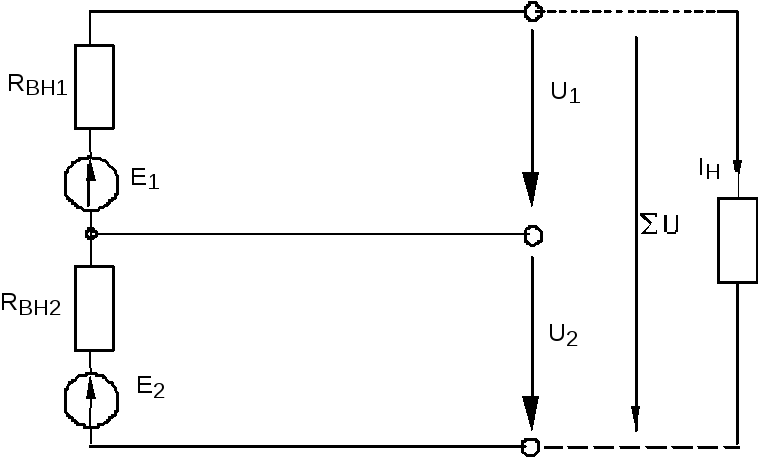
Для схемы рис. 3.17 имеем но поэтому .
Задающий ток эквивалентного источника равен алгебраической сумме задающих токов источников, включенных параллельно . Со знаком «плюс» учитываются те из них, чьи стрелки направлены по отношению к узлам так же, как стрелка эквивалентного источника .
Параллельное соединение источников напряжения с различными ЭДС не имеет физического смысла.
3.5.3. Эквивалентное преобразование последовательного
соединения ЕиRв параллельное соединение JиG
По второму закону Кирхгофа для схемы с последовательным соединением и по первому закону для схемы с параллельным соединением(рис. 3.18) можно записать:
Эти выражения тождественны лишь при равенстве слагаемых, как не зависящих от тока I ,так и пропорциональных ему. Поэтому
В обеих схемах сопротивление одинаково, а ЭДС и задающий ток источников связаны законом Ома.
3. 5.4. Параллельное соединение активных
ветвей
5.4. Параллельное соединение активных
ветвей
Воспользовавшись уже известными преобразованиями (переход от одной схемы к другой на рис. 3.19 по стрелкам), найдем:
тогда
В общем случае n параллельных ветвей
В числителе предпоследней формулы сумма алгебраическая: со знаком «плюс» записываются ЭДС тех источников, чьи стрелки направлены по отношению к узлам так же, как и ,со знаком «минус» – направленные в противоположную сторону.
3.5.5. Перенос источника ЭДС через узел (рис. 3.20)
Пусть
тогда в исходной схеме
Включим в каждую из ветвей одинаковые по
величине ЭДСЕ , направленные от узла 4. При этом потенциалы узлов 2 и 3 не
изменятся. В первой ветви две ЭДС скомпенсируют действие друг друга и их можно
удалить. В эквивалентной схеме и
т.е. изменился лишь потенциал узла 4, а
ЭДС оказалась «вытесненной» из одной ветви во все остальные. Это преобразование
удобно применять, когда в схеме есть активная ветвь без сопротивления.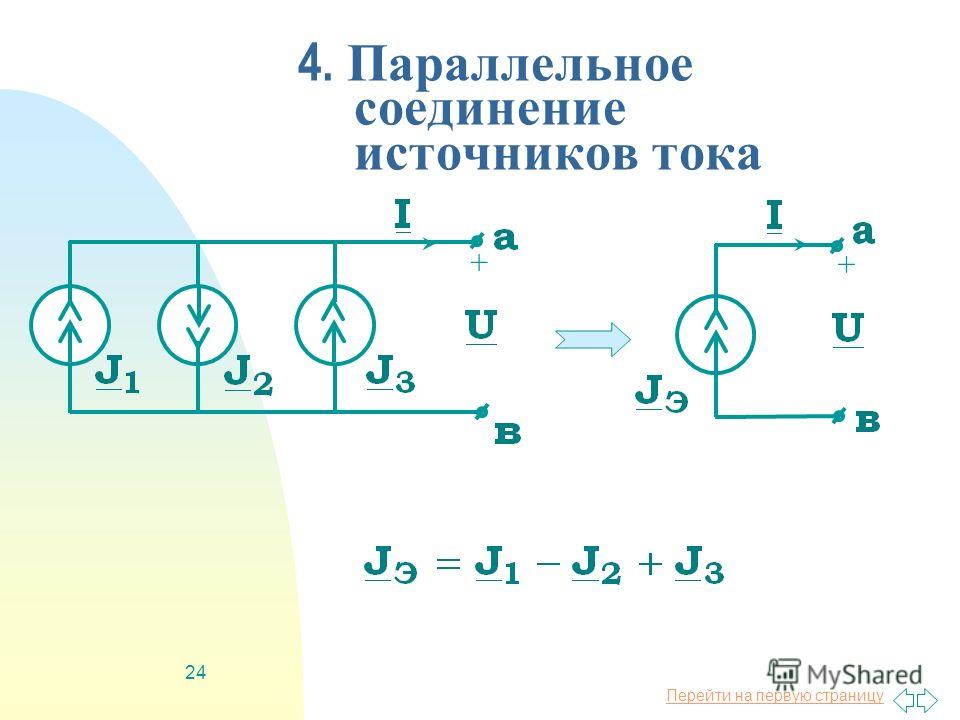 После
него эта («особая») ветвь может быть устранена вместе с одним из узлов.
После
него эта («особая») ветвь может быть устранена вместе с одним из узлов.
3.5.6. Перенос источника тока в контуре
В схеме рис. 3.21,а выделены две ветви с сопротивлениями и ,образующие с источником тока замкнутый контур. Включим последовательно с одним источником тока еще один такой же и подключим точку их соединения к узлу 3 (рис. 3.21,б). При этом мы не нарушили первый закон Кирхгофа и не изменили режим работы остальной части цепи(I = 0).
Заменим параллельное соединение источников токаJ с пассивной и активной ветвями последовательным соединением источниковЭДС с теми же сопротивлениями. Получим схему рис. 3.21,в, в которой действуют новые ЭДС и . По сравнению с исходной схемой удалось избавиться от одного («особого») контура. Токи в сопротивлениях этого контура после преобразования изменятся, а в остальной части схемы сохранят прежние значения.
Это
преобразование легко распространить на любое число ветвей, образующих контур с
источником тока.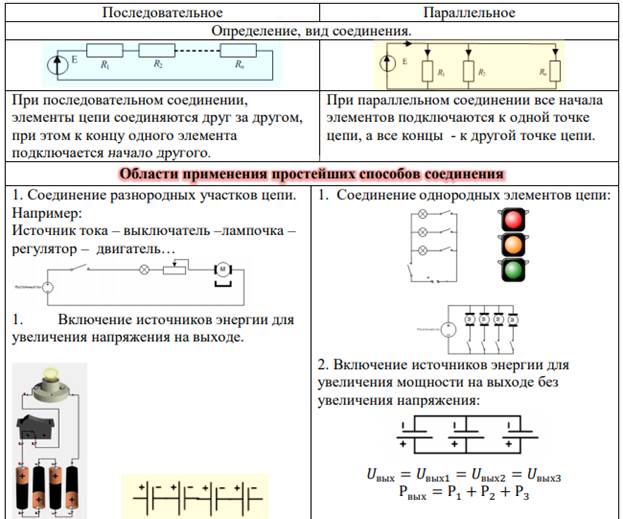
3.5.7. Преобразование треугольника в звезду и обратно
Если в одной из ветвей треугольника есть источник ЭДС (рис. 3.23), то в лучах эквивалентной звезды, подключенных к тем же узлам, что и активная ветвь треугольника, появляются две ЭДС, пропорциональные их сопротивлениям:
где
что легко доказывается с помощью уже известных преобразований. Сопротивлениялучей эквивалентной звезды вычисляются так же, как и в случае с пассивными звездой и треугольником.
Направление стрелок эквивалентных ЭДС по отношению к узлам такое же, как и у ЭДС в ветвях треугольника.
Варианты с несколькими ЭДС сводятся к рассмотренному посредством переноса ЭДС через узел. Преобразование активной звезды в треугольник трудностей не представляет.
На практике несколько источников электрической энергии соединяются в группу — батарею источников электрической энергии. Соединение в батарею может быть последовательное, параллельное и смешанное.
При последовательном соединении положительный полюс предыдущего источника соединяется с отрицательным полюсом последующего.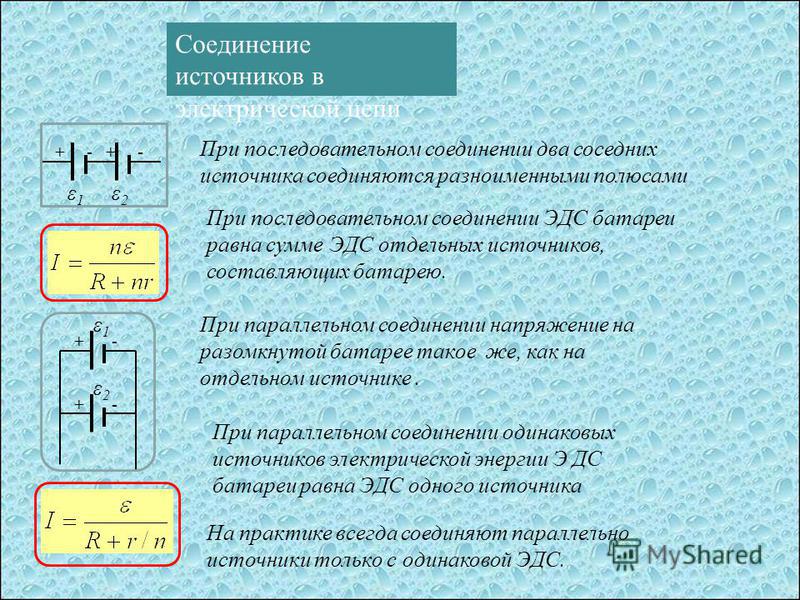 Дневники скромные апортаменты mrloft.ru/apartamenty .
Дневники скромные апортаменты mrloft.ru/apartamenty .
Полная ЭДС цепи равна алгебраической сумме ЭДС отдельных элементов, а внутреннее сопротивление батареи равно сумме сопротивлений источников:
Объяснить это можно тем, что при последовательном соединении электрический заряд поочередно проходит через источник электрической энергии и в каждом из них приобретает энергию. Внутреннее сопротивление батареи также увеличивается.
При последовательном соединении одинаковых источников с ЭДС е и внутренним сопротивлением г ЭДС батареи и ее внутреннее сопротивление равны.
где п — число источников.
Закон Ома для полной цепи при последовательном соединении одинаковых источников тока записывается в виде;
где e и r — ЭДС и внутреннее сопротивление одного источника, R — сопротивление внешнего участка цепи, I — сила тока в цепи.
Например, полная цепь содержит несколько источников тока, ЭДС которых равны E1,E2,E3 а внутренние сопротивления-r1,r2,r3, соответственно. ЭДС, действующая в цепи, равна:
ЭДС, действующая в цепи, равна:
eб=e1 -e2+e3-e4
Сопротивление батареи равно:
r, = r, + r, + r, + г.
При этом учитываем, что положительными являются те ЭДС, которые повышают потенциал в направлении обхода цепи, т.е. направление обхода цепи совпадает с переходом внутри источника от отрицательного полюса источника к положительному.
Последовательное соединение источников тока применяется в тех случаях, когда нужно повысить напряжение на внешней цепи, причем сопротивление внешней цепи велико по сравнению с внутренним сопротивлением одного источника.
Рис. 9
При параллельном соединении источников все их положительные
полюсы присоединены к одному проводнику, а отрицательные-к другому.
Полная ЭДС цепи (всей батареи равна ЭДС одного источника: eб= e,а внутреннее сопротивление батареи равно:
где п — число параллельно соединенных источников.
При параллельном соединении ток одного источника электрической энергии уже не проходит через другие, и поэтому каждый заряд получает энергию только в одном источнике.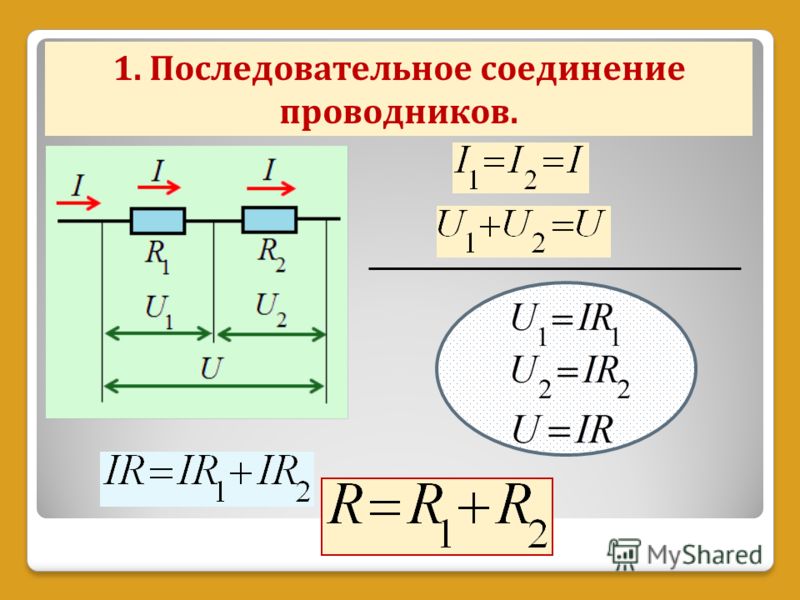 Сопротивление батареи меньше сопротивления одного источника, так как через каждый источник электрической энергии проходит только часть зарядов, перемещающихся во внешней цепи.
Сопротивление батареи меньше сопротивления одного источника, так как через каждый источник электрической энергии проходит только часть зарядов, перемещающихся во внешней цепи.
Закон Ома для полной цепи при параллельном соединении одинаковых источников тока записывается в виде:
Если заменить один источник тока батареей параллельно соединенных источников, то ток в цепи возрастает.
Параллельное соединение источников тока применяется в тех случаях, когда нужно усилить ток во внешней цепи, не изменяя напряжения, причем сопротивление внешней цепи мало по сравнению с сопротивлением одного источника.
Если ЭДС источников различны, то для источников тока напряжений и ЭДС в различных участках цепи удобно пользоваться правилами Кирхгофа, сформулированными в 1847 г. немецким Физиком Густавом Робертом Кирхгофом (1824-1887).
1. Первое правило (правило узлов).
Алгебраическая сумма сил токов, сходящихся в любом узле, равна нулю:
где п — число проводников, сходящихся в узле.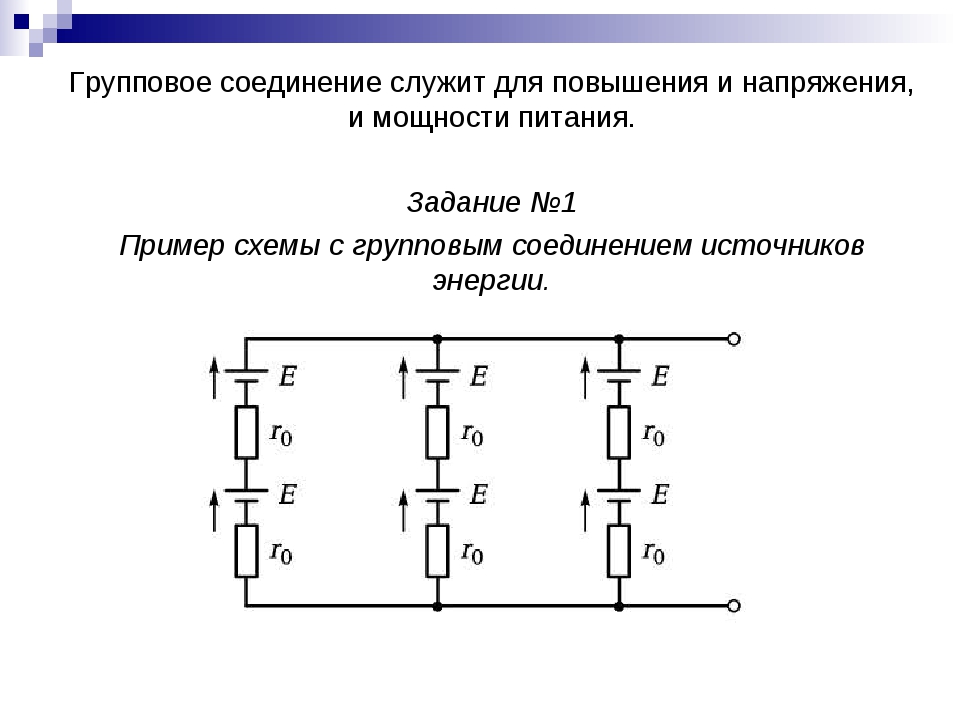 Узлом в разветвленной цепи называется точка, в которой сходится не менее трех проводников. Токи, текущие к узлу, считаются положительными, а токи, текущие от узла, отрицательными.
Узлом в разветвленной цепи называется точка, в которой сходится не менее трех проводников. Токи, текущие к узлу, считаются положительными, а токи, текущие от узла, отрицательными.
Рис. 10
Узел токов. I1+I2+I4=I3+I5 или I1+I2-I3+I4-I5=0.
2 Второе правило (правило контуров).
Химические источники э. д. с. (аккумуляторы, элементы) включаются между собой последовательно, параллельно и смешанно.
1, Последовательное соединение источников э. д. с. На рис. 56, а представлены три соединенных между собой аккумулятора. Такое
соединение аккумуляторов, когда минус каждого предыдущего источника соединен с плюсом последующего источника, называется последовательным соединением. Группа соединенных между собой аккумуляторов или элементов называется батареей.
Внутреннее сопротивление батареи равно сумме внутренних сопротивлений отдельных аккумуляторов:
Схематически последовательное
соединение трех аккумуляторов в батарею показано на рис. 56, б . Так как э. д. с. аккумуляторов в этом
случае совпадают по направлению, э. д. с. всей батареи равна их сумме
Так как э. д. с. аккумуляторов в этом
случае совпадают по направлению, э. д. с. всей батареи равна их сумме
Если батарея окажется замкнутой на внешнее сопротивление r, то ток в цепи будет найден по формуле
Последовательно соединяют аккумуляторы в том случае, когда напряжение потребителя выше э. д. с. одного аккумулятора.
Практически приходится соединять между собой в батареи только однотипные аккумуляторы, т. е. имеющие одинаковые э. д. с, внутренние сопротивления и емкости.
Внутреннее сопротивление батареи
Ток батареи, замкнутой на внешнее сопротивление, будет
В этом случае э. д. с. батареи, состоящей из п аккумуляторов, равна:
Пример 1. Батарея из пяти аккумуляторов, обладающих э. д. с. 1,2 в и внутренним сопротивлением 0,2 ом, замкнута на внешнее сопротивление 11 ом. Определить ток, отдаваемый батареей в сеть:
2. Параллельное соединение источников э. д. с. Если положительные зажимы (плюсы) нескольких аккумуляторов соединить
между собой и вывести общий
плюс, а отрицательные зажимы (минусы) этих же аккумуляторов также соединить
между собой и вывести общий минус, то такое соединение будет называться
параллельным.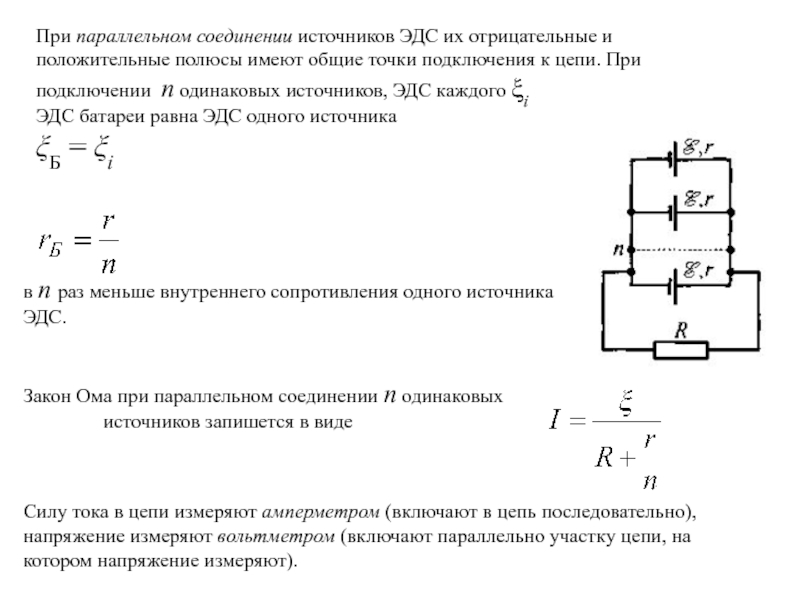 На рис. 57, а представлено параллельное I соединение трех аккумуляторов,
а на рис. 57, б дана схема того же соединения.
На рис. 57, а представлено параллельное I соединение трех аккумуляторов,
а на рис. 57, б дана схема того же соединения.
Обязательным условием для параллельного соединения аккумуляторов является равенство их э. д. с, внутренних сопротивлений и емкостей, так как иначе между аккумуляторами будут протекать уравнительные токи, вредные для батареи.
Э. д. с. батареи при параллельном соединении равна э. д. с. одного аккумулятора:
При параллельном соединении аккумуляторов батарея в целом может отдать в сеть ток, больший, чем каждый аккумулятор в отдельности.
Внутреннее сопротивление батареи, состоящей из n параллельно включенных аккумуляторов, будет и в n раз меньше сопротивления каждого аккумулятора:
Ток, отдаваемый батареей в сеть, будет
Параллельное соединение аккумуляторов применяется в том случае, когда напряжение потребителя равно э.д.с. аккумулятора, а ток, необходимый потребителю, больше разрядного тока одного аккумулятора.
Пример 2 . Определить ток, отдаваемый в сеть батареей, состоящей из двух
параллельно включенных аккумуляторов, если э. д. с. каждого аккумулятора равна
2 в, а внутреннее сопротивление — 0,02 ом. Внешнее сопротивление равно 1,99 ом:
Определить ток, отдаваемый в сеть батареей, состоящей из двух
параллельно включенных аккумуляторов, если э. д. с. каждого аккумулятора равна
2 в, а внутреннее сопротивление — 0,02 ом. Внешнее сопротивление равно 1,99 ом:
3. Смешанное соединение источников э. д. с. Комбинируя последовательное и параллельное соединения, мы получим смешанное соединение аккумуляторов. На рис. 58, а представлено смешанное соединение четырех аккумуляторов из двух параллельных групп по два элемента в каждой группе, а на рис. 58, б дана схема этого соединения. Э. д. с. батареи со смешанным соединением аккумуляторов равна сумме э. д. с. элементов, последовательно включенных в каждую группу (п):
Внутреннее сопротивление аккумуляторов в группе
Внутреннее сопротивление батареи, состоящей из m групп,
Ток, отдаваемый батареей в сеть сопротивлением r ом,
Смешанное соединение аккумуляторов применяется в том случае, когда напряжение и ток потребителя
соответственно больше з д. с. и разрядного тока одного аккумулятора.
с. и разрядного тока одного аккумулятора.
Пример 3. Имеется батарея, состоящая из двух параллельно соединенных групп аккумуляторов по три аккумулятора в группе. Батарея замкнута на сопротивление 1,65 ом, э. д. с. аккумулятора 1,2 в, внутреннее сопротивление 0,1 ом. Определить ток во внешней цепи:
Мы оазобоали ряд случаев соединения источников э. д. с. Какой же способ является наиболее выгодным с точки зрения максимальной отдачи мощности во внешней цепи? Математическое исследование дает ответ на этот вопрос. Оказывается, что для получения во внешней цепи максимальной мощности необходимо равенство сопротивлений внутренней и внешней части цепи:
Задачи дня самостоятельного решения
1. Сколько мг цинка выделится из раствора цинковой соли при прохождении через раствор 50 к электричества?
2. Через ванну с раствором медного купороса проходит ток 5 а в течение 20 мин. Определить количество выделенной из раствора меди.
3. При никелировании в качестве анода подвешена пластинка никеля весом 20 г. В какое время
израсходуется никелевая пластинка, если через раствор проходит ток 10 А?
При никелировании в качестве анода подвешена пластинка никеля весом 20 г. В какое время
израсходуется никелевая пластинка, если через раствор проходит ток 10 А?
4. Металлическую пластинку площадью 2 дм 2 покрывают слоем цинка толщиной 0,05 мм . Сколько времени будет продолжаться покрытие, если ток ранен 1 о, а удельный вес цинка 7,1?
5. Металлический предмет размером 10X40X60 мм покрывают серебром. Какой ток необходимо пропустить, чтобы покрыть предмет слоем серебра толщиной 0,01 мм в течение 0,5 ч? Удельный вес серебра 10,5.
6. Имеется батарея из четырех аккумуляторов с э. д. с. по 1,2 в и внутренним сопротивлением по 0,2 ом. Батарея замкнута на сопротивление 4 ом. Определить ток батареи в случае, если аккумуляторы соединены: а) последовательно, б) параллельно.
7. Четыре
аккумулятора с э. д. с. по 1,2 в и внутренним сопротивлением по 0,3 ом включены
последовательно. Внешнее сопротивление равно 8,4 ом. Определить величину тока и напряжения батареи.
Определить величину тока и напряжения батареи.
8. Три параллельные группы аккумулятора по пять последовательно включенных аккумуляторов в каждой группе работают на внешнюю сеть сопротивлением 4,995 ом. Э. д. е.; аккумулятора 2 в, внутреннее сопротивление 0,003 ом. Определить ток, напряжение батареи и мощность, отдаваемую ею во внешнюю цепь.
Контрольные вопросы
1. Что называется электролизом?
2. От чего зависит количество вещества, выделившегося на электродах при электролизе?
3. Что называется электрохимическим эквивалентом вещества?
4. В чем сущность закона Фарадея?
5. Укажите области технического применения электролиза.
6. Как устроен простейший гальванический элемент?
7. Как устроены и работают аккумуляторы?
8. Как соединяются между собой электрохимические источники напряжения?
9. Каковы особенности каждого соединения?
Параллельное соединение — источник — Большая Энциклопедия Нефти и Газа, статья, страница 2
Параллельное соединение — источник
Cтраница 2
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников. [17]
[17]
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей, отдаваемых источниками. [18]
Несмотря на то, что параллельное соединение источников не приводит к увеличению ЭДС, его целесообразно применять в тех случаях, когда требуется получить источник тока с малым внутренним сопротивлением. [20]
Пусть схема замещения реального генератора представляет собой параллельное соединение источника тока io и резистивного сопротивления R. [21]
В настоящее время в связи с выпуском про-мышленностыо источников питания большой мощности параллельное соединение источников питания применяется сравнительно редко. [22]
Не допускается включение нуллора к идеализированным источникам, точно так же, как не допускается параллельное соединение источников напряжения с разными задающими напряжениями и последовательное соединение источников тока с различными задающими токами, как противоречащие законам Кирхгофа.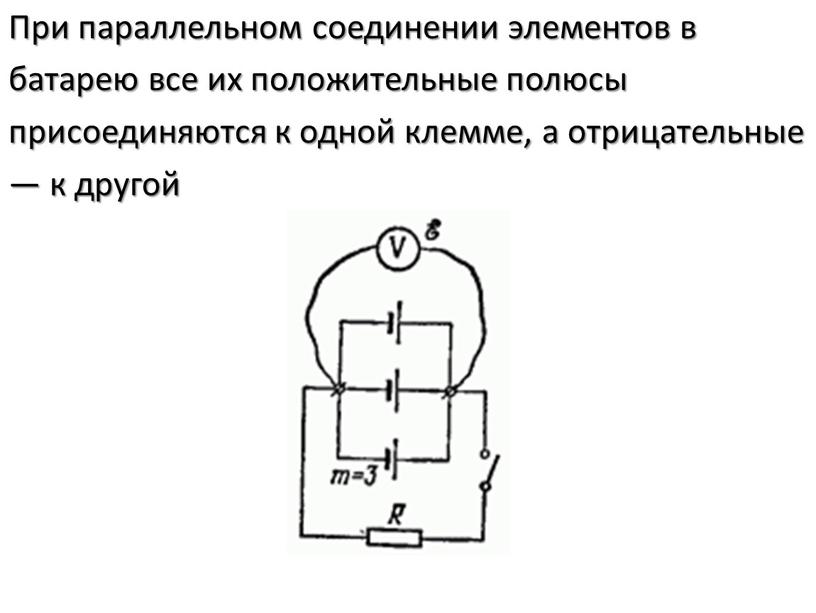 [23]
[23]
Смешение токов звуковой и высокой частоты ( подмагничивание на выходе УЗ может производиться при последовательном или параллельном соединении источников колебаний. [24]
Величина тока каждого источника ограничена его номинальным значением / ном, сверх которого нагружать источник нельзя. Параллельное соединение источников применяется для увеличения общего тока, благодаря чему достигается увеличение мощности потребления энергии без изменения напряжения. [26]
Величина тока каждого источника ограничена его номинальным значением /, сверх которого нагружать источник нельзя. Параллельное соединение источников применяется для увеличения общего тока, благодаря чему достигается увеличение мощности потребления энергии без изменения напряжения. [27]
При этом сопротивление батареи минимально. Итак, выгоднее параллельное соединение источников, при котором наибольший коэффициент полезного действия, но не самая большая из возможных сила тока.
[28]
Итак, выгоднее параллельное соединение источников, при котором наибольший коэффициент полезного действия, но не самая большая из возможных сила тока.
[28]
Таким образом, этот источник электрической энергии является источником тока. При расчете цепей он обычно заменяется эквивалентной схемой ( рис. 3.5), состоящей из параллельного соединения источника постоянного внутреннего тока J и внутренней проводимости GB, величина которой учитывает все причины изменения внешнего тока при нагрузке. [29]
Три одинаковых источника тока соединены последовательно и замкнуты проводником, сопротивление которого R 2 Ом. При параллельном соединении источников в том же проводнике идет ток силой / 2 0 9 А. [30]
Страницы: 1 2 3
резисторов последовательно и параллельно
Резисторы серии
Общее сопротивление в цепи с последовательно включенными резисторами равно сумме отдельных сопротивлений.
Цели обучения
Рассчитайте общее сопротивление в цепи с последовательно включенными резисторами
Основные выводы
Ключевые моменты
- Одинаковый ток течет через каждый резистор последовательно.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
- Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений: [латекс] \ text {RN} (\ text {series}) = \ text {R} _1 + \ text {R} _2 + \ text {R} _3 +… + \ text {R} _ \ text {N} [/ latex].
Ключевые термины
- серия : ряд элементов, которые следуют одно за другим или связаны друг за другом.
- сопротивление : Противодействие прохождению электрического тока через этот элемент.
Обзор
В большинстве схем есть более одного компонента, называемого резистором, который ограничивает поток заряда в цепи.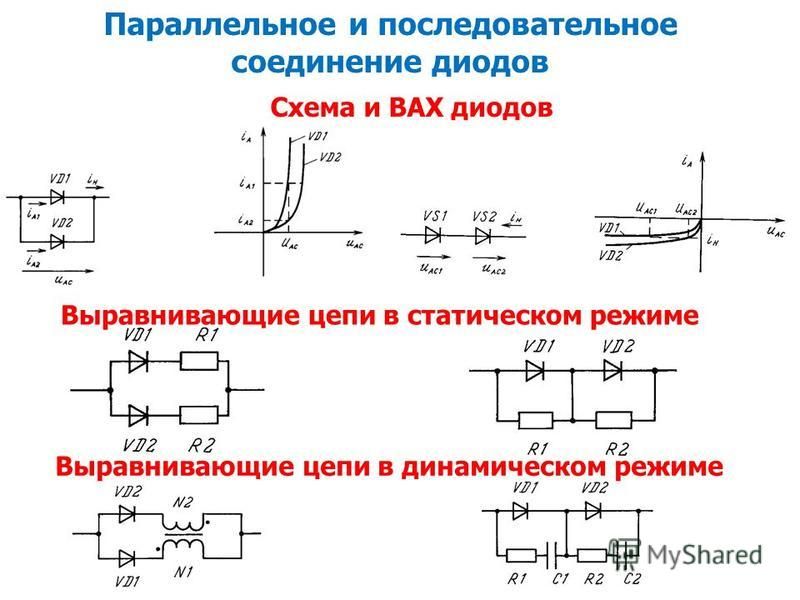 Мера этого предела расхода заряда называется сопротивлением. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они подключены.
Мера этого предела расхода заряда называется сопротивлением. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они подключены.
Цепи серии : Краткое введение в анализ последовательных и последовательных цепей, включая закон Кирхгофа по току (KCL) и закон Кирхгофа по напряжению (KVL).
Резисторы серии
Резисторы включены последовательно, когда заряд или ток должны проходить через компоненты последовательно.
Резисторы в серии : Эти четыре резистора соединены последовательно, потому что, если бы ток подавался на один конец, он бы протекал через каждый резистор последовательно до конца.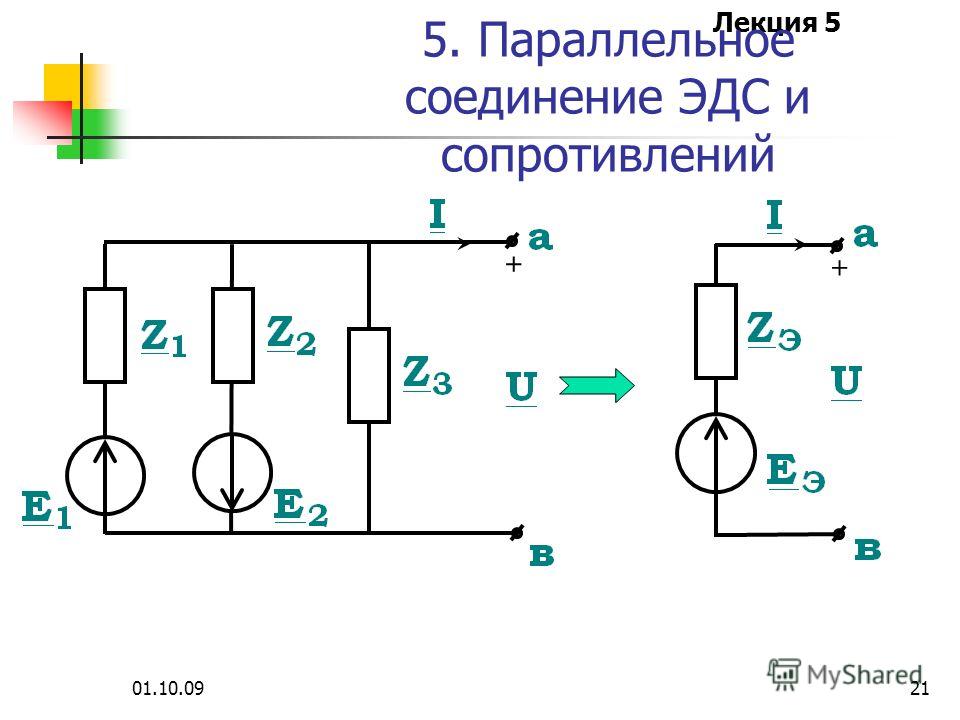
показывает резисторы, последовательно подключенные к источнику напряжения. Общее сопротивление в цепи равно сумме отдельных сопротивлений, так как ток должен последовательно проходить через каждый резистор.
Резисторы, подключенные последовательно : три резистора, подключенные последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Использование закона Ома для расчета изменений напряжения в резисторах серии
В соответствии с законом Ома падение напряжения V на резисторе при протекании через него тока рассчитывается с помощью уравнения V = IR, где I — ток в амперах (A), а R — сопротивление в омах (Ω). .
Таким образом, падение напряжения на R 1 составляет В 1 = IR 1 , на R 2 составляет В 2 = IR 2 , а на R 3 составляет В 3 = IR 3 .Сумма напряжений будет равна: V = V 1 + V 2 + V 3 , исходя из сохранения энергии и заряда. Если подставить значения отдельных напряжений, получим:
Если подставить значения отдельных напряжений, получим:
[латекс] \ text {V} = \ text {IR} _1 + \ text {IR} _2 + \ text {IR} _3 [/ latex]
или
[латекс] \ text {V} = \ text {I} (\ text {R} _1 + \ text {R} _2 + \ text {R} _3) [/ латекс]
Это означает, что полное сопротивление в серии равно сумме отдельных сопротивлений. Следовательно, для каждой цепи с Н количество резисторов, включенных последовательно:
[латекс] \ text {RN} (\ text {series}) = \ text {R} _1 + \ text {R} _2 + \ text {R} _3 +… + \ text {R} _ \ text {N }.[/ латекс]
Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, и последовательно соединенные сопротивления просто складываются.
Поскольку напряжение и сопротивление имеют обратную зависимость, отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Об этом свидетельствует пример, когда две лампочки соединены в последовательную цепь с аккумулятором. В простой схеме, состоящей из одной батареи 1,5 В и одной лампочки, падение напряжения на лампочке будет равно 1.5V через него. Однако, если две лампочки были соединены последовательно с одной и той же батареей, на каждой из них было бы падение напряжения 1,5 В / 2 или 0,75 В. Это будет очевидно по яркости света: каждая из двух последовательно соединенных лампочек будет вдвое слабее, чем одиночная лампочка. Следовательно, резисторы, подключенные последовательно, потребляют такое же количество энергии, как и один резистор, но эта энергия распределяется между резисторами в зависимости от их сопротивлений.
В простой схеме, состоящей из одной батареи 1,5 В и одной лампочки, падение напряжения на лампочке будет равно 1.5V через него. Однако, если две лампочки были соединены последовательно с одной и той же батареей, на каждой из них было бы падение напряжения 1,5 В / 2 или 0,75 В. Это будет очевидно по яркости света: каждая из двух последовательно соединенных лампочек будет вдвое слабее, чем одиночная лампочка. Следовательно, резисторы, подключенные последовательно, потребляют такое же количество энергии, как и один резистор, но эта энергия распределяется между резисторами в зависимости от их сопротивлений.
Параллельные резисторы
Общее сопротивление в параллельной цепи равно сумме обратных сопротивлений каждого отдельного сопротивления.
Цели обучения
Рассчитайте полное сопротивление в цепи с резисторами, включенными параллельно
Основные выводы
Ключевые моменты
- Общее сопротивление в параллельной цепи меньше наименьшего из отдельных сопротивлений.

- Каждый резистор, включенный параллельно, имеет то же напряжение, что и приложенный к нему источник (напряжение в параллельной цепи постоянное).
- Не каждый параллельный резистор получает полный ток; они делят его (ток зависит от номинала каждого резистора и общего количества резисторов в цепи).
Ключевые термины
- сопротивление : Противодействие прохождению электрического тока через этот элемент.
- параллельно : Расположение электрических компонентов, при котором ток течет по двум или более путям.
Обзор
Резисторы в цепи можно подключать последовательно или параллельно. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они подключены.
Parallel Circuits : Краткий обзор анализа параллельных цепей с использованием таблиц VIRP для студентов-физиков средней школы.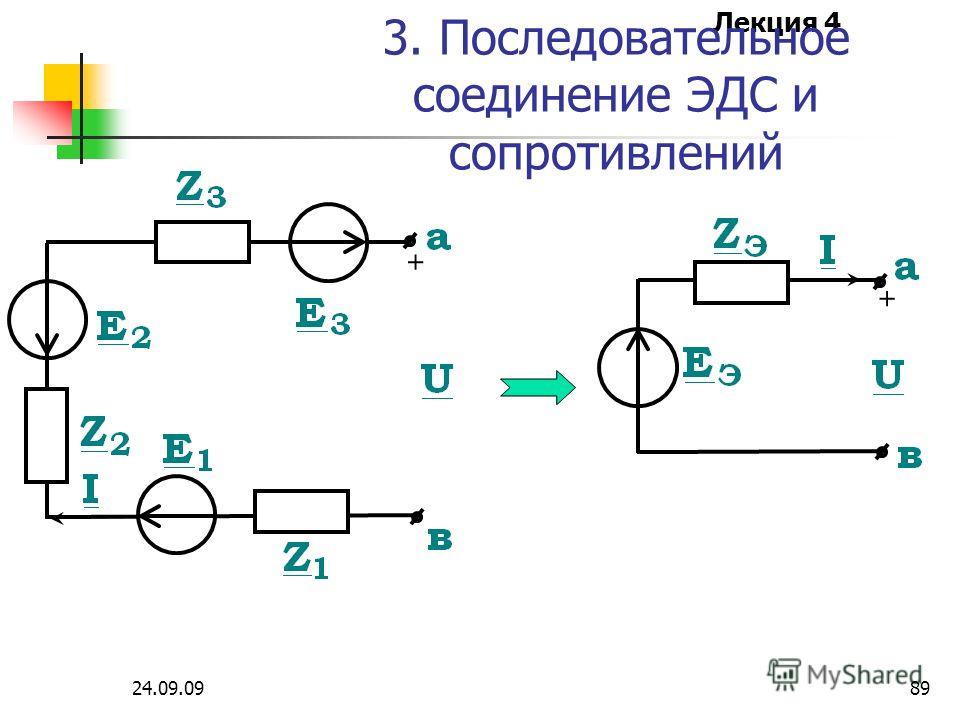
Параллельные резисторы
Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения путем соединения проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Параллельное соединение резисторов : Параллельное соединение резисторов.
Каждый резистор потребляет такой же ток, как если бы он был единственным резистором, подключенным к источнику напряжения. Это верно для схем в доме или квартире. Каждая розетка, подключенная к прибору («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.
ЗаконОм и параллельные резисторы
Каждый резистор в цепи имеет полное напряжение. Согласно закону Ома, токи, протекающие через отдельные резисторы, равны [латекс] \ text {I} _1 = \ frac {\ text {V}} {\ text {R} _1} [/ latex], [latex] \ text {I} _2 = \ frac {\ text {V}} {\ text {R} _2} [/ latex] и [latex] \ text {I} _3 = \ frac {\ text {V}} {\ text {R} _3} [/ латекс]. Сохранение заряда подразумевает, что полный ток является суммой этих токов:
Сохранение заряда подразумевает, что полный ток является суммой этих токов:
Параллельные резисторы : Три резистора, подключенные параллельно батарее, и эквивалентное одиночное или параллельное сопротивление.
[латекс] \ text {I} = \ text {I} _1 + \ text {I} _2 + \ text {I} _3. [/ Latex]
Подстановка выражений для отдельных токов дает:
[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R} _1} + \ frac {\ text {V}} {\ text {R} _2} + \ frac {\ текст {V}} {\ text {R} _3} [/ latex]
или
[латекс] \ text {I} = \ text {V} (\ frac {1} {\ text {R} _1} + \ frac {1} {\ text {R} _2} + \ frac {1} { \ text {R} _3}) [/ latex]
Это означает, что полное сопротивление в параллельной цепи равно сумме обратных сопротивлений каждого отдельного сопротивления.Следовательно, для каждой схемы с числом [latex] \ text {n} [/ latex] или параллельно подключенных резисторов —
[латекс] \ text {R} _ {\ text {n} \; (\ text {parallel})} = \ frac {1} {\ text {R} _1} + \ frac {1} {\ text { R} _2} + \ frac {1} {\ text {R} _3}… + \ frac {1} {\ text {R} _ \ text {n}}.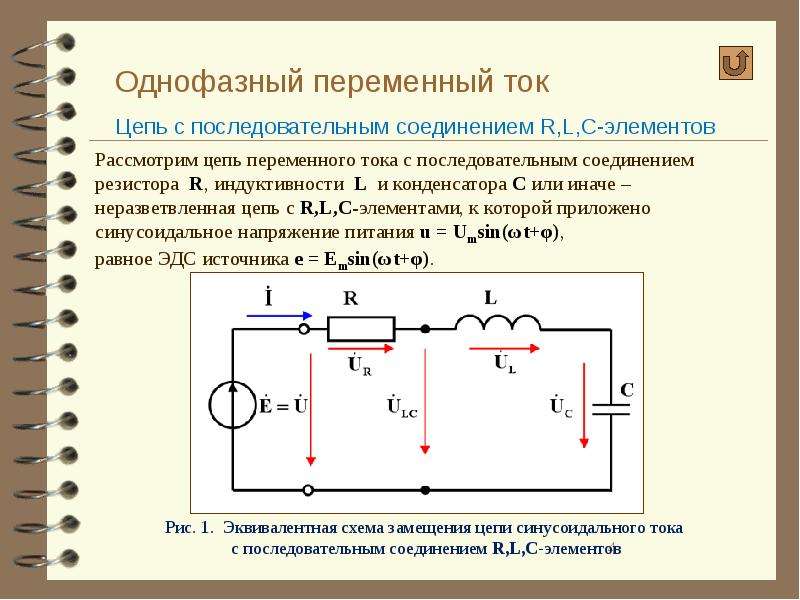 [/ Latex]
[/ Latex]
Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений. Когда резисторы подключены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Каждый резистор, включенный параллельно, имеет такое же полное напряжение источника, как на него, но делит общий ток между ними. Примером может служить соединение двух лампочек в параллельную цепь с аккумулятором на 1,5 В. В последовательной цепи две лампочки будут вдвое менее тусклыми при подключении к одному источнику батареи. Однако, если бы две лампочки были подключены параллельно, они были бы столь же яркими, как если бы они были подключены к батарее по отдельности. Поскольку к обеим лампочкам подается одинаковое полное напряжение, батарея также разряжается быстрее, поскольку она по существу обеспечивает полную энергию обеими лампочками.В последовательной цепи батарея будет работать столько же, сколько и с одной лампочкой, только тогда яркость будет разделена между лампочками.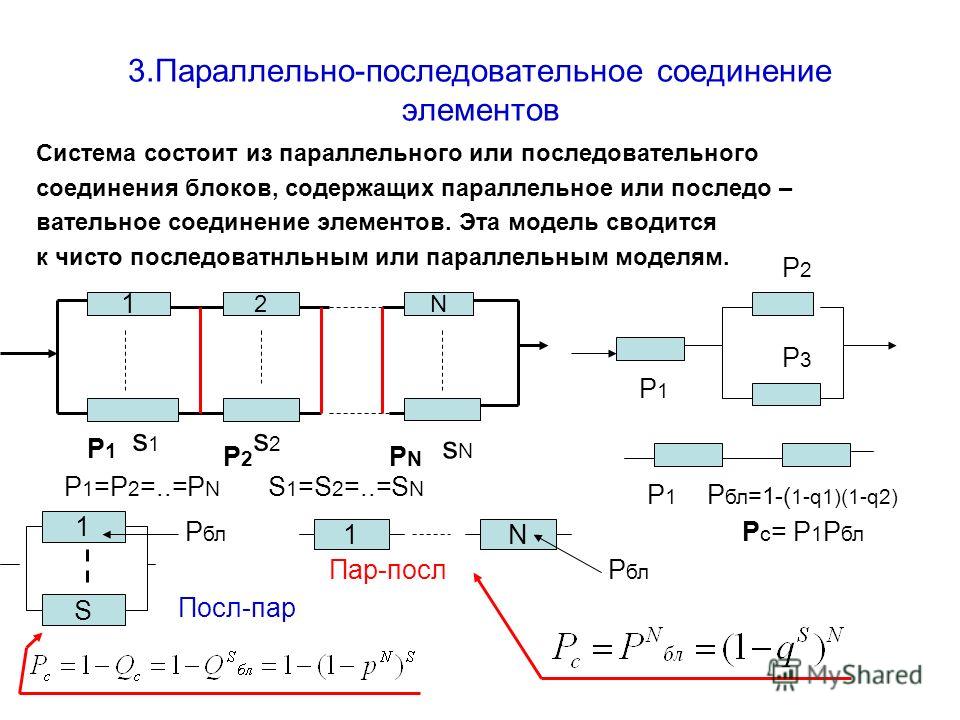
Комбинированные схемы
Комбинированная цепь может быть разбита на аналогичные части, которые работают последовательно или параллельно.
Цели обучения
Описать расположение резисторов в комбинированной цепи и его практическое значение
Основные выводы
Ключевые моменты
- Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного.
- Различные части комбинированной схемы могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление.
- Сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление в проводах относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными и повлиять на выходную мощность в бытовые приборы.
Ключевые термины
- серия : ряд элементов, которые следуют одно за другим или связаны друг за другом.

- параллельно : Расположение электрических компонентов, при котором ток течет по двум или более путям.
- Комбинированная схема : электрическая цепь, содержащая несколько резисторов, соединенных в комбинации как последовательного, так и параллельного соединения.
Комбинированные схемы
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Это часто встречается, особенно если учитывать сопротивление проводов.В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинированная цепь может быть разбита на аналогичные части, которые являются последовательными или параллельными, как показано на схеме. На рисунке общее сопротивление может быть вычислено путем соединения трех резисторов друг с другом последовательно или параллельно. R 1 и R 2 соединены параллельно друг другу, поэтому мы знаем, что для этого подмножества сопротивление, обратное сопротивлению, будет равно:
Сеть резисторов : В этой комбинированной схеме цепь может быть разбита на последовательный компонент и параллельный компонент.
Комбинированные схемы : Два параллельных резистора, соединенные последовательно с одним резистором.
[латекс] \ frac {1} {\ text {R} _1} + \ frac {1} {\ text {R} _2} [/ latex] или [латекс] \ frac {\ text {R} _1 \ text {R} _2} {\ text {R} _1 + \ text {R} _2} [/ latex]
R 3 соединены последовательно с как R 1 , так и R 2 , поэтому сопротивление будет рассчитываться как:
[латекс] \ text {R} = \ frac {\ text {R} _1 \ text {R} _2} {\ text {R} _1 + \ text {R} _2} + \ text {R} _3 [/ латекс ]
Сложные комбинированные схемы
Для более сложных комбинированных схем различные части могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление, как показано на. На этом рисунке комбинация из семи резисторов идентифицирована как включенные последовательно или параллельно. На исходном изображении две обведенные кружком секции показывают резисторы, включенные параллельно.
На этом рисунке комбинация из семи резисторов идентифицирована как включенные последовательно или параллельно. На исходном изображении две обведенные кружком секции показывают резисторы, включенные параллельно.
Сокращение комбинированной схемы : Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждый из них идентифицируется и уменьшается до эквивалентного сопротивления, а затем уменьшается до тех пор, пока не будет достигнуто одно эквивалентное сопротивление.
Уменьшение этих параллельных резисторов до одного значения R позволяет нам визуализировать схему в более упрощенном виде.На верхнем правом изображении мы видим, что обведенная кружком часть содержит два последовательно соединенных резистора. Мы можем дополнительно уменьшить это до другого значения R, добавив их. Следующий шаг показывает, что два обведенных резистора включены параллельно. Уменьшение тех бликов, что последние два включены последовательно и, таким образом, могут быть уменьшены до одного значения сопротивления для всей цепи.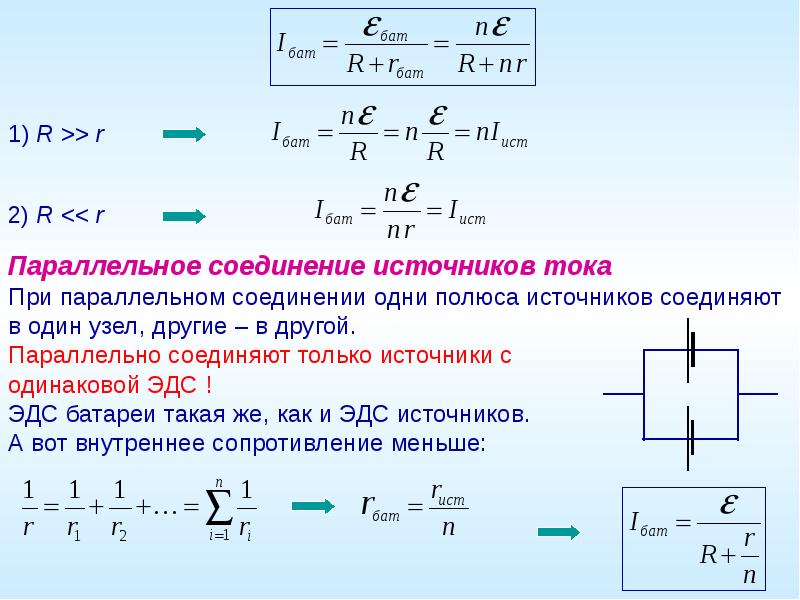
Практическое применение комбинированной схемы состоит в том, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Комбинированная цепь может быть преобразована в последовательную цепь на основе понимания эквивалентного сопротивления параллельных ветвей комбинированной цепи. Последовательная цепь может использоваться для определения общего сопротивления цепи. По сути, сопротивление провода является последовательным с резистором. Таким образом, увеличивается общее сопротивление и уменьшается ток. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение ИК-излучения в проводах также может быть значительным.
Зарядка аккумулятора: последовательные и параллельные ЭДС
При последовательном включении источников напряжения их ЭДС и внутренние сопротивления складываются; параллельно они остаются прежними.
Цели обучения
Сравните сопротивления и электродвижущие силы для источников напряжения, подключенных с одинаковой и противоположной полярностью, последовательно и параллельно
Основные выводы
Ключевые моменты
- ЭДС, соединенные последовательно с одинаковой полярностью, являются аддитивными и приводят к более высокой общей ЭДС.

- Две ЭДС, соединенные последовательно с противоположной полярностью, имеют общую ЭДС, равную разнице между ними, и могут использоваться для зарядки источника более низкого напряжения.
- Два источника напряжения с идентичными ЭДС, соединенные параллельно, имеют чистую ЭДС, эквивалентную одному источнику ЭДС, однако общее внутреннее сопротивление меньше и, следовательно, дает более высокий ток.
Ключевые термины
- параллельно : Расположение электрических компонентов, при котором ток течет по двум или более путям.
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
- серия : ряд элементов, которые следуют одно за другим или соединяются одно за другим.
Когда используется более одного источника напряжения, они могут быть подключены последовательно или параллельно, аналогично резисторам в цепи.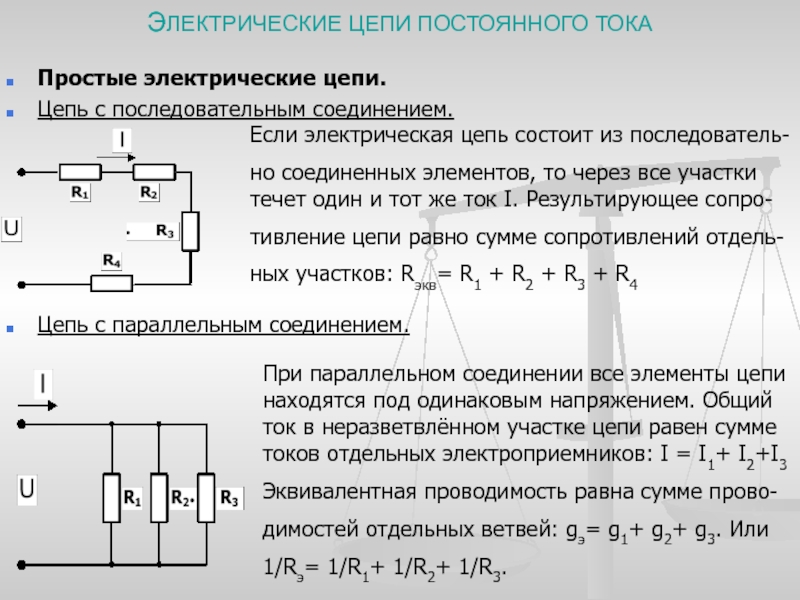 Когда источники напряжения включены последовательно в одном направлении, их внутренние сопротивления складываются, а их электродвижущая сила, или ЭДС, складывается алгебраически. Эти типы источников напряжения распространены в фонариках, игрушках и других устройствах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС.
Когда источники напряжения включены последовательно в одном направлении, их внутренние сопротивления складываются, а их электродвижущая сила, или ЭДС, складывается алгебраически. Эти типы источников напряжения распространены в фонариках, игрушках и других устройствах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС.
Фонарик и лампочка : Последовательное соединение двух источников напряжения в одном направлении. Эта схема представляет собой фонарик с двумя последовательно включенными ячейками (источниками напряжения) и одной лампочкой (сопротивление нагрузки).
Батарея — это соединение нескольких гальванических элементов. Однако недостатком такого последовательного соединения ячеек является то, что их внутреннее сопротивление увеличивается. Иногда это может быть проблематично. Например, если вы поместите в машину две батареи на 6 В вместо обычной батареи на 12 В, вы добавите как ЭДС, так и внутреннее сопротивление каждой батареи. Таким образом, вы получите ту же ЭДС 12 В, хотя внутреннее сопротивление тогда будет удвоено, что вызовет у вас проблемы, когда вы захотите запустить двигатель.
Таким образом, вы получите ту же ЭДС 12 В, хотя внутреннее сопротивление тогда будет удвоено, что вызовет у вас проблемы, когда вы захотите запустить двигатель.
Но, если ячейки противостоят друг другу, например, когда одна вставляется в прибор задом наперед, общая ЭДС меньше, так как это алгебраическая сумма отдельных ЭДС. Когда он перевернут, он создает ЭДС, которая противодействует другой, и приводит к разнице между двумя источниками напряжения.
Зарядное устройство : представляет два источника напряжения, соединенных последовательно с противоположными ЭДС. Ток течет в направлении большей ЭДС и ограничивается суммой внутренних сопротивлений.(Обратите внимание, что каждая ЭДС представлена на рисунке буквой E.) Зарядное устройство, подключенное к аккумулятору, является примером такого подключения. Зарядное устройство должно иметь большую ЭДС, чем аккумулятор, чтобы через него протекал обратный ток.
Когда два источника напряжения с идентичными ЭДС соединены параллельно и также подключены к сопротивлению нагрузки, общая ЭДС будет такой же, как и отдельные ЭДС. Но общее внутреннее сопротивление уменьшается, поскольку внутренние сопротивления параллельны. Таким образом, параллельное соединение может производить больший ток.
Но общее внутреннее сопротивление уменьшается, поскольку внутренние сопротивления параллельны. Таким образом, параллельное соединение может производить больший ток.
Две идентичные ЭДС : Два источника напряжения с одинаковыми ЭДС (каждый помечен буквой E), соединенные параллельно, создают одинаковую ЭДС, но имеют меньшее общее внутреннее сопротивление, чем отдельные источники. Параллельные комбинации часто используются для подачи большего тока.
ЭДС и напряжение на клеммах
Выходное напряжение или напряжение на клеммах источника напряжения, такого как аккумулятор, зависит от его электродвижущей силы и внутреннего сопротивления.
Цели обучения
Выразите взаимосвязь между электродвижущей силой и напряжением на клеммах в форме уравнения
Основные выводы
Ключевые моменты
- Электродвижущая сила (ЭДС) — это разность потенциалов источника при отсутствии тока.
- Напряжение на клеммах — это выходное напряжение устройства, измеренное на его клеммах.

- Напряжение на клеммах рассчитывается по формуле V = ЭДС — Ir.
Ключевые термины
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
- напряжение на клеммах : выходное напряжение устройства, измеренное на его клеммах.
- разность потенциалов : разница в потенциальной энергии между двумя точками в электрическом поле; разница в заряде между двумя точками в электрической цепи; Напряжение.
Когда вы забываете выключить автомобильные фары, они постепенно тускнеют по мере разряда аккумулятора. Почему они просто не мигают, когда батарея разряжена? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разряда батареи. Причина снижения выходного напряжения для разряженных или перегруженных батарей заключается в том, что все источники напряжения состоят из двух основных частей — источника электрической энергии и внутреннего сопротивления.
Электродвижущая сила
Все источники напряжения создают разность потенциалов и могут подавать ток, если подключены к сопротивлению. В небольшом масштабе разность потенциалов создает электрическое поле, которое воздействует на заряды, вызывая ток. Мы называем эту разность потенциалов электродвижущей силой (сокращенно ЭДС). ЭДС — это вообще не сила; это особый тип разности потенциалов источника при отсутствии тока. Единицы измерения ЭДС — вольт.
Электродвижущая сила напрямую связана с источником разности потенциалов, например с конкретной комбинацией химических веществ в батарее.Однако при протекании тока ЭДС отличается от выходного напряжения устройства. Напряжение на выводах батареи, например, меньше, чем ЭДС, когда батарея подает ток, и оно уменьшается дальше, когда батарея разряжается или разряжается. Однако, если выходное напряжение устройства можно измерить без потребления тока, то выходное напряжение будет равно ЭДС (даже для сильно разряженной батареи).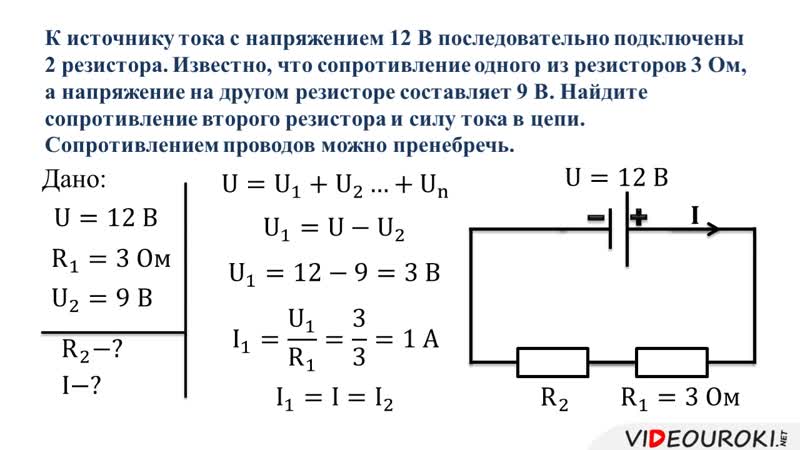
Напряжение на клеммах
представляет схематическое изображение источника напряжения.Выходное напряжение устройства измеряется на его выводах и называется напряжением на выводах В . Напряжение на клеммах определяется уравнением:
Схематическое изображение источника напряжения : Любой источник напряжения (в данном случае углеродно-цинковый сухой элемент) имеет ЭДС, связанную с источником разности потенциалов, и внутреннее сопротивление r, связанное с его конструкцией. (Обратите внимание, что сценарий E означает ЭДС.) Также показаны выходные клеммы, на которых измеряется напряжение на клеммах V.Поскольку V = ЭДС-Ir, напряжение на клеммах равно ЭДС, только если ток не течет.
[латекс] \ text {V} = \ text {emf} — \ text {Ir} [/ latex],
, где r — внутреннее сопротивление, а I — ток, протекающий во время измерения.
I является положительным, если ток течет от положительного вывода. Чем больше ток, тем меньше напряжение на клеммах. Точно так же верно, что чем больше внутреннее сопротивление, тем меньше напряжение на клеммах.
Точно так же верно, что чем больше внутреннее сопротивление, тем меньше напряжение на клеммах.
ЭДС последовательно и параллельно
Когда используется более одного источника напряжения, они могут быть подключены последовательно или параллельно, аналогично резисторам в цепи.Когда источники напряжения включены последовательно в одном направлении, их внутренние сопротивления складываются, а их электродвижущая сила, или ЭДС, складывается алгебраически. Эти типы источников напряжения распространены в фонариках, игрушках и других устройствах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС.
Фонарик и лампочка
Последовательное соединение двух источников напряжения в одном направлении. Эта схема представляет собой фонарик с двумя последовательно включенными ячейками (источниками напряжения) и одной лампочкой (сопротивление нагрузки).
Батарея — это соединение нескольких гальванических элементов. Однако недостатком такого последовательного соединения ячеек является то, что их внутреннее сопротивление увеличивается. Иногда это может быть проблематично. Например, если вы поместите в машину две батареи на 6 В вместо обычной батареи на 12 В, вы добавите как ЭДС, так и внутреннее сопротивление каждой батареи. Таким образом, вы получите ту же ЭДС 12 В, хотя внутреннее сопротивление тогда будет удвоено, что вызовет у вас проблемы, когда вы захотите запустить двигатель.
Однако недостатком такого последовательного соединения ячеек является то, что их внутреннее сопротивление увеличивается. Иногда это может быть проблематично. Например, если вы поместите в машину две батареи на 6 В вместо обычной батареи на 12 В, вы добавите как ЭДС, так и внутреннее сопротивление каждой батареи. Таким образом, вы получите ту же ЭДС 12 В, хотя внутреннее сопротивление тогда будет удвоено, что вызовет у вас проблемы, когда вы захотите запустить двигатель.
Но, если ячейки противостоят друг другу, например, когда одна вставляется в прибор задом наперед, общая ЭДС меньше, так как это алгебраическая сумма отдельных ЭДС. Когда он перевернут, он создает ЭДС, которая противодействует другой, и приводит к разнице между двумя источниками напряжения.
Зарядное устройство
Это два источника напряжения, соединенных последовательно с противоположными ЭДС. Ток течет в направлении большей ЭДС и ограничивается суммой внутренних сопротивлений.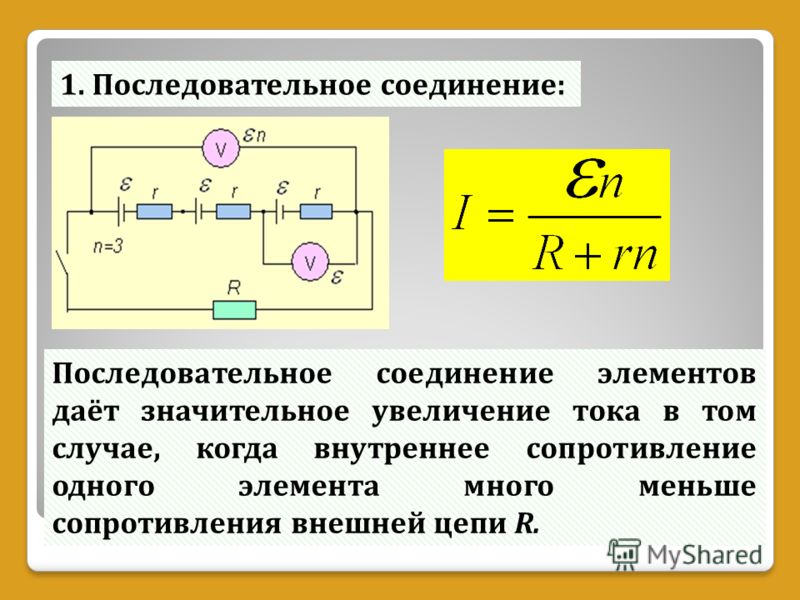 (Обратите внимание, что каждая ЭДС представлена на рисунке буквой E.) Зарядное устройство, подключенное к аккумулятору, является примером такого подключения. Зарядное устройство должно иметь большую ЭДС, чем аккумулятор, чтобы через него протекал обратный ток.
(Обратите внимание, что каждая ЭДС представлена на рисунке буквой E.) Зарядное устройство, подключенное к аккумулятору, является примером такого подключения. Зарядное устройство должно иметь большую ЭДС, чем аккумулятор, чтобы через него протекал обратный ток.
Когда два источника напряжения с идентичными ЭДС соединены параллельно и также подключены к сопротивлению нагрузки, общая ЭДС будет такой же, как и отдельные ЭДС. Но общее внутреннее сопротивление уменьшается, поскольку внутренние сопротивления параллельны.Таким образом, параллельное соединение может производить больший ток.
Две одинаковые ЭДС
Два источника напряжения с идентичными ЭДС (каждый из которых обозначен надписью E), подключенные параллельно, создают одинаковую ЭДС, но имеют меньшее общее внутреннее сопротивление, чем отдельные источники. Параллельные комбинации часто используются для подачи большего тока.
ЭДС и внутреннее сопротивление
ЭДС и внутреннее сопротивлениеследующий: резисторы последовательно и Up: Electric Current Предыдущий: Сопротивление и удельное сопротивление Теперь настоящие батареи изготавливаются из материалов с ненулевым удельным сопротивлением.
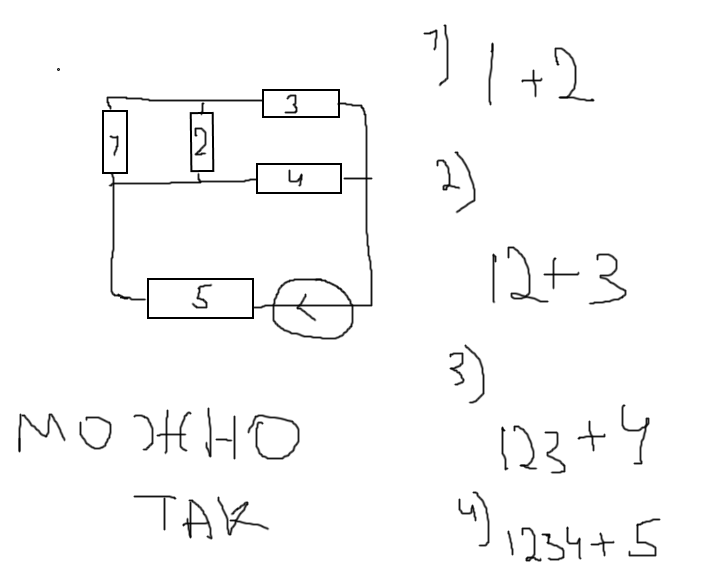 Отсюда следует, что настоящие батареи — это не просто источники чистого напряжения. Они также обладают внутренние сопротивления .
Между прочим, чистое напряжение
Источник обычно обозначается как ЭДС (что означает электродвижущую силу ). Конечно,
ЭДС измеряется в вольтах.
Аккумулятор можно смоделировать как ЭДС, включенную последовательно с резистором.
, который представляет его внутреннее сопротивление. Предположим, что такие
батарея используется для управления током через внешний нагрузочный резистор, так как
изображенный на рис.17.
Обратите внимание, что на принципиальных схемах ЭДС представлена двумя близко расположенными параллельными
линии неравной длины. Электрический потенциал более длинной линии больше, чем
тот из более коротких по вольтам. Резистор представлен как
зигзагообразная линия.
Отсюда следует, что настоящие батареи — это не просто источники чистого напряжения. Они также обладают внутренние сопротивления .
Между прочим, чистое напряжение
Источник обычно обозначается как ЭДС (что означает электродвижущую силу ). Конечно,
ЭДС измеряется в вольтах.
Аккумулятор можно смоделировать как ЭДС, включенную последовательно с резистором.
, который представляет его внутреннее сопротивление. Предположим, что такие
батарея используется для управления током через внешний нагрузочный резистор, так как
изображенный на рис.17.
Обратите внимание, что на принципиальных схемах ЭДС представлена двумя близко расположенными параллельными
линии неравной длины. Электрический потенциал более длинной линии больше, чем
тот из более коротких по вольтам. Резистор представлен как
зигзагообразная линия. Рассмотрим батарею на рисунке.Напряжение аккумулятора равно
определяется как разность электрического потенциала между его положительным и
отрицательные клеммы: т.е. , точки и соответственно. Когда мы переходим от к
, электрический потенциал увеличивается на вольт, когда мы пересекаем
ЭДС, но затем уменьшается на вольт, когда мы пересекаем внутренний резистор.
Падение напряжения на резисторе следует из закона Ома, из которого следует, что
падение напряжения на резисторе, по которому течет ток
, находится в том направлении, в котором
текущие потоки.Таким образом, напряжение аккумулятора связано с его ЭДС.
и внутреннее сопротивление через
| (133) |
Обычно мы думаем, что ЭДС батареи по существу постоянная (поскольку она зависит только от химической реакции, происходящей внутри батареи, которая преобразует химическая энергия в электрическую), поэтому мы должны сделать вывод, что напряжение батарея на самом деле уменьшается по мере увеличения тока, потребляемого от нее.
 Фактически, напряжение равно только
ЭДС при пренебрежимо малом токе. Текущий розыгрыш
от аккумулятора обычно не может превышать критического значения
Фактически, напряжение равно только
ЭДС при пренебрежимо малом токе. Текущий розыгрыш
от аккумулятора обычно не может превышать критического значения | (134) |
поскольку напряжение становится отрицательным (что может произойти только если резистор нагрузки также отрицательный: это практически невозможно). Отсюда следует, что если мы закоротим аккумулятор, подключив его положительные и отрицательные клеммы вместе с помощью проводящего провода с незначительным сопротивлением, ток, потребляемый от батареи, ограничен ее внутренним сопротивлением.Фактически в этом случае сила тока равна максимально возможной. Текущий .
Настоящая батарея обычно характеризуется
его ЭДС ( т.е. , его
напряжение при нулевом токе) и максимальный ток, который он может подавать.
Например, стандартный сухой элемент (, т. Е. , своего рода
аккумулятор, используемый для питания калькуляторов и фонарей) обычно рассчитан на
и скажи) . Таким образом, ничего действительно катастрофического не произойдет.
произойдет, если мы закоротим сухой элемент.Мы разрядим батарею через
сравнительно короткий промежуток времени, но опасно большой ток не будет
поток. С другой стороны, автомобильный аккумулятор обычно рассчитывается на
и что-то вроде (такой ток нужен для
запустить стартер). Понятно, что автомобильный аккумулятор должен иметь много
более низкое внутреннее сопротивление, чем у сухого элемента. Отсюда следует, что если
мы были достаточно глупы, чтобы замкнуть автомобильный аккумулятор, в результате
довольно катастрофичен (представьте себе всю энергию, необходимую для запуска двигателя
автомобиль собирается тонким проводом, соединяющим клеммы аккумулятора вместе).
Е. , своего рода
аккумулятор, используемый для питания калькуляторов и фонарей) обычно рассчитан на
и скажи) . Таким образом, ничего действительно катастрофического не произойдет.
произойдет, если мы закоротим сухой элемент.Мы разрядим батарею через
сравнительно короткий промежуток времени, но опасно большой ток не будет
поток. С другой стороны, автомобильный аккумулятор обычно рассчитывается на
и что-то вроде (такой ток нужен для
запустить стартер). Понятно, что автомобильный аккумулятор должен иметь много
более низкое внутреннее сопротивление, чем у сухого элемента. Отсюда следует, что если
мы были достаточно глупы, чтобы замкнуть автомобильный аккумулятор, в результате
довольно катастрофичен (представьте себе всю энергию, необходимую для запуска двигателя
автомобиль собирается тонким проводом, соединяющим клеммы аккумулятора вместе).
следующий: резисторы последовательно и Up: Electric Current Предыдущий: Сопротивление и удельное сопротивление Ричард Фицпатрик 2007-07-14
Батареи последовательно и Батареи параллельно
Батарейные элементы
Батарея — это электрический элемент, в котором в результате химической реакции создается электрический потенциал.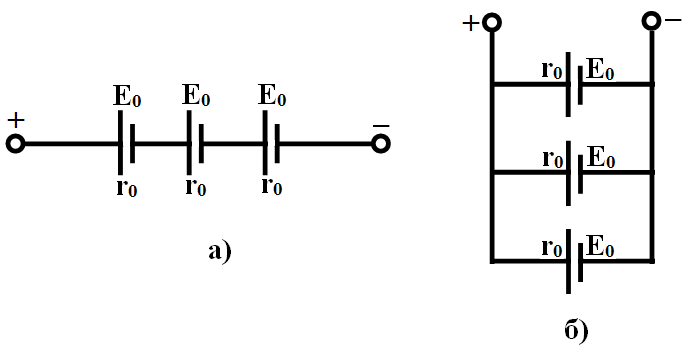 Каждая электрохимическая реакция имеет предел создания разности электрических потенциалов между двумя электродами.
Каждая электрохимическая реакция имеет предел создания разности электрических потенциалов между двумя электродами.
Батарейные элементы — это элементы, в которых происходят эти электрохимические реакции с образованием ограниченной разности электрических потенциалов. Для достижения желаемой разности электрических потенциалов на клеммах батареи необходимо последовательно соединить несколько ячеек. Отсюда можно сделать вывод, что батарея — это комбинация нескольких ячеек, где ячейка — это единица батареи. Например, никель-кадмиевые элементы батареи обычно вырабатывают около 1,2 В на элемент, в то время как свинцово-кислотные батареи вырабатывают около 2 В на элемент.Таким образом, 12-вольтная батарея будет иметь в общей сложности 6 последовательно соединенных ячеек.
ЭДС батареи
Если кто-нибудь просто измеряет разность электрических потенциалов между двумя выводами батареи, когда нагрузка не подключена к батарее, он или она получит напряжение, развиваемое в батарее, когда через нее не течет ток.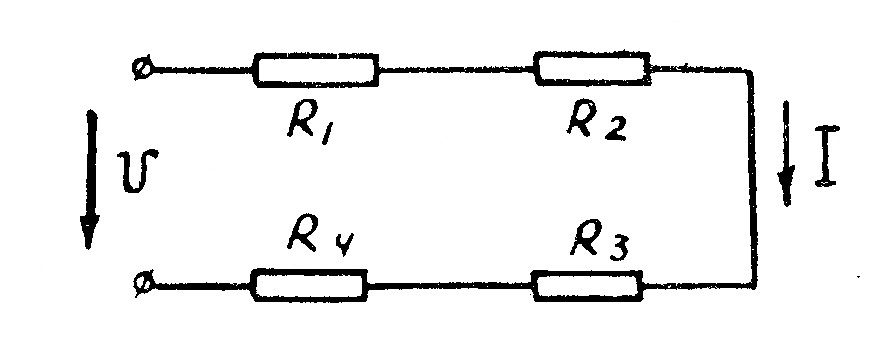 Это напряжение обычно называют электродвижущей силой или ЭДС батареи . Это также называется напряжением холостого хода аккумулятора.
Это напряжение обычно называют электродвижущей силой или ЭДС батареи . Это также называется напряжением холостого хода аккумулятора.
Напряжение на клеммах батареи
Напряжение на клеммах батареи — это разность потенциалов на ее клеммах, когда от нее отводится ток.Фактически, когда нагрузка подключена к батарее, через нее будет течь ток нагрузки. Поскольку батарея является электрическим оборудованием, внутри нее должно быть электрическое сопротивление. Из-за внутреннего сопротивления аккумулятора на нем будут некоторые падения напряжения. Таким образом, если кто-либо измеряет напряжение на клеммах нагрузки, то есть напряжение на клеммах батареи , когда нагрузка подключена, он или она получит напряжение, которое меньше, чем ЭДС батареи, из-за внутреннего падения напряжения батареи.
Если E — ЭДС или напряжение холостого хода батареи, а V — напряжение на клеммах нагрузки нагрузки батареи, то E — V = внутреннее падение напряжения батареи.
Согласно закону Ома, это внутреннее падение напряжения является не чем иным, как продуктом электрического сопротивления батареи и протекающего через нее тока.
Внутреннее сопротивление батареи
Все сопротивление, с которым сталкивается ток, как если бы он протекал через батарею от отрицательной клеммы к положительной клемме, называется внутренним сопротивлением батареи .
Параллельные батареи серииБатарейные элементы могут подключаться последовательно, параллельно, а также в сочетании последовательного и параллельного.
Батареи серии Когда в батарее положительная клемма одной ячейки соединена с отрицательной клеммой следующей ячейки, то говорят, что элементы соединены последовательно, или просто батарея серии . Здесь общая ЭДС батареи представляет собой алгебраическую сумму всех отдельных ячеек, соединенных последовательно.Но общий ток разряда батареи не превышает ток разряда отдельных ячеек.
Если E — общая ЭДС батареи, объединенная n числом ячеек, а E 1 , E 2 , E 3 , …………… E n — ЭДС отдельных элементов.
Аналогично, если r 1 , r 2 , r 3 , …………… r n — это внутренние сопротивления отдельных ячеек, то внутреннее сопротивление аккумулятора будет равно сумме внутреннего сопротивления отдельных ячеек i.е.
Параллельные батареи
Когда положительные выводы всех ячеек соединены вместе и аналогично отрицательные выводы этих ячеек соединены вместе в батарее, то говорят, что элементы соединены параллельно. Эти комбинации также обозначаются как параллельных батарей . Если ЭДС каждой ячейки идентична, то ЭДС батареи, объединенная числом n элементов, соединенных параллельно, равна ЭДС каждой ячейки. Результирующее внутреннее сопротивление комбинации составляет,
Ток, отдаваемый батареей, является суммой токов, подаваемых отдельными элементами.
Смешанное группирование батарей или последовательно параллельных батарей
Как мы уже говорили ранее, элементы в батарее также могут быть соединены как последовательно, так и параллельно. Эти комбинации некоторое время называются параллельной батареей серии . Нагрузке может потребоваться как напряжение, так и ток больше, чем у отдельного элемента батареи. Для достижения требуемого напряжения нагрузки желаемое количество аккумуляторных элементов может быть объединено последовательно, а для достижения требуемого тока нагрузки желаемое количество этих последовательных комбинаций соединяется параллельно.Пусть m — номера серий, каждая из которых содержит n номеров одинаковых ячеек, соединены параллельно.
Снова предположим, что ЭДС каждой ячейки равна E, а внутреннее сопротивление каждой ячейки равно r. Поскольку в каждой серии подключено n элементов, ЭДС каждой серии, а также батареи будет nE. Эквивалентное сопротивление серии — nr. As, m количество последовательно соединенных параллельно эквивалентное внутреннее сопротивление этой серии и параллельной батареи составляет nr / m.
Видео-презентация о последовательных параллельных батареях
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
Физика — Электродвижущая сила — Бирмингемский университет
Электродвижущая сила (ЭДС) равна разности потенциалов на клеммах при отсутствии тока. ЭДС и разность потенциалов на клеммах ( В, ) измеряются в вольтах, но это не одно и то же. ЭДС ( ϵ ) — это количество энергии ( E ), обеспечиваемое батареей для каждого проходящего кулон заряда ( Q ).
ЭДС и разность потенциалов на клеммах ( В, ) измеряются в вольтах, но это не одно и то же. ЭДС ( ϵ ) — это количество энергии ( E ), обеспечиваемое батареей для каждого проходящего кулон заряда ( Q ).
Как рассчитать ЭДС?
ЭДС можно записать через внутреннее сопротивление батареи ( r ) где: ϵ = I (r + R )
Что из закона Ома, мы можем изменить это с точки зрения оконечного сопротивления: ϵ = В + Ir
ЭДС ячейки может быть определена путем измерения напряжения на ячейке с помощью вольтметра и тока в цепи с помощью амперметра для различных сопротивлений.Затем мы можем настроить схему для определения ЭДС, как показано ниже.
ЭДС и внутреннее сопротивление электрических элементов и батарей
Исследование ЭМП
Как закон Фарадея соотносится с ЭМП?
Закон Фарадея гласит, что любое изменение магнитного поля катушки будет индуцировать в катушке ЭДС (а следовательно, и ток). Он пропорционален минус скорости изменения магнитного потока ( ϕ ) (примечание: N — количество витков в катушке).
Он пропорционален минус скорости изменения магнитного потока ( ϕ ) (примечание: N — количество витков в катушке).
Согласно закону Фарадея, общество извлекло выгоду из таких важных технологий, как трансформаторы, которые используются для передачи электроэнергии в национальной энергосистеме Великобритании, которая сейчас необходима в наших домах. Также он используется в электрических генераторах и двигателях, таких как плотины гидроэлектростанций, которые производят электричество, которое сейчас является неотъемлемой частью наших современных технологических потребностей. Текущий исследовательский проект в Бирмингеме, MAG-DRIVE, направлен на поиск способов разработки и улучшения материалов с постоянными магнитами, которые можно использовать в электромобилях следующего поколения.ЭМП также генерируется солнечными батареями, поэтому он важен для исследований в области возобновляемых источников энергии.
Лабораторные признания
Исследователи подкаста In the Laboratory Confessions рассказывают о своем лабораторном опыте в контексте практических экзаменов A Level.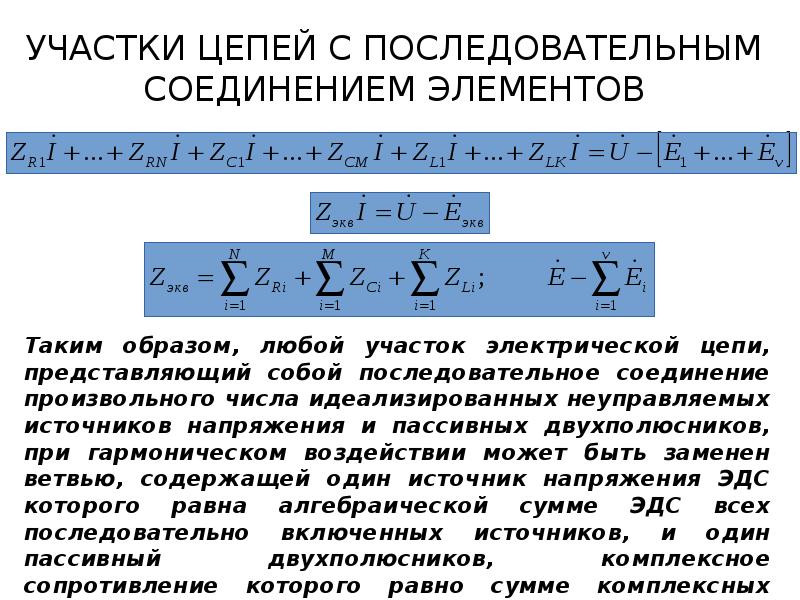 Эпизоды, посвященные правильному использованию цифровых инструментов (простое гармоническое движение), правильному построению принципиальных схем (удельное сопротивление в проводе) и использованию источников питания постоянного тока (конденсаторов), имеют отношение к эксперименту по ЭДС, ниже вы можете услышать удельное сопротивление. в проводном подкасте.
Эпизоды, посвященные правильному использованию цифровых инструментов (простое гармоническое движение), правильному построению принципиальных схем (удельное сопротивление в проводе) и использованию источников питания постоянного тока (конденсаторов), имеют отношение к эксперименту по ЭДС, ниже вы можете услышать удельное сопротивление. в проводном подкасте.
Как мы интерпретируем наши данные?
По мере увеличения сопротивления переменного резистора величина тока будет уменьшаться. График зависимости напряжения от тока должен давать линейную зависимость, где градиент линии дает отрицательное внутреннее сопротивление ячейки ( -r ), а точка пересечения дает ЭДС (напряжение, при котором ток равен 0).
Выполнение нескольких измерений при разных значениях сопротивления даст больше точек на графике V-I, что сделает подбор более надежным.Также рекомендуется повторить измерения, поскольку ячейка будет постепенно стекать, что повлияет на показания. Во избежание разряда элемента / батареи ее следует отключать между измерениями.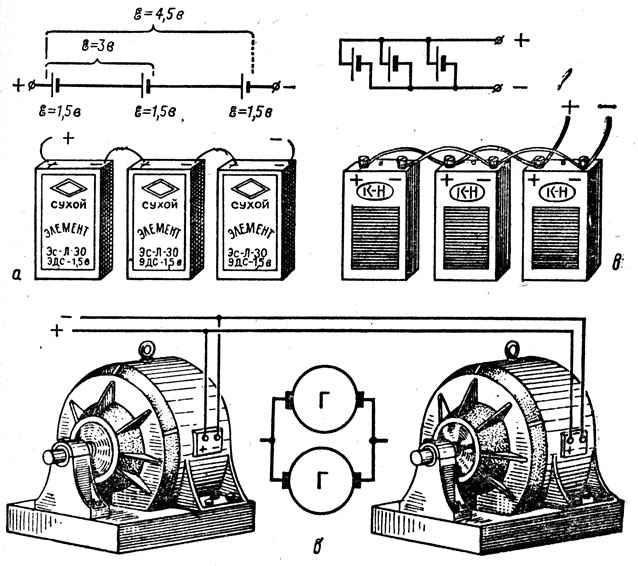 Как вариант, в схему можно включить выключатель. Также рекомендуется не использовать перезаряжаемые батареи, поскольку они имеют низкое внутреннее сопротивление.
Как вариант, в схему можно включить выключатель. Также рекомендуется не использовать перезаряжаемые батареи, поскольку они имеют низкое внутреннее сопротивление.
Хотя этот эксперимент довольно прост, он поможет вам отличить конечную разницу от ЭДС, что может быть сложной концепцией для понимания учащимися.Поскольку люди становятся все более зависимыми от электричества, исследования, связанные с ЭМП, важны для развития и технического прогресса электричества.
Следующие шаги
Эти ссылки предоставлены только для удобства и в информационных целях; они не означают одобрения или одобрения Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте. Бирмингемский университет не несет ответственности за точность, законность или содержание внешнего сайта или за содержание последующих ссылок.Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы относительно его содержания.
Напряжение
НАПРЯЖЕНИЕ
Прочитав этот раздел, вы сможете сделать следующее:
- Определите ЭДС и объясните, как она измеряется.

- Объясните, почему ЭДС важна для протекания электрического тока.
- Перечислите несколько примеров источников электродвижущей силы.
Нам также нужно кое-что знать о силе, которая заставляет электроны двигаться в электрической цепи. Эта сила называется электродвижущей силой или ЭДС . Иногда удобно думать об ЭДС как об электрическом давлении. Другими словами, это сила, которая заставляет электроны двигаться в определенном направлении внутри проводника.
Но как нам создать это «электрическое давление» для генерации электронного потока? Источников ЭМП много.Вот некоторые из наиболее распространенных: батареи, генераторы и фотоэлектрические элементы, и это лишь некоторые из них.
Батареи сконструированы таким образом, что в одном материале слишком много электронов, а в другом — недостаточно. Электроны хотят уравновесить электростатический заряд, перемещаясь от материала с избыточными электронами к материалу с нехваткой электронов. Однако они не могут этого сделать, потому что для них нет проводящего пути. Однако, если эти два несбалансированных материала в батарее соединены вместе с помощью проводника, электрический ток будет течь по мере того, как электрон перемещается из отрицательно заряженной области в положительно заряженную область.Когда вы используете батарею, вы позволяете электронам проходить от одного конца батареи через проводник и что-то вроде лампочки к другому концу батареи. Батарея будет работать до тех пор, пока на обоих концах батареи не будет баланса электронов. Предупреждение: вы никогда не должны подключать проводник к двум концам батареи, не позволяя электронам проходить через что-то вроде лампочки, которая замедляет токи. Если позволить электронам течь слишком быстро, проводник станет очень горячим, и он и аккумулятор могут быть повреждены.
Однако они не могут этого сделать, потому что для них нет проводящего пути. Однако, если эти два несбалансированных материала в батарее соединены вместе с помощью проводника, электрический ток будет течь по мере того, как электрон перемещается из отрицательно заряженной области в положительно заряженную область.Когда вы используете батарею, вы позволяете электронам проходить от одного конца батареи через проводник и что-то вроде лампочки к другому концу батареи. Батарея будет работать до тех пор, пока на обоих концах батареи не будет баланса электронов. Предупреждение: вы никогда не должны подключать проводник к двум концам батареи, не позволяя электронам проходить через что-то вроде лампочки, которая замедляет токи. Если позволить электронам течь слишком быстро, проводник станет очень горячим, и он и аккумулятор могут быть повреждены.
В следующем разделе мы обсудим, как электрические генераторы используют магнетизм для создания ЭДС. Фотоэлектрические элементы превращают световую энергию таких источников, как солнце, в энергию.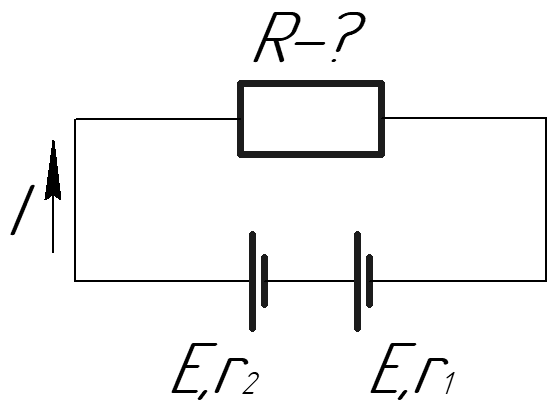 Чтобы понять фотовольтаический процесс, вам необходимо знать о полупроводниках, поэтому мы не будем рассматривать их в этом материале.
Чтобы понять фотовольтаический процесс, вам необходимо знать о полупроводниках, поэтому мы не будем рассматривать их в этом материале.
Перейдите по этой ссылке, чтобы узнать больше о вольте: Что такое вольт?
Как усилитель и вольт работают вместе в электричестве?
Чтобы понять, как связаны напряжение и сила тока, иногда полезно провести аналогию с водой.Посмотрите на изображение воды, текущей в садовом шланге. Представьте, что электричество течет по проводу так же, как вода течет по шлангу. Напряжение, заставляющее электрический ток течь в проводе, можно рассматривать как давление воды в кране, которое заставляет воду течь. Если бы мы увеличили давление в гидранте, по шлангу потекло бы больше воды. Точно так же, если мы увеличим электрическое давление или напряжение, в провод будет течь больше электронов.
Имеет ли смысл, что если бы мы сбросили давление в гидранте, отключив его, вода перестала бы течь? То же самое и с электрической схемой.

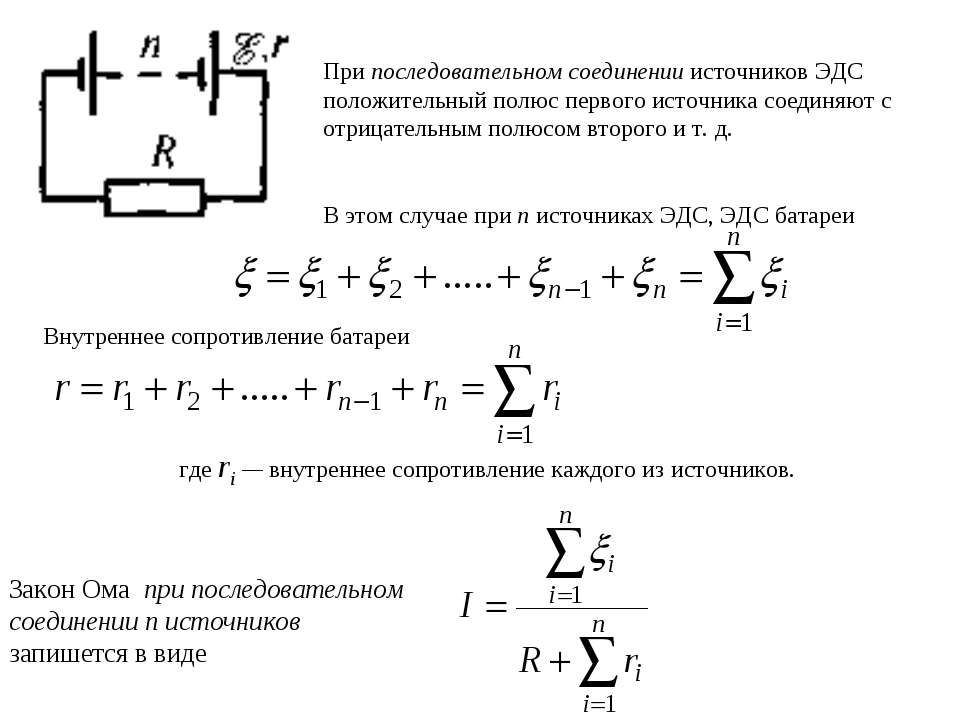

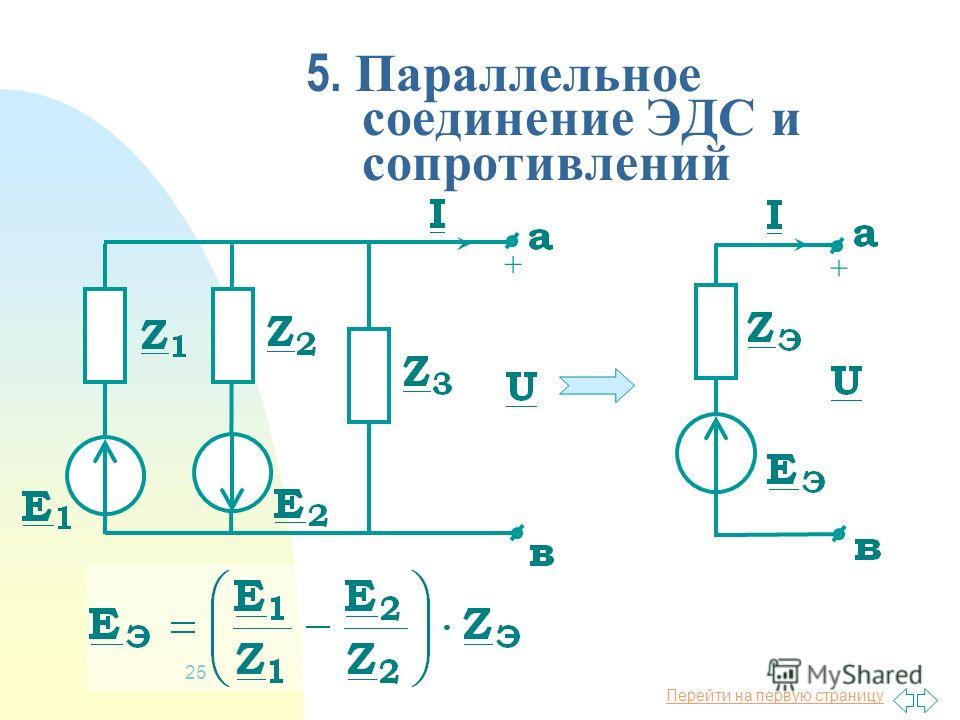
 В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.