Последовательное соединение проводников | Физика

Электрические цепи, используемые на практике, содержат, как правило, несколько потребителей электроэнергии. Эти потребители могут быть по-разному соединены друг с другом, например последовательно или параллельно.

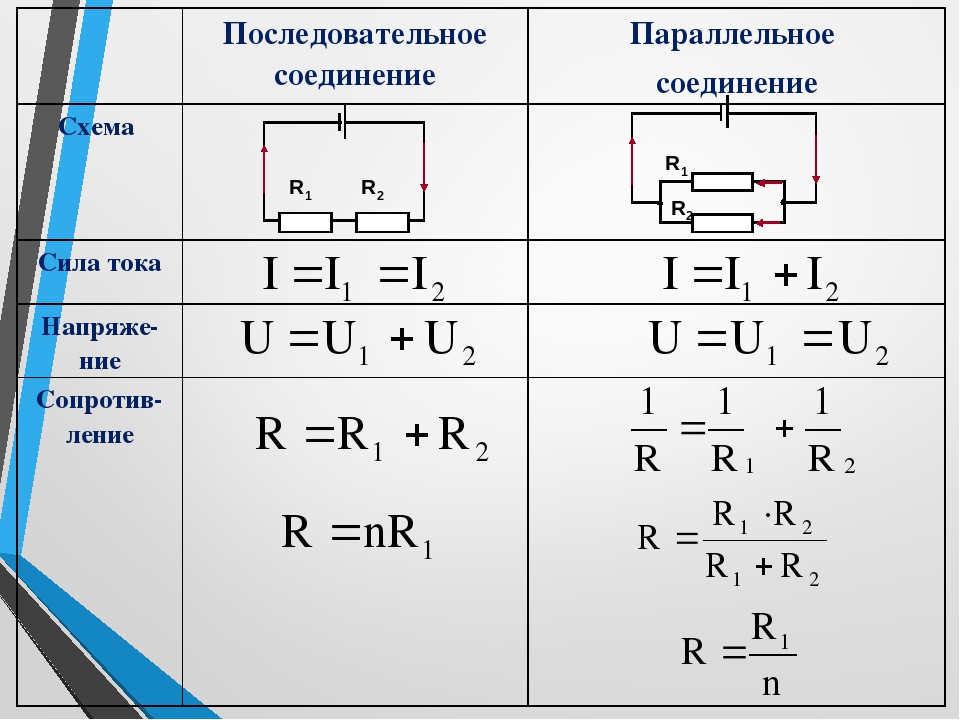
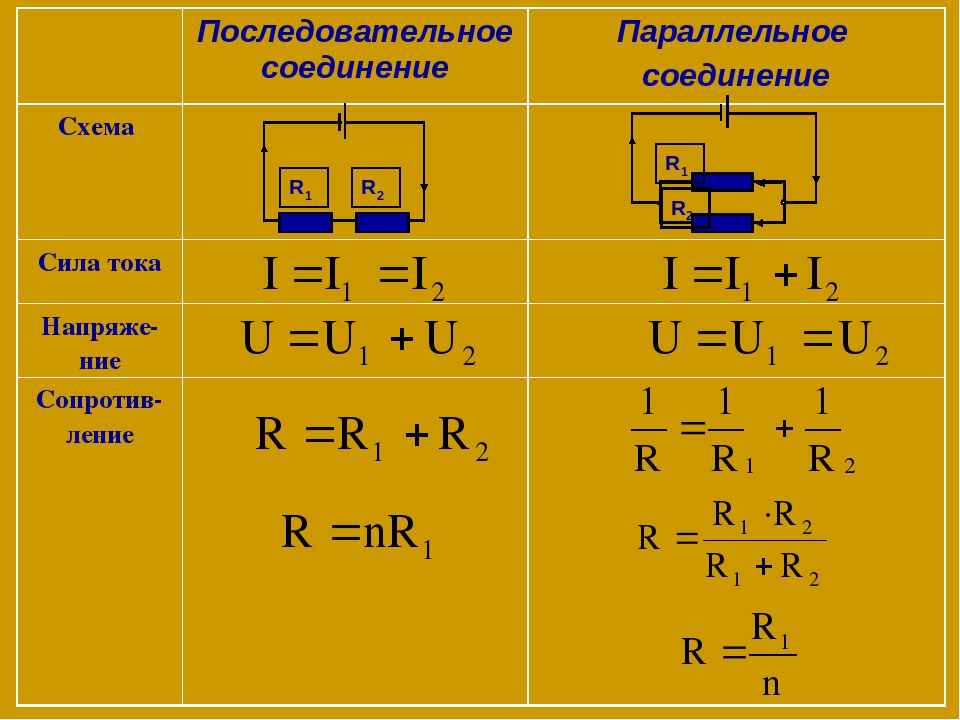
При последовательном соединении потребителей они включаются в цепь поочередно друг за другом без разветвлений проводов между ними. Именно так соединены резисторы, изображенные на рисунке 41. Форма линий, обозначающих при этом соединительные провода, не играет роли, и потому схема цепи при одном и том же типе соединения может выглядеть по-разному.

Обозначим через I₁, U₁ и R₁ силу тока, напряжение и сопротивление на первом участке цепи (первом резисторе на рисунке 41, а), а через I₂, U₂ и R₂ силу тока, напряжение и сопротивление на втором участке цепи (втором резисторе на рисунке 41, а). Общее сопротивление обоих участков обозначим через R, общее напряжение на них — через U, а общую силу тока, которая совпадает с силой тока внутри источника, — через I. Тогда связь между общими значениями силы тока, напряжения и сопротивления с их значениями на отдельных участках цепи может быть выражена в виде следующих соотношений:

I = I₁ = I₂, (16.1) U = U₁ + U₂, (16.2) R = R₁ + R₂. (16.3)

Чтобы убедиться в справедливости этих соотношений, следует собрать соответствующую цепь и с помощью амперметра и вольтметра произвести необходимые измерения.

Итак, при последовательном соединении проводников сила тока везде одинакова, напряжение в цепи равно сумме напряжений на отдельных участках, а общее сопротивление складывается из сопротивлений отдельных проводников.

Соотношения (16.1)-(16.3) допускают обобщение: все приведенные закономерности справедливы для любого числа последовательно соединенных проводников.

Из равенства (16.3) следует, что общее сопротивление последовательно соединенных проводников всегда превышает сопротивление любого из них. Это и понятно: ведь, соединяя проводники последовательно, мы как бы увеличиваем их общую длину, а с увеличением длины возрастает и сопротивление.

При последовательном соединении n одинаковых элементов (резисторов, ламп и т. д.) их общее сопротивление R превышает сопротивление R

1 одного из них в n раз:

R = nR₁

Общее напряжение U при этом делится на n равных частей, так что каждый из элементов цепи оказывается под напряжением U1 в n раз меньшим общего значения. Например, при включении в сеть с напряжением U = 220 В десяти последовательно соединенных одинаковых ламп каждая из них оказывается под напряжением U₁ = U/10 = 22 В.

Отличительной особенностью последовательного соединения проводников является то, что при отказе в работе хотя бы одного из них ток прекращается сразу во всей цепи. Вывернув, например, одну из ламп, изображенных на рисунке 42, мы увидим, как тут же перестанет гореть и другая (оставшаяся) лампа. Так что, если вы украсите новогоднюю елку гирляндой из последовательно соединенных лампочек и какая-то из них перегорит, то погаснет не только она, но и все остальные тоже. Поэтому, чтобы определить, какая из лампочек перегорела, вам придется проверить всю гирлянду.

1. Какое соединение проводников называют последовательным? 2. Начертите схему цепи, изображенной на рисунке 42. 3. Какие три закономерности справедливы для последовательного соединения проводников? 4. Как находится общее сопротивление последовательно соединенных проводников в случае, когда они одинаковые? Как в этом случае распределяется между проводниками общее напряжение?

Последовательное соединение элементов — Энциклопедия по машиностроению XXL

Система с последовательным соединением элементов (рис. 21,а). В этом случае вся система выходит из строя, если отказал хотя бы один элемент системы.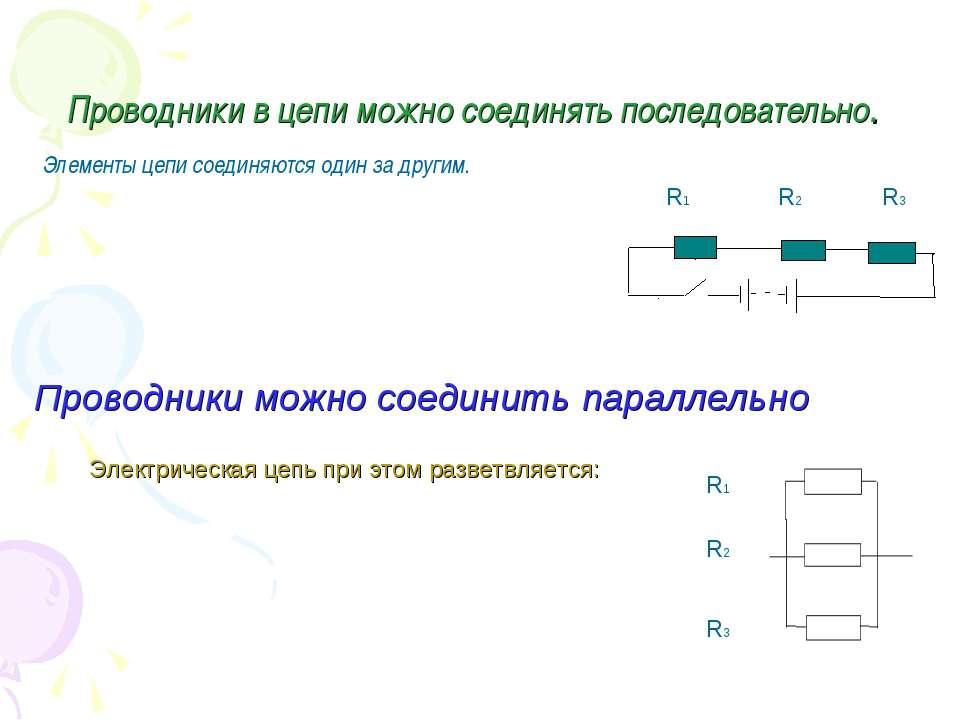 Если в системе отказы элементов статистически независимы, то надежность всей системы будет [17]  [c.79]

Вероятность безотказной работы всего прибора при последовательном соединении элементов 6  [c.175]

Последовательным называют соединение, при котором полезное сопротивление предыдущего элемента является движущей силой для последующего. Коэффициент полезного действия машины (механизма), состоящей из последовательно соединенных элементов, равен произведению к. п. д. этих элементов  

[c.258]

Пример 157. Определить мощность, теряемую на преодоление вредных сопротивлений в сложной машине, состоящей из семи последовательно соединенных элементов t]i = 0,72, г 2 = 0,74, т]з = 0,9, ri4 = 0,8, г]5 = 0,90, г]б = 0,97, т), = 0,8, если потребляемая мощность равна  [c.264]

При последовательном соединении элементов (рис. 5.5) общим для всех элементов является ток и поэтому уравнение движения в системе целесообразно записать в виде (И  [c.189]

Сравнение дуальных электрических цепей показывает, что последовательному соединению элементов цепи, построенной по первой системе электромеханических аналогий, соответствует параллельное соединение элементов цепи, построенной по второй системе электромеханических аналогий. Напряжения в первой цепи распределяются подобно токам второй, а ток первой цепи аналогичен падению напряжения между узлами второй цепи.  

[c.208]

Последовательные соединения элементов или машин. Пусть цепь состоит из п элементов или мащин, КПД каждого или каждой из которых известны. Определим общий КПД такой  [c.95]

На рис. 142 показана установка логических элементов в блоке управления и соединения входов и выходов согласно формулам включения. Каждый элемент умножения показан в виде квадрата с названием операции И и трех линий. По верхней линии подходит сигнал первого множителя, по боковой — второго множителя, сигнал произведения идет по третьей линии.

Против выходов и /1 поставлено по одному элементу умножения, а против выхода 2 два последовательно соединенных элемента. После установки этих элементов остается соединить входы и выходы по формулам включения.  [c.257]

ЛИНИИ ПОДХОДИТ сигнал первого множителя, по боковой — второго множителя, сигнал произведения идет по третьей линии. Против выходов f- и fi поставлено по одному элементу умножения, а против выхода /г—два последовательно соединенных элемента. После установки этих элементов для получения схемы блока управления остается соединить входы и выходы по формулам включения.  

[c.541]

Рис, 57. Последовательное соединение элементов сложной системы  [c.183]

Наиболее характерен случай, когда отказ одного элемента выводит из строя всю систему, как это имеет место при последовательном соединении элементов (рис. 57, а).  [c.183]

Резервирование систем. Рассматривая систему, состоящую из п последовательно соединенных элементов, можно предложить несколько вариантов ее резервирования.  [c.186]

При последовательном соединении элементов складываются обратные величины пропускных способностей  [c.35]

Если состояния элементов х, системы являются событиями, связанными в указанном выше смысле, то для последовательного соединения элементов можно записать, обобщая (4.28),  [c.160]

Таким образом, получен важный и интересный вывод если в результате испытаний элементов системы не было зафиксировано ни одного отказа, то нижняя оценка вероятности безотказной работы системы, состоящей из последовательно соединенных элементов, совпадает с соответствующей оценкой для элемента, объем испытаний которого был наименьшим. На первый взгляд может показаться, что нижняя доверительная оценка надежности для системы должна бы быть ниже, чем полученная оценка (4.167).  

[c.275]

Рассматриваемая система состоит из Л последовательно соединенных элементов с интенсивностями отказов 0,. По признаку автономности диагностирования элементы группируются в М контролируемых блоков, имеющих интенсивности отказов А.о,-, i = 1, М. Длительность и полнота диагностирования связаны зависимостями а,- = ф или Г,- (а,), где — длительность полного теста i-ro контроли-  [c.312]

Неполный аппаратурный контроль и защита с помощью КТ. Система состоит из N последовательно соединенных элементов. Каждый элемент имеет основное оборудование с интенсивностью отказов Xgj и встроенное контрольное оборудование с интенсивностью отказов Поэтому интенсивность отказов i-ro элемента X,- = Xgj +  

[c.319]

Метод равномерного распределения. Если система состоит из /, последовательно соединенных элементов примерно равной сложности, то можно заданный показатель надежности П типа вероятности безотказной работы, коэффициента оперативной готовности или коэффициента готовности распределять по правилу Я, = = 1, Задаваемое среднее время безотказной работы -го элемента приближенно равно в этом случае Т = пТ, > = 1, п, где Т — заданное среднее время безотказной работы системы.  

[c.394]

Указанные модели вязкоупругого тела становятся весьма наглядными, если их представить в зиде комбинации простейших элементов —упругого и вязкого. Упругий элемент имеет вид пружины (см. рис. 7.4, а) с линейной характеристикой, т. е. о = Ее. Вязкий элемент представляет собой цилиндр (рис. 7.4, б) с вязкой жидкостью, в котором перемещается поршень с отверстием или с зазором вдоль стенки цилиндра, благодаря чему жидкость может перетекать из одной части цилиндра в другую. При постоянной силе поршень перемещается с постоянной скоростью, или, иначе говоря, а = В модели Максвелла деформации в упругом и вязком элементах суммируются, а напряжения одинаковы. Это соответствует последовательному соединению элементов (рис. 7.5, а). В модели Фойгта суммируются напряжения в элементах, а их деформации одинаковы. Такая картина получится, если элементы соединить параллельно (рис.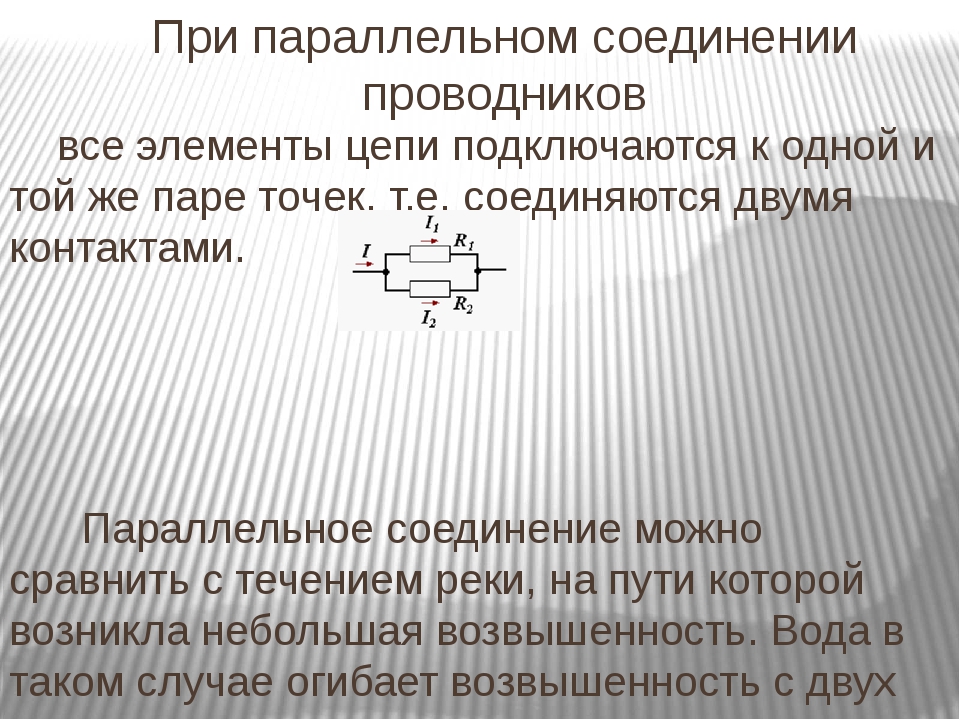 7.5, б).  [c.757]

К классу I отнесем динамические модели механизмов, образованные последовательным соединением элементов. Для облегчения необходимых пояснений воспользуемся следующей символической записью, характеризующей структуру динамической модели или ее составного элемента  [c.51]

К классу II отнесены динамические модели цикловых механизмов, образованных при параллельно-последовательном соединении элементов (модификация 1) и модели, элементы которых образуют замкнутые контуры (модификация 2).  [c.52]

ОБРАЗОВАННЫХ ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ  [c.179]

Формула (2.46) представляет собой искомый стохастический алгоритм. Определив стохастический алгоритм и зная из 2.1 структуру первого и третьего блоков алгоритма исследования надежности условных систем, конструкцию алгоритма исследования надежности условных систем для последовательного соединения элементов  [c.106]

Алгоритм получения времени безотказной работы для рассматриваемой системы может быть представлен зна-. чительно проще. В самом деле, система, изображенная на рис. 3.14, представляет собой последовательное соединение устройств, каждое из которых состоит из mj + 1 отдельных элементов (устройств). Поэтому на основании формул, полученных для последовательного соединения элементов,  [c.178]

При последовательном соединении элементов в основной и резервной подсистемах  [c.225]

Общее падение давления во всей системе Ро — Рп равно сумме разностей давления на концах последовательно соединенных элементов системы (труб, камер)  [c.515]

В качестве иллюстрации вышеизложенной методики рассмотрим задачу оптимального распределения надежности для конструкции, состоящей из четырех последовательно соединенных элементов — трех цилиндрических оболочек и плоского днища в виде круглой симмвт 4Ч4в наг женной пластины (рис.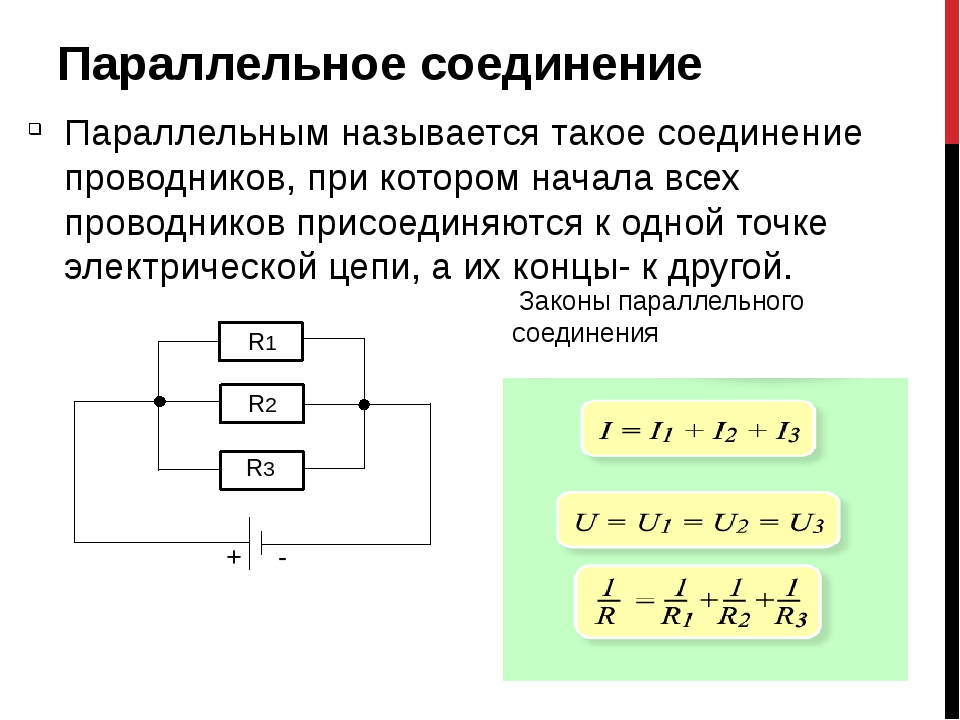 22). Дня цилиндрических оболочек будем считать определяющей надежность по прочности, для днища — надежность пв жесткости. Величины нагрузок и несущей способности для каждого элемента будем считать некоррелированными случайными величинами со следующими вероятностными характе1 стиками  [c.89]

Пример. Определить КПД плоского четырехшарнирника (см. рис. 2.8). Решение. Этот механизм состоит из четырех звеньев, последовательно соединенных во вращательные кинематические пары О, А, В и С. Полагая КПД одинаковым для всех кинематических пар и применив формулу (5.49), найдем КПД ц = Рв. Заметим, что равенство (5.49) свидетельствует о несовершенстве последовательного соединения элементов или машин с энергетической точки зрения.  [c.96]

Далее процесс повторяется и может автокаталитически ускоряться при устранении возможности конвекционного обмена состава внутрищелевого раствора с окружающей средой. Естественно, что отдельные стадии этого процесса могут накладываться друг на друга. Указанную мно-гостадийность процесса коррозионного растрескивания можно представить в виде модели последовательно соединенных элементов электрической цепи выход из строя любого элемента этой цепи прекращает ток  [c.70]

В направлении армирования по епоеобу суммирования используются характеристики аЕ компонентов, а для коэффициента расширения в поперечном направлении — только а. Модуль упругости в поперечном направлении и модуль сдвига , лучше всего (в смысле большей точности совпадения с экспериментом) представляются формулой последовательного соединения элементов Рейсса.  [c.257]

Система с последовательным соединением элементов, непополняемым резервом времени и необесценивающими отказами. Система содержит N последовательно соединенных элементов с постоянными интенсивностями отказов X.. и произвольными распределениями времени восстановления F M), i = 1,N. Все отказы элементов обнаруживаются мгновенно и достоверно, после обнаружения отказа элемент сразу поступает в ремонт. Прй этом остальные элементы выключаются до полного восстановления работоспособности системы. Система выполняет задание, требующее суммарной наработки не менее t. Для выполнения задания выделяется непополняемый резерв времени t, расходуемый только на восстановление работоспособности. Задание будет выполнено в срок, если к моменту достижения наработки t суммарное время восстановления не превысит т. Обозначим вероятность выполнения задания через P(t,x). Она находится из интегрального уравнения [145]  [c.206]

Система с последовательным соединением элементов, непополняе-мым резервом времени и обесценивающими отказами. Система функционирует так же, как система в предыдущем параграфе, но отличается от нее тем, что каждый отказ элемента вызывает потерю всей полезной наработки, поэтому после восстановления работоспособности задание выполняется заново. Вероятность выполнения задания находят из уравнения  [c.208]

Система с последовательным соединением элементов, непополняе-мым резервом времени и частично обесценивающими отказами. В системе с непрерывным идеальным контролем для уменьшения объема обесцененной наработки задание разбивается на п этапов одинаковой длительности Г = t/n. После выполнения очередного этапа в отсутствие отказов фиксируются результаты и создается так называемая контрольная точка. На ее создание и переход к следующему этапу затрачивается время При возникновении отказа обесценивается наработка только в пределах текущего этапа. Задание считается выполненным, если последовательно выполнены все его этапы и затраты времени на восстановление работоспособности и повторение работ не превысили резервного времени т.  [c.210]

Система с последовательным соединением элементов, мгновенно пополняемым резервом времени и необесценивающими отказами. Система состоит из N последовательно соединенных элементов с постоянными интенсивностями отказов и произвольными распределениями времени восстановления Fg, (t). Отказ i-ro элемента не считается отказом системы, если время его устранения не превышает индивидуального резерва времени т,. Время восстановления, не превышающее резервного, включается в полезную наработку. Время т,- в общем случае является случайной величиной с известным распределением Di(t). Вероятность выполнения задания находится как решение уравнения  [c.211]

Система с последовательным соединением элементов, комбинированным резервом времени и необесиенивающими отказами. Система имеет кроме индивидуального резерва времени Тд,- еще и общий непо-полняемый резерв времени т . Резерв Хд,- является мгновенно пополняемым, т.е. сразу же после восстановления работоспособности он восстанавливается до исходного уровня. Показатели надежности системы существенно зависят от того, как взаимодействуют между собой обе составляющие резерва и какова стратегия их использования. Поэтому далее рассматриваются различные модели, учитывающие эти факторы. Общее правило состоит, однако, в том, что сначала используется индивидуальный резерв, а после него (или параллельно с ним) — непополняемый общий резерв.  [c.213]

Система с последовательным соединением элементов и промежуточными накопителями продукции (многофазная система). Система состоит из N последовательно соедийенных элементов, каждый из которых характеризуется интенсивностью отказов X,-, распределени-216  [c.216]

Здесь коэффициент потерь обратно пропорционален частоте. Помимо этого, и действительная часть (7.10) зависит от частоты. На низких частотах она близка к нулю, а на высо- ких частотах стремится к пределу Сь Физически это очевидно (см. рис. 7.2, б) на частотах, близких к нулю, податливость (т. е. обратная величина жесткости) последовательного соединения элементов j и Г] определяется в основном демпфером, относительное смещение на нем значительно больше, чем относительное смещение концов пружины, благодаря чему энергия рассеянная в демпфере, значительно превышает энергию Wo, накапливаемую в пружине, а коэффициент потерь согласно (7. 7) на низких частотах может достигать больших значений т)((о) = (сот/)». Многие реальные тела (стекло, некоторые металлы) демонстрируют подобную зависимость ri((a) на низких частотах (явление пластического течения). На рис. 7.5 крестиками изображены экспериментальные значения коэффициента потерь серебра при изгибных колебаниях пластинок [282]. На низких частотах наблюдается увеличение г), обусловленное пластическим течением. Сплошная кривая на рис. 7.5 соответствует формулам (7.11) —  [c.213]

Таким образом, из рассмотрения аналитических алгоритмов исследования надежности даже такой простой системы, как система с последовательным соединением элементов, следует, что такие алгоритмы при любом законе надежности, кроме разве экспоненциального, требуют довольно большой вычислительной работы, а это вызывает необходимость использования УЦВМ. Поэтому, целесообразным является применение стохастических алгоритмов для исследования надежности не только системы рис. 2.21, но главным образом сложных радиоэлектронных систем в классе условных систем с резервным соединением элементов.  [c.121]

---

Последовательное соединение потребителей(элементов) в цепи с…

Привет, мой друг, тебе интересно узнать все про последовательное соединение, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое последовательное соединение,цепь rlc,режимы работы rlc-цепи , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства

Последовательным соединением участков электрической цепи называют соединение, при котором через все участки проходит один ток (рис.3.5).

Напряжение на каждом последовательно включенном участке пропорционально величине сопротивления этого участка.

При последовательном соединении потребителей с сопротивлениями R₁, R₂ и R₃ (рис.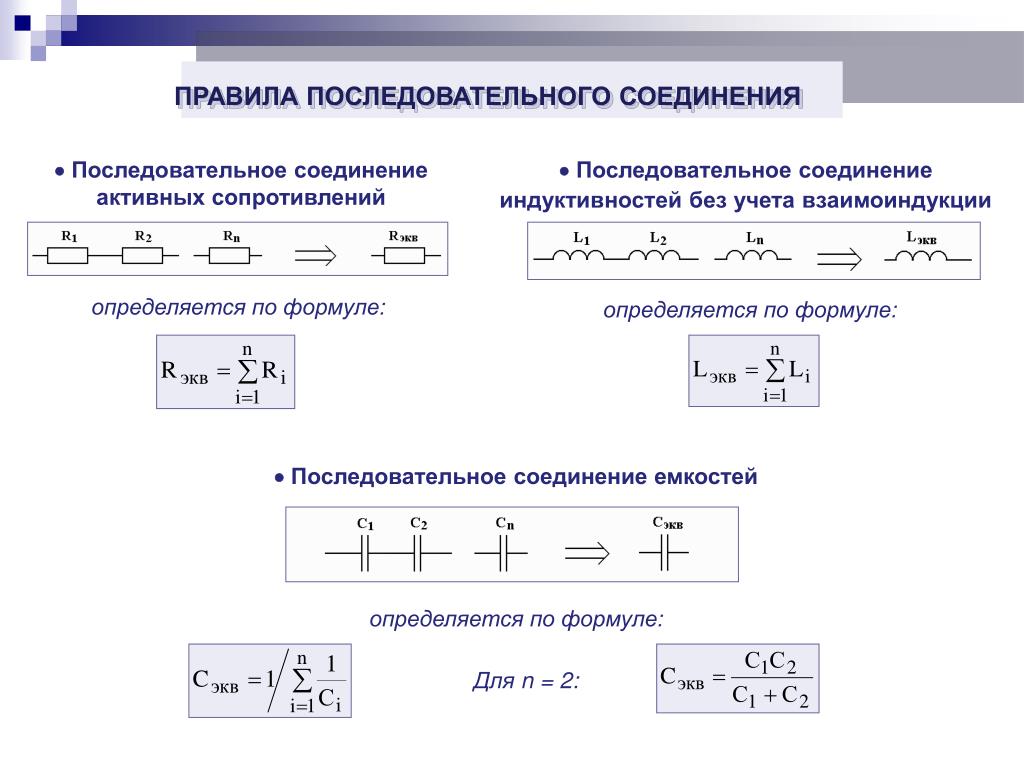 3.5) напряжение на их зажимах равно

Воспользовавшись вторым законом Кирхгофа для рассматриваемой цепи (рис. 3.5), можно записать

или (1.28)

Откуда (1.29)

Таким образом, общее (эквивалентное) сопротивление R последовательно включенных сопротивлений (потребителей) равно сумме этих сопротивлений.

Ток в цепи последовательно включенных потребителей (рис. 3.5) определяется выражением

Нетрудно понять, что при изменении сопротивления хотя бы одного потребителя изменяется ток цепи, а следовательно, и режим работы (напряжение) всех последовательно включенных потребителей.

Поэтому последовательное соединение сопротивлений не нашло широкого практического применения.

Следует заметить, что при последовательном соединении резисторов на большем сопротивлении тратится большая мощность

По второму закону Кирхгофа в комплексной форме

закон Ома

Zэкв – модуль эквивалентного сопротивления (полное сопротивление определяет связь между U и I)
— аргумент, связь между начальными фазами

Треугольники сопротивлений и напряжений

Из треугольника:

Треугольник напряжений

Режимы работы электрических RLC цепей переменного тока

При протекании токов по элементам электрической цепи, элементы которой соединены последовательно, параллельно или имеют смешанное соединение, могут получаться различные режимы работы этой цепи.
В этом параграфе будут рассмотрены следующие режимы работы электрических цепей.

1) Резонанс напряжений

Резонанс в цепи с последовательным соединением элементов. (Резонанс напряжений). (Рис. 63).

Рис. 63.

Режим работы RLC цепи или LC—цепи, при условии равенства реактивных сопротивлений X_{C= XL, когда общее напряжение цепи совпадает по фазе с ее током , называется резонансом напряжения.}

X_C= X_L – условие резонанса

RLC цепь LC цепь.

Признаки резонанса напряжения:

1 . Об этом говорит сайт https://intellect.icu . Напряжение на входе совпадает по фазе с током, т.е. сдвиг фаз между I и U φ = 0, cos φ = 1

2. Ток в цепи будет наибольшим и как следствие P_max= I²_maxR тоже максимальна, а реактивная мощность равна нулю.

3. Резонансная частота

4.

Резонанс можно достигнуть, изменяя L, C или ω.

Векторные диаграммы при резонансе напряжений

LC цепь RLC цепь

2) Резонанс токов

Резонанс в цепи с параллельным соединением элементов. (Резонанс токов). (Рис. 64).

Рис. 64.
Резонанс в цепи с параллельным соединением реальных элементов, т.е. резонанс с учетом потерь в активных сопротивлениях катушки и соединительных проводов. (Рис. 65).

Рис. 65.

Эти режимы работы имеют важное практическое значение и обязательны для изучения.

Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.

Условие резонанса токов:

В₁ – реактивная проводимость первой ветви,

В₂ – реактивная проводимость второй ветви

Признаки резонанса токов:

1. Реактивные составляющие токов ветвей равны I_PC= I_PL и находятся в противофазе в случае, когда напряжение на входе чисто активное;
2. Токи ветвей превышают общий ток цепи, который имеет минимальное значение;
3. совпадают по фазе

RLC – цепь Векторная диаграмма

LC – цепь Векторная диаграмма

Резонансная частота

Случаи резонансных цепей цепей

Если R₂=0 резонанс наступит, при

Случаи резонанса токов

Случай 1. Один резонанс в цепи, при условии:

Случай 2. Два резонанса в цепи, при определенном соотношении сопротивлений элементов

Случай 3. Нет резонанса в цепи – частота является величиной неопределенной, при

Частотные характеристики колебательного контура

Баланс мощностей в цепях переменного тока

Коэффициент мощности

• Генератор или электрооборудование энергетически выгодно эксплуатировать, если оно совершает максимальную работу. Работа в электрической цепи определяется активной мощностью Р.
• Коэффициент мощности показывает, насколько эффективно используется генератор или электрооборудование λ=P/S=cosφ≤1

С уменьшением коэффициента мощности стоимость потребляемой электроэнергии возрастает .

Способы увеличения коэффициента мощности

• Мощность максимальна в случае, когда Р = S, т.е. в случае резистивной цепи.
• Генератор осуществляет только необратимые преобразования энергии и не участвует в колебательных процессах обмена энергией с электромагнитным полем приемников, в режиме максимальной мощности.
• Потребители электрической энергии в основном имеют схему замещения RL элемента, поэтому увеличение коэффициента мощности возможен с помощью компенсации реактивной мощности подключением емкостного элемента (Q_L—Q_С), подключение емкостного элемента снижает ток в линии электропередачи, что позволяет уменьшить сечение электропроводов, а это приводит к экономии электропроводящих материалов.
• Значение коэффициента мощности в энергосистемах зависит насколько грамотно эксплуатируется электротехнические установки и приборы.
• сosφ может снижаться, если установки работают в режиме холостого хода, или недогружены.

3) Критический режим в последовательной RLC-цепи

Критический режим в последовательной RLC-цепи (критический случай апериодического режима) наблюдается, когда корни характеристического полинома последовательной RLC-цепи являются кратными

При этом (согласно уравнению состояния последовательной RLC-цепи, подключенной к источнику напряжения u₀ = const) решение

действительно не содержит колебательной составляющей (как и при рассмотрении апериодического режима).

При начальных условиях

получим А₁ = 0, следовательно,

График критического процесса приведен на рис. 23 (где линейная функция и экспонента намечены штриховыми линиями; периодическая составляющая в графике отсутствует, а максимум соответствует постоянной времени τ = 1/α).

См. также

Как ты считаеешь, будет ли теория про последовательное соединение улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое последовательное соединение,цепь rlc,режимы работы rlc-цепи и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электротехника, Схемотехника, Аналоговые устройства

   На рис. 2.1 изображена электрическая цепь с последовательно соединенными сопротивлениями.

Рис. 2.1

Напряжение на зажимах источника ЭДС равно величине электродвижущей силы. Поэтому часто источник на схеме не изображают.
Падения напряжений на сопротивлениях определяются по формулам

В соответствии со вторым законом Кирхгофа, напряжение на входе электрической цепи равно сумме падений напряжений на сопротивлениях цепи.

        где   — эквивалентное сопротивление.

    Эквивалентное сопротивление электрической цепи, состоящей из n последовательно включенных элементов, равно сумме сопротивлений этих элементов.

2.2. Параллельное соединение элементов

электрических цепей

На рис. 2.2 показана электрическая цепь с параллельным соединением сопротивлений.

Рис. 2.2

Токи в параллельных ветвях определяются по формулам:

        где — проводимости 1-й, 2-й и n-й ветвей.

      В соответствии с первым законом Кирхгофа, ток в неразветвленной части схемы равен сумме токов в параллельных ветвях.

        где      Эквивалентная проводимость электрической цепи, состоящей из n параллельно включенных элементов, равна сумме проводимостей параллельно включенных элементов.
Эквивалентным сопротивлением цепи называется величина, обратная эквивалентной проводимости

  Пусть электрическая схема содержит три параллельно включенных сопротивления.
Эквивалентная проводимость

  Эквивалентное сопротивление схемы, состоящей из n одинаковых элементов, в n раз меньше сопротивлений R одного элемента

Возьмем схему, состоящую из двух параллельно включенных сопротивлений (рис. 2.3). Известны величины сопротивлений и ток в неразветвленной части схемы. Необходимо определить токи в параллельных ветвях.

Рис. 2.3 Эквивалентная проводимость схемы

,

    а эквивалентное сопротивление

      Напряжение на входе схемы

       Токи в параллельных ветвях

       Аналогично

      Ток в параллельной ветви равен току в неразветвленной части схемы, умноженному на сопротивление противолежащей, чужой параллельной ветви и деленному на сумму сопротивлений чужой и своей параллельно включенных ветвей.

2.3.Преобразование треугольника сопротивлений

в эквивалентную звезду

Встречаются схемы, в которых отсутствуют сопротивления, включенные последовательно или параллельно, например, мостовая схема, изображенная на рис. 2.4. Определить эквивалентное сопротивление этой схемы относительно ветви с источником ЭДС описанными выше методами нельзя. Если же заменить треугольник сопротивлений
R1-R2-R3, включенных между узлами 1-2-3, трехлучевой звездой сопротивлений, лучи которой расходятся из точки 0 в те же узлы 1-2-3, эквивалентное сопротивление полученной схемы легко определяется.

Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений всех сторон треугольника.
В соответствии с указанным правилом, сопротивления лучей звезды определяются по формулам:

    Эквивалентное соединение полученной схемы определяется по формуле

       Сопротивления R0 и R?1 включены последовательно, а ветви с сопротивлениями R?1 + R4 и R?3 + R5 соединены параллельно.

2.4.Преобразование звезды сопротивлений

в эквивалентный треугольник

Иногда для упрощения схемы полезно преобразовать звезду сопротивлений в эквивалентный треугольник.
Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R1-R2-R3 эквивалентным треугольником сопротивлений R?1-R?2-R?3, включенных между узлами 1-2-3.

2.5. Преобразование звезды сопротивлений
в эквивалентный треугольник

Сопротивление стороны эквивалентного треугольника сопротивлений равно сумме сопротивлений двух прилегающих лучей звезды плюс произведение этих же сопротивлений, деленное на сопротивление оставшегося (противолежащего) луча. Сопротивления сторон треугольника определяются по формулам:

1.5. Способы соединения элементов и преобразования цепей

1.5. Способы соединения элементов и преобразования цепей

При расчетах часто возникает необходимость упростить схему. В основе

различных методов преобразования электрических цепей лежит понятие эквивалентности. Согласно этому понятию напряжения и токи в ветвях цепи, не затронутых преобразованием, остаются неизменными. Наиболее часто электрические цепи представляют собой последовательное и паралельное соединение резистивных, емкостных, индуктивных элементов и источников питания.

Последовательное соединение резисторов показано на рис. 1.12.

 

Рис. 1.12. Последовательное соединение резисторов.

На основании второго закона Кирхгофа для цепи рис. 1.12 можно записать следующее выражение:

,        где        

Из полученного выражения видно, что при последовательном соединении резисторов их общее электрическое сопротивление равно сумме электрических сопротивлений всех резисторов цепи.

.                                                          (1.24)

Последовательное  соединение емкостей показано на рис. 1.13

Рис. 1.13. Последовательное соединение емкостей.

Напряжение на каждой емкости в сумме дает напряжение, приложенное к батарее емкостей. Учитывая, что напряжение на емкости

для схемы рис. 1.13 можно записать:.                                  (1.25)

Отношение u к q дает величину, обратную суммарной емкости CΣ. Следовательно

.

Т.е. при последовательном соединении величина, обратная суммарной емкости, равна сумме величин, обратных емкостям.

Последовательное соединение индуктивностей показано на рис. 1.14.

Рис. 1.14. Последовательное соединение индуктивностей.

Напряжение на каждой индуктивности в сумме дает напряжение, приложенное к суммарной индуктивности LΣ.

.

Разделив u на

получим общую индуктивность, т. е..                                                  (1.26)

При последовательном соединении индуктивностей общая индуктивность равна сумме всех индуктивностей, включенных в электрическую цепь.

Последовательное соединение источников напряжения показано на рис. 1.15.

Рис. 1.15. Последовательное соединение источников напряжения.

Учитывая, что источники, действующие в одном направлении, суммируются, а в противоположных направлениях вычитаются; на основании рис. 1.15 имеем

.                                  (1.27)

При последовательном соединении источников напряжения общая величина напряжения равна алгебраической сумме напряжений на каждом источнике.

Параллельное соединение резисторов показано на рис. 1.16,а.

Рис. 1.16. Параллельное соединение резисторов (а), индуктивных (б) и емкостных (в) элементов.

Из рис. 1.16 видно, что при параллельном соединении элементов к ним приложено одно и тоже напряжение u. Согласно первому закону Кирхгофа для тока каждой из схем, изображенных на рис. 1.16 можно записать:

.                                                          (1.28)

На основании этого уравнения и учитывая, что для резистивного элемента

, получаем:,        где        .                  (1.29)

При параллельном соединении резистивных элементов общая проводимость цепи равна сумме проводимостей всех резистивных элементов, включенных в электрическую цепь.

Параллельное соединение индуктивностей показано на рис. 1.16,б. Ток в индуктивности равен

.Подставляя значение тока в выражение (1.28) будем иметь:,        где        .                  (1.30)

При параллельном соединении индуктивных элементов обратная величина индуктивности всей цепи равна сумме обратных величин каждой индуктивности, включенной в электрическую цепь.

Параллельное соединение емкостей показано на рис. 1.16,в.

Ток в емкостном элементе равен

. Подставляя значения тока в выражение (1.28) получаем,        где        .                  (1.31)

При параллельном соединении емкостных элементов общая емкость цепи равна сумме всех емкостей, включенных в электрическую цепь.

Следовательно, электрическую цепь, состоящую из n последовательно или параллельно соединенных резистивных, индуктивных  или емкостных элементов можно заменить одним эквивалентным резистивным, индуктивным или емкостным элементом с параметрами, вычисленными по формулам (1.24÷1.26) и (1.29÷1.31).

Способы соединения элементов питания.

«Питайтесь» правильно!

При питании радиоаппаратуры от батареек и аккумуляторов полезно знать распространённые схемы соединения батарей и аккумуляторов. Дело в том, что каждый вид батареек имеет допустимый разрядный ток.

Разрядный ток – наиболее оптимальное значение тока, который потребляется от батареи. Если потреблять от батарейки ток, превышающий разрядный, то надолго этой батарейки не хватит, она не сможет полностью отдать свою расчётную мощность.

Наверное, замечали, что для электромеханических часов используются “пальчиковые” (формата АА) или “мизинцевые” (формата ААА) батарейки, а для переносного лампового фонаря батарейки побольше (формат R14 или R20), которые способны отдать значительный ток и имеют большую ёмкость. Размер батарейки имеет значение!

Иногда требуется обеспечить батарейное электропитание прибора, который потребляет значительный ток, но стандартные батареи (например R20, R14) не могут дать необходимый ток, он для них выше разрядного. Что делать в этом случае?

Ответ прост!

Необходимо взять несколько однотипных батареек и соединить их в батарею.

Параллельное соединение элементов питания.

Так, например, если необходимо обеспечить значительный ток для аппарата применяют параллельное соединение батареек. В таком случае общее напряжение составной батареи будет равно напряжению одного элемента питания, а разрядный ток будет во столько раз больше, сколько батареек применяется.

На рисунке составная батарея из трёх 1,5 вольтовых батареек G1, G2, G3. Если учесть, что среднее значение разрядного тока для 1 батарейки формата АА 7-7,5 mA (при сопротивлении нагрузки 200 Ом), то  разрядный ток составной батареи составит 3 _* 7,5 = 22,5 mA. Вот так, приходится брать количеством.

Последовательное соединение элементов питания.

Бывает, что необходимо обеспечит напряжение 4,5 – 6 вольт, применяя батарейки на 1,5 вольта. В таком случае нужно соединить батарейки последовательно, как на рисунке.

Разрядный ток такой составной батареи составит значение для одного элемента, а общее напряжение будет равно сумме напряжений трёх батареек. Для трёх элементов формата АА (“пальчиковых”) разрядный ток составит 7-7,5 mA (при сопротивлении нагрузки 200 Ом), а суммарное напряжение – 4,5 Вольт.

Итак, подведём итоги.

• Если необходимо обеспечить значительный ток, то применяется параллельное соединение элементов питания. Рассчитать значения напряжения и разрядного тока для параллельно составленной батареи питания:

  I=I_G1* N  — общий разрядный ток параллельно составленной батареи.

   где N – количество однотипных элементов питания.

  I_G1 – разрядный ток одного элемента питания.

  U=U_G1 — общее напряжение параллельно составленной батареи.

  где U_G1 – напряжение одного элемента питания.

  Понятно, что никакого выигрыша по напряжению при параллельном соединении мы не получим.

• Если требуется обеспечить напряжение в разы большее напряжения отдельного элемента питания, то применяется последовательная схема соединения.

  Рассчитать значения напряжения и разрядного тока для последовательно составленной батареи питания:

  U=U_G1* N — общее напряжение последовательно составленной батареи.

  I=I_G1 — общий ток последовательно составленной батареи.

  В таком случае мы получаем выигрыш по напряжению.

• А как быть, если необходимо получить выигрыш и по напряжению и по току? Тогда применяется смешанное соединение элементов питания.

  Взгляните на рисунок, думаю, Вам всё станет понятно.

  При таком соединении составная батарейка из 6 элементов типоразмера АА обеспечит напряжение 4,5 Вольт и разрядный ток на нагрузке в 200 Ом – 2 _* 7,5 = 15mA.

Рассчитывается всё довольно просто. Сначала, вычисляем напряжение на 3 последовательно соединённых элементах одного из плеч. Ток последовательно соединённых элементов будет равен току одного элемента.

Далее складываем токи каждого плеча из трёх элементов. В данном случае у нас два плеча. Напряжение параллельно соединённых элементов равно напряжению одного элемента. Здесь 3 последовательно соединённых батарейки представляют как бы один элемент питания на 4,5 Вольт.

В радиолюбительской практике не всегда необходимо вычислять разрядный ток, так как потребляемый приборами ток, как правило, нестабилен, всё зависит от режима работы конкретного аппарата.

Понятно, что магнитола потребляет больший ток в режиме воспроизведения, нежели в режиме прослушивания радио. В режиме воспроизведения ток потребления возрастает из-за работы двигателя протяжки ленты, тогда как в режиме радио необходимо лишь усилить принятый сигнал.

Необходимо просто правильно оценивать токовую нагрузку на составную батарею, ведь некоторые приборы могут потреблять значительный ток и в таких случаях можно добавить пару дополнительных элементов питания. В таком случае автономное время работы Вашего прибора возрастёт.

Главная &raquo Радиоэлектроника для начинающих &raquo Текущая страница

Также Вам будет интересно узнать:

 

Физическая формула расчета (определения) эквивалентного сопротивления в цепи

Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.

Метод свёртывания цепи

Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.

Последовательное соединение элементов

В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.

При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.

Последовательное подключение приборов

Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:

I = U/R.

Из вышестоящего выражения получаем значение R:

R = U/I (1).

Поскольку при последовательном соединении:

• I = I1 = I2 =…= IN (2),
• U = U1 + U2 +…+ UN (3),

формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:

• Rэкв = (U1 + U2 + …+ UN)/I,
• Rэкв = R1 + R2 + … + RN (4).

Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:

Rобщ = N·R (5).

Параллельное соединение

При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.

Параллельное соединение

Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.

В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.

Если имеются N резистивных устройств, подключенных таким образом, то:

I = I1 + I2  + … + IN (6),

U = U1 = U2 = … = UN (7).

Из выражений (1), (6) и (7) имеем:

• Rобщ = U/(I1 + I2 + …+ IN),
• 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).

Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:

Rобщ = R · R / N·R = R / N (9).

Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.

Расчёт при смешанном соединении устройств

В случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.

При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.

Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:

• R1 = 1Ом,
• R2 = 2Ом,
• R3 = 3Ом,
• R4 = 6Ом,
• R5 = 9Ом,
• R6 = 18Ом,
• R7 = 2,8Ом,
• U = 32В.

Электрическая схема

Из закона Ома имеем: 

I = U/R,

где R – суммарное сопротивление всех приборов.

Его будем находить, воспользовавшись методом сворачивания цепи.

Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:

R2,3= R2·R3 / (R2+R3).

R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:

1/R4,5,6 = 1/R4+1/R5+1/R6.

Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.

Эквивалентная схема

Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.

Rобщ может быть найдено по формуле:

Rобщ = R1 + R2,3 + R4,5,6 + R7.

Подставляем числовые значения и рассчитываем R для определённых участков:

• R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
• 1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
• R4,5,6 = 3Ом,
• Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.

Теперь, после того, как нашли Rэкв, можно вычислять значение I:

I = 32В / 8Ом = 4А.

После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.

Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:

I1 = I2,3 = I4,5,6 = I7 = I = 4А.

На участке R2,3 напряжение находим по формуле:

• U2,3 = I2,3·R2,3,
• U2,3 = 4А·1,2Ом = 4,8В.

Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:

• I2 = U2 / R2,
• I2 = 4,8В / 2Ом = 2,4А,
• I3 = U3 / R3,
• I3 = 4,8В / 3Ом = 1,6А.

Проверяем правильность решения:

• I2,3 = I2 + I3,
• I2,3 = 2,4А + 1,6А = 4А.

На участке R4,5,б напряжение также находим, исходя из закона Ома:

• U4,5,6 = I4,5,6·R4,5,6,
• U4,5,6 = 4А·3Ом = 12В.

Так как R4, R5, Rб подключены параллельно друг к другу, то:

U4,5,6 = U4 = U5 = U6 = 12В.

Вычисляем I4, I5, I6:

• I4 = U4 / R4,
• I4 = 12В / 6Ом = 2А,
• I5 = U5 / R5,
• I5 = 12В / 9Ом » 1,3А,
• I6 = U6 / R6,
• I5 = 12В / 18Ом » 0,7А.

Проверяем правильность решения:

I4,5,6 = 2А + 1,3А + 0,7А = 4А.

Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.

Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.

Видео

Оцените статью:Цепи простой серии

| Последовательные и параллельные схемы

На этой странице мы изложим три принципа, которые вы должны понимать в отношении последовательных цепей:

1. Ток : величина тока одинакова для любого компонента в последовательной цепи.
2. Сопротивление : Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
3. Напряжение : напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.

Давайте взглянем на несколько примеров последовательных цепей, демонстрирующих эти принципы.

Начнем с последовательной схемы, состоящей из трех резисторов и одной батареи:

Первый принцип, который нужно понять о последовательных схемах, заключается в следующем:

Величина тока в последовательной цепи одинакова для любого компонента в цепи.

Это связано с тем, что в последовательной цепи существует только один путь прохождения тока.Поскольку электрический заряд проходит через проводники, как шарики в трубке, скорость потока (скорость мрамора) в любой точке цепи (трубки) в любой конкретный момент времени должна быть одинаковой.

Использование закона Ома в последовательных цепях

По расположению 9-вольтовой батареи мы можем сказать, что ток в этой цепи будет течь по часовой стрелке от точки 1 к 2, к 3 к 4 и обратно к 1. Однако у нас есть один источник напряжение и три сопротивления. Как мы можем использовать здесь закон Ома?

Важная оговорка к закону Ома заключается в том, что все величины (напряжение, ток, сопротивление и мощность) должны относиться друг к другу в терминах одних и тех же двух точек в цепи.Мы можем увидеть эту концепцию в действии на примере схемы с одним резистором ниже.

Использование закона Ома в простой цепи с одним резистором

В схеме с одной батареей и одним резистором мы можем легко вычислить любое количество, потому что все они относятся к одним и тем же двум точкам в цепи:

Поскольку точки 1 и 2 соединены вместе проводом с незначительным сопротивлением, как и точки 3 и 4, мы можем сказать, что точка 1 электрически является общей с точкой 2, а точка 3 электрически общей с точкой 4.Поскольку мы знаем, что у нас есть 9 вольт электродвижущей силы между точками 1 и 4 (непосредственно через батарею), и поскольку точка 2 является общей для точки 1, а точка 3 — общей для точки 4, мы также должны иметь 9 вольт между точками 2 и 3. (прямо через резистор).

Следовательно, мы можем применить закон Ома (I = E / R) к току через резистор, потому что мы знаем напряжение (E) на резисторе и сопротивление (R) этого резистора. Все термины (E, I, R) относятся к одним и тем же двум точкам в цепи, к одному и тому же резистору, поэтому мы можем безоговорочно использовать формулу закона Ома.

Использование закона Ома в схемах с несколькими резисторами

В схемах, содержащих более одного резистора, мы должны соблюдать осторожность при применении закона Ома. В приведенном ниже примере схемы с тремя резисторами мы знаем, что у нас есть 9 вольт между точками 1 и 4, что является величиной электродвижущей силы, управляющей током через последовательную комбинацию R ₁ , R ₂ и R _{. 3} . Однако мы не можем взять значение 9 вольт и разделить его на 3 кОм, 10 кОм или 5 кОм, чтобы попытаться найти значение тока, потому что мы не знаем, какое напряжение есть на любом из этих резисторов по отдельности.

Цифра 9 вольт составляет всего величин для всей цепи, тогда как цифры 3 кОм, 10 кОм и 5 кОм представляют собой отдельных величин для отдельных резисторов. Если бы мы включили цифру для общего напряжения в уравнение закона Ома с цифрой для отдельного сопротивления, результат не будет точно соответствовать какой-либо величине в реальной цепи.

Для R ₁ закон Ома будет связывать величину напряжения на R ₁ с током через R ₁ , учитывая сопротивление R ₁ , 3 кОм:

Но, поскольку нам неизвестно напряжение на R ₁ (только полное напряжение, подаваемое батареей на комбинацию из трех последовательных резисторов), и нам не известен ток через R ₁ , мы можем t делать какие-либо вычисления с любой формулой.То же самое касается R ₂ и R ₃ : мы можем применять уравнения закона Ома тогда и только тогда, когда все члены представляют свои соответствующие величины между одними и теми же двумя точками в цепи.

Итак, что мы можем сделать? Нам известно напряжение источника (9 вольт), приложенное к последовательной комбинации R ₁ , R ₂ и R ₃ , и мы знаем сопротивление каждого резистора, но поскольку эти величины не входят в В том же контексте мы не можем использовать закон Ома для определения тока в цепи.Если бы мы только знали, что такое общее сопротивление для цепи: тогда мы могли бы вычислить общий ток с нашей цифрой для общего напряжения (I = E / R).

Объединение нескольких резисторов в эквивалентный общий резистор

Это подводит нас ко второму принципу последовательной схемы:

Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.

Это должно иметь интуитивный смысл: чем больше последовательно соединенных резисторов, через которые должен протекать ток, тем труднее будет протекать ток.

В примере задачи у нас были последовательно подключены резисторы 3 кОм, 10 кОм и 5 кОм, что дало нам общее сопротивление 18 кОм:

По сути, мы вычислили эквивалентное сопротивление для R ₁ , R ₂ и R ₃ вместе взятых. Зная это, мы могли бы перерисовать схему с одним эквивалентным резистором, представляющим последовательную комбинацию R ₁ , R ₂ и R ₃ :

.

Расчет тока цепи по закону Ома

Теперь у нас есть вся необходимая информация для расчета тока цепи, потому что у нас есть напряжение между точками 1 и 4 (9 вольт) и сопротивление между точками 1 и 4 (18 кОм):

Расчет напряжений компонентов по закону Ома

Зная, что ток одинаков во всех компонентах последовательной цепи (и мы только что определили ток через батарею), мы можем вернуться к нашей исходной принципиальной схеме и отметить ток через каждый компонент:

Теперь, когда мы знаем величину тока, протекающего через каждый резистор, мы можем использовать закон Ома для определения падения напряжения на каждом из них (применяя закон Ома в его надлежащем контексте):

Обратите внимание на падение напряжения на каждом резисторе и на то, как падает сумма напряжений (1.5 + 5 + 2,5) равно напряжению аккумулятора (питания): 9 вольт.

Это третий принцип последовательных цепей:

Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.

Анализ простых последовательных цепей с помощью «табличного метода» и закона Ома

Однако метод, который мы только что использовали для анализа этой простой последовательной схемы, можно упростить для лучшего понимания. Используя таблицу для перечисления всех напряжений, токов и сопротивлений в цепи, становится очень легко увидеть, какие из этих величин могут быть правильно связаны в любом уравнении закона Ома:

Правило с такой таблицей — применять закон Ома только к значениям в каждом вертикальном столбце.Например, E _R1 только с I _R1 и R ₁ ; E _R2 только с I _R2 и R ₂ ; и т.д. Вы начинаете свой анализ с заполнения тех элементов таблицы, которые даны вам с самого начала:

Как видно из расположения данных, мы не можем подать 9 вольт ET (полное напряжение) ни на одно из сопротивлений (R ₁ , R ₂ или R ₃ ) ни при каких условиях. Формула закона Ома, потому что они находятся в разных столбцах.Напряжение батареи 9 В составляет , а не , приложенное непосредственно к R ₁ , ₂ R или ₃ R. Однако мы можем использовать наши «правила» для последовательных цепей, чтобы заполнить пустые места в горизонтальном ряду. В этом случае мы можем использовать правило ряда сопротивлений для определения общего сопротивления из суммы отдельных сопротивлений:

Теперь, когда значение общего сопротивления вставлено в крайний правый столбец («Всего»), мы можем применить закон Ома I = E / R к общему напряжению и общему сопротивлению, чтобы получить общий ток 500 мкА:

Затем, зная, что ток распределяется поровну между всеми компонентами последовательной цепи (еще одно «правило» последовательной схемы), мы можем заполнить токи для каждого резистора из только что рассчитанного значения тока:

Наконец, мы можем использовать закон Ома для определения падения напряжения на каждом резисторе, по столбцу за раз:

Проверка расчетов с помощью компьютерного анализа (SPICE)

Ради удовольствия, мы можем использовать компьютер для автоматического анализа этой самой схемы.Это будет хороший способ проверить наши расчеты, а также познакомиться с компьютерным анализом. Во-первых, мы должны описать схему компьютеру в формате, распознаваемом программным обеспечением.

Программа SPICE, которую мы будем использовать, требует, чтобы все электрически уникальные точки в цепи были пронумерованы, а размещение компонентов понималось по тому, какие из этих пронумерованных точек или «узлов» они разделяют. Для ясности я пронумеровал четыре угла схемы в нашем примере с 1 по 4. SPICE, однако, требует, чтобы где-то в схеме был нулевой узел, поэтому я перерисую схему, немного изменив схему нумерации:

Все, что я здесь сделал, это перенумеровал нижний левый угол цепи 0 вместо 4.Теперь я могу ввести несколько строк текста в компьютерный файл, описывающий схему в терминах, понятных SPICE, вместе с парой дополнительных строк кода, предписывающих программе отображать данные о напряжении и токе для нашего удовольствия от просмотра. Этот компьютерный файл известен как список цепей в терминологии SPICE:

последовательная цепь
v1 1 0
r1 1 2 3к
r2 2 3 10к
r3 3 0 5k
.dc v1 9 9 1
.print dc v (1,2) v (2,3) v (3,0)
.конец
 

Теперь все, что мне нужно сделать, это запустить программу SPICE для обработки списка соединений и вывода результатов:

версия 1	в (1,2)	в (2,3)	в (3)	я (v1)
9.000E + 00	1.500E + 00	5.000E + 00	2.500E + 00	-5.000E-04

Эта распечатка сообщает нам, что напряжение батареи составляет 9 вольт, а падение напряжения на R ₁ , R ₂ и R ₃ составляет 1,5 В, 5 В и 2,5 В соответственно. Падения напряжения на любом компоненте в SPICE обозначаются номерами узлов, между которыми находится компонент, поэтому v (1,2) относится к напряжению между узлами 1 и 2 в цепи, которые являются точками, между которыми находится R ₁ . .

Порядок номеров узлов важен: когда SPICE выводит число для v (1,2), он учитывает полярность так же, как если бы мы держали вольтметр с красным измерительным проводом на узле 1 и черным измерительным проводом на узел 2. У нас также есть дисплей, показывающий ток (хотя и с отрицательным значением) на уровне 0,5 мА или 500 мкА. Итак, наш математический анализ был подтвержден компьютером. Эта цифра отображается как отрицательное число в анализе SPICE из-за необычного способа обработки текущих вычислений SPICE.

Таким образом, последовательная цепь определяется как имеющая только один путь, по которому может течь ток. Из этого определения следуют три правила последовательных цепей: все компоненты имеют одинаковый ток; сопротивления складываются, чтобы равняться большему общему сопротивлению; а падение напряжения в сумме равняется большему общему напряжению. Все эти правила находят корень в определении последовательной цепи. Если вы полностью понимаете это определение, то правила — не что иное, как сноски к определению.

ОБЗОР:

• Компоненты в последовательной цепи имеют одинаковый ток: I _Всего = I ₁ = I ₂ =.. . Я _n
• Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений: RTotal = R ₁ + R ₂ +. . . Р _н
• Общее напряжение в последовательной цепи равно сумме отдельных падений напряжения E _Всего = E ₁ + E ₂ +. . . En

Попробуйте наш Калькулятор закона Ома в разделе Инструменты .

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

Рабочий лист параллельных цепей постоянного тока серии

— Электрические цепи постоянного тока

Позвольте электронам сами дать вам ответы на ваши собственные «практические проблемы»!

Примечания:

По моему опыту, студентам требуется много практики с анализом цепей, чтобы стать профессионалом. С этой целью инструкторы обычно предоставляют своим ученикам множество практических задач, над которыми нужно работать, и дают ученикам ответы, с которыми они могут проверить свою работу.Хотя такой подход позволяет студентам овладеть теорией схем, он не дает им полноценного образования.

Студентам нужна не только математическая практика. Им также нужны настоящие практические схемы построения схем и использование испытательного оборудования. Итак, я предлагаю следующий альтернативный подход: ученики должны построить свои собственные «практические задачи» с реальными компонентами и попытаться математически предсказать различные значения напряжения и тока. Таким образом, математическая теория «оживает», и учащиеся получают практические навыки, которых они не приобрели бы, просто решая уравнения.

Еще одна причина для использования этого метода практики — научить студентов научному методу : процессу проверки гипотезы (в данном случае математических предсказаний) путем проведения реального эксперимента. Студенты также разовьют реальные навыки поиска и устранения неисправностей, поскольку они время от времени делают ошибки при построении схем.

Выделите несколько минут времени со своим классом, чтобы ознакомиться с некоторыми «правилами» построения схем, прежде чем они начнутся. Обсудите эти проблемы со своими учениками в той же сократической манере, в которой вы обычно обсуждаете вопросы рабочего листа, вместо того, чтобы просто говорить им, что они должны и не должны делать.Я никогда не перестаю удивляться тому, насколько плохо студенты понимают инструкции, представленные в типичном формате лекции (монолог инструктора)!

Примечание для тех инструкторов, которые могут жаловаться на «потраченное впустую» время, необходимое ученикам для построения реальных схем вместо того, чтобы просто математически анализировать теоретические схемы:

Какова цель студентов, посещающих ваш курс?

Если ваши ученики будут работать с реальными схемами, им следует по возможности учиться на реальных схемах.Если ваша цель — обучить физиков-теоретиков, то во что бы то ни стало придерживайтесь абстрактного анализа! Но большинство из нас планирует, чтобы наши ученики что-то делали в реальном мире с образованием, которое мы им даем. «Потраченное впустую» время, потраченное на создание реальных схем, принесет огромные дивиденды, когда им придет время применить свои знания для решения практических задач.

Кроме того, когда студенты создают свои собственные практические задачи, они учатся выполнять первичное исследование , тем самым давая им возможность продолжить свое образование в области электрики / электроники в автономном режиме.

В большинстве наук реалистичные эксперименты намного сложнее и дороже, чем электрические схемы. Профессора ядерной физики, биологии, геологии и химии хотели бы, чтобы их студенты применяли передовую математику в реальных экспериментах, не представляющих опасности для безопасности и стоивших меньше, чем учебник. Они не могут, но вы можете. Воспользуйтесь удобством, присущим вашей науке, и заставьте своих учеников практиковать математику на множестве реальных схем!

Схемы серии

(часть 1) — Видеолекция по схемам

В начале четвертой главы мы упомянули, что собираемся рассмотреть четыре основных способа построения схем, и первый метод, который мы собираемся рассмотреть, и самый простой — это последовательные схемы.

Техническому специалисту важно разбираться в последовательных схемах. Последовательная схема характеризуется как имеющая только один путь для прохождения тока, поэтому здесь у нас есть источник ЭДС и подключенный компонент, так как здесь внизу у нас есть источник напряжения и компонент, подключенный, в данном случае лампочка, но в обоих В этих случаях существует только один путь для прохождения тока. Есть только один способ протекания тока, нет альтернативных путей, есть только один путь, и это делает его последовательной схемой.

Компоненты серии

соединены таким образом, что существует только один путь для прохождения тока без каких-либо ответвлений в цепи.

Цепи серии

Если каждый электрон, который покидает отрицательный вывод источника питания, имеет только один путь для прохождения тока, тогда схема представляет собой последовательную цепь, и в этом случае вы видите здесь отрицательную сторону этого… и положительную… каждый проходящий электрон имеет только один путь для тока, поэтому мы будем называть его последовательной схемой.В последовательной цепи, поскольку существует только один путь для прохождения тока, через каждый компонент протекает тот же ток, что и через всю цепь. Это важный аспект последовательной цепи. Поскольку существует только один путь для прохождения тока, то это тот же ток, который проходит через R2, R3 и R1, то есть такая же величина. Это похоже на то, как мы говорили об этой гидравлической системе и о том, что в гидравлической системе есть насос, и если это контур, то такое же количество жидкости, которое проходит через него, проходит через это, и это была аналогия с гидравлическим насосом, который мы говорилось в предыдущих уроках.

Теперь, вот эта конкретная схема, у меня есть вопрос по вышеуказанным последовательным схемам … ну, это, очевидно, последовательная схема … в этом случае мы начинаем с нашего источника напряжения, ток входит и проходит через все … ток от источник идет от R2, но теперь у нас есть то, что мы называем разветвлением, и это будет параллельная схема, поэтому схема будет проходить через эту ветвь резисторов здесь, а затем вернуться через эту схему. Это уже не действительно последовательная схема.Это последовательная схема, но здесь есть параллельная ветвь, и позже в этой главе мы рассмотрим параллельные схемы.

Интуитивные отношения

Цепи серии

, этот раздел называется интуитивными отношениями, а интуитивные отношения — это вещи, которые просто имеют смысл, а в последовательных цепях есть некоторые вещи, которые просто интуитивно понятны для последовательной цепи, и в вашем тексте будет немного обсуждения. каждый из них, если неясно, как я это преодолел.Во-первых, все токи в последовательной цепи равны, весь ток через эту конкретную цепь будет одинаковым. Общее сопротивление больше любого сопротивления. Возможно, это очевидно, но общее сопротивление всех компонентов будет больше, чем какое-либо одно сопротивление. Аналогичным образом, общая мощность больше, чем рассеиваемая мощность любого одного компонента, поэтому общая рассеиваемая мощность этой схемы будет больше, чем рассеиваемая мощность любого отдельного компонента. Падение большего сопротивления приводит к большему падению напряжения.Это может быть не так очевидно, но если мы вспомним, что напряжения … помните, мы говорили о том, что такое напряжение с точки зрения закона Ома? Мы сказали, что напряжение равно I, умноженному на R, теперь помните, что у нас есть один и тот же ток, протекающий по всей цепи, поэтому мы говорим, что ток будет таким, мы просто покажем плоскую стрелку, показывающую горизонтальную, плоское соотношение не изменится. Если сопротивление увеличивается, то падение напряжения на этом компоненте будет увеличиваться, и поэтому у нас здесь три компонента, это самые большие 30 кОм, поэтому это будет самое большое падение напряжения, основанное на формуле, согласно которой ток, умноженный на сопротивление, равен напряжению и самое большое сопротивление и все токи равны, падение здесь будет самым большим.

Наконец, последнее интуитивное соотношение, полное напряжение больше, чем напряжение любого компонента, поэтому общее напряжение в этом случае составляет 120 вольт, и оно будет больше, чем падение любого отдельного напряжения, и эти отношения называются интуитивными отношениями для последовательных цепей. схемы.

Математические отношения

Математические соотношения, в последовательной цепи существуют следующие соотношения в отношении текущего напряжения и сопротивления. Первый, у нас есть что-то здесь, называемое IA, в этом случае A имеет отношение к приложенному току, ток, который выходит из нашего источника питания, равен тому, который проходит через R1, R2 и R3, и математически это то, что состояния.Сопротивление, в данном случае RT — это полное сопротивление. В этом случае общее сопротивление всех компонентов будет равно R1 + R2 + R3. Затем у нас есть VT для напряжения, и снова это общее напряжение, в данном случае 120 вольт, но оно будет равно падению напряжения на R1, R2 и R3. Приложенное напряжение в замкнутом контуре равно сумме падений составляющих напряжения. Это важное соотношение известно как закон напряжения Кирхгофа.

Полярность падений напряжения

Когда через резистор протекает ток, на этом резисторе возникает соответствующее падение напряжения.Точка, где ток входит в резистор, является отрицательной, а точка выхода тока будет положительной. Итак, здесь у нас есть источник питания, он подает ток, ток течет в этом направлении, и обратите внимание, что мы находимся здесь на отрицательной клемме, но первая точка здесь, где мы вводим компонент, полярность будет отрицательной, а затем другая сторона будет положительной. Когда мы будем моделировать наши схемы, вы сможете использовать вольтметр, чтобы измерить это и подтвердить, что это действительно так.Полярность здесь будет минус к положительному, минус к положительному, минус к положительному. Это имеет смысл, если вы думаете, что у вас есть батарея, и у вас есть только один компонент, вот этот компонент, и батарея имеет положительный или отрицательный полюс, что полярность в компоненте будет такой же; положительное будет на положительной стороне, отрицательное — на отрицательной. В любом случае, точка, где ток входит в компонент, будет отрицательной стороной компонента.

Замкнутые уравнения

Следующая процедура может использоваться для создания уравнения с обратной связью для описания последовательной цепи.В этом есть два шага. Сначала пометьте полярность падений напряжения и источников, так что здесь у нас есть полярность, мы делали это ранее нормально, положительный к минусу, а затем минус к положительному минусу к положительному минусу к положительному. Начните с любой точки схемы и запишите напряжения, указывающие полярность, по мере продвижения по петле в любом направлении. Помните, что полярность падения напряжения определяется направлением тока. Наконец, переместитесь по контуру и запишите напряжения на выходных концах компонентов.

Закон Кирхгофа о напряжении

Мы можем это сделать… перейдем к следующему слайду; на следующем слайде немного больше места. На самом деле мы применяем закон напряжения Кирхгофа, и другой способ сформулировать этот закон состоит в том, что алгебраическая сумма всех падений напряжения и всех источников напряжения в любом замкнутом контуре равна нулю. Вы можете сделать это, суммируя полярность каждого компонента в зависимости от того, где этот ток входит в компоненты. Мы смотрим на это и думаем, что ток течет в этом направлении, и мы собираемся оценить полярность на основе того, где ток входит в этот конкретный компонент.Давайте начнем с этого момента. Полярность, при которой ток поступает в источник питания, положительная, поэтому мы начинаем со 120, а затем собираемся суммировать на основе того, где ток входит в компонент. Мы начинаем здесь с положительного значения, затем мы входим в этот компонент, и у нас есть знак «минус», поэтому мы идем -60 и продолжаем около -40, продолжаем примерно до -20. Если мы сложим эти значения, сумма будет равна нулю. Это то, о чем мы упоминали на предыдущем слайде, что сумма всех напряжений по кругу будет равна нулю, и это еще один способ сформулировать закон Кирхгофа.Если бы вы были обычным человеком и хотели бы пойти в другом направлении, вы могли бы сделать это с тем же успехом, но вы должны быть последовательны, если собираетесь это делать. Если мы скажем, что положительные силы движутся в этом направлении, тогда мы начнем с этого момента, и мы начнем с -120, идущим в этом направлении, + 20, +40, а затем +60, но снова сумма будет нулем.

Теперь я собираюсь посоветовать вам прочитать текст по этой конкретной теме, и есть несколько симуляций схем, которые вы можете сделать в мультисимметричной симуляции, чтобы подтвердить это, и вам нужно иметь возможность войти в симуляцию, подключить мультиметр и фактически измерить их. падает и убедитесь сами, что это так и закон Кирхгофа имеет смысл.Если вы алгебраически просуммируете все значения в последовательной схеме, сумма будет равна нулю.

Здесь мы рассмотрели закон напряжения Кирхгофа при решении уравнения замкнутого контура, мы рассмотрели полярность и падение напряжения, мы рассмотрели математические зависимости, мы рассмотрели некоторые интуитивно понятные взаимосвязи между последовательными цепями и мы посмотрели, что такое последовательная цепь. и что не является последовательной схемой. На этом мы завершаем наш раздел, посвященный последовательным схемам.

Видеолекции, созданные Тимом Фигенбаумом в Общественном колледже Северного Сиэтла.

Учебное пособие по физике: два типа соединений

Когда в цепи с источником энергии присутствуют два или более электрических устройства, существует несколько основных способов их соединения. Их можно подключить последовательно или подключить параллельно . Предположим, что в одну цепь включены три лампочки. При последовательном соединении они соединяются таким образом, чтобы отдельный заряд проходил через каждую из лампочек последовательно.При последовательном соединении заряд проходит через каждую лампочку. При параллельном подключении один заряд, проходящий через внешнюю цепь, будет проходить только через одну из лампочек. Лампочки помещаются в отдельную ветвь, и заряд, проходящий через внешнюю цепь, проходит только через одну из ветвей на обратном пути к клемме с низким потенциалом. Способы подключения резисторов будут иметь большое влияние на общее сопротивление цепи, общий ток в цепи и ток в каждом резисторе.В Уроке 4 мы исследуем влияние типа подключения на общий ток и сопротивление цепи.

Обычная физическая лаборатория состоит в построении обоих типов цепей с лампами, подключенными последовательно, и лампами, подключенными параллельно. Эти две схемы сравниваются и противопоставляются.

Основные вопросы, вызывающие беспокойство при такой лабораторной деятельности, как правило, следующие:

• Что происходит с общим током в цепи при увеличении количества резисторов (лампочек)?
• Что происходит с общим сопротивлением в цепи при увеличении количества резисторов (лампочек)?
• Если один из резисторов выключен (т.е.е., лампочка гаснет ), что происходит с другими резисторами (лампочками) в цепи? Они остаются включенными (т.е. горят)?

Изучение последовательных подключений

При проведении лабораторных работ для двух типов цепей производятся совершенно разные наблюдения. Последовательная цепь может быть построена путем соединения лампочек таким образом, чтобы оставался единственный путь для потока заряда; луковицы добавляются к той же линии без точки ветвления.По мере того, как добавляется все больше и больше лампочек, яркость каждой лампочки постепенно уменьшается. Это наблюдение является индикатором того, что ток в цепи уменьшается.

Итак, для последовательных цепей по мере добавления резисторов общий ток в цепи уменьшается. Это уменьшение тока согласуется с выводом о том, что общее сопротивление увеличивается.

Последнее наблюдение, которое является уникальным для последовательных цепей, — это эффект вынимания лампы из розетки.Если одна из трех лампочек в последовательной цепи вывинчивается из своего патрона, то наблюдается, что остальные лампочки сразу же гаснут. Чтобы устройства в последовательной цепи работали, каждое устройство должно работать. Если один погаснет, погаснут все. Предположим, что вся бытовая техника на домашней кухне подключена последовательно. Чтобы холодильник работал на этой кухне, должны быть включены тостер, посудомоечная машина, мусоропровод и верхний свет. Чтобы одно устройство, включенное последовательно, работало, все они должны работать.Если ток равен , отрежьте от любого из них, он отключается от всех. Совершенно очевидно, что приборы на кухне не подключены последовательно.

Исследование параллельных подключений

Используя тот же набор проводов, D-элементов и лампочек, можно таким же образом исследовать параллельные цепи. Можно исследовать влияние количества резисторов на общий ток и общее сопротивление.На схемах ниже изображены обычные способы построения схемы с параллельным подключением лампочек. Следует отметить, что исследование общего тока для параллельных соединений требует добавления индикаторной лампы . Лампа индикатора размещена вне ответвлений и позволяет наблюдать влияние дополнительных резисторов на общий ток. Лампочки, размещенные в параллельных ветвях, служат только индикатором тока через эту конкретную ветвь.Поэтому, исследуя влияние количества резисторов на общий ток и сопротивление, нужно внимательно следить за лампочкой индикатора, а не за лампочками, помещенными в ответвления. На диаграмме ниже показаны типичные наблюдения.

Из показаний лампочек индикаторов на приведенных выше схемах видно, что добавление большего количества резисторов приводит к тому, что лампочка индикатора становится ярче. Для параллельных цепей с увеличением количества резисторов общий ток также увеличивается.Это увеличение тока согласуется с уменьшением общего сопротивления. Добавление резисторов в отдельную ветвь приводит к неожиданному результату уменьшения общего сопротивления!

Если отдельная лампочка в параллельной ветви вывинчивается из патрона, то ток в общей цепи и в других ветвях все равно остается. Удаление третьей лампочки из патрона приводит к преобразованию схемы из параллельной цепи с тремя лампами в параллельную цепь с двумя лампами.Если бы приборы на домашней кухне были подключены параллельно, то холодильник мог бы работать без включения посудомоечной машины, тостера, мусоропровода и верхнего освещения. Одно устройство может работать без включения других. Поскольку каждое устройство находится в своей отдельной ветви, выключение этого устройства просто прекращает подачу заряда в эту ветвь. По другим ответвлениям к другим приборам по-прежнему будет поступать заряд. Совершенно очевидно, что бытовая техника в доме подключена параллельно.

Аналогия с платной кабиной

Эффект добавления резисторов совершенно иной, если они добавляются параллельно, по сравнению с их последовательным соединением. Последовательное добавление большего количества резисторов означает увеличение общего сопротивления; однако добавление большего количества резисторов параллельно означает уменьшение общего сопротивления. Тот факт, что можно добавить больше резисторов параллельно и добиться меньшего сопротивления, многих очень беспокоит. Аналогия может помочь прояснить причину этой изначально надоедливой правды.

Поток заряда по проводам цепи можно сравнить с потоком автомобилей по платной дороге в очень густонаселенном мегаполисе. Основными источниками сопротивления на платных дорогах являются посты. Остановка автомобилей и принуждение их к уплате дорожных сборов не только замедляет движение автомобилей, но и в районе с интенсивным движением, также приведет к возникновению узких мест с резервной копией на многие мили. Скорость, с которой автомобили проезжают через точку на этой платной системе, значительно снижается из-за наличия платы за проезд.Понятно, что пункты пропуска дороги — это главный фактор, препятствующий потоку автомобилей.

Теперь предположим, что в попытке увеличить скорость потока Управление взимания платы за проезд решает добавить еще две точки взимания платы за проезд на определенной станции взимания платы, где узкое место создает проблемы для путешественников. Они рассматривают два возможных способа подключения своих платных пунктов оплаты — последовательно или параллельно. При последовательном добавлении платных постов (т. Е. Резисторов) они добавляли бы их таким образом, чтобы каждая машина, движущаяся по шоссе, должна была бы последовательно останавливаться на каждой плате за проезд.При наличии только одного пути через пункты взимания платы за проезд каждая машина должна будет останавливаться и платить за проезд в каждой будке. Вместо того, чтобы платить 60 центов один раз в одной будке, теперь им придется платить по 20 центов трижды в каждой из трех платных. Совершенно очевидно, что добавление платных постов последовательно имело бы общий эффект увеличения общего сопротивления и уменьшения общей скорости потока автомобиля (т. Е. Тока).

Другим способом добавления двух дополнительных пунктов взимания платы на этой конкретной станции сбора платы за проезд может быть параллельное добавление пунктов взимания платы.Каждую будку можно разместить в отдельном филиале. Машины, движущиеся по платной дороге, останавливались только у одной из трех будок. У автомобилей будет три возможных пути, по которым они будут проезжать через станцию ​​сбора платы за проезд, и каждая машина выберет только один из путей. Совершенно очевидно, что параллельное добавление платных постов приведет к уменьшению общего сопротивления и увеличению общей скорости потока автомобилей (т. Е. Тока) вдоль платной дороги. Как и в случае добавления дополнительных электрических резисторов параллельно, добавление дополнительных плат в параллельных ветвях создает меньшее общее сопротивление.Обеспечивая большее количество путей (то есть ответвлений), по которым заряд и автомобили могут проходить через узкие места, скорость потока может быть увеличена.

Мы хотели бы предложить … Зачем просто читать об этом и когда можно с ним взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, расположить и подключить их так, как вам нужно. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).

Проверьте свое понимание

1. Обратите внимание на электрическую проводку, указанную ниже. Укажите, являются ли соединения последовательными или параллельными. Объясните каждый выбор.

2. Ниже показаны две электрические цепи. Для каждой цепи укажите, какие два устройства подключены последовательно, а какие — параллельно.

Последовательно? ___________________ Параллельно? _________________	Последовательно? ___________________ Параллельно? _________________

2.2.3 Цепи с последовательными и параллельными элементами

Большинство энергосистем фактически настроено как «цепи» или контуры, и нам может потребоваться найти эквивалентное последовательно-параллельное сопротивление от начала контура до конца. На рисунке ниже показан особенно неприятный пример, но мы можем разбить его на несколько простых шагов.

Рисунок 2.7: Сложная последовательно-параллельная схема

Щелкните здесь, чтобы увидеть текстовое описание рисунка 2.7

Схема представлена ​​прямоугольником, который разделен по вертикали на большую и меньшую секции.Слева находится закрашенный кружок со знаком плюс и минус, обозначенный как 120V. В цепи 4 резистора. Первый находится в верхней части большой части прямоугольника и обозначен как 4 Ом. Следующий находится в верхней части маленькой стороны схемы и обозначен как 3 Ом. В правой части прямоугольника есть резистор, обозначенный как 6 Ом. Последний резистор находится на делении и имеет маркировку 18 Ом. Под резистором 4 Ом находится стрелка, указывающая вправо, с надписью i _s .Резистор на 18 Ом имеет направленную вниз стрелку, обозначенную i ₁ , а резистор на 6 Ом имеет направленную вниз стрелку, обозначенную i ₂ .

Источник: Сет Блумсак

На этом рисунке у нас есть источник 120 В (например, небольшая батарея), который передает ток через показанную сеть резисторов. Какое эквивалентное сопротивление во всей цепи, от положительной до отрицательной клеммы аккумулятора?

Шаг 1. Возьмем резистор 3 Ом и резистор 6 Ом и вычислим эквивалентное последовательное сопротивление следующим образом: 3 Ом + 6 Ом = 9 Ом.Это дает новое представление схемы ниже.

Рисунок 2.8: Первый шаг упрощения сложной схемы

Щелкните здесь, чтобы увидеть текстовое описание рисунка 2.8

Схема представлена ​​прямоугольником, который разделен по вертикали на большую и меньшую части. Слева находится закрашенный кружок со знаком плюс и минус, обозначенный как 120V. В цепи 3 резистора. Первый находится в верхней части большой части прямоугольника и обозначен как 4 Ом.В правой части прямоугольника есть резистор, обозначенный как 9 Ом. Последний резистор находится на делении и имеет маркировку 18 Ом.

Источник: Сет Блумсак

На шаге 2 мы вычислим эквивалентное параллельное сопротивление элементов 9 Ом и 18 Ом. Мы рассчитываем это как:

1 (19 + 118) = 1 (218 + 118) = 1 (16) = 6 Ом

Рисунок 2.9: Второй шаг упрощения сложной схемы

Щелкните здесь, чтобы увидеть текстовое описание рисунка 2.9

На схеме показана более простая схема, представленная прямоугольником со встроенным кружком с левой стороны.Внутри круга есть символы плюса и минуса, обозначенные как 120 В. В верхней части схемы находится резистор с маркировкой 4 Ом, а с правой стороны схемы — резистор с маркировкой 6 Ом

.

Источник: Сет Блумсак

На последнем этапе мы возьмем последовательное сопротивление элементов 4 Ом и 6 Ом: 4 Ом + 6 Ом = 10 Ом.

В этих нескольких шагах мы показали, что две цепи на рисунке ниже имеют точно такое же эквивалентное сопротивление.

Фигура 2.10: Сложная последовательно-параллельная схема (слева) и ее эквивалентная простая схема (справа)

Щелкните здесь, чтобы увидеть текстовое описание рисунка 2.10

Схема с рисунка 2.8 рядом с простой схемой. Простая схема представлена ​​прямоугольником со встроенным кружком с левой стороны с символом плюс и минус внутри, обозначенным 120 В. На правой стороне схемы расположен резистор с маркировкой 10 Ом.

Источник: Сет Блумсак

Характеристики параллельной цепи

Обновлено 28 декабря 2020 г.

Автор: S.Hussain Ather

Электрические цепи могут иметь элементы схемы, расположенные последовательно или параллельно. В последовательных цепях элементы соединяются с помощью одной и той же ветви, которая пропускает электрический ток через каждую из них один за другим. В параллельных цепях элементы имеют свои отдельные ответвления. В этих цепях ток может проходить по разным путям.

Поскольку ток может проходить по разным путям в параллельной цепи, ток не является постоянным во всей параллельной цепи.Вместо этого для ветвей, которые соединены параллельно друг с другом, падение напряжения или потенциала на каждой ветви является постоянным. Это связано с тем, что ток распределяется по каждой ветви в количестве, обратно пропорциональном сопротивлению каждой ветви. Это приводит к тому, что ток становится наибольшим там, где сопротивление наименьшее, и наоборот.

Эти качества позволяют параллельным цепям пропускать заряд по двум или более путям, что делает его стандартным кандидатом в домах и электрических устройствах через стабильную и эффективную систему питания.Он позволяет электричеству течь через другие части цепи, когда какая-либо часть повреждена или сломана, и они могут распределять мощность равномерно по разным зданиям. Эти характеристики можно продемонстрировать с помощью диаграммы и примера параллельной цепи.

Схема параллельной цепи

••• Syed Hussain Ather

На схеме параллельной цепи вы можете определить поток электрического тока, создавая потоки электрического тока от положительного конца батареи к отрицательному.Положительный конец обозначен плюсом на источнике напряжения, а отрицательный -.

По мере прохождения тока по ветвям параллельной цепи помните, что весь ток, входящий в один узел или точку в цепи, должен равняться всему току, выходящему или выходящему из этой точки. Также имейте в виду, что падение напряжения вокруг любого замкнутого контура в цепи должно равняться нулю. Эти два утверждения являются схемными законами Кирхгофа.

Характеристики параллельной цепи

В параллельных цепях используются ответвления, которые позволяют току проходить по различным маршрутам через цепь.Ток проходит от положительного конца батареи или источника напряжения к отрицательному. Напряжение остается постоянным по всей цепи, в то время как ток изменяется в зависимости от сопротивления каждой ветви.

Примеры параллельных цепей

Чтобы найти полное сопротивление резисторов, установленных параллельно друг другу, используйте формулу

\ frac {1} {R_ {total}} = \ frac {1} {R_1} + \ frac { 1} {R_2} + \ frac {1} {R_3} + … + \ frac {1} {R_n}

, в котором сопротивление каждого резистора суммируется в правой части уравнения.На приведенной выше диаграмме общее сопротивление в Ом (Ом) можно рассчитать следующим образом:

1. 1 / R _всего = 1/5 Ом + 1/6 Ом + 1/10 Ом
2. 1 / R _всего = 6/30 Ом + 5/30 Ом + 3/30 Ом
3. 1 / R _всего = 14/30 Ом
   
4. R _всего = 15/7 Ом или около 2,14 Ом

Обратите внимание, что вы можете «перевернуть» обе стороны уравнения с шага 3 на шаг 4 только тогда, когда есть только один член с обеих сторон уравнения (в данном случае 1 / R _всего слева и 14/30 Ом справа).

После того, как вы рассчитали сопротивление, ток и напряжение, можно рассчитать по закону Ома V = I / R , в котором V — напряжение, измеренное в вольтах, I — ток, измеренный в амперах. , а R — сопротивление в Ом. В параллельных цепях сумма токов, протекающих по каждому пути, является полным током от источника. Ток на каждом резисторе в цепи можно рассчитать, умножив напряжение на сопротивление резистора.Напряжение остается постоянным по всей цепи, поэтому напряжение является напряжением батареи или источника напряжения.

Параллельная и последовательная цепь

••• Syed Hussain Ather

В последовательных цепях ток постоянен на всем протяжении, падение напряжения зависит от сопротивления каждого резистора, а общее сопротивление складывается из каждого отдельного резистора. В параллельных цепях напряжение постоянно, ток зависит от каждого резистора, а величина, обратная величине общего сопротивления, является суммой величин, обратных величине каждого отдельного резистора.

Конденсаторы и катушки индуктивности могут использоваться для изменения заряда в последовательной и параллельной цепях с течением времени. В последовательной цепи общая емкость схемы (заданная переменной C ), потенциал конденсатора для накопления заряда с течением времени, является обратной суммой обратных величин каждой отдельной емкости, а общая индуктивность ( I ), мощность индукторов, выделяющих заряд с течением времени, является суммой каждой индуктивности. Напротив, в параллельной цепи общая емкость является суммой каждого отдельного конденсатора, а величина, обратная величине полной индуктивности, является суммой обратных величин каждой индивидуальной индуктивности.

Последовательные и параллельные цепи также имеют разные функции. В последовательной цепи, если одна часть сломана, ток вообще не будет течь по цепи. В параллельной цепи открытие отдельной ветви останавливает только ток в этой ветви. Остальные ветви будут продолжать работать, потому что у тока есть несколько путей, которые он может пройти по цепи.

Последовательно-параллельная цепь

••• Syed Hussain Ather

Цепи, в которых есть оба разветвленных элемента, которые также соединены таким образом, что ток течет в одном направлении между этими ветвями, являются последовательными и параллельными.В этих случаях вы можете применять правила как для последовательного, так и для параллельного подключения, в зависимости от схемы. В приведенном выше примере R1 и R2 параллельны друг другу, чтобы сформировать R5 , а также R3 и R4 , чтобы сформировать R6 . . Их можно суммировать параллельно следующим образом:

1. 1 / R5 = 1/1 Ом + 1/5 Ом
2. 1 / R5 = 5/5 Ом + 1/5 Ом
3. 1 / R5 = 6/5 Ом
   
4. R5 = 5/6 Ом или около 0,83 Ом

1. 1 / R6 = 1/7 Ом + 1/2 Ом
2. 1 / R6 = 2/14 Ом + 7/14 Ом
3. 1 / R6 = 9/14 Ом
   
4. R6 = 14/9 Ом или около 1.56 Ом

••• Syed Hussain Ather

Схема может быть упрощена для создания схемы, показанной непосредственно выше, с R5 и R6 . Эти два резистора могут быть добавлены просто, как если бы цепь была последовательной.

R_ {total} = 5/6 \ Omega + 14/9 \ Omega = 2.38 \ Omega

При напряжении 20 В в качестве напряжения закон Ома определяет, что общий ток равен В / R . , или 20 В / (43/18 Ом) = 360/43 А или около 8.37 A. Используя этот общий ток, вы также можете определить падение напряжения на R5 и R6, используя закон Ома ( В = I / R ).

V_5 = \ frac {360} {43} \ times 5/6 = 6.98 \ text {V}

V_5 = \ frac {360} {43} \ times 14/9 = 13.02 \ text {V}

Наконец, эти падения напряжения для R5 и R6 можно разделить обратно на исходные параллельные цепи для расчета тока R1 и R2 для R5, и . R2 и R3 для R6 с использованием закона Ома.

I1 = (1800/258 В) / 1 Ом = 1800/258 А или около т 6,98 А.

I2 = (1800/258 В) /5 Ом = 1500/43 А или около т 34,88 А.

I3 = ( 680/129 В ) / 7 Ом = 4760/129 A или примерно 36,90 A .

I3 = ( 680/129 В ) / 2 Ом = 1360/129 A или около 10.54 A.

Последовательные конденсаторы | Приложения

Конденсаторы серийные

Как и другие электрические элементы, конденсаторы бесполезны, когда используются в цепи по отдельности. Они подключаются к другим элементам цепи одним из двух способов: последовательно или параллельно. В некоторых случаях полезно соединить несколько конденсаторов последовательно для создания функционального блока:

Анализ

Когда этот блок подключен к источнику напряжения, каждый конденсатор в блоке сохраняет равное количество заряда, что означает, что общий заряд равномерно распределяется по всем конденсаторам, независимо от их емкости.Количество заряда, накопленного на каждом конденсаторе, равно:

, где Q _всего — это общая сумма заряда в полном блоке, а от Q ₁ до Q _n — это заряды на каждом отдельном конденсаторе.

Чтобы объяснить, почему заряды на каждом конденсаторе взаимно равны и равны общему количеству заряда, хранящегося в полном блоке последовательного соединения, давайте предположим, что все конденсаторы были разряжены в один момент времени. Когда напряжение сначала подается на блок, одинаковый ток течет через все конденсаторы, и в результате происходит сдвиг заряда.Электроны переносятся от одной пластины каждого конденсатора к другой, что означает, что заряд, накопленный пластиной любого из конденсаторов, должен исходить от пластины соседнего конденсатора. Это означает, что носители заряда (электроны) просто прошли через все конденсаторы, что является причиной того, что заряды на каждом конденсаторе равны.

При этом следует отметить, что напряжения на каждом конденсаторе не равны и рассчитываются для каждого конденсатора по известной формуле:

, где Q _n — количество заряда на каждом конденсаторе в последовательном соединении, C _n — емкость конденсатора, а V _n — напряжение на конденсаторе.

Применяя закон Кирхгофа к блоку последовательного подключения, напряжение на блоке равно сумме напряжений на отдельных конденсаторах:

Подставляя приведенную выше формулу для напряжения на конденсаторе в это уравнение, имея в виду, что заряд на каждом конденсаторе равен общему заряду, накопленному в последовательном соединении, мы получаем следующую формулу:

, что дает:

, где C _eq — эквивалентная емкость, а от C ₁ до C _n — значения емкости каждого отдельного конденсатора в последовательном соединении.

Другими словами, обратное значение эквивалентной емкости равно сумме значений обратной емкости для каждого конденсатора в последовательном соединении.

Приложения

Делитель напряжения емкостной

Делитель напряжения — это устройство, которое делит приложенное напряжение на два или более выходных напряжения с заданным соотношением. Они могут быть построены с использованием резисторов или реактивных элементов, таких как конденсаторы. Когда конденсаторы соединены последовательно и через это соединение подается напряжение, напряжения на каждом конденсаторе обычно не равны, но зависят от значений емкости.

Точнее, отношение напряжений на отдельных конденсаторах обратно пропорционально отношению значений емкости каждого отдельного конденсатора в серии. Следует отметить, что для практических целей емкостные делители напряжения полезны только в цепях переменного тока, поскольку конденсаторы не пропускают сигналы постоянного тока, а также потому, что они имеют определенную утечку напряжения. На следующем рисунке показан емкостной делитель напряжения:

Повышенное рабочее напряжение

Иногда желательно использовать последовательное соединение конденсаторов, чтобы иметь возможность работать с более высокими напряжениями.Например, предположим, что источник питания 5 кВ необходимо фильтровать с помощью конденсаторов, и что единственные доступные конденсаторы рассчитаны на 1 кВ и имеют одинаковые значения емкости. В этом случае при последовательном соединении пяти или более таких конденсаторов высокое напряжение будет разделено на все конденсаторы, и максимальный номинальный ток не будет превышен.

Другой пример использования последовательно соединенных конденсаторов — возможная замена автомобильного аккумулятора конденсаторной батареей из суперконденсаторов.Поскольку их максимальное номинальное напряжение составляет всего около 2,7 В, при последовательном подключении шести таких суперконденсаторов рабочее напряжение батареи повышается до уровней, приемлемых для использования в автомобилях. Преимущество использования суперконденсаторов по сравнению с батареями — это преимущество в весе, однако эта технология все еще нуждается в улучшении из-за токов утечки и гораздо большей емкости, предлагаемой батареями.

Безопасность

Следует ввести определенный запас прочности при использовании цепи последовательного конденсатора, и в этом примере в хорошей конструкции должно быть использовано более пяти конденсаторов по двум причинам.Первая причина заключается в том, что конденсаторы имеют определенный допуск по емкости, и они не могут иметь одинаковые значения емкости. Как следствие, конденсатор с немного меньшим значением емкости будет подвергаться воздействию немного большего напряжения, чем максимальное номинальное напряжение в этом примере. Вторая причина в том, что в реальности конденсаторы иногда выходят из строя. Если один из конденсаторов выйдет из строя и произойдет короткое замыкание, приложенное напряжение 5 кВ будет разделено между оставшимися 4 конденсаторами номиналом всего 1 кВ, и это вызовет каскад отказов, в конечном итоге закорачивая источник напряжения и приводя к полной разрушение фильтра.

.

No related posts.