Еще раз популярно про закон Ома
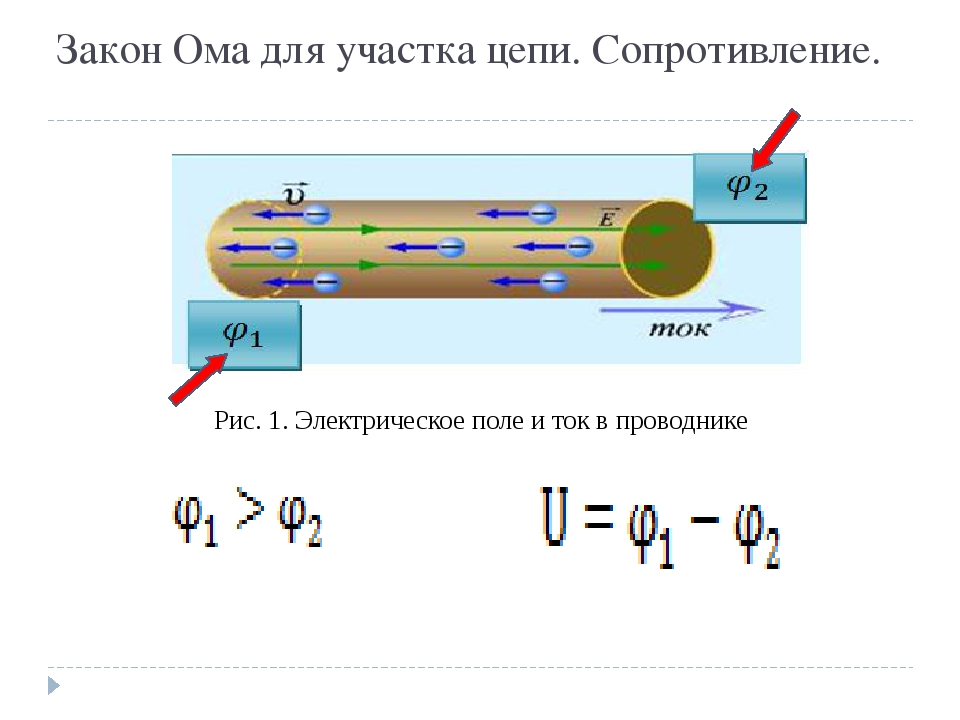
Закон Ома
1. Дифференциальная форма записи закона Ома
Самый главный закон электротехники – это, конечно, закон Ома. О его существовании знают даже люди, не имеющие отношения к электротехнике. Но между тем вопрос «А знаешь ли ты закон Ома?» в технических ВУЗах является ловушкой для зарвавшихся и самонадеянных школяров. Товарищ, разумеется, отвечает, что закон Ома знает отлично, и тогда к нему обращаются с просьбой привести этот закон в дифференциальной форме. Тут-то и выясняется, что школяру или первокурснику еще учиться и учиться.
Однако дифференциальная форма записи закона Ома на практике почти неприменима. Она отражает зависимость между плотностью тока и напряженностью поля:
j=G*E,
где G – это проводимость цепи; Е – напряженность электрического тока.
Все это – попытки выразить электрический ток, принимая во внимание только физические свойства материала проводника, без учета его геометрических параметров (длина, диаметр и тому подобное).
Дифференциальная форма записи закона Ома – это чистая теория, знание ее в быту совершенно не требуется.
2. Интегральная форма записи закона Ома для участка цепи
Иное дело – интегральная форма записи. Она тоже имеет несколько разновидностей. Самой популярной из них является закон Ома для участка цепи: I=U/R
Говоря по-другому, ток в участке цепи всегда тем выше, чем больше приложенное к этому участку напряжение и чем меньше сопротивление этого участка.
Вот этот «вид» закона Ома просто обязателен к запоминанию для всех, кому хоть иногда приходится иметь дело с электричеством. Благо, и зависимость-то совсем простая. Ведь напряжение в сети можно считать неизменным. Для розетки оно равно 220 вольт. Поэтому получается, что ток в цепи зависит только от сопротивления цепи, подключаемой к розетке. Отсюда простая мораль: за этим сопротивлением надо следить.
Короткие замыкания, которые у всех на слуху, случаются именно по причине низкого сопротивления внешней цепи.
Предположим, что из-за неправильного соединения проводов в ответвительной коробке фазный и нулевой провода оказались напрямую соединены между собой. Тогда сопротивление участка цепи резко снизится практически до нуля, а ток так же резко возрастет до очень большой величины. Если электропроводка выполнена правильно, то сработает автоматический выключатель, а если его нет, или он неисправен или подобран неправильно, то провод не справится с возросшим током, нагреется, расплавится и, возможно, вызовет пожар.
Но бывает, что приборы, включенные в розетку и отработавшие уже далеко не один час, становятся причиной короткого замыкания. Типичный случай – вентилятор, обмотки двигателя которого подверглись перегреву из-за заклинивания лопастей. Изоляция обмоток двигателя не рассчитана на серьезный нагрев, она быстро приходит в негодность. В результате появляются межвитковые короткие замыкания, которые снижают сопротивление и, в соответствии с законом Ома, также ведут к увеличению тока.
Повышенный ток, в свою очередь, приводит изоляцию обмоток в полную негодность, и наступает уже не межвитковое, а самое настоящее, полноценное короткое замыкание.
Ток идет помимо обмоток, сразу из фазного в нулевой провод. Правда, все сказанное может случиться только с совсем простым и дешевым вентилятором, не оборудованным тепловой защитой.
Закон Ома для переменного тока
Надо отметить, что приведенная запись закона Ома описывает участок цепи с постоянным напряжением. В сетях переменного напряжения существует дополнительное реактивное сопротивление, а полное сопротивление приобретает значение квадратного корня из суммы квадратов активного и реактивного сопротивления.
Закон Ома для участка цепи переменного тока принимает вид: I=U/Z,
где Z – полное сопротивление цепи.
Но большое реактивное сопротивление свойственно, прежде всего, мощным электрическим машинам и силовой преобразовательной технике. Внутреннее электрическое сопротивление бытовых приборов и светильников практически полностью является активным. Поэтому в быту для расчетов можно пользоваться самой простой формой записи закона Ома: I=U/R.
3. Интегральная форма записи для полной цепи
Раз есть форма записи закона для участка цепи, то существует и закон Ома для полной цепи: I=E/(r+R).
Здесь r – внутреннее сопротивление источника ЭДС сети, а R – полное сопротивление самой цепи.
За физической моделью для иллюстрации этого подвида закона Ома далеко ходить не надо – это бортовая электрическая сеть автомобиля, аккумулятор в которой является источником ЭДС. Нельзя считать, что сопротивление аккумулятора равно абсолютному нулю, поэтому даже при прямом замыкании между его клеммами (отсутствии сопротивления R) ток вырастет не до бесконечности, а просто до высокого значения. Однако этого высокого значения, конечно, хватит для того, чтобы вызвать расплавление проводов и возгорание обшивки авто. Поэтому электрические цепи автомобилей защищают от короткого замыкания при помощи предохранителей.
Такой защиты может оказаться недостаточно, если замыкание произойдет до блока предохранителей относительно аккумулятора, или если вовсе один из предохранителей заменен на кусок медной проволоки.
Тогда спасение только в одном – необходимо как можно быстрее разорвать цепь полностью, откинув «массу», то есть минусовую клемму.
4. Интегральная форма записи закона Ома для участка цепи, содержащего источник ЭДС
Следует упомянуть и о том, что есть и еще одна разновидность закона Ома – для участка цепи, содержащего источник ЭДС:
I=(U+E)/(r+R)
или
I=(U-E)/(r+R)
Здесь U – это разность потенциалов в начале и в окончании рассматриваемого участка цепи. Знак перед величиной ЭДС зависит от направленности ее относительно напряжения. Воспользоваться законом Ома для участка цепи нередко приходится при определении параметров цепи, когда часть схемы недоступна для детального изучения и не интересует нас. Допустим, она скрыта неразъемными деталями корпуса. В оставшейся схеме имеется источник ЭДС и элементы с известным сопротивлением. Тогда, замерив напряжение на входе неизвестной части схемы, можно вычислить ток, а после этого – и сопротивление неизвестного элемента.
Выводы
Таким образом, мы можем увидеть, что «простой» закон Ома далеко не так прост, как кому-то, возможно, казалось. Зная все формы интегральной записи законов Ома, можно понять и легко запомнить многие требования электробезопасности, а также приобрести уверенность в обращении с электричеством.
Александр Молоков, http://electrik.info
Закон Ома ? для участка цепи, формула. Закон Ома ? в дифференциальной форме для полной цепи и её участка
Автор Даниил Леонидович На чтение 5 мин. Просмотров 3.7k. Опубликовано Обновлено
Физический закон ома получен путём экспериментов. 3 формулировки ома – одни из основополагающих в физике, устанавливающие связь между электротоком, сопротивлением и энергонапряжением. Год открытия – 1826.
Впервые все 3 физических закона ома сформулировал физик-экспериментатор немецкого происхождения Георг Ом, с фамилией которого связано их определение.
Мнемоническая схема
Согласно мнемосхеме, чтобы высчитать электросопротивление по закону ома для участка цепи постоянного тока, необходимо комплексное напряжение на участке цепи разделить на силу тока для полной цепи. Однако, с физико-математической точки зрения, формулу ома для участка цепи для вычисления только по первому закону ома принято считать неполной.
Альтернативный способ вычислить токовое сопротивление по закону ома кратко подразумевает умножение электросопротивления материи, из которой выполнен проводник, на длину с последующим делением на площадь пересекающегося сечения.
Для выполнения вычислений сформулируйте по закону ома для участка цепи уравнение, исходя из имеющихся числовых данных:
Применение на линии электропередач
В процессе доставки на линию электропередач потери энергии должны быть минимизированы.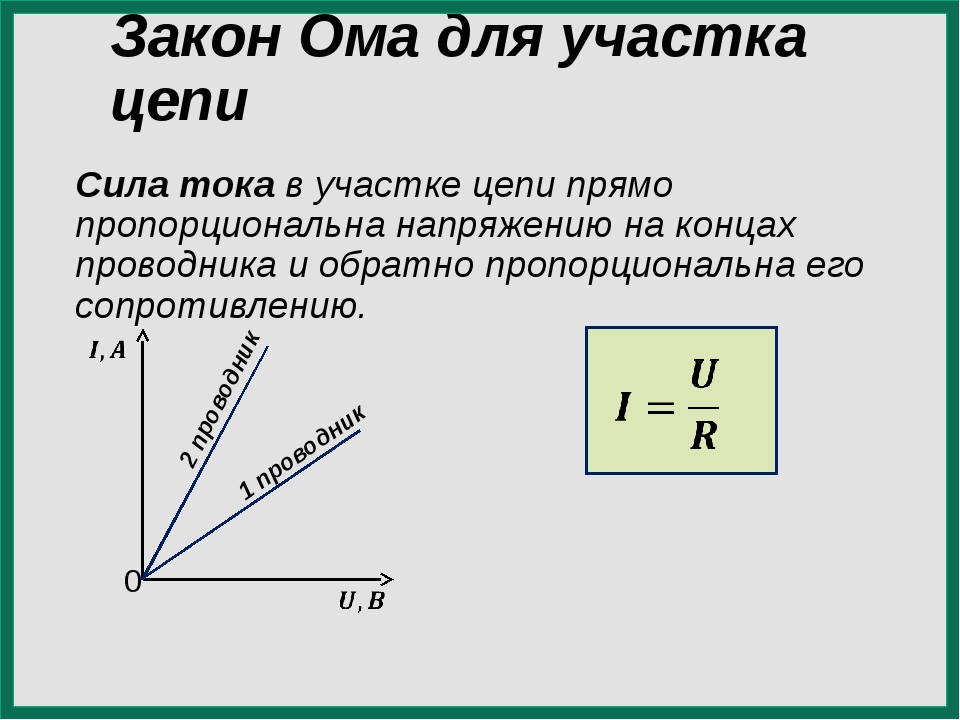
Причиной энергетических потерь является нагрев провода, во время которого энергия электротока превращается в теплоэнергию.
Чтобы дать определение по закону ома потерянной мощности, необходимо показатель электрической мощности во второй степени умножить на внутреннее сопротивление источника напряжения и разделить на ЭДС в квадрате.
Из этого следует, что рост потери энергомощности осуществляется пропорционально протяжённости линии электропередач и квадрату электродвижущей силы.
Поскольку электродвижущую силу ограничивает прочность обмотки генератора, то повышение энергонапряжения возможно после того, как из генератора выйдет электроток, на участке входа линии.
Переменный ток легче всего распределяется по линии через трансформатор. Однако, поскольку следствием повышения энергонапряжения является потеря коронирования, а надёжность изоляции обеспечивается с трудом, напряжение на участке цепи протяжённой линии электропередач не превышает миллиона вольт.
Внимание!
Поведение линии электропередач в пространстве подобно антенне, ввиду чего берётся во внимание потеря на излучение.
Отображение в дифференциальной форме
На подсчёт сопротивления влияет тип материи, по которой протекает электроток, а также геометрические габариты проводника.
Дифференциальная форма формулировки Ома, записывающаяся достаточно кратко, отображает электропроводящие характеристики изотропных материалов и заключается в умножении удельной проводимости на вектор напряжённости электрополя с целью вычисления вектора плотности энерготока.
Для выполнения требуемых вычислений, уравнение сформулируйте по закону ома:
Интересно!
Если исходить из научных данных, следует сделать вывод о законе ома в дифференциальной форме об отсутствии зависимого соотношения геометрических габаритов.
При использовании анизотропеновых электроэлементов нередко встречается несовпадение вектора плотности токового энергонапряжения. Данное суждение справедливо для закона ома в интегральной и дифференциальной формах.
Переменный ток
Величины являются комплексными, если речь идёт о синусоидальных формах энерготока с циклической частотой, в цепях которых присутствуют активная ёмкость с индуктивностью.
В перечень комплексных величин входят:
- разность между потенциалами;
- сила тока;
- комплексное электросопротивление;
- модуль импеданса;
- разность индуктивного и ёмкостного сопротивлений;
- омическое электросопротивление;
- фаза импеданса.
Если несинусоидальный энерготок допустимо измерить временными показателями, закон ома для неполной электрической цепи может быть представлен в виде сложенных синусоидальных Фурье-компонентов. В линейной цепи составные элементы фурье-разложения являются независимо функционирующими. В нелинейных цепях образуются гармоники и множество колебаний. Таким образом, можно сделать вывод о невозможности выполнения правила Ома для нелинейной электроцепи.
Внимание!
Гармоника – это колебание, частота которого кратна частоте напряжения.
Как трактуется правило Ома
Так как обобщённая формула ома не считается основополагающей, правило применяется для описания разновидностей проводников в условиях приближения незначительной частоты, плотности тока и напряжения электрополя. Следует отметить, что в ряде случаев как первый закон, так и второй закон, применяемый для полной цепи, не соблюдаются.
Существует теория Друде, для выражения которой используются следующие величины:
- удельная электропроводимость;
- концентрированное размещение электронов;
- показатель элементарного заряда;
- время затихания по импульсам;
- эффективная масса электрона.
Внимание!
Все формулы Ома – первый, второй физический закон ома и третий распространяются на омические компоненты.
Перечень условий, при которых становится невозможным соблюдения правила Ома:
- высокие частоты с чрезмерно большой скоростью изменения электротока;
- пониженная температура сверхпроводимого вещества;
- перегрев проводника проходящим электротоком;
- в ситуации пробоя, возникшего в результате подсоединения к проводниковому элементу высокого напряжения;
- в вакуумной или газонаполненной электролампе;
- для гетерогенного полупроводникового прибора;
- при образовании пространственного диэлектрического заряда в контакте металлического диэлектрика.
Интерпретация
Определяющаяся действием приложенного напряжения мощностная сила тока является пропорциональной показателю его напряжения. К примеру, при двойном увеличении приложенного напряжения, интенсивность постоянного тока также удваивается.
Интересно!
Наиболее часто правило Ома применяется для металла и керамики.
Методы запоминания формулы
Чтобы легче запомнить формулу расчёта напряжения на участке цепи, следует выписать на бумажном листе все величины, из которых она состоит, в которую также входит сопротивление и сила тока. Искомую величину закрыть пальцем, вследствие чего соотношение оставшихся величин будет отображать действие, которое необходимо совершить для её вычисления.
Ниже будет представлено видео с подробным объяснением всех правил и формул, относящихся к рассматриваемой теме.
Закон Ома – один из самых несложных для понимания, который входит в программу школьных учебников физики начального уровня. Пользуясь графическим приёмом расчёта величин – при необходимости или для самопроверки, можно получить безошибочные результаты вычислений.
Формула закона Ома в физике
Содержание:
Определение и формула закона Ома
Определение
Закон был получен Омом опытным путем. Построив вольт – амперную характеристику для проводника можно увидеть, что сила тока (I), текущего через проводник пропорциональна напряжению (U) на нем $(I \sim U)$.
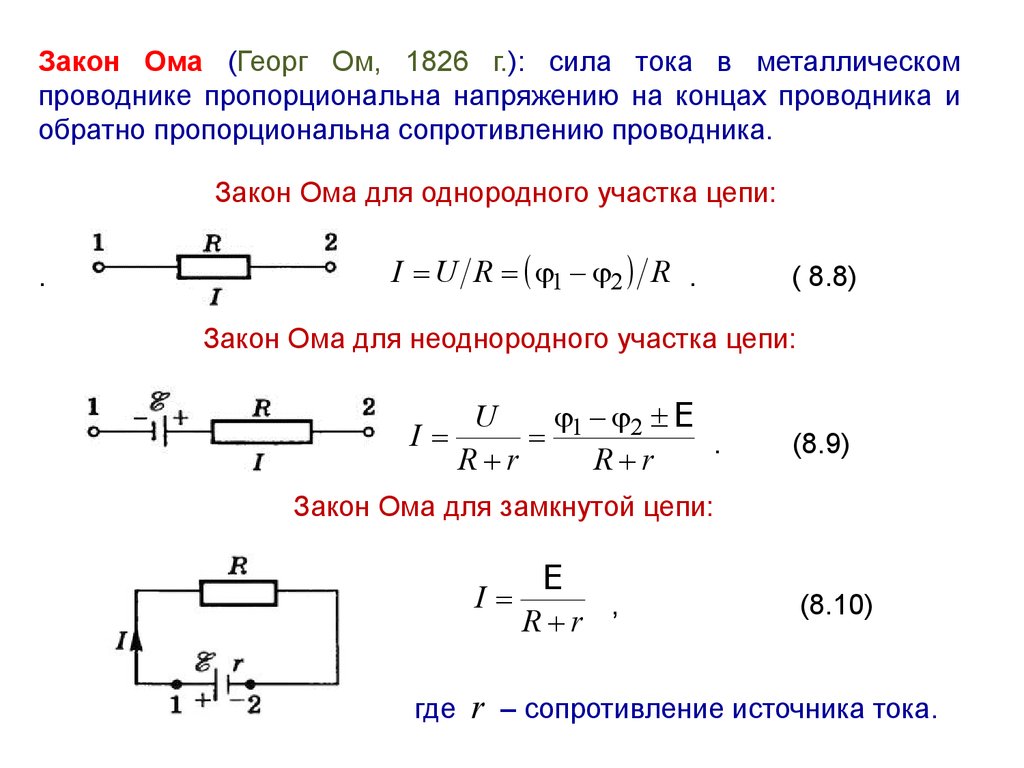
Закон Ома для участка цепи
Если на рассматриваемом участке цепи, содержащей проводник, источников ЭДС нет $\left(U_{21}=\varphi_{1}-\varphi_{2}\right)$, то формула закона Ома является предельно простой:
$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}}{R}(1)$$где R – сопротивление проводника (совокупности проводников, участка цепи).
Если источник тока в участок цепи включен и характеризуется при помощи ЭДС ($\varepsilon$), то формула закона Ома преобразуется к виду:
$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(2)$$Закон Ома для замкнутой цепи
где под R=Rvnesh+rist понимают полное сопротивление цепи, которое включает так называемое внешнее сопротивление (Rvnesh) и сопротивление источника ЭДС (rist).
Формула закона Ома в дифференциальной форме
Все выше приведенные формулы закона Ома были представлены в интегральной форме. Этот закон можно записать в дифференциальной форме, которая характеризует электрическое состояние в точке.
$$\bar{j}=\sigma \bar{E}(4)$$где $\sigma=\frac{1}{\rho}$ – удельная проводимость,
$\rho$ – удельное сопротивление,
$\bar{j}$ – вектор плотности тока,
$\bar{E}$ – вектор напряженности электрического поля.
{d} \frac{1}{\left(\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d}\right.} r\right) \frac{d r}{S}=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)}\left[\ln \left(d \sigma_{2}\right)-\ln \left(d \sigma_{1}\right)\right]= \\
=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)(1.2)
\end{array}
$$
Подставим найденное в (1.2) сопротивление в (1.1), получим искомую силу тока:
$I=\frac{U}{\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$Ответ. $I=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$
Слишком сложно?
Формула закона Ома не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какой будет плотность тока в металлическом проводнике (удельное сопротивление считать равным $\rho$) постоянного сечения, имеющем длину l, если напряжение, которое приложено к проводу равно U?
Решение.
Плотность тока для проводника, который имеет постоянное сечение S можно найти как:
Силу тока можно вычислить, если использовать формулу Закона Ома для участка цепи не имеющего ЭДС:
$$I=\frac{U}{R}(2.2)$$Сопротивление провода найдем, применяя формулу:
$$R=\rho \frac{l}{S}(2.3)$$Подставим, необходимые величины в (2.1), получим:
$$j=\frac{U}{S R}=\frac{U S}{S \rho l}$$Ответ. $j=\frac{U S}{S \rho l}$
Читать дальше: Формула мощности тока.
Закон Ома для участка цепи, формула, определение
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит.
Возьмем замкнутую электрическую цепь (рисунок 1) и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I — ток, протекающий по участку цепи.
- R — сопротивление этого участка.
- φ1-φ2 — разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R
Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
ПРАВИЛО ЗНАКОВ ДЛЯ ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной (рис.3.1). В противном случае — ЭДС считается отрицательной (рис.3.2).
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3.
При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ
Закон Ома для полной цепи — его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r).
Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС.
Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r — сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной.
Закон Ома рассмотрен здесь достоточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
© 2012-2020 г. Все права защищены.
Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов
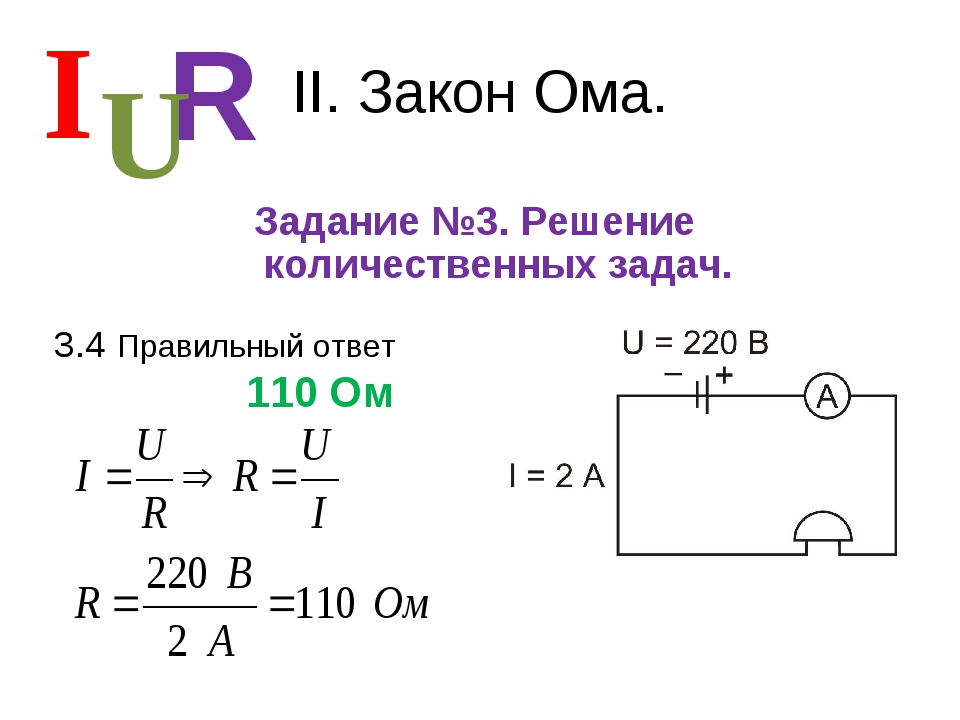
Закон Ома 1 курс (СПО)
Урок по физике в 10классе по теме «Закон Ома для полной цепи»
Электрический ток,
Электрический ток,
Утверждают, что ты –
Электронов поток,
И болтает к тому же
Досужий народ,
Что тобой управляют
Катод и анод.
Электрический ток,
Электрический ток,
Говорят, ты порою
Бываешь жесток.
Может жизни лишить
Твой коварный укус.
Ну и пусть,
Все равно я тебя не боюсь!
Цель урока:
Обучающая: Ввести понятия электродвижущей силы; сформулировать закон Ома для полной цепи; сформировать у учащихся представление о различии между ЭДС, напряжением и разностью потенциалов.
Воспитательная: Работу в коллективе, волевая саморегуляция, следовать основным нормам поведения, Т.Б. на уроке, формирование социальной роли ученика, положительное отношение к учению.
Развивающая: Навыки работы с приборами, логическое мышление, проводить связь с жизнью.
Тип урока:
Комбинированный урок
Используемые учебники и учебные пособия:
1. Физика-10. Базовый и профильный уровни / авт.
Мякишев Г.Я., БуховцевБ.Б., СотскийС.С. – М.: «Просвещение», 2008.
2. Сборник задач для 10-11 класса, автор Рымкевич А.П. – Дрофа, 2008.
3. Поурочные разработки по физике.10класс. Волков В.А.- М: «ВАКО»,2008.
4. Поурочные планы по учебнику Г.Я.Мякишева и др.-Волгограл,2008.
Используемое оборудование:
Источник питания, вольтметр, амперметр, реостат, резистор, провода, ключ, карточки с заданием.
I. Организационный момент (готовность класса к уроку, внешний вид, порядок в классе, часть доски закрыта, схема участка цепи).
II. Проверка домашнего задания:
1) Фронтальный опрос:
1. В каком движении участвуют свободные электроны в металле?
2. Происходит ли при этом перенос электрического заряда?
3. В каком случае происходит перенос заряда через поперечное сечение проводника?
4. Что такое электрический ток?
5. Что представляет собой ток в металлах?
6. Что принимают за направление тока?
7.
Как можно обнаружить электрический ток?
8. Какие действия тока мы знаем?
9. Какая величина служит основной количественной характеристикой
электрического тока?
10. Как рассчитать силу тока?
11. От каких величин зависит сила тока?
12. Какие условия необходимы для создания электрического тока?
13. Что собой представляет вольтамперная характеристика проводника с током?
14. Сформулируйте закон Ома для участка цепи.
15. Что характеризует электрическое сопротивление проводника?
16. От каких величин зависит электрическое сопротивление проводника?
17. Какие виды соединений мы знаем?
18. Как выгодно включать потребители к осветительной цепи?
19. Что совершает электрический ток, перенося заряд вдоль проводника?
20. Чему равна работа тока?
21. Что определяет работа тока?
22. Сформулируйте закон Джоуля-Ленца?
23. Что характеризует мощность тока?
24. Чему равна работа на замкнутом участке цепи?
2) Физический диктант:
1вариант:1.
Закон Ома для участка цепи.
2. Скорость упорядоченного движения электронов в проводнике.
3. Чему равно напряжение на концах проводника?
4. Записать законы параллельного соединения проводников.
5. Записать всевозможные формулы для расчета мощности тока.
6. Определить цену деления амперметра.
2вариант:1. Закон Джоуля-Ленца.
2. Чему равна сила тока?
3. Формула для расчета удельного сопротивления проводника.
4. Записать законы последовательного соединения проводников.
5. Записать всевозможные формулы для работы тока.
6. Определить цену деления вольтметра.
( сначала взаимопроверка вариантов, затем проверка на доске- открыть доску –проставление оценок).
http://www.naukamira.ru/board/
III. Изучение нового материала:
к деятельности
Психологическая мотивация: на доске изображен участок эл. цепи.
Что здесь изображено?
Из каких частей состоит эл.
цепь?
Все ли составные части присутствуют в данной цепи?
Итак, это только участок цепи.
Как выглядит Закон Ома для участка цепи?
Смотрят,
Слушают,
Отвечают.
Сопоставляют.
Анализируют.
2.
Выделение проблемного поля
Покажем полную цепь.
Какие элементы добавились?
Что не учитывает закон Ома для участка цепи?
Анализируют.
Сопоставляют.
Дают ответы.
3.
Совместная с учащимися постановка целей
Как вы думаете, чему будет посвящен урок? Каких целей мы должны достичь?
Что мы должны узнать?
Дети предлагают свои варианты и формулируют тему урока.
Формулируют цели урока:
-назначение источника тока;
-закон Ома для полной цепи.
4.
Совместный поиск решения проблемы
Поэтому нам надо в первую очередь уточнить назначение источника тока?
Зачем нужно эл. поле?
Каким образом?
Создать эл.
поле.
Разделения эл. зарядов.
Обсуждение вариантов ответов.
Давайте рассмотрим 2шарика, несущие заряды противоположных знаков, соединив их проводником. Что происходит?
Надолго?
Т.е. заряды нейтрализуются и эл. ток исчезнет. Что дальше? Тока больше нет.
Т.е нужен источник тока. Каково же его назначение?
Анализ рис.
Могут ли это сделать кулоновские силы?
Значит?
Да! В источнике тока на заряды кроме кулоновских сил должны действовать силы неэлектрического происхождения. Их называют сторонними — это любые силы, действующие на эл. заряды, за исключением сил кулоновских. Они необходимы для постоянного разделения зарядов внутри источника тока.
Давайте обратимся к закону сохранения энергии, чтобы сделать правильный вывод о необходимости сторонних сил. Эл. поле потенциально, т.е. работа этих сил по перемещению заряженных частиц вдоль замкнутой эл. цепи равна …
Значит, В любой цепи должен быть источник энергии, поставляющий ее в цепь, но кроме кулоновских сил.
Обязательно должны действовать сторонние силы, т.е. непотенциальные силы, работа которых вдоль замкнутого контура не равнялась нулю. Именно в процессе совершения работы этими силами, заряженные частицы приобретают внутри источника энергию и отдают ее затем в проводниках эл. цепи. Итак, сторонние силы приводят в движение заряженные частицы внутри всех источников тока на электростанциях, гальванических элементов, аккумуляторов и т. д.
Во всей остальной цепи заряженные частицы приводят в движение кулоновские силы.
Природа сторонних сил разнообразна: в генераторах — магнитные силы, в гальваническом элементе – химические силы.
Действие сторонних сил
характеризуется физ. величиной, называющейся электродвижущей силой ЭДС
ε= Аст/q; ε- ЭДС [В]
( дать аналогию между эл. током и течением жидкости по трубам)
Ну а теперь рассмотрим нашу простейшую полную (замкнутую) цепь. Давайте начертим ее на доске и соберем на демонстрационном столе.
Рассмотрим замкнутый контур
Апол =Аст + Ак, Ак=0 по закону сохранения энергии
Апол=Аст по закону Джоуля—Ленца
Апол=I²Rt+I²rt Аст=εq=εtI
Вызвать ученика решить данное уравнение, после преобразований получаем
I=ε/R+r закон Ома для полной цепи.
Как его прочитать?
Сила тока зависит:
1.E 2.R 3.R
Если R→0, то возникает ток короткого замыкания.
Iк.з.=ε/r Ток короткого замыкания очень опасен, приводит к пожарам зданий.
Чтобы избежать короткого замыкания включают предохранители, автоматические выключатели.
Физ-минутка ( упражнения для глаз).
В проводнике возникает ток
Ток прекратится как только все электроны перейдут с шара «-» на шар «+»
Нужен источник зарядов.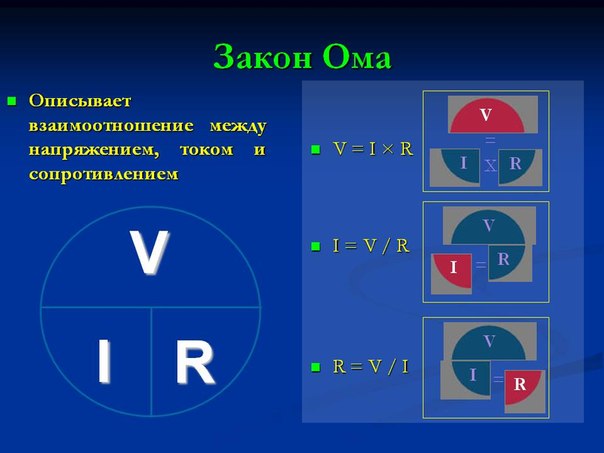
Двигать е к «-», а + к «+»
Нет?
Нужны другие силы.
Нулю.
Небольшое сообщение – сравнение- аналогия дается учеником.
Учащиеся по желанию выходят начертить схему и собрать ее (двое учащихся)
Дети делают вывод.
Дети формулируют закон:
Сила тока в полной цети равна отношению эдс цепи к ее полному сопротивлению
Дают ответы
5
Закрепление нового материала.
а) практическое закрепление опыта;
б) самостоятельная работа с
самопроверкой,
взаимопроверкой,
самооценкой;
в)закрепление во внешней речи.
Выполняем эксперимент по определению ЭДС и внутреннего сопротивления, проводим математическую обработку результатов эксперимента.
Порядок выполнения работы:
1.Собрать эл.цепь.
2.Создать необходимые условия для проведения эксперимента, Т.
Б.
3.Проверить работу цепи при разомкнутом и замкнутом ключе.
4.Осуществить наблюдения и измерения в запланированной последовательности.
5.Записать и вычислить искомые величины.
Р № 820.
1.Что означает запись на батарейке?
2.Какие силы называются сторонними?
3.Что такое ЭДС?
4.Как читается закон Ома для полной цепи?
5.Что такое ток короткого замыкания?
Снимают показания и решают экспериментальную задачу на определение ЭДС и внутреннего сопротивления источника тока.(один у доски, остальные в тетради)
Решают.
Дают ответы.
6
Рефлексия
Шкала анализа:
Актуальность, эмоции, значимость
§ 109, 110.№ 817, № 821.СПАСИБО ЗА УРОК!
Электрический ток,
Электрический ток,
Говорят, ты порою
Бываешь жесток.
Может жизни лишить
Твой коварный укус.
Ну и пусть,
Все равно я тебя не боюсь!
Электрический ток,
Электрический ток,
Утверждают, что ты –
Электронов поток,
И болтает к тому же
Досужий народ,
Что тобой управляют
Катод и анод.
Закон Ома | Физика
В предыдущих параграфах были рассмотрены три величины, характеризующие протекание электрического тока в цепи,— сила тока I, напряжение U и сопротивление R. Между этими величинами существует определенная связь. Закон, выражающий эту связь, был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя.
Выделим в произвольной электрической цепи участок, обладающий сопротивлением R и находящийся под напряжением U (рис. 37). Согласно закону Ома:
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.
Математически закон Ома записывается в виде следующей формулы:
I = U/R (14.1)
Закон Ома позволяет установить, что будет происходить с силой тока на участке цепи при изменении его сопротивления или напряжения.
1. При неизменном сопротивлении сила тока прямо пропорциональна напряжению: чем больше напряжение U на концах участка цепи, тем больше сила тока I на этом участке.
Увеличив (или уменьшив) напряжение в несколько раз, мы во столько же раз увеличим (или уменьшим) силу тока.
Проиллюстрируем эту закономерность на опыте. Соберем электрическую цепь из источника тока, лампы, амперметра и ключа (рис. 38, а). В качестве источника тока будем использовать устройство, позволяющее регулировать выходное напряжение от 4 до 12 В. Измеряя силу тока в цепи при разных напряжениях, можно убедиться в том, что она действительно пропорциональна напряжению.
2. При неизменном напряжении сила тока обратно пропорциональна сопротивлению: чем больше сопротивление R участка цепи, тем меньше сила тока I в нем.
Для проверки этой закономерности заменим в используемой цепи лампу на магазин сопротивлений (рис. 38, б). Измеряя силу тока при разных сопротивлениях, мы увидим, что сила тока I и сопротивление R действительно находятся в обратно пропорциональной зависимости.
При уменьшении сопротивления сила тока возрастает. Если сила тока превысит допустимое для данной цепи значение, включенные в нее приборы могут выйти из строя; провода при этом могут раскалиться и стать причиной пожара.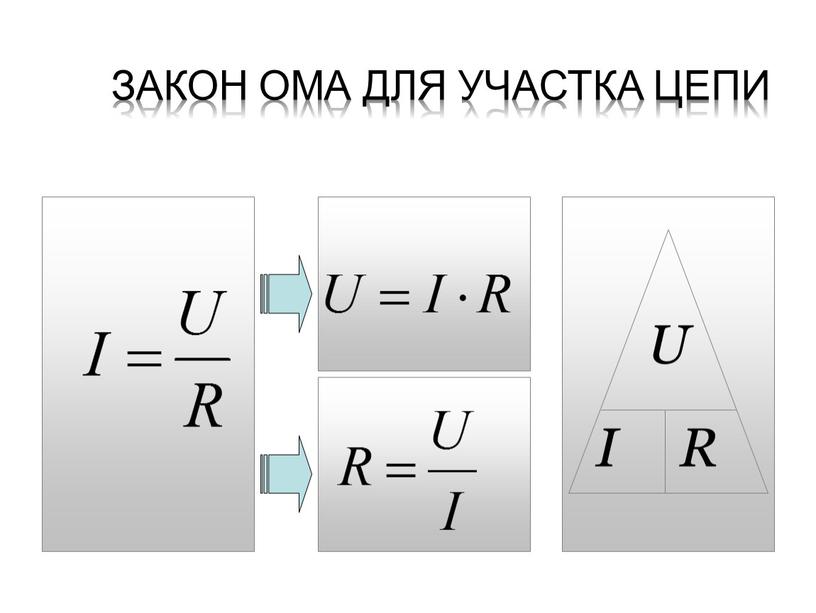
Именно такая ситуация возникает при коротком замыкании. Так называют соединение двух точек электрической цепи, находящихся под некоторым напряжением, коротким проводником, обладающим очень малым сопротивлением.
Короткое замыкание может возникнуть при соприкосновении оголенных проводов, при небрежном ремонте проводки под током, при большом скоплении пыли на монтажных платах и даже при случайном попадании какого-нибудь насекомого внутрь прибора.
На законе Ома основан экспериментальный способ определения сопротивления. Из формулы (14.1) следует, что
R = U/I (14.2)
Поэтому для нахождения сопротивления R участка цепи надо измерить на нем напряжение U, затем силу тока I, после чего разделить первую из этих величин на вторую. Соответствующая этому схема цепи изображена на рисунке 39.
Если, наоборот, известны сопротивление R и сила тока I на участке цепи, то закон Ома позволяет рассчитать напряжение U на его концах.
Из формулы (14.1) получаем
U = IR (14.3)
Чтобы найти напряжение U на концах участка цепи, надо силу тока I на этом участке умножить на его сопротивление R.
Опубликовав книгу, в которой излагался открытый им закон «Теоретические исследования электрических цепей», Георг Ом написал, что «рекомендует ее добрым людям с теплым чувством отца, не ослепленного обезьяньей любовью к детям, но довольствующегося указанием на открытый взгляд, с которым его дитя смотрит на злой мир». Мир действительно оказался для него злым, и уже через год после выхода его книги в одном из журналов появилась статья, в которой работы Ома были подвергнуты уничтожающей критике. «Тот, кто благоговейными глазами взирает на вселенную,— говорилось в статье,— должен отвернуться от этой книги, являющейся плодом неисправимых заблуждений, преследующих единственную цель — умалить величие природы».
Злобные и безосновательные нападки на Ома не прошли бесследно. Теорию Ома не приняли.
И вместо продолжения научных исследований он должен был тратить время и энергию на полемику со своими оппонентами. В одном из своих писем Ом написал: «Рождение «Электрических цепей» принесло мне невыразимые страдания, и я готов проклясть час их зарождения».
Но это были временные трудности. Постепенно, сначала в России, а затем и в других странах, теория Ома получила полное признание. Закон Ома внес такую ясность в правила расчета токов и напряжений в электрических цепях, что американский ученый Дж. Генри, узнав об открытиях Ома, не удержался от восклицания: «Когда я первый раз прочел теорию Ома, то она мне показалась молнией, вдруг осветившей комнату, погруженную во мрак».
??? 1. Сформулируйте закон Ома. 2. Как изменится сила тока на участке цепи, если при неизменном сопротивлении увеличить напряжение на его концах? 3. Как изменится сила тока, если при неизменном напряжении увеличить сопротивление участка цепи? 4. Как с помощью вольтметра и амперметра можно измерить сопротивление проводника? 5.
По какой формуле находится напряжение, если известны сила тока и сопротивление данного участка? 6. Что называют коротким замыканием? Почему при этом увеличивается сила тока? 7. Объясните причину короткого замыкания в ситуациях, изображенных на рисунке 40.
Основные электрические законы. Базовые формулы и расчеты
В предыдущей статье мы познакомились с основными электрическими понятиями, такими как электрический ток, напряжение, сопротивление и мощность. Настал черед основных электрических законов, так сказать, базиса, без знания и понимания которых невозможно изучение и понимание электронных схем и устройств.
Закон Ома
Электрический ток, напряжение, сопротивление и мощность, безусловно, между собой связаны. А взаимосвязь между ними описывается, без сомнения, самым главным электрическим законом – законом Ома. В упрощенном виде этот закон называется: закон Ома для участка цепи. И звучит этот закон следующем образом:
«Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи».
Для практического применения формулу закона Ома можно представить в виде вот такого треугольника, который помимо основного представления формулы, поможет определить и остальные величины.
Работает треугольник следующим образом. Чтобы вычислить одну из величин, достаточно закрыть ее пальцем. Например:
В предыдущей статье мы проводили аналогию между электричеством и водой, и выявили взаимосвязь между напряжением, током и сопротивлением. Также хорошей интерпретацией закона Ома может послужить следующий рисунок, наглядно отображающий сущность закона:
На нем мы видим, что человечек «Вольт» (напряжение) проталкивает человечка «Ампера» (ток) через проводник, который стягивает человечек «Ом» (сопротивление). Вот и получается, что чем сильнее сопротивление сжимает проводник, тем тяжелее току через него проходить («сила тока обратно пропорциональна сопротивлению участка цепи» – или чем больше сопротивление, тем хуже приходится току и тем он меньше).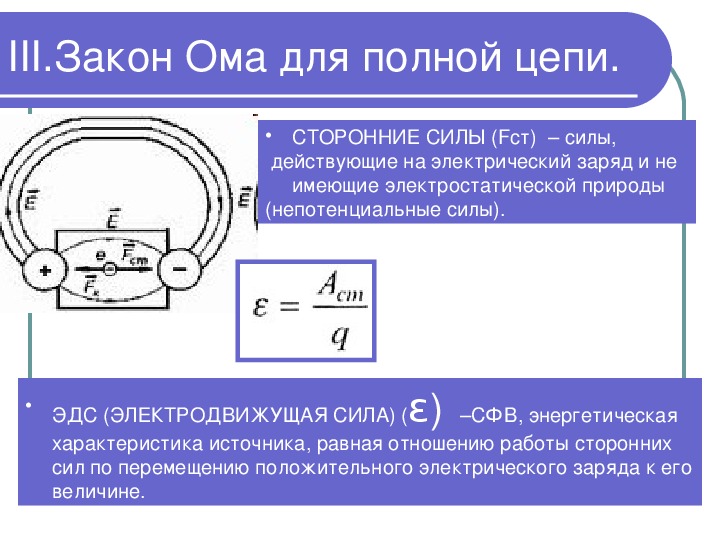
Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).
Когда фонарик начинает слабо светить, мы говорим – «разрядилась батарейка». Что с ней произошло, что значит разрядилась? А значит это, что напряжение батарейки снизилось и оно больше не в состоянии «помогать» току преодолевать сопротивление цепей фонарика и лампочки. Вот и получается, что чем больше напряжение – тем больше ток.
Последовательное подключение – последовательная цепь
При последовательном подключении потребителей, например обычных лампочек, сила тока в каждом потребителе одинаковая, а вот напряжение будет отличаться. На каждом из потребителей напряжение будет падать (снижаться).
А закон Ома в последовательной цепи будет иметь вид:
При последовательном соединении сопротивления потребителей складываются. Формула для расчета общего сопротивления:
Параллельное подключение – параллельная цепь
При параллельном подключении, к каждому потребителю прикладывается одинаковое напряжение, а вот ток через каждый из потребителей, в случае, если их сопротивление отличается – будет отличаться.
Закон Ома для параллельной цепи, состоящей из трех потребителей, будет иметь вид:
При параллельном соединении общее сопротивление цепи всегда будет меньше значения самого маленького отдельного сопротивления. Или еще говорят, что «сопротивление будет меньше наименьшего».
Общее сопротивление цепи, состоящей из двух потребителей, при параллельном соединении:
Общее сопротивление цепи, состоящей из трех потребителей, при параллельном соединении:
Для большего числа потребителей расчет производится исходя из того, что при параллельном соединении проводимость (величина обратная сопротивлению) рассчитывается как сумма проводимостей каждого потребителя.
Электрическая мощность
Мощность – это физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Рассчитывается мощность по следующей формуле:
Таким образом зная, напряжение источника и измерив потребляемый ток, мы можем определить мощность потребляемую электроприбором.
И наоборот, зная мощность электроприбора и напряжение сети, можем определить величину потребляемого тока. Такие вычисления порой необходимы. Например, для защиты электроприборов используются предохранители или автоматические выключатели. Чтобы правильно подобрать средство защиты нужно знать потребляемый ток. Предохранители, применяемые в бытовой технике, как правило подлежат ремонту и для их восстановления достаточно подобрать и заменить проволоку.
Применив закон Ома, можно рассчитать мощность и по другой формуле:
При расчетах надо учитывать, что часть потребляемой электроэнергии расходуется на нагрев и преобразуется в тепло. При работе греются не только электрообогреватели, но и телевизоры, и компьютеры и другая бытовая техника.
И в завершение, в качестве бонуса, вот такая шпаргалка, которая поможет определить любой из основных электрических параметров, по уже известным.
Закон первого Ома — MR WATT Shop
Мы можем сказать, что в электрической цепи, если разность потенциалов, приложенная между двумя ее точками, равна 1 вольту, а частичное сопротивление участка между этими двумя точками составляет 1 Ом на этом участке.
циркулирует ток 1 ампер.
Закон Ома очень просто устанавливает взаимосвязь между тремя следующими электрическими величинами: напряжением (В), током (I) и сопротивлением (R).
Этот закон был провозглашен известным немецким физиком Джорджем Симоном Омом и, безусловно, является наиболее подходящим. важны из тех, что касаются электричества.
Заявление звучит именно так:
«Сила тока в цепи прямо пропорциональна приложенному к ней напряжению и обратно пропорциональна сопротивлению самой цепи».
Его математическое выражение:
I = V / R
, которое позволяет рассчитать ток, зная напряжение и сопротивление. Получено по этой формуле:
V = I * R
R = V / I
, что позволяет определить напряжение или сопротивление, когда две другие величины известны.Если схема применяется к одному ф.э.м. (Электродвижущая сила) значения E, мы видим, что формула закона Ома принимает следующий вид:
I = E / (R + r)
где «r» — внутреннее сопротивление генератора.
. Если мы рассмотрим схему с одним резистором и предположим, что разность потенциалов между клеммами A и B имеет значение V, ток, протекающий через сопротивление R, будет:
I = V / R
Тогда как с другой стороны, схема с двумя резисторами, питаемыми от ЭДС генератора E и внутренним сопротивлением r, если R1 и R2 являются внешними резисторами или нагрузкой, соединенными последовательно, мы будем иметь:
I = E / (R1 + R2 + r)
, что дает
E = I (R1 + R2 + r) = I R1 + I R2 + I r.
Продукты I R1, I R2 и I r (резисторы тока) соответственно выражают разность потенциалов, существующую между точками (AC) и (CB), а также внутреннее падение напряжения генератора.
Мы видим, что ф.э.м. И приложенная к цепи сумма разностей парциальных потенциалов равна сумме, которую еще называют «падениями напряжения».
Падения напряжения IR1 и IR2 возникают во внешней цепи и могут иметь полезный эффект.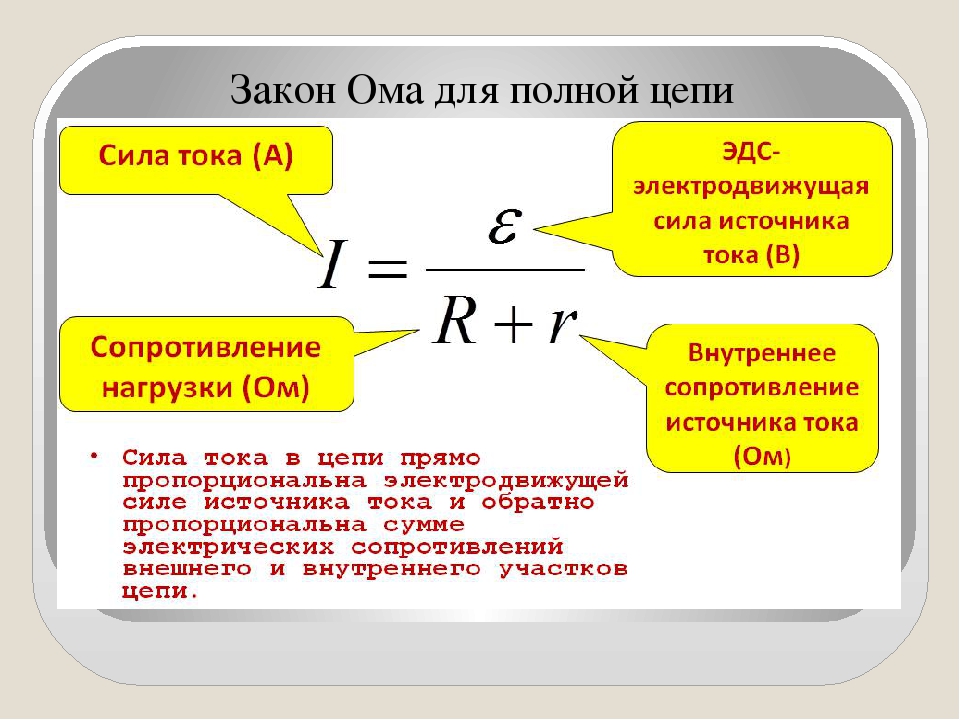
Падение напряжения Ir возникает внутри генератора и не имеет значения.
Предположим, что теперь переключатель разомкнут: в цепи нет тока и, поскольку I = 0, внутреннее падение напряжения будет нулевым, а ddp между двумя выводами A и B генератора будет равно ЭДС самого генератора. : VAB = E.
Если вместо этого цепь замкнута и циркулирует ток I, между A и B будет разность потенциалов (ddp)
VAB = E — I * r
Другой случай, при котором возникает условие VAB = E — это когда внутреннее сопротивление генератора равно нулю (r = 0).
Несмотря на то, что большинство из нас знает и правильно использует «Закон Ома», мы не должны забывать, что есть люди, начинающие, которые, зная о существовании этого закона, не знают, как использовать его на практике, чтобы получить как можно больше преимуществ. .
Мы обращаемся к симулятору за любыми примерами и приложениями.
Ток и закон Ома
Переменный ток:
Электрический ток, периодически меняющий направление на противоположное.
Цепь:
Полный или частичный путь, по которому может течь ток.
Сопротивление:
Свойство проводника, с помощью которого он препятствует прохождению электрического тока, что приводит к выделению тепла в проводящем материале.
Напряжение:
Электродвижущая сила или разность электрических потенциалов, выраженная в вольтах.
Ток:
Поток или скорость электрического заряда в проводнике или среде между двумя точками, имеющими разность потенциалов, обычно выражаемую в амперах.
Ток и закон Ома
Закон Ома — самый важный, основной закон электричества. Он определяет соотношение между тремя основными электрическими величинами: током, напряжением и сопротивлением. Когда напряжение подается на цепь, содержащую только резистивные элементы (т.е.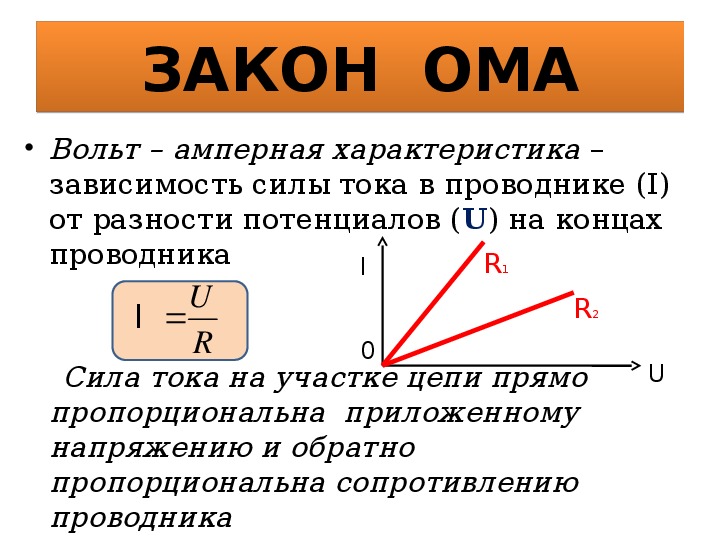
е. без катушек) ток течет по закону Ома, который показан ниже.
I = V / R
| Где: | |
Я = | Электрический ток (амперы) |
V = | Напряжение (Напряжение) |
R = | Сопротивление (Ом) |
Закон Ома гласит, что электрический ток (I ), протекающий в цепи, пропорционален напряжению (В ) и обратно пропорционален сопротивлению (R) .Следовательно, если напряжение увеличивается, ток будет увеличиваться при условии, что сопротивление цепи не изменится.
Точно так же увеличение сопротивления цепи снижает ток, если напряжение не изменяется. Формулу можно реорганизовать, чтобы можно было легко увидеть взаимосвязь для всех трех переменных.
Приведенный ниже Java-апплет позволяет пользователю изменять каждый из этих трех параметров в законе Ома и видеть влияние на два других параметра. Значения можно вводить в диалоговые окна, или сопротивление и напряжение также можно изменять, перемещая стрелки в апплете.Ток и напряжение отображаются так, как если бы они отображались на осциллографе, где по оси X отложено время, а по оси Y — амплитуда тока или напряжения. Закон Ома действует как для постоянного (DC), так и для переменного (AC) тока. Обратите внимание, что в цепях переменного тока, состоящих из чисто резистивных элементов, ток и напряжение всегда находятся в фазе друг с другом.
Упражнение: Используйте интерактивный апплет ниже, чтобы исследовать взаимосвязь переменных в законе Ома.Измените напряжение в цепи, щелкнув и перетащив стрелку, отмеченную буквой V.
Сопротивление в цепи можно увеличить, перетащив стрелку под переменный резистор, отмеченный R. Вертикальная шкала экрана осциллографа автоматически подстраивается под значение тока.
Посмотрите, что происходит с напряжением и током при увеличении сопротивления в цепи. Что произойдет, если в цепи недостаточно сопротивления? Если сопротивление увеличивается, что должно произойти, чтобы поддерживать ток на том же уровне?
Щелкните здесь, чтобы запустить приложение JavaScript на основе закона Ома.
ЗаконОма: что это такое и почему это важно?
Обновлено 28 декабря 2020 г.
Ли Джонсон
Электрические цепи повсеместно встречаются в нашей повседневной жизни. От сложных интегральных схем, управляющих устройством, которое вы читаете в этой статье, до проводки, которая позволяет вам включать и выключать лампочку в вашем доме, вся ваша жизнь была бы радикально другой, если бы вы не были окружены цепями повсюду. вы идете.
Но большинство людей на самом деле не изучают мельчайших деталей того, как работают схемы, и довольно простые уравнения, такие как закон Ома, которые объясняют взаимосвязь между ключевыми понятиями, такими как электрическое сопротивление, напряжение и электрический ток.
Однако более глубокое погружение в физику электроники может дать вам более глубокое понимание основных правил, лежащих в основе большинства современных технологий.
Что такое закон Ома?
Закон Ома — одно из самых важных уравнений, когда дело доходит до понимания электрических цепей, но если вы собираетесь его понять, вам понадобится хорошее понимание основных понятий, которые он связывает: напряжение , ток и сопротивление . Закон Ома — это просто уравнение, которое описывает соотношение между этими тремя величинами для большинства проводников.
Напряжение — это наиболее часто используемый термин для обозначения разности электрических потенциалов между двумя точками, который обеспечивает «толчок», который позволяет электрическому заряду перемещаться по проводящей петле.
Электрический потенциал — это форма потенциальной энергии, как и потенциальная энергия гравитации, и определяется как электрическая потенциальная энергия на единицу заряда.
Единицей измерения напряжения в системе СИ является вольт (В), а 1 В = 1 Дж / Кл, или один джоуль энергии на кулон заряда. Иногда его также называют электродвижущей силой , или ЭДС.
Электрический ток — это скорость прохождения электрического заряда через заданную точку в цепи, в системе СИ единицей измерения является ампер (А), где 1 А = 1 Кл / с (один кулон заряда в секунду). Он имеет форму постоянного (DC) и переменного (AC) тока, и, хотя постоянный ток проще, цепи переменного тока используются для подачи энергии в большинство домашних хозяйств по всему миру, потому что его проще и безопаснее передавать на большие расстояния.
Последняя концепция, которую вам нужно понять, прежде чем приступить к рассмотрению закона Ома, — это сопротивление, которое является мерой сопротивления току, протекающему в цепи.Единицей измерения сопротивления в системе СИ является ом (в котором используется греческая буква омега, Ом), где 1 Ом = 1 В / А.
Уравнение закона Ома
Немецкий физик Георг Ом описал взаимосвязь между напряжением, током и сопротивлением в своем одноименном уравнении.
Формула закона Ома:
В = IR
, где В, — это напряжение или разность потенциалов, I — величина тока, а сопротивление R — конечная величина.
Уравнение можно легко переформулировать, чтобы получить формулу для расчета тока на основе напряжения и сопротивления или сопротивления на основе тока и напряжения.Если вам неудобно переставлять уравнения, вы можете найти треугольник закона Ома (см. Раздел «Ресурсы»), но это довольно просто для любого, кто знаком с основными правилами алгебры.
Ключевыми моментами, которые показывает уравнение закона Ома, являются то, что напряжение прямо пропорционально электрическому току (поэтому, чем выше напряжение, тем выше ток), и этот ток обратно пропорционален сопротивлению (поэтому чем выше сопротивление, тем ниже электрический ток).
Вы можете использовать аналогию с потоком воды, чтобы запомнить ключевые моменты, в основе которой лежит труба, один конец которой находится на вершине холма, а другой конец — внизу.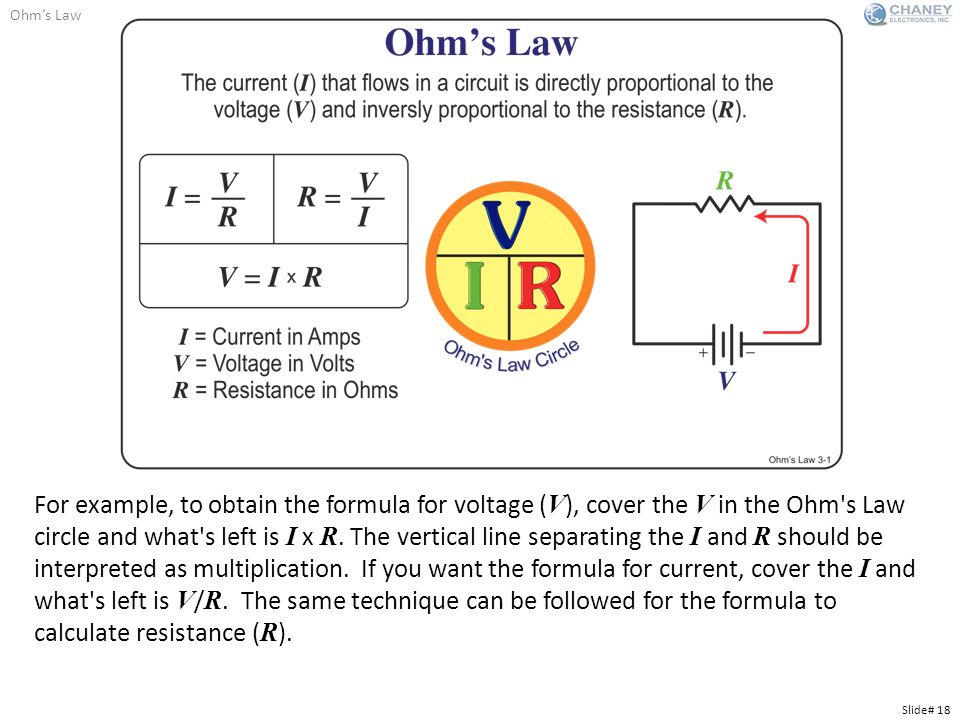
Напряжение похоже на высоту холма (более крутой и высокий холм означает большее напряжение), текущий поток похож на поток воды (вода течет быстрее по крутому склону), а сопротивление похоже на трение между сторонами трубы. и вода (более тонкая труба создает большее трение и снижает скорость потока воды, как более высокое сопротивление для электрического тока).
Почему важен закон Ома?
Закон Ома жизненно важен для описания электрических цепей, поскольку он связывает напряжение с током, а значение сопротивления регулирует взаимосвязь между ними.Из-за этого вы можете использовать закон Ома для управления величиной тока в цепи, добавляя резисторы для уменьшения тока и убирая их, чтобы увеличить величину тока.
Его также можно расширить, чтобы описать электрическую мощность (скорость потока энергии в секунду), потому что мощность P = IV, и поэтому вы можете использовать ее, чтобы гарантировать, что ваша схема обеспечивает достаточно энергии, например, для 60-ваттного прибора.
Для студентов-физиков наиболее важным в законе Ома является то, что он позволяет анализировать принципиальные схемы, особенно когда вы объединяете его с законами Кирхгофа, которые следуют из него.
Закон Кирхгофа по напряжению гласит, что падение напряжения вокруг любого замкнутого контура в цепи всегда равно нулю, а закон тока утверждает, что величина тока, протекающего в переходе или узле в цепи, равна величине, вытекающей из Это. Вы можете использовать закон Ома с законом напряжения, в частности, для расчета падения напряжения на любом компоненте схемы, что является общей проблемой, возникающей в классах электроники.
Примеры закона Ома
Вы можете использовать закон Ома, чтобы найти любую неизвестную величину из трех, при условии, что вам известны две другие величины для рассматриваемой электрической цепи.Работа с некоторыми базовыми примерами показывает, как это делается.
Во-первых, представьте, что у вас есть 9-вольтовая батарея, подключенная к цепи с общим сопротивлением 18 Ом.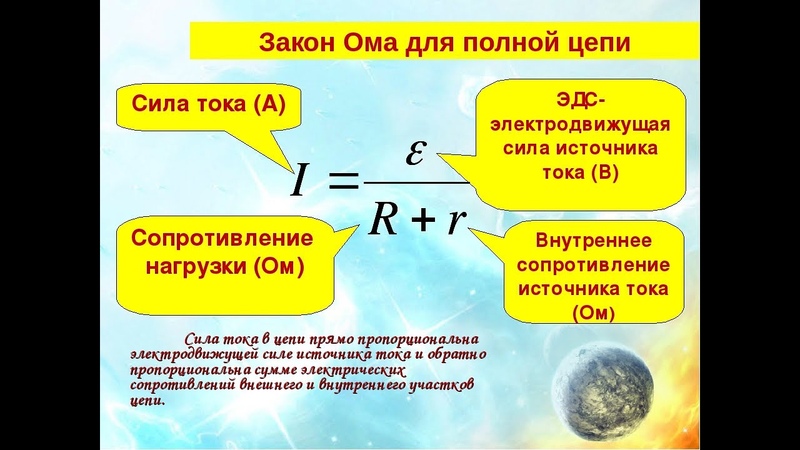
Сколько тока течет при подключении цепи? Изменив закон Ома (или используя треугольник), вы можете найти:
\ begin {align} I & = \ frac {V} {R} \\ & = \ frac {9 \ text {V}} {18 \ text {Ω}} \\ & = 0.5 \ text {A} \ end {align}
Итак, 0,5 ампер тока течет по цепи. Теперь представьте, что это идеальная величина тока для компонента, который вы хотите запитать, но у вас есть только батарея на 12 В.Какое сопротивление нужно добавить, чтобы обеспечить оптимальное значение тока для компонента? Опять же, вы можете переставить закон Ома и решить его, чтобы найти ответ:
\ begin {align} R & = \ frac {V} {I} \\ & = \ frac {12 \ text {V}} {0.5 \ text {A}} \\ & = 24 \ text {Ω} \ end {align}
Итак, вам понадобится резистор 24 Ом для завершения вашей схемы. Наконец, каково падение напряжения на резисторе 5 Ом в цепи с током 2 А, протекающим через нее? На этот раз стандартная форма закона V = IR работает нормально:
\ begin {выровнены} V & = IR \\ & = 2 \ text {A} × 5 \ text {Ω} \\ & = 10 \ text {V} \ end {align}
Омические и неомические резисторы
Вы можете использовать закон Ома в огромном диапазоне ситуаций, но есть ограничения на его применимость — это не действительно фундаментальный закон физики.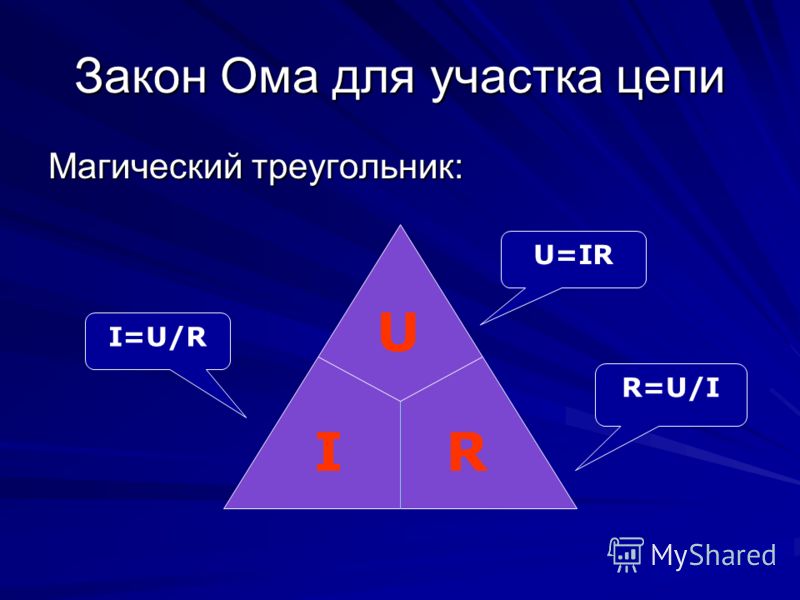
Закон описывает линейную зависимость между напряжением и током, но эта зависимость сохраняется только в том случае, если резистор или резистивный элемент схемы, с которым вы работаете, имеет постоянное сопротивление при различных значениях напряжения В и тока I .
Материалы, которые подчиняются этому правилу, называются омическими резисторами, и хотя большинство физических проблем связано с омическими резисторами, вы знакомы со многими неомическими резисторами из своей повседневной жизни.
Лампочка — прекрасный пример неомического резистора.Когда вы строите график зависимости В от I для омических резисторов, он показывает полностью прямолинейную зависимость, но если вы сделаете это для чего-то вроде лампочки, ситуация изменится. По мере того как нить накала в лампе нагревается, сопротивление лампы увеличивается на , что означает, что график становится кривой, а не прямой линией, и закон Ома не действует.
19,1 Закон Ома — Физика
Постоянный и переменный ток
Так же, как вода течет с большой высоты на низкую, электроны, которые могут свободно перемещаться, будут перемещаться из места с низким потенциалом в место с высоким потенциалом.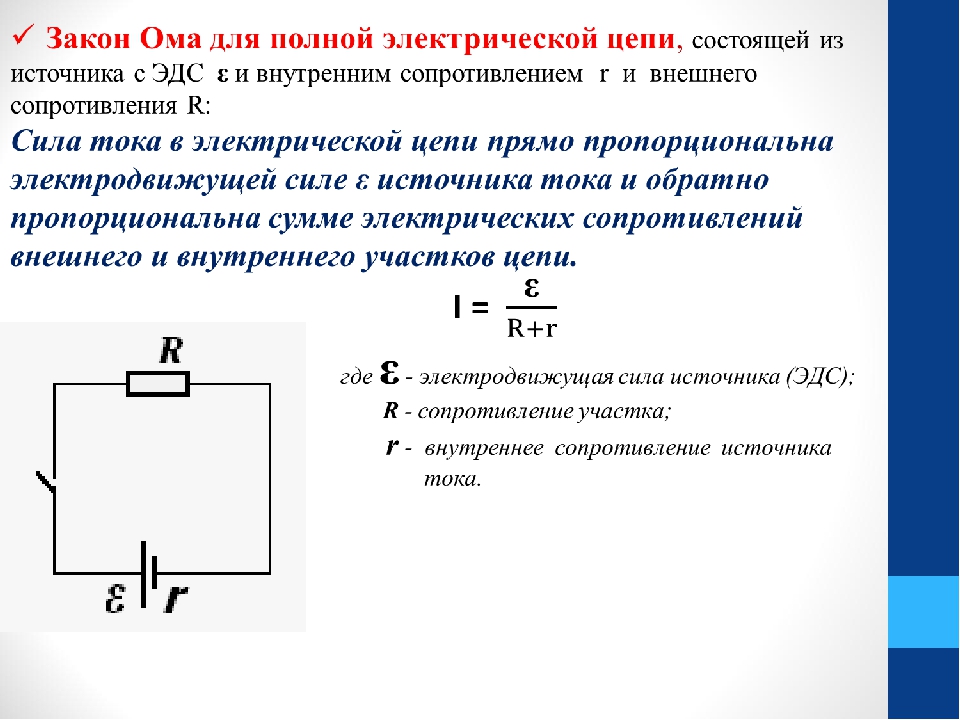
Батарея имеет две клеммы с разным потенциалом. Если клеммы соединены проводом, электрический ток (заряды) будет течь, как показано на рисунке 19.2. Затем электроны будут перемещаться от низкопотенциальной клеммы батареи (отрицательный конец ) через провод и попадут в высокопотенциальную клемму батареи (положительный конец ).
Рисунок 19.2 У батареи есть провод, соединяющий положительную и отрицательную клеммы, который позволяет электронам перемещаться от отрицательной клеммы к положительной.
Поддержка учителя
Поддержка учителя
Подчеркните, что электроны движутся от отрицательной клеммы к положительной, потому что они несут отрицательный заряд, поэтому они отталкиваются кулоновской силой от отрицательной клеммы.
Электрический ток — это скорость движения электрического заряда. Большой ток, такой как тот, который используется для запуска двигателя грузовика, перемещает большую величину очень быстро, тогда как небольшой ток, такой как тот, который используется для работы портативного калькулятора, перемещает небольшое количество заряда медленнее.
В форме уравнения электрический ток I определяется как
, где ΔQΔQ — это количество заряда, которое проходит через заданную область, а ΔtΔt — время, за которое заряд проходит мимо этой области. Единицей измерения электрического тока в системе СИ является ампер (А), названный в честь французского физика Андре-Мари Ампера (1775–1836). Один ампер — это один кулон в секунду, или
Электрический ток, движущийся по проволоке, во многом похож на ток воды, движущийся по трубе.Чтобы определить поток воды через трубу, мы можем подсчитать количество молекул воды, которые проходят мимо данного участка трубы. Как показано на рисунке 19.3, электрический ток очень похож. Мы подсчитываем количество электрических зарядов, протекающих по участку проводника; в данном случае провод.
Рис. 19.3 Электрический ток, движущийся по этому проводу, — это заряд, который проходит через поперечное сечение A, деленный на время, необходимое этому заряду, чтобы пройти через участок A .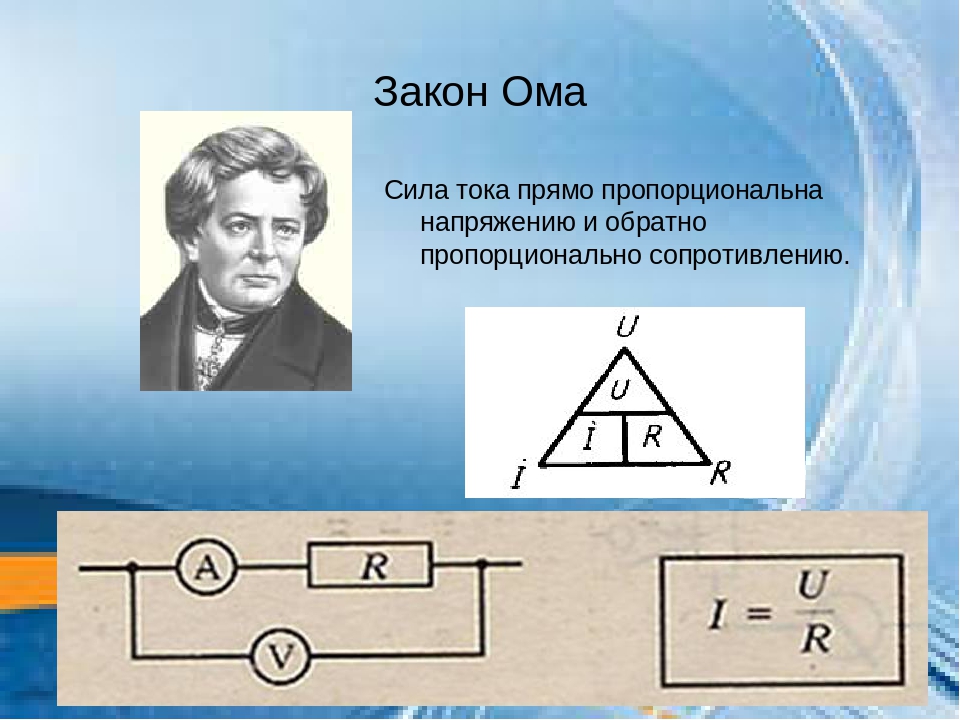
Поддержка учителя
Поддержка учителя
Обратите внимание на то, что носители заряда на этом рисунке положительны, поэтому они движутся в том же направлении, что и электрический ток.
Предположим, что каждая частица q на рисунке 19.3 несет заряд q = 1nCq = 1nC, и в этом случае общий показанный заряд будет ΔQ = 5q = 5nCΔQ = 5q = 5nC. Если эти заряды пройдут мимо области A и за время Δt = 1 нсΔt = 1 нс, то ток будет
I = ΔQΔt = 5nC1ns = 5A.I = ΔQΔt = 5nC1ns = 5A.19,1
Обратите внимание, что мы присвоили зарядам на рис. 19.3 положительный заряд. Обычно отрицательные заряды — электроны — являются подвижным зарядом в проводах, как показано на рисунке 19.2. Положительные заряды обычно застревают в твердых телах и не могут свободно перемещаться. Однако, поскольку положительный ток, движущийся вправо, совпадает с отрицательным током такой же величины, движущимся влево, как показано на рисунке 19.
4, мы определяем обычный ток, который течет в том направлении, в котором протекал бы положительный заряд, если бы он мог двигаться. . Таким образом, если не указано иное, предполагается, что электрический ток состоит из положительных зарядов.
Также обратите внимание, что один кулон — это значительная величина электрического заряда, поэтому 5 А — это очень большой ток.Чаще всего вы увидите ток порядка миллиампер (мА).
Рис. 19.4 (а) Электрическое поле направлено вправо, ток движется вправо, а положительные заряды движутся вправо. (б) Эквивалентная ситуация, но с отрицательными зарядами, движущимися влево. Электрическое поле и ток по-прежнему справа.
Поддержка учителя
Поддержка учителя
Укажите, что электрическое поле одинаково в обоих случаях, и что ток направлен в направлении электрического поля.
Предупреждение о заблуждении
Убедитесь, что учащиеся понимают, что ток — это , определяемый как как направление, в котором будет течь положительный заряд, даже если электроны чаще всего являются мобильными носителями заряда.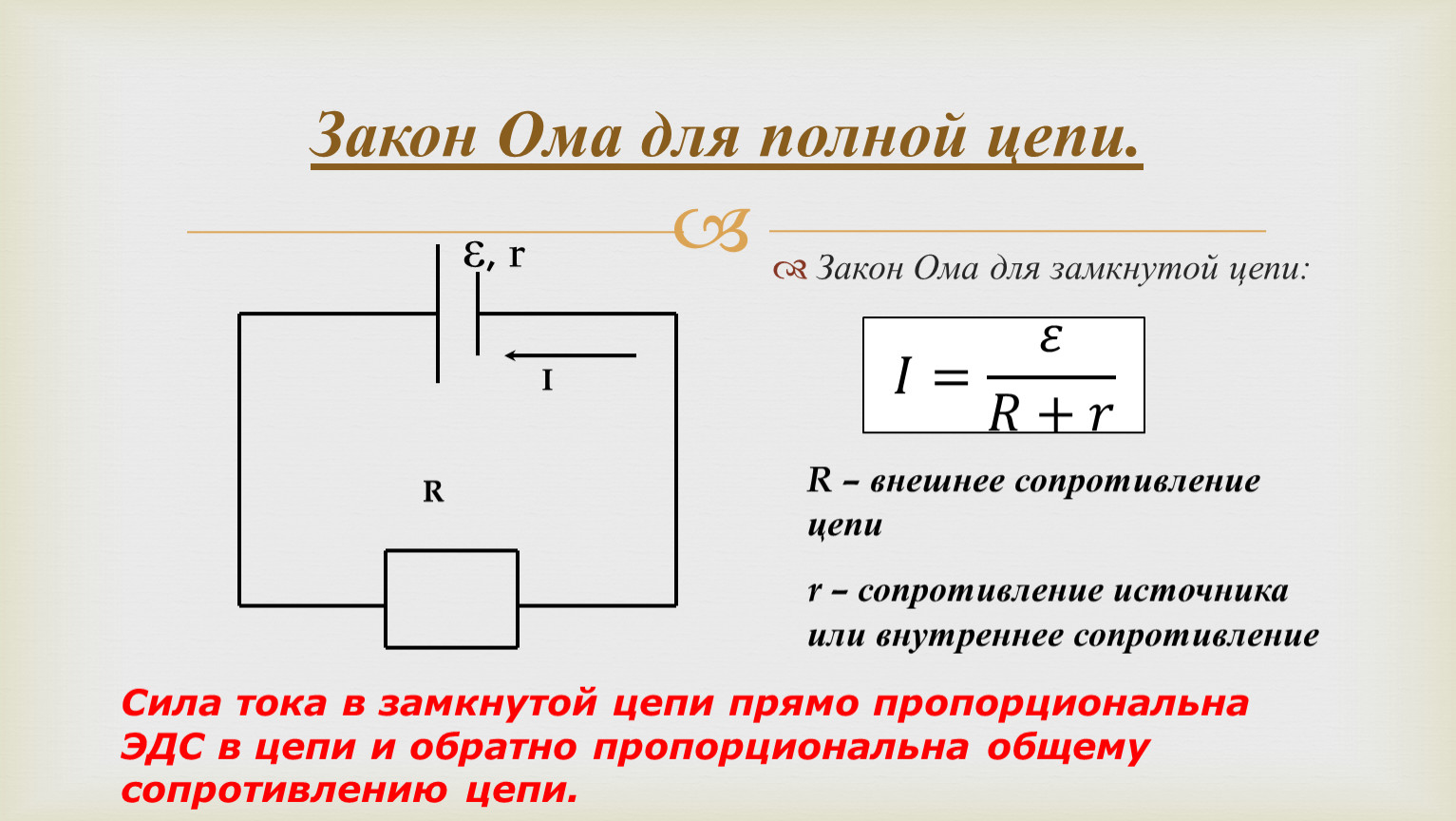
Математически результат один и тот же, независимо от того, предполагаем ли мы положительный заряд в одном направлении или отрицательный заряд в противоположном направлении. Однако физически ситуация совершенно иная (хотя разница уменьшается после определения отверстий).
Snap Lab
Vegetable Current
Эта лабораторная работа помогает студентам понять, как работает ток.Учитывая, что частицы, заключенные в трубе, не могут занимать одно и то же пространство, толкание большего количества частиц в один конец трубы вытеснит такое же количество частиц из противоположного конца. Это создает поток частиц.
Найдите соломинку и сушеный горох, которые могут свободно перемещаться в соломе. Положите соломинку на стол и засыпьте ее горошком. Когда вы вдавливаете одну горошину с одного конца, другая горошина должна выходить из другого конца. Эта демонстрация представляет собой модель электрического тока.Определите часть модели, которая представляет электроны, и часть модели, которая представляет собой подачу электроэнергии.
В течение 30 секунд подсчитайте, сколько горошин вы можете протолкнуть через соломинку. Когда закончите, рассчитайте горошин, текущий , разделив количество горошин на время в секундах.
Обратите внимание, что поток гороха основан на том, что горох физически сталкивается друг с другом; электроны толкают друг друга за счет взаимно отталкивающих электростатических сил.
Проверка захвата
Предположим, у вас есть резервуар с горохом, каждый заправлен до 1 нКл.Если вы пропустите горошек через соломинку со скоростью четыре горошины в секунду, как бы вы рассчитали электрический ток, переносимый заряженным горошком?
- Измерьте длину соломинки, затем разделите на расход гороха и умножьте на расход на горошину.
- Умножьте расход гороха на расход гороха.
- Измерьте длину соломинки, затем умножьте на скорость потока гороха и разделите на количество заряда на горошину.
- Разделите скорость потока гороха на расход на горох.
Направление обычного тока — это направление, в котором будет течь положительный заряд . В зависимости от ситуации могут перемещаться положительные заряды, отрицательные заряды или и то, и другое. В металлических проводах, как мы видели, ток переносится электронами, поэтому отрицательные заряды движутся. В ионных растворах, таких как соленая вода, движутся как положительно заряженные, так и отрицательно заряженные ионы. То же самое и с нервными клетками.Чистые положительные токи относительно редки, но встречаются. История считает, что американский политик и ученый Бенджамин Франклин описал ток как направление, в котором положительные заряды проходят через провод. Он назвал тип заряда, связанный с электронами, отрицательным задолго до того, как стало известно, что они переносят ток во многих ситуациях.
Когда электроны движутся по металлической проволоке, они сталкиваются с препятствиями, такими как другие электроны, атомы, примеси и т.
Д. Электроны рассеиваются от этих препятствий, как показано на рисунке 19.5. Обычно электроны теряют энергию при каждом взаимодействии. Таким образом, для поддержания движения электронов требуется сила, создаваемая электрическим полем. Электрическое поле в проводе направлено от конца провода с более высоким потенциалом к концу провода с более низким потенциалом. Электроны, несущие отрицательный заряд, движутся в среднем (или дрейф ) в направлении, противоположном электрическому полю, как показано на рисунке 19.5.
Рис. 19.5. Свободные электроны, движущиеся в проводнике, совершают множество столкновений с другими электронами и атомами.Показан путь одного электрона. Средняя скорость свободных электронов находится в направлении, противоположном электрическому полю. Столкновения обычно передают энергию проводнику, поэтому для поддержания постоянного тока требуется постоянный запас энергии.
До сих пор мы обсуждали ток, который постоянно движется в одном направлении.
Это называется постоянным током, потому что электрический заряд течет только в одном направлении. Постоянный ток часто называют током DC .
Многие источники электроэнергии, такие как плотина гидроэлектростанции, показанная в начале этой главы, вырабатывают переменный ток, направление которого меняется взад и вперед.Переменный ток часто называют Переменный ток . Переменный ток движется вперед и назад через равные промежутки времени, как показано на рисунке 19.6. Переменный ток, который исходит из обычной розетки, не меняет направление внезапно. Скорее, он плавно увеличивается до максимального тока, а затем плавно уменьшается до нуля. Затем он снова растет, но в противоположном направлении, пока не достигнет того же максимального значения. После этого он плавно уменьшается до нуля, и цикл начинается снова.
Рисунок 19.6 При переменном токе направление тока меняется на противоположное через равные промежутки времени.
График вверху показывает текущую зависимость от времени. Отрицательные максимумы соответствуют движению тока влево. Положительные максимумы соответствуют току, движущемуся вправо. Ток регулярно и плавно чередуется между этими двумя максимумами.
Teacher Support
Teacher Support
Помогите ученикам интерпретировать график, подчеркнув, что ток не меняет направление мгновенно, а плавно переходит от одного максимума к противоположному максимуму и обратно.Объясните, что четыре изображения внизу показывают ток в соответствующих максимумах. Обратите внимание, что для упрощения интерпретации операторы мобильной связи на изображении считаются положительными.
Устройства, использующие переменный ток, включают пылесосы, вентиляторы, электроинструменты, фены и многие другие. Эти устройства получают необходимую мощность, когда вы подключаете их к розетке. Настенная розетка подключена к электросети, которая обеспечивает переменный потенциал (потенциал переменного тока).
Когда ваше устройство подключено к сети, потенциал переменного тока толкает заряды вперед и назад в цепи устройства, создавая переменный ток.
Однако во многих устройствах используется постоянный ток, например в компьютерах, сотовых телефонах, фонариках и автомобилях. Одним из источников постоянного тока является аккумулятор, который обеспечивает постоянный потенциал (потенциал постоянного тока) между своими выводами. Когда ваше устройство подключено к батарее, потенциал постоянного тока толкает заряд в одном направлении через цепь вашего устройства, создавая постоянный ток. Другой способ получения постоянного тока — использование трансформатора, который преобразует переменный потенциал в постоянный. Маленькие трансформаторы, которые вы можете подключить к розетке, используются для зарядки вашего ноутбука, мобильного телефона или другого электронного устройства.Люди обычно называют это зарядным устройством или батареей , но это трансформатор, который преобразует напряжение переменного тока в напряжение постоянного тока.
В следующий раз, когда кто-то попросит одолжить зарядное устройство для ноутбука, скажите им, что у вас нет зарядного устройства для ноутбука, но они могут одолжить ваш преобразователь.
Рабочий пример
Ток при ударе молнии
Удар молнии может передать до 10201020 электронов из облака на землю. Если удар длится 2 мс, каков средний электрический ток в молнии?
Стратегия
Используйте определение тока, I = ΔQΔtI = ΔQΔt.Заряд ΔQΔQ из 10201020 электронов составляет ΔQ = neΔQ = ne, где n = 1020n = 1020 — количество электронов, а e = −1.60 × 10−19Ce = −1.60 × 10−19C — заряд электрона. Это дает
ΔQ = 1020 × (-1,60 × 10-19 ° C) = -16,0 ° C. ΔQ = 1020 × (-1,60 × 10-19 ° C) = -16,0 ° C.19,2
Время Δt = 2 × 10–3 с Δt = 2 × 10–3 с — это продолжительность удара молнии.
Решение
Ток при ударе молнии
I = ΔQΔt = −16,0C2 × 10−3s = −8kA.I = ΔQΔt = −16,0C2 × 10−3s = −8kA.19,3
Обсуждение
Отрицательный знак отражает тот факт, что электроны несут отрицательный заряд. Таким образом, хотя электроны текут от облака к земле, положительный ток должен течь от земли к облаку.
Рабочий пример
Средний ток для зарядки конденсатора
В цепи, содержащей конденсатор и резистор, заряд конденсатора емкостью 16 мкФ с использованием батареи 9 В. занимает 1 мин. Какой средний ток в это время?
Стратегия
Мы можем определить заряд конденсатора, используя определение емкости: C = QVC = QV.Когда конденсатор заряжается 9-вольтовой батареей, напряжение на конденсаторе будет V = 9VV = 9V. Это дает заряд
Подставляя это выражение для заряда в уравнение для тока, I = ΔQΔtI = ΔQΔt, мы можем найти средний ток.
Решение
Средний ток
I = ΔQΔt = CVΔt = (16 × 10−6F) (9V) 60s = 2,4 × 10−6A = 2,4 мкА I = ΔQΔt = CVΔt = (16 × 10−6F) (9V) 60s = 2,4 × 10−6A = 2,4 мкА.19,5
Обсуждение
Этот небольшой ток типичен для тока, встречающегося в таких цепях.
Сопротивление и закон Ома
Как упоминалось ранее, электрический ток в проводе во многом похож на воду, текущую по трубе. На поток воды, который может течь по трубе, влияют препятствия в трубе, такие как засорения и узкие участки в трубе. Эти препятствия замедляют ток через трубу. Точно так же электрический ток в проволоке может быть замедлен многими факторами, включая примеси в металле проволоки или столкновения между зарядами в материале.Эти факторы создают сопротивление электрическому току. Сопротивление — это описание того, насколько провод или другой электрический компонент препятствует прохождению через него заряда. В XIX веке немецкий физик Георг Симон Ом (1787–1854) экспериментально обнаружил, что ток через проводник пропорционален падению напряжения на проводнике с током.
Константа пропорциональности — это сопротивление материала R , что приводит к
Это соотношение называется законом Ома.Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Закон Ома — это эмпирический закон, подобный закону трения, что означает, что это явление наблюдается экспериментально. Единицы сопротивления — вольт на ампер или В / А. Мы называем V / A Ом , что обозначается заглавной греческой буквой омега (ΩΩ). Таким образом,
1 Ом = 1 В / А (1,4). 1 Ом = 1 В / А (1,4).Закон Ома справедлив для большинства материалов и при обычных температурах. При очень низких температурах сопротивление может упасть до нуля (сверхпроводимость).При очень высоких температурах тепловое движение атомов в материале препятствует потоку электронов, увеличивая сопротивление. Многие вещества, для которых действует закон Ома, называются омическими. Омические материалы включают хорошие проводники, такие как медь, алюминий и серебро, и некоторые плохие проводники при определенных обстоятельствах. Сопротивление омических материалов остается практически неизменным в широком диапазоне напряжения и тока.
Watch Physics
Введение в электричество, цепи, ток и сопротивление
В этом видео представлен закон Ома и показана простая электрическая схема.Оратор использует аналогию давления, чтобы описать, как электрический потенциал заставляет заряд двигаться. Он называет электрический потенциал электрическим давлением . Другой способ размышления об электрическом потенциале — это представить, что множество частиц одного знака скопилось в небольшом замкнутом пространстве. Поскольку эти заряды имеют одинаковый знак (все они положительные или все отрицательные), каждый заряд отталкивает другие вокруг себя. Это означает, что множество зарядов постоянно выталкивается за пределы пространства.Полная электрическая цепь похожа на открытие двери в небольшом пространстве: какие бы частицы ни толкали к двери, теперь есть способ убежать. Чем выше электрический потенциал, тем сильнее каждая частица сталкивается с другими.
Проверка захвата
Если вместо одного резистора R на схеме, показанной в видео, нарисовать два резистора с сопротивлением R каждый, что вы можете сказать о токе в цепи?
- Сила тока в цепи должна уменьшиться вдвое.
- Количество тока в цепи должно увеличиться вдвое.
- Ток в цепи должен оставаться неизменным.
- Количество тока в цепи будет удвоено.
Виртуальная физика
Закон Ома
Это моделирование имитирует простую схему с батареями, обеспечивающими источник напряжения, и резистором, подключенным к батареям.Посмотрите, как на ток влияет изменение сопротивления и / или напряжения. Обратите внимание, что сопротивление моделируется как элемент, содержащий малых рассеивающих центров . Они представляют собой загрязнения или другие препятствия, препятствующие прохождению тока.
Проверка захвата
В цепи, если сопротивление оставить постоянным, а напряжение удвоить (например, с 3 В до 6 В), как изменится ток? Соответствует ли это закону Ома?
- Сила тока удвоится.Это соответствует закону Ома, поскольку ток пропорционален напряжению.
- Сила тока удвоится. Это не соответствует закону Ома, поскольку ток пропорционален напряжению.
- Ток увеличится вдвое. Это соответствует закону Ома, поскольку ток пропорционален напряжению.
- Ток уменьшится вдвое. Это не соответствует закону Ома, поскольку ток пропорционален напряжению.
Рабочий пример
Сопротивление фары
Каково сопротивление автомобильной фары, через которую проходит 2,50 А при подаче на нее 12,0 В?
Стратегия
ЗаконОма говорит нам, что Vheadlight = IRheadlightVheadlight = IRheadlight. Падение напряжения при прохождении через фару — это просто повышение напряжения, обеспечиваемое аккумулятором, Vheadlight = VbatteryVheadlight = Vbattery. Мы можем использовать это уравнение и изменить закон Ома, чтобы найти сопротивление RheadlightRheadlight фары.
Решение
Решение закона Ома для сопротивления фары дает
Vheadlight = IRheadlight Vbattery = IRheadlight Rheadlight = VbatteryI = 12V2.5A = 4.8Ω. Vheadlight = IRheadlightVbattery = IRheadlightRheadlight = VbatteryI = 12V2.5A = 4.8Ω.19,6
Обсуждение
Это относительно небольшое сопротивление. Как мы увидим ниже, сопротивление в цепях обычно измеряется в кВт или МВт.
Рабочий пример
Определите сопротивление по графику «ток-напряжение»
Предположим, вы прикладываете к цепи несколько различных напряжений и измеряете ток, протекающий по цепи.График результатов показан на рисунке 19.7. Какое сопротивление цепи?
Рисунок 19.7 Линия показывает зависимость тока от напряжения. Обратите внимание, что ток указан в миллиамперах. Например, при 3 В ток составляет 0,003 А или 3 мА.
Стратегия
График показывает, что ток пропорционален напряжению, что соответствует закону Ома. По закону Ома (V = IRV = IR) константа пропорциональности — это сопротивление R . Поскольку на графике показан ток как функция напряжения, мы должны изменить закон Ома в следующей форме: I = VR = 1R × VI = VR = 1R × V.Это показывает, что наклон линии I по сравнению с V составляет 1R1R. Таким образом, если мы найдем наклон линии на рисунке 19.7, мы сможем вычислить сопротивление R .
Решение
Наклон линии равен подъему , разделенному на подъем . Глядя на нижний левый квадрат сетки, мы видим, что линия поднимается на 1 мА (0,001 А) и проходит через напряжение 1 В. Таким образом, наклон линии равен
. наклон = 0.001A1V. Наклон = 0,001A1V.19,7
Приравнивая наклон к 1R1R и решая для R , получаем
1R = 0,001A1R = 1V0,001A = 1000 Ом 1R = 0,001A1R = 1V0,001A = 1000 Ом19,8
или 1 кОм.
Обсуждение
Это сопротивление больше, чем то, что мы обнаружили в предыдущем примере. Подобные сопротивления часто встречаются в электрических цепях, как мы узнаем в следующем разделе. Обратите внимание, что если бы линия на рисунке 19.7 не была прямой, то материал не был бы омическим, и мы не смогли бы использовать закон Ома.Материалы, которые не подчиняются закону Ома, называются безомными.
ЗАКОН ОМА После прочтения этого раздела вы сможете сделать следующее:
Вероятно, наиболее важным математическим соотношением между напряжением, током и сопротивлением в электричестве является то, что называется «законом Ома».Человек по имени Джордж Ом опубликовал эту формулу в 1827 году, основываясь на своих экспериментах с электричеством. Эта формула используется для расчета электрических величин, чтобы мы могли проектировать схемы и использовать электричество с пользой. Закон Ома показан ниже.
Давайте посмотрим, что говорит нам закон Ома. В первой версии формулы I = V / R закон Ома говорит нам, что электрический ток в цепи можно рассчитать, разделив напряжение на сопротивление. Другими словами, ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.Таким образом, увеличение напряжения будет увеличивать ток, пока сопротивление остается постоянным. В качестве альтернативы, если сопротивление в цепи увеличивается, а напряжение не изменяется, ток будет уменьшаться. Вторая версия формулы говорит нам, что напряжение можно рассчитать, если известны ток и сопротивление в цепи. Из уравнения видно, что если в цепи увеличивается ток или сопротивление (в то время как другое остается неизменным), напряжение также должно увеличиваться. Третья версия формулы говорит нам, что мы можем рассчитать сопротивление в цепи, если известны напряжение и ток. Если ток остается постоянным, увеличение напряжения приведет к увеличению сопротивления. В качестве альтернативы увеличение тока при поддержании постоянного напряжения приведет к уменьшению сопротивления. Следует отметить, что закон Ома верен для полупроводников, но для широкого спектра материалов (например, металлов) сопротивление является фиксированным и не зависит от величины тока или величины напряжения. Как видите, напряжение, ток и сопротивление математически, а также физически связаны друг с другом. Мы не можем иметь дело с электричеством без учета всех трех этих свойств. (Символ Ом выглядит как подкова и изображен после цифры «100» на диаграмме выше.) Обзор
|
Понимание закона Ома — Pi My Life Up
Закон Ома — одна из основ электроники и невероятно удобен для быстрого расчета тока, напряжения или сопротивления цепи. Вам нужно будет знать как минимум два значения.
Закон Ома определяет математическое соотношение между током, напряжением и сопротивлением сети.
Этот закон был назван в честь немецкого физика и математика XIX века Георга Ома.Ом обнаружил эту взаимосвязь еще в то время, когда не было возможности легко измерить ток, напряжение или сопротивление.
Несмотря на то, что при первой публикации он был встречен холодно, он стал обязательным для всех, кто интересуется электрическими схемами. Закон Ома стал частью нашего нынешнего понимания электрических схем.
Если вы занимаетесь каким-либо из наших проектов электроники Raspberry Pi, которые связаны со схемами, то этот учебник может оказаться вам полезным.
Что такое закон Ома?
Закон Ома гласит, что ток, проходящий через проводник между двумя точками, прямо пропорционален напряжению в этих двух точках и обратно пропорционален сопротивлению между двумя точками.
Проще говоря, если в цепи удваивается ток, то удваивается и напряжение. Точно так же, если сопротивление в цепи увеличится вдвое, ток упадет вдвое.
Хотя это может показаться немного сложным, фактическая математика, лежащая в основе этой теории, невероятно проста для понимания и запоминания.
Формула закона Ома
К счастью для нас, формула закона Ома невероятно проста для понимания.
Закон Ома можно выразить математической формулой, как показано ниже.
Эта формула говорит, что напряжение ( В, ) равно току ( I ), умноженному на сопротивление ( R ).
Во всех формулах закона Ома мы используем следующие переменные.
- В = напряжение, выраженное в вольтах.
- I = ток, выраженный в амперах.
- R = Сопротивление, выраженное в Ом.
Хотя формулу можно использовать для расчета напряжения, ею также можно управлять, чтобы вместо этого вычислить ток или сопротивление в цепи.
Для начала давайте изменим формулу так, чтобы мы могли вычислить ток ( I ) цепи.
Мы также можем изменить базовую формулу закона Ома, чтобы мы могли вычислить сопротивление ( R ) цепи.
Калькулятор закона Ома
Чтобы использовать этот калькулятор закона Ома, сначала выберите, хотите ли вы рассчитать напряжение, ток или сопротивление.
При выбранном режиме все, что вам нужно сделать, это ввести два требуемых значения. Калькулятор автоматически рассчитает правильные значения.
Треугольник закона Ома
Один из самых простых способов запомнить три различных формулы закона Ома — это треугольник.
Средний горизонтальный делитель треугольника представляет деление, то есть всякий раз, когда в формуле участвует напряжение ( В, ), все остальные буквы делятся на него.
Например, если мы хотим вычислить ток ( I ), нам нужно разделить напряжение ( В, ) на сопротивление ( R ).
Обведя кружком « I » в треугольнике, мы увидим, что формула остается в треугольнике с V по R .
Мы также можем использовать тот же треугольник, чтобы разработать формулу для расчета сопротивления ( R ) цепи.
Обведя сопротивление ( R ), мы можем увидеть формулу, которую мы должны использовать: напряжение ( В, ), деленное на ток ( I )
Вертикальная линия в треугольнике представляет собой умножение.Эта линия используется только при расчете напряжения (В).
Снова используя треугольник закона Ома, мы можем быстро увидеть формулу, которую нам нужно использовать, обведя кружком « V », поскольку это значение, которое мы хотим вычислить.
Из этого легко понять, что для расчета напряжения ( В, ) все, что нам нужно сделать, это умножить ток ( I ) на сопротивление ( R ).
Пример закона Ома в действии
Далее мы рассмотрим три различных примера схем.
Эти примеры касаются использования каждого варианта трех различных формул закона Ома.
Пример напряжения
В этом первом примере мы собираемся начать с формулы закона основного сопротивления для расчета напряжения цепи.
Для расчета напряжения нам необходимо знать сопротивление ( R ) и ток ( I ) цепи.
В этой примерной схеме вы можете видеть, что у нас есть сопротивление ( R ) 200 Ом и ток ( I ) 5 А.
Чтобы рассчитать напряжение, нам нужно вставить два наших значения в формулу закона Ома.
После заполнения формулы вы можете видеть, что все, что нам нужно сделать, это умножить 200 на 5 , чтобы рассчитать напряжение.
Умножив сопротивление и ток, мы увидим, что напряжение для схемы в примере равно 1000 вольт .
Пример тока
В этом втором примере мы будем использовать модифицированную версию формулы закона Ома для расчета тока следующей цепи.
Из этой схемы мы знаем, что сопротивление ( R ) составляет 50 Ом, и что напряжение ( В, ) составляет 24 В, .
Нам нужно поместить эти значения в формулу закона Ома, которая была изменена для расчета тока ( I ).
Используя значения сопротивления и напряжения, введенные в формулу, мы видим, что нам нужно разделить 24 на 50 , чтобы вычислить ток.
Используя закон Ома, мы вычисляем ток в цепи как 0.48 ампер .
Пример сопротивления
В нашем третьем и последнем примере мы будем использовать третью версию формулы закона Ома. В этом случае мы будем использовать формулу для расчета сопротивления цепи.
Чтобы рассчитать сопротивление цепи, нам нужно знать напряжение ( В, ) и ток ( I ) цепи.
Из этой примерной схемы мы можем видеть, что наша примерная схема имеет ток 10 А, и напряжение 20 Вольт .
Нам нужно вставить эти два значения в формулу сопротивления закона Ома.
Исходя из этого, мы можем рассчитать необходимое сопротивление, разделив напряжение 20 на 10 ампер .
Рассчитав это, мы видим, что сопротивление нашей схемы в нашем примере должно быть 2 Ом .
Надеюсь, что теперь у вас есть понимание закона Ома и то, как его использовать. Мы рассмотрели, как можно использовать треугольник закона Ома как простой способ запоминания трех различных формул.
Вы найдете эти уравнения очень удобными в проектах, в которых используются схемы, таких как все наши проекты Arduino.
Если у вас есть какие-либо советы или отзывы, не стесняйтесь оставлять комментарии ниже.
Сопротивление и резисторы | Безграничная физика
Закон Ома
ЗаконОма гласит, что ток пропорционален напряжению; цепи являются омическими, если они подчиняются соотношению V = IR.
Цели обучения
Контрастная форма вольт-амперных графиков для омических и неомических цепей
Основные выводы
Ключевые моменты
- Напряжение управляет током, а сопротивление препятствует ему. Закон
- Ома относится к пропорциональному соотношению между напряжением и током. Это также относится к конкретному уравнению V = IR, которое действительно при рассмотрении схем, содержащих простые резисторы (сопротивление которых не зависит от напряжения и тока).
- Цепи или компоненты, которые подчиняются соотношению V = IR, известны как омические и имеют линейные зависимости тока от напряжения, проходящие через начало координат.
- Есть неомические компоненты и цепи; их графики I-V нелинейны и / или не проходят через начало координат.
Ключевые термины
- простая схема : Схема с одним источником напряжения и одним резистором.
- омический : То, что подчиняется закону Ома.
Закон Ома
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и условно называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов V, которая создает электрическое поле.Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток. Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению V. Немецкий физик Георг Симон Ом (1787-1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению: [латекс] \ text {I} \ propto \ text {V} [/ latex ].
Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием.Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда. Напомним, что в то время как напряжение управляет током, сопротивление ему препятствует. Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток. Таким образом, ток обратно пропорционален сопротивлению: [latex] \ text {I} \ propto \ frac {1} {\ text {R}} [/ latex].
Простая схема : Простая электрическая цепь, в которой замкнутый путь для прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленной красными параллельными линиями.Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.
Единицей измерения сопротивления является Ом, где 1 Ом = 1 В / А. Мы можем объединить два приведенных выше соотношения, чтобы получить I = V / R. Это соотношение также называется законом Ома. В этой форме закон Ома действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых действует закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах.Омические материалы имеют сопротивление R, которое не зависит от напряжения V и тока I. Объект с простым сопротивлением называется резистором, даже если его сопротивление невелико.
Падение напряжения : Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Дополнительное понимание можно получить, решив I = V / R для V, что дает V = IR. Это выражение для V можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I.Для этого напряжения часто используется фраза «падение ИК-излучения». Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывая ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления. Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию).В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку E = qΔV, и через каждую из них протекает одинаковое q. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.
В истинно омическом устройстве одно и то же значение сопротивления будет вычислено из R = V / I независимо от значения приложенного напряжения V. То есть отношение V / I является постоянным, и когда ток отображается как В зависимости от напряжения кривая является линейной (прямая линия).Если напряжение принудительно устанавливается равным некоторому значению V, тогда это напряжение V, деленное на измеренный ток I, будет равно R. Или, если ток будет увеличен до некоторого значения I, тогда измеренное напряжение V, деленное на этот ток I, также будет R. график I против V как прямая линия. Однако есть компоненты электрических цепей, которые не подчиняются закону Ома; то есть их взаимосвязь между током и напряжением (их ВАХ) нелинейна (или неомична). Примером может служить диод с p-n переходом.
Кривые «ток-напряжение» : ВАХ четырех устройств: двух резисторов, диода и батареи.Два резистора подчиняются закону Ома: график представляет собой прямую линию, проходящую через начало координат. Два других устройства не подчиняются закону Ома.
Закон Ома : Краткий обзор закона Ома.
Температура и сверхпроводимость
Сверхпроводимость — это явление отсутствия электрического сопротивления и выброса магнитных полей в некоторых материалах при температуре ниже критической.
Цели обучения
Описать поведение сверхпроводника ниже критической температуры и в слабом внешнем магнитном поле
Основные выводы
Ключевые моменты
- Сверхпроводимость — это сверхпроводимость. Сверхпроводимость — это термодинамическая фаза, обладающая определенными отличительными свойствами, которые в значительной степени не зависят от микроскопических деталей.
- В сверхпроводящих материалах характеристики сверхпроводимости проявляются при понижении температуры ниже критической. Возникновение сверхпроводимости сопровождается резкими изменениями различных физических свойств.
- Когда сверхпроводник помещается в слабое внешнее магнитное поле H и охлаждается ниже температуры перехода, магнитное поле выбрасывается.
- Сверхпроводники могут поддерживать ток без приложенного напряжения.
Ключевые термины
- высокотемпературные сверхпроводники : материалы, которые ведут себя как сверхпроводники при необычно высоких температурах (выше примерно 30 K).
- критическая температура : В сверхпроводящих материалах характеристики сверхпроводимости проявляются при этой температуре (и сохраняются ниже).
- сверхпроводимость : Свойство материала, при котором он не оказывает сопротивления прохождению электрического тока.
Сверхпроводимость — это явление точно нулевого электрического сопротивления и выброса магнитных полей, возникающее в некоторых материалах при охлаждении ниже критической температуры.Он был обнаружен Хайке Камерлинг-Оннес (на фото) 8 апреля 1911 года в Лейдене.
Хайке Камерлинг-Оннес : Хайке Камерлинг-Оннес (1853-1926).
Большинство физических свойств сверхпроводников варьируются от материала к материалу, такие как теплоемкость и критическая температура, критическое поле и критическая плотность тока, при которых сверхпроводимость разрушается. С другой стороны, существует класс свойств, не зависящих от основного материала.Например, все сверхпроводники имеют точно нулевое удельное сопротивление по отношению к низким приложенным токам, когда нет магнитного поля или если приложенное поле не превышает критического значения. Существование этих «универсальных» свойств подразумевает, что сверхпроводимость является термодинамической фазой и, таким образом, обладает определенными отличительными свойствами, которые в значительной степени не зависят от микроскопических деталей.
В сверхпроводящих материалах характеристики сверхпроводимости появляются, когда температура T понижается ниже критической температуры T c .Возникновение сверхпроводимости сопровождается резкими изменениями различных физических свойств — отличительным признаком фазового перехода. Например, электронная теплоемкость пропорциональна температуре в нормальном (несверхпроводящем) режиме. При сверхпроводящем переходе он претерпевает прерывистый скачок и после этого перестает быть линейным, как показано на.
Когда сверхпроводник помещается в слабое внешнее магнитное поле H и охлаждается ниже температуры перехода, магнитное поле выбрасывается.Эффект Мейснера не вызывает полного выброса поля. Скорее, поле проникает в сверхпроводник на очень малое расстояние (характеризуемое параметром λ), называемое лондонской глубиной проникновения. Он экспоненциально спадает до нуля в объеме материала. Эффект Мейснера — определяющая характеристика сверхпроводимости. Для большинства сверхпроводников лондонская глубина проникновения составляет порядка 100 нм.
Сверхпроводящий фазовый переход : Поведение теплоемкости (cv, синий) и удельного сопротивления (ρ, зеленый) при сверхпроводящем фазовом переходе.
Сверхпроводники также способны поддерживать ток без какого-либо приложенного напряжения — свойство, используемое в сверхпроводящих электромагнитах, таких как те, что используются в аппаратах МРТ. Эксперименты показали, что токи в сверхпроводящих катушках могут сохраняться годами без какого-либо измеримого ухудшения. Экспериментальные данные указывают на текущую продолжительность жизни не менее 100 000 лет. Теоретические оценки времени жизни постоянного тока могут превышать расчетное время жизни Вселенной, в зависимости от геометрии провода и температуры.
Значение этой критической температуры варьируется от материала к материалу. Обычно обычные сверхпроводники имеют критические температуры в диапазоне от примерно 20 К до менее 1 К. Твердая ртуть, например, имеет критическую температуру 4,2 К. По состоянию на 2009 год самая высокая критическая температура, найденная для обычного сверхпроводника, составляет 39 К. для магния. диборид (MgB 2 ), хотя экзотические свойства этого материала вызывают некоторые сомнения в правильности его классификации как «обычного» сверхпроводника.Высокотемпературные сверхпроводники могут иметь гораздо более высокие критические температуры. Например, YBa 2 Cu 3 O 7 , один из первых открытых купратных сверхпроводников, имеет критическую температуру 92 К; Были обнаружены купраты на основе ртути с критическими температурами, превышающими 130 К. Следует отметить, что химический состав и кристаллическая структура сверхпроводящих материалов могут быть довольно сложными, как показано в.
Элементарная ячейка сверхпроводника YBaCuO : Элементарная ячейка сверхпроводника YBaCuO.Атомы обозначены разными цветами.
Сопротивление и удельное сопротивление
Сопротивление и удельное сопротивление описывают степень, в которой объект или материал препятствуют прохождению электрического тока.
Цели обучения
Определить свойства материала, которые описываются сопротивлением и удельным сопротивлением
Основные выводы
Ключевые моменты
- Сопротивление объекта (т. Е. Резистора) зависит от его формы и материала, из которого он состоит.
- Удельное сопротивление ρ является внутренним свойством материала и прямо пропорционально общему сопротивлению R, внешней величине, которая зависит от длины и площади поперечного сечения резистора.
- Удельное сопротивление различных материалов сильно различается. Точно так же резисторы могут иметь разные порядки величины.
- Резисторы расположены последовательно или параллельно. Эквивалентное сопротивление цепи последовательно включенных резисторов является суммой всех сопротивлений.Сопротивление, обратное эквивалентному сопротивлению цепи параллельно включенных резисторов, является суммой обратных сопротивлений каждого резистора.
Ключевые термины
- последовательное эквивалентное сопротивление : сопротивление сети резисторов, расположенных таким образом, что напряжение в сети является суммой напряжений на каждом резисторе. В этом случае эквивалентное сопротивление — это сумма сопротивлений всех резисторов в сети.
- параллельное эквивалентное сопротивление : сопротивление сети, при котором на каждый резистор действует одинаковая разность потенциалов (напряжение), так что токи, проходящие через них, складываются.В этом случае сопротивление, обратное эквивалентному сопротивлению, равно сумме обратных сопротивлений всех резисторов в сети.
- удельное сопротивление : Обычно сопротивление материала электрическому току; в частности, степень сопротивления материала потоку электричества.
Сопротивление и удельное сопротивление
Сопротивление — это электрическое свойство, препятствующее прохождению тока. Ток, протекающий через провод (или резистор), подобен воде, протекающей по трубе, а падение напряжения на проводе подобно перепаду давления, которое проталкивает воду по трубе.Сопротивление пропорционально тому, сколько давления требуется для достижения заданного потока, в то время как проводимость пропорциональна тому, сколько потока возникает при заданном давлении. Проводимость и сопротивление взаимны. Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорционально его длине L, подобно сопротивлению трубы потоку жидкости.Чем длиннее цилиндр, тем больше зарядов столкнется с его атомами. Чем больше диаметр цилиндра, тем больше тока он может пропускать (опять же, аналогично потоку жидкости по трубе). Фактически, R обратно пропорционально площади поперечного сечения цилиндра A.
Цилиндрический резистор : однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению, оказываемому трубой потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление.Чем больше площадь его поперечного сечения A, тем меньше его сопротивление.
Как уже упоминалось, для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы обладают разным сопротивлением потоку заряда. Мы определяем удельное сопротивление ρ вещества так, чтобы сопротивление R объекта было прямо пропорционально ρ. Удельное сопротивление ρ является внутренним свойством материала, независимо от его формы или размера. Напротив, сопротивление R — это внешнее свойство, которое зависит от размера и формы резистора.(Аналогичная внутренняя / внешняя связь существует между теплоемкостью C и удельной теплоемкостью c). Напомним, что объект, сопротивление которого пропорционально напряжению и току, называется резистором.
Типичный резистор : Типовой резистор с осевыми выводами.
Что определяет удельное сопротивление? Удельное сопротивление разных материалов сильно различается. Например, проводимость тефлона примерно в 1030 раз ниже, чем проводимость меди. Почему такая разница? Грубо говоря, металл имеет большое количество «делокализованных» электронов, которые не застревают в каком-либо одном месте, но могут свободно перемещаться на большие расстояния, тогда как в изоляторе (например, тефлоне) каждый электрон прочно связан с одним атомом и требуется большая сила, чтобы оторвать его.Точно так же резисторы могут иметь разные порядки величины. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 12 Ом или более. Сопротивление сухого человека может составлять 10 5 Ом, тогда как сопротивление человеческого сердца составляет примерно 10 3 Ом. Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10 −5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны). Разность потенциалов (напряжение), наблюдаемая в сети, является суммой этих напряжений, поэтому общее сопротивление (последовательное эквивалентное сопротивление) можно найти как сумму этих сопротивлений:
[латекс] \ text {R} _ {\ text {eq}} = \ text {R} _ {1} + \ text {R} _ {2} + \ cdots + \ text {R} _ {\ text {N}} [/ латекс].
В качестве особого случая сопротивление N резисторов, соединенных последовательно, каждый из которых имеет одинаковое сопротивление R, определяется как NR. Каждый резистор в параллельной конфигурации подвержен одной и той же разности потенциалов (напряжению), однако протекающие через них токи складываются . Таким образом, можно вычислить эквивалентное сопротивление (Req) сети:
[латекс] \ frac {1} {\ text {R} _ {\ text {eq}}} = \ frac {1} {\ text {R} _ {1}} + \ frac {1} {\ text {R} _ {2}} + \ cdots + \ frac {1} {\ text {R} _ {\ text {N}}} [/ latex].
Параллельное эквивалентное сопротивление может быть представлено в уравнениях двумя вертикальными линиями «||» (как в геометрии) как упрощенное обозначение.Иногда вместо «||» используются две косые черты «//», если на клавиатуре или шрифте отсутствует символ вертикальной линии. Для случая двух параллельно подключенных резисторов это можно рассчитать по формуле:
[латекс] \ text {R} _ {\ text {eq}} = \ text {R} _ {1} \ parallel \ text {R} _ {2} = \ frac {\ text {R} _ {1 } \ text {R} _ {2}} {\ text {R} _ {1} + \ text {R} _ {2}} [/ latex].
В качестве особого случая сопротивление N резисторов, соединенных параллельно, каждый из которых имеет одинаковое сопротивление R, определяется как R / N. Сеть резисторов, которая представляет собой комбинацию параллельного и последовательного соединения, может быть разбита на более мелкие части, которые являются одним или другим, как показано на.
Сеть резисторов : В этой комбинированной схеме цепь может быть разбита на последовательный компонент и параллельный компонент.
Однако некоторые сложные сети резисторов не могут быть решены таким образом. Это требует более сложного анализа схем. Одно из практических применений этих соотношений состоит в том, что нестандартное значение сопротивления обычно может быть синтезировано путем соединения ряда стандартных значений последовательно или параллельно. Это также можно использовать для получения сопротивления с более высокой номинальной мощностью, чем у отдельных используемых резисторов.В частном случае N идентичных резисторов, все подключенных последовательно или все подключенных параллельно, номинальная мощность отдельных резисторов умножается на N.
Сопротивление, резисторы и удельное сопротивление : краткий обзор сопротивления, резисторов и удельного сопротивления.
Зависимость сопротивления от температуры
Удельное сопротивление и сопротивление зависят от температуры, причем зависимость линейна для малых изменений температуры и нелинейна для больших.
Цели обучения
Сравнить температурные зависимости удельного сопротивления и сопротивления при больших и малых изменениях температуры
Основные выводы
Ключевые моменты
- При изменении температуры на 100ºC или меньше удельное сопротивление (ρ) изменяется с изменением температуры ΔT как: [latex] \ text {p} = \ text {p} _ {0} (1 + \ alpha \ Delta \ text {T }) [/ latex] где ρ 0 — исходное удельное сопротивление, а α — температурный коэффициент удельного сопротивления.
- При больших изменениях температуры наблюдается нелинейное изменение удельного сопротивления с температурой.
- Сопротивление объекта демонстрирует такую же температурную зависимость, как и удельное сопротивление, поскольку сопротивление прямо пропорционально удельному сопротивлению.
Ключевые термины
- удельное сопротивление : Обычно сопротивление материала электрическому току; в частности, степень сопротивления материала потоку электричества.
- температурный коэффициент удельного сопротивления : эмпирическая величина, обозначаемая α, которая описывает изменение сопротивления или удельного сопротивления материала в зависимости от температуры.
- полупроводник : Вещество с электрическими свойствами, промежуточными между хорошим проводником и хорошим изолятором.
Удельное сопротивление всех материалов зависит от температуры. Некоторые материалы могут стать сверхпроводниками (нулевое сопротивление) при очень низких температурах (см.). И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Так как атомы колеблются быстрее и на больших расстояниях при более высоких температурах, электроны, движущиеся через металл, например, создают больше столкновений, эффективно увеличивая удельное сопротивление.При относительно небольших изменениях температуры (около 100 ° C или менее) удельное сопротивление ρ изменяется с изменением температуры ΔT, как выражено в следующем уравнении:
Сопротивление образца ртути : Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры его сопротивление совершает внезапный скачок, а затем увеличивается почти линейно. с температурой.
[латекс] \ text {p} = \ text {p} _ {0} (1 + \ alpha \ Delta \ text {T}) [/ latex]
, где ρ 0 — исходное удельное сопротивление, а α — температурный коэффициент удельного сопротивления.Для более значительных изменений температуры α может изменяться, или для нахождения ρ может потребоваться нелинейное уравнение. По этой причине обычно указывается суффикс для температуры, при которой измерялось вещество (например, α 15 ), и соотношение сохраняется только в диапазоне температур вокруг эталона. Обратите внимание, что α положителен для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Температурный коэффициент обычно составляет от + 3 · 10 −3 K −1 до + 6 · 10 −3 K −1 для металлов, близких к комнатной температуре.Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Например, манганин (состоящий из меди, марганца и никеля) имеет α, близкое к нулю, поэтому его удельное сопротивление незначительно меняется с температурой. Это полезно, например, для создания не зависящего от температуры эталона сопротивления.
Отметим также, что α отрицательна для полупроводников, что означает, что их удельное сопротивление уменьшается с увеличением температуры. Они становятся лучшими проводниками при более высоких температурах, потому что повышенное тепловое перемешивание увеличивает количество свободных зарядов, доступных для переноса тока.Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках.
Сопротивление объекта также зависит от температуры, поскольку R 0 прямо пропорционально ρ. Для цилиндра мы знаем, что R = ρL / A, поэтому, если L и A не сильно изменяются с температурой, R будет иметь ту же температурную зависимость, что и ρ. (Исследование коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, и поэтому влияние температуры на L и A примерно на два порядка меньше, чем на ρ.) Таким образом,
[латекс] \ text {R} = \ text {R} _ {0} (1 + \ alpha \ Delta \ text {T}) [/ latex]
— это температурная зависимость сопротивления объекта, где R 0 — исходное сопротивление, а R — сопротивление после изменения температуры T. Многие термометры основаны на влиянии температуры на сопротивление (см.). Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для определения его температуры.