Параллельное соединение резисторов | Электротехника
Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
Рис. 26. Схемы параллельного соединения приемников
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или
I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/Rэк = 1/R1 + 1/R2 + 1/R3 (24)
Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Rэк=R1R2/(R1+R2)
при трех параллельно включенных резисторах
Rэк=R1R2R3/(R1R2+R2R3+R1R3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.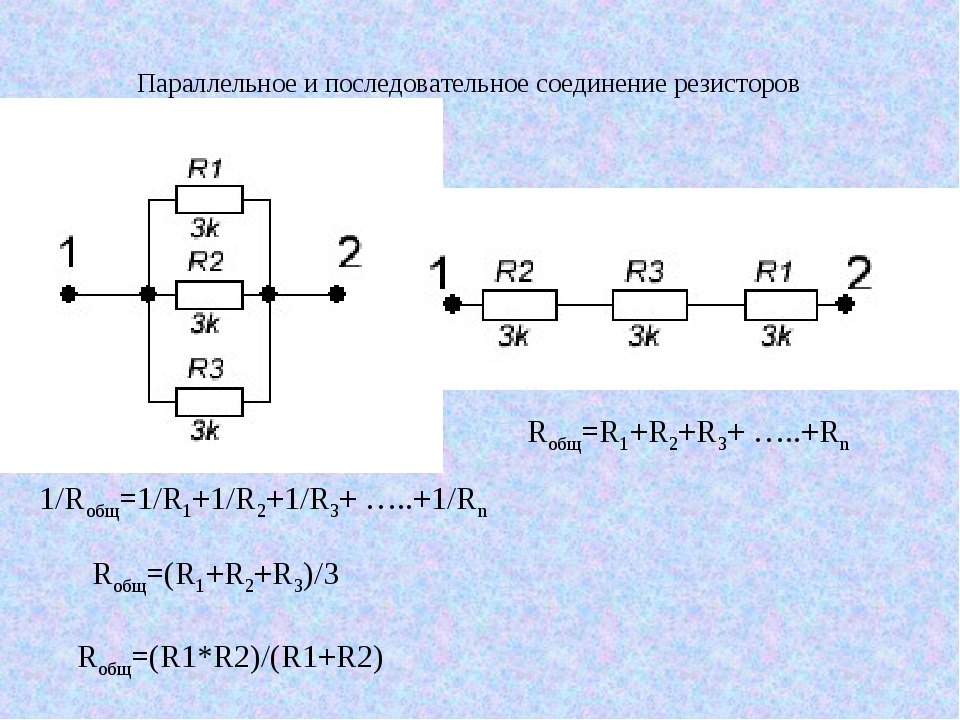
Rэк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.

Параллельное соединение резисторов: расчет и формулы
В случае последовательного соединения прохождение тока осуществляется только через один проводник. Параллельное соединение резисторов предполагает распределение электрического тока среди нескольких проводников. При добавлении еще одного резистора в электрическую цепь, ток будет частично проходить через разные резисторы.
Схемы последовательного и параллельного соединения
Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами.
При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений.
При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.
Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.
Если последовательное и параллельное соединение резисторов рассматривается с точки зрения радиоэлектроники, необходимо четко представлять себе, что представляет собой данный элемент и какова его роль в электронных схемах. Эта деталь является неотъемлемой частью многих устройств, благодаря такому свойству, как сопротивление электрическому току. Резисторы могут быть двух типов – постоянными и переменными, то есть подстроечными. При создании тех или иных электрических схем требуется резистор установленного номинала, которого в данный момент может не оказаться в наличии. Поэтому приходится использовать элементы с другими номинальными значениями, формула для каждого из которых подтверждает их физические свойства.
Последовательное соединение считается наиболее простым. Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.
Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.
Отличие параллельного и последовательного соединения
Последовательное и параллельное соединение резисторов отличаются между собой значениями напряжения. В каждой части параллельных контуров этот показатель будет одинаковым. Однако, при одном и том же напряжении, сила тока в контурах будет разной. Кроме того, сопротивление резисторов при параллельном соединении будет существенно отличаться от того же показателя при последовательном соединении.
В процессе использования последовательной схемы наблюдаются обратные явления. Сила тока в каждом сопротивлении будет одна и та же, а напряжение на каждом участке будет отличаться. Это связано с тем, что во время протекания тока, каждый резистор частично забирает приложенное напряжение.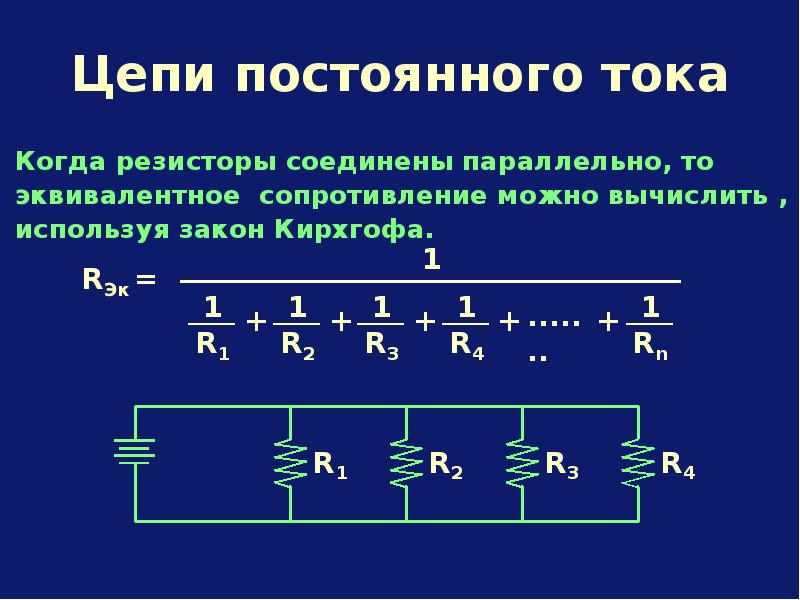 Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено. Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты.
Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено. Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты.
Таким образом, параллельное соединение резисторов, находящихся под одинаковым напряжением, не влияет на режим работы каждого из них. То есть, они совершенно не зависят друг от друга, и ток, проходящий по одному приемнику, не может существенно влиять на другие приемники.
Формула расчета параллельного соединения резисторов
Свои особенности имеет и ток при параллельном соединении резисторов. Попадая в первый узел соединения, он разделяется на столько частей, сколько имеется резисторов, подключенных параллельно. То есть, через сопротивление R1 будет протекать ток I1, а через R2 – ток I2. При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2.
При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2.
Если какой-либо резистор вышел из строя, то остальные будут нормально функционировать. В этом заключается основное преимущество параллельного соединения. Особенно, это касается двигателей и электрических ламп, работающих от определенного номинального напряжения.
Расчет общего номинального сопротивления осуществляется с помощью формулы: R(общ)=1/(1/R1+1/R2+1/R3+1/R n), где R(общ) – является общим сопротивлением, а R1, R2, R3 и Rn – параллельно подключенными резисторами. Если выполняется параллельное соединение двух резисторов, при котором используется всего лишь два элемента, то в этом случае для расчетов используется следующая схема: R(общ)=R1хR2/R1+R2.
Очень часто в радиоэлектронике приходится пользоваться следующим правилом: если резисторы, подключенные параллельно, имеют один и тот же номинал, то итоговое сопротивление высчитывается путем деления номинала на число подключенных элементов. Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1\n, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов.
Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1\n, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов.
Для того чтобы рассчитать параллельное соединение резисторов, следует учитывать, что итоговое сопротивление всех подключенных элементов будет всегда ниже, чем сопротивление резистора с самым низким номиналом. В качестве примера можно рассмотреть схему с тремя резисторами, сопротивления которых составляют 30, 100 и 150 Ом. При использовании основной формулы будет получен следующий результат: R(общ)=1/(1/30+1/100+1/150) =1/(0,03+0,01+0,007)=1/0,047=21,28Ом. Таким образом, три резистора, соединенные параллельно, с минимальным номиналом 30 Ом, в итоге дадут общее сопротивление электрической цепи 21,28 Ом.
Онлайн калькулятор
В случае больших объемов вычислений, расчет параллельного соединения резисторов выполняется с помощью онлайн-калькулятора.
Как найти параллельное сопротивление формула
Из закона Ома и первого и второго правил Кирхгофа следует:
При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.
При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.
Поскольку 1/R = G, т.е. проводимость, то
при параллельном соединении электрические проводимости отдельных ветвей складываются
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Сопротивление проводников. Параллельное и последовательное соединение проводников.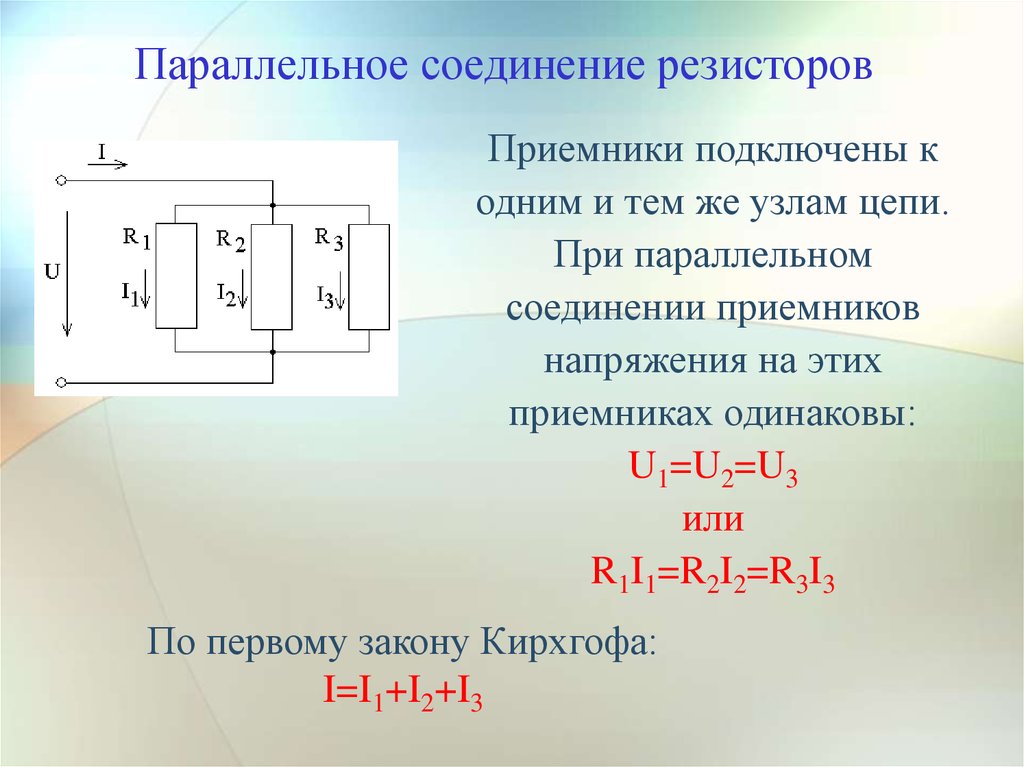
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
где R – электрическое сопротивление всей цепи. Отсюда следует:
Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Параллельное соединение проводников
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Формула расчета сопротивления при параллельном соединении резистора
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.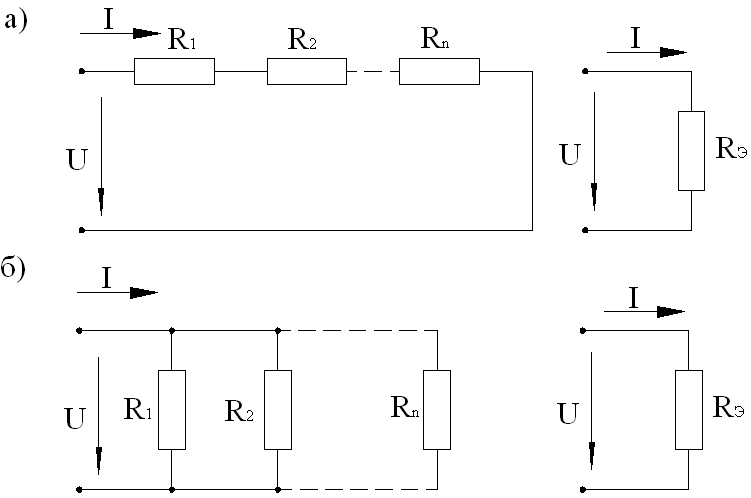
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Резисторы R2 и R3 соединены последовательно (группа 2).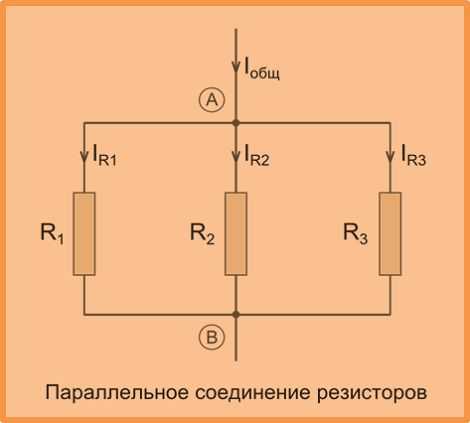 Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
- Таким образом, протекающий общий ток в цепи можно определить как:
- I = I1 + I2
- Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
- Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
- Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
- Таким образом, общий ток будет равен:
- I = 0,545 мА + 0,255 мА = 0,8 мА
- Это также можно проверить, используя закон Ома:
- I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
- где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
- И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.
Источник: http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/
Последовательное и параллельное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток.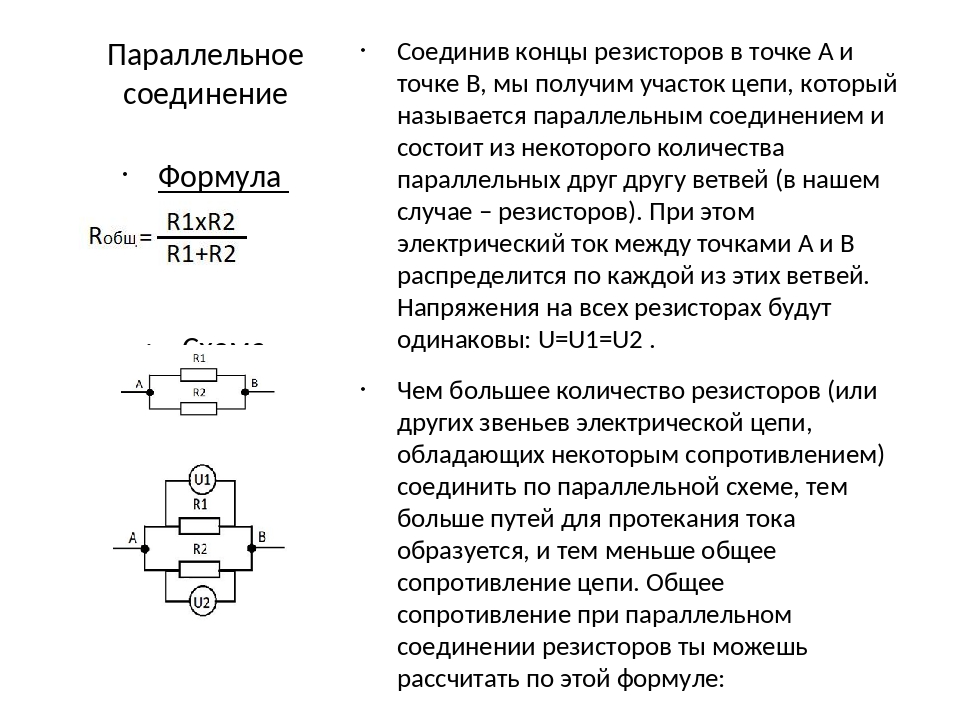 Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Источник: http://hightolow.ru/resistor3.php
Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
- При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
- Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.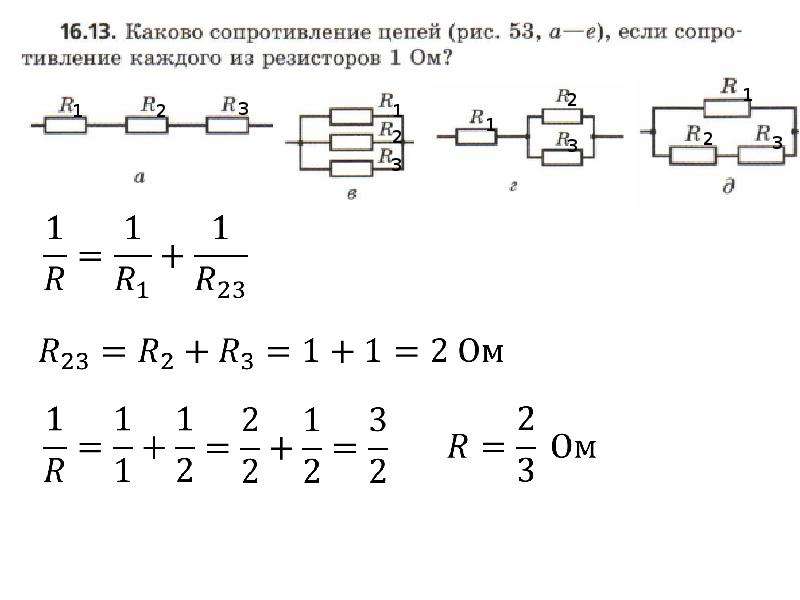
Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
2. Делитель токов.
Источник: https://kurstoe.ru/osnovnie-svedeniya/preobrazovanie-tcepej/parallelnoe-soedinenie.html
Последовательное и параллельное соединение резисторов
Последовательное и параллельное соединение резисторов в схемах являются самыми распространенными, также — это база для расчета более сложных схем.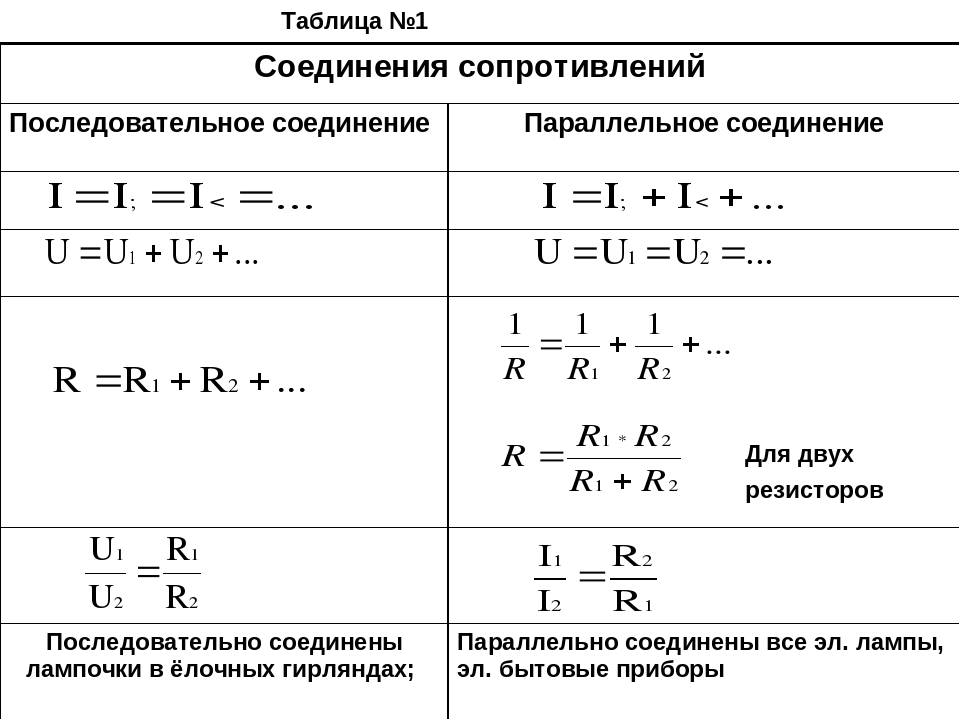
Последовательное подключение
Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше.
Рис. Последовательное подключение.
Обозначение:
Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.
Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам.
В последовательных цепях — складываем, в параллельных — это обратно пропорциональная величина.
Параллельное соединение
Рис. Параллельное подключение.
Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т. е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах — //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле. Более наглядно это можно представить в виде формул: 1. Каждый вид соединения находится под одинаковым напряжением: U = U1 = U2; 2. Суммарная сила тока равняется суммарному значению тока каждого участка I = I1 + I2; 3. Сопротивление цепи равно сумме величина обратных сопротивлению участка: 1/R = 1/R1 + 17R2 + . . . + 1/Rn; 4. Сила тока пропорциональна сопротивлению каждого участка I1/I2=R2/R1.
е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах — //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле. Более наглядно это можно представить в виде формул: 1. Каждый вид соединения находится под одинаковым напряжением: U = U1 = U2; 2. Суммарная сила тока равняется суммарному значению тока каждого участка I = I1 + I2; 3. Сопротивление цепи равно сумме величина обратных сопротивлению участка: 1/R = 1/R1 + 17R2 + . . . + 1/Rn; 4. Сила тока пропорциональна сопротивлению каждого участка I1/I2=R2/R1.
Далее рассмотрим схему как работает не только последовательное параллельное, но и смешанное соединение резисторов.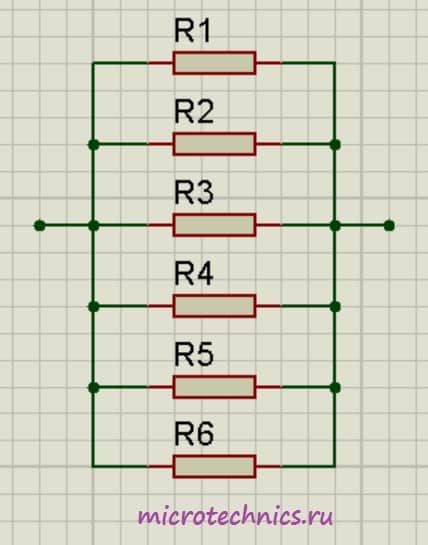
Смешанное подключение
Рис. Смешанное подключение резисторов
В электрических схемах используются не только типовые схемы, но и смешанное, созданное из критерий определенных требований. Чаще всего в схемах встречается третий вариант, представляющий набор из элементарных типов схем. В смешанных участках учитываются не только элементы, но и направления движения тока. При вычислении мощности резисторов смешанного подключения используются формулы для параллельного и последовательного соединения резисторов, формула также является составной.
Основные законы электротехники, наиболее часто используемые для расчетов
Рассмотрим основные законы электротехники и свойства последовательного и параллельного соединения резисторов для участка цепи
Закон Ома
Напряжение находится по закону Ома по формуле I=U/R — чем больше сопротивление, тем меньше ток. Напряжение можно найти из этой же формулы. U=R*I, ток умножается на сопротивление. Запишем эту формулу для каждого участка U1=R1· I1, Un=Rn · In.
Законы Кирхгофа
Первый закон
Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два.
Рис. иллюстрация к пояснению действия первого закона Кирхгофа.
Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю. Если посмотреть на схему, I1 — это ток, который заходит в узел, I2 и I3 — это электроны, которые вытекают из него. Применяя формулировку первого закона можно записать формулу по-другому:
I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.
Второй закон Кирхгофа
Рис. иллюстрация к пояснению действия второго закона Кирхгофа.
Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре. E1- Е2 = — UR1 — UR2 или E1 = Е2 — UR1 — UR2.
Параллельное и последовательное соединение резисторов, решение задач
Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно.
Рис. Порядок замещения при расчете сложных позиций более простыми.
Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. Рассмотрим схему №1 на рис.
На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1).
Как же правильно определить параллельное и последовательное соединение резисторов?
Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.
Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом. Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше (рис 3).
Теперь образовалась ситуация — включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех.
Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом. Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.
Схема с подключением сопротивлений «треугольником»
Рис. Расчетная схема соединения резисторов в треугольник.
Иногда некоторые затруднения возникают при разборе схемы соединения в треугольник.
Рассмотрим на примере рисунка расчет резисторов по этому подключению. Из схемы видно, что R1 и R2 соединены последовательно Rэ12 будет соединяться R3 последовательно.
Затем Rэ123 соединяется с сопротивлением R4, R5 в последовательную цепь. Затем все это объединяется с Rэ в //.
Проведем несложные вычисления учитывая, что R1, R2, R4, R5 равняется 1 Ом. R3, R7 — 2 Ом.
RЭ1,2 = R1+R2 = 1+1=2 Ом.
Вычисляем параллельное подключение: Rэ 12 с R3. Rэ1,3 = (Rэ12*R3) /(Rэ12+R3) = (2*2) /(2+2) = 1Ом.
Далее мы видим последовательное: RЭ123 + R4 + R5 = 1+1+1 = 3 Ом. И последнее — Rэ123 4 5 с R6 — параллельное.
Общее сопротивление цепи Rц = Rоб = (RЭ1,2,3,4,5 *R6) /(RЭ1,2,3,4,5+R6) = (3 * 2) / (3+2) = 1,2 Ом. Как видно, что расчет подобного варианта также не сложный.
Расчет последовательного и параллельного подключения резисторов онлайн
Подсчитать значение мощность и сопротивлений подставляя их в формулы можно только в учебных целях, или, когда объемы не очень большие.
Наиболее практичный вариант расчета является онлайн калькуляторы, которые расположены на многочисленных интернет ресурсах.
Для расчёта любой сложности нужно правильно определить тип соединения резисторов последовательное или параллельное и внести данные для расчета в поля калькулятора.
Также такая форма расчета подойдет и для проверки результатов решения учебных задач.
Последовательное и параллельное соединение резисторов и конденсаторов
Электрические цепи состоят не только из резисторов, в них применяется большое количество различных деталей, например, конденсатор, которые подключаются в последовательное, // и смешанное соединение.
Рис. Замещения последовательно включенных элементов.
Определение этому элементу можно дать следующее: Конденсатор — это совокупность проводящих тел служащий для накопления электрического заряда. Элементарный конденсатор имеет две пластины, форма этих пластин может быть различной: сферической, круглой, цилиндрической, прямоугольной — по форме пластин разделяется и тип конденсатора.
Важное свойство. Одно из важных свойств конденсатора: если заряжается одна пластина конденсатора, то благодаря явлению электростатической индукции заряжается и вторая половина, но с противоположным знаком.
Устройство конденсатора
Плоский конденсатор состоит из двух плоских пластин отстоящих друг от друга на маленькое расстояние. У конденсатора к двум пластинам припаивается вывод всего их получается два.
Типовые схемы подключения конденсаторов
Рассмотрим различные виды подключения конденсатора.
Последовательное
Первый вид — это последовательное соединение. Предположим, что емкость этих конденсаторов будут равны.
Тогда заряды также будут равны: q1=q2=q3, как и в примере с резисторами, сложный тип позиций с конденсатором можно упростить, заменив несколько элементов одним.
У элементов соединенных друг за другом, общая емкость будет обратно пропорциональная всем имеющимся элементам. То есть: Rэк будет равняться 1/С1 + 1/С2 +…. 1/Сn/
Напряжение складывается, U эк = U1 + U2+ … Un.
Параллельное
Второй тип подключения конденсаторов — это соединение в паралель
Рис. Схема замещения элементов, включенных в параллель.
- Соответственно эти конденсаторов обозначены C1, C2, … Cn заряды: Q1, Q2, … Qn и напряжение: U1, U2, … Un.
- У элементов в // емкость складывается Сэ = C1 + C2 + … C n. Напряжение Un на каждом конденсаторе будет равно напряжению на эквивалентном
- Uэ = U1 = U2 =… = Un — это особенность параллельного подсоединения всех элементов цепи.
- Емкость будет складываться из суммы отдельных элементов Сэ =С1 + С2 + … Сп.
Рис. Расчетные позиции элементов при различном включении.
Простая позиция, которая не требует преобразования №1 — последовательное подключение. По известной формуле для этих поз. запишем 1/Сэ = 1/С1 +1/С2 +1/С3, подставив формулу значения, которые даны в условии задачи, получим 1/Сэ = 1/С1 +1/С2 +1/С3 = 59 мФ.
Не требует преобразования и 2 схема: емкость общего конденсатора будет равняться сумме конденсаторов которые включены в параллельной цепи: Сэ =С1 +С2 +С3 Сэ = 100 + 200 + 500 = 800 мФ.
Рассмотрев рис. №3 видно, что пара конденсаторов включена параллельно и один последовательно. Алгоритм преобразования таких цепей мы уже рассматривали, поэтому: сразу же находим емкость конденсатора Сэ соединения: Сэ = С1+С2 = 200+500 = 700 мФ.
Теперь находим общие эквивалентную емкость элементов с последовательным подключением 1/Сэ = 1/С2,3 +1/ С1 = 89 мф. Практическая задача решена.
Источник: http://themechanic.ru/posledovatelnoe-i-parallelnoe-soedinenie-rezistorov/
Соединение резисторов
Радиоэлектроника для начинающих
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно.
Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов
- В жизни последовательное соединение резисторов имеет вид:
- Последовательно соединённые резисторы серии МЛТ
- Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
- Общее номинальное сопротивление составного резистора обозначено как Rобщ.
- Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
- Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Что это значит?
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом.
Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом.
Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов
- Можно соединять резисторы и параллельно:
- Два резистора МЛТ-2, соединённых параллельно
- Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
- Замер общего сопротивления при последовательном соединении
- Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
- Измерение сопротивления при параллельном соединении
- Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Главная » Радиоэлектроника для начинающих » Текущая страница
Также Вам будет интересно узнать:
Источник: https://go-radio.ru/connection-of-resistors.html
Параллельное соединение резисторов
Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов. Сегодня я бы хотел вам рассказать про другой возможный вид соединения – параллельное.
Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье. Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам .
- А) – Последовательное соединение
- В) – Параллельное соединение
- Рисунок 1 – Последовательное и параллельное соединение
- Как мы видим из рисунка 1, параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.
Сейчас наша задача будет разобраться, как ведут себя токи, напряжения, сопротивления и мощности при таком подключении. Для этого прошу вас взглянуть на рисунок 2, где подробно разрисован расклад дел для параллельного соединения. Будем полагать, что мы знаем величины R1, R2 и R3, а также величину приложенного к схеме напряжения U. Про токи же мы ничего не знаем.
Рисунок 2 – Параллельное соединения
Что мы видим на рисунке 2? Ну, в первую очередь – два узла А и B. В узел А сходятся одни концы всех резисторов, а в узел В – другие концы. Пусть узел А имеет потенциал φ1, а узел В – потенциал φ2. Из рисунка 2 видно, что для всех резисторов R1, R2 и R3 у нас одна и та же разность потенциалов U.
Как следует из статьи про потенциалы, это означает, что напряжение на всех резисторах у нас одинаково и равно приложенному напряжению U. Это важный вывод, его следует хорошо запомнить.
С токами дело обстоит по-другому. Проанализируем рисунок 2 слева направо. Пусть у нас в цепи течет ток I. Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа? А то, что ток I в узле А разделится на три тока I1, I2, I3. При этом будет выполняться равенство
То есть через резистор R1 будет протекать ток I1, через резистор R2 – ток I2, а через резистор R3 – ток I3.
Итак, у нас в системе уже тихо-мирно текут себе три тока. И все хорошо, пока они не наткнуться на узел В. Тут снова вступает в силу первый закон Кирхгофа. Эти три тока I1, I2, I3 вновь соединятся в один ток I. Причем после узла В ток будет иметь такую же величину I, какой он был до узла А.
То есть если все вышесказанное воплотить в лаконичный язык наскальной живописи, положение дел можно представить себе вот так
Как же найти эти самые токи I1, I2, I3? Господа, полагаю, вы уже догадались, что на помощь нам придет горячо нами всеми любимый закон Ома. Действительно, мы знаем сопротивления резисторов и, кроме того, нам известно, что на всех них падает одно и тоже напряжение U. Поэтому легко находим токи
Отлично, мы разобрались с напряжениями и с токами в такой схеме. А помните в статье про последовательное сопротивление мы ловко преобразовали три резистора в один с эквивалентным им сопротивлением? Нельзя ли и здесь сделать что-то подобное? Оказывается, вполне себе можно. Как мы помним, токи в схеме распределены таким вот образом
- Обзовем эквивалентное сопротивление буковкой R. И подставим в это выражение только что найденные нами токи I1, I2, I3
- Видим, что здесь без проблем можно сократить левую и правую части на U. Получаем
- Господа, важный вывод: при параллельном соединении резисторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных резисторов.
- То есть для упрощения различных расчетов электрических схем такую вот цепочку параллельно соединенных резисторов можно заменить одним резистором с соответствующим сопротивлением, как показано на рисунке 3.
- Рисунок 3 – Преобразование параллельного соединение
Весьма частый случай на практике, когда соединены параллельно не много резисторов, а всего два. Поэтому полезно знать наизусть итоговое сопротивление такой схемы. Давайте посмотрим, чему оно равно:
То есть, если у вас два сопротивления соединены параллельно, то по этой формуле вы легко высчитаете общее сопротивление. Рассмотрим пример. Пусть у нас параллельно соединены два резистора 10 кОм и 15 кОм. Чему равно их общее сопротивление?
Заметьте, господа, итоговое сопротивление у нас получилось 6 кОм, что меньше 10 кОм и 15 кОм. То есть при параллельном соединении общее сопротивление меньше любого из составляющих.
Это всегда верно для любого количества резисторов, а не только для двух. Итоговое сопротивление всегда уменьшается (в отличии от последовательного сопротивления, где итоговое сопротивление всегда растет).
Этот факт полезно запомнить.
Еще один часто встречающийся на практике случай – когда параллельно соединены несколько резисторов с одинаковым сопротивлением. Допустим, каждый из них обладает сопротивлением R1 и всего их N штук. Тогда по нашей общей формуле для эквивалентного сопротивления
- То есть при параллельном соединении N одинаковых резисторов с сопротивлением R1 итоговое сопротивление будет в N раз меньше этого самого сопротивления R1.
- Так-с, с током разобрались, с напряжением разобрались, с эквивалентным сопротивлением вроде тоже…осталась мощность. Для этого воспользуемся вот этим выражением, которое мы писали чуть выше в статье
- Умножим левую и правую части на напряжение U.
- Как мы помним из статьи про мощность произведение тока на напряжение есть мощность. То есть мы можем записать
- где Р – мощность, выдаваемая источником;
- P1 – мощность, рассеиваемая на резисторе R1;
- P2 – мощность, рассеиваемая на резисторе R2;
- P3 – мощность, рассеиваемая на резисторе R3.
Заметьте, господа, формула в точности такая же, как и для случая последовательного соединения резисторов. И там и там мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на резисторах цепи.
Итак, господа, мы рассмотрели основные соотношения при параллельном соединении резисторов. Теперь осталось поговорить, где это параллельное соединение можно использовать и для чего.
1) Ну, во-первых, параллельное соединение применяют во всех случаях, когда хотят запитать несколько нагрузок от одного источника напряжения. При этом пользуются тем свойством, что при параллельном соединении напряжения на всех нагрузках одинаково.
То есть, допустим, вы берете источник напряжения, выставляете на нем напряжение 5 В и цепляете к этому источнику сразу несколько своих устройств. Узлами А и В в этом случае будут клеммы источника. На каждое из устройств в этом случае придет напряжение 5 В.
Да и все устройства в вашей квартире (лампочки, компьютеры, телевизоры и все прочее) соединены между собой параллельно.
2) Второе возможное применение встречается не так часто, но, думаю, о нем тоже следует рассказать. Допустим, вы делаете какую-то схему, где необходим очень точный подгон сопротивления. Скажем, надо получить сопротивление 6 кОм. Такое сопротивление найти нелегко, их просто не продают. Зато у вас есть два сопротивления 10 кОм и 15 кОм.
Вы их соединяете параллельно и получаете требуемые 6 кОм. Как показывает практика, 3 параллельных резисторов достаточно для получения итогового результирующего сопротивления требуемого номинала с весьма хорошей точностью. Конечно, таких вещей лучше избегать и, если есть возможность, всегда стараться применять стандартные сопротивления.
Но бывают случаи, когда это невозможно, и тогда приходит на помощь этот метод.
3) Третий пункт будет немного похож на первый. Его суть заключается в следующим. Допустим, нам надо снять с источника питания 10 Вт мощности. А у нас в наличии только резисторы, которые позволяют рассеивать на себе 1 Вт. Что делать? Можно соединить 10 резисторов параллельно и с каждого снимать по 1 Вт. Мы же помним нашу формулу
Конечно, лучше брать не 10 резисторов, а хотя бы 15 и рассеивать на них меньше, чем 1 Вт. Работать на пределе никогда не следует.
Кстати, тут очень вовремя к моменту написания статьи пришли платы с производства! Господа, прошу вас взглянуть на рисунок 4.
Рисунок 4 – Плата нагревателя
На нем изображена плата нагревателя (флешка для масштаба). В чем суть? Имеется весьма сложное устройство, предназначенное для работы в арктических условиях.
Найти же компоненты, которые надежно функционировать при температурах минус 55 градусов и при этом стоят адекватных денег и обладают адекватными размерами бывает непросто. Обычно элементная база в лучшем случае рассчитана на минус 40 градусов.
И было принято решение разработать вот такой вот нагреватель для прогрева чувствительных к холоду аналоговых узлов устройства. Он управляется с микроконтроллера и автоматически включается при температурах меньше минус 40 градусов.
Как вы можете видеть из рисунка 4, этот нагреватель представляет собой 30 параллельно соединенных резисторов с сопротивлениями 150 Ом. Каждый резистор, согласно документации, способен рассеивать до 1 Вт мощности. Используя изученные формулки, мы можем посчитать, что в сумме такая система обладает сопротивлением
- и теоретически может рассеивать мощность
Ну, с сопротивлением вопросов нет, оно действительно равно 5 Ом. Ну, плюс-минус 5 % на допуск резисторов, что в данном случае вообще не критично. А вот с мощностью тут не так все однозначно. Помните про закон Джоуля-Ленца, который мы рассматривали? Резисторы будут греться, причем не слабо.
Как показывает практика, если нагружать резисторы по полной, то есть рассеивать на каждом по 1 Вт, то в течении нескольких секунд их температура улетит за 150 градусов. Такая высокая температура критична для резистора и может привести к его разрушению.
Я был готов к такому развитию событий, поэтому заложил для платы нагревателя максимальное напряжение 9 вольт. Это значит, что на каждом резисторе будет выделяться
- что почти в два раза меньше максимально допустимой мощности в 1 Вт. В сумме на всей плате выделялось, соответственно
Эксперимент показал, что резисторы достигли температуры с комнатных 25 градусов до критичных 120 градусов приблизительно за 10 секунд работы и температура продолжала уверенно расти.
Очевидно, если оставить на длительное время включенным такой нагреватель при комнатной температуре, он неминуемо выйдет из строя.
Возможно, при работе на минус 55 градусах перегрев бы не был столь критичным, однако хотелось исключить вариант спалить плату на столе, поэтому я понизил напряжение, подаваемое на плату на 3 вольта: стал подавать 6 вольт. Теперь на каждом резисторе рассеивалось
- а на всей плате
Теперь температура поднималась до 100-110 градусов примерно за 30-40 секунд работы и оставалась на этом уровне (выходила в точку термодинамического равновесия). Эта температура вполне подходит для нагревателя.
Однако пока это были лишь эксперименты на столе при комнатной температуре, главный эксперимент – в термокамере на минус 55 градусах – впереди. Возможно, по его результатам потребуется чуть увеличить рассеиваемую мощность.
А может все останется как есть и этой мощности будет достаточно для вывода девайса на режим за адекватное время, время покажет .
На сегодня все, господа. Удачи вам и до новых встреч!
Источник: http://myelectronix.ru/postoyannyy-tok/40-parallelnoe-soedinenie-rezistorov
Как отличается параллельное и последовательное соединение резисторов?
Большое разнообразие схем основано на двух видах соединений – последовательное параллельное. Для каждого типа существуют свои собственные законы и принципы. Именно это и позволяет создавать устройства с самыми различными техническими параметрами, в том числе и резисторы. Что же такое резистор?
Резистор – радиодеталь, созданная для контроля напряжения и тока в цепи, увеличивая либо понижая его. Резисторы могут быть двух видов – постоянные и переменные. Так, например, светодиоды требуют для себя совсем небольшого тока. Для этого в электрическую цепочку перед светодиодом устанавливается резистор, который обеспечивает необходимое напряжение для работы последнего.
В статье подробны рассмотрены все аспекты последовательного и параллельного подключения резисторов. Бонусом к статье являются видеоролик и детальная информационная статья на рассматриваемую тему.
Последовательное подключение
Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше. Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.
Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях — складываем, в параллельных — это обратно пропорциональная величина.
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).
Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.
Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Последовательное подключение.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Будет интересно➡ SMD резисторы: что это такое и для чего используются?
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.
Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Материал по теме: Как проверить варистор мультиметром.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Параллельное подключение резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.
То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков».
То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи.
В случае с параллельным соединением резисторов — от их номинала.
Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.
Схема параллельного соединения
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна.
Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно.
Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала.
Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.
Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Параллельное соединение резисторов
Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи.
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn.
Формулы расчета параллельного и последовательного подключения.
Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора. Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле: Rобщ= R1*R2/R1+R2.
Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.
Заменяя лампы резисторами с сопротивлениями R1, R2, R3, При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома: I1=U/R1; I2=U/R2; I3=U/R3.
Источник: https://ElectroInfo.net/radiodetali/rezistory/kak-otlichaetsja-parallelnoe-i-posledovatelnoe-soedinenie-rezistorov.html
Параллельная схема: характеристики, преимущества и недостатки
Параллельное соединение проводников
Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
| Рисунок 4. Схема параллельного соединения проводников |
Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:
I = I1 + I2 + I3.
Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:
то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа. Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.
Видео 2. Первый закон Кирхгофа
Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.
Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.
Общий ток, приходящий к точке А, равен:
Токи в каждой из ветвей имеют значения:
По формуле первого закона Кирхгофа
I = I1 + I2 + I3
или
Вынося U в правой части равенства за скобки, получим:
Сокращая обе части равенства на U, получим формулу подсчета общей проводимости:
или
g = g1 + g2 + g3.
Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость.
Пример 3. Определить общее сопротивление трех параллельно включенных сопротивлений, если r1 = 2 Ом, r2 = 3 Ом, r3 = 4 Ом.
откуда
Пример 4. Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:
откуда
Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.
Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r1, деленному на число ветвей n:
Пример 5. Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:
Для проверки попробуем найти сопротивление разветвления по формуле:
откуда
Как видим, ответ получается тот же.
Пример 6. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а.
| Рисунок 5. К примеру 6 |
Найдем общее сопротивление цепи:
откуда
Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б).
Падение напряжения на участке между точками А и Б будет:
U = I × r = 22 × 1,09 = 24 В.
Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А и Б.
Рассматривая первую ветвь разветвления с сопротивлением r1, мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:
Ток второй ветви
Ток третьей ветви
Проверим по первому закону Кирхгофа
I = I1 + I2 + I3 = 12 + 6 + 4 = 22 А.
Следовательно, задача решена верно.
Обратим внимание на то, как распределяются токи в ветвях нашего параллельного соединения. Первая ветвь: r1 = 2 Ом, I1 = 12 А
Вторая ветвь: r2 = 4 Ом, I2 = 6 А. Третья ветвь: r3 = 6 Ом, I3 = 4 А
Первая ветвь: r1 = 2 Ом, I1 = 12 А. Вторая ветвь: r2 = 4 Ом, I2 = 6 А. Третья ветвь: r3 = 6 Ом, I3 = 4 А.
Как видим, сопротивление первой ветви в два раза меньше сопротивление второй ветви, а ток первой ветви в два раза больше тока второй ветви. Сопротивление третьей ветви в три раза больше сопротивления первой ветви, а ток третьей ветви в три раза меньше тока первой ветви. Отсюда можно сделать вывод, что токи в ветвях при параллельном соединении распределяются обратно пропорционально сопротивлениям этих ветвей. Таким образом, по ветви с большим сопротивлением потечет ток меньший, чем по ветви с малым сопротивлением.
Для двух параллельных ветвей можно также, конечно, пользоваться данной выше формулой.
Однако общее сопротивление проводника при параллельном соединении в этом случае легче подсчитать по формуле:
или окончательно:
Последовательное соединение ламп накаливания.
Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.
Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.
Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.
Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.Но повторюсь – это редкий случай.
Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания. В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.
Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.
Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.
Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.
На следующем рисунке показаны три лампы соединенные последовательно.
На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.
Так же примером последовательного соединения могут служить новогодние гирлянды. Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.
Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.
P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.
Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.
Вывод:
Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.
А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.
Первый закон Кирхгофа
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Примеры использования
- Батареи гальванических элементов или аккумуляторов, в которых отдельные химические источники тока соединены последовательно (для увеличения напряжения) или параллельно (для увеличения тока).
- Регулировка мощности электрического устройства, состоящего из нескольких одинаковых потребителей электроэнергии, путём их переключения с параллельного на последовательное соединение. Таким способом регулируется мощность конфорки электрической плиты, состоящей из нескольких спиралей; мощность (скорость движения) электровоза, имеющего несколько тяговых двигателей.
- Делитель напряжения
- Балласт
- Шунт
Какой способ лучше?
Метод «шлейфов» не слишком удобен только тем, что любой потребитель по цепи зависит от предыдущего. Например, если произойдёт обрыв провода на второй розетке, то третья и четвёртая также останутся без напряжения. Но при этом нельзя не выделить экономию проводника при начальном монтаже электропроводки.
Рисунок 3: Комбинированное соединение розеток
К тому же, «шлейфом» очень удобно проводить линии, когда необходимо минимизировать количество штроб в стенах. А делают это при монтаже проводки по полу или потолку, в специальной гофрированной трубе. Тогда остаётся провести только основные штробы к розеткам и между ними.
Вывод: прокладка электропроводки «шлейфом» удобна и экономична, не занимает много времени в процессе монтажа, имеет длительный эксплуатационный срок и совсем незначительные недостатки, которые можно оставить без внимания.
Последовательное соединение ламп накаливания.
Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.
Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.
Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.
Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.Но повторюсь – это редкий случай.
Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания. В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.
Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.
Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.
Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.
На следующем рисунке показаны три лампы соединенные последовательно.
На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.
Так же примером последовательного соединения могут служить новогодние гирлянды. Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.
Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.
P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.
Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.
Вывод:
Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.
А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.
Как выглядит формула Георга Ома
Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.
Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:
U1 = U2 = U.
Схема параллельного соединения
Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:
I = I1 + I2.
Расчет силы тока при помощи закона Ома записывается как:
I = U/R;
I1 = U1/R1;
I2 = U2/R2.
Из формулы следует:
U/R = U1/R1 + U2/R2;
U = U1 = U2;
1/R = 1/R1 + 1/R2.
Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * . Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
- Таким образом, протекающий общий ток в цепи можно определить как:
- I = I1 + I2
- Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
- Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
- Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
- Таким образом, общий ток будет равен:
- I = 0,545 мА + 0,255 мА = 0,8 мА
- Это также можно проверить, используя закон Ома:
- I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
- где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
- И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Последовательное соединение источников питания
Теперь давайте представим вот такую ситуацию. Что будет, если в нашей обрезанной водобашне полной воды добавим еще одну такую же сверху полную воды? Схематически это будет выглядеть примерно вот так:
Как вы думаете, уменьшится давление на землю, или увеличится? Понятное дело, что увеличится! Да еще и ровно в два раза! Почему так произошло? Уровень воды стал выше, следовательно, давление на дно увеличилось.
Если “минус” одной батарейки соединить с “плюсом” другой батарейки, то их общее напряжение суммируется.
Полностью заряженная батарейка будет выглядеть как башня, полностью залитая водой с учетом того, что работает насос автоматической подачи воды. По аналогии, насос – это ЭДС.
Наполовину разряженная батарейка будет уже выглядеть примерно вот так:
Можно сказать, насос уже не справляется.
Батарейка посаженная в “ноль” будет выглядеть вот так:
Насос автоматической подачи воды сломался.
Естественно, что если вы соедините полностью заряженную и наполовину дохлую батарейку последовательно, то их общее напряжение будет выглядеть примерно вот так:
Давайте все это продемонстрируем на практике. Итак, у нас есть 2 литий-ионных аккумулятора. Я их пометил цифрами 1 и 2. С плюса каждого аккумулятора я вывел красный провод, а с минуса – черный.
Давайте замеряем напряжение аккумулятора под №1 с помощью мультиметра. Как это сделать, я еще писал в статье Как измерить ток и напряжение мультиметром.
На первом аккумуляторе у нас напряжение 3,66 Вольт. Это типичное значение литий-ионного аккумулятора.
Таким же способом замеряем напряжение на аккумуляторе №2
О, как совпало). Те же самые 3,66 Вольт.
Для того, чтобы соединить последовательно эти аккумуляторы, нам надо сделать что-то подобное:
Также как и в башнях, нам надо соединить основание одной башни с верхушкой другой башни. В источниках питания, типа аккумуляторов или батареек, нам надо соединить минус одной батарейки с плюсом другой. Так мы и сделаем. Соединяем плюс одной батарейки с минусом другой и получаем… сумму напряжений каждой батарейки! Как вы помните, на первой батарейке у нас было напряжение 3,66 В, на второй тоже 3,66 В. 3,66+3,6=7,32 В.
Мультиметр показывает 7,33 В. 0,01В спишем на погрешность измерений.
Это свойство прокатывает не только с двумя аккумуляторами, но также с их бесконечным множеством. Думаю, не стоит говорить, что если выставить в ряд штук 100 таких аккумуляторов, соединить последовательно и коснуться крайних полюсов голыми руками, то все это может завершиться даже летальным исходом.
Оцените статью:Калькулятор параллельных сопротивлений • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов.
Пример. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно.
Входные данные
Добавить резистор
Выходные данные
Эквивалентное сопротивление
R ом (Ом)
Введите величины сопротивлений в поля R1, R2 и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы сопротивления в миллиомах (мОм), омах (Ом), килоомах (кОм) или мегаомах (МОм) и нажмите кнопку Рассчитать.
1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.
Эквивалентное сопротивление Req группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.
или
Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:
Эта формула для Req и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:
Если параллельно соединены только два резистора, формула упрощается:
или
Если имеется n соединенных параллельно одинаковых резисторов R, то их эквивалентное сопротивление будет равно
Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.
При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.
Различные постоянные и переменные резисторы
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Установленный в мультиметре шунт для измерения ток до 20 ампер. Отметим, что если этим мультиметром измеряется большой ток непрерывно более 10 секунд, шунт перегреется и его сопротивление изменится, что приведет к ошибке измерения
Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Резисторы поверхностного монтажа на печатной плате
Параллельное соединение резисторов таблица. Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление , используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
R(общ)=R1*R2/R1+R2.
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Универсальная схема расчета
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.
Пример расчета
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Заключение
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.
Сопротивление проводника
Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.
Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.
При расчёте сопротивления используется известная из школьного курса физики формула:
R = ρ · l/S, S — площадь сечения; l — длина.
Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.
и нагрев проводника
Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:
δ = I/S, I — ток, S — сечение.
Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.
Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.
Правилами регламентируется производить расчёт проводников на нагрев.
Способы соединения проводников
Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.
На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .
Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.
Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.
Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.
Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.
R2,3,4 = R2,3 · R4/(R2,3 + R4).
Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.
Виды проводников
В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.
Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.
Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.
Расчёт проводов на нагрев
Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).
На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.
Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.
Расчёт проводников на потерю напряжения
При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.
Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.
R л = ρ · 2L/S,
Здесь S — сечение провода линии, мм 2 .
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.
С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Виды соединений
Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:
- Постоянные.
- Переменные.
Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:
- Последовательное.
- Параллельное.
- Смешанное.
Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.
Последовательное соединение проводников
В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.
Примером последовательного соединения проводников в быту является ёлочная гирлянда.
Параллельное соединение резисторов
При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.
Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.
В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.
Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.
Примеры параллельного соединения проводников:
- Освещение.
- Розетки в квартире.
- Производственное оборудование.
Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.
Смешанное соединение проводников
Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.
В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.
Формулы и калькулятор »Электроника
Формулы, расчеты и калькулятор для определения общего сопротивления резисторов, установленных последовательно и параллельно.
Учебное пособие по сопротивлению Включает:
Что такое сопротивление
Закон Ома
Омические и неомические проводники
Сопротивление лампы накаливания
Удельное сопротивление
Таблица удельного сопротивления для распространенных материалов
Температурный коэффициент сопротивления
Электрическая проводимость
Последовательные и параллельные резисторы
Таблица параллельных резисторов
Резисторы могут быть размещены во многих конфигурациях в электрической или электронной схеме — иногда последовательно, иногда параллельно.
Когда они размещаются в этих конфигурациях, важно иметь возможность рассчитать общее сопротивление. Этого можно довольно легко добиться, если использовать правильные формулы — есть простые формулы как для последовательных, так и для параллельных резисторов.
При проектировании электронной схемы или по другой причине возможность вычисления сопротивления комбинации резисторов может быть очень полезной.
В электронных схемах комбинации резисторов могут быть сведены к последовательным элементам и параллельным элементам, хотя при использовании других электронных компонентов комбинации могут быть более сложными.Однако во многих случаях расчет значений последовательного и параллельного сопротивления имеет большое значение.
Резисторы серии
Самая простая конфигурация электронной схемы — это резисторы, включенные последовательно. Это может произойти, если несколько этих электронных компонентов соединены последовательно, или необходимо добавить сопротивление кабеля к сопротивлению резистора и т. Д.
Если резисторы соединены последовательно, то общее сопротивление является просто суммой отдельных резисторов.
Последовательные резисторыВеличину резисторов или сопротивлений, включенных последовательно, можно математически выразить следующим образом:
Пример расчета последовательных резисторов:
В качестве примера, если три резистора, имеющие номиналы 1 кОм, 2 кОм и 3 кОм, соединены последовательно, то общее сопротивление составит 1 + 2 + 3 кОм = 6 кОм.
В реальных жизненных ситуациях и аспектах проектирования электрических и электронных схем будет много областей, где есть электронные компоненты, такие как резисторы или другие элементы, вносящие сопротивление, где количество последовательно соединенных сопротивлений, которые необходимо суммировать.
Резисторы параллельно
Есть также много случаев, когда электронные компоненты, такие как резисторы, а также другие элементы, вызывающие сопротивление, появляются в электрической или электронной цепи параллельно.
Если резисторы размещены параллельно, они разделяют ток, и ситуацию немного сложнее рассчитать, но все же довольно легко.
1Rtotal = 1R1 + 1R2 + 1R3 + ……
Пример расчета сопротивления резисторов, включенных параллельно:
Чтобы дать пример, если есть три резистора, подключенных параллельно со значениями 1 кОм, 2 кОм и Омега и 3 кОм, то можно вычислить общее значение комбинации:
1 / R Итого = 1/1000 + 1/2000 + 1/3000
1 / R Итого = 1/1000 + 1/2000 + 1/3000
1 / R Итого = 6/6000 + 3/6000 + 2/6000
1 / R Итого = 11/6000
R Всего = 6000/11 Ом или 545 Ом
Корпус только двух резисторов, включенных параллельно
Во многих конструкциях электронных схем наиболее распространенный экземпляр параллельных резисторов состоит только из двух электронных компонентов.
Часто бывает так, что один резистор подключается параллельно другому. Или другой случай может быть, когда резистор помещается на клеммы для цепи или сети, которая имеет определенное сопротивление. В этом случае необходимо только рассчитать общее сопротивление для двух параллельно включенных резисторов.
Если необходимо рассчитать общее значение для двух параллельных резисторов, уравнением можно манипулировать и значительно упростить его, как показано ниже:
Эта формула значительно упрощает вычисление номинала двух параллельных резисторов, так как требует только одного умножения, одного сложения и одного деления.Часто это можно сделать мысленно или на клочке бумаги. В качестве альтернативы можно использовать наш простой калькулятор для двух параллельно включенных резисторов, приведенный ниже.
Калькулятор для двух резисторов, включенных параллельно
Этот калькулятор параллельного сопротивления обеспечивает простой метод расчета общего сопротивления для двух резисторов, соединенных параллельно.
Хотя вычисление номиналов параллельных резисторов для двух резисторов упрощается до простой формулы, иногда гораздо проще и быстрее использовать калькулятор.
Чтобы использовать калькулятор параллельных резисторов, просто введите значения параллельных резисторов в Ом, Ом или кОм и т. Д. В два поля ввода, но обратите внимание, что все значения должны быть в одних и тех же единицах, то есть оба в Ом кОм МОм и т. Д. Затем вычислитель параллельных резисторов предоставит общее сопротивление двух резисторов в тех же единицах, что и вход.
Введите два значения для резисторов, R1 и R2, в поля, представленные в калькуляторе ниже, нажмите «Расчет», и будет предоставлено общее сопротивление.
Калькулятор параллельного сопротивления
Калькулятор параллельных резисторов обеспечивает простой способ рассчитать сопротивление двух резисторов, включенных параллельно, экономя записывать все и прибегая к ручке и бумаге или калькулятору какой-либо формы.
Знание того, как рассчитать значения резисторов, включенных последовательно и параллельно, является ключом к пониманию того, как работают электрические и электронные схемы. Эти концепции используются как вторая натура при проектировании электрических и электронных схем.
Другие основные концепции электроники:
Напряжение
Текущий
Мощность
Сопротивление
Емкость
Индуктивность
Трансформеры
Децибел, дБ
Законы Кирхгофа
Q, добротность
Радиочастотный шум
Вернуться в меню «Основные понятия электроники». . .
10.3: Последовательные и параллельные резисторы
Цели обучения
К концу раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)).В последовательной схеме выходной ток первого резистора течет на вход второго резистора; следовательно, ток одинаков в каждом резисторе. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Рисунок \ (\ PageIndex {1} \): (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое.Резисторы серии
Считается, что резисторывключены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \).Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.На рисунке \ (\ PageIndex {2} \) ток, исходящий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор. Согласно закону Ома, падение потенциала \ (V \) на резисторе при протекании через него тока рассчитывается с использованием уравнения \ (V = IR \), где \ (I \) — ток в амперах (\ (A \)), а \ (R \) — сопротивление в Ом \ ((\ Omega) \).N V_i = 0. \]
Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе. На рисунке \ (\ PageIndex {2} \) сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
\ [\ begin {align *} V — V_1 — V_2 — V_3 & = 0, \\ [4pt] V & = V_1 + V_2 + V_3, \\ [4pt] & = IR_1 + IR_2 + IR_3, \ end { выровнять *} \]
Решение для \ (I \)
\ [\ begin {align *} I & = \ frac {V} {R_1 + R_2 + R_3} \\ [4pt] & = \ frac {V} {R_ {S}}.\ end {align *} \]
Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления (\ (R_ {S} \)), которое представляет собой просто сумму сопротивлений отдельных резисторов. N R_i.\ label {серия эквивалентных сопротивлений} \]
Одним из результатов подключения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что внутреннее сопротивление батареи незначительно.
- Рассчитайте эквивалентное сопротивление цепи.
- Рассчитайте ток через каждый резистор.
- Рассчитайте падение потенциала на каждом резисторе.
- Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Решение
- Эквивалентное сопротивление — это алгебраическая сумма сопротивлений (Уравнение \ ref {серия эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 10 \, \ Омега = 90 \, \ Омега.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W. \ nonumber \]
Значение
Есть несколько причин, по которым мы использовали бы несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серию по девять луковиц.Если перегорает слишком много лампочек, в конечном итоге открываются шунты. Что вызывает это?
- Ответ
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление будет 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \). Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к сгоранию шунта.№ Р_и. \]
- Один и тот же ток последовательно проходит через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке \ (\ PageIndex {4} \) показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Рисунок \ (\ PageIndex {4} \): Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.Ток, протекающий от источника напряжения на рисунке \ (\ PageIndex {4} \), зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы \ (R_1 \) и \ (R_2 \). По мере того, как заряды идут от аккумулятора, некоторые проходят через резистор \ (R_1 \), а некоторые — через резистор \ (R_2 \).Сумма токов, текущих в переход, должна быть равна сумме токов, текущих из перехода:
\ [\ sum I_ {in} = \ sum I_ {out}. {- 1}.{-1}. \ label {10.3} \]
Это соотношение приводит к эквивалентному сопротивлению \ (R_ {P} \), которое меньше наименьшего из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример \ (\ PageIndex {2} \): Анализ параллельной цепи
Три резистора \ (R_1 = 1,00 \, \ Omega \), \ (R_2 = 2,00 \, \ Omega \) и \ (R_3 = 2,00 \, \ Omega \) подключены параллельно.Параллельное соединение подключается к источнику напряжения \ (V = 3,00 \, V \).
- Какое эквивалентное сопротивление?
- Найдите ток, подаваемый источником в параллельную цепь.
- Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.
- Рассчитайте мощность, рассеиваемую каждым резистором.
- Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью уравнения \ ref {10.3}. (Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив \ (R_ {P} \) на полное сопротивление \ (I = \ frac {V} {R_ {P}} \).
(c) Отдельные токи легко вычислить по закону Ома \ (\ left (I_i = \ frac {V_i} {R_i} \ right) \), поскольку каждый резистор получает полное напряжение.{-1} = 0,50 \, \ Omega. \ Nonumber \] Общее сопротивление с правильным количеством значащих цифр равно \ (R_ {eq} = 0,50 \, \ Omega \). Как и предполагалось, \ (R_ {P} \) меньше наименьшего индивидуального сопротивления.
- Полный ток можно найти из закона Ома, заменив полное сопротивление \ (R_ {P} \). Это дает \ [I = \ frac {V} {R_ {P}} = \ frac {3.00 \, V} {0.50 \, \ Omega} = 6.00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
- Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом, \ [I_1 = \ frac {V} {R_1} = \ frac {3.00 \, V} {1.00 \, \ Omega} = 3.00 \, A. \ nonumber \] Аналогично, \ [I_2 = \ frac {V } {R_2} = \ frac {3.00 \, V} {2.00 \, \ Omega} = 1.50 \, A \ nonumber \] и \ [I_3 = \ frac {V} {R_3} = \ frac {3.00 \, V } {2.00 \, \ Omega} = 1.50 \, A. \ nonumber \] Полный ток — это сумма отдельных токов: \ [I_1 + I_2 + I_3 = 6.2} {2.00 \, \ Omega} = 4.50 \, W. \ nonumber \]
- Общую мощность также можно рассчитать несколькими способами. Выбор \ (P = IV \) и ввод общей текущей доходности \ [P = IV = (6.00 \, A) (3.00 \, V) = 18.00 \, W. \ nonumber \]
Значение
Общая мощность, рассеиваемая резисторами, также 18,00 Вт:
\ [P_1 + P_2 + P_3 = 9,00 \, W + 4,50 \, W + 4,50 \, W = 18,00 \, W. \ nonumber \]
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
Упражнение \ (\ PageIndex {2A} \)
Рассмотрим одну и ту же разность потенциалов \ ((V = 3,00 \, V) \), приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
- Раствор
Эквивалент последовательной схемы будет \ (R_ {eq} = 1.00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Упражнение \ (\ PageIndex {2B} \)
Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?
- Раствор
Река, текущая по горизонтали с постоянной скоростью, разделяется на две части и течет через два водопада. Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение — это потенциальная энергия на каждом резисторе.
При рассмотрении энергии аналогия быстро разрушается. В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
Суммируем основные характеристики резисторов параллельно:
- Эквивалентное сопротивление находится по формуле \ ref {10.3} и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, входящий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Как вы помните, в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. Таблица \ (\ PageIndex {1} \) суммирует уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
Таблица \ (\ PageIndex {1} \): сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях Комбинация серий Параллельная комбинация Эквивалентная емкость \ [\ frac {1} {C_ {S}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +.N R_i \ nonumber \] \ [\ frac {1} {R_ {P}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +. . . \ nonumber \] Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учесть сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного подключения можно свести к одному эквивалентному сопротивлению, используя технику, показанную на рисунке \ (\ PageIndex {5} \).Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Рисунок \ (\ PageIndex {5} \): (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, и эквивалентное сопротивление равно \ (R_ {34} = 10 \, \ Omega \). (c) Шаг 2: сокращенная схема показывает, что резисторы \ (R_2 \) и \ (R_ {34} \) включены параллельно, с эквивалентным сопротивлением \ (R_ {234} = 5 \, \ Omega \).(d) Шаг 3: сокращенная схема показывает, что \ (R_1 \) и \ (R_ {234} \) включены последовательно с эквивалентным сопротивлением \ (R_ {1234} = 12 \, \ Omega \), которое является эквивалентное сопротивление \ (R_ {eq} \). (e) Уменьшенная схема с источником напряжения \ (V = 24 \, V \) с эквивалентным сопротивлением \ (R_ {eq} = 12 \, \ Omega \). Это приводит к току \ (I = 2 \, А \) от источника напряжения.Обратите внимание, что резисторы \ (R_3 \) и \ (R_4 \) включены последовательно. Их можно объединить в одно эквивалентное сопротивление.Один из методов отслеживания процесса — включить резисторы в качестве индексов. {- 1} = 5 \, \ Omega.\ nonumber \]
Этот шаг процесса сокращает схему до двух резисторов, как показано на рисунке \ (\ PageIndex {5d} \). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
\ [R_ {eq} = R_ {1234} = R_1 + R_ {234} = 7 \, \ Omega + 5 \ Omega = 12 \, \ Omega. \ nonumber \]
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен \ (I = \ frac {V} {R_ {eq}} = \ frac {24 \, V} {12 \, \ Omega} = 2 \, A \). Этот ток проходит через резистор \ (R_1 \) и обозначается как \ (I_1 \). Падение потенциала на \ (R_1 \) можно найти с помощью закона Ома:
\ [V_1 = I_1R_1 = (2 \, A) (7 \, \ Omega) = 14 \, V. \ nonumber \]
Глядя на рисунок \ (\ PageIndex {5c} \), это оставляет \ (24 \, V — 14 \, V = 10 \, V \) отбрасывать в параллельной комбинации \ (R_2 \) и \ ( R_ {34} \).Ток через \ (R_2 \) можно найти по закону Ома:
\ [I_2 = \ frac {V_2} {R_2} = \ frac {10 \, V} {10 \, \ Omega} = 1 \, A. \ nonumber \]
Резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, поэтому токи \ (I_3 \) и \ (I_4 \) равны
.\ [I_3 = I_4 = I — I_2 = 2 \, A — 1 \, A = 1 \, A. \ nonumber \]
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные капли равны \ (V_3 = I_3R_3 = 6 \, V \) и \ (V_4 = I_4R_4 = 4 \, V \).2 (4 \, \ Omega) = 4 \, W, \\ [4pt] P_ {рассеивается} & = P_1 + P_2 + P_3 + P_4 = 48 \, W. \ end {align *} \]
Общая энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет
\ [\ begin {align *} P_s & = IV \\ [4pt] & = (2 \, A) (24 \, V) = 48 \, W \ end {align *} \]
Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
Пример \ (\ PageIndex {3} \): объединение последовательных и параллельных цепей
На рисунке \ (\ PageIndex {6} \) показаны резисторы, подключенные последовательно и параллельно.Мы можем считать \ (R_1 \) сопротивлением проводов, ведущих к \ (R_2 \) и \ (R_3 \).
- Найдите эквивалентное сопротивление цепи.
- Какое падение потенциала \ (V_1 \) на резисторе \ (R_1 \)?
- Найдите ток \ (I_2 \) через резистор \ (R_2 \).
- Какую мощность рассеивает \ (R_2 \)?
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения \ (R_2 \) и \ (R_3 \). Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с \ (R_1 \).
(b) Ток через \ (R_1 \) можно найти с помощью закона Ома и приложенного напряжения. Ток через \ (R_1 \) равен току от батареи. Падение потенциала \ (V_1 \) на резисторе \ (R_1 \) (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.{-1} = 5.10 \, \ Omega. \ Nonumber \] Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чисто параллельной (\ (20.0 \, \ Omega \) и \ (0.804 \, \ Omega \) ), соответственно).
- Ток через \ (R_1 \) равен току, обеспечиваемому батареей: \ [I_1 = I = \ frac {V} {R_ {eq}} = \ frac {12.0 \, V} {5.10 \, \ Omega} = 2.35 \, A. \ nonumber \] Напряжение на \ (R_1 \) равно \ [V_1 = I_1R_1 = (2.35 \, A) (1 \, \ Omega) = 2.35 \, V. \ nonumber \] Напряжение, приложенное к \ (R_2 \) и \ (R_3 \), меньше напряжения, подаваемого батареей, на величину \ (V_1 \).Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных \ (R_2 \) и \ (R_3 \).
- Чтобы найти ток через \ (R_2 \), мы должны сначала найти приложенное к нему напряжение. Напряжение на двух параллельных резисторах одинаковое: \ [V_2 = V_3 = V — V_1 = 12.0 \, V — 2.35 \, V = 9.65 \, V. \ nonumber \] Теперь мы можем найти ток \ (I_2 \) через сопротивление \ (R_2 \) по закону Ома: \ [I_2 = \ frac {V_2} {R_2} = \ frac {9.65 \, V} {6.00 \, \ Omega} = 1.2 (6.00 \, \ Omega) = 15.5 \, W. \ nonumber \]
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.
Упражнение \ (\ PageIndex {3} \)
Учитывайте электрические цепи в вашем доме.Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
- Раствор
Все цепи верхнего освещения параллельны и подключены к основному питанию, поэтому при перегорании одной лампочки все верхнее освещение не гаснет. У каждого верхнего света будет по крайней мере один переключатель, включенный последовательно с источником света, так что вы можете включать и выключать его.
В холодильнике есть компрессор и лампа, которая загорается при открытии дверцы.Обычно для подключения холодильника к стене используется только один шнур. Цепь, содержащая компрессор, и цепь, содержащая цепь освещения, параллельны, но есть переключатель, включенный последовательно со светом. Термостат управляет переключателем, который включен последовательно с компрессором, чтобы контролировать температуру холодильника.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке \ (\ PageIndex {7} \). Устройство, обозначенное символом \ (R_3 \), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, обозначенных \ (R_1 \), уменьшая напряжение на лампочке (которое равно \ (R_2 \)), которое затем заметно гаснет.
Рисунок \ (\ PageIndex {7} \): Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
- Точно определите, что необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей.
- Проверьте, являются ли ответы разумными и последовательными.
Пример \ (\ PageIndex {4} \): объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно \ ((R_1, \, R_2) \), соединены с двумя резисторами, включенными параллельно \ ((R_3, \, R_4) \).Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Через резистор \ (R_1 \) проходит ток 2,00 А. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
Рисунок \ (\ PageIndex {8} \): Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.- Нарисуйте четкую принципиальную схему (Рисунок \ (\ PageIndex {8} \)).
- Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы \ (R_1 \) и \ (R_2 \) включены последовательно, а резисторы \ (R_3 \) и \ (R_4 \) включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов \ (R_3 \) и \ (R_4 \) последовательно с последовательной конфигурацией резисторов \ (R_1 \) и \ (R_2 \).{-1} = 5,00 \, \ Омега. \ nonumber \] Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление схемы равно \ (R_ {eq} = R_1 + R_2 + R_ {34} = (25.00 \, \ Omega \). поэтому напряжение, подаваемое батареей, равно \ (V = IR_ {eq} = 2,00 \, A (25,00 \, \ Omega) = 50,00 \, V \).
- Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами. Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
Поскольку мощность, рассеиваемая резисторами, равна мощности, обеспечиваемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При нахождении \ (R_ {eq} \) для параллельного соединения необходимо с осторожностью относиться к обратному. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Авторы и ссылки
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
— learn.sparkfun.com
Добавлено в избранное Любимый 48 Серияи параллельные резисторы
Резисторы постоянно соединяются вместе в электронике, обычно в последовательной или параллельной схеме. Когда резисторы объединены последовательно или параллельно, они создают общее сопротивление , которое можно рассчитать с помощью одного из двух уравнений.Знание того, как сочетаются значения резисторов, пригодится, если вам нужно создать конкретное значение резистора.
Резисторы серииПри последовательном соединении значения резисторов просто складываются.
резисторов Н. Общее сопротивление — это сумма всех последовательных резисторов.
Так, например, если у вас всего , у вас должно быть , 12,33 кОм; резистор, найдите некоторые из наиболее распространенных номиналов резисторов 12 кОм; и 330 Ом, и соединить их последовательно.
Резисторы параллельные
Найти сопротивление параллельно включенных резисторов не так-то просто. Общее сопротивление параллельно включенных резисторов Н и обратно пропорционально сумме всех обратных сопротивлений. Это уравнение может иметь больше смысла, чем последнее предложение:
резисторов Н, включенных параллельно. Чтобы найти общее сопротивление, инвертируйте каждое значение сопротивления, сложите их, а затем инвертируйте.
(Обратное сопротивление на самом деле называется проводимостью , поэтому короче: проводимость параллельных резисторов является суммой каждой из их проводимостей).
В качестве частного случая этого уравнения: если у вас только два резистора , подключенных параллельно, их полное сопротивление можно рассчитать с помощью этого чуть менее инвертированного уравнения:
В качестве даже , более особого случая этого уравнения, если у вас есть два параллельных резистора равного значения , общее сопротивление составляет половину их значения. Например, если два 10k & ohm; резисторы включены параллельно, их полное сопротивление 5кОм.
Сокращенно сказать, что два резистора подключены параллельно, можно с помощью оператора параллельности: || .Например, если R 1 параллельно с R 2 , концептуальное уравнение может быть записано как R 1 || R 2 . Намного чище и скрывает все эти неприятные фракции!
Резисторные сети
В качестве специального введения в вычисление общего сопротивления, учителя электроники просто любят , когда они знакомят своих учеников с сумасшедшими, запутанными цепями резисторов.
Приручить резисторный сетевой вопрос может быть что-то вроде: «какое сопротивление между выводами A, и B в этой цепи?»
Чтобы решить такую проблему, начните с задней части схемы и упростите ее до двух терминалов.В этом случае R 7 , R 8 и R 9 все идут последовательно и могут складываться вместе. Эти три резистора подключены параллельно с R 6 , поэтому эти четыре резистора можно превратить в один с сопротивлением R 6 || (R 7 + R 8 + R 9 ). Делаем нашу схему:
Теперь четыре крайних правых резистора можно упростить еще больше. R 4 , R 5 и наша совокупность R 6 — R 9 все последовательно и могут быть добавлены.Тогда все эти последовательные резисторы подключены параллельно R 3 .
И это всего лишь три последовательных резистора между выводами A и B . Добавьте их! Таким образом, общее сопротивление этой цепи составляет: R 1 + R 2 + R 3 || (R 4 + R 5 + R 6 || (R 7 + R ) 8 + R 9 )).
← Предыдущая страница
Номинальная мощность6.2 последовательных и параллельных резистора — Введение в электричество, магнетизм и схемы
ЦЕЛИ ОБУЧЕНИЯ
По окончании раздела вы сможете:- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где. В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (рисунок 6.2.1). В последовательной цепи выходной ток первого резистора течет на вход второго резистора; следовательно, ток одинаков в каждом резисторе. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
(рисунок 6.2.1)
Рисунок 6.2.1 (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое.Резисторы серии
Считается, что резисторывключены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок 6.2.2, на котором показаны три последовательно включенных резистора с приложенным напряжением, равным.Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
(рисунок 6.2.2)
Рисунок 6.2.2 (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.На рисунке 6.2.2 ток, исходящий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор. Согласно закону Ома падение потенциала на резисторе при протекании через него тока рассчитывается по формуле, где — ток в амперах (), а — сопротивление в омах (). Поскольку энергия сохраняется, а напряжение равно потенциальной энергии на заряд, сумма напряжения, приложенного к цепи источником, и падения потенциала на отдельных резисторах вокруг контура должны быть равны нулю:
Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе.На рисунке 6.2.2 сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления, которое представляет собой просто сумму сопротивлений отдельных резисторов.
Любое количество резисторов может быть подключено последовательно. Если резисторы соединены последовательно, эквивалентное сопротивление равно
.(6.2.1)
Одним из результатов подключения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
ПРИМЕР 6.2.1
Эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах подключена к цепи, состоящей из четырех и одного последовательно соединенных резисторов (рисунок 6.2.3). Предположим, что внутреннее сопротивление батареи незначительно. (а) Рассчитайте эквивалентное сопротивление цепи. (б) Рассчитайте ток через каждый резистор. (c) Рассчитайте падение потенциала на каждом резисторе. (d) Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
(рисунок 6.2.3)
Рисунок 6.2.3 Простая последовательная схема с пятью резисторами.Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.Ток в цепи можно найти из закона Ома и равен напряжению, деленному на эквивалентное сопротивление. Падение потенциала на каждом резисторе можно найти с помощью закона Ома. Мощность, рассеиваемая каждым резистором, может быть найдена с помощью, а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, обеспечиваемую аккумулятором, можно найти с помощью.
Решение
а. Эквивалентное сопротивление — это алгебраическая сумма сопротивлений:
г.Ток в цепи одинаков для каждого резистора в последовательной цепи и равен приложенному напряжению, деленному на эквивалентное сопротивление:
г. Падение потенциала на каждом резисторе можно найти с помощью закона Ома:
Обратите внимание, что сумма падений потенциала на каждом резисторе равна напряжению, подаваемому батареей.
г. Мощность, рассеиваемая резистором, равна, а мощность, отдаваемая аккумулятором, равна:
Значение
Есть несколько причин, по которым мы использовали бы несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи.Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов. Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
ПРОВЕРЬТЕ ПОНИМАНИЕ 6.2
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи.«Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серию по девять луковиц. Если перегорает слишком много лампочек, в конечном итоге открываются шунты. Что вызывает это?
Кратко обозначим основные характеристики последовательно соединенных резисторов:
Сопротивления серии- суммируются, чтобы получить эквивалентное сопротивление:
- Один и тот же ток последовательно проходит через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке 6.2.4 показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома, где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
(рисунок 6.2.4)
Рисунок 6.2.4 (a) Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.Ток, протекающий от источника напряжения на рисунке 6.2.4, зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы и. По мере того, как заряды проходят от батареи, некоторые проходят через резистор, а некоторые — через резистор. Сумма токов, текущих в переход, должна быть равна сумме токов, текущих из перехода:
Это уравнение называется правилом соединения Кирхгофа и будет подробно обсуждено в следующем разделе.На рисунке 6.2.4 показано правило соединения. В этой схеме есть две петли, которые приводят к уравнениям и Обратите внимание, что напряжение на резисторах, включенных параллельно, одинаковое (), а ток является аддитивным:
Обобщая для любого количества резисторов, эквивалентное сопротивление параллельного соединения связано с отдельными сопротивлениями на
(6.2.2)
Это соотношение приводит к эквивалентному сопротивлению, которое меньше наименьшего из отдельных сопротивлений.Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
ПРИМЕР 6.2.2
Анализ параллельной цепи
Три резистора, и соединены параллельно. Параллельное соединение подключается к источнику напряжения. а) Какое эквивалентное сопротивление? (b) Найдите ток, подаваемый источником в параллельную цепь. (c) Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.(d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью.
(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.)(b) Ток, подаваемый источником, можно найти из закона Ома, заменив полное сопротивление.
(c) Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение.Полный ток — это сумма отдельных токов:.
(d) Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. Давайте использовать, так как каждый резистор получает полное напряжение.
(e) Общую мощность также можно рассчитать несколькими способами, используйте.
Решение
а. Общее сопротивление для параллельной комбинации резисторов находится с помощью уравнения 6.2.2.Ввод известных значений дает
Общее сопротивление с правильным количеством значащих цифр составляет. Как и предполагалось, меньше минимального индивидуального сопротивления.
г. Полный ток можно найти из закона Ома, заменив полное сопротивление. Это дает
Ток для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример). Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
г. Отдельные токи легко вычислить по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,
Аналогично
и
Общий ток складывается из отдельных токов:
г. Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.Давайте использовать, так как каждый резистор получает полное напряжение. Таким образом,
Аналогично
и
e. Суммарную мощность также можно рассчитать несколькими способами. Выбор и ввод общей текущей доходности
Значение
Общая мощность, рассеиваемая резисторами, также составляет:
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
ПРОВЕРЬТЕ ПОНИМАНИЕ 6.3
Рассмотрим одинаковую разность потенциалов, приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
ПРОВЕРЬТЕ ПОНИМАНИЕ 6.4
Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?
Суммируем основные характеристики резисторов параллельно:
- Эквивалентное сопротивление находится из
и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это.Ток, входящий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Вы можете вспомнить, что в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. В таблице 6.2.1 приведены уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
(таблица 6.2.1)
Комбинация серий Параллельная комбинация Эквивалентная емкость Эквивалентное сопротивление Таблица 10.1 Сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях
Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения.Такие комбинации обычны, особенно если учесть сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Последовательные и параллельные комбинации можно уменьшить до одного эквивалентного сопротивления, используя методику, показанную на рисунке 6.2.5. Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден.Здесь мы отмечаем эквивалентное сопротивление как.
(рисунок 6.2.5)
Обратите внимание, что резисторы и включены последовательно. Их можно объединить в одно эквивалентное сопротивление. Один из методов отслеживания процесса — включить резисторы в качестве индексов. Здесь эквивалентное сопротивление и равно
.Теперь схема сокращается до трех резисторов, показанных на Рисунке 6.2.5 (c). Перерисовывая, мы теперь видим, что резисторы и составляют параллельную цепь.Эти два резистора можно уменьшить до эквивалентного сопротивления:
Этот шаг процесса сокращает схему до двух резисторов, показанных на Рисунке 6.2.5 (d). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен. Этот ток проходит через резистор и обозначен как. Падение потенциала можно найти с помощью закона Ома:
Глядя на рис. 6.2.5 (c), остается отбросить параллельную комбинацию и. Проходной ток можно найти с помощью закона Ома:
Резисторы и включены последовательно, поэтому токи и равны
.Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах.Потенциальные падения равны и. Окончательный анализ — это посмотреть на мощность, подаваемую источником напряжения, и мощность, рассеиваемую резисторами. Мощность, рассеиваемая резисторами
Общая энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, равна. Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
ПРОВЕРЬТЕ ПОНИМАНИЕ 6.5
Учитывайте электрические цепи в вашем доме. Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если протекает большой ток, провал в проводах также может быть значительным и проявляться в виде тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на Рисунке 6.2.7. Устройство, представленное значком, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток.Этот увеличенный ток вызывает большее падение в проводах, представленных значком, уменьшая напряжение на лампочке (которая есть), которое затем заметно гаснет.
(рисунок 6.2.7)
Рисунок 6.2.7 Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения.Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
- Точно определите, что необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные.Есть один список для серий, а другой — для параллелей.
- Проверьте, являются ли ответы разумными и последовательными.
ПРИМЕР 6.2.4
Объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно, подключены к двум резисторам, включенным параллельно. Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление.Ток проходит через резистор. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
- Нарисуйте четкую принципиальную схему (рисунок 6.2.8).
(рисунок 6.2.8)
Рисунок 6.2.8 Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи. - Неизвестно напряжение аккумулятора.Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы и включены последовательно, а резисторы и включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов и последовательно с последовательной конфигурацией резисторов и.
- Напряжение, подаваемое батареей, можно найти, умножив ток от батареи на эквивалентное сопротивление цепи.Ток от батареи равен току через и равен. Нам нужно найти эквивалентное сопротивление, уменьшив схему. Чтобы уменьшить схему, сначала рассмотрите два резистора, включенных параллельно. Эквивалентное сопротивление составляет. Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление цепи равно. Таким образом, напряжение, подаваемое батареей, составляет.
- Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами.Мощность, подаваемая аккумулятором, составляет
Поскольку они включены последовательно, сквозной ток равен сквозному току. Т.к. ток через каждый будет. Мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором:
Поскольку мощность, рассеиваемая резисторами, равна мощности, подаваемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При поиске параллельного подключения необходимо соблюдать осторожность. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Кандела Цитаты
Лицензионный контент CC, конкретная атрибуция
- Загрузите бесплатно с http: // cnx………………………………………………………………………………………………………………………………………………………………………………………………………………………………………… ».org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Учебное пособие по физике: Параллельные схемы
Как упоминалось в предыдущем разделе Урока 4, два или более электрических устройства в цепи могут быть соединены последовательным или параллельным соединением. Когда все устройства соединены с использованием параллельных соединений, схема называется параллельной цепью .В параллельной схеме каждое устройство помещается в свою отдельную ветвь . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить через внешнюю цепь. Каждый заряд, проходящий через контур внешней цепи, будет проходить через единственный резистор, присутствующий в одной ветви. Прибыв в место разветвления или узел, заряд делает выбор , через какую ветвь пройти на обратном пути к терминалу с низким потенциалом.
Краткое сравнение и контраст между последовательными и параллельными цепями было сделано в предыдущем разделе Урока 4. В этом разделе было подчеркнуто, что добавление большего количества резисторов в параллельную цепь приводит к довольно неожиданному результату — уменьшению общего сопротивления. . Поскольку существует несколько путей, по которым может протекать заряд, добавление еще одного резистора в отдельную ветвь обеспечивает еще один путь, по которому заряд может проходить через основную область сопротивления в цепи.Это уменьшенное сопротивление в результате увеличения количества ветвей будет иметь эффект увеличения скорости, с которой течет заряд (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платными дорогами. Плата за проезд — это основное место сопротивления автомобильному потоку на платной дороге. Добавление дополнительных пунктов сбора платы за проезд в пределах их собственного отделения на платной дороге обеспечит больше путей для автомобилей, проезжающих через станцию сбора платы за проезд. Эти дополнительные пункты пропуска снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.
ТекущийСкорость, с которой заряд проходит через цепь, называется током. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами таким образом, что в одном месте ток меньше, чем в другом. В параллельной схеме заряд делит на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой.Тем не менее, если брать в целом, общая сумма тока во всех ветвях при сложении равна величине тока в местах за пределами ветвей. Правило, что ток везде одинаковый все еще работает, только с закруткой. Сила тока вне ветвей равна сумме токов в отдельных ветвях. Это все еще та же величина тока, только разделенная на несколько путей.
В форме уравнения этот принцип можно записать как
I итого = I 1 + I 2 + I 3 +…, где I total — общая величина тока вне ветвей (и в батарее), а I 1 , I 2 и I 3 представляют ток в отдельных ветвях цепи.
В этом блоке широко использовалась аналогия между расходом заряда и расходом воды. Еще раз вернемся к аналогии, чтобы проиллюстрировать, как сумма текущих значений в ветвях равна сумме вне ветвей.Поток заряда в проводах аналогичен потоку воды в трубах. Рассмотрим приведенные ниже схемы, на которых поток воды в трубах делится на отдельные ответвления. В каждом узле (место разветвления) вода проходит двумя или более отдельными путями. Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ветвях за пределами узла. Точно так же, когда две или более ветви подаются в узел, скорость, с которой вода вытекает из узла, будет равна сумме расходов в отдельных ветвях, которые подаются в узел.
Тот же принцип разделения потока применяется к электрическим цепям. Скорость, с которой заряд поступает в узел, равна сумме расходов в отдельных ветвях за пределами узла. Это проиллюстрировано в приведенных ниже примерах. В примерах вводится новый символ схемы — буква A, заключенная в круг. Это символ амперметра — устройства, используемого для измерения силы тока в определенной точке. Амперметр способен измерять ток, оказывая при этом незначительное сопротивление потоку заряда.
На диаграмме A показаны два резистора, подключенные параллельно узлам в точках A и B. Заряд течет в точку A со скоростью 6 ампер и делится на два пути — один через резистор 1, а другой через резистор 2. Ток в ветви с резистором 1 — 2 ампера, а ток в ветви с резистором 2 — 4 ампера. После того, как эти две ветви снова встретятся в точке B, чтобы сформировать единую линию, ток снова станет 6 ампер. Таким образом, мы видим, что принцип, согласно которому ток вне ветвей равен сумме тока в отдельных ветвях, справедлив.
I всего = I 1 + I 26 ампер = 2 ампера + 4 ампера
Схема B выше может быть немного сложнее, если три резистора расположены параллельно. На схеме обозначены четыре узла, обозначенные буквами A, B, C и D. Заряд течет в точку A со скоростью 12 ампер и делится на два пути: один проходит через резистор 1, а другой направляется к точке B (и резисторам 2). и 3). 12 ампер тока делятся на 2-амперную (через резистор 1) и 10-амперную (в направлении точки B).В точке B происходит дальнейшее разделение потока на два пути — один через резистор 2, а другой через резистор 3. Ток в 10 ампер, приближающийся к точке B, делится на 6-амперный канал (через резистор 2) и 4-канальный. -амперный тракт (через резистор 3). Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера, и что сумма значений тока в отдельных ветвях равна току вне ветвей.
I всего = I 1 + I 2 + I 312 А = 2 А + 6 А + 4 А
Анализ потока в точках C и D также может быть проведен, и будет замечено, что сумма расходов потока в этих точках равна скорости потока, находящейся непосредственно за этими точками.
Эквивалентное сопротивлениеФактическое количество тока всегда изменяется обратно пропорционально общему сопротивлению. Существует четкая взаимосвязь между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая, когда два резистора помещены в параллельные ветви, каждый из которых имеет одинаковое значение сопротивления 4 Ом.Поскольку схема предлагает два равных путей для потока заряда, только половина заряда выберет для прохождения через данную ветвь. В то время как каждая отдельная ветвь предлагает сопротивление 4 Ом любому заряду, который проходит через нее, только половина всего заряда, протекающего по цепи, будет встречать сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается батареи, которая накачивает заряд, наличие двух параллельно подключенных резисторов 4 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи.Таким же образом, наличие двух параллельно подключенных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом. А наличие двух параллельных резисторов 12 Ом было бы эквивалентно наличию в цепи одного резистора 6 Ом.
Теперь давайте рассмотрим другой простой случай, когда три резистора включены параллельно, каждый из которых имеет одинаковое сопротивление 6 Ом. При трех равных путях прохождения заряда через внешнюю цепь только одна треть заряда будет проходить через данную ветвь.Каждая отдельная ветвь обеспечивает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через определенную ветвь, означает, что общее сопротивление цепи составляет 2 Ом. Что касается батареи, которая нагнетает заряд, наличие трех параллельных резисторов 6 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи. Таким же образом, наличие трех параллельно подключенных резисторов сопротивлением 9 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом.А наличие трех параллельных резисторов 12 Ом было бы эквивалентно наличию одного резистора 4 Ом в цепи.
Это концепция эквивалентного сопротивления. Эквивалентное сопротивление схемы — это величина сопротивления, которая потребуется одному резистору, чтобы сравняться с общим эффектом от набора резисторов, присутствующих в схеме. Для параллельных цепей математическая формула для вычисления эквивалентного сопротивления (R eq ) составляет
. 1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 +…, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, подключенных параллельно. Приведенные выше примеры можно рассматривать как простые случаи, в которых все пути обладают одинаковым сопротивлением отдельному заряду, который проходит через них. Приведенные выше простые случаи были выполнены без использования уравнения. Тем не менее, это уравнение подходит как для простых случаев, когда резисторы ответвления имеют одинаковые значения сопротивления, так и для более сложных случаев, когда резисторы ответвления имеют разные значения сопротивления.Например, рассмотрим применение уравнения к одному простому и одному сложному случаю ниже.
Случай 1 : Три резистора 12 Ом включены параллельно 1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (12 Ом) + 1 / (12 Ом) + 1 / (12 Ом)
Использование калькулятора …
1 / R экв. = 0,25 Ом -1
R экв = 1 / (0,25 Ом -1 )
R экв = 4,0 Ом
Случай 2 : резисторы 5,0 Ом, 7,0 Ом и 12 Ом подключены параллельно 1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (5.0 Ом) + 1 / (7,0 Ом) + 1 / (12 Ом)
Использование калькулятора …
1 / R экв = 0,42619 Ом-1
R экв = 1 / (0,42619 Ом -1 )
R экв = 2,3 Ом
Ваша очередь попробовать Нужно больше практики? Используйте Два параллельных резистора , виджет ниже, чтобы попробовать некоторые дополнительные проблемы.Введите любые два желаемых значения сопротивления. Используйте свой калькулятор, чтобы определить значения R eq . Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте столько раз, сколько хотите, с разными значениями сопротивления. Падения напряжения для параллельных ветвейВ разделе «Схемы» учебного пособия «Физический класс» подчеркивалось, что любое повышение напряжения, полученное за счет заряда в батарее, теряется из-за заряда, когда он проходит через резисторы внешней цепи.Общее падение напряжения во внешней цепи равно увеличению напряжения при прохождении заряда через внутреннюю цепь. В параллельной схеме заряд не проходит через каждый резистор; скорее, он проходит через единственный резистор. Таким образом, полное падение напряжения на этом резисторе должно соответствовать напряжению батареи. Не имеет значения, проходит ли заряд через резистор 1, резистор 2 или резистор 3, падение напряжения на резисторе, которое выбирает для прохождения через , должно равняться напряжению батареи.В форме уравнения этот принцип можно было бы выразить как
V аккумулятор = V 1 = V 2 = V 3 = …Если три резистора размещены в параллельных ветвях и питаются от 12-вольтовой батареи, то падение напряжения на каждом из трех резисторов составляет 12 вольт. Заряд, протекающий по цепи, встретит только один из этих трех резисторов и, таким образом, столкнется с одним падением напряжения на 12 вольт.
Диаграммы электрических потенциалов были представлены в Уроке 1 этого устройства и впоследствии использовались для иллюстрации последовательных падений напряжения, происходящих в последовательных цепях.Диаграмма электрических потенциалов — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим приведенную ниже принципиальную схему и соответствующую диаграмму электрических потенциалов.
Как показано на диаграмме электрических потенциалов, все позиции A, B, C, E и G имеют высокий электрический потенциал. Один заряд выбирает только один из трех возможных путей; таким образом, в позиции B один заряд будет двигаться к точкам C, E или G, а затем проходит через резистор, находящийся в этой ветви.Заряд не теряет свой высокий потенциал до тех пор, пока он не пройдет через резистор, либо от C к D, от E к F или от G к H. После того, как он пройдет через резистор, заряд вернется почти до 0 вольт и вернется к отрицательному значению. клемму аккумуляторной батареи для повышения ее напряжения. В отличие от последовательных цепей, заряд в параллельной цепи встречает единственное падение напряжения на своем пути через внешнюю цепь.
Ток через заданную ветвь можно предсказать, используя уравнение закона Ома, падение напряжения на резисторе и сопротивление резистора.Поскольку падение напряжения на каждом резисторе одинаково, фактором, определяющим, что резистор имеет наибольший ток, является сопротивление. Резистор с наибольшим сопротивлением испытывает наименьший ток, а резистор с наименьшим сопротивлением — наибольший ток. В этом смысле можно сказать, что заряд (как и люди) выбирает путь наименьшего сопротивления. В форме уравнения это может быть указано как
I 1 = Δ V 1 / R 1 I 2 = Δ V 2 / R 2 I 3 = Δ V 3 / R 3 Этот принцип иллюстрируется схемой, показанной ниже.Произведение I • R одинаково для каждого резистора (и равно напряжению батареи). Тем не менее, ток у каждого резистора разный. Ток наибольший там, где сопротивление наименьшее, и ток наименьший, где сопротивление наибольшее.
Математический анализ параллельных цепейПриведенные выше принципы и формулы могут использоваться для анализа параллельной цепи и определения значений тока и разности электрических потенциалов на каждом из резисторов в параллельной цепи.Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока через батарею (I — ), а также падений напряжения и тока для каждого из трех резисторов.
Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.
1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 = (1/17 Ω) + (1/12 Ω) + (1/11 Ω)1 / R экв = 0.23306 Ом -1
R экв = 1 / (0,23306 Ом -1 )
R экв = 4,29 Ом
(округлено от 4,29063 Ом)
Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в батарее важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R.Расчет показан здесь:
I tot = ΔV аккумулятор / R eq = (60 В) / (4,29063 Ом)I общ = 14,0 А
(округлено от 13,98396 А)
Напряжение батареи 60 В представляет собой усиление электрического потенциала за счет заряда, проходящего через батарею. Заряд теряет такое же количество электрического потенциала при любом прохождении через внешнюю цепь.То есть падение напряжения на каждом из трех резисторов такое же, как и напряжение, полученное в батарее:
ΔV аккумулятор = ΔV 1 = ΔV 2 = ΔV 3 = 60 ВОсталось определить три значения — ток каждого отдельного резистора. Закон Ома снова используется для определения значений тока для каждого резистора — это просто падение напряжения на каждом резисторе (60 В), деленное на сопротивление каждого резистора (указанное в формулировке задачи).Расчеты показаны ниже.
I 1 = ΔV 1 / R 1 I 1 = (60 В) / (17 Ом)
I 1 = 3,53 А
I 2 = ΔV 2 / R 2 I 2 = (60 В) / (12 Ом)
I 2 = 5,00 А
I 3 = ΔV 3 / R 3 I 3 = (60 В) / (11 Ом)
Я 3 = 5.45 А
В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли вычисленные значения принципу, согласно которому сумма значений тока для каждого отдельного резистора равна общему току в цепи (или в батарее). . Другими словами, I tot = I 1 + I 2 + I 3 ?
Является ли I tot = I 1 + I 2 + I 3 ?Из 14.0 ампер = 3,53 ампер + 5,00 ампер + 5,45 ампер?
14,0 А = 13,98 А?
Да !!
(Разница в 0,02 ампера — это просто результат предыдущего округления значения I до с 13,98.)
Математический анализ этой параллельной цепи включал смесь концепций и уравнений. Как это часто бывает в физике, отделение понятий от уравнений при принятии решения физической проблемы является опасным актом.Здесь необходимо учитывать концепции, согласно которым падение напряжения на каждом из трех резисторов равно напряжению батареи, и что сумма тока в каждом резисторе равна общему току. Эти представления необходимы для завершения математического анализа. В следующей части Урока 4 будут исследованы комбинированные или составные схемы, в которых одни устройства включены параллельно, а другие — последовательно.
Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже.Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ. Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, расположить и подключить их так, как вам нужно. Вольтметры и амперметры позволяют измерять ток и падение напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).
Проверьте свое понимание1. По мере того, как в цепь добавляется все больше и больше резисторов, эквивалентное сопротивление цепи ____________ (увеличивается, уменьшается), а общий ток цепи ____________ (увеличивается, уменьшается).
2.Три одинаковые лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают местоположения вдоль цепи. Какое из следующих утверждений верно?
а. Ток в точке Y больше, чем ток в точке Q.
г. Ток на Y больше, чем на P.
.г. Ток в точке Y больше, чем ток в точке Z.
г. Ток в точке P больше, чем ток в точке Q.
.e.Ток на Q больше, чем на P.
.ф. Сила тока одинакова во всех местах.
3. Три одинаковые лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают местоположения вдоль цепи. В каком (а) месте (ах), если таковые имеются, будет ток …
а. … так же, как у X?
г…. такой же, как у Q?
г. … так же, как у Y?
г. … меньше, чем у Q?
e. … меньше, чем у P?
ф. … вдвое больше, чем у Z?
г. … в три раза больше, чем в Y?
4. Какие изменения можно внести в схему ниже, чтобы уменьшить ток в ячейке? Перечислите все подходящие варианты.
а. Увеличьте сопротивление лампы X.
г. Уменьшите сопротивление лампы X.
г. Увеличьте сопротивление лампы Z.
.г. Уменьшите сопротивление лампы Z.
.e. Увеличьте напряжение ячейки (как-нибудь).
ф. Уменьшите напряжение ячейки (как-нибудь).
г. Снять лампу Y.
.5.Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключаются, как показано на рисунке. Ток в резисторе 12 Ом равен ____ току в резисторе 4 Ом.
а. 1/3
г. 1/2
г. 2/3
г. то же, что
e.1,5 раза
ф. дважды
г. трижды
ч. четыре раза
6. Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключены, как показано.Падение напряжения на резисторе 12 Ом равно ____ падению напряжения на резисторе 4 Ом.
а. 1/3
г. 1/2
г. 2/3
г. то же, что
e. 1,5 раза
ф.дважды
г. трижды
ч. четыре раза
7. Аккумулятор на 12 В и резистор на 12 Ом подключаются, как показано на схеме. Резистор на 6 Ом добавлен к резистору на 12 Ом, чтобы создать цепь Y, как показано.Падение напряжения на резисторе 6 Ом в цепи Y равно ____ падению напряжения на резисторе в цепи X.
а. больше, чем
г. меньше
г. то же, что
8. Используйте свое понимание эквивалентного сопротивления, чтобы заполнить следующие утверждения:
а. Два резистора сопротивлением 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.
г. Три резистора 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
г. Три резистора сопротивлением 8 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.
г. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
e. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом размещены параллельно.Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
ф. Три резистора с сопротивлением 12 Ом, 6 Ом и 21 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
9. На основании ваших ответов на вышеуказанный вопрос заполните следующую формулировку:
Общее или эквивалентное сопротивление трех параллельно включенных резисторов будет _____.
а. больше, чем сопротивление самого большого значения R.
г. меньше, чем сопротивление наименьшего значения R из трех.
г. где-то между наименьшим значением R и наибольшим значением R.
г. … бред какой то! Такого обобщения сделать нельзя. Результаты меняются.
10. Три резистора включены параллельно.Если поместить в цепь с источником питания 12 В. Определите эквивалентное сопротивление, полный ток цепи, падение напряжения и ток в каждом резисторе.
Серияи параллельные резисторы
- Изучив этот раздел, вы сможете:
- Рассчитайте значения общего сопротивления в цепях с последовательным сопротивлением.
- Используйте соответствующие формулы для расчета сопротивления в цепях с параллельным сопротивлением.
- • Вычисление суммы обратных величин.
- • Произведение над суммой.
- Рассчитайте значения общего сопротивления в последовательных / параллельных сетях.
Расчеты в последовательно- и параллельных резисторных цепях
Компоненты, включая резисторы в цепи, могут быть соединены вместе двумя способами:
ПОСЛЕДОВАТЕЛЬНО, так что один и тот же ток течет через все компоненты, но различная разность потенциалов (напряжение) может существовать на каждом из них.
ПАРАЛЛЕЛЬНО, так что одна и та же разность потенциалов (напряжение) существует на всех компонентах, но каждый компонент может проводить разный ток.
Рис. 4.2.1 Резисторы серии
Рис. 4.2.2 Параллельные резисторы
В любом случае (для резисторов) полное сопротивление той части цепи, которая содержит резисторы, может быть рассчитано с использованием методов, описанных ниже.
Возможность рассчитать суммарное (общее) значение резисторов таким способом позволяет легко вычислить неизвестные значения сопротивления, тока и напряжения для довольно сложных цепей, используя относительно простые методы.Это очень полезно при поиске неисправностей.
ПЕРЕД ДАЛЬНЕЙШЕЙ ДАЛЬНЕЙШЕЙ ПОПРАКТИКОЙ ИСПОЛЬЗУЙТЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА ОБЩИХ ЗНАЧЕНИЙ СЕРИЙНЫХ И ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ.
Для резисторов в серии:
Общее сопротивление двух или более резисторов, подключенных последовательно , определяется простым сложением индивидуальных значений резисторов, чтобы найти общую сумму (R TOT ):
Для резисторов, включенных параллельно:
Для расчета общего сопротивления цепи, в которой используются параллельные резисторы, можно использовать следующую формулу.
Обратите внимание, однако, что эта формула НЕ дает вам полного сопротивления R TOT . Это дает вам ВЗАИМОДЕЙСТВИЕ R TOT или:
Это совсем другое значение — и НЕ является полным сопротивлением. Он делится на 1, разделенный на TOT . Чтобы получить правильное значение для R TOT (которое будет обратным 1 / R TOT , т. Е. TOT /1, просто нажмите соответствующую клавишу на вашем калькуляторе (отмеченную 1 / x или x-1) .
Другой способ расчета параллельных цепей.
Суммарное сопротивление двух резисторов, включенных параллельно , которое не включает обратных величин, определяется по формуле:
Эту формулу часто называют «произведение над суммой».
Рассчитывает только ДВА резистора параллельно? Ну да, но это не большая проблема. Если имеется более двух параллельных резисторов, просто выберите два из них и определите общее сопротивление для этих двух — затем используйте это общее сопротивление, как если бы это был один резистор, и составьте еще одну пару с третьим резистором.Определите новую сумму и так далее, пока вы не включите все параллельные резисторы в этой конкретной сети.
О, еще одна вещь, которую нужно помнить о произведении над суммой, видите скобки вокруг суммы (нижняя часть) формулы? Это означает, что вы должны решить это, прежде чем использовать его для разделения продукта (верхняя часть) на. Если вы этого не сделаете, ваш ответ будет неправильным.
Звучит сложно? Не совсем, это просто вопрос повторения, и на практике вы не часто встречаетесь с множеством параллельных сетей с гораздо более чем двумя резисторами.Тем не менее, какую формулу вы выберете, зависит от вас, взаимная или сумма продукта.
подсказки
Использование обратного метода
Если вы используете МЕТОД ВЗАИМОДЕЙСТВИЯ для параллельных цепей, НЕ ЗАБУДЬТЕ, когда вы добавили обратные величины отдельных резисторов — вы должны снова найти обратную величину. 1 / R1 + 1 / R2 + 1 / R3 = 1 / R TOT и чтобы найти R TOT , вы должны найти обратное 1 / R TOT .
Упрощающие схемы
Для комбинированных последовательных и параллельных цепей сначала разработайте секцию цепи (последовательную или параллельную).Затем перерисуйте схему, заменив участок, сопротивление которого вы нашли, одним резистором. Теперь у вас есть упрощенная схема, в которой можно найти R TOT .
Вы можете использовать формулу «произведение на сумму»:
Для цепей с более чем двумя параллельными резисторами просто вычислите два параллельных резистора одновременно, используя формулу произведения на сумму, а затем перерисуйте схему, заменив два резистора одним резистором, значение которого является объединенным сопротивлением двух .
Теперь вы можете использовать первое комбинированное значение в качестве единственного резистора со следующим параллельным резистором и так далее. Таким образом, можно выработать большое количество параллельных резисторов с использованием произведения на сумму.
Когда все параллельные резисторы одинакового номинала.
Если подключено несколько идентичных параллельных резисторов, общее сопротивление будет равно номиналу резистора, умноженному на обратную величину количества резисторов.
, т.е. два параллельных резистора 12 кОм имеют общее сопротивление
.12K x 1/2 = 6K
Три параллельно включенных резистора 12 кОм имеют суммарное сопротивление
12K x 1/3 = 4K и т. Д.
Проверяю ответ
Суммарное значение любого количества параллельных резисторов всегда будет МЕНЬШЕ, чем значение наименьшего отдельного резистора в сети. Используйте этот факт, чтобы проверить свои ответы.
Серияи параллельная комбинация
Попробуйте несколько вычислений, основанных на последовательной и параллельной цепях резисторов. Для этого вам просто нужно использовать информацию на этой странице и на странице «Советы по расчету резисторов». Вас просят вычислить общее сопротивление для каждой цепи.Вы можете выбрать, какую формулу использовать
Вы также можете получить помощь по математике, загрузив нашу бесплатную брошюру «Советы по математике».
Прежде чем начать, подумайте об этих нескольких советах. Они упростят задачу, если вы будете внимательно им следовать.
1. Разработайте ответы с помощью карандаша и бумаги; перерисуйте схему, над которой работаете.
2. Конечно, ответ — это не просто число, это будет определенное количество Ом, не забудьте указать правильную единицу (например.грамм. Ω, KΩ или MΩ) или ваш ответ не имеет смысла.
3. Когда вы вводите значения в калькулятор, преобразуйте все значения KΩ или MΩ в Ом с помощью клавиши EXP. Если вы здесь ошибетесь, то получите действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.
Итак, вы прочитали эти инструкции и готовы приступить к работе. Вот способ решить типичную проблему на бумаге, чтобы (со временем) вы не запутались.
Пример последовательной и параллельной цепи.
Хорошо, есть что вспомнить, так почему бы не попробовать несколько практических вопросов в модуле резисторов 4.5 по определению общего сопротивления некоторых цепей резисторов?
резисторов последовательно и параллельно
резисторов последовательно и параллельно
Далее: Правила Кирхгофа Up: Электрический ток Предыдущее: ЭДС и внутреннее сопротивление Резисторы, вероятно, встречаются чаще всего. компоненты в электронных схемах.Практические схемы часто содержат очень сложные комбинации резисторов. Поэтому полезно иметь набор правил для поиска эквивалентных сопротивление некоторой общей схемы резисторов. Оказывается, мы можем всегда находите эквивалентное сопротивление повторным применением два простых правил. Эти правила относятся к резисторам, включенным последовательно, и в параллели.Рисунок 18: Два резистора соединены последовательно. Рассмотрим два резистора, соединенных в серию , как показано на рис.18. Понятно, что через оба резистора протекает одинаковый ток. Ибо, если бы это было не так, заряд накапливался бы в одном или другом резисторов, которые не соответствовали бы установившаяся ситуация (таким образом нарушая основное предположение этого раздела). Предположим, что падение потенциала от точки к точке есть. Это падение представляет собой сумму потенциальных падает и на двух резисторах и соответственно. Таким образом,
(135)
Согласно закону Ома, эквивалентное сопротивление между и — отношение падения потенциала в этих точках и ток, протекающий между ними.Таким образом,(136)
давая(137)
Здесь мы использовали тот факт, что ток является общим для все три резистора. Следовательно, правилоЭквивалентное сопротивление двух последовательно соединенных резисторов равно сумма отдельных сопротивлений.
Для резисторов, соединенных последовательно, уравнение.(137) обобщает к .Рисунок 19: Два резистора подключены параллельно. Рассмотрим два резистора, соединенных по параллельно , как показано на рис. 19. Это Из рисунка видно, что падение потенциала на двух резисторах равно одно и тоже. В общем, однако, токи и которые протекают через резисторы и соответственно разные. По закону Ома эквивалентное сопротивление между и — отношение падения потенциала через эти точки и текущий которая течет между ними.Этот ток должен равняться сумме токи и протекающие через два резистора, в противном случае заряд будет накапливаться на одном или обоих переходах в цепи. Таким образом,
(138)
Следует, что(139)
давая(140)
Здесь мы использовали тот факт, что падение потенциала является общим для всех трех резисторов.Ясно, что правилоОбратное эквивалентное сопротивление двух сопротивлений. подключенных параллельно — это сумма обратных величин индивидуальные сопротивления.
Для резисторов, соединенных параллельно, уравнение. (140) обобщает на .
Далее: Правила Кирхгофа Up: Электрический ток Предыдущее: ЭДС и внутреннее сопротивление Ричард Фицпатрик 2007-07-14 .


