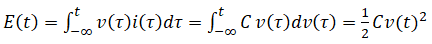В электрических цепях применяются различные способы соединения конденсаторов . Соединение конденсаторов может производиться: последовательно , параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
У начинающих электронщиков при сборке любого самодельного устройства могут возникнуть проблемы с соединением конденсатора. Ведь даже у заядлого любителя электроники может не оказаться под рукой конденсатора с нужным номиналом, особенно когда нужно срочно отремонтировать бытовой прибор. Из сложившейся проблемы легко выйти, соединив последовательно или параллельно несколько конденсаторов.
Приготовьте:
- конденсаторы;
- вольтметр;
- провода;
- кусачки.
Способы подключения конденсаторов в электрическую цепь
Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей. Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.
Параллельное включение конденсаторов в цепь
Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.
Параллельное соединение конденсаторов:
Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.
Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.
При параллельном соединении конденсаторов емкость равняется:
Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.
Конденсаторы, соединенные параллельно, имеют напряжение:
Последовательное включение конденсаторов в цепь
Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.
Последовательное соединение конденсатора:
При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния. По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.
Формула нахождения заряда на конденсаторе, схема подключения конденсатора:
Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости. Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.
Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.
Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:
Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:
Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:
Смешанное включение емкостных накопителей в схему
Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.
Участок цепи подсоединенных смешанным включением накопителей емкости:
Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:
- разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
- вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
- проводим нахождение эквивалентной емкости на параллельном участке;
- когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
- рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.
Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:
- Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.
- Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
- Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.
Вывод
Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников. В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.
Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.
Соединение конденсаторов
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Соединение конденсаторов Параллельное соединение конденсаторов
П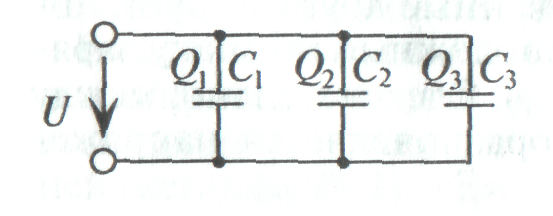
ри параллельном соединении конденсаторов к каждому конденсатору приложено одинаковое напряжениеU, а величина заряда на обкладках каждого конденсатора Q пропорциональна его емкости (рис. 2).
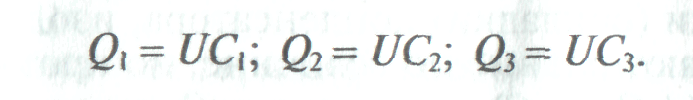
Общий заряд Q всех конденсаторов
Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.
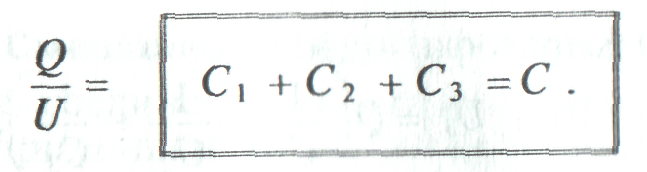
Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов применяется для увеличения емкости.
4)Если параллельно включены т одинаковых конденсаторов емкостью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением
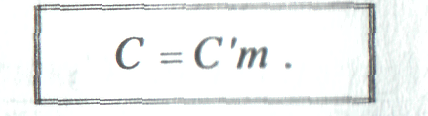
Последовательное соединение конденсаторов
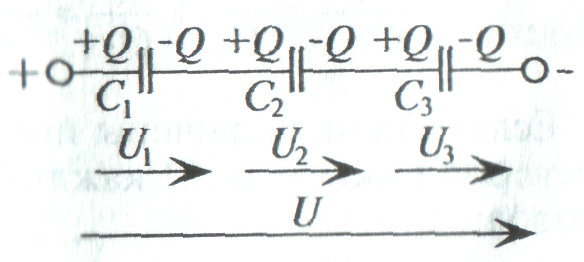
На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U, появятся заряды одинаковые по величине с противоположными знаками.
Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:
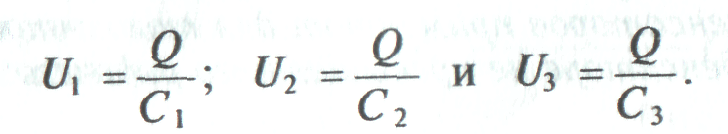
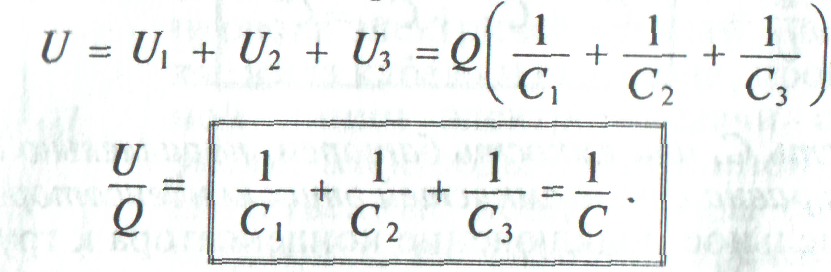
Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.
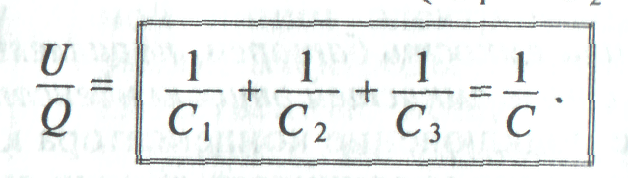
При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:
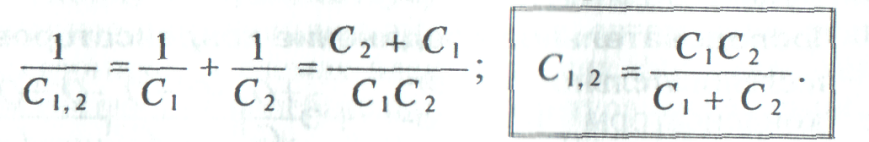
Если в цепь включены последовательно п одинаковых конденсаторов емкостью С каждый, то общая емкость этих конденсаторов:
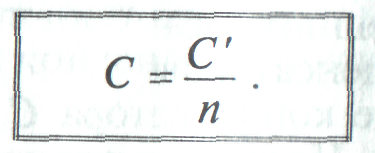
Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.
На практике может оказаться , что допустимое рабочее напряжение Up конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего Up. Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения Up.
Смешанное соединение конденсаторов
Смешанное соединение (последовательно-параллельное) конденсаторов применяют тогда, когда необходимо увеличить емкость и рабочее напряжение батареи конденсаторов.
Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.
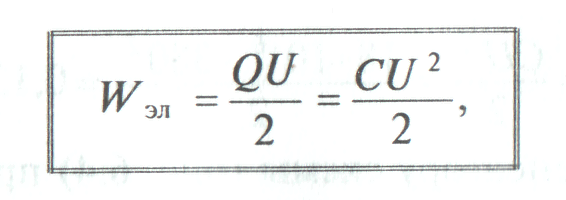
где Q — заряд конденсатора или конденсаторов, к которым приложено напряжение U; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U.
Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.
15.Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)
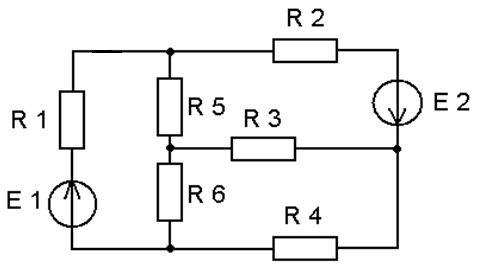
Рисунок 5- Схема электрическая
Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.
На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.
1.Схемы замещения элементов электрических цепей
На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).
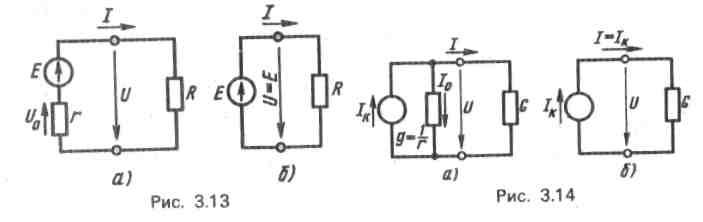
Приr= 0 внутреннее падение напряженияUо = 0, поэтому
напряжение на зажимах источника при любом токе равно
В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияIK, а вместо внутреннего сопротивления в расчет вводится внутренняя проводимостьg=1/r.
Возможность такой замены можно доказать, разделив равенство (3.1) на r:
где U/r = Io—некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E/r = IK — ток короткого замыкания источника;
Вводя новые обозначения, получим равенство IK = Io + I, которому удовлетворяет эквивалентная схема рис. 3.14,а.
В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):
Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.
Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.
{SOURCE}
Проводники и диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.
Проводники и диэлектрики в электростатическом поле
Вещества в природе можно разделить на проводники и диэлектрики.
Основная особенность — наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.
Типичные проводники — металлы.
Диэлектрическая проницаемость вещества
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.
В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.
Физическая величина, равная отношению модуля напряженности \(\vec{E}_0\) внешнего электрического поля в вакууме к модулю напряженности \(\vec{E}\) полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества \(\varepsilon\).
\[\varepsilon=\dfrac{\vec{E}_0}{\vec{E}}\]
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда \(q\) одного из проводников к разности потенциалов \(\Delta \varphi\) между ними:
\[\fbox{$C=\dfrac{q}{\Delta \varphi}$}\]
Единицы измерения: \(\displaystyle [\text{Ф}]\) (фарад).
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.
Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, — обкладками.
Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.
Электроемкость плоского конденсатора
Разность потенциалов \(\Delta \varphi\) между пластинами в однородном электрическом поле равна \(Ed\), где \(d\) — расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
\[C=\dfrac{q}{\Delta \varphi}=\dfrac{\sigma S}{Ed}=\dfrac{\varepsilon_0S}{d}\]
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в \(\varepsilon\) раз:
\[\fbox{$C=\dfrac{\varepsilon_0\varepsilon S}{d}$}\]
Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
\[\fbox{$U=U_1+U_2$}\]
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
\[\dfrac{q}{C}=\dfrac{q}{C_1}+\dfrac{q}{C_2}\]
Сократив выражение на \(Q\), получим формулу:
\[\fbox{$\dfrac{1}{C}=\dfrac{1}{C_1}+\dfrac{1}{C_2}$}\]
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
\[\fbox{$C=\dfrac{C_1C_2}{C_1+C_2}$}\]
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
\[\fbox{$q=q_1+q_2$}\]
Так как заряд конденсатора
\[q=CU\]
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
\[CU=C_1U+C_2U\]
\[\fbox{$C=C_1+C_2$}\]
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии того, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.
Вычислим эту энергию: начнём с плоского воздушного конденсатора.
Ответим на такой вопрос: какова силу притяжения его обкладок друг к другу. Величины используем следующие: заряд конденсатора \(q\), площадь обкладок \(S\). Возьмём на второй обкладке настолько маленькую площадку, что заряд \(q_0\) этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
\[F_0 = q_0E_1,\]
где \(E_1\) — напряжённость поля первой обкладки:
\[E_1=\dfrac{\sigma}{2\varepsilon_0}=\dfrac{q}{2\varepsilon_0S}\]
Значит
\[F_0=\dfrac{qq_0}{2\varepsilon_0S}\]
Направлена эта сила параллельно линиям поля (т.е. перпендикулярно пластинам). Результирующая сила \(F\) притяжения второй обкладки к первой складывается из всех этих сил \(F_0\), с которыми притягиваются к первой обкладке всевозможные маленькие заряды \(q_0\) второй обкладки. При этом суммировании постоянный множитель \(\displaystyle\dfrac{q}{2\varepsilon_0S}\) вынесется за скобку, а в скобке просуммируются все \(q_0\) и дадут \(q\). В результате получим
\[F=\dfrac{q^2}{2\varepsilon_0S}\]
Предположим теперь, что расстояние между обкладками изменилось от начальной величины \(d_1\) до конечной величины \(d_2\). Сила притяжения пластин совершает при этом работу \[A = F(d_1 -d_2)\]
Знак правильный: если пластины сближаются \((d_2 < d_1)\), то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины \((d_2 > d_1)\), то работа силы притяжения получается отрицательной, как и должно быть.
Получаем
\[A=\dfrac{q^2}{2\varepsilon_0S}(d_1-d_2)=\dfrac{q^2d_1}{2\varepsilon_0S}-\dfrac{q^2d_2}{2\varepsilon_0S}=\dfrac{q^2}{2C_1}-\dfrac{q^2}{2C_2}=W_1-W_2\]
Это можно переписать следующим образом: \[A =-(W_2-W_1) =-\Delta W,\]
где \[\fbox{$W=\dfrac{q^2}{2C}$}, (1)\]
Работа потенциальной силы \(F\) притяжения обкладок оказалась равна изменению со знаком минус величины \(W\). Это как раз и означает, что \(W\) — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора. Используя соотношение \(q = CU\), можно получить ещё две формулы для энергии конденсатора (проделать это самостоятельно).
\[\fbox{$W=\dfrac{qU}{2}$}, (2)\]
\[\fbox{$W=\dfrac{CU^2}{2}$}, (3)\]
Формулы (1)—(3) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
Автор Aluarius На чтение 5 мин. Просмотров 324 Опубликовано
Для чего предназначены резисторы и конденсаторы
Резисторы – одни из наиболее распространённых элементов в электронике. Их главное назначение – сопротивление течению тока и преобразовывать его в тепло. Главной характеристикой данных элементов является значение R.
Чем больше величина R, тем большая часть электроэнергии сможет рассеется в тепло. В схемах, которые питаются небольшим напряжением от 5 до 12 В, чаще всего используют резисторы имеющие величину R от 100 Ом до 100 кОм.
Конденсаторы – устройства, главная задача которых накапливать электрические заряды. Стоит отметить, что эту же функцию выполняет и аккумулятор, но в отличие от батареи конденсатор сразу же отдаёт весь накопившийся заряд. Величина, которую способно накопить устройство, называют «ёмкость».
Когда подсоединяется цепь к источнику электроэнергии: через конденсатор течет электрический ток. Сила тока в начале прохождения через устройство имеет наивысшее значение, в это же время напряжение станет низким.
После того, как устройство начнет накопление заряда, сила тока упадёт до нуля, а напряжение наоборот станет увеличиваться.
Особенности соединения резистора и конденсатора в цепи
Существует два типа соединения резисторов и конденсаторов: параллельное и последовательное.
Параллельное соединение резистора и конденсатора
Для того, чтобы осуществить параллельное соединение резистора и конденсатора, необходимо объединить все элементы цепи двумя узлами. Они не должны иметь связи с другими элементами.
При таком соединении, величина напряжения между обоими узлами станет падать, и оно станет равным для каждого элемента. А величина, которая обратна общему R, будет равняться сумме величин, которые обратны R всех проводников.
Когда осуществляется параллельное соединение резисторов, проводимость всех резисторов станет равняться проводимости цепи.
Если резистор соединить к заряженному конденсатору то вполне возможно короткое замыкание.
Последовательное соединение
Последовательное соединение – связка элементов между собой так, чтобы начальный участок цепи не имел ни одного узла. При таком соединении величина тока на проводниках станет равна между собой.
Когда осуществляется последовательное соединение всех элементов, то их общая ёмкость имеет формулу 1/Собщ = 1/С1 + 1/С2 + … + 1/Сn.
Как рассчитать импеданс в цепи
Импеданс – полное R тока, который обозначается Z. Этот параметр – отражение меняющегося во времени значения тока. Импеданс – векторная величина, которая состоит из двух значений: активное и реактивное сопротивление.
Активная часть импеданса, которая обозначается R – это мера степени, с которой материал будет противостоять движению электронов между атомными частицами. Чем легче атомные частицы освобождают или принимают электроны, тем ниже и сопротивление.
К материалам с минимальным сопротивлением можно отнести сталь, алюминий, золото. Самое большое значение R имеют стекло, слюда, полиэтилен и чаще всего их называют изоляторы или диэлектрики.
Стоит отметить! Активное R, имеет одно и тоже значение, как при последовательном, так и при параллельном соединении.
Если использовать резисторы в цепях синусоидального тока, то термин «импеданс» будет использоваться для обозначения сопротивления R=Z.
Практические расчеты импеданса чаще всего выполняются по следующей формуле:
Z = Um/Im.
Реактивное сопротивление обозначается X и является выражением степени, с которой электронный компонент схемы станет хранить или высвобождать электроэнергию, в то время, когда сила тока и значение напряжения станет колебаться при каждом цикле. Реактивное сопротивление выражается в числе Ом.
Энергия будет храниться и выделяться в двух типах:
- Магнитного поля. Реактивная часть является индуктивной.
- Электрического поля.
Как рассчитать время разряда и заряда конденсатора через резистор
Чтобы осуществить заряд устройства, нужно включить устройство в цепь и присоединить к зажимам генератора. Как вы уже знаете, генератор имеет внутреннее сопротивление.
Если резистор подключить к заряженному конденсатору то ключ будет замкнут и конденсатор начнёт зарядку до напряжения между обкладками, которая станет равна э.д.с генератора и равна Uc=E. При этом, обкладка которая соединена с положительным зажимом, получит положительный заряд, вторая же получит отрицательный заряд.
Чтобы обе обкладки устройства полностью зарядились, нужно, чтобы одни из них приобрела определенное количество электронов, а вторая столько же потеряла.
Зарядный ток в цепи будет протекать сотые доли секунды, пока величина напряжения на устройстве достигнет такой же уровня, что и на генераторе. В то время, пока конденсатор будет заряжаться, по всей цепи будет проходить зарядный ток. Вначале он будет иметь максимальную величину, т.к. величина напряжения станет равна 0.
По мере того как конденсатор станет заряжаться, величина R на нём будет падать.
Время процесса зарядки будет зависеть от следующих величин:
- Внутреннее сопротивление электрического генератора.
- Способность конденсатора принять количество тока.
Для того, чтобы разрядить устройство нужно отключить его от генератора переменного тока и присоединить к его обкладкам сопротивление. Дело в том, что на обкладках уже есть разность потенциалов, поэтому в цепи потечет ток.
Он будет проходить от одной обкладки через сопротивление к другой. Процесс разряда будет проходить до тех пор, пока обе обкладки не станут равны, т.е. пока напряжение между ними станет равно 0.
В самом начале, напряжение будет максимальным, сила тока – наибольшая. Как только начнется разрядка, напряжение и сила тока будут уменьшаться.
Продолжительность разряда устройства имеет зависимость от:
- Отношению заряда к разности потенциалов;
- Удельному электрическому сопротивлению.
Чем значение сопротивления выше, тем дольше будет происходить разряд конденсатора. Это можно объяснить тем, что при максимальном сопротивлении, сила тока небольшая, а величина заряда станет медленно уменьшаться.
Важно! Заряженный конденсатор не станет пропускать постоянный ток, потому что диэлектрик между его положительной и отрицательной обкладками будет размыкать цепь.
Для того, чтобы рассчитать время заряда и разряда на устройстве, лучше всего воспользоваться онлайн калькулятором.
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим необходимый конденсатор. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь 2 – 3 конденсатора на 470 микрофарад. Ставить конденсатор на 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров за одним конденсатором?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное .
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение конденсаторов. На практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С 1 – ёмкость первого конденсатора;
С 2 – ёмкость второго конденсатора;
С 3 – ёмкость третьего конденсатора;
С N – ёмкость N -ого конденсатора;
C общ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости конденсаторов нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если рассчитываем ёмкости в микрофарадах, то нужно указывать ёмкость C 1 , C 2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады или нанофарады можно воспользоваться специальной таблицей. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно пересчитать значения величин.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Для большего количества последовательно включенных конденсаторов потребуется другая формула. Она более запутанная, да и не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении конденсаторов их результирующая ёмкость будет всегда меньше наименьшей ёмкости, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсатор ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость составного конденсатора будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C 1 – ёмкость конденсатора.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из конденсаторов.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате ёмкость составного конденсатора составит 5 нанофарад.
Проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул для расчёта.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.), другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ с функцией измерения ёмкости конденсаторов и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости последовательно соединённых конденсаторов
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения конденсаторов. Проверим результат с помощью тестера (см. фото).
Измерение ёмкости параллельно соединённых конденсаторов
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединить конденсаторы?
Во-первых, не стоит забывать, что кроме ёмкости у конденсаторов есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально ёмкостям этих конденсаторов. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое должно быть у конденсатора взамен которого мы ставим составной конденсатор.
Если же используются конденсаторы одинаковой ёмкости, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов строго соблюдайте полярность! При параллельном соединении электролитических конденсаторов всегда соединяйте минусовой вывод одного конденсатора с минусовым выводом другого. Плюсовой вывод с плюсовым.
Параллельное соединение электролитических конденсаторов
Схема параллельного соединения
В последовательном соединении электролитических конденсаторов ситуация обратная. Необходимо соединять плюсовой вывод с минусовым. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитических конденсаторов
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из этих конденсаторов будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамически
Соединение конденсаторов — Студопедия
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторовможет производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
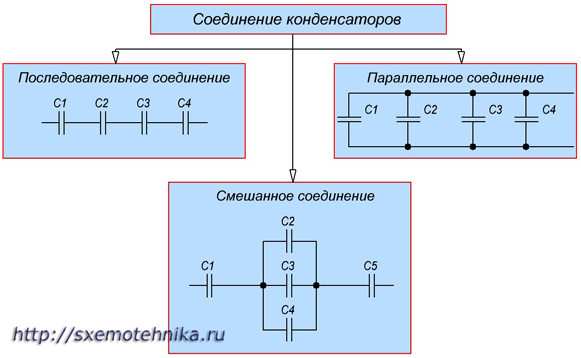
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
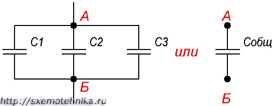
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
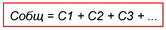
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
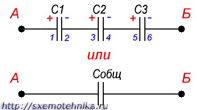
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
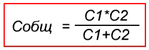
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
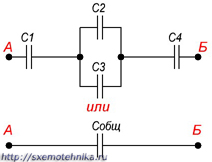
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
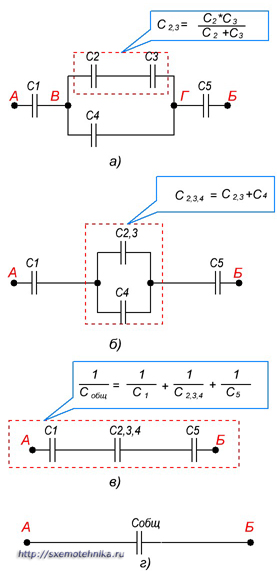
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
Конденсаторыпараллельно »Руководство по конденсаторам
Конденсаторы, как и другие электрические элементы, могут быть подключены к другим элементам последовательно или параллельно. Иногда полезно соединить несколько конденсаторов параллельно, чтобы создать функциональный блок, такой как на рисунке. В таких случаях важно знать эквивалентную емкость блока параллельного соединения. Эта статья будет посвящена анализу параллельного подключения конденсаторов и возможных приложений для таких цепей.
Анализ
Все конденсаторы в параллельном соединении имеют одинаковое напряжение на них, что означает:
, где V 1 — V n представляют напряжение на каждом соответствующем конденсаторе. Это напряжение равно напряжению, приложенному к параллельному соединению конденсаторов через входные провода. Однако количество заряда, хранящегося на каждом конденсаторе, не одинаково и зависит от емкости каждого конденсатора по формуле:
, где Q n — это количество заряда, накопленного на конденсаторе, C n — это емкость конденсатора, а V n — это напряжение, приложенное к конденсатору, которое равно напряжению, приложенному к полной параллельной цепи. блок подключения.Общее количество заряда, которое хранится в блоке конденсаторов, представлено как Q и разделено между всеми конденсаторами, присутствующими в этой цепи. Это представлено:
Следующее уравнение используется для определения эквивалентной емкости для параллельного подключения нескольких конденсаторов:
, где C eq — эквивалентная емкость параллельного соединения конденсаторов, V — напряжение, приложенное к конденсаторам через входные провода, и Q 1 — Q n представляют заряды, хранящиеся на каждом соответствующем конденсаторе.Это приводит нас к важному выводу:
, что означает, что эквивалентная емкость параллельного соединения конденсаторов равна сумме отдельных емкостей. Этот результат также интуитивно понятен — конденсаторы параллельно можно рассматривать как один конденсатор, площадь пластины которого равна сумме площадей пластины отдельных конденсаторов.
приложений
Конденсаторы — устройства, используемые для хранения электрической энергии в форме электрического заряда.При параллельном подключении нескольких конденсаторов полученная схема способна накапливать больше энергии, поскольку эквивалентная емкость представляет собой сумму отдельных емкостей всех задействованных конденсаторов. Этот эффект используется в некоторых приложениях.
Источники питания постоянного тока
Одним из примеров являются источники постоянного тока, которые иногда используют несколько параллельных конденсаторов для лучшей фильтрации выходного сигнала и устранения пульсации переменного тока. Используя этот подход, можно использовать конденсаторы меньшего размера, которые имеют превосходные характеристики пульсации при одновременном получении более высоких значений емкости.
Более высокие значения емкости
Есть некоторые приложения, которые просто требуют значений емкости, которые намного выше, чем доступные в продаже конденсаторы. Конденсаторные банки используются в таких приложениях. Одним из примеров являются конденсаторные батареи, используемые для коррекции коэффициента мощности с индуктивными нагрузками. Другим примером являются банки конденсаторов накопления энергии, которые объявлены для использования в автомобильной промышленности, а именно KERS (Kinetic Energy Recovery System), используемая для рекуперативного торможения в больших транспортных средствах, таких как трамваи, а также в гибридных автомобилях.
Импульсные нагрузки
Одна лаборатория с сильным магнитным полем обеспечивает работу самого мощного в мире магнита, способного создавать магнитное поле почти в 100 тесла, сохраняя энергию в конденсаторной батарее. Накопленная энергия высвобождается через магнитную катушку за очень короткое время, создавая очень мощное магнитное поле.
В любом случае конденсаторные батареи могут достигать очень высоких значений емкости. При использовании нескольких суперконденсаторов, соединенных параллельно, возможны емкости в несколько десятков килофарад, особенно с учетом того, что суперконденсаторы способны достигать значений емкости более 2000 фарад.
Проектные ограничения
При параллельном подключении конденсаторов необходимо учитывать некоторые моменты. Один из них заключается в том, что максимальное номинальное напряжение параллельного соединения конденсаторов является таким же высоким, как и минимальное номинальное напряжение всех конденсаторов, используемых в системе. Таким образом, если несколько конденсаторов, рассчитанных на 500 В, подключены параллельно к конденсатору, рассчитанному на 100 В, максимальное номинальное напряжение всей системы составляет всего 100 В, поскольку одинаковое напряжение подается на все конденсаторы в параллельной цепи.
Безопасность
Еще один момент, о котором следует помнить, это то, что конденсаторные батареи могут быть опасными из-за количества накопленной энергии и того факта, что конденсаторы способны выделять накопленную энергию за очень короткое время. Эта накопленная энергия иногда эффективна, чтобы вызвать серьезные травмы или повреждение электропроводки и устройств при случайном замыкании.
,- Программирование
- электроника
- Компоненты
- Компоненты электроники: конденсаторы параллельно и серии
By Doug Lowe
Вы можете комбинировать конденсаторы в последовательных или параллельных сетях для создания любого значения емкости, которое вам нужно в электронной схеме. Например, если вы объединяете три конденсатора емкостью 100 мкФ параллельно, общая емкость цепи составляет 300 мкФ.
Объединить конденсаторы параллельно
Расчет общей емкости двух или более конденсаторов параллельно прост: просто сложите значения отдельных конденсаторов, чтобы получить общую емкость.
Это правило имеет смысл, если задуматься. Когда вы подключаете конденсаторы параллельно, вы по существу подключаете пластины отдельных конденсаторов. Таким образом, параллельное подключение двух одинаковых конденсаторов по существу удваивает размер пластин, что фактически удваивает емкость.
Здесь две цепи имеют одинаковую емкость. Первая схема выполняет работу с одним конденсатором, вторая — с тремя. Таким образом, схемы эквивалентны.
Всякий раз, когда вы видите два или более конденсаторов параллельно в цепи, вы можете заменить один конденсатор, значение которого является суммой отдельных конденсаторов. Точно так же, каждый раз, когда вы видите один конденсатор в цепи, вы можете заменить два или более конденсаторов параллельно, если их значения в сумме составляют первоначальное значение.
Общая емкость параллельных конденсаторов всегда больше емкости любого из отдельных конденсаторов. Это потому, что каждый конденсатор добавляет свою общую емкость к общей.
Подключите конденсаторы последовательно
Вы также можете комбинировать конденсаторы последовательно для создания эквивалентных емкостей. Когда вы делаете, однако, математика немного сложнее. Оказывается, что расчеты, необходимые для последовательно соединенных конденсаторов, такие же, как и для параллельных вычислений резисторов.
Вот правила для расчета емкости последовательно:
Если конденсаторы имеют одинаковую ценность, вам повезло. Все, что вам нужно сделать, это разделить значение одного из отдельных конденсаторов на количество конденсаторов. Например, общая емкость двух конденсаторов емкостью 100 мкФ составляет 50 мкФ.
Если задействованы только два конденсатора, используйте этот расчет:
В этой формуле C1 и C2 являются значениями двух конденсаторов.
Вот пример, основанный на последовательно соединенных конденсаторах 220 мкФ и 470 мкФ:
Для трех или более последовательно соединенных конденсаторов формула:
Обратите внимание, что многоточие в конце выражения указывает на то, что вы продолжаете складывать обратные значения емкостей для стольких конденсаторов, сколько у вас есть.
Вот пример для трех конденсаторов со значениями 100 мкФ, 220 мкФ и 470 мкФ:
Как видите, окончательный результат 59.9768 мкФ. Если ваше имя не является Споком, вы, вероятно, не заботитесь о том, чтобы ответ был настолько точным, поэтому вы можете безопасно округлить его до 60 мкФ.
Формулы для расчета общей емкости конденсаторной сети противоположны правилам, которым вы руководствуетесь при расчете резисторных сетей. Другими словами, формула, которую вы используете для последовательных резисторов, применяется к конденсаторам параллельно, а формула, которую вы используете для резисторов параллельно, применяется к конденсаторам последовательно.Разве не смешно, что науке иногда нравится возиться с твоим разумом?
,, параллельные и последовательно-параллельные цепи, их сравнение и применение
Почему параллельное соединение предпочтительнее последовательного соединения?
Использование, применение и важность последовательного и параллельного соединения сегодня нельзя переоценить. Применение последовательного и параллельного соединения можно увидеть в наших домах, школьных залах и в наших уличных фонарях.С нажатием кнопки все Бобы в наших гостиных включаются. некоторые ссылаются на то, что у бобов в их домах должны быть разные выключатели.
Ну, это не волшебство, когда более чем три электрических удара или нагрузки управляются одним выключателем. Нагрузка — это все, что угодно, т. Е. Это могут быть приборы, электробобы или даже потолочные вентиляторы, которые потребляют электроэнергию при подключении к источнику питания. Электрические бобы, телевизоры, холодильники и т. Д. Можно назвать нагрузкой.Бобс преобразует электрическую энергию в форму света и тепла. Вентиляторы преобразуют электрическую энергию в механическую.
Тип подключения наших потолочных вентиляторов, электрические бобы будут определять, будет ли у них общий выключатель или нет. Последовательное соединение цепей дает нам возможность подключать более двух нагрузок к общему коммутатору. Уличные фонари являются очень хорошим примером этого. Параллельное соединение цепей позволяет нам подключать нагрузки к их отдельным выключателям.Как последовательное, так и параллельное соединение хорошо, но одно по большей части предпочтительнее другого по той или иной причине. Прежде чем говорить о причине, по которой параллельное соединение предпочтительнее последовательного, давайте вспомним, какие последовательные и параллельные соединения являются первыми.
Последовательная цепь
Последовательная цепь — это цепь, в которой резисторы или нагрузки подключены вплотную, так что цепь будет иметь только один путь, по которому течет электрический ток.Таким образом, когда несколько резисторов соединены последовательно, эффективное сопротивление (полное сопротивление в цепи) получается путем сложения индивидуального сопротивления алгебраически. То есть, если у нас есть резисторы с сопротивлением R1, R2, R3… Rn , соединенные последовательно , то;
R и = R T = R 1 + R 2 + R 3 +… R n .
При последовательном соединении один и тот же ток протекает через все ветви цепей, но разное напряжение на нем, поэтому резисторы имеют различное напряжение на них.Каждый резистор или нагрузка будет испытывать падение напряжения. Приложенное напряжение равно сумме падения напряжения на разных участках цепи. Падение напряжения пропорционально току сопротивления, который одинаков во всей цепи. Когда нагрузки соединены последовательно, нагрузки будут иметь общий выключатель. Этот вид связи используется в школьных залах, уличных фонарей.
Как подключить фонари в серии?Использование и применение последовательного соединения
Некоторые люди последовательно подключают охранные фонари в своих домах, что позволяет им иметь общий выключатель.Проблема с этим типом соединения заключается в том, что, когда нагрузка создает проблему, другая подключенная система выйдет из строя. Это соединение типа «все или ничего». Пока нагрузка получает энергию до того, как она доставит ее другому, а та, которая доставит, не получится, произойдет отключение.
Серийные соединения сериишироко распространены и широко используются в электрооборудовании. Нити трубки в небольших радиоприемниках обычно бывают последовательными. Устройства контроля тока всегда соединены последовательно с устройством, которое они защищают.Предохранители соединены последовательно с устройством, которое они защищают, автоматическое отопительное оборудование имеет термостат, электромагнитные катушки и защитные выключатели, соединенные последовательно с источником напряжения и т. Д.
Недостатки последовательной цепи
- Разрыв в проводе неисправность или отсоединение какой-либо одной лампы нарушит цепь и приведет к тому, что все остальные перестанут работать, поскольку в цепи протекает только один путь тока.
- Если в последовательную цепь освещения будет добавлено больше ламп, их яркость уменьшится.потому что напряжение распределяется в последовательной цепи. Если мы добавим больше нагрузок в последовательную цепь, то падение перенапряжения будет увеличиваться, что не является хорошим знаком для защиты электрических приборов. Серия
- Проводка типа «ВСЕ или НЕТ» означает, что все устройства будут работать одновременно или все они отключатся, если произойдет сбой в любом из подключенных устройств в последовательной цепи.
- Высокое напряжение питания необходимо, если нам нужно добавить больше нагрузки (лампочки, электрические обогреватели, кондиционер и т. Д.) В последовательную цепь.Например, если пять последовательно соединенных ламп 220 В, напряжение питания должно быть: 5 x 220 В = 1,1 кВ.
- Общее последовательное сопротивление цепи увеличивается (и уменьшается ток) при увеличении нагрузки в цепи.
- В соответствии с будущими потребностями, в эту последовательную цепь тока должны быть добавлены только те электрические приборы, если они имеют такой же номинальный ток, что и ток в каждой точке последовательной цепи. Тем не менее, мы знаем, что электрические приборы и устройства я.е. лампочки, вентилятор, обогреватель, кондиционер и т. д. имеют различную номинальную силу тока, поэтому они не могут быть подключены в последовательную цепь для бесперебойной и эффективной работы.
Светильники, подключенные последовательно Серия
Преимущества Соединение серии
- При последовательной разводке требуется меньший размер проводного кабеля.
- Мы используем для защиты цепи для последовательного подключения плавких предохранителей и автоматических выключателей с другими приборами. Схема серии
- не может легко перегружаться из-за высокого сопротивления при увеличении нагрузки в цепи.
- Срок службы батареи в последовательной цепи больше по сравнению с параллельной.
- Это самый простой метод электропроводки, и неисправность можно легко обнаружить и устранить по сравнению с параллельной или последовательно-параллельной проводкой.
Параллельная цепь
Резисторы, нагрузки, как говорят, соединены параллельно, когда конец каждого из резисторов или нагрузок имеет общую точку или соединение, а другие концы также связаны с общей точкой или переходом.Такие схемы известны как параллельные схемы.
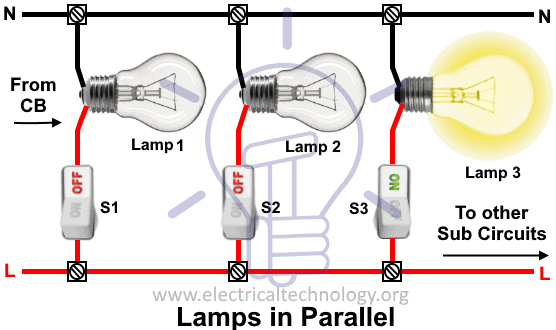
Лампочки, подключенные параллельноВ отличие от последовательного соединения цепей, при нахождении полного (эффективного) сопротивления в параллельной цепи берется обратная величина для отдельного сопротивления. Таким образом, когда несколько сопротивлений соединены параллельно, обратная величина эффективного сопротивления задается арифметической или алгебраической суммой обратной величины индивидуального сопротивления.
1 / R и или 1 / R T = 1 / R 1 + 1 / R 2 + 1 / R 3 … 1 / R n .
Подключение параллельных цепей имеет одинаковое напряжение, протекающее по всем ветвям цепей. Разные резисторы имеют свои индивидуальные токи.
Использование и применение параллельного соединения
Параллельное соединение очень распространено в использовании. Различные лампы и электроприборы в наших домах соединены параллельно, так что каждая из ламп или ламп и приборов может работать независимо. Для того чтобы мы могли контролировать отдельные лампы или нагрузки, они должны быть подключены параллельно.
Преимущества параллельной цепи
- Каждое подключенное электрическое устройство и прибор независимы от других. Таким образом, включение / выключение устройства не повлияет на другие устройства и их работу.
- В случае обрыва кабеля или удаления какой-либо лампы не будут нарушены все цепи и подключенные нагрузки, другими словами, другие лампы / лампы и электроприборы будут работать без сбоев.
- Если в параллельные цепи освещения будет добавлено больше ламп, их яркость уменьшаться не будет (как это происходит только в последовательных цепях освещения).Потому что напряжение одинаково в каждой точке параллельной цепи. Короче говоря, они получают то же напряжение, что и напряжение источника.
- Можно добавить больше осветительных приборов и точек нагрузки в параллельных цепях в соответствии с будущими потребностями, если цепь не перегружена.
- Добавление дополнительных устройств и компонентов не увеличит сопротивление, но уменьшит общее сопротивление цепи, особенно при использовании устройств с высоким номинальным током, таких как кондиционер и электрические нагреватели.
- параллельная проводка более надежна, безопасна и проста в использовании. Неисправности в параллельных цепях освещения
Недостатки параллельных соединений
- В кабельной проводке параллельного освещения используется больший размер кабеля и провода.
- Необходим больший ток, если в параллельной цепи добавлена дополнительная лампочка.
- Батарея быстрее разряжается для установки постоянного тока.
- Конструкция параллельной разводки является более сложной по сравнению с последовательной разводкой.
Похожие сообщения: Какая лампа светится ярче при последовательном и параллельном подключении и почему?
Последовательные параллельные соединения и цепи
Схема является последовательной или параллельной на следующем рисунке, т.е. это последовательная схема. Первые три лампы (B 1 , B 2 и B 3 ) подключены параллельно, а переключатели (S 1 , S 2 и S 3 ) подключены последовательно.B 7 , B 8 , B 9 и B 10 расположены последовательно друг с другом, параллельно двум первым лампам (B 1 , B 2 и B 3 ) в то время как переключатели (S5 и S6) параллельно соединены с лампой (B 10 ). Кроме того, лампочки (B 4 , B 5 и B 6 ) и выключатель (S 7 ) соединены последовательно друг с другом, параллельно (B 1 , B 2 и B (3 ) и так далее.
Поскольку схема представляет собой комбинацию последовательных и параллельных, мы не можем упростить ток, напряжение, сопротивление и мощность с помощью простого закона Ома. Мы должны применять различные теоремы, такие как теорема Нортона, Тевенина, максимальная передача мощности и т. Д., Или упростим схему в основных последовательных и параллельных цепях, чтобы найти все эти величины.
Наиболее распространенная в настоящее время установка электропроводки в домашних условиях с использованием этого метода электропроводки.
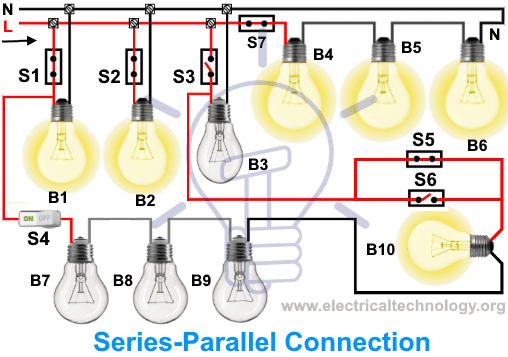
Последовательное и параллельное освещение цепиСравнение между последовательным и параллельным подключением
Ниже в данной таблице показаны основные различия между последовательными и параллельными соединениями.
| S № | Последовательная схема | Параллельная схема |
| Ток (I) | Ток одинаков в каждой точке последовательной цепи: I = I = 2 = I 3 =…. I n | Ток является аддитивным в последовательной цепи: I 1 + I 2 + I 3 +…. I n |
| Напряжение (В) | Напряжение является аддитивным в последовательной цепи: В 1 + V 2 + V 3 +….V n | В каждой точке параллельной цепи напряжения одинаковы: V 1 = V 2 = V 3 =…. V n |
| Сопротивление (R) и найти (R) | Сопротивление аддитивно в последовательной цепи: R 1 + R 2 + R 3 +… R n = R eff = R T | Сопротивление делится при увеличении нагрузки в цепи. 1 / R T = 1 / R 1 + 1 / R 2 + 1 / R 3 … 1 / R n или I = G 1 + G 2 + G 3 +… G n |
| Найти ток (I) | I = V 1 / R 1 = V 2 / R 2 = V 3 / R 3 = V n / R n | I = V 1 / R 1 + V 2 / R 2 + V 3 / R 3 + V n / R n |
| Найти напряжение (В) | V = I 1 R 1 + I 2 R 2 + I 3 R 3 +… I n R n | V = I 1 R 1 = I 2 R 2 = I 3 R 3 =… I n R n |
P = I 2 R 1 + I 2 R 2 +… I 2 R n или P = V 1 2 / R 1 + V 2 2 / R 2 +… V n 2/ R n | P = V 2 / R 1 + V 2 / R 2 +… V 2/ R n или P = I 1 2 R 1 + I 2 2 R 2 +… I n 2 R n | |
| Правило деления тока и напряжения | V 1 = V T (R 1 / R T ), V 2 = V T (R 2 / R T ) | I 1 = I T (G 1 / G T 900 32), I 2 = I T (G 2 / G T ) |
| Пути протекания электрического тока | Только один путь | Два или более путей |
| Яркость лампы | Диммер, если добавлено больше ламп (P = V x I) | Ярче из-за одинаковых напряжений |
| Если в цепи возникают обрывы | Вся цепь бесполезна | Остальная часть Цепь все еще будет работать |
| Состояние батареи | Батарея разряжается медленно (батарея заряжается) | Батарея быстро разряжается (батарея заряжается время и токи) |
| Применения | Используется для защиты цепи во время работы Подключение плавких предохранителей и автоматических выключателей последовательно с подключенными приборами | Используется в большинстве бытовых электропроводок |
Преимущества параллельного подключения по сравнению с последовательным подключением
Последовательное подключение — это соединение типа «все или ничего».Это означает, что если один из устройств выходит из строя, все другие устройства также выходят из строя, поэтому этот тип соединения хорош только тогда, когда мы хотим защитить устройство.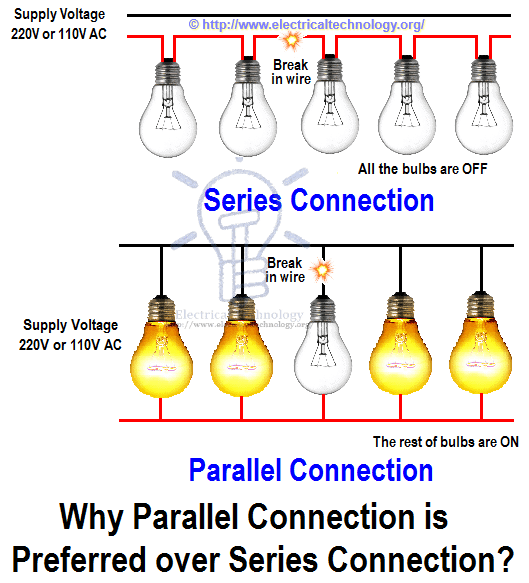 
Если предохранитель перегорел, например, из-за высокого тока, то защищаемое им устройство не будет повреждено, так как ток больше не достигнет его. В то время как последовательное соединение является полным или нулевым, параллельное соединение дает вам возможность распределять нагрузки и устройства по отдельности. Параллельное соединение обеспечивает сопротивление потоку тока по сравнению с последовательным соединением.
Недостатки схемы последовательного освещенияСопротивление 100 Ом и резисторы 150 Ом, подключенные параллельно, будут оказывать меньшее влияние на электрический ток по сравнению с последовательно подключенными резисторами 50 Ом и 40 Ом. В электронных устройствах параллельное соединение имеет первостепенное значение. Ячейки в банке питания все соединены параллельно. Параллельное соединение делает электрическую энергию дольше. Сами элементы имеют свое внутреннее сопротивление, поэтому, если они были подключены последовательно, часть энергии будет потеряна при преодолении внутреннего сопротивления, так как его эффект высок при последовательном соединении, чем при параллельном подключении.
Похожие сообщения:
конденсаторов MCQ с пояснительными ответами
конденсаторов MCQ с пояснительными ответами1. Маркировка на керамических или неполяризованных конденсаторах — «104». Какова стоимость конденсатора?
- 104 мкФ
- 10000 мкФ
- 10000 нФ
- 100000 пФ
Показать пояснительный ответ
Ответ: 4. 100000 пФ
Объяснение :
Здесь обозначение конденсатора «104»
Это означает, что = 10 + 4 нуля = 1 000,00 пФ
= 100 нФ = 0.1 мкФ
2. Конденсатор проходит переменный ток и блокирует постоянный ток
- Верный
- Ложь
Показать пояснительный ответ
Ответ: (1)
Емкостная реактивность дается как:
X c = 1/2 πfC
Где f — частота приложенного напряжения к обкладкам конденсатора, а C — емкость.
Для постоянного тока значение f равно нулю и, следовательно, емкостное сопротивление равно бесконечности. Поскольку емкостное реактивное сопротивление обозначает сопротивление потоку тока так же, как и сопротивление, это подразумевает, что конденсатор блокирует прохождение постоянного тока.
Поскольку частота сигналов переменного тока не равна нулю или меньше его, емкостное сопротивление имеет конечное значение для питания переменного тока и позволяет пропускать переменный ток.
3. Выводы всех конденсаторов поляризованы.
- True
- False
Показать пояснительный ответ
Ответ: (2)
Конденсаторы бывают двух типов в зависимости от их полярности — электролитные и неполяризованные конденсаторы. В то время как электролитические конденсаторы имеют поляризованные выводы, неполяризованные конденсаторы, такие как керамика, слюда и т. Д.есть эквивалентные выводы.
4. Значение приведенного ниже дискового керамического конденсатора составляет:
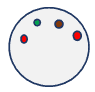
- 400pF , +/- 5% допуск
- 250pF , +/- 2% допуск
- 300pF , допуск +/- 4%
- 100 нФ , допуск +/- 2%
Показать пояснительный ответ
Ответ: (2)
Согласно цветовому коду для дискового керамического конденсатора, первый два цвета представляют значение емкости, третий цвет представляет множитель, а последний цвет представляет допуск.
Таким образом, обращаясь к таблице цветов, мы приходим к следующему выводу:
- Первый цвет: красный. Следовательно первая цифра 2
- Второй цвет: зеленый. Следовательно вторая цифра 5
- Таким образом, значение емкости составляет 25
- Третий цвет: коричневый. Следовательно, множитель 10 пФ
- Четвертый цвет: красный. Следовательно, допуск составляет +/- 2%
. Следовательно, значение конденсатора составляет 25 x 10 пФ, +/- 2%, то есть 250 пФ, допуск +/- 2%.
5. Показание приведенного ниже конденсатора составляет
- 46 x 10 пФ, допуск +/- 5%, 250 вольт
- 50 х 100 пФ, допуск +/- 2%, 100 вольт
- 35 x 10 мкФ, допуск +/- 1%, 60 вольт
- 50 Допуск x 100 нФ, +/- 4%, 250 вольт
Показать пояснительный ответ
Ответ: (1)
Согласно Цветовой код для трубчатого конденсатора, первые два цвета представляют значение емкости, третий цвет представляет множитель, четвертый цвет представляет допуск, а последний цвет представляет максимально допустимое напряжение на конденсаторе.
Таким образом, обращаясь к таблице цветов, мы приходим к следующему выводу:
- Первый цвет: желтый. Следовательно первая цифра 4
- Второй цвет: синий. Следовательно, вторая цифра равна 6
- . Таким образом, значение емкости равно 46.
- Третий цвет: коричневый. Следовательно, множитель 10 пФ
- Четвертый цвет: зеленый. Следовательно, допуск составляет +/- 5%
- Пятый цвет: красный. Следовательно, напряжение составляет 250 Вольт
Таким образом, значение конденсатора составляет: 46 x 10 пФ, допуск +/- 5%, 250 Вольт.
6. Для конденсаторов, подключенных параллельно, общая емкость будет:
- Произведение отдельных емкостей
- Сумма отдельных емкостей
- Обратное значение суммы обратных значений конденсаторов
- эти
Показать пояснительный ответ
Ответ: (2)
Рассмотрим нижеприведенное параллельное соединение конденсаторов
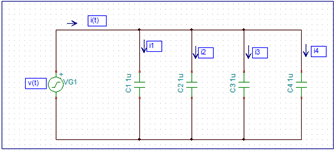
Применяя текущий закон Кирхгофа, мы получаем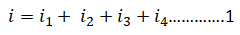 
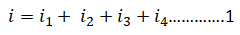
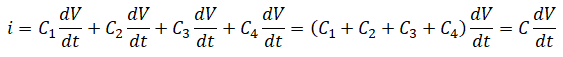
Таким образом, для параллельного подключения конденсаторов общая емкость представляет собой сумму отдельных емкостей.
7. Для конденсаторов, включенных последовательно, общая емкость равна:
- То же, что и значение общих сопротивлений в параллельном соединении
- Сумма отдельных значений
- То же, что и значение общих значений последовательные сопротивления
- Ни одно из этих
Показать пояснительный ответ
Ответ: (1)
Рассмотрим схему, приведенную ниже :
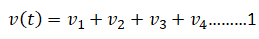
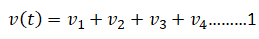
Теперь напряжение на конденсаторе N,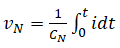 
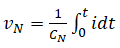
Поскольку ток в контуре одинаков.Следовательно, уравнение 1 становится следующим:
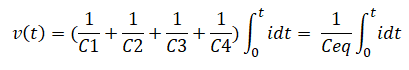
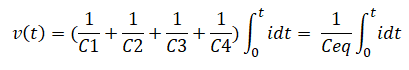
Таким образом, общая емкость для последовательно соединенных конденсаторов равна суммарному сопротивлению параллельно.
8. Энергия, накопленная в конденсаторе:
- ¼ CV
- ½ CV 2
- CV 2
- Show / 2CV 000 Пояснительный ответ
Ответ: (2)
Когда на конденсатор подается напряжение v (t), через него протекает ток I.Энергия, запасенная в конденсаторе, является интегралом мгновенной мощности.
Таким образом, энергия,
Таким образом, энергия, накопленная в конденсаторе, E = 1 / 2CV 2
9. Значение ESR для фактических конденсаторов находится в диапазоне:
- Милли Ом до
- Ом до Милли Ом
- Ом до Мега
- Нано Ом до
Показать Пояснительный ответ
Ответ: (1)
Хотя теоретически диэлектрический материал между пластинами Конденсатор имеет бесконечное удельное сопротивление, он имеет некоторое конечное удельное сопротивление, которое приводит к протеканию тока, известного как ток утечки.- 4 джоулей, 72 x 10 -4 джоулей
- 0 джоулей, 144 x 10 -5 джоулей, 72 x 10 -5 джоулей
- 72 x 10 9 -4 Джоулей, 144 микро Джоулей, 0 Джоулей
- Ни один из этих
Показать пояснительный ответ
Ответ: (2)
Дано: Напряжение на конденсаторе, C1 = 0
Следовательно, энергия накапливается в конденсаторе , C1 = 0 Джоулей
Напряжение на конденсаторе, C2 = 12В
Следовательно, энергия, накопленная в конденсаторе, C2 = 1 / 2CV 2 = 144 x 10 -5 Джоулей
Напряжение на конденсаторе, C3 = 12V
Следовательно, энергия, накопленная в конденсаторе, C3 = 1 / 2CV 2 = 72 x 10 -5 Джоулей
11. Для приведенной ниже цепи ток через конденсатор составляет ———-?
- 0.2cos 100πt
- 0.15cos 100πt
- 0.1cos 100πt
- 0.25cos 100πt
Показать пояснительный ответ
Данные
(t) = 30sin (100 πt)Емкость, C1 = 50 мкФ
Таким образом, ток через конденсатор, i (t) = Кдв (т) / dt = 50 x 10 -6 d (30sin 100πt) / dt = 50 x 10 -6 x 30 x 100 x πcos 100 πt = 15 x 10 -2 cos 100πt
12. Конденсатор работает в ———–
- Электрическое поле
- Магнитное поле
- Ни один из этих
- Оба
Показать пояснительный ответ
Ответ: (1)
Конденсатор состоит из двух электрических проводники разнесены на расстояние d с диэлектрическим материалом. Когда на проводники подается напряжение, разность потенциалов между проводниками заряжает проводники, что создает однородное электрическое поле между проводниками.Это электрическое поле определяется как сила на единицу заряда. Таким образом, конденсатор работает в электрическом поле.
13. Емкость конденсатора — это мера его способности ——-
- Сопротивление течению тока
- Накопительный заряд
- Допустимое течение тока
- Ни один из этих
Показать пояснительный ответ
Ответ: (2)
Емкость — это мера конденсатора для хранения заряда для данного электрического потенциала.Если он заряжается до напряжения «V», он сохраняет заряд + Q на одной пластине и зарядку -Q на другой пластине. Емкость 1 Фарад обозначает накопление 1 кулоновского заряда для разности потенциалов 1 В.
14. Когда на конденсатор подается напряжение постоянного тока, оно ———–
- Действует как короткое замыкание в момент приложения напряжения, а затем как разомкнутая цепь после полной зарядки
- Действует как разомкнутая цепь с самого начала применяется к конденсатору, первоначально высокий ток проходит через пластины конденсатора, когда он начинает заряжаться.По истечении времени «t» значение тока падает до нуля, когда пластины конденсатора полностью заряжаются. Это время «t» задается как обратная величина RC, где R — значение резистора R1.
15. Конденсаторы используются в системе электроснабжения для ——–
- Повышение коэффициента мощности
- Уменьшение линейного тока
- Обеспечение стабильности напряжения
- Все эти
Показать пояснительный ответ
Ответ: (4)
Большинство систем электроснабжения имеют индуктивные нагрузки, что вызывает запаздывающее влияние на ток питания.Это вызывает увеличение полной или реактивной мощности и увеличивает ток питания.
.