Параллельное соединение — урок. Физика, 8 класс.

При параллельном соединении все потребители подключены к источнику тока независимо друг от друга и образуют разветвлённую цепь.

При параллельном соединении все потребители подключены к одному источнику тока, между клеммами которого имеется определённое напряжение.

Каждый потребитель получает полное напряжение цепи.
 

U=U1=U2=U3=…

При параллельном соединении общий ток является суммой токов, протекающих через отдельные потребители.

 

I=I1+I2+I3+…

 

Общее сопротивление потребителей, находящихся в параллельном соединении, будет наименьшим (меньше, чем наименьшее из сопротивлений параллельно подключённых потребителей).
Если параллельно соединены \(n\) потребителей, а сопротивление каждого из них одинаково и равно \(R\), тогда общее сопротивление цепи будет равно \(R : n\).

Можно сделать вывод о том, что при увеличении числа потребителей общая сила тока неограниченно возрастает, что может привести к пожару.

 

Обрати внимание!

В одну розетку нельзя включать несколько мощных потребителей, так как перенагруженные провода нагреваются и могут загореться.

В квартире потребители включены в параллельное соединение. Подводка электричества, входящего в квартиру, состоит из нескольких проводов, которые проходят через счётчик, измеряющий потребление электроэнергии. Электрический ток течёт через предохранители, которые подключены последовательно и предусмотрены для определённой силы тока в цепи. Они размыкают цепь в случае опасной перегрузки.

Электрический кабель, который используется в электрической цепи квартиры, имеет три провода. Третий провод является заземлением.

Преимуществом параллельного соединения является то, что при отключении одного из потребителей, остальные продолжают работать.

Источники:

 

http://www.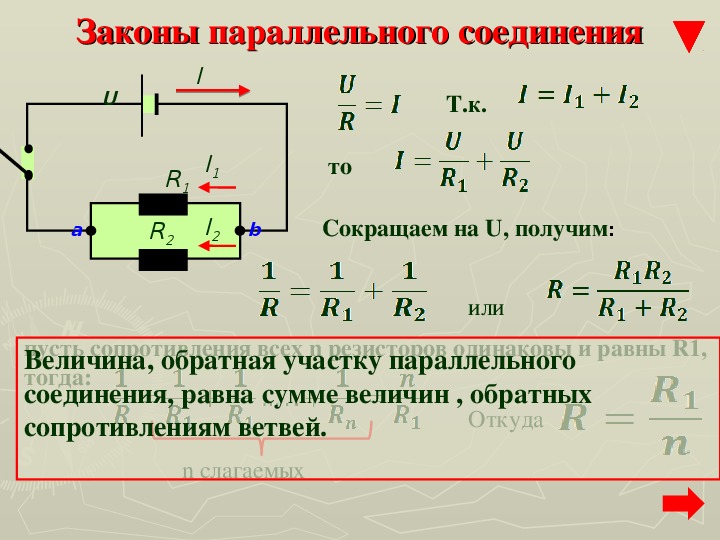 ndg.lv/latvian/Macibas/FizInter/b2.2.4.htm
http://www.goerudio.com/demo/paralelais_slegums
http://www.ndg.lv/latvian/Macibas/FizInter/b2.2.4.htm

Параллельное соединение проводников | Физика

При параллельном соединении все проводники (резисторы, лампы и т.д.) подключаются к одной и той же паре точек A и B (рис. 43). Связь между общими значениями силы тока, напряжения и сопротивления с их значениями на отдельных участках цепи при этом отличается от той, что была при последовательном соединении. Теперь соответствующие формулы имеют вид

I = I₁ + I₂, (17.1)     U = U₁ = U₂, (17.2)      R = (R₁R₂) / (R₁ + R₂). (17.3)

Чтобы убедиться в справедливости этих соотношений, следует собрать цепь и с помощью амперметра и вольтметра произвести необходимые измерения.

Итак, при параллельном соединении проводников напряжение на всех участках цепи одно и то же, общая сила тока равна сумме сил токов на отдельных проводниках, а общее сопротивление двух проводников находится как отношение произведения их сопротивлений к их сумме.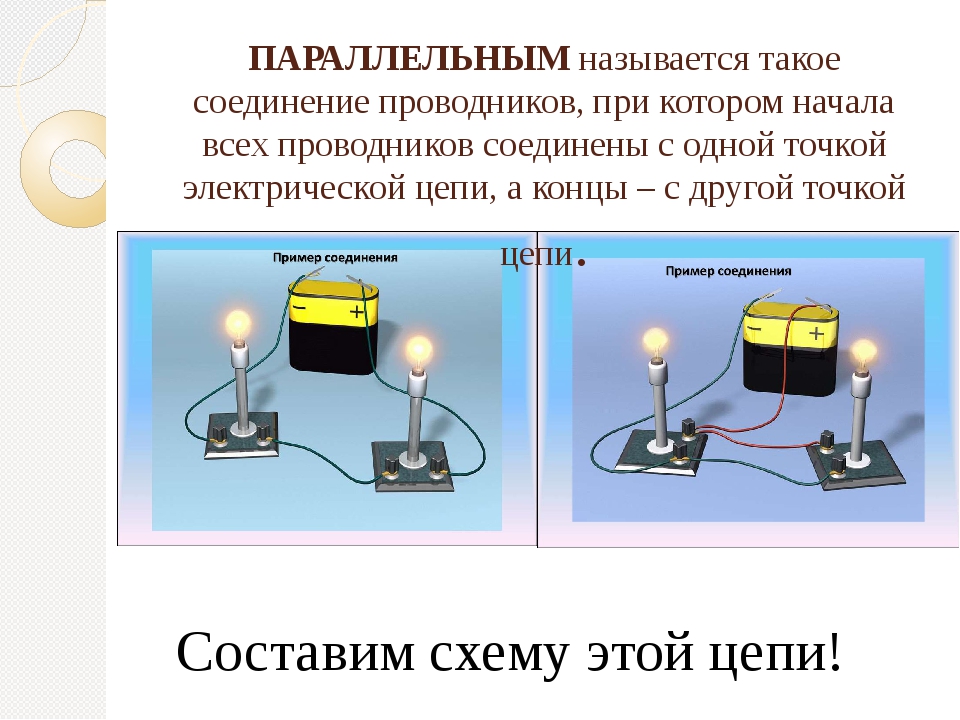

Первые две из этих закономерностей справедливы для любого числа параллельно соединенных проводников, последняя — только для двух.

Если R₁ = R₂, то

R = (R₁R₂) / (R₁ + R₂) = R₁²/2R₁ = R₁/2      (17.4)

Мы видим, что общее сопротивление двух одинаковых проводников в 2 раза меньше сопротивления одного проводника. Эта закономерность допускает обобщение: если параллельно соединено n одинаковых потребителей электроэнергии (резисторов, ламп и т.д.), то их общее сопротивление в n раз меньше сопротивления каждого из них:

R = R₁

/n      (17.5)

Отсюда следует, что с увеличением числа проводников общее сопротивление будет становиться все меньше и меньше. Это может показаться странным. На самом деле ничего удивительного в этом нет: ведь при параллельном соединении проводников происходит как бы увеличение общей площади их поперечного сечения, а с увеличением площади сечения проводника, как известно, его сопротивление уменьшается.

Отличительной особенностью параллельного соединения нескольких потребителей является то, что при выключении одного из них остальные продолжают работать. Так, например, вывернув одну лампу в цепи, изображенной на рисунке 44, мы увидим, что другая будет по-прежнему гореть.

Большинство потребителей электроэнергии — электронагревательные приборы, холодильники, швейные машины, магнитофоны, телевизоры и т. д. — рассчитаны на напряжение сети 220 В. Поэтому все они должны включаться в сеть параллельно, ибо только в этом случае они окажутся под одним и тем же напряжением (220 В) и будут продолжать работать при выключении одного из них.

На рисунке 45 приведена упрощенная схема квартирной электропроводки. Провода сети, между которыми существует напряжение 220 В, обозначены буквами Ф и О. Первый из них называют фазным, второй — нулевым. Нулевой провод соединен с землей. Именно с ним соединяют все потребители. И наоборот, все выключатели соединяют с фазным проводом. Такой порядок подключения потребителей и выключателей обеспечивает наибольшую безопасность человека.

??? 1. Какое соединение называют параллельным? 2. Начертите схему цепи, изображенной на рисунке 44. 3. Какие три закономерности справедливы для параллельного соединения проводников? 4. Как находится общее сопротивление параллельно соединенных проводников, когда они одинаковые? 5. Перечислите все элементы электрической цепи, изображенной на рисунке 45. 6. Предположим, что при замене лампы человек случайно коснулся металлического контакта в патроне лампы и одновременно с этим какой-либо заземленной части здания (например, батареи отопления). Под каким напряжением он окажется? Рассмотрите ситуацию, когда лампа и выключатель подсоединены к проводам сети так, как это показано на рисунке 45. Что произойдет, если лампу и выключатель поменять местами? 7. Почему у вольтметров делают большое внутреннее сопротивление, а у амперметров — малое?

Виды соединения проводников

При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.

Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.

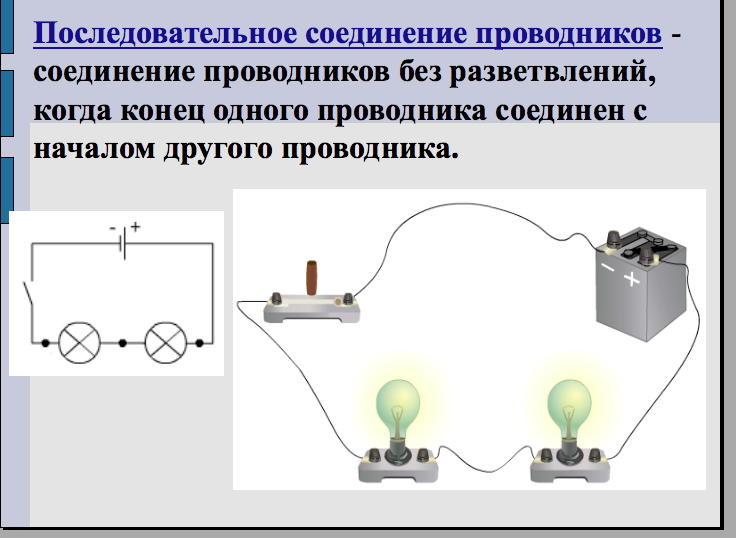
Последовательное соединение

Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.

При последовательном соединении сопротивления элементов суммируются. 

Параллельное соединение

Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.

При параллельном соединении эквивалентное сопротивление находится как:

В случае двух параллельно соединенных резисторов

В случае трех параллельно подключенных резисторов:

Смешанное соединение

Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.

Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R₃

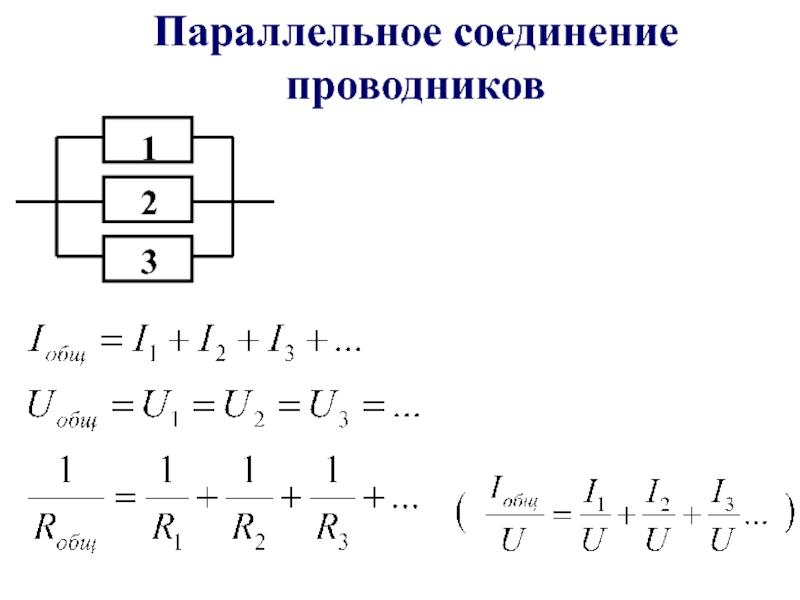. Следует понимать, что после преобразования эквивалентное сопротивление R₁R₂ и резистор R₃, соединены последовательно.

 

Итак, остается самое интересное и самое сложное соединение проводников.

Мостовая схема

Мостовая схема соединения представлена на рисунке ниже.

Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.

И находят сопротивления R₁, R₂ и R₃. 

Затем находят общее эквивалентное сопротивление, учитывая, что резисторы R₃,R₄ и R₅,R₂ соединены между друг другом последовательно, а в парах параллельно. 

На этом всё! Примеры расчета сопротивления цепей тут.

Просмотров: 38654

Параллельное соединение сопротивлений в электрической цепи.

Параллельное соединение конденсаторов и катушек.

Определение параллельного соединения

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов. 

Графическое обозначение схемы параллельного соеднинения

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения). 

  

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

 

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений.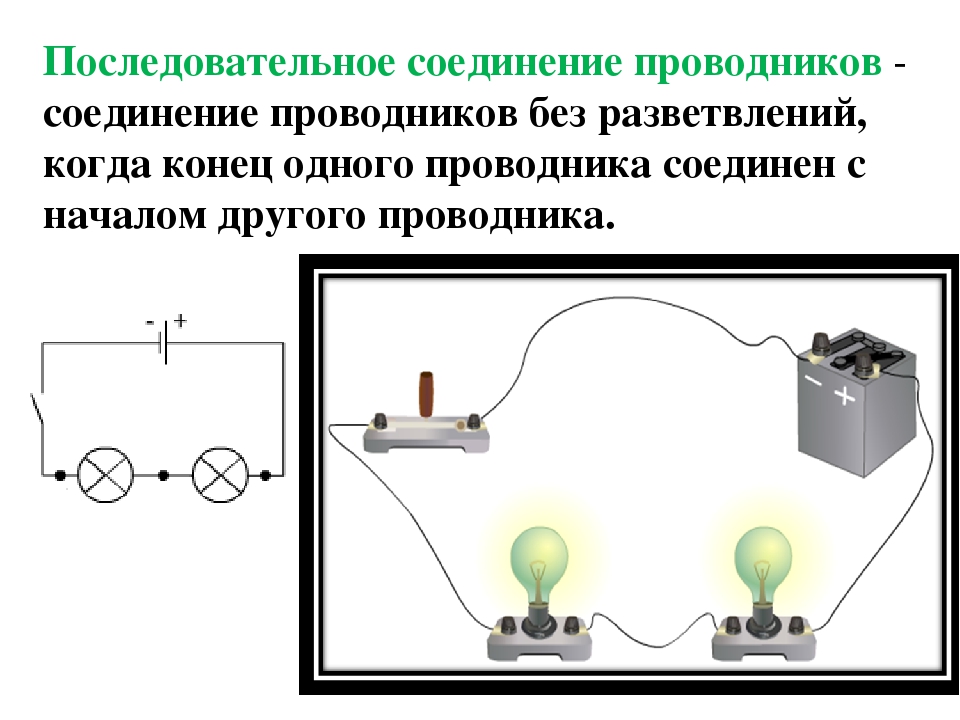 Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

 

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

 

 В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

 

Формулы для частного рассчета вытекают из основной формулы. 

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

 

Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении: 

 

Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления  

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

 

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.

Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении 

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

2. Делитель токов.

Параллельное соединение проводников: напряжение соединения, формулы

Существует множество схем с различным видом подключения. Для каждого электроприбора существует свой тип подключения проводника. В этой статье представлены формулы последовательного и параллельного соединения в проводниках.

Определение параллельного соединения

При таком виде, все проводники устанавливаются параллельно друг с другом. Они соединены в одну общую точку и все концы также скрепляются вместе. Если рассматривать энное количество одинаковых проводников, соединенных по данному принципу, то он будет называться разветвленным.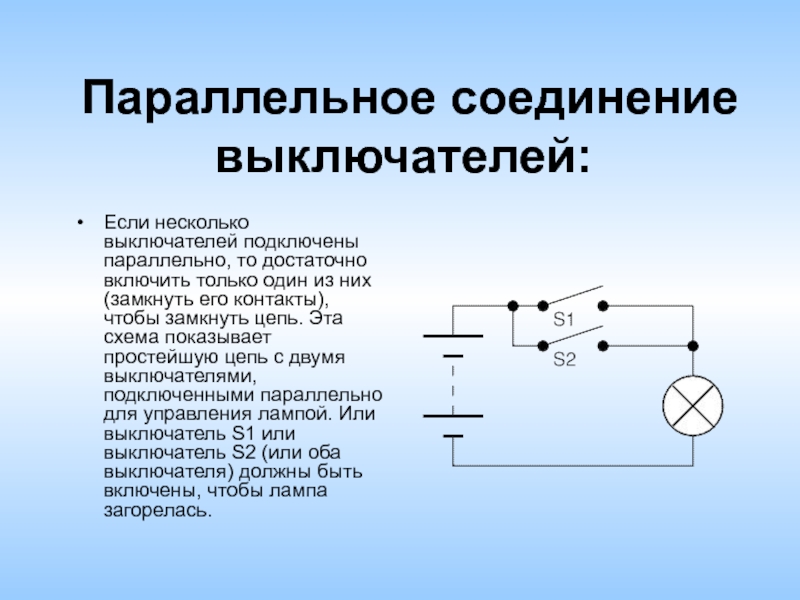

Какие виды подключений бывают

В каждом отсеке располагается один проводник. Поток электронов в виде тока, доходит до отметки ветвления, переходит на каждый проводник, и будет равен суммарным токам на всех сопротивлениях. Напряжение при таком подключении также будет равное.

Все проводники можно сменить одним общим резистором. Если применить правило Ома, то можно получить параметры сопротивления. При параллельном сопротивлении складываются показатели обратные их значениям.

Формулы для разных последовательностей

Сила тока при параллельном подключении

Если было использовано последовательное подключение в цепи, то сила не изменится ни на одном участке ветви. Найти напряжение можно, применяя стандартное правило — нужно суммировать все показатели, которые присутствуют на концах каждого из резисторов, в итоге получится результат. Но при параллельном соединения намного сложней найти силу тока.

Даже при малой нагрузке в цепи будет формироваться определенное сопротивление. И тогда оно будет мешать продвижению электрического тока и будут потери. В общем, ток перемещается постепенно, от источника по подключенным заранее резисторам к нагруженным деталям.

Классическая формула Ома

Чтобы выполнить доступное прохождение тока по резисторам, нужно, чтобы он мог быстро и просто отдавать электроны, проще говоря иметь проводимость.

В современное время в основном применяются медные проводники, а важным элементом будут приемники электрической энергии. Такой элемент вызывает небольшую нагрузку и имеет свое сопротивление. Ниже описаны формулы для последовательного и параллельного соединения сопротивлений.

Также при подключении необходимо использовать катушку индуктивности. Она способна подавлять помехи в электроцепи.

Как выглядит формула Георга Ома

Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.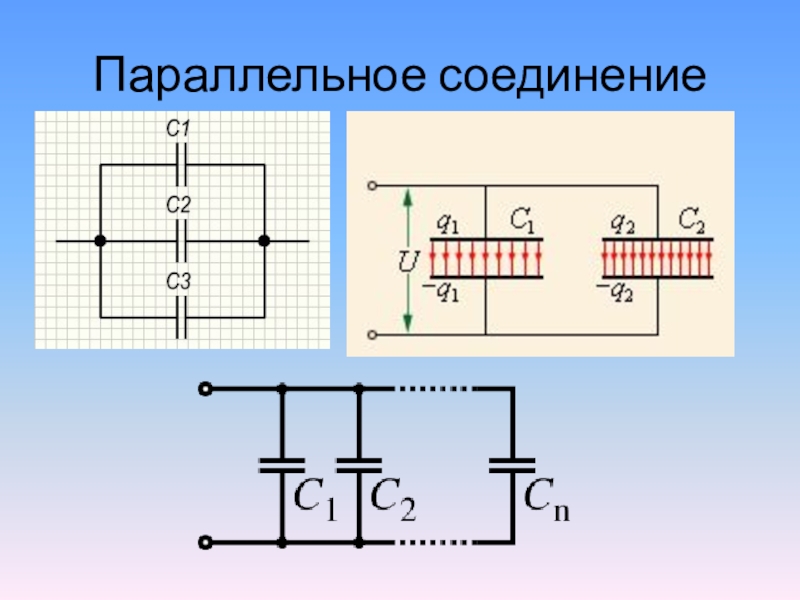

Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:

U1 = U2 = U.

Схема параллельного соединения

Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:

I = I1 + I2.

Расчет силы тока при помощи закона Ома записывается как:

I = U/R;

I1 = U1/R1;

I2 = U2/R2.

Из формулы следует:

U/R = U1/R1 + U2/R2;

U = U1 = U2;

1/R = 1/R1 + 1/R2.

Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.

Отличия между двумя видами подключений

Схема последовательного подключения говорит о том, что проводники установлены в особом расположении друг за другом.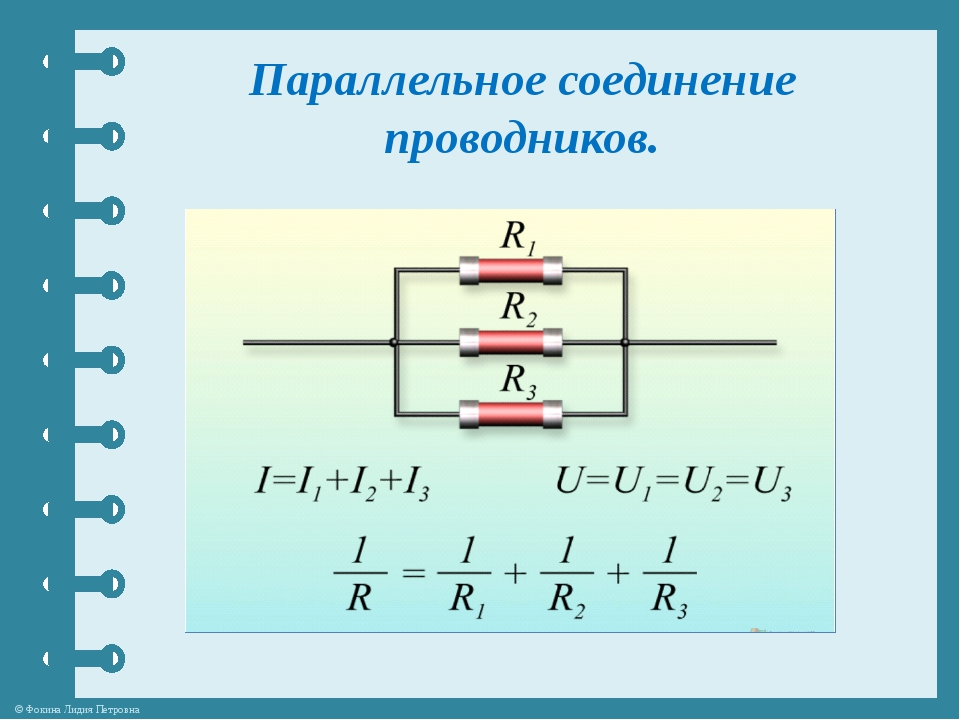 Поэтому сила тока у них одинаковая. Эти элементы создают в цепи Uобщее.

 

Пример подключения с предохранителем

Заряды не собираются в узлах электрической цепи, иначе было бы видно, как напряжение меняется. Минусом этой схемы будет то, что если любой элемент сломается, то вся цепь разорвется и перестанет работать. Например, если взять новогоднюю гирлянду. Если одна лампочка перестала работать, то другие тоже не загораются. Это и будет главным различием между последовательным и параллельным соединением. Ниже описана характеристика резисторов при параллельном объединении.

Свойства резисторов при параллельном подключении

При данном виде соединении скачки напряжения будут одинаковы на всех участках цепи. При этом показатель, обратный суммарному сопротивлению цепи, равен общей величине резисторов.

Обратите внимание! F тока в неразветвленной точке цепи равняется суммарной силе тока на отдельных участках проводника.

Стандартная формула напряжения

Формула для вычисления напряжения

При данном виде соединения все линии будут находиться в двух точках.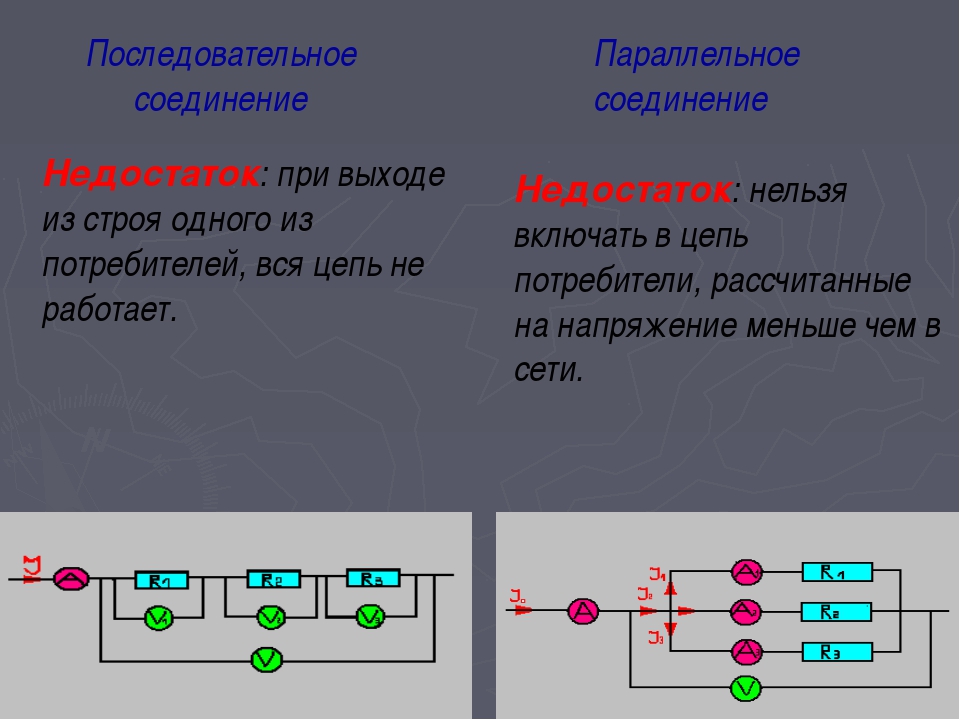 Потому напряжение для всех резисторов будет равным.

При подсоединении двух и более приборов друг с другом, напряжение на выводах такой схемы — это показатель на каждом резисторе.

Напряжения условно обозначаются как U. По закону Ома, зная, что I = U/R, можно рассчитать по формуле:

U = U1 = U2 = … = Uобщ.

Обратите внимание! Помимо вычисления напряжения, рекомендуется знать мощность проводников. Они не должны сильно отличаться друг от друга. Параллельное соединение также можно встретить в лампочках, кабелях сигнализации автомобиля, фарах и прочем.

Также иногда можно встретить смешанный вид подключения. Это когда в цепи применяется два типа подключения, и параллельное, и последовательное. Оно чаще всего используется в контурных обогревателях.

Желательно изучить каждый вид подключения и схемы к ним. Профессиональные электрики рекомендует не выполнять подключений самостоятельно, если у человека совсем нет опыта в этой сфере. Так как в цепи может случиться короткое замыкание или возгорание, в лучшем случае выход из строя прибора.

Определение мощности на примере ламп

В заключении необходимо отметить, каждому человеку желательно знать свойства последовательного и параллельного соединения проводников. Чтобы в будущем не путаться при выполнении простых работ в электрике своего дома.

Как отличить параллельное соединение от последовательного

В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.

Последовательное соединение

При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.

Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.

Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.

Параллельное соединение

В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.

Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.

Применение

Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.

Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.

Работа тока

Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:

А = I х U х t, где А – работа тока, t – время течения по проводнику.

Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.

Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:

Р=Р1 + Р2

Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.

Влияние схемы соединения на новогоднюю гирлянду

После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:

С= q/(U1 + U2 + U3)

Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.

Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.

Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.

Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.

Теперь используем формулу расчета сопротивления:

• Первая формула для последовательного вида соединения.
• Далее, для параллельной схемы.
• И окончательно для последовательной схемы.

Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.

В физике изучается тема про параллельное и последовательное соединение, причем это могут быть не только проводники, но и конденсаторы. Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.

Как различить эти два соединения?

Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.

Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.

Формулы для силы тока

О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину силы тока в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.

Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:

Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.

Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при параллельном соединении проводников:

Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.

Формулы для напряжения

Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.

Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:

Другая ситуация складывается, если рассматривается параллельное соединение резисторов. Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:

Формулы для электрического сопротивления

Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.

Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:

• последовательно, значит, нужно равенство для напряжения — I_общ * R_общ = I₁ * R₁ + I₂ * R_2;
• параллельно необходимо пользоваться формулой для силы тока — U_общ / R_общ = U₁ / R₁ + U₂ / R₂ .

Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:

1. R _общ = R ₁ + R ₂ (для последовательного соединения проводников).
2. 1 / R _общ = 1 / R ₁ + 1 / R ₂ (при параллельном соединении).

При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.

Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.

Работа тока

Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t, где А — работа тока, t — время его прохождения по проводнику.

Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U ₁ + U ₂) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.

Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А ₁ + А ₂.

Мощность тока

При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р ₁ + Р ₂.

То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.

Как влияет соединение проводников на ремонт новогодней гирлянды?

Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее – и гирлянда станет работать.

Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.

Что происходит с цепью, если в нее включены не резисторы, а конденсаторы?

При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:

Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С. В ней С — емкость конденсатора.

Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:

Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С ₁ + 1 / С ₂.

Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное. Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:

С = (q 1 + q 2 ) / U.

То есть эта величина считается, как сумма каждого из использованных в соединении приборов:

Как определить общее сопротивление произвольного соединения проводников?

То есть такого, в котором последовательные участки сменяют параллельные, и наоборот. Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.

Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).

Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.

Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.

Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:

• сначала ту, которая приведена для последовательного соединения;
• потом для параллельного;
• и снова для последовательного.

Подобным образом можно развернуть любую, даже очень сложную схему.

Задача на последовательное соединение проводников

Условие. В цепи друг за другом подсоединены две лампы и резистор. Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?

Решение. Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.

Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.

Ответ. Сопротивление резистора равно 2,5 Ом.

Задача на соединение конденсаторов, параллельное и последовательное

Условие. Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.

Решение. Проще начать с параллельного подключения. В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.

Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.

Ответ. Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.

В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.

Последовательное соединение

При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.

Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.

Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.

Параллельное соединение

В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.

Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.

Применение

Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.

Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.

Работа тока

Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:

А = I х U х t, где А – работа тока, t – время течения по проводнику.

Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.

Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:

Р=Р1 + Р2

Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.

Влияние схемы соединения на новогоднюю гирлянду

После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:

С= q/(U1 + U2 + U3)

Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.

Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.

Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.

Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.

Теперь используем формулу расчета сопротивления:

• Первая формула для последовательного вида соединения.
• Далее, для параллельной схемы.
• И окончательно для последовательной схемы.

Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.

Параллельное соединение резисторов определение — Морской флот

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

1. Номинал резистора в 16 Ом подойдет.
2. Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

1. Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
2. Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

1. Ток не изменяется на участке цепи.
2. Общее напряжение равно сумме падений напряжений на каждом резисторе.
3. Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

1. I = I1 = I2 = 0,5 (А).
2. Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
3. Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Электрическое сопротивление характеризует свойство проводника препятствовать прохождению через него электрического тока. У каждого материала есть свое удельное сопротивление. Это табличная величина, и условно она считается постоянной.

Условно, потому что во многом эта характеристика зависит от внешних условий, например температуры. Сопротивление же какого-либо конкретного элемента (мы будем говорить о резисторах) складывается из многих факторов, например, из геометрических параметров, а когда речь идет о цепи переменного тока, то в расчеты включают также индуктивное и емкостное сопротивление, но об этом мы расскажем позже. Пока же — немного теории.

Закон Ома

В 1826 году немецкий физик Георг Ом на основе своих опытов вывел закон, согласно которому сила тока на участке цепи прямо пропорциональна напряжению, которое к нему приложено, и обратно пропорциональна сопротивлению участка. Из школьного курса мы знаем этот закон:

I=U/R

Позже он был сформулирован и для полной цепи:

I=ε/(R+r)

Где ε — ЭДС источника, R — сопротивление цепи, а r — сопротивление источника.

Мощность прибора

Электрический заряд при своем перемещении совершает работу. Может быть, это незаметно глазу, но вот пощупать результат этой работы можно: электроприборы у нас греются, а иногда нагрев — это цель, а не побочное явление. Не верите — ну, электроплитки, ТЭНы, утюги как раз это свойство и эксплуатируют. Правда, руками это проверять не советую.

Мощностью у нас называют работу, совершенную за единицу времени. Попробуем вычислить мощность электроприбора, включенного в цепь.2/R

Последовательное и параллельное соединение

В реальной жизни мы редко имеем дело с одним проводником и одним источником. Достаточно взглянуть в любую принципиальную электрическую схему, например, такую простенькую:

(это схема микроволновки «Электроника»)

можно увидеть, что элементы в схеме соединены по-разному, но мы покажем вам базовые закономерности, которые работают в цепях.

Правила Кирхгофа

Если взять замкнутую электрическую цепь, по которой течет заряд, то можно определенно сказать: он никуда не денется. Сумма всех зарядов, которые текут в одной цепи, всегда одинакова. Это называется законом сохранения заряда, частным случаем общего закона сохранения (как говорится, если в одном месте что-то убудет, в другом непременно прибудет).

Отсюда мы и выводим тот факт, что в каждом узле цепи сумма токов равна нулю. То есть, если ток «приходит» в точку по ветке и «уходит» по двум — значит, первый равен сумме второго и третьего.

На этой картинке мы видим, что I1+I4=I2+I3

Это называется первым правилом Кирхгофа.

Если наша цепь не будет содержать узлов, значит, ток в ней будет величиной постоянной, а элементы, один за другим поставленные в цепь, будут давать падение напряжения. При этом общее напряжение в цепи останется тем же. Отсюда вытекает второе правило Кирхгофа: сумма напряжений на участках цепи будет равна ЭДС источников тока, входящий в эту цепь. Если у нас источник один, то будет верно равенство:

ε=U1+U2+U3+…+Un

Сумма падений напряжения будет, таким образом, нулевой.

В ситуациях, когда мы имеем дело с переменным током, падение будет наблюдаться на участках с конденсаторами и катушками — в цепях переменного тока у них появляется сопротивление (об этом позже).

Теперь, когда мы познакомились с теоретической частью, можем перейти к более приближенному к суровой реальности вопросу, а именно — расчету последовательного и параллельного соединения резисторов.

Примеры расчетов

Рассчитаем параметры цепей с разным типом соединения.

Как мы видим из рисунка, резисторы соединены один за другим, последовательным способом.2/R

Исходя из вышеперечисленных закономерностей, вы сможете рассчитывать самые причудливые соединения резисторов, можете попрактиковаться, взяв в библиотеке задачник.

Типы резисторов

Как уже было сказано ранее, элемент, который ставится в цепь для нагрузки, называется резистором. Ставят его для разных целей, главным образом для того, чтобы изменить тот или иной параметр на участке цепи. Например, понизить напряжение или силу тока, чтобы деталь, стоящая за резистором, не сгорела.

Предприятиями выпускается большой ассортимент таких изделий, и их можно по-разному классифицировать. Номинально резистор имеет то сопротивление, которое указано на нем, а по факту оно может зависеть от напряжения в сети (нелинейность), иметь разброс параметра (иногда до 20% доходит). По применяемой технологии резисторы можно разделить на:

1. проволочные;
2. композитные;
3. металлофольговые;
4. угольные;
5. интегральные.

Фактическое сопротивление такого элемента может зависеть от температуры окружающей среды и даже от частоты, если мы имеем дело с переменным током. Дело в том, что часть ассортимента резисторов выполнены по проволочной технологии, то есть фактически они представляют собой мини-катушку. При малых частотах (50 Гц) это в расчет не берется, а вот на высоких (мегагерцы) паразитная индуктивность и индуктивное сопротивление может сказаться на работе схемы. Поэтому при выборе резистора для работы с высокочастотными схемами внимательно смотрите. по какой технологии он сделан. Отдайте предпочтение тонкослойным и композиционным изделиям.

Помимо этого, большое распространение получили переменные резисторы, значение сопротивления которых можно регулировать. Делается это чаще всего отверткой. Необходимость в таких изделиях продиктована разбросом параметров у обычных резисторов, а подстроечный вариант позволяет регулировать сопротивление.

Все вышесказанное актуально для цепей постоянного тока и переменного при невысоких частотах, и все это — при нормальных условиях внешней среды. Расчеты цепей при нарушении этих условий нуждаются в дополнительной корректировке: это связано с ограниченностью действия закона Ома. С чем связаны ограничения? Вот несколько примеров:

1. при сверхнизких температурах многие проводники проявляют такое интересное явление, как сверхпроводимость;
2. также сопротивление может разниться при нагревании;
3. неприменим закон Ома для описания электрического тока в газах;
4. наконец, обычный резистор можно просто пробить высоким напряжением.

Все это прекрасно работает. Не верите — можете поэкспериментировать у себя дома или провести замеры тестером. Например, изучить елочную гирлянду или показания счетчиков при включенных электроприборах (напомню, что в гирлянде лампочки соединены последовательно, а розетки в доме — параллельно). Удачи!

Что такое «последовательные» и «параллельные» схемы? | Последовательные и параллельные схемы

Цепи, состоящие только из одной батареи и одного сопротивления нагрузки, очень просто анализировать, но они не часто встречаются на практике. Обычно мы находим цепи, в которых вместе соединено более двух компонентов.

Серия

и параллельные схемы

Существует два основных способа соединения более двух компонентов схемы: серии и параллельно .

Схема конфигурации серии

Сначала пример последовательной схемы:

Здесь у нас есть три резистора (с маркировкой R ₁ , R ₂ и R ₃ ), соединенных длинной цепочкой от одного вывода батареи к другому. (Следует отметить, что нижний индекс — эти маленькие цифры в правом нижнем углу буквы «R» — не связаны со значениями резистора в омах. Они служат только для идентификации одного резистора от другого.)

Определяющей характеристикой последовательной цепи является то, что существует только один путь для прохождения тока. В этой схеме ток течет по часовой стрелке от точки 1 до точки 2, от точки 3 до точки 4 и обратно до 1.

Конфигурация параллельной цепи

Теперь давайте посмотрим на другой тип схемы, параллельную конфигурацию:

Опять же, у нас есть три резистора, но на этот раз они образуют более одного непрерывного пути прохождения тока.Есть один путь от 1 к 2 до 7 к 8 и снова к 1. Есть еще один от 1 до 2 до 3 до 6 до 7 до 8 и снова 1. И затем есть третий путь от 1 до 2 до 3 до 4 до 5 до 6 до 7 до 8 и снова обратно к 1. Каждый отдельный путь (через ₁ рандов, ₂ рандов и ₃ рандов) называется ветвью .

Определяющей характеристикой параллельной цепи является то, что все компоненты подключены между одним и тем же набором электрически общих точек. Глядя на схематическую диаграмму, мы видим, что все точки 1, 2, 3 и 4 электрически общие.То же самое и с точками 8, 7, 6 и 5. Обратите внимание, что все резисторы, а также батарея подключены между этими двумя наборами точек.

И, конечно же, сложность не ограничивается простыми последовательностями и параллелями! У нас могут быть цепи, которые представляют собой комбинацию последовательной и параллельной цепи.

Последовательно-параллельная схема конфигурации

В этой схеме у нас есть две петли для протекания тока: одна от 1 до 2 до 5 до 6 и снова обратно к 1, а другая от 1 до 2 до 3 до 4 до 5 до 6 и снова обратно к 1 .Обратите внимание, как оба пути тока проходят через R ₁ (от точки 1 к точке 2). В этой конфигурации мы бы сказали, что R ₂ и R ₃ параллельны друг другу, а R ₁ — последовательно с параллельной комбинацией R ₂ и R ₃ .

Это всего лишь предварительный обзор того, что будет в будущем. Не волнуйся! Мы рассмотрим все эти схемы подробно, по очереди! Вы можете сразу перейти к следующим страницам, посвященным последовательным и параллельным схемам, или к разделу Что такое последовательно-параллельная схема? в главе 7.

Основы последовательного и параллельного подключения

Что такое последовательное соединение?

Основная идея «последовательного» соединения заключается в том, что компоненты соединяются встык в линию, образуя единый путь, по которому может течь ток:

Что такое параллельное соединение?

С другой стороны, основная идея «параллельного» подключения состоит в том, что все компоненты подключаются через выводы друг друга. В чисто параллельной схеме никогда не может быть более двух наборов электрически общих точек, независимо от того, сколько компонентов подключено.Есть много путей для прохождения тока, но только одно напряжение на всех компонентах:

Конфигурации последовательных и параллельных резисторов

имеют очень разные электрические свойства. В следующих разделах мы рассмотрим свойства каждой конфигурации.

ОБЗОР:

• В последовательной цепи все компоненты соединены встык, образуя единый путь для прохождения тока.
• В параллельной цепи все компоненты соединены друг с другом, образуя ровно два набора электрически общих точек.
• «Ветвь» в параллельной цепи — это путь для электрического тока, образованный одним из компонентов нагрузки (например, резистором).

СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:

электрических цепей — Каково формальное определение последовательного и параллельного соединения?

электрические цепи — Каково формальное определение последовательного и параллельного соединения? — Обмен физическими стеками

Сеть обмена стеков

Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

2. 0
3. +0
6. Авторизоваться Зарегистрироваться

Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 7 месяцев назад

Просмотрено 73 раза

$ \ begingroup $

Кажется, что половину времени я просто гадаю, последовательное оно или параллельное, разве нет способа окончательно определить, является ли данное соединение последовательным или параллельным, просто взглянув на него?

Qmechanic ♦

147k2828 золотых знаков347347 серебряных знаков17421742 бронзовых знака

Создан 10 сен.

$ \ endgroup $ 1 $ \ begingroup $

Для двух элементов серии , ток, протекающий через один из них, затем течет через другой: они разделяют один и тот же ток.Сумма их падений напряжения равна напряжению питания.

Для двух элементов в , параллельном , напряжение на одном из них также и на другом: они имеют одинаковое напряжение. Полный ток — это сумма их индивидуальных токов.

Создан 10 сен.

Нильс Нильсен

53.7k1212 золотых знаков6868 серебряных знаков136136 бронзовых знаков

$ \ endgroup $ $ \ begingroup $

Просто чтобы вы знали, что есть SE Electrical Engineering, и люди могут быть более заинтересованы в этом. На ваш вопрос невозможно ответить для всех типов схем. Некоторые части могут быть включены последовательно, другие — параллельно. Если есть только два компонента, такие как источник питания и светодиод, они включены как последовательно, так и параллельно.Обычно параллельность означает, что в какой-то момент два рассматриваемых электрических элемента соединены с обоих концов, а последовательно только один из них соединяет их вместе.

Создан 10 сен.

УинстонУинстон

3,100966 серебряных знаков3030 бронзовых знаков

$ \ endgroup $ $ \ begingroup $

Вот один из способов взглянуть на правила.S: два резистора включены последовательно, если вы можете провести линию вдоль провода от одного к другому, не встретив стыка в проводе.

P: два резистора включены параллельно, если вы можете соединить резисторы сверху вниз и снизу вниз, используя линии, которые не проходят через какие-либо другие резисторы.

А вот алгоритм сокращения любой цепи, которая представляет собой комбинацию последовательно и параллельно резисторов.

1. Выберите резистор и найдите все резисторы, включенные последовательно, с помощью правила (S), приведенного выше.Сгруппируйте эти резисторы, вычислите их эквивалентное сопротивление и заново начертите схему так, чтобы они выглядели как один резистор.
2. Повторяйте шаг 1 до тех пор, пока не останутся последовательно подключенные разгруппированные резисторы.
3. Выберите резистор и найдите все резисторы, подключенные параллельно ему, используя правило (P) выше. Сгруппируйте эти резисторы, рассчитайте их эквивалентное сопротивление и заново прочертите схему.
4. Повторяйте шаг 1 до тех пор, пока не исчезнут какие-либо упрощения. Практически в любом домашнем задании это заканчивается одним резистором.

Дополнительная заслуга: Найдите схему, которая не сводится к одному резистору после этого алгоритма. Подсказка: требуется не менее 5 резисторов.

Создан 11 сен.

Люк Притчетт, Люк Притчетт

5,18222 золотых знака1212 серебряных знаков1616 бронзовых знаков

$ \ endgroup $ Physics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

Принимать все файлы cookie Настроить параметры

Почему батарея рассчитана в Ач (ампер-час), а не в ВА.

Почему номинальная мощность батареи указывается в Ач (ампер-час), а не в ВА или ваттах.

Аккумулятор накапливает заряд в виде химической энергии, а затем преобразует его в электрическую, которую можно использовать в течение определенного времени. Количество доступного заряда — это емкость элемента или батареи, которая может быть выражена в Ач (ампер-час). Более того, в заряженной батарее количество молекул ограничено для создания потока электронов в электрических цепях, поэтому в элементе / батарее должно быть ограниченное количество электронов, которые они побуждают через цепь к полной разрядке.

Теперь у нас есть возможность оценивать емкость батареи в виде количества протекающих электронов за определенное время, но это будет головной болью, потому что в ней огромное количество электронов. Таким образом, у нас есть другой вариант ( 1C (кулон) = 6,25 x 10 ¹⁸ электронов, или 6,250,000,000,000,000,000 электронов.

Кроме того, 1A (ампер) = 1 кулон электронов в секунду и,

1 час (ч ) = 3600 секунд

Следовательно;

1Ah = (1A) x (3600s) = (C / s) x (3600s) = 3600 C.

∴ A (1 ампер) = 1 кулон в секунду = C / s

Но,

Зачем составлять новый блок для оценки емкости батареи, если старый блок работает нормально? Конечно! Чтобы усложнить вам жизнь техников и студентов;). Так же, как и с электрическими единицами… т.е. 1 единица электроэнергии = 1 кВтч = 1 доска торговой единицы.

Почему аккумулятор не имеет номинальных значений в ВА (вольт-амперах) или ваттах?

VA — вольт-амперы. Это измерение полной мощности одного из трех типов мощности в цепях переменного тока.Два других — это истинная мощность, измеряемая в ваттах, и реактивная мощность, измеряемая в VARS (вольт-амперы, реактивные). Взаимосвязь между этими тремя определяет высокий коэффициент мощности, который вам нужен в цепи переменного тока. Батареи работают от постоянного тока с коэффициентом мощности, равным единице (т. Е. P.f не применяется в цепях постоянного тока из-за нулевой частоты).

Кроме того, аккумулятор не является источником постоянного напряжения, т.е. нас интересует только емкость аккумулятора, которая рассчитана только на определенное время, поэтому мы также не можем использовать для аккумулятора Wh вместо Ah.Вот почему батарея не измеряется в ВА или Вт вместо Ач.

Вы также можете прочитать:

Разница между последовательной и параллельной схемами (со сравнительной таблицей)

Решающее различие между последовательной и параллельной цепью существует на основе ориентации компонентов в цепи. В последовательной схеме несколько компонентов соединяются каскадом, то есть хвост одного компонента соединяется с головкой другого.

В параллельной схеме несколько компонентов соединены в ориентации голова к голове и хвост к хвосту.

Содержание: серия против параллельной цепи

1. Таблица сравнения
2. Определение
3. Ключевые отличия
4. Заключение

Сравнительная таблица

Основа для сравнения	Последовательная цепь	Параллельная цепь
Ориентация компонентов	Компоненты соединяются друг за другом.	Здесь компоненты соединены голова к голове и хвост к хвосту.
Ток	Одинаковый ток течет через все компоненты в цепи.	Через каждый компонент цепи протекает разный ток.
Напряжение	На каждом компоненте существует разность потенциалов (напряжение).	Разность потенциалов (напряжение), существующая на различных компонентах цепи, одинакова.
Количество путей	Один	Несколько (зависит от количества компонентов).
Неисправность	Неисправность в одном из компонентов цепи приводит к нарушению работы всей цепи.	Неисправность отдельного компонента не мешает работе остальной цепи.
Устранение неисправностей	Сложно.	Довольно просто.
Эквивалентное сопротивление	Эквивалентное сопротивление всегда больше, чем максимальное значение сопротивления в последовательном соединении.	Эквивалентное сопротивление всегда меньше, чем у любого из отдельных резисторов, подключенных параллельно.

Определение последовательной цепи

В последовательной цепи компоненты в цепи подключаются один за другим или, можно сказать, каскадно. Более конкретно, мы можем сказать, что последовательная схема позволяет соединение таким образом, что хвост одного компонента напрямую соединяется с головкой другого и так далее, что соответствует двум концам батареи.

На рисунке ниже показано последовательное соединение 4 резисторов в цепи:

Как мы можем ясно видеть, что компоненты соединены каскадом в одну линию, таким образом, одинаковый ток, я буду течь через все резисторы в последовательной сети.Между тем между различными резисторами цепи существует разная разность потенциалов.

Это можно понять таким образом, что если одинаковый ток течет между всеми резисторами, то падение на каждом резисторе будет зависеть от сопротивления, предлагаемого каждым резистором в цепи. Таким образом, можно сказать, что в последовательной цепи из-за наличия единственного пути один и тот же ток течет через все компоненты. Тем самым возникает различная разность потенциалов (напряжение) на каждом компоненте.

Определение параллельной цепи

В параллельной схеме компоненты расположены таким образом, что головки каждого компонента соединены вместе с общей точкой. Пока хвосты соединены между собой еще одной общей точкой. Тем самым образуя несколько параллельных ветвей в цепи. На рисунке показано параллельное соединение 4 резисторов в цепи:

Как мы видим здесь, параллельная схема имеет 4 ветви, и через каждую ветвь протекает разный ток.Но поскольку ветви имеют общие точки, таким образом, одинаковый потенциал существует в двух точках по отношению к двум концам потенциала батареи.

Это также можно понять так, что на каждом резисторе в цепи существует одинаковая разность потенциалов. Тогда фактический ток, протекающий через каждую ветвь, будет автоматически зависеть от сопротивления каждого резистора в цепи.

Таким образом, мы можем сказать, что из-за наличия нескольких ветвей в цепи общий ток от источника питания делится на несколько ветвей, поскольку напряжение на точках одинаково.

Ключевые различия между последовательной и параллельной схемами

1. Компоненты в последовательной цепи расположены по единственному пути от одного конца источника питания к другому. Однако несколько компонентов в параллельной схеме расположены в множественных путях, по отношению к двум концевым выводам батареи.
2. В последовательной цепи общий ток протекает через все компоненты схемы. В параллельной цепи через каждую параллельную ветвь цепи протекает разное количество тока.
3. В последовательной цепи различное напряжение существует на каждом компоненте в цепи. В то время как в параллельной цепи одинаковое напряжение присутствует на нескольких компонентах в цепи.
4. Неисправность в одном из компонентов последовательной цепи вызывает помехи в работе всей цепи. В отличие от неисправности одного компонента в параллельной сети, не мешает функционированию другой части схемы.
5. Обнаружение неисправности в случае последовательной цепи сложно, но довольно легко в параллельной цепи.
6. Эквивалентное сопротивление в случае последовательной цепи всегда больше, чем наивысшее значение сопротивления в последовательном соединении. При этом эквивалентное сопротивление в параллельной цепи всегда меньше, чем любое из отдельных сопротивлений в параллельной комбинации.

Заключение

Итак, исходя из этого обсуждения, мы можем сказать, что в последовательной цепи протекающий ток остается неизменным в каждой части цепи. В параллельных цепях напряжение на двух конечных точках ветвей совпадает с подаваемым напряжением.

Параллельная цепь серии

: определение и примеры | Последовательно-параллельные резисторы

В целом схема на рис. 1 не является ни последовательной, ни параллельной цепью. Однако R ₂ и R ₃ подключены между одними и теми же двумя точками в цепи и должны иметь одинаковое падение напряжения. Следовательно, эти два резистора включены параллельно, и мы можем рассчитать для них одно эквивалентное сопротивление.

При измерении от клемм источника напряжения упрощенная схема Рис. 2 эквивалентна исходной схеме на Рис. 1.На рисунке 2 R ₁ включены последовательно с эквивалентным сопротивлением R ₂ и R ₃ параллельно. Следовательно, мы можем решить схему на Рисунке 2 как простую последовательную схему.

Рисунок 1 Простая последовательно-параллельная схема

Рисунок 2 Эквивалентная схема для Рисунка 1

В схеме, показанной на Рисунок 3 (a) , R ₂ и R ₃ имеют одинаковый ток через них и, следовательно, включены последовательно.Мы можем заменить их эквивалентным резистором, как показано на Рисунок 3 (b) . Теперь мы можем решить упрощенную схему на рис. 3 (b) как простую параллельную схему.

Рисунок 3 (а) Последовательно-параллельная схема; (b) Эквивалентная схема

Последовательно-параллельная Определение схемы

Мы определяем последовательно-параллельную схему как такую, в которой некоторые части схемы имеют характеристики простых последовательных цепей, в то время как другие части имеют характеристики простых параллельные цепи.

Решение для последовательной параллельной схемы с использованием метода эквивалентной схемы

Мы можем решить последовательно-параллельные схемы, заменяя эквивалентные сопротивления для различных частей схемы, пока исходная схема не будет сведена либо к простой последовательной, либо к простой параллельной схеме .

Пример 1

Найдите падение напряжения, ток и мощность для каждого резистора на принципиальной схеме на Рисунке 4.

Решение

Шаг 1

Нарисуйте полностью помеченную принципиальную схему для этого конкретного схема.

Рисунок 4 Принципиальная схема для примера 1

Шаг 2

Так как R ₂ и R ₃ работают параллельно,

\ [{{\ operatorname {R}} _ {eq }} = \ frac {{{R} _ {3}} \ times {{R} _ {3}}} {{{R} _ {2}} + {{R} _ {3}}} = \ frac {10 \ times 40} {10 + 40} = 8 \ Omega \]

Общее сопротивление цепи составляет

$ {{R} _ {T}} = {{R} _ {1}} + {{\ operatorname {R}} _ {eq}} = 12 + 8 = 20 \ Omega $

Шаг 3

Из закона Ома,

\ [{{I} _ {T}} = \ frac {E} {{{R} _ {T}}} = \ frac {100V} {20 \ Omega} = 5A \]

Шаг 4

Поскольку _{рандов 1} последовательно с источником,

$ {{I} _ {1}} = {{I} _ {T}} = 5A $

Шаг 5

Применение закона Ома к _{рандов 1} ,

$ {{V} _ { 1}} = {{I} _ {1}} {{R} _ {1}} = 5A \ times 12 \ Omega = 60V $

Step 6

Из закона напряжения Кирхгофа,

$ {{ V} _ {eq}} = E — {{V} _ {1}} = 100-60 = 40 В $

Теперь вернемся к исходной цепи,

$ {{V} _ {2}} = {{V} _ {3}} = {{V} _ {eq}} = 40 В $

Шаг 7

Применение закона Ома к R ₂ и R ₃ ,

$ \ begin {align} & {{I} _ {2}} = \ frac {{{V} _ {2}}} {{{R} _ {2}}} = \ frac {40V} {10 \ Omega} = 4A \\ & {{I} _ {3}} = \ frac {{{V} _ {3}}} {{{R} _ {3}}} = \ frac {40V} {40 \ Omega} = 1A \\\ end {align} $

Чтобы проверить наши расчеты, мы можем проверить, что рассчитанные нами токи удовлетворяют действующему закону Кирхгофа для этой цепи:

$ {{I} _ {1}} = {{I} _ {2}} + {{I} _ {3}} $

Шаг 8

Так как,

$ P = VI $

Итак,

$ \ begin {align} & {{P} _ {1}} = {{V} _ {1}} {{I} _ {1}} = 60В \ раз 5А = 0.30 кВт \\ & {{P} _ {2}} = {{V} _ {2}} {{I} _ {2}} = 40 В \ times 4A = 0,16 кВт \\ & {{P} _ {1 }} = {{V} _ {1}} {{I} _ {1}} = 40 В \ times 1A = 40 Вт \\ & {{P} _ {1}} = {{V} _ {1}} {{I} _ {1}} = 100 В \ times 5A = 0,50 кВт \\\ end {align} $

Мы можем проверить наши расчеты, проверив, что:

$ {{P} _ {T} } = {{P} _ {1}} + {{P} _ {2}} + {{P} _ {3}} $

Принцип делителя напряжения

Для последовательной схемы на Рисунке 5 , Закон Кирхгофа утверждает, что E = V ₁ + V ₂ + V ₃ .Другими словами, общее приложенное напряжение делится между тремя резисторами. Мы можем подключить вольтметр к шести возможным комбинациям клемм A, B, C и D, как показано на рисунке 5. Таким образом, последовательная комбинация R ₁ , R ₂ и R ₃ действует как делитель напряжения.

Рисунок 5 Принцип делителя напряжения

Чтобы найти шесть напряжений на Рисунке 5, мы могли бы вычислить R _T , найти I из закона Ома, а затем вычислить падение напряжения на каждом сопротивлении из V ₁ = IR ₁ , V ₂ = IR ₂ и т. Д.Однако мы можем рассчитать каждое напряжение за один шаг. Свойство цепей серии , которое часто называют принципом делителя напряжения:

В цепи серии соотношение между любыми двумя падениями напряжения равно отношению двух сопротивлений, на которых возникают эти падения напряжения.

Следовательно, для любого резистора R _n в делителе напряжения

\ [\ begin {align} & \ frac {{{V} _ {n}}} {E} = \ frac {{{R } _ {n}}} {{{R} _ {T}}} \\ & и \\ & \ begin {matrix} {{V} _ {n}} = E \ times \ frac {{{R} _ {n}}} {{{R} _ {T}}} & {} & \ left (1 \ right) \\\ end {matrix} \\\ end {align} \]

Пример 2

Какое напряжение между клеммами B и D в схеме на Рисунке 5?

Решение

\ [\ begin {align} & {{V} _ {BD}} = E \ times \ frac {{{R} _ {2}} + {{R} _ {3}} } {{{R} _ {1}} + {{R} _ {2}} + {{R} _ {3}}} \\ & = 350V \ times \ frac {\ left (5k \ Omega + 10k \ Omega \ right)} {\ left (20k \ Omega + 5k \ Omega + 10k \ Omega \ right)} \\ & = 150V \\\ end {align} \]

Использование переменного резистора в качестве делителя напряжения обеспечивает бесступенчато регулируемое напряжение на клеммах, как показано на рисунке 6.

Рисунок 6 Схема потенциометра

Делители напряжения

Делители напряжения широко используются в источниках питания для электронных схем, так что один источник напряжения может подавать все различные напряжения, необходимые для части оборудования, уменьшая стоимость, размер и вес оборудования.

Последовательно понижающий резистор, показанный на Рисунке 7, обеспечивает простейший метод получения требуемого падения напряжения на конкретном элементе схемы.

Рисунок 7 Последовательный понижающий резистор

Пример 3

Часть электронной схемы требует рабочего напряжения 15 В и тока 20 мА. Если напряжение на клеммах питания составляет 25 В, какое значение резистора для последовательного включения требуется?

Решение

Из закона Ома мы можем представить эту цепь нагрузки резистором, как показано на рисунке 7.

\ [{{R} _ {L}} = \ frac {{{V} _ {L }}} {{{I} _ {L}}} = \ frac {15V} {20mA} = 750 \ Omega \]

Согласно закону Кирхгофа, падение напряжения на резисторе последовательного понижения должно быть

$ {{V} _ {D}} = E — {{V} _ {L}} = 25-15 = 10V $

Поскольку понижающий резистор и нагрузка включены последовательно,

$ \ begin {align} & {{I} _ {D}} = {{I} _ {L}} = 20 мА \\ & {{R} _ {S}} = \ frac {{{V} _ {D}}} {{{ I} _ {D}}} = \ frac {10V} {20mA} = 500 \ Omega \\\ end {align} $

Для завершения проектирования мы находим минимальную номинальную мощность для R _S :

$ P = VI = 10 В \ раз 20 мА = 0.20 Вт $

Резистор мощностью 0,5 Вт будет хорошим выбором, поскольку он будет работать при более низких температурах, чем резистор 0,25 Вт, и, следовательно, с меньшей вероятностью выйдет из строя.

Преимущество простого последовательного резистора заключается в том, что единственным стоком на источнике питания является ток, протекающий через нагрузку. Но эта схема имеет недостаток , заключающийся в том, что любое изменение сопротивления нагрузки изменяет ток через последовательно понижающий резистор, который, в свою очередь, изменяет падение напряжения на резисторе и напряжение, подаваемое на нагрузку.

В схемах, где нагрузка представляет собой транзистор, R _L может стать очень большим. В таких условиях падение напряжения на последовательно падающем резисторе почти равно нулю, а напряжение на нагрузке близко к полному приложенному напряжению, которое может быть достаточно высоким, чтобы повредить транзистор.

Чтобы предотвратить такое повреждение , некоторые конструкции делителей напряжения включают в себя спускной резистор, включенный параллельно нагрузке, как показано на рисунке 8. Сопутствующий резистор обеспечивает постоянное прохождение тока через последовательно понижающий резистор для поддержания заметного падения напряжения. через это.Следовательно, напряжение нагрузки не может подняться до полного приложенного напряжения.

Рисунок 8 Делитель напряжения с ограничивающим сопротивлением

В источниках питания для электронного оборудования ток утечки в 10–25% от общего тока, потребляемого от источника, обеспечивает достаточную защиту от чрезмерного напряжения нагрузки при сопротивлении нагрузки увеличивается.

Чем больше ток утечки, тем меньшее количество колебаний тока нагрузки влияет на напряжение нагрузки. Таким образом, улучшенное регулирование напряжения достигается за счет дополнительного стока тока от источника и дополнительного тепла, выделяемого в резисторах делителя напряжения.

При разработке делителей напряжения для нагрузок, состоящих из одного транзистора, регулирование напряжения имеет большее значение, чем несколько дополнительных миллиампер тока утечки.

В схемах, которые получают несколько различных напряжений от одного источника питания, удобно иметь общую точку отсчета для всех измерений напряжения.

Часто металлический каркас или шасси схемы подключается к цепи и используется в качестве контрольной точки. Шасси также может быть подключено к земле, обычно через заземляющий провод электрической системы.

Символ внизу Рис. 9 указывает на то, что контрольная точка заземлена. Следовательно, мы можем сказать, что напряжение в точке A составляет 1250 В относительно земли. Символ в середине Рис. 10 указывает точку, в которой шасси электрически подключено к цепи.

Что касается шасси, напряжение в точке A в этой цепи составляет 112 В, а напряжение в точке B — 212 В.

Рисунок 9 Делитель напряжения с несколькими выходными напряжениями

Транзисторные цепи могут потребовать положительного или положительного напряжения. отрицательные напряжения относительно обычного соединения шасси, и многие схемы требуют и того, и другого.Мы можем получить эти положительные и отрицательные напряжения от одного источника питания, подключив отвод делителя напряжения к шасси, как показано на Рис. 10 .

Рисунок 10 Делитель напряжения источника питания для транзисторного усилителя

Пример 5

При полной нагрузке источник питания на Рисунке 10 имеет напряжение на клеммах 24 В постоянного тока. Разработайте делитель напряжения для обеспечения 112 В и 212 В по отношению к шасси, когда потребляемый ток составляет 400 мА при 112 В и 200 мА при 212 В.Общий ток, потребляемый источником питания, составляет 500 мА.

Решение

Поскольку R1 параллелен нагрузке 1, V1 5 12 В. Применяя закон Кирхгофа к переходу A,

$ \ begin {align} & I1 = 200mA-400mA = 100mA \\ & {{ R} _ {1}} = \ frac {{{V} _ {1}}} {{{I} _ {1}}} = \ frac {12V} {100mA} = 120 \ Omega \\ & P1 = {{V} _ {1}} {{I} _ {1}} = 12 В \ times 100 мА = 1,2 Вт \\\ end {align} $

Аналогично

$ \ begin {align} & {{V } _ {2}} = 12 В, \\ & и \\ & {{I} _ {2}} = 500 мА-200 мА = 300 мА \\ & {{R} _ {2}} = \ frac {12 В} { 300 мА} = 40 \ Омега \\ & {{P} _ {2}} = 12 В \ умноженное на 300 мА = 3.6W \\\ end {align} $

Принцип делителя тока

Принцип делителя тока можно описать как:

В параллельной цепи отношение между любыми двумя токами ветви равно отношению двух проводимость, по которой протекают эти токи.

Поскольку напряжение одинаково для резисторов, включенных параллельно,

\ [V = \ frac {{{I} _ {1}}} {{{G} _ {1}}} = \ frac {{{I } _ {2}}} {{{G} _ {2}}} = \ frac {{{I} _ {n}}} {{{G} _ {n}}} = \ frac {{{I } _ {T}}} {{{G} _ {T}}} \]

и

\ [\ begin {matrix} {{I} _ {n}} = {{I} _ {T} } \ times \ frac {{{G} _ {n}}} {{{G} _ {T}}} & {} & \ left (2 \ right) \\\ end {matrix} \]

Подстановка G _n = 1 / R _n , а GT = 1 / R _eq в уравнении 2 дает

\ [\ begin {matrix} {{I} _ {n}} = {{I} _ { T}} \ times \ frac {{{\ operatorname {R}} _ {eq}}} {{{R} _ {n}}} & {} & \ left (3 \ right) \\\ end {matrix } \]

Следовательно, мы можем переформулировать принцип делителя тока:

В параллельной цепи отношение между любыми двумя токами ветви обратно пропорционально отношению сопротивлений ветвей.

Для двух резисторов, включенных параллельно,

$ \ begin {align} & {{\ operatorname {R}} _ {eq}} = \ frac {{{R} _ {1}} \ times {{R} _ {2}}} {{{R} _ {1}} + {{R} _ {2}}} \\ & {{I} _ {1}} = {{I} _ {T}} \ times \ frac {{{R} _ {1}} \ times {{R} _ {2}}} {{{R} _ {1}} \ left ({{R} _ {1}} + {{ R} _ {2}} \ right)} \\\ end {align}

$

И

\ [\ begin {align} & \ begin {matrix} {{I} _ {1}} = {{I } _ {T}} \ times \ frac {{{R} _ {2}}} {\ left ({{R} _ {1}} + {{R} _ {2}} \ right)} & { } & \ left (4 \ right) \\\ end {matrix} \\ & аналогично, \\ & \ begin {matrix} {{I} _ {1}} = {{I} _ {T}} \ times \ frac {{{R} _ {1}}} {\ left ({{R} _ {1}} + {{R} _ {2}} \ right)} & {} & \ left (5 \ right ) \\\ end {matrix} \\\ end {align} \]

Пример 6

Рассчитайте ток утечки в делителе напряжения, если сопротивление нагрузки равно 3.0 кОм, как показано на рисунке 11.

Рисунок 11 Принципиальная схема для примера 6

Решение

Эквивалентное сопротивление спускного резистора и сопротивления нагрузки параллельно составляет

$ \ begin {align } & {{\ Operatorname {R}} _ {eq}} = \ frac {{{R} _ {1}} \ times {{R} _ {2}}} {{{R} _ {1}} + {{R} _ {2}}} = \ frac {300 \ Omega \ times 3k \ Omega} {300 \ Omega + 3k \ Omega} = 273 \ Omega \\ & {{R} _ {T}} = {{\ operatorname {R}} _ {eq}} + {{R} _ {S}} = 143 + 273 = 416 \ Omega \\ & {{I} _ {T}} = \ frac {E} { {{R} _ {T}}} = \ frac {25V} {416 \ Omega} = 60.1 мА \\ & {I} _ {B} = {{I} _ {T}} \ times \ frac {{{R} _ {L}}} {{{R} _ {B}} + {{R } _ {L}}} = 60,1 мА \ times \ frac {3k \ Omega} {3,3k \ Omega} = 55 мА \\\ end {align} $

Ячейки последовательно-параллельные

Последовательно-параллельные Подключение батареи, как показано на рисунке 12, обеспечивает большее напряжение и большую емкость, чем отдельные элементы. Элементы должны быть идентичными, чтобы избежать циркуляции токов внутри батареи. Общая емкость аккумулятора определяется количеством параллельно соединенных рядов.

Рисунок 12 Эквивалентная схема последовательно-параллельно соединенной батареи

Для батареи, состоящей из P параллельных рядов с S ячеек, включенных последовательно в каждом ряду, ЭДС батареи является ЭДС одной последовательной строки, то же, что и для последовательного подключения батареи:

$ {{E} _ {bat}} = S {{E} _ {cell}} $

Общее внутреннее сопротивление — это комбинация P идентичных параллельных рядов S резисторов в серии, где каждый резистор имеет сопротивление R _{, ячейка} , поэтому

\ [\ begin {matrix} {{R} _ {bat}} = \ frac {сопротивление \ text {} of \ text {} each \ text {} row} {number \ text {} of \ text {} rows} = \ frac {S {{R} _ {cell}}} {P} & {} & \ left (6 \ right) \\\ конец {matrix} \]

Пример 7

Двадцать идентичных ячеек соединены в четыре параллельных ряда, по пять ячеек в каждой последовательно.Каждая ячейка имеет внутреннее сопротивление 0,20 В. Батарея подает ток 5,0 А на резистор 1,25 В, как показано на рисунке 13. Рассчитайте ЭДС каждой ячейки.

Решение

$ \ begin {align} & {{R} _ {bat}} = \ frac {S {{R} _ {cell}}} {P} = \ frac {5 \ times 0.20 \ Омега} {4} = 0,25 \ Omega \\ & {{E} _ {bat}} = {{I} _ {L}} {{R} _ {T}} = 5A \ times \ left (0,25 \ Omega +1,25 \ Omega \ right) = 7,5 В \\ & {{E} _ {cell}} = \ frac {{{E} _ {bat}}} {S} = \ frac {7,5 В} {5} = 1,5 В \\\ end {align} $

Рисунок 13 Эквивалентная схема для примера 7

5.1: Что такое «последовательные» и «параллельные» схемы?

Серия

и параллельные схемы

Существует два основных способа соединения более двух компонентов схемы: серии и параллельно . Сначала пример последовательной схемы:

Здесь у нас есть три резистора (с маркировкой R ₁ , R ₂ и R ₃ ), соединенных длинной цепочкой от одного вывода батареи к другому. (Следует отметить, что обозначение нижним индексом — эти маленькие цифры в правом нижнем углу буквы «R» — не связаны со значениями резистора в омах.Они служат только для того, чтобы отличить один резистор от другого.) Определяющей характеристикой последовательной цепи является то, что существует только один путь для прохождения электронов. В этой цепи электроны движутся против часовой стрелки, от точки 4 к точке 3, к точке 2, к точке 1 и обратно до 4.

Теперь давайте посмотрим на другой тип схемы, параллельную конфигурацию:

Опять же, у нас есть три резистора, но на этот раз они образуют более одного непрерывного пути для прохождения электронов.Есть один путь от 8 к 7, от 2 к 1 и снова к 8. Еще один — от 8 до 7, от 6 до 3, до 2, до 1 и снова до 8. И затем есть третий путь от 8 до 7 до 6 до 5 до 4 до 3 до 2 к 1 и снова обратно к 8. Каждый отдельный путь (через ₁ рандов, ₂ рандов и ₃ рандов) называется ветвью .

Определяющей характеристикой параллельной цепи является то, что все компоненты подключены между одним и тем же набором электрически общих точек. Глядя на схематическую диаграмму, мы видим, что все точки 1, 2, 3 и 4 электрически общие.То же самое с точками 8, 7, 6 и 5. Обратите внимание, что все резисторы, а также батарея подключены между этими двумя наборами точек.

И, конечно же, сложность не ограничивается простыми последовательностями и параллелями! У нас также могут быть цепи, которые представляют собой комбинацию последовательной и параллельной цепи:

В этой схеме у нас есть два контура для прохождения электронов: один от 6 до 5, от 2 до 1 и снова обратно к 6, а другой от 6 до 5 до 4, до 3, от 2 до 1 и снова обратно к 6.Обратите внимание, как оба пути тока проходят через R ₁ (от точки 2 до точки 1). В этой конфигурации мы бы сказали, что R ₂ и R ₃ параллельны друг другу, а R ₁ — последовательно с параллельной комбинацией R ₂ и R ₃ .

Это всего лишь предварительный обзор того, что будет в будущем. Не волнуйся! Мы рассмотрим все эти схемы подробно, по очереди!

Изучите основные идеи последовательного и параллельного подключения

Основная идея «последовательного» соединения заключается в том, что компоненты соединяются встык в линию, образуя единый путь для прохождения электронов:

С другой стороны, основная идея «параллельного» подключения состоит в том, что все компоненты подключаются через выводы друг друга.В чисто параллельной схеме никогда не может быть более двух наборов электрически общих точек, независимо от того, сколько компонентов подключено. Есть много путей для прохождения электронов, но только одно напряжение на всех компонентах:

Конфигурации последовательных и параллельных резисторов

имеют очень разные электрические свойства. В следующих разделах мы рассмотрим свойства каждой конфигурации.

Определение параллели по физике.

Примеры параллелей в следующих темах:

• Комбинации конденсаторов: последовательные и параллельные

  • Как и любой другой вид электрического схемного устройства, конденсаторы могут использоваться последовательно и / или параллельно внутри схем.
  • Схема может содержать конденсаторы, которые включены как последовательно, так и параллельно .
  • Однако они оба находятся в параллельно с C3.
  • На этом изображении показаны конденсаторы C1, C2 и так далее до Cn в параллельно .
  • Рассчитайте общую емкость конденсаторов, соединенных последовательно и параллельно

• Параллельные резисторы

  • Резисторы в цепи могут быть подключены последовательно или параллельно .
  • Следовательно, для каждой цепи с числом $ n $ или резисторами, подключенными параллельно , ,
  • $ R_ {n \; ( параллельно )} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} … + \ frac {1} { R_n}. $
  • Три резистора, подключенных по параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление .
  • Рассчитайте общее сопротивление в цепи с резисторами, подключенными параллельно

• Комбинированные схемы

  • Комбинированная схема может быть разбита на аналогичные части, которые являются последовательными или параллельными .
  • В этом случае сопротивление провода последовательно с другими сопротивлениями, которые находятся в параллельно .
  • На исходном изображении две обведенные кружком секции показывают резисторы, которые соединены параллельно .
  • Следующий шаг показывает, что два обведенных кружком резистора подключены к параллельно .
  • Эта комбинация из семи резисторов состоит из последовательных и параллельных частей.

• Конденсатор с параллельными пластинами

  • Параллельный конденсатор с пластинами — это электрический компонент, используемый для хранения энергии в электрическом поле между двумя заряженными плоскими поверхностями.
  • Для этого атома мы сосредоточимся на параллельных -пластинчатых конденсаторах.
  • Для конденсатора с параллельными пластинами емкость (C) связана с диэлектрической проницаемостью (ε), площадью поверхности (A) и расстоянием между пластинами (d):
  • Краткий обзор параллельных пластин и эквипотенциальных линий с точки зрения электростатики.

• Конденсатор с параллельными пластинами

  • Конденсатор с параллельными пластинами — это конденсатор, который включает в себя две проводящие пластины, каждая из которых соединена с проводами, отделенными друг от друга тонким пространством.
  • Один из наиболее часто используемых конденсаторов в промышленности и в учебных заведениях — это конденсатор с параллельными пластинами .
  • Назначение конденсатора — накапливать заряд, а в конденсаторе с параллельными пластинами и одна пластина принимает на себя избыток положительного заряда, а другая становится более отрицательной.

• Зарядка аккумулятора: последовательные и параллельные ЭДС

  • При последовательном включении источников напряжения их ЭДС и внутренние сопротивления складываются; в параллельно они остаются прежними.
  • Когда используется более одного источника напряжения, они могут быть подключены последовательно или параллельно , аналогично резисторам в цепи.
  • Но общее внутреннее сопротивление уменьшается, так как внутренние сопротивления параллельны .
  • Таким образом, параллельное соединение может производить больший ток.
  • Параллельные комбинации часто используются для подачи большего тока.

• При постоянной скорости получается прямолинейный

  • Если скорость заряженной частицы равна параллельно магнитному полю, то результирующая сила отсутствует и частица движется по прямой линии.
  • Если магнитное поле и скорость параллельны (или антипараллельны), то sinθ равен нулю и сила отсутствует.
  • Если находится между 0 и 90 градусами, то компонент v , параллельный к B, остается неизменным.
  • В приведенном выше случае магнитная сила равна нулю, потому что скорость параллельна силовым линиям магнитного поля.

• Магнитная сила между двумя параллельными проводниками

  • Параллельные проводов, по которым проходит ток, создают значительные магнитные поля, которые, в свою очередь, создают значительные силы на токи.
  • Параллельные проводов, по которым проходит ток, создают значительные магнитные поля, которые, в свою очередь, создают значительные силы для токов.
  • Для параллельных проводов, расположенных на расстоянии одного метра друг от друга, каждый из которых несет один ампер, сила на метр составляет:
  • Это означает, что один ампер тока через два бесконечно длинных параллельных проводников (разделенных одним метром в пустом пространстве и без каких-либо других магнитных полей) вызывает силу 2 × 10-7 Н / м на каждый провод.

• Емкость

  • Наиболее распространенный конденсатор известен как конденсатор с параллельными пластинами , который состоит из двух отдельных проводящих пластин, отделенных друг от друга диэлектриком.
  • Для конденсатора с параллельными пластинами это уравнение можно использовать для расчета емкости:
  • В конденсаторе с параллельными пластинами это можно упростить до:

• Сопротивление и удельное сопротивление

  • Эквивалентное сопротивление параллельно может быть представлено в уравнениях двумя вертикальными линиями «||» (как в геометрии) как упрощенное обозначение.
  • Для случая двух резисторов, подключенных параллельно , это можно рассчитать по формуле:
  • В качестве особого случая сопротивление резисторов N, подключенных параллельно , каждый из которых имеет одинаковое сопротивление R, определяется как R / N.

    No related posts.