Введение

Се­го­дняш­ний урок будет по­свя­щен яв­ле­нию элек­тро­маг­нит­ной ин­дук­ции. Яв­ле­ни­ем элек­тро­маг­нит­ной ин­дук­ции на­зы­ва­ет­ся яв­ле­ние воз­ник­но­ве­ния элек­три­че­ско­го тока в про­вод­ни­ке под дей­стви­ем пе­ре­мен­но­го маг­нит­но­го поля.

Важно, что в дан­ном слу­чае про­вод­ник дол­жен быть за­мкнут. В на­ча­ле XIX в. после опы­тов дат­ско­го уче­но­го Эр­сте­да стало ясно, что элек­три­че­ский ток со­зда­ет во­круг себя маг­нит­ное поле. После встал во­прос о том, нель­зя ли по­лу­чить элек­три­че­ский ток за счет маг­нит­но­го поля, т.е. про­из­ве­сти об­рат­ные дей­ствия. Если элек­три­че­ский ток со­зда­ет маг­нит­ное поле, то, на­вер­ное, и маг­нит­ное поле долж­но со­зда­вать элек­три­че­ский ток. В пер­вой по­ло­вине XIX века уче­ные об­ра­ти­лись имен­но к таким опы­там: стали ис­кать воз­мож­ность со­зда­ния элек­три­че­ско­го тока за счет маг­нит­но­го поля.

Опыты Фарадея

Впер­вые уда­лось до­стичь успех в этом (т.е. по­лу­чить элек­три­че­ский ток за счет маг­нит­но­го поля) ан­глий­ско­му фи­зи­ку Май­к­лу Фа­ра­дею. Итак, об­ра­тим­ся к опы­там Фа­ра­дея.

Рис. 1. Опыт, ана­ло­гич­ный опыту Фа­ра­дея. При дви­же­нии маг­ни­та в ка­туш­ке, в ее цепи ре­ги­стри­ру­ет­ся элек­три­че­ский ток

Пер­вая схема была до­воль­но про­стой. Во-пер­вых, М. Фа­ра­дей ис­поль­зо­вал в своих опы­тах ка­туш­ку с боль­шим чис­лом вит­ков. Ка­туш­ка на­ко­рот­ко была при­со­еди­не­на к из­ме­ри­тель­но­му при­бо­ру, мил­ли­ам­пер­мет­ру (мА). Нужно ска­зать, что в те вре­ме­на не было до­ста­точ­но хо­ро­ших ин­стру­мен­тов для из­ме­ре­ния элек­три­че­ско­го тока, по­это­му поль­зо­ва­лись необыч­ным тех­ни­че­ским ре­ше­ни­ем: брали маг­нит­ную стрел­ку, рас­по­ла­га­ли рядом с ней про­вод­ник, по ко­то­ро­му про­те­кал ток, и по от­кло­не­нию маг­нит­ной стрел­ки су­ди­ли о про­те­ка­ю­щем токе. Так вот в дан­ном слу­чае токи могли быть очень неве­ли­ки, по­это­му ис­поль­зо­вал­ся при­бор мА, т.е. тот, ко­то­рый из­ме­ря­ет ма­лень­кие токи.

Вдоль ка­туш­ки М. Фа­ра­дей пе­ре­ме­щал по­сто­ян­ный маг­нит – от­но­си­тель­но ка­туш­ки маг­нит дви­гал­ся вверх и вниз.

Об­ра­ща­ем ваше вни­ма­ние на то, что в этом экс­пе­ри­мен­те впер­вые было за­фик­си­ро­ва­но на­ли­чие элек­три­че­ско­го тока в цепи в ре­зуль­та­те из­ме­не­ния маг­нит­но­го по­то­ка, ко­то­рый про­хо­дит сквозь ка­туш­ку.

Фа­ра­дей об­ра­тил вни­ма­ние и на тот факт, что стрел­ка мА от­кло­ня­ет­ся от сво­е­го ну­ле­во­го зна­че­ния, т.е. по­ка­зы­ва­ет, что в цепи су­ще­ству­ет элек­три­че­ский ток толь­ко тогда, когда маг­нит дви­жет­ся. Стоит толь­ко маг­ни­ту оста­но­вить­ся, стрел­ка воз­вра­ща­ет­ся в пер­во­на­чаль­ное по­ло­же­ние, в ну­ле­вое по­ло­же­ние, т.е. ни­ка­ко­го элек­три­че­ско­го тока в цепи в этом слу­чае нет.

Вто­рая за­слу­га Фа­ра­дея – уста­нов­ле­ние за­ви­си­мо­сти на­прав­ле­ния ин­дук­ци­он­но­го элек­три­че­ско­го тока от по­ляр­но­сти маг­ни­та и на­прав­ле­ния его дви­же­ния. Сто­и­ло Фа­ра­дею из­ме­нить по­ляр­ность маг­ни­тов и про­пус­кать маг­нит через ка­туш­ку с боль­шим чис­лом вит­ков, как тут же ме­ня­лось на­прав­ле­ние ин­дук­ци­он­но­го тока, того, ко­то­рый воз­ни­ка­ет в за­мкну­той элек­три­че­ской цепи.

Т.о. мы при­шли к тому, с чего на­чи­на­ли урок: под­твер­ди­лась ги­по­те­за, что элек­три­че­ский ток воз­ни­ка­ет, когда из­ме­ня­ет­ся маг­нит­ное поле.

Итак, неко­то­рое за­клю­че­ние. Из­ме­ня­ю­ще­е­ся маг­нит­ное поле со­зда­ет элек­три­че­ский ток. На­прав­ле­ние элек­три­че­ско­го тока за­ви­сит от того, какой полюс маг­ни­та про­хо­дит в дан­ный мо­мент через ка­туш­ку, в каком на­прав­ле­нии дви­жет­ся маг­нит.

И еще: ока­зы­ва­ет­ся, на зна­че­ние элек­три­че­ско­го тока вли­я­ет ко­ли­че­ство вит­ков в ка­туш­ке. Чем боль­ше вит­ков, тем и зна­че­ние тока будет боль­ше.

Об­ра­тим­ся те­перь ко вто­ро­му экс­пе­ри­мен­ту Фа­ра­дея. В чем он за­клю­чал­ся?

Рис. 2. Вто­рой экс­пе­ри­мент по ис­сле­до­ва­нию яв­ле­ния элек­тро­маг­нит­ной ин­дук­ции

Две ка­туш­ки раз­ме­ща­лись близ­ко друг с дру­гом. Одна ка­туш­ка с боль­шим чис­лом вит­ков под­клю­ча­лась к ис­точ­ни­ку тока, в этой цепи был ключ, ко­то­рый за­мы­кал и раз­мы­кал цепь. Вто­рая ка­туш­ка, тоже с боль­шим чис­лом вит­ков, под­клю­чен­ная к мил­ли­ам­пер­мет­ру на­пря­мую, ни­ка­ких ис­точ­ни­ков тока нет. Как толь­ко цепь за­мы­ка­лась, мил­ли­ам­пер­метр по­ка­зы­вал на­ли­чие элек­три­че­ско­го тока в цепи. Как толь­ко цепь раз­мы­ка­лась, мил­ли­ам­пер­метр вновь ре­ги­стри­ро­вал на­ли­чие элек­три­че­ско­го тока, но на­прав­ле­ние элек­три­че­ско­го тока из­ме­ня­лось на про­ти­во­по­лож­ное. Пока цепь была за­мкну­та, т.е. пока в цепи про­те­кал элек­три­че­ский ток, мил­ли­ам­пер­метр ни­ка­ко­го тока в элек­три­че­ской цепи не ре­ги­стри­ро­вал.

Выводы из экспериментов

Какие вы­во­ды были сде­ла­ны М.Фа­ра­де­ем в ре­зуль­та­те этих экс­пе­ри­мен­тов? Ин­дук­ци­он­ный элек­три­че­ский ток по­яв­ля­ет­ся в за­мкну­той цепи толь­ко тогда, когда су­ще­ству­ет пе­ре­мен­ное маг­нит­ное поле. При­чем это маг­нит­ное поле долж­но из­ме­нять­ся.

От чего зависит индукционный ток?

Если из­ме­не­ния маг­нит­но­го поля не про­ис­хо­дит, то не будет ни­ка­ко­го элек­три­че­ско­го тока. Даже если маг­нит­ное поле су­ще­ству­ет. Мы можем ска­зать, что ин­дук­ци­он­ный элек­три­че­ский ток прямо про­пор­ци­о­на­лен, во-пер­вых, числу вит­ков, во-вто­рых, ско­ро­сти маг­нит­но­го поля, с ко­то­рой из­ме­ня­ет­ся это маг­нит­ное поле от­но­си­тель­но вит­ков ка­туш­ки.

Рис. 3. От чего за­ви­сит ве­ли­чи­на ин­дук­ци­он­но­го тока?

Для ха­рак­те­ри­сти­ки маг­нит­но­го поля ис­поль­зу­ет­ся ве­ли­чи­на, ко­то­рая на­зы­ва­ет­ся маг­нит­ный поток. Она ха­рак­те­ри­зу­ет маг­нит­ное поле в целом, мы об этом будем го­во­рить на сле­ду­ю­щем уроке. Сей­час от­ме­тим лишь, что имен­но из­ме­не­ние маг­нит­но­го по­то­ка, т.е. числа линий маг­нит­но­го поля, про­ни­зы­ва­ю­щих кон­тур с током (ка­туш­ку, на­при­мер), при­во­дит к воз­ник­но­ве­нию в этом кон­ту­ре ин­дук­ци­он­но­го тока.

Читайте также:

Рекомендуемые страницы:

Поиск по сайту

poisk-ru.ru

От каких факторов зависит сила индукционного тока. От чего зависит индукционный ток

9.5. Индукционный ток

9.5.1. Тепловое действие индукционного тока

Возникновение ЭДС приводит к появлению в проводящем контуре индукционного тока , сила которого определяется по формуле

I i = | ℰ i | R ,

где ℰ i — ЭДС индукции, возникающая в контуре; R — сопротивление контура.

При протекании индукционного тока в контуре выделяется теплота , количество которой определяется одним из выражений:

Q i = I i 2 R t , Q i = ℰ i 2 t R , Q i = I i | ℰ i | t ,

где I i — сила индукционного тока в контуре; R — сопротивление контура; t — время; ℰ i — ЭДС индукции, возникающая в контуре.

Мощность индукционного тока вычисляется по одной из формул:

P i = I i 2 R , P i = ℰ i 2 R , P i = I i | ℰ i | ,

где I i — сила индукционного тока в контуре; R — сопротивление контура; ℰ i — ЭДС индукции, возникающая в контуре.

При протекании индукционного тока в проводящем контуре через площадь поперечного сечения проводника переносится заряд , величина которого вычисляется по формуле

q i = I i ∆t ,

где I i — сила индукционного тока в контуре; Δt — интервал времени, в течение которого по контуру течет индукционный ток.

Пример 21. Кольцо, изготовленное из проволоки с удельным сопротивлением 50,0 ⋅ 10 −10 Ом ⋅ м, находится в однородном магнитном поле с индукцией 250 мТл. Длина проволоки равна 1,57 м, а площадь ее поперечного сечения составляет 0,100 мм 2 . Какой максимальный заряд пройдет по кольцу при выключении поля?

Решение . Появление ЭДС индукции в кольце вызвано изменением потока вектора индукции, пронизывающего плоскость кольца, при выключении магнитного поля.

Поток индукции магнитного поля через площадь кольца определяется формулами:

• до выключения магнитного поля

Ф 1 = B 1 S  cos α,

где B 1 — первоначальное значение модуля индукции магнитного поля, B 1 = 250 мТл; S — площадь кольца; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости кольца;

• после выключения магнитного поля

Ф 2 = B 2 S  cos α = 0,

где B 2 — значение модуля индукции после выключения магнитного поля, B 2 = 0.

∆Ф = Ф 2 − Ф 1 = −Ф 1 ,

или, с учетом явного вида Ф 1 ,

∆Ф = −B 1 S  cos α.

Среднее значение ЭДС индукции, возникающей в кольце при выключении поля,

| ℰ i | = | Δ Ф Δ t | = | − B 1 S cos α Δ t | = B 1 S | cos α | Δ t ,

где ∆t — интервал времени, за который происходит выключение поля.

Наличие ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = B 1 S | cos α | R Δ t ,

где R — сопротивление кольца.

При протекании индукционного тока по кольцу переносится индукционный заряд

q i = I i Δ t = B 1 S | cos α | R .

Максимальному значению заряда соответствует максимальное значение функции косинус (cos α = 1):

q i max = I i Δ t = B 1 S R .

Полученная формула определяет максимальное значение заряда, который пройдет по кольцу при выключении поля.

Однако для расчета заряда необходимо получить выражения, которые позволят найти площадь кольца и его сопротивление.

Площадь кольца — площадь круга радиусом r , периметр которого определяется формулой длины окружности и совпадает с длиной проволоки, из которой изготовлено кольцо:

l = 2πr ,

где l — длина проволоки, l = 1,57 м.

Отсюда следует, что радиус кольца определяется отношением

r = l 2 π ,

а его площадь —

S = π r 2 = π l 2 4 π 2 = l 2 4 π .

Сопротивление кольца задается формулой

R = ρ l S 0 ,

где ρ — удельное сопротивление материала проволоки, ρ = 50,0 × × 10 −10 Ом ⋅ м; S 0 — площадь поперечного сечения проволоки, S 0 = = 0,100 мм 2 .

Подставим полученные выражения для площади кольца и его сопротивления в формулу, определяющую искомый заряд:

q i max = B 1 l 2 S 0 4 π ρ l = B 1 l S 0 4 π ρ .

Вычислим:

q i max = 250 ⋅ 10 − 3 ⋅ 1,57 ⋅ 0,100 ⋅ 10 − 6 4 ⋅ 3,14 ⋅ 50,0 ⋅ 10 − 10 = 0,625 Кл = 625 мКл.

При выключении поля по кольцу проходит заряд, равный 625 мКл.

Пример 22. Кон

medicinye.ru

Электромагнитная индукция — Википедия

Электромагни́тная инду́кция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении во времени магнитного поля или при движении материальной среды в магнитном поле^[1]. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года^[2]. Он обнаружил, что электродвижущая сила (ЭДС), возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.

Согласно закону электромагнитной индукции Фарадея (в СИ):

E=−dΦBdt,{\displaystyle {\mathcal {E}}=-{{d\Phi _{B}} \over dt},}

где

E{\displaystyle {\mathcal {E}}} — электродвижущая сила, действующая вдоль произвольно выбранного контура,

ΦB{\displaystyle \Phi _{B}} =∬SB→⋅dS→{\displaystyle =\iint \limits _{S}{\vec {B}}\cdot d{\vec {S}}} — магнитный поток через поверхность, ограниченную этим контуром.

Знак «минус» в формуле отражает правило Ленца, названное так по имени российского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

E=−NdΦBdt=−dΨdt,{\displaystyle {\mathcal {E}}=-N{{d\Phi _{B}} \over dt}=-{{d\Psi } \over dt},}

где

E{\displaystyle {\mathcal {E}}} — электродвижущая сила,

N{\displaystyle N} — число витков,

ΦB{\displaystyle \Phi _{B}} — магнитный поток через один виток,

Ψ{\displaystyle \Psi } — потокосцепление катушки.

Векторная форма[править | править код]

В дифференциальной форме закон Фарадея можно записать в следующем виде:

rotE→=−∂B→∂t{\displaystyle \operatorname {rot} \,{\vec {E}}=-{\partial {\vec {B}} \over \partial t}} (в системе СИ)

или

rotE→=−1c∂B→∂t{\displaystyle \operatorname {rot} \,{\vec {E}}=-{1 \over c}{\partial {\vec {B}} \over \partial t}} (в системе СГС).

В интегральной форме (эквивалентной):

∮∂S⁡E→⋅dl→=−∂∂t∫SB→⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-{\partial \over \partial t}\int _{S}{\vec {B}}\cdot {\vec {ds}}}(СИ)

или

∮∂S⁡E→⋅dl→=−1c∂∂t∫SB→⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-{1 \over c}{\partial \over \partial t}\int _{S}{\vec {B}}\cdot {\vec {ds}}} (СГС).

Здесь E→{\displaystyle {\vec {E}}} — напряжённость электрического поля, B→{\displaystyle {\vec {B}}} — магнитная индукция, S {\displaystyle S\ } — произвольная поверхность, ∂S{\displaystyle \partial S} — её граница. Контур интегрирования ∂S{\displaystyle \partial S} подразумевается фиксированным (неподвижным).

Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).

• В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)^[3].

Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство E=−dΦ/dt{\displaystyle {\mathcal {E}}=-{{d\Phi }/dt}} продолжает соблюдаться, но ЭДС в левой части теперь не сводится к ∮⁡E→⋅dl→{\displaystyle \oint {\vec {E}}\cdot {\vec {dl}}} (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула остаётся справедливой, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).

• Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год^[4] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле E=−dΦ/dt{\displaystyle {\mathcal {E}}=-{{d\Phi }/dt}} в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)^[5]. В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
• Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной. Дело в том, что, по крайней мере для определённых ситуаций, это совпадение оказывается очевидным проявлением принципа относительности. А именно, например, для случая относительного движения катушки с присоединённым к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчёта, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчёта, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчёта мы её рассчитали.

Потенциальная форма[править | править код]

При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:

E→=−∂A→∂t{\displaystyle {\vec {E}}=-{\partial {\vec {A}} \over \partial t}} (в случае отсутствия безвихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).

В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:

E→=−∇φ−∂A→∂t{\displaystyle {\vec {E}}=-\nabla \varphi -{\partial {\vec {A}} \over \partial t}}

Подробнее

Поскольку вектор магнитной индукции по определению выражается через векторный потенциал так:

B→=rot A→≡∇×A→,{\displaystyle {\vec {B}}=rot\ {\vec {A}}\equiv \nabla \times {\vec {A}},}

то можно подставить это выражение в

rot E→≡∇×E→=−∂B→∂t,{\displaystyle rot\ {\vec {E}}\equiv \nabla \times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}

получая

∇×E→=−∂(∇×A→)∂t,{\displaystyle \nabla \times {\vec {E}}=-{\frac {\partial (\nabla \times {\vec {A}})}{\partial t}},}

и, поменяв местами дифференцирование по времени и пространственным координатам (ротор):

∇×E→=−∇×∂A→∂t.{\displaystyle \nabla \times {\vec {E}}=-\nabla \times {\frac {\partial {\vec {A}}}{\partial t}}.}

Отсюда, поскольку ∇×E→{\displaystyle \nabla \times {\vec {E}}} полностью определяется правой частью последнего уравнения, видно, что вихревая часть электрического поля (та часть, которая имеет ротор, в отличие от безвихревого поля ∇φ{\displaystyle \nabla \varphi }) полностью определяется выражением

−∂A→∂t.{\displaystyle -{\frac {\partial {\vec {A}}}{\partial t}}.}

То есть в случае отсутствия безвихревой части можно записать

E→=−∂A→∂t,{\displaystyle {\vec {E}}=-{\frac {\partial {\vec {A}}}{\partial t}},}

а в общем случае

E→=−∇φ−dA→dt.{\displaystyle {\vec {E}}=-\nabla \varphi -{\frac {d{\vec {A}}}{dt}}.}

В 1820 году Ганс Христиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 году в своём дневнике. Многие годы настойчиво ставил он различные опыты, но безуспешно, и только 29 августа 1831 года наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, состояла из кольца из мягкого железа примерно 2 см шириной и 15 см диаметром. На каждой половине кольца было намотано много витков медной проволоки. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.

В это же время американский физик Джозеф Генри также успешно проводил опыты по индукции токов, но пока он собирался опубликовать результаты своих опытов, в печати появилось сообщение М. Фарадея об открытии им электромагнитной индукции.

М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.

1. ↑ Миллер М. А., Пермитин Г. В. Электромагнитная индукция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 537—538. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
2. ↑ Faraday, Michael. The philosopher’s tree: a selection of Michael Faraday’s writings / Michael Faraday, P. Day. — CRC Press, 1999-02-01. — P. 71. — ISBN 978-0-7503-0570-9.
3. ↑ Это уравнение Максвелла может быть переписано в эквивалентном виде

   ∮∂S⁡E→⋅dl→=−∫S∂B→∂t⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-\int _{S}{\frac {\partial {\vec {B}}}{\partial t}}\cdot {\vec {ds}}}

   (здесь просто производная по t внесена под знак интеграла). В таком виде уравнение также может быть включено в систему уравнений Максвелла, причем оговорка о неподвижности контура интегрирования теряет актуальность, так как производная теперь очевидно не действует на границу области (на пределы интегрирования), а само интегрирование в любом случае полагается «мгновенным». В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).
4. ↑ М. Лившиц. Закон электромагнитной индукции или «правило потока»? // Квант. — 1998. — № 3. — С. 37—38.
5. ↑ Такой отказ объясняется тем, что, в отличие от закона для циркуляции электрического поля, выполняющегося всегда, «правило» корректно работает лишь для случаев, когда контур, в котором вычисляется ЭДС, совпадает физически с проводником (то есть совпадает их движение; в противном же случае правило может не работать (самый известный пример — униполярная машина Фарадея; контур, который в этом случае трудно определить, но кажется довольно очевидным, что он не меняется; во всяком случае, довольно затруднительно указать разумное определение для контура, который бы в этом случае менялся), то есть проявляется парадокс, что для «закона природы» недопустимо.

ru.wikipedia.org

Электромагнитная индукция – FIZI4KA

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ​\( S \)​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​\( B \)​, площади поверхности ​\( S \)​, пронизываемой данным потоком, и косинуса угла ​\( \alpha \)​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ​\( \Phi \)​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​\( \alpha \)​ магнитный поток может быть положительным (\( \alpha \) < 90°) или отрицательным (\( \alpha \) > 90°). Если \( \alpha \) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​\( N \)​ витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​\( R \)​:

При движении проводника длиной ​\( l \)​ со скоростью ​\( v \)​ в постоянном однородном магнитном поле с индукцией ​\( \vec{B} \)​ ЭДС электромагнитной индукции равна:

где ​\( \alpha \)​ – угол между векторами ​\( \vec{B} \)​ и \( \vec{v} \).

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​\( \varepsilon_{is} \)​, возникающая в катушке с индуктивностью ​\( L \)​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ​\( \Phi \)​ через контур из этого проводника пропорционален модулю индукции ​\( \vec{B} \)​ магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ​\( L \)​ между силой тока ​\( I \)​ в контуре и магнитным потоком ​\( \Phi \)​, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• закона электромагнитной индукции;
• ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

6. Решение проверить.

Электромагнитная индукция

fizi4ka.ru

Направление индукционного тока. Правило Ленца

Направление индукционного тока. Правило Ленца

«Физика — 11 класс»

Направление индукционного тока

Направление индукционного тока, возникающего в катушке, зависит от того, приближается магнит к катушке или удаляется от нее.

Возникающий индукционный ток может притягивать или отталкивать магнит, т.к. катушка становится подобной магниту с двумя полюсами — северным и южным.
На основе закона сохранения энергии можно предсказать, в каких случаях катушка будет притягивать магнит, а в каких отталкивать его.

Взаимодействие индукционного тока катушки с магнитом.

В чем состоит различие двух опытов: приближение магнита к катушке и его удаление?

Если магнит приближать к катушке

Число линий магнитной индукции, пронизывающих витки катушки, или, что то же самое, магнитный поток, увеличивается.
Катушка становится подобной магниту, обращенному одноименным полюсом к приближающемуся к ней магниту.
Линии индукции ‘ магнитного поля, созданного возникшим в катушке индукционным током, выходят из верхнего конца катушки.
В катушке появляется индукционный ток такого направления, что магнит обязательно отталкивается.
Для сближения магнита и катушки нужно совершить положительную работу.

Если магнит удалять от катушки

Число линий магнитной индукции, пронизывающих витки катушки, или, что то же самое, магнитный поток, уменьшается.
Линии индукции ‘ магнитного поля, созданного возникшим в катушке индукционным током, входят в верхний конец катушки.
Катушка с током становится аналогична магниту, северный полюс которого находится снизу.
В катушке возникает ток такого направления, что проявляется притягивающая магнит сила.

Аналогично можно рассмотреть опыт, когда на концах стержня, который может свободно вращаться вокруг вертикальной оси, закреплены два проводящих алюминиевых кольца (одно из них с разрезом).

С разрезанным кольцом магнит не взаимодействует, так как разрез препятствует возникновению в кольце индукционного тока.
Отталкивает или притягивает другое кольцо магнит, зависит от направления индукционного тока, возникающего в кольце.
Поэтому закон сохранения энергии позволяет сформулировать правило, определяющее направление индукционного тока.

Правило Ленца

Существует правило, позволяющее определить направление индукционного тока, которое было установлено русским физиком Э. X. Ленцем:

Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван.

или более кратко:

Индукционный ток направлен так, чтобы препятствовать причине, его вызывающей.

При увеличении магнитного потока через витки катушки индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует усилению магнитного потока через витки катушки.
Ведь линии индукции ‘ этого поля направлены против линий индукции поля, изменение которого порождает электрический ток.
Если же магнитный поток через катушку ослабевает, то индукционный ток создает магнитное поле с индукцией ‘ увеличивающее магнитный поток через витки катушки.

Применение правила Ленца:

1. Определить направление линий магнитной индукции внешнего магнитного поля.

2. Выяснить, увеличивается ли поток вектора магнитной индукции этого поля через поверхность, ограниченную контуром (ΔФ > 0), или уменьшается (ΔФ < 0).

3. Установить направление линий магнитной индукции ‘ магнитного поля индукционного тока. Эти линии должны быть согласно правилу Ленца направлены противоположно линиям магнитной индукции В при ΔФ > 0 и иметь одинаковое с ними направление при ΔФ <0.

4. Зная направление линий магнитной индукции ‘, найти направление индукционного тока, пользуясь правилом буравчика.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитная индукция. Физика, учебник для 11 класса — Класс!ная физика

Электромагнитная индукция. Магнитный поток — Направление индукционного тока. Правило Ленца — Закон электромагнитной индукции — ЭДС индукции в движущихся проводниках. Электродинамический микрофон — Вихревое электрическое поле — Самоиндукция. Индуктивность. Энергия магнитного поля тока — Электромагнитное поле — Примеры решения задач — Краткие итоги главы

class-fizika.ru

Электромагнитная индукция. | Объединение учителей Санкт-Петербурга

www.eduspb.com

Индукционный ток — Какое направление индукционного тока? — Росиндуктор

ИНДУКЦИОННЫЙ ТОК — это электрический ток, возникающий при изменении потока магнитной индукции в замкнутом проводящем контуре. Это явление носит название электромагнитной индукции. Хотите узнать какое направление индукционного тока? Росиндуктор — это торговый информационный портал, где вы найдете информацию про ток.

Содержание

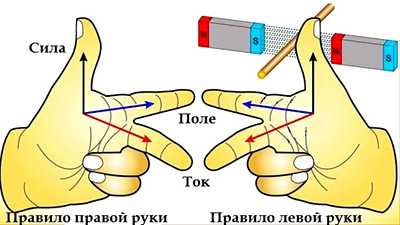
Индукционный ток правило

Определяющее направление индукционного тока правило звучит следующим образом: «Индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван». Правая рука развернута ладонью навстречу магнит¬ным силовым линиям, при этом большой палец направлен в сторону движения проводника, а четыре пальца по-казывают, в каком направлении будет течь индукционный ток. Перемещая проводник, мы перемещаем вместе с проводчиком все электроны, заключенные в нем, а при перемещении в магнитном поле электрических зарядов на них будет действовать сила по правилу левой руки.

Направление индукционного тока

Направление индукционного тока, как и его величина, определяется правилом Ленца, в котором говорится, что направление индукционного тока всегда ослабляет действие фактора, возбудившего ток. При изменении потока магнитного поля через контур направление индукционного тока будет таким, чтобы скомпенсировать эти изменения. Когда магнитное поле возбуждающее ток в контуре создается в другом контуре, направление индукционного тока зависит от характера изменений: при увеличении внешнего тока индукционный ток имеет противоположное направление, при уменьшении — направлен в ту же сторону и стремиться усилить поток.

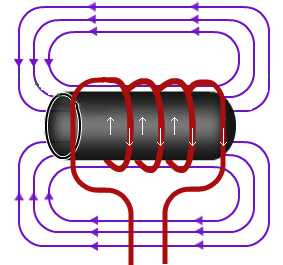
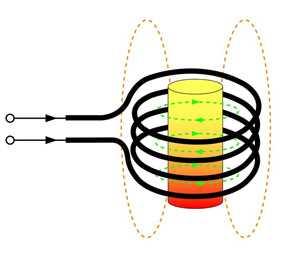
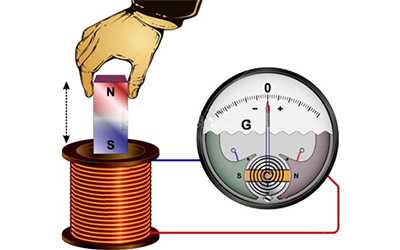
Индукционный ток в катушке

Катушка с индукционным током имеет два полюса (северный и южный), которые определяются в зависимости от направления тока: индукционные линии выходят из северного полюса. Приближение магнита к катушке вызывает появление тока с направлением, отталкивающим магнит. При удалении магнита ток в катушке имеет направление, способствующее притягиванию магнита.

Индукционный ток возникает

Индукционный ток возникает в замкнутом контуре, находящемся в переменном магнитном поле. Контур может быть как неподвижным (помещенным в изменяющийся поток магнитной индукции), так и движущимся (движение контура вызывает изменение магнитного потока). Возникновение индукционного тока обуславливает вихревое электрическое поле, которое возбуждается под воздействием магнитного поля.

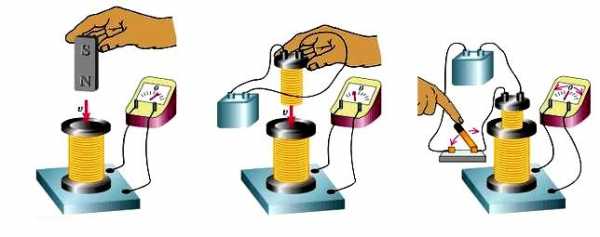
Как создать индукционный ток

О том, как создать кратковременный индукционный ток можно узнать из школьного курса физики.

Для этого есть несколько способов:

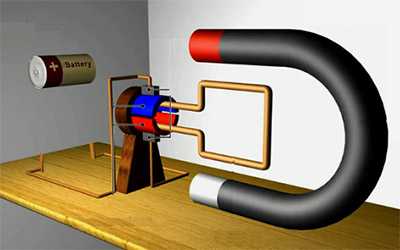
• — перемещение постоянного магнита или электромагнита относительно катушки,
• — перемещение сердечника относительно вставленного в катушку электромагнита,
• — замыкание и размыкание цепи,
• — регулирование тока в цепи.

Сила индукционного тока

Основной закон электродинамики (закон Фарадея) гласит, что сила индукционного тока для любого контура равна скорости изменения магнитного потока, проходящего через контур, взятой со знаком минус. Сила индукционного тока носит название электродвижущей силы.

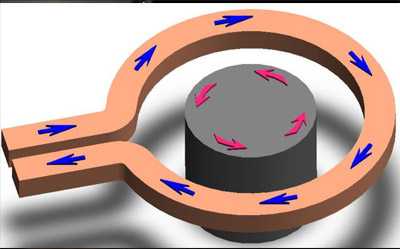
zavodrr.ru