Закон Ома. Формула Закона Ома

Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.

Георг Симон Ом

Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.

Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.

Формула закона Ома записывается в следующем виде:

где

I – сила тока в проводнике, единица измерения силы тока — ампер [А];

U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];

R – электрическое сопротивление проводника, единица измерения электрического сопротивления — ом [Ом].

Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза

И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.

Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:

Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.

Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.

Где и когда можно применять закон Ома?

Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.

Значение Закона Ома

Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.

Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.

Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.

Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:

Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

zakon-oma.ru

Закон Ома

Закон Ома

— физический закон, определяющий зависимость между электрическими величинами — напряжением, сопротивлением и током для проводников.
Впервые открыл и описал его в 1826 году немецкий физик Георг Ом, показавший (с помощью гальванометра) количественную связь между электродвижущей силой, электрическим током и свойствами проводника, как пропорциональную зависимость.
Впоследствии свойства проводника, способные противостоять электрическому току на основе этой зависимости, стали называть электрическим сопротивлением (Resistance), обозначать в расчётах и на схемах буквой R и измерять в Омах в честь первооткрывателя.
Сам источник электрической энергии также обладает внутренним сопротивлением, которое принято обозначать буквой r.

Закон Ома для участка цепи

Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома:

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.

I = U/R

Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.

Отсюда следуют ещё два полезных соотношения:

Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).

U = IR

Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.

R = U/I

Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R.
Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.

Предлагается простой Онлайн-калькулятор для практических расчётов.

Закон Ома. Расчёт напряжения, сопротивления, тока, мощности.
После сброса ввести два любых известных параметра.

I=U/R;   U=IR;   R=U/I; P=UI   P=U²/R;   P=I²R; R=U²/P;   R=P/I²   U=√(PR)   I= √(P/R)

---

Закон Ома для замкнутой цепи

Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:

I — Сила тока в цепи.
— Электродвижущая сила (ЭДС) — величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника.
r — Внутреннее сопротивление источника питания.

Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .

Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR.
Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания.
С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы.
По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = — I*r.
Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах

U.
Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.

В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС ( ≈ U ) независимо от сопротивления внешней цепи R.
Такой источник питания называют источником напряжения.

---

Закон Ома для переменного тока

При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.
В таком случае запись Закона Ома будет иметь вид:

I = U/Z

Здесь

Z — полное (комплексное) сопротивление цепи — импеданс. В него входит активная R и реактивная X составляющие.
Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.
Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.

С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:

— комплексная амплитуда тока. = I_ampe ^jφ
— комплексная амплитуда напряжения. = U_ampe ^jφ
— комплексное сопротивление. Импеданс.
φ — угол сдвига фаз между током и напряжением.

e — константа, основание натурального логарифма.
j — мнимая единица.
I_amp , U_amp — амплитудные значения синусоидального тока и напряжения.

Нелинейные элементы и цепи

Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников.
Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы.

Такие элементы и цепи, в которых они используются, называют нелинейными.

Похожие статьи: Постоянный ток. Переменный ток.

---

Замечания и предложения принимаются и приветствуются!

tel-spb.ru

формулы и определения / Блог

Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.

 

Закон Ома для участка цепи:

Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

1. I — сила тока (в системе СИ измеряется — Ампер)
   • Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
   • Формула: I=\frac{U}{R}
2. U — напряжение (в системе СИ измеряется — Вольт)
3. R — электрическое сопротивление (в системе СИ измеряется — Ом).
   • Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
   • Формула R=\frac{U}{I}

 

Определение единицы сопротивления — Ом

1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1(Вольт) протекает ток 1 (Ампер).

 

Закон Ома для полной цепи

Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

 

Формула I=\frac{\varepsilon}{R+r}

• \varepsilon — ЭДС источника напряжения, В;
• I — сила тока в цепи, А;
• R — сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

 

Как запомнить формулы закона Ома

Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

.

 



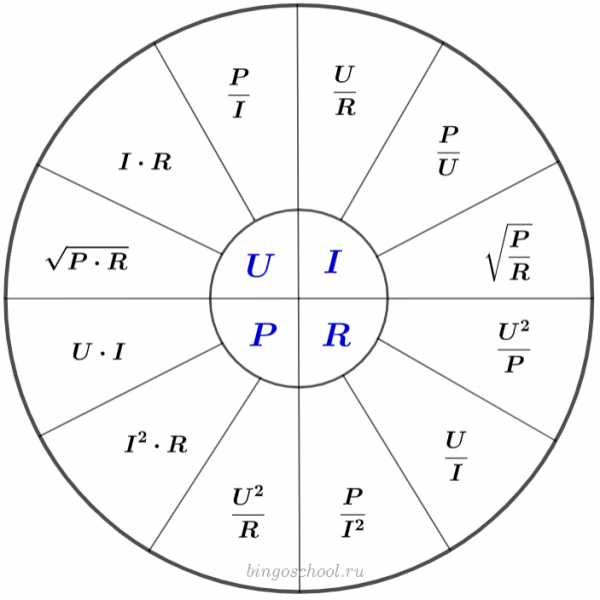
• U — электрическое напряжение;
• I — сила тока;
• P — электрическая мощность;
• R — электрическое сопротивление

---

 

Смотри также:

 

Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.

bingoschool.ru

Закон Ома для полной цепи

Закон Ома для полной цепи – эмпирический (полученный из эксперимента) закон, который устанавливает связь между силой тока, электродвижущей силой (ЭДС) и внешним и внутренним сопротивлением в цепи.

При проведении реальных исследований электрических характеристик цепей с постоянным током необходимо учитывать сопротивление самого источника тока. Таким образом в физике осуществляется переход от идеального источника тока к реальному источнику тока, у которого есть свое сопротивление (см. рис. 1).

Рис. 1. Изображение идеального и реального источников тока

Рассмотрение источника тока с собственным сопротивлением обязывает использовать закон Ома для полной цепи.

Сформулируем закона Ома для полной цепи так (см. рис. 2): сила тока в полной цепи прямо пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи, где под полным сопротивлением понимается сумма внешних и внутренних сопротивлений.

Рис. 2. Схема закона Ома для полной цепи.

Формула закона Ома для полной цепи

• R – внешнее сопротивление [Ом];
• r – сопротивление источника ЭДС (внутреннее) [Ом];
• I – сила тока [А];
• ε– ЭДС источника тока [В].

Рассмотрим некоторые задачи на данную тему. Задачи на закон Ома для полной цепи, как правило, дают ученикам 10 класса, чтобы они могли лучше усвоить указанную тему.

I. Определите силу тока в цепи с лампочкой, сопротивлением 2,4 Ом и источником тока, ЭДС которого равно 10 В, а внутреннее сопротивление 0,1 Ом.

По определению закона Ома для полной цепи, сила тока равна:

II. Определить внутреннее сопротивление источника тока с ЭДС 52 В. Если известно, что при подключении этого источника тока к цепи с сопротивлением 10 Ом амперметр показывает значение 5 А.

Запишем закон Ома для полной цепи и выразим из него внутреннее сопротивление:

III. Однажды школьник спросил у учителя по физике: «Почему батарейка садится?» Как грамотно ответить на данный вопрос?

Мы уже знаем, что реальный источник обладает собственным сопротивлением, которое обусловлено либо сопротивлением растворов электролитов для гальванических элементов и аккумуляторов, либо сопротивлением проводников для генераторов. Согласно закону Ома для полной цепи:

следовательно, ток в цепи может уменьшаться либо из-за уменьшения ЭДС, либо из-за повышения внутреннего сопротивления. Значение ЭДС у аккумулятора почти постоянный. Следовательно, ток в цепи понижается за счет повышения внутреннего сопротивления. Итак, «батарейка» садится, так как её внутреннее сопротивление увеличивается.

zakon-oma.ru

Закон Ома для переменного тока

После открытия в 1831 году Фарадеем электромагнитной индукции, появились первые генераторы постоянного, а после и переменного тока. Преимущество последних заключается в том, что переменный ток передается потребителю с меньшими потерями.

При увеличении напряжения в цепи, ток будет увеличиваться аналогично случаю с постоянным током. Но в цепи переменного тока сопротивление оказывается катушкой индуктивности и конденсатор. Основываясь на этом, запишем закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

где
• I [А] – сила тока,
• U [В] – напряжение,
• Z [Ом] – полное сопротивление цепи.

Полное сопротивление цепи

В общем случае полное сопротивление цепи переменного тока (рис. 1) состоит из активного (R [Ом]), индуктивного, и емкостного сопротивлений. Иными словами, ток в цепи переменного тока зависит не только от активного омического сопротивления, но и от величины емкости (C [Ф]) и индуктивности (L [Гн]). Полное сопротивление цепи переменного тока можно вычислить по формуле:

где
• — индуктивное сопротивление, оказываемое переменному току, обусловленное индуктивностью электрической цепи, создается катушкой.
• — емкостное сопротивление, создается конденсатором.

Полное сопротивление цепи переменного тока можно изобразить графически как гипотенузу прямоугольного треугольника, у которого катетами являются активное и индуктивное сопротивления.

Рис.1. Треугольник сопротивлений



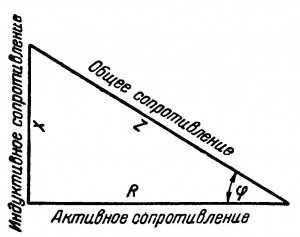
Учитывая последние равенства, запишем формулу закона Ома для переменного тока:

– амплитудное значение силы тока.

Рис.2. Последовательная электрическая цепь из R, L, C элементов.

Из опыта можно определить, что в такой цепи колебания тока и напряжения не совпадают по фазе, а разность фаз между этими величинами зависит от индуктивности катушки и емкости конденсатора:

Решение задач:

Цепь переменного тока состоит из последовательно соединенных конденсатора (емкостью С), катушки индуктивности (L) и активного сопротивления (R). На зажимы цепи подается действующее напряжение (U), частота которого ν. Чему равно действующее значение силы тока в цепи?

zakon-oma.ru

Ома закон — это… Что такое Ома закон?

Зако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.

Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка.

Ток, А	Напряжение, В	Сопротивление, Ом	Мощность, Вт
I	U	R	P

История закона Ома

Георг Ом, проводя эксперименты с проводником, установил, что сила тока I в проводнике пропорциональна напряжению U, приложенному к его концам:

,

или

.

Коэффициент пропорциональности назвали электропроводностью, а величину принято именовать электрическим сопротивлением проводника.

Закон Ома был открыт в 1827 году.

Закон Ома в интегральной форме

Схема, иллюстрирующая три составляющие закона Ома

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления

Закон Ома для участка электрической цепи имеет вид:

U = RI

где:

• U — напряжение или разность потенциалов,
• I — сила тока,
• R — сопротивление.

Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

где:

Закон Ома в дифференциальной форме

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re^—iδ — комплексное сопротивление (импеданс),
• R = (R_a²+R_r²)^1/2 — полное сопротивление,
• R_r = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = —arctg R_r/R_a — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U₀sin(ωt + φ) подбором такой , что . Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Объяснение закона Ома

Закон Ома можно просто объяснить при помощи теории Друде

См. также

Wikimedia Foundation. 2010.

dic.academic.ru

ЗАКОН ОМА

На рисунке показана схема знакомой вам простейшей электрической цепи. Эта замкнутая цепь состоит из трех элементов: источника напряжения — батареи GB, потребителя тока — нагрузки R, которой может быть, например, нить накала электрической лампы или резистор, и проводников, соединяющих источник напряжения с нагрузкой. Между прочим, если эту цепь дополнить выключателем, то получится полная схема карманного электрического фонаря.

Нагрузка R, обладающая определенным сопротивлением, является участком цепи. Значение тока на этом участке цепи зависит от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем большим ток будет идти по участку цепи. Эта зависимость тока от напряжения и сопротивления выражается следующей формулой:


I = U/R

где I — ток, выраженный в амперах, А; U — напряжение в вольтах, В; R — сопротивление в омах, Ом. Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и обратно пропорционален его сопротивлению. Это основной закон электротехники, именуемый законом Ома (по фамилии Г. Ома), для участка электрической цепи. Используя закон Ома, можно по двум известным электрическим величинам узнать неизвестную третью. Вот несколько примеров практического применения закона Ома.

Первый пример: На участке цепи, обладающем сопротивлением 5 Ом, действует напряжение 25 В. Надо узнать значение тока на этом участке цепи.
Решение: I = U/R = 25 / 5 = 5 А.
Второй пример: На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Прежде всего ток 20 мА нужно выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.
Третий пример: Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Здесь, как и в предыдущем примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10кОм = 10000Ом). Следовательно, U = IR = 0,02 х 10000 = 200 В. На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем говорят эти сведения? О том, что лампочка будет нормально светиться при токе 0,28 А, который обусловливается напряжением 3,5 В, Пользуясь законом Ома, нетрудно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом. Это, подчеркиваю, сопротивление накаленной нити лампочки. А сопротивление остывшей нити значительно меньше. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.
В связи с этим приведу еще один пример: Напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Примерно такой ток потребляет электрический паяльник.
Всеми этими формулами, вытекающими из закона Ома, можно пользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.
Закон Ома и производные от него расчетные формулы, достаточно легко запомнить, если пользоваться вот этой графической схемой, т. н. треугольник закона Ома:

>Пользоваться этим треугольником легко, достаточно четко запомнить, что горизонтальная линия в треугольнике означает знак деления (по аналогии дробной черты), а вертикальная линия в треугольнике означает знак умножения.

Теперь рассмотрим такой вопрос: как влияет на ток резистор, включаемый в цепь последовательно с нагрузкой или параллельно ей? Разберем такой пример. У нас имеется лампочка от круглого электрического, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, начальное напряжение которой 4,5 В? Нетрудно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, почти вдвое превышающий тот ток, на который она рассчитана. Такой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все же можно питать от батареи 336Л, если последовательно в цепь включить добавочный резистор сопротивлением 25 Ом, как это показано на рис..



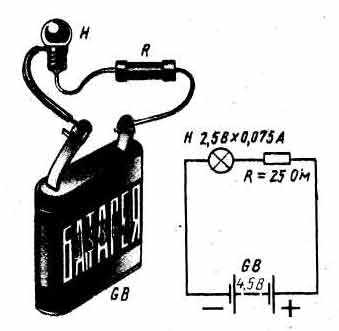
В этом случае общее сопротивление внешней цепи будет равно примерно 55 Ом, т.е. 30 Ом — сопротивление нити лампочки Н плюс 25 Ом — сопротивление добавочного резистора R. В цепи, следовательно, потечет ток, равный примерно 0,08 А, т.е. почти такой же, на который рассчитана нить накала лампочки. Эту лампочку можно питать от батареи и с более высоким напряжением и даже от электроосветительной сети, если подобрать резистор соответствующего сопротивления. В этом примере добавочный резистор ограничивает ток в цепи до нужного нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В данном случае в цепь было включено последовательно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при последовательном соединении сопротивлений ток одинаков во всех точках цепи. Можно включать амперметр в любую точку цепи, и всюду он будет показывать одно значение. Это явление можно сравнить с потоком воды в реке. Русло реки на различных участках может быть широким или узким, глубоким или мелким. Однако за определенный промежуток времени через поперечное сечение любого участка русла реки всегда проходит одинаковое количество воды.
Добавочный резистор, включаемый в цепь последовательно с нагрузкой (как, например, на рис. выше), можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится добавочным резистором или, как говорят, падает на нем, будет тем большим, чем больше сопротивление этого резистора. Зная ток и сопротивление добавочного резистора, падение напряжения на нем легко подсчитать все по той же знакомой вам формуле U = IR, Здесь U — падение напряжения, В; I — ток в цепи, A; R — сопротивление добавочного резистора, Ом. Применительно к нашему примеру резистор R ( на рис.) погасил избыток напряжения: U = IR = 0,08 х 25 = 2 В. Остальное напряжение батареи, равное приблизительно 2,5 В, упало на нити лампочки. Необходимое сопротивление резистора можно найти по другой знакомой вам формуле R = U/I, где R — искомое сопротивление добавочного резистора, Ом; U-напряжение, которое необходимо погасить, В; I — ток в цепи, А. Для нашего примера сопротивление добавочного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать или увеличивать напряжение, которое падает на добавочном резисторе, и таким образом регулировать ток в цепи. Но добавочный резистор R в такой цепи может быть переменным, т.е. резистором, сопротивление которого можно изменять (см. рис. ниже).

В этом случае с помощью движка резистора можно плавно изменять напряжение, подводимое к нагрузке Н, а значит, плавно регулировать ток, протекающий через эту нагрузку. Включенный таким образом переменный резистор называют реостатом, С помощью реостатов регулируют токи в цепях приемников, телевизоров и усилителей. Во многих кинотеатрах реостаты использовали для плавного гашения света в зрительном зале. Есть, однако, и другой способ подключения нагрузки к источнику тока с избыточным напряжением — тоже с помощью переменного резистора, но включенного потенциометром, т.е. делителем напряжения, как показано на рис..

Здесь R1 — резистор, включенный потенциометром, a R2 — нагрузка, которой может быть та же лампочка накаливания или какой — то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое частично или полностью может быть подано к нагрузке R2. Когда движок резистора находится в крайнем нижнем положении, к нагрузке напряжение вообще не подается (если это лампочка, она гореть не будет). По мере перемещения движка резистора вверх мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в крайнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 — лампочка карманного фонаря, а напряжение источника тока большое, нить лампочки перегорит). Можно опытным путем найти такое положение движка переменного резистора, при котором к нагрузке будет подано необходимое ей напряжение. Переменные резисторы, включаемые потенциометрами, широко используют для регулирования громкости в приемниках и усилителях. Резистор может быть непосредственно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет двумя параллельными путями: через добавочный резистор и основную нагрузку. Наибольший ток будет в ветви с наименьшим сопротивлением. Сумма же токов обеих ветвей будет равна току, расходуемому на питание внешней цепи. К параллельному соединению прибегают в тех Случаях, когда надо ограничить ток не во всей цепи, как при последовательном включении добавочного резистора, а только на каком — то участке. Добавочные резисторы подключают, например, параллельно миллиамперметрам, чтобы ими можно было измерять большие токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.

Спасибо lessonradio.narod.ru

www.radioingener.ru

No related posts.