Расчет сопротивления цепи

Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью. 

Пример 1

 

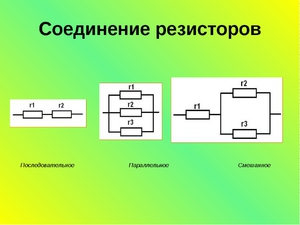
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.

Допустим, что R₁=10 Ом R₂=20 Ом, тогда 

Пример 2

 

Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R₁,R₂ такие же как и в примере 1) 

Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз. 

Пример 3

 

В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R

1,R₂ прежние, R₃=105 Ом) 

 

Пример 4

 

Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R₁ и R₂ соединенных параллельно, а затем общее сопротивление, как сумму R₁₂ и R₃ соединенных последовательно. 

 Пример 5

Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.

R₄=20 Ом, R₅=40 Ом, R₆=15 Ом 

Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.  

Просмотров: 23653

electroandi.ru

параллельная, последовательная и комбинированная цепь

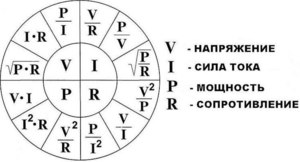
Решая задачи в области электроники и электрики, приходится сталкиваться с различными вычислениями. Чаще всего они связаны с упрощением электрических схем. Для этого используется метод эквивалента, когда часть цепи заменяется на один элемент с характеристиками, аналогичными ей. Но чтобы это сделать, необходимо знать, как посчитать сопротивление участка цепи и какие виды соединений бывают.

Определение величины

Ток — это упорядоченное движение носителей заряда под действием электрического поля. Способность вещества проводить ток называют электропроводимостью. Чем больше носителей частиц имеет материал, тем большей проводимостью он обладает. В зависимости от этой характеристики все вещества разделяют на три вида:

1. Проводники. Характеризуются хорошей электропроводностью. К ним относят металлы и их сплавы, а также электролиты.
2. Диэлектрики. Вещества, практически не проводящие электрический ток. В основном это газы, каучук, минеральные масла, пластмассы.
3. Полупроводники. Материалы, обладающие двумя видами проводимости одновременно — дырочной и электронной. Это вещества, имеющие ковалентную связь: кремний, германий, селен.

Величина, обратная электропроводимости, называется электрическим сопротивлением. То есть это физическая величина, препятствующая прохождению тока. Кроме способности любого материала ограничивать количество проходящих через него зарядов, существует специальный радиоэлемент, ограничивающий силу тока — резистор.

Таким образом, существует два понятия сопротивления: радиоэлемент и физическая величина.

Сопротивление радиоэлемента

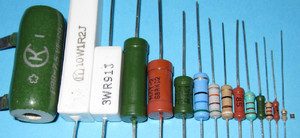Термин «резистор» произошёл от латинского слова resisto — «сопротивляемость». Все резисторы делятся на постоянные и переменные. Последние позволяют изменять своё сопротивление. На схемах и в литературе такая радиодеталь подписывается латинской буквой R. Единицей измерения считается Ом. Графически резистор обозначается в виде прямоугольника с двумя выводами от середины краёв. Кроме номинального сопротивления, он характеризуется рассеиваемой мощностью и классом точности.

По своей сути это пассивный радиоэлемент, преобразующий часть электрической энергии в тепловую. Тем самым он ограничивает ток, линейно преобразовывая его силу в напряжение и наоборот. Главный параметр, описывающий сопротивление, находится согласно закону Ома для участка цепи по следующей формуле: R = U/I, где:

• R — электрическое сопротивление, Ом.
• U — разность потенциалов приложенная к элементу, В.
• I — сила тока, преходящая через резистор, А.

Но тут следует отметить, что этот закон справедлив только для резистивных цепей. То есть для тех, при расчёте которых ёмкостью и индуктивностью пренебрегают. Если же эту формулу применить к реактивным элементам, то для катушки индуктивности сопротивление будет равным нулю, а для конденсатора — бесконечным. Но это верно для постоянного тока и напряжения.

При переменных величинах напряжение на индуктивности не будет равно нулю, как и ток, проходящий через конденсатор. Такие случаи сопротивлением уже не описываются, поскольку оно предполагает постоянные значения тока и напряжения.

Удельный параметр вещества

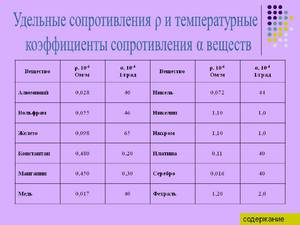Чтобы различать понятие и элемент, было введено название удельное электрическое сопротивление. Обозначается оно греческим символом ρ. В Международной системе единиц эта величина измеряется в Омах, умноженных на метр. Зависит она исключительно от свойства материала.

Для расчёта электрического сопротивления однородного вещества используется формула: R = ρ* l/S, где:

• l — длина проводника, м;
• S — площадь поперечного сечения, м².

Поэтому в физическом смысле удельное сопротивление материала — это величина, обратная удельной проводимости, представляющая собой сопротивление однородного проводника единичной длины и площади поперечного сечения. А значит, она численно равна импедансу участка электрической цепи, выполненному из вещества длиною один метр и площадью поперечного сечения один метр квадратный.

Для каждого вещества удельное сопротивление известно и является справочной величиной. Например, для меди — 0,01724 Ом*мм²/м, алюминия — 0,0262 Ом*мм²/м, висмута — 1,2 Ом*мм²/м, нихром — 1,05 Ом*мм²/м. Эти данные получены при температуре t = 20 °C, так как материалы обладают свойством изменять свою удельную характеристику при изменениях температуры. Так, проводимость металлов увеличивается при снижении температуры, а полупроводников — уменьшается.

Эквивалентная схема

При расчётах сопротивления электрических цепей широко используется понятие «эквивалентная схема замещения». Её назначение — упростить сложную схему до вида, состоящую из минимума элементов. Иными словами, каждый сложный радиоэлемент можно представить в виде соответствующих ему эквивалентных простых радиодеталей: резистор, ёмкость, индуктивность, источники тока и напряжения. Это позволяет не только математически описать любую схему, но и рассчитать её параметры.

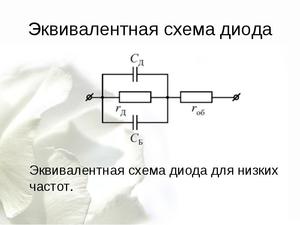
При этом обычно радиоэлементы идеализируются, то есть их паразитные параметры не учитываются. Так и для подсчёта сопротивления цепи каждый компонент представляется как идеальный резистор. После чего схема перерисовывается, и в результате на ней остаются только подключённые разными способами друг к другу резисторы.

Существует два вида подключения:

• последовательное;
• параллельное.

Основными элементами электрической цепи являются узел, ветвь и контур. Узел — это место соединения двух и более ветвей. Ветвь — это последовательный участок цепи между двумя узлами, а контур — любая замкнутая цепь. Последовательное соединение состоит из элементов, при котором все компоненты цепи связаны так, что участок цепи, образованный из них, не имеет ни одного узла. А при параллельном соединении все компоненты электрической цепи контактируют между собой в двух узлах. При этом эти узлы напрямую не связаны.

Расчёт импеданса

Методы вычисления общего сопротивления зависят от способа соединения резисторов. При расчётах общего импеданса за основу берутся законы Кирхгофа.

Так, первый его закон гласит: сумма токов в узле равна нулю. Или, если его перефразировать, значение тока, втекающего в узел, равно сумме токов, вытекающих из этого узла. Второй закон связан с электродвижущей силой, и его формулировка звучит так: сумма разности потенциалов в контуре равна сумме падений разности потенциалов на каждом резисторе в цепи.

При последовательном соединении все элементы располагаются друг за другом без ответвлений. Так как согласно правилу Кирхгофа в любом месте ветви сила тока одинаковая I = I1 = In, то падение напряжения на первом элементе: U1 = I*R1, а на n: Un = I*Rn, где:

• In — сила тока, протекающая через резистор, А.
• Un — значение падения напряжения на резисторе, В.
• Rn — величина сопротивления элемента, Ом.

Общая разность потенциалов равна сумме всех напряжений, поэтому можно записать: U = U1+…+Un = I*(R1+…+Rn) = IRo.

В результате формула для расчёта сопротивления цепи в этом случае будет выглядеть следующим образом:

Ro = R1 +…+ Rn, где:

• Ro — общее сопротивление ветви.
• R1 — значение импеданса первого элемента.
• Rn — величина сопротивления n-го элемента.

Если цепь параллельная то это значит, что на этом участке несколько ветвей расходятся, а после опять соединяются. Получается, что сила тока в каждой ветви будет своя, а величина напряжения одинакова. Поэтому Uo = U1=…= Un, а Io = I1+…+In. Используя закон Ома, можно записать:

Uo/Ro = U1/R1+…+Un/Rn, или

1/Ro = 1/R1+…1/Rn.

В итоге эквивалентное сопротивление при параллельном соединении рассчитывается как произведение значений резисторов, делённое на сумму их произведений. Для двух резисторов формулу для нахождения общего сопротивления можно записать в виде: Ro = (R1*R2) / (R1+R2).

Браузерный онлайн-калькулятор

Если элементов в цепи немного, то, упрощая схему, довольно легко посчитать, используя формулы для параллельного и последовательного включения резисторов, общий импеданс цепи. Но если в схеме много элементов, да ещё она такая, что содержит и то, и другое соединение (комбинированная), проще воспользоваться браузерными онлайн-калькуляторами.

В их основе используются всё те же формулы для расчёта эквивалентного резистора, но все вычисления происходят автоматически. Существует огромное количество предложений таких калькуляторов. Но при этом все они работают одинаково. Онлайн-расчёт представляет собой программный код, в котором заложен алгоритм вычисления. Потребителю необходимо только в специальных ячейках указать, какой вид соединения используется, сколько элементов в контуре и сопротивления резисторов. Далее надо нажать кнопку «Рассчитать» и через считанные секунды получить ответ.

Необходимо отметить, что, если даже это в программе не указано, все значения вводятся только в Международной системе единиц, сила тока — ампер, напряжение — вольт, сопротивление — Ом. Тогда и ответ получится в Омах.

Бонусом является и то, что многие такие программы сразу рассчитывают и мощность элемента. Для этого используется формула: P = U²/Ro = I²*Ro, Вт.

Практическое применение

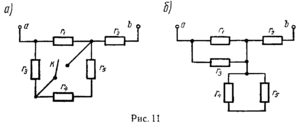Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.

Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.

Простое соединение

Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.

R3 = 1 кОм = 1000 Ом.

Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.

Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:

1/Ro = 1/R1 + 1/R2 +1/R3.

Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).

Подставив исходные данные в эту формулу, получим:

Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.

Комбинированный контур

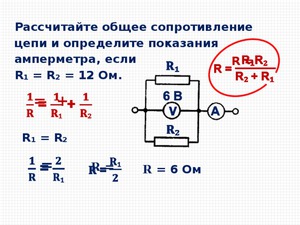Необходимо вычислить мощность и эквивалентное сопротивление смешанной цепи, состоящей из четырёх резисторов. Резистор R1 =R2 =5 Ом, R3= 10 Ом, R4 =3 Ом. На схему подаётся питание пять вольт.

Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:

Rp = (R3*R4)/(R3+R4).

Rp = (10*3)/ (10+3) = 2,3 Ом.

Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:

Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.

Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:

I = U/R = 5/2,3 = 2,2 A.

P = I*U = 2,2*5= 11 Вт.

Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.

220v.guru

Физическая формула расчета эквивалентного сопротивления в цепи

Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).

Эквивалентное сопротивление резисторов

Определение эквивалентного сопротивления

При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.

Последовательное соединение элементов

Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.

Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.

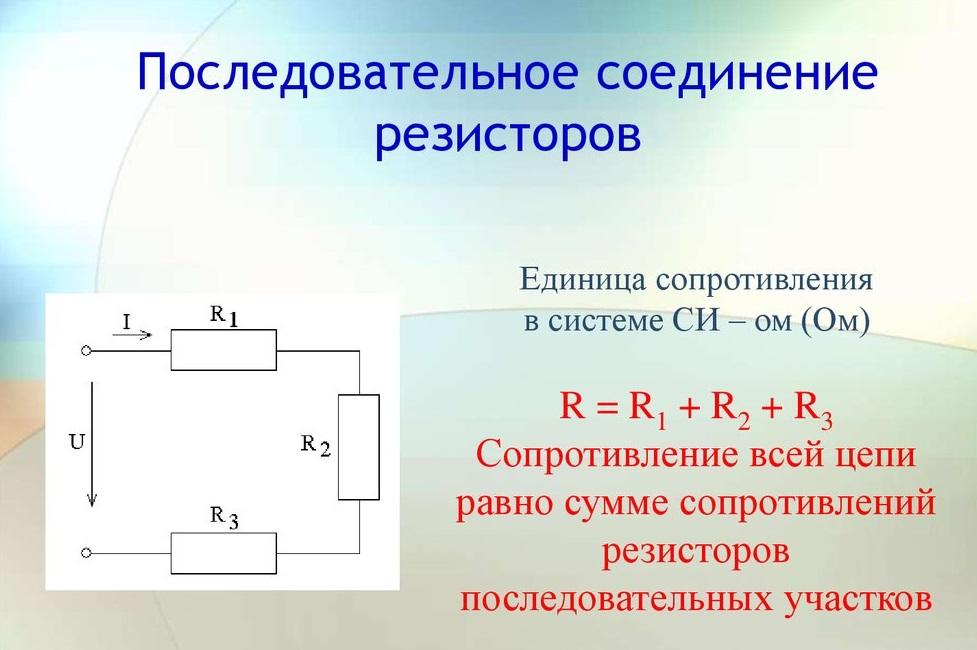
Последовательное включение резисторов

В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:

I = U/R.

Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:

R = U/I.

Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.

Проходящий по цепи ток везде одинаковый:

I = I1= I2= … = In.

Прикладываемое напряжение является суммой напряжений на каждом резисторе:

U = U1 + U2+ … + Un.

Следовательно, рассчитать можно общее:

Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.

Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.

Параллельное соединение

Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.

Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:

• общий ток: I = I1 + I2 + … + In;
• общее напряжение: U = U1 = U2 = … = Un;
• Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.

Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.

Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.

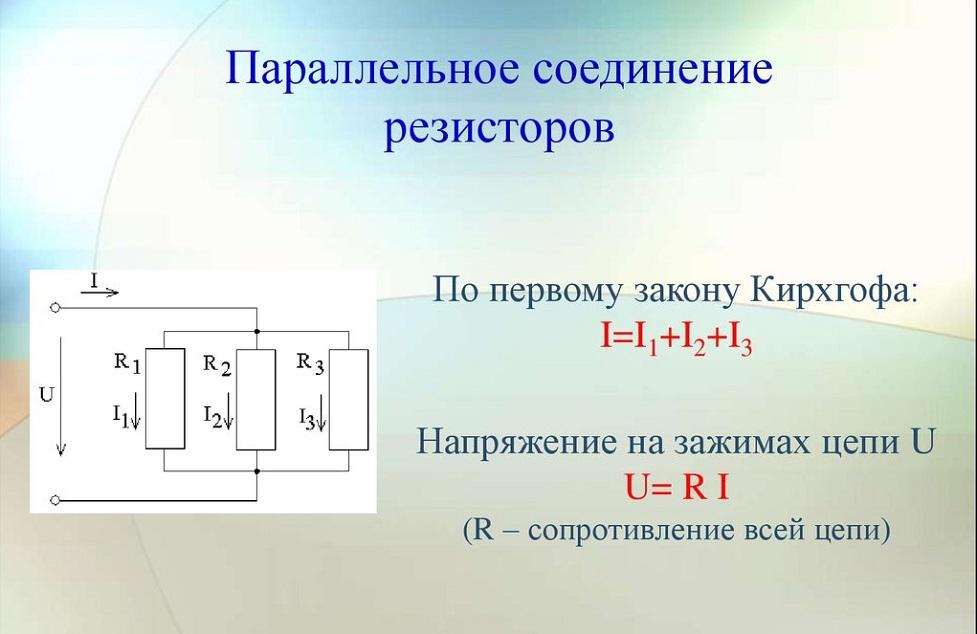
Параллельное включение резисторов

Расчёт при смешанном соединении устройств

Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.

Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.

Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.

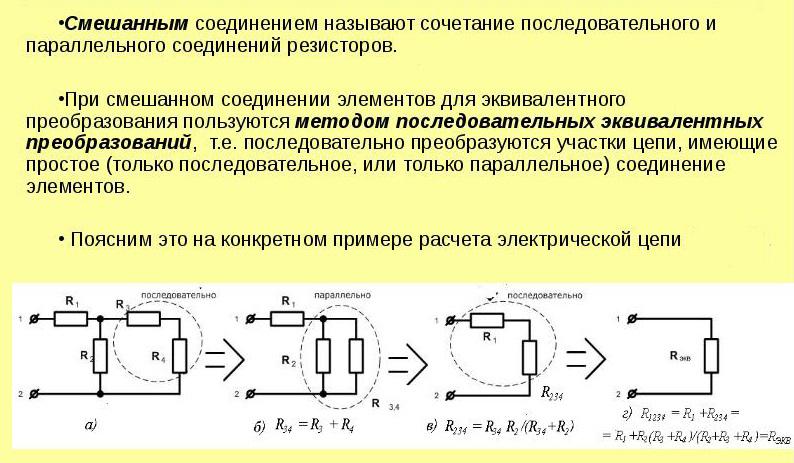
Способ расчёта при смешанном соединении

Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.

Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.

Физические формулы и примеры вычислений

Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:

• параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
• последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.

У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.

Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:

• R1 = 1 Ом;
• R2 = 2 Ом;
• R3 = 3 Ом;
• R4 = 6 Ом;
• R5 = 9 Ом;
• R6 = 18 Ом;
• R7 = 2Ом;
• R8 = 2Ом;
• R9 = 8 Ом;
• R10 = 4 Ом.

Напряжение, поданное на схему:

U = 24 В.

Требуется рассчитать токи на всех резистивных элементах.

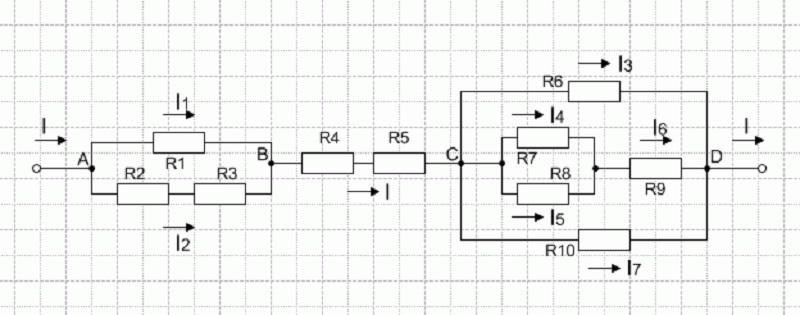
Исходная цепь

Для расчётов применяется закон Ома:

I = U/R, подставляя вместо R эквивалентное сопротивление.

Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.

Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.

На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:

• АВ – участок, имеющий две параллельных ветви;
• ВС – отрезок, вмещающий в себя последовательное сопряжение;
• CD – отрезок схемы с расположением трёх параллельных цепочек.

Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.

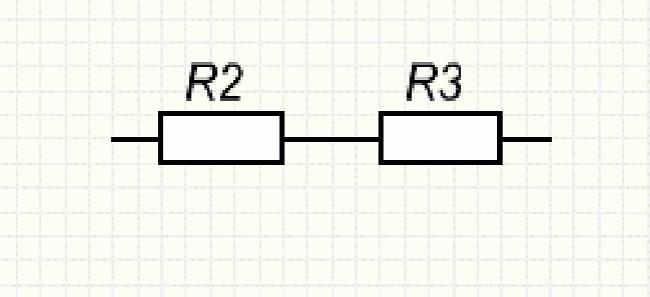
Последовательно соединённые резисторы R2 и R3

Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.

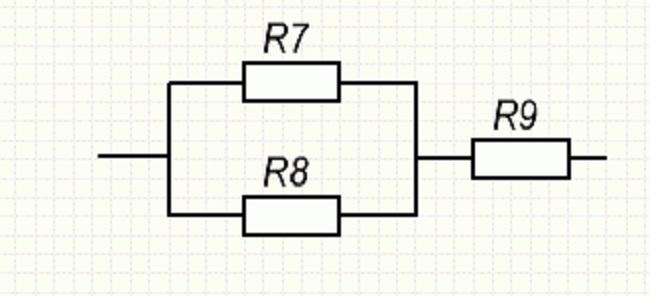
Смешанное включение на участке CD

Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:

• Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
• Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
• Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.

Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.

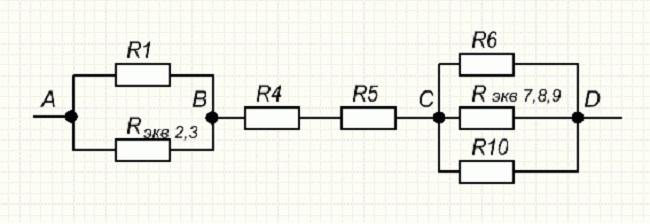
Результат первого свёртывания

Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:

• Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
• Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
• 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.

В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.

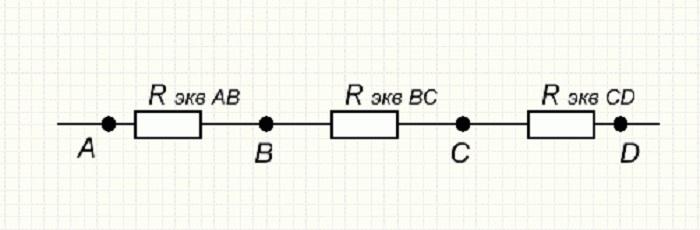
Результат последующего свёртывания

Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:

Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.

Далее, используя закон Ома, находят ток в последнем последовательном участке:

I = U/ Rэкв. = 24/56,83 = 0,42 А.

Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:

• UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
• UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
• UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.

Следующим шагом станет определение токов на параллельных отрезках AB и CD:

• I1 = UAB/R1 = 0,35/1 = 0,35 А;
• I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
• I3 = UCD/R6 = 0,17/18 = 0,009 А;
• I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
• I7 = UCD/R10 = 0,17/4 = 0,04 А.

Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.

U9 = R9*I6 = 8*0,02 = 0,16 В.

Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.

U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.

После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:

• I4 = U7,8/R7 = 1/2 = 0,5 A;
• I5 = U7,8/R8 = 1/2 = 0,5 A.

Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.

Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.

Видео

amperof.ru

Электрическое сопротивление участка цепи

Электрическое сопротивление для участка цепи определяется при помощи закона Ома. Для того, чтобы понять процессы, происходящие в элементах электрической цепи постоянного тока, необходимо дать общее определение закона Ома.

Закон Ома

Сила тока на участке цепи всегда прямо пропорциональна напряжению на данном участке и обратно пропорциональна сопротивлению участка.

Подобное определение будет верно также для растворов электролитов. Общий закон Ома характерен при описании однородного участка цепи, который не содержит источников тока.

При составлении формул вводятся дополнительные характеристики. Среди них коэффициент пропорциональности. Его записывают в виде $1=R$. Отсюда следует, что $I = \frac{U}{R}$.

$R$ – сопротивление проводника.

Сопротивление принято измерять в омах (Ом).

Закон Ома является главным законом в электротехнике. С помощью его:

• изучаются и рассчитываются электрические цепи;
• устанавливается логическое соотношение между сопротивлением и напряжением.

Определение 1

Вольтамперная характеристика – функциональная зависимость элемента участка цепи. Она является очень важной величиной электрических свойств элемента. Такую зависимость можно представить в виде $I = I(U)$.

Подобные характеристики в зависимости от ситуации могут приобретать различные формы и выражения. Наиболее простой вид вольтамперной характеристики выразил в формуле Георг Ом, в честь которого была названа единица сопротивления тока. Ученый подтвердил свою теорию многочисленными экспериментами, применяя опыты к металлическому проводнику.

Закон Ома необходимо понимать на теоретическом и практическом уровне, чтобы решать различные задачи. Если неправильно применять основные параметры закона, то результат приобретает неправильные черты, поэтому допускаются многочисленные ошибки.

Применение закона Ома для участка цепи

Каждый участок электрической цепи можно описать с помощью трех основных величин:

• сопротивления;
• напряжения;
• тока.

Такое сочетание также называют «треугольником Ома», поскольку величины характеризуют все процессы электротехники.

Все производимые расчеты имеют смысл только в тех случаях, когда напряжение на участке цепи выражается в вольтах (В), сопротивление — в омах (Ом), а ток – в амперах (А). При использовании иных единиц измерений или их кратных значений необходимо осуществлять дополнительный ряд действий, чтобы искомый результат полностью соответствовал задачам и целям расчетов. Для этого кратные единицы используемых величин переводят в традиционные величины.

Кратные единицы измерений:

• милливольты;
• миллиамперы;
• мегаомы.

При произведении расчетов в кратных единицах измерений величин напряжение всегда выражается в вольтах.

Для расчета сопротивления на участке цепи по закону Ома необходимо сначала определить ток на заданном участке цепи. Напряжение при этом делят на сопротивление конкретного участка цепи. Эти действия можно производить на любом участке без погрешности.

Для определения напряжения в цепи используют формулу $U = IR$.

Согласно указанной формуле, напряжение на обоих концах участка электрической цепи прямо пропорционально сопротивлению и току. Иными словами, если не стремиться все время изменять сопротивление на данном участке, то при увеличении тока применяется способ увеличения напряжения.

Значительному напряжению в цепи будет соответствовать больший ток. Эти правила действуют при постоянном сопротивлении. Для получении одинакового тока при различных сопротивлениях большее напряжение должно соответствовать большему сопротивлению.

Падение напряжения – это напряжение на определенном участке цепи. Это означает, что напряжение и падение напряжения – идентичные понятия, а слово «падение» никак не связано с потерей некоторого количества напряжения в цепи. Потерю напряжения следует различать от падения напряжения.

Расчет сопротивления

Сопротивление на участке цепи рассчитывается по классической формуле $R = \frac{U}{I}$. Для этого необходимо установить значения напряжения и тока. Сопротивление – отношение напряжения к току.

При многократном увеличении или уменьшении напряжения ток также изменяется в несколько раз в ту или иную сторону. Отношение напряжения к току, которое равно сопротивлению, всегда остается на неизменном уровне.

Сопротивление определенного проводника не зависит от напряжения и тока. Оно будет лежать в зависимости от материала проводника, его длины и площади сечения. Формула для расчета сопротивления на участке цепи очень похожа на формулу для определения тока, однако существует между ними принципиальное различие.

Оно состоит в том, что ток на конкретном участке цепи зависит от напряжения и сопротивления, поэтому изменяется таким же образом. Сопротивление на данном участке цепи – постоянная величина. Она не зависит от изменения значений тока и напряжения, однако равно отношению этих величин.

Вольтамперная характеристика

Закон Ома представляют в виде вольтамперной характеристики. Зависимость между двумя пропорциональными величинами выражается прямой линией на графике. Она проходит через начало координат. Подобную прямую пропорциональную зависимость величин также называют линейной зависимостью.

В графическом выражении закона Ома для участка цепи при отрицательных значениях напряжения и тока также рисуют прямую линию. Это означает, что ток в цепи проходит в разных направлениях одинаково. При большем сопротивлении меньшее значение имеет ток с таким же напряжением.

Вольтамперную характеристику составляют при помощи специальных приборов. Линейными называют такие приборы, у которых характеристика выражается прямой линией, и она проходит через начало координат.

Специалисты при составлении вольтамперной характеристики применяют также понятия линейные сопротивления и линейные цепи.

Определение 2

Нелинейными называют приборы, у которых сопротивление меняется при изменении тока или напряжения. Для таких случаев уже не действует закон Ома.

spravochnick.ru

Для знатоков физики! Необходимо определить общее сопротивление цепи…

Ответ Rобщ. =R*(1+КОРЕНЬ (3))=2,732R Могу прислать очень простое доказательство (решение). <img src=»//otvet.imgsmail.ru/download/c7d16c238368c7d1b95e1baa38c62ff3_i-4.jpg» ><img src=»//otvet.imgsmail.ru/download/c7d16c238368c7d1b95e1baa38c62ff3_i-5.jpg» >

а есть какие то цифры, значение?

R/n n-количество проводников

Посмотри уравнение Кирхгоффа

скорее всего ответ R

Интересная последовательность, но я практик и теорию обойду: Rsum приблизительно = 2 R + мелочь)) ) (посадите меня голой задницей на горячий паяльник, если неправ))) ( R парал участка стремится к нулю в бесконечности ряда)

Считаешь токи по веткам: _ ___ ____ _| _|_| _|_|_| …U/(3R), U/(6R), U/(9R) … Затем суммируешь: U/(3R)*[1 + 1/2 + 1/3 + .+1/n] = Hn*U/(3R), где Hn — частичная сумма гармонического ряда, n — число веток. Делишь напряжение на этот ток, получается: Общее сопротивление = 3R/Hn. Если число элементов бесконечно, то ответ — ноль.

Красивая задача! Будет (1+корень из 3)R, или примерно 2,732R. Готов доказать, если это требуется 😉 P.S. Блин, меня опередили, пока считал 🙁

Оветили тебе уже верно, а решение очень красиво, у нас оно называется «методом Иона Тихого» — это герой С. Лема. Как-то приехал Ион Тихий на новую планету, а там была гостинница с бесконечным числом номеров. Но свободых номеров всё равно не было :-(. Что делать? И тогда Тихий попросил администрацию одномоментно переселить жильца первого номера — во второй, второго в третий, n-ого в n+1-ый. Когда номеров бесконечно, это очевидно можно сделать! И освободился первый номер. Теперь решение ясно? Кстати ещё такие методы носят название методов самосогласованного поля или эффективной среды, и основаны на том, что если от бесконечной цепочки сопротивлением Х откусит первое звено — сопротивление оставшейся части всё равно будет Х — ведь БЕСКОНЕЧНАЯ цепочка отсутствия первого звена не заметит!

touch.otvet.mail.ru

No related posts.