3.5. Обрыв фаз и обрыв линейного провода при соединении источников и потребителей треугольником
3.5.1. Обрыв фазы ab
Рассмотрим электрическую схему, изображённую на рис.3.20.
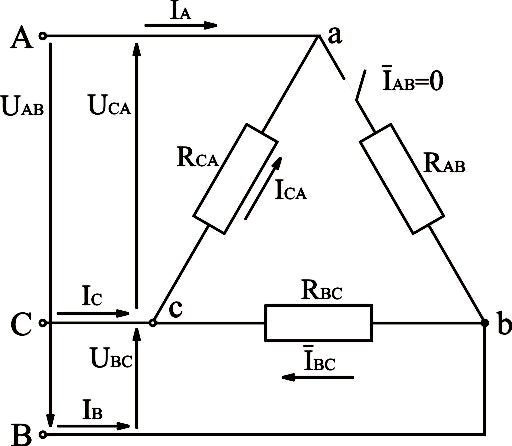
Рис.3.20. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенной фазой
При
обрыве фазы ab вектор тока 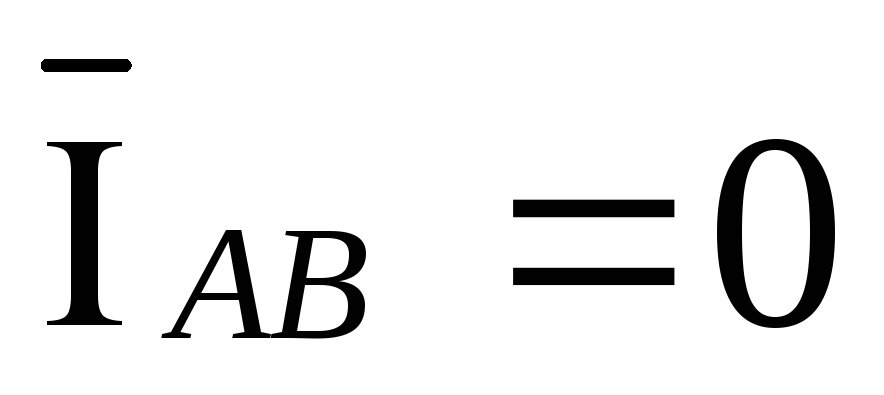 ,
тогда выражения (3.14) преобразуются в
следующий вид:
,
тогда выражения (3.14) преобразуются в
следующий вид:
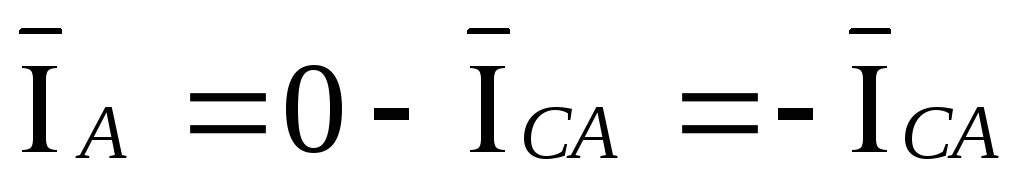 ,
, 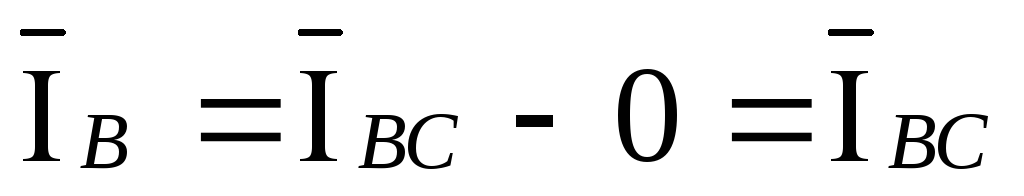 ,
, 
На рис.3.21 приведена векторная диаграмма напряжений и токов при обрыве фазы аb нагрузки, соединённой треугольником.
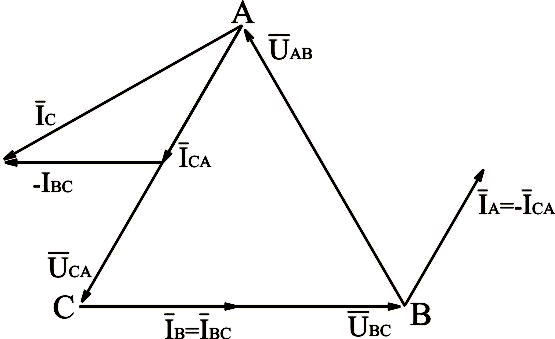
Рис.3.21. Векторная диаграмма напряжений и токов для нагрузки, соединённой треугольником, с отключенной фазой
3.5.2. Обрыв фаз ab и bc
Рассмотрим электрическую схему, изображённую на рис.3.22.
При
обрыве фаз ab и bc векторы токов 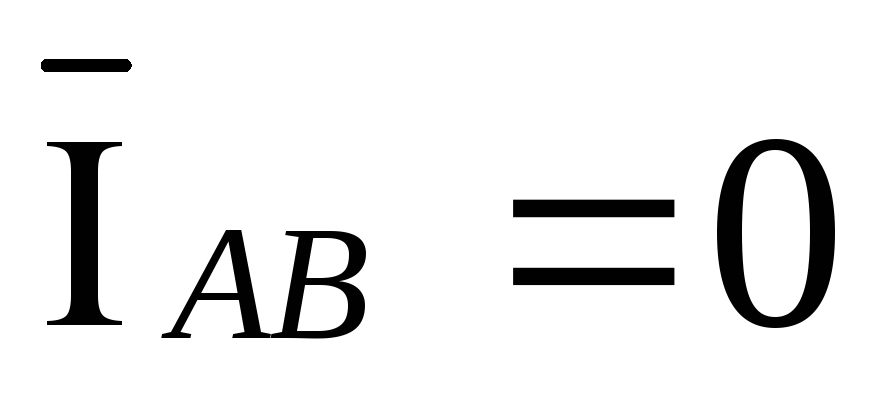
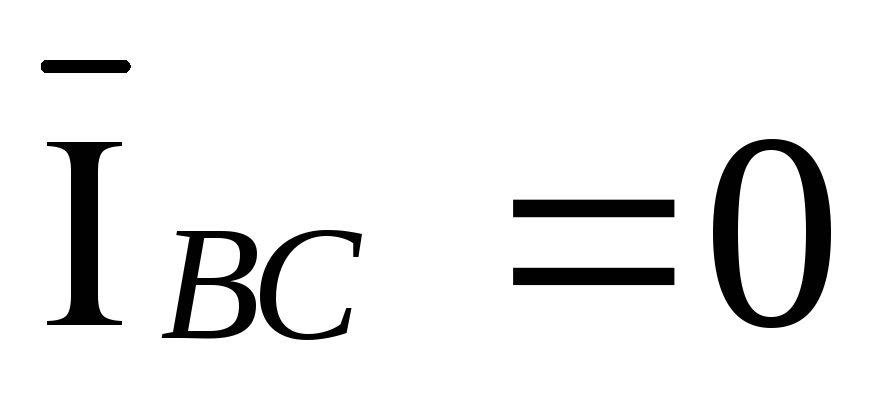 ,
тогда выражения (3.14) преобразуются в
следующий вид:
,
тогда выражения (3.14) преобразуются в
следующий вид: 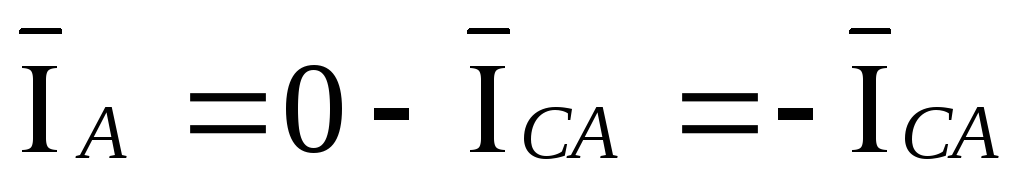 ,
, 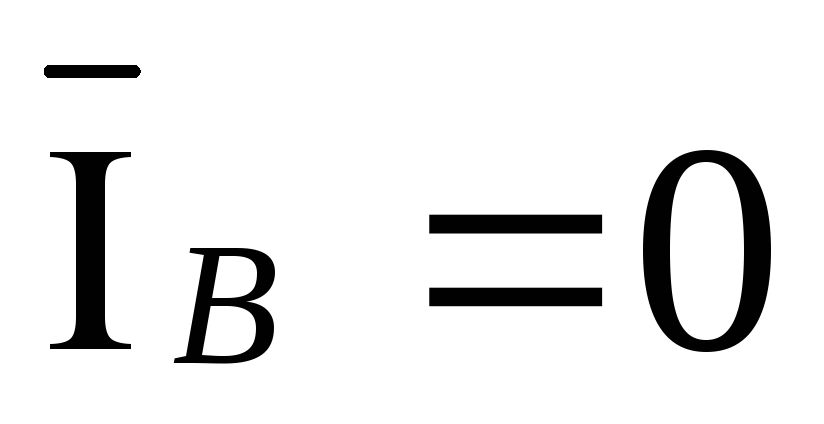 ,
, 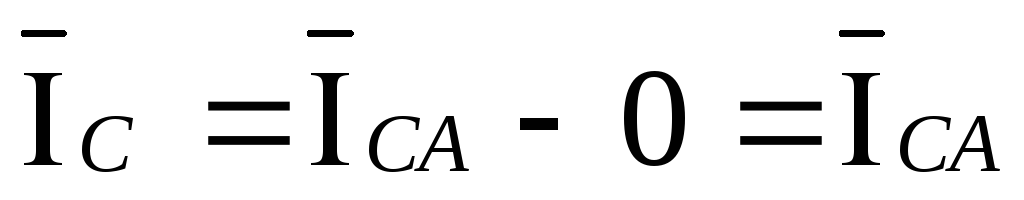 .
(3.17)
.
(3.17)
На рис.3.23 приведена векторная диаграмма напряжений и токов при обрыве фаз аb
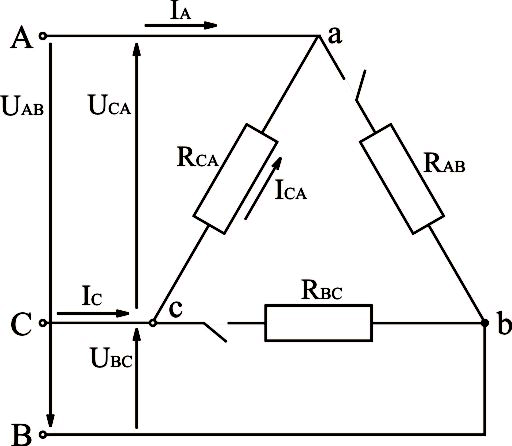
Рис.3.22. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенными двумя фазами
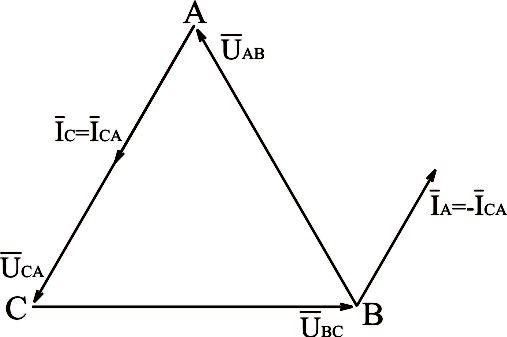
Рис.3.23. Векторная диаграмма напряжений и токов для нагрузки, соединённой треугольником, с отключенными двумя фазами
3.5.3. Обрыв линейного провода
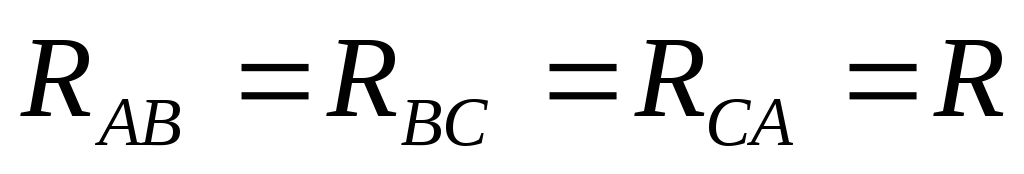 .
. 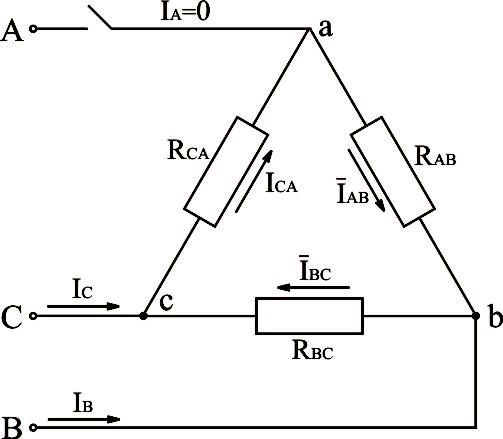
Рис.3.24. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенным линейным проводом
При
обрыве линейного провода Аa вектор
тока 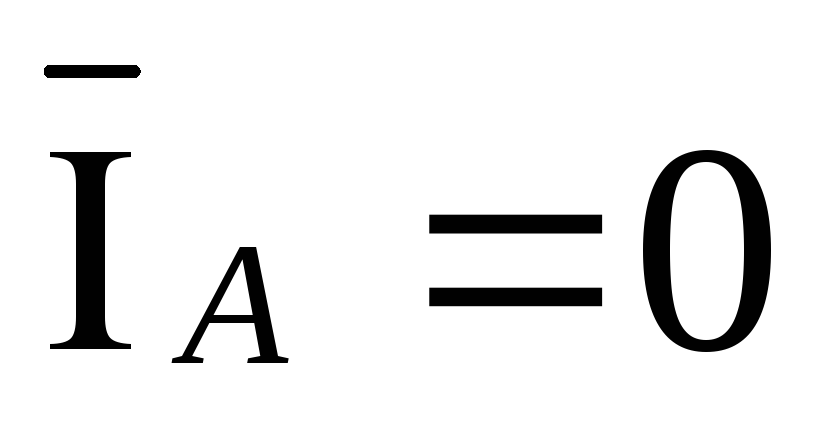 .
Преобразуем схему рис.3.24 в схему рис.3.25.
.
Преобразуем схему рис.3.24 в схему рис.3.25.
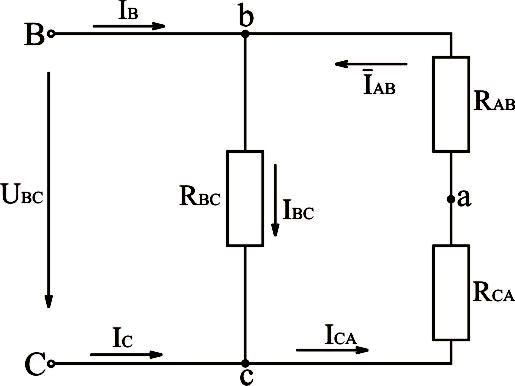
Рис.3.25. Преобразование трёхфазной электрической схемы, соединённой треугольником, с отключенным линейным проводом в однофазную электрическую схему
Из преобразованной схемы следует:
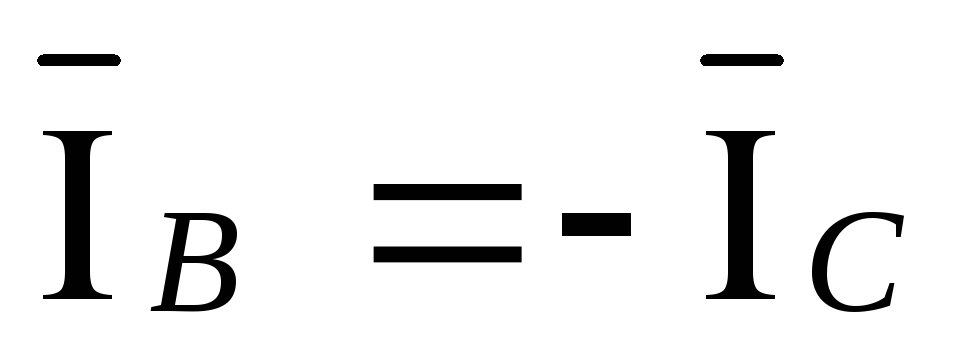 ,
,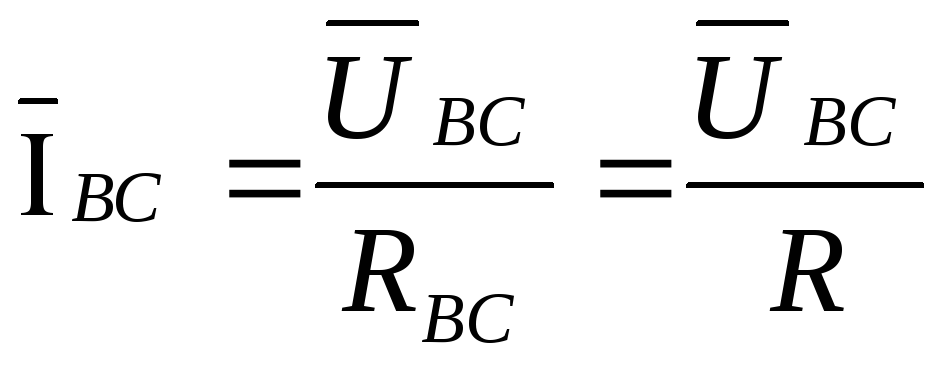 ,
,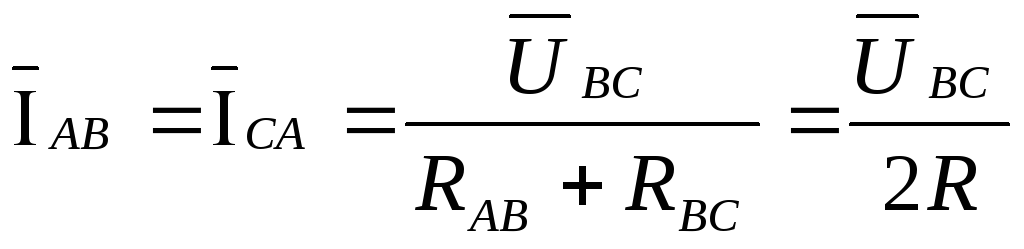 .
(3.18)
.
(3.18)
По первому закону Кирхгофа:
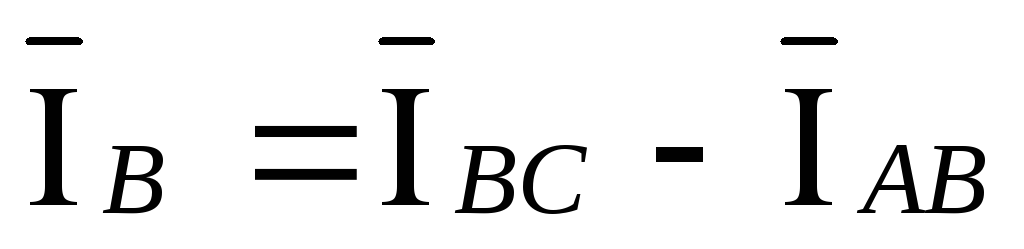 ;
; .
(3.19)
.
(3.19)Используя формулы (3.18) и (3.19), построим векторную диаграмму:
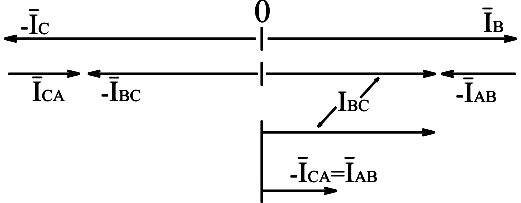
Рис.3.26. Векторная диаграмма токов преобразованной схемы
3.6. Мощность трёхфазной цепи
При симметричной нагрузке активная мощность трёхфазной цепи равна сумме активных мощностей фаз:
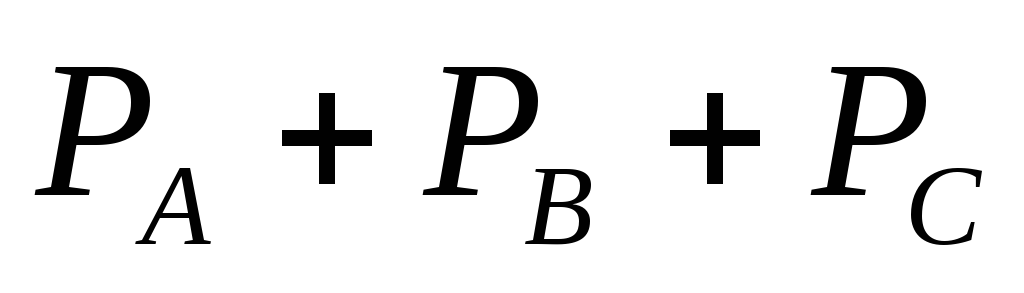 .
Активную мощность трёхфазной цепи можно
выразить через фазные значения напряжения
и тока:
.
Активную мощность трёхфазной цепи можно
выразить через фазные значения напряжения
и тока: P =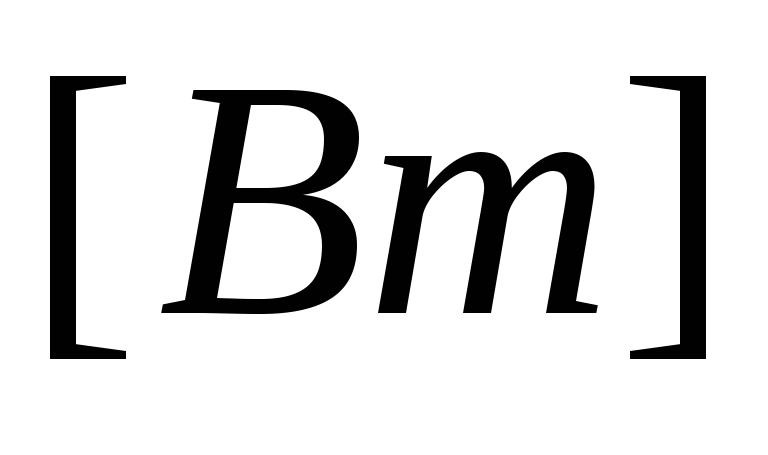 .
(3.20)
.
(3.20)
При
соединении звездой соотношения между
фазными и линейными напряжениями и
токами равны: 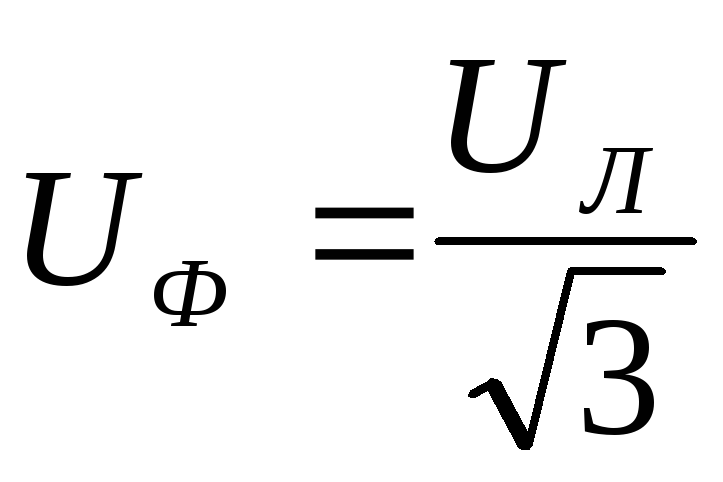 ,
, 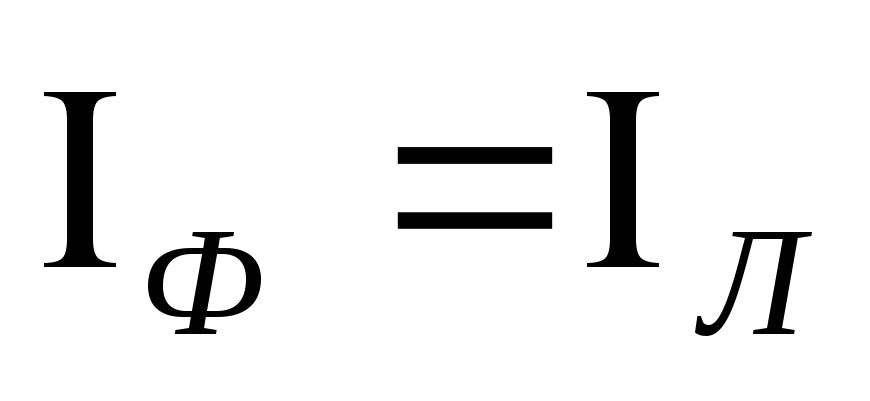
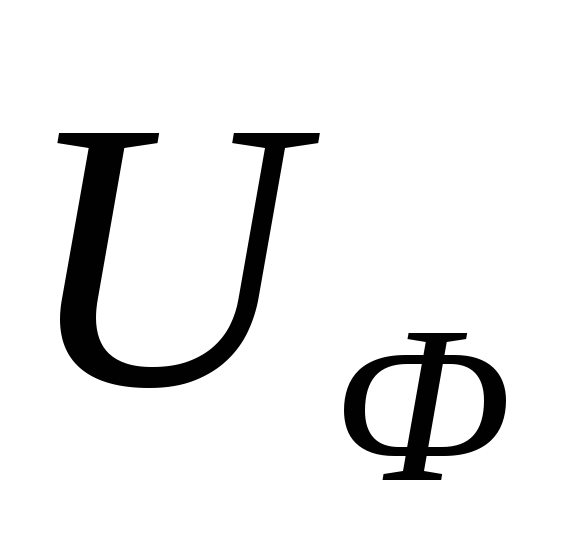 =
=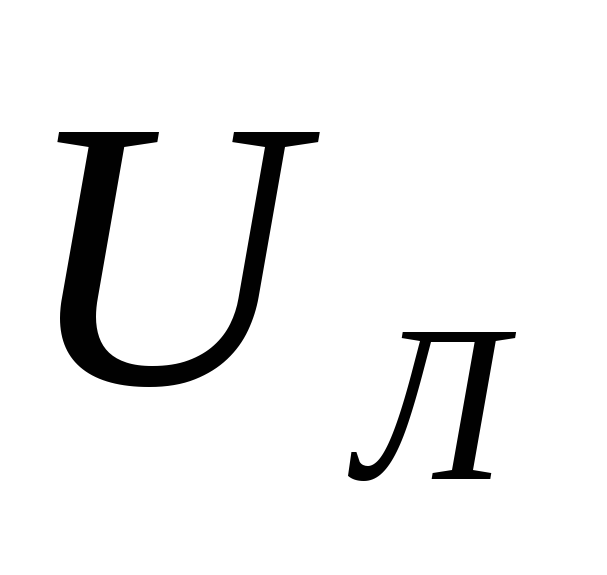 ,
, 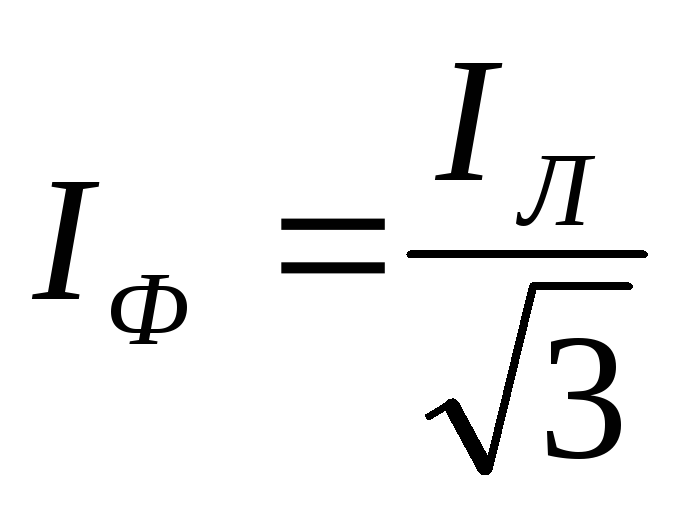 .
В обоих случаях
.
В обоих случаях 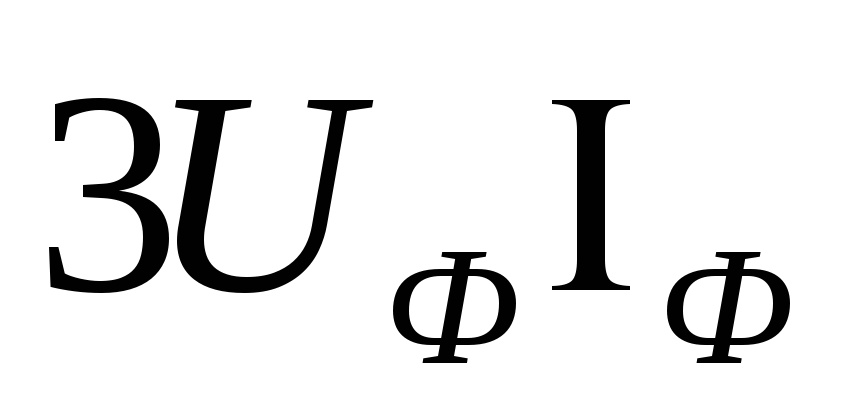
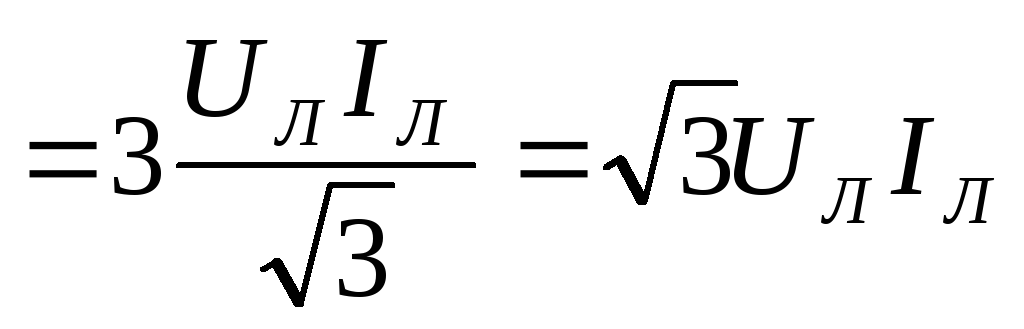 .
Тогда активную мощность можно выразить
через линейные значения напряжения и
тока:
.
Тогда активную мощность можно выразить
через линейные значения напряжения и
тока:
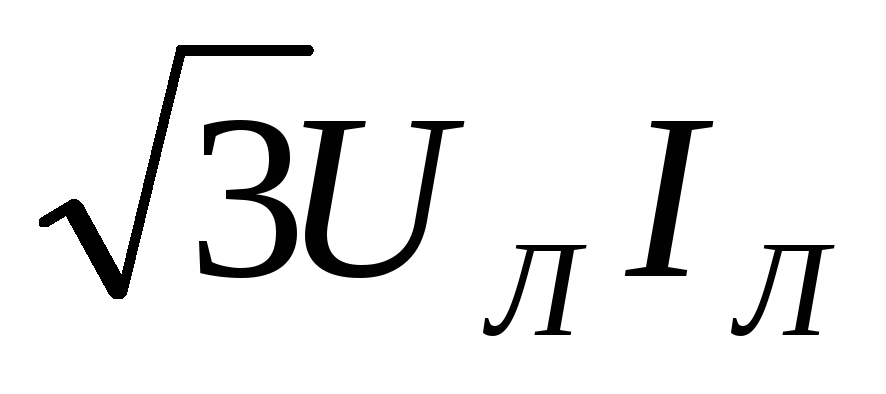
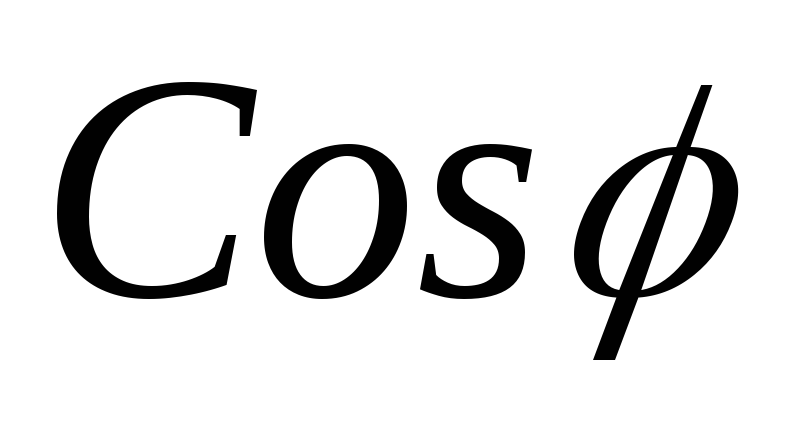
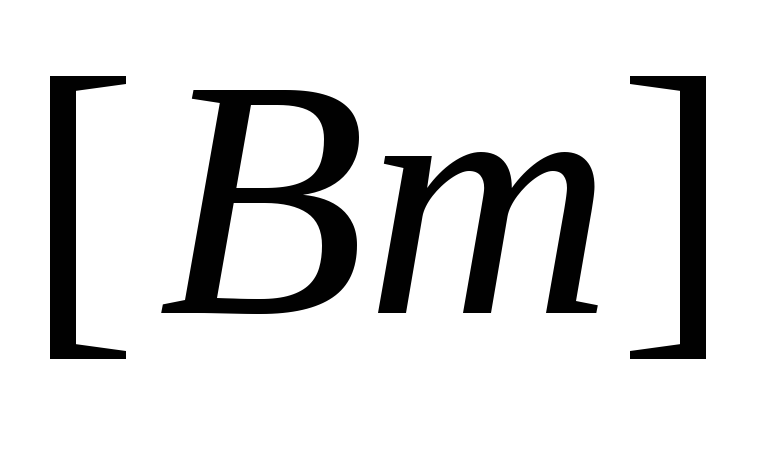 .
(3.21)
.
(3.21)Реактивная мощность трёхфазной цепи:
Q = =
=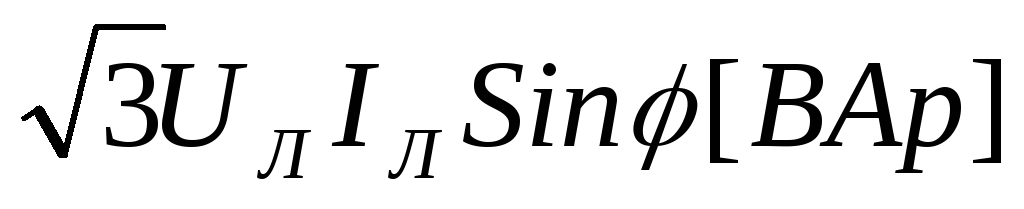 .
(3.22)
.
(3.22)
Полная мощность трёхфазной цепи:
S =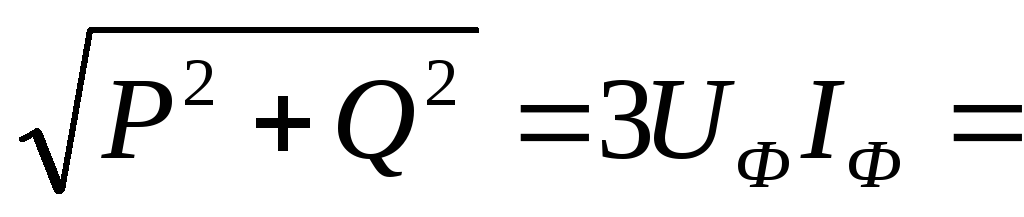
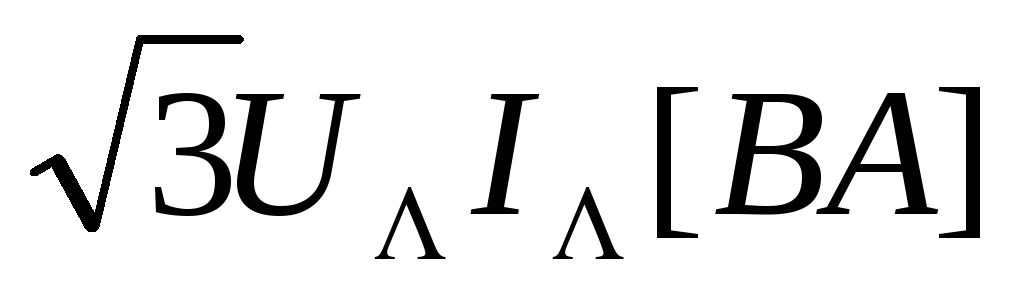 .
(3.23)
.
(3.23)
При расчётах удобно пользоваться следующими формулами:
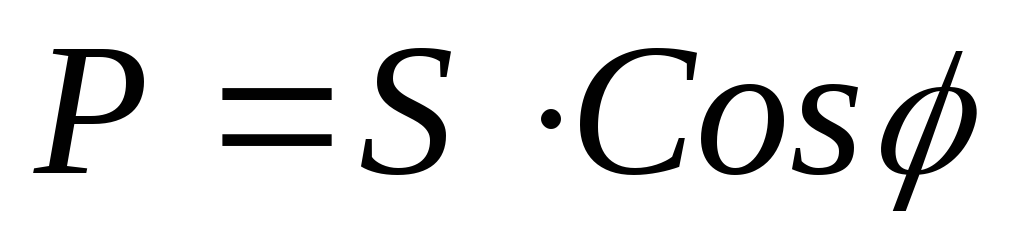 ;
;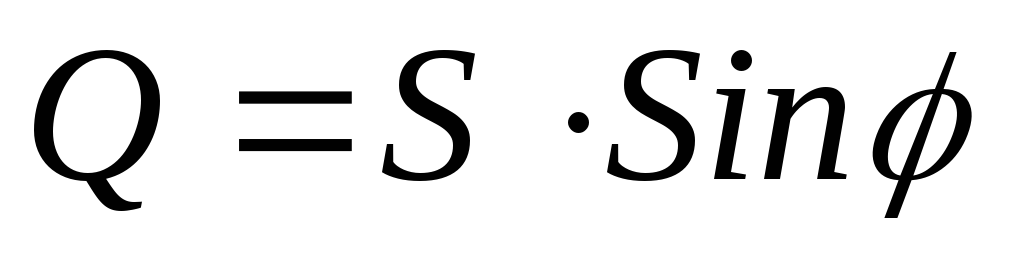 ;
;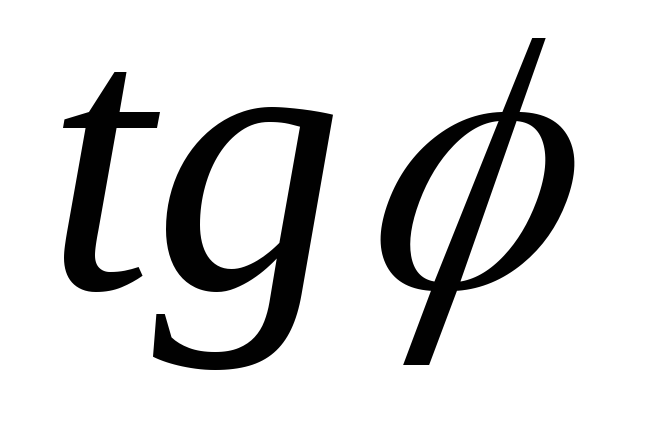
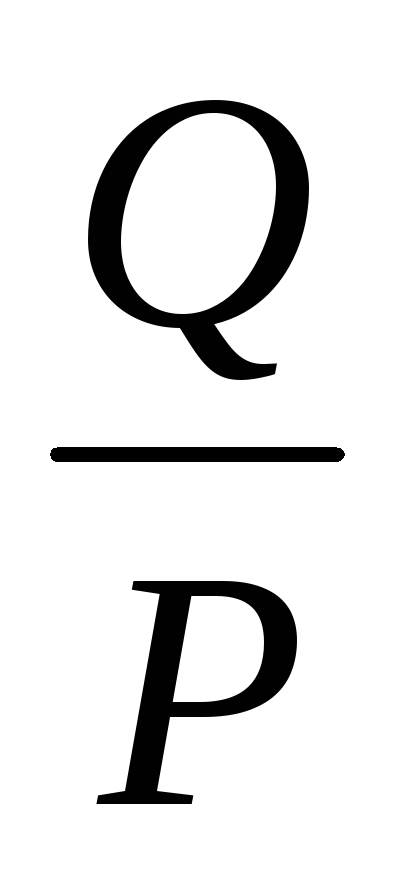 ;
;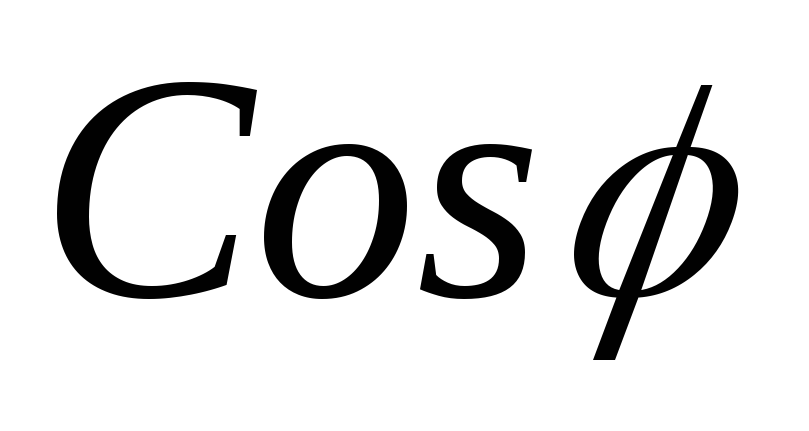 =
=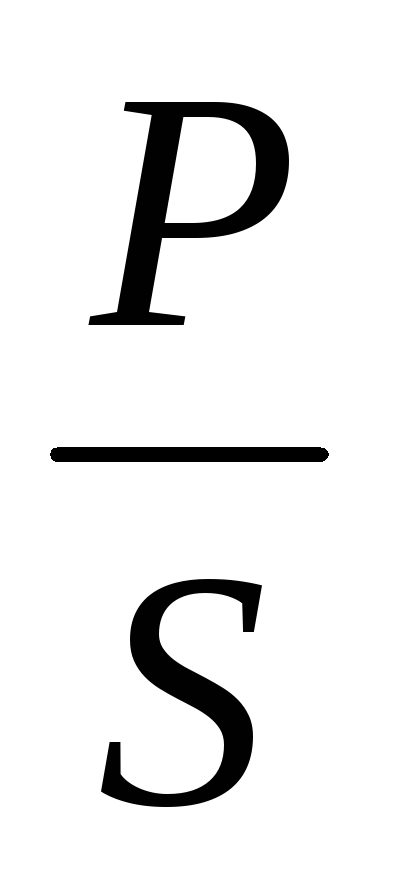 ;
; 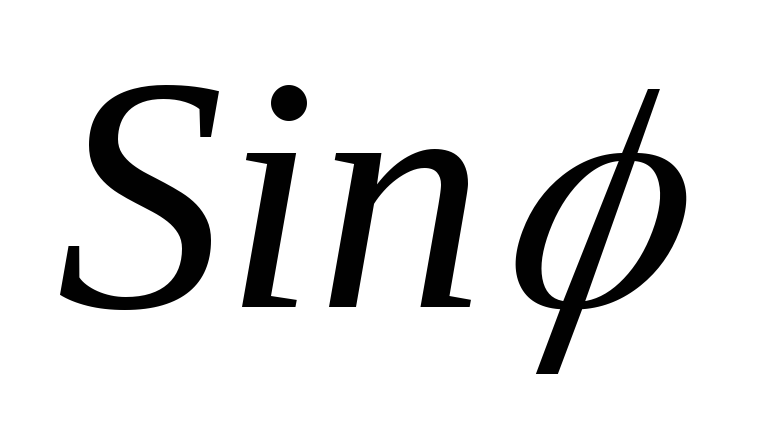 =
=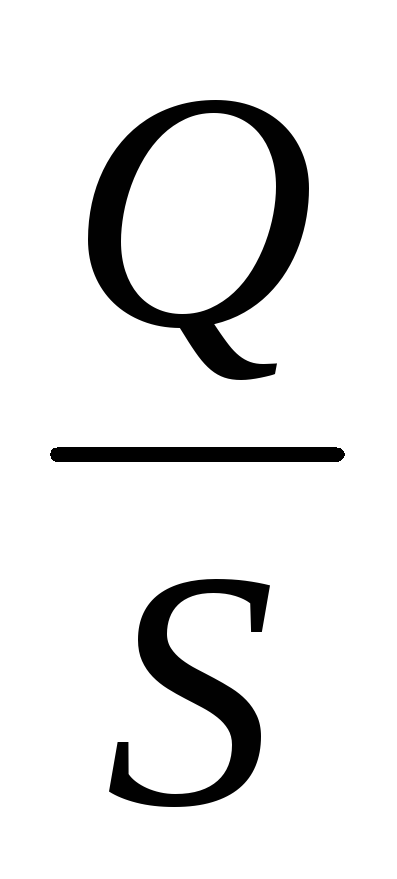 .
.При несимметричных нагрузках, соединённых звездой или треугольником, активную мощность рассчитывают по формулам:
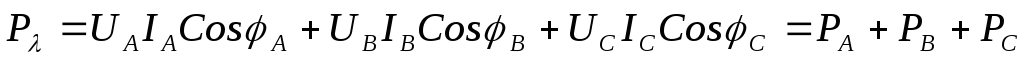 ;
;
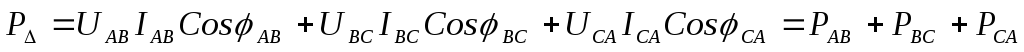 .
.
studfile.net
Обрыв фазы при симметричной нагрузке в схеме с нулевым проводом
При обрыве провода, например, в фазе А ток этой фазы становится равным нулю, напряжения и токи в фазах В и С не изменяются, а в нулевом проводе появляется ток
IN = IB + I
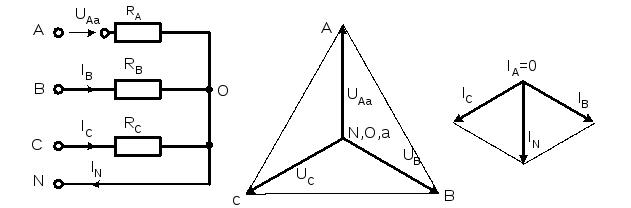
Рис.8.4.2
Обрыв фазы при симметричной нагрузке в схеме без нулевого провода
При
обрыве, например, фазы А сопротивления
RAи RBоказываются соединёнными
последовательно и к ним приложено
линейное напряжение UBC. Напряжение
на каждом из сопротивлений составляет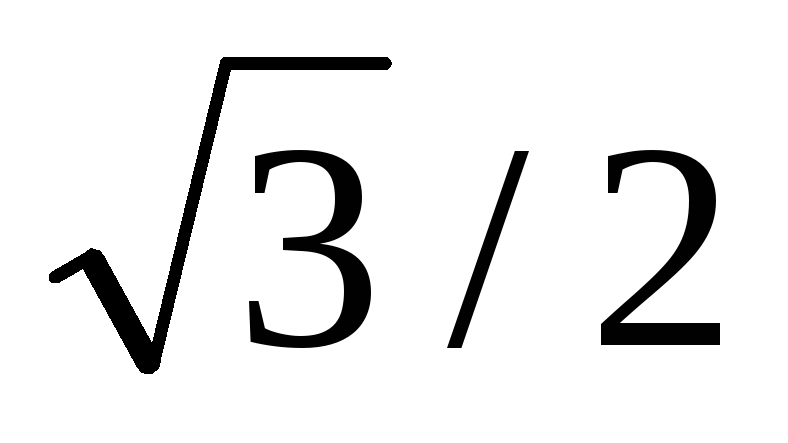 от фазного напряжения в нормальном
режиме. Нулевая точка нагрузки на
векторной диаграмме напряжений смещается
на линию ВС и при RB= RCнаходится точно в середине отрезка ВС
(рис.8.4.3
от фазного напряжения в нормальном
режиме. Нулевая точка нагрузки на
векторной диаграмме напряжений смещается
на линию ВС и при RB= RCнаходится точно в середине отрезка ВС
(рис.8.4.3
)
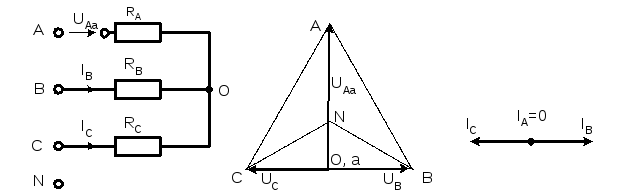
Рис.8.4.3
Короткие замыкания
При
коротком замыкании фазы нагрузки в
схеме с нулевым проводом ток в этой фазе
становится очень большим (теоретически
бесконечно большим) и это приводит к
аварийному отключению нагрузки защитой.
В схеме без нулевого провода при
замыкании, например, фазы А, нулевая
точка нагрузки смещается в точку «А»
генератора. Тогда к сопротивлениям фаз
В и С прикладываются линейные напряжения.
Токи в этих фазах возрастают в 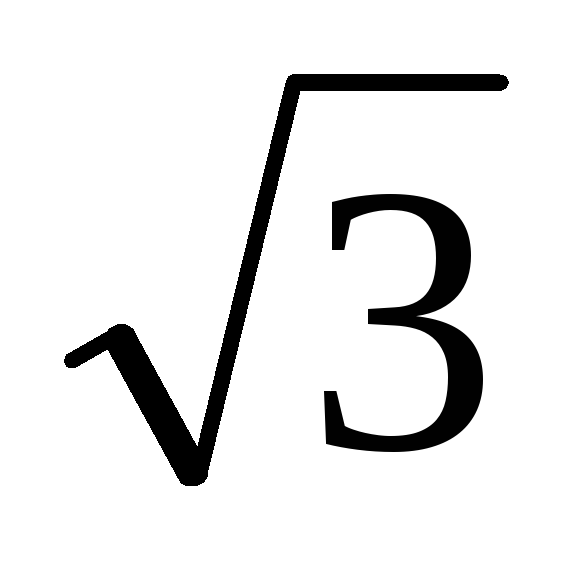 раз, а ток в фазе А – в 3 раза (рис. 8.4.4).
раз, а ток в фазе А – в 3 раза (рис. 8.4.4).
Короткие замыкания между линейными проводами и в той и в другой схеме приводят к аварийному отключению нагрузки.
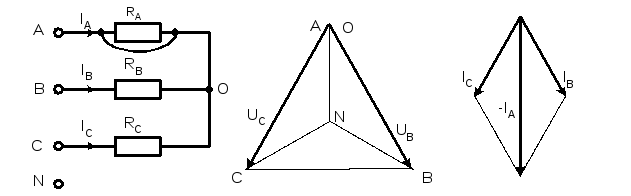
Рис.8.4.4
8.4.2. Экспериментальная часть Задание
Экспериментально исследовать аварийные режимы трёхфазной цепи при соединении нагрузки в звезду.
Порядок выполнения работы
Соберите цепь цепь согласно схеме (рис.8.4.5) с сопротивлениями фаз RA=RB=RC=1кОм.Измерения токов можно производить одним – двумя амперметрами, переключая их из одной фазы в другую, либо виртуальными приборами.
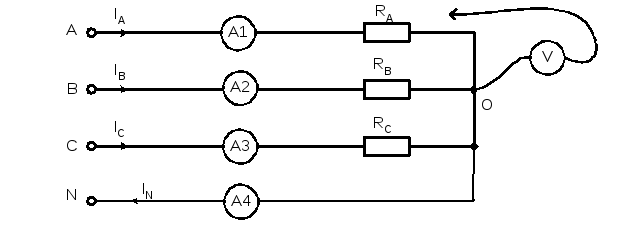
Рис.8.4.5
Убедитесь, что обрыв (отключение) нейтрали не приводит к изменению фазных токов.
Убедитесь, что в схеме с нулевым проводом происходит отключение источника защитой при коротких замыканиях как в фазах нагрузки, так и между линейными проводами.
Убедитесь, что в схеме без нулевого провода короткое замыкание в фазе нагрузки не приводит к отключению, а при коротком замыкании между линейными проводами установка отключается.
Проделайте измерения токов и напряжений всех величин, указанных в табл. 8.4.1 в различных режимах и по экспериментальным данным постройте векторные диаграммы для каждого случая в выбранном масштабе.
Ответьте на контрольные вопросы.
Таблица 8.4.1
Режим | UAO, B | UBO, B | UCO, B | UON, B | IA, мА | IB, мА | IC, мА | IN, мА |
RA=1 кОм RB=680 Ом RC=330 Ом Обрыв нейтрали | ||||||||
RA=RB=RC=1 кОм Схема с нейтралью Обрыв фазы А | ||||||||
RA=RB=RC=1 кОм Схема без нейтрали Обрыв фазы А | ||||||||
RA=RB=RC=1 кОм Схема без нейтрали К. З. фазы А |
Векторные диаграммы
RA=1 кОм, RB=680 Ом, RC=330 Ом. Обрыв нейтрали
2. RA= RB= RC =1 кОм, Схема с нейтралью, обрыв фазы А
3. RA= RB= RC =1 кОм, Схема без нейтрали, обрыв фазы А
4. RA= RB= RC =1 кОм, Схема без нейтрали, короткое замыкание фазы А
В опрос:Как изменяется мощность трёхфазной
нагрузки при обрыве фазы в схеме с
нулевым проводом и без него? Как изменяется
мощность при коротком замыкании одной
фазы?
опрос:Как изменяется мощность трёхфазной
нагрузки при обрыве фазы в схеме с
нулевым проводом и без него? Как изменяется
мощность при коротком замыкании одной
фазы?
Ответ: …………
studfile.net
Контроль трехфазных электрических сетей
ОБРЫВ ФАЗЫ
Обрыв фазы может привести к тому, что двигатели перестанут запускаться или будут забирать необходимый ток из других фаз. Такая ситуация приводит к неравномерным нагрузкам на обмотку двигателя и может вызвать его поломку.
ПОВЫШЕННОЕ И ПОНИЖЕННОЕ НАПРЯЖЕНИЕ
Длительная эксплуатация электрооборудова ния, включенного в сеть с напряжением, выхо дящим за пределы допустимого, может привес ти к нежелательным последствиям. Повышенное напряжение приводит к нагреву подключенного оборудования. Если своевременно не обнару жить перенапряжение, то оно может привести к повреждению или даже разрушению обору дования.
Пониженное напряжение приводит к воз никновению нестабильного состояния в работе оборудования. При пониженном напряжении не гарантируется надежный пуск двигателей. Если на катушку контактора подается пониженное на пряжение, контакты могут неправильно работать при переключении (занимают неопределенное положение).
АСИММЕТРИЯ
Если из-за неравномерного распределения нагрузки в трехфазной сети напряжение питания двигателя становится несимметричным, часть энергии двигателя превращается в реактивную мощность. Производительность падает, кроме того, двигатель подвергается повышенной теп ловой нагрузке и может выйти из строя, если в устройствах тепловой защиты электродвигателя нет функции контроля асимметрии фаз.
ОБРЫВ НЕЙТРАЛЬНОГО ПРОВОДА
Окажет или нет влияние на работу оборудования обрыв нейтрального провода, зависит от того, симметричная или асимметричная нагрузка в сети. Примерами симметричной нагрузки яв ляются электродвигатели или трехфазные обог реватели. В большинстве других случаев подключаемое оборудова ние представляет собой асимметричную нагрузку для электрической сети. В случае симметричной нагрузки обрыв нейтрального провода не оказывает никакого влияния на сеть. При обрыве нейтрального провода в сети с ассиметричной нагрузкой в отдельных фазах возни кают колебания напряжения, способные нанести значительный ущерб подключенному оборудованию. В этом случае необходимо принять соответствующие меры защиты, как это показано ниже, в примере «Обнаружение обрыва нулевого провода».
ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ
Двигатель с рекуперацией энергии
(двигатель, способный генерировать энергию в сеть)
Обрыв фазы работающего трехфазного двигателя может быть четко зафиксирован при помощи реле контроля асимметрии фаз. В номинальном режиме сразу после подачи напряжения питания реле контроля фиксирует правильность чередования фаз L 1- L 2- L 3 и соответствие всех напряжений диапазону U мин./ U макс. Тем самым гарантируется отсутствие перенапряжений, пониженного напряжения и обрыва фазы (рис. За). Только после этого двигатель запускается.
При обрыве фазы (в примере, фаза Ц) фазный ток IL2 становится равным 0, а фазное напряжение UL2 уменьшается на величину ДЦ Величина остаточного напряжения UL2 может составлять до 95% от номинального, в зависимости от типа используемого двигателя, на грузки и других факторов. Приборы контроля фаз и пониженного напряжения контролируют пропадание фаз только до 60 % от но минального напряжения. Таким образом, обрыв фазы работающего двигателя нельзя с достаточной уверенностью определить при помощи реле контроля фазы или пониженного напряжения. Надежное определение данной неисправности может гарантировать только контроль асимметрии фаз. При обнаружении асимметрии фаз реле контроля асимметрии отключает двигатель, чтобы предотвратить его повреждение (рис. 36).
ОБНАРУЖЕНИЕ ОБРЫВА НУЛЕВОГО ПРОВОДА
Как уже говорилось выше, последствия обрыва нулевого прово да зависят от вида нагрузки в трехфазной сети. Ток, протекающий через нулевой провод IN , согласно закону Кирхгофа, определяется как сумма всех фазных токов.
www.energycenter.ru
3) Обрыв фазы
Ra = ; Rb = Rc;
a) четырехпроводная звезда
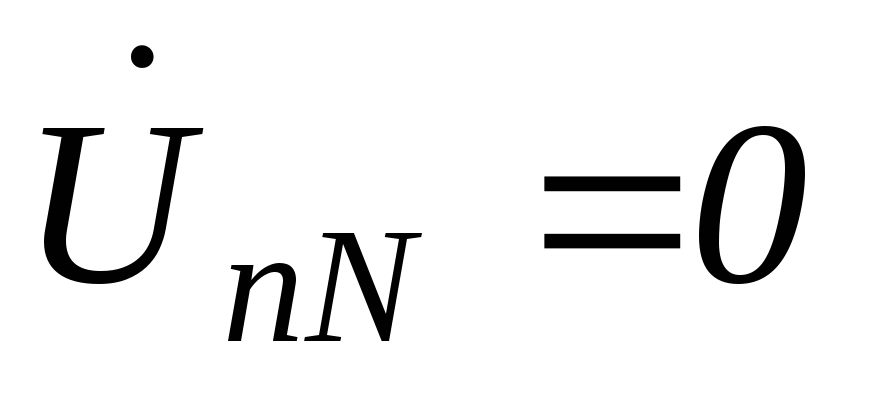 ;
;
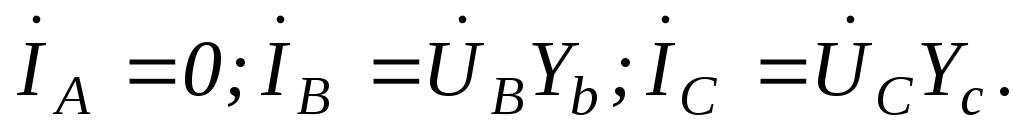
Векторная диаграмма (Рис. 4 .67) демонстрирует работу четырехпроводной системы.
б) трехпроводная звезда
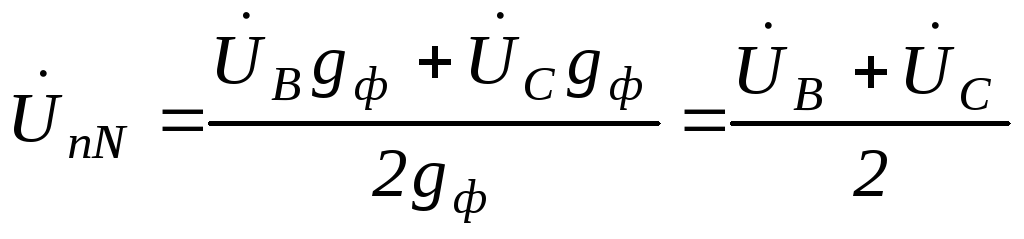 .
.
Напряжение
смещения 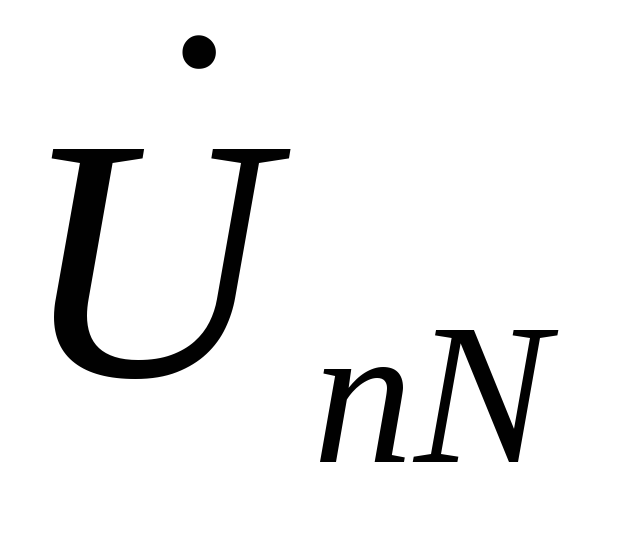 можно также определить методом засечек,
как показано на Рис. 4 .68.
можно также определить методом засечек,
как показано на Рис. 4 .68.
 ;
;
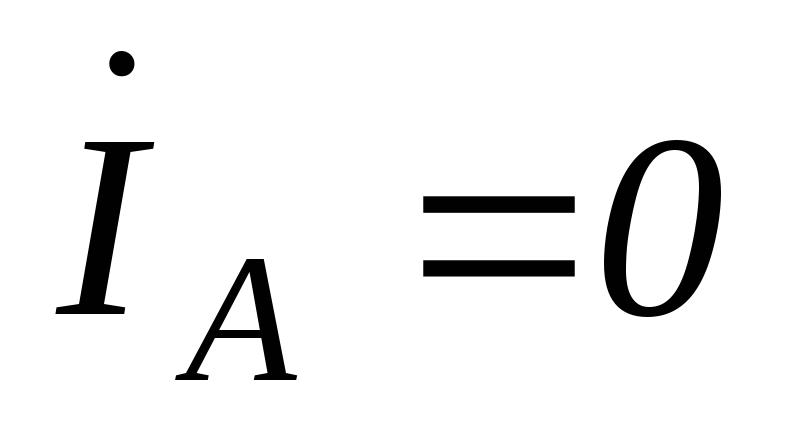 ;
;
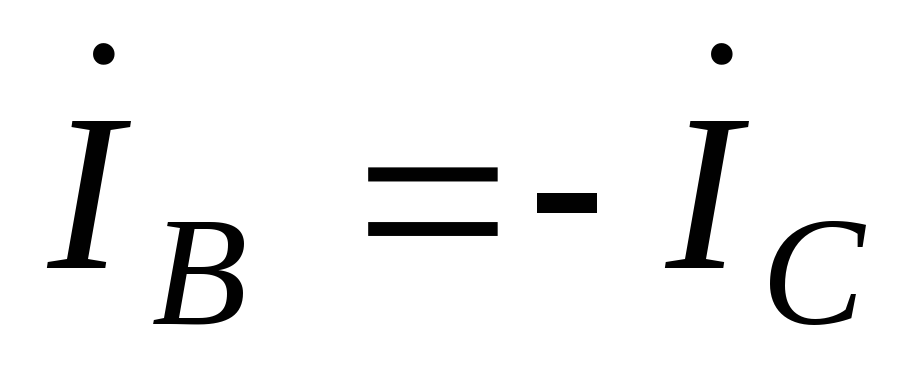 .
.
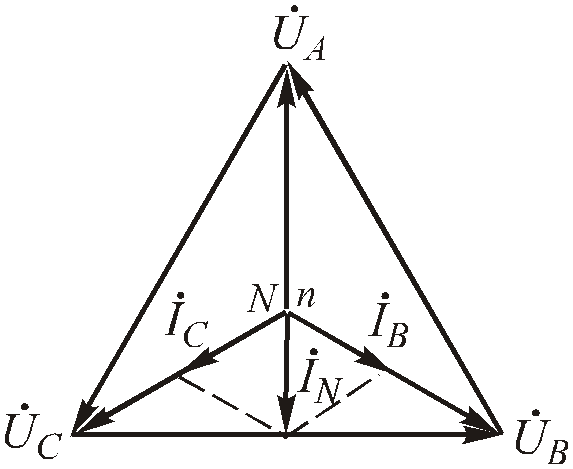
Рис.4.67. Векторная диаграмма для обрыва фазы в четырехпроводной системе
Токи в фазах bисдолжны находиться в противофазе.
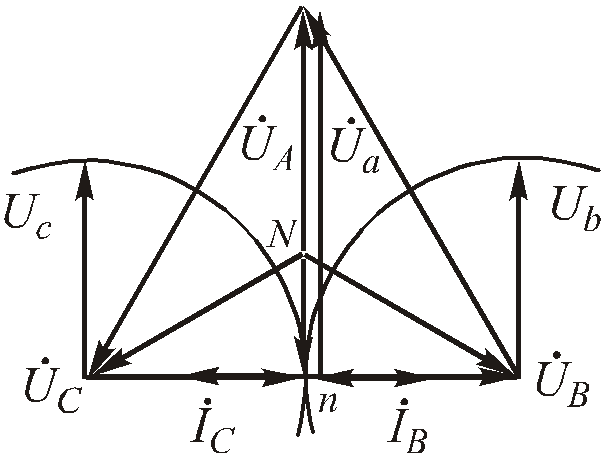
Рис.4.68. Векторная диаграмма для обрыва фазы в трехпроводной системе
4) Короткое замыкание фазы
Ra = 0; Rb = Rc;
а) четырехпроводная звезда
В четырехпроводной системе при коротком замыкании фазы приемника получаем короткое замыкание фазы источника.
б) трехпроводная звезда
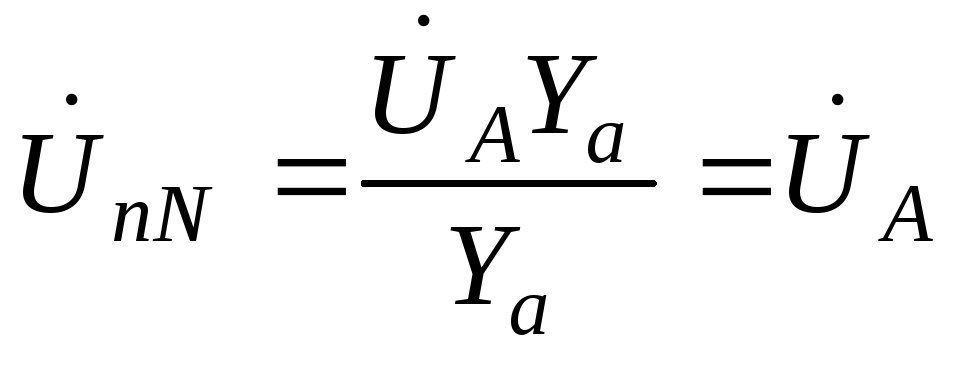 .
.
Фазные напряжения приемника:
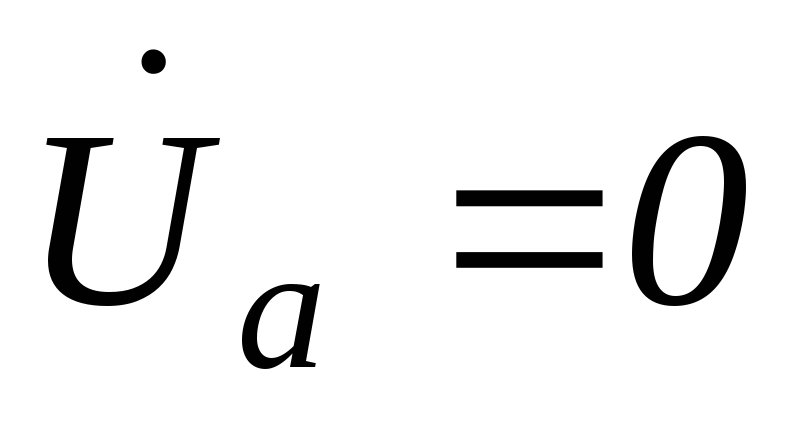 ;
;
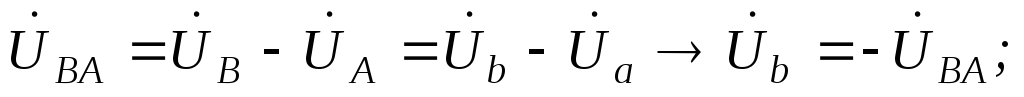
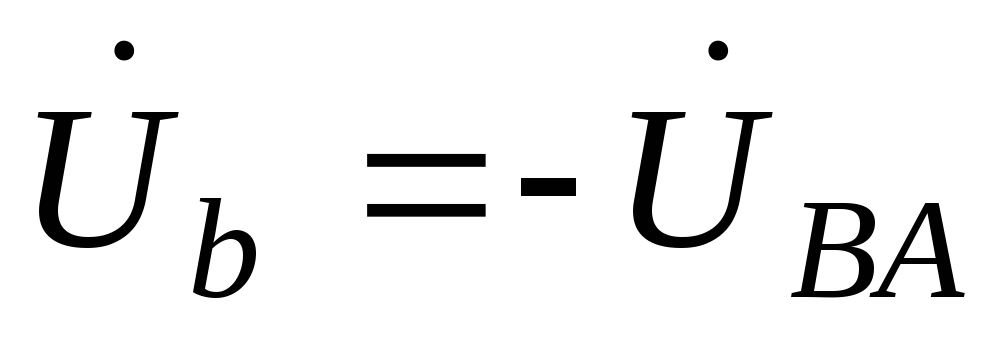 ;
;
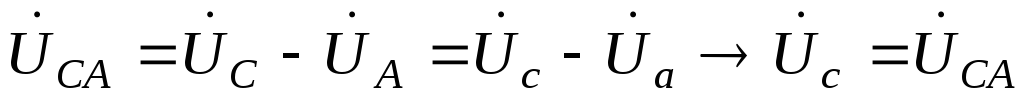 ;
;
т.е. фазные напряжения увеличились до линейных напряжений, соответственно, токи фаз:
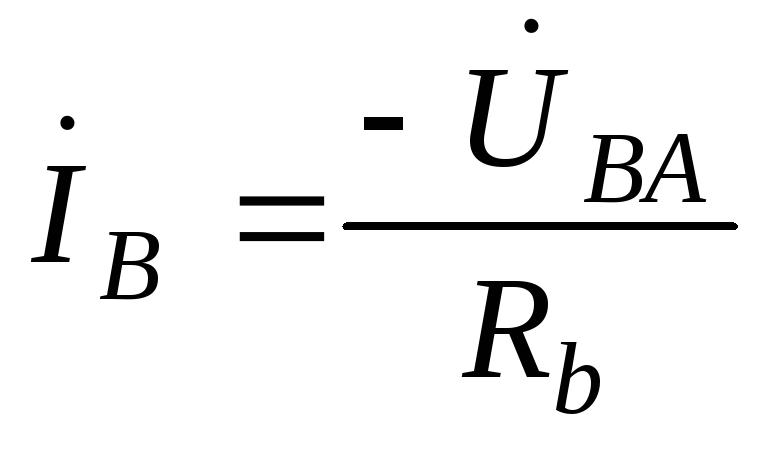 ;
;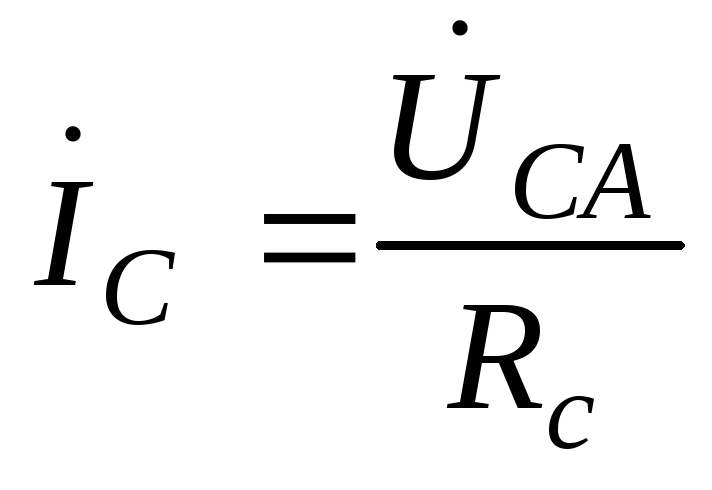 увеличились в
увеличились в раз.
раз.
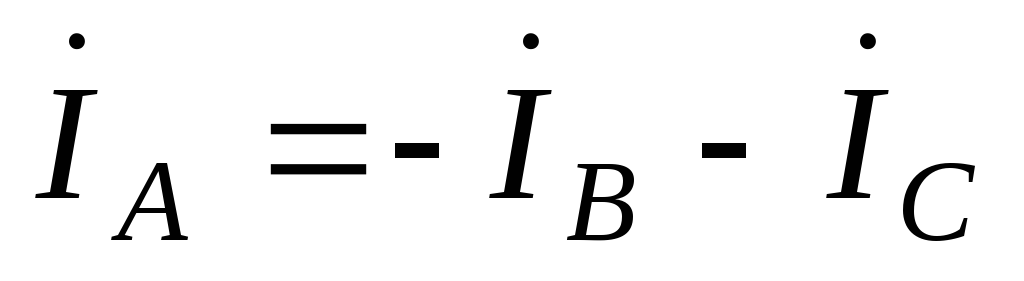 .
.
Построение векторной диаграммы показано на Рис. 4 .69.
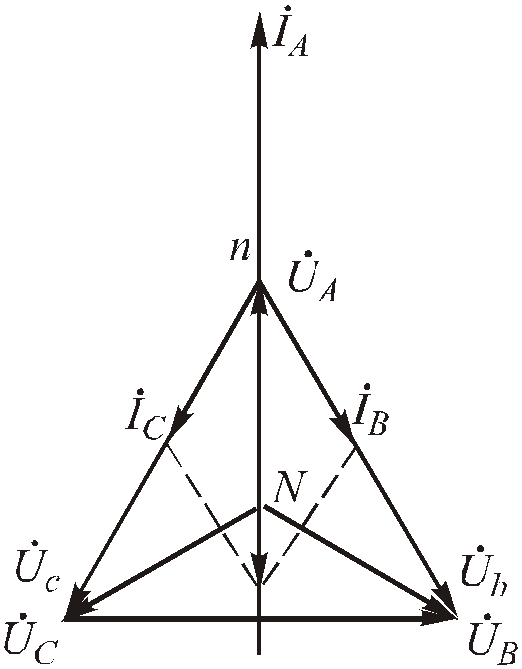
Рис.4.69. Векторная диаграмма для короткого замыкания фазыА
5) Разнородная нагрузка
а) четырехпроводная звезда
Сравнив схемы соединения потребителей трех- и четырехпроводной звездой, можно сделать вывод, что однофазные приемники надо включать по схеме четырехпроводной звезды, чтобы обеспечить постоянство напряжений на зажимах этих приемников.
По схеме трехпроводной звезды включают трехфазные симметричные приемники, например, трехфазные асинхронные и синхронные двигатели.
Соединение потребителей «треугольником»
Рассмотрим различные режимы работы приемника при соединении его фаз треугольником.
Вновь будем считать, что в качестве потребителей в фазах включены активные сопротивления (для простоты построений).
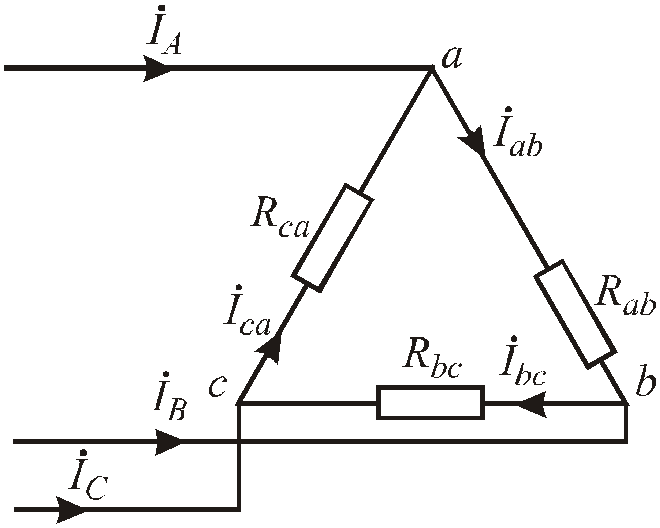
Рис.4.70. Соединение фаз приемника «треугольником»
а) симметричный режим.
Rab = Rbc = Rca = Rф.
На Рис. 4 .62 построена векторная диаграмма для симметричной нагрузки при соединении фаз приемника «треугольником».
Токи равны по модулю и отличаются только по фазе:
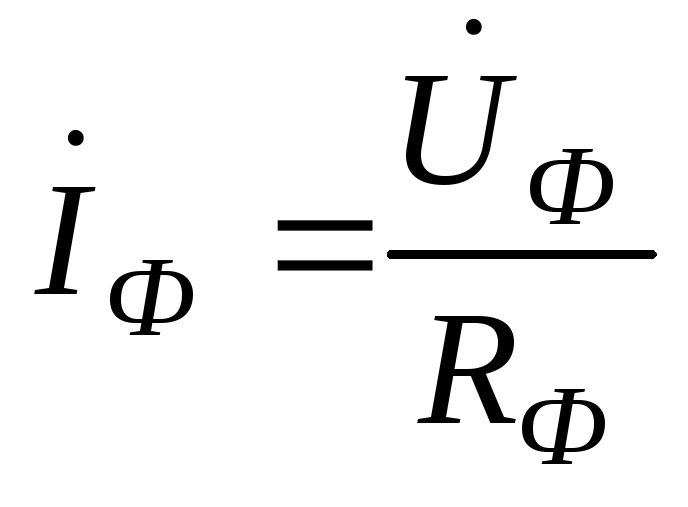 .
.
Линейные токи:
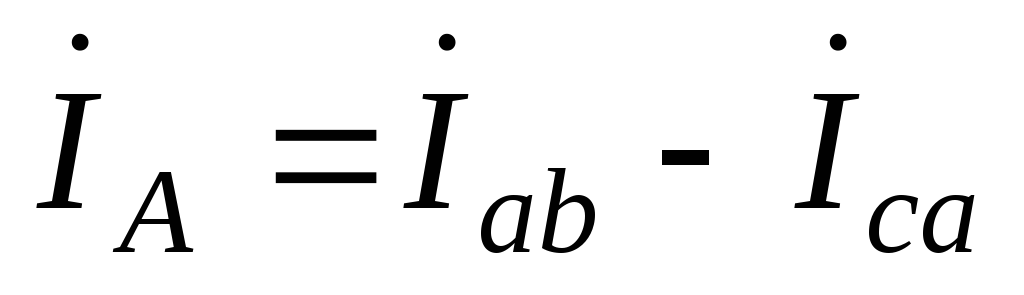 ;
;
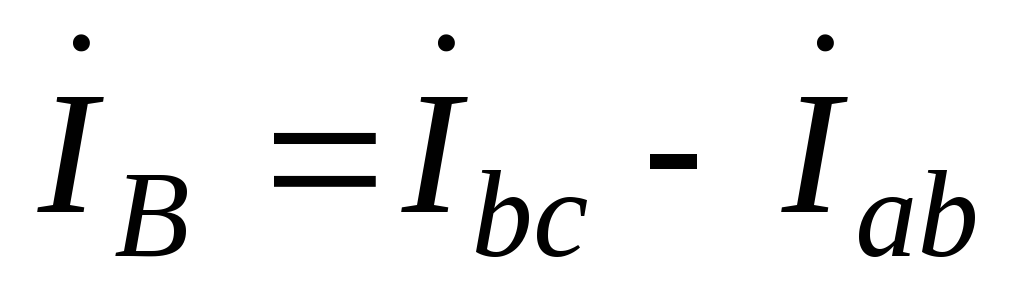 ;98(4.91)
;98(4.91)
;
.
в) несимметричные режим.
Rab Rbc = Rca;
Фазы по-прежнему работают независимо друг от друга и поэтому фазные токи:
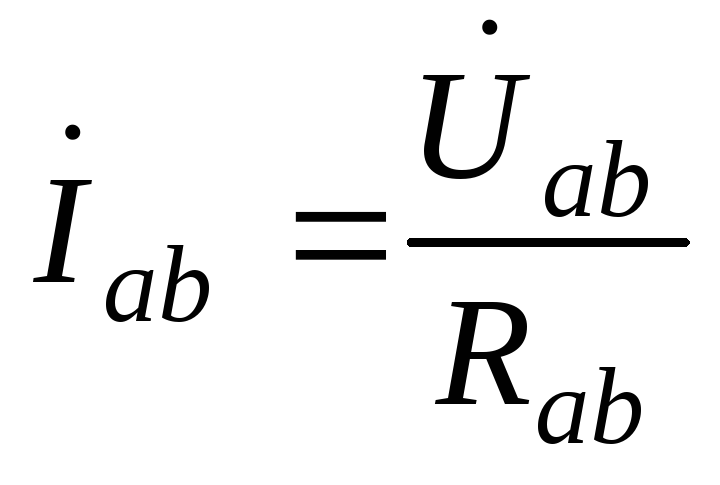 ;
;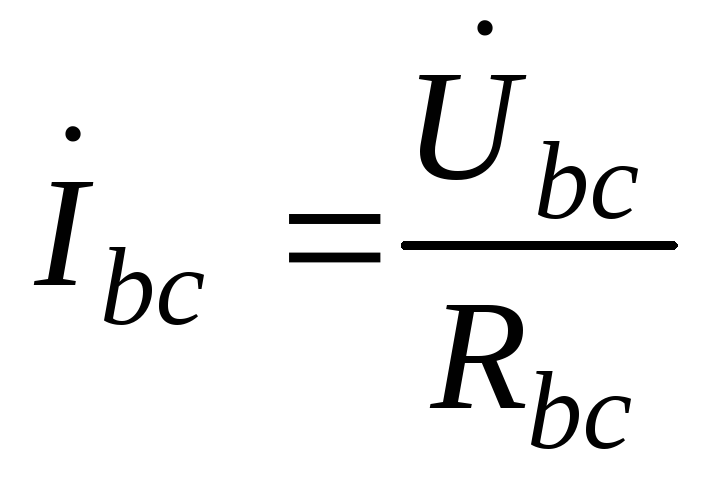 ;
;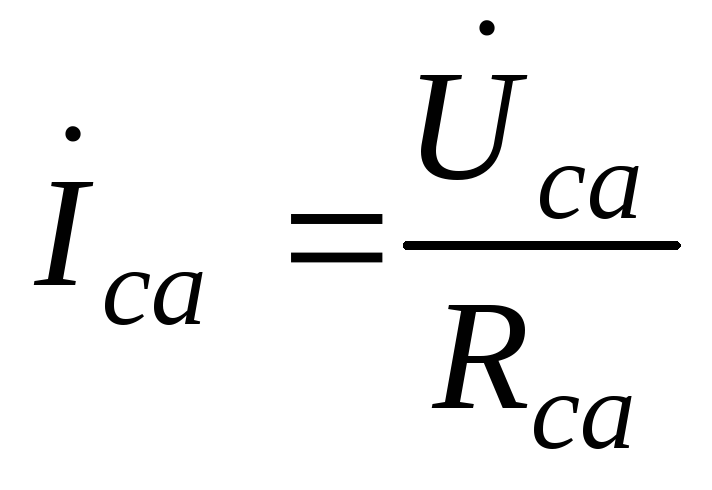 ;
;
Линейные токи определяются соответственно по формулам ( 4 .91). На рис.4.16 представлены векторные диаграммы для несимметричной нагрузки приемников соединенных «треугольником».
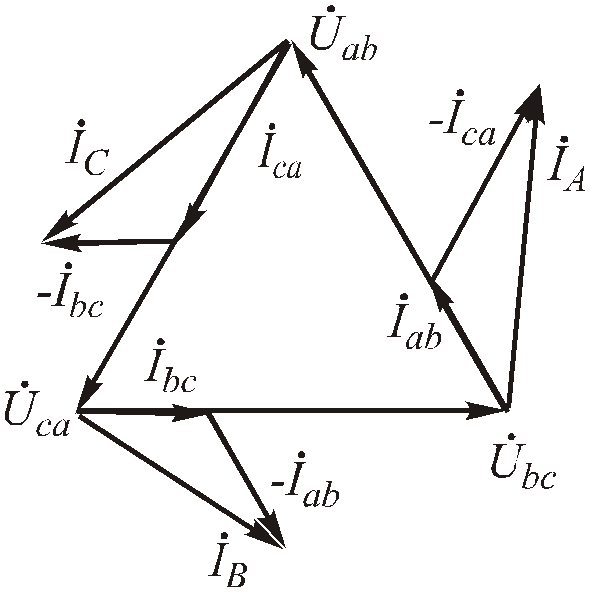
Рис.4.71. Векторные диаграммы для несимметричной нагрузки приемников соединенных «треугольником».
с) обрыв фазы.
Rab = ; Rbc = Rca .
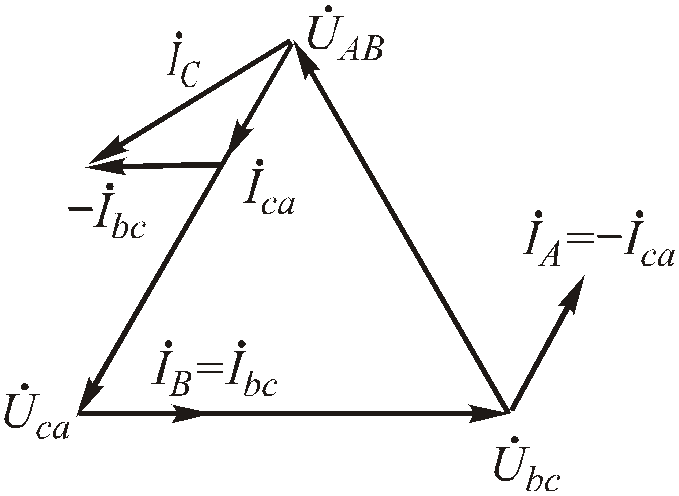
Рис.4.72. Векторная диаграмма для обрыва фазы при соединении приемников треугольником
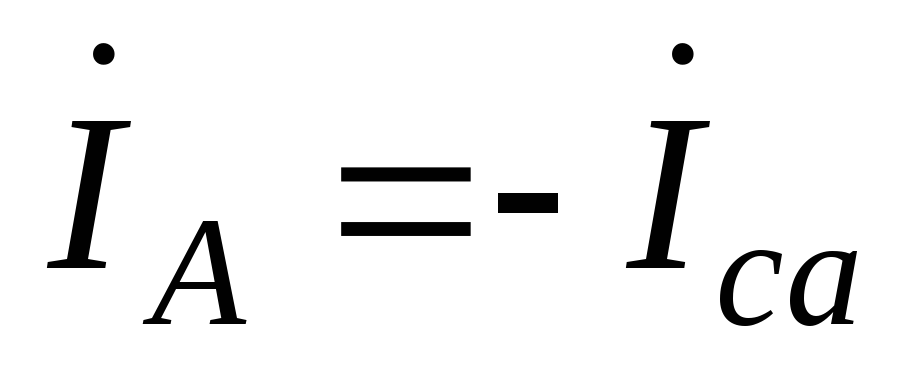 ;
;
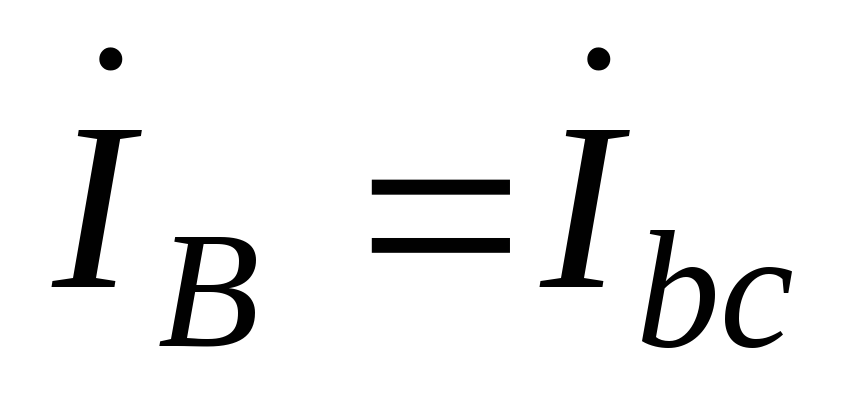 ;
;
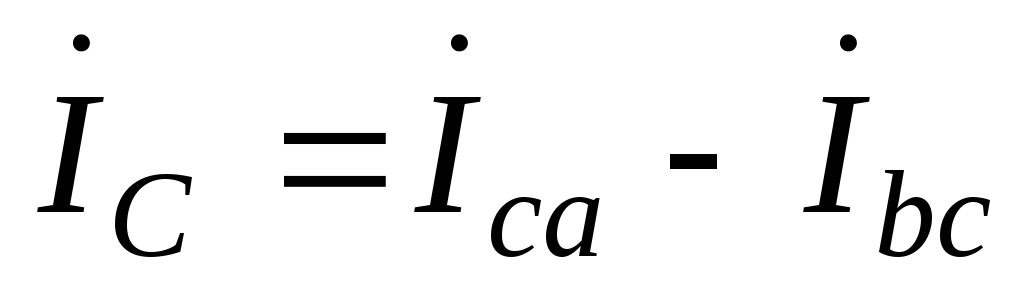 .
.
При разнородной нагрузке методика расчета не меняется.
Мощность трехфазной цепи
Рассмотрим расчет мощности при соединении приемников по схеме четырехпроводной звезды и допустим, что нагрузка несимметрична. Если учесть, что сопротивление нейтрального провода не равно нулю и активное, то имеем:
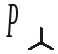
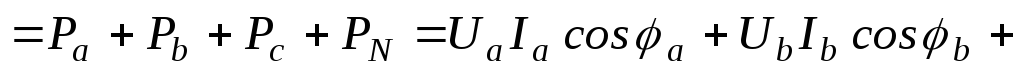
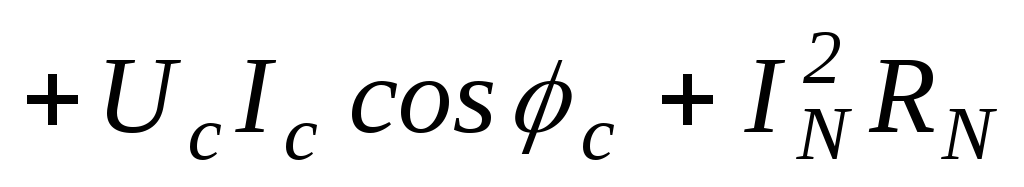 ;
;
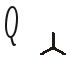
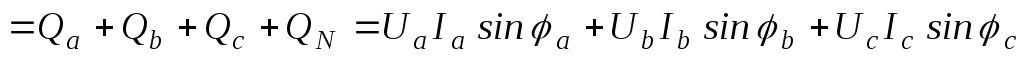 ;
;
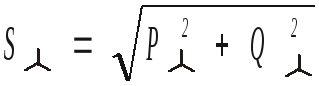 .
.
При симметричной нагрузке для трех- и четырехпроводной системы:
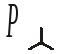
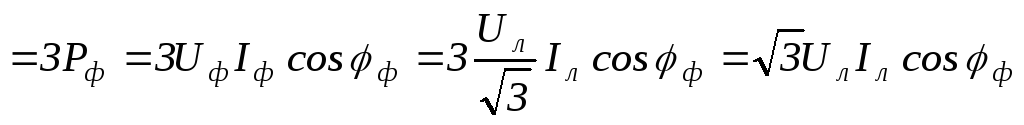 ;99(4.92)
;99(4.92)
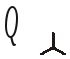
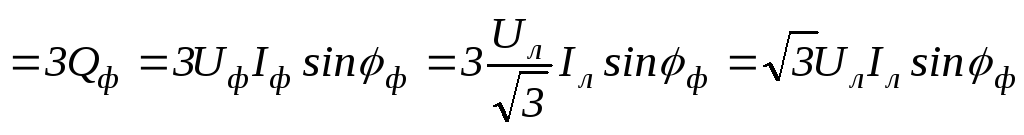 ;100(4.93)
;100(4.93)
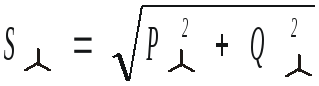
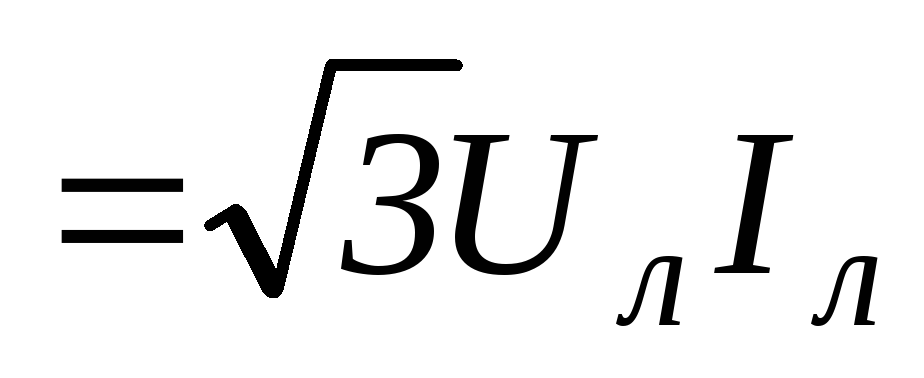 .101(4.94)
.101(4.94)
При соединении фаз приемника треугольником и несимметрии нагрузки имеем:
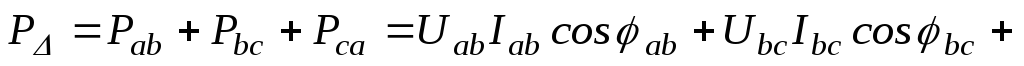
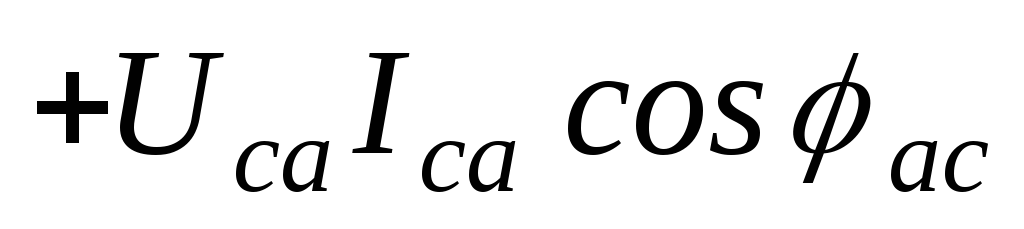 ;
;
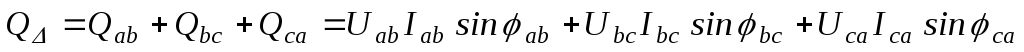 ;
;
.
При симметричной нагрузке:
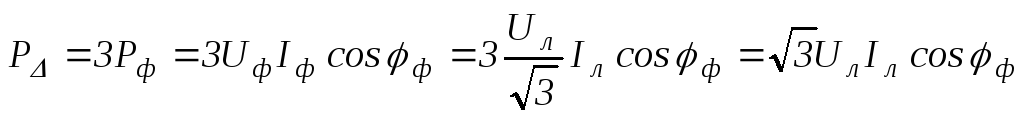 ;102(4.95)
;102(4.95)
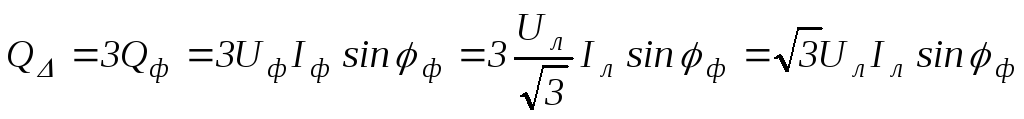 ;103(4.96)
;103(4.96)
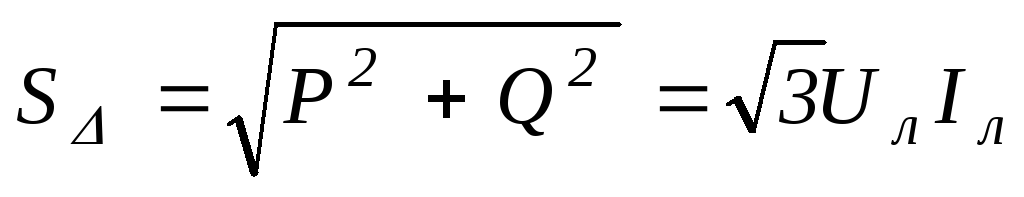 .104(4.97)
.104(4.97)
При этом необходимо учесть, что одинаковые формулы для подсчета мощности не означают одинаковые численные значения.
Пример.Пусть трехфазный приемник с сопротивлением фазыZф соединен «звездой», тогда активная мощность
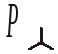
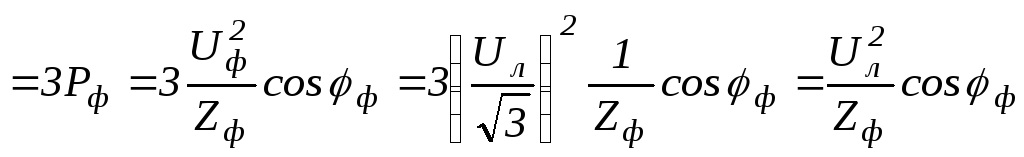 .
.
Теперь фазы того же приемника соединим «треугольником» и подключим к тому же трехфазному источнику:
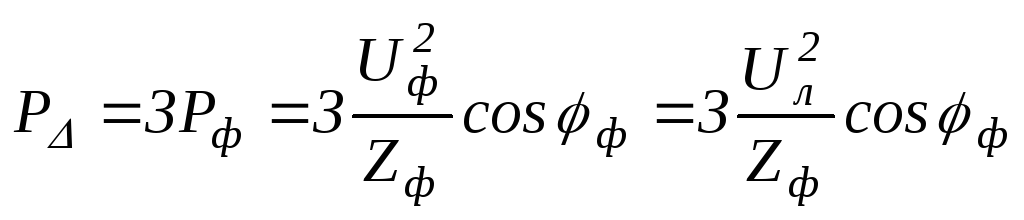 ,
,
т.е. 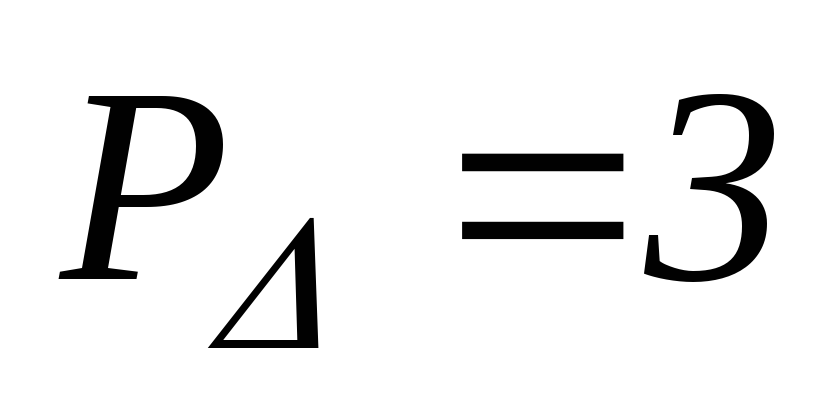
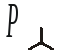 .
.
studfile.net
3) Обрыв фазы
Ra = ; Rb = Rc;
a) четырехпроводная звезда
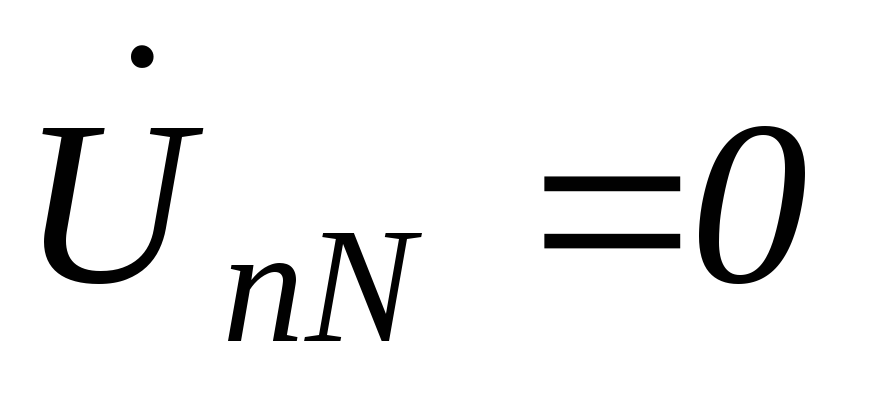 ;
;
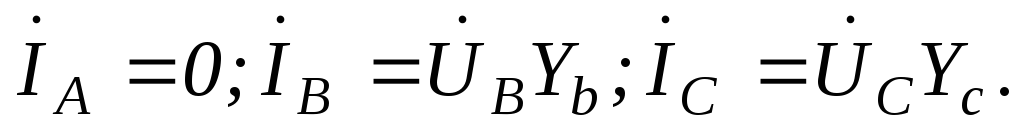
Векторная диаграмма (Рис. 4 .67) демонстрирует работу четырехпроводной системы.
б) трехпроводная звезда
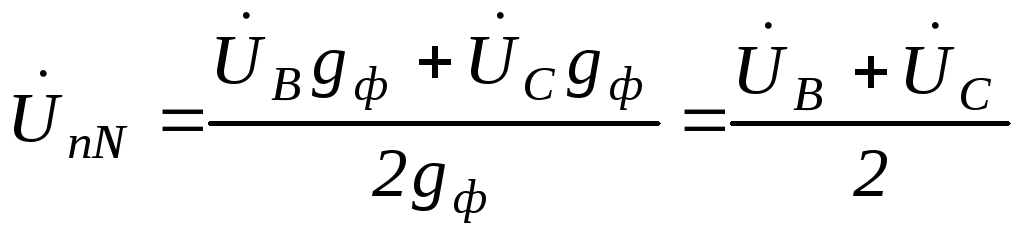 .
.
Напряжение
смещения 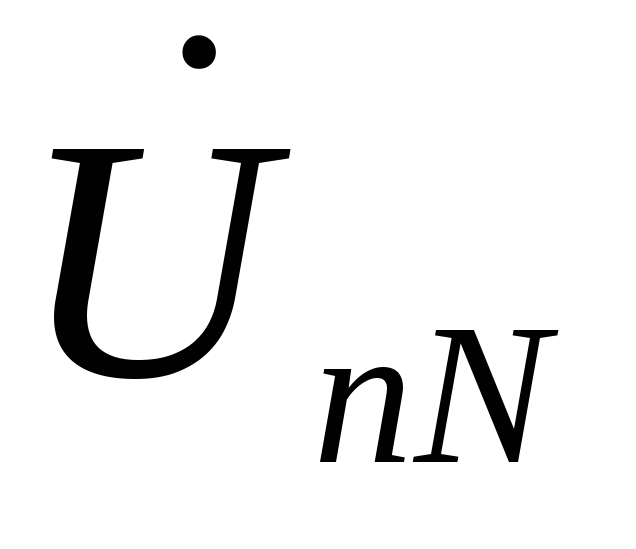 можно также определить методом засечек,
как показано на Рис. 4 .68.
можно также определить методом засечек,
как показано на Рис. 4 .68.
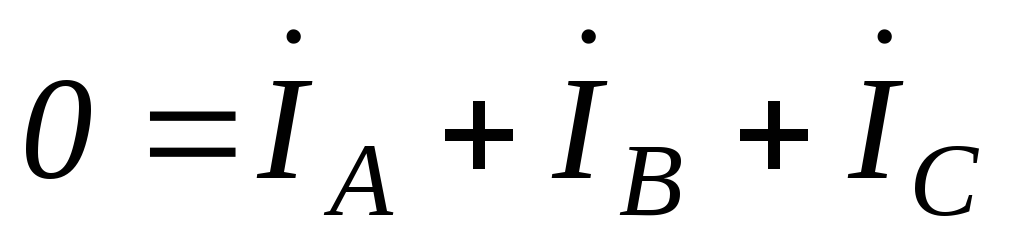 ;
;
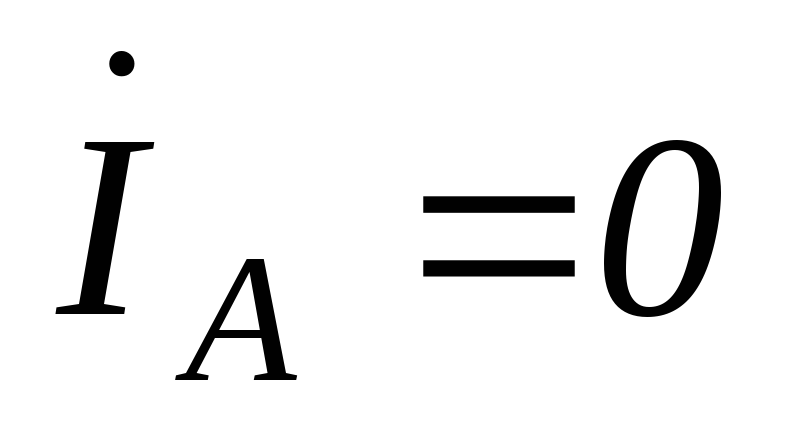 ;
;
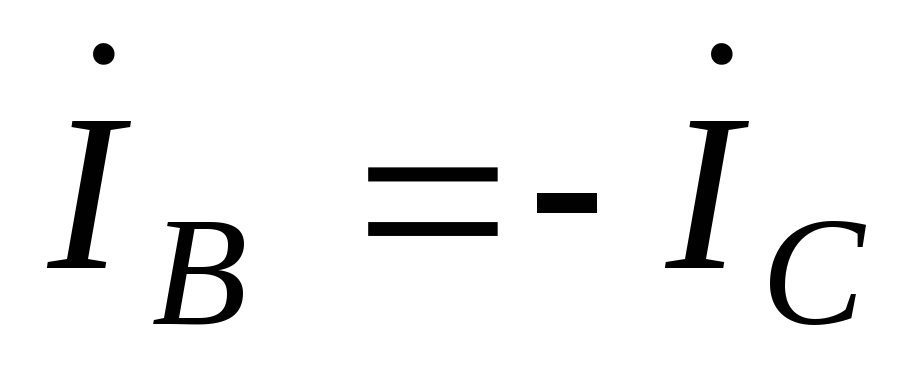 .
.
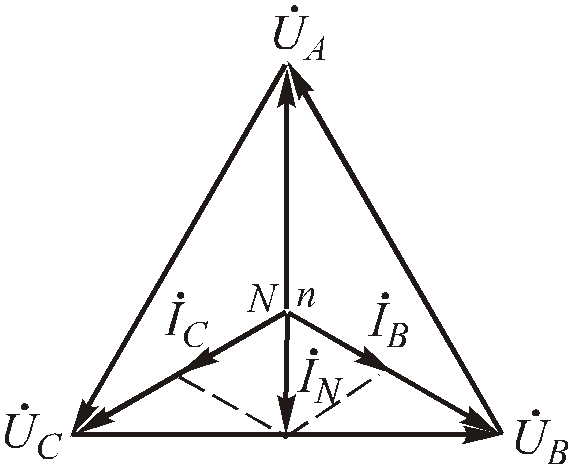
Рис.4.67. Векторная диаграмма для обрыва фазы в четырехпроводной системе
Токи в фазах bисдолжны находиться в противофазе.
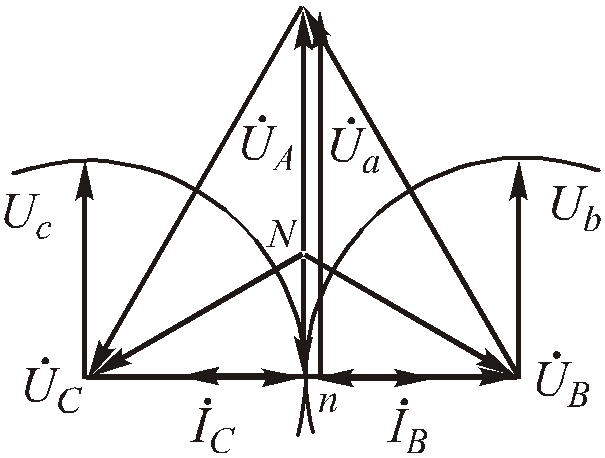
Рис.4.68. Векторная диаграмма для обрыва фазы в трехпроводной системе
4) Короткое замыкание фазы
Ra = 0; Rb = Rc;
а) четырехпроводная звезда
В четырехпроводной системе при коротком замыкании фазы приемника получаем короткое замыкание фазы источника.
б) трехпроводная звезда
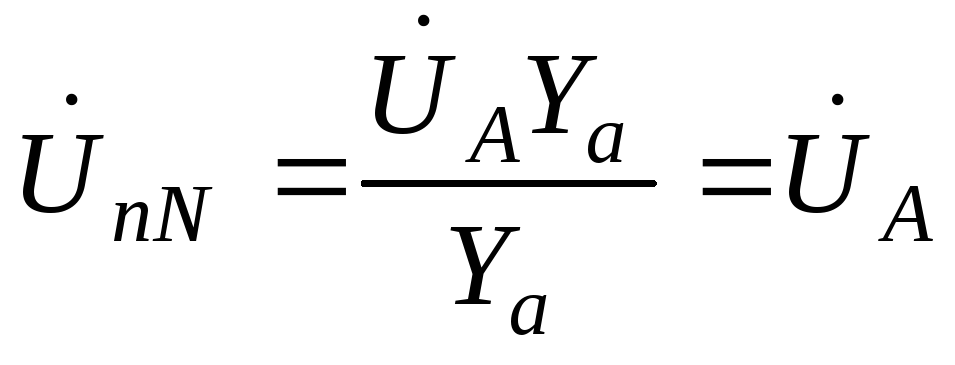 .
.
Фазные напряжения приемника:
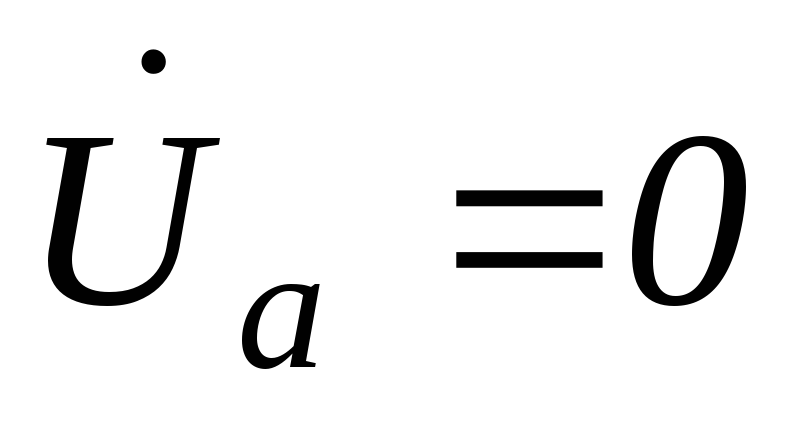 ;
;
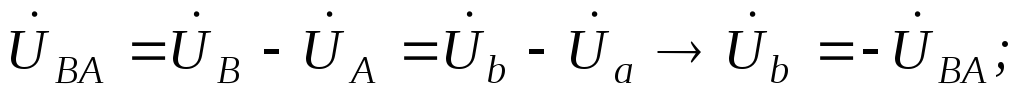
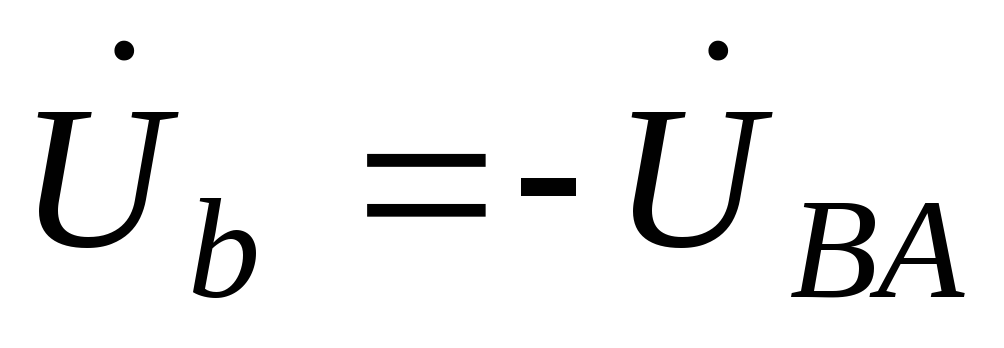 ;
;
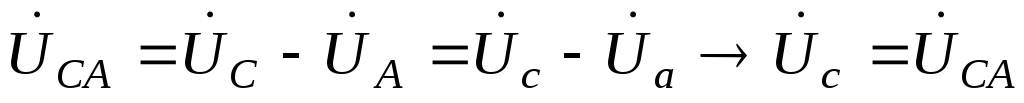 ;
;
т.е. фазные напряжения увеличились до линейных напряжений, соответственно, токи фаз:
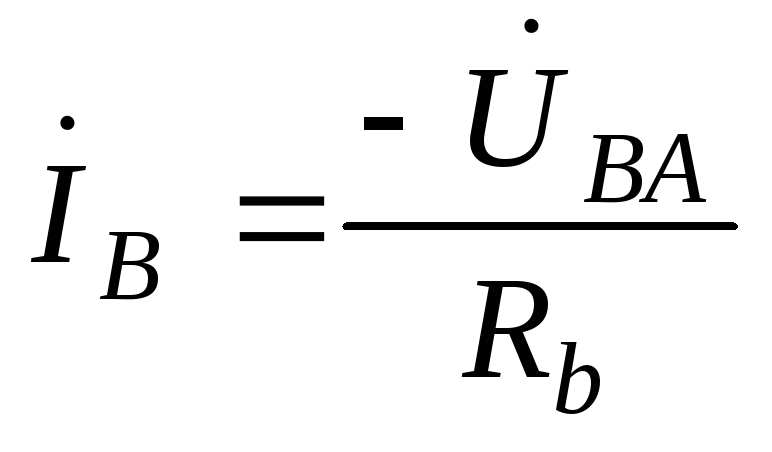 ;
;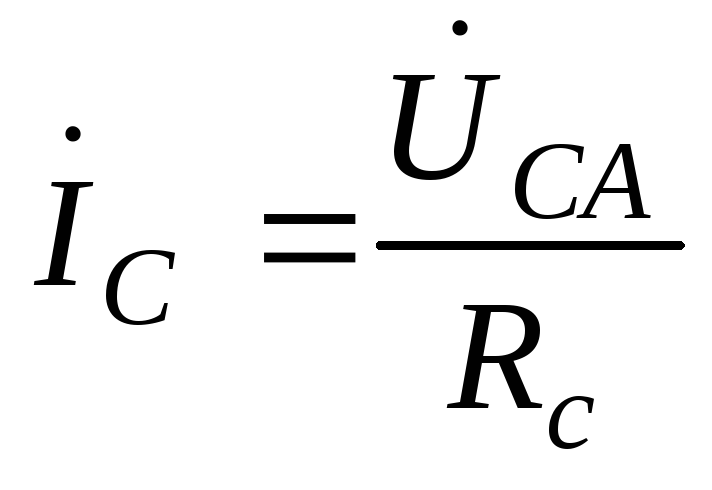 увеличились в
увеличились в раз.
раз.
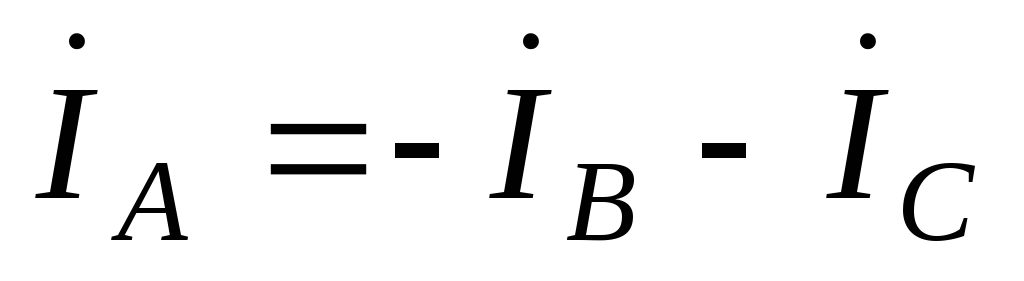 .
.
Построение векторной диаграммы показано на Рис. 4 .69.
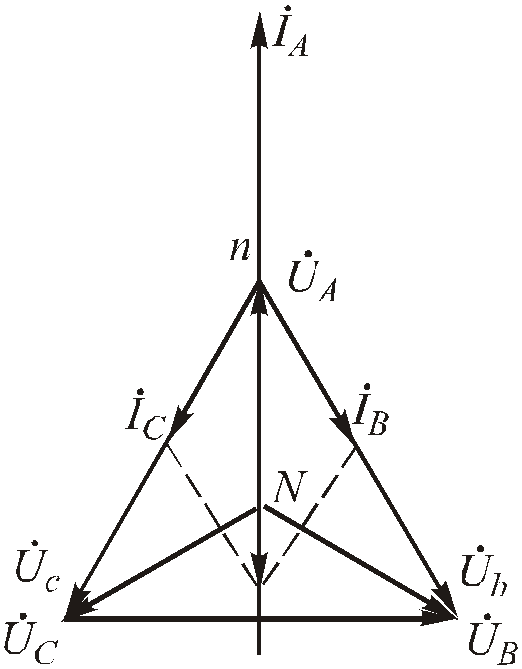
Рис.4.69. Векторная диаграмма для короткого замыкания фазыА
5) Разнородная нагрузка
а) четырехпроводная звезда
Сравнив схемы соединения потребителей трех- и четырехпроводной звездой, можно сделать вывод, что однофазные приемники надо включать по схеме четырехпроводной звезды, чтобы обеспечить постоянство напряжений на зажимах этих приемников.
По схеме трехпроводной звезды включают трехфазные симметричные приемники, например, трехфазные асинхронные и синхронные двигатели.
Соединение потребителей «треугольником»
Рассмотрим различные режимы работы приемника при соединении его фаз треугольником.
Вновь будем считать, что в качестве потребителей в фазах включены активные сопротивления (для простоты построений).
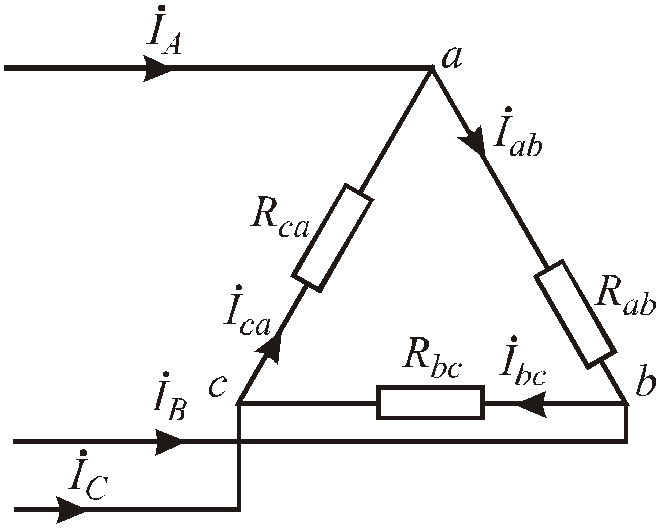
Рис.4.70. Соединение фаз приемника «треугольником»
а) симметричный режим.
Rab = Rbc = Rca = Rф.
На Рис. 4 .62 построена векторная диаграмма для симметричной нагрузки при соединении фаз приемника «треугольником».
Токи равны по модулю и отличаются только по фазе:
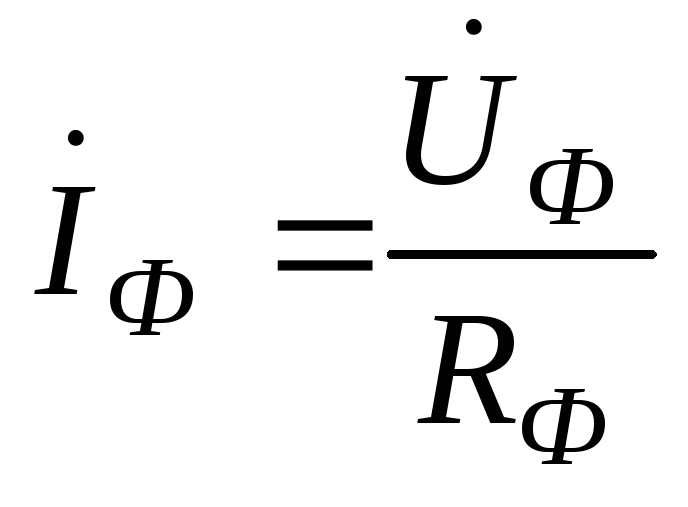 .
.
Линейные токи:
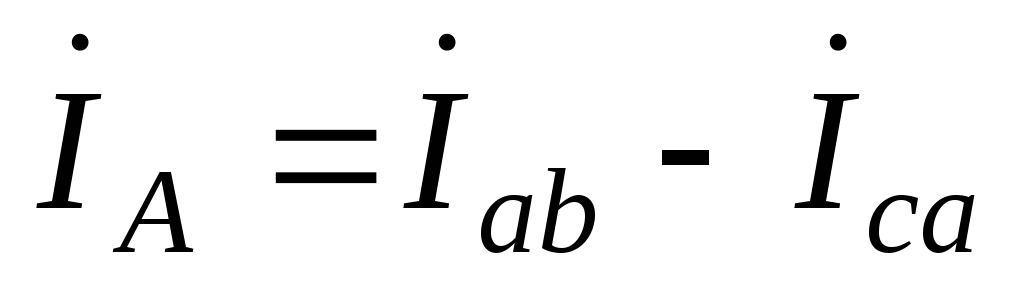 ;
;
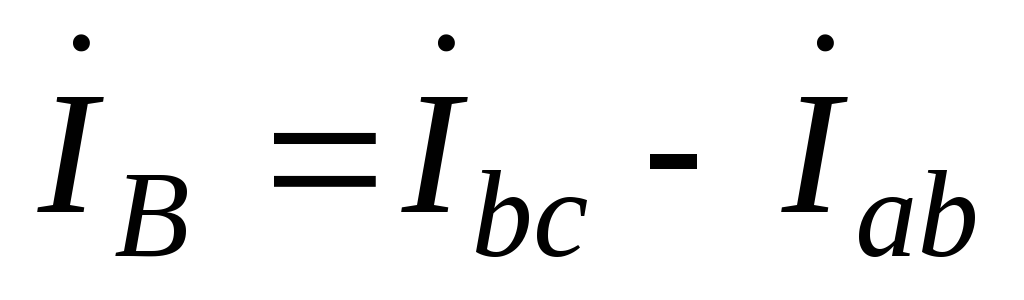 ;98(4.91)
;98(4.91)
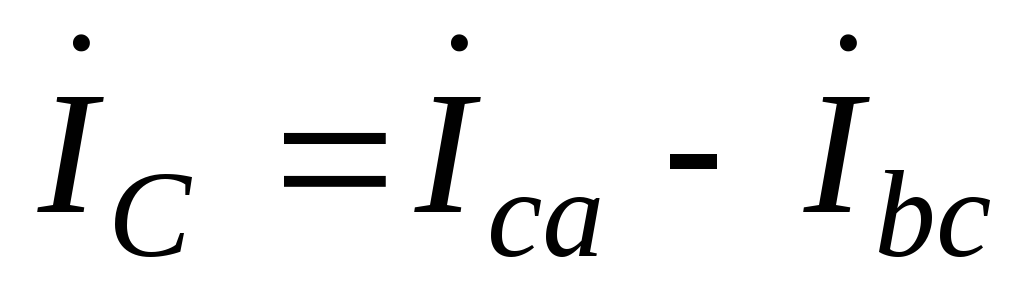 ;
;
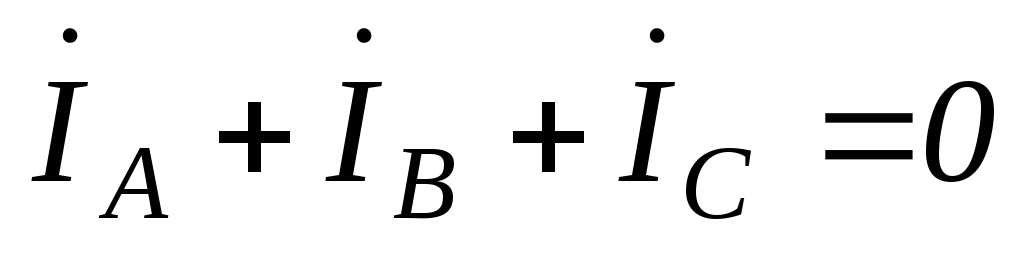 .
.
в) несимметричные режим.
Rab Rbc = Rca;
Фазы по-прежнему работают независимо друг от друга и поэтому фазные токи:
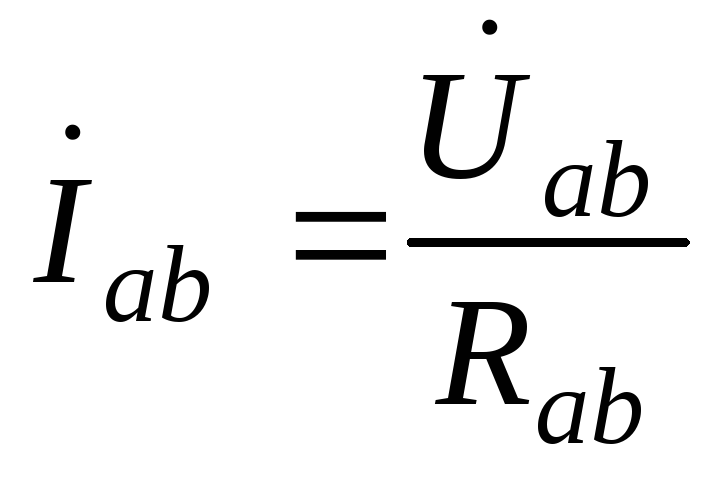 ;
;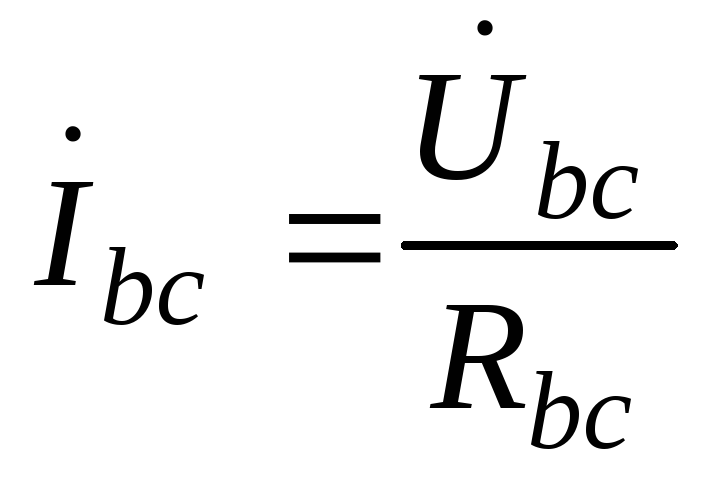 ;
;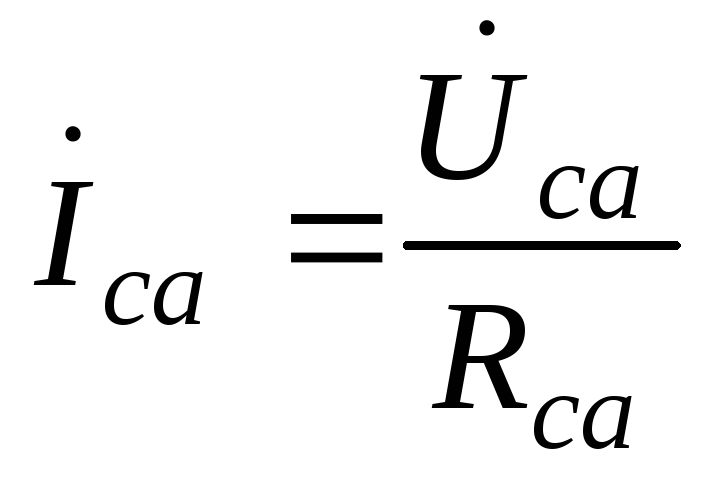 ;
;
Линейные токи определяются соответственно по формулам ( 4 .91). На рис.4.16 представлены векторные диаграммы для несимметричной нагрузки приемников соединенных «треугольником».
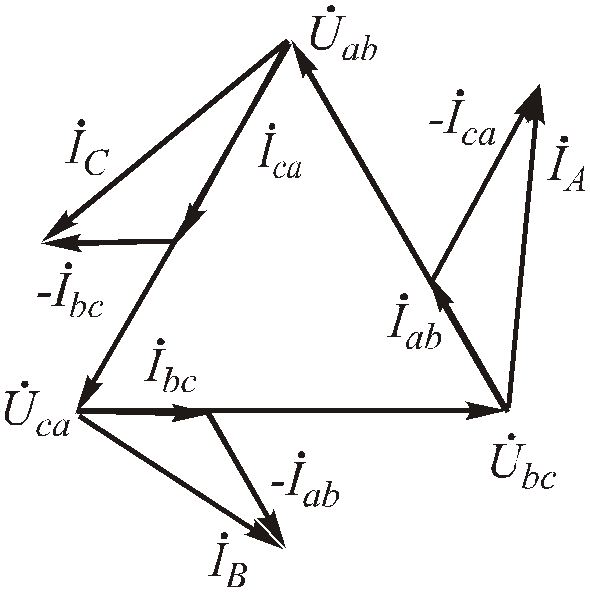
Рис.4.71. Векторные диаграммы для несимметричной нагрузки приемников соединенных «треугольником».
с) обрыв фазы.
Rab = ; Rbc = Rca .
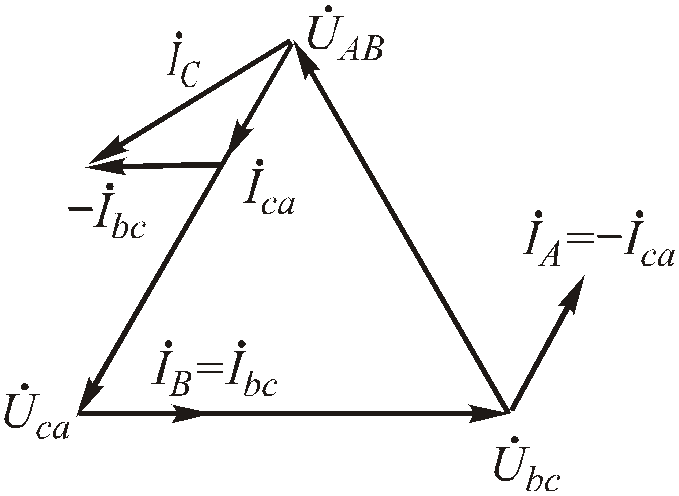
Рис.4.72. Векторная диаграмма для обрыва фазы при соединении приемников треугольником
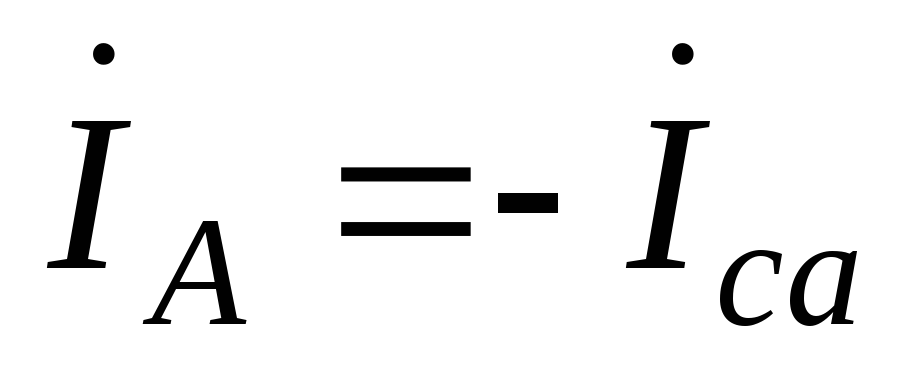 ;
;
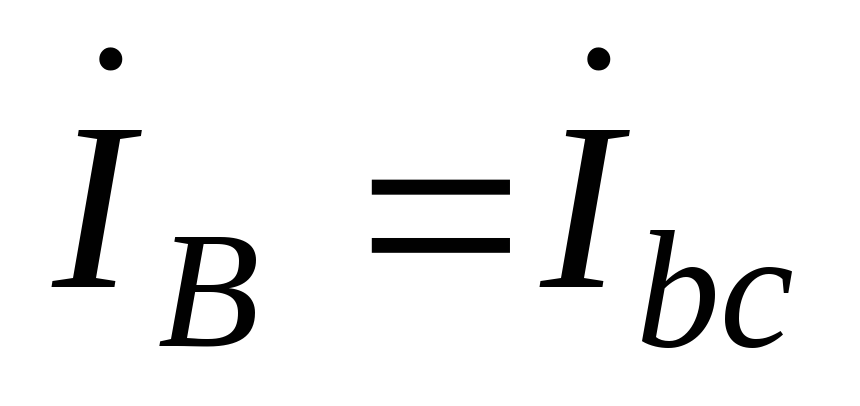 ;
;
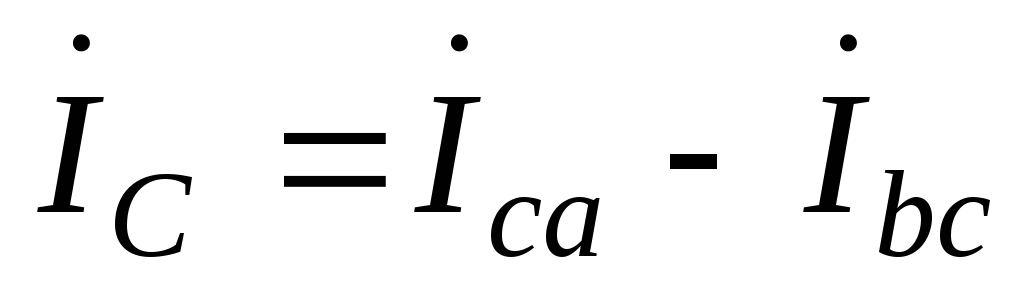 .
.
При разнородной нагрузке методика расчета не меняется.
Мощность трехфазной цепи
Рассмотрим расчет мощности при соединении приемников по схеме четырехпроводной звезды и допустим, что нагрузка несимметрична. Если учесть, что сопротивление нейтрального провода не равно нулю и активное, то имеем:
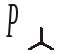
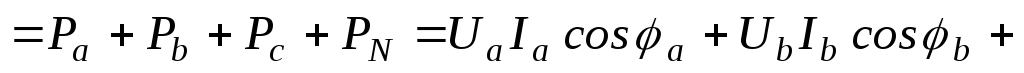
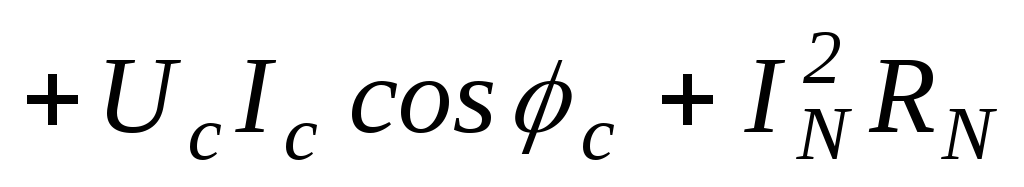 ;
;
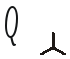
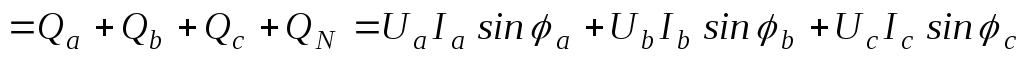 ;
;
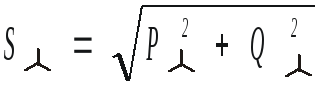 .
.
При симметричной нагрузке для трех- и четырехпроводной системы:
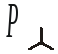
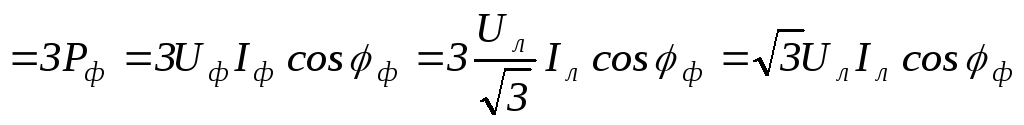 ;99(4.92)
;99(4.92)
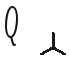
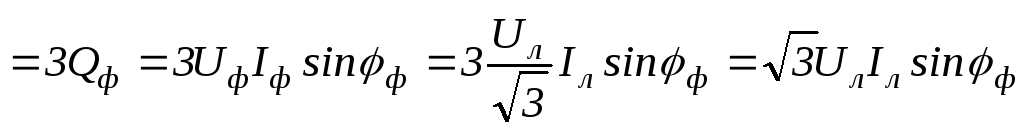 ;100(4.93)
;100(4.93)
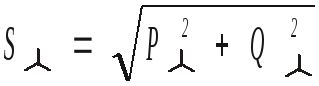
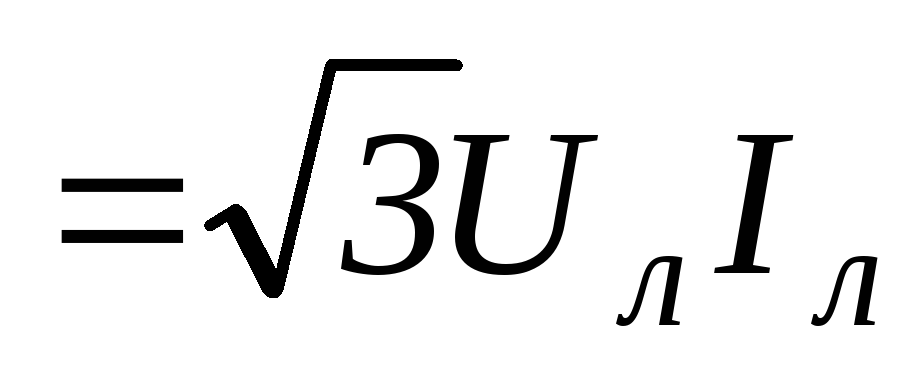 .101(4.94)
.101(4.94)
При соединении фаз приемника треугольником и несимметрии нагрузки имеем:
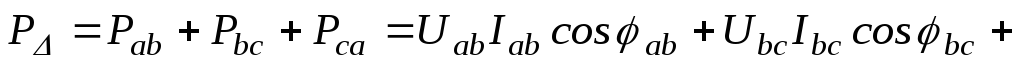
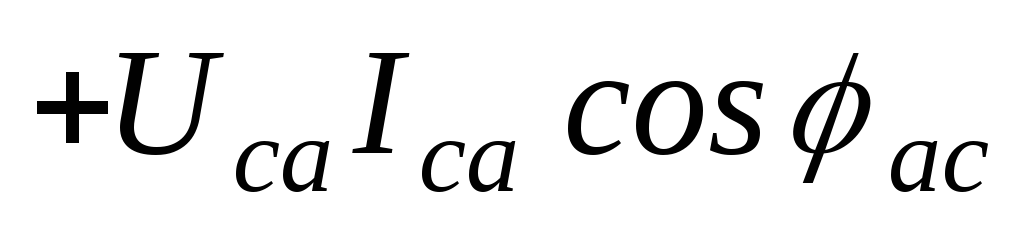 ;
;
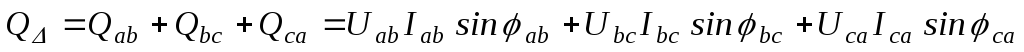 ;
;
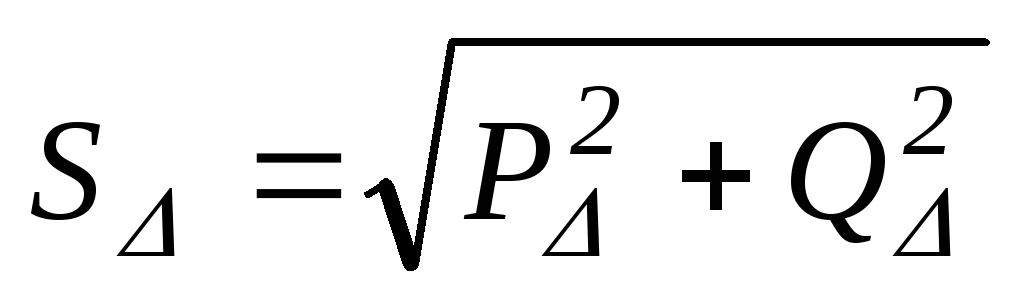 .
.
При симметричной нагрузке:
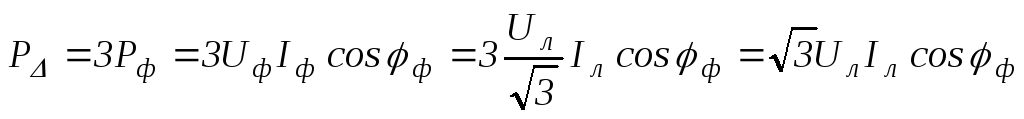 ;102(4.95)
;102(4.95)
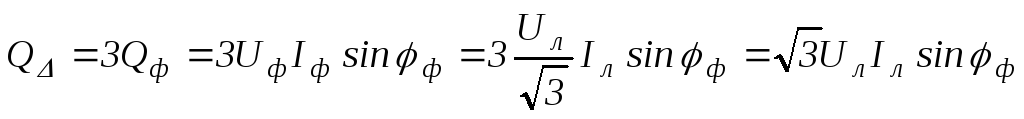 ;103(4.96)
;103(4.96)
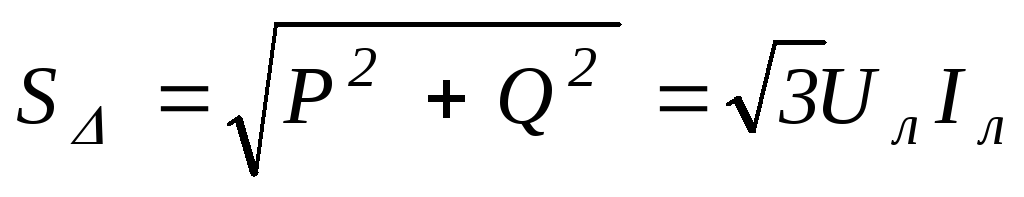 .104(4.97)
.104(4.97)
При этом необходимо учесть, что одинаковые формулы для подсчета мощности не означают одинаковые численные значения.
Пример.Пусть трехфазный приемник с сопротивлением фазыZф соединен «звездой», тогда активная мощность
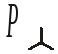
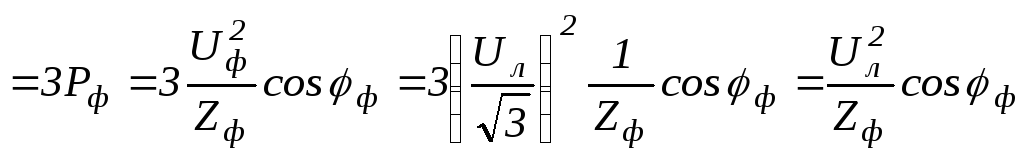 .
.
Теперь фазы того же приемника соединим «треугольником» и подключим к тому же трехфазному источнику:
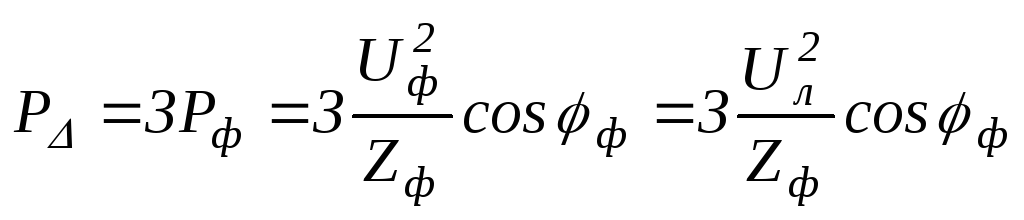 ,
,
т.е. 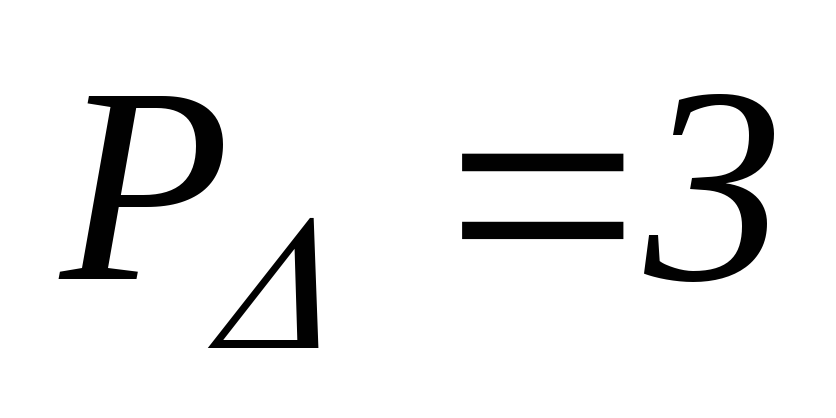
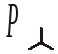 .
.
studfile.net
3.5. Обрыв фаз и обрыв линейного провода при соединении источников и потребителей треугольником
3.5.1. Обрыв фазы ab
Рассмотрим электрическую схему, изображённую на рис.3.20.
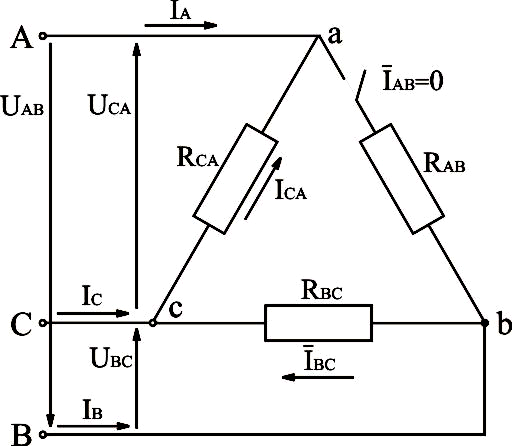
Рис.3.20. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенной фазой
При
обрыве фазы ab вектор тока 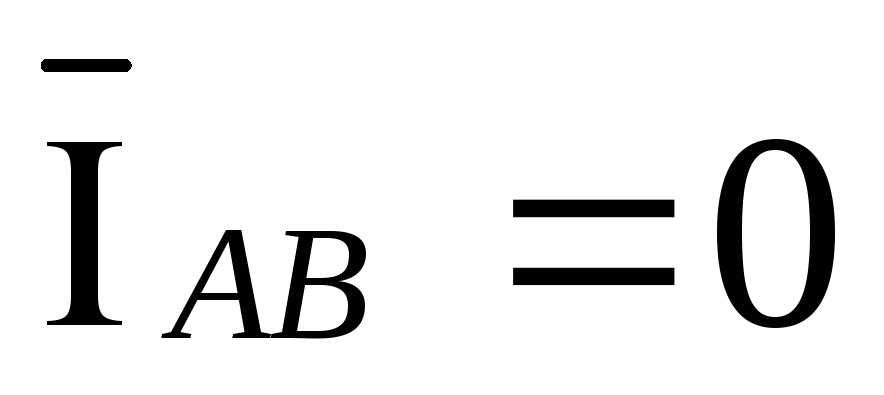 ,
тогда выражения (3.14) преобразуются в
следующий вид:
,
тогда выражения (3.14) преобразуются в
следующий вид:
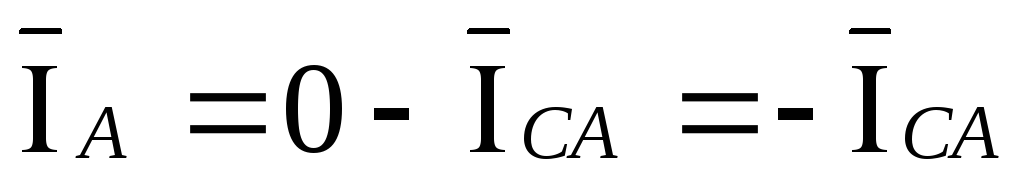 ,
, 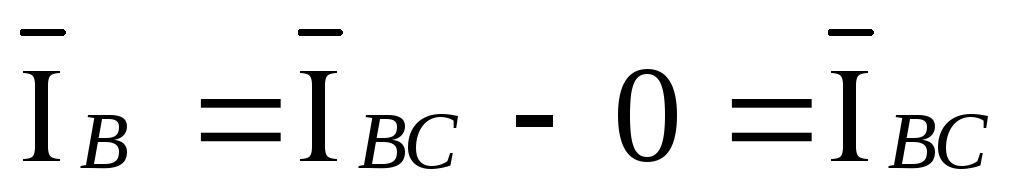 ,
,  .
(3.16)
.
(3.16)
На рис.3.21 приведена векторная диаграмма напряжений и токов при обрыве фазы аb нагрузки, соединённой треугольником.
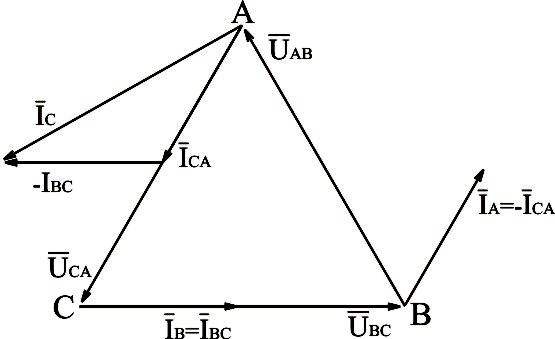
Рис.3.21. Векторная диаграмма напряжений и токов для нагрузки, соединённой треугольником, с отлюченной фазой
3.5.2. Обрыв фаз ab и bc
Рассмотрим электрическую схему, изображённую на рис.3.22.
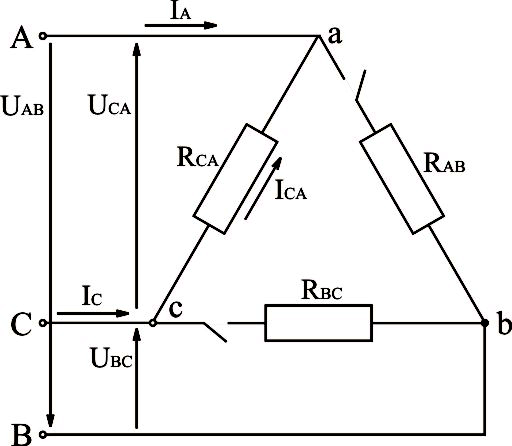
Рис.3.22. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенными двумя фазами
При
обрыве фаз ab и bc векторы токов 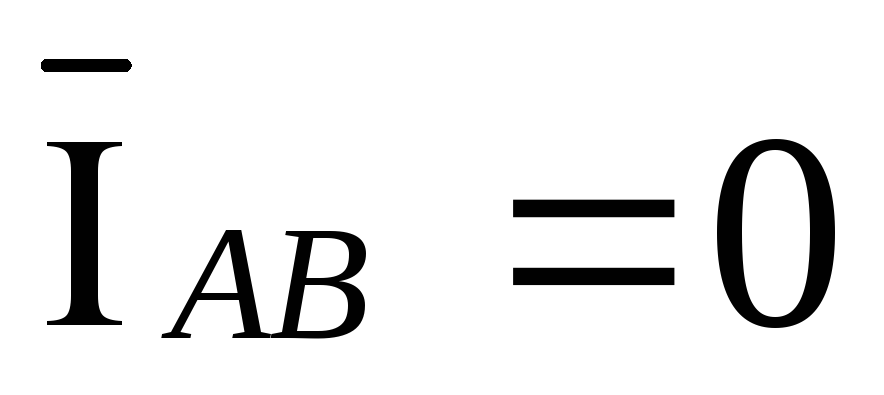 и
и 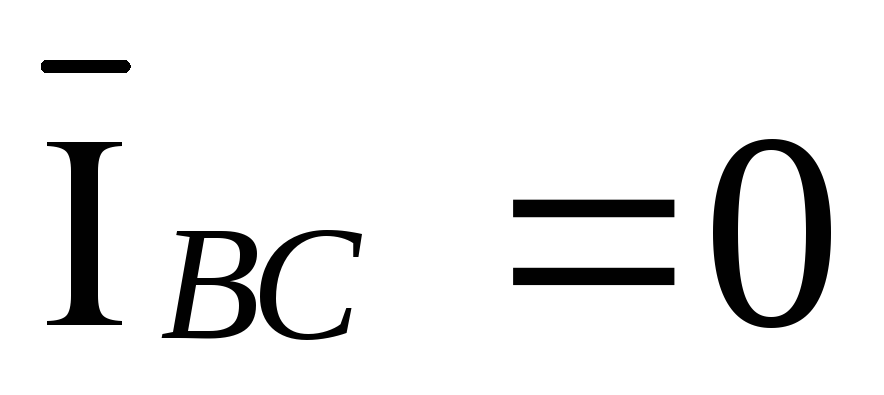 ,
тогда выражения (3.14) преобразуются в
следующий вид:
,
тогда выражения (3.14) преобразуются в
следующий вид:
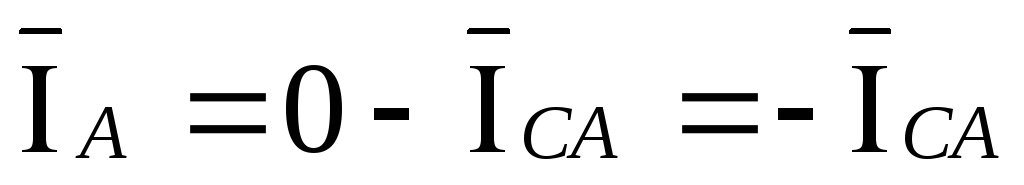 ,
, 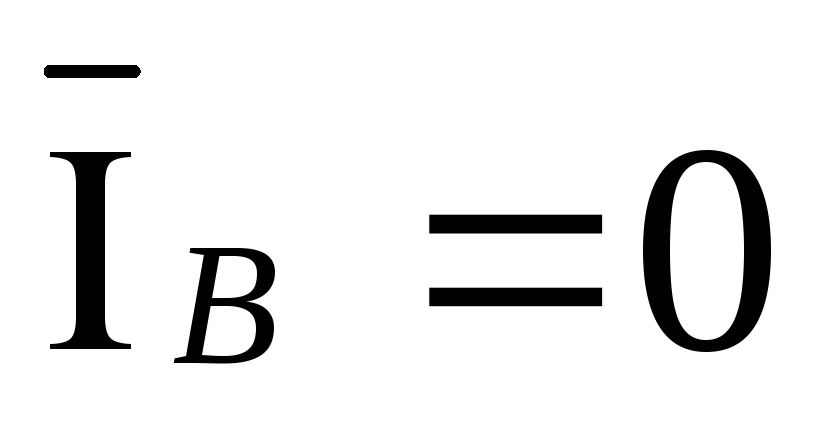 ,
,  .
(3.17)
.
(3.17)
На рис.3.23 приведена векторная диаграмма напряжений и токов при обрыве фаз аb и bc нагрузки, соединённой треугольником.
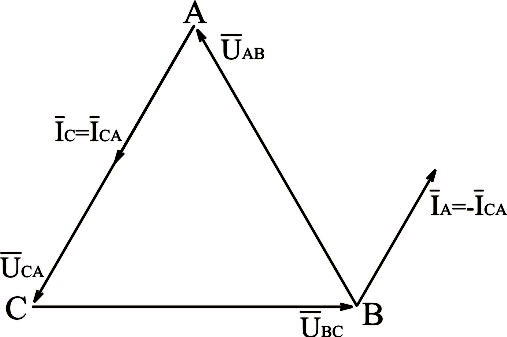
Рис.3.23. Векторная диаграмма напряжений и токов для нагрузки, соединённой треугольником, с отлюченными двумя фазами
3.5.3. Обрыв линейного провода
Рассмотрим
электрическую схему, изображённую на
рис.3.24. Пусть 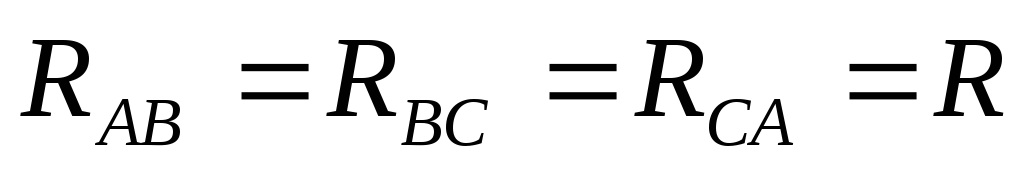 .
.
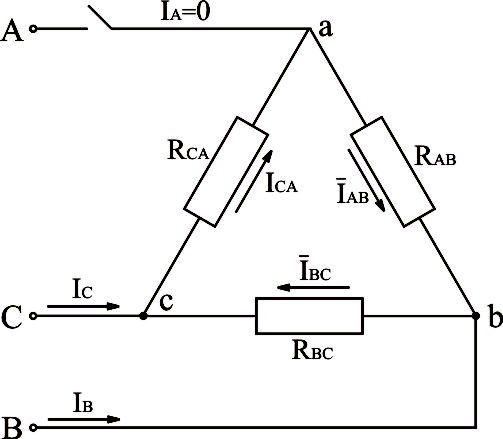
Рис.3.24. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенным линейным проводом
При
обрыве линейного провода Аa вектор
тока 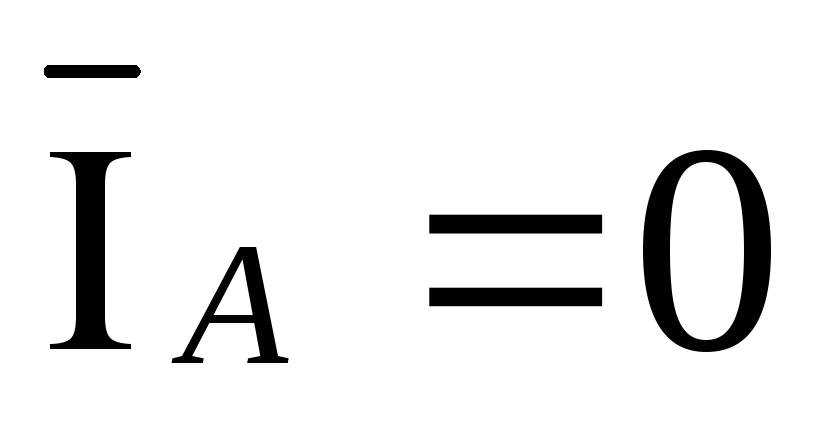 .
Преобразуем схему рис.3.24 в схему рис.3.25.
.
Преобразуем схему рис.3.24 в схему рис.3.25.
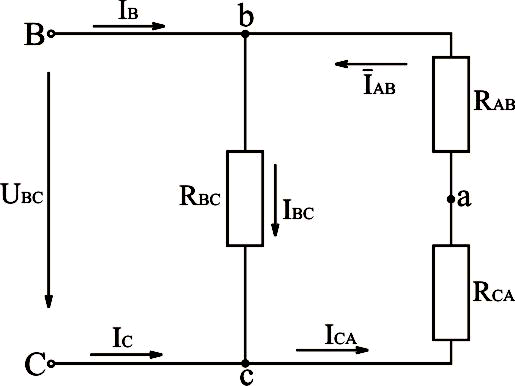
Рис.3.25. Преобразование трёхфазной электрической схемы, соединённой треугольником, с отключенным линейным проводом в однофазную электрическую схему
Из преобразованной схемы следует:
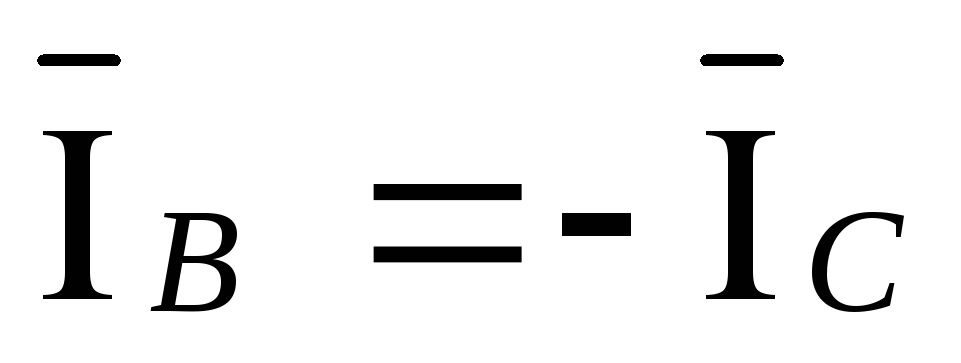 ,
,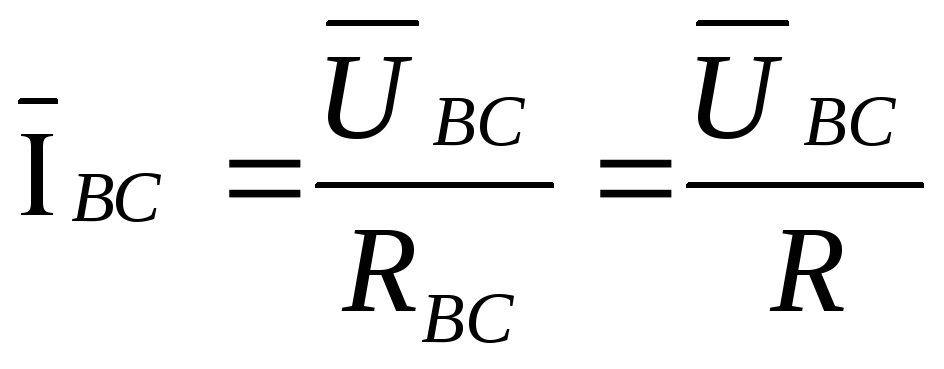 ,
,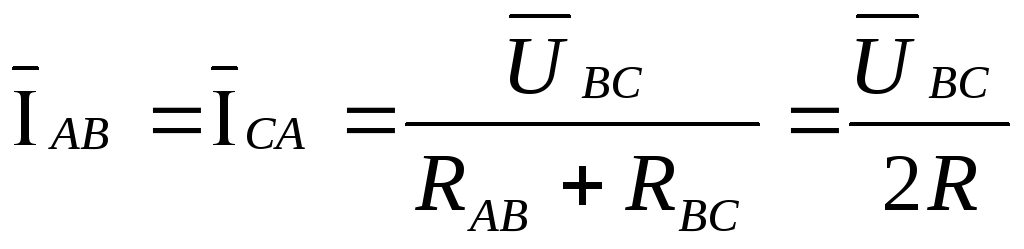 .
(3.18)
.
(3.18)
По первому закону Кирхгофа:
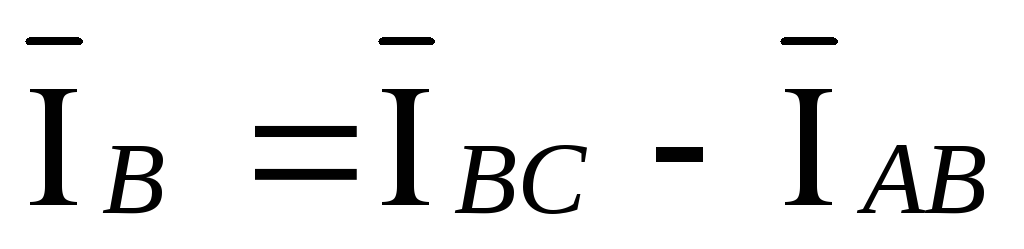 ;
; .
(3.19)
.
(3.19)
Используя формулы (3.18) и (3.19), построим векторную диаграмму:
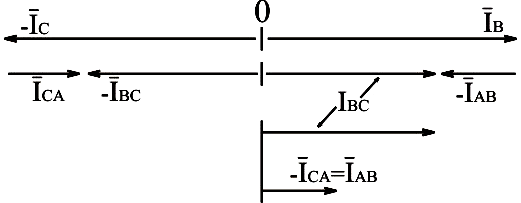
Рис.3.26. Векторная диаграмма токов преобразованной схемы
3.6. Мощность трёхфазной цепи
При
симметричной нагрузке активная мощность
трёхфазной цепи равна сумме активных
мощностей фаз: P
=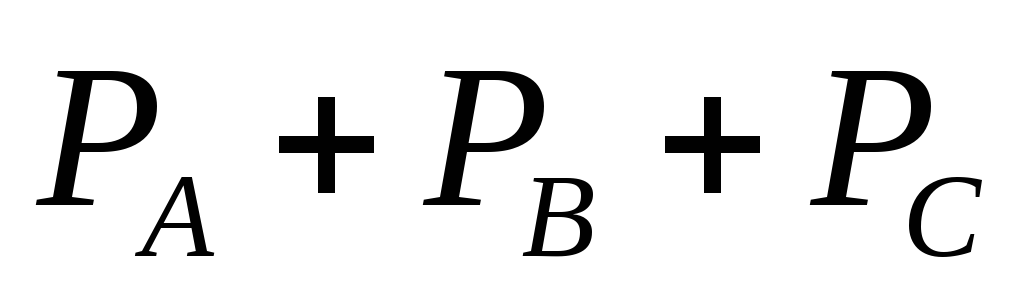 .
Активную мощность трёхфазной цепи можно
выразить через фазные значения напряжения
и тока:
.
Активную мощность трёхфазной цепи можно
выразить через фазные значения напряжения
и тока:
P
=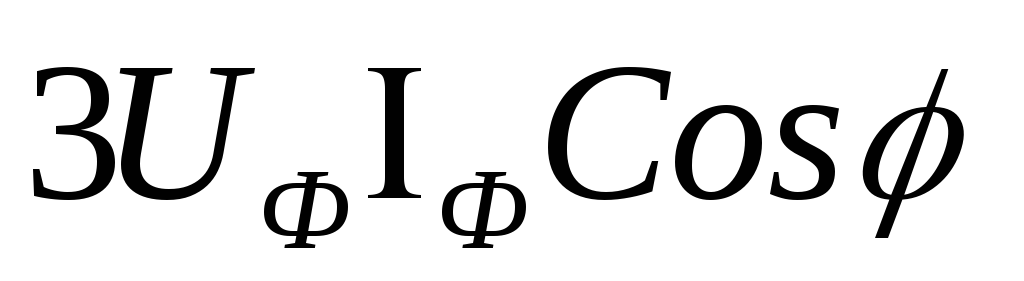
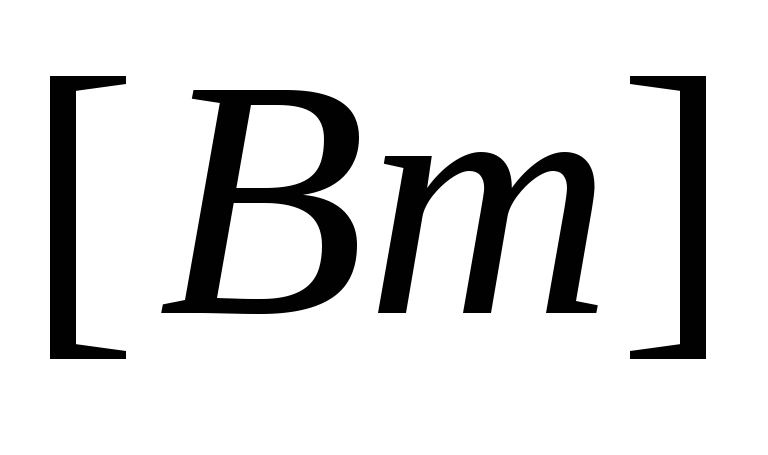 .
(3.20)
.
(3.20)
При
соединении звездой соотношения между
фазными и линейными напряжениями и
токами равны: 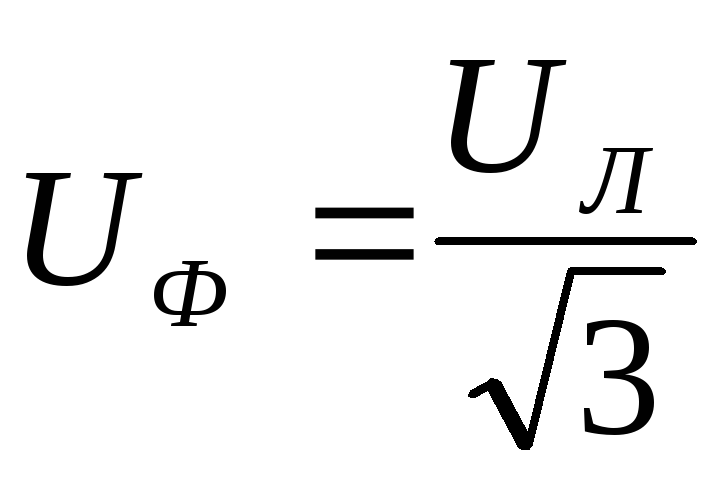 ,
, 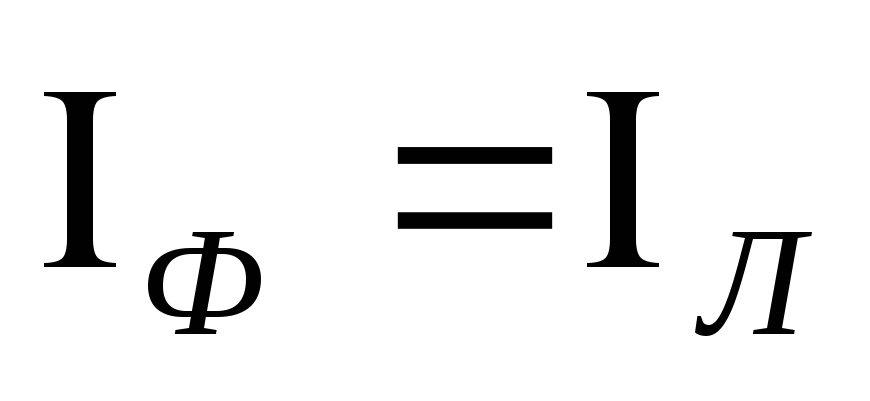 .
При соединении треугольником эти
соотношения равны:
.
При соединении треугольником эти
соотношения равны: 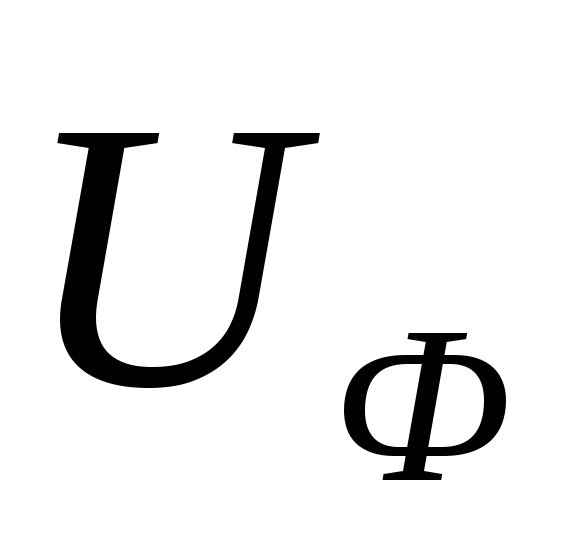 =
=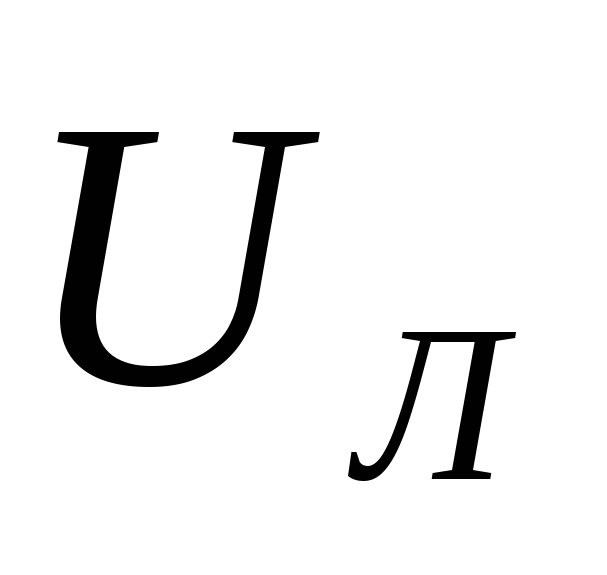 ,
, 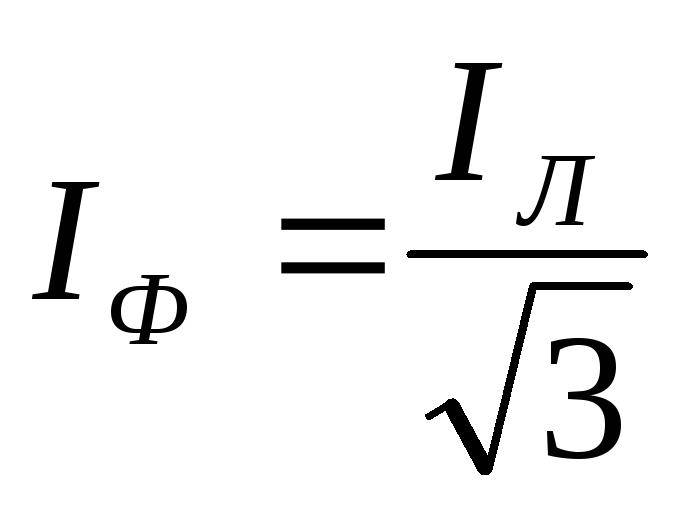 .
В обоих случаях
.
В обоих случаях 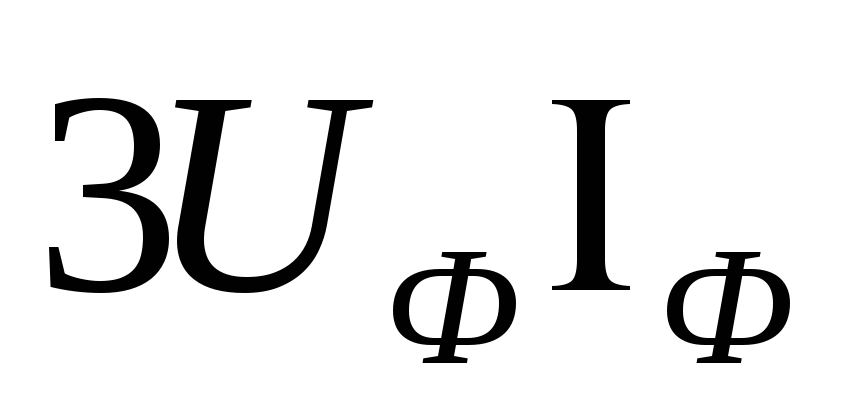
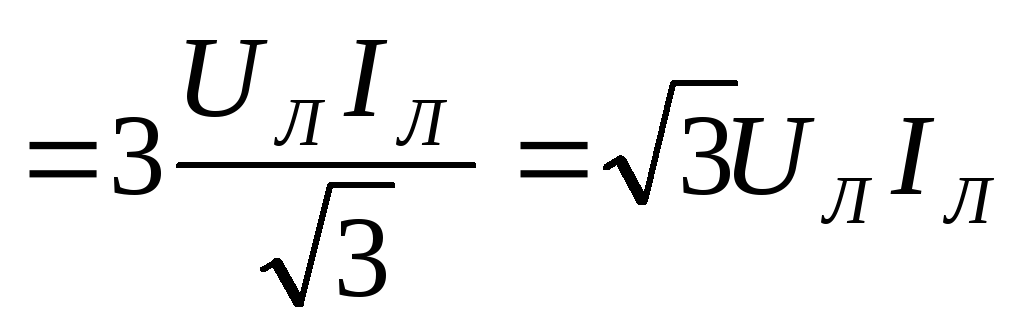 .
Тогда активную мощность можно выразить
через линейные значения напряжения и
тока:
.
Тогда активную мощность можно выразить
через линейные значения напряжения и
тока:
P
=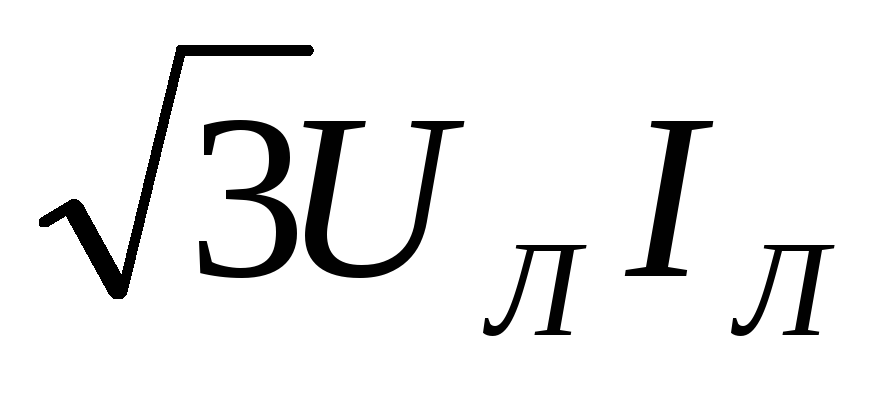
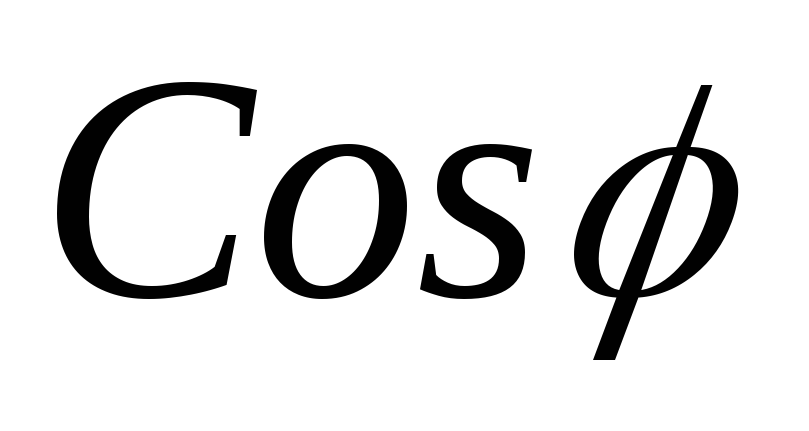
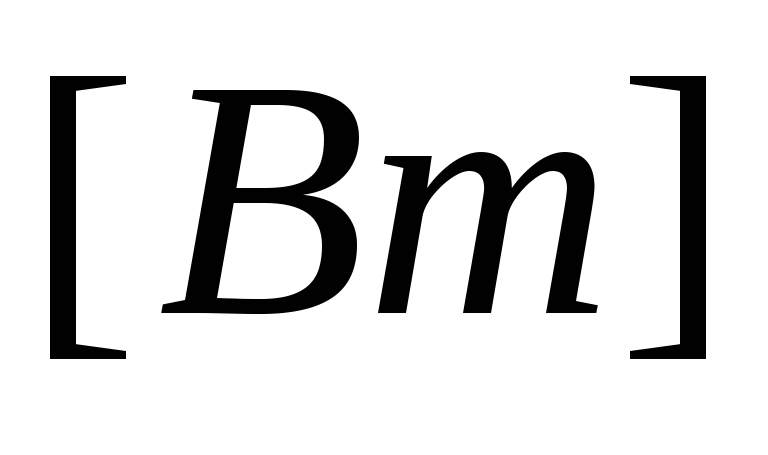 .
(3.21)
.
(3.21)
Реактивная мощность трёхфазной цепи
Q
=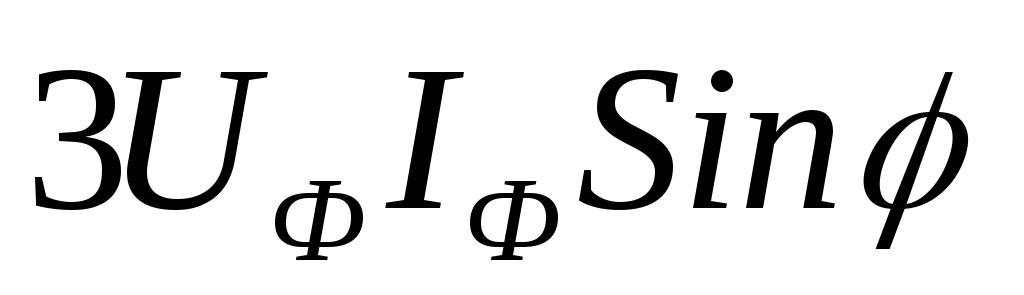 =
=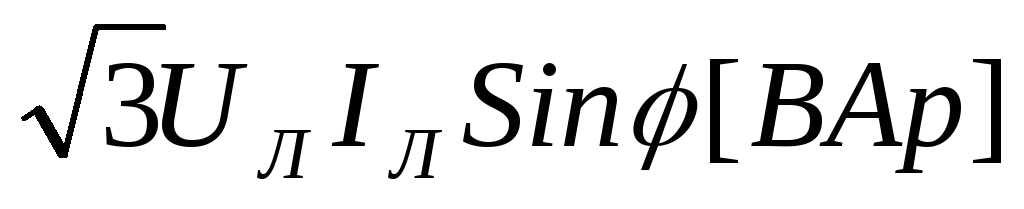 .
(3.22)
.
(3.22)
Полная мощность трёхфазной цепи
S
=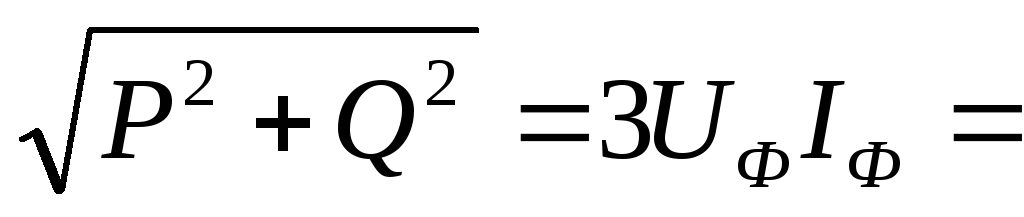
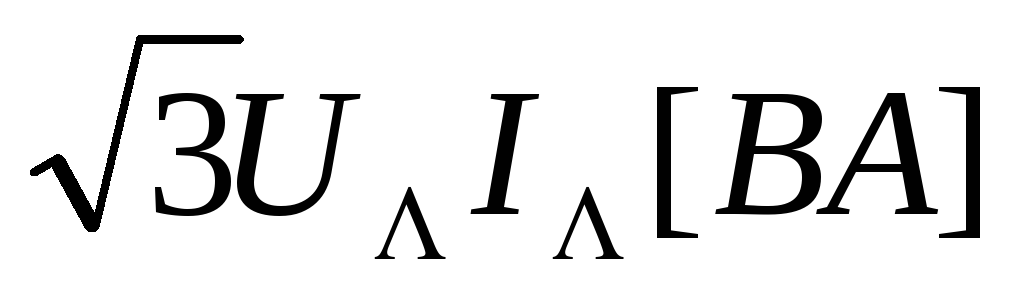 .
(3.23)
.
(3.23)
При расчётах удобно пользоваться следующими формулами:
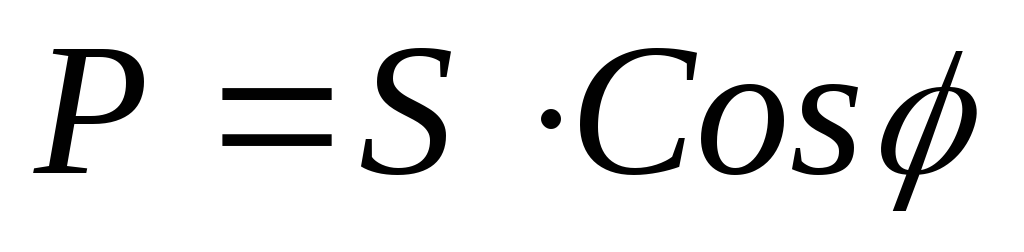 ;
;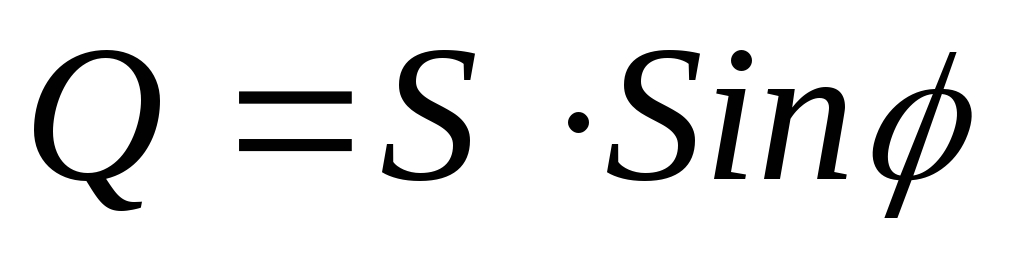 ;
;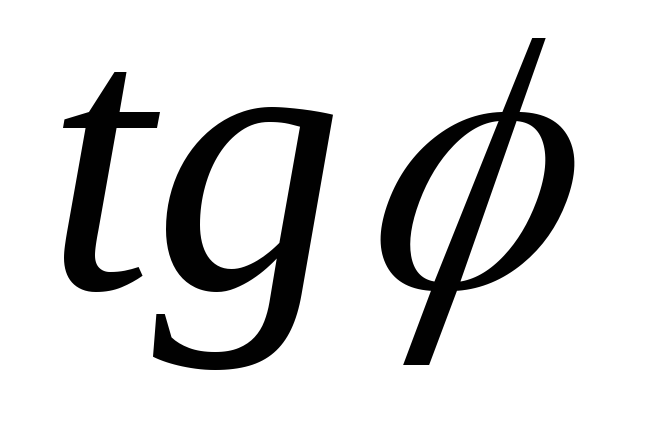 =
=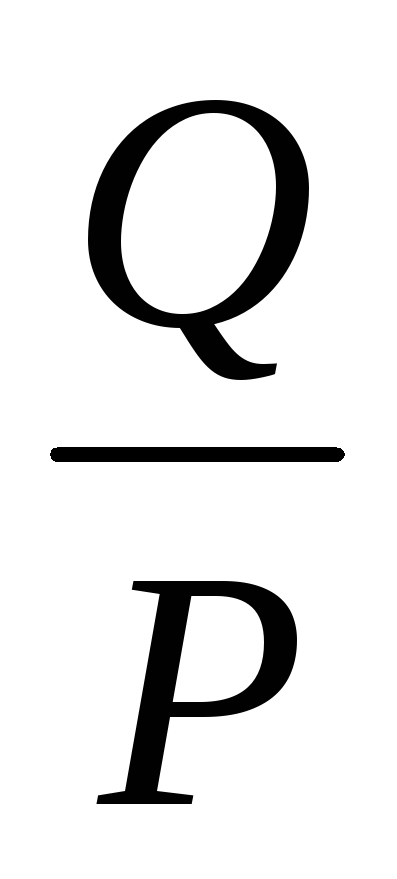 ;
;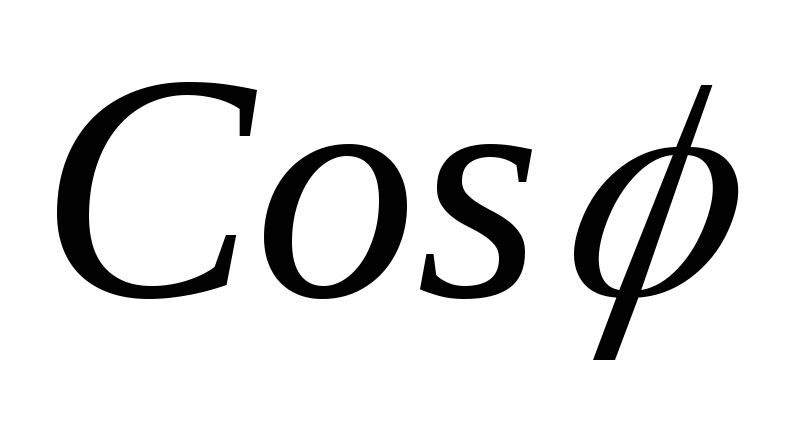 =
=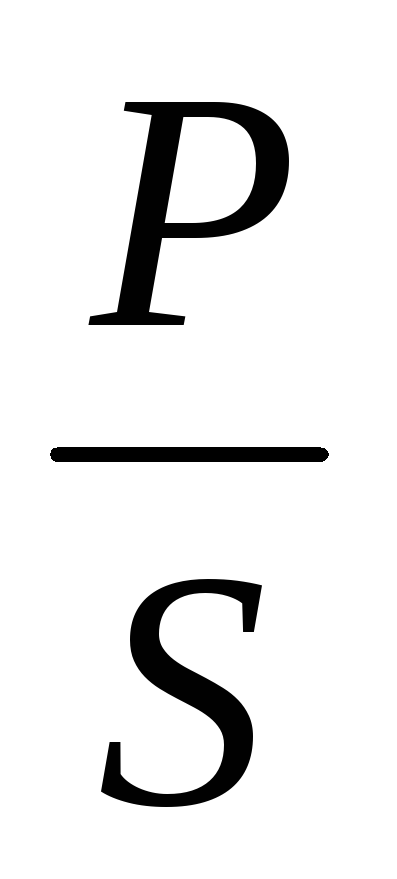 ;
; 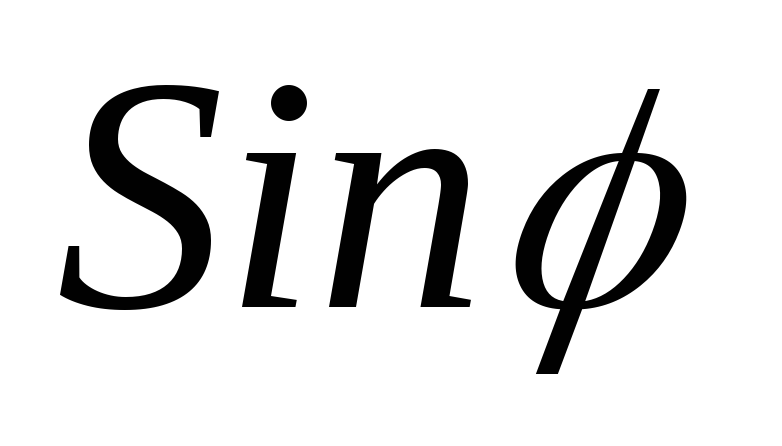 =
=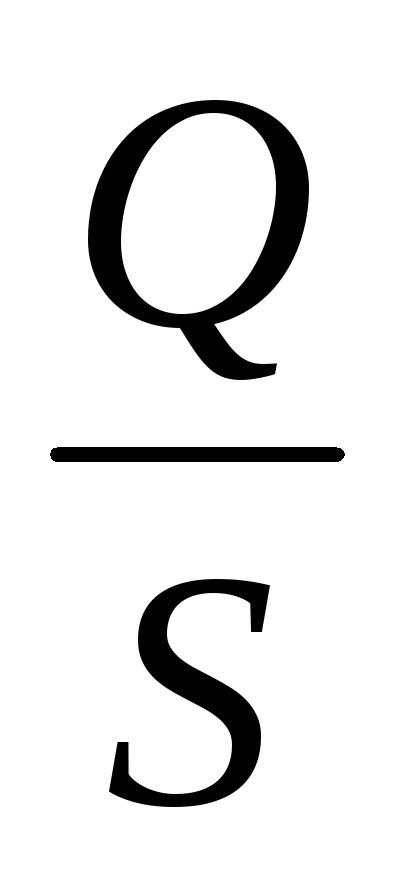 .
.
При несимметричных нагрузках, соединённых звездой или треугольником, активную мощность рассчитывают по формулам:
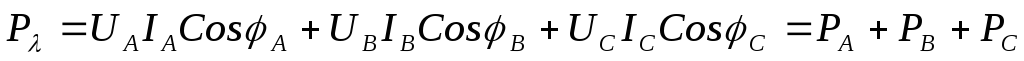 ;
;
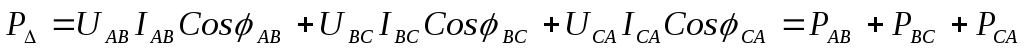 .
.
studfile.net
3.5. Обрыв фаз и обрыв линейного провода при соединении источников и потребителей треугольником
3.5.1. Обрыв фазы ab
Рассмотрим электрическую схему, изображённую на рис.3.20.
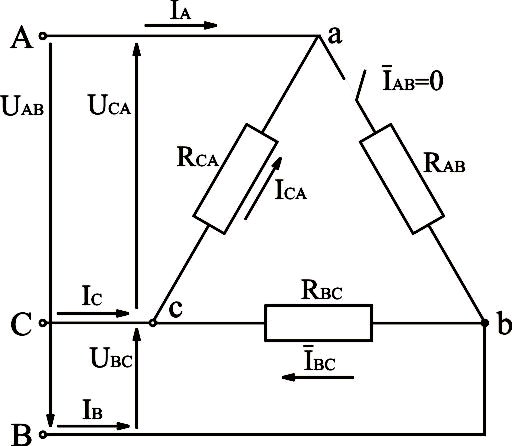
Рис.3.20. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенной фазой
При
обрыве фазы ab вектор тока 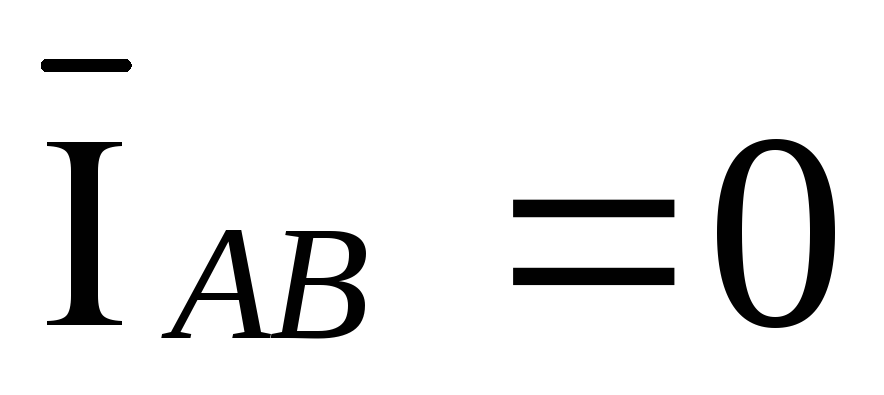 ,
тогда выражения (3.14) преобразуются в
следующий вид:
,
тогда выражения (3.14) преобразуются в
следующий вид:
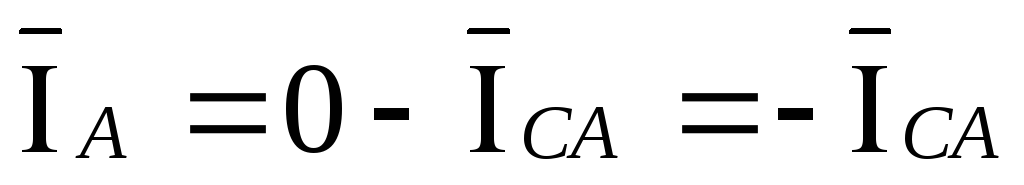 ,
, 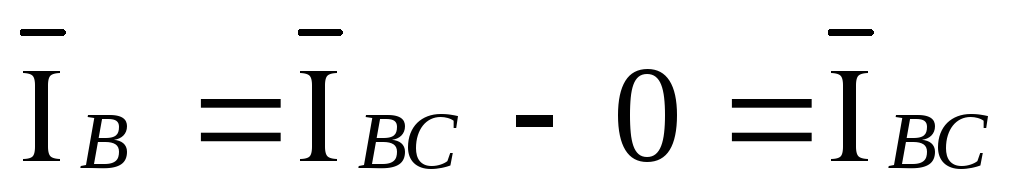 ,
,  .
(3.16)
.
(3.16)
На рис.3.21 приведена векторная диаграмма напряжений и токов при обрыве фазы аb нагрузки, соединённой треугольником.
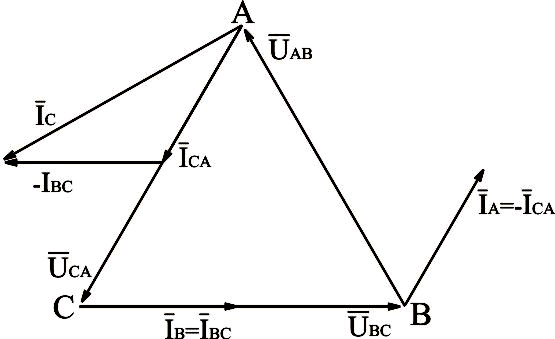
Рис.3.21. Векторная диаграмма напряжений и токов для нагрузки, соединённой треугольником, с отлюченной фазой
3.5.2. Обрыв фаз ab и bc
Рассмотрим электрическую схему, изображённую на рис.3.22.
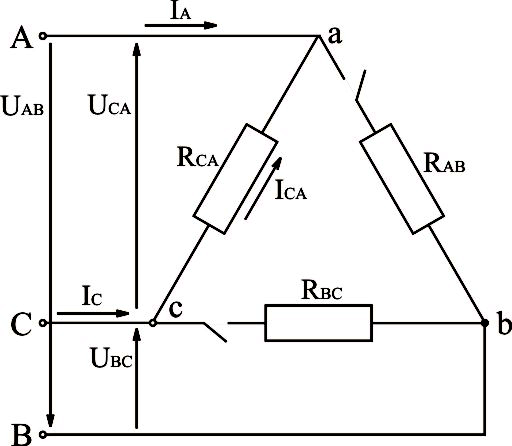
Рис.3.22. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенными двумя фазами
При
обрыве фаз ab и bc векторы токов 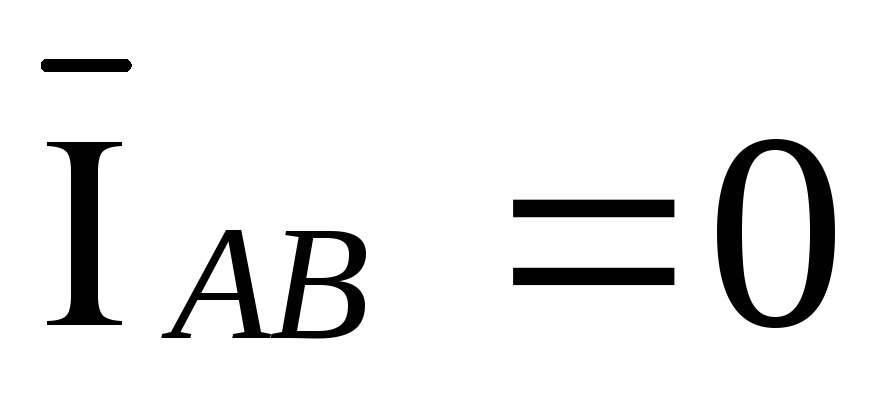 и
и 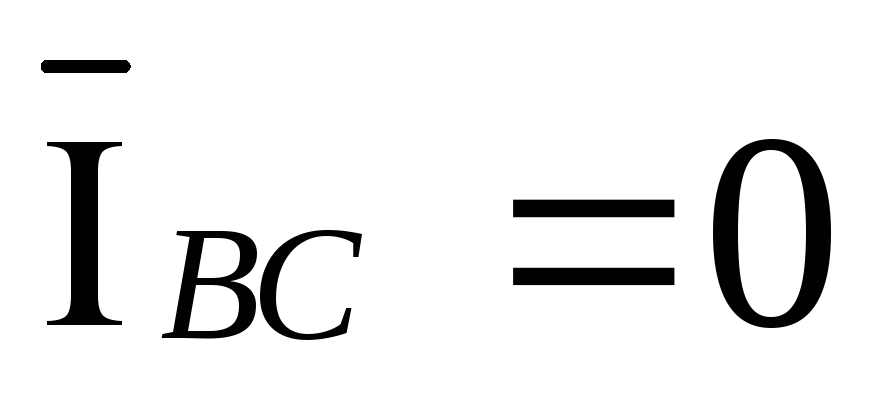 ,
тогда выражения (3.14) преобразуются в
следующий вид:
,
тогда выражения (3.14) преобразуются в
следующий вид:
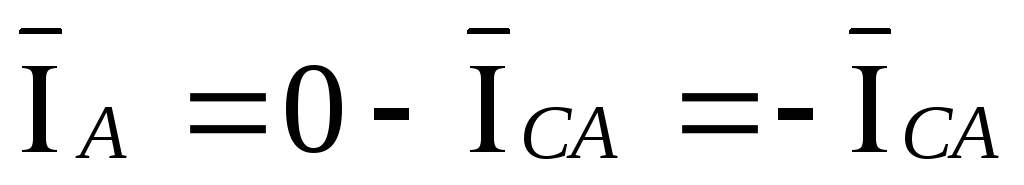 ,
, 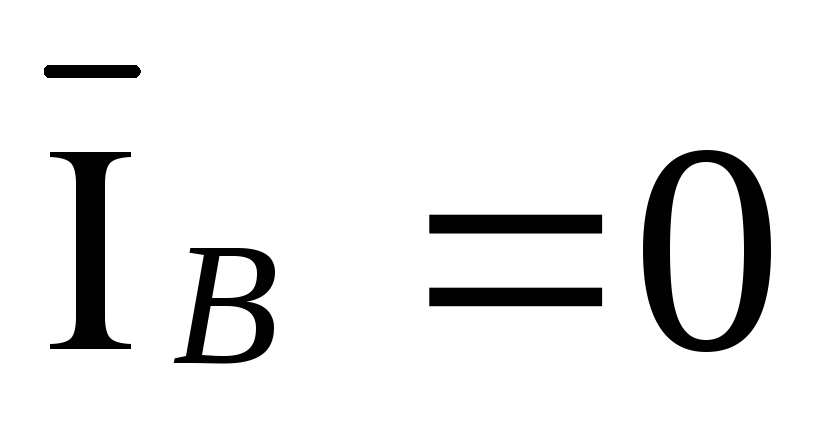 ,
, 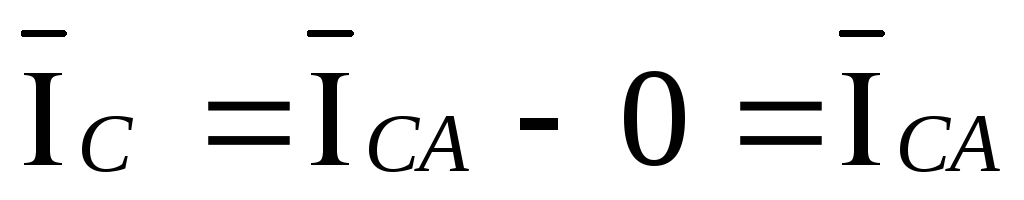 .
(3.17)
.
(3.17)
На рис.3.23 приведена векторная диаграмма напряжений и токов при обрыве фаз аb и bc нагрузки, соединённой треугольником.
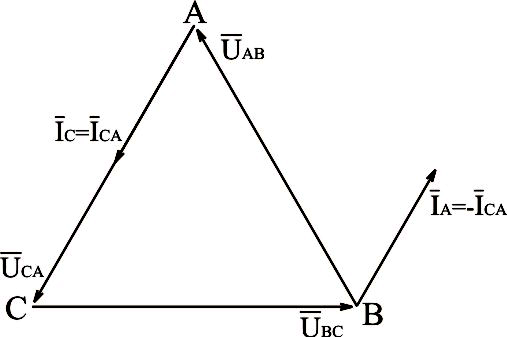
Рис.3.23. Векторная диаграмма напряжений и токов для нагрузки, соединённой треугольником, с отлюченными двумя фазами
3.5.3. Обрыв линейного провода
Рассмотрим
электрическую схему, изображённую на
рис.3.24. Пусть 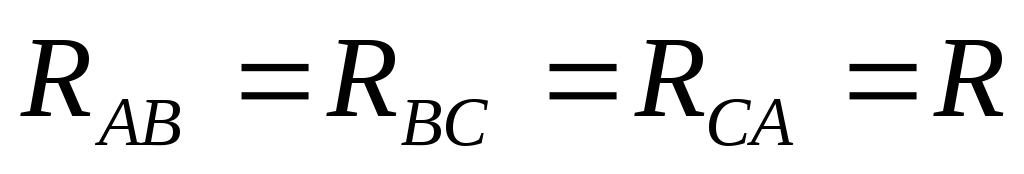 .
.
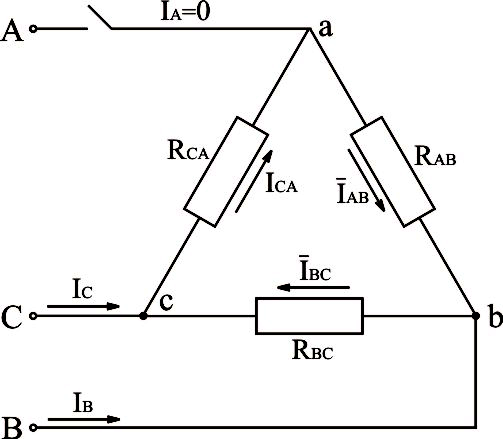
Рис.3.24. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенным линейным проводом
При
обрыве линейного провода Аa вектор
тока 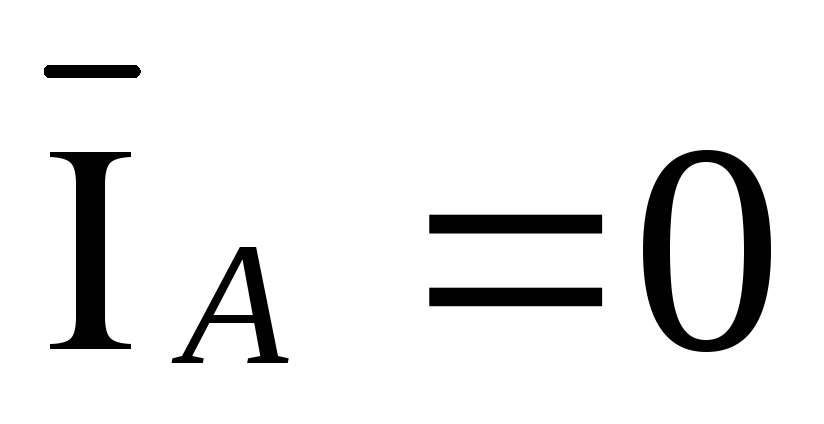 .
Преобразуем схему рис.3.24 в схему рис.3.25.
.
Преобразуем схему рис.3.24 в схему рис.3.25.
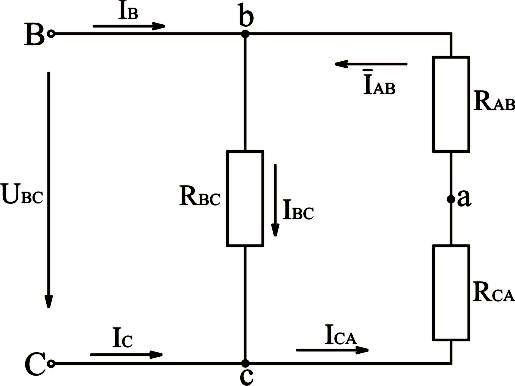
Рис.3.25. Преобразование трёхфазной электрической схемы, соединённой треугольником, с отключенным линейным проводом в однофазную электрическую схему
Из преобразованной схемы следует:
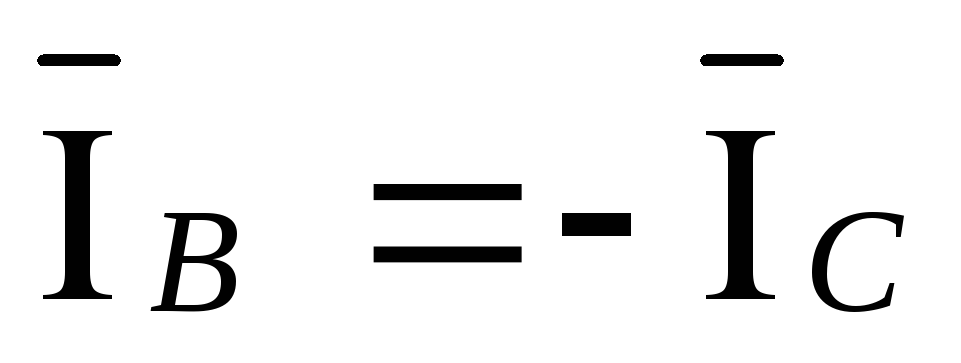 ,
,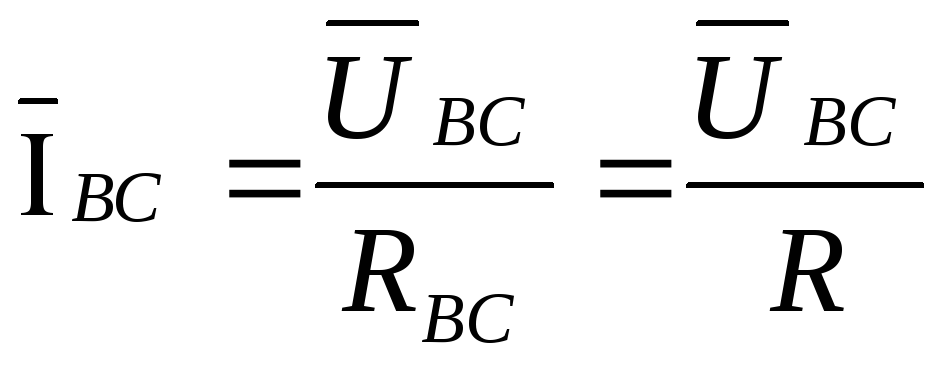 ,
,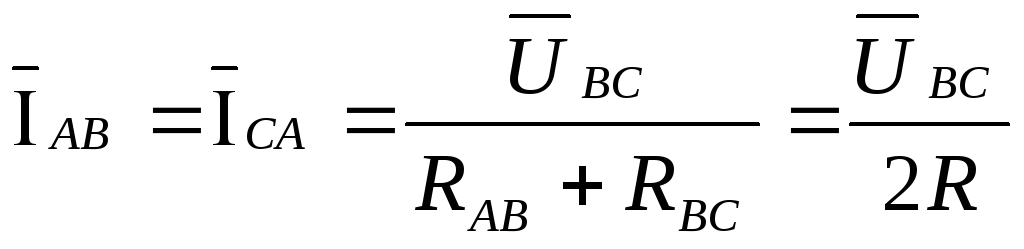 .
(3.18)
.
(3.18)
По первому закону Кирхгофа:
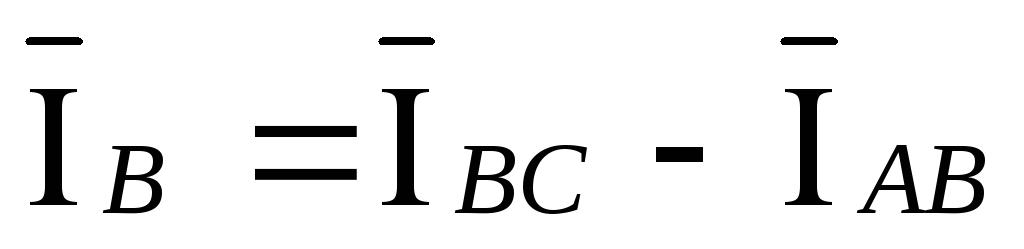 ;
; .
(3.19)
.
(3.19)
Используя формулы (3.18) и (3.19), построим векторную диаграмму:
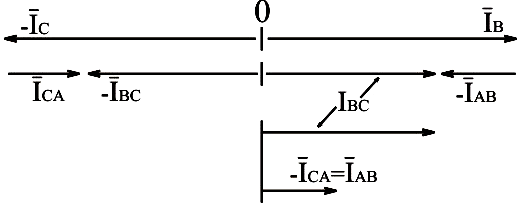
Рис.3.26. Векторная диаграмма токов преобразованной схемы
3.6. Мощность трёхфазной цепи
При
симметричной нагрузке активная мощность
трёхфазной цепи равна сумме активных
мощностей фаз: P
=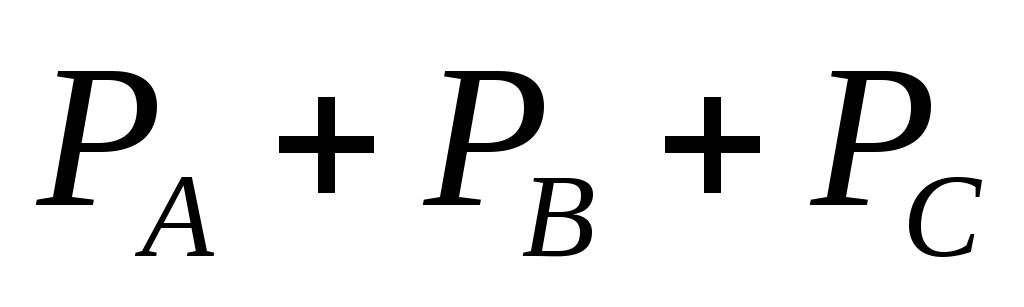 .
Активную мощность трёхфазной цепи можно
выразить через фазные значения напряжения
и тока:
.
Активную мощность трёхфазной цепи можно
выразить через фазные значения напряжения
и тока:
P
=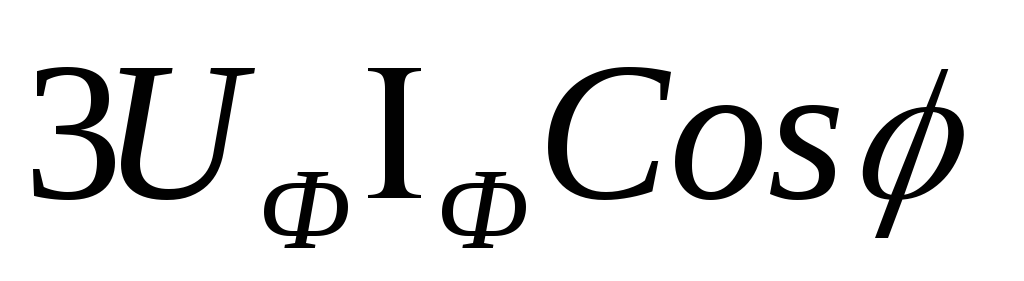
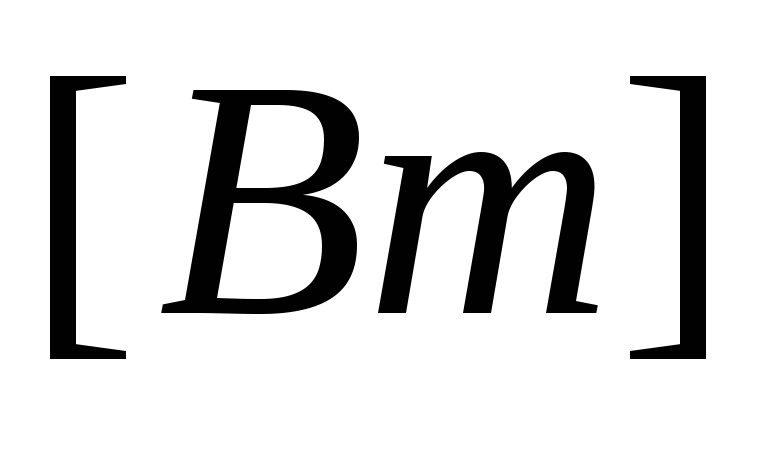 .
(3.20)
.
(3.20)
При
соединении звездой соотношения между
фазными и линейными напряжениями и
токами равны: 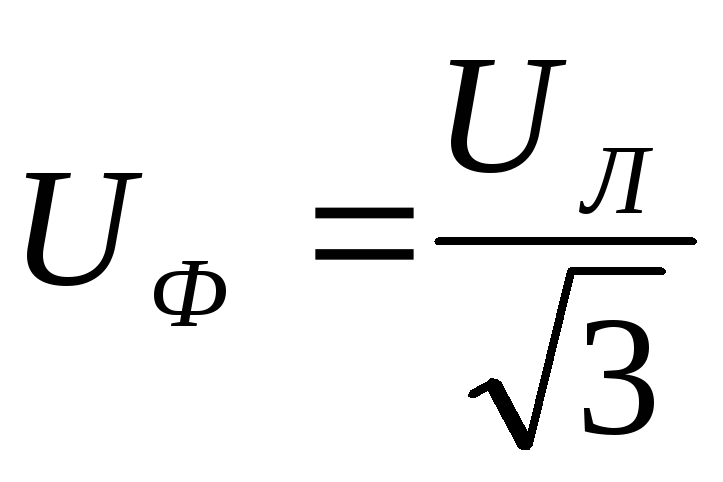 ,
, 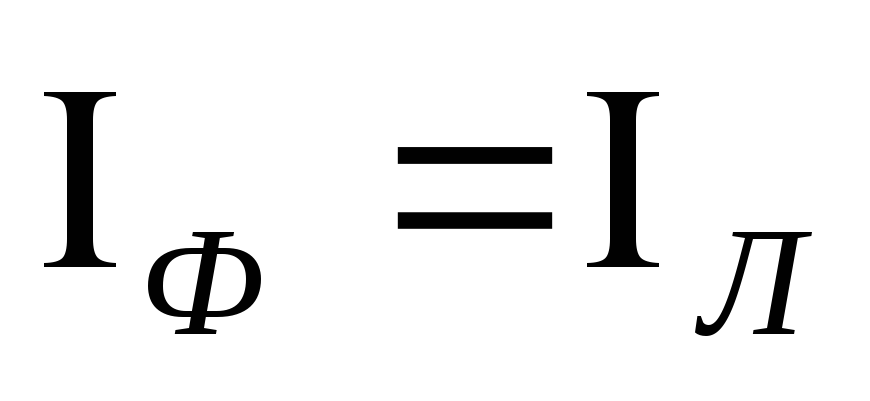 .
При соединении треугольником эти
соотношения равны:
=
.
При соединении треугольником эти
соотношения равны:
=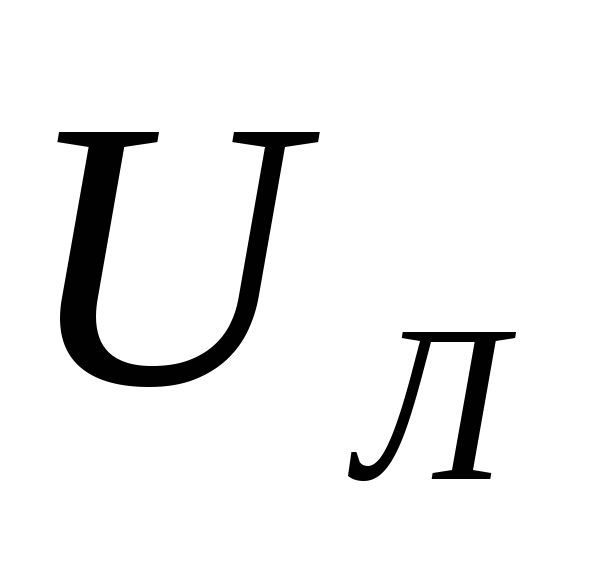 ,
, 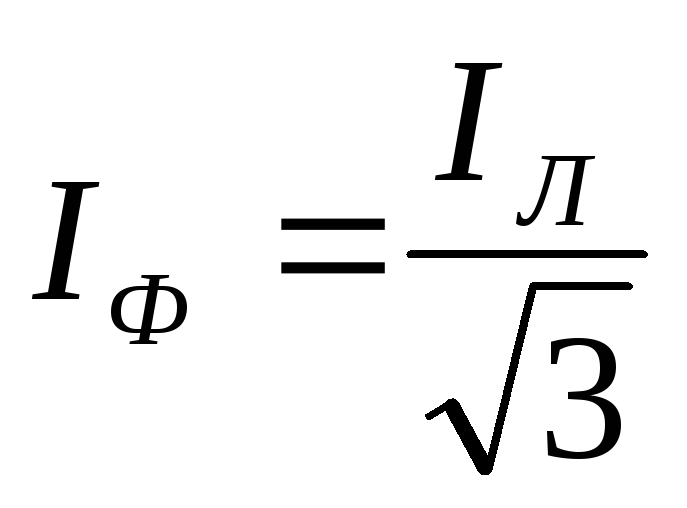 .
В обоих случаях
.
В обоих случаях 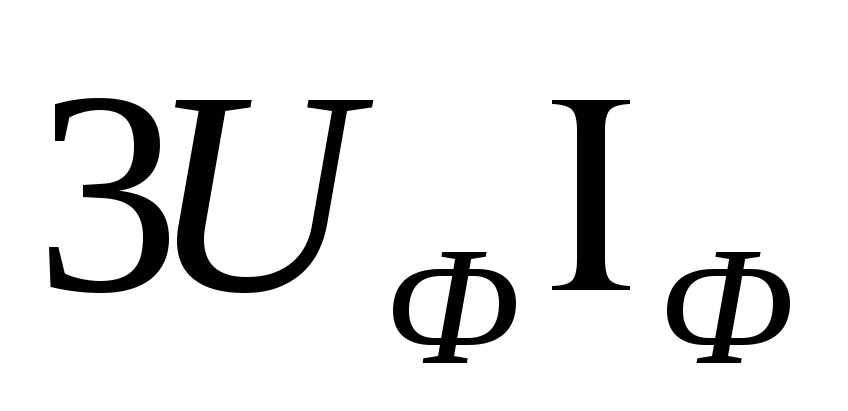
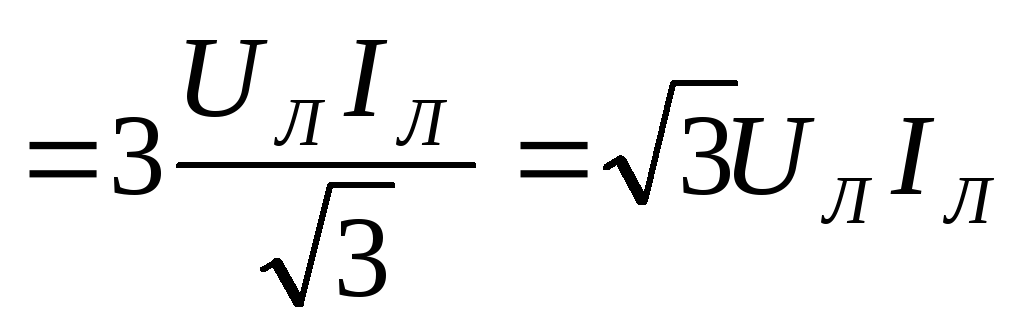 .
Тогда активную мощность можно выразить
через линейные значения напряжения и
тока:
.
Тогда активную мощность можно выразить
через линейные значения напряжения и
тока:
P
=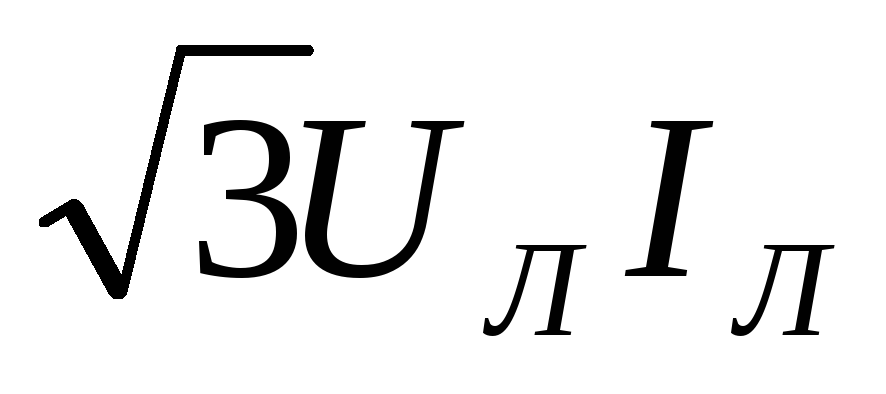
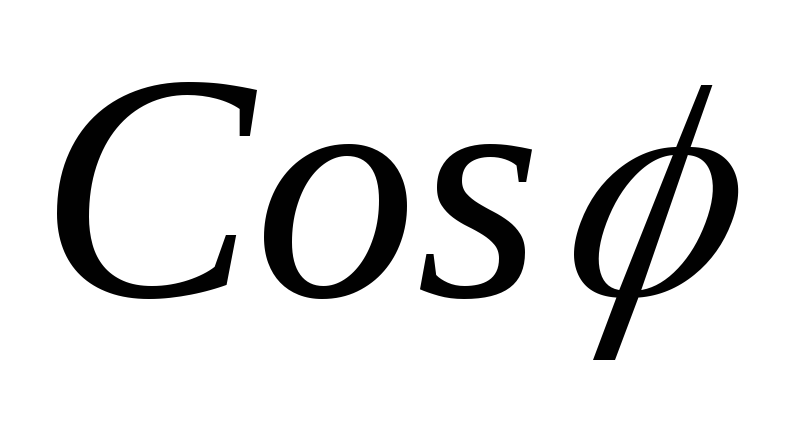
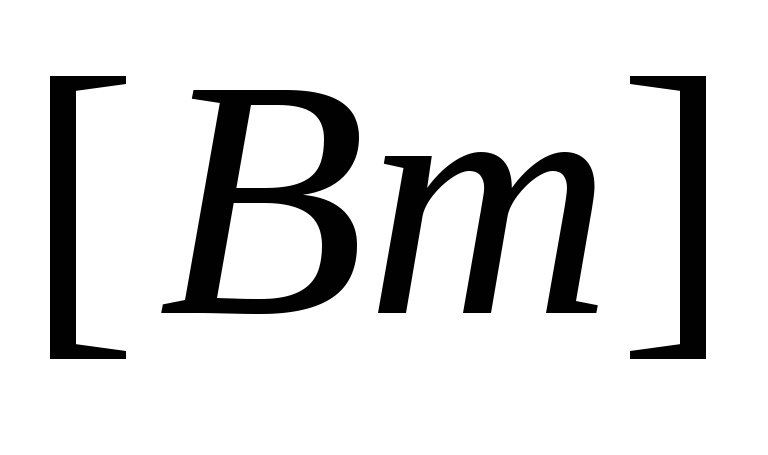 .
(3.21)
.
(3.21)
Реактивная мощность трёхфазной цепи
Q
=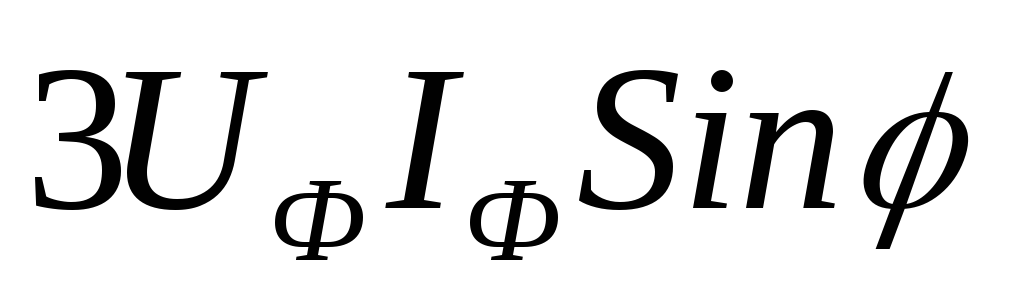 =
=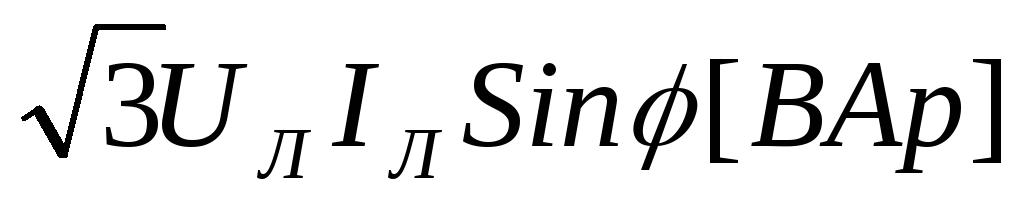 .
(3.22)
.
(3.22)
Полная мощность трёхфазной цепи
S
=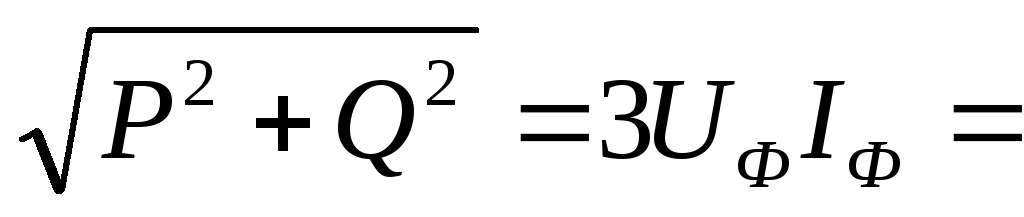
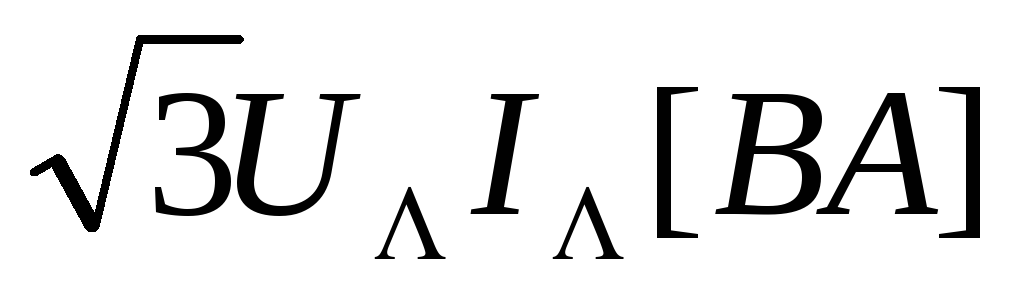 .
(3.23)
.
(3.23)
При расчётах удобно пользоваться следующими формулами:
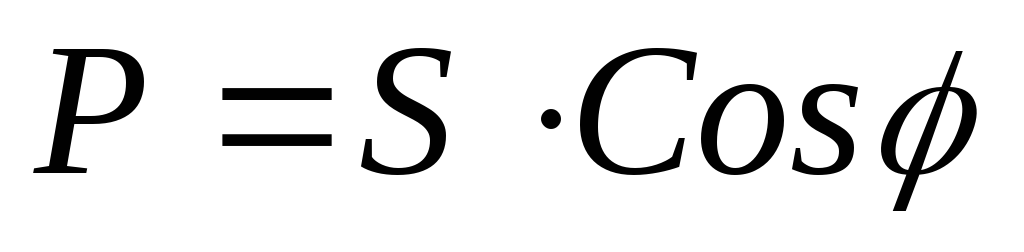 ;
;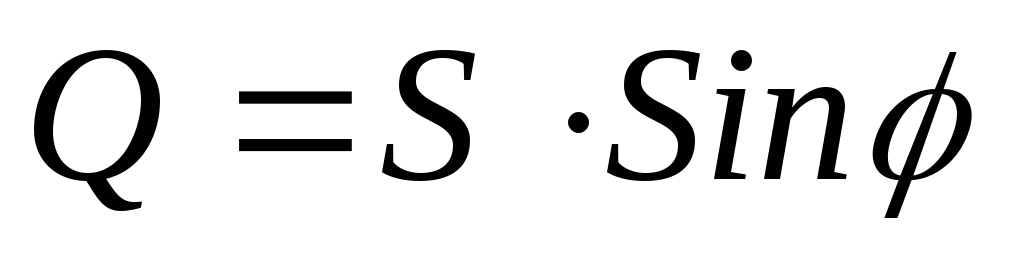 ;
;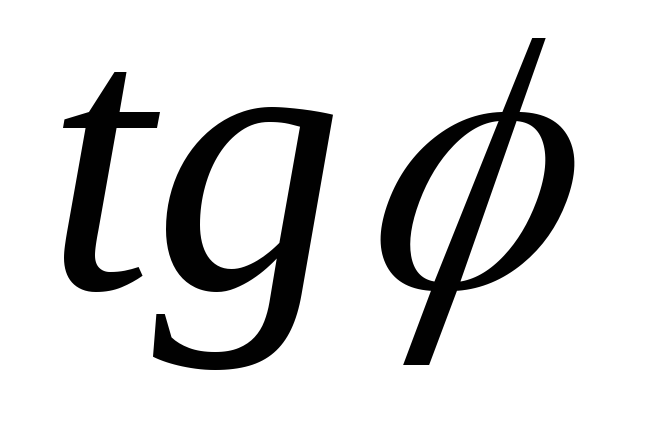 =
= ;
;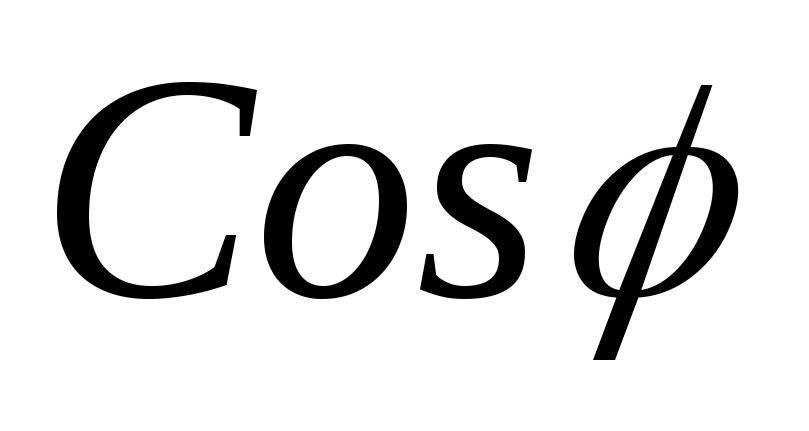 =
=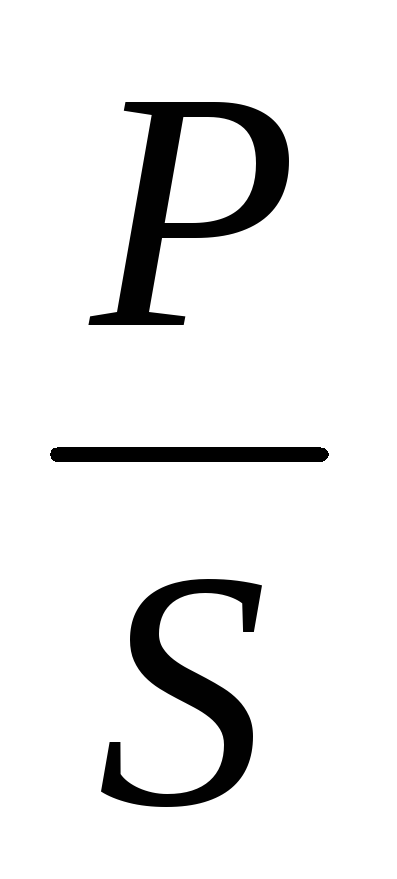 ;
; 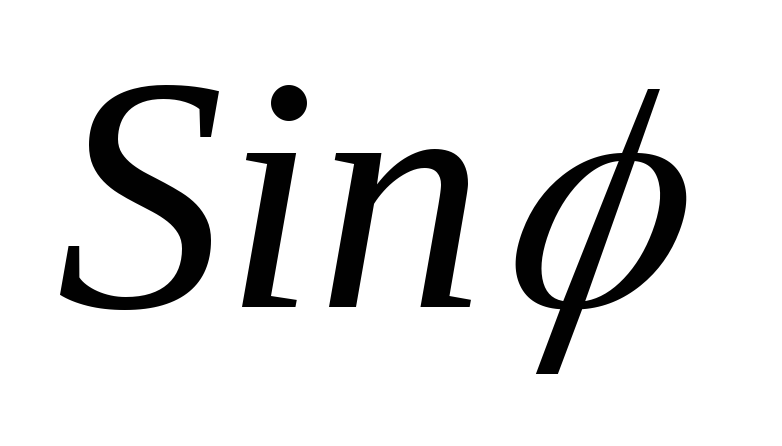 =
=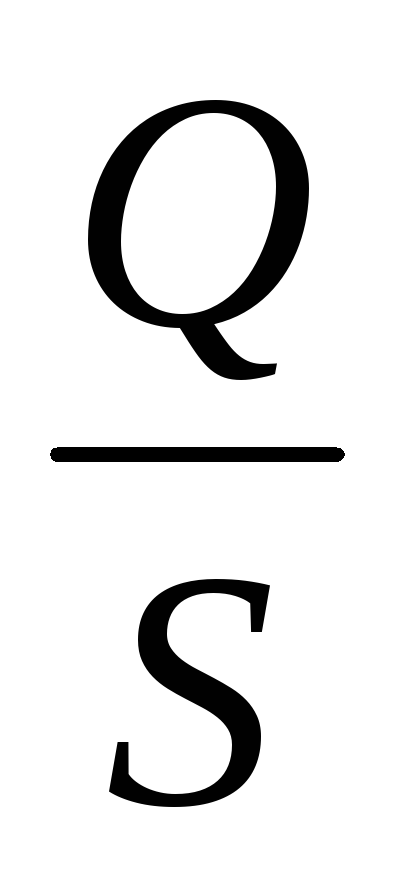 .
.
При несимметричных нагрузках, соединённых звездой или треугольником, активную мощность рассчитывают по формулам:
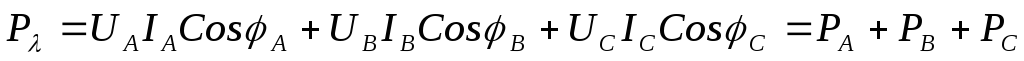 ;
;
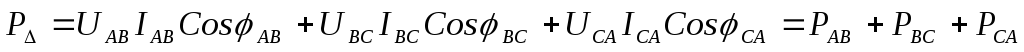 .
.
studfile.net
