Что дает последовательное соединение конденсаторов. Соединение конденсаторов

Вопрос о том, как соединить конденсаторы может возникнуть у любого человека, интересующегося электроникой и пайкой . Чаще всего, необходимость в этом возникает в случаях отсутствия под рукой устройства подходящего номинала при сборке или ремонте какого-либо прибора.

К примеру, человеку нужно отремонтировать устройство, заменив в нем электролитический конденсатор ёмкостью 1000 микрофарад или больше, на руках подходящие по номиналу детали отсутствуют, но есть несколько изделий с меньшими параметрами. В этом случае есть три варианта выхода из сложившейся ситуации:

1. Поставить вместо конденсатора на 1000 микрофарад устройство с меньшим номиналом.
2. Поехать в ближайший магазин или радио-рынок для покупки подходящего варианта.
3. Соединить несколько элементов вместе для получения необходимой ёмкости.

От установки радиоэлемента меньшего номинала лучше отказаться, так как подобные эксперименты не всегда заканчиваются успешно.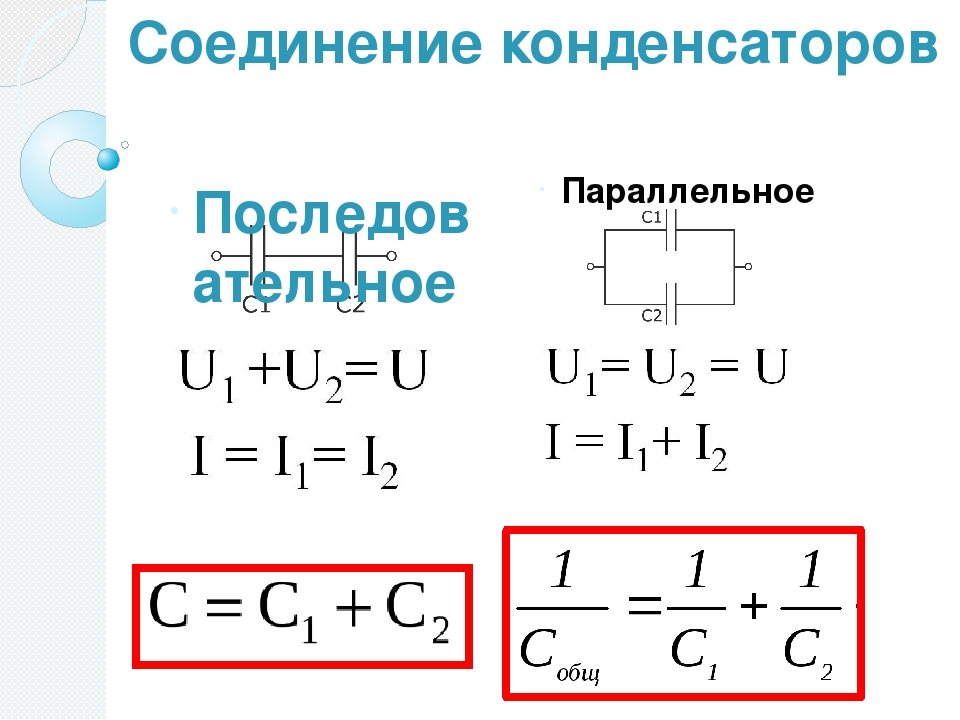

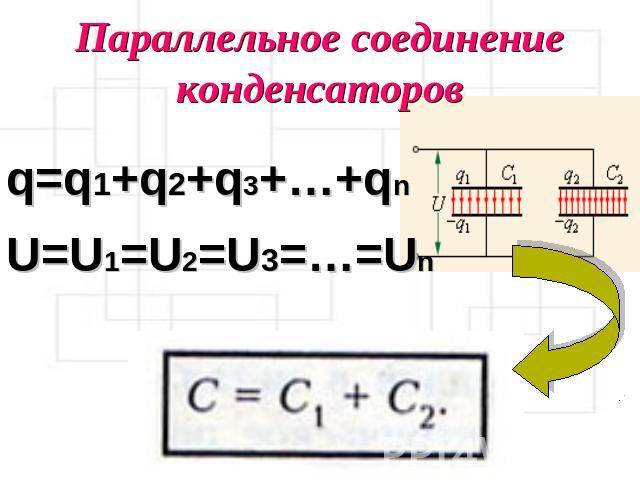
Можно съездить на рынок или в магазин, но это требует немало времени. Потому в сложившейся ситуации чаще соединяют несколько конденсаторов и получают необходимую емкость.

Параллельное соединение конденсаторов

Параллельная схема подключения конденсаторов предполагает соединение в две группы всех обкладок приборов. В одну группу соединяются первые выводы, а в другую группу – вторые выводы. На рисунке ниже представлен пример.

Конденсаторы, соединенные параллельно между собой, подключаются к одному источнику напряжения, поэтому на них существует две точки напряжения или разности потенциалов . Следует учитывать, что на всех выводах подключенных параллельно конденсаторов напряжение будет иметь одинаковую величину.

Параллельная схема образует из элементов единую ёмкость, величина которой равняется сумме ёмкостей всех подключенных в группу конденсаторов. При этом через конденсаторы в процессе работы устройства будет протекать ток разной величины. Параметры проходящего через изделия тока зависят от индивидуальной ёмкости устройства.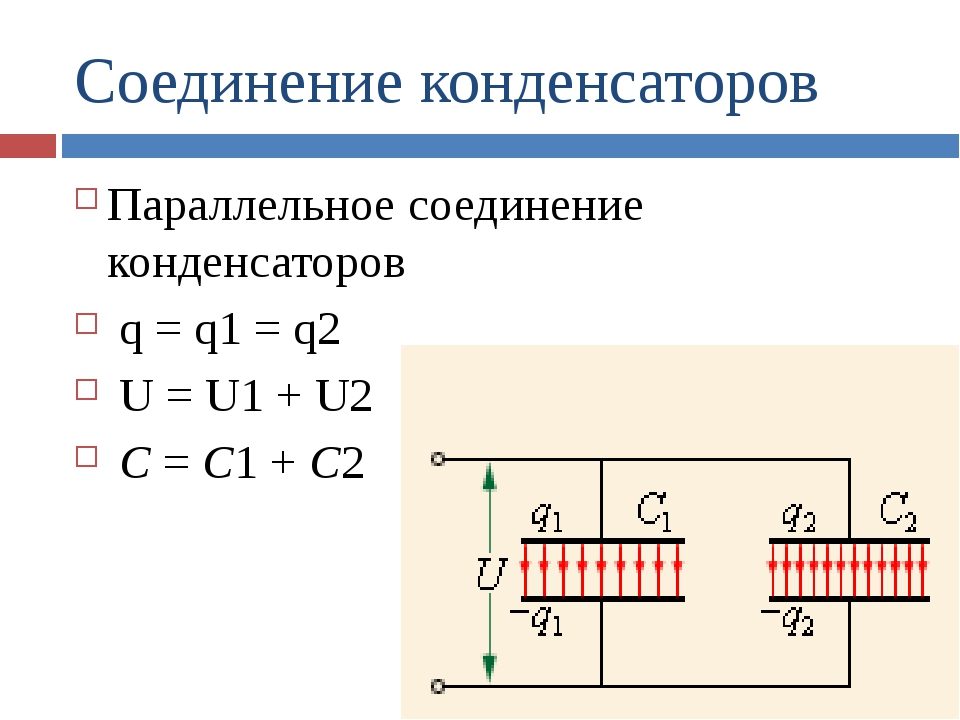 Чем выше ёмкость, тем больший по величине ток пройдет через него. Формула, характеризующее параллельное соединение, имеет следующий вид:

Параллельная схема чаще всего используется в быту, она позволяет собрать необходимую ёмкость из любого числа отдельных, различных по номиналу элементов.

Последовательное соединение конденсаторов

Схема последовательного подключения представляет собой цепочку, в которой первая обкладка конденсатора соединяется со второй обкладкой предыдущего устройства, а вторая обкладка – с первой обкладкой следующего прибора. Первый вывод первого конденсатора и второй вывод последней детали в цепи соединяются с источником электрического тока, благодаря чему между ними осуществляется перераспределение электрических зарядов. Все промежуточные обкладки имеют одинаковые по величине заряды, чередующиеся по знаку.

На рисунке ниже представлен пример последовательного подключения.

Через соединенные в группу конденсаторы протекает ток одинаковой величины. Общая мощность ограничивается площадью обкладок устройства с наименьшим номиналом, так как после зарядки наименьшего по ёмкости устройства, вся цепь перестанет пропускать ток.

Несмотря на явные недостатки, данный способ обеспечивает увеличение изоляции между отдельными обкладками до суммы расстояний между выводами на всех последовательно соединенных конденсаторах. То есть, при последовательном соединении двух элементов с рабочим напряжением 200 В, изоляция между их выводами сможет выдерживать напряжение до 1000 В. Ёмкость по формуле:

Данный способ позволяет получить эквивалент меньшего по ёмкости конденсатора в группе, способной работать при высоких напряжениях. Всего этого можно достичь путем покупки одного единственного элемента подходящего номинала, потому на практике последовательные соединения практически не встречаются.

Эта формула актуальна для расчета общей ёмкости цепи последовательно соединенных двух конденсаторов. Для определения общей ёмкости цепи с большим числом приборов необходимо воспользоваться формулой:

Смешанная схема

Пример смешанной схемы подключения представлен ниже.

Чтобы определить общую ёмкость нескольких устройств, всю схему необходимо разделить на имеющиеся группы последовательного и параллельного соединения и рассчитать параметры ёмкости для каждой из них.

На практике данный способ встречаются на различных платах, с которыми приходиться работать радиолюбителям.

ИССЛЕДОВАНИЕ ПОСЛЕДОВАТЕЛЬНОГО, ПАРАЛЛЕЛЬНОГО И СМЕШАННОГО СОЕДИНЕНИЯ КОНДЕНСАТОРОВ

Цель работы: Научиться составлять батареи конденсаторов и определять их емкость.

Теоретическая часть

Соединение конденсаторов параллельно

При параллельной схеме подключения все обкладки конденсаторов соединяются в две группы, причем один вывод с каждого конденсатора соединяется в одну группу с другими, а второй — в другую. Наглядный пример параллельного соединения и схема

на картинке

Все параллельно соединенные конденсаторы подключаются к одному источнику напряжения, поэтому существует на них две точки разности потенциалов или напряжения. На всех выводах конденсаторов будет абсолютно одинаковое напряжение.

При подключении параллельно все конденсаторы вместе, образуют принципиально одну емкость, величина которой будет равняться сумме всех емкостей подключенных в цепи конденсаторов. При параллельном подключении через каждый из конденсаторов потечет разный ток, который будет зависеть от величины емкости каждого из них. Чем выше емкость, тем больший ток потечет через неё.

Параллельное соединение очень часто встречается в жизни. С его помощью можно из группы конденсаторов собрать любую необходимую емкость. Например, для запуска 3 фазного электродвигателя в однофазной сети 220 Вольт в результате расчетов Вы получили что необходима рабочая емкость 125 мкФ. Такой емкости конденсаторов Вы не найдете в продаже. Для того, что бы получить необходимую емкость придется купить и соединить параллельно 3 конденсатора один на 100 мкФ, второй- на 20, и третий на 5 мкФ.

Соединение конденсаторов последовательно

При последовательном соединении конденсаторов каждая из обкладок соединяется только в одной точке с одной обкладкой другого кон­денсатора. Получается цепочка конденсаторов. Крайние два вывода подключаются к источнику тока, в результате чего происходит перераспределение между ними электрических зарядов. Заряды на всех промежуточных обкладках одинаковые величине с чередованием по знаку.

Через все соединенные конденсаторы последовательно протекает одинаковой величины ток, потому что у него нет другого пути прохождения.

Общая же емкость будет ограничиваться площадью обкладок самого маленького по величине, потому что как только зарядится полностью конденсатор с самой маленькой емкостью- вся цепочка перестанет пропускать ток и заряд остальных прервется. Высчитывается же ем

кость по этой формуле:

Но при последовательном соединении увеличивается расстояние (или изоляция) между обкладками до величины равной сумме расстояний между обкладками всех последовательно подключенных конденсаторов. Например, если взять два конденсатора с рабочим напряжением 200 Вольт и соединить последовательно, то изоляция между их обкладками сможет выдержать 1000 Вольт при подключении в схему.

Из выше сказанного можно сделать вывод , что последовательно соединять необходимо:

1. Для получения эквивалентного меньшего по емкости конденсатора.

2. Если необходима емкость , работающая на более высоких напряжениях.

3. Для создания емкостного делителя напряжения, который позволяет получить меньшей величины напряжение из более высокого.

Практически, для получения первого и второго достаточно просто купить один конденсатор с необходимой величиной емкости или рабочим напряжением. Поэтому данный метод соединения в жизни не встречается.

В этой статье мы попытаемся раскрыть тему соединения конденсаторов разными способам. Из статьи про соединения резисторов мы знаем,что существует последовательное, параллельное и смешанное соединение, это же правило справедливо и для этой статьи. Конденсатор (от лат. слова «condensare» — «уплотнять», «сгущать»)– это очень широко распространённый электрический прибор.

Это два проводника (обкладки), между которыми находится изоляционный материал.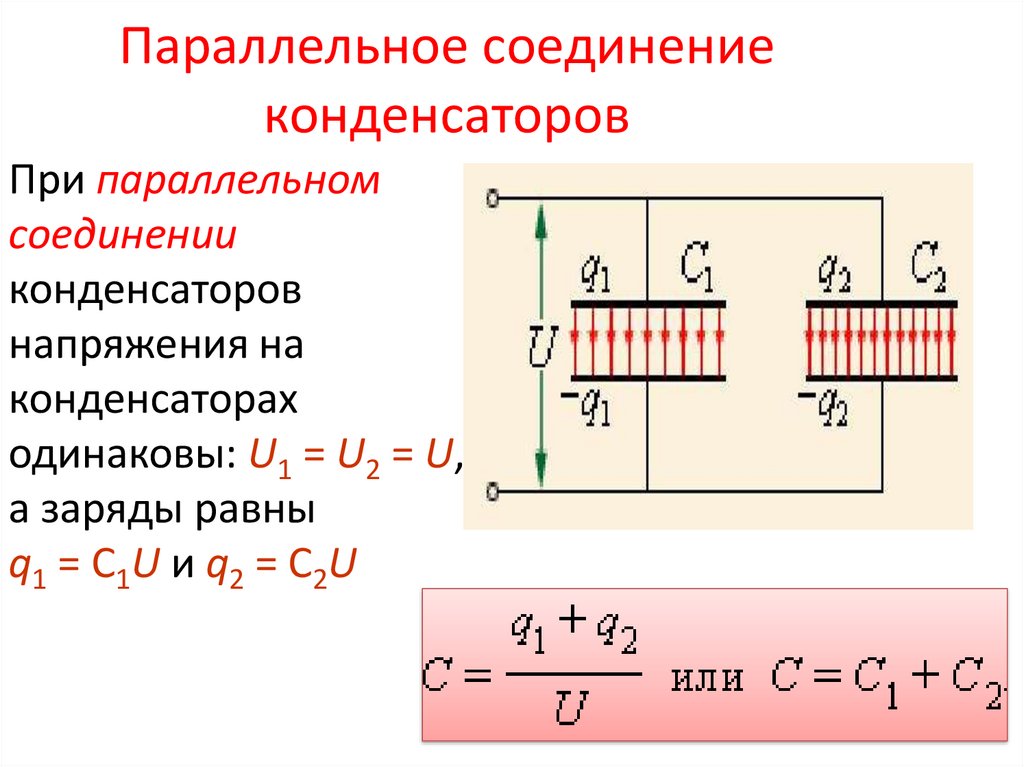 Если на него подать напряжение (U), то на его проводниках накопится электрический заряд(Q). Основная его характеристика – ёмкость (C). Свойства конденсатора описываются уравнением Q = UC , заряд на обкладках и напряжение прямо пропорциональны друг другу.

Условное обозначение конденсатора на схеме

Пусть на конденсатор подается переменное напряжение. Он заряжается по мере роста напряжения, электрический заряд на обкладках увеличивается. Если напряжение уменьшается, то уменьшается и заряд на его обкладках и он разряжается.

Отсюда следует, что по проводам, соединяющим конденсатор с остальной цепью, электрический ток протекает тогда, когда напряжение на конденсаторе изменяется. При этом не важно, что происходит в диэлектрике между проводниками. Сила тока равна общему заряду, протекшему в единицу времени по подключенному к конденсатору проводу. Она зависит от его емкости и скорости изменения питающего напряжения.

Ёмкость зависит от характеристик изоляции, а также размеров и формы проводника. Единица измерения ёмкости кондёра — фарада (Ф), 1 Ф=1 Кл/В. Однако на практике емкость измеряется чаще в микро- (10-6) или пико- (10-12) фарадах.

В основном используются конденсаторы для построения цепей с частотной зависимостью, для получения мощного короткого электрического импульса, там, где необходимо накапливать энергию. За счёт изменения свойств пространства между обкладками можно использовать их для измерения уровня жидкости.

Параллельное соединение

Параллельное соединение – это соединение, при котором выводы всех конденсаторов имеют две общие точки – назовём их входом и выходом схемы. Так все входы объединены в одной точке, а все выходы – в другой, напряжения на всех конденсаторах равны:

Параллельное соединение предполагает распределение полученного от источника заряда на обкладках нескольких конденсаторов, что можно записать так:

Так как напряжение на всех конденсаторах одинаковое, заряды на их обкладках зависят только от ёмкости:

Суммарная емкость параллельной группы конденсаторов:

Суммарная ёмкость такой группы конденсаторов равна сумме емкостей включенных в схему.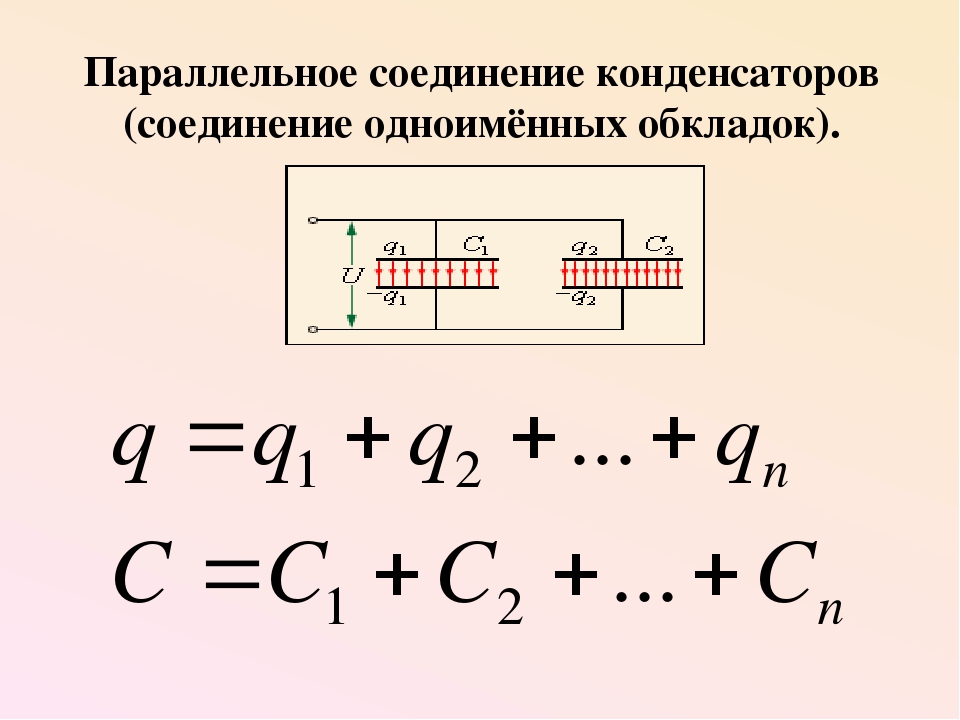

Блоки конденсаторов широко используются для повышения мощности и устойчивости работы энергосистем в линиях электропередач. При этом затраты на более мощные элементы линий можно снизить. Повышается стабильность работы ЛЭП, устойчивость ЛЭП к сбоям и перегрузкам.

Последовательное соединение

Последовательное соединение конденсаторов – это их подключение непосредственно друг за другом без разветвлений проводника. От источника напряжения заряды поступают на обкладки первого и последнего в цепи конденсаторов.

В силу электростатической индукции на внутренних обкладках смежных конденсаторов происходит выравнивание заряда на электрически соединённых обкладках смежных конденсаторов, поэтому на них появляются равные по величине и обратные по знаку электрические заряды.

При таком соединении электрические заряды на обкладках отдельных кондёров по величине равны:

Общее напряжение для всей цепи:

Очевидно, что напряжение между проводниками для каждого конденсатора зависит от накопленного заряда и ёмкости, т.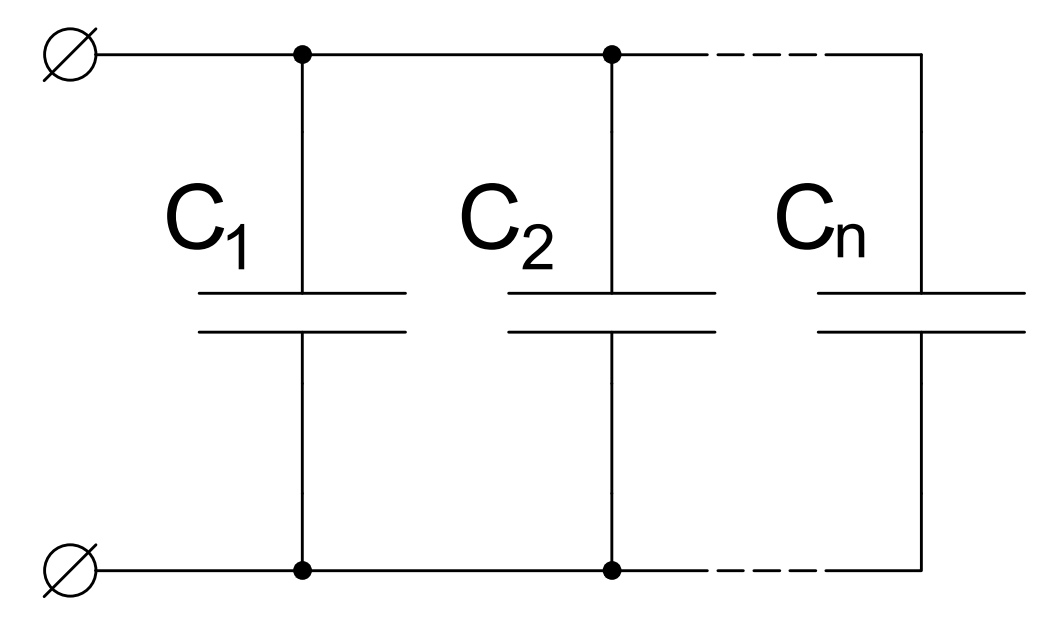 е.:

Поэтому эквивалентная ёмкость последовательной цепи равна:

Отсюда следует, что величина, обратная общей емкости, равна сумме величин, обратных емкостям отдельных конденсаторов:

Смешанное соединение

Смешанным соединение конденсаторов называют такое соединение, при котором присутствует соединение последовательное и параллельное одновременно. Чтобы более подробно разобраться, давайте рассмотрим это соединение на примере:

На рисунке видно,что соединены два конденсатора последовательно вверху и внизу и два параллельно. Можно вывести формулу из выше описанных соединении:

Основой любой радиотехники является конденсатор, он используется в самых разнообразных схемах-это и источники питания и применение для аналоговых сигналов хранения данных, а также в телекоммуникационных связи для регулирования частоты.

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим.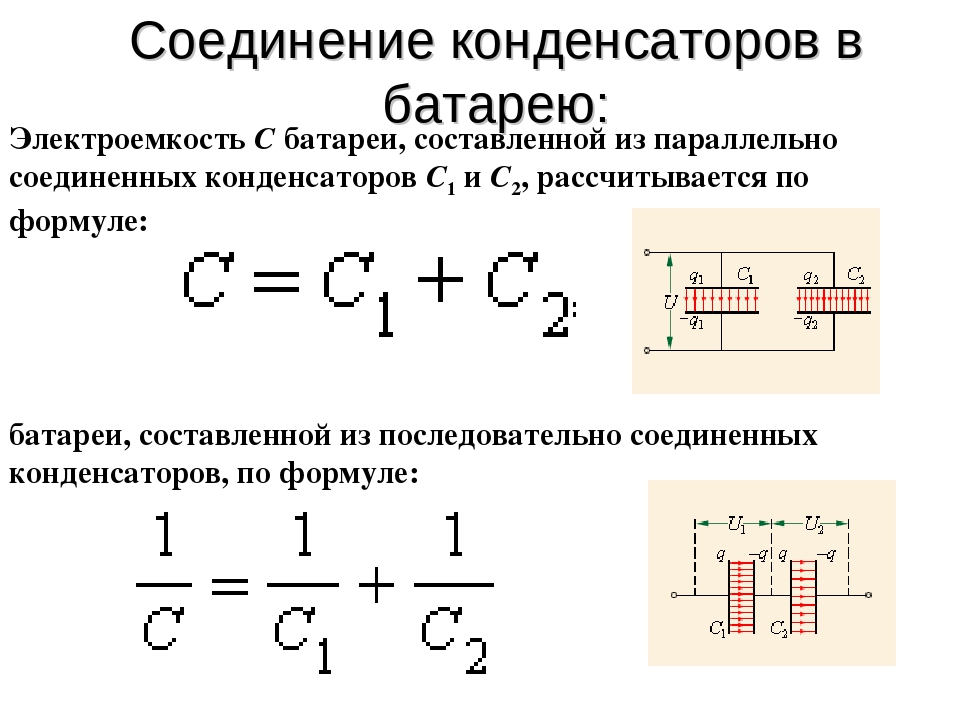 Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное .

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение.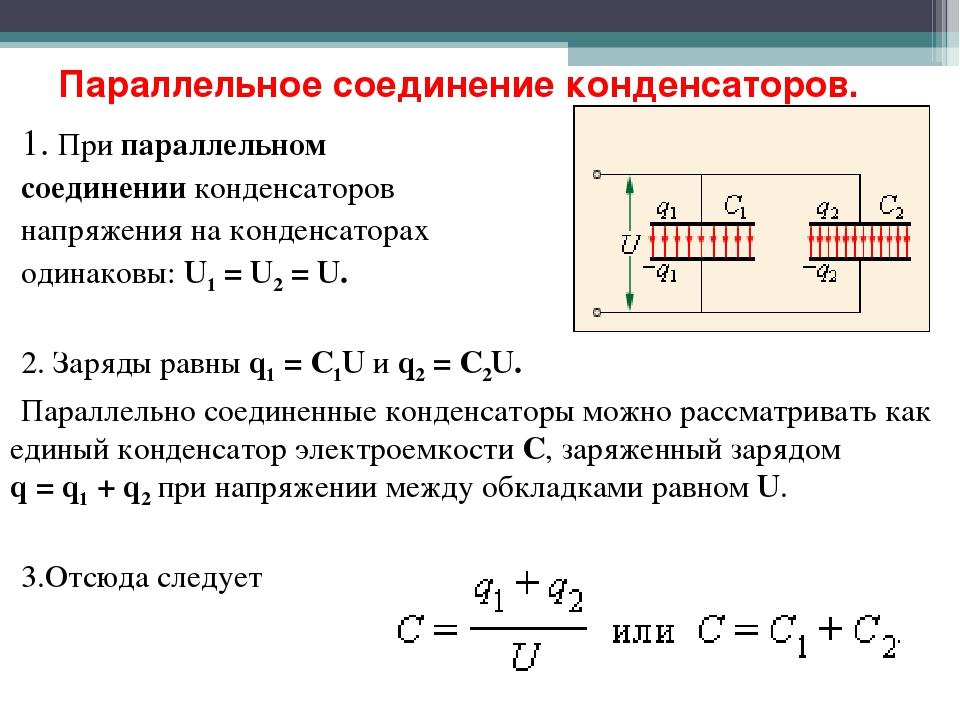 Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С 1 – ёмкость первого;

С 2 – ёмкость второго;

С 3 – ёмкость третьего;

С N – ёмкость N -ого конденсатора;

C общ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C 1 , C 2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте .

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C 1 – его ёмкость.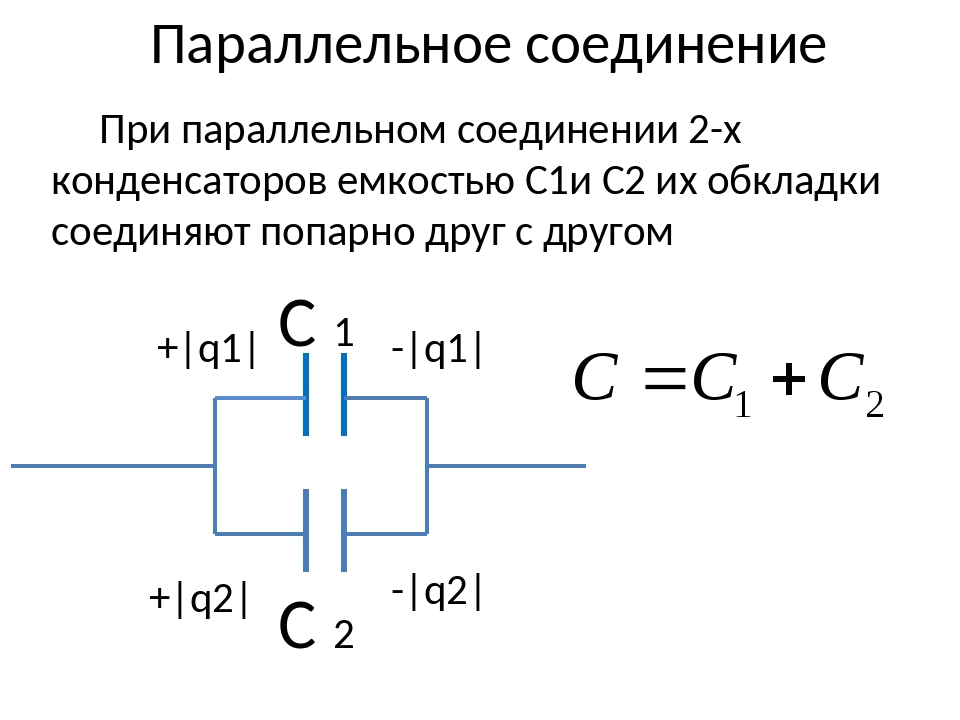

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор , замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

Последовательное соединение электролитов

Схема последовательного соединения

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены:)

Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!

Под последовательным соединением подразумевают случаи, когда два или больше элемента имеют вид цепи, при этом каждый из них соединяется с другим только в одной точке.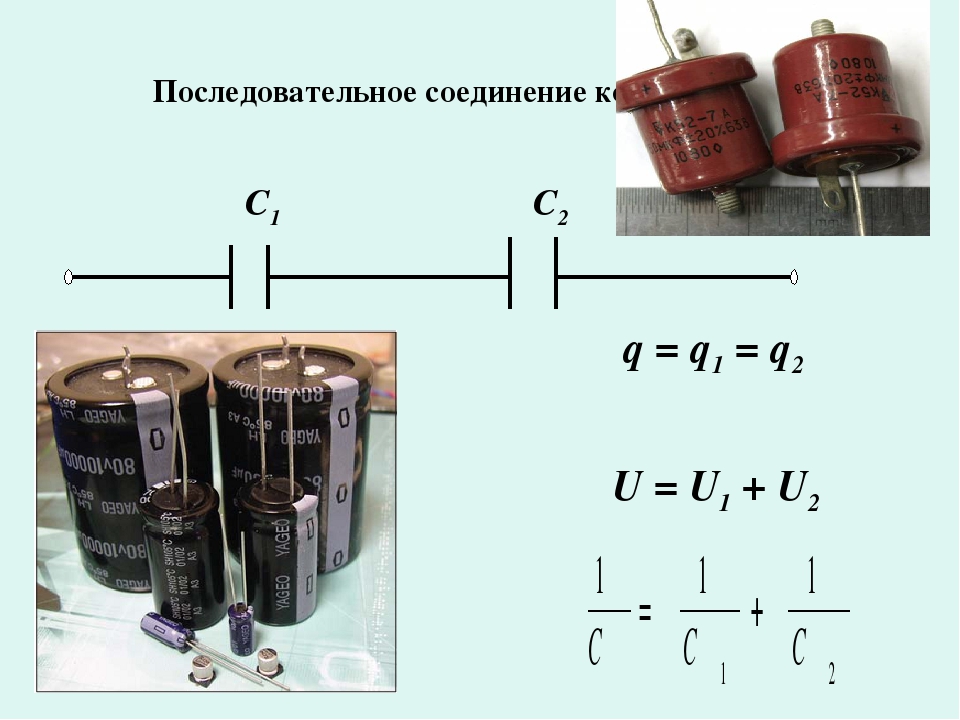 Зачем конденсаторы так размещаются? Как это правильно сделать? Что необходимо знать? Какие особенности последовательное соединение конденсаторов имеет на практике? Какая формула результата?

Что необходимо знать для правильного соединения?

Увы, но здесь не всё так легко сделать, как может показаться. Многие новички думают, что если на схематическом рисунке написано, что необходим элемент на 49 микрофарад, то достаточно его просто взять и установить (или заменить равнозначным). Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно. Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим. Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет.

Зачем так делают?

Когда с ними проводятся такие манипуляции, то электрические заряды на обкладках отдельных элементов будут равны: КЕ=К 1 =К 2 =К 3 . КЕ — конечная емкость, К — пропускаемое значение конденсатора. Почему так? Когда заряды поступают от источника питания на внешние обкладки, то на внутренних может быть осуществлен перенос величины, которая является значением элемента с наименьшими параметрами. То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ — то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ. Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула:

• ОЕ — общая емкость;
• Н — напряжение;
• КЕ — конечная емкость.

Что ещё необходимо знать, чтобы правильно соединить конденсаторы?

Для начала не забывайте, что кроме ёмкости они ещё обладают номинальным напряжением.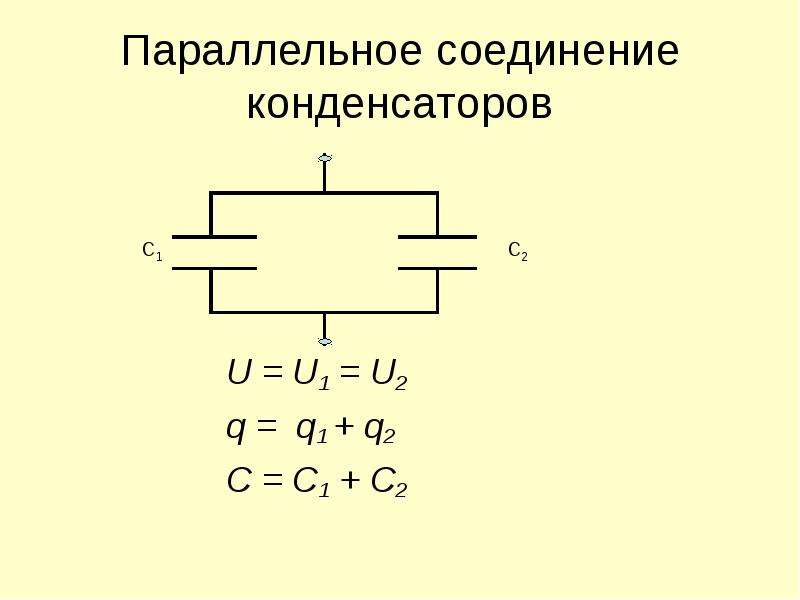 Почему? Когда осуществляется последовательное соединение, то напряжение распределяется обратно пропорционально их ёмкостям между ними самими. Поэтому использовать такой подход имеет смысл только в тех случаях, когда любой конденсатор сможет предоставить минимально необходимые параметры работы. Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну. Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов. Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы.

Ток при последовательном соединении

Из-за того, что у него существует только один возможный путь протекания, он будет иметь одно значение для всех конденсаторов.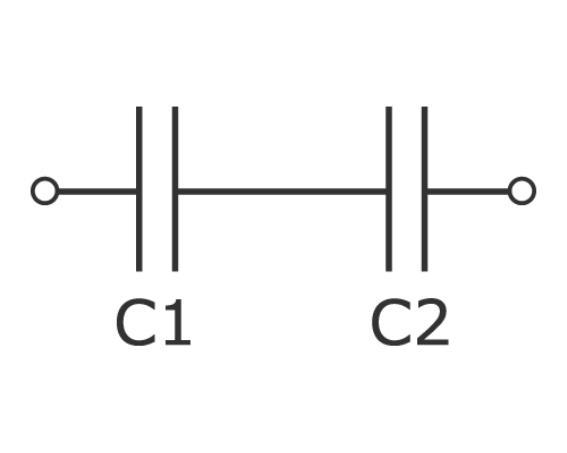 При этом количество накопленного заряда везде обладает одинаковым значением. От емкости это не зависит. Посмотрите на любую схему последовательного соединения конденсаторов. Правая обкладка первого соединена с левой второго и так далее. Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи. Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток. И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться.

Падение напряженности и общая емкость

Каждый элемент понемногу рассеивает напряжение. Учитывая, что емкость ему обратно пропорциональна, то чем она меньше, тем большим будет падение. Как уже упоминалось ранее, последовательно соединённые конденсаторы обладают одинаковым электрическим зарядом. Поэтому при делении всех выражений на общее значение можно получить уравнение, которое покажет всю емкость. В этом последовательное и параллельное соединение конденсаторов сильно разнятся.

Пример № 1

Давайте воспользуемся представленными в статье формулами и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300. Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ.

Пример № 2

Давайте, чтобы закрепить наработки, решим ещё одну задачу. Имеется 100 конденсаторов. Емкость каждого элемента составляет 2 мкФ. Необходимо определить их общую емкость. Нужно их количество умножить на характеристику: 100*2=200 мкФ. Итак, общая емкость конденсатора при последовательном соединении составляет 200 микрофарад. Как видите, ничего сложного.

Заключение

Итак, мы проработали теоретические аспекты, разобрали формулы и особенности правильного соединения конденсаторов (последовательно) и даже решили несколько задачек. Хочется напомнить, чтобы читатели не упускали из внимания влияние номинального напряжения. Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект.

Параллельное соединение конденсаторов формула — Стройпортал Biokamin-Doma.ru

Соединение конденсаторов

Как правильно соединять конденсаторы?

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.

В реальности это выглядит так:

Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С₁ – ёмкость первого;

С₂ – ёмкость второго;

С₃ – ёмкость третьего;

С_N – ёмкость N-ого конденсатора;

C_общ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C₁, C₂ в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается

.

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C₁ – его ёмкость.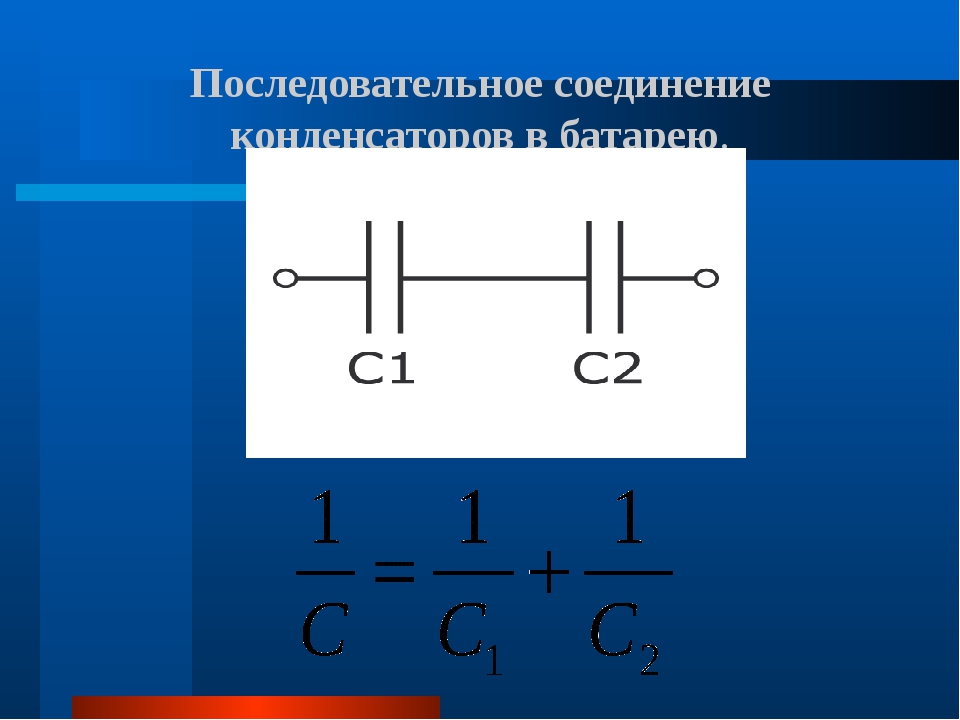

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см.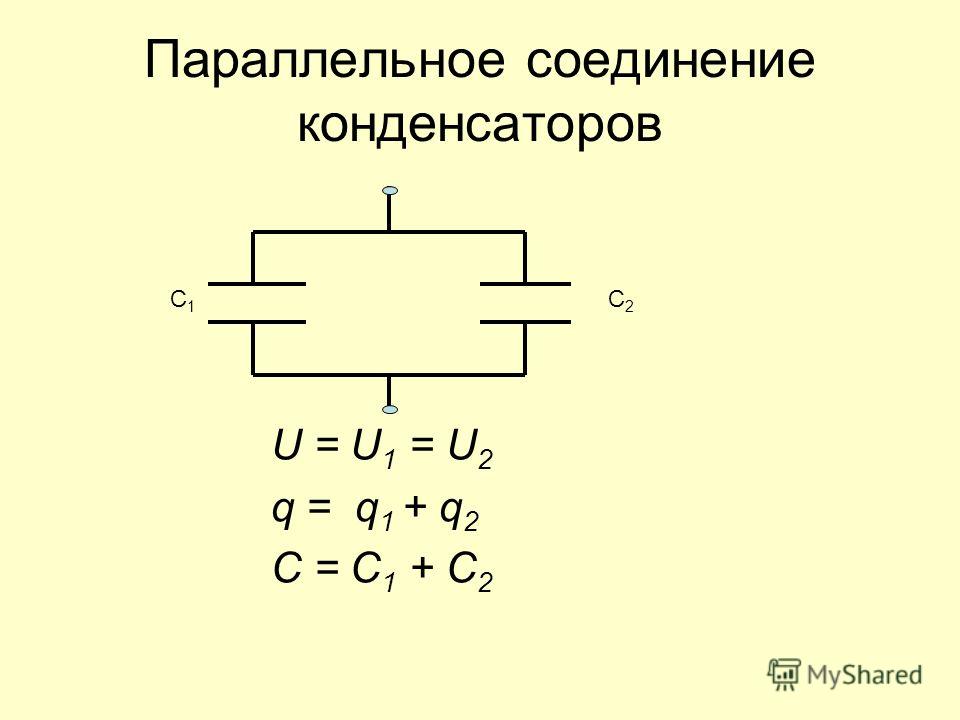 фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.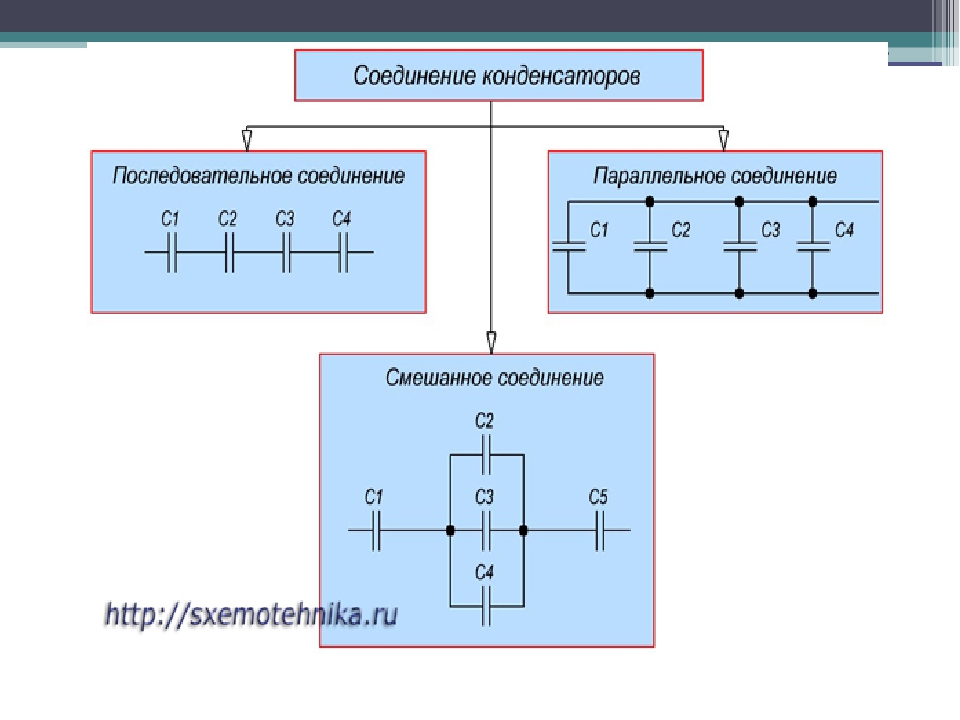

Параллельное соединение электролитов
Схема параллельного соединения

В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитов
Схема последовательного соединения

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел

). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂

Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!

Последовательное и параллельное соединение конденсаторов

Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.

Последовательное соединение конденсаторов

При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

Напряжение на данном участке цепи соотносятся следующим образом:

Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

Сократив выражение на Q, получим знакомую формулу:

Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

Параллельное соединение конденсаторов

При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

Так как заряд конденсатора

А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов

Пример 1

Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С₁ = 10 мкФ, C₂ = 2 мкФ, C₃ = 5 мкФ, а C₄ = 1 мкФ?

При последовательном соединении общая емкость равна:

При параллельном соединении общая емкость равна:

Пример 2

Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С₁ = 7 мкФ, С₂ = 2 мкФ, С₃ = 1 мкФ.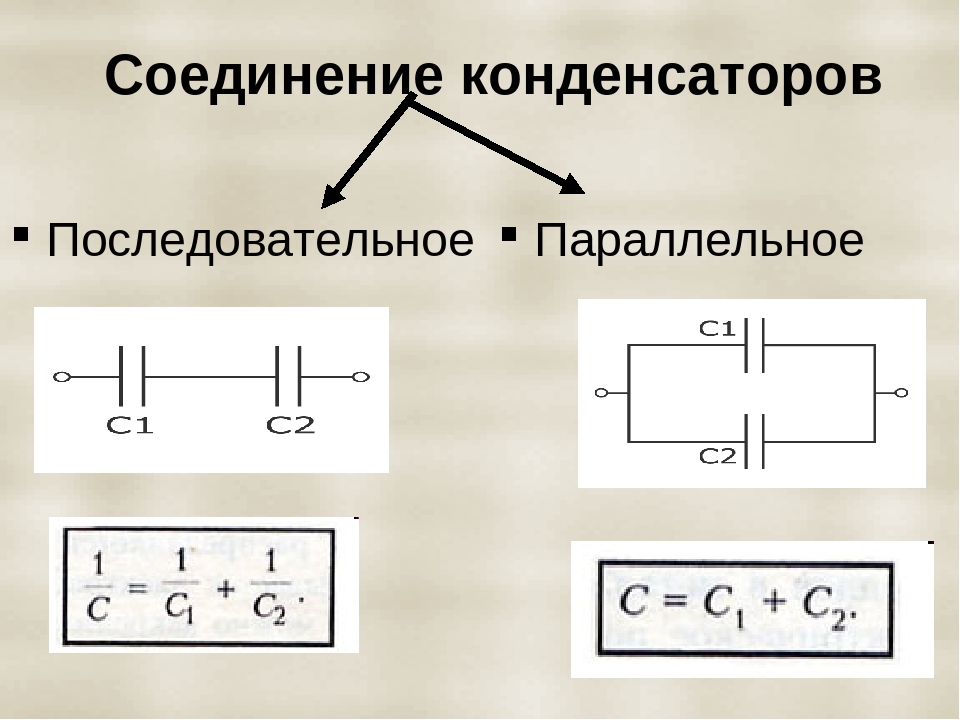

Сначала найдем общую емкость параллельного участка цепи:

Затем найдем общую емкость для всей цепи:

По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.

Способы подключения конденсаторов в электрическую цепь

Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей. Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.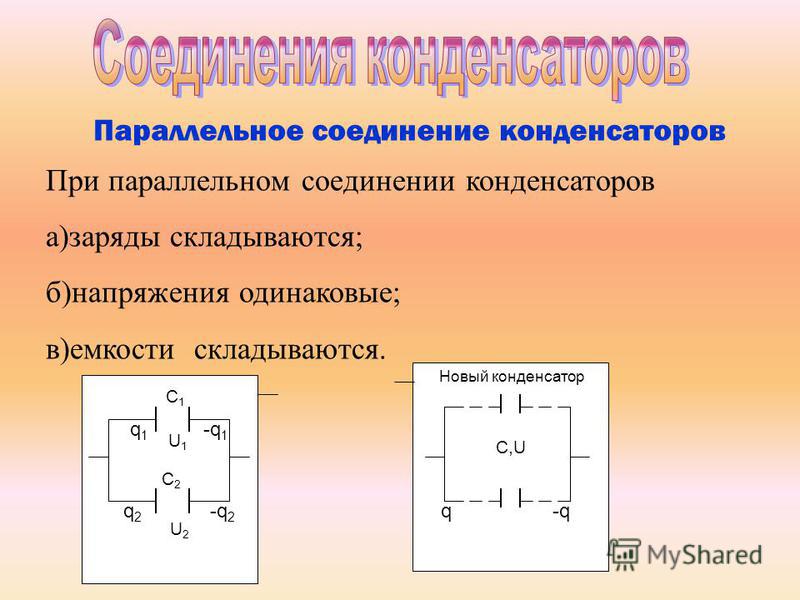

Параллельное включение конденсаторов в цепь

Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.

Параллельное соединение конденсаторов:

Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.

Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.

При параллельном соединении конденсаторов емкость равняется:

Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.

Конденсаторы, соединенные параллельно, имеют напряжение:

Последовательное включение конденсаторов в цепь

Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.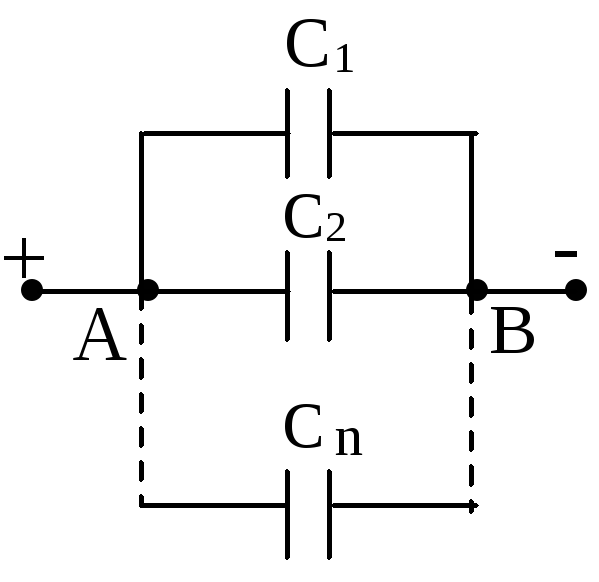

Последовательное соединение конденсатора:

При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния. По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.

Формула нахождения заряда на конденсаторе, схема подключения конденсатора:

Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости. Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.

Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.

Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:

Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:

Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:

Смешанное включение емкостных накопителей в схему

Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.

Участок цепи подсоединенных смешанным включением накопителей емкости:

Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:

• разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
• вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
• проводим нахождение эквивалентной емкости на параллельном участке;
• когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
• рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.

Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:

1. Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.
2. Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
3. Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.

Вывод

Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников. В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.

Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.

Соединение конденсаторов

В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.

Рисунок 1. Способы соединения конденсаторов.

Параллельное соединение конденсаторов.

Если группа конденсаторов включена в цепь таким обра­зом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).

Рисунок 2. Параллельное соединение конденсаторов.

При заряде группы конденсаторов, соединенных параллель­но, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количе­ство электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из кон­денсаторов, так как заряд каждого их конденсаторов проис­ходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединен­ных конденсаторов можно рассматривать как один эквива­лентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.

Обозначим суммарную емкость соединенных в батарею конденсаторов бук­вой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:

Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и во­обще при любом числе конденсаторов.

Последовательное соединение конденсаторов.

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последо­вательным (рисунок 3).

Рисунок 2. Последовательное соединение конденсаторов.

При последовательном соединении все конденса­торы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заря­жаются через влияние. При этом заряд пла­стины 2 будет равен по величине и противо­положен по знаку за­ряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пла­стины 2 и т. д.

Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.

Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.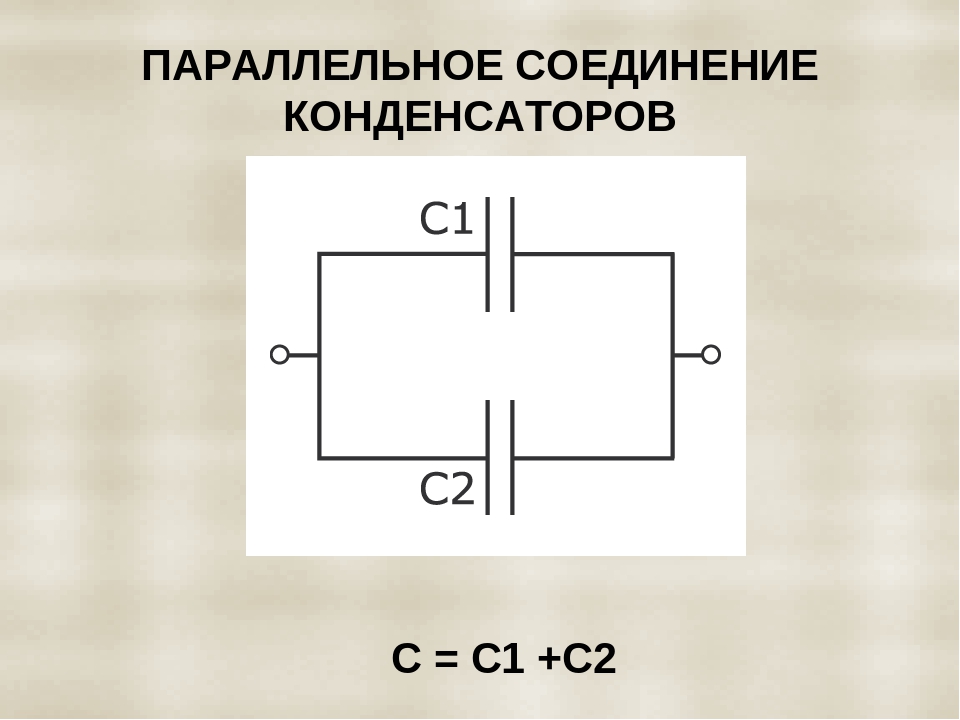

Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.

Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряже­ния, существующего на всей группе конденсаторов. Напря­жение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединен­ных последовательно, меньше емкости самого малого конден­сатора в группе.

Для вычисления общей емкости при последовательном со­единении конденсаторов удобнее всего пользоваться следую­щей формулой:

Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:

Последовательно-параллельное (смешанное) соединение конденсаторов

Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.

На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.

Рисунок 4. Последовательно-параллельное соединение конденсаторов.

При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:

1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.

Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.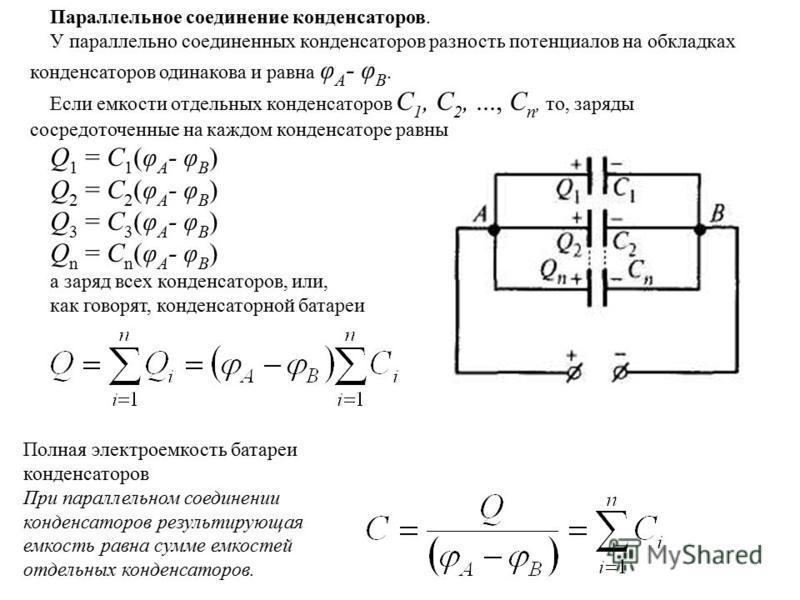

Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Соединение конденсаторов: руководство для начинающих

В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.

Параллельное соединение

Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии

Схема параллельного крепления

Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.

Схема — напряжение на накопителях

В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:

Последовательное соединение

Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.

Схема — схема последовательного соединения

Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.

Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:

i = i_c1 = i_c2 = i_c3 = i_c4, то есть токи проходящие через каждый конденсатор равны между собой.

Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:

А так определяется общая суммарная емкость конденсаторов при последовательном соединении:

Видео: как соединять конденсаторы параллельным и последовательным методом

Смешанное подключение

Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.

Схема: смешанное соединение конденсаторов

Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:

1. Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
2. Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
3. Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока. Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
4. Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.

Последовательное и параллельное соединение конденсаторов

Все наверняка уже знают, что собой представляют последовательное и параллельное соединения.
Соединение, при котором конец одного устройства соединен с началом следующего, называется последовательным.

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов, получаемая цепь выглядит следующим образом:

Эта схема состоит из следующих элементов: трех конденсаторов C1 , C2 , С3 и источника электрической энергии E .

Мы видим, что конденсаторы подключены по всем правилам последовательного соединения, то есть вывод конденсатора C1 соединён с началом конденсатора C2 , ну а конец конденсатора C2 соединен с началом третьего конденсатора C3 .
Стоит обратить внимание на то, как распределяются ёмкости каждого.

При таком соединении, все ёмкостя следующим образом.

Дело в том, что общая емкость всех включенных конденсаторов не будит превышать емкости любого из конденсаторов. Проще говоря, если в данной группе конденсаторов, будит конденсатор с наименьшей емкостью, например, в 100 миро фарад, то общая емкость трех конденсаторов не будит превышать этих ста микрофарад.
Общую емкость можно рассчитать по следующей формуле:

Если в цепи имеются всего лишь два последовательно соединенных конденсатора, то общая емкость определяется по формуле:

Параллельное соединение конденсаторов

При параллельном соединении, начала всех конденсаторов соединяются в одну точку, а концы в другую, как показано на рисунке ниже:

Так при параллельном соединении, емкости всех конденсаторов складываются:

То есть, емкость каждого конденсатора, включенного параллельно суммируется и получается одна большая емкость, которую можно на схеме представить одним конденсатором.

Это как два пишем один в уме, только в данном случаи один рисуем, а три в уме.

Смешанное соединение конденсаторов

Смешанное соединение конденсаторов выглядит следующим образом:

И представляет с собой различные сочетания параллельного и последовательного соединений.
Для вычисления общей емкости таких соединений, применяют метод замещения: все конденсаторы делят на последовательно и параллельно соединенные группы, рассчитывают ёмкость каждой группы в отдельности, так что в конце выйдет две параллельных или последовательных емкостей, которые можно без труда посчитать.
Например, дана следующая схема и следующие данные:
C1=0.4Ф
C2=0.8Ф
C3=0,73Ф
Необходимо найти общую емкость всех трех конденсаторов.
Как мы видим конденсаторы C1 и C2 соединены последовательно, а конденсатор C3 по отношению к первым двум параллельно.
Посчитав общую емкость последовательно соединенных конденсаторов C1 и C2, их можно представить, как один конденсатор C1,2.

Теперь нам не составит труда посчитать емкость двух параллельно соединенных конденсаторов, просто сложив их ёмкости.

Применения параллельного и последовательного соединений конденсаторов нашло свое применение в тех случаях, когда необходимо получить ту или иную величину емкости. Допустим у вас нет подходящего конденсатора, но есть куча других. Выполнив несколько не хитрых расчетов можно подобрать необходимую емкость.

проверенный способ соединения, формула, типы подключений

Если нужно срочно отремонтировать технику, а нужного конденсатора нет, то можно увеличить емкость конденсатора, как известно из школьной программы, соединив несколько приборов в одну цепь.

Такая проблема может также возникнуть, если, например, нужного номинала нет в продаже, то есть для нестандартных подключений, например, в радиотехнических опытах.

Электрическая емкость

При соединении приборов для конденсации заряда, как правило, техника интересует электрическая емкость, которая получится в итоге.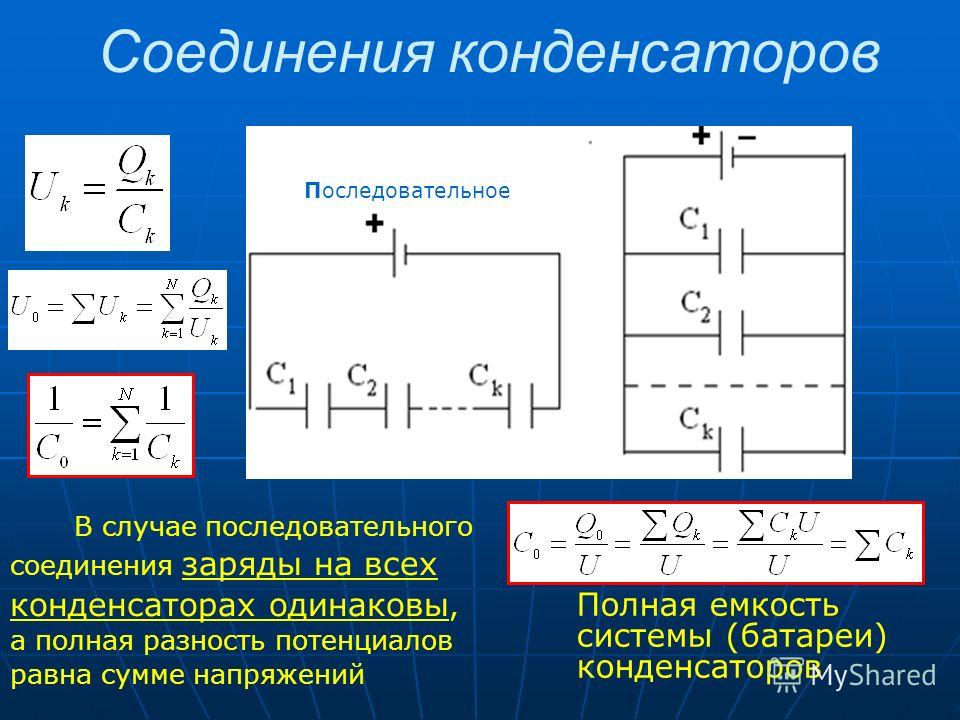

Электроемкость показывает способность двухполюсника накапливать в себе заряд и измеряется в фарадах. Может показаться, что чем выше это значение, тем лучше, но на практике не существует возможности создать все возможные на свете емкости, более того, часто это и не нужно, так как во всех приборах, использующихся повседневно, применяются стандартные приборы для конденсации.

Можно соединить несколько приборов для конденсации в цепь, создав одну конденсирующую емкость, при этом значение характерной величины будет зависеть от типа подключения, и для его расчета есть давно известные формулы.

Параллельное соединение

Существует два типа подключения приборов в цепь: последовательное и параллельное. Каждый из них обладает своими свойствами, но, как правило, используется параллельное соединение конденсаторов.

Параллельное соединение обладает такими свойствами:

1. Емкость составного двухполюсника увеличивается по сравнению с каждым отдельным прибором.
2. Напряжение в сети не изменяется.

Соединить конденсаторы для увеличения емкости, как показывают свойства, лучше этим способом. Для этого нужно соединить выводы с каждого двухполюсника по группам: у каждого из них два вывода. Нужно создать две группы: в одну соединить все конденсаторы с одного вывода, а во вторую с оставшегося.

При таком соединении приборы для конденсации образуют одну емкость, поэтому верна такая формула: С=С1+С2+…СN, где N — количество конденсаторов в цепи.

Например, если имеются номинальные значения 50мкф, 100мкф и 150мкф, то при последовательном подключении общее значение в цепи будет 300мкф.

В жизни это подключение используют довольно часто, например, если при расчетах оказалось, что требуется такой двухполюсник, которого в продаже точно не найти. С помощью этого способа можно варьировать емкость конденсатора так, как это потребуется, при этом не изменяя напряжение в сети.

Последовательное включение конденсаторов

Свойства последовательного включения конденсаторов:

1. Емкость последовательно соединенных приборов для конденсации заряда в отличие от емкости параллельно соединенных конденсаторов уменьшается.
2. Напряжение на приборах растет.

Для такого подключения нужно просто соединять выводы двухполюсников один с другим, образуя цепочку: вывод первого будет соединен с выводом второго, оставшийся вывод второго с выводом третьего и так далее.

Формула подключения: 1/(1/С1+1/С2+…+1/СN), где N — это количество приборов в соединении.

Например, есть три конденсатора по 100мкф. 1/100+1/100+1/100=0,03мкф. 1/0,03=33мкф.

Заряды распределятся с чередующимся знаком, а емкостное значение будет ограничено только им же для самого слабого звена в цепи. Как только он получит свой заряд, передача тока в цепи прекратится.

Для чего тогда нужен подобный способ подключения? Такая цепь более устойчива и может выдержать большее напряжение при подключении в схему при меньшем емкостном номинале конденсатора. Однако в продаже имеются приборы, которые и без того обладают нужными свойствами, поэтому-то такое подключение в жизни практически не используется, а если используется, то для специфических задач.

Смешанный способ

Сочетает в себе параллельное и последовательное подключения.

При этом для участков с последовательным соединением характерны свойства последовательного соединения, а для участков с параллельным — свойства параллельного.

Оно используется, когда ни электроемкость, ни номинальное напряжение приборов, имеющихся в продаже, не подходят для задачи. Обычно такая проблема возникает в радиотехнике.

Чтобы определить общее значение электроемкости, нужно будет сначала определить это же значение для параллельно соединенных двухполюсников, а потом для их последовательного соединения.

Сравнение различных вариантов

	Емкость	Напряжение
Параллельное	Увеличивается	Не изменяется
Последовательное	Уменьшается	Увеличивается
Смешанное	Изменяется	Увеличивается

Для выбора соединения можно воспользоваться такой таблицей. Слева тип соединения приборов, сверху свойства прибора для конденсации заряда.

Если требуется увеличить емкость, то нужно использовать параллельное соединение, а если увеличить напряжение — то последовательное. Если же требуется и то, и то, то нужно будет рассчитывать смешанное подключение конденсаторов в цепь.

Схемные соединения в конденсаторах — CoderLessons.com

В цепи конденсатор может быть подключен последовательно или параллельно. Если набор конденсаторов был подключен в цепи, тип подключения конденсатора имеет дело со значениями напряжения и тока в этой сети.

Конденсаторы в серии

Давайте посмотрим, что происходит, когда несколько конденсаторов подключены последовательно. Рассмотрим три конденсатора с разными значениями, как показано на рисунке ниже.

емкость

Когда рассматривается емкость сети, чьи конденсаторы включены последовательно, обратная величина емкостей всех конденсаторов добавляется для получения обратной величины общей емкости. Чтобы получить это более ясно,

 гидроразрыва1CT= гидроразрыва1C1 + гидроразрыва1C2 + гидроразрыва1C3

Следуя той же формуле, если просто два конденсатора соединены последовательно, то

CT,= гидроразрываC1 разC2C1 + :C2

Где C ₁ — емкость на 1- ^м конденсаторе, C ₂ — емкость на 2- ^м конденсаторе, а C ₃ — емкость на 3- ^м конденсаторе в вышеупомянутой сети.

вольтаж

Напряжение на каждом конденсаторе зависит от значения отдельных емкостей. Что значит

VС1= гидроразрываQTC1VС2= гидроразрываQTC2VС3= гидроразрываQTC3

Общее напряжение на цепи последовательных конденсаторов,

VT,=VС1 +VС2 +VС3

Где V _c1 — это напряжение на 1- ^м конденсаторе, V _c2 — это напряжение на 2- ^м конденсаторе, а V _c3 — это напряжение на 3- ^м конденсаторе в вышеуказанной сети.

Текущий

Общее количество тока, протекающего через набор конденсаторов, соединенных последовательно, одинаково во всех точках. Поэтому конденсаторы будут хранить одинаковое количество заряда независимо от значения их емкости.

Тока через сеть,

I=I1=I2=I3

Где I ₁ — ток через 1- ^й конденсатор, I ₂ — ток через 2- ^й конденсатор, а I ₃ — ток через 3- ^й конденсатор в вышеуказанной сети.

Поскольку ток одинаков, накопление заряда одинаково, поскольку любая пластина конденсатора получает свой заряд от соседнего конденсатора, и, следовательно, конденсаторы, соединенные последовательно, будут иметь одинаковый заряд.

QT,=Q1=Q2=Q3

Конденсаторы параллельно

Давайте посмотрим, что происходит, когда несколько конденсаторов подключены параллельно. Рассмотрим три конденсатора с разными значениями, как показано на рисунке ниже.

емкость

Общая Емкость цепи эквивалентна сумме отдельных емкостей конденсаторов в сети.

CT,=C1 +C2 +C3

Где C ₁ — емкость на 1- ^м конденсаторе, C ₂ — емкость на 2- ^м конденсаторе, а C ₃ — емкость на 3- ^м конденсаторе в вышеупомянутой сети.

вольтаж

Напряжение, измеренное в конце цепи, совпадает с напряжением на всех конденсаторах, соединенных в параллельную цепь.

VT,=V1=V2=V3

Где V _c1 — это напряжение на 1- ^м конденсаторе, V _c2 — это напряжение на 2- ^м конденсаторе, а V _c3 — это напряжение на 3- ^м конденсаторе в вышеуказанной сети.

Текущий

Общий протекающий ток равен сумме токов, протекающих через каждый конденсатор, подключенный к параллельной сети.

IT,=I1 +I2 +I3

Где I ₁ — ток через 1- ^й конденсатор, I ₂ — ток через 2- ^й конденсатор, а I ₃ — ток через 3- ^й конденсатор в вышеуказанной сети.

Параллельное включение конденсаторов. Соединение конденсаторов Как правильно соединять конденсаторы

В электрических цепях применяются различные способы соединения конденсаторов . Соединение конденсаторов может производиться: последовательно , параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.

Рисунок 1. Способы соединения конденсаторов.

Параллельное соединение конденсаторов.

Если группа конденсаторов включена в цепь таким обра­зом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2. ).

Рисунок 2. Параллельное соединение конденсаторов.

При заряде группы конденсаторов, соединенных параллель­но, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количе­ство электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из кон­денсаторов, так как заряд каждого их конденсаторов проис­ходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединен­ных конденсаторов можно рассматривать как один эквива­лентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.

Обозначим суммарную емкость соединенных в батарею конденсаторов бук­вой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:

Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и во­обще при любом числе конденсаторов.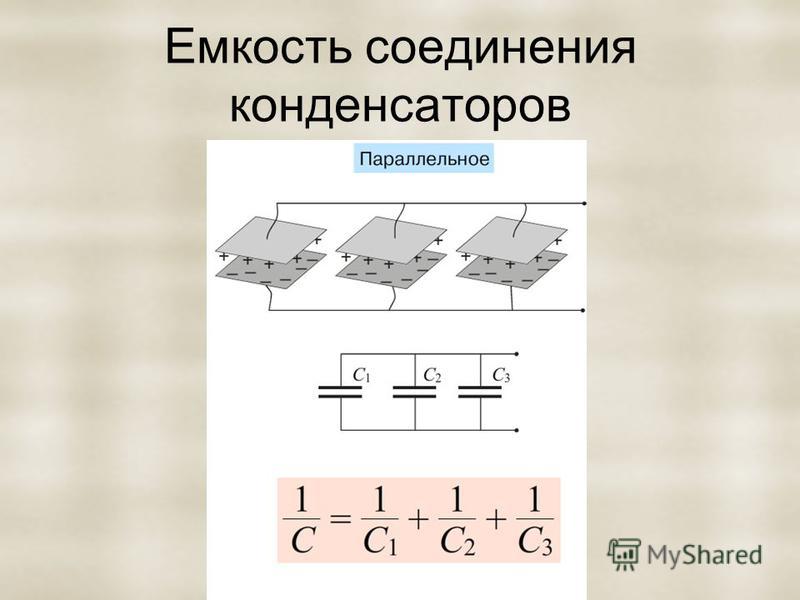

Последовательное соединение конденсаторов.

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последо­вательным (рисунок 3).

Рисунок 2. Последовательное соединение конденсаторов.

При последовательном соединении все конденса­торы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заря­жаются через влияние. При этом заряд пла­стины 2 будет равен по величине и противо­положен по знаку за­ряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пла­стины 2 и т. д.

Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.

Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.

Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.

Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряже­ния, существующего на всей группе конденсаторов. Напря­жение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединен­ных последовательно, меньше емкости самого малого конден­сатора в группе.

Для вычисления общей емкости при последовательном со­единении конденсаторов удобнее всего пользоваться следую­щей формулой:

Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:

Последовательно-параллельное (смешанное) соединение конденсаторов

Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.

На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.

Рисунок 4. Последовательно-параллельное соединение конденсаторов.

При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:

1.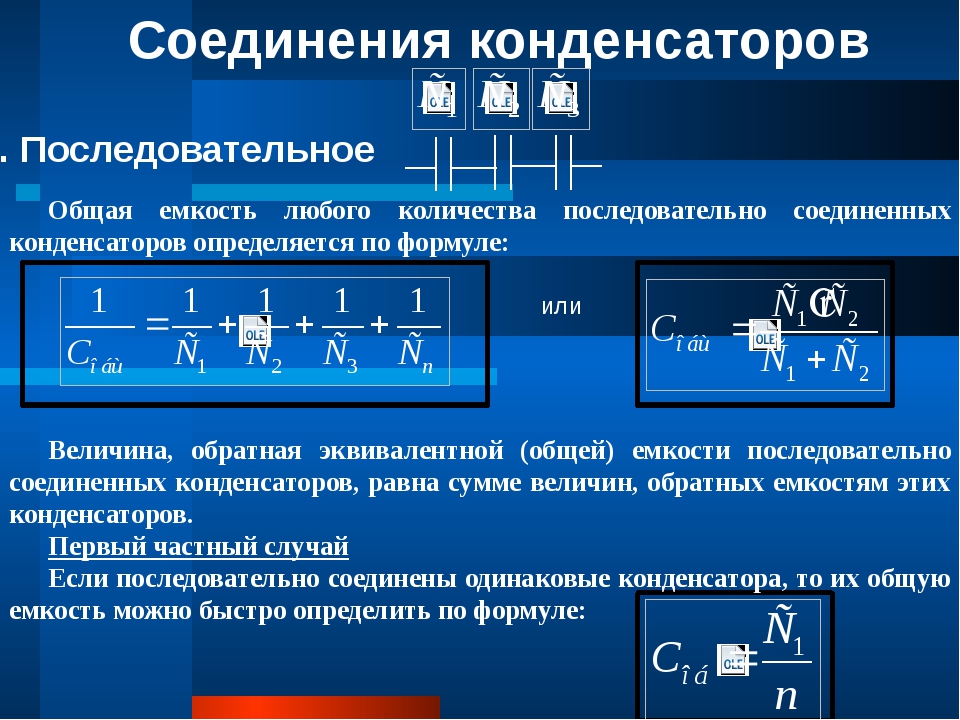 Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.

Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.

У начинающих электронщиков при сборке любого самодельного устройства могут возникнуть проблемы с соединением конденсатора. Ведь даже у заядлого любителя электроники может не оказаться под рукой конденсатора с нужным номиналом, особенно когда нужно срочно отремонтировать бытовой прибор. Из сложившейся проблемы легко выйти, соединив последовательно или параллельно несколько конденсаторов.

Приготовьте:

• конденсаторы;
• вольтметр;
• провода;
• кусачки.

Если последовательно соединяются два конденсатора с равными емкостями, то в результате получится общая емкость с меньшим значением в 2 раза, а напряжение — увеличится. В реальных случаях схемы с последовательным соединением встречается редко, в основном в высоковольтных источниках питания. Для низковольтных источников питания применяется параллельное соединение, так как при этом сглаживается пульсация. Общая емкость соединенных параллельно конденсаторов будет складываться, а напряжение — равно значению напряжения того конденсатора, который имеет меньший параметр. Например, имеется три конденсатора по 30 микрофарад с напряженностью 100 В и соединяются параллельно. Значение всего набора будет вычисляться: 90 мкф * 100.

Существует комбинированный способ соединения — последовательно-параллельное, который встречается крайне редко. Для расчета общей емкости цепь разделяют на несколько участков и вычисляют каждую отдельно.

Для соединения электролитических конденсаторов нужно учитывать полярность. При параллельном способе минусовый вывод одного конденсатора должен соединяться с минусовым выводом другого. При последовательном — минус с плюсовым выводом.

При присоединении конденсаторов следует учитывать значение номинального напряжения. Если один из конденсаторов будет с меньшим номинальным напряжением, то, скорее всего, в ближайшее время устройство выйдет из строя.

Соединяйте конденсаторы только тогда, когда они полностью отсоединены от других элементов схемы. Подключение проводят изолированными проводами. После любого соединения и отсоединения проверьте работу с помощью вольтметра.

Для составного конденсатора старайтесь брать однотипные конденсаторы, а если возможно — то с одной партии. Конденсаторы бывают керамические, пленочные, металлобумажные, слюдяные.

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим необходимый конденсатор. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь 2 – 3 конденсатора на 470 микрофарад. Ставить конденсатор на 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров за одним конденсатором?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное .

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение конденсаторов. На практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С 1 – ёмкость первого конденсатора;

С 2 – ёмкость второго конденсатора;

С 3 – ёмкость третьего конденсатора;

С N – ёмкость N -ого конденсатора;

C общ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости конденсаторов нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если рассчитываем ёмкости в микрофарадах, то нужно указывать ёмкость C 1 , C 2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады или нанофарады можно воспользоваться специальной таблицей. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно пересчитать значения величин.

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Для большего количества последовательно включенных конденсаторов потребуется другая формула. Она более запутанная, да и не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении конденсаторов их результирующая ёмкость будет всегда меньше наименьшей ёмкости, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсатор ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость составного конденсатора будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C 1 – ёмкость конденсатора.

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из конденсаторов.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате ёмкость составного конденсатора составит 5 нанофарад.

Проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул для расчёта.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.), другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ с функцией измерения ёмкости конденсаторов и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости последовательно соединённых конденсаторов

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения конденсаторов. Проверим результат с помощью тестера (см. фото).

Измерение ёмкости параллельно соединённых конденсаторов

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединить конденсаторы?

Во-первых, не стоит забывать, что кроме ёмкости у конденсаторов есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально ёмкостям этих конденсаторов. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое должно быть у конденсатора взамен которого мы ставим составной конденсатор.

Если же используются конденсаторы одинаковой ёмкости, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

При соединении электролитических конденсаторов строго соблюдайте полярность! При параллельном соединении электролитических конденсаторов всегда соединяйте минусовой вывод одного конденсатора с минусовым выводом другого. Плюсовой вывод с плюсовым.

Параллельное соединение электролитических конденсаторов

Схема параллельного соединения

В последовательном соединении электролитических конденсаторов ситуация обратная. Необходимо соединять плюсовой вывод с минусовым. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитических конденсаторов

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из этих конденсаторов будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше будет, если они взяты из одной партии.

Конечно, возможно и смешанное (комбинированное) соединение конденсаторов, но в практике оно не применяется (я не видел ). Расчёт ёмкости смешанного соединения конденсаторов обычно достаётся тем, кто решает задачи по физике и сдаёт экзамены:)

Как соединить конденсаторы? Последовательное и параллельное соединение

Вопрос о том, как соединить конденсаторы может возникнуть у любого человека, интересующегося электроникой и пайкой. Чаще всего, необходимость в этом возникает в случаях отсутствия под рукой устройства подходящего номинала при сборке или ремонте какого-либо прибора.

К примеру, человеку нужно отремонтировать устройство, заменив в нем электролитический конденсатор ёмкостью 1000 микрофарад или больше, на руках подходящие по номиналу детали отсутствуют, но есть несколько изделий с меньшими параметрами. В этом случае есть три варианта выхода из сложившейся ситуации:

1. Поставить вместо конденсатора на 1000 микрофарад устройство с меньшим номиналом.
2. Поехать в ближайший магазин или радио-рынок для покупки подходящего варианта.
3. Соединить несколько элементов вместе для получения необходимой ёмкости.

От установки радиоэлемента меньшего номинала лучше отказаться, так как подобные эксперименты не всегда заканчиваются успешно. Можно съездить на рынок или в магазин, но это требует немало времени. Потому в сложившейся ситуации чаще соединяют несколько конденсаторов и получают необходимую емкость.

Параллельное соединение конденсаторов

Параллельная схема подключения конденсаторов предполагает соединение в две группы всех обкладок приборов. В одну группу соединяются первые выводы, а в другую группу – вторые выводы. На рисунке ниже представлен пример.

Конденсаторы, соединенные параллельно между собой, подключаются к одному источнику напряжения, поэтому на них существует две точки напряжения или разности потенциалов. Следует учитывать, что на всех выводах подключенных параллельно конденсаторов напряжение будет иметь одинаковую величину.

Параллельная схема образует из элементов единую ёмкость, величина которой равняется сумме ёмкостей всех подключенных в группу конденсаторов. При этом через конденсаторы в процессе работы устройства будет протекать ток разной величины. Параметры проходящего через изделия тока зависят от индивидуальной ёмкости устройства. Чем выше ёмкость, тем больший по величине ток пройдет через него. Формула, характеризующее параллельное соединение, имеет следующий вид:

Параллельная схема чаще всего используется в быту, она позволяет собрать необходимую ёмкость из любого числа отдельных, различных по номиналу элементов.

Последовательное соединение конденсаторов

Схема последовательного подключения представляет собой цепочку, в которой первая обкладка конденсатора соединяется со второй обкладкой предыдущего устройства, а вторая обкладка – с первой обкладкой следующего прибора. Первый вывод первого конденсатора и второй вывод последней детали в цепи соединяются с источником электрического тока, благодаря чему между ними осуществляется перераспределение электрических зарядов. Все промежуточные обкладки имеют одинаковые по величине заряды, чередующиеся по знаку.

На рисунке ниже представлен пример последовательного подключения.

Через соединенные в группу конденсаторы протекает ток одинаковой величины. Общая мощность ограничивается площадью обкладок устройства с наименьшим номиналом, так как после зарядки наименьшего по ёмкости устройства, вся цепь перестанет пропускать ток.

Несмотря на явные недостатки, данный способ обеспечивает увеличение изоляции между отдельными обкладками до суммы расстояний между выводами на всех последовательно соединенных конденсаторах. То есть, при последовательном соединении двух элементов с рабочим напряжением 200 В, изоляция между их выводами сможет выдерживать напряжение до 1000 В. Ёмкость по формуле:

Данный способ позволяет получить эквивалент меньшего по ёмкости конденсатора в группе, способной работать при высоких напряжениях. Всего этого можно достичь путем покупки одного единственного элемента подходящего номинала, потому на практике последовательные соединения практически не встречаются.

Эта формула актуальна для расчета общей ёмкости цепи последовательно соединенных двух конденсаторов. Для определения общей ёмкости цепи с большим числом приборов необходимо воспользоваться формулой:

Смешанная схема

Пример смешанной схемы подключения представлен ниже.

Чтобы определить общую ёмкость нескольких устройств, всю схему необходимо разделить на имеющиеся группы последовательного и параллельного соединения и рассчитать параметры ёмкости для каждой из них.

На практике данный способ встречаются на различных платах, с которыми приходиться работать радиолюбителям.

Параллельное соединение конденсаторов | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

В условиях массового применения кон­денсаторов невозможно организовать изготов­ление конденсаторов всех возможных зна­чений электроемкости и рабочей разности потенциалов на обкладках. Для получения необходимых параметров стандартные кон­денсаторы определенным образом соединя­ют между собой. На практике применяют параллельное, последовательное и смешан­ное соединение конденсаторов.

Рис. 4.76. Параллельное соединение кон­денсаторов

При параллельном соединении конден­саторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рис. 4.76 изображена схема такого соеди­нения. Каждая группа обкладок имеет оди­наковый потенциал.

Если полученную батарею параллельных конденсаторов зарядить, то между обклад­ками каждого конденсатора будут одина­ковые разности потенциалов

Δφ₁ = Δφ₂ = Δφ₃ = … = Δφ_n.

Общий заряд на пластинах будет равен сумме зарядов каждого конденсатора:

Q = Q₁ + Q₂ + Q₃ + … + Q_n.

Учитывая, что Q = CΔφ, получим

CΔφ = C₁Δφ + C₂Δφ + C₃Δφ + … + C_nΔφ,

или

C = C₁ + C₂ + C₃ + …+ C_n.

Электроемкость батареи параллельно со­единенных конденсаторов равна сумме элект­роемкостей всех конденсаторов.

Рис. 4.78. Строение и схема плоского конденсатора с несколькими пластина­ми

Если батарея состоит из n конденсаторов емкостью Q каждый, то емкость батареи

C = nC₀.

Увеличение емкости при параллельном соединении конденсаторов можно объяс­нить также тем, что при этом увеличивается площадь пластин, которые имеют одина­ковые потенциалы.

Емкость конденсаторов можно увеличить путем их параллельно­го соединения. Материал с сайта http://worldofschool.ru

Примером параллельного соединения кон­денсаторов является плоский конденсатор, имеющий n пластин, разделенных диэлект­риком (рис. 4.78). Пластины этого конден­сатора через одну соединены между собой. Но количество этих конденсаторов всегда на один меньше, чем пластин. Из рис. 4.78, а видно, что шесть пластин образуют пять кон­денсаторов, соединенных параллельно (рис. 4.78, б). Каждая внутренняя пластина яв­ляется одновременно обкладкой двух кон­денсаторов. Поэтому при вычислении элект­роемкости плоского сложного конденсатора пользуются формулами:

C = (n — 1)C₀,

C = (εε₀S / d) • (n — 1).

где C — общая электроемкость; Q — элект­роемкость конденсатора из двух пластин; n — общее количество пластин.

На этой странице материал по темам:

• Закон параллельного соединения конденсаторов

• Параллельное соединение конденсатора применяют

• Последовательное и параллельное соединение конденсаторов реферат

• Физика параллельное соединение катушки и конденсатора лабораторная работа

• Чего достигают соединенияя конденсаторы паралельно? посдедоватильно?

Вопросы по этому материалу:

• С какой целью конденсаторы объединяют в батареи?

• Чего достигают, соединяя конденсаторы параллельно?

• Чему равна общая электроемкость соединенных параллельно кон­денсаторов?

• Как рассчитать емкость плоского конденсатора из многих пластин?

конденсаторов последовательно и параллельно

Цели обучения

К концу этого раздела вы сможете:

• Выведите выражения для полной емкости последовательно и параллельно.
• Обозначает последовательные и параллельные части при соединении конденсаторов.
• Рассчитайте эффективную емкость последовательно и параллельно с учетом индивидуальных емкостей.

Несколько конденсаторов могут быть соединены вместе в различных приложениях.Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Существует два простых и распространенных типа соединений, называемых серией и параллельной , для которых мы можем легко вычислить общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного.

Емкость серии

На рисунке 1а показано последовательное соединение трех конденсаторов с приложенным напряжением.Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением [латекс] C = \ frac {Q} {V} \\ [/ latex].

Обратите внимание на рисунок 1, что противоположные заряды величиной Q протекают по обе стороны от первоначально незаряженной комбинации конденсаторов, когда приложено напряжение В, . Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов были созданы заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах.Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов. (См. Рисунок 1b.) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.

Рис. 1. (a) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине равна Q. (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d.Последовательные соединения дают общую емкость, которая меньше, чем у любого из отдельных конденсаторов.

Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение [латекс] C = \ frac {Q} {V} \\ [/ latex] для В дает [латекс ] V = \ frac {Q} {C} \\ [/ latex]. Таким образом, напряжения на отдельных конденсаторах равны [латексному] V_1 = \ frac {Q} {C_1}, V_2 = \ frac {Q} {C_2}, \ text {и} V_3 = \ frac {Q} {C_3} \\ [/латекс].

Общее напряжение складывается из отдельных напряжений:

В = В ₁ + В ₂ + В ₃ .

Теперь, называя общую емкость C _S последовательной емкостью, считайте, что

[латекс] V = \ frac {Q} {C _ {\ text {S}}} = V_1 + V_2 + V_3 \\ [/ latex].

Вводя выражения для V ₁ , V ₂ и V ₃ , получаем

[латекс] \ frac {Q} {C _ {\ text {S}}} = \ frac {Q} {C_ {1}} + \ frac {Q} {C_ {2}} + \ frac {Q} { C_ {3}} \\ [/ латекс].

Отменяя Q s, мы получаем уравнение для полной емкости в серии C _S равным

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} { C_ {3}} + \ точки, \\ [/ latex]

, где «…» означает, что выражение действительно для любого количества конденсаторов, соединенных последовательно.Выражение этой формы всегда приводит к общей емкости C _S , которая меньше любой из отдельных емкостей C ₁ , C ₂ ,…, как показано в примере 1.

Общая емкость в серии,

C _с

Общая емкость в серии:

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} { C_ {3}} + \ dots \\ [/ latex]

Пример 1. Что такое серийная емкость?

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны 1.000, 5.000 и 8.000 мкФ.

Стратегия

Имея данную информацию, общую емкость можно найти, используя уравнение для емкости в серии.

Решение

Ввод заданных емкостей в выражение для [latex] \ frac {1} {C _ {\ text {S}}} \\ [/ latex] дает [latex] \ frac {1} {C _ {\ text {S} }} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} \\ [/ latex].

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {1.000 \ mu \ text {F}} + \ frac {1} {5.000 \ mu \ text {F} } + \ frac {1} {8.000 \ mu \ text {F}} = \ frac {1.325} {\ mu \ text {F}} \\ [/ latex]

Преобразование для нахождения C _S дает [латекс] C _ {\ text {S}} = \ frac {1.325} {\ mu \ text {F}} = 0,755 \ mu \ text {F} \\ [/ латекс].

Обсуждение

Общая последовательная емкость C _с меньше наименьшей индивидуальной емкости, как было обещано. При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только вычисления целых чисел) равен 40.Таким образом,

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {40} {40 \ mu \ text {F}} + \ frac {8} {40 \ mu \ text {F} } + \ frac {5} {40 \ mu \ text {F}} = \ frac {53} {40 \ mu \ text {F}} \\ [/ latex]

так что

[латекс] C _ {\ text {S}} = \ frac {40 \ mu \ text {F}} {53} = 0,755 \ mu \ text {F} \\ [/ latex]

Конденсаторы параллельно

На рисунке 2а показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти легче, чем в последовательном случае. Чтобы найти эквивалентную общую емкость C, , _p , сначала отметим, что напряжение на каждом конденсаторе составляет В, , то же самое, что и у источника, поскольку они подключены непосредственно к нему через проводник.(Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют такие же заряды, как и при индивидуальном подключении к источнику напряжения. Общая сумма начислений Q представляет собой сумму отдельных начислений: Q = Q ₁ + Q ₂ + Q ₃ .

Рис. 2. (a) Параллельное соединение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, и поэтому общая параллельная емкость — это просто сумма отдельных емкостей.(b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.

Используя соотношение Q = CV , мы видим, что общий заряд составляет Q = C _p V , а отдельные расходы составляют Q ₁ = C ₁ V , Q ₂ = C ₂ V , и Q ₃ = C ₃ V .Ввод их в предыдущее уравнение дает

C _p V = C ₁ V + C ₂ V + C ₃ V .

Исключая из уравнения В , получаем уравнение для полной емкости параллельно

C _p : C _p = C ₁ + C ₂ + C ₃ +….

Общая емкость, подключенная параллельно, — это просто сумма отдельных емкостей. (И снова «… » означает, что выражение действительно для любого количества конденсаторов, подключенных параллельно.) Так, например, если конденсаторы в Примере 1 были подключены параллельно, их емкость составила бы

C _p = 1.000 мкФ + 5.000 мкФ + 8.000 мкФ = 14000 мкФ.

Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на рисунке 2b.

Общая емкость параллельно,

C _p

Общая емкость параллельно C _p = C ₁ + C ₂ + C ₃ +…

Более сложные соединения конденсаторов иногда могут быть последовательными и параллельными. (См. Рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую.

Рис. 3. (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C ₁ и C ₂ находятся последовательно; их эквивалентная емкость C _S меньше, чем у любого из них. (c) Обратите внимание, что C _S параллельно с C ₃ . Таким образом, общая емкость составляет сумму C _S и C ₃ .

Пример 2. Смесь последовательной и параллельной емкостей

Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех десятичных знаков ( C ₁ = 1.000 мкФ, C ₂ = 3.000 мкФ и C ₃ = 8.000 мкФ) и округлите ответ до трех десятичных знаков.

Стратегия

Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы включены последовательно, а какие — параллельно.Конденсаторы C ₁ и C ₂ идут последовательно. Их комбинация, обозначенная на рисунке C _S , параллельна C ₃ .

Решение

Поскольку C ₁ и C ₂ включены последовательно, их общая емкость определяется как [латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} { C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} \\ [/ latex]. Ввод их значений в уравнение дает

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} = \ frac {1} { 1.000 \ mu \ text {F}} + \ frac {1} {5.000 \ mu \ text {F}} = \ frac {1.200} {\ mu \ text {F}} \\ [/ latex].

Инвертирование дает C _S = 0,833 мкФ.

Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; Таким образом, общая сумма составляет

[латекс] \ begin {array} {lll} C _ {\ text {tot}} & = & C _ {\ text {S}} + C _ {\ text {S}} \\\ text {} & = & 0.833 \ mu \ text {F} +8.000 \ mu \ text {F} \\\ text {} & = & 8.833 \ mu \ text {F} \ end {array} \\ [/ latex]

Обсуждение

Этот метод анализа комбинаций конденсаторов по частям, пока не будет получена общая сумма, может быть применен к более крупным комбинациям конденсаторов.

Сводка раздела

• Общая емкость последовательно [латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ гидроразрыв {1} {C_ {3}} + \ dots \\ [/ latex]
• Общая емкость параллельно C _p = C ₁ + C ₂ + C ₃ +…
• Если схема содержит комбинацию конденсаторов, включенных последовательно и параллельно, определите последовательную и параллельную части, вычислите их емкости, а затем найдите общую сумму.

Концептуальные вопросы

1. Если вы хотите хранить большое количество энергии в конденсаторной батарее, подключите ли вы конденсаторы последовательно или параллельно? Объяснять.

Задачи и упражнения

1. Найдите общую емкость комбинации конденсаторов на Рисунке 4.

   Рисунок 4. Комбинация последовательного и параллельного подключения конденсаторов.

2. Предположим, вам нужна конденсаторная батарея с общей емкостью 0.750 Ф, и у вас есть множество конденсаторов емкостью 1,50 мФ. Какое наименьшее число вы могли бы связать вместе, чтобы достичь своей цели, и как бы вы их связали?
3. Какую общую емкость можно получить, соединив конденсатор 5,00 мкФ и конденсатор 8,00 мкФ?
4. Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.

   Рисунок 5. Комбинация последовательного и параллельного подключения конденсаторов.

5. Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.

   Рисунок 6. Комбинация последовательного и параллельного подключения конденсаторов.

6. Необоснованные результаты. (a) Конденсатор емкостью 8,00 мкФ подключен параллельно другому конденсатору, что дает общую емкость 5,00 мкФ. Какая емкость у второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?

Избранные решения проблем и упражнения

1. 0,293 мкФ

3.3,08 мкФ в последовательном соединении, 13,0 мкФ в параллельном соединении

4. 2,79 мкФ

6. (a) –3,00 мкФ; (б) У вас не может быть отрицательного значения емкости; (c) Предположение, что конденсаторы были подключены параллельно, а не последовательно, было неверным. Параллельное соединение всегда дает большую емкость, в то время как здесь предполагалась меньшая емкость. Это могло произойти, только если конденсаторы подключены последовательно.

конденсаторов параллельно | Приложения

Конденсаторы, как и другие электрические элементы, могут подключаться к другим элементам последовательно или параллельно.Иногда бывает полезно подключить несколько конденсаторов параллельно, чтобы получился функциональный блок, подобный показанному на рисунке. В таких случаях важно знать эквивалентную емкость блока параллельного подключения. В этой статье мы сосредоточимся на анализе параллельного соединения конденсаторов и возможных сферах применения таких схем.

Анализ

Все конденсаторы в параллельном соединении имеют одинаковое напряжение на них, что означает:

, где от V ₁ до V _n представляют напряжение на каждом соответствующем конденсаторе.Это напряжение равно напряжению, приложенному к параллельному соединению конденсаторов через входные провода. Однако количество заряда, накопленного на каждом конденсаторе, не одинаково и зависит от емкости каждого конденсатора по формуле:

, где Q _n — количество заряда, накопленного на конденсаторе, C _n — емкость конденсатора, а V _n — напряжение, приложенное к конденсатору, которое равно напряжению, приложенному ко всей параллели. блок подключения.Общее количество заряда, которое хранится в блоке конденсаторов, обозначается Q и делится между всеми конденсаторами, присутствующими в этой цепи. Это представлено:

Следующее уравнение используется для определения эквивалентной емкости для параллельного соединения нескольких конденсаторов:

, где C _eq — эквивалентная емкость при параллельном соединении конденсаторов, V — напряжение, приложенное к конденсаторам через входные провода, а Q ₁ — Q _n представляют собой заряды, накопленные на каждом соответствующем конденсаторе.Это подводит нас к важному выводу, что:

, что означает, что эквивалентная емкость при параллельном соединении конденсаторов равна сумме индивидуальных емкостей. Этот результат также интуитивно понятен — конденсаторы, включенные параллельно, можно рассматривать как один конденсатор, площадь пластин которого равна сумме площадей пластин отдельных конденсаторов.

Приложения

Конденсаторы — это устройства, которые используются для хранения электрической энергии в виде электрического заряда.При параллельном подключении нескольких конденсаторов полученная схема может хранить больше энергии, поскольку эквивалентная емкость является суммой индивидуальных емкостей всех задействованных конденсаторов. Этот эффект используется в некоторых приложениях.

Источники питания постоянного тока

Одним из примеров являются источники постоянного тока, в которых иногда используется несколько параллельных конденсаторов для лучшей фильтрации выходного сигнала и устранения пульсаций переменного тока. Используя этот подход, можно использовать конденсаторы меньшего размера, которые имеют лучшие характеристики пульсации, при этом получая более высокие значения емкости.

Более высокие значения емкости

Для некоторых приложений просто требуются значения емкости, которые намного выше, чем могут предложить коммерчески доступные конденсаторы. В таких приложениях используются конденсаторные батареи. Одним из примеров являются конденсаторные батареи, используемые для коррекции коэффициента мощности с индуктивными нагрузками. Другим примером являются батареи накопителей энергии, которые заявлены для использования в автомобильной промышленности, а именно KERS (система рекуперации кинетической энергии), используемая для рекуперативного торможения в больших транспортных средствах, таких как трамваи, а также в гибридных автомобилях.

Импульсные нагрузки

Одна лаборатория с сильным магнитным полем приводит в действие самый мощный в мире магнит, способный создавать магнитное поле почти 100 тесла за счет хранения энергии в конденсаторной батарее. Накопленная энергия высвобождается через магнитную катушку за очень короткое время, создавая очень мощное магнитное поле.

В любом случае конденсаторные батареи могут достигать очень высоких значений емкости. При использовании нескольких суперконденсаторов, соединенных параллельно, возможны емкости в несколько десятков килофарад, особенно с учетом того, что суперконденсаторы могут достигать значений емкости более 2000 фарад.

Ограничения по конструкции

При параллельном подключении конденсаторов следует помнить о некоторых моментах. Во-первых, максимальное номинальное напряжение при параллельном соединении конденсаторов равно минимальному номинальному напряжению всех конденсаторов, используемых в системе. Таким образом, если несколько конденсаторов на 500 В подключены параллельно к конденсатору на 100 В, максимальное номинальное напряжение всей системы составляет всего 100 В, поскольку на все конденсаторы в параллельной цепи подается одинаковое напряжение.

Безопасность

Еще один момент, о котором следует помнить, заключается в том, что батареи конденсаторов могут быть опасными из-за количества хранимой энергии и того факта, что конденсаторы могут высвобождать накопленную энергию за очень короткое время. Эта накопленная энергия иногда эффективна, чтобы вызвать серьезные травмы или повреждение электропроводки и устройств в случае случайного короткого замыкания.

Серия

и параллельные схемы — learn.sparkfun.com

Добавлено в избранное Любимый 53 Конденсаторы серии

и параллельные

Объединение конденсаторов аналогично объединению резисторов… только наоборот. Как бы странно это ни звучало, это абсолютная правда. Почему это могло быть?

Конденсатор — это просто две пластины, расположенные очень близко друг к другу, и его основная функция — удерживать целую группу электронов. Чем больше значение емкости, тем больше электронов она может удерживать. Если размер пластин увеличивается, емкость увеличивается, потому что физически больше места для электронов. И если пластины отодвинуть дальше друг от друга, емкость падает, потому что напряженность электрического поля между ними уменьшается с увеличением расстояния.

Теперь предположим, что у нас есть два конденсатора по 10 мкФ, соединенные последовательно, и предположим, что они оба заряжены и готовы к разрядке в друга, сидящего рядом с вами.

Помните, что в последовательной цепи есть только один путь для прохождения тока. Отсюда следует, что количество электронов, выходящих из колпачка снизу, будет таким же, как и количество электронов, выходящих из колпачка наверху. Значит, емкость не увеличилась?

На самом деле все еще хуже.Разместив конденсаторы последовательно, мы эффективно раздвинули пластины друг от друга, потому что расстояние между пластинами двух конденсаторов складывается. Так что у нас нет 20 мкФ или даже 10 мкФ. У нас 5 мкФ. Результатом этого является то, что мы добавляем значения последовательного конденсатора так же, как мы добавляем значения параллельного резистора. И метод «произведение над суммой», и метод взаимности действительны для последовательного добавления конденсаторов.

Может показаться, что нет смысла добавлять конденсаторы последовательно. Но следует отметить, что мы получили вдвое большее напряжение (или номинальное напряжение).Как и в случае с батареями, когда мы соединяем конденсаторы последовательно, напряжения складываются.

Добавление конденсаторов параллельно похоже на добавление резисторов последовательно: значения просто складываются, никаких уловок. Почему это? Их параллельное расположение эффективно увеличивает размер пластин без увеличения расстояния между ними. Чем больше площадь, тем больше емкость. Простой.

---

← Предыдущая страница
Практические правила для последовательных и параллельных резисторов

Работа конденсаторов в последовательной и параллельной цепях

Последовательные и параллельные конденсаторы

Конденсаторы серии

Последовательные конденсаторы означают, что два или более конденсатора соединены в одну линию i.Положительная пластина одного конденсатора соединена с отрицательной пластиной следующего конденсатора. Все конденсаторы, соединенные последовательно, имеют одинаковый заряд (Q) и одинаковый зарядный ток (i _C ).

Рассмотрим N- количество конденсаторов, подключенных последовательно, тогда

Q _T = Q ₁ = Q ₂ = Q ₃ = ———- = Q _N

I _C = I ₁ = I ₂ = I ₃ = ——— = I _N

Вернуться к списку

Конденсаторы в последовательном соединении:

Следующие схемы показывают последовательное соединение группы конденсаторов.

Последовательное соединение N-количество конденсаторов:

Последовательное соединение 2-х конденсаторов:

В этой схеме заряд (Q), хранящийся во всех конденсаторах, одинаков, потому что каждый конденсатор имеет заряд, который течет от соседнего конденсатора. Падение напряжения на всех конденсаторах отличается друг от друга. Но полное падение напряжения, приложенное между входными и выходными линиями схемы, равно сумме всех индивидуальных падений напряжения каждого конденсатора.Эквивалентная емкость цепи составляет C _eq = Q / V.

Таким образом,

V _T = V ₁ + V ₂

C _экв = Q / V ₁ + Q / V ₂

1 / C _экв = (V ₁ + V ₂ ) / Q

V _T = Q / C _экв = Q / C ₁ + Q / C ₂

Вернуться к списку

Конденсаторы серии Equation

1 / Ceq = 1 / C1 + 1 / C2 +……… + 1 / CN

Когда конденсаторы соединены последовательно, величина, обратная эквивалентной емкости, равна сумме обратных величин отдельных емкостей конденсаторов в цепи.

На рисунке 2 величина, обратная эквивалентной емкости цепи, равна сумме значений обратных емкостей двух конденсаторов C ₁ и C ₂ , выражение приведено ниже.

1 / C _экв = 1 / C ₁ + 1 / C ₂

Вернуться к списку

Конденсаторы в серии Пример № 1:

Мы предполагаем, что номиналы двух конденсаторов на рисунке 2 выше 0.4 мкФ и 0,5 мкФ соответственно. Теперь мы можем рассчитать эквивалентную емкость для двух последовательно соединенных конденсаторов как

1 / C _экв = 1 / C ₁ + 1 / C ₂

1 / C _экв = (C ₁ + C ₂ ) / C ₁ C ₂

C _экв = (C ₁ C ₂ ) / (C ₁ + C ₂ )

C _экв = (0,4 мкФ * 0,5 мкФ) / (0.4 мкФ + 0,5 мкФ)

C _экв = 0,22 мкФ

Мы знаем, что эквивалентная емкость конденсаторов, соединенных последовательно, меньше, чем значение наименьшего конденсатора в цепи. Таким образом, здесь мы также получаем эквивалентное значение 0,22 мкФ, что меньше наименьшей емкости 0,4 мкФ в последовательном соединении данной цепи из двух конденсаторов.

Вернуться к списку

Конденсаторы в серии Пример № 2

Вычислите эквивалентную емкость, и отдельные падения напряжения на наборе из двух последовательно соединенных конденсаторов имеют 0.1 мкФ и 0,2 мкФ соответственно при подключении к 12 В переменного тока. поставлять.

1 / C _экв = 1 / C ₁ + 1 / C ₂

C _экв = (C ₁ C ₂ ) / (C ₁ + C ₂ )

C _экв = (0,1 мкФ * 0,2 мкФ) / (0,1 мкФ + 0,2 мкФ)

C _экв = 0,066 мкФ = 66 нФ

Падение напряжения на двух последовательно соединенных конденсаторах составляет:

V ₁ = (C ₂ * V _T ) / (C ₁ + C ₂ ) = (0.2 мкФ * 12 В) / (0,1 мкФ + 0,2 мкФ) = 8 В

V ₂ = (C ₁ * V _T ) / (C ₁ + C ₂ ) = (0,1 мкФ * 12 В) / (0,1 мкФ + 0,2 мкФ) = 4 В

Из этих результатов мы заметили, что эквивалентная емкость 66 нФ меньше, чем наименьшая емкость 0,1 мкФ из данных двух конденсаторов. Отдельные падения напряжения на данных двух конденсаторах различны. Но сумма отдельных падений напряжения на обоих конденсаторах равна общему напряжению.т.е. 8 В + 4 В = 12 В.

Теперь посчитаем заряд, накопленный в отдельном конденсаторе,

Q ₁ = В ₁ * C ₁ = 8 В * 0,1 мкФ = 0,8 мкКл

Q ₂ = V ₂ * C ₂ = 4 В * 0,2 мкФ = 0,8 мкКл

Здесь мы наблюдали, что одинаковый заряд 0,8 мкКл сохраняется в обоих конденсаторах C ₁ и C ₂ , которые соединены последовательно.

Вернуться к списку

Конденсаторы в серии Сводка:

Эквивалентная емкость конденсаторов, соединенных последовательно, обратная эквивалентная емкость равна сумме обратных величин всех индивидуальных емкостей последовательно соединенных конденсаторов.Все конденсаторы, соединенные последовательно, имеют одинаковый заряд (Q). Зарядный ток (i _C ) также одинаков для всех отдельных конденсаторов, которые соединены последовательно, например, i _C = i ₁ = i ₂ и т. Д.

Падение напряжения для отдельных конденсаторов в Последовательное соединение разные. Но сумма всех отдельных падений напряжения равна общему напряжению в цепи. т.е. V _T = V ₁ + V ₂ и т. д.Большое значение емкости приведет к меньшему падению напряжения, а небольшое значение емкости приведет к большему падению напряжения.

Вернуться к списку

Конденсаторы в параллельных цепях

Конденсаторы, включенные параллельно, означает, что два или более конденсатора подключены параллельно, т. Е. Оба их вывода подключены к каждому выводу другого конденсатора или конденсаторы соответственно. Все конденсаторы, подключенные параллельно, имеют одинаковое напряжение, равное V _T , приложенному между входными и выходными клеммами схемы.Тогда на параллельные конденсаторы подается «общее напряжение». т.е. V _T = V ₁ = V ₂ и т. д.

Эквивалентная емкость C _eq цепи, в которой конденсаторы соединены параллельно, равна сумме всех отдельных емкостей конденсаторов, сложенных вместе. Это связано с тем, что верхняя пластина каждого конденсатора в цепи соединена с верхней пластиной соседних конденсаторов. Таким же образом нижняя пластина каждого конденсатора в цепи соединяется с нижней пластиной соседних конденсаторов.

Следующие схемы показывают параллельное соединение между группами конденсаторов.

Параллельное соединение n конденсаторов:

Параллельное соединение 2-х конденсаторов:

На рисунке 4 общий заряд (Q) в цепи разделен между двумя конденсаторами, что означает, что заряд Q распределяется между конденсаторами, подключенными параллельно. Потому что падение напряжения на отдельных конденсаторах одинаково, а также равно общему напряжению, приложенному к цепи.Но общий заряд Q равен сумме всех зарядов отдельных конденсаторов, соединенных параллельно. т.е. из приведенного выше рисунка 4 два разных конденсатора C1 и C2 имеют два разных заряда Q ₁ и Q ₂ соответственно. Здесь Q = Q ₁ + Q ₂

Теперь мы видим эквивалентную емкость конденсаторов C1 и C2, соединенных параллельно, что показано на рисунке 4 выше.

Мы знаем формулу:

Q = C _экв V _T

Здесь Q = Q ₁ + Q ₂

И V _T = V ₁ = V ₂

C _экв = Q / V _T = (Q ₁ + Q ₂ ) / V _T = (Q ₁ / V _T ) + (Q ₂ / V _T )

Вернуться к списку

Параллельные конденсаторы Уравнение:

C _{eq =} C ₁ + C ₂ + C ₃ + ———— + C _N

Эквивалентная емкость конденсаторов, подключенных в параллельность равна сумме отдельных емкостей конденсаторов в цепи.

На рисунке 4 значение эквивалентной емкости (C _экв. ) равно сумме значений емкости C ₁ и C ₂ , выражение показано ниже.

Ceq = C1 + C2

Вернуться к списку

Конденсаторы параллельно Пример № 1:

Рассмотрим значения емкости двух конденсаторов C ₁ = 0,2 мкФ и C ₂ = 0,3 мкФ, которые показаны на рисунке 4 выше.Теперь рассчитайте эквивалентную емкость цепи.

Мы знаем, что эквивалентная емкость

C _экв = C ₁ + C ₂

C _экв = 0,2 мкФ + 0,3 мкФ

C _экв = 0,5 мкФ

Один важный момент, который следует помнить о параллельно соединенных конденсаторных цепях, эквивалентная емкость (C _eq ) любых двух или более конденсаторов, соединенных вместе параллельно, всегда будет больше, чем значение самого большого конденсатора в цепи, поскольку мы складываем значения .Таким образом, в нашем примере выше C _eq = 0,5 мкФ, тогда как конденсатор наибольшей емкости в цепи составляет всего 0,3 мкФ.

Вернуться к списку

Параллельные конденсаторы Пример № 2:

Рассчитайте эквивалентную емкость на наборе из двух параллельно включенных конденсаторов, показанном на рисунке 4.

(а) Один конденсатор 0,1 мкФ, подключенный параллельно с 0,2 мкФ.

(b) Один конденсатор емкостью 750 нФ, подключенный параллельно с 0.5 мкФ.

(а) Эквивалентная емкость,

C _экв. = C ₁ + C ₂

_{C экв. = 0,1 мкФ + 0,2 мкФ}

C _экв = 0,3 мкФ

(b) Эквивалентная емкость,

C _экв = C ₁ + C ₂

C _экв = 750 нФ + 0,5 мкФ

C _экв = 750 нФ + 500 нФ

C _{экв =} 1250 нФ = 1.25 мкФ

В двух вышеупомянутых случаях мы наблюдали, что значение эквивалентной емкости (C _eq ) двух конденсаторов, соединенных параллельно, больше, чем значение самого большого конденсатора в цепи, поскольку мы складываем значения. В разделе (а) значение C _eq = 0,3 мкФ, тогда как конденсатор с наибольшей емкостью составляет всего 0,2 мкФ. В разделе (b) значение C _eq = 1,25 мкФ, тогда как самый большой конденсатор в цепи составляет всего 0,5 мкФ.

Вернуться к списку

Конденсаторы, соединенные параллельно

Эквивалентная емкость группы конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов.то есть C _{eq =} C ₁ + C ₂ . Потому что падение напряжения на отдельном конденсаторе равно общему напряжению, приложенному между входными и выходными клеммами схемы. т.е. V _T = V ₁ = V ₂ . Заряды, хранящиеся в отдельных конденсаторах, различны, но сумма всех зарядов отдельных конденсаторов равна полному потоку заряда в цепи. то есть Q = Q ₁ + Q ₂ .

Зарядный ток, протекающий в цепи, распределяется на все конденсаторы в цепи.Но общий зарядный ток равен сумме всех отдельных зарядных токов конденсаторов в цепи. т.е. i _C = i ₁ + i ₂ и т. д. Эквивалентное значение емкости группы конденсаторов, соединенных параллельно, всегда больше, чем значение наибольшего конденсатора в цепи.

Вернуться к списку

Емкостное реактивное сопротивление

— Как найти последовательные и параллельные конденсаторы

Найдите емкостное реактивное сопротивление цепи с последовательными или параллельными конденсаторами, используя этот простой двухэтапный процесс.

Шаг 1: Найдите общую емкость цепи

Предположим, у нас есть три конденсатора, 12 Ф, 20 Ф и 30 Ф, подключенных к источнику с частотой 60 Гц. Каково полное емкостное реактивное сопротивление (X _C ) при последовательном или параллельном подключении?

1А. Для конденсаторов серии

Когда конденсаторы соединены последовательно, общая емкость меньше, чем любая из отдельных емкостей последовательных конденсаторов.Если два или более конденсатора соединены последовательно, общий эффект будет таким, как у одного (эквивалентного) конденсатора, имеющего суммарное расстояние между пластинами отдельных конденсаторов.

Конденсаторы серии

Пример:

1/12 = 0,083, 1/20 = 0,050, 1/30 = 0,033

0,083 + 0,050 + 0,033 = 0,166

1 / 0,163 = 6,02 мкФ

Примечание: математические расчеты упрощены для иллюстрации. Для более точных чисел воспользуйтесь калькулятором.

1Б. Для параллельных конденсаторов

При параллельном подключении конденсаторов общая емкость представляет собой сумму емкостей отдельных конденсаторов. Если два или более конденсатора подключены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.

Параллельные конденсаторы Пример:

12 + 20 + 30 = 62 мкФ

---

Шаг 2. Определите емкостное сопротивление

Как и сопротивление, реактивное сопротивление измеряется в Ом, но ему присваивается символ X, чтобы отличать его от чисто резистивного значения R, и, поскольку рассматриваемый компонент является конденсатором, реактивное сопротивление конденсатора называется емкостным реактивным сопротивлением (X _C ) который измеряется в Ом.

Поскольку конденсаторы заряжаются и разряжаются пропорционально скорости изменения напряжения на них, чем быстрее изменяется напряжение, тем больше тока протекает. Точно так же, чем медленнее изменяется напряжение, тем меньше будет протекать ток. Это означает, что реактивное сопротивление конденсатора переменного тока «обратно пропорционально» частоте источника питания.

X _C — емкостное реактивное сопротивление в омах, f — частота в герцах, а C — емкость переменного тока в фарадах. Очень важно преобразовать наш пример из микрофарад в фарады, чтобы получить правильный результат!

1 мкФ = 0,000001 F

Серия 60 Гц Пример:

6,02 мкФ = 0,000006 F (упрощенно)
2 х 3,14 х 60 х 0,000006 = 0,0022608
1 / 0,0022608 = 442,32 Ом

60 Гц Параллельный Пример:

62 мкФ = 0,000062 F
2 х 3.14 х 60 х 0,000062 = 0,0233616
1 / 0,0233616 = 42,805 Ом

Теперь посмотрим, что произойдет при изменении частоты на 400 Гц :

Серия 400 Гц Пример:

2 х 3,14 х 400 х 0,000006 = 0,015072
1 / 0,015072 = 66,34 Ом

Параллельный 400 Гц Пример:

2 х 3,14 х 400 х 0,000062 = 0,155744
1 / 0,155744 = 6,42 Ом

---

Полезные ссылки

на комментарий.

Конденсаторы последовательно и параллельно

Конденсаторы последовательно

Давайте подключим n из конденсаторов последовательно . Через эту последовательную комбинацию конденсаторов подается напряжение V вольт.

Рассмотрим емкость конденсаторов C ₁ , C ₂ , C ₃ …… .C _n соответственно, а эквивалентная емкость последовательной комбинации конденсаторов равна C. Падения напряжения на конденсаторах равны считается V ₁ , V ₂ , V ₃ …….V _n соответственно.

Теперь, если Q кулонов — это заряд, передаваемый от источника через эти конденсаторы, тогда

Поскольку заряд, накопленный в каждом конденсаторе и I, вся последовательная комбинация конденсаторов будет одинакова, и это считается Q.
Теперь, уравнение (i) можно записать как:

Параллельные конденсаторы

Конденсатор предназначен для хранения энергии в форме своего электрического поля, т. е. электростатической энергии. Всякий раз, когда возникает необходимость увеличить емкость накопления электростатической энергии, требуется подходящий конденсатор с увеличенной емкостью.Конденсатор состоит из двух металлических пластин, соединенных параллельно и разделенных диэлектрической средой, такой как стекло, слюда, керамика и т. Д. Диэлектрик обеспечивает непроводящую среду между пластинами и обладает уникальной способностью удерживать заряд, а также способностью конденсатора для хранения заряда определяется как емкость конденсатора. Когда к пластинам конденсатора подключается источник напряжения, на одной пластине осаждается положительный заряд, а на другой — отрицательный. Общее количество накопленного заряда (q) прямо пропорционально источнику напряжения (V), так что,

Где, C — константа пропорциональности i.е. емкость. Его значение зависит от физических размеров конденсатора.

Где ε = диэлектрическая проницаемость, A = эффективная площадь пластины и d = расстояние между пластинами.

Чтобы увеличить значение емкости конденсатора, два или более конденсатора подключаются параллельно как две одинаковые пластины, соединенные вместе, затем их эффективная площадь перекрытия складывается с постоянным интервалом между ними, и, следовательно, их эквивалентное значение емкости становится равным удвоение (C ∝ A) индивидуальной емкости.Конденсаторная батарея используется в различных производственных и перерабатывающих отраслях и включает конденсаторы, включенные параллельно, чтобы обеспечить требуемую емкость в соответствии с требованиями, регулируя подключение конденсаторов, подключенных параллельно, и, таким образом, она эффективно используется в качестве статического компенсатора для баланса реактивной мощности. в компенсации энергосистемы. Когда два конденсатора подключены параллельно, тогда напряжение (В) на каждом конденсаторе одинаковое, т.е. ( _{В, эквивалент} = В _{, а} = В _{, b} ), а ток (i _{, эквивалентный} ) делится на две части: _а и я _б .Поскольку известно, что
Подставляя значение q из уравнения (1) в приведенное выше уравнение,

Последний член становится равным нулю (поскольку емкость конденсатора постоянна). Следовательно,

Применение закона Кирхгофа по току на входящем узле параллельного соединения


Наконец, мы получаем,

Следовательно, всякий раз, когда n конденсаторов подключены параллельно, эквивалентная емкость всего соединения определяется следующим уравнением, которое похоже эквивалентному сопротивлению резисторов при последовательном включении.

Метод определения выражения эквивалентной емкости параллельного конденсатора

Подключим n конденсаторов параллельно через источник напряжения V вольт.

Рассмотрим емкость конденсаторов C ₁ , C ₂ , C ₃ … ..C _n соответственно, а эквивалентная емкость комбинации конденсаторов равна C. Как у . конденсаторы подключаются параллельно , вроде ток заряда в каждом конденсаторе будет одинаковым.Общий заряд параллельной комбинации будет разделен в каждом конденсаторе в соответствии с его значением емкости, но напряжение на каждом конденсаторе будет одинаковым, а в установившемся режиме оно точно равно приложенному напряжению.

Где, Q ₁ , Q ₂ , Q ₃ , …… .Q _n — заряд конденсатора C ₁ , C ₂ , C ₃ … .. C _n соответственно.

Теперь уравнение (2) можно записать как:

Конденсаторы серии

и параллельные | Блестящая вики по математике и науке

Если конденсаторы включены последовательно, соответствующие выводы всех конденсаторов больше не соединяются вместе.Скорее, терминалы подключаются последовательно, один за другим, в цепочку, как показано выше. В результате все конденсаторы должны нести одинаковый заряд. Чтобы понять, почему, рассмотрим, что происходит между последовательными конденсаторами: если заряд на одной «пластине» конденсатора равен + Q + Q + Q, то заряд пластины, подключенной к этой пластине, должен быть -Q -Q -Q.

Таким образом, хотя разность потенциалов на каждом последовательном конденсаторе может быть разной в зависимости от его геометрии, заряд на каждом из них должен быть одинаковым.В результате Q / Ci = Vi Q / C_i = V_i Q / Ci = Vi и

∑iQCi = ∑iViQ∑i1Ci = Vtot. \ Begin {align} \ sum_i \ frac {Q} {C_i} & = \ sum_i V_i \\ Q \ sum_i \ frac {1} {C_i} & = V_ \ text {tot}. \ end {align} i∑ Ci Q Qi∑ Ci 1 = i∑ Vi = Vобщ.

Учитывая некоторый общий потенциал Vtot V_ \ text {tot} Vtot, весь массив последовательно соединенных конденсаторов достигает некоторого заряда QQQ на каждом конденсаторе с константой пропорциональности ∑i1Ci \ sum_i \ frac {1} {C_i} ∑i Ci 1. Таким образом, эффективная емкость Ceff C_ \ text {eff} Ceff равна

.

1Ceff = ∑i1Ci.\ frac {1} {C_ \ text {eff}} = \ sum_i \ frac {1} {C_i}. Ceff 1 = i∑ Ci 1.

Какова эффективная емкость двух последовательно соединенных конденсаторов 2 нФ 2 \, \ text {nF} 2 нФ?

---

Эффективная емкость определяется как

112 нФ + 12 нФ = 1 нФ. \ frac {1} {\ frac {1} {2 \, \ text {nF}} + \ frac {1} {2 \, \ text {nF}}} = 1 \, \ text {nF}. 2nF1 + 2nF1 1 = 1nF.

32Q \ frac {3} {2} Q23 Q 98Q \ frac {9} {8} Q89 Q 89Q \ frac {8} {9} Q98 Q 43Q \ frac {4} {3} Q34 Q

Вышеупомянутая схема представляет собой схему, состоящую из трех конденсаторов с одинаковой емкостью C.C.C. Когда переключатель разомкнут, количество электрического заряда во всей цепи составляет Q.Q.Q. Если переключатель замкнут, сколько будет электрического заряда во всей цепи?

C2 \ frac {C} {2} 2C 2C2C2C 2C3 \ frac {2C} {3} 32C 3C3C3C

Конденсаторы последовательно и параллельно

Каждый конденсатор на приведенной выше схеме имеет емкость CCC.Какая эквивалентная емкость?

0,4 мкФ и 2,5 мкФ 1,5 мкФ и 2 мкФ.5 мк \ мкФ 2,5 мкФ и 1,5 мкФ 0,4 мкФ и 1,5 мкФ

На двух диаграммах выше показаны конденсаторы A и B с их соответствующей емкостью 0.50,50,5 мкФ и 222 мкФ, подключенные к электрической цепи двумя разными способами.