Последовательное и параллельное соединение.
Иногда нужно увеличить ёмкость или сопротивление, а подходящих деталей на нужное сопротивление нет, или размеры конструкции не позволяют вставить один большой конденсатор на 3000 мкф.
В этом случае можно набрать необходимые ёмкость или сопротивление из нескольких деталей, а вместо конденсатора на 3000 микрофарад вставить 3 штуки по 1000 микрофарад.
Для увеличения ёмкости конденсаторы соединяются параллельно.

Для увеличения сопротивления резисторы соединяются последовательно.
Вода через трубу с двумя валенками течёт хуже, чем через трубу с одним валенком.

Последовательное соединение — когда детали стоят друг за дружкой, «в очереди», будто за колбасой, потому оно так и называется.
Не путайте эти соединения, для увеличения ёмкости конденсаторы соединяются параллельно, а резисторы для увеличения сопротивления последовательно !
Со сложением ёмкостей и сопротивлений всё легко.
С параллельным соединением резисторов и последовательным соединением конденсаторов слегка посложнее, но к нашему счастью конденсаторы довольно редко соединяют последовательно, а резисторы параллельно.
Последовательное соединение конденсаторов может понадобиться например в сборке гаусс-гана (электромагнитной стрелялки), когда под рукой конденсаторы только на 400 вольт, а нам нужен 800-вольтовый конденсатор, а их редко где найдёшь и они дорогие.
Параллельное соединение резисторов считается вот по какой формуле:

Через три трубы, в которых в каждой по валенку, вода лучше потечёт, чем через одну трубу с одним валенком. Или если в бочке проковырять три дырки, то вода быстрее выльется, чем если бы мы проковыряли одну дырку.
Последовательное соединение конденсаторов считается по той же формуле.

Если два одинаковых конденсатора по 680uF с максимальным напряжением 400В поставить последовательно, то получится конденсатор на 340 uF с напряжением 800 вольт.
Соединение конденсаторов
Как правильно соединять конденсаторы?

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов:
В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:

С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается 

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).

Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.

Параллельное соединение электролитов

Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитов

Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел  ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂
). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

Напряжение на данном участке цепи соотносятся следующим образом:

Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

Сократив выражение на Q, получим знакомую формулу:

Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

Так как заряд конденсатора

А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов


Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С1 = 10 мкФ, C2 = 2 мкФ, C3 = 5 мкФ, а C4 = 1 мкФ?
При последовательном соединении общая емкость равна:

При параллельном соединении общая емкость равна:

Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С1 = 7 мкФ, С2 = 2 мкФ, С3 = 1 мкФ.

Сначала найдем общую емкость параллельного участка цепи:

Затем найдем общую емкость для всей цепи:

По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Параллельное и последовательное соединение конденсаторов
Элементы цепи могут быть подключены двумя способами:
Проиллюстрируем данные подключения на примере двух конденсаторов (рис. 1).
- последовательное соединение конденсаторов
Рис. 1. Последовательное соединение конденсаторов
Логическая зарядка конденсаторов происходит как показано на рис.1. Приходя из цепи, электрон останавливается на левой обкладке (пластине) конденсатора. При этом, благодаря своему электрическому полю (электризация через влияние), он выбивает другой электрон с правой обкладки, уходящий дальше в цепь (рис. 1.1). Этот образовавшийся электрон приходит на левую обкладку следующего конденсатора, соединённого последовательно. И всё повторяется снова. Таким образом, в результате «прохождения» через последовательную цепь конденсаторов «одного» электрона, мы получаем заряженную систему с одинаковыми по значению зарядами на каждом из конденсаторов (рис. 1.2).
Кроме того, напряжение на последовательно соединённой батареи конденсаторов есть сумма напряжений на каждом из элементов (аналог последовательного сопротивления проводников).
Рис. 2. Последовательное соединение конденсаторов
Часть задач школьной физики касается поиска общей электроёмкости участка цепи, логика такого поиска: найти такую электроёмкость, которым можно заменить цепь, чтобы параметры напряжения и заряда остались неизменными (рис. 2). Пусть заряд на обоих конденсаторах — (помним, что они одинаковы), электроёмкости — , и соответствующие напряжения — и .
- где
- — напряжение на первом конденсаторе,
- — электроёмкость первого конденсатора,
- — заряд конденсатора.
- где
- — напряжение на втором конденсаторе,
- — электроёмкость второго конденсатора,
- — заряд конденсатора.
- где
- — напряжение полной цепи,
- — электроёмкость общего конденсатора,
- — заряд общего конденсатора.
Памятуя о том, что конденсаторы соединены последовательно, получаем:
Или в общем виде:
- где
- — электроёмкость последовательно соединённых конденсаторов,
- — сумма обратных емкостей.
Для цепи из двух последовательных соединений:
- параллельное соединение конденсаторов
Рис. 3. Параллельное соединение конденсаторов
Параллельное подключение конденсаторов представлено на рисунке 3. При внесении электрона в систему, у него есть выбор: пойти на верхний или нижний конденсатор. При большом количестве электронов заполнение обкладок конденсатора происходит прямо пропорционально электроёмкости конденсаторов.
Рис. 4. Параллельное соединение конденсаторов. Поиск полной электроёмкости
Опять попробуем решить задачу по поиску полной ёмкости конденсаторов (рис. 4). Помним, что при параллельном подключении напряжения на элементах одинаковы, тогда:
- где
- — заряд на первом конденсаторе,
- — электроёмкость первого конденсатора,
- — напряжение на первом конденсаторе.
- где
- — заряд на втором конденсаторе,
- — электроёмкость второго конденсатора,
- — напряжение на втором конденсаторе.
- где
- — заряд на общем конденсаторе,
- — электроёмкость полного конденсатора,
- — напряжение на общем конденсаторе.
С учётом того, что , получим:
Или в общем виде:
- где
- — электроёмкость параллельно соединённых конденсаторов,
- — сумма электроёмкостей последовательно соединённой цепи.
Вывод: в задачах, в которых присутствует цепь, необходимо рассмотреть, какое конкретно соединение рассматривается, а потом использовать соответствующую логику рассуждений:
- для последовательного соединения
- заряды всех конденсаторов одинаковы: .
- напряжение во всей цепи есть сумма напряжений на каждом из элементов: ,
- полная электроёмкость цепи конденсаторов, соединённых последовательно равна: .
- для параллельного соединения
- заряд системы конденсаторов есть сумма зарядов на каждом из них: ,
- напряжение на каждом из элементов одинаково: ,
- полная электроёмкость цепи конденсаторов, соединённых параллельно равна: .
Поделиться ссылкой:
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
{SOURCE}
Условие задачи:
Два последовательно соединенных конденсатора с электроемкостью 1 и 3 мкФ подключены к источнику напряжения 220 В. Найти напряжение на каждом конденсаторе.
Задача №6.4.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(C_1=1\) мкФ, \(C_2=3\) мкФ, \(U=220\) В, \(U_1-?\), \(U_2-?\)
Решение задачи:
Пусть \(U_1\) – напряжение между обкладками первого конденсатора, а \(U_2\) – напряжение между обкладками второго. Известно, что при последовательном соединении конденсаторов заряд на их обкладках одинаковый, поэтому запишем формулу электроемкости и выразим из нее заряд \(q\):
\[C = \frac{q}{U}\]
\[q = CU\;\;\;\;(1)\]
Также известно, что при таком соединении конденсаторов общее напряжение равно сумме напряжений на каждом из конденсаторов. Учитывая все написанное и пользуясь формулой (1), мы можем получить такую систему:
\[\left\{ \begin{gathered}
{C_1}{U_1} = {C_2}{U_2} \hfill \\
U = {U_1} + {U_2} \hfill \\
\end{gathered} \right.\]
Из верхнего равенства системы выразим напряжение \(U_2\):
\[{U_2} = {U_1}\frac{{{C_1}}}{{{C_2}}}\;\;\;\;(2)\]
Полученное выражение подставим в нижнее равенство системы:
\[U = {U_1} + {U_1}\frac{{{C_1}}}{{{C_2}}}\]
\[U = {U_1}\frac{{{C_1} + {C_2}}}{{{C_2}}}\]
Откуда напряжение на первом конденсаторе \(U_1\) равно:
\[{U_1} = \frac{{U{C_2}}}{{{C_1} + {C_2}}}\]
Используя формулу (2), найдем напряжение на втором конденсаторе \(U_2\):
\[{U_2} = \frac{{U{C_2}}}{{{C_1} + {C_2}}} \cdot \frac{{{C_1}}}{{{C_2}}}\]
\[{U_2} = \frac{{U{C_1}}}{{{C_1} + {C_2}}}\]
Мы получили две формулы для расчета напряжений, считаем численные ответы:
\[{U_1} = \frac{{220 \cdot 3 \cdot {{10}^{ – 6}}}}{{1 \cdot {{10}^{ – 6}} + 3 \cdot {{10}^{ – 6}}}} = 165\;В = 0,165\;кВ\]
\[{U_2} = \frac{{220 \cdot 1 \cdot {{10}^{ – 6}}}}{{1 \cdot {{10}^{ – 6}} + 3 \cdot {{10}^{ – 6}}}} = 55\;В = 0,055\;кВ\]
Ответ: 0,165 кВ; 0,055 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Условие задачи:
Напряжение на батарее из двух последовательно включенных конденсаторов электроемкостью 20 и 30 мкФ равно 1 кВ. Чему равна разность напряжений на первом и втором конденсаторе?
Задача №6.4.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(C_1=20\) мкФ, \(C_2=30\) мкФ, \(U=1\) кВ, \(\Delta U-?\)
Решение задачи:
Для начала запишем формулу электроемкости:
\[C = \frac{q}{U}\]
Выразим из этой формулы заряд \(q\):
\[q = CU\;\;\;\;(1)\]
Пусть \(U_1\) – напряжение между обкладками первого конденсатора, а \(U_2\) – напряжение между обкладками второго. Известно, что при последовательном соединении конденсаторов заряд на их обкладках одинаковый, а общее напряжение равно сумме напряжений на каждом из конденсаторов. Учитывая все написанное и пользуясь формулой (1), мы можем получить такую систему:
\[\left\{ \begin{gathered}
{C_1}{U_1} = {C_2}{U_2} \hfill \\
U = {U_1} + {U_2} \hfill \\
\end{gathered} \right.\]
Из верхнего равенства системы выразим напряжение \(U_2\):
\[{U_2} = {U_1}\frac{{{C_1}}}{{{C_2}}}\;\;\;\;(2)\]
Полученное выражение подставим в нижнее равенство системы:
\[U = {U_1} + {U_1}\frac{{{C_1}}}{{{C_2}}}\]
\[U = {U_1}\frac{{{C_1} + {C_2}}}{{{C_2}}}\]
Откуда напряжение на первом конденсаторе \(U_1\) равно:
\[{U_1} = \frac{{U{C_2}}}{{{C_1} + {C_2}}}\;\;\;\;(3)\]
Используя формулу (2), найдем напряжение на втором конденсаторе \(U_2\):
\[{U_2} = \frac{{U{C_2}}}{{{C_1} + {C_2}}} \cdot \frac{{{C_1}}}{{{C_2}}}\]
\[{U_2} = \frac{{U{C_1}}}{{{C_1} + {C_2}}}\;\;\;\;(4)\]
Так как из данных задачи видно, что \({C_2} > {C_1}\), то из формул (3) и (4) видно, что \({U_1} > {U_2}\), поэтому искомую разность напряжений \(\Delta U\) будем искать по формуле:
\[\Delta U = {U_1} – {U_2}\]
Используя выражения (3) и (4), получим:
\[\Delta U = \frac{{U{C_2}}}{{{C_1} + {C_2}}} – \frac{{U{C_1}}}{{{C_1} + {C_2}}}\]
\[\Delta U = \frac{{U\left( {{C_2} – {C_1}} \right)}}{{{C_1} + {C_2}}}\]
Задача решена, остается только посчитать ответ:
\[\Delta U = \frac{{1000 \cdot \left( {30 \cdot {{10}^{ – 6}} – 20 \cdot {{10}^{ – 6}}} \right)}}{{20 \cdot {{10}^{ – 6}} + 30 \cdot {{10}^{ – 6}}}} = 200\;В = 0,2\;кВ\]
Ответ: 0,2 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Условие задачи:
Два конденсатора электроемкостью 4 и 1 мкФ соединены последовательно и подключены к источнику постоянного напряжения 220 В. Каково напряжение на конденсаторе меньшей емкости?
Задача №6.4.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(C_1=4\) мкФ, \(C_2=1\) мкФ, \(U=220\) В, \(U_2-?\)
Решение задачи:
Для начала запишем формулу электроемкости:
\[C = \frac{q}{U}\]
Выразим из этой формулы заряд \(q\):
\[q = CU\;\;\;\;(1)\]
Пусть \(U_1\) – напряжение на первом конденсаторе, а \(U_2\) – напряжение на втором. Известно, что при последовательном соединении конденсаторов заряд на их обкладках одинаковый, а общее напряжение равно сумме напряжений на каждом из конденсаторов. Учитывая все написанное и пользуясь формулой (1), получим такую систему:
\[\left\{ \begin{gathered}
{C_1}{U_1} = {C_2}{U_2} \hfill \\
U = {U_1} + {U_2} \hfill \\
\end{gathered} \right.\]
Из верхнего равенства системы выразим напряжение \(U_1\):
\[{U_1} = {U_2}\frac{{{C_2}}}{{{C_1}}}\]
Полученное выражение подставим в нижнее равенство системы:
\[U = {U_2}\frac{{{C_2}}}{{{C_1}}} + {U_2}\]
\[U = {U_2}\frac{{{C_1} + {C_2}}}{{{C_1}}}\]
Откуда искомое напряжение на втором конденсаторе \(U_2\) (который имеет меньшую емкость) равно:
\[{U_2} = \frac{{U{C_1}}}{{{C_1} + {C_2}}}\]
Задача решена, посчитаем численный ответ:
\[{U_2} = \frac{{220 \cdot 4 \cdot {{10}^{ – 6}}}}{{4 \cdot {{10}^{ – 6}} + 1 \cdot {{10}^{ – 6}}}} = 176\;В = 0,176\;кВ\]
Ответ: 0,176 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Условие задачи:
Два одинаковых плоских воздушных конденсатора соединены последовательно и подключены к источнику с постоянной ЭДС. Пространство между обкладками одного из конденсаторов заполняется диэлектриком с диэлектрической проницаемостью \(\varepsilon=3\). Во сколько раз изменится напряженность поля в этом конденсаторе.
Задача №6.4.64 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\varepsilon=3\), \(\frac{E}{E_0}-?\)
Решение задачи:
Напряженность поля плоского конденсатора \(E\) и напряжение между его обкладками \(U\) связаны по такой формуле:
\[E = \frac{U}{d}\]
Так как расстояние между пластинами \(d\) в этой задаче не меняется, то поиск отношения \(\frac{E}{E_0}\) сведется к поиску отношения напряжений \(\frac{U}{U_0}\), то есть:
\[\frac{E}{{{E_0}}} = \frac{U}{{{U_0}}}\;\;\;\;(1)\]
Вначале, когда конденсаторы имели одинаковую электроемкость \(C_0\), напряжение на них было одинаковым и равным половине ЭДС источника \(\rm E\):
\[{U_0} = \frac{{\rm E}}{2}\;\;\;\;(2)\]
После того, как один из конденсаторов заполнят диэлектриком, напряжение на конденсаторах изменится, но заряд на конденсаторах всегда будет оставаться одинаковым (но не постоянным, учтите это!). Поэтому будет правильно записать:
\[{C_0}{U_1} = CU\]
Здесь \(U_1\) – конечное значения напряжения на первом конденсаторе (который остается воздушным), \(U\) – конечное значения напряжения на втором конденсаторе (в который вводится диэлектрик), \(C\) – конечное значение электроемкости второго конденсатора. Последнее можно найти по формуле:
\[C = \varepsilon {C_0}\]
Тогда:
\[{C_0}{U_1} = \varepsilon {C_0}U\]
\[{U_1} = \varepsilon U\;\;\;\;(3)\]
Очевидно, что сумма напряжений на конденсаторах есть ЭДС источника, поэтому:
\[{\rm E} = {U_1} + U\]
Учитывая (3), получим:
\[{\rm E} = \varepsilon U + U\]
\[{\rm E} = U\left( {\varepsilon + 1} \right)\]
\[U = \frac{{\rm E}}{{\varepsilon + 1}}\;\;\;\;(4)\]
А теперь подставим (2) и (4) в (1):
\[\frac{E}{{{E_0}}} = \frac{{{\rm E} \cdot 2}}{{\left( {\varepsilon + 1} \right) \cdot {\rm E}}}\]
\[\frac{E}{{{E_0}}} = \frac{2}{{\varepsilon + 1}}\]
Посчитаем ответ:
\[\frac{E}{{{E_0}}} = \frac{2}{{3 + 1}} = 0,5\]
Так как ответ получился менее 1, значит напряженность поля в конденсаторе уменьшится. Поэтому, чтобы найти во сколько раз оно уменьшится, правильнее находить отношение \(\frac{E_0}{E}\):
\[\frac{{{E_0}}}{E} = \frac{{\varepsilon + 1}}{2}\]
\[\frac{{{E_0}}}{E} = \frac{{3 + 1}}{2} = 2\]
Таким образом, мы выяснили, что напряженность поля уменьшится в 2 раза.
Обратите Ваше внимание, что ответ не совпал с ответом в указанном сборнике задач. Там указан ответ для случая, если бы требовалось найти изменение напряжения на первом конденсаторе.
Ответ: уменьшится в 2 раза.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
- Предисловие
- Блок 1. Термодинамика
- 1 Температура и тепло
- 1 Температура и температура
- Введение
- 1.1 Температура и тепловое равновесие
- 1.2 Термометры и температурные шкалы
- 1.3 Тепловое расширение
- 1.4 Теплопередача, удельная теплоемкость и калориметрия
- 1.5 Изменения фазы
- 1.6 Механизмы теплопередачи
- Обзор главы
- Ключевые термины
- Ключевые уравнения
- Резюме
- Концептуальные вопросы
- Проблемы
- Дополнительные проблемы
- Дополнительные проблемы
- Дополнительные проблемы Задачи
- 2 Кинетическая теория газов
- Введение
- 2.1 Молекулярная модель идеального газа
- 2.2 Давление, температура и среднеквадратичная скорость
- 2.3 Тепловая мощность и распределение энергии
- 2.4 Распределение молекулярных скоростей
- Обзор главы
- Ключевые термины
- Ключевые уравнения
- Резюме
- Концептуальные вопросы
- Проблемы
- Дополнительные проблемы
- Задачи испытаний
- 3 Первый закон термодинамики
- Введение
- 3.1 Термодинамические системы
- 3.2 Работа, тепло и внутренняя энергия
- 3.3 Первый закон термодинамики
- 3.4 Термодинамические процессы
- 3.5 Теплопроизводительность идеального газа
- 3.6 Адиабатические процессы для идеального газа
- Обзор главы
- Ключевые термины
- Ключевые уравнения
- Резюме
- Концептуальные вопросы
- Задачи
- Дополнительные задачи
- Задачи задачи
- 4 Второй закон термодинамики
- Введение
- 4.1 Обратимые и необратимые процессы
- 4.2 Тепловые двигатели
- 4.3 Холодильники и тепловые насосы
- 4.4 Утверждения второго закона термодинамики
- 4.5 Цикл Карно
- 4.6 Энтропия
- 4.7 Энтропия на микроскопическом уровне
- 4,7 Энтропия на микроскопическом уровне
- 4,7 Энтропия на микроскопическом уровне
- Ключевые термины
- Ключевые уравнения
- Резюме
- Концептуальные вопросы
- Проблемы
- Дополнительные проблемы
- Задачи задачи
- 1 Температура и тепло
- 5 Электрические заряды и поля
- Введение
- 5.1 Электрический заряд
- 5.2 Проводники, изоляторы и зарядка по индукции
- 5.3 Закон Кулона
- 5.4 Электрическое поле
- 5.5 Расчет электрических полей распределения
- 5.6 Линии электрического поля
- 5.7 Электрические диполи
- Обзор главы
- Ключевые термины
- Ключевые уравнения
- Резюме
- Концептуальные вопросы
- Задачи
- Дополнительные проблемы
- Введение
- ,1 Electric Flux
- 6.2. Объяснение закона Гаусса
- 6.3 Применение закона Гаусса
- 6.4 Проводники в электростатическом равновесии
конденсаторы могут быть подключены параллельно:
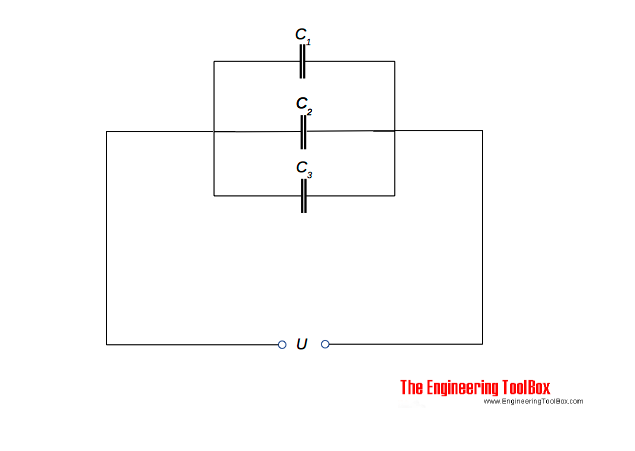
Эквивалентная емкость для конденсаторов с параллельным подключением может быть рассчитана как
C = C 1 + C 2 +. , + C n (1)
, где
C = эквивалентная емкость для параллельно соединенной цепи (Фарад, F, мкФ)
C 1..n = емкостные конденсаторы (Фарад, F, мкФ)
Обычно в качестве единицы измерения емкости используется мкФ .
Конденсаторы серии
Конденсаторы могут быть подключены последовательно:
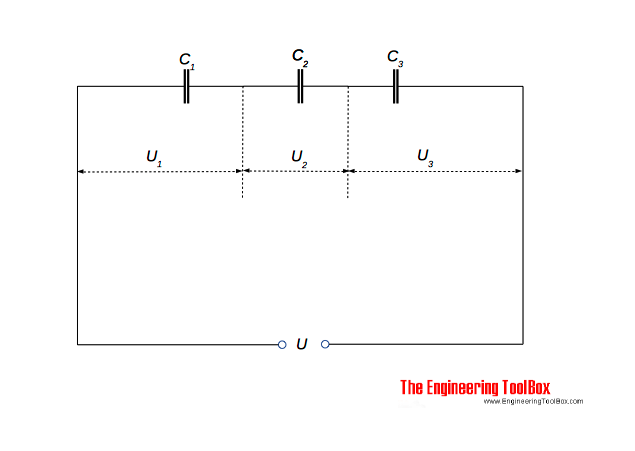
Эквивалентную емкость для последовательно соединенных конденсаторов можно рассчитать как
1 / C = 1 / C 1 + 1 / C 2 +. , + 1 / C n (2)
Для особого случая с двумя последовательно соединенными конденсаторами емкость можно выразить как
1 / C = ( C 1 + C 2 ) / (C 1 C 2 ) (2b)
— или преобразовано в
C = C 1 C 2 / (C 1 + C 2 ) (2c)
Пример — конденсаторы, подключенные параллельно и последовательно
Эквивалентную емкость двух конденсаторов с емкостью 10 мкФ и 20 мкФ можно рассчитать как
параллельно
C = (10 мкФ) + (20 мкФ)
= 30 (мкФ)
в серии
1 / С = 1 / (10 мкФ) + 1 / (20 мкФ)
= 0.15 (1 / мкФ)
или
C = 1 / 0,15 (1 / мкФ)
= 6,7 (мкФ)
Конденсаторы серии
Три конденсатора C 1 = 3 мкФ, С 2 = 6 мкФ и С 3 = 12 мкФ соединены последовательно, как показано на рисунке выше. Напряжение в цепи составляет 230 В.
Эквивалентную емкость цепи можно рассчитать с помощью (2)
1 / C = 1 / ( 3 мкФ ) + 1 / (6 мкФ ) + 1/ ( 12 мкФ )
= (4 + 2 + 1) / 12
= 0.58 1 / мкФ
— или с преобразованием
C = 12 / (4 + 2 + 1)
= 1,7 мкФ
Общий заряд в цепи может рассчитывается с
Q = UC
, где
Q = заряд (кулон, C)
U = электрический потенциал (В)
— или со значениями
Q = (230 В) (1.7 10 -6 F)
= 3,91 10 -4 C
= 391 мкК
Поскольку конденсаторы соединены последовательно — заряд составляет 391 мкК на каждом из них.
Напряжение на конденсаторе 1 можно рассчитать
U 1 = Q / C 1
= (391 мкК) / (3 мкФ)
= 130 В
Напряжение на конденсаторе 2 можно рассчитать
U 2 = Q / C 2
= (391 мкК) / (6 мкФ)
= 65 В
Напряжение через конденсатор 3 можно рассчитать
U 3 = Q / C 3
= (391 мкК) / (12 мкФ)
= 33 В
Емкость двух коаксиальных Баллоны
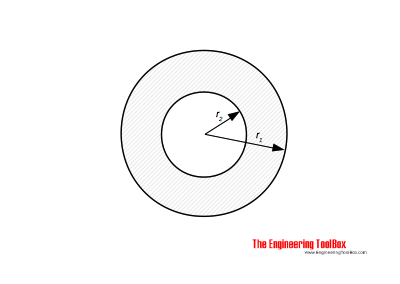
Емкость двух коаксиальных цилиндров, как показано на рисунке, можно рассчитать как
C = 2 π ε o ε r л / лн (r 2 / r 1 )(3)
, где
ε o = абсолютная диэлектрическая проницаемость, вакуумная диэлектрическая проницаемость (8.85 10 -12 Ф / м, Фарад / м)
ε r = относительная диэлектрическая проницаемость
l = длина цилиндров
r 2 = радиус внутреннего цилиндра
r 1 = радиус внешнего цилиндра
.КонденсаторКонденсатор является одним из наиболее часто используемых электронных компонентов. Он обладает способностью накапливать энергию внутри него в форме электрического заряда, создающего статическое напряжение (разность потенциалов) на его пластинах. Просто конденсатор похож на небольшой аккумулятор. Конденсатор представляет собой просто комбинацию двух проводящих или металлических пластин, расположенных параллельно и электрически разделенных хорошим изолирующим слоем (также называемым диэлектрик) , состоящим из вощеной бумаги, слюды, керамики, пластика и т. Д.
Существует много применений конденсатора в электронике, некоторые из них перечислены ниже:
- накопитель энергии
- Мощность кондиционирования
- Коррекция коэффициента мощности
- Фильтрация
- Генераторы
Теперь дело в , как работает конденсатор ? Когда вы подключаете источник питания к конденсатору, он блокирует постоянный ток из-за изолирующего слоя и позволяет напряжению присутствовать на пластинах в форме электрического заряда.Итак, вы знаете, как работает конденсатор и каковы его применения или применение, но вы должны научиться тому, как использовать конденсатор в электронных схемах.
Как подключить конденсатор в электронную схему?
Здесь мы собираемся продемонстрировать вам соединения конденсатора и эффект от него на примерах.
- Конденсатор серии
- Параллельный конденсатор
- Конденсатор в цепи переменного тока
Конденсатор в последовательной цепи
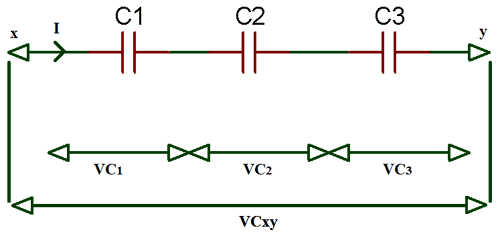
В цепи, когда вы подключаете конденсаторы последовательно, как показано на рисунке выше, общая емкость уменьшается.Последовательный ток через конденсаторы равен (то есть i T = i 1 = i 2 = i 3 = i n ). Следовательно, заряд, сохраняемый конденсаторами, также является тем же самым (то есть Q T = Q 1 = Q 2 = Q 3 ), потому что заряд, накопленный пластиной любого конденсатора, исходит от пластины соседних конденсатор в цепи.
Применяя Закон напряжения Кирхгофа (KVL) в цепи, мы получаем
V T = V C1 + V C2 + V C3 … уравнение (1)
Как мы знаем,
Q = CV Итак, V = Q / C
, где V C1 = Q / C 1 ; V C2 = Q / C 2 ; V C3 = Q / C 3
Теперь, поместив вышеуказанные значения в уравнение (1)
(1 / С Т ) = (1 / С 1 ) + (1 / С 2 ) + (1 / С 3 )
Для n числа конденсаторов в серии уравнение будет
(1 / С Т ) = (1 / С 1 ) + (1 / С 2 ) + (1 / С 3 ) +….+ (1 / Cn)
Следовательно, вышеприведенное уравнение представляет собой уравнение конденсаторов серии .
Где, C T = Общая емкость цепи
C 1 … n = емкость конденсаторов
Уравнение емкости для двух особых случаев определяется ниже:
Случай I: , если два последовательно соединенных конденсатора, при различном значении емкость будет выражаться как:
(1 / C T ) = (C 1 + C 2 ) / (C 1 * C 2 ) Или, C T = (C 1 * C 2 ) / (C 1 + C 2 )… уравнение (2)
Случай II: , если два последовательно соединенных конденсатора, при одинаковом значении емкость будет выражаться как:
(1 / C T ) = 2C / C 2 = 2 / C Или, C T = C / 2
Пример последовательной цепи конденсатора:
Теперь в следующем примере мы покажем вам, как рассчитать общую емкость и индивидуальное среднеквадратичное падение напряжения на каждом конденсаторе.
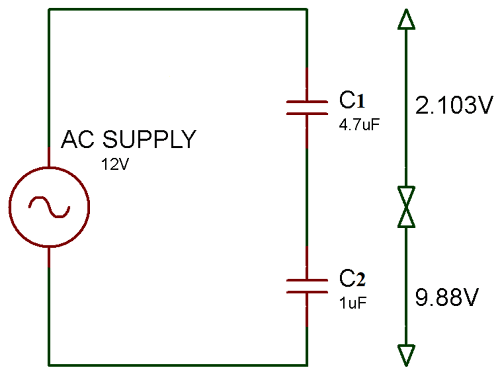
Согласно приведенной выше принципиальной схеме два конденсатора соединены последовательно с разными значениями. Таким образом, падение напряжения на конденсаторах также неравномерно. Если подключить два конденсатора с одинаковым значением, падение напряжения также будет одинаковым.
Теперь для общего значения емкости будем использовать формулу из уравнения (2)
So, C T = (C 1 * C 2 ) / (C 1 + C 2 ) Здесь C 1 = 4.7 мкФ и С 2 = 1 мкФ C T = (4,7 мкФ * 1 мкФ) / (4,7 мкФ + 1 мкФ) C T = 4,7 мкФ / 5,7 мкФ C T = 0,824 мкФ
Теперь падение напряжения на конденсаторе C 1 составляет:
VC 1 = (C T / C 1 ) * V T VC 1 = (0,824 мкФ / 4,7 мкФ) * 12 VC 1 = 2,103 В
Теперь падение напряжения на конденсаторе C 2 составляет:
VC 2 = (C T / C 2 ) * V T VC 2 = (0.824 мкФ / 1 мкФ) * 12 VC 2 = 9,88 В
Конденсатор в параллельной цепи
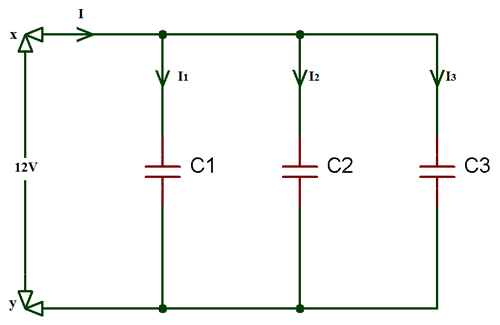
При параллельном подключении конденсаторов общая емкость будет равна сумме всех емкостей конденсаторов. Потому что верхняя пластина всех конденсаторов соединена вместе, а нижняя также. Таким образом, при касании друг друга эффективная площадь пластины также увеличивается. Следовательно, емкость пропорциональна отношению площади и расстояния.
Применив Текущий закон Кирхгофа (KCL) в вышеупомянутой цепи,
i T = i 1 + i 2 + i 3
Как мы знаем, ток через конденсатор выражается как;
i = C (DV / dt ) Итак, я T = C 1 (DV / dt ) + C 2 (DV / dt ) + C 3 (DV / dt ) А, i T = (C 1 + C 2 + C 3 ) * (DV / dt ) i T = C T (дв / dt )… уравнение (3)
Из уравнения (3) уравнение параллельной емкости:
C T = C 1 + C 2 + C 3
Для n конденсаторов, соединенных параллельно, приведенное выше уравнение выражается как:
C T = C 1 + C 2 + C 3 +… + Cn
Пример параллельной конденсаторной цепи
На приведенной ниже принципиальной схеме три конденсатора соединены параллельно .Поскольку эти конденсаторы подключены параллельно, эквивалентная или полная емкость будет равна сумме отдельной емкости.
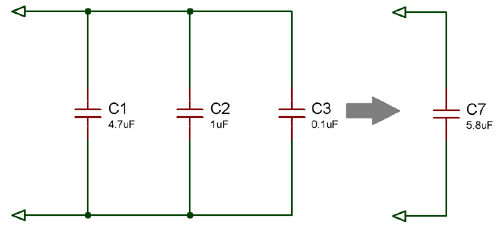
C T = C 1 + C 2 + C 3 , где С 1 = 4,7 мкФ; C 2 = 1 мкФ и C 3 = 0,1 мкФ Итак, C T = (4,7 +1 + 0,1) UF C T = 5,8 мкФ
Конденсатор в цепях переменного тока
Когда конденсатор подключен к источнику постоянного тока, конденсатор начинает медленно заряжаться.И когда напряжение тока зарядки конденсатора равно напряжению питания, говорят, что оно полностью заряжено. Здесь в этом состоянии конденсатор работает как источник энергии, пока подается напряжение. Кроме того, конденсаторы не позволяют току проходить через него после того, как он полностью зарядится.
Всякий раз, когда на конденсатор подается переменное напряжение, как показано на приведенной выше чисто емкостной схеме. Затем конденсатор заряжается и разряжается непрерывно до каждого нового уровня напряжения (заряжается при положительном уровне напряжения и разряжается при отрицательном уровне напряжения).Емкость конденсатора в цепях переменного тока зависит от частоты входного напряжения, подаваемого в цепь. Ток прямо пропорционален скорости изменения напряжения, приложенного к цепи.
i = dQ / dt = C (dV / dt )
Фазовая диаграмма для конденсатора в цепи переменного тока
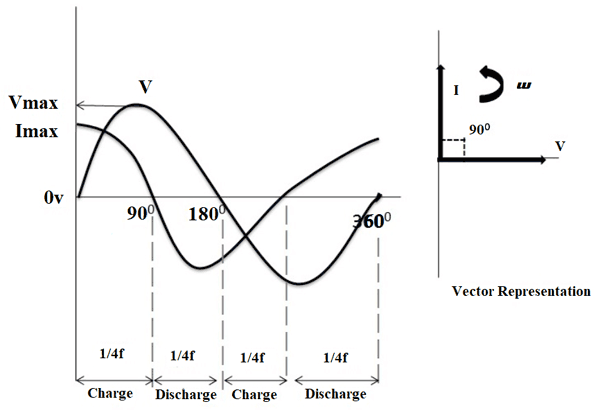
Как вы видите фазовую диаграмму для конденсатора переменного тока на изображении ниже, ток и напряжение представлены в синусоиде.При наблюдении при 0 ° зарядный ток достигает своего пикового значения, поскольку напряжение постоянно увеличивается в положительном направлении.
Теперь при 90 ° ток не проходит через конденсатор, потому что напряжение питания достигает максимального значения. При 180 ° напряжение начинает медленно уменьшаться до нуля, а ток достигает максимального значения в отрицательном направлении. И снова заряд достигает своего пикового значения при 360⁰, поскольку напряжение питания находится на минимальном значении.
Таким образом, из приведенного выше сигнала мы можем наблюдать, что ток опережает напряжение на 90⁰.Итак, мы можем сказать, что переменное напряжение отстает от тока на 90⁰ в идеальной конденсаторной цепи .
Реактивное сопротивление конденсатора (Xc) в цепи переменного тока
Рассмотрим приведенную выше принципиальную схему, так как мы знаем, что входное напряжение переменного тока выражается как,
V = V м Грех вес
А, заряд конденсатора Q = CV,
Итак, Q = CV м Грех вес
А, ток через конденсатор, i = dQ / dt
Итак,
i = d (CV м Грех вес ) / дт i = C * d (В м Грех вес ) / дт i = C * V м Cos мас. * w i = w * C * V м Грех (вес + π / 2) ат, вес = 0 sin (wt + π / 2) = 1 отсюда, я м = WCV м В м / м = 1 / wC
Как мы знаем, w = 2πf
Итак,
Емкостное реактивное сопротивление (Xc) = V м / i м = 1 / 2πfC
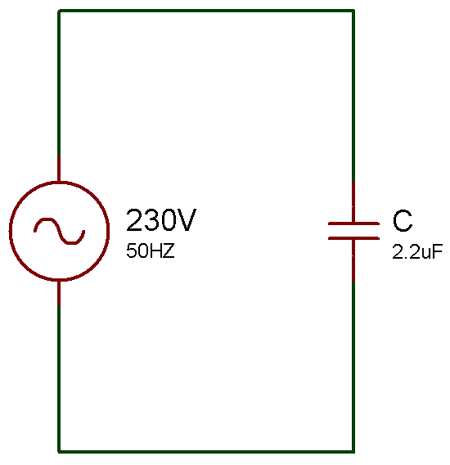
Пример емкостного сопротивления в цепи переменного тока
диаграмма
Давайте рассмотрим значение C = 2.2 мкФ и напряжение питания V = 230 В, 50 Гц,
Теперь емкостное реактивное сопротивление (Xc) = V м / i м = 1 / 2πfC Здесь C = 2,2 мкФ и f = 50 Гц Итак, Xc = 1/2 * 3,1414 * 50 * 2,2 * 10 -6 Xc = 1446,86 Ом.
Что такое конденсатор (C)
Что такое конденсатор и расчеты конденсаторов.
Что такое конденсатор
Конденсатор — это электронный компонент, который хранит электрический заряд. Конденсатор состоит из 2-х тесных проводников (обычно пластин), которые разделены диэлектрическим материалом. Пластины накапливаются электрический заряд при подключении к источнику питания. Одна тарелка накапливает положительный заряд, а другая пластина накапливает отрицательный заряд.
Емкость — это количество электрического заряда, который накапливается в конденсаторе при напряжении 1 Вольт.
Емкость измеряется в единицах Фарад (F).
Конденсатор отключает ток в цепях постоянного тока (DC) и короткое замыкание в цепях переменного тока (AC).
Конденсаторные картинки
Конденсаторные символы
Емкость
Емкость (C) конденсатора равна электрическому заряду (Q), деленному на напряжение (V):
C — емкость в Фарадах (F)
Q — электрический заряд в кулонах (С), который накапливается на конденсаторе
В — напряжение между обкладками конденсатора в вольтах (В)
Емкость пластин емкостных
Емкость (C) конденсатора пластин равна диэлектрической проницаемости (ε), умноженной на площадь пластины (A), деленную на зазор или расстояние между пластинами (d):
C — емкость конденсатора, в Фарадах (F).
ε — диэлектрическая проницаемость конденсаторного материала в Фарадах на метр (Ф / м).
A — площадь пластины конденсатора в квадратных метрах (м 2 ).
d — расстояние между пластинами конденсатора в метрах (м).
Конденсаторы в серии
Общая емкость конденсаторов последовательно, C1, C2, C3, ..:
Конденсаторы параллельно
Общая емкость конденсаторов параллельно, C1, C2, C3 ,., :
C Итого = C 1 + C 2 + C 3 + …
Ток конденсатора
Моментальный ток конденсатора i c (т) равен емкости конденсатора,
раз производная напряжения мгновенного конденсатора v c (т):
Напряжение на конденсаторе
Временное напряжение конденсатора v c (t) равно начальному напряжению конденсатора,
плюс 1 / C, умноженное на интеграл тока мгновенного конденсатора i c (t) за время t:
Энергия конденсатора
накопленная энергия конденсатора E C в джоулях (J) равен емкости C, в Фарадах (F)
Враз больше квадратного напряжения конденсатора В С в вольтах (В) делится на 2:
E C = C × V C 2 /2
цепи переменного тока
Угловая частота
ω = 2 π f
ω — угловая скорость, измеренная в радианах в секунду (рад / с)
f — частота измеряется в герцах (Гц).
Реактивное сопротивление конденсатора
Конденсаторное сопротивление
Декартова форма:
Полярная форма:
Z C = X C ∟-90º
Типы конденсаторов
| Переменный конденсатор | Переменный конденсатор имеет переменную емкость |
| Электролитический конденсатор | Электролитические конденсаторы используются, когда требуется высокая емкость.Большинство электролитических конденсаторов поляризованы |
| Сферический конденсатор | Сферический конденсатор имеет форму шара |
| Силовой конденсатор | Силовые конденсаторы используются в высоковольтных энергосистемах. |
| Керамический конденсатор | Керамический конденсатор имеет керамический диэлектрический материал. Имеет функцию высокого напряжения. |
| Танталовый конденсатор | Танталоксидный диэлектрический материал. Имеет высокую емкость |
| Слюдяной конденсатор | Высокоточные конденсаторы |
| Бумажный конденсатор | Бумажный диэлектрический материал |
